Прогулка по лунолётам. 3 - Оживляем "Кон-тики"
Все прогулки: первая, вторая, третья и четвёртая.
На предыдущей прогулке мы успешно запрограммировали модель, позволяющую управлять лунолётом в динамике вблизи безвоздушных планет. Однако, вывод оперативной информации о полёте представлял собой только поток ежесекундно меняющихся цифр. Пришла пора добавить графику и перейти в двумерное пространство.
Возможности даже UserRPL (у SysRPL они выше) по работе с графикой весьма богаты: отображение функций, точнее, их кривых, рисование на уровне примитивов "линия", "дуга", "прямоугольник", "круг", вывод двоичных графических объектов в определенное место экрана, анимация по заданной последовательности изображений и многое другое.
Тем не менее, UserRPL не ориентирован на вывод графики в динамическом режиме. Если вы попробуете делать это стандартными способами - очистить экран, добавить объекты, сохранить экран, показать, повторить в цикле - то картинка начнет мерцать. Скорости обработки не хватает.
Поэтому для динамики потребуется не совсем стандартный подход, накладывающий некоторые ограничения. Суть его в том, что мы не очищаем экран всякий раз, а инвертируем точки по двум состояниям объекта: предыдущему и текущему. "Исключающее ИЛИ" с предыдущим состоянием погасит точки, оно же высветит их для текущего. Это касается двоичных объектов (GROB). Из функций рисования такими свойствами обладает лишь TLINE. Её то мы и будем использовать для обрисовки "Кон-тики" под разными углами атаки.
Для рисования векторного изображения лунолёта нам должно хватить восьми точек. Для простоты расчетов возьмём полярную систему координат с центром, вокруг которого будет вращаться корабль.
Вот необходимая нам математика.
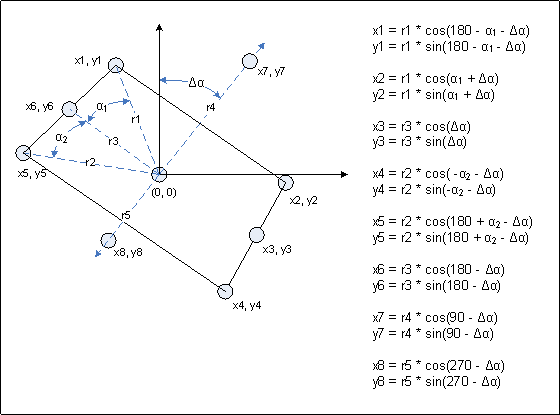
Наша задача - отработать блок отрисовки лунолёта, поэтому программа (см. прикрепленный файл и текст ниже) будет упрощенной. Не будем пока реализовывать блок расхода топлива, расчета координат и многочисленных проверок. Ограничимся управлением стрелками: приращение ускорения будем всё так же производить вертикальными, а горизонтальные подключим для изменения угла атаки. Выведем также значения вертикальной и горизонтальной скоростей.
Кнопки "A" и "Q" будут служить для выхода из программы. Кнопка "M" позволяет переключать приращение угла между 1 и 10 (см. цифру справа от значения Δα).
Обратите внимание на использование стека, локальных переменных и организацию подпрограмм. Нам это всё обязательно понадобится на следующей прогулке.
Пробуем набрать скорость в вертикальном полете

Начинаем отклоняться вправо
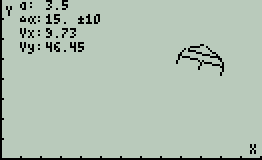
Лунолёт под углом 45°

Снимки экрана получены с эмулятора. На реальном устройстве графика смотрится гораздо чётче.
Не совсем пока ясна концепция показа траектории. Как нагляднее мог бы выглядеть такой показ: просто кривая, построенная по контрольным точкам с изменением масштаба при выходе за пределы координатной сетки, или еще что-то?
На следующей прогулке нам предстоит решить этот вопрос и добавить все недостающие реалистичному симулятору блоки для полёта.
%%HP: T(0)A(D)F(.);
«
PUSH
1.62 'g' STO @ Lunar acceleration of gravity, m/sec2
0. 'a' STO @ Current acceleration
0. 'an1' STO @ Acceleration N-1 (previous step)
0.5 'da' STO @ Acceleration increment
0. 'ac' STO @ angle of climb in degrees
0. 'acn1' STO
1. 'dac' STO @ Angle increment
1. 'dacn1' STO
0. 'u' STO @ vertical velocity
0. 'un1' STO
0. 'v' STO @ horisontal velosity
0. 'vn1' STO
1. 'dt' STO @ Maneuver discrete time in sec
@ Points to draw lunar ship
20. 'alpha1' STO
20. 'alpha2' STO
10. 'r1' STO
12. 'r2' STO
11. 'r3' STO
8. 'r4' STO
4. 'r5' STO
100. 'x0' STO
30. 'y0' STO
@ Application flags
0 'tostop' STO
1 'toinit' STO
«
1 \->GROB PICT UNROT REPL
» 'showrepl' STO
«
\-> valn1 valn coord toinit
«
IF toinit valn1 valn \=/ OR
THEN
IF toinit NOT
THEN
PICT coord valn1 1 \->GROB GXOR
END
PICT coord valn 1 \->GROB GXOR
END
»
» 'showgxor' STO
«
\-> r phi
«
r phi COS * x0 + R\->B
y0 r phi SIN * - R\->B
2 \->LIST
»
» 'getpoint' STO
«
\-> phi
«
r1 180 alpha1 - phi -
getpoint
r1 alpha1 phi -
getpoint
r3 0 phi -
getpoint
r2 alpha2 NEG phi -
getpoint
r2 180 alpha2 + phi -
getpoint
r3 180 phi -
getpoint
r4 90 phi -
getpoint
r5 270 phi -
getpoint
\-> p1 p2 p3 p4 p5 p6 p7 p8
«
p1 p2 TLINE
p2 p3 TLINE
p3 p4 TLINE
p3 p6 TLINE
p5 p6 TLINE
p1 p6 TLINE
p1 p7 TLINE
p2 p7 TLINE
x0 R\->B y0 R\->B 2 \->LIST p8 TLINE
»
»
» 'showship' STO
DEG
DO
IF toinit
THEN
0. 100 XRNG
0. 50 YRNG
ERASE
DRAX
LABEL
{#0d, #0d} PVIEW
{#10d, #0d} "a:"
showrepl
{#10d, #7d} "\GD\Ga:"
showrepl
{#10d, #14d} "Vx:"
showrepl
{#10d, #21d} "Vy:"
showrepl
END
an1 a {#23d, #0d} toinit
showgxor
IF toinit
dac dacn1 \=/ OR
ac acn1 \=/ OR
THEN
acn1 \->STR " \177" dacn1 \->STR + +
ac \->STR " \177" dac \->STR + +
{#23d, #7d} toinit
showgxor
END
vn1 2 RND v 2 RND {#23d, #14d} toinit
showgxor
un1 2 RND u 2 RND {#23d, #21d} toinit
showgxor
@ Calculate points as a function of "ac"
IF toinit ac acn1 \=/ OR
THEN
IF toinit NOT
THEN
acn1
showship
END
ac
showship
END
dt WAIT
@ Prevoius iteration values
a 'an1' STO
ac 'acn1' STO
v 'vn1' STO
u 'un1' STO
dac 'dacn1' STO
WHILE KEY
REPEAT
\-> k
«
CASE
k 25 == THEN a da + 'a' STO END
k 34 == THEN ac dac - 'ac' STO END
k 35 == THEN a da - 'a' STO END
k 36 == THEN ac dac + 'ac' STO END
k 41 == THEN
IF dac 1 == THEN 10 ELSE 1 END 'dac' STO
END
k 11 ==
k 51 == OR THEN 1 'tostop' STO END
END
»
END
v a dt * ac SIN * + 'v' STO
u a ac COS * g - dt * + 'u' STO
0 'toinit' STO
UNTIL
tostop 1 ==
END
{
'g',
'a', 'an1', 'da',
'ac', 'acn1', 'dac', 'dacn1'
'v', 'vn1',
'u', 'un1',
'dt',
'tostop', 'toinit'
'alpha1', 'alpha2' 'r1', 'r2', 'r3', 'r4', 'r5', 'x0', 'y0',
'showrepl', 'showgxor', 'getpoint', 'showship'
} PURGE
POP
»
HOME
'Lunar' PURGE
'Lunar' STO
CLEAR
CLLCD
@ show the VAR menu
2. MENU
11.1 KEYEVAL
