1 чем отличается непрерывный сигнал от дискретного. Непрерывные и дискретные сигналы: ключевые отличия и особенности

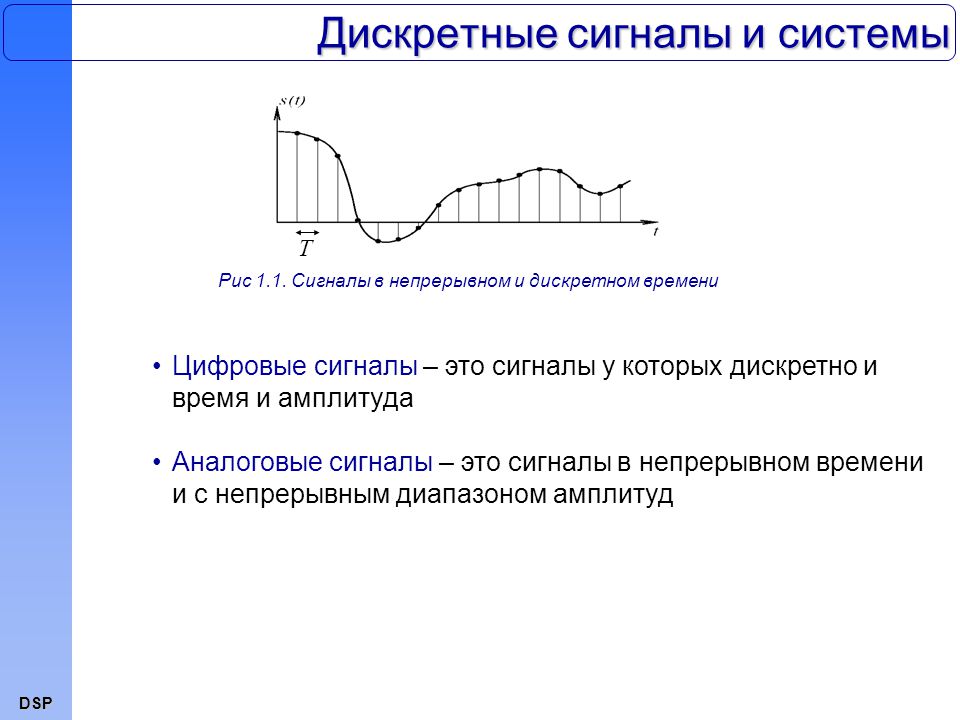
Чем характеризуются непрерывные и дискретные сигналы. Какие основные отличия между ними существуют. Как происходит преобразование непрерывных сигналов в дискретные. Где применяются разные типы сигналов.

Что такое непрерывные и дискретные сигналы

Непрерывные и дискретные сигналы — это два фундаментальных типа сигналов, используемых в обработке информации и электронике. Рассмотрим их основные характеристики и отличия:

Непрерывные сигналы

Непрерывные сигналы характеризуются следующими свойствами:

• Могут принимать любые значения в заданном диапазоне
• Определены для любого момента времени
• Описываются непрерывными математическими функциями
• Примеры: аналоговые звуковые и видеосигналы, напряжение в электрической цепи

Дискретные сигналы

Основные характеристики дискретных сигналов:

• Принимают только определенные значения из конечного набора
• Определены только в дискретные моменты времени
• Описываются последовательностями чисел
• Примеры: цифровые аудио и видеосигналы, импульсные сигналы

Ключевые отличия непрерывных и дискретных сигналов

Рассмотрим основные различия между непрерывными и дискретными сигналами:

Область определения

Непрерывные сигналы определены для любого момента времени, образуя непрерывную функцию. Дискретные сигналы заданы только в определенные моменты времени, образуя последовательность отсчетов. Можно ли определить значение сигнала в произвольный момент времени? Для непрерывного — да, для дискретного — нет.

Множество значений

Непрерывные сигналы могут принимать любые значения в заданном диапазоне. Дискретные сигналы ограничены конечным набором возможных значений. Сколько различных значений может принимать сигнал? Для непрерывного — бесконечно много, для дискретного — конечное число.

Математическое описание

Непрерывные сигналы описываются непрерывными функциями времени. Дискретные сигналы представляются числовыми последовательностями. Какой математический аппарат используется для описания? Для непрерывных — дифференциальное и интегральное исчисление, для дискретных — разностные уравнения.

Спектральный состав

Спектр непрерывного сигнала может содержать бесконечное число гармоник. Спектр дискретного сигнала ограничен частотой Найквиста. Какова максимальная частота в спектре сигнала? Для непрерывного — бесконечность, для дискретного — половина частоты дискретизации.

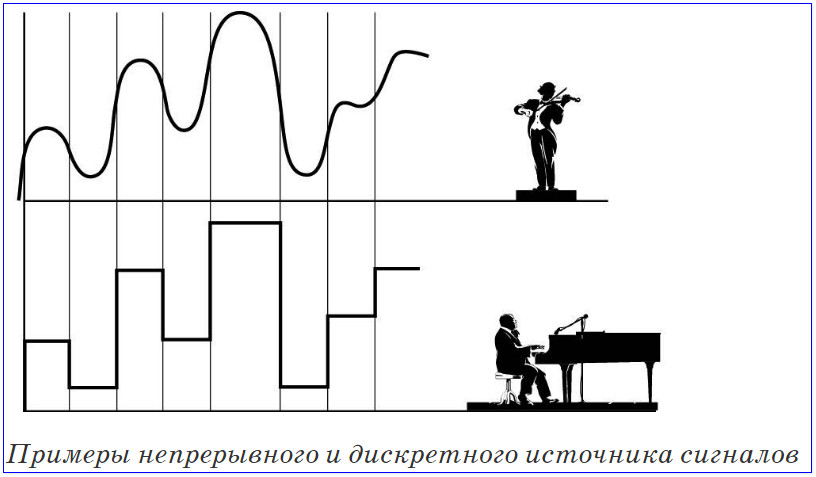
Преобразование непрерывных сигналов в дискретные

Для обработки непрерывных сигналов на цифровых устройствах необходимо преобразовать их в дискретную форму. Этот процесс включает следующие этапы:

Дискретизация по времени

Непрерывный сигнал измеряется через равные промежутки времени, образуя последовательность отсчетов. Частота дискретизации выбирается в соответствии с теоремой Котельникова.

Квантование по уровню

Мгновенные значения сигнала округляются до ближайших дискретных уровней. Количество уровней определяется разрядностью АЦП.

Кодирование

Квантованные значения представляются в двоичном коде для обработки на цифровых устройствах.

Какие искажения вносит процесс дискретизации? Возникают ошибки квантования и ограничение спектра сигнала.

Области применения непрерывных и дискретных сигналов

Непрерывные и дискретные сигналы имеют свои сферы применения:

Использование непрерывных сигналов

• Аналоговые системы связи
• Аудио и видеотехника
• Измерительные приборы
• Системы автоматического управления

Применение дискретных сигналов

• Цифровые системы связи
• Компьютерная техника
• Цифровая обработка сигналов
• Системы передачи данных

Где чаще используются непрерывные, а где дискретные сигналы? Непрерывные — в аналоговой технике, дискретные — в цифровых системах.

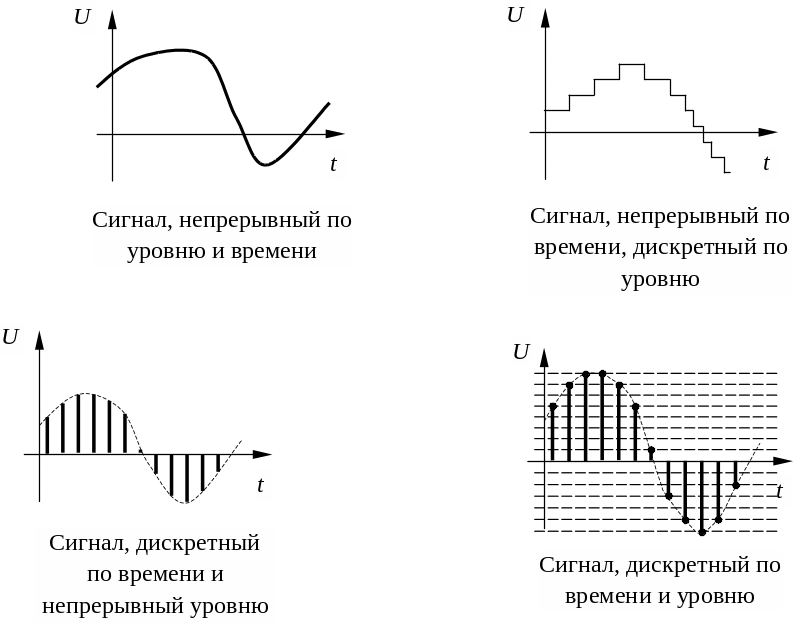
Преимущества и недостатки разных типов сигналов

Рассмотрим основные достоинства и ограничения непрерывных и дискретных сигналов:

Преимущества непрерывных сигналов

• Высокая точность представления информации
• Неограниченный частотный диапазон
• Простота генерации и обработки аналоговыми устройствами

Недостатки непрерывных сигналов

• Чувствительность к помехам и искажениям
• Сложность хранения и передачи на большие расстояния
• Ограниченные возможности цифровой обработки

Преимущества дискретных сигналов

• Высокая помехоустойчивость
• Простота хранения, передачи и обработки на ЭВМ
• Возможность применения цифровых методов обработки

Недостатки дискретных сигналов

• Ограниченная точность представления из-за квантования
• Ограниченный частотный диапазон
• Необходимость аналого-цифрового преобразования

Какой тип сигналов лучше использовать в конкретном приложении? Это зависит от требований к точности, помехоустойчивости и методам обработки.

Методы анализа непрерывных и дискретных сигналов

Для анализа сигналов разных типов применяются различные математические методы:

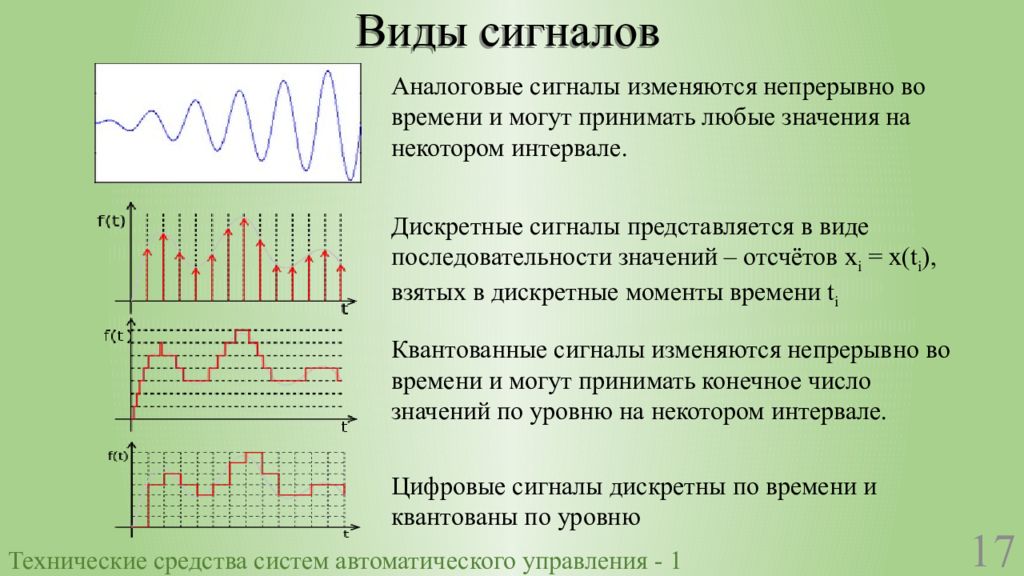
Анализ непрерывных сигналов

• Преобразование Фурье
• Интегральные преобразования (Лапласа, Меллина и др.)
• Спектральный анализ
• Корреляционный анализ

Анализ дискретных сигналов

• Дискретное преобразование Фурье
• Z-преобразование
• Цифровая фильтрация
• Статистические методы анализа последовательностей

Какие методы позволяют наиболее эффективно анализировать сигналы? Для непрерывных — интегральные преобразования, для дискретных — методы цифровой обработки сигналов.

Тенденции развития методов обработки сигналов

Современные тенденции в области обработки сигналов включают:

• Развитие методов цифровой обработки сигналов
• Повышение производительности АЦП и ЦАП
• Применение искусственного интеллекта для анализа сигналов
• Разработка программно-определяемых радиосистем
• Совершенствование алгоритмов сжатия данных

Какие направления будут наиболее перспективными в ближайшем будущем? Вероятно, методы машинного обучения для интеллектуального анализа сигналов и систем.

Заключение

Непрерывные и дискретные сигналы имеют свои особенности и области применения. Понимание их ключевых отличий позволяет эффективно применять методы обработки сигналов в различных приложениях. Развитие цифровых технологий способствует все более широкому использованию дискретных сигналов, однако непрерывные сигналы по-прежнему играют важную роль во многих областях науки и техники.

Чем отличается непрерывный сигнал от дискретного • Мир электрики

На чтение: 3 минОбновлено:

23.06.2021Рубрика: Основы электротехникиАвтор: admin

Содержание

1. Особенности непрерывного сигнала
2. Что такое дискретный
3. Отличия двух видов сигналов

Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные (НС) и дискретные сигналы (ДС).

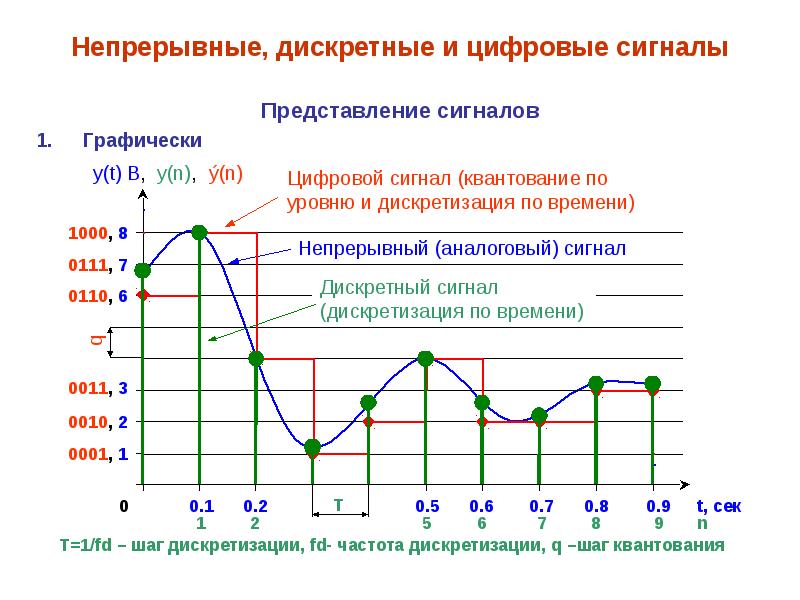
Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом

Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции. Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.

Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:

• пониженную помехозащищённость — это свойство связано с тем, что из-за непрерывности системы помеху, попавшую в сигнал, невозможно отличить от самого сигнала;
• затруднения при передаче сигналов управления;
• трудности при сопряжении с компьютером и другими цифровыми устройствами;
• трудности шифрования.

Что такое дискретный

Дискретность применяется в вычислительной технике для пакетной передачи данных

Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.

Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС.

В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.

Достоинствами цифровых систем, работающих на ДС, являются:

• высокая помехозащищённость и возможность работы каналов связи при больших шумах;
• простота передачи команд управления каналами;
• возможность цифровой обработки сигналов;
• лёгкость засекречивания.

Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно. Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.

Все значения дискретного сигнала можно пронумеровать целыми числами

Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.

К недостаткам систем, использующих ДС, можно отнести:

• увеличение полосы частот, требуемой для передачи сообщений;
• для обеспечения точного воспроизведения непрерывного сигнала при дискретизации требуется значительное количество уровней квантования и высокая частота;
• требование синхронизации;
• плохая совместимость с уже имеющимися аналоговыми системами.

Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее. Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.

Рейтинг

( Пока оценок нет )

0

admin/ автор статьи

Понравилась статья? Поделиться с друзьями:

Чем отличается непрерывный сигнал от дискретного

by Realist

Основы электротехники

Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные (НС) и дискретные сигналы (ДС).

Содержание статьи

• 1 Особенности непрерывного сигнала
• 2 Что такое дискретный
• 3 Отличия двух видов сигналов

Особенности непрерывного сигнала

Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом

Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции. Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.

Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:

• пониженную помехозащищённость — это свойство связано с тем, что из-за непрерывности системы помеху, попавшую в сигнал, невозможно отличить от самого сигнала;
• затруднения при передаче сигналов управления;
• трудности при сопряжении с компьютером и другими цифровыми устройствами;
• трудности шифрования.

Что такое дискретный

Дискретность применяется в вычислительной технике для пакетной передачи данных

Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.

Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС. В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.

Достоинствами цифровых систем, работающих на ДС, являются:

• высокая помехозащищённость и возможность работы каналов связи при больших шумах;
• простота передачи команд управления каналами;
• возможность цифровой обработки сигналов;
• лёгкость засекречивания.

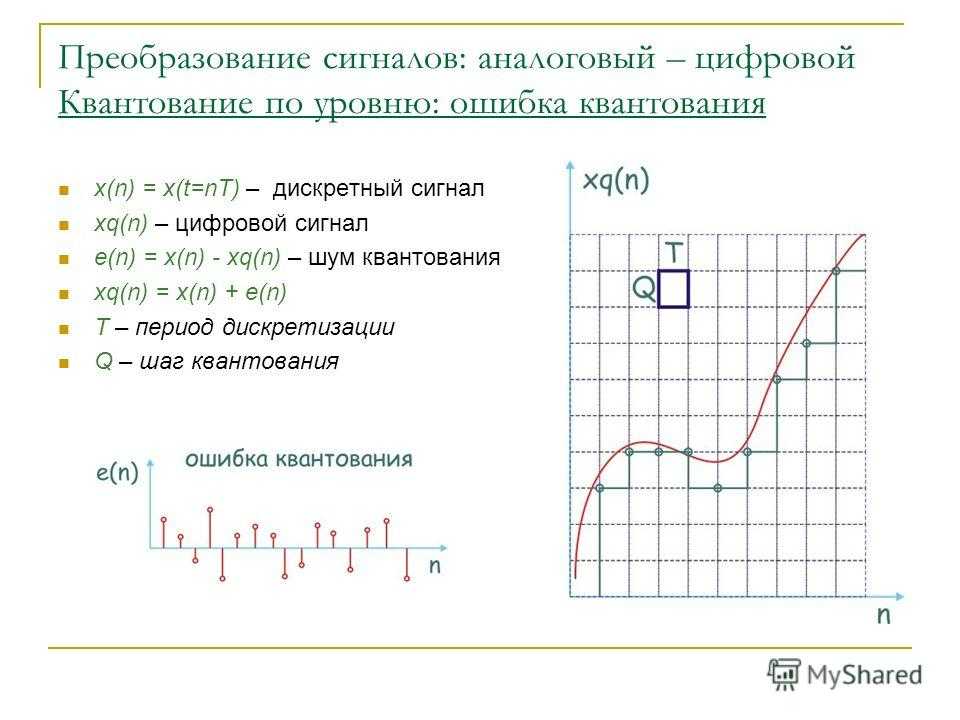
Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно. Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.

Отличия двух видов сигналов

Все значения дискретного сигнала можно пронумеровать целыми числами

Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.

К недостаткам систем, использующих ДС, можно отнести:

• увеличение полосы частот, требуемой для передачи сообщений;
• для обеспечения точного воспроизведения непрерывного сигнала при дискретизации требуется значительное количество уровней квантования и высокая частота;
• требование синхронизации;
• плохая совместимость с уже имеющимися аналоговыми системами.

Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее. Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.

10.7: Дискретная обработка сигналов непрерывного времени

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

23163

• Richard Baraniuk et al.
• Университет Райса

Введение

Цифровые компьютеры могут обрабатывать дискретные сигналы времени, используя чрезвычайно гибкие и мощные алгоритмы. Однако большинство представляющих интерес сигналов представляют собой непрерывные сигналы во времени, именно так данные почти всегда появляются в природе. Теперь, когда была обсуждена теория, поддерживающая методы генерации дискретного сигнала времени из непрерывного сигнала времени путем дискретизации и последующего точного восстановления исходного сигнала из его выборок без ошибок, будет показано, как это можно применить для реализации непрерывного времени, линейного инвариантные во времени системы, использующие дискретное время, линейные инвариантные во времени системы. Это имеет ключевое значение для многих современных технологий, поскольку позволяет использовать возможности цифровых вычислений для обработки аналоговых сигналов.

Дискретная обработка сигналов непрерывного времени

Структура процесса

С целью обработки сигналов непрерывного времени с использованием системы дискретного времени мы рассмотрим одну из наиболее распространенных структур технологий цифровой обработки сигналов. В качестве обзора принятого подхода исходный сигнал непрерывного времени \(x\) преобразуется в сигнал дискретного времени \(x_s\) таким образом, что периоды спектра выборок \(X_s\) максимально близки возможным по форме к спектру \(X\). Затем применяется дискретный, линейный во времени инвариантный фильтр \(H_2\), который изменяет форму спектра отсчетов \(X_s\), но не может увеличить предел полосы пропускания \(X_s\), чтобы создать другой сигнал \(y_s\ ). Это восстанавливается с помощью подходящего фильтра реконструкции для получения выходного сигнала непрерывного времени \(y\), тем самым эффективно реализуя некоторую систему непрерывного времени \(H_1\). Этот процесс показан на рисунке \(\PageIndex{1}\), а спектры показаны для конкретного случая на рисунке \(\PageIndex{2}\).

Рисунок \(\PageIndex{1}\): Показана блок-схема обработки сигналов непрерывного времени с использованием систем дискретного времени.

Необходимо дальнейшее обсуждение каждого из этих шагов, и мы начнем с обсуждения аналого-цифрового преобразователя, часто обозначаемого АЦП или АЦП. Понятно, что для обработки сигнала непрерывного времени с использованием методов дискретного времени мы должны произвести выборку сигнала в качестве начального шага. По сути, это и есть цель АЦП, хотя есть и практические вопросы, которые будут обсуждаться позже. АЦП принимает аналоговый сигнал с непрерывным временем в качестве входного сигнала и формирует цифровой сигнал с дискретным временем в качестве выходного с идеальным случаем бесконечной точности, соответствующим выборке. Как утверждает теорема Найквиста-Шеннона о дискретизации, для того, чтобы сохранить всю информацию об исходном сигнале, нам обычно требуется выборка выше частоты Найквиста \(\omega_s≥2B\), где полоса исходного сигнала ограничена до \((−B, Б)\). Когда невозможно гарантировать это условие, следует использовать фильтр сглаживания.

В фильтре дискретного времени происходят преднамеренные изменения информации о сигнале. Это обычно делается в программном обеспечении для цифровых компьютеров после того, как сигнал был оцифрован аппаратным АЦП и до того, как он будет использован аппаратным ЦАП для создания выходного сигнала. Это позволяет описанной выше настройке быть достаточно гибкой в ​​фильтре, который она реализует. Если выборка выше частоты Найквиста. Любые изменения, которые дискретный фильтр вносит в эту форму, могут быть переданы в непрерывный временной сигнал, предполагающий идеальную реконструкцию. Следовательно, описанный процесс реализует непрерывный во времени линейный инвариантный во времени фильтр. Это будет объяснено более математически подробно в следующем разделе. Как обычно, есть, конечно, практические ограничения, которые будут обсуждаться позже.

Наконец, мы обсудим цифро-аналоговый преобразователь, часто обозначаемый ЦАП или ЦАП. Поскольку фильтры непрерывного времени имеют входы непрерывного времени и выходы непрерывного времени, мы должны создать сигнал непрерывного времени из нашего отфильтрованного сигнала дискретного времени. Предполагая, что мы произвели выборку с ограниченной полосой пропускания с достаточно высокой скоростью, в идеальном случае это было бы сделано с использованием идеальной реконструкции с помощью интерполяционной формулы Уиттакера-Шеннона. Однако, опять же, есть практические проблемы, препятствующие этому, которые будут обсуждаться позже.

Рисунок \(\PageIndex{2}\): Спектры показаны черным цветом для каждого шага реализации фильтра непрерывного времени с использованием фильтра дискретного времени для определенного сигнала. Частотные характеристики фильтра показаны синим цветом, и обе они должны иметь максимальное значение 1, несмотря на вертикальную шкалу, предназначенную только для спектров сигналов. Предполагается, что АЦП и ЦАП идеальны.

Фильтр дискретного времени

После некоторого начального обсуждения процесса, показанного на рисунке \(\PageIndex{1}\), связь между инвариантным линейным фильтром непрерывного времени \(H_1\) и дискретным временем, линейным временем инвариантный фильтр \(H_2\) можно изучить. Мы будем предполагать использование идеальных АЦП и ЦАП с бесконечной точностью, которые выполняют дискретизацию и идеальную реконструкцию соответственно, используя частоту дискретизации \(\omega_s=2 \pi /T_s≥2B\), где входной сигнал \(x\) равен полоса ограничена до \((−B,B)\). Обратите внимание, что эти аргументы терпят неудачу, если это условие не выполняется и происходит псевдоним. В этом случае для сохранения этих аргументов необходимо предварительное применение фильтра сглаживания. 9{\infty} H_{1}\left(\frac{\omega-2 \pi k}{T_{s}}\right)(u(\omega-(2k-1) \pi) -u(\ омега-(2k+1) \pi)). \nonumber \]

Проще говоря, \(H_2\) является \(2 \pi\) периодическим и \(H_2(\omega)=H_1( \omega /T_s)\) для \(\omega \in[ -\пи, \пи)\).

При заданном непрерывном линейном инвариантном во времени фильтре \(H_1\) приведенное выше уравнение решает задачу проектирования системы при условии, что мы знаем, как реализовать \(H_2\). Фильтр \(H_2\) должен быть выбран таким, чтобы он имел частотную характеристику, где каждый период имел ту же форму, что и частотная характеристика \(H_1\) на \(\left(-\pi / T_{s}, \ pi / T_{s}\right)\). Это показано на частотных характеристиках, показанных на рисунке \(\PageIndex{2}\).

Мы могли бы также рассмотреть задачу системного анализа, в которой задан конкретный дискретный, линейный во времени инвариантный фильтр \(H_2\), и мы хотим описать фильтр \(H_1\). Таких фильтров много, но мы можем описать их частотные характеристики на \(\left(-\pi / T_{s}, \pi / T_{s}\right)\), используя приведенное выше уравнение. Выделение одного периода \(H_2(\omega)\) приводит к выводу, что \(H_{1}(\omega)=H_{2}\left(\omega T_{s}\right)\) для \(\ омега \in\left(-\pi / T_{s}, \pi / T_{s}\right)\). Поскольку предполагалось, что \(x\) ограничен полосой до \(\left(-\pi / T_{s}, \pi / T_{s}\right)\), значение частотной характеристики в другом месте не имеет значения.

Практические соображения

Как упоминалось ранее, существует несколько практических соображений, которые необходимо учитывать на каждом этапе процесса, показанного на рисунке \(\PageIndex{1}\). Некоторые из них будут кратко рассмотрены здесь, а более полная модель дискретной обработки сигналов непрерывного времени представлена ​​на рисунке \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\): Более полная модель того, как дискретная обработка сигналов непрерывного времени реализуется на практике.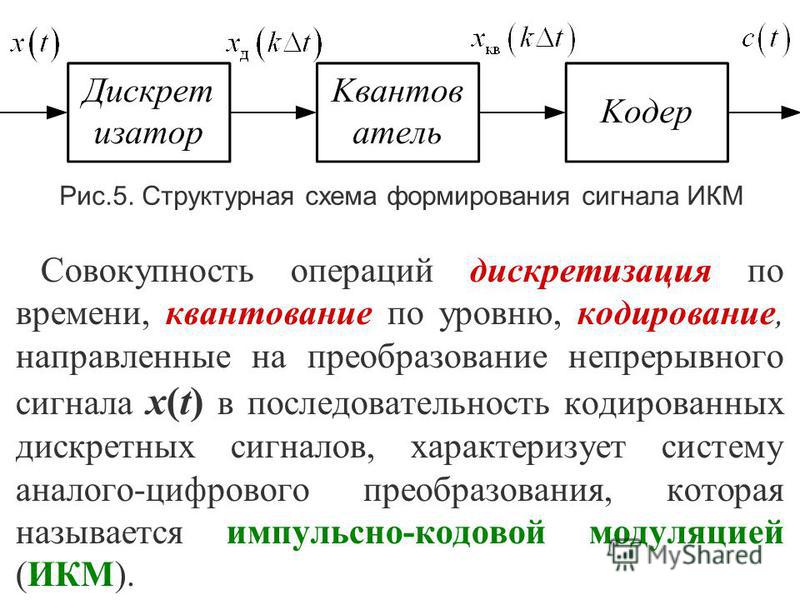 Обратите внимание на добавление фильтров сглаживания и защиты от изображения, чтобы способствовать ограничению входной и выходной полосы пропускания. Показано, что АЦП выполняет выборку с квантованием. Далее указывается, что цифровой фильтр является причинным. Показано, что ЦАП выполняет несовершенную реконструкцию, в этом случае сохраняется нулевой порядок.

Anti-Aliasing Filter

В действительности мы обычно не можем гарантировать, что входной сигнал будет иметь определенную полосу пропускания, и не всегда может быть достигнута достаточно высокая частота дискретизации. Поскольку крайне важно, чтобы высокочастотные компоненты не маскировались под более низкочастотные компоненты посредством наложения спектров, необходимо использовать сглаживающие фильтры с частотой среза, меньшей или равной \(\omega_s/2\) АЦП. Блок-схема на рисунке \(\PageIndex{3}\) отражает это дополнение.

Как описано в предыдущем разделе, идеальный фильтр нижних частот, удаляющий всю энергию на частотах выше \(\omega_s/2\), был бы оптимален.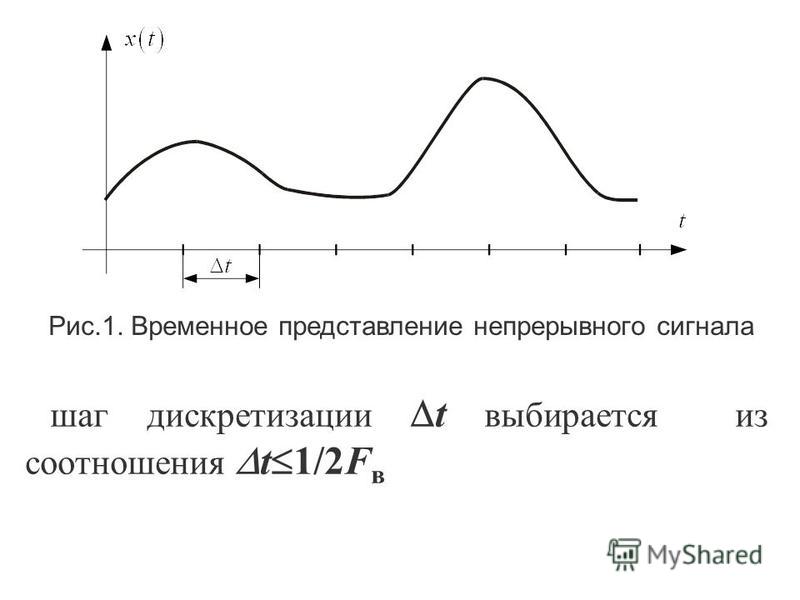 Конечно, это недостижимо, поэтому необходимо принять аппроксимацию идеального фильтра нижних частот с низким коэффициентом усиления выше \(\omega_s/2\). Это означает, что некоторый алиасинг неизбежен, но его можно уменьшить до незначительного уровня.

Квантование сигнала

В нашем предыдущем обсуждении дискретной обработки сигналов с непрерывным временем мы предположили идеальный случай, в котором АЦП точно выполняет выборку. Однако, хотя АЦП преобразует непрерывный сигнал времени в сигнал дискретного времени, он также должен преобразовывать аналоговые значения в цифровые значения для использования в цифровом логическом устройстве, что называется квантованием. Подсистема ADC на блок-схеме на рисунке \(\PageIndex{3}\) отражает это дополнение.

Данные, полученные АЦП, должны храниться в виде конечного числа бит внутри цифрового логического устройства. Таким образом, существует только конечное число значений, которые может принимать цифровая выборка, а именно \(2N\), где \(N\) — количество битов, в то время как аналоговая выборка может принимать неисчислимое множество значений. Следовательно, что-то должно быть потеряно в процессе квантования. В результате квантование ограничивает как диапазон, так и точность выходного сигнала АЦП. Оба являются конечными, и улучшение одного при постоянном числе битов требует жертвовать качеством другого.

Реализуемость фильтра

В реальных условиях, если входной сигнал является функцией времени, будущие значения сигнала не могут использоваться для вычисления выходного сигнала. Таким образом, цифровой фильтр \(H_2\) и система в целом \(H_1\) должны быть причинно-следственными. Аннотация фильтра на рисунке \(\PageIndex{3}\) отражает это добавление. Если искомая система не является причинной, но имеет импульсную характеристику, равную нулю до некоторого времени \(t_0\), можно ввести задержку, чтобы сделать ее причинной. Однако, если эта задержка чрезмерна или импульсная характеристика имеет бесконечную длину, для практического решения проблемы становится необходимой оконная схема. Умножение на окно для уменьшения длины импульсной характеристики может уменьшить необходимую задержку и уменьшить требования к вычислениям.

Возьмем, к примеру, идеальный фильтр нижних частот. Она акаузальна и бесконечна по протяженности в обоих направлениях. Таким образом, мы должны довольствоваться приближением. Можно предположить, что эти аппроксимации могут быть достигнуты путем усечения синхроимпульсной характеристики фильтра нижних частот на одном из его нулей, эффективно обрабатывая его прямоугольным импульсом. Однако это приведет к плохим результатам в частотной области, так как результирующая свертка значительно расширит энергию сигнала. Другие оконные функции, которых существует множество, меньше распространяют сигнал в частотной области и, таким образом, гораздо полезнее для получения этих приближений.

Anti-Image Filter

В нашем предыдущем обсуждении дискретной обработки сигналов непрерывного времени мы предположили идеальный случай, в котором ЦАП выполняет идеальную реконструкцию. Однако при рассмотрении практических вопросов важно помнить, что функция sinc, используемая для интерполяции Уиттакера-Шеннона, бесконечна по длине и акаузальна. Следовательно, для ЦАП было бы невозможно реализовать идеальную реконструкцию.

Вместо этого ЦАП реализует причинно-следственную фиксацию нулевого порядка или другую простую схему реконструкции относительно частоты дискретизации \(\omega_s\), используемой АЦП. Однако это приведет к тому, что функция не будет ограничена пропускной способностью \((−\omega_s/2,\omega_s/2)\). Следовательно, к выходу необходимо применить дополнительный фильтр нижних частот, называемый фильтром подавления изображений. Процесс, показанный на рисунке \(\PageIndex{3}\), отражает эти добавления. Фильтр подавления изображений пытается ограничить полосу пропускания сигнала до \((−\omega_s/2,\omega_s/2)\), поэтому оптимальным будет идеальный фильтр нижних частот. Однако, как уже было сказано, это невозможно. Следовательно, должны быть приняты приближения идеального фильтра нижних частот с низким коэффициентом усиления выше \(\omega_s/2\). Фильтр подавления изображений обычно имеет те же характеристики, что и фильтр сглаживания.

Дискретная обработка сигналов непрерывного времени Резюме

Как было показано, выборка и реконструкция могут использоваться для реализации систем непрерывного времени с использованием систем дискретного времени, которые очень эффективны благодаря универсальности, гибкости и скорости цифровых компьютеров. . Однако существует большое количество практических соображений, которые необходимо учитывать при попытке выполнить это, включая шум квантования и сглаживание в аналого-цифровом преобразователе, реализуемость фильтра в дискретном временном фильтре, оконную реконструкцию и связанные с этим проблемы. в цифро-аналоговом преобразователе. Многие современные технологии решают эти проблемы и используют этот процесс.

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Ричард Баранюк и др.

   Лицензия

   СС BY

   Программа OER или Publisher

   OpenStax CNX

2. Теги

   На этой странице нет тегов.

Терминология сигналов и графиков

Сигнал — это описание того, как один параметр зависит от другого параметра. Например, наиболее распространенным типом сигнала в аналоговой электронике является напряжение, изменяющееся во времени. Поскольку оба параметра могут принимать непрерывный диапазон значений, мы будем называть это непрерывным сигналом. Для сравнения, прохождение этого сигнала через аналого-цифровой преобразователь приводит к квантованию каждого из двух параметров. Например, представьте, что преобразование выполняется с 12 битами с частотой дискретизации один килогерц. Напряжение урезано до 4096 возможных двоичных уровней, и время определяется только с шагом в одну миллисекунду. Сигналы, сформированные из параметров, квантованных таким образом, называются дискретными сигналами или оцифрованными сигналами. По большей части непрерывные сигналы существуют в природе, тогда как дискретные сигналы существуют внутри компьютеров (хотя вы можете найти исключения для обоих случаев). Также возможны сигналы, в которых один параметр является непрерывным, а другой — дискретным. Поскольку эти смешанные сигналы довольно редки, им не даются специальные имена, и природа двух параметров должна быть указана явно.

На рис. 2-1 показаны два дискретных сигнала, которые могут быть получены с помощью цифровой системы сбора данных. Вертикальная ось может представлять напряжение, интенсивность света, звуковое давление или бесконечное количество других параметров. Поскольку мы не знаем, что он представляет в данном конкретном случае, мы дадим ему общую метку: амплитуда. Этот параметр также называют несколькими другими именами: ось Y, зависимая переменная, диапазон и ордината.

Горизонтальная ось представляет другой параметр сигнала, имеющий такие названия, как: ось x, независимая переменная, домен и абсцисса. Время является наиболее распространенным параметром, отображаемым на горизонтальной оси полученных сигналов; однако в конкретных приложениях используются другие параметры. Например, геофизик может провести измерения плотности горных пород на равном расстоянии друг от друга по поверхности земли. Для общего понимания мы просто обозначим горизонтальную ось номером образца. Если бы это был непрерывный сигнал, пришлось бы использовать другую метку, например: время, расстояние, х и т. д.

Два параметра, формирующих сигнал, обычно не взаимозаменяемы. Говорят, что параметр по оси y (зависимая переменная) является функцией параметра по оси x (независимая переменная). Другими словами, независимая переменная описывает, как и когда берется каждый образец, а зависимая переменная представляет собой фактическое измерение. Имея конкретное значение на оси x, мы всегда можем найти соответствующее значение на оси y, но обычно не наоборот.

Обратите особое внимание на слово: домен, очень широко используемый термин в DSP. Например, говорят, что сигнал, который использует время в качестве независимой переменной (т. е. параметр на горизонтальной оси), находится во временной области. Другой распространенный сигнал в DSP использует частоту в качестве независимой переменной, что приводит к термину «частотная область». Точно так же говорят, что сигналы, которые используют расстояние в качестве независимого параметра, находятся в пространственной области (расстояние является мерой пространства). Тип параметра на горизонтальной оси — это домен сигнала; это так просто. Что, если ось X помечена чем-то очень общим, например номером образца? Авторы обычно называют эти сигналы сигналами во временной области. Это связано с тем, что выборка через равные промежутки времени является наиболее распространенным способом получения сигналов, и у них нет более конкретного названия для этого.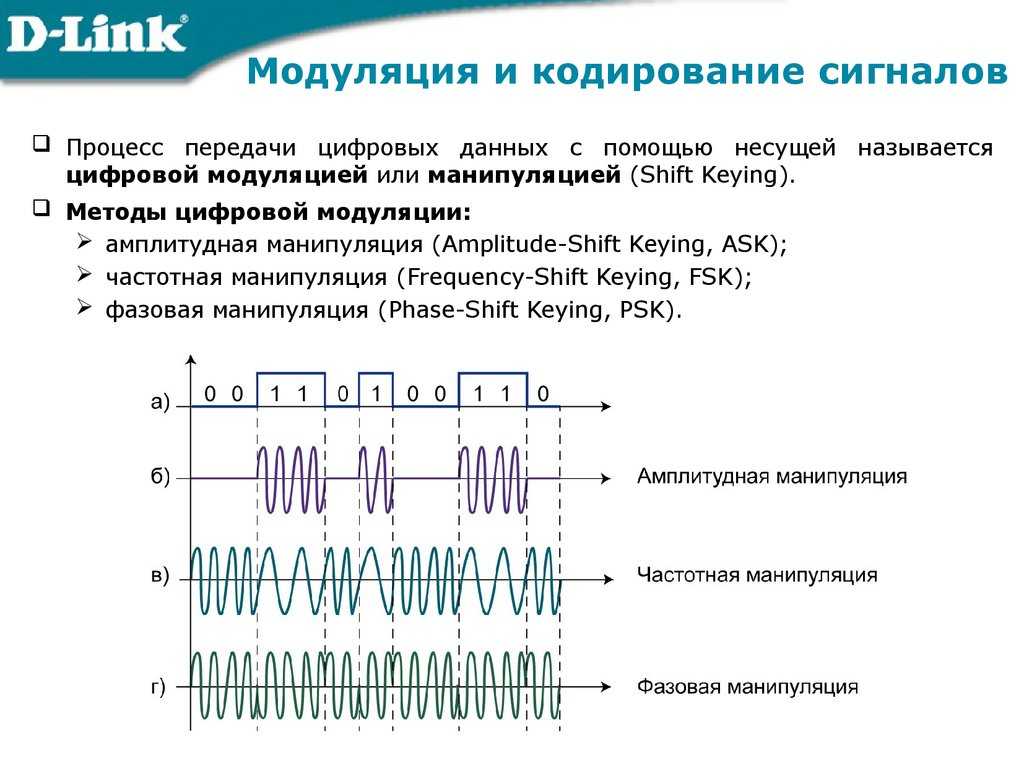

Хотя сигналы на рис. 2-1 дискретны, на этом рисунке они отображаются сплошными линиями. Это связано с тем, что существует слишком много семплов, чтобы их можно было различить, если бы они отображались как отдельные маркеры. На графиках, отображающих более короткие сигналы, скажем, менее 100 отсчетов, обычно отображаются отдельные маркеры. Непрерывные линии могут быть или не быть нарисованы для соединения маркеров, в зависимости от того, как автор хочет, чтобы вы просматривали данные. Например, непрерывная линия может указывать на то, что происходит между выборками, или просто помогать читателю следить за тенденцией в зашумленных данных. Дело в том, что изучите маркировку горизонтальной оси, чтобы определить, работаете ли вы с дискретным или непрерывным сигналом. Не полагайтесь на способность иллюстратора рисовать точки.

Переменная N широко используется в DSP для представления общего количества выборок в сигнале. Например, N = 512 для сигналов на рис. 2-1.

Чтобы данные были организованы, каждому образцу присваивается номер образца или индекс.