1 магнитное поле тока. Магнитное поле тока: основные понятия, взаимодействия и законы

Что такое магнитное поле тока. Как оно взаимодействует с проводниками и заряженными частицами. Какие основные законы описывают магнитное поле. Как определить направление магнитного поля и действующих в нем сил.

Природа и свойства магнитного поля

Магнитное поле — это особый вид материи, который возникает вокруг движущихся электрических зарядов и постоянных магнитов. Основные свойства магнитного поля:

• Создается движущимися электрическими зарядами и постоянными магнитами
• Действует только на движущиеся заряженные частицы и проводники с током
• Характеризуется векторной величиной — магнитной индукцией B
• Силовые линии магнитного поля всегда замкнуты
• Магнитное поле не совершает работу над движущимися зарядами

Магнитное поле тесно связано с электрическим полем — вместе они образуют единое электромагнитное поле. При движении заряда электрическое поле порождает магнитное, и наоборот.

Источники магнитного поля

Основными источниками магнитного поля являются:

• Движущиеся электрические заряды
• Проводники с электрическим током
• Постоянные магниты
• Электромагниты

Магнитное поле постоянных магнитов обусловлено упорядоченным движением электронов в атомах вещества. Фактически, внутри магнитов существуют незатухающие микроскопические токи.

Характеристики магнитного поля

Основной характеристикой магнитного поля является вектор магнитной индукции B. Он показывает силу действия магнитного поля на движущиеся заряды и токи. Единица измерения магнитной индукции — Тесла (Тл).

Магнитное поле можно графически изобразить с помощью линий магнитной индукции. Это воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора B. Густота линий пропорциональна величине магнитной индукции.

Сила Лоренца

На движущуюся заряженную частицу в магнитном поле действует сила Лоренца. Она определяется формулой:

F = qvB sin α

где q — заряд частицы, v — ее скорость, B — магнитная индукция, α — угол между векторами скорости и магнитной индукции.

Направление силы Лоренца определяется по правилу левой руки: если расположить левую руку так, чтобы линии магнитной индукции входили в ладонь, а отогнутый на 90° большой палец показывал направление движения положительного заряда, то четыре вытянутых пальца покажут направление силы Лоренца.

Сила Ампера

На проводник с током в магнитном поле действует сила Ампера. Она определяется формулой:

F = IBl sin α

где I — сила тока в проводнике, B — магнитная индукция, l — длина проводника, α — угол между направлением тока и вектором магнитной индукции.

Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца показывали направление тока, то отогнутый на 90° большой палец покажет направление силы Ампера.

Закон Био-Савара-Лапласа

Закон Био-Савара-Лапласа позволяет рассчитать магнитную индукцию поля, создаваемого проводником с током. Согласно этому закону, магнитная индукция dB, создаваемая элементом проводника dl с током I в точке, находящейся на расстоянии r от этого элемента, определяется выражением:

dB = (μ0/4π) * (I dl sin α) / r^2

где μ0 — магнитная постоянная, α — угол между элементом тока I dl и радиус-вектором r.

Магнитное поле прямого проводника с током

Магнитные линии прямого проводника с током представляют собой концентрические окружности, лежащие в плоскостях, перпендикулярных проводнику. Направление линий определяется по правилу буравчика: если направление поступательного движения буравчика совпадает с направлением тока, то направление вращения ручки буравчика совпадает с направлением линий магнитной индукции.

Величина магнитной индукции поля прямого бесконечно длинного проводника с током на расстоянии r от него определяется формулой:

B = (μ0 * I) / (2πr)

Магнитное поле кругового тока

Магнитные линии кругового тока подобны линиям поля полосового магнита. В центре витка магнитное поле направлено перпендикулярно плоскости витка. Направление поля в центре витка определяется по правилу буравчика: если направление вращения буравчика совпадает с направлением тока в витке, то направление поступательного движения буравчика совпадает с направлением магнитного поля в центре витка.

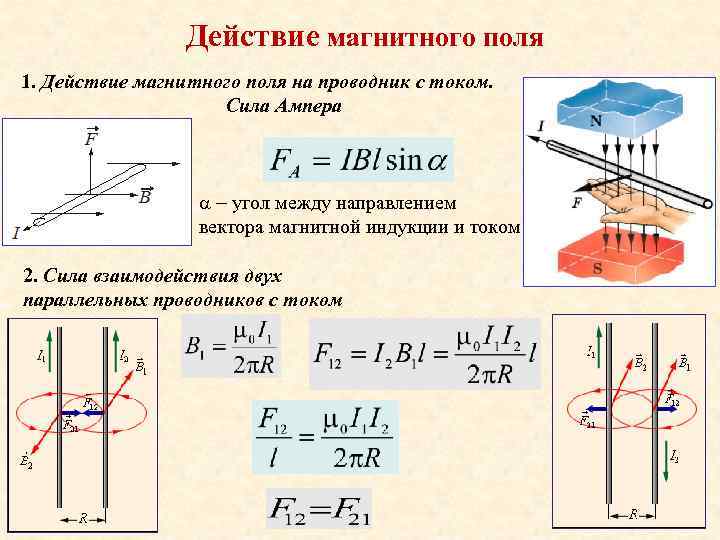
Магнитная индукция в центре кругового витка радиуса R с током I определяется формулой:

B = (μ0 * I) / (2R)

Магнитное поле соленоида

Соленоид — это катушка с током, намотанная на цилиндрический каркас. Внутри длинного соленоида магнитное поле практически однородно. Его направление определяется по правилу буравчика: если направление вращения буравчика совпадает с направлением тока в витках, то направление поступательного движения буравчика совпадает с направлением магнитного поля внутри соленоида.

Магнитная индукция внутри длинного соленоида определяется формулой:

B = μ0 * n * I

где n — число витков на единицу длины соленоида, I — сила тока в обмотке.

Взаимодействие параллельных токов

Два параллельных проводника с токами взаимодействуют между собой посредством своих магнитных полей. Если токи в проводниках направлены в одну сторону, проводники притягиваются. Если токи направлены в противоположные стороны — отталкиваются.

Сила взаимодействия двух параллельных проводников длиной l, расположенных на расстоянии r друг от друга, определяется формулой:

F = (μ0 * I1 * I2 * l) / (2πr)

где I1 и I2 — силы токов в проводниках.

Движение заряженных частиц в магнитном поле

Траектория заряженной частицы в однородном магнитном поле зависит от угла между векторами скорости частицы и магнитной индукции:

• Если частица влетает в поле перпендикулярно линиям индукции, она движется по окружности
• Если частица влетает под углом к линиям индукции, траектория представляет собой спираль
• Если частица движется вдоль линий индукции, траектория остается прямолинейной

Радиус окружности, по которой движется заряженная частица в однородном магнитном поле, определяется формулой:

R = (m * v) / (q * B)

где m — масса частицы, v — ее скорость, q — заряд, B — магнитная индукция.

Применение магнитного поля

Магнитное поле находит широкое применение в науке и технике:

• Электродвигатели и генераторы
• Электромагниты
• Трансформаторы
• Ускорители заряженных частиц
• Масс-спектрометры
• Магнитно-резонансные томографы
• Магнитная левитация
• Магнитная запись информации

Понимание свойств и законов магнитного поля имеет огромное значение для развития современных технологий и научных исследований в области физики, электротехники и других областях.

Общая электротехника с основами электроники

Общая электротехника с основами электроники

Попов В. С., Николаев С. А. Общая электротехника с основами электроники, М., «Энергия», 1972, — 504 c. В книге рассмотрены электрические цепи, электрические машины и трансформаторы, электротехнические намерения и приборы, электропривод и аппаратура управления, передача и распределение электрической энергии, электронные лампы, газоразрядные приборы, полупроводниковые приборы, фотоэлектрические приборы, усилители и генераторы, Книга предназначена для учащихся техникумов неэлектротехнических специальностей. Оглавление Предисловие Введение Часть первая. Общая электротехника 1-1. Основные понятия 1-2. Электрическое напряжение. Потенциал 1-3. Электропроводность 1-4. Электрическая емкость. Конденсаторы 1-5. Соединение конденсаторов 1-6. Энергия электрического поля 1-8. Электроизоляционные материалы Глава вторая. Электрические цепи постоянного тока 2-1. Электрический ток 2-2. Электрическая цепь и ее элементы 2-3. Закон Ома 2-4. Электрические сопротивление и проводимость 2-5. Зависимость сопротивления от температуры 2-6. Проводниковые материалы 2-7. Работа и мощность 2-8. Преобразование электрической энергии в тепловую 2-9. Электрическая нагрузка проводов и защита их от перегрузки 2-10. Потеря напряжения в проводах 2-11. Первый закон Кирхгофа 2-12. Последовательное соединение сопротивлений — приемников энергии 2-13. Параллельное соединение сопротивлений — приемников энергии 2-14. Смешенное соединение сопротивлений 2-15. Два режима работы источника питания 2-16. Второй закон Кирхгофа 2-17. 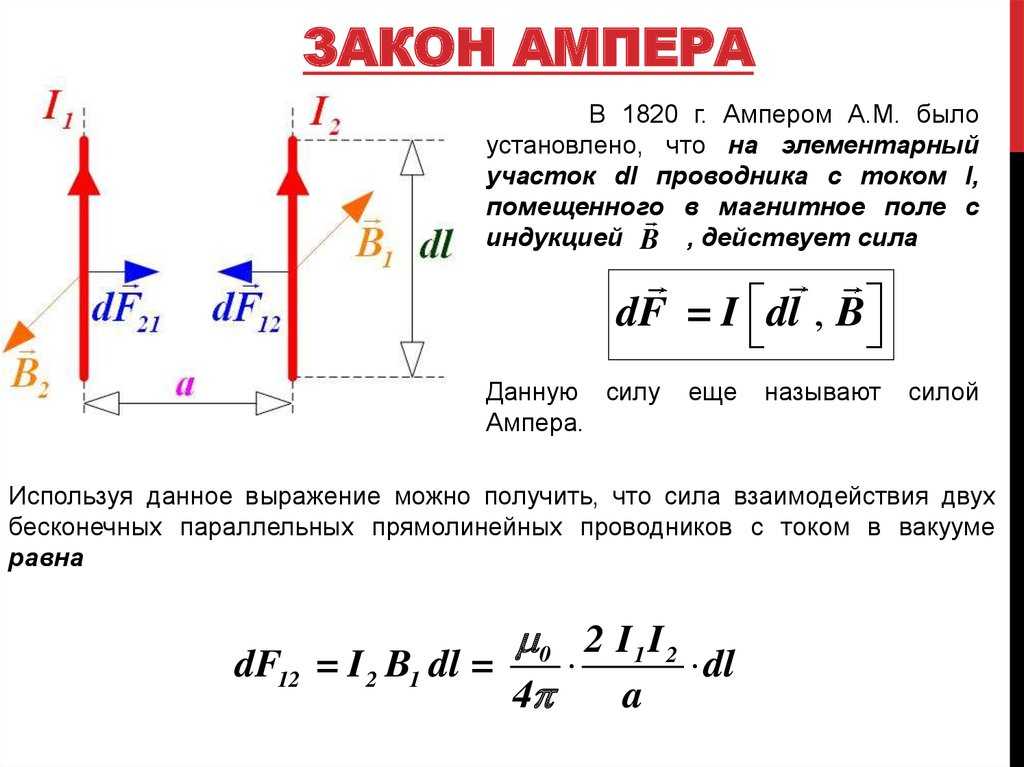Расчет сложных цепей 2-18. Химические источники питания 2-19. Соединение химических источников питания 2-20. Нелинейные электрические цепи 2-21. Лабораторная работа. Потеря напряжения в линии Глава третья. Электромагнетизм 3-1. Магнитное поле тока. Магнитная индукция. Магнитный поток 3-2. Электромагнитная сила 3-3. Взаимодействие параллельных проводов с токами 3-4. Магнитная проницаемость 3-5. Напряженность магнитного поля. Магнитное напряжение 3-6. Закон полного тока 3-7. Магнитное поле катушки с током 3-8. Ферромагнетики, их намагничивание и перемагничивание 3-9. Ферромагнитные материалы 3-10. Магнитная цепь и ее расчет 3-11. Электромагниты 3-12. Электромагнитная индукция 3-13. Принцип работы электрического генератора 3-14. Принцип работы электродвигателя 3-15. Вихревые токи 3-16. Индуктивность. Электродвижущая сила самоиндукции 3-17. Энергия магнитного поля 3-18. Взаимная индуктивность Глава четвертая. Электрические машины постоянного тока 4-1. Назначение машин постоянного тока 4-2. Устройство машины постоянного тока 4-3. Принцип работы машины постоянного тока 4-4. Устройство обмотки якоря 4-5. Электродвижущая сила обмотки якоря 4-6. Электромагнитный момент на валу машины 4-7. Механическая мощность машины постоянного тока 4-8. Реакция якоря машины постоянного тока 4-9. Коммутация тока 4-10. Понятие о номинальных данных и характеристиках электрических машин 4-11. Генератор с независимым возбуждением 4-12. Генератор с параллельным возбуждением 4-13. Генератор со смешанным возбуждением 4-14. Электродвигатели постоянного тока 4-15. Электродвигатель с параллельным возбуждением 4-16. Электродвигатель с независимым возбуждением 4-17. Электродвигатели с. последовательным и со смешанным возбуждением 4-18. Потери и коэффициент полезного действия 4-19. Лабораторная работа. Электродвигатель с параллельным возбуждением 4-20. 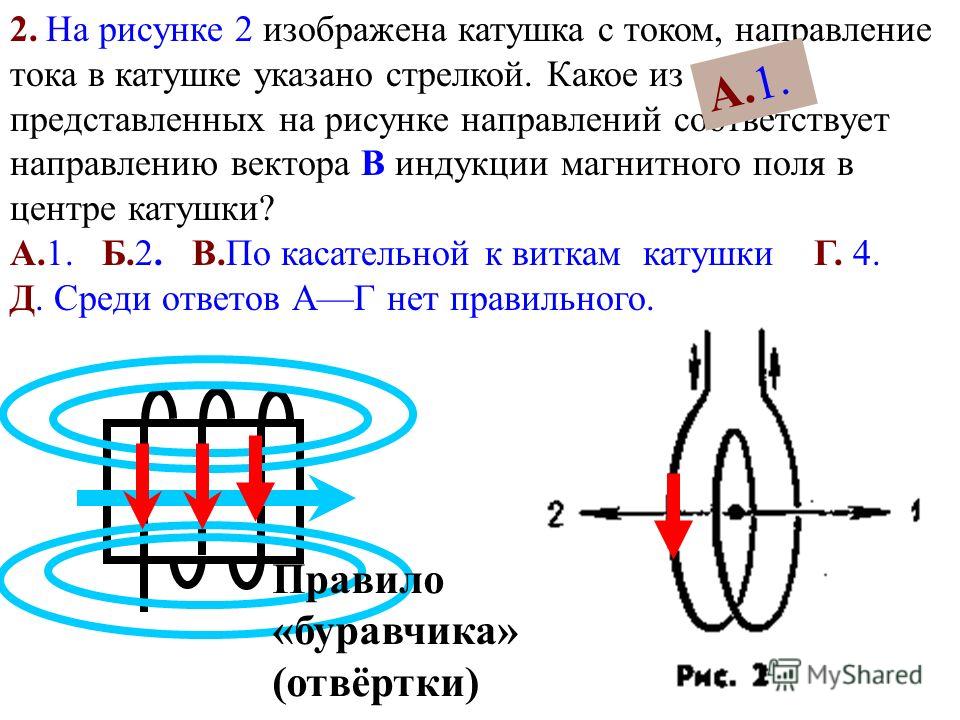Лабораторная работа. Генератор с параллельным возбуждением Главе пятая. Основные понятия, относящиеся к переменным токам 5-1. Переменный ток 5-2. Получение синусоидальной э. д. с. 5-3. Сдвиг фаз 5-4. Действующие значения тока и напряжения 5-5. Векторная диаграмма Глава шестая. Цепи переменного тока 6-1. Особенности цепей переменного тока 6-2. Цепь с сопротивлением 6-3. Цепь с индуктивностью 6-4. Цепь с активным сопротивлением и индуктивностью 6-5. Неразветвленная цепь с активными сопротивлениями и индуктивностями 6-6. Разветвленная цепь с активными сопротивлениями и индуктивностями 6-7. Цепь с емкостью 6-8. Колебательный контур 6-9. Резонанс напряжений 6-10. Резонанс токов 6-11. Коэффициент мощности 6-12. Активная и реактивная энергия 6-13. Лабораторная работа. Цепь переменного тока с активным сопротивлением, индуктивностью и емкостью 6-14. Лабораторная работа. Параллельное соединение катушки и конденсатора Глава седьмая. 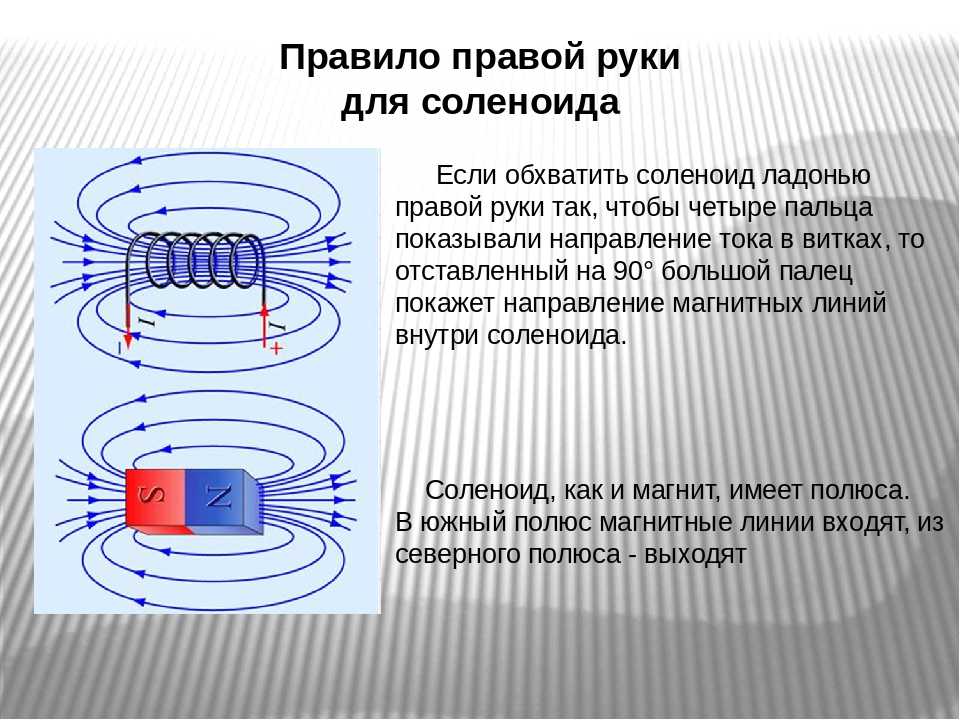Трехфазные цепи 7-1. Трехфазные системы 7-2. Соединение обмоток генератора звездой 7-3. Соединение обмоток генератора треугольником 7-4. Соединение приемников энергии звездой 7-5. Соединение приемников энергии треугольником 7-6. Лабораторная работа. Трехфазные цепи Глава восьмая. Электротехнические измерения и приборы 8-1. Основные понятия 8-2. Классификация электроизмерительных приборов 8-3. Измерительные механизмы приборов 8-4. Измерение тока и напряжения 8-5. Измерение мощности 8-6. Измерение электрической энергии 8-7. Измерение сопротивлений 8-8. Измерение неэлектрических величин электрическими методами 8-9. Лабораторная работа. Измерение сопротивлений 8-10. Лабораторная работа. Поверка индукционного счетчика 8-11. Лабораторная работа. Измерение мощности в трехфазной цепи Глава девятая. Трансформаторы 9-1. Назначение трансформаторов 9-2. Принцип действия и устройство однофазного трансформатора 9-3. Холостой ход однофазного трансформатора 9-4. Работа нагруженного трансформатора и диаграмма магнитодвижущих сил (м. д. с.) 9-5. Изменение напряжения трансформатора при нагрузке 9-6. Мощность потерь в обмотках нагруженного трансформатора 9-7. Трехфазный трансформатор 9-8. Регулирование напряжения трансформаторов 9-9. Автотрансформаторы 9-10. Трансформаторы для дуговой электросварки 9-11. Измерительные трансформаторы 9-12. Коэффициент полезного действия трансформатора 9-13. Нагрев и охлаждение трансформаторов 9-14. Лабораторная работа. Однофазный трансформатор Глава десятая. Электрические машины переменного тока 10-1. Назначение машин переменного тока. Асинхронные электродвигатели 10-2. Получение вращающегося магнитного поля 10-3. Обмотка статора асинхронного электродвигателя 10-4. Обмотка ротора асинхронного двигателя 10-5. Принцип действия асинхронного двигателя 10-6. Электродвижущие силы в обмотках статора и ротора 10-7. Сопротивления обмотки ротора 10-8. Токи в обмотке ротора 10-9. Вращающий момент двигателя 10-10. Пуск в ход асинхронных двигателей 10-11. Регулирование частоты вращения асинхронного двигателя 10-12. Однофазный асинхронный двигатель 10-13. Потери и к. п. д. асинхронного двигателя 10-14. Синхронные машины 10-15. Универсальный коллекторный двигатель 10-16. Лабораторная работа. Трехфазный асинхронный электродвигатель Глава одиннадцатая. Электропривод и аппаратура управления 11-1. Система электропривода 11-2. Нагрев и охлаждение электрических машин 11-3. Выбор мощности двигателя при продолжительном режиме 11-4. Выбор мощности двигателя при кратковременном режиме 11-5. Выбор мощности двигателя при повторно-кратковременном режиме 11-6. Рубильники 11-7. Пакетные выключатели 11-8. Реостаты для пуска и регулирования электродвигателей 11-9. Контроллеры 11-10. Плавкие предохранители 11-11. Автоматические воздушные выключатели 11-12. Контакторы 11-13. Реле 11-14. Схема управления асинхронным двигателем с помощью реверсивного магнитного пускателя 11-15. Схема включения двухскоростного асинхронного двигателя 11-16. Автоматический пуск асинхронного двигателя с кольцами 11-17. Автоматический пуск двигателя постоянного тока с параллельным возбуждением 11-18. Лабораторная работа. Сборка и проверка работы схемы релейноконтакторного управления трехфазным асинхронным двигателем с короткозамкнутым ротором Глава двенадцатая. Передача и распределение электрической энергии 12-1. Схемы электроснабжения промышленных предприятий. 12-2. Трансформаторные подстанции и распределительные устройства промышленных предприятий 12-3. Электрические сети промышленных предприятий 12-4. Защитное заземление Часть вторая. Основы промышленной электроники 13-1. Классификация и применение электронных приборов 13-2. Движение электронов в электрическом поле 13-3. Движение электронов в магнитном поле 13-4. Электронная эмиссия 13-5. Катоды электровакуумных приборов 13-6. Двухэлектродные электронные лампы — диоды 13-7. Применение двухэлектродных ламп Глава четырнадцатая. Трехэлектродные лампы. Четырех- и пятиэлектродные лампы. Усилители 14-1. Устройство и принцип работы триода 14-2. Статические характеристики триода 14-3. Параметры триода 14-4. Простейший каскад усиления 14-5. Характеристики и параметры простейшего каскада усиления 14-6. Типы триодов 14-7. Четырехэлектродные лампы — тетроды 14-8. Пятиэлектродные лампы — пентоды 14-9. Комбинированные и многосеточные лампы. Типы ламп 14-10. Общие понятия, относящиеся к усилителям 14-11. Режимы работы усилителей 14-12. Многокаскадные ламповые усилители 14-13. Обратная связь в усилителях 14-14. Лабораторная работа. Снятие анодных и анодно-сеточных характеристик триода и определение по ним статических параметров 14-15. Лабораторная работа. Снятие частотных характеристик усилителя напряжения низкой частоты Глава пятнадцатая. Газоразрядные приборы и их применение 15-1. Виды газового разряда и его вольт-амперная характеристика 15-2. Ионные приборы с несамостоятельным дуговым разрядом 15-3. Приборы с тлеющим разрядом 15-4. Ионные приборы с самостоятельным дуговым разрядом 15-5. Обозначения газоразрядных приборов 15-6. Лабораторная работа. Снятие анодносеточных и пусковых характеристик тиратрона Глава шестнадцатая. Электронные генераторы. Осциллографы 16-1. Генераторы синусоидальных напряжений 16-2. Зарядка и разряд конденсатора 16-3. Релаксационные генераторы (генераторы пилообразного напряжения) 16-4. Мультивибраторы 16-5. Электроннолучевые трубки 16-6. Электроннолучевой осциллограф 16-7. Обозначения электроннолучевых трубок 16-8. Лабораторная работа. Экспериментальное, определение кривых напряжений в схемах выпрямителей Глава семнадцатая. Полупроводниковые приборы и их применение 17-1. Собственная электропроводность полупроводников 17-2. Примесная электропроводность полупроводников 17-3. Полупроводниковый вентиль 17-4. Германиевые и кремниевые диоды 17-5. Меднозакисные и селеновые диоды 17-6. Применение полупроводниковых вентилей и схемы выпрямителей 17-7. Обозначения полупроводниковых диодов 17-8. Кремниевые стабилитроны (опорные диоды) 17-9. Транзисторы 17-10. Применение транзисторов для усиления колебаний 17-11. Схемы включения и характеристики транзисторов 17-12. Обозначения полупроводниковых триодов 17-13. Лабораторная работа. Снятие характеристик транзистора Глава восемнадцатая. Фотоэлектронные приборы и электронные реле 18-1. Фотоэлементы с внешним фотоэффектом 18-2. Фоторезисторы 18-3. Полупроводниковые фотоэлементы 18-4. Электронные и ионные реле 18-5. Лабораторная работа. Электронное реле — триггер

Глава 22. Магнитные взаимодействия. Магнитная индукция.Силы Лоренца и Ампера

Если заряд движется, то наряду с электрическим полем он создает еще одно поле — магнитное, которое действует на другие движущиеся заряды. В результате возникает дополнительное (наряду с кулоновским) взаимодействие движущихся электрических зарядов, которое называется магнитным. В результате магнитного взаимодействия возникает взаимодействие проводников с током.

В 1820 г. датский физик Х. Эрстед обнаружил, что проводник с током действует на магнитную стрелку. После этого стало ясно, что магнитное взаимодействие движущихся электрических зарядов и токов и взаимодействие постоянных магнитов имеют одну и ту же природу. На основании подробных исследований А. Ампер установил, что взаимодействие постоянных магнитов между собой и с токами можно объяснить, если предположить, что внутри магнитов есть электрические токи (в настоящее время известно, что эти токи имеют внутримолекулярную природу).

Для характеристики магнитного поля вводится векторная величина, которая называется индукцией магнитного поля и которая позволяет найти силы, действующие со стороны магнитного поля на движущиеся заряды. Как правило, эту величину обозначают буквой . Для нахождения индукции в каждой точке магнитного поля, созданного проводником с током, используется закон Био-Савара-Лапласа и принцип суперпозиции. Закон Био-Савара-Лапласа позволяет найти поле , созданное бесконечно малым элементом проводника, а принцип суперпозиции требует сложить векторы индукции, созданные всеми элементами проводников. Закон Био-Савара-Лапласа в школьный курс физики, однако, не входит. В задачи ЕГЭ входят только вопросы, связанные с направлением вектора магнитной индукции (но не с величиной). Существует несколько вариантов правила нахождения направления вектора . Наиболее удобным является правило буравчика — оно более универсально, чем правило левой руки. Правило буравчика утверждает, что если вкручивать правыйбуравчик¹ по току в проводнике, то направление движения ручки в каждой точке пространства покажет направление вектора индукции магнитного поля в этой точке. Относительно величины достаточно помнить, что чем дальше от проводника, тем меньше индукция, и что внутри бесконечной катушки (бесконечного соленоида) магнитное поле направлено вдоль оси катушки и однородно.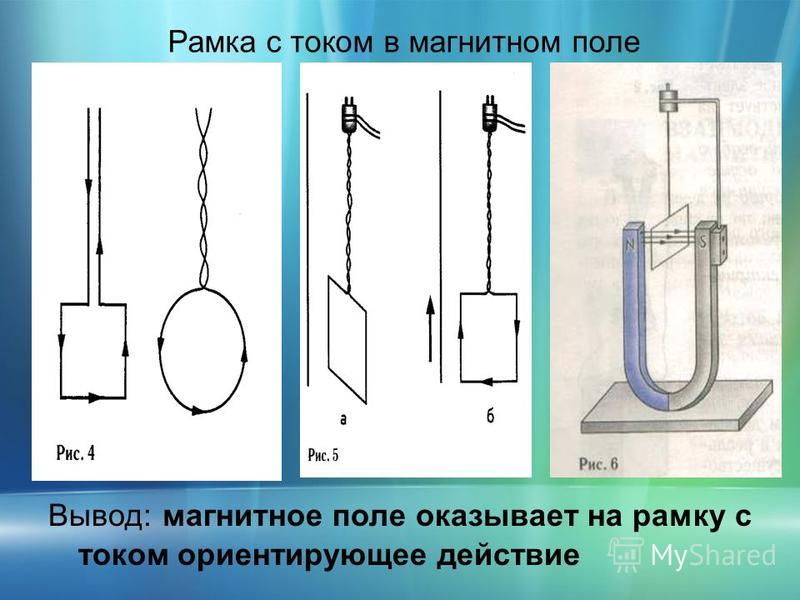

Магнитное поле можно изобразить графически с помощью линий магнитной индукции. Линии магнитной индукции — воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора в этой точке. Линии магнитной индукции проводят так, что их густота в каждой области пространства пропорциональна величине индукции в этой области. В отличие от силовых линий электрического поля линии магнитной индукции всегда являются замкнутыми.

На электрический заряд величиной , движущийся со скоростью в магнитном поле с индукцией , со стороны магнитного поля действует сила, которая называется силой Лоренца

(22.1)

где — угол между скоростью и вектором индукции. Направление силы Лоренца определяется следующим образом (см. рисунок).

1. Сила Лоренца перпендикулярна плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля (на рисунке эта плоскость показана тонким пунктиром).

2. Выбор между двумя перпендикулярными направлениями осуществляется с помощью правила буравчика (или правила левой руки): если вращать правый буравчик так, что его ручка движется от вектора к вектору , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд (траектория ручки буравчика показана на рисунке изогнутой стрелкой).

3. Для отрицательного заряда направление силы Лоренца противоположно.

Можно также определять направление силы Лоренца по правилу левой руки: левую руку нужно расположить так, чтобы вектор входил в ладонь, направление четырех пальцев совпадало с направлением вектора скорости заряда, тогда направление отогнутого под прямым углом к четырем пальцам большого пальца покажет направление силы, действующей на положительный заряд (на отрицательный заряд действует сила противоположного направления).

Поскольку магнитное поле действует на движущиеся заряды, то магнитное поле действует и на проводник, по которому течет электрический ток.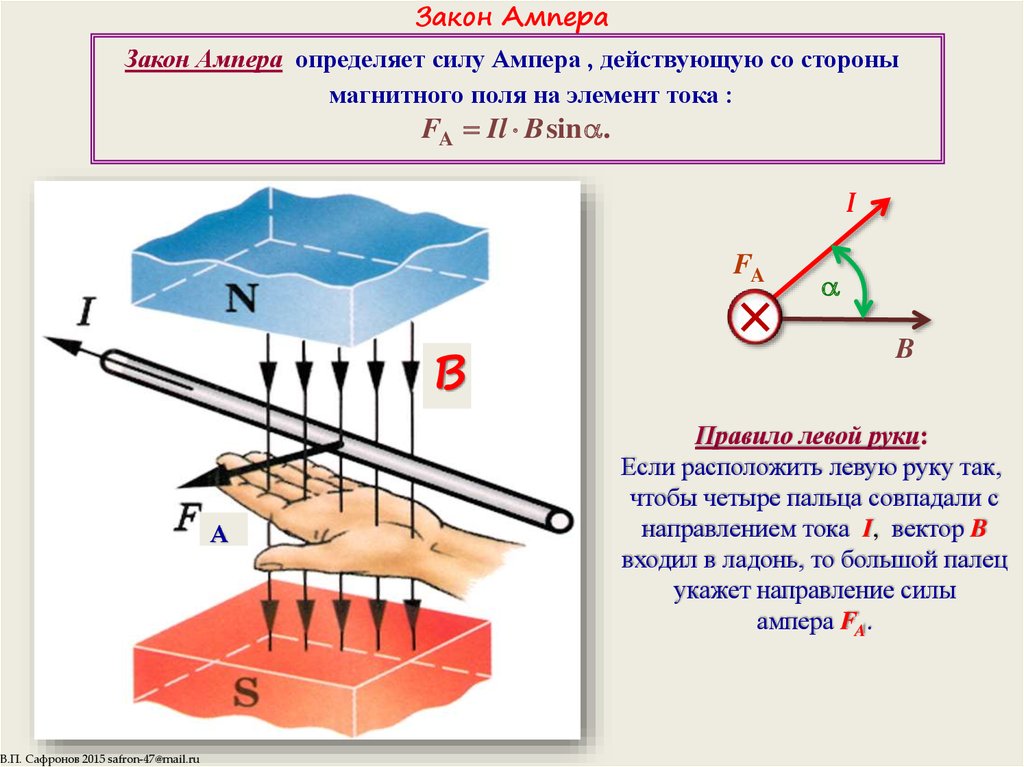 Если в магнитном поле с индукцией находится проводник длиной , по которому течет ток , то на этот проводник действует сила

(22.2)

где — угол между током и вектором индукции. Направлен вектор силы (22.2) перпендикулярно плоскости, в которой лежат вектор и проводник, причем в таком направлении, что если поставить правый буравчик перпендикулярно указанной плоскости и вращать его так, что ручка вращается от тока к вектору , то направление его вкручивания покажет направление силы (см. рисунок; плоскость в которой лежат проводник и вектор индукции обозначена тонким пунктиром, движение ручки буравчика — изогнутой стрелкой). Также для нахождения направления силы можно использовать правило левой руки. Сила (22.2), действующая со стороны магнитного поля на проводник с током, называется силой Ампера.

Рассмотрим теперь задачи.

Правильный ответ в задаче 22.1.1 — 4 (магнитное поле создается движущимися заряженными телами), в задаче 22. 1.2 — 2 (в магнитном веществе есть незатухающие электрические токи). Что же касается того, заряжен магнит или нет, то от этого существование магнитного поля (если магнит покоится) не зависит.

В задаче 22.1.3 следует воспользоваться правилом буравчика. Если вкручивать буравчик по направлению тока в проводнике, то в точке его ручка будет двигаться за чертеж. Следовательно, за чертеж направлен в точке и вектор индукции магнитного поля (ответ 1).

Если вкручивать буравчик по току в кольце (в любой точке кольца), то ручка буравчика в центре кольца будет двигаться за чертеж. Поэтому правильный ответ в задаче 22.1.4 — 3.

Поскольку угол между скоростью заряда и вектором магнитной индукции равен нулю (задача 22.1.5), то согласно формуле (22.1) сила Лоренца, действующая на этот заряд, равна нулю (ответ 4).

Применим к проводнику с током из задачи 22.1.6 формулу (22.2) для силы Ампера. Имеем (ответ 2).

Как следует из формулы (22. 2) сила Ампера равна нулю, если угол между током и индукцией равен нулю или 180°. Из приведенных на рисунке в задаче 22.1.7 проводников, таковым является только проводник 1. Поэтому на него магнитное поле не действует (ответ 1).

Применяем к частице из задачи 22.1.8 (см. рисунок) правила нахождения направления силы Лоренца (пункты 1-3 после формулы (22.1)). Во-первых, сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля — т.е. либо за чертеж, либо на нас. Во-вторых, при вращении ручки буравчика, поставленного на чертеж в ту точку, где находится заряд, от вектора к вектору (в направлении меньшего угла между ними), буравчик будет «выкручиваться» из чертежа. А по-скольку частица заряжена положительно, сила Лоренца направлена «на нас» (ответ 1).

Используя правила для силы Ампера (формула (22.2) и текст после нее), найдем, что сила Ампера, действующая со стороны магнитного поля на проводник с током в задаче 22. 1.9, направлена «от нас» (ответ 3).

В задаче 22.1.10 следует сначала найти направление вектора магнитной индукции поля провода в той точке, где находится заряд, а затем использовать правила для силы Лоренца (формула (22.1) и текст за ней). Согласно результатам задачи 22.1.3, вектор в той точке, где находится заряд, направлен за чертеж (см. рисунок).

Вектор силы Лоренца направлен перпендикулярно плоскости, в которой лежат векторы и , т.е. либо к проводу, либо от него. Ставим буравчик перпендикулярно этой плоскости и вращаем его так, что ручка движется от вектора к вектору (см. рисунок; буравчик нужно вращать по часовой стрелке, если смотреть снизу). При таком вращении буравчик будет вкручиваться вверх. А поскольку электрон заряжен отрицательно, то действующая на него сила направлена противоположно, т.е. от провода (ответ 2).

В задаче 22.2.1 используем принцип суперпозиции. Ток в горизонтальном кольце создает поле в его центре с индукцией, направленной вверх, ток в вертикальном кольце — с индукцией, направленной вправо (см. задачу 22.1.4.). Результат сложения этих векторов — индукция суммарного магнитного поля — направлена на «северо-восток» (ответ 1).

Ток в верхнем проводе (задача 22.2.2) создает поле с индукцией, направленной «за чертеж», ток в нижнем — «на нас». Результат их сложения зависит от величин этих векторов. Поскольку поле нижнего провода в точке больше поля верхнего (меньше расстояние), то вектор суммы направлен «на нас» (ответ 1).

Сила Лоренца в любой момент времени перпендикулярна скорости частицы. Поэтому угол между бесконечно малым перемещением частицы в любой момент времени и силой Лоренца, действующей на частицу в этот момент времени, — прямой. А поскольку в формулу для работы силы на бесконечно малом участке перемещения входит косинус угла между силой и перемещением, то работа силы Лоренца равна нулю (задача 22.2.3 — ответ 3). Из этих рассуждений и теоремы об изменении кинетической энергии следует, что заряженная частица, движущаяся под действием магнитного поля, изменяет направление, но не величину своей скорости.

Если заряженная частица влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, то она движется по окружности, причем эта окружность лежит в плоскости, перпендикулярной линиям магнитной индукции. Радиус окружности можно найти из второго закона Ньютона для этой частицы

(22.3)

где и — масса частицы и ее заряд, — ускорение, — скорость, которая не изменяется по величине (см. предыдущую задачу), — индукция магнитного поля. В формуле (22.3) использовано известное выражение для центростремительного ускорения . Из формулы (22.3) получаем для радиуса окружности

(22.4)

Применяя формулу (22.4) к задаче 22.2.4 находим отношение радиусов окружности первой и второй частиц

(ответ 2).

Найдем сначала скорости протона и -частицы, ускоренных одним и тем же напряжением (задача 22.2.5). По теореме об изменении кинетической энергии имеем

где и — масса частицы и ее заряд, — скорость, которую частица приобретает после разгона (здесь предполагается, что начальная скорость частицы равна нулю). Из этой формулы находим отношение скоростей протона и -частицы , ускоренных одним и тем же напряжением

Поскольку заряд протона вдвое меньше заряда -частицы, а масса вчетверо меньше, то . Теперь из формулы (22.4) находим отношение радиусов окружности протона и  -частицы, ускоренных одним и тем же электрическим напряжением и движущихся в одном и том же магнитном поле

(ответ 4).

Период обращения заряженной частицы в магнитном поле (задача 22. 2.6) можно найти из следующих соображений. В однородном магнитном поле частица движется по окружности и за период проходит путь, равный длине этой окружности , где — ее радиус. Используя формулу (22.4) для радиуса траектории, получим для периода обращения

где — скорость частицы, — ее масса, — заряд, — индукция магнитного поля. Отсюда заключаем, что период обращения заряженной частицы в магнитном поле не зависит от ее скорости (ответ 3).

Индукция магнитного поля в задаче 22.2.7 должна быть направлена так, чтобы сила Лоренца, действующая на электрон, была направлена к центру окружности, по которой он движется (см. рисунок). А поскольку сила Лоренца перпендикулярна скорости и индукции, то вектор индукции может быть направлен в этой ситуации только «за чертеж» или «на нас». Воспользуемся далее правилом буравчика (см. текст после формулы (22.1)): если вращать буравчик так, что его ручка будет вращаться от скорости заряда к индукции магнитного поля , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд. Для электрона ( < 0) направление силы противоположно. Непосредственной проверкой убеждаемся, что вектор индукции направлен «за чертеж» (ответ 4).

В области среднего провода (задача 22.2.8) ток в верхнем проводе создает магнитное поле с индукцией, направленной «от нас», ток в нижнем — «на нас» (см. задачу 22.1.3). Но ток в нижнем проводе вдвое меньше тока в верхнем, а индукция поля — пропорциональна току. Поэтому индукция суммарного поля верхнего и нижнего проводов в области среднего провода направлена «от нас». Согласно правилам нахождения направления силы Ампера (см. текст после формулы (22.2)) находим, что сила, действующая на средний провод со стороны магнитного поля верхнего и нижнего проводов, направлена вверх (ответ 1). Отметим, что из приведенных рассуждений также следует, что два параллельных провода, по которым текут токи одинакового направления притягиваются, противоположного — отталкиваются.

В задаче 22.2.9 магнитное поле действует на рамку следующим образом. На стороны и , которые параллельны линиям индукции, поле не действует. На стороны и действуют силы Ампера, равные по величине , где — ток в рамке, — индукция магнитного поля, — длина стороны. Сила, действующая на сторону , направлена «на нас», на сторону — «от нас». Поскольку суммарная сила, действующая на рамку, равна нулю, как целое рамка перемещаться в пространстве не будет, а будет вращаться вокруг оси, показанной на рисунке пунктиром (ответ 4).

Задача 22.2.10 по формуле (22.2) находим силы Ампера, действующие на стороны треугольника

где — ток в контуре, и — длины сторон и , — индукция магнитного поля (последняя из приведенных формул следует из того, что сторона параллельна линиям индукции). Из теоремы синусов для треугольника

заключаем, что , а из правил для направления силы Ампера — что один из векторов или направлен «за чертеж», один — «на нас» (в зависимости от направления тока в контуре). Поэтому правильный ответ в задаче — 3.

Правило правой руки

Ориентация для левшей показана слева, а для правшей — справа.

Использование правой руки.

В математике и физике правило правой руки является общепринятой мнемоникой для понимания условных обозначений векторов в трех измерениях. Он был изобретен для использования в электромагнетизме британским физиком Джоном Амброузом Флемингом в конце 19 века.

При выборе трех векторов, которые должны быть под прямым углом друг к другу, есть два различных решения, поэтому при выражении этой идеи в математике необходимо устранить неоднозначность того, какое решение имеется в виду.

Существуют вариации мнемоники в зависимости от контекста, но все вариации связаны с одной идеей выбора условности.

Contents 1 Direction associated with an ordered pair of directions 2 Direction associated with a rotation 3 Applications 4 External links

Direction associated with an ordered пара направлений

Одна из форм правила правой руки используется в ситуациях, когда над двумя векторами a и b должна быть выполнена упорядоченная операция, результатом которой является вектор c , перпендикулярный как a , так и б . Наиболее распространенным примером является векторное перекрестное произведение. Правило правой руки требует следующей процедуры выбора одного из двух направлений.

• Когда большой, указательный и средний пальцы находятся под прямым углом друг к другу (указательный палец направлен прямо), средний палец указывает в направлении c , когда большой палец представляет a , а указательный палец представляет b .

Возможны другие (эквивалентные) назначения пальцев. Например, первый (указательный) палец может представлять a , первый вектор в произведении; второй (средний) палец, b , второй вектор; и большой палец, c , продукт.

Направление, связанное с вращением

Прогноз направления поля ( B ), учитывая, что ток I течет в направлении большого пальца.

Другая форма правила правой руки, иногда называемая правилом захвата правой рукой , используется в ситуациях, когда вектор должен быть назначен вращению тела, магнитного поля или жидкости.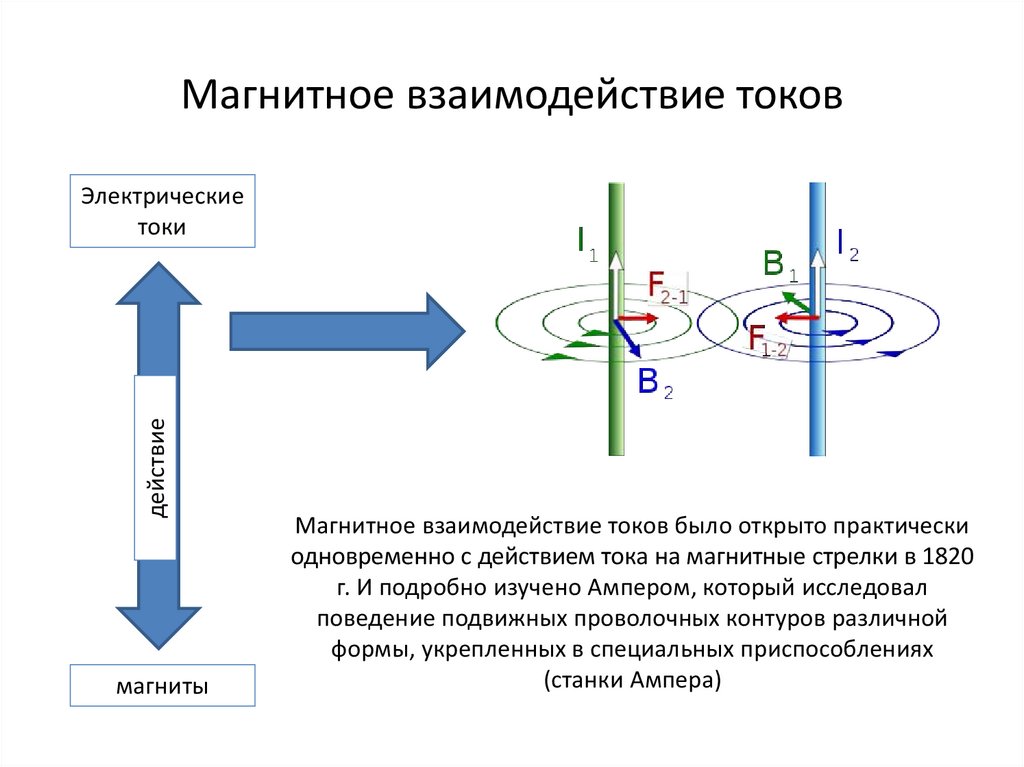 В качестве альтернативы, когда вращение задается вектором и необходимо понять, каким образом происходит вращение, применимо правило захвата правой рукой.

Эта версия правила используется в двух взаимодополняющих приложениях закона Ампера:

1. Электрический ток проходит через соленоид, в результате чего возникает магнитное поле. Когда вы обхватываете соленоид правой рукой пальцами в направлении обычного тока, ваш большой палец указывает в направлении северного магнитного полюса.
2. По прямому проводу проходит электрический ток. Здесь большой палец указывает в направлении условного тока (от положительного к отрицательному), а пальцы указывают в направлении линий магнитного потока.

Этот принцип также используется для определения направления вектора крутящего момента. Если вы захватите воображаемую ось вращения вращающей силы так, что ваши пальцы будут указывать в направлении силы, то вытянутый большой палец будет указывать в направлении вектора крутящего момента.

Правило захвата правой рукой является соглашением, полученным из соглашения о правиле правой руки для векторов. Например, при применении правила к току в прямом проводе направление магнитного поля (против часовой стрелки, а не по часовой стрелке, если смотреть с кончика большого пальца) является результатом этого соглашения, а не лежащим в основе физическим явлением.

Приложения

Первая форма правила используется для определения направления векторного произведения двух векторов. Это приводит к широкому использованию в физике везде, где встречается перекрестное произведение. Ниже приведен список физических величин, направления которых связаны правилом правой руки. (Некоторые из них связаны с перекрестными произведениями только косвенно и используют вторую форму.)

• Угловая скорость вращающегося объекта и скорость вращения любой точки объекта
• Крутящий момент, вызывающая его сила и положение точки приложения силы
• Магнитное поле, положение точки, в которой оно определяется, и электрический ток (или изменение электрического потока), который вызывает его
• Магнитное поле в витке провода и электрический ток в проводе
• Сила магнитного поля, действующая на заряженную частицу, само магнитное поле и скорость объекта
• Завихренность в любой точке в области течения жидкости
• Индуцированный ток от движения в магнитном поле (известный как правило правой руки Флеминга)

Внешние ссылки

• Демонстрация правила правой руки на physics. syr.edu
• Определение на mathworld.wolfram.com

Правило правой руки для заряда в магнитном поле

Все ресурсы AP Physics 2

6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Учитесь по концепции

AP Физика 2 Справка » Электричество и магнетизм » Магнетизм и электромагнетизм » Правило правой руки для заряда в магнитном поле

Электроны вращаются против часовой стрелки в плоскости экрана. Каково направление магнитного поля в центре вращения, создаваемого этими электронами?

Возможные ответы:

В экран

В центре нет поля

Вне экрана

Влево

Правильно

Правильный ответ:

В экран

Объяснение:

Согласно правилу правой руки, вращающийся против часовой стрелки заряд создаст поле, выходящее за пределы экрана; однако, поскольку электроны заряжены отрицательно, они создают противоположное поле. Поэтому поле, создаваемое этими электронами, уходит в экран.

Сообщить об ошибке

Кусок металла с ЭДС движения движется через магнитное поле, попадая на страницу (обозначается крестиком) с величиной . Длина металлической детали (длина по вертикали, а не длина по горизонтали) . Найдите модуль скорости тела.

Возможные ответы:

Правильный ответ:

Пояснение:

В металле есть свободные электроны, которые движутся в магнитном поле вместе с металлом. Это заряды, движущиеся через магнитное поле. Они чувствуют силу, действующую на них

Используя правило правой руки, можно показать, что электроны будут двигаться к верхней части стержня, оставляя нижнюю часть с положительным зарядом. Теперь между верхом и низом металлического стержня существует электрическое поле. На частицы бруска действует электрическая сила

где — электрическое поле. Электрическая сила теперь будет равна и противоположна магнитной силе, поэтому заряды осядут и не продолжат двигаться из стержня. Уравняв эти силы, заряд разделится.

Электрическое поле — это просто ЭДС движения на единицу длины,

Решение для v,

Сообщить об ошибке

Предположим, что электрон движется прямо на восток в присутствии ориентированного магнитного поля так, чтобы он был направлен наружу, в сторону от зрителя. В каком направлении действует магнитная сила на этот электрон?

Возможные ответы:

North

South

Вдали от зрителя

к зрителю

East

Правильный ответ:

South

Пояснение:

В этом вопросе нам предлагается сценарий, в котором электрон движется на восток в магнитном поле, направленном от наблюдателя. Нас просят определить направление, в котором указывает магнитная сила, действующая на этот электрон.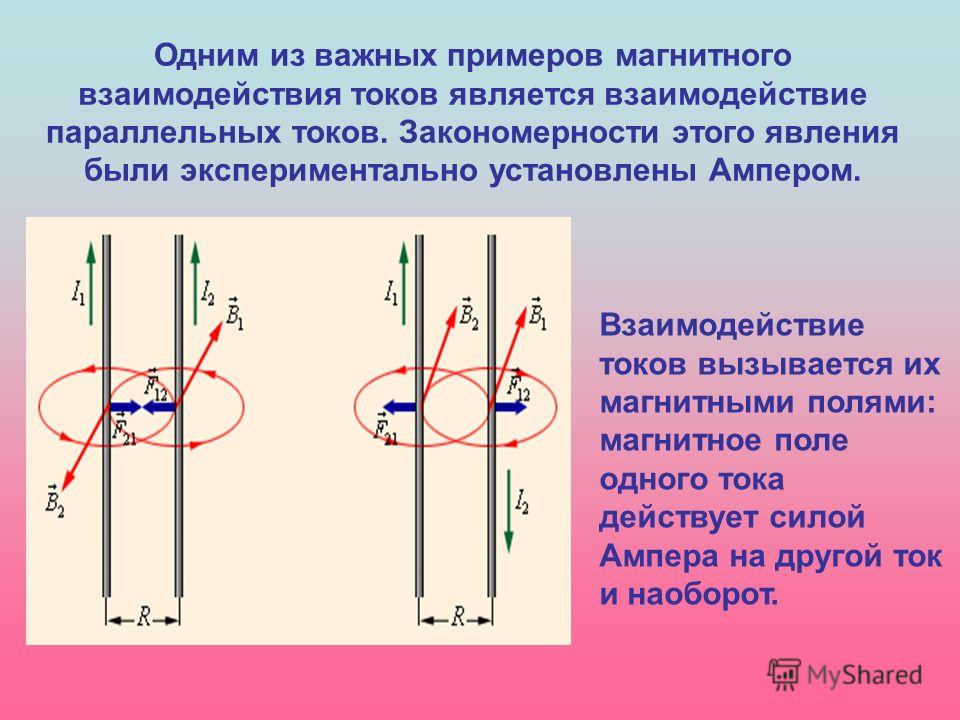

Чтобы ответить на этот вопрос, нам нужно использовать «правило правой руки». Это полезный трюк, который позволяет нам связать относительную ориентацию трех величин:

1) Скорость положительно заряженной частицы, движущейся в магнитном поле

2) Направление магнитного поля

3) Магнитная сила испытывается движущейся частицей

Кроме того, существует уравнение, связывающее эти три величины:

В такой ситуации все три вышеуказанные величины ориентированы перпендикулярно друг другу. Правило правой руки — полезный способ запомнить, как каждый термин ориентирован по отношению друг к другу. Используя правую руку, большой палец представляет направление скорости частицы. Указательный палец представляет направление внешнего магнитного поля. И, наконец, направление, к которому обращена ладонь, совпадает с направлением магнитной силы, действующей на движущуюся частицу.

Имейте в виду, что эта ориентация верна для положительно заряженных частиц. Чтобы определить относительную ориентацию этих терминов для отрицательной частицы, просто измените направление силы.

В этой задаче частица движется на восток (вправо), а магнитное поле направлено наружу, в сторону от наблюдателя. Следовательно, если мы используем правую руку и направляем большой палец вправо, а указательный палец от себя, наша ладонь обращена вверх. Но поскольку это отрицательно заряженный электрон, нам нужно изменить направление силы на противоположное. Следовательно, вместо направления вверх (север) сила направлена ​​вниз (юг).

Сообщить об ошибке

На положительно заряженный объект, движущийся на запад по экватору, действует магнитная сила, направленная в небо. Каково направление преобладающего магнитного поля в этом месте?

Возможные ответы:

Юг

Запад

Север

Восток

Северо-Запад

Юг Правильный ответ:

3 Объяснение:

Используйте правило правой руки.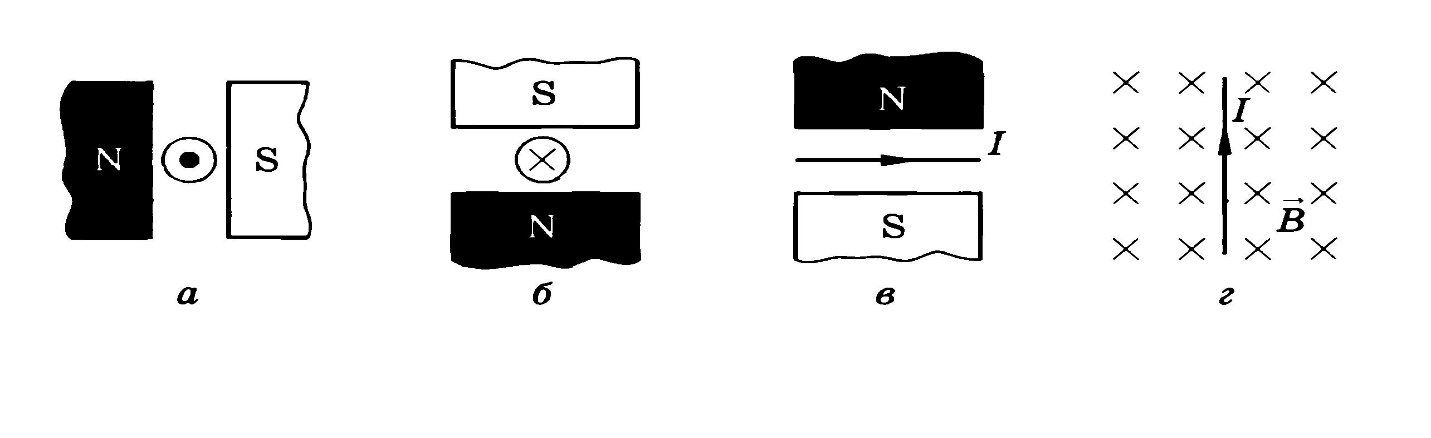 Первый вектор скорости представлен большим пальцем, указывающим на запад. Результирующий вектор, средний палец (или ладонь) направлен в небо. Указательный палец направлен на юг.

Сообщить об ошибке

В каком направлении будет действовать сила на протон, движущийся влево на месте ?

Возможные ответы:

Вниз, вниз экрана

Вправо

Влево

Вверх, вверх экрана

Ни один из этих ответов

3 4 010302 9 Правильный ответ

Вниз, к низу экрана

Пояснение:

Используя правило правой руки для магнитных полей, видно, что магнитное поле направлено на страницу в точке . Используя правило правой руки для силы, действующей на движущуюся положительно заряженную частицу, видно, что сила действует вниз.

Сообщить об ошибке

Электрон в точке движется вправо. Как будет направлена ​​магнитная сила?

Возможные ответы:

На страницу

Вне страницы

Вниз, к низу страницы

Ни один из этих

Вверх, к началу страницы Правильный ответ

4 :

2

Вниз, к нижней части страницы

Объяснение:

Согласно правилу правой руки для провода с током магнитное поле направлено на страницу.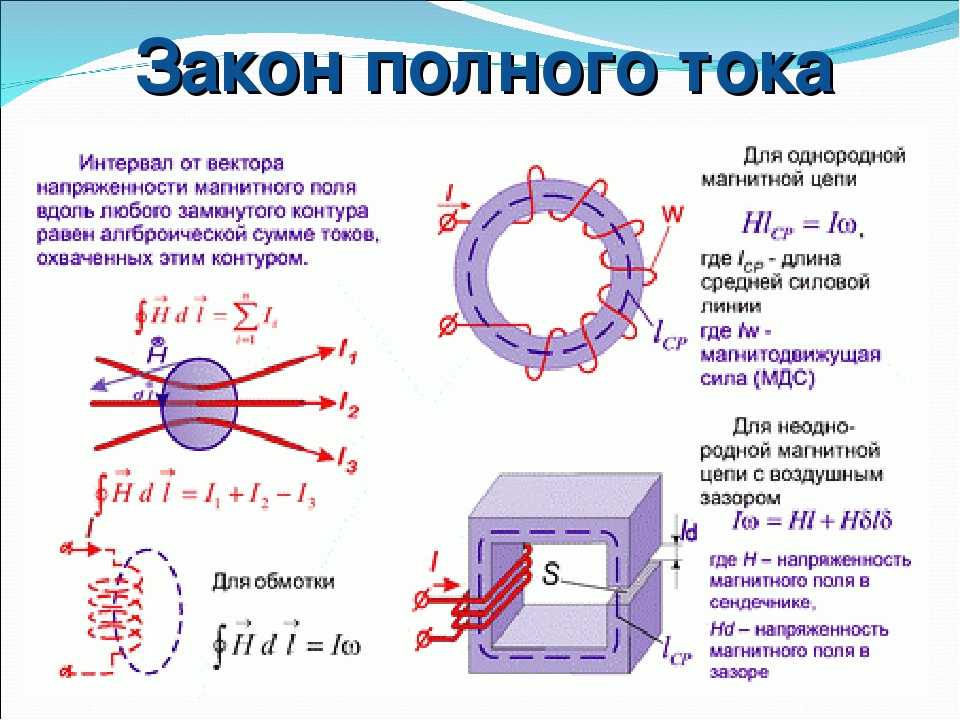 Согласно правилу правой руки для магнитной силы, сила направлена ​​вниз на отрицательно заряженный электрон.

Сообщить об ошибке

Электрон попадает на экран, в то время как другой электрон выходит из экрана. Они достаточно далеко, чтобы не столкнуться друг с другом. Будут ли магнитные силы между ними притягивающими или отталкивающими?

Возможные ответы:

Отталкивающий

Привлекательные и отталкивающие силы отменяют друг друга

Ни

Ни один из этих

Привлекательный

Правильный ответ:

Привлекательный

Объяснение:

Согласно общепринятым символам, «X» представляет электроны, входящие в страницу, а «точка» представляет электроны, выходящие из страницы. Выбор любого из электронов и использование правила правой руки для движения тока, а затем изменение направления отрицательного заряда электрона дает нам направление магнитного поля на другом электроне. Снова используя правило правой руки для перемещения зарядов в магнитном поле, а затем обращая его для отрицательного заряда электрона, мы показываем, что заряды будут испытывать магнитную силу притяжения.

Сообщить об ошибке

Предположим, что электрон ускоряется наружу, в плоскости страницы, против часовой стрелки, как показано на рисунке ниже. В каком направлении должно быть направлено магнитное поле, чтобы заставить электрон двигаться таким образом?

Возможные ответы:

Вниз

Вниз и влево

На страницу/экран

Вверх

За пределы страницы/экрана

Правильный ответ:

Вне страницы/экрана

Пояснение:

В этом вопросе нам показан путь, по которому движется электрон против часовой стрелки. Нас просят найти правильную ориентацию магнитного поля, которая заставит электрон двигаться именно так.

В этом вопросе следует отметить несколько моментов. Во-первых, мы знаем, что электрон движется по окружности. Это верно даже при том, что он ускоряется наружу. Таким образом, он должен испытывать некоторую форму центростремительной силы, чтобы оставаться на своем частично круговом пути.

Кроме того, источником этой центростремительной силы должно быть магнитное поле. Мы знаем, что в него не может вноситься гравитация, так как заряд электрона делает его гравитационную массу незначительной.

Поскольку магнитная сила является источником центростремительной силы, мы можем использовать это, чтобы определить, как должно быть ориентировано магнитное поле. Для этого воспользуемся правилом правой руки. Хотя существует несколько способов использования этого правила, мы можем использовать один из них; большой палец указывает в направлении движущегося заряда, остальные пальцы указывают в направлении магнитного поля, а ладонь обращена в направлении вектора магнитной силы. И помните, это работает только правой рукой!

Если мы используем большой палец для представления движения электрона, наши пальцы будут указывать вперед (указывая на страницу).