Десятичное число 17 в двоичной системе счисления записывается как?? А1.Десятичное число 17 в двоичной системе…
записывается как … а) 10010 б) 1001 в) 11000 г) 10001 А2.Двоичному числу 1010 в десятичной системе счисления соответствует число … а) 8 б) 9 в) 10 г) 11 А3 .Сколько байтов информации содержит слово БИТ ? а) 24 б) 8 в) 3 г) 16 А4.Файл — это: а) единица измерения количества информации б) программа в оперативной памяти в) программа или данные на диске, имеющие имя г) текст, распечатанный на принтере А5.Тип информации в файле можно определить, зная его… а) размер б) имя в) расширение г) место хранения А6.Укажите недостающее понятие: человек – записная книжка, компьютер — … а) клавиатура б) жесткий диск в) видеокарта г) процессор А7.Визуальной называют информацию, воспринимаемую органами… а) слуха б) зрения в) обоняния г) осязания А8.В какой из последовательностей единицы измерения указаны в порядке убывания а) гигабайт, байт, килобайт, мегабайт б) гигабайт, мегабайт, килобайт, байт в) гигабайт, килобайт, мегабайт, байт г) байт, килобайт, мегабайт, гигабайт 3 А9. Мысленное разделение объекта на составные части или выделение при-знаков объекта – это а) анализ б) синтез в) сравнение г) обобщение А10.Выберите единичное понятие а) водитель б) озеро в) Антарктида г) дом А11.К какому типу суждений относится следующее суждение: «Ни один ко-мар не является слоном» а) общеутвердительное б) общеотрицательное в) частноутвердительное г) частноотрицательное А12. Дополните суждение подходящей логической связкой «Чтобы утолить жажду, … выпить стакан воды» а) необходимо б) достаточно в) необходимо и достаточно А13.В каком отношении между собой находятся следующие два понятия — «книга» и «учебник математики» а) тождество б) пересечение в) подчинение г) противоположность А14.Что можно считать алгоритмом? а) прогноз погоды б) домашнее задание в дневнике в) инструкция по сборке шифоньера г) расписание движения автобусов А15. Алгоритм, в котором некоторая группа команд выполняется много-кратно, пока соблюдается некоторое заранее установленное условие, назы-вается … а) линейным б) циклическим в) ветвлением 4 А16.
Мысленное разделение объекта на составные части или выделение при-знаков объекта – это а) анализ б) синтез в) сравнение г) обобщение А10.Выберите единичное понятие а) водитель б) озеро в) Антарктида г) дом А11.К какому типу суждений относится следующее суждение: «Ни один ко-мар не является слоном» а) общеутвердительное б) общеотрицательное в) частноутвердительное г) частноотрицательное А12. Дополните суждение подходящей логической связкой «Чтобы утолить жажду, … выпить стакан воды» а) необходимо б) достаточно в) необходимо и достаточно А13.В каком отношении между собой находятся следующие два понятия — «книга» и «учебник математики» а) тождество б) пересечение в) подчинение г) противоположность А14.Что можно считать алгоритмом? а) прогноз погоды б) домашнее задание в дневнике в) инструкция по сборке шифоньера г) расписание движения автобусов А15. Алгоритм, в котором некоторая группа команд выполняется много-кратно, пока соблюдается некоторое заранее установленное условие, назы-вается … а) линейным б) циклическим в) ветвлением 4 А16.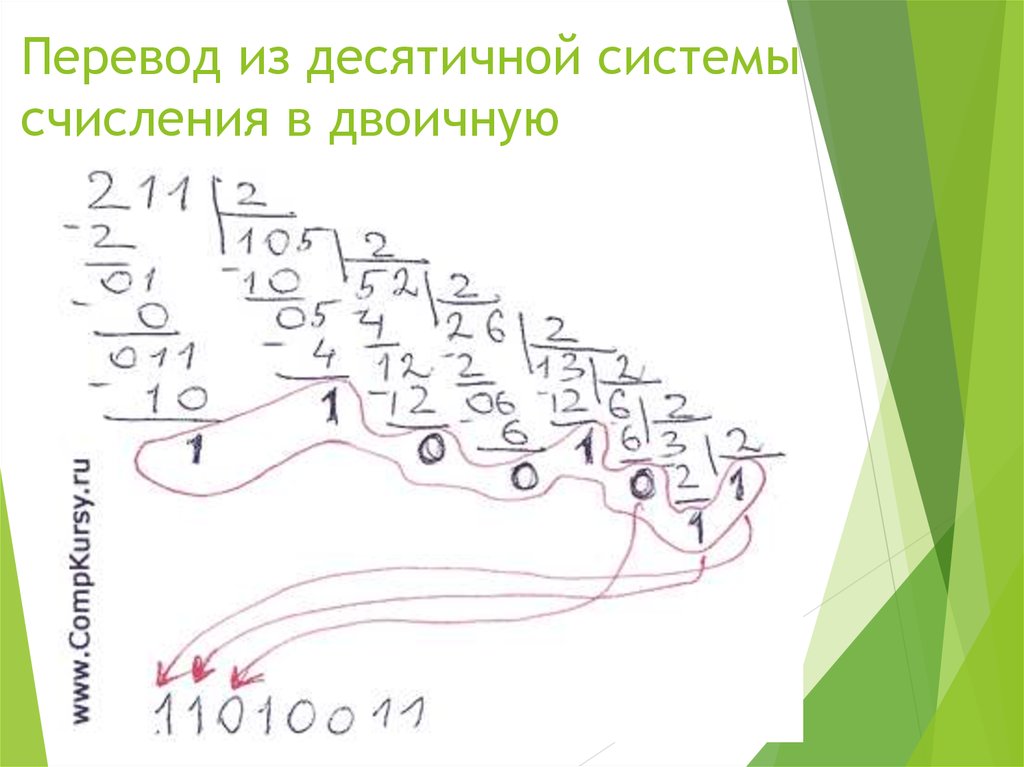 Геометрическая фигура используется в блок-схемах для обозначения … а) начала или конца алгоритма б) принятия решения в) ввода или вывода г) выполнения действия А17.Считая, что каждый символ кодируется одним байтом, определите ин-формационный объём следующего текста: В 1642 году Б.Паскаль создал первую механическую счетную машину. а) 64 бита б) 512 бит в) 54 байта г) 512 байт А18.Расширения txt, rtf, doc имеют: а) исполняемые файлы б) графические файлы в) текстовые файлы г) звуковые файлы А19. Что такое байт, килобайт, мегабайт и гигабайт? а) единицы измерения времени б) единицы измерения информации в) единицы измерения массы г) единицы измерения длины А20.Представление информации с помощью последовательности нулей и единиц называется а) компьютерным кодированием б) двоичным кодированием в) шифрованием информации А21.Среди следующих словосочетаний отметьте все понятия: а) Двоичные коды б) Всего существует 256 различных цепочек из 8 нулей и единиц. в) Графический файл г) Текстовый документ д) В вычислительной технике применяется двоичная система счисления е) Система счисления ж) Файл — это информация, хранящаяся во внешней памяти как единое целое и обозначенная именем А22.
Геометрическая фигура используется в блок-схемах для обозначения … а) начала или конца алгоритма б) принятия решения в) ввода или вывода г) выполнения действия А17.Считая, что каждый символ кодируется одним байтом, определите ин-формационный объём следующего текста: В 1642 году Б.Паскаль создал первую механическую счетную машину. а) 64 бита б) 512 бит в) 54 байта г) 512 байт А18.Расширения txt, rtf, doc имеют: а) исполняемые файлы б) графические файлы в) текстовые файлы г) звуковые файлы А19. Что такое байт, килобайт, мегабайт и гигабайт? а) единицы измерения времени б) единицы измерения информации в) единицы измерения массы г) единицы измерения длины А20.Представление информации с помощью последовательности нулей и единиц называется а) компьютерным кодированием б) двоичным кодированием в) шифрованием информации А21.Среди следующих словосочетаний отметьте все понятия: а) Двоичные коды б) Всего существует 256 различных цепочек из 8 нулей и единиц. в) Графический файл г) Текстовый документ д) В вычислительной технике применяется двоичная система счисления е) Система счисления ж) Файл — это информация, хранящаяся во внешней памяти как единое целое и обозначенная именем А22. Отметьте логические приёмы формирования понятий: а) анализ б) обобщение в) понятие г) суждение д) умозаключение е) синтез 5 А23.Алгоритм, в котором команды выполняются в порядке их записи, то есть последовательно друг за другом, называется а) линейным б) циклическим в) ветвлением А24.Команды, которые может выполнять конкретный исполнитель, образу-ют а) систему знаний исполнителя б) систему знаков исполнителя в) систему видов исполнителя г) систему команд исполнителя А25.Отметьте формы мышления: а) умозаключение б) синтез в) анализ г) понятие д) обобщение е) суждение А26.Укажите кнопку формирования маркированного списка в текстовом редакторе.
Отметьте логические приёмы формирования понятий: а) анализ б) обобщение в) понятие г) суждение д) умозаключение е) синтез 5 А23.Алгоритм, в котором команды выполняются в порядке их записи, то есть последовательно друг за другом, называется а) линейным б) циклическим в) ветвлением А24.Команды, которые может выполнять конкретный исполнитель, образу-ют а) систему знаний исполнителя б) систему знаков исполнителя в) систему видов исполнителя г) систему команд исполнителя А25.Отметьте формы мышления: а) умозаключение б) синтез в) анализ г) понятие д) обобщение е) суждение А26.Укажите кнопку формирования маркированного списка в текстовом редакторе.
Знаешь ответ?
Как написать хороший ответ?Как написать хороший ответ?
Будьте внимательны!
- Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. 🙂
- Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
0 /10000
Задача №1.
 Перевод из одной системы в другую, сравнение чисел в различных системах.
Перевод из одной системы в другую, сравнение чисел в различных системах. Автор материалов — Лада Борисовна Есакова.
Системы счисления и их разновидности.
Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.
Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.
1. Непозиционные системы счисления.
В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.
Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.
Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.
Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:
Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число
Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.
2. Позиционные системы счисления.
В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.
Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.
Разница обусловлена положением цифры в числе.
Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).
Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.
Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».
2.1. Однородные системы счисления.
В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.
Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.
2.2. Смешанные системы счисления.
В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2.
Переведем десятичное число 672 в восьмеричную систему счисления.Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т. е.
е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Десятичные дроби и смешанные числа в разных системах счисления.
Автор — Лада Борисовна Есакова.
Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.
1. Перевод смешанного числа в десятичную систему счисления из любой другой.
Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Пример 1.
Переведите число 105,4 из восьмеричной системы в десятичную.
Решение:
Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :
Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:
Ответ:
2. Перевод десятичных дробей из десятичной системы счисления в любую другую.
Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.
Пример 2
Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.
Решение:
Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:
Ответ:
Пример 3.
Переведите десятичное число 0,8125 в восьмеричную систему.
Решение:
Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:
Ответ:
3. Перевод смешанных чисел из десятичной системы счисления в любую другую
Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.
Пример 4.
Сколько единиц в двоичной записи десятичного числа 14,125?
Решение:
Переведем целую часть числа в двоичную систему:
Переведем дробную часть числа в двоичную систему:
Соединим целую и дробную части:
14,12510 = 1110,0012
Количество единиц равно 4.
Ответ: 4
17 в двоичном формате — Как преобразовать 17 из десятичного в двоичный?
17 в двоичном формате равно 10001. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты). Мы использовали 5 бит для представления 17 в двоичном виде. В этой статье давайте узнаем, как преобразовать десятичное число 17 в двоичное.
В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты). Мы использовали 5 бит для представления 17 в двоичном виде. В этой статье давайте узнаем, как преобразовать десятичное число 17 в двоичное.
Как преобразовать 17 в двоичный код?
Шаг 1: Разделите 17 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0,9.0005
| Дивиденд | Остаток |
|---|---|
| 17/2 = 8 | 1 |
| 8/2 = 4 | 0 |
| 4/2 = 2 | 0 |
| 2/2 = 1 | 0 |
| 1/2 = 0 | 1 |
Шаг 2: Запишите остаток снизу вверх, т.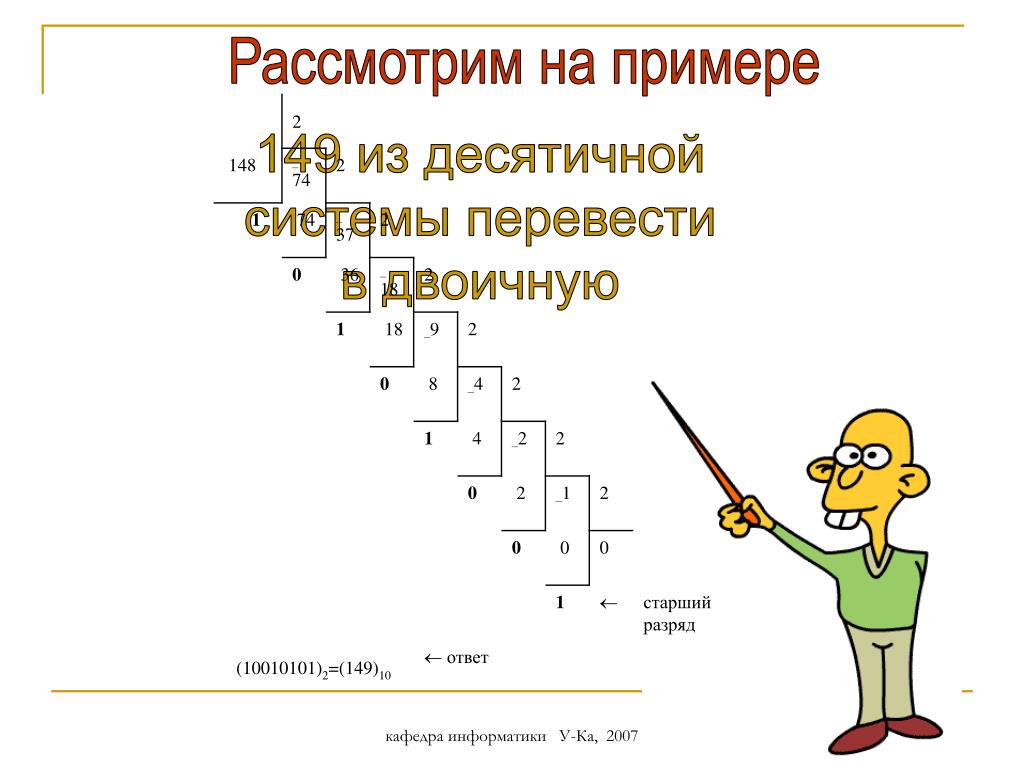 е. в обратном хронологическом порядке. Это даст двоичный эквивалент 17,9.0005
е. в обратном хронологическом порядке. Это даст двоичный эквивалент 17,9.0005
Таким образом, двоичный эквивалент десятичного числа 17 равен 10001.
☛ Калькулятор десятичной записи в двоичную
Давайте посмотрим на значение десятичного числа 17 в различных системах счисления.
- 17 в двоичном виде: 17₁₀ = 10001₂
- 17 в восьмеричной системе: 17₁₀ = 21₈
- 17 в шестнадцатеричном формате: 17₁₀ = 11₁₆
- 10001₂ в десятичном формате: 17₁₀
Описание проблемы:
Часто задаваемые вопросы о 17 в двоичном формате
Что такое 17 в двоичном формате?
17 в двоичном формате равно 10001. Чтобы найти десятичный эквивалент в двоичном, разделите 17 последовательно на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.
☛ Двоичное преобразование в десятичное
Найдите значение 1 × 17 в двоичной форме.

Мы знаем, что 17 в двоичном формате равно 10001, а 1 равно 1. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0, 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 10001 × 1 = 10001, что равно 17 в десятичной системе счисления. [17 × 1 = 17]
Сколько бит имеет 17 в двоичном формате?
Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 17 в двоичном формате, т. е. 10001. Таким образом, мы использовали 5 бит для представления 17 в двоичном формате.
Как преобразовать 17 в двоичный эквивалент?
Мы можем разделить 17 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге.
- 17 mod 2 = 1 — LSB (младший значащий бит)
- 8 мод 2 = 0
- 4 мод 2 = 0
- 2 мод 2 = 0
- 1 mod 2 = 1 — MSB (старший бит)
Записать остатки от MSB до LSB. Таким образом, десятичное число 17 в двоичном виде можно представить как 10001.
Что такое двоичный эквивалент 17 + 79?
17 в двоичной системе счисления равно 10001, а 79 равно 1001111. Мы можем сложить двоичный эквивалент 17 и 79, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (10001)₂ + (1001111)₂ = (1100000)₂, что равно 9.6.
☛ Двоично-десятичный калькулятор
☛ Также проверьте:
- 252 в двоичном формате — 11111100
- 41 в двоичном формате — 101001
- 1 в двоичном формате — 1
- 24 в двоичном формате — 11000
- 63 в двоичном формате — 111111
- 31 в двоичном формате — 11111
- 157 в двоичном формате — 10011101
Рабочие листы по математике и визуальный учебный план
Преобразование десятичного числа 17 в двоичное
Как записать 17 в двоичном формате (с основанием 2)?
17 равно 10001 в двоичной форме
|
||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответы на такие вопросы, как: Преобразование десятичного числа 17 в двоичное или Преобразование десятичного числа в двоичное.
Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответы на такие вопросы, как: Преобразование десятичного числа 17 в двоичное или Преобразование десятичного числа в двоичное.
| Декабрь | Шестнадцатеричный | Октябрь | Бин | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 29 6 00021 | ||||||||||||||||||||||
| 1 | 1 | 1 | 1 | |||||||||||||||||||||
| 2 | 2 | 2 | 10 | |||||||||||||||||||||
| 3 | 3 | 3 | 11 | |||||||||||||||||||||
| 4 | 4 | 4 | 100 | |||||||||||||||||||||
| 5 | 5 | 5 | 101 | |||||||||||||||||||||
| 110026 | 6 | 6 | 110026 | 6 | 6 | 110026 | 6 | 110026 | 6 | 110026 | 6 | 110026 | 6 | 110026 | 6 | .0026 | 111 | |||||||
| 8 | 8 | 10 | 1000 | |||||||||||||||||||||
| 9 | 9 | 11 | 1001 | |||||||||||||||||||||
| 10 | A | 12 | 1010 | |||||||||||||||||||||
| 11 | B | 13 | 1011 | |||||||||||||||||||||
| 12 | C | 14 | 1100 | |||||||||||||||||||||
| 13 | D | 15 | 1101 | |||||||||||||||||||||
| 14 | E | 16 | 1110 | |||||||||||||||||||||
| 15 | F | 17 | 1111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 22 | 10010 |
| 19 | 13 | 23 | 10011 |
| 20 | 14 | 24 | 10100 |
| 21 | 15 | 25 | 10101 |
| 22 | 16 | 26 | 10110 |
| 23 | 17 | 27 | 10111 |
| 24 | 18 | 30 | 11000 |
| 25 | 19 | 31 | 11001 |
| 26 | 1A | 32 | 11010 |
| 27 | 1B | 33 | 11011 |
| 28 | 1C | 34 | 11100 |
| 29 | 1D | 35 | 11101 |
| 30 | 1E | 36 | 11110 |
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | |
| 33 | 21 | 41 | 100001 | |
| 34 | 22 | 42 | 100010 | |
| 35 | 23 | 43 | 100011 | |
| 36 | 24 | 44 | 100100 | |
| 37 | 25 | 45 | 100101 | |
| 38 | 26 | 46 | 100110 | |
| 39 | 27 | 47 | 100111 | |
| 40 | 28 | 50 | 101000 | |
| 41 | 29 | 51 | 101001 | |
| 42 | 2A | 52 | 101010 | |
| 43 | 2B | 53 | 101011 | |
| 44 | 2C | 54 | 101100 | |
| 45 | 2D | 55 | 101101 | |
| 46 | 2E | 56 | 101110 | |
| 47 | 2F | 57 | 1011111126 | 99 | 2999999999999999999999999999999999999999999999теля 999999999999999999999999999999999999999999999999999999999999999999999н0018Hex | Oct | Bin |
| 48 | 30 | 60 | 110000 | |
| 49 | 31 | 61 | 110001 | |
| 50 | 32 | 62 | 110010 | |
| 51 | 33 | . 0026 0026 | 65 | 110101 |
| 54 | 36 | 66 | 110110 | |
| 55 | 37 | 67 | 110111 | |
| 56 | 38 | 70 | 111000 | |
| 57 | 39 | 71 | 111001 | |
| 58 | 3A | 72 | 111010 | |
| 59 | 3B | 73 | 111011 | |
| 60 | 3C | 74 | 111100 | |
| 61 | 3D | 75 | 111101 | |
| 62 | 3E | 76 | 111110 | |
| 63 | 3F | 77 | 111111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 64 | 40 | 100 | 1000000 |
| 65 | 41 | 101 | 1000001 |
| 66 | 42 | 102 | 1000010 |
| 67 | 43 | 103 | 1000011 |
| 68 | 44 | 104 | 1000100 |
| 69 | 45 | 105 | 1000101 |
| 70 | 46 | 106 | 1000110 |
| 71 | 47 | 107 | 1000111 |
| 72 | 48 | 110 | 1001000 |
| 73 | 49 | 111 | 1001001 |
| 74 | 4A | 1001010 | |
| 75 | 4B | 113 | |
| 9 | 99 | 9 | .114 | 1001100 |
| 77 | 4D | 115 | 1001101 |
| 78 | 4E | 116 | 1001110 |
| 79 | 4F | 117 | 1001111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 80 | 50 | 120 | 1010000 |
| 81 | 51 | 121 | 1010001 |
| 82 | 52 | 122 | 1010010 |
| 83 | 53 | 123 | 1010011 |
| 84 | 54 | 124 | 1010100 |
| 85 | 55 | 125 | 1010101 |
| 86 | 56 | 126 | 1010110 |
| 87 | 57 | 127 | 1010111 |
| 88 | 58 | 130 | 1011000 |
| 89 | 59 | 131 | 1011001 |
| 90 | 5A | 132 | 1011010 |
| 91 | 5B | 133 | 1011011 |
| 92 | 5C | 134 | 1011100 |
| 93 | 5D | 135 | 1011101 |
| 94 | 5E | 136 | 1011110 |
| 95 | 5F | 137 | 1011111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 96 | 60 | 140 | 1100000 |
| 97 | 61 | 141 | 1100001 |
| 98 | 62 | 142 | 1100010 |
| 99 | 63 | 143 | 1100011 |
| 100 | 64 | 144 | 1100100 |
| 101 | 65 | 145 | 1100101 |
| 102 | . 0026 0026 | ||
| 104 | 68 | 150 | 1101000 |
| 105 | 69 | 151 | 1101001 |
| 106 | 6A | 152 | 1101010 |
| 107 | 6B | 153 | 1101011 |
| 108 | .0026 | ||
| 110 | 6E | 156 | 1101110 |
| 111 | 6F | 157 | 1101111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 112 | 70 | 160 | 1110000 |
| 113 | 71 | 161 | 1110001 |
| 114 | 72 | 162 | 1110010 |
| 115 | 73 | 163 | 1110011 |
| 116 | 74 | 164 | 1110100 |
| 117 | 75 | 165 | 1110101 |
| 118 | 76 | 166 | 1110110 |
| 119 | 77 | 167 | 1110111 |
| 120 | 78 | 170 | 1111000 |
| 121 | 79 | 171 | 1111001 |
| 122 | 7A | 172 | 1111010 |
| 123 | 7B | 173 | 1111011 |
| 124 | 7C | 174 | 1111100 |
| 125 | 7D | 175 | 1111101 |
| 126 | 7E | 176 | 1111110 |
| 127 | 7F | 177 | 1111111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 128 | 80 | 200 | 10000000 |
| 129 | 81 | 201 | 10000001 |
| 130 | 82 | 202 | 10000010 |
| 131 | 83 | 203 | 10000011 |
| 132 | 84 | 204 | 10000100 |
| 133 | 85 | 205 | 10000101 |
| 134 | 86 | 206 | 10000110 |
| 135 | 87 | 207 | 10000111 |
| 136 | 88 | 210 | 10001000 |
| 137 | 89 | 211 | 10001001 |
| 138 | 8A | 212 | 10001010 |
| 139 | 8B | 213 | 10001011 |
| 140 | 8C | 214 | 10001100 |
| 141 | 8D | 215 | 10001101 |
| 142 | 8E | 216 | 10001110 |
| 143 | 8F | 217 | 10001111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 144 | 90 | 220 | 10010000 |
| 145 | 91 | 221 | 10010001 |
| 146 | 92 | 222 | 10010010 |
| 147 | 93 | 223 | 10010011 |
| 148 | 94 | 224 | 10010100 |
| 149 | 95 | 225 | 10010101 |
| 150 | 96 | 226 | 10010110 |
| 151 | 97 | 227 | 10010111 |
| 152 | 98 | 230 | 10011000 |
| 153 | 99 | 231 | 10011001 |
| 154 | 9A | 232 | 10011010 |
| 155 | 9B | 233 | 10011011 |
| 156 | 9C | 234 | 10011100 |
| 157 | 9D | 235 | 10011101 |
| 158 | 9E | 236 | 10011110 |
| 159 | 9F | 237 | 10011111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 160 | A0 | 240 | 10100000 |
| 161 | A1 | 241 | 10100001 |
| 162 | A2 | 242 | 10100010 |
| 163 | A3 | 243 | 10100011 |
| 164 | A4 | 244 | 10100100 |
| 165 | A5 | 245 | 10100101 |
| 166 | A6 | 246 | 10100110 |
| 167 | A7 | 247 | 10100111 |
| 168 | A8 | 250 | 10101000 |
| 169 | A9 | 251 | 10101001 |
| 170 | AA | 252 | 10101010 |
| 171 | AB | 253 | 10101011 |
| 172 | AC | 254 | 10101100 |
| 173 | AD | 255 | 10101101 |
| 174 | AE | 256 | 10101110 |
| 175 | AF | 257 | 10101111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 176 | B0 | 260 | 10110000 |
| 177 | B1 | 261 | 10110001 |
| 178 | B2 | 262 | 10110010 |
| 179 | B3 | 263 | 10110011 |
| 180 | B4 | 264 | 10110100 |
| 181 | B5 | 265 | 10110101 |
| 182 | B6 | 266 | 10110110 |
| 183 | B7 | 267 | 10110111 |
| 184 | B8 | 270 | 10111000 |
| 185 | B9 | 271 | 10111001 |
| 186 | BA | 272 | 10111010 |
| 187 | BB | 273 | 10111011 |
| 188 | BC | 274 | 10111100 |
| 189 | BD | 275 | 10111101 |
| 190 | BE | 276 | 10111110 |
| BF | 7777769 | ||
. 0026 0026 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 192 | C0 | 300 | 11000000 |
| 193 | C1 | 301 | 11000001 |
| 194 | C2 | 302 | 11000010 |
| 195 | C3 | 303 | 11000011 |
| 196 | C4 | 304 | 11000100 |
| 197 | C5 | 305 | 11000101 |
| 198 | C6 | 306 | 11000110 |
| 199 | C7 | 307 | 11000111 |
| 200 | C8 | 310 | 11001000 |
| 201 | C9 | 311 | 11001001 |
| 202 | CA | 312 | 11001010 |
| 203 | CB | 313 | 11001011 |
| 204 | CC | 314 | 11001100 |
| 205 | CD | 315 | 11001101 |
| 206 | CE | 316 | 11001110 |
| 207 | CF | 317 | 11001111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 208 | D0 | 320 | 11010000 |
| 209 | D1 | 321 | 11010001 |
| 210 | D2 | 322 | 11010010 |
| 211 | D3 | 323 | 11010011 |
| 212 | D4 | 324 | 11010100 |
| 213 | D5 | 325 | 11010101 |
| 214 | D6 | 326 | 11010110 |
| 215 | D7 | 327 | 11010111 |
| 216 | D8 | 330 | 11011000 |
| 217 | D9 | 331 | 11011001 |
| 218 | DA | 332 | 11011010 |
| 219 | DB | 333 | 11011011 |
| 220 | DC | 334 | 11011100 |
| 221 | DD | 335 | 11011101 |
| 222 | DE | 336 | 11011110 |
| 223 | DF | 337 | 11011119 |
9999999 2
99999999999999999
 0018
0018
| Bin | |||
|---|---|---|---|
| 240 | F0 | 360 | 11110000 |
| 241 | F1 | 361 | 11110001 |
| 242 | F2 | 362 | 11110010 |
| 243 | F3 | 363 | 11110011 |
| 244 | F4 | 364 | 11110100 |
| 245 | F5 | 365 | 11110101 |
| 246 | F6 | 366 | 11110110 |
| 247 | F7 | 367 | 11110111 |
| 248 | F8 | 370 | 11111000 |
| 249 | F9 | 371 | 11111001 |
| 250 | FA | 372 | 11111010 |
| 251 | FB | 373 | 11111011 |
| 252 | FC | 374 | 11111100 |
| 253 | FD | 375 | 11111101 |
| 254 | FE | 376 | 11111110 |
| 255 | FF | 377 | 11111111 |


 0026
0026 