1С целочисленное деление. Целочисленное деление в 1С 8: эффективные методы и приемы

Как выполнить целочисленное деление в 1С 8. Какие встроенные функции можно использовать. Как получить целую часть от деления чисел. Какие особенности нужно учитывать при целочисленном делении в 1С.

Встроенные функции для целочисленного деления в 1С 8

В платформе 1С:Предприятие 8 предусмотрено несколько встроенных функций для выполнения целочисленного деления:

• Цел() — возвращает целую часть числа, отбрасывая дробную
• Окр() — округляет число до указанного количества знаков после запятой
• Int() — возвращает целую часть числа (аналог Цел)

Рассмотрим, как можно использовать эти функции для целочисленного деления.

Функция Цел()

Функция Цел() отбрасывает дробную часть числа и возвращает целую часть. Ее можно использовать следующим образом:

Результат = Цел(10 / 3); // вернет 3

В этом случае результатом деления 10 на 3 будет 3.3333…, а функция Цел() вернет целую часть — число 3.

Функция Окр()

Функция Окр() позволяет округлить число до нужного количества знаков после запятой. Для целочисленного деления можно использовать округление до 0 знаков:

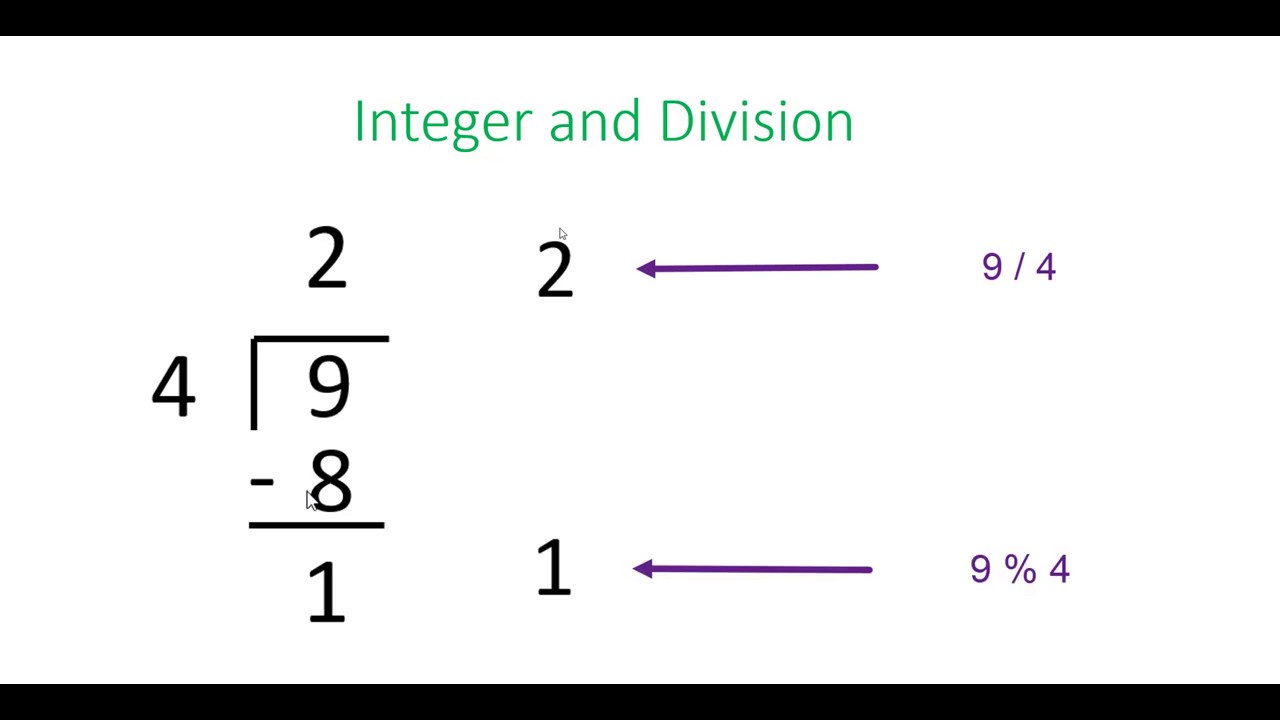
Результат = Окр(10 / 3, 0); // вернет 3

Здесь результат деления 10 на 3 будет округлен до целого числа 3.

Функция Int()

Функция Int() является аналогом Цел() и также возвращает целую часть числа:

Результат = Int(10 / 3); // вернет 3

Результатом будет целое число 3, полученное отбрасыванием дробной части.

Особенности целочисленного деления отрицательных чисел

При целочисленном делении отрицательных чисел в 1С нужно учитывать некоторые особенности:

• Функции Цел() и Int() округляют в сторону нуля
• Функция Окр() округляет по математическим правилам

Например:

Результат1 = Цел(-10 / 3);  // вернет -3
Результат2 = Окр(-10 / 3, 0); // вернет -3
Результат3 = Int(-10 / 3);   // вернет -3

Результат4 = Цел(-11 / 3);  // вернет -3 
Результат5 = Окр(-11 / 3, 0); // вернет -4
Результат6 = Int(-11 / 3);   // вернет -3
 

Как видим, функции Цел() и Int() всегда округляют в сторону нуля, а Окр() может округлить и в меньшую сторону.

Получение остатка от целочисленного деления

Для получения остатка от целочисленного деления в 1С можно использовать оператор %:

Остаток = 10 % 3; // вернет 1

Здесь 10 делится на 3 с остатком 1.

Также можно использовать функцию Mod():

Остаток = Mod(10, 3); // вернет 1

Функция Mod() возвращает остаток от деления первого аргумента на второй.

Проверка делимости чисел нацело

Чтобы проверить, делится ли одно число на другое нацело, можно использовать оператор % или функцию Mod():

Если 10 % 2 = 0 Тогда
  // 10 делится на 2 нацело
КонецЕсли;

Если Mod(10, 3) = 0 Тогда 
  // 10 делится на 3 нацело
КонецЕсли; 

Если остаток равен 0, значит число делится нацело.

Оптимизация целочисленного деления в циклах

При выполнении целочисленного деления в циклах можно применить некоторые оптимизации:

• Вынести вычисление делителя за пределы цикла, если это возможно
• Использовать битовые операции вместо деления, если делитель является степенью двойки
• Заменить деление умножением на обратное число, если делитель известен заранее

Например, вместо:

Для i = 1 По 1000 Цикл
  Результат = Цел(i / 16);
КонецЦикла;

Можно использовать битовый сдвиг:

Для i = 1 По 1000 Цикл
  Результат = i >> 4; // эквивалентно делению на 16
КонецЦикла;

Это позволит ускорить выполнение цикла.

Целочисленное деление в запросах 1С

В запросах 1С для целочисленного деления можно использовать функцию ЦЕЛОЕ():

ВЫБРАТЬ
  ЦЕЛОЕ(Сумма / 100) КАК ЦелаяЧасть
ИЗ
  Документ.РасходнаяНакладная
 

Функция ЦЕЛОЕ() вернет целую часть от деления Суммы на 100.

Также в запросах можно использовать оператор // для целочисленного деления:

ВЫБРАТЬ
  Сумма // 100 КАК ЦелаяЧасть 
ИЗ
  Документ.РасходнаяНакладная

Оператор // выполнит целочисленное деление Суммы на 100.

Особенности целочисленного деления на ноль

При делении на ноль в 1С возникает ошибка выполнения. Чтобы избежать этого, нужно предусмотреть соответствующую проверку:

Если Знаменатель <> 0 Тогда
  Результат = Цел(Числитель / Знаменатель);
Иначе
  // Обработка деления на ноль
  Результат = 0; // или другое значение по умолчанию
КонецЕсли;

Такая проверка позволит корректно обработать ситуацию деления на ноль.

Применение целочисленного деления в бухгалтерском учете

Целочисленное деление часто применяется в бухгалтерском учете, например, при расчете НДС или округлении сумм. Рассмотрим несколько примеров:

Расчет НДС

СуммаБезНДС = 1000;
СтавкаНДС = 20;

СуммаНДС = Окр(СуммаБезНДС * СтавкаНДС / 100, 2);
ИтоговаяСумма = СуммаБезНДС + СуммаНДС;

Здесь мы округляем сумму НДС до 2 знаков после запятой.

Округление сумм

СуммаКОплате = 2345.67;
ОкругленнаяСумма = Окр(СуммаКОплате, 0);

Разница = СуммаКОплате - ОкругленнаяСумма;

В этом примере мы округляем сумму до целых рублей и вычисляем разницу для учета копеек.

Использование целочисленного деления при работе с датами

Целочисленное деление может быть полезно при работе с датами в 1С. Например, для определения квартала по номеру месяца:

НомерМесяца = Месяц(ТекущаяДата());
Квартал = Цел((НомерМесяца - 1) / 3) + 1;

Здесь мы используем целочисленное деление для определения номера квартала по номеру месяца.

Другой пример — расчет количества полных недель между датами:

ДатаНачала = '20230101';
ДатаОкончания = '20230331';

КолвоДней = ДатаОкончания - ДатаНачала;
ПолныхНедель = Цел(КолвоДней / 7);

В этом случае целочисленное деление позволяет определить количество полных недель в заданном периоде.

Похожие видео ролики → Python: Уроки Python #4 | Целочисленное деление и остаток от деления

Навигатор по видео

• Технологии цифровизации
  • Искусственный интеллект ¹⁰³
  • Бизнес-анализ, BPM, BI, CPM, ⁴³⁷
  • Большие данные — Big Data ⁷⁶
  • CRM, SRM, клиенты, маркетинг ⁶⁹⁸
  • Управление предприятием, ERP, MES ⁴⁵⁵
  • Логистика, склад, WMS, TMS ⁶⁹⁵
  • Управление производством ³³³
  • Ремонты, ТОиР, ТО, EAM ⁵³⁰
  • Управление проектами ¹⁹¹
  • Проектирование и моделирование, САПР, CAD/CAM/CAE, 3D ⁶³⁸
  • Моделирование, цифровой двойник, BIM ⁵²⁵
  • Управление жизненным циклом продукции, PLM ²⁹⁷
  • Управление технологическим процессом, АСУ ТП, SCADA ¹²²²
  • Документоборот, СЭД, ECM ⁷⁵¹
  • Торговля, кассы, маркировка, retail ⁴³⁵
  • Финансы и бухгалтерия, FIN ⁸²²
  • Управление персоналом, HRM, НСM ¹⁰³
  • ITSM, ITIL, CobiT, Service Desk ²²¹
  • Роботизация RPA ²³¹
  • Контакт-центр, колл-центр, Call center ⁷⁶
  • Интернет вещей, встраиваемые системы, умный город, IoT ¹⁹²
  • Сервера и сети ³⁷²
  • Системы хранения данных ⁵²
  • ЦОД, центр обработки данных ²²⁰
  • Интернет, Порталы, CMS ²⁴²
  • Cloud-сервисы, облака ⁵¹⁷
  • Безопасность ¹⁷⁹⁹
    • Предотвращение утечки данных, DLP ²¹⁸
    • Антивирусное ПО ²⁹⁸
  • Мобильные технологии, Приложения ²¹²
  • Коммуникации, голосовые технологии, мессенджеры, боты ²¹⁰
  • Видеонаблюдение, видеоаналитика, видеоконференцсвязь ⁵⁸
  • Геоинформационные системы ⁷⁹⁸
  • Навигация и мониторинг ¹¹⁵
  • Робототехника ³⁸
  • Презентации и новинки ⁴²⁴
  • ИТ-аутсорсинг ⁴
  • Советы ²⁰
• Цифровизация по отраслям
  • Банки, финансы ¹⁴⁵
  • Строительство ¹¹⁶
  • Жилищное хозяйство ²⁹
  • Ресторан, общепит ⁵⁹
  • Телекоммуникации и связь ³²
  • Гостиницы, отели, салоны ³⁸
  • Здравоохранение и медицина ⁷⁴
  • СМИ ¹
  • Библиотеки ⁹
  • Сельское хозяйство, АПК ⁷¹
  • Транспорт ²¹
  • Электронная/онлайн школа ⁷
• Разработка ПО и приложений
  • DevOps, Software Testing & QA ⁹⁶⁰
  • Разработка на Java ⁹²²
  • Разработка на Python ⁴¹⁰
  • Разработка 1С ⁹²⁵
  • Разработка на PHP ⁷⁶⁰
  • Разработка на C# ⁸⁷⁰
  • Разработка IoT ⁴⁰⁸
  • Разработка на C / C++ ²⁰
  • Database, СУБД ³⁷
  • Веб-дизайн ¹⁰²
  • Разработка на Go ⁹⁷
• События и мероприятия
  • Интервью ⁵⁸⁷
  • Подкасты ³⁹
  • Вебинары ¹⁸¹²
  • Отзывы ¹¹⁴
  • Хакатоны ³⁷⁷
  • Конкурсы ²²
    • ЯБ2018 ⁸²
• Карьера и образование
  • Карьера ¹⁸⁵
  • Образование ²¹⁵
  • Курсы, онлайн-курсы ¹⁵¹
• Цифровая экономика
  • Цифровизация ²⁴⁸⁵
  • Цифровизация: другой взгляд ³⁶
• Разное
  • Мир вокруг ⁴⁰
  • Обзоры ¹³
  • Game Zone ¹⁶
  • Юмор ¹¹
  • ИТ-вкусно готовить ⁹
• ITBION. RU
  • Биоинформационные технологии и медицина ⁶⁴
  • Кластеры, технопарки ¹²¹
  • Стартапы ⁵⁶

Pine Script. Оператор модуля в TradingView — Прочее

Помимо арифметических операторов в Pine Script есть еще один оператор для выполнения вычислений: оператор модуля (%). Что делает этот оператор и как мы можем его использовать?

Когда мы выполняем целочисленное деление в Pine Script, любой дробный остаток теряется. Об этом мы говорили в предыдущей статье.

Но иногда нам нужно узнать именно остаток от целочисленного деления, а не отбрасывать его. Для этого мы используем оператор модуля (%). Этот оператор выполняет действие на двумя операндами и возвращает остаток от целочисленного деления. В других языках программирования его называют оператором остатка.

Например, 5 % 3 возвращает 2 (5/3 = 1 с остатком 2), а 25 % 3 дает 1 (25/3 = 8, остаток 1).   При помощи оператора модуля можно найти сколько раз одно число содержится в другом (например 3, один раз содержится в 5, и 8 раз в 25).

Простой пример использования оператора модуля

//@version=5 indicator(title=»modul», overlay=false) plot(series=bar_index % 5)

//@version=5 indicator(title=»modul», overlay=false)   plot(series=bar_index % 5)

bar_index — номер текущего бара.

Функция plot выводит остаток от деления номера бара на 5:

Как видите, наш график колеблется между 0 и 4. Каждый 5-й бар выражение (bar_index % 5) возвращает 0.

Как найти каждый N-ый бар при помощи оператора модуля

//@version=5 indicator(title=»modul», overlay=true) Colour = (bar_index % 15 == 0) ? color.new(color.maroon, 70) : na bgcolor(color=Colour)

//@version=5 indicator(title=»modul», overlay=true)   Colour = (bar_index % 15 == 0) ? color. new(color.maroon, 70)  : na bgcolor(color=Colour)

При помощи условного тернарного оператора проверяем условие: какой остаток получается при делении номера (bar_index) на 15. Если остаток равен 0, значит бар индекс кратен 15, тогда в переменную Colour передаем цвет — color.new(color.maroon, 70). Если остаток не равен 0, то возвращаем n/a.

Функция bgcolor — заливает фон каждого 15-го бара указанным цветом, который хранится в переменной Colour.

Так выглядит график, на котором подсвечивается каждый 15-й бар:

Поиск четных и нечетных чисел при помощи оператора модуля

Если при делении числа на 2 в остатке получаем 0, значит делимое число четное. Давайте выделим четные и нечетные бары стрелочками разного цвета.

//@version=5 indicator(title=»modul_2″, overlay=true) Bar = (bar_index % 2 == 0) ? 1 : -1 plotarrow(series=Bar, colorup=color.fuchsia, colordown=color. black, maxheight=12)

//@version=5 indicator(title=»modul_2″, overlay=true)   Bar = (bar_index % 2 == 0) ? 1 : -1 plotarrow(series=Bar, colorup=color.fuchsia, colordown=color.black, maxheight=12)

Номер бара делим на 0 и проверяем остаток. Если остаток равен 0, то тернарный оператор возвращает 1 в переменную Bar, если остаток не равен 0, то возвращаем -1.

При помощи функции plotarrow выводим на график разные стрелочки. colorup определяет цвет стрелок, направленных вверх, а colordown — цвет стрелок направленных вниз.

maxheight — максимально возможный размер стрелок в пикселях (по умолчанию 100), мы поменяли на 12.

Так выглядит график, на котором отмечены четные и нечетные бары:

Заключение

• Оператор модуля (%) возвращает остаток от целочисленного деления.
• С помощью модуля мы можем кратна ли заданная величина какому-то определенному числу, проверив равен ли остаток 0.
• Также можно узнать четное или не четное число, проверив делится ли оно на 2 с остатком или без.

элементарная теория чисел. Является ли целочисленное деление однозначно определенным в математике?

спросил 10 лет, 7 месяцев назад

Изменено 7 лет, 2 месяца назад

Просмотрено 4к раз

$\begingroup$

В настоящее время я изучаю программирование на Java, и меня немного потрясла концепция целочисленного деления. Я предполагаю, что это просто вопрос привыкания к тому, что $1/2=0$, но я боюсь, что это может занять некоторое время, учитывая, что это свойство оператора деления (/) несовместимо с математикой.

Или это? Чтение раздела Википедии о делении целых чисел, кажется, подразумевает, что это неоднозначное понятие (см. следующую ссылку). Утверждение о том, что множество целых чисел не замкнуто при делении (т. е. целочисленное деление может дать элементы, которые не являются целыми числами), имеет для меня смысл, как и вариант 2 в следующем списке. Однако список меня озадачивает. Его существование подразумевает, что у нас есть выбор в этом вопросе, и что один из них (вариант 4) позволяет вам назвать «$1/2=0$» истинным утверждением.

Значит, целочисленное деление — дело вкуса? Может ли «$1/2=0$» быть истинным утверждением даже в строгом математическом смысле, в зависимости от того, как вы его интерпретируете?

• элементарная теория чисел

$\endgroup$

7

$\begingroup$

Все зависит от того, что вы хотите, чтобы ваша операция «разделения» выполнялась. Другими словами, каким свойствам он должен удовлетворять. В действительных числах (или рациональных, или комплексных и т. д.) наиболее существенное свойство связывает $/$ с $\times$:

Деление обратно умножению: $a/b = c$ тогда и только тогда, когда $b \times c = a$.

Однако даже в привычных системах счисления операция не закрыта. $a/0$ не определено (поскольку не существует действительного (или рационального, или комплексного) $c$ такого, что $0 \times c = a$. Ситуация еще более ограничена в целых числах, где $a/b$ может только быть определено, когда $b$ делит $a$

Операция «целочисленное деление» (существующая во многих компьютерных приложениях с использованием одного и того же символа «$/$») фиксирует свойство замыкания (то есть $a/b$ определяется для всех целых чисел, за исключением случаев, когда $b=0$), но в целом не имеет свойства Inverse. ИМХО, должно быть отдельное обозначение, такое как функция «Частное» в Mathematica:

Частное[a,b] = целочисленное частное $a$ и $b$, примерно, сколько целых раз $b$ входит в $a$.

Когда вы говорите о согласованности, это всегда относится к свойствам операции. Частное не обладает теми же свойствами, что и $/$, и является четко определенной функцией целых чисел (кроме случаев, когда делитель равен $0$).

Надеюсь, это поможет!

$\endgroup$

4

$\begingroup$

Вспомните истинный смысл деления: мы говорим, что $a/b=c$ тогда и только тогда, когда $a = b \cdot c$. Но поскольку не существует целого числа $z$, такого что $2z = 1$, это означает, что простое определение деления целых чисел по необходимости является неполным: $1/2$ в этом смысле просто не существует.

С другой стороны, есть довольно простое решение, которое на самом деле также предоставляется распространенными языками программирования: Вы можете определить деление как деление с остатком, то есть: Мы говорим, что $a/b$ равно $q$ с остатком $r$ тогда и только тогда, когда $a = bq + r$. Указав, что, например, $0 \le r < b$, это определение дает уникальные результаты для всех $a$ и $b \neq 0$, а значение $q$ равно для натуральных $a$ и $b$ , ровно $\mathtt{a/b}$ для большинства языков программирования. В языках, производных от C (например, Java), остаток $r$ задается как $\mathtt{a\%b}$.

$\endgroup$

3

$\begingroup$

Как уже упоминалось, математическая нотация сильно перегружена, когда один символ может использоваться для нескольких потенциально несовместимых понятий. Правильное понятие (обычно) дается или может быть выведено из контекста, по крайней мере, до необходимого уровня детализации. Языки программирования усугубляют эту проблему.

В конце концов, любой символ может означать что угодно, если вы даете определение. Тем не менее, целочисленное деление не является специальным изобретением, хотя, возможно, оно неправильно реализовано в большинстве языков программирования. Взяв «основное свойство» деления Шона, мы можем ослабить его до другого свойства, полностью характеризующего целочисленное деление. Пусть $b$ — натуральное число, а $a$ и $c$ — любые целые числа. Тогда следующее свойство (связность или присоединение Галуа) характеризует целочисленное деление: $$\textrm{forall}a \textrm{ и } c\quad a\times{}b \leq c\quad \textrm{тогда и только тогда, когда}\quad a \leq c/b$$ Обратите внимание, что это также эквивалентно $$\textrm{forall}a \textrm{ и } c\quad a\times{}b \gt c\quad \textrm{тогда и только тогда, когда}\quad a \gt c/b$$ Так что же должно быть $5/3$? Если мы скажем $0$, то для всех $a$, $a \gt 5/3 = 0$ следует $a\times{}3 \gt 5$, что неверно для $a=1$. Если мы скажем $2$, то для всех $a$, $a \leq 5/3 = 2$ следует $a\times{}3 \leq 5$, что неверно для $a=2$. $a=1$ удовлетворяет этому свойству. Что еще интереснее, определите, какой должна быть $(-5)/3$, и сравните ее с вашим любимым языком программирования.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

элементарная теория чисел. Какие приемы позволяют быстро выполнить целочисленное деление?

спросил 1 год, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 166 раз

$\begingroup$

По какой-то причине на моем уроке элементарной теории чисел они хотят, чтобы мы занимались такими вещами, как запись наибольшего общего делителя больших чисел в виде их линейной комбинации или китайская теорема об остатках для больших чисел. Это очень утомительный, долгий, разочаровывающий и подверженный ошибкам процесс.

Например, нужно было найти целые числа $a,b$ такие, что $1680a+ 294b =\gcd(1680, 294)$. Чтобы применить алгоритм Евклида, сначала нужно разделить 1680$ на 294$.