Что такое закон Ома и как он применяется в электрических цепях. Как рассчитать напряжение, силу тока и сопротивление. Какие материалы являются омическими. Как устроены простые электрические схемы.
Что такое закон Ома и почему он так важен
Закон Ома — это один из фундаментальных законов электротехники, описывающий связь между напряжением, силой тока и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1827 году и назван в его честь.
Согласно закону Ома, сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Математически это выражается формулой:
I = U / R
где:
- I — сила тока (в амперах, А)
- U — напряжение (в вольтах, В)
- R — сопротивление (в омах, Ом)
Почему закон Ома так важен? Он позволяет:
- Рассчитывать параметры электрических цепей
- Проектировать электронные устройства
- Анализировать работу электрических схем
- Находить неисправности в электрооборудовании
Без понимания закона Ома невозможно грамотно работать с электричеством. Это базовый закон, на котором строится вся современная электротехника.
Как применять закон Ома на практике
Закон Ома позволяет легко рассчитать любую из трех величин — ток, напряжение или сопротивление, если известны две другие. Рассмотрим несколько примеров:
Расчет силы тока
Допустим, к резистору сопротивлением 100 Ом приложено напряжение 12 В. Какой ток будет протекать через резистор?
I = U / R = 12 В / 100 Ом = 0,12 А
Расчет напряжения
Через лампочку с сопротивлением 20 Ом протекает ток 0,5 А. Какое напряжение приложено к лампочке?
U = I * R = 0,5 А * 20 Ом = 10 В
Расчет сопротивления
К неизвестному резистору приложено напряжение 9 В, при этом через него протекает ток 0,3 А. Чему равно сопротивление резистора?
R = U / I = 9 В / 0,3 А = 30 Ом
Как видим, зная закон Ома, можно легко производить расчеты параметров электрических цепей.
Омические и неомические материалы: в чем разница
Закон Ома справедлив не для всех материалов и устройств. Материалы и компоненты, для которых выполняется закон Ома, называются омическими. К ним относятся:
- Металлические проводники (медь, алюминий, серебро и др.)
- Резисторы
- Нагревательные элементы
Для омических материалов характерна линейная вольт-амперная характеристика — график зависимости тока от напряжения представляет собой прямую линию.
К неомическим материалам и компонентам относятся:
- Полупроводниковые приборы (диоды, транзисторы)
- Газоразрядные лампы
- Электрическая дуга
Для них характерна нелинейная вольт-амперная характеристика. Зависимость тока от напряжения для таких элементов более сложная и не описывается законом Ома.
Простые электрические цепи: из чего они состоят
Простейшая электрическая цепь включает в себя следующие основные элементы:
- Источник питания (батарейка, аккумулятор, блок питания)
- Потребитель электроэнергии (лампочка, двигатель, нагреватель)
- Соединительные провода
- Выключатель
Рассмотрим простую схему с лампочкой:
В данной схеме:
- Батарея создает электрическое напряжение
- Лампочка является потребителем и обладает электрическим сопротивлением
- Провода соединяют элементы цепи
- Выключатель позволяет замыкать и размыкать цепь
Когда выключатель замкнут, в цепи начинает протекать электрический ток, и лампочка загорается. При размыкании выключателя ток прекращается.
Как измерить напряжение, ток и сопротивление
Для измерения электрических величин используются специальные приборы:
Вольтметр
Измеряет напряжение. Подключается параллельно участку цепи, на котором нужно измерить напряжение.
Амперметр
Измеряет силу тока. Включается последовательно в разрыв цепи.
Омметр
Измеряет сопротивление. Подключается к обесточенному участку цепи или компоненту.
Современные цифровые мультиметры совмещают функции всех этих приборов и позволяют измерять напряжение, ток и сопротивление одним устройством.
Применение закона Ома в быту и промышленности
Закон Ома находит широкое применение как в бытовой технике, так и в промышленном оборудовании:
Бытовая техника
- Расчет мощности электроприборов
- Выбор сечения проводов для проводки
- Настройка яркости светодиодных ламп
Промышленность
- Проектирование электрических сетей
- Расчет систем электроснабжения
- Настройка систем защиты от перегрузок
Понимание закона Ома критически важно для всех, кто работает с электричеством — от домашних мастеров до профессиональных электриков и инженеров.
Ограничения закона Ома
Несмотря на широкое применение, закон Ома имеет ряд ограничений:
- Справедлив только для постоянного тока или медленно меняющегося переменного тока
- Не работает для сверхпроводников
- Не применим к полупроводниковым приборам
- Нарушается при очень сильных токах и напряжениях
В этих случаях для расчетов используются более сложные модели. Однако для большинства практических задач закон Ома остается надежным инструментом анализа электрических цепей.
Заключение
Закон Ома — это фундаментальный закон электротехники, описывающий связь между током, напряжением и сопротивлением. Его понимание необходимо для работы с любыми электрическими цепями и устройствами.
Ключевые моменты:
- Закон Ома: I = U / R
- Позволяет рассчитывать параметры электрических цепей
- Справедлив для омических материалов и устройств
- Широко применяется в быту и промышленности
- Имеет ограничения для некоторых случаев
Освоив закон Ома и принципы его применения, вы сможете лучше понимать работу электрических устройств и грамотно обращаться с электричеством.
Закон Ома для участка цепи
В § 8-и мы начали знакомство с физической величиной «электрическое сопротивление». Продолжим его – проделаем опыт. Нам потребуются источник электроэнергии, амперметр, вольтметр, реостат и два резистора (две нихромовые спирали) с различными сопротивлениями.
Соберём цепь, как показано на рисунке слева или на схеме в конце параграфа. Перемещая движок реостата, поочерёдно установим значения силы тока 0,4 А, 0,6 А, 0,8 А, 1 А. Запишем показания амперметра и вольтметра в таблицу. Повторим опыт, заменив резистор, и дополним таблицу:
| Первый резистор | Второй резистор | |||||||
| I , A | 0,4 | 0,6 | 0,8 | 1,0 | 0,4 | 0,6 | 0,8 | 1,0 |
| U , В | 1,6 | 2,4 | 3,2 | 4,0 | 2,4 | 3,6 | 4,8 | 6,0 |
| Поделив напряжение на силу тока, обнаружим закономерность: | ||||||||
| R = U/I | 4 | 4 | 4 | 4 | 6 | 6 | 6 | 6 |
Закономерность в том, что вне зависимости от значений напряжения и силы тока их частное остаётся постоянным для каждого резистора. Проверьте: после деления каждого числа строки (U, В) на расположенное над ним число строки (I, А) получаются одинаковые результаты во всех колонках левой половины таблицы: 4 В/А и во всех колонках правой половины таблицы: 6 В/А. Это показывает, что величина R является характеристикой именно изучаемого участка цепи – резистора.
Проверьте: после деления каждого числа строки (U, В) на расположенное над ним число строки (I, А) получаются одинаковые результаты во всех колонках левой половины таблицы: 4 В/А и во всех колонках правой половины таблицы: 6 В/А. Это показывает, что величина R является характеристикой именно изучаемого участка цепи – резистора.
Заметим, что эта закономерность всегда справедлива для металлических проводников в твёрдом или жидком состоянии; для других проводников она справедлива не всегда. Однако величину R, равную отношению U/I, всегда называют электрическим сопротивлением проводника независимо от его материала и состояния, а 1 В/А называют 1 Ом. Следовательно, 1 Ом – сопротивление такого проводника, в котором возникнет ток 1 А, если на концах проводника напряжение 1 В.
Связь между величинами U, I, R обычно записывается в виде формулы, известной как закон Ома для участка цепи:
| I = | U | I – сила тока в участке цепи, А U – приложенное напряжение, В R – сопротивление участка цепи, Ом | |||
| R |
Чтобы выяснить, как следует прочитать эту формулу, вспомним знания по алгебре о видах пропорциональности величин.
| прямая пропорциональность: | Y = k · X | → | I = 1/R · U |
| обратная пропорциональность: | Y = k / X | → | I = U / R |
Из первой строки следует: при постоянном сопротивлении величина 1/R тоже постоянна, поэтому сила тока прямо пропорциональна напряжению на концах участка цепи. Из второй строки: при постоянном напряжении сила тока обратно пропорциональна сопротивлению участка цепи. Объединяя это, получаем формулировку закона Ома для участка цепи: сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению этого участка.
Из второй строки: при постоянном напряжении сила тока обратно пропорциональна сопротивлению участка цепи. Объединяя это, получаем формулировку закона Ома для участка цепи: сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению этого участка.
Примечание. С точки зрения алгебры, формулу закона Ома можно записать в такой форме: U=I·R. Применим её для изучения цепи, изображённой на схеме. Допустим, клеммы A и B присоединены к источнику с напряжением 10 В, однако вольтметр позволяет измерить напряжение не более 6 В (см. рисунок в начале параграфа). Поэтому нам нужно создать падение напряжения на реостате на 4 В или более. Как это сделать? Чем правее мы смещаем движок, тем больше сопротивление реостата, и, согласно формуле U=I·R, больше напряжение на реостате, которое и называют падением напряжения.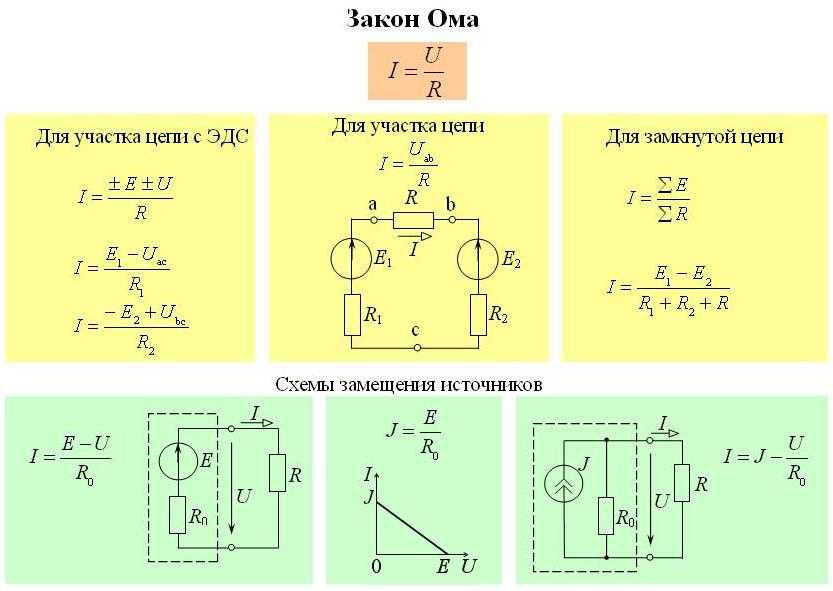 В результате на резисторе напряжение снижается и может стать менее 6 В, что нам и нужно.
В результате на резисторе напряжение снижается и может стать менее 6 В, что нам и нужно.
Закон Ома для цепи переменного тока. Резонанс в электрической цепи. Школьный курс физики
Главная | Физика 11 класс | Закон Ома для цепи переменного тока
Закон Ома для цепи переменного тока.
Рассмотрим более общий случай электрической цепи, в которую последовательно включены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор ёмкостью С. Если напряжение на концах такой цепи меняется по закону u = Umsin ωt, то сила тока в цепи меняется по закону
i = Imsin (ωt-φc),
где φc — разность фаз между колебаниями силы тока и колебаниями напряжения в цепи.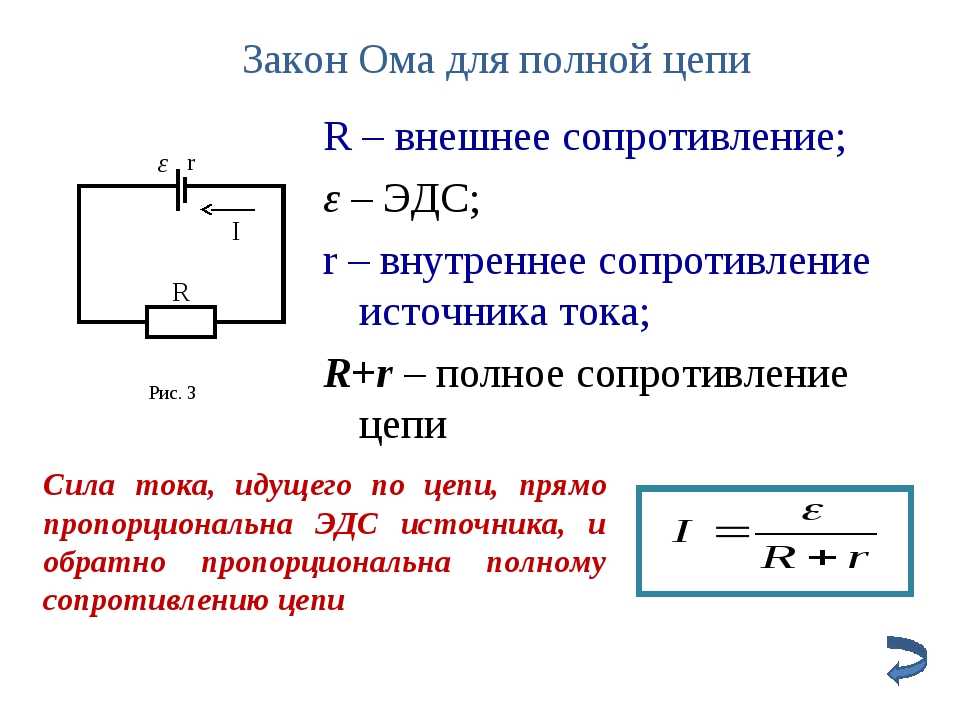
В результате математических преобразований можно получить соотношение между амплитудами колебаний силы тока и напряжения в RLC-контуре:
Сдвиг фаз φc будет определяться выражением
Выражение (1) имеет вид закона Ома Im = Um / Z, где
Величина Z — это полное сопротивление цепи. Закон Ома для цепи переменного тока (1) записан для амплитудных значений силы тока и напряжения.
Резонанс в цепи переменного тока 1.
1 Существуют два основных вида резонанса в цепи переменного тока: резонанс напряжений, который возникает при последовательном соединении элементов цепи, и резонанс токов, происходящий при их параллельном соединении. В этом параграфе будет рассмотрен резонанс напряжений.
Аналогия между законами механических и электромагнитных колебаний позволяет сделать заключение о существовании резонанса в колебательном контуре, обладающем определённой собственной частотой колебаний.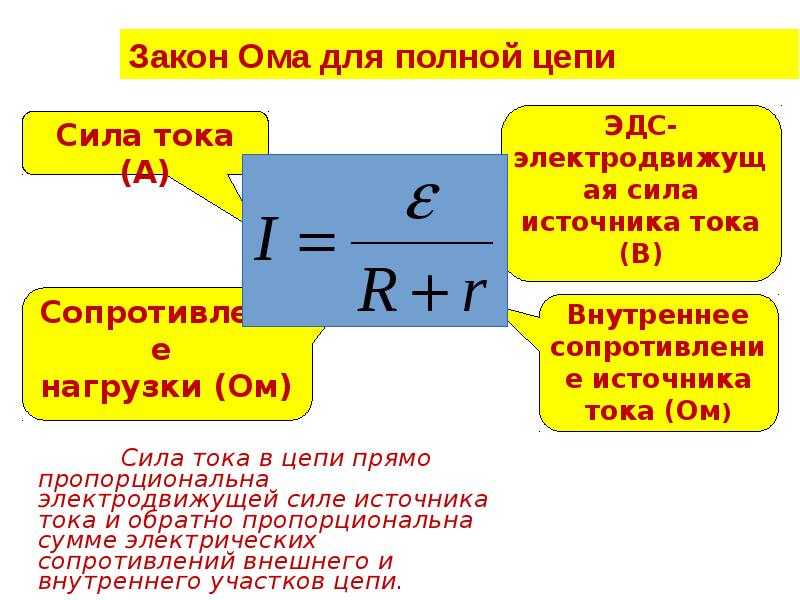
Амплитуда силы тока при вынужденных электромагнитных колебаниях в контуре, совершающихся под действием внешнего гармонически изменяющегося напряжения, определяется формулой (1). При фиксированном напряжении Um и заданных значениях R, L и C амплитуда колебаний силы тока достигает максимума при частоте ω, удовлетворяющей соотношению
Знаменатель в формуле (1) становится при этом минимальным, и амплитуда колебаний силы тока достигает максимального значения:
Амплитуда силы тока особенно велика при малом R. Из уравнения (3) можно определить циклическую частоту переменного тока, при которой сила тока максимальна:
Эта частота совпадает с частотой свободных колебаний в контуре с малым активным сопротивлением (см. § 31 «Свободные электромагнитные колебания. Колебательный контур»).
Резкое возрастание амплитуды установившихся вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением происходит при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.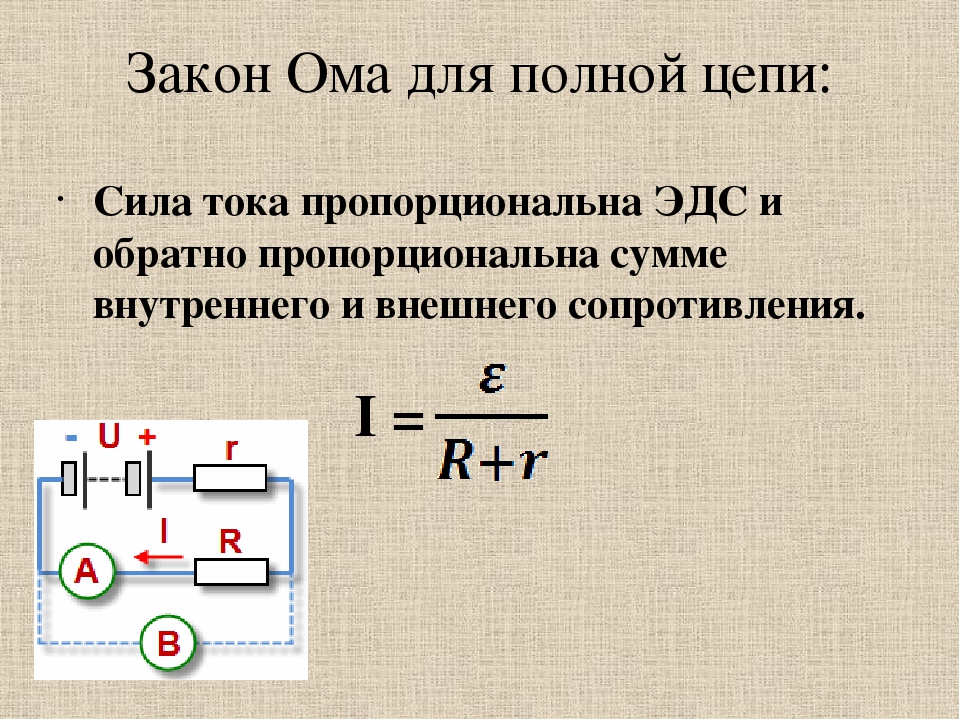 В этом состоит явление резонанса в колебательном контуре.
В этом состоит явление резонанса в колебательном контуре.
Резонанс выражен тем отчётливее, чем меньше энергетические потери в цепи, т. е. чем меньше сопротивление R. При R → 0 резонансное значение силы тока неограниченно возрастает: Iрез → ∞.
C увеличением R максимальное значение силы тока уменьшается, и при больших
R говорить о резонансе уже не имеет смысла. Зависимость амплитуды силы тока от частоты при различных сопротивлениях показана на рисунке 6.28 (R1 < R2 < R3).
Рис. 6.28
Одновременно с увеличением силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Они становятся одинаковыми и во много раз превосходят внешнее напряжение, которое связано с резонансной силой тока следующим образом:
При резонансе сдвиг фаз между силой тока и напряжением становится, согласно формуле (2), равным нулю. Наглядно это можно пояснить так. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсируют друг друга
Наглядно это можно пояснить так. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсируют друг друга
Явление электрического резонанса учитывают в радиотехнике при расчётах электрических цепей, в схемах настройки радиоприёмников, радиопередатчиков, усилителей, генераторов высокочастотных колебаний.
В некоторых случаях резонанс в электрической цепи может принести большой вред. Если цепь не рассчитана на работу в условиях резонанса, то возникновение резонанса приведёт к аварии. Чрезмерно большие токи могут перегреть провода, а большие напряжения приведут к пробою изоляции.
Вопросы:
1. Что представляет собой RLC-контур?
2. Какое соотношение выражает закон Ома для цепи переменного тока?
3. В чём заключается явление резонанса в электрическом колебательном контуре?
В чём заключается явление резонанса в электрическом колебательном контуре?
Вопросы для обсуждения:
1.Как будет изменяться накал нити лампы при изменении частоты переменного тока от 0 до ∞ в цепях, изображённых на рисунке 6.29? Амплитуда колебаний напряжения источника переменного тока не изменяется.
Рис. 6.29
2. Можно ли установить режим резонанса в цепи переменного тока, не изменяя индуктивности катушки и ёмкости конденсатора в цепи? Если да, то как это сделать?
3. Сравните явление резонанса в механических и электрических колебательных системах.
Пример решения задачи
Катушка с активным сопротивлением 10 Ом и индуктивностью 0,05 Гн соединена последовательно с конденсатором ёмкостью 2 мкФ. К цени подведено напряжение с амплитудой 100 В при частоте переменного тока, равной 50 Гц (рис. 6.30). Определите амплитуду силы тока в цепи.
Рис. 6.30
Запишем закон Ома для цени переменного тока и найдём силу тока:
Ответ: Im ≈ 0,06 А.
Упражнения:
1. Электрическая цепь состоит из последовательно соединённых резистора сопротивлением 4 Ом, катушки с индуктивным сопротивлением 8 Ом И конденсатора с ёмкостным сопротивлением 5 Ом. К концам цени приложено переменное напряжение 120 В. Найдите силу тока в цепи и напряжения на всех участках цепи.
2. В цепь включены последовательно катушка индуктивностью 50 мГн и конденсатор ёмкостью 20 мкФ. Какой частоты переменный ток нужно пропустить через эту цепь, чтобы наступил резонанс?
3. Конденсатор и катушка соединены последовательно в цепи переменного тока. Индуктивность катушки равна 0,01 Гн. При какой ёмкости конденсатора сила тока частотой 1 кГц будет максимальной?
4. Конденсатор и катушка соединены последовательно в цепи переменного тока. Ёмкостное сопротивление конденсатора равно 5000 Ом. Какой должна быть индуктивность катушки, чтобы резонанс наступил в цепи при частоте тока 20 кГц?
5. Резонансная частота колебательного контура равна 50 кГц. Как нужно изменить расстояние между пластинами плоского конденсатора в этом контуре, чтобы резонансная частота стала равной 70 кГц?
Как нужно изменить расстояние между пластинами плоского конденсатора в этом контуре, чтобы резонансная частота стала равной 70 кГц?
Предыдущая страницаСледующая страница
Страница поддержки закона Ома — Концептуальная физика 8
Страница поддержки закона Ома
|
Сопротивление и простые схемы – Физика Колледжа Дугласа 1104 Индивидуальный учебник – Зима и лето 2020 г.
Глава 15 Электрический ток, сопротивление и закон Ома
Резюме
- Объясните происхождение закона Ома.
- Расчет напряжения, тока или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он применяет разность потенциалов [латекс]\boldsymbol{V}[/латекс], которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению [латекс]\boldsymbol{V}[/латекс]. Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению :
.[латекс]\boldsymbol{I \propto V}.[/латекс]
Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.
Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением RR размером 12{R} {}. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или
Сопротивление определяется как обратно пропорциональное току, или
[латекс]\boldsymbol{I \propto}[/латекс] [латекс]\boldsymbol{\frac{1}{R}}.[/латекс]
Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает
[латекс]\boldsymbol{I =}[/латекс] [латекс]\boldsymbol{\frac{V}{R}}.[/латекс]
Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы обладают сопротивлением [латекс]\boldsymbol{R}[/латекс], которое не зависит от напряжения [латекс]\boldsymbol{V}[/латекс] и тока [латекс]\boldsymbol{I}[/латекс]. Объект, который имеет простое сопротивление, называется резистор , даже если его сопротивление мало. Единицей сопротивления является ом, который обозначается символом [латекс]\Омега[/латекс] (греческая омега в верхнем регистре). Перестановка [латекс]\boldsymbol{I = V/R}[/латекс] дает [латекс]\boldsymbol{R = V/I}[/латекс], поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:
Единицей сопротивления является ом, который обозначается символом [латекс]\Омега[/латекс] (греческая омега в верхнем регистре). Перестановка [латекс]\boldsymbol{I = V/R}[/латекс] дает [латекс]\boldsymbol{R = V/I}[/латекс], поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:
[латекс]\boldsymbol{1 \;\Omega = 1}[/латекс] [латекс]\boldsymbol{\frac{V}{A}}[/латекс]
На рис. 1 показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в [латекс]\boldsymbol{R}[/латекс].
Рисунок 1. Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 1. Расчет сопротивления: автомобильная фара
Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?
Стратегия
Мы можем переформулировать закон Ома, как указано [latex]\boldsymbol{I=V/R}[/latex], и использовать его для нахождения сопротивления.
Решение
Перестановка [латекс]\boldsymbol{I = V/R}[/латекс] и подстановка известных значений дает
[латекс]\жирныйсимвол{R =}[/латекс] [латекс]\жирныйсимвол{ \frac{V}{I}}[/latex] [латекс]\boldsymbol{=}[/latex] [латекс]\boldsymbol{\frac{12,0 \;\textbf{V}}{2,50 \;\textbf{ A}}}[/латекс] [латекс]\boldsymbol{= 4,80 \;\Омега }[/латекс]
Обсуждение
Это относительно небольшое сопротивление, но оно больше морозостойкости фары. Как мы увидим в главе 20.3. Сопротивление и удельное сопротивление, сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева. {-5} \;\Омега}[/латекс], а сверхпроводники вообще не имеют сопротивления (они не омический). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в главе 20.3 Сопротивление и удельное сопротивление.
{-5} \;\Омега}[/латекс], а сверхпроводники вообще не имеют сопротивления (они не омический). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в главе 20.3 Сопротивление и удельное сопротивление.
Дополнительную информацию можно получить, решив [латекс]\жирныйсимвол{I = V/R}[/латекс], что даст
[латекс]\boldsymbol{V = IR}.[/латекс]
Это выражение для [latex]\boldsymbol{V}[/latex] можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока [latex]\boldsymbol{I}[/latex]. Фраза [латекс]\boldsymbol{IR}[/латекс] падение часто используется для обозначения этого напряжения. Например, фара в примере 1 имеет падение [латекс]\жирный символ{ИК}[/латекс] 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается в источнике напряжения и уменьшается у резистора. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку [latex]\boldsymbol{PE = q \Delta V}[/latex] и тот же [ латекс]\boldsymbol{q}[/latex] проходит через каждый. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 2.)
Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку [latex]\boldsymbol{PE = q \Delta V}[/latex] и тот же [ латекс]\boldsymbol{q}[/latex] проходит через каждый. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 2.)
Создание соединений: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.
Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.
PhET Исследования: Закон Ома
Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Рис. 3. Закон Ома- Простая схема — это схема, в которой есть один источник напряжения и одно сопротивление.
- Одно из утверждений закона Ома дает взаимосвязь между током [латекс]\жирныйсимвол{I}[/латекс], напряжением [латекс]\жирныйсимвол{В}[/латекс] и сопротивлением [латекс]\жирныйсимвол{R}[/ латекс] в простой схеме должен быть [латекс]\boldsymbol{I = \frac{V}{R}}[/латекс].
- Сопротивление выражается в омах ([латекс]\boldsymbol{\Omega}[/латекс]), связанных с вольтами и амперами как [латекс]\жирныйсимвол{1 \;\Omega = 1 \;\textbf{V} / \ textbf{A}}[/латекс].
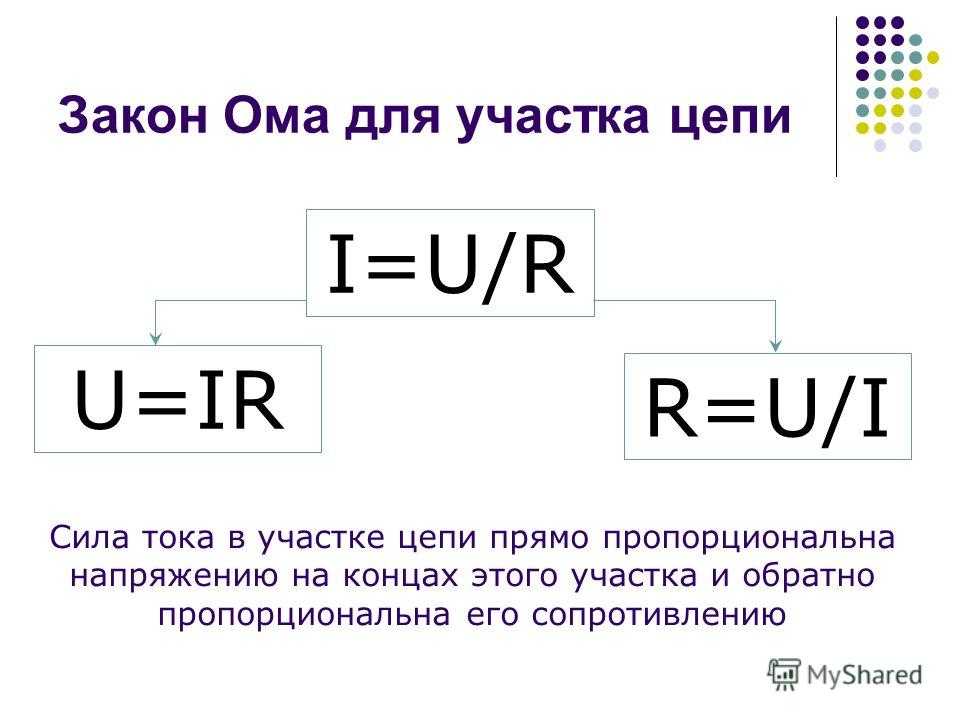

 А в поле тока электричества есть ΔV = I • R.
А в поле тока электричества есть ΔV = I • R.  Чем больше напряжение батареи (т. е. разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток. Заряд течет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. В самом деле, двукратное увеличение напряжения батареи приведет к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
Чем больше напряжение батареи (т. е. разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток. Заряд течет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. В самом деле, двукратное увеличение напряжения батареи приведет к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения. 

 Кухонные приборы, такие как электрические смесители и регуляторы освещенности, работают, изменяя ток на нагрузке путем увеличения или уменьшения сопротивления цепи. Нажатие различных кнопок на электрическом миксере может изменить режим с смешивания на взбивание, уменьшив сопротивление и позволив большему току присутствовать в миксере. Точно так же поворот диска на диммерном переключателе может увеличить сопротивление его встроенного резистора и, таким образом, уменьшить ток.
Кухонные приборы, такие как электрические смесители и регуляторы освещенности, работают, изменяя ток на нагрузке путем увеличения или уменьшения сопротивления цепи. Нажатие различных кнопок на электрическом миксере может изменить режим с смешивания на взбивание, уменьшив сопротивление и позволив большему току присутствовать в миксере. Точно так же поворот диска на диммерном переключателе может увеличить сопротивление его встроенного резистора и, таким образом, уменьшить ток.  Батарея может быть добавлена к блоку батарей, и процесс может быть повторен несколько раз, чтобы получить набор данных I-ΔV. График зависимости I от ΔV даст линию с наклоном, эквивалентным обратной величине сопротивления резистора. Это можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и достоверность уравнения закона Ома.
Батарея может быть добавлена к блоку батарей, и процесс может быть повторен несколько раз, чтобы получить набор данных I-ΔV. График зависимости I от ΔV даст линию с наклоном, эквивалентным обратной величине сопротивления резистора. Это можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и достоверность уравнения закона Ома.  Было бы разумно часто обращаться к этому списку или даже сделать свою собственную копию и дополнять ее по мере продвижения модуля. Некоторые учащиеся считают полезным сделать пятую колонку, в которой указано определение каждой величины.
Было бы разумно часто обращаться к этому списку или даже сделать свою собственную копию и дополнять ее по мере продвижения модуля. Некоторые учащиеся считают полезным сделать пятую колонку, в которой указано определение каждой величины. 
 )
) 