3 и не таблица истинности: Таблицы истинности логических функций

Таблицы истинности логических функций

⇐ ПредыдущаяСтр 15 из 19Следующая ⇒

x1 x2	f1	f2	f3	f4	f5	f6	f7
		Λ	V	~	→	↓	|	⊕

 

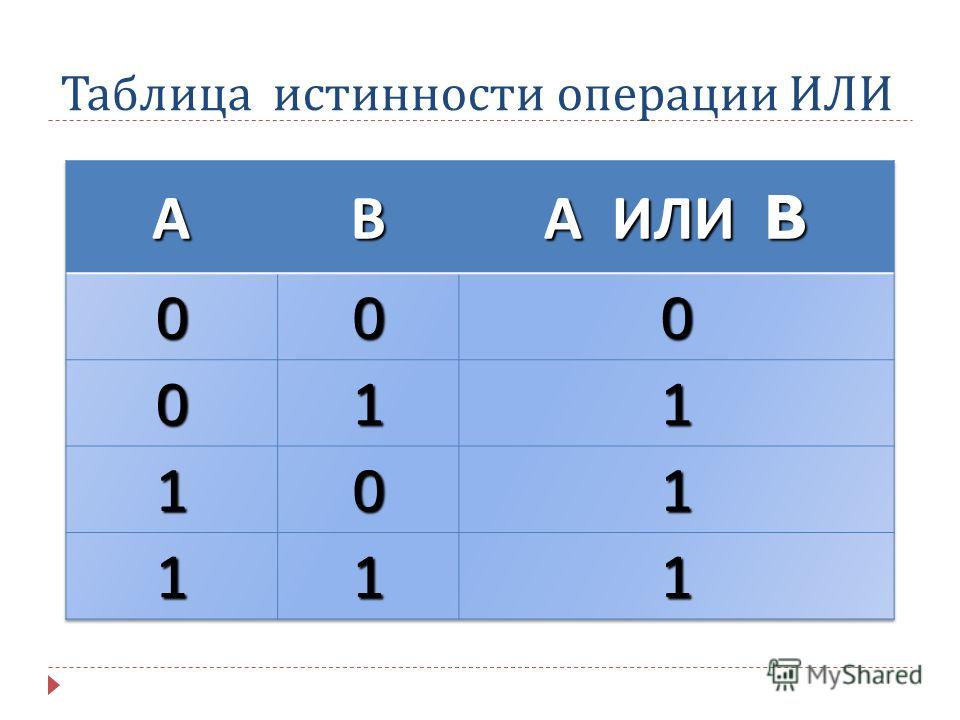
Дизъюнкция (логическое сложение, ИЛИ)

Конъюнкция (логическое умножение, И)

Равнозначность

Импликация

Функция Вебба (стрелка Пирса, ИЛИ-НЕ)

Функция Шеффера (И-НЕ)

Функция сложения по модулю два (полусумматор)

Как можно представить логические функции с помощью электрических переключающих схем? Так как логические переменные могут иметь только два дискретных значения, то следует обратить внимание на схемы, которые могут находиться в двух легко различимых рабочих состояниях.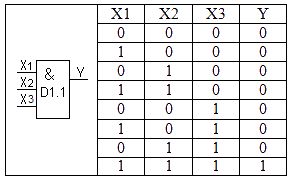 Простейшим способом реализации логической переменной является ключ.

 

Можно условиться, что разомкнутый ключ эквивалентен логическому нулю, а замк­нутый –логической единице. Таким обра­зом, ключ реализует переменную х, если он замкнут при х = 1, и переменную , ес­ли он разомкнут при х = 1.

Рассмотрим сначала, какая логическая функция будет реализована, если два клю­ча и соединить последовательно.

 

Значение зависимой переменной у характеризуется тем, будет ли замкнута или разомкнута составная коммутируемая цепь, расположенная ме­жду входными клеммами. Очевидно, что рассматриваемая цепь будет замкнута только тогда, когда и замкнуты, т.е. равны единице. Таким образом, последова­тельное включение ключей реализует функ­цию И.

Функция ИЛИ может быть получе­на, если ключи включить параллельно.

С помощью такой схемной логики можно наглядно показать справедливость ранее приведенных теорем.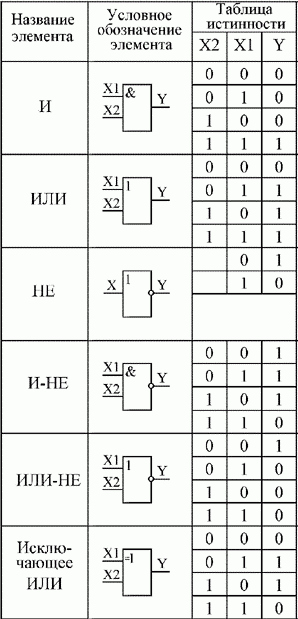

Рассмотрим это на примере правила повторения.

На рис. показана реализация обеих частей выражения правила повторения с помощью коммутируе­мой цепи. Легко заметить, что рассматри­ваемое тождество выполняется, поскольку два включенных последовательно ключа, замыкание и размыкание которых проис­ходит одновременно, воздействуют на внешние цепи как один такой ключ.

 

Другой возможностью представления логических переменных является электри­ческое напряжение, имеющее два раз­личных уровня: высокий и низкий. Этим уровням можно поставить в соответствие логи­ческие состояния 1 и 0. Эта система обо­значений: высокий = 1 и низкий = 0 – на­зывается позитивной логикой. Но возмож­на также и обратная система обозначений: высокий = 0 и низкий = 1, которая назы­вается негативной логикой.

Основные логические функции могут быть реализованы с помощью соответ­ствующих электронных схем. Эти схемы имеют один или несколько входов и один выход.

Как правило, они называются логи­ческими элементами. Уровень выходного напряжения определяется уровнями напря­жения на входах и характером логической функции. Для реализации одной и той же логической функции существует большое число различных электронных схем. По­этому с целью упрощения документации были введены символы, которые обозна­чают лишь только логическую функцию и не раскрывают внутреннее строение схемы.

 

В цифровой технике задача, как правило, формулируется в форме таблицы переключений, которая называется также таблицей истинности. Прежде всего требуется найти такую логическую функцию, которая соответствовала бы этой таблице. На следующем этапе эту функцию преобразуют в простейшую форму, которую потом реализуют с помощью соответствующей комбинации базовых логических схем. Логические функции записывают, как правило, в

дизъюнктивной совершенной нормальной форме (ДСНФ). При этом поступают следующим образом.

1. В таблице истинности выделяют строки, в которых выходная переменная у имеет значение 1.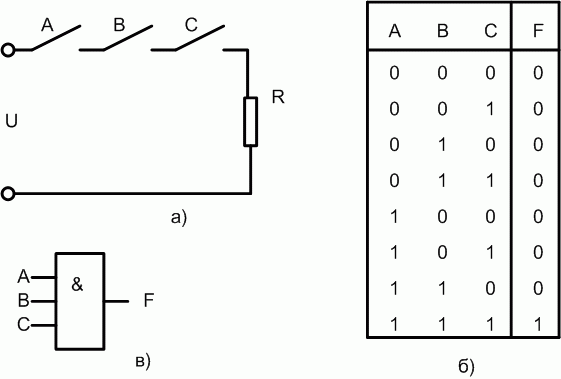

2. Для каждой такой строки составляют конъюнкцию всех входных переменно причем записывают сомножитель , если рассматриваемая переменная принимает значение 1, в противном случае записывают . Таким образом, составляется столько произведений, сколько имеется строк с у = 1.

3. Наконец, записывая логическую сумму всех найденных произведений, получают искомую функцию.

 

Формулы склеивания:

Формулы поглощения:

 

Минимизация методом Карно

При минимизации методом Карно логическую функцию в виде карты. При размещении различных комбинаций значений входных переменных следует выбирать таким, чтобы при переходе от одной ячейки к соседней изменялась только одна переменная (используют код Грэя). Склеивание возможно, если одинаковые значения функции располагаются рядом.

Желательно образовывать контуры возможно большей протяженности. Контуры могут охватывать 1, 2, 4,8 и т. д. единиц (или нулей). В результате исчезает та переменная, которая меняет знак при обходе контура. При организации контуров следует считать, что карту можно навернуть на цилиндр.

Если обхватывать контурами единицы, то результат получим в ДСНФ, если нули – то в КСНФ (конъюнктивная совершенная нормальная форма).

	f

2-х разрядная карта Карно

 

Результат:

 

Элементарная база цифровых микросхем. Логические элементы И, ИЛИ, НЕ на диодах, биполярных и полевых транзисторах. Базовые логические элементы диодно-транзисторной, транзисторно-транзисторной, эмиттерно-связанной логики. Логические элементы на однотипных и комплементарных МДП-транзисторах. Логические элементы с тремя выходными состояниями. Микросхемы с открытым коллектором. Совместное применение микросхем разных серий.

 

 

Эволюция цифровой логики:

1) РТЛ – резисторно-транзисторная логика.

2) ДТЛ – диодно-транзисторная логика.

3) ТТЛ –транзисторно-транзисторная логика.

Элемент три «И-НЕ» на ДТЛ.

Напряжение <0.4B считается логическим нулем, при U>2.4 – логическая единица.

Элементы на основе ТТЛ.

В основе – многоэммитерный транзистор.

Серия 155.

Если на всех входах «1» , то на коллекторе эмиттерный переход закрыт, а коллекторный открыт и напряжение на базе VT1=1.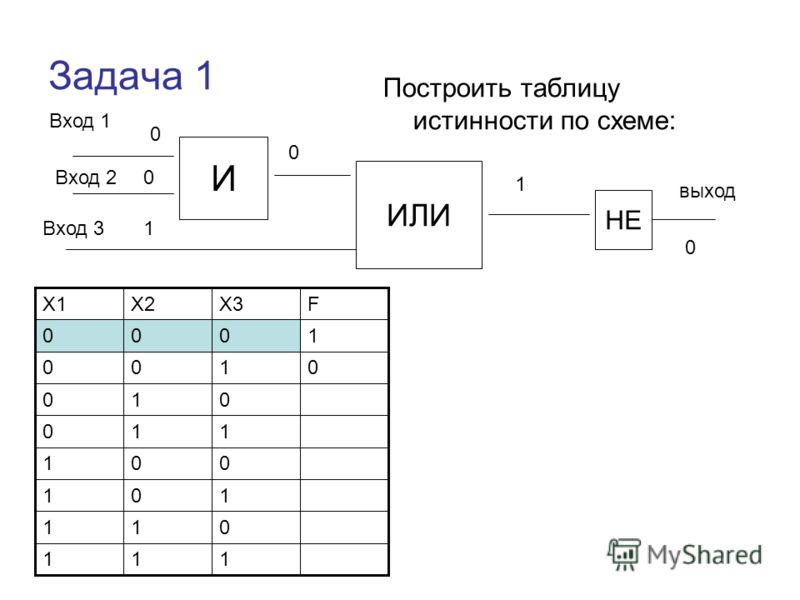

8 В. VT2 и VT5 открыты, VD4 –предназначен для надежного запирания VT4. R3, R4 и VT3 действуют как резистор и предназначены для увеличения помехоустойчивости.

Если на любом из входов «0», то VT1 переключается из инверсного в активный режим и отпирается. В этом случае напряжение на его коллекторе (0,8В) уже недостаточно для отпирания VT4 и VT5. VT4 при этом открыт и на выходе появляется логическая единица.

R5 предназначен для защиты выходов при кратковременном замыкании на землю.

 

 

Серия повышенного быстродействия.

VT1, VT2 – VT5 – используются транзисторы Шотке.

Следующим шагом к повышению быстродействия стало использование транзистора Шотке.

 

Если на базу подать большое напряжение, то транзистор может войти в режим насыщения и его быстродействие уменьшается.

У диода Шотке напряжение отпирания 0,3-0,4 В. Напряжение на базе транзистора Шотке не может превышать напряжение на его коллекторе более, чем на 0,4 В, т.

е. коллекторный переход никогда полностью не открывается транзистор не заходит в режим насыщения, что резко увеличивает его быстродействие.

 

Читайте также:

 

ЕГЭ по информатике — Задание 2 (Мощнейший метод)

Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.

Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).

С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую

логическую операцию, и давайте рассмотрим их.

Порядок выполнения логических операций:

1. () — операции в скобках
2. ¬ — логическое отрицание
3. ∧ — логическое умножение
4. ∨ — логическое сложение
5. ⟶ — следование
6. ≡ — равнозначность

Так же на ЕГЭ по информатике будет полезно знать логические формулы :
Ещё соотношения:

Передём к решению задач из ЕГЭ по информатике

Задача 1 (лёгкая)

Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Решение:

Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице).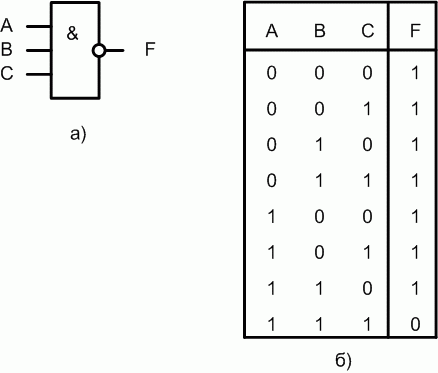 Значит каждое выражение в нашей функции должно равняться единице.

Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.

Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.

Ответ: zyxw

Задача 2 (средний уровень)

Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.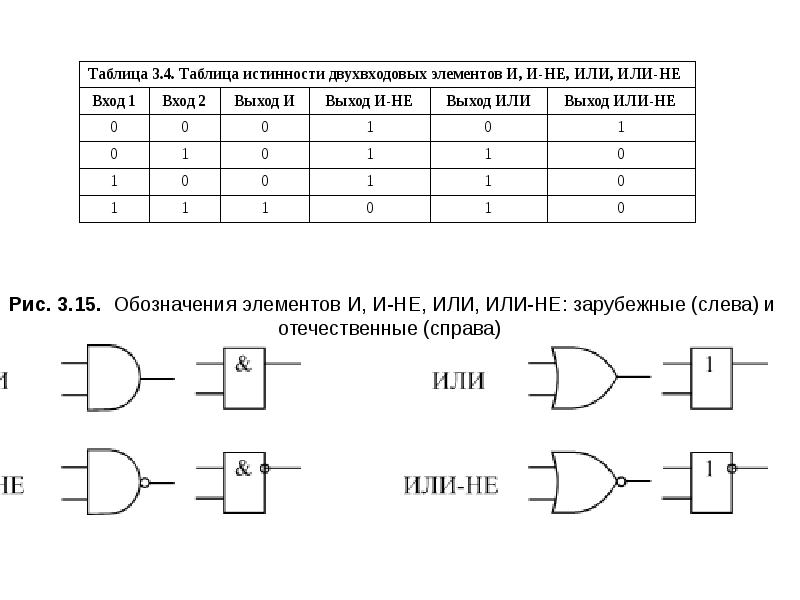 Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Решение:

Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.

Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).

Самым слабым звеном является переменная w, потому что она стоит одна.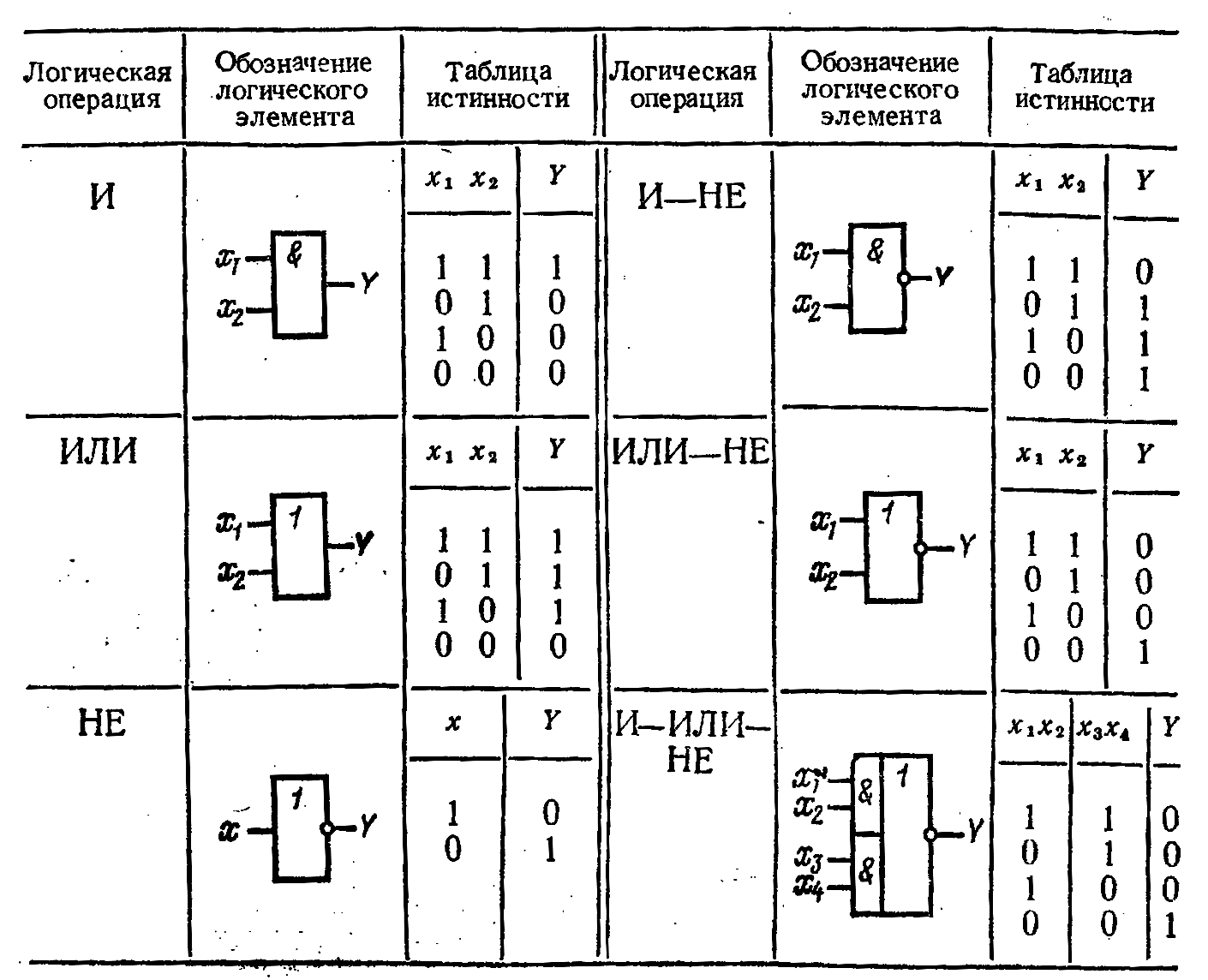 Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.

Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!

Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).

Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).

Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.

Осталось разобраться с z и y.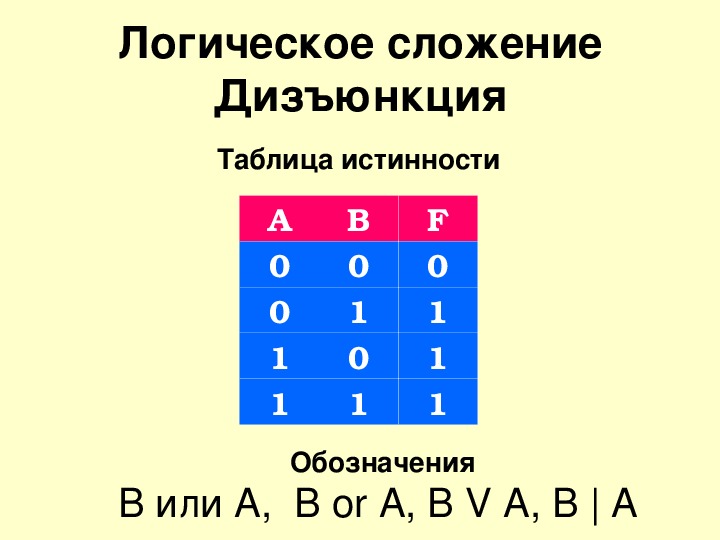 Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.

Тогда ответ будет равен yxwz.

Ответ: yxwz

Мощнейший метод для решения второго задания из ЕГЭ по информатике

Задача 3 (хороший уровень)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. 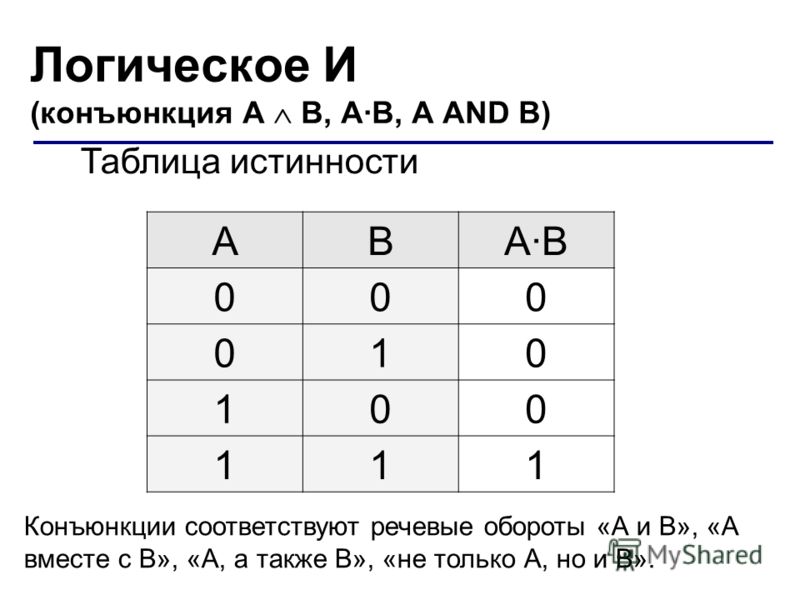д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Решение:

«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).

Тогда каждое выражение должно равняться 0(нулю).

Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 2⁴).

Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).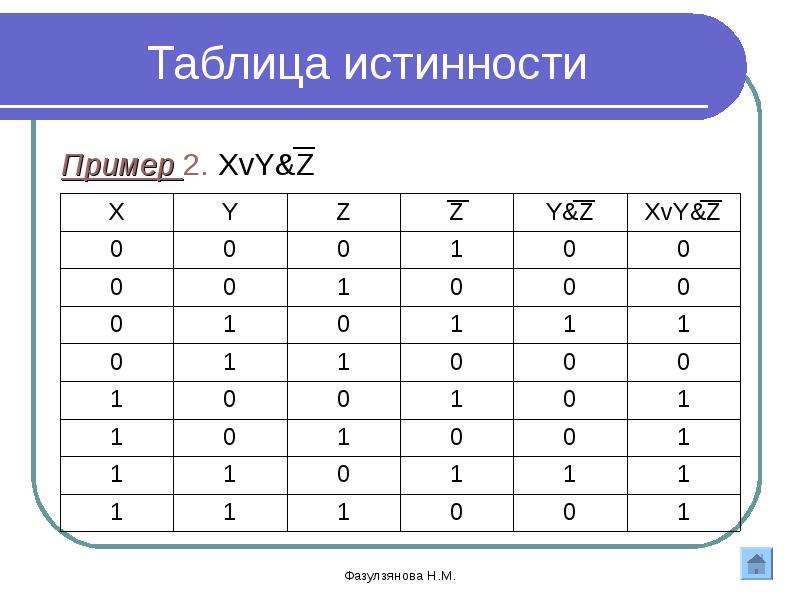

При небольшой тренировке анализ подобных выражений занимает сущие секунды!

У нас получается 4 строчки, которые удовлетворяют нашей функции:

Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).

Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.

Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец

Ответ: ywzx.

На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!

Пока!

СОСТАВЛЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ — МегаЛекции

СЛОЖНЫЕ СУЖДЕНИЯ

Сложные суждения – это суждения, образованные из простых с помощью логических связок.

Связь между элементами сложного суждения осуществляется с помощью логических союзов (логических связок).

 

Логические связки:

 

Главная их особенность в том, что логические союзы однозначны, тогда как грамматические союзы имеют множество смыслов и оттенков.

 

1. КОНЪЮНКЦИЯ (от лат. сonjunctio – союз, связь).

Знак: ˄ или &

В русском языке конъюнкции соответствуют союзы: «и», «а», «но», «да», «хотя», «который», «зато», «однако», «при этом» и т.п.

 

Суждение «Она любит яблочный сок и зелёный чай» является конъюнкцией (связью) двух простых суждений: «она любит яблочный сок» и «она любит зелёный чай».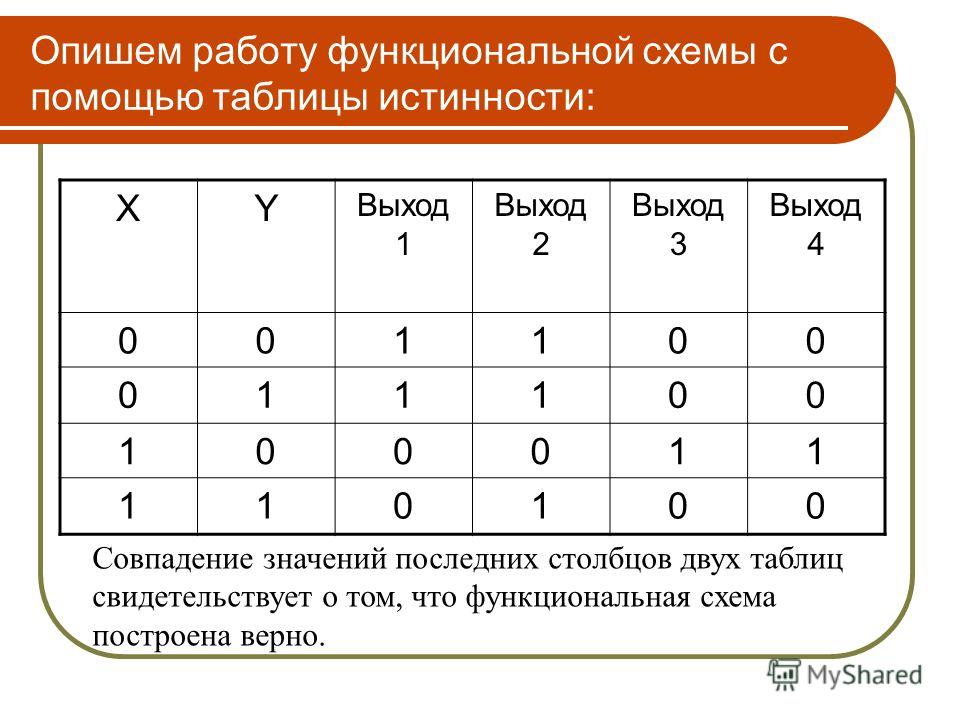

Запись этого суждения с помощью логических связок будет выглядеть: а ˄ bилиа & b

2. ДИЗЪЮНКЦИЯ (от лат. disjunctio – разобщение).

Знак: ˅

В русском языке конъюнкции соответствуют союзы: «или», «либо», «то ли… то ли».

 

Суждение «Мы пойдём в кино или в парк» является дизъюнкцией двух простых суждений: «мы пойдём в кино» или «мы пойдём в парк». Данная связка не является строгой, то есть не предполагает только один выбор, так как мы можем пойти и в кино, и погулять в парке.

Запись этого суждения с помощью логических связок будет выглядеть: а ˅ b

 

СТРОГАЯ ДИЗЪЮНКЦИЯ

Знак: .

Союз «или» может употребляться в строгом смысле – когда члены дизъюнкции исключают друг друга.

 

Суждение «Автор «Войны и мира» то ли Толстой, то ли Достоевский» является строгой дизъюнкцией

Запись этого суждения с помощью логических связок будет выглядеть:

 

4. ИМПЛИКАЦИЯ (от лат. implico – тесно связываю)

Знак: → .

В языке аналоги этой связки союзы: «если…, то»; «когда…, тогда»; «коль скоро…, то» и т.п.

Обычно с помощью импликации выражаются причинно-следственные отношения типа: «Если выглянет Солнце, то станет тепло». a → b.Первый элемент импликации называется основанием (антецедентом), второй – следствием (консеквентом).

 

5. ЭКВИВАЛЕНЦИЯ (от позднелат. aequivalens – равнозначный; равноценный)

Знак: ↔ или ≡ .

В языке аналоги этой связки союзы: «если и только если»; «тогда и только тогда, когда…»; «лишь при условии, что…, то».

 

Суждение: «Только тогда ребёнок получит конфету, когда доест весь суп» является эквиваленцией.

Запись этого суждения с помощью логической связки будет выглядеть: a ↔ bилиa ≡ b

 

6. ОТРИЦАНИЕ

Знак: ~ или . ставятся перед суждением ~а или а ; или черта, которая ставится над суждением

В языке отрицание выражается союзами и словами: «не», «неверно» и т.п.

Суждение: «Не заводится машина» записывается как ~а

Суждение: «Любит или не любит» содержит строгую дизъюнкцию и отрицание.

Упражнения: Запишите суждения в виде логической формы с помощью логических связок.

 

1. Он в кафе закажет чай или мороженое.	a ˅ b
2.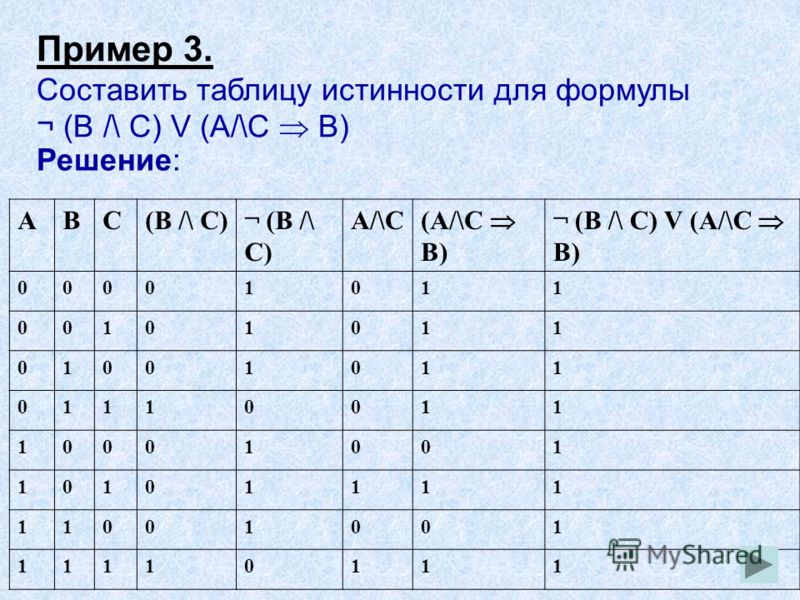 Преступление может быть умышленным или совершённым по неосторожности.	a b
3. Если число делится на два без остатка, то оно чётное.	a → b
4. Простое число больше единицы и имеет только два натуральных делителя.	а ˄ b
5. «Пять» больше единицы, но не простое число.	а ˄ ~b

 

Самопроверка:Запишите суждения в виде логической формы с помощью логических связок

Для самопроверки выделите столбец «формула» и измените цвет шрифта

Суждение	Формула
1. Когда придёт весна, то станет тепло и растает весь снег.	a → (b ˄ с)
2. Если число больше единицы и имеет только два натуральных делителя, то оно является простым.	(а ˄ b) → c
3. студент получит зачёт-автомат по логике, только если он будет посещать занятия и правильно выполнит все задания.	a ↔ (b ˄ с)
4. Если болезнь запущена, то её трудно излечить. Однако, если болезнь не запущена, то её трудно распознать, но её не трудно излечить.	(а → b) ˄ ~a → (c ˄ ~b)

ТАБЛИЦЫ ИСТИННОСТИ

 

Значение истинности сложных суждений определяется с помощью таблиц истинности, где буквы a, b, c– переменные, обозначающие простые суждения; буква «и» обозначает истину, а «л» — ложь.

 

а	b	а ˄ b	а ˅ b	а b	a → b	a ↔ b	~а	~b
и	и	и	и	л	и	и	л	л
и	л	л	и	и	л	л	л	и
л	и	л	и	и	и	л	и	л
л	л	л	л	л	и	и	и	и

 

Также возможно обозначать истину нулём «1», а ложь единицей «0».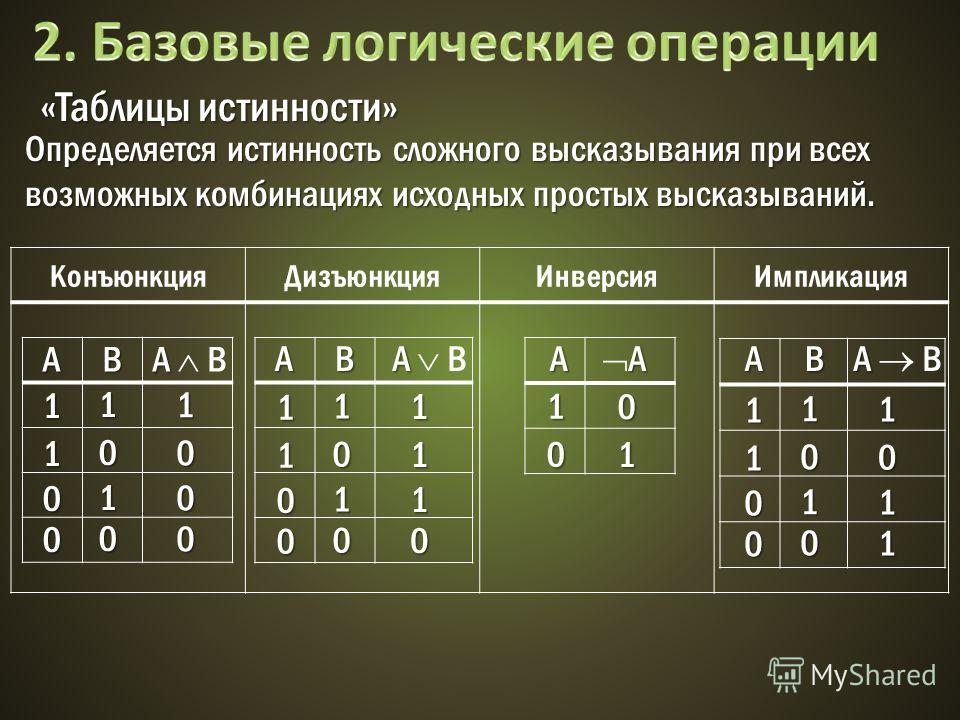

 

а	b	а ˄ b	а ˅ b	а b	a → b	a ↔ b	~а	~b

 

1. КОНЪЮНКЦИЯ а ˄ bилиа & b

 

Конъюнкция будет истинна в том и только в том случае, если суждения а и b оба истинны.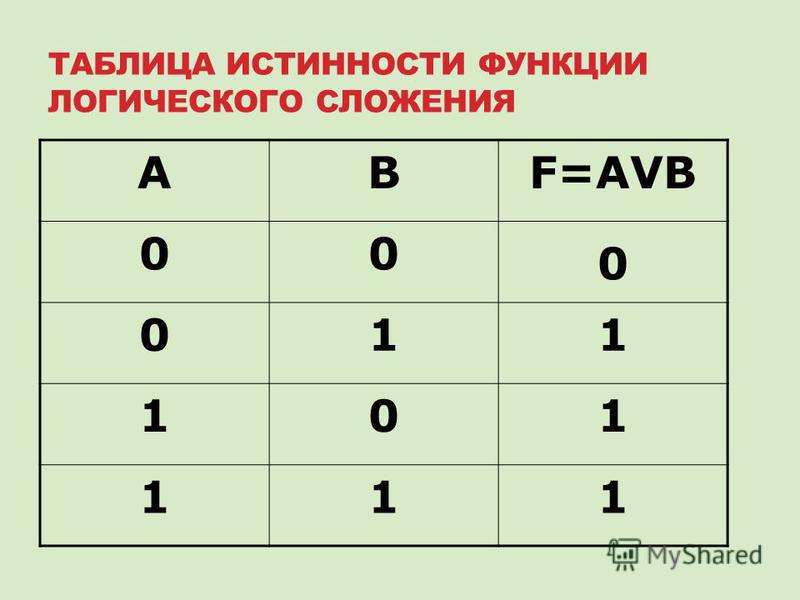

2. ДИЗЪЮНКЦИЯ а ˅ b

 

Сложное суждение истинно, если истинно хотя бы одно из составляющих его простых суждений, и ложно, если оба простых суждения ложны.

СТРОГАЯ ДИЗЪЮНКЦИЯ

 

Сложное суждение истинно, если истинно лишь одно из составляющих его простых суждений, так как элементы сложной дизъюнкции исключают друг друга.

 

4. ИМПЛИКАЦИЯ a → b

 

Сложное суждение, соединённое импликацией, ложно только в одном случае: если основание (первое суждение) истинно, а следствие (второе суждение) ложно.

 

5. ЭКВИВАЛЕНЦИЯ a ↔ bилиa ≡ b

Сложное суждение, соединённое эквиваленцией, истинно только в тех случаях, когда составляющие его простыt суждения, либо оба истинны, либо оба ложны.

6. ОТРИЦАНИЕ ~аили аили ~b; b;

Если а истинно, то его отрицание ложно.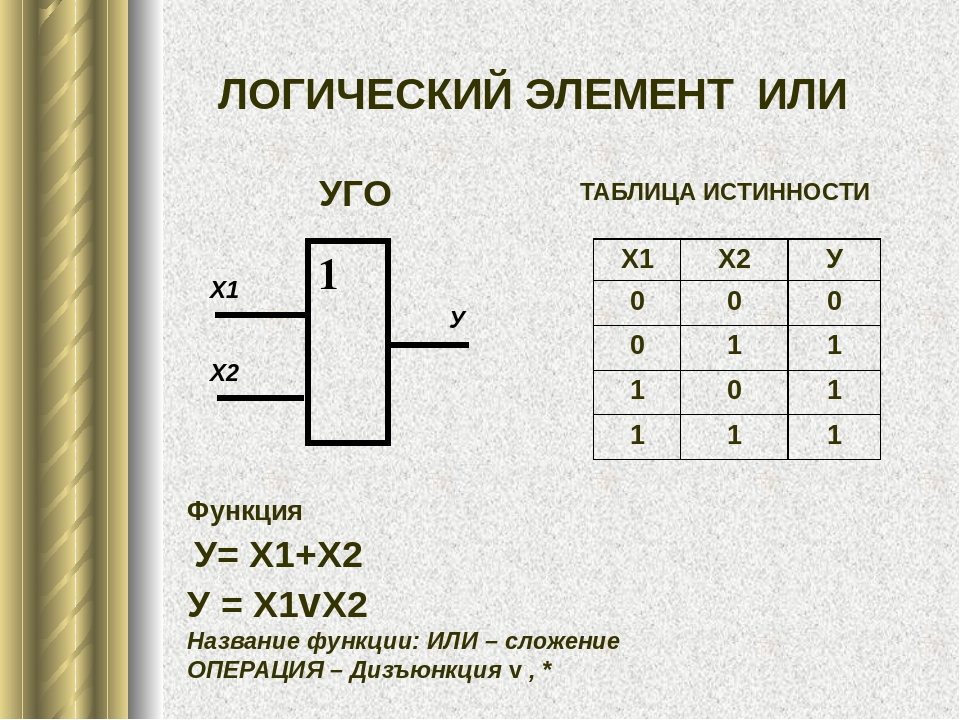 Если а ложно, то не-а (~а) – истинно.

Если b истинно, то его отрицание ложно. Если b ложно, то не-b (~b) – истинно.

 

Если отрицание стоит внутри суждения перед связкой «есть», то мы имеем дело с простым отрицательным суждением типа «Черепахи не летают». Если же отрицание присоединяется к суждению снаружи – «Неверно, что черепахи летают», то мы имеем дело с логической связкой, преобразующей простое суждение в сложное.

Если знак отрицания стоит непосредственно перед а или b, то есть ~а; ~b,то отрицание применяется только к одному суждению.

Если знак отрицания стоит перед скобкой ~(a → b), то отрицанию будет подвержена операция, указанная в скобках. В данном примере, ̶ это отрицание импликации. Сначала выполняется импликация, затем результат подвергается отрицанию.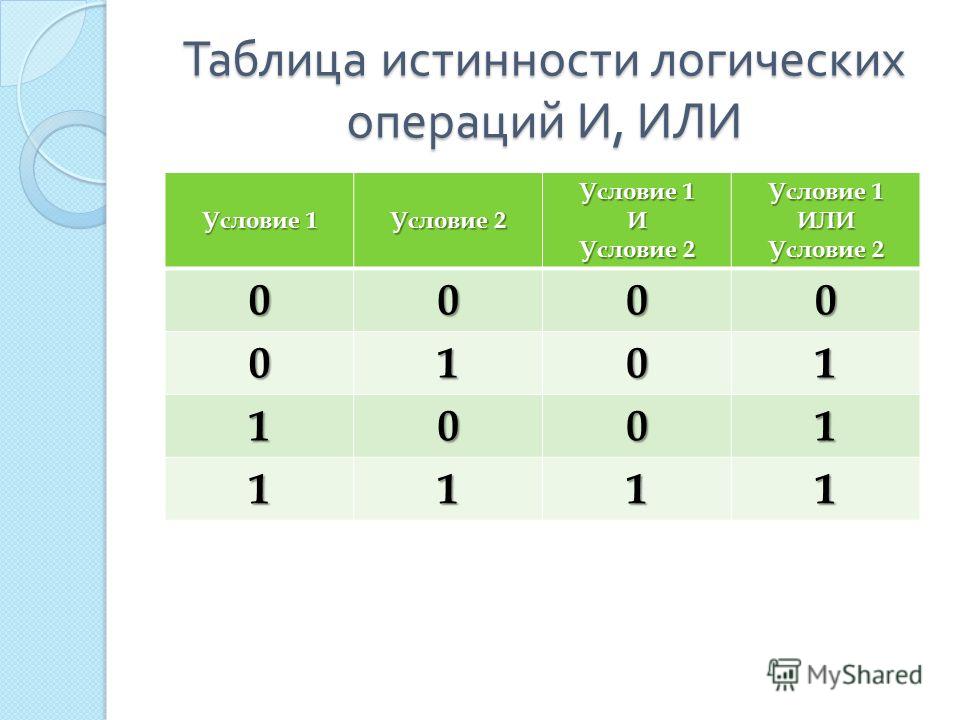

Выполнимата формула, которая может принимать по крайней мере одно значение «истина».

Тождественно-истинная формулата, которая при любых комбинациях значений для входящих в неё переменных принимают значение «истина» (иначе она называется законом логики).

Тождественно-ложная формула та, которая принимает только значение «ложь» (иначе ‒ противоречие).

!!! Следует помнить, что логику интересует не содержание, а исключительно форма мысли!

Устанавливать истинность сложных суждений в логике, опираясь на здравый смысл или жизненный опыт, или обращение к действительности, ̶ неправильно!

Формально-логические связки не в состоянии учитывать многих смысловых оттенков естественного языка. Значения истинности некоторых сложных суждений достаточно близки к здравому смыслу, но другие могут показаться странными.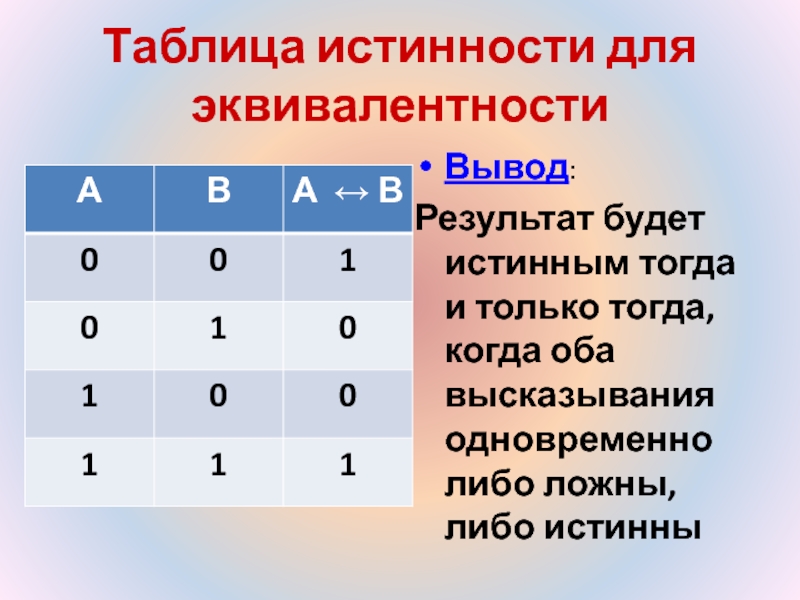 Поэтому то, то с точки зрения содержания может выглядеть непривычно, с точки зрения формы будет являться правильным.

СОСТАВЛЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ

 

Чтобы проверить сложное суждение с помощью таблицы истинности, необходимо грамотно её составить.

Например, нужно проверить суждение: «Если пойдёт дождь, то дорога будет мокрая».

 

1. Определим все простые суждения, составляющие данное сложное высказывание и узнаем количество переменных n :

а – пойдёт дождь; b – дорога будет мокрая

 

Получилось две переменных (а, b), соединённых союзом «если, то»

 

2. Количество строк (k) в таблице определяется по формуле: k = 2ⁿ , где n – количество переменных (то есть количество простых суждений, составляющих сложное).

 

В данном примере k = 2² = 4 Значит будет четыре строчки в таблице.

 

3. Количество столбцов в таблице будет зависеть от количества операций (логических связок) в сложном суждении.

Сначала в первых столбцах распределяются все возможные значения истины и лжи для переменных.

а	b

 

В данном примере две переменные, следовательно, четыре строки.

 

 

а	b
	и
	л
	и
	л

В самом правом столбце (b) чередуют «и» и «л» по одному, начиная всегда с «истины»

 

Во втором справа столбце (а) чередуют подряд два значения «и» и два значения «л», начиная всегда с «истины».

а	b
и	и
и	л
л	и
л	л

 

Затем направо выписывают логические формы всех сложных суждений, входящих в рассматриваемое суждение. В данном примере указана одна логическая связка «если, то» – импликация.

 

а	b	a → b
и	и
и	л
л	и
л	л

 

Осталось определить значения истинности для импликации. Сложное суждение, соединённое импликацией, ложно только в одном случае: если основание (первое суждение) истинно, а следствие (второе суждение) ложно.

а	b	a → b
и	и	и
и	л	л
л	и	и
л	л	и

 

 

1. Дождь пошёл, дорога мокрая. а – истина; b – истина. Следовательно, если а, то b (a → b) – истина

2. Дождь пошёл, но дорога не стала мокрая. а – истина; b – ложь. Следовательно, если а, то b (a → b) – ложно. Невозможно, чтобы причина была, а следствие не наступило.

3. Дождь не пошёл, но дорога мокрая а – ложь; b – истина. Следовательно, a → b–истина. Дорога может быть мокрой и по другой причине.

4. Дождь не пошёл и дорога не намокла. а – ложь; b – ложь. Следовательно, a → b– истина.

Если сложное суждение составлено из трёх простых, то есть состоит из трёх переменных (а, b, c), то таблица истинности, включающая все возможные комбинации истинности или ложности её переменных, будет состоять из 2³ = 8 строк.

Алгоритм распределения значений «и» и «л» для трёх переменных таков:

 

а	b	с		Начинаем распределять значения с крайнего правого столбца (с) и распределяем значения «и» и «л» попеременно, начиная с «истины».   Затем распределяем значения во втором столбце справа (b), распределяем значения «и» и «л», чередуя подряд по два значения «и», затем по два значения «л»; затем опять два значения «и» и два значения «л».   В крайнем левом столбце (а) чередуем «и» и «л», чередуя подряд сначала четыре значения «и» и затем четыре значения «л»
и	и	и
и	и	л
и	л	и
и	л	л
л	и	и
л	и	л
л	л	и
л	л	л

Упражнения:

1. Запишите высказывание в виде логической формы, используя логические связки: «Если ты сможешь доказать мне свои добрые намерения, то я поверю тебе или же мне придётся вызвать полицию и обвинить тебя в лжесвидетельстве» (Г. Каттнер. Источник миров).

 

Выпишем все простые суждения, входящие в состав сложного высказывания:

а – ты сможешь доказать мне свои добрые намерения

b – я поверю тебе

с – мне придётся вызвать полицию

d – (мне придётся) обвинить тебя в лжесвидетельствовании.

Определим связки между элементами: если а, то b или с и d

 

(a → b) ˅ (c ˄ d)

---

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

{k} \ to \ mathbb {A},} где k {\ displaystyle k \!} — неотрицательное целое число, а A {\ displaystyle \ mathbb {A}} — область логических значений {false, true}. {k} \ to \ mathbb {B},} где k {\ displaystyle k \!} — неотрицательное целое число, а B {\ displaystyle \ mathbb {B}} — логическая область {0,1}.{\ displaystyle \ {0,1 \}. \!} В большинстве приложений false {\ displaystyle \ operatorname {false}} представлен 0 {\ displaystyle 0 \!}, а true {\ displaystyle \ operatorname {true}} представлен 1 {\ displaystyle 1 \!}, но возможно и обратное представление, в зависимости от общего представления функций истинности как логических функций. Остальная часть статьи предполагает обычное представление, принимая как должное уравнения F = 0 {\ displaystyle \ operatorname {F} = 0} и T = 1 {\ displaystyle \ operatorname {T} = 1}.

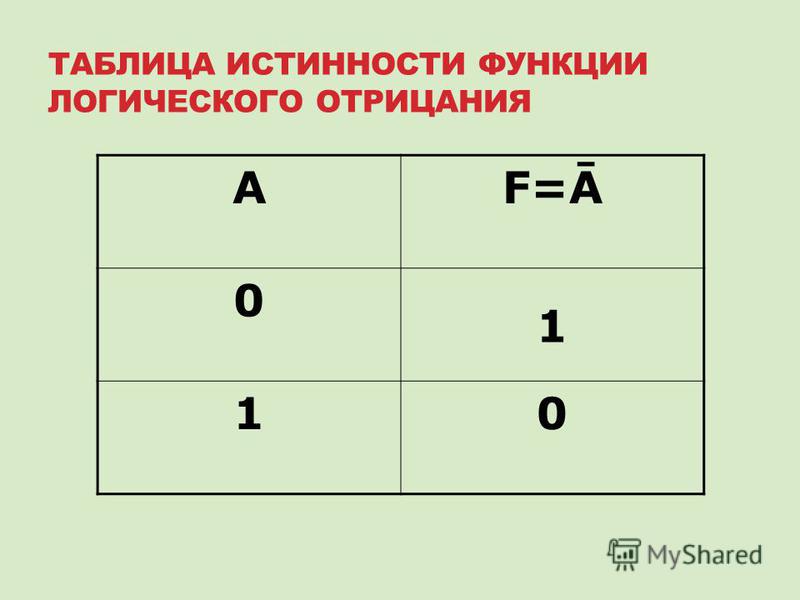
Логическое отрицание — это операция над одним логическим значением, обычно значением предложения, которая дает значение true , когда его операнд ложный, и значение false , когда его операнд истинен.

Таблица истинности NOT⁡ p, {\ displaystyle \ operatorname {NOT} ~ p,} также записывается как ¬p, {\ displaystyle \ lnot p, \!} Отображается ниже:

Отрицание пропозиции p {\ displaystyle p \!} Может быть обозначено различными способами в различных контекстах применения, часто просто для удобства типографики.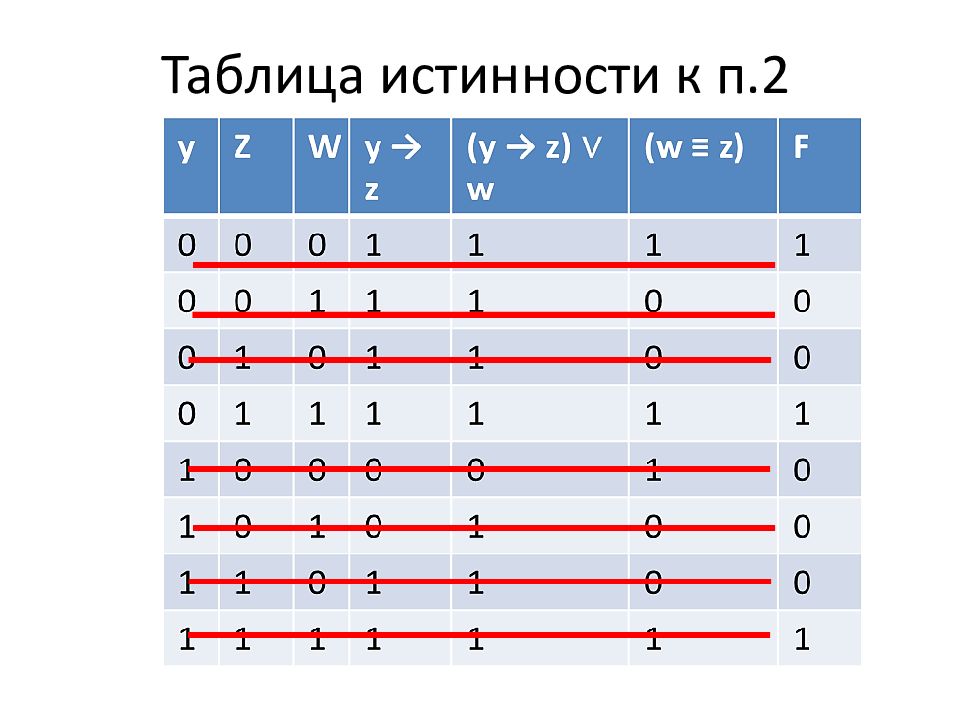 Среди этих вариантов можно выделить следующие:

Логическое соединение — это операция над двумя логическими значениями, обычно значениями двух предложений, которая производит значение истинно тогда и только тогда, когда оба его операнда истинны.

Таблица истинности p AND⁡ q, {\ displaystyle p ~ \ operatorname {AND} ~ q,} также записывается как p∧q {\ displaystyle p \ land q \!} Или p⋅q, {\ displaystyle p \ cdot q, \!} появится ниже:

Логическая дизъюнкция , также называемая логическим чередованием , представляет собой операцию над двумя логическими значениями, обычно значениями двух предложений, которая производит значение false тогда и только тогда, когда оба его операнда ложны.

Таблица истинности p OR⁡ q, {\ displaystyle p ~ \ operatorname {OR} ~ q,} также записывается как p∨q, {\ displaystyle p \ lor q, \!}, Появляется ниже:

Логическое равенство — это операция над двумя логическими значениями, обычно значениями двух предложений, которая дает значение истина тогда и только тогда, когда оба операнда ложны или оба операнда истинны.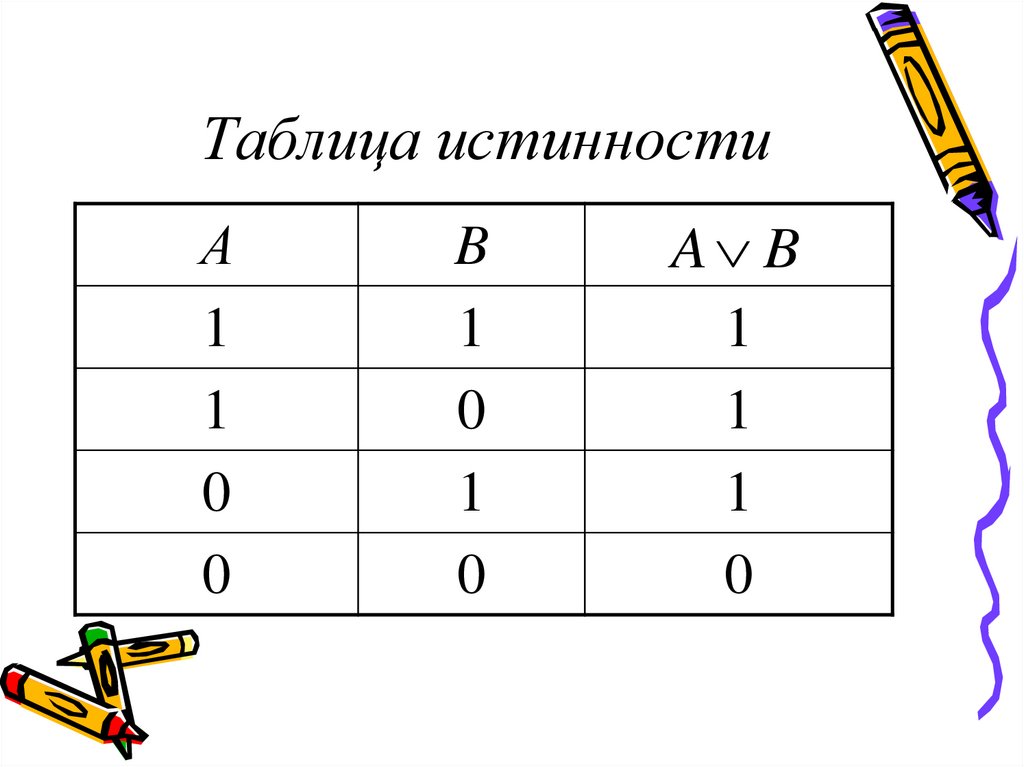

Таблица истинности p EQ⁡ q, {\ displaystyle p ~ \ operatorname {EQ} ~ q,} также записывается как p = q, {\ displaystyle p = q, \!} P⇔q, {\ displaystyle p \ Стрелка влево-вправо q, \!} Или p≡q, {\ displaystyle p \ Equiv q, \!} Появляется ниже:

Исключительная дизъюнкция , также известная как логическое неравенство или симметричная разность , представляет собой операцию над двумя логическими значениями, обычно значениями двух предложений, которая дает значение истинное на случай, если ровно один из его операндов правда.

Таблица истинности p XOR⁡ q, {\ displaystyle p ~ \ operatorname {XOR} ~ q,} также написана

таблиц истинности, продолжение 6.3 и 6.4 14 марта. 6.3 Таблицы истинности для предложений Помните: таблица истинности дает значение истинности сложного предложения.

Презентация на тему: «Таблицы истинности, продолжение 6.3 и 6.4, 14 марта. 6.3 Таблицы истинности для предложений Помните: таблица истинности дает значение истинности составного предложения». — Стенограмма презентации:

1 Таблицы истинности, продолжение 6.3 и 6,4 14 марта

2 6.3 Таблицы истинности для предложений Помните: таблица истинности дает значение истинности составного предложения для всех возможных значений истинности его простых компонентов. Каждое возможное расположение значений истинности получает строку в таблице истинности. В результате общее количество строк равно количеству возможных комбинаций значений истинности для простых предложений.

3 6.3 таблицы истинности предложений L = количество строк n = количество различных простых предложений L = 2 n ПРИМЕР: рассмотрим утверждение, (A ⋅ B) ⊃ C A, B, C — три простых утверждения 2 3 L = 8 L =

4 6. 3 Таблица истинности — демонстрация ПРИМЕР: (A V ~ B) ⊃ B Два разных предложения 2 2 = 4, поэтому четыре строки

5 6.3 Таблица истинности — демонстрационный ПРИМЕР: (A V ~ B) ⊃ B Два разных предложения 2 2 = 4, поэтому четыре строки (A V ~ B) ⊃ B T T F T T T T T T F F F F F F T T T F T T F T F

6 6.3. Классификация утверждений Тавтологии Тавтологические утверждения, также известные как логически истинные утверждения, верны независимо от значений истинности их компонентов. Примеры: — A V ~ A — (A ⊃ B) ⊃ (B ⊃ A)

7 6.3 Классификация утверждений Самопротиворечивые утверждения Самопротиворечивые утверждения, также известные как логически ложные утверждения, ложны независимо от значений истинности их компонентов. Примеры: — A ⋅ ~ A — (B V C) ≡ (~ B ⋅ ~ C)

8 6. 3 Классификация утверждений. Условные утверждения. Условные утверждения верны или ложны в зависимости от значений истинности их компонентов. Примеры: — A V B — B ⊃ C

9 6.3 Ваша очередь Тавтологична, противоречива или условна? 1. N ⊃ (N ⊃ N) 2. (A ⊃ B) ⋅ (A ⋅ ~ B) 3. [C ⊃ (D ⊃ E)] ≡ [(C ⊃ D) ⊃ E]

10 6.3 Ваш ход Тавтологичный, противоречивый или случайный? 1. N ⊃ (N ⊃ N) тавтологично 2. (A ⊃ B) ⋅ (A ⋅ ~ B) противоречиво 3. [C ⊃ (D ⊃ E)] ≡ [(C ⊃ D)

8.3 Таблицы истинности для аргументного анализа

Таблица истинности анализа аргументов

Мы почти закончили с таблицами истинности.Следующее, для чего мы можем использовать их в логике, — это определить, является ли аргумент в логике высказываний действительным или недействительным.

Ключ состоит в том, чтобы знать, что значит сказать, что аргумент действителен, и знать, как отобразить это в таблице истинности.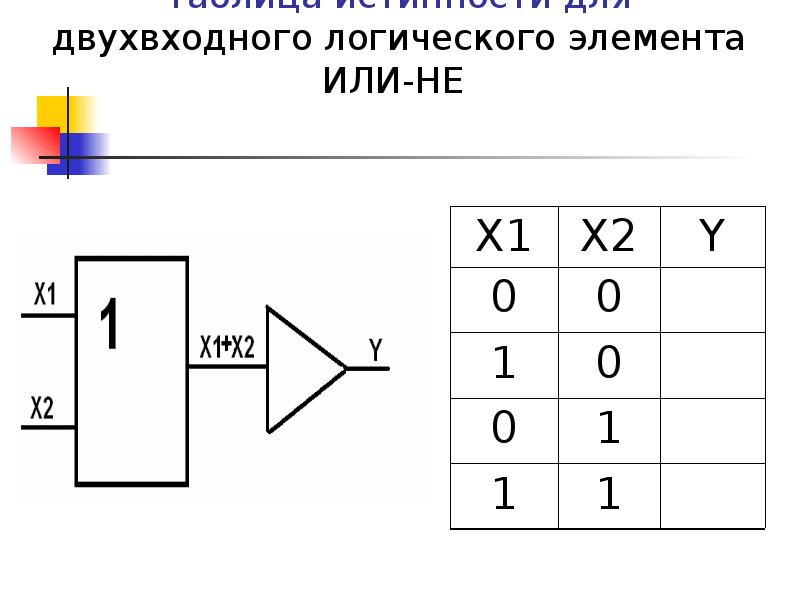

Это означает, что , если все предпосылки верны, невозможно, чтобы заключение было ложным . Это не означает, что посылки все верны, но что , если они верны, они потребуют истинного заключения.

К этому можно также плодотворно подойти со стороны недействительности. «Недействительный» означает, что даже если все предпосылки верны, они не требуют, чтобы заключение было верным.

Итак, если вы нашли строку в таблице истинности для аргумента, по которому заключение было F, но все предпосылки были T, аргумент будет недействительным. И если вы нашли линию, на которой заключение было T, и все посылки также были T, но затем на другой строке вывод был F, а посылки были T, аргумент также был бы неверным.То есть не должно быть строки без строки , на которой были бы все помещения T и вывод F, чтобы таблица показывала, что он действителен.

Подход с использованием таблицы истинности означает, что если аргумент недействителен, он действителен. Итак, вы должны проверить аргумент на недействительность, и для этого вы должны четко понимать, что искать.

Как вы думаете, что вы должны сказать о аргументе, имеющем противоречивые посылки?

Давайте посмотрим на несколько примеров.

Во-первых, обратите внимание, что я ввел косые черты.Это означает, что у нас есть аргумент. Для отделения помещений друг от друга используется одинарная косая черта. Перед заключением ставится двойная косая черта, которая всегда будет отображаться как самое правое утверждение.

(стр.	>	к)	/ ~ с	// ~ д
т	т	Т	Ф	f
т	Ф	F	Ф	т
Ф	т	Т	т	f
Ф	т	F	т	т

Это правильно заполнено. Значения для помещений выделены жирным шрифтом , , а значения вывода — строчными. Есть четыре варианта, то есть четыре строки для чтения. В первой строке не обе посылки верны, поэтому вывод F еще не означает, что он неверен. Во второй строке обе посылки — F, поэтому эта строка нам ничего не говорит. В третьей строке обе посылки обозначены буквой T, а вывод — буквой F, что означает, что он неверен, потому что это случай, когда истинный вывод не генерируется, несмотря на то, что все предпосылки истинны.Это все, что нам нужно знать, мы можем перестать это читать. Но давайте все равно зачитаем четвертую строчку, потому что она поучительна. В четвертой строке обе посылки — буква Т, как и заключение. Что мы думаем об этом?

Ничего. Это ничего не значит, поскольку третья строка показывает, что этот аргумент не гарантирует T выводов из T предпосылок, но допускает возможность F выводов. Это делает форму ненадежной, не на сто процентов надежной, недействительной.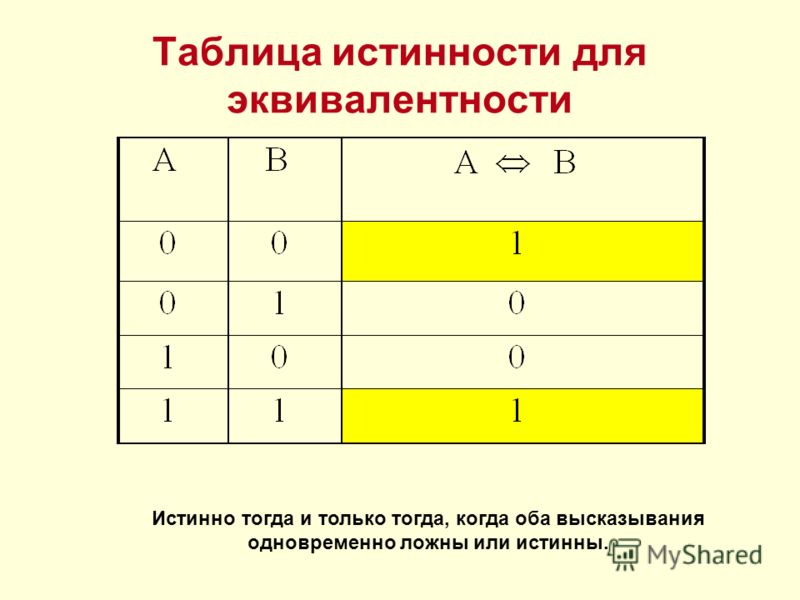

Надеюсь, вы узнали эту форму; он известен по фразе, описывающей то, что делают его помещения.(Отрицая антецедент.)

[youtube] [/ youtube]

У этого есть имя, которое вы также должны знать:

(стр.	>	к)	/ кв	// п.
т	Т	Т	Т	Т
т	F	F	F	Т
Ф	Т	Т	Т	F
Ф	Т	F	F	F

Недействительность здесь также показана в третьей строке, где обе посылки — T, а заключение — F.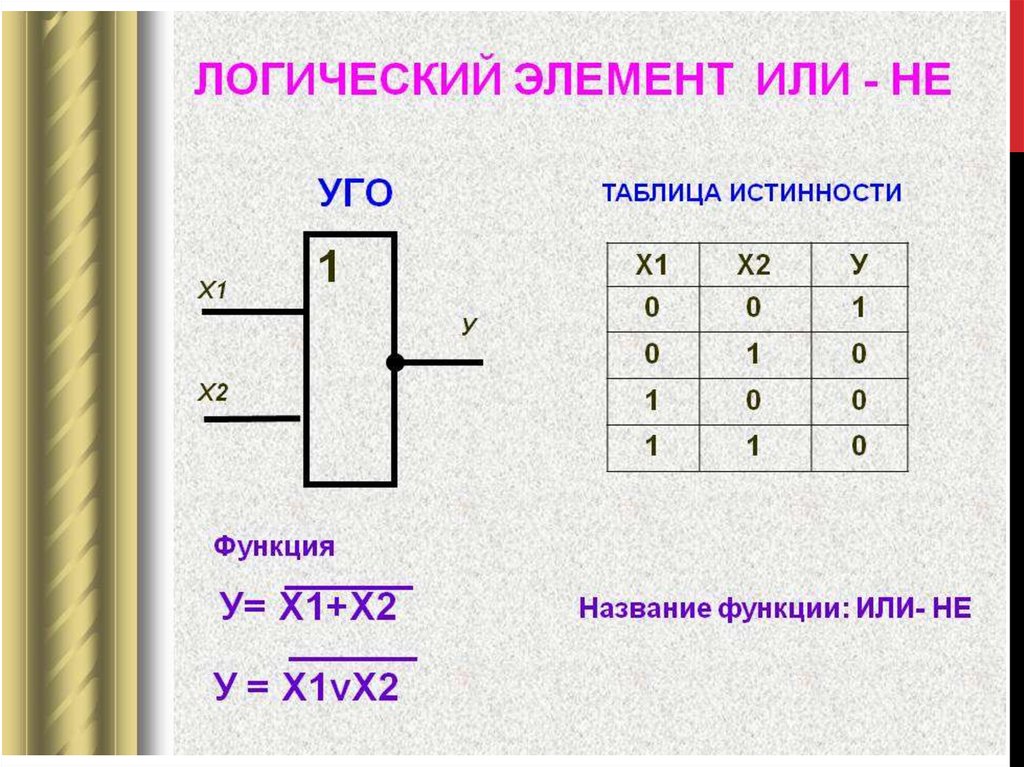 Первая строка, в которой и посылки, и заключение являются T, не указывает ничего, что могло бы противодействовать тому, что показывает третья строка, а именно, что эта форма допускает возможность T посылок и F вывода.

Это Подтверждающее Следствие .

Вот еще один вариант:

~	(G	∙	М)	/ M	v	~ G	// ~ G
Ф	Т	Т	Т	Т	т	F	F
т	Т	F	F	F	Ф	F	F
т	F	F	Т	т	т	Т	т
т	F	F	F	F	т	Т	т

В помещении сказано: «Не одновременно G и M.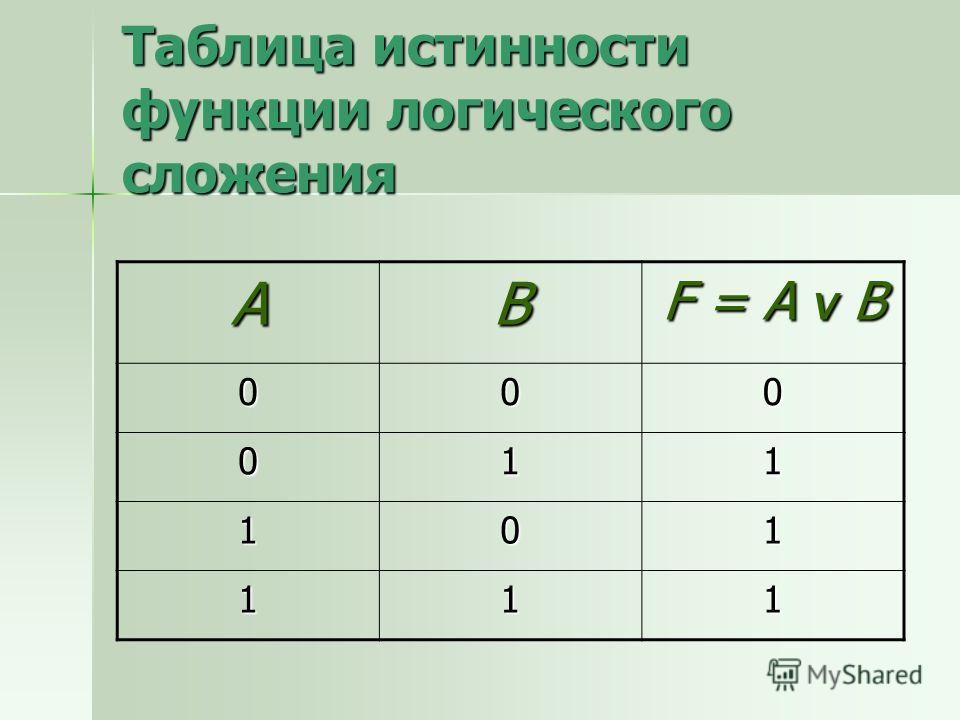 Либо M, либо G ложны ». Вывод: «Не Г.».

Это может быть

Неверно, что и Гарфилд, и Мармадьюк — собаки. Либо Мармадьюк собака, либо не Гарфилд. Следовательно, Гарфилд не один.

Что показывает таблица? Это показывает, что всякий раз, когда вывод — F, по крайней мере, одна посылка тоже F. В первой и второй строках вывод — F. Но в первой строке первая посылка — это F (смотрите под знаком ~), а во второй строке вторая посылка — F (смотрите под v).Это показывает, что он не недействителен, следовательно, действителен.

В следующих двух строках показаны все посылки T и заключение T. Но даже если мы не будем внимательно смотреть на них, мы можем сказать, что оно верное, потому что единственный шанс на его недействительность — это когда вывод F, и мы уже видел все возможности этого.

8 Таблицы истинности аргументов

Вот несколько упражнений, над которыми вы можете практиковаться:

1. P ≡ ~ N // N v P

2. K ≡ ~ L / ~ (L ∙ ~ K) // K> L

3. Z // E> (Z> E)

4. C ≡ D / E v ~ D // E> C

5. A> (B v C) / ~ C v B // A> B

6. J> (K> L) / K> (J> L) // (J v K)> L

7. Если Сартр экзистенциалист, то Витгенштейн написал Трактат, следовательно, если Витгенштейн написал Трактат, Сартр экзистенциалист.

8. Херли — президент, так что либо он президент, либо Аккерманн — декан.

9.Если «время летит» — это метафора, это не совсем так. Если это не совсем так, тогда время не летит, поэтому, если «время летит» — метафора, то время не летит.

10. Если аргумент от дизайна слабый, это слабая аналогия. Чтобы быть слабой аналогией, оно должно проводить неоправданное сравнение, поэтому аргумент, исходящий от дизайна, дает неоправданное сравнение.

11. Зима холодная, а лето жаркое, поэтому либо лето жаркое, либо луна сделана из зеленого сыра.

12.Рассел был либо реалистом, либо эмпириком. Если первое, то он не был идеалистом, значит, он не был эмпириком.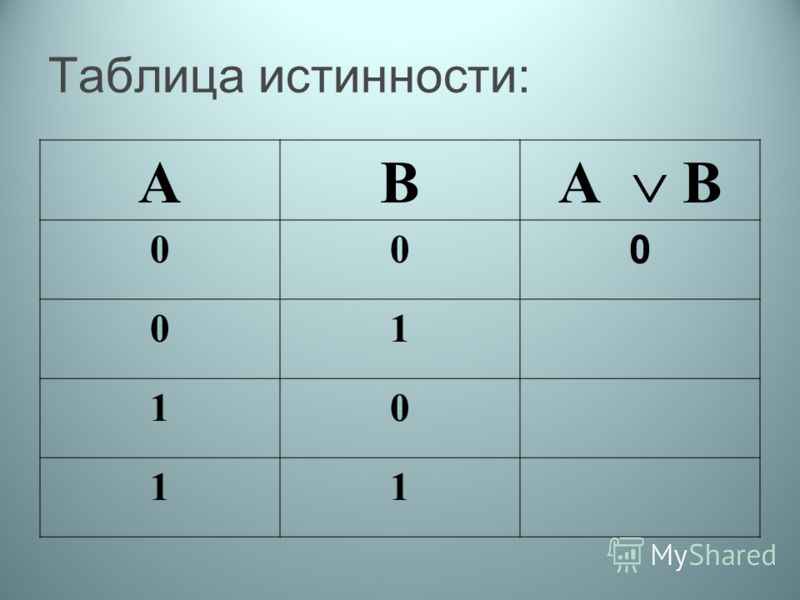

13. Если он любит ее, он женится на ней. Поэтому, если он ее не любит, он не женится на ней.

14. Если люди смогут поселиться на Луне, они смогут поселиться на Марсе. Если они смогут поселиться на Марсе, они смогут поселиться на Юпитере. Итак, если Луна может быть заселена, то и Юпитер может.

15. Этот аргумент недействителен тогда и только тогда, когда он может иметь истинные посылки и ложный вывод.Следовательно, он недействителен, так как имеет ложное заключение.

16. Тот факт, что животные менее умны, чем мы, не означает, что мы можем пренебрегать их благополучием. Если мы пренебрегаем их благополучием, тогда мы бесчеловечны и ничем не лучше самих животных. Таким образом, если мы пренебрегаем их благополучием, будет ошибкой считать, что они менее умны, чем мы.

17. Если Швеция находится в Северной Африке, то либо египтяне голубоглазые, либо шведы смуглые и красивые. Швеция находится не в Северной Африке, поэтому египтяне не голубоглазые.