Как рассчитать общее сопротивление при параллельном и последовательном соединении резисторов. Какие формулы используются для расчетов. В каких случаях применяется каждый тип соединения. Как распределяются ток и напряжение в цепи при разных соединениях.
Особенности последовательного соединения резисторов
При последовательном соединении резисторы подключаются друг за другом, образуя неразветвленную цепь. Основные характеристики такого соединения:
- Общее сопротивление равно сумме сопротивлений всех резисторов: R = R1 + R2 + R3 + …
- Сила тока одинакова во всех участках цепи: I = I1 = I2 = I3
- Общее напряжение равно сумме напряжений на каждом резисторе: U = U1 + U2 + U3
- Напряжение распределяется пропорционально сопротивлениям: U1 : U2 : U3 = R1 : R2 : R3
Таким образом, при последовательном соединении общее сопротивление увеличивается, а сила тока уменьшается по сравнению с отдельными резисторами.
Формула расчета общего сопротивления при последовательном соединении
Для расчета общего сопротивления при последовательном соединении используется формула:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Например, если соединить последовательно резисторы 10 Ом, 20 Ом и 30 Ом, общее сопротивление составит:
R = 10 + 20 + 30 = 60 Ом
Особенности параллельного соединения резисторов
При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Основные характеристики:
- Общая проводимость равна сумме проводимостей резисторов: 1/R = 1/R1 + 1/R2 + 1/R3 + …
- Напряжение одинаково на всех резисторах: U = U1 = U2 = U3
- Общий ток равен сумме токов через каждый резистор: I = I1 + I2 + I3
- Токи распределяются обратно пропорционально сопротивлениям: I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3
При параллельном соединении общее сопротивление уменьшается, а сила тока увеличивается по сравнению с отдельными резисторами.
Формула расчета общего сопротивления при параллельном соединении
Для расчета общего сопротивления при параллельном соединении используется формула:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Для двух параллельно соединенных резисторов формула упрощается:
R = (R1 * R2) / (R1 + R2)
Например, если соединить параллельно резисторы 10 Ом и 20 Ом, общее сопротивление составит:
R = (10 * 20) / (10 + 20) = 200 / 30 ≈ 6,67 Ом
Применение последовательного соединения резисторов
Последовательное соединение резисторов применяется в следующих случаях:
- Для увеличения общего сопротивления цепи
- Для снижения тока в цепи
- Для распределения напряжения между несколькими потребителями
- В делителях напряжения
- В предохранителях и выключателях для разрыва всей цепи
Классический пример — елочная гирлянда, где лампочки соединены последовательно. При перегорании одной лампочки гаснет вся гирлянда.
Применение параллельного соединения резисторов
Параллельное соединение резисторов используется в таких случаях:
- Для уменьшения общего сопротивления цепи
- Для увеличения общего тока
- Для обеспечения независимой работы потребителей
- В бытовой электропроводке для подключения розеток и приборов
- В осветительных приборах для соединения ламп
Например, в люстре все лампочки подключены параллельно. При перегорании одной лампы остальные продолжают работать.
Смешанное соединение резисторов
На практике часто используется смешанное (последовательно-параллельное) соединение резисторов. Оно позволяет получить нужное общее сопротивление, комбинируя имеющиеся номиналы резисторов.
Для расчета общего сопротивления при смешанном соединении используют метод постепенного преобразования схемы:
- Рассчитывают сопротивление параллельных участков
- Заменяют их эквивалентными резисторами
- Рассчитывают общее сопротивление последовательно соединенных участков
Например, для схемы из трех резисторов R1 и R2 параллельно, а R3 последовательно с ними, общее сопротивление составит:
R = (R1 * R2) / (R1 + R2) + R3
Как выбрать способ соединения резисторов?
При выборе способа соединения резисторов следует учитывать:
- Требуемое общее сопротивление цепи
- Необходимые значения тока и напряжения
- Мощность рассеивания
- Надежность работы схемы
Последовательное соединение увеличивает сопротивление и уменьшает ток. Параллельное — уменьшает сопротивление и увеличивает ток. Смешанное соединение позволяет достичь компромисса между этими параметрами.
Правильный выбор способа соединения резисторов позволяет оптимизировать работу электрической цепи под конкретные задачи.
Параллельное соединение резисторов
Физика > Параллельное соединение резисторов
Чему равно сопротивление резисторов при параллельном соединении: общее сопротивление цепи, схема параллельного соединения, формула закона Ома, расчет.
В параллельной цепи полное сопротивление достигает суммы инверсии каждого.
Задача обучения
- Определить общее сопротивление.
Основные пункты
- В параллельном соединении полное сопротивление меньше, чем наименьшее из отдельных.
- Каждый резистор наделен одним напряжением.
- Параллельные резисторы получают общее количество тока, но и делят его.
Термины
- Параллельность – расположение электрических составляющих так, чтобы ток протекал вдоль двух или более путей.
- Сопротивление – противодействие потоку электрического тока.
Обзор
Резисторы в электрической схеме цепи могут располагаться последовательно или параллельно. Полное сопротивление зависит от индивидуальных значений и метода связи.
Параллельное соединение
Мы сталкиваемся с параллельным соединением резисторов, если каждый резистор подключается к источнику напряжения индивидуально. Поэтому каждый обладает полным напряжением. Ниже представлена схема параллельного соединения резисторов в электрической цепи.
Параллельное соединение резисторов
Резисторы используют столько тока, как если бы они были единственными в цепи. Это применяют в доме, чтобы обеспечить независимую работу прибора.
Закон Ома в параллельном подключении
У каждого резистора есть полное напряжение. Тогда закон Ома будет выглядеть как:
I1 = V/R1
I2 = V/R2
I3 = V/R3.
Суммарный ток будет приравниваться к результату сложения отдельных:
Три резистора в параллельном соединении с батареей и эквивалентным сопротивлением
I = I1 + I2 + I3.
Подставим выражение для отдельных токов: I = V/R1 + V/R2 + V/R3 или I = V (1/R1 + 1/R2 + 1/R3).
Мы видим, что общее сопротивление в параллельном подключении достигает суммы инверсии каждого отдельного. Поэтому выходим на формулу:
Rn(параллельно) = 1/R1 + 1/R2 + 1/R3 … + 1/Rn.
Подобное соотношение выводит на суммарное сопротивление, которое уступает наименьшему из индивидуальных. При параллельном подключении больше тока протекает от источника, чем поток для каждого по отдельности, поэтому сопротивление ниже.
Каждый резистор обладает полным напряжением источника, но и разделяют общий ток. Например, у нас есть батарея 1.5В. В последовательном подключении две лампочки будут гореть также ярко, как если бы это была всего одна. Однако батарея расходуется быстрее, потому что гарантирует полную энергию сразу для двух лампочек.
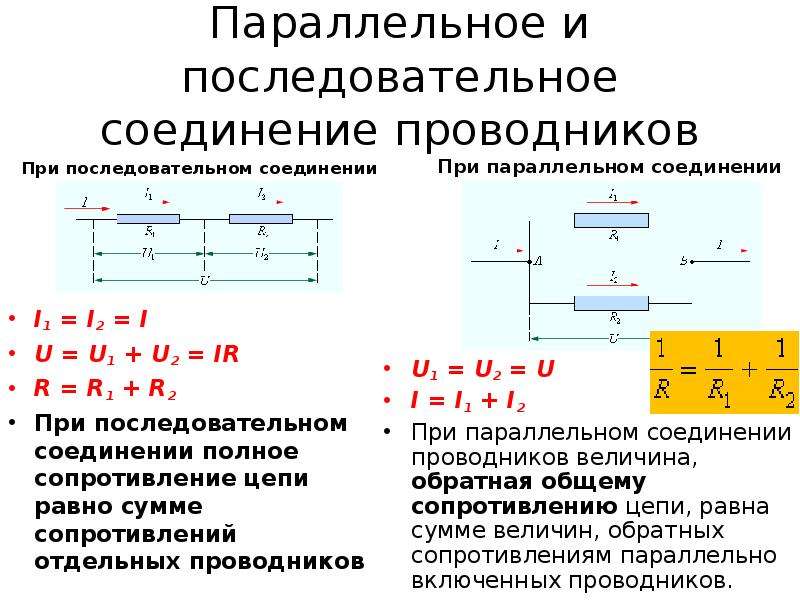
Последовательное и параллельное соединение проводников резисторов. Параллельное соединение сопротивлениий (резисторов)
1. При последовательном соединении проводников
1. Сила тока во всех проводниках одинакова :
I 1 = I 2 = I
2. Общее напряжение U на обоих проводниках равно сумме напряжений U 1 и U 2 на каждом проводнике :
U = U 1 + U 2
3. По закону Ома, напряжения U 1 и U 2 на проводниках равны U 1 = IR 1 , U 2 = IR 2 а общее напряжение U = IR где R – электрическое сопротивление всей цепи, тогда IR = IR 1 + I R 2. Отсюда следует
R = R 1 + R 2
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
2. При параллельном соединении проводников
1. Напряжения U 1 и U 2 на обоих проводниках одинаковы
U 1 = U 2 = U
2. Сумма токов I 1 + I 2 , протекающих по обоим проводникам, равна току в неразветвленной цепи :
I = I 1 + I 2
Этот результат следует из того, что в точках разветвления токов (узлы A и B ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд I Δt , а утекает от узла за то же время заряд I 1 Δt + I 2 Δt . Следовательно, I = I 1 + I 2 .
3. Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получимПри параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рисунке приведен пример такой сложной цепи и указана последовательность вычислений. Сопротивления всех проводников указаны в омах (Ом).
На пракутике одного источника тока в цепи бывает недостаточно, и тогда источники тока тоже соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединяются разноименными полюсами.
Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.
Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε 1 + ε 2 + ε 3
2 . Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников r батареи = r 1 + r 2 + r 3
Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε 1, а сопротивление r батареи = nr 1
3.
При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.
Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).
Параллельно соединяют только источники с одинаковой ЭДС . Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε 1 = ε 2 = ε 3
2.
Сопротивление батареи меньше, чем сопротивление одного источника
r батареи = r 1 /n
3.
Сила тока в такой цепи по закону Ома
Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы — параллельно или последовательно.
Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Для параллельного соединения сопротивлений характерны следующие свойства:
Напряжения на зажимах всех сопротивлений одинаковы:
U 1 = U 2 =U 3 =U ;
Проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:
1/R = 1/R 1 + 1/R 2 + 1/R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 /R 1 R 2 R 3 ,
где R — эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае R 1 , R 2 и R 3 ) .
Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости. Следовательно, сопротивление параллельного разветвления из трёх резисторов:
R = R 1 R 2 R 3 /R 1 R 2 + R 2 R 3 + R 1 R 3 .
Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.
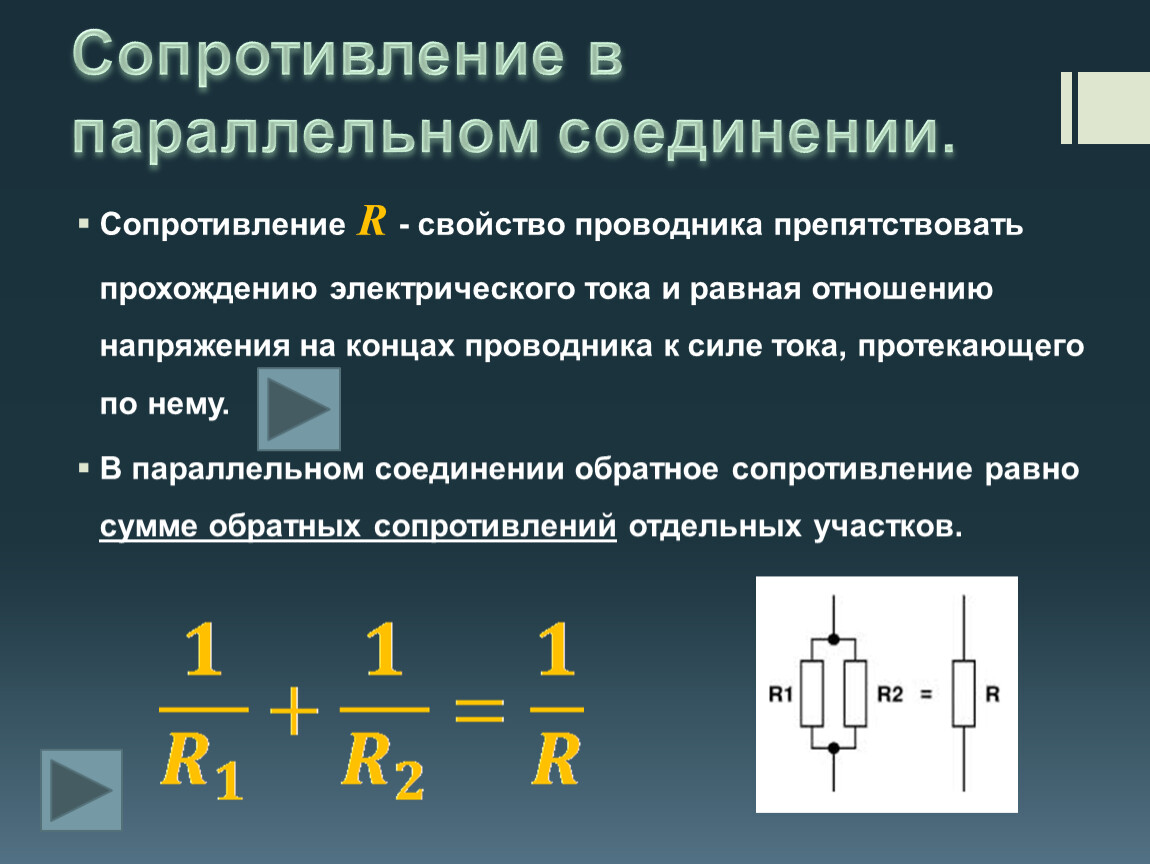
Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.
При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.
На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.
Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений R 1 и R 2 (см. рис.). Проводимость первой ветви равна 1/R 1 , проводимость второй ветви — 1/R 2 . Общая проводимость:
1/R = 1/R 1 + 1/R 2 .
Приведём к общему знаменателю:
1/R = R 2 + R 1 /R 1 R 2 ,
отсюда эквивалентное сопротивление
R = R 1 R 2 /R 1 + R 2 .
Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.
Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.
При параллельном соединении n равных сопротивлений R 1 эквивалентное сопротивление их будет в n раз меньше, т.е.
R = R 1 /n .
На схеме, изображённой на последнем рисунке, включено пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R будет
R = R 1 /5 = 30/5 = 6 Ом.
Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:
I = I 1 + I 2 + I 3 .
Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то
U = I 1 R 1 и U = I 2 R 2 .
Левые части этих равенств одинаковы, следовательно, равны и правые части:
I 1 R 1 = I 2 R 2 ,
или
I 1 /I 2 = R 2 /R 1 ,
Т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.
Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.
При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.
Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить общее сопротивление цепи R общ .
Решение. R общ = R 1 R 2 /R 1 + R 2 = 25 . 50 / 25 + 50 ≈ 16, 6 Ом.
Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1, 5 ампера и третьей I 3 = 2, 5 ампера. Определить общий ток цепи накала ламп усилителя I общ .
Решение. I общ = I 1 + I 2 + I 3 = 1 + 1, 5 + 2, 5 = 5 ампер.
Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.
Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов
.
При последовательном соединении
нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)
где R
эк
=
R 1 + R 2 + R 3
.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов
. При параллельном соединении
нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов
. Смешанным соединением
называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
Параллельное и последовательное соединение резисторов
Автор Alexey На чтение 5 мин. Просмотров 724 Опубликовано Обновлено
В электротехнике и электронике очень широко используются резисторы. Применяются они в основном для регулирования в схемах тока и напряжения. Основные параметры : электрическое сопротивление (R) измеряется в Омах, мощность (Вт) , стабильность и точность их параметров в процессе эксплуатации. Можно вспомнить ещё множество его параметров , — ведь это обычное промышленное изделие.
Последовательное соединение
Последовательное соединение — это такое соединение, при котором каждый последующий резистор подключается к предыдущему, образуя неразрывную цепь без разветвлений. Ток I=I1=I2 в такой цепи будет одинаковым в каждой её точке. Напротив, напряжение U1, U2 в различных её точках будет разным, причём работа по переносу заряда через всю цепь, складывается из работ по переносу заряда в каждом из резисторов, U=U1+U2. Напряжение U по закону Ома равно току, умноженному на сопротивление, и предыдущее выражение можно записать так:
IR=IR1+IR2,
где R — общее сопротивление цепи. То есть по простому идет падение напряжения в точках соединения резисторов и чем больше подключенных элементов , тем больше происходит падение напряжения
Отсюда следует, что , общее значение такого соединения определяется суммированием сопротивлений последовательно . Наши рассуждения справедливы для любого количества последовательно соединяемых участков цепи.
Параллельное соединение
Объединим начала нескольких резисторов (точка А). В другой точке (В) мы соединим все их концы. В результате получим участок цепи, который называется параллельным соединением и состоит из некоторого количества параллельных друг другу ветвей (в нашем случае – резисторов). При этом электрический ток между точками А и B распределится по каждой из этих ветвей.
Напряжения на всех резисторах будут одинаковы: U=U1=U2=U3, их концы — это точки А и В.
Заряды, прошедшие за единицу времени через каждый резистор, в сумме образуют заряд, прошедший через весь блок. Поэтому суммарный ток через изображенную на рисунке цепь I=I1+I2+I3.
Теперь, использовав закон Ома, последнее равенство преобразуется к такому виду:
U/R=U/R1+U/R2+U/R3.
Отсюда следует, что для эквивалентного сопротивления R справедливо:
1/R=1/R1+1/R2+1/R3
или после преобразования формулы мы можем получить другую запись, такого вида : .
Чем большее количество резисторов (или других звеньев электрической цепи, обладающих некоторым сопротивлением) соединить по параллельной схеме, тем больше путей для протекания тока образуется, и тем меньше общее сопротивление цепи.
Следует отметить, что обратная сопротивлению величина называется проводимостью. Можно сказать, что при параллельном соединении участков цепи складываются проводимости этих участков, а при последовательном соединении – их сопротивления.
Примеры использования
Понятно, что при последовательном соединении, разрыв цепи в одном месте приводит к тому, что ток перестает идти по всей цепи. Например, ёлочная гирлянда перестаёт светить, если перегорит всего одна лампочка, это плохо.
Но последовательное соединение лампочек в гирлянде даёт возможность использовать большое количество маленьких лампочек, каждая из которых рассчитана на напряжение сети (220 В), делённое на количество лампочек.
Последовательное соединение резисторов на примере 3-х лампочек и ЭДСЗато при последовательном подключении предохранительного устройства его срабатывание (разрыв плавкой вставки) позволяет обесточить всю электрическую цепь, расположенную после него и обеспечить нужный уровень безопасности, и это хорошо. Выключатель в сеть питания электроприбора включается также последовательно.
Параллельное соединение также широко используется. Например, люстра – все лампочки соединены параллельно и находятся под одним и тем же напряжением. Если одна лампа перегорит, — не страшно, остальные не погаснут, они остаются под тем же самым напряжением.
Параллельное соединение резисторов на примере 3-х лампочек и генератораПри необходимости увеличения способности схемы рассеивать тепловую мощность, выделяющуюся при протекании тока, широко используются и последовательное, и параллельное объединение резисторов. И для последовательного, и параллельного способов соединения некоторого количества резисторов одного номинала общая мощность равна произведению количества резисторов на мощность одного резистора.
Смешанное соединение резисторовТакже часто используется смешанное соединение . Если ,например необходимо получить сопротивление определенного номинала, но его нет в наличии можно воспользоваться одним из выше описанных способов или воспользоваться смешанным соединением.
Отсюда , можно вывести формулу которая и даст нам необходимое значение:
Rобщ.=(R1*R2/R1+R2)+R3
В нашу эпоху развития электроники и различных технических устройств в основе всех сложностей лежать простые законы, которые поверхностно рассматриваются на данном сайте и думаю, что вам они помогут успешно применять в своей жизни. Если например взять ёлочную гирлянду , то соединения лампочек идет друг за другом , т.е. грубо говоря это отдельно-взятое сопротивление.
Не так давно гирлянды стали соединятся смешанным способом. Вообще , в совокупности все эти примеры с резисторами взяты условно , т.е. любым элементом сопротивления может быть ток проходящий через элемент с падением напряжения и выделением тепла.
последовательное, параллельное, смешанное соединение. Расчет сопротивления
электрика, сигнализация, видеонаблюдение, контроль доступа (СКУД), инженерно технические системы (ИТС)
Резисторы между собой могут быть соединены двумя основными способами: последовательно и параллельно. Смешанное соединение резисторов является их комбинацией.
Сочетания любых соединений резисторов можно привести к одному резистору, расчетом сопротивления которого (R) мы сейчас займемся.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Давайте рассчитаем общее сопротивление такой цепи (рисунок 1). Для этого нам понадобится закон Ома — I=U/R и закон Кирхгофа — I=I1+I2+..In
С учетом этого имеем:
- I=U/R
- I1=U/R1
- I2=U/R2
- In=U/Rn
- U/R=U/R1+U/R2+…U/Rn
- 1/R=1/R1+1/R2+…1/Rn
Последняя формула является основной для расчета сопротивления цепи параллельно соединенных резисторов. Для двух резисторов ее можно записать более удобно: R=(R1*R2)/(R1+R2).
Отсюда следует, что в случае параллельного соединения двух одинаковых по номиналу резисторов (R1=R2) их общее сопротивление будет вдвое меньше любого из них. Это полезно помнить.
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Используя уже упомянутые законы для цепи последовательно соединенных резисторов (рисунок 2) можем записать:
- U=I*R
- I=I1=I2=…In
- U=U1+U2+…Un
- I*R=I*R1+I*R2+…I*Rn
- R=R1+R2+…Rn
То есть общее сопротивление резисторов при последовательном соединении равно сумме их сопротивлений.
СМЕШАННОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Такое соединение всегда можно представить как комбинацию последовательного и параллельного соединений (рис.3).
Расчет общего сопротивления цепи при этом производится поэтапно. В приведенном примере рассчитываем:
- последовательное сопротивление резисторов Rпосл=R1+R2
- параллельное соединение R=(Rпосл*R3)/(Rпосл+R3)
Безусловно, могут встретиться более сложные варианты, но методика расчета их сопротивления та же.
Несколько слов про то, когда возникает необходимость соединять резисторы тем или иным способом:
- Отсутствие «под рукой» резистора нужного номинала. При этом следует помнить, что погрешности резисторов будут суммироваться.
Например, для рисунка 3.a, если фактическая погрешность R1 составляет +10%, а R2 имеет +15%, то для Rпосл она будет +25%.
Здесь следует обращать внимание на знак, то есть для -10% и +15% в результате получим +5%.
- Необходимость получить большую мощность.
Здесь надо учесть, что при одинаковых номиналах сопротивлений и мощностей соединяемых резисторов, как при последовательном, так и при параллельном их соединении итоговая мощность будет равна сумме мощностей.
В противном случае следует ее рассчитать, используя закон Ома и формулу для определения рассеиваемой мощности P=I*U.
Про мощность и номиналы резисторов можно почитать здесь.
© 2012-2021 г. Все права защищены.
Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов
Формулы параллельного, последовательного и смешанного соединения резисторов
Автор Aluarius На чтение 7 мин. Просмотров 4.5k. Опубликовано
Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.
Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».
Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC).
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC
О разнице подключения звезда и треугольник читайте здесь.
Чему равна сила тока в цепи при параллельном соединении резисторов
Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.
Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.
Решение задачи производится путем разделения резистивных элементов на системные группы.
Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.
Считаем сопротивление Rобщ1 = R2+R3+R4.
Выделяем вторую группу из последовательных элементов R1, R5, R6.
Считаем сопротивление Rобщ2 = R1+R5+R6.
Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
Схемы соединения резисторов
Последовательное соединение резисторов
Последовательное соединение резисторов
Iобщ = I1 = I2 = I3
Uобщ = U1 + U2 + U3
Параллельное соединение резисторов
Параллельное соединение резисторов
Iобщ = I1 + I2 + I3
Uобщ = U1 = U2 = U3
Реостат
Реостат – это переменный резистор, который включается в цепь последовательно с потребителем нагрузки.
Изменяя положение ползунка, в цепи меняется ток от 0 до max.
Реостат применяется для изменения тока в цепи.
В электрических схемах встречается понятие – реостатное включение нагрузки.
Реостатное включение нагрузки
| T1 I = | Uист Rр + Rн |
→ max |
RP = 0
| T2 I = | Uист Rр + Rн |
→ min |
Гасящий резистор
В радиосхемах возникает необходимость подавать на потребитель напряжение меньше чем развивает источник, тогда между источником и нагрузкой включается гасящий резистор.
Применение – в схеме создания напряжения смещения на участке эмиттер-база транзистора.
Гасящий резистор
Uгас = Uист – URн
PRгас = I2 – Rгас
Делитель напряжения
Делитель напряжения
Делитель напряжения – это цепь, состоящая из нескольких последовательно соединённых резисторов обеспечивающих подачу на потребитель некоторой части напряжения источника.
Потенциометр
Потенциометр – это переменный резистор, с части которого снимается напряжения источника.
Потенциометр
Применение – регулировка громкости на входе усилителя низкой частоты.
| НОВОСТИ ФОРУМА Рыцари теории эфира |
13.06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> [center][Youtube]tXZcSDqQ9A4[/Youtube][/center] |
[center][b]Гибель пчел в Курчатовском районе [/center]
[center][b]Массовая гибель пчёл 2019. г. Павловск Воронежской об [/center]л
[center][b]Массовая гибель пчел в Добринском районе. В чем причина? [/center]
Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь понять, а не обижаться)
Горькая истина заключается в том, что людская толпа – это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна.
Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди,
даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция – есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов.
Последовательное соединение резисторов
Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).
Рисунок 2. Последовательное соединение резисторов.
То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток.
Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:
Rобщ = R1 + R2 + R3+. + Rn.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).
Рисунок 3. Параллельное соединение резисторов.
При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:
1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn
Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:
Rобщ= R1*R2/R1+R2
Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них.
Смешанное соединение резисторов
Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
На рисунке 4 показан простейший пример смешанного соединения резисторов.
Рисунок 4. Смешанное соединение резисторов.
На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.
Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.
Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
резисторов последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
- Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Contrast (Контраст), как рассчитывается общее сопротивление для резисторов, включенных последовательно и параллельно.
- Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Вычислить общее сопротивление цепи, которая содержит смесь резисторов, включенных последовательно и параллельно.
Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Рис. 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток протекает через человека, держащего отвертку, и попадает в Землю, тогда R 1 на Рисунке 1 (а) может быть сопротивлением вала отвертки, R 2 сопротивлением ее ручки , R 3 сопротивления тела человека и R 4 сопротивления его обуви.На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. прибор, уменьшающий рабочий ток.)
Рис. 2. Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на рисунке 2. Согласно закону Ома, падение напряжения, В, , на резистор, когда через него протекает ток, рассчитывается по формуле V = IR , где I равно току в амперах (A), а R — сопротивление в омах (Ω).Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , что на R 2 составляет В 2 = IR 2 и что для R 3 это V 3 = IR 3 .Сумма этих напряжений равна выходному напряжению источника; то есть
В = В 1 + В 2 + В 3 .
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV , где q — электрический заряд, а V — напряжение. Таким образом, энергия, подаваемая источником, составляет кв.кв. , а энергия, рассеиваемая резисторами, равна
.qV 1 + qV 2 + qV 3 .
Установление связей: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые гласят, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии.Таким образом, qV = qV 1 + qV 2 + qV 3 . Плата q аннулируется, давая V = V 1 + V 2 + V 3 , как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.) Теперь подстановка значений для отдельных напряжений дает
В = IR 1 + IR 2 + IR 3 = I ( R 1 + R 2 + R 3 ).
Обратите внимание, что для эквивалентного сопротивления одной серии R с , мы имеем
В = ИК с .
Это означает, что полное или эквивалентное последовательное сопротивление R с трех резисторов составляет R с = R 1 + R 2 + R 3 .Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление R с последовательного соединения составляет
R с = R 1 + R 2 + R 3 +…,
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 2 равно 12.0 В, а сопротивления равны R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
[латекс] \ begin {array} {lll} {R} _ {\ text {s}} & = & {R} _ {1} + {R} _ {2} + {R} _ {3} \ \ & = & 1.00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].
Стратегия и решение для (b)
Ток определяется по закону Ома: В = IR . Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
[латекс] I = \ frac {V} {{R} _ {\ text {s}}} = \ frac {12.0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].
Стратегия и решение для (c)
Напряжение — или падение IR — на резисторе определяется законом Ома.Ввод тока и значения первого сопротивления дает
.В 1 = IR 1 = (0,600 A) (1,0 Ом) = 0,600 В.
Аналогично
В 2 = IR 2 = (0,600 A) (6,0 Ом) = 3,60 В
и
V3 = IR 3 = (0,600 A) (13,0 Ом) = 7,80 В.
Обсуждение для (c)
Три капли IR добавляют к 12.0 В, прогноз:
В 1 + В 2 + В 3 = (0,600 + 3,60 + 7,80) В = 12,0 В.
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , P = IV , где P — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома V = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
P 1 = I 2 R 1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт
Аналогично
P 2 = I 2 R 2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт
и
P 3 = I 2 R 3 = (0.{2}} {R} \\ [/ latex], где В, — это падение напряжения на резисторе (а не полное напряжение источника). Будут получены те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P = IV , где В, — напряжение источника. Это дает
P = (0,600 A) (12,0 В) = 7,20 Вт.
Обсуждение для (e)
Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
P 1 + P 2 + P 3 = (0,360 + 2,16 + 4,68) W = 7,20 Вт.
Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Последовательные сопротивления добавить: R с = R 1 + R 2 + R 3 +….
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
На рисунке 3 показаны резисторы , включенные параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления R p , давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} \\ [/ latex] , [латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} \\ [/ latex] и [латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} \\ [/ латекс]. Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:
I = I 1 + I 2 + I 3 .
Подстановка выражений для отдельных токов дает
[латекс] I = \ frac {V} {{R} _ {1}} + \ frac {V} {{R} _ {2}} + \ frac {V} {{R} _ {3}} = V \ left (\ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} \ справа) \\ [/ латекс].
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
[латекс] I = \ frac {V} {{R} _ {p}} = V \ left (\ frac {1} {{R} _ {p}} \ right) \\ [/ latex].
Члены в круглых скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление R p параллельного соединения связано с отдельными сопротивлениями на
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ гидроразрыв {1} {{R} _ {\ text {.} 3}} + \ text {.} \ Text {…} \\ [/ latex]
Это соотношение приводит к общему сопротивлению R p , которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как в ранее рассмотренном последовательном соединении: В = 12.0 В, R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения.Ввод известных значений дает
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} = \ frac {1} {1 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {6 \ text {. } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} \\ [/ latex].
Таким образом,
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1.00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.) Мы должны перевернуть это, чтобы найти полное сопротивление R p . Это дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {1 \ text {.} \ Text {2436}} \ text {} \ Omega = 0 \ text {.} \ Text { 8041} \ text {} \ Omega \\ [/ latex].
Общее сопротивление с правильным количеством значащих цифр составляет R p = 0,804 Ом
Обсуждение для (а)
R p , как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление R p . Это дает
[латекс] I = \ frac {V} {{R} _ {\ text {p}}} = \ frac {\ text {12.0 V}} {0.8041 \ text {} \ Omega} = \ text {14} \ text {.} \ text {92 A} \\ [/ latex].
Обсуждение для (б)
Ток I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
[латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} = \ frac {12.0 \ text {V}} {1.00 \ text {} \ Omega} = 12.0 \ text {A} \\ [/ латекс].
Аналогично
[латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} = \ frac {12.0 \ text {V}} {6.00 \ text {} \ Omega} = 2 \ text {.} \ text {00} \ text {A} \\ [/ latex]
и
[латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} = \ frac {\ text {12} \ text {.} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].
Обсуждение для (c)
Общий ток складывается из отдельных токов:
I 1 + I 2 + I 3 = 14,92 A.
Это соответствует сохранению заряда.{2}} {13.0 \ text {} \ Omega} = 11.1 \ text {W} \\ [/ latex].
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбрав P = IV и введя полный ток, получим
P = IV = (14,92 A) (12,0 В) = 179 Вт.
Обсуждение для (e)
Общая мощность, рассеиваемая резисторами, также составляет 179 Вт:
P 1 + P 2 + P 3 = 144 Вт + 24,0 Вт + 11,1 Вт = 179 Вт
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики резисторов, подключенных параллельно
- Параллельное сопротивление определяется из [latex] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {1}} + \ frac {1} { {R} _ {2}} + \ frac {1} {{R} _ {3}} + \ text {…} \\ [/ latex], и оно меньше любого отдельного сопротивления в комбинации.
- На каждый параллельно включенный резистор подается такое же полное напряжение источника. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно свести к одному эквивалентному сопротивлению, используя технику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс более трудоемкий, чем трудный.
Рис. 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.
Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 4, также является наиболее поучительной, поскольку она используется во многих приложениях.Например, R 1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R 2 и R 3 могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3. Расчет сопротивления,
IR Падение, ток и рассеиваемая мощность: объединение последовательных и параллельных цепейНа рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — сочетание последовательного и параллельного.Можно считать R 1 сопротивлением проводов, ведущих к R 2 и R 3 . (а) Найдите полное сопротивление. (b) Что такое падение IR в R 1 ? (c) Найдите текущие значения с I 2 по R 2 . (d) Какую мощность рассеивает R 2 ?
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация включена последовательно с R 1 .
Стратегия и решение для (а)
Чтобы найти полное сопротивление, отметим, что R 2 и R 3 находятся параллельно, и их комбинация R p находится последовательно с R 1 . Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
.R до = R 1 + R p .
Сначала мы находим R p , используя уравнение для параллельных резисторов и вводя известные значения:
[латекс] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3 }} = \ frac {1} {6 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].
Инвертирование дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {0,2436} \ text {} \ Omega = 4.11 \ text {} \ Omega \\ [/ latex].
Таким образом, общее сопротивление равно
.R до = R 1 + R p = 1,00 Ом + 4,11 Ом = 5,11 Ом.
Обсуждение для (а)
Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом и 0,804 Ом соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение IR в R 1 , отметим, что полный ток I протекает через R 1 . Таким образом, его падение IR составляет
.В 1 = ИК 1
Мы должны найти I , прежде чем сможем вычислить V 1 .Полный ток I находится с помощью закона Ома для схемы. То есть
[латекс] I = \ frac {V} {{R} _ {\ text {tot}}} = \ frac {\ text {12.0} \ text {V}} {5.11 \ text {} \ Omega} = 2.35 \ text {A} \\ [/ latex].
Вводя это в выражение выше, мы получаем
В 1 = IR 1 = (2,35 A) (1,00 Ом) = 2,35 В.
Обсуждение для (б)
Напряжение, приложенное к R 2 и R 3 , меньше полного напряжения на величину В 1 .Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R 2 и R 3 .
Стратегия и решение для (c)
Чтобы найти ток через R 2 , мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение В p , потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное как к R 2 , так и к R 3 , уменьшается на величину В 1 , и поэтому оно составляет
В p = V — V 1 = 12.0 В — 2,35 В = 9,65 В.
Теперь ток I 2 через сопротивление R 2 находится по закону Ома:
[латекс] {I} _ {2} = \ frac {{V} _ {\ text {p}}} {{R} _ {2}} = \ frac {9.65 \ text {V}} {6.00 \ текст {} \ Omega} = 1,61 \ text {A} \\ [/ latex].
Обсуждение для (c)
Ток меньше, чем 2,00 А, которые протекали через R 2 , когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.
Стратегия и решение для (d)
Мощность, рассеиваемая R 2 равна
P 2 = ( I 2 ) 2 R 2 = (1,61 A) 2 (6,00 Ом) = 15,5 Вт
Обсуждение для (d)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное номером R 3 , имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, представленных R 1 , уменьшая напряжение на лампе (которое составляет R 2 ), которое затем заметно гаснет.
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
Проверьте свое понимание
Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.
Решение Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему.
Стратегии решения проблем для последовательных и параллельных резисторов
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении R необходимо соблюдать осторожность.
- Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Сводка раздела
Концептуальные вопросы
1. Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и очень большое в разомкнутом, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.
Рис. 7. Переключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
2. Какое напряжение на разомкнутом переключателе на Рисунке 7?
3. На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?
4. Почему мощность, рассеиваемая замкнутым переключателем, как на Рисунке 7, мала?
5. Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и гаснет, когда выключатель замкнут. (Не пытайтесь — батарея сильно разряжается!)
Рис. 8. Ошибка подключения. Включите этот переключатель параллельно устройству, обозначенному [латекс] R [/ латекс].(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
6. Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он поражен им? Объяснять.
7. Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
8. Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?
9.Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10. Предположим, вы проводите физическую лабораторию, в которой вас просят вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?
11. Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление.Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.
12. У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей нити необходимо для трех режимов мощности?
Задачи и упражнения
Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
1. (a) Каково сопротивление десяти последовательно соединенных резисторов сопротивлением 275 Ом? (б) Параллельно?
2. (a) Каково сопротивление последовательно соединенных резисторов 1,00 × 10 2 Ом, 2,50 кОм и 4,00 кОм? (б) Параллельно?
3. Какое наибольшее и наименьшее сопротивление можно получить, соединив резисторы на 36,0 Ом, 50,0 Ом и 700 Ом?
4. Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если они подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5. Фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)
6.(a) Учитывая батарею на 48,0 В и резисторы на 24,0 и 96,0 Ом, найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.
7. Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите I 3 двумя следующими способами: (a) по известным значениям I и I 2 ; (б) используя закон Ома для R 3 . В обеих частях явно показано, как вы следуете шагам, описанным выше в стратегии решения проблем для последовательных и параллельных резисторов .
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация включена последовательно с R 1 .
8. Ссылаясь на рисунок 5: (a) Вычислите P 3 и обратите внимание на его сравнение с P 3 , найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
9. См. Рисунок 6 и обсуждение затемнения света при включении тяжелого прибора. (a) Учитывая, что источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
10. Линия электропередачи на 240 кВ, имеющая 5,00 × 10 2 , подвешена к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление 1,00 × 10 9 Ом (рис. 9 (а)). Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы следуете шагам, описанным выше в стратегии решения проблем для последовательных и параллельных резисторов .
Рис. 9. Высоковольтная (240 кВ) линия электропередачи 5,00 × 10 2 подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает сопротивление 1,00 × 10 9 Ом каждый.
11. Покажите, что если два резистора R 1 и R 2 объединены, и один из них намного больше другого ( R 1 >> R 2 ): (a ) Их последовательное сопротивление почти равно большему сопротивлению R 1 .(б) Их параллельное сопротивление почти равно меньшему сопротивлению R 2 .
12. Необоснованные результаты Два резистора, один из которых имеет сопротивление 145 Ом, подключены параллельно, чтобы получить общее сопротивление 150 Ом. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
13. Необоснованные результаты Два резистора, один из которых имеет сопротивление 900 кОм, соединены последовательно, чтобы получить общее сопротивление 0.500 МОм. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Глоссарий
- серия:
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор:
- компонент, обеспечивающий сопротивление току, протекающему через электрическую цепь
- сопротивление:
- вызывает потерю электроэнергии в цепи
- Закон Ома:
- соотношение между током, напряжением и сопротивлением в электрической цепи: В = IR
- напряжение:
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором
- падение напряжения:
- потеря электроэнергии при прохождении тока через резистор, провод или другой компонент
- ток:
- поток заряда через электрическую цепь мимо заданной точки измерения
- Закон Джоуля:
- взаимосвязь между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемая следующим образом: [latex] {P} _ {e} = \ text {IV} [/ latex]
- параллельно:
- разводку резисторов или других компонентов в электрической цепи, так что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Избранные решения проблем и упражнения
1.(а) 2,75 кОм (б) 27,5 Ом
3. (а) 786 Ом (б) 20,3 Ом
5. 29,6 Вт
7. (а) 0,74 А (б) 0,742 А
9. (а) 60,8 Вт (б) 3,18 кВт
11. (a) [латекс] \ begin {array} {} {R} _ {\ text {s}} = {R} _ {1} + {R} _ {2} \\ \ Rightarrow {R} _ {\ text {s}} \ приблизительно {R} _ {1} \ left ({R} _ {1} \ text {>>} {R} _ {2} \ right) \ end {array} \\ [/ латекс]
(b) [латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2} } = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ [/ latex],
, так что
[латекс] \ begin {array} {} {R} _ {p} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ приблизительно \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1}} = {R} _ {2} \ left ({R} _ {1 } \ text {>>} {R} _ {2} \ right) \ text {.} \ end {array} \\ [/ latex]
13. (a) –400 кОм (b) Сопротивление не может быть отрицательным. (c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.
резисторов параллельно | Прядильные числа
Компоненты находятся в параллельных , если они совместно используют два узла, например,
Мы раскрываем свойства параллельного соединения, рассматривая схемы резисторов. Определить параллельные резисторы немного сложнее, чем последовательные резисторы.
Автор Вилли Макаллистер.
Содержание
Параллельное соединение
Компоненты работают параллельно, когда их два терминала подключены к одним и тем же узлам.
На следующем изображении $ \ text R1 $, $ \ text R2 $ и $ \ text R3 $ расположены параллельно. Две горизонтальные линии представляют два узла, общие для всех трех резисторов.
Просмотрите определение узла
Просмотрите определения узла и распределенного узла в этой статье о терминологии схемы.Еще один хороший ресурс, который поможет вам разобраться в параллельных схемах, — это статья об эквивалентности схем.
Поскольку резисторы подключены к одним и тем же узлам, на каждом параллельном резисторе появляется одинаковое напряжение.
Сопротивления на следующем изображении — это , а не , подключенные параллельно. Есть дополнительные компоненты (оранжевые прямоугольники), разделяющие общие узлы между резисторами. Эта схема имеет четыре отдельных узла, поэтому $ \ text R1 $, $ \ text R2 $ и $ \ text R3 $ не имеют одного и того же напряжения.
Резисторы параллельно
Вот схема с параллельными резисторами. В этой схеме есть источник тока. Мы не используем их очень часто, так что это должно быть весело.
Текущий источник $ \ text I_ \ text s $ направляет текущий $ i $ к $ \ text R1 $, $ \ text R2 $ и $ \ text R3 $. Текущий $ i $ возвращается на нижний терминал текущего источника. но мы еще не знаем, какое напряжение $ v $ или как $ i $ распадается на токи трех резисторов.
То, что мы знаем,
- Текущее значение $ i $ — некоторое заданное постоянное значение.
- Сумма токов трех резисторов должна составлять $ i $.
- Напряжение $ v $ появляется на всех трех резисторах.
С помощью всего лишь этого небольшого количества знаний и закона Ома мы можем найти то, чего не знаем,
- Нам пока неизвестно напряжение $ v $, появляющееся на резисторах и источнике тока.
- Мы не знаем, как $ i $ распадается на токи трех резисторов.
Используя то, что мы знаем, мы можем записать эти выражения,
$ i = i _ {\ text R1} + i _ {\ text R2} + i _ {\ text R3}
$$ v = i _ {\ text R1} \, \ text R1 \ qquad v = i _ {\ text R2} \, \ text R2 \ qquad v = i _ {\ text R3} \, \ text R3 $
Переставьте три выражения закона Ома, чтобы найти ток,
$ i _ {\ text R1} = \ dfrac {v} {\ text R1} \ qquad i _ {\ text R2} = \ dfrac {v} {\ text R2} \ qquad i _ {\ text R3} = \ dfrac { v} {\ text R3}
долларов СШАПодставляем эти выражения в сумму токов,
$ i = \ dfrac {v} {\ text R1} + \ dfrac {v} {\ text R2} + \ dfrac {v} {\ text R3}
$Выносим за скобки общий термин $ v $,
$ i = v \ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ dfrac {1} {\ text R3} \ right) $
Помните, что мы уже знаем $ i $ (он установлен в текущем источнике), поэтому мы можем решить для $ v $,
$ v = i \, \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ dfrac {1} {\ text R3} \ right )}
долларовВзгляните на это уравнение.Это похоже на закон Ома, $ v = i \, \ text R $, но с резисторами, представленными в виде большого двойного взаимного выражения, где обычно появляется $ \ text R $.
Заключаем,
Для резисторов, включенных параллельно, общее сопротивление обратно пропорционально сумме обратных величин отдельных резисторов.
(Это полнота. Легче понять уравнение, чем произносить его вслух.)
Эквивалентный параллельный резистор
Предыдущее уравнение предлагает способ определения нового резистора , эквивалентного трем параллельным резисторам.
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ dfrac {1} { \ text R3} \ right)}
долларов СШАНовый резистор является величиной, обратной сумме обратных величин. Это эквивалентно в том смысле, что для данного $ i $, вытекающего из источника тока, появляется такое же напряжение $ v $.
Мы можем записать это немного меньше, перевернув гигантское число, равное
.$ \ dfrac {1} {\ text R _ {\ text {parallel}}} = \ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ dfrac {1} {\ text R3}
долларовВы можете заменить три параллельных резистора одним эквивалентным резистором, и $ i $ и $ v $ останутся неизменными.
С «точки зрения» источника тока невозможно отличить эквивалентный резистор от трех параллельных резисторов.
$ \ text N $ резисторы параллельно
Мы можем обобщить уравнение параллельного резистора для любого количества резисторов, включенных параллельно. Вывод этой формулы для резисторов $ \ text N $, включенных параллельно, следует точно таким же шагам, которые мы проделали выше для трех резисторов, включенных параллельно.
$ \ dfrac {1} {\ text R _ {\ text {parallel}}} = \ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ ldots + \ dfrac {1} {\ text {R} _ \ text N}
долларов США$ \ qquad \ quad $
Ток распределяется между резисторами, включенными параллельно
Давайте выясним, как основной ток $ i $ разделяется и течет через каждый резистор.Мы ищем $ i _ {\ text R1} $, $ i _ {\ text R2} $ и $ i _ {\ text R3} $.
Примените закон Ома к отдельным резисторам. $ v $ одинаково в каждом уравнении,
$ i _ {\ text R1} = v / \ text R_1 \ qquad i _ {\ text R2} = v / \ text R_2 \ qquad i _ {\ text R3} = v / \ text R_3 $
Основной ток $ i $ разделяется на три отдельных тока. Эти токи соединяются и текут обратно к источнику тока. Это означает, что отдельные токи резистора должны суммироваться с основным током.
Величина тока в каждом резисторе составляет обратно пропорционально номиналу резистора.
Это будет лучше, если мы сделаем пример с действительными числами.
Проверка концепции
ПРОБЛЕМА 1
а. Найдите напряжение $ v $.
г. Найдите токи в трех резисторах.
г. Покажите, как в сумме токи отдельных резисторов составляют $ i $.
Шаги к решению:
- Найдите эквивалентное параллельное сопротивление $ \ text R _ {\ text {parallel}} $.
- Найдите напряжение $ v $, используя закон Ома.
- Найдите отдельные токи, снова используя закон Ома.
- Убедитесь, что токи резистора в сумме соответствуют требуемым.
Часть а. Эквивалент $ \ text R _ {\ text {parallel}} $ равен обратной обратной сумме трех резисторов.
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {50 \, \ Omega} + \ dfrac {1} {100 \, \ Omega} + \ dfrac {1} {500 \, \ Omega} \ right)}
долларов США$ \ text R _ {\ text {parallel}} = \ dfrac {1} {(0.02 + 0,01 + 0,002)} = \ dfrac {1} {0,032} = 31,25 \, \ Omega $
Теперь мы знаем ток и эквивалентное сопротивление. Мы можем найти напряжение $ v $ на всех резисторах, используя закон Ома
.$ v = i \, \ text R _ {\ text {parallel}}
$$ v = 100 \, \ text {mA} \ cdot 31.25 \, \ Omega = 3.125 \, \ text V $
Часть б. Зная $ v $, мы можем вернуться и вычислить токи отдельных резисторов,
$ i _ {\ text R1} = \ dfrac {v} {\ text R1} = \ dfrac {3.125 \, \ text V} {\ text {50}} = 62,5 \, \ text {mA}
долларов США$ i _ {\ text R2} = \ dfrac {v} {\ text R2} = \ dfrac {3.125 \, \ text V} {\ text {100}} = 31.25 \, \ text {mA} $
$ i _ {\ text R3} = \ dfrac {v} {\ text R3} = \ dfrac {3.125 \, \ text V} {\ text {500}} = \ phantom {0} 6.25 \, \ text {mA } $
Вот как выглядит решение,
Часть c. Проверка: Суммируются ли токи резистора с током источника?
$ 62.5 \, \ text {mA} + 31.25 \, \ text {mA} + 6.25 \, \ text {mA} = 100 \, \ text {mA} \ qquad \ checkmark $ Да!
Как электроны «знают», через какой резистор пройти?Распространенный вопрос о параллельных цепях: «Когда ток достигает первого резистора, как электроны« выбирают »или« знают », через какой резистор протекать?» Или «Как электроны« решают », куда идти? ”
Как известно, электроны — не люди, у них нет маленьких электронных мозгов (насколько нам известно).Здесь нет выбора или принятия решения. Они не выбирают и не решают, через какой резистор протекать, точно так же, как молекула воды «решает» или «выбирает», через какую сторону камня она будет проходить в потоке. В любой цепи, включая параллельные цепи, каждый электрон реагирует только на электрические силы, исходящие от напряжения и от отталкивающего роя окружающих электронов.
На основе только что найденных токов резисторов,
ПРОБЛЕМА 2
Через какой резистор проходит наибольшая доля тока?
Выберите один: $ \ quad $ наименьший $ \ quad $ средний $ \ quad $ наибольший
показать ответСамый маленький резистор несет наибольшую долю тока.
ПРОБЛЕМА 3
Через какой резистор проходит наименьшая доля тока?
Выберите один: $ \ quad $ наименьший $ \ quad $ средний $ \ quad $ наибольший
показать ответСамый большой резистор проводит наименьшую долю тока.
ПРОБЛЕМА 4
Каков относительный размер эквивалентного резистора по сравнению с параллельными резисторами?
- $ \ text {R} _ \ text {parallel} $ больше, чем самый большой резистор.
- $ \ text {R} _ \ text {parallel} $ находится между самым большим и самым маленьким резистором.
- $ \ text {R} _ \ text {parallel} $ меньше самого маленького резистора.
Эквивалентный параллельный резистор меньше самого маленького параллельного резистора. Всегда.
Проблема 5
Какой резистор имеет наибольшее напряжение?
Выберите один: $ \ quad $ наименьший $ \ quad $ средний $ \ quad $ наибольший
показать ответВопрос с подвохом.Все три резистора имеют одинаковое напряжение. Вот что значит быть параллельным. Все они имеют одинаковое напряжение.
Особый случай — резисторы по 2 доллара параллельно
Из общего уравнения два резистора, включенных параллельно, имеют эквивалентное сопротивление
Ом.$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} \ right)} $
Мы можем немного поработать алгеброй, чтобы придумать альтернативное выражение с одной дробью.Вместо того, чтобы просто сказать вам ответ, это обряд посвящения в самостоятельную работу с алгеброй в первый раз. Ответ спрятан, так что вы можете попробовать это самостоятельно, прежде чем посмотреть. Посмотрим, сможете ли вы получить выражение для $ \ text R _ {\ text {parallel}} $ в виде одной дроби.
Два резистора параллельно$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} \ right)} $
Обработайте знаменатель, чтобы очистить дроби. Общий знаменатель — $ \ text R1 \, \ text R2 $.
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} \, \ dfrac {\ text R2} {\ text R2} \ right) + \ left (\ dfrac {1} {\ text R2} \, \ dfrac {\ text R1} {\ text R1} \ right)} $
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {\ text R2} {\ text R1 \, \ text R2} \ right) + \ left (\ dfrac {\ текст R1} {\ text R1 \, \ text R2} \ right)} $
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {\ text R1 + \ text R2} {\ text R1 \, \ text R2} \ right)} $
Переверните большую дробь, чтобы получить уравнение для двух параллельных резисторов,
$ \ text R _ {\ text {parallel}} = {\ dfrac {\ text R1 \, \ text R2} {\ text R1 + \ text R2}} $
Произведение на сумму.Это стоит запомнить.
Особый случай — резисторы равной 2 $, включенные параллельно
Что делать, если два параллельно включенных резистора имеют одинаковое значение. Что эквивалентно $ \ text R _ {\ text {parallel}} $?
Пусть $ \ text R1 = \ text R2 $. Мы назовем его просто $ \ text R $.
$ \ text R _ {\ text {parallel}} = \ dfrac {\ text R \, \ text R} {\ text R + \ text R} = \ dfrac {\ text R \, \ text R} {2 \ , \ text R}
долларов США$ \ text R _ {\ text {parallel}} = \ dfrac {1} {2} \, \ text
R $Два идентичных резистора, включенных параллельно, имеют эквивалентное сопротивление, равное половине значения любого резистора.Ток распределяется между ними поровну.
Резюме
Параллельно подключенные компоненты имеют одинаковое напряжение.
Общий вид параллельно включенных резисторов:
$ \ dfrac {1} {\ text R _ {\ text {parallel}}} = \ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ ldots + \ dfrac {1} {\ text {R} _ \ text N}
долларов СШАИспользуйте это уравнение, если у вас параллельно подключено три или более резистора.
Если у вас есть два параллельных резистора, вы можете использовать общую форму или объединить их как произведение на сумму,
$ \ text R _ {\ text {parallel}} = \ dfrac {\ text R1 \, \ text R2} {\ text R1 + \ text R2} $
Эквивалентный резистор $ \ text R _ {\ text {parallel}} $ всегда меньше наименьшего параллельного резистора.
Самый большой ток протекает через наименьший резистор.
Резисторы— learn.sparkfun.com
Добавлено в избранное Любимый 50 Резисторы сериии параллельные
Резисторы постоянно соединяются вместе в электронике, обычно в последовательной или параллельной схеме. Когда резисторы соединены последовательно или параллельно, они создают общее сопротивление , которое можно рассчитать с помощью одного из двух уравнений.Знание того, как сочетаются значения резисторов, пригодится, если вам нужно создать конкретное значение резистора.
Резисторы серииПри последовательном соединении значения резисторов просто складываются.
Н резисторов последовательно. Общее сопротивление — это сумма всех последовательных резисторов.
Так, например, если у вас всего , нужно иметь , 12,33 кОм; резистор, найдите некоторые из наиболее распространенных номиналов резисторов 12 кОм; и 330 Ом, и соединить их последовательно.
Резисторы параллельные
Определить сопротивление параллельно включенных резисторов не так-то просто. Общее сопротивление резисторов N , включенных параллельно, является обратной суммой всех обратных сопротивлений. Это уравнение может иметь больше смысла, чем последнее предложение:
Н резисторов параллельно. Чтобы найти общее сопротивление, инвертируйте каждое значение сопротивления, сложите их, а затем инвертируйте.
(Сопротивление, обратное сопротивлению, на самом деле называется проводимостью , , поэтому короче: проводимость , параллельных резисторов — это сумма каждой из их проводимостей).
В качестве частного случая этого уравнения: если у вас только два резистора , подключенных параллельно, их полное сопротивление можно рассчитать с помощью этого чуть менее инвертированного уравнения:
В качестве даже более особого случая этого уравнения, если у вас есть два параллельных резистора равного значения , общее сопротивление составляет половину их значения. Например, если два 10k & ohm; резисторы включены параллельно, их полное сопротивление 5кОм.
Сокращенно обозначить, что два резистора включены параллельно, можно с помощью оператора параллельности: || .Например, если R 1 находится параллельно с R 2 , концептуальное уравнение может быть записано как R 1 || R 2 . Намного чище и скрывает все эти неприятные фракции!
Резисторные сети
В качестве специального введения в вычисление полного сопротивления учителя электроники любят подвергать своих учеников сумасшедшим, запутанным цепям резисторов.
Приручить резисторный сетевой вопрос может быть что-то вроде: «какое сопротивление между выводами A, и B в этой цепи?»
Чтобы решить такую проблему, начните с задней части схемы и упростите ее к двум клеммам.В этом случае R 7 , R 8 и R 9 идут последовательно и могут складываться вместе. Эти три резистора включены параллельно с R 6 , поэтому эти четыре резистора можно превратить в один с сопротивлением R 6 || (R 7 + R 8 + R 9 ). Делаем нашу схему:
Теперь четыре крайних правых резистора можно упростить еще больше. R 4 , R 5 и наш конгломерат R 6 — R 9 все последовательно и могут быть добавлены.Тогда все эти последовательные резисторы подключены параллельно с R 3 .
И это всего три резистора между клеммами A и B . Добавьте их! Таким образом, общее сопротивление этой цепи составляет: R + R 2 + R 3 || (R 4 + R 5 + R 6 || (R 7 + R ). 8 + Р 9 )).
← Предыдущая страница
Номинальная мощность
L4: Последовательные и параллельные резисторы
Содержание
- Эквивалентные сопротивления
- Последовательные резисторы
- Пример серии 1: Решить для тока
- Шаг 1: Решить для общего сопротивления
- Шаг 2: Решить для тока I с эквивалентом сопротивление
- Пример серии 2: Решить для тока
- Проверить нашу работу в симуляторе схемы
- Пример серии 1: Решить для тока
- Делители напряжения
- Пример 1: Решить для напряжения на VB
- Шаг 1: Решить для тока через схема
- Шаг 2: Рассчитайте падение напряжения на резисторах
- Шаг 3: Теперь вычислите VB
- Шаблон делителя напряжения
- Получение уравнения делителя напряжения
- Пример 1: Решить для напряжения на VB
- Параллельные резисторы
- Параллельный пример 1: Решите параллельный пример 1: Решите \ (I_ {Total} \)
- Шаг 1. Обратите внимание, что \ (I_ {Total} \) разбивает int o ветви
- Шаг 2: Определите и присвойте имя узлам
- Шаг 3: Определите \ (V_A \)
- Шаг 4: Решите для \ (I_1 \) и \ (I_2 \)
- Шаг 5: Наконец, решите для \ (I_ {Total} \)
- Шаг 6: Используйте эквивалентное сопротивление для проверки нашей работы
- Проверьте нашу работу в симуляторе схем
- Параллельный пример 1: Решите параллельный пример 1: Решите \ (I_ {Total} \)
- Activity
- Ресурсы
- Следующий урок
По закону Ома На уроке мы проанализировали относительно простые схемы с одним резистором.Эти схемы помогли нам заложить основу и концептуальное понимание закона Ома и того, как его применять; однако большинство схем не так просты.
В этом уроке мы собираемся распространить закон Ома на более сложные схемы: резисторы серии и резисторы параллельно . Вкратце:
- Резисторы в серии делят напряжение и являются одной из наиболее распространенных (и полезных) схемных конфигураций при работе с микроконтроллерами и резистивными датчиками, такими как потенциометры, силовые резисторы и фотоэлементы.
- Параллельно подключенные резисторы делят ток (и больший ток проходит по нисходящим путям с меньшим сопротивлением). Параллельные схемы полезны, например, для питания нескольких светодиодов.
Рисунок. Пример резисторов серии (слева) и параллельных резисторов (справа). Изображения сделаны в PowerPoint.
Эквивалентные сопротивления
Используя законы Кирхгофа для цепей, мы можем получить «эквивалентные» сопротивления для последовательных и параллельных цепей.
Для последовательных резисторов суммируем сопротивления, чтобы найти суммарное сопротивление \ (R_ {эквивалент} \):
\ [R_ {эквивалент} = R_ {1} + R_ {2} + … + R_ {N-1 } + R_ {N} \]Для параллельных резисторов все немного сложнее:
\ [R_ {equal} = \ frac {1} {\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + … + \ frac {1} {R_ {N-1}} + \ frac {1} {R_ {N}}} \]Да, уравнение параллельного сопротивления немного загадочно но вы можете вывести его самостоятельно (или даже забыть все вместе), если вы знаете закон Ома и законы Кирхгофа.
Для нас наиболее важным и полезным понятием является то, что резисторы серии делят напряжение (мы будем использовать это позже в наших схемах микроконтроллера) и что параллельные резисторы делят ток (с больше, чем ток, протекающий через ветви с меньшим сопротивлением). Изображение ниже пытается кратко объяснить это.
Рисунок. Обзор того, как работают резисторы серии (ток одинаков на каждом резисторе, но напряжение делится на ) и как работают параллельные резисторы (напряжение одинаково на каждом резисторе, но ток делится на ).Найдите минутку, чтобы изучить и понять, почему это может быть. Щелкните изображение правой кнопкой мыши и выберите «Открыть в новой вкладке», чтобы увеличить. Изображение сделано в PowerPoint.
И хотя способность вручную понимать и анализировать схему важна для физических вычислений, если вы запутаетесь, вы всегда можете использовать симулятор схем, например CircuitJS.
Резисторы серииРезисторы последовательно подключаются по схеме «голова к хвосту».
Рисунок. Компоненты соединены последовательно, если они соединены встык (или конец к концу) в последовательности, как указано выше.Изображение слева из Академии Хана. Изображение сделано в PowerPoint.
Из закона Ома мы знаем, что на резисторах падает напряжение (действительно, падение напряжения \ (V_ {R} \) на резисторе \ (R \) равно \ (V_ {R} = I * R \)) . Таким образом, несколько резисторов «в ряд» (последовательно) , каждый вызовет падение напряжения — и величина этого падения пропорциональна резистору (большее сопротивление, большее падение напряжения).
Обычно, когда мы пытаемся проанализировать схему с несколькими конфигурациями резисторов (последовательными, параллельными или комбинациями), первым шагом является определение эквивалентного сопротивления .То есть, как мы можем объединить все сопротивление в цепи в одно значение (называемое \ (R_ {total} \) или \ (R_ {эквивалент} \)), которое позволяет нам применять закон Ома ко всей цепи. В случае расчета по току это будет \ (I = \ frac {V} {R_ {total}} \)
Итак, давайте попробуем!
Серия, пример 1: Решить для тока
Давайте начнем с простейшей схемы последовательного резистора: батарея 9 В с последовательно включенными резисторами 100 Ом и 1 кОм.
Рисунок. Простая схема с двумя последовательными резисторами (100 Ом и 1 кОм) и батареей на 9 В. Сколько тока \ (I \) протекает по этой цепи?
Шаг 1: Найдите общее сопротивление
Первый шаг — найти полное сопротивление в нашей цепи. Мы знаем, что мы суммируем сопротивления последовательно, поэтому: \ (R_ {Total} = R_ {1} + R_ {2} \ Rightarrow 100Ω + 1000Ω \ Rightarrow 1100Ω \). Общее сопротивление составляет \ (1100 Ом \).
Рисунок. Чтобы найти эквивалентное сопротивление этой цепи (назовем это \ (R_ {Total} \)), мы можем объединить последовательные резисторы, суммируя их.
Шаг 2: Решите для тока I с эквивалентным сопротивлением
Теперь мы можем использовать это эквивалентное значение сопротивления \ (R_ {Total} \), чтобы найти ток \ (I \), используя закон Ома: \ (I = 9V / 1100Ω \ Rightarrow 0.0082A \ Rightarrow 8.2mA \)
Рис. Теперь мы решаем по току \ (I \) просто по закону Ома: \ (I = 9V / 1100Ω \ Rightarrow 8.2mA \)
Вот и все. Мы сделали это! Полный ток равен \ (I = 8,2 мА \).
Серия, пример 2: Решить для текущего
Чтобы укрепить понимание, давайте попробуем еще раз, но с тремя резисторами вместо двух.На этот раз \ (R_ {1} = 2,2 кОм \), \ (R_ {2} = 1 кОм \) и \ (R_ {3} = 470 Ом \).
Опять же, мы начинаем с нахождения \ (R_ {Total} \), что составляет:
\ [R_ {Total} = R_ {1} + R_ {2} + R_ {3} \\ R_ {Total} = 2200 Ом. + 1000Ω + 470Ω \\ R_ {Total} = 3670Ω \]Затем мы можем использовать это эквивалентное значение сопротивления для определения тока \ (I \), который равен \ (I = \ frac {9V} {3670Ω} \ Rightarrow 0,0025 A \ Стрелка вправо 2,5 мА \).
Рисунок. На изображении выше мы вычисляем ток с тремя последовательными резисторами.Сначала просуммируйте сопротивления (потому что они включены последовательно), а затем используйте это совокупное сопротивление (\ (R_ {Total} \)), чтобы определить ток по закону Ома: \ (I = \ frac {V} {R_ {Total}} \ Rightarrow \ frac {9V} {3670Ω $} \ Rightarrow 2.5mA \)
Проверьте нашу работу в симуляторе схем
Мы можем проверить нашу работу в нашем любимом симуляторе схем, который вам нравится. 🙂
Я буду использовать открытый инструмент CircuitJS. Конкретная симуляция здесь.
Мы можем щелкнуть по проводам, чтобы волшебным образом показать, какой ток проходит по ним, или показать их электрический потенциал (напряжение) относительно земли.И, конечно же, вы увидите, что действительно \ (2,5 мА \) проходит по цепи. Что еще вы наблюдаете?
Хорошо, вспомните, как мы подчеркивали, что напряжения делятся на , на или на на последовательно включенные резисторы. Вы тоже это ясно видите! Напряжение составляет \ (9 В \) в верхнем узле, но падает на \ (5,4 В \) на резисторе \ (2,2 кОм \) до \ (3,6 В \), которое затем падает на \ (2,4 В \) в течение резистор \ (1кОм \) оставляет только \ (1,2В \) электрического потенциала, прежде чем окончательно упасть до \ (0В \) или \ (GND \) на резисторе \ (470Ом \).Мы поговорим об этом позже!
Рисунок. В этом видео показано моделирование CircuitJS базовой схемы с тремя последовательными резисторами. Здесь вы можете поиграть со схемой.
Делители напряжения
Представление о том, что резисторы серии делят напряжение , является критически важным при работе с микроконтроллерами. Итак, это заслуживает отдельного внимания.
Главное запомнить: на каждом резисторе наблюдается падение напряжения (это всегда так, а не только в конфигурации последовательной цепи).Таким образом, между каждым резистором у нас есть различный электрический потенциал , или напряжение. А поскольку микроконтроллеры «считывают» напряжение, а не ток, мы можем использовать это свойство для управления динамическим вводом в наш микроконтроллер!
Давайте рассмотрим несколько примеров.
Пример 1: Решить для напряжения на VB
С этой идеей падения напряжения на каждом резисторе, давайте посмотрим, как рассчитать напряжение в узле \ (V_ {B} \) относительно земли (и помните, что узел — это просто любая точка соединения с двумя или более соединениями в цепи).
Перед тем, как продолжить наш пример, остановитесь и спросите себя: как бы вы рассчитали напряжение в \ (V_ {B} \)?
Шаг 1: Найдите ток в цепи
Как и раньше, первым шагом будет вычисление тока в цепи. Мы делаем это снова, найдя эквивалентное сопротивление \ (R_ {Total} \) и используя закон Ома. Итак, \ (I = \ frac {V} {R_ {Total}} \ Rightarrow \ frac {9V} {250Ω} \ Rightarrow 36mA \).
Шаг 2: Расчет падения напряжения на резисторах
Теперь, когда мы знаем полный ток, протекающий по нашей цепи (\ (36 мА \)), мы можем использовать это для вычисления удельного падения напряжения на каждом резисторе.Назовем падение напряжения более \ (R_ {1} \): \ (V_ {1} \) и падение напряжения более \ (R_ {2} \): \ (V_ {2} \). И поскольку нас интересует вычисление напряжения, мы будем использовать эту формулировку закона Ома: \ (V = I * R \).
Таким образом:
\ [{V_1} = I * R_1 \ Rightarrow 0.0036A * 100Ω \ Rightarrow 3.6V \\ {V_2} = I * R_2 \ Rightarrow 0.0036A * 150Ω \ Rightarrow 5.4V \]И так же Быстрая проверка нашей работы (и не вдаваясь в подробности), мы знаем из схем Кирхгофа, что \ (V_ {Total} = V_1 + V_2 \ Rightarrow 9V = 3.6 В + 5,4 В \ Стрелка вправо 9 В = 9 В \). Итак, пока все идет хорошо!
Шаг 3: Теперь вычислите VB
Теперь просто вычислить \ (V_B \). Мы знаем, что \ (V_A = 9V \) и \ (R_1 \) вызывает падение напряжения \ (3.6V \). Итак, \ (V_B \) должен быть равен \ (9V — 3.6V \), что составляет 5,4V.
Схема делителя напряжения
Подобную конфигурацию с двумя резисторами мы называем делителем напряжения именно потому, что, как вы можете видеть, он делит напряжения.В этом случае мы использовали последовательно резисторы \ (100 Ом \) и \ (150 Ом \) для вывода \ (5,4 В \) на \ (V_B \).
Используя закон Ома, мы можем вывести уравнение делителя напряжения для \ (V_B \) в терминах входного напряжения (\ (V_A \)) в нашу сеть делителя напряжения и двух резисторов: верхнего резистора \ (R_1 \) и нижний резистор \ (R_2 \).
Это уравнение делителя напряжения, таким образом, выглядит следующим образом: \ (V_ {B} = V_ {A} * \ frac {R_2} {R_1 + R_2} \)
Или чаще записывается как \ (V_ {out} = V_ { in} * \ frac {R_2} {R_1 + R_2} \)
Рис. Схема и уравнение делителя напряжения. Изображение сделано в PowerPoint. См. Академию Хана для получения дополнительной информации.
Важно, как вы можете понять из уравнения, значение , а не абсолютных сопротивлений, а скорее отношение \ (R_1 \) к \ (R_2 \), которое контролирует \ (V_ {out} \). Таким образом, для целей деления напряжений , установка \ (R_1 = 100 Ом \) и \ (R_2 = 100 Ом \) будет такой же, как \ (R_1 = 2,2 кОм \) и \ (R_2 = 2,2 кОм \), они оба делят напряжения равномерно. Итак, \ (V_ {out} \) будет равно \ (4.5V \), если \ (V_ {in} = 9V \).
Однако величина тока между двумя цепями будет значительно отличаться в первом случае: \ (I = \ frac {9V} {200Ω} \ Rightarrow 45mA \), а во втором: \ (I = \ frac {9V} {4.4kΩ} \ Rightarrow 2.0mA \).
Разве не было бы круто динамически управлять одним из этих значений резистора для вывода переменного напряжения на уровне \ (V_ {out} \)? Да! И это основа потенциометра, о котором мы узнаем на следующем уроке.
Получение уравнения делителя напряжения
Учитывая то, что вы изучаете о схемах, теперь у вас есть знания, чтобы вывести уравнение делителя напряжения или, по крайней мере, понять , как оно получается из .Давайте взглянем!
Рисунок. Вывод уравнения делителя напряжения. См. Академию Хана для получения дополнительной информации.
Используя приведенный выше рисунок, давайте определим и запишем то, что мы знаем. Мы знаем, что падение напряжения на \ (R2 \) равно \ (V_ {out} \) (действительно, это одно и то же) и что \ (V_R2 = I * R2 \):
\ [V_ {out } = V_ {R2} = I * R2 \]Мы также знаем, что \ (V_in \) равно \ (V_R1 + V_R2 \) с учетом закона Кирхгофа о напряжении.
\ [V_ {in} = V_ {R1} + V_ {R2} \]Используя закон Ома, мы можем заменить \ (I * R1 \) на \ (V_ {R1} \) и \ (I * R2 \ ) для \ (V_ {R2} \).
\ [V_ {in} = I * R1 + I * R2 \]Теперь переставим уравнение \ (V_ {in} \), используя алгебру:
\ [V_ {in} = I * (R1 + R2) \ Стрелка вправо I = \ frac {V_ {in}} {(R1 + R2)} \]Возвращаясь к \ (V_ {out} = I * R2 \), мы можем заменить \ (I \), учитывая формулировку выше:
\ [V_ {out} = I * R2 = \ frac {V_ {in}} {(R1 + R2)} * R2 \]Наконец, измените приведенное выше, чтобы получить популярное уравнение делителя напряжения:
\ [V_ {out } = V_ {in} * \ frac {R2} {(R1 + R2)} \]Примечание: для выполнения этого уравнения делителя напряжения ток \ (I \), протекающий через \ (R_1 \), должен быть ( в основном) равным \ (R_2 \).То есть, если мы подключим ответвление к \ (V_ {out} \), как мы это делали ниже, тогда эта ветвь должна иметь очень высокое сопротивление, чтобы в эту ветвь «просачивался» очень небольшой ток. То есть \ (R_ {Load} \) должно быть больше, чем \ (R1 + R2 \). Однако в случае входов микроконтроллера это , к счастью, случай, к которому мы вернемся позже.
Рисунок. Уравнение делителя напряжения выполняется только тогда, когда \ (R_ {Load} \) велико, что будет, когда мы начнем использовать микроконтроллеры (которые считывают изменения уровней напряжения и имеют «высокий входной импеданс»)
Параллельные резисторы
Принимая во внимание Резисторы серии имеют одинаковый ток, но делят напряжение, * параллельные резисторы * имеют такое же напряжение, но делят ток.Компоненты, включенные параллельно, выглядят так:
Рисунок. Компоненты работают параллельно, если их голова совместно использует узел, а их хвост — общий узел. Изображение слева из Академии Хана. Изображение сделано в PowerPoint.
Параллельный пример 1: Решите для \ (I_ {Total} \)
В приведенной ниже схеме у нас есть два параллельных резистора \ (R_1 = 100 Ом \) и \ (R_2 = 1 кОм \). Давайте решим полный ток \ (I_ {Total} \) в цепи.
Шаг 1. Обратите внимание на то, что \ (I_ {Total} \) разбивается на ветви
Первое, что нужно признать, это то, что \ (I_ {Total} \) разбивается на две ветви.Назовем ток в этих двух ветвях \ (I_1 \) и \ (I_2 \). Из законов Кирхгофа мы знаем, что \ (I_ {Total} = I_1 + I_2 \). Это связано с сохранением энергии — в нашем контуре не теряются заряды (они просто текут вокруг и вокруг).
Шаг 2: Идентифицируйте и присвойте имя узлам
Также обратите внимание на то, что в нашей цепи всего два узла . Мы можем пометить их как \ (Узел A \) и \ (Узел B \).
Шаг 3: Определите \ (V_A \)
Поскольку \ (Узел A \) напрямую подключен к положительной клемме батареи, он имеет электрический потенциал 9 В.Назовем это \ (V_A = 9V \). Точно так же \ (Узел B \) напрямую подключен к отрицательному выводу батареи, поэтому давайте назовем его \ (GND \) или \ (OV \).
Шаг 4: Решите для \ (I_1 \) и \ (I_2 \)
Используя закон Ома, теперь мы можем решить для \ (I_1 \) и \ (I_2 \), где: \ (I_1 = \ frac {V_A} {R_1} \) и \ (I_2 = \ frac {V_A} {R_2} \). Таким образом, \ (I_1 = \ frac {9V} {100Ω} \ Rightarrow 90mA \) и \ (I_2 = \ frac {9V} {1000Ω} \ Rightarrow 9mA \).
Остановитесь на мгновение.Подумайте об этих результатах. Имеют ли смысл концептуально ?
Используя закон Ома, мы обнаружили, что , в 10 раз превышающее тока, проходит через ветвь \ (I_2 \), чем через ветвь \ (I_1 \). Действительно, это точно соответствует соотношению двух резисторов \ (R_1 \) к \ (R_2 \) — \ (R_2 \) на в 10 раз больше, чем на , чем \ (R_1 \), и, таким образом, будет ограничивать гораздо больший ток. В этом есть смысл: точно так же, как больше воды будет течь через ветвь с меньшим сопротивлением, также будет больше тока течь по пути с меньшим сопротивлением.
Шаг 5: Наконец, решите для \ (I_ {Total} \)
Наконец, мы можем использовать \ (I_ {Total} = I_1 + I_2 \) для решения \ (I_ {Total} \). В этом случае \ (I_ {Total} = 90 мА + 9 мА \ Rightarrow 99 мА \).
Шаг 6: Используйте эквивалентное сопротивление для проверки нашей работы
Помните, как мы ввели уравнение для эквивалентного сопротивления в параллельных цепях резисторов? Уравнение:
\ [R_ {эквивалент} = \ frac {1} {\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + … + \ frac {1 } {R_ {N-1}} + \ frac {1} {R_ {N}}} \]Кстати, если вам интересно узнать о его происхождении, посмотрите этот урок Академии Хана, но, вкратце, вы можно вывести это из закона Ома (и шагов, которые мы выполнили выше).
Мы можем использовать это уравнение для более быстрого решения для \ (I_ {Total} \), которое равно \ (I_ {Total} = \ frac {V_A} {R_ {equal}} \).
Мы знаем, что \ ({R_ {equal} = \ frac {1} {\ frac {1} {100Ω} + \ frac {1} {1kΩ}}} \ Rightarrow 90.9Ω \)
Таким образом, \ ( I_ {Total} = \ frac {9V} {90.91Ω} \ Rightarrow 99mA \).
Проверить нашу работу на симуляторе схем
Мы также можем проверить нашу работу на симуляторе схем. Я построил такую же схему в CircuitJS, которую вы можете просмотреть здесь.
Соответствует ли визуализация вашим ожиданиям?
Рисунок. В этом видео показано моделирование CircuitJS базовой параллельной схемы с двумя резисторами. Здесь вы можете поиграть со схемой.
Activity
Придумайте две цепи последовательных резисторов и две параллельные цепи резисторов. Используя то, что вы узнали, вручную решите по току в каждой цепи (карандаш + бумага или в цифровом виде). Покажите свою пошаговую работу. Проверьте свою работу, построив симуляцию в CircuitJS.
В свои журналы прототипирования включите эскиз схемы (может быть изображение смартфона, состоящее из бумаги и карандаша), вашу ручную работу, которую необходимо решить для текущего \ (I \) (опять же, может быть бумага + карандаш), и снимок экрана. схемы CircuitJS вместе с прямой ссылкой.(Помните, что вы можете создать ссылку CircuitJS, выбрав «Файл» -> «Экспортировать как ссылку»).
Ресурсы
Следующий урок
В следующем уроке мы узнаем больше о резисторах, о том, как они сделаны, как их использовать, как они характеризуются и как рассчитать их рассеиваемую мощность.
Предыдущая: Схема Следующая: Резисторы
Все материалы с открытым исходным кодом созданы лабораторией Makeability Lab и профессором Джоном Э. Фрелихом. Нашли ошибку? Отправьте сообщение о проблеме на GitHub.
Резисторы сериии параллельные [Analog Devices Wiki]
Цель:
Целью этой лабораторной работы является исследование последовательно и параллельно включенных резисторов.
Серияи параллельные схемы
Простые схемы, состоящие всего из нескольких компонентов, обычно просты для понимания новичками. Но все усложняется, когда в смесь входит большее количество компонентов.Куда идет ток? Что делают узловые напряжения? Можно ли упростить схему и облегчить понимание? Следующая информация должна помочь.
В этой лабораторной работе мы сначала обсудим разницу между последовательными цепями и параллельными цепями, используя цепи, содержащие самые основные компоненты, резисторы и батареи (или источники напряжения), чтобы показать разницу между двумя конфигурациями.
Прежде чем мы углубимся в объяснение, нам нужно определить, что такое узел схемы.Узел в цепи — это не что иное, как электрическое соединение между двумя или более компонентами. Когда схема изображена на схеме, такой как рисунок 1, узлы представлены проводами (линиями) между компонентами.
Рисунок 1, Пример схемы узла
На схеме изображена схема с 4 резисторами и источником напряжения. Также есть четыре уникальных узла. Цветные узлы (линии) Красный соединяет (+) конец источника напряжения с резистором R 1 , оранжевый соединяет R 1 и R 2 вместе, синий соединяет R 2 с R 3 и R 4 и зеленый соединяет (-) конец источника напряжения с R 3 и R 4 .Обратите внимание, что мы обычно определяем один узел как общий узел, на который ссылаются все остальные узлы, в данном случае это зеленый наземный узел.
Нам также необходимо понять, как ток течет по цепи. Обычный ток течет от более высокого или более положительного напряжения к более низкому или менее положительному напряжению в цепи. Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки с наименьшим напряжением, обычно называемой землей (0 вольт). Используя приведенную выше схему в качестве примера, вот как ток будет течь от положительной клеммы источника напряжения к отрицательной клемме.
Обратите внимание, что в некоторых узлах (например, между R 1 и R 2 ) ток на входе такой же, как на выходе. В других узлах (в частности, трехсторонний переход между R 2 , R 3 и R 4 ) основной (красный) ток разделяется на два разных: фиолетовый ток, протекающий в R 3 и оранжевый ток протекает в R 4 . Также обратите внимание, что токи I R3 и I R4 рекомбинируют в зеленый ток.Это подчеркивает ключевое различие между последовательным и параллельным подключением.
Определение цепей серииКогда резисторы соединены последовательно (как показано на рисунке 2), вывод одного резистора подключается непосредственно к выводу следующего резистора, без каких-либо других возможных путей, так что весь ток в одном резисторе должен течь в следующий и скоро.
Когда резисторы включены последовательно, они могут быть объединены или объединены в один эквивалентный резистор с сопротивлением, равным сумме последовательных сопротивлений, i.е. , г.
Рисунок 2: Последовательные резисторы, R СЕРИЯ = R 1 + R 2 + R 3 +…
Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление. Итак, для приведенной выше последовательной схемы:
Мы знаем, что все резисторы имеют одинаковый ток I S .
Аналогично для остальных трех резисторов так:
Или за вычетом I S :
Таким образом, полное эквивалентное сопротивление — это просто сумма их значений.
Определение параллельных цепей
Когда резисторы включены параллельно (как показано на рисунке 3), все их первые выводы соединены вместе, а все их вторые выводы соединены вместе.
Когда резисторы включены параллельно, они могут быть объединены или объединены в один эквивалентный одиночный резистор, значение которого определяется следующим уравнением:
Для двух параллельно подключенных резисторов это упрощает:
Рисунок 3: Параллельные резисторы
Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление.Итак, для вышеуказанной параллельной схемы:
Мы знаем, что все резисторы имеют одинаковое напряжение В S .
Ток, подаваемый источником напряжения В S , является суммой токов в резисторах.
Подставляя четыре резистора, получаем:
Или за вычетом V S :
Преобразуя сопротивление, получаем полное эквивалентное сопротивление:
Эксперименты
Материалы:
Аппаратный модуль ADALM1000
Макетная плата без пайки и перемычки
Резисторы 3 — 100 Ом
Резисторы 3 — 470 Ом
резисторов в серии:
Поместите три резистора 100 Ом последовательно на беспаечную макетную плату, как показано на рисунке 4.Соедините с помощью перемычек, подключите вход CH A к левой стороне первого резистора, а вход CH B — к правой стороне того же резистора.
Рисунок 4, последовательно соединенные резисторы
Запустите прибор ALICE M1K Ohm Meter. Здесь показан экран. Программное обеспечение использует известный резистор для проверки неизвестного резистора. ADALM1000 имеет встроенный резистор 50 Ом, который можно использовать для этого. Убедитесь, что выбран параметр Int. Уровень напряжения, который используется для измерения резистора, может быть установлен.Тестирование при максимальном напряжении 5,0 В дает наилучшие результаты для большинства номиналов резисторов. Нажмите Run, и вы должны увидеть что-то подобное с единственным резистором 100 Ом.
Переместите перемычку CH B к правому концу второго резистора, как показано ниже.
Рисунок 5, два резистора последовательно
Омметр должен теперь показать значение для двух последовательно соединенных резисторов или около 200 Ом. Теперь переместите перемычку CH B к правому концу третьего резистора, как показано ниже.
Рисунок 6, три резистора последовательно
Омметр должен теперь показать значение трех последовательно соединенных резисторов или около 300 Ом.
параллельных резисторов:
Теперь замените резисторы 100 Ом на резисторы 470 Ом, как показано на рисунке 7.
Измерение одного резистора 470 Ом
Омметр должен теперь показать значение одиночного резистора или около 470 Ом. Переместите средний резистор 470 Ом так, чтобы он был параллелен резистору справа, как показано ниже.
Измерение двух резисторов 470 Ом, включенных параллельно
Омметр должен теперь показать значение для двух резисторов 470 Ом, включенных параллельно. Соответствует ли измеренное значение формуле для параллельных резисторов?
Переместите третий резистор 470 Ом так, чтобы он был параллелен двум другим резисторам справа, как показано ниже.
Измерение трех резисторов 470 Ом, включенных параллельно
Омметр должен теперь показать значение для трех резисторов 470 Ом, включенных параллельно.Соответствует ли измеренное значение формуле для параллельных резисторов?
Поэкспериментируйте с другими комбинациями резисторов и номиналов, чтобы убедиться, что формулы верны для любого номинала резистора.
Комбинированные схемы
Более сложные соединения резисторов обычно представляют собой просто комбинации последовательного и параллельного соединения. Это часто встречается, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная схема может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на рисунке 7. На рисунке общее сопротивление может быть вычислено путем соединения трех резисторов друг с другом последовательно или параллельно.
Комбинированные последовательные и параллельные резисторы
R 2 и R 3 соединены параллельно друг другу, поэтому мы знаем, что для этих двух резисторов эквивалентное сопротивление будет:
Комбинированное сопротивление R 2 и R 3 последовательно с R1, поэтому общее эквивалентное сопротивление будет:
Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.
Для дальнейшего изучения:
Академия Хана — Резисторные схемы
Безграничная физика
Последовательные и параллельные схемы (по физике)
Вернуться к разделу «Введение в работу электротехнической лаборатории» Содержание
Параллельная цепь серии| Примеры последовательной параллельной цепи
Определение последовательной параллельной цепи
Не все схемы являются простыми последовательными или параллельными схемами.Многие из них представляют собой комбинации параллельных резисторов, соединенных последовательно с другими резисторами или объединенные с другими параллельными группами. Их можно описать как последовательно-параллельную цепь.
Самый простой подход к анализу последовательно-параллельной цепи — это разделить каждую чисто последовательную группу на ее единственное эквивалентное сопротивление и разделить каждую параллельную группу резисторов на ее эквивалентное сопротивление. Процесс повторяется столько раз, сколько необходимо.
Как и во всех типах цепей, условия разомкнутой цепи и короткого замыкания влияют на токи и падения напряжения во всей цепи.
Последовательно-параллельные резистивные схемы
Простые последовательно-параллельные цепи
Последовательно-параллельные резистивные цепи состоят из комбинаций последовательно соединенных и параллельно соединенных резисторов. На рисунке 1 показана принципиальная схема очень простой последовательно-параллельной схемы с тремя резисторами. Видно, что резисторы R 2 и R 3 подключены параллельно, а резистор R 1 включен последовательно с параллельными комбинациями R 2 и R 3 .Токи в цепи меняются от ветви к ветви, а падение напряжения компонентов зависит от токов ветви и от сопротивлений компонентов. Ток питания зависит от напряжения питания и сопротивления цепи источника напряжения. Законы Кирхгофа для напряжения и тока применяются для анализа последовательно-параллельных цепей.
Рис.1: Принципиальная схема последовательно-параллельной цепи
Эквивалентные последовательно-параллельные схемы
В схеме, показанной на рисунке 2 (а), резисторы R 2 и R 2 включены параллельно , и вместе они идут последовательно с R 1 .Уровень тока, снимаемого с источника питания, легко вычислить, если сначала заменить R 2 и R 3 их эквивалентным сопротивлением (R 2 || R 3 ), как показано на рисунке 2 (b). Теперь схема становится простой последовательной схемой с двумя резисторами.
Рис. 2: Последовательно-параллельная цепь и эквивалентная схема
Пример 1 Последовательно-параллельная схема
Рассчитайте ток, потребляемый от источника питания в цепи, показанной на рисунке 2 (a).
Решение
Изобразите эквивалентную схему, как на рисунке 2 (b), с
$ {{R} _ {eq}} = {{R} _ {2}} || {{R} _ {3 }} $
Для вычисления эквивалентного сопротивления:
\ [{{R} _ {eq}} = \ frac {{{R} _ {2}} * {{R} _ {3}}} {{{ R} _ {2}} + {{R} _ {3}}} = \ frac {20 * 30} {20 + 30} = 12 \ Omega \]
\ [I = \ frac {E} {{ {R} _ {1}} + {{R} _ {eq}}} = \ frac {25} {38 + 12} = 0,5A \]
На рисунке 3 (a) другая последовательно-параллельная комбинация резисторов Показано. В этом случае схема сводится к простой параллельной схеме, когда R 2 и R 3 заменяются их эквивалентным сопротивлением.[См. Рис. 3 (b)]
Рис. 3: Последовательно-параллельная схема и ее эквивалентная схема
Пример 2-й последовательной параллельной схемы
Определите уровень тока питания для схемы, показанной на рис. (а).
Решение
Изобразите эквивалентную схему, как на рисунке 3 (b).
$ {{R} _ {eq}} = {{R} _ {2}} + {{R} _ {3}} = 35 + 40 = 75 \ Omega $
R 1 и рандов eq параллельно:
$ R = {{R} _ {1}} || {{R} _ {eq}} $
Для вычисления эквивалентного сопротивления:
\ [R = \ frac {{{ R} _ {1}} * {{R} _ {eq}}} {{{R} _ {1}} + {{R} _ {eq}}} = \ frac {50 * 75} {50+ 75} = 30 \ Omega \]
\ [I = \ frac {E} {R} = \ frac {75} {30} = 2.5A \]
Ток в последовательно-параллельной цепи
Схема на рисунке 2 (a) воспроизведена на рисунке 4 с идентифицированными токами и напряжениями ответвления. Видно, что ток питания протекает через резистор R 1 и разделяется на I 2 и I 3 , чтобы протекать через R 2 и R 3 . Возвращаясь к отрицательной клемме питания, ток снова равен I. Видно, что
$ I = {{I} _ {2}} + {{I} _ {3}} $
Рис.4: Ток и напряжение в последовательно-параллельной цепи
Точно так же ток питания распределяется между резисторами на рисунке 5, который воспроизводит схему, показанную на рисунке 3 (a). Здесь I 1 протекает через R 1 , а I 2 протекает через R 2 и R 3 , а ток питания составляет
$ I = {{I} _ {1}} + { {I} _ {2}} $
Рис.5: Токи и напряжения в последовательно-параллельной цепи
В каждом из этих случаев ток через отдельные резисторы можно легко вычислить с помощью правила делителя тока.
Падение напряжения в последовательно-параллельной цепи
Как всегда, падение напряжения на любом резисторе является произведением значения сопротивления и тока через резистор. На рисунке 4
$ {{V} _ {1}} = I {{R} _ {1}}
$ и
$ {{V} _ {2}} = {{I} _ { 2}} {{R} _ {2}} = {{V} _ {3}} = {{I} _ {3}} {{R} _ {3}}
долларов СШАКроме того,
долларов США E = {{V} _ {1}} + {{V} _ {2}} $
Аналогично, на рисунке 5
$ {{V} _ {1}} = {{I} _ {1} } {{R} _ {1}}
$$ {{V} _ {2}} = {{I} _ {2}} {{R} _ {2}}
$$ {{V} _ {3}} = {{I} _ {2}} {{R} _ {3}}
$$ E = {{V} _ {1}} = {{V} _ {2}} + {{V} _ {3}} $
Пример последовательной параллельной цепи 3
Используя теорему о делителе напряжения, проанализируйте схему на рисунке (a) ниже, чтобы определить падение напряжения на резисторе и токи ответвления.
Рис. Пример последовательной параллельной цепи
Решение
\ [{{R} _ {eq}} = {{R} _ {2}} || {{R} _ {3}} \]
\ [{{R} _ {eq}} = \ frac {{{R} _ {2}} * {{R} _ {3}}} {{{R} _ {2}} + {{R} _ {3}}} = \ frac {20 * 30} {20 + 30} = 12 \ Omega \]
Для делителя напряжения R 1 и R eq , как показано на рисунке (b ) выше:
\ [{{V} _ {2}} = E * \ frac {{{R} _ {eq}}} {{{R} _ {1}} + {{R} _ {eq }}} = 25 * \ frac {12} {38 + 12} = 6V \]
\ [{{V} _ {1}} = E * \ frac {{{R} _ {1}}} { {{R} _ {1}} + {{R} _ {eq}}} = 25 * \ frac {38} {38 + 12} = 19V \]
Для токов ответвления:
\ [I = \ frac {{{V} _ {1}}} {{{R} _ {1}}} = \ frac {19} {38} = 0.5A \]
\ [{{I} _ {2}} = \ frac {{{V} _ {2}}} {{{R} _ {2}}} = \ frac {6} {20} = 0,3A \]
\ [{{I} _ {3}} = \ frac {{{V} _ {3}}} {{{R} _ {3}}} = \ frac {6} { 30} = 0,2A \]
Разрыв цепи и короткое замыкание в последовательно-параллельной цепи
Влияние состояния разомкнутой цепи или короткого замыкания на последовательно-параллельную цепь зависит от того, где именно в в цепи возникает неисправность. Рассмотрим рисунок 6, где в конце R 1 показан обрыв цепи. Это имеет тот же эффект, что и разрыв цепи в линии питания, так что все уровни тока равны нулю.Кроме того, поскольку токи равны нулю, на резисторах нет падений напряжения, и, следовательно, все напряжение питания E появляется на разомкнутой цепи.
Рис.6: Разрыв цепи на резисторе R 1
Разрыв в одной ветви последовательно-параллельной цепи обычно изменяет уровни тока в нескольких ветвях цепи.
В случае обрыва цепи на одном конце параллельных резисторов, как показано на рисунке 7, I 2 переходит в ноль.Ток через R 1 и R 2 теперь равен току питания и рассчитывается как
\ [I = \ frac {E} {{{R} _ {1}} + {{R} _ {2}}} \]
Также из-за отсутствия тока через R 3 на нем нет падения напряжения, а напряжение в разомкнутой цепи равно 2 В.
Рис. 7: Обрыв цепи на резисторе R 3
Для состояния короткого замыкания, показанного на рисунке 8, сопротивление между выводами R 1 фактически равно нулю.Следовательно, напряжение питания появляется параллельно R 2 и R 3 . Это дает ток питания
\ [I = \ frac {E} {{{R} _ {2}} || {{R} _ {3}}} \]
И токи ответвления равны
\ [{{I} _ {2}} = \ frac {E} {{{R} _ {2}}} \]
и
\ [{{I} _ {3}} = \ frac { E} {{{R} _ {3}}} \]
Видно, что уровни тока через R 2 и R 3 были увеличены по сравнению с нормальным (до короткого замыкания) состоянием. Это может привести к чрезмерному рассеянию мощности в компонентах, если они ранее работали с максимальным номиналом.
Рис. 8: Короткое замыкание через резистор R 1
Короткое замыкание в одной ветви последовательно-параллельной цепи обычно изменяет уровни тока в нескольких ветвях цепи.
Состояние короткого замыкания, показанное на рисунке 9, эффективно снижает I 2 и I 3 до нуля и увеличивает ток питания до
\ [I = \ frac {E} {{{R} _ {1 }}} \]
Очевидно, что ток через R 1 теперь больше, чем обычно, и снова рассеивание мощности может представлять проблему.
Рис.9: Короткое замыкание на резисторе R 3
Анализ последовательно-параллельной цепи
Процедура анализа последовательно-параллельных цепей резисторов выглядит следующим образом:
- Нарисуйте принципиальную схему, идентифицирующую все Компоненты по номерам и с указанием всех токов и падений напряжения на резисторе.
- Преобразуйте все последовательные ветви двух или более резисторов в одно эквивалентное сопротивление.
- Преобразуйте все параллельные комбинации двух или более резисторов в одно эквивалентное сопротивление.
- Повторяйте процедуры 2 и 3 до тех пор, пока не будет достигнут желаемый уровень упрощения.
Конечная цепь должна быть прямой последовательной или параллельной цепью, которая может быть проанализирована обычным способом. После того, как станет известен ток через каждое эквивалентное сопротивление или напряжение на нем, исходная схема может быть использована для определения токов и напряжений отдельных резисторов.
Резисторы в параллельной формуле
В электрических цепях часто можно заменить группу резисторов одним эквивалентным резистором.Эквивалентное сопротивление ряда резисторов, включенных параллельно, можно найти, используя обратное сопротивление, 1 / R. Обратная величина эквивалентного сопротивления равна сумме обратных величин каждого сопротивления. Единицей измерения сопротивления является Ом (Ом), который равен Вольт на Ампер (1 Ом = 1 В / А). Также распространены резисторы большего размера с сопротивлением килоом (1 кОм = 10 3 Ом) или мегаом (1 МОм = 10 6 Ом).
R экв = эквивалентное сопротивление (Ом или более единицы)
R 1 = сопротивление первого резистора (Ом)
R 2 = сопротивление второго резистора (Ом)
R 3 = сопротивление третьего резистора (Ом)
Параллельные резисторы Вопросы по формуле:
1) Какое эквивалентное сопротивление 1000 кОм и 250 Ом.Резистор 0 кОм подключен параллельно?
Ответ: Оба сопротивления выражены в килоомах, поэтому нет необходимости изменять их единицы. Эквивалентное сопротивление можно найти в кОм по формуле:
.
Последний шаг — инвертировать значения с обеих сторон формулы, чтобы найти эквивалентное сопротивление:
R экв = 200,0 кОм
Эквивалентное сопротивление 1000 кОм и 250.Параллельно подключенные резисторы 0 кОм составляют 200,0 кОм.
2) Три резистора включены параллельно в электрическую цепь. Их сопротивления составляют 400 Ом, 40,0 кОм и 4,00 МОм. Какое эквивалентное сопротивление?
Ответ: Три значения сопротивления выражены в разных единицах измерения. Первым шагом к нахождению эквивалентного сопротивления является преобразование их в общую единицу. Два значения можно преобразовать в ту же единицу, что и третье. В этом решении все значения будут преобразованы в Ом.

