4 д куб. Четырехмерный гиперкуб (тессеракт): свойства, визуализация и особенности

Что такое четырехмерный гиперкуб (тессеракт). Как он устроен. Каковы его основные свойства и характеристики. Как можно визуализировать тессеракт. Какие существуют способы представления четырехмерных объектов в трехмерном пространстве.

Что такое четырехмерный гиперкуб (тессеракт)

Четырехмерный гиперкуб, также известный как тессеракт — это геометрическая фигура в четырехмерном пространстве, являющаяся аналогом куба в трехмерном пространстве. Тессеракт можно представить как результат «вытягивания» трехмерного куба в четвертое измерение.

Основные характеристики тессеракта:

• Состоит из 16 вершин
• Имеет 32 ребра
• Ограничен 24 двумерными гранями (квадратами)
• Содержит 8 трехмерных ячеек (кубов)

Тессеракт можно рассматривать как четырехмерный аналог последовательности: точка (0D) — отрезок (1D) — квадрат (2D) — куб (3D). Каждая следующая фигура получается «вытягиванием» предыдущей в новое измерение.

Свойства и характеристики тессеракта

Рассмотрим основные свойства четырехмерного гиперкуба:

1. Все ребра тессеракта имеют одинаковую длину и пересекаются под прямыми углами.
2. Все двумерные грани тессеракта являются квадратами.
3. Все трехмерные ячейки тессеракта представляют собой кубы.
4. В каждой вершине тессеракта сходятся 4 ребра под прямыми углами друг к другу.
5. Тессеракт имеет симметрию гиперкуба — любые две вершины можно совместить путем вращений и отражений.

Таким образом, тессеракт обладает высокой степенью симметрии, аналогичной симметрии куба в трехмерном пространстве.

Визуализация тессеракта в трехмерном пространстве

Полностью визуализировать четырехмерный объект в трехмерном пространстве невозможно. Однако существует несколько способов представления тессеракта, позволяющих получить некоторое представление о его структуре:

1. Проекция на трехмерное пространство

При проецировании тессеракта на трехмерное пространство получается фигура, состоящая из двух вложенных кубов, соединенных ребрами. Это наиболее распространенный способ изображения тессеракта.

2. Развертка

Тессеракт можно развернуть в трехмерном пространстве, получив 8 соединенных кубов. Это аналогично развертке куба на плоскости в виде креста из 6 квадратов.

3. Сечения

Можно представить, как выглядят трехмерные сечения тессеракта при его прохождении через наше пространство. Сечения будут меняться от точки до куба и обратно.

4. Анимация

Вращение проекции тессеракта позволяет лучше понять его структуру. При этом внутренний и внешний кубы меняются местами.

Как мыслить в четырех измерениях

Полностью представить четырехмерное пространство человеческий мозг не способен. Однако есть несколько подходов, позволяющих развить интуитивное понимание четвертого измерения:

• Аналогия с переходом от 2D к 3D — представьте, как двумерное существо воспринимало бы трехмерный мир.
• Рассмотрение времени как четвертого измерения в пространстве-времени.
• Изучение свойств и закономерностей четырехмерных объектов математически.
• Работа с проекциями и сечениями четырехмерных фигур.

Хотя полностью визуализировать четырехмерное пространство невозможно, понимание его свойств позволяет расширить представления о структуре реальности.

Применение концепции четырехмерного пространства

Идея четвертого пространственного измерения находит применение в различных областях:

• Теоретическая физика — теория струн предполагает существование дополнительных измерений.
• Компьютерная графика — работа с четырехмерными объектами для создания сложных 3D-эффектов.
• Криптография — использование свойств многомерных пространств для шифрования данных.
• Философия и фантастика — осмысление реальности за пределами трех измерений.

Таким образом, концепция четырехмерного пространства, хотя и недоступна для прямого восприятия, играет важную роль в современной науке и культуре.

Заключение

Четырехмерный гиперкуб (тессеракт) представляет собой fascinating geometric объект, позволяющий заглянуть за пределы нашего трехмерного восприятия. Хотя полностью визуализировать его невозможно, изучение свойств и способов представления тессеракта позволяет развить интуитивное понимание многомерных пространств. Это не только расширяет границы нашего мышления, но и находит практическое применение в различных областях науки и технологий.

Гиперкуб

Гиперкуб

☰ Оглавление

• Первая страница
• Онлайн инструменты ▽
  • Редактор иконок favicon.ico онлайн
  • Игра «Жизнь» онлайн
  • Онлайн навигатор по множеству (фракталу) Мандельброта
  • Онлайн конвертер PNG в favicon.ico
  • Интерактивная схема солнечной системы
  • Пересчёт дат в Юлианские дни
  • Объяснение и онлайн-демо, как работает HTML5 canvas transform
  • Онлайн генератор периодических фонов
  • Онлайн конвертер цветов из HSV в RGB
  • Онлайн URL-перекодировщик
  • Онлайн генератор QR-кодов
  • Покрутить 4D-гиперкуб
  • Получение географических координат точки на карте
  • «Сапёр» на бесконечном поле онлайн
  • Черепаший язык онлайн
  • Калькулятор индекса массы тела
  • Для самых маленьких ▽
    • Рисовалка для детей до трёх лет
    • «Робот» для детей с трёх-четырёх лет
    • «Морской бой» для самых маленьких
  • Простой чат
• Инструменты ▽
  • Docker ▽
    • Docker устанавливаем и разбираемся
    • Пример использования Docker для изучения Ruby on Rails
    • Пример использования Docker для запуска MySQL
    • Почему docker требует root-прав
  • JavaScript ▽
    • Букмарклеты для JavaSctipt/HTML-разработчика
    • Использование «use strict» в JavaScript
    • Небольшая памятка по JavaScript
    • Простой минификатор/оптимизатор JavaScript
    • Мои плагины для хрома
  • Python ▽
    • Сводная таблица методов основных типов данных Python 2 и 3
    • Инструменты для Python-разработчика
    • Удобная командная строка Python
    • Утечки памяти в Python: метод __del__ и сборка мусора
    • Работа с нитями в Python
  • Файловая система ▽
    • FS: перемещение, переименование, архивирование
    • Монтирование sshfs с помощью systemd
  • Shell ▽
    • Работа с историей команд bash
    • Консоль/bash.
      настройка
    • Отправка e-mail с картинками чистым shell скриптом
    • Конвертирование аудио
    • Конвертирование видео
  • Управляем тактовой частотой процессора
  • Совместный доступ к mercurial по SSH
  • Передача файлов по сети
  • Безопасное хранение и передача данных
  • Нотификатор
  • Xorg. Настройка
  • Xorg. Настройка нестандартной клавиатуры
  • Synergy: Много мониторов с одной клавиатурой и мышкой
  • Ssh. Настройка
  • Ssh. Настройка туннелирования через NAT и firewall
  • Pidgin для хакеров
  • Печать
  • USB-Flash. монтирование
  • Доступ к данным по MTP
  • Настройка aspell
  • Iptables. Port knocking
  • Sudo, sudoers, visudo
  • Swap в файле в Linux
  • Добрый kill (gdb)
  • Изменить размер tmp (tmpfs)
  • Установка Arch Linux на USB-Flash
  • Эмуляция в QEMU
  • GRUB2 вручную
  • Системные утилиты
  • Настройка редактора vi
  • Краткое руководство по vi
  • HTML-валидатор
  • VDS/VPS
    • Начальная настройка
    • Сборка nginx
    • Настройка nginx
    • Сборка uWSGI (Django+CGI)
    • Настройка uWSGI
  • Управление сетью в Ubuntu с помощью netctl (Arch Linux)
  • Настройка WiFi точки доступа под Linux
• CS: Искусственный интеллект ▽
  • Метрики в машинном обучении: precision, recall и не только
  • Оценка точности классификатора
  • Нейронные сети на простейших примерах
    • Что такое нейрон (очень коротко)
    • Пример задачи и демонстрация, как нейрон её решает
    • Пример обучения нейрона
    • Что осталось за сценой в задаче для одного нейрона
  • Деревья принятия решений
  • Байесовское машинное обучение
  • Примеры кода numpy, scipy, matplotlib
    • Метод наименьших квадратов
    • Построение системы рекомендаций, на основе текстов
    • Диффузионные реакции (реакции с диффузией)
• CS: Разное ▽
  • RSA-шифрование на пальцах
  • SQRT-декомпозиция
  • О пользе рекурсии
  • Дискретная бисекция
  • Top-K из N (куча)
  • Быстрое возведение в степень и подсчёт чисел Фибоначчи
  • Алгебра логики
  • Небольшая памятка по C++
  • Проблема останова
  • Примеры простейших серверов на Python
    • Простейший форкающийся сервер
    • Простейший prefork-сервер
    • Простейший многонитевой сервер
    • Многонитевой сервер с простым взаимодействием между нитями
    • Асинхронный сервер
  • Кумулятивное вычисление статистических характеристик
  • Пять задач, которые хорошо бы уметь решать за час
• Теория относительности ▽
  • Об этих заметках
  • Пространство-время как геометрия
  • Физическая интерпретация
  • Универсальность скорости света
  • Эквивалентность инерциальных систем отсчёта
  • Относительность пространственных и временных интервалов
  • Движение быстрее света
  • Парадокс близнецов
  • Заключение
• Теория вероятностей ▽
  • Как нас обманывает интуиция
  • Парадокс Монти Холла
  • Парадокс двух конвертов
• Квантовая механика ▽
  • Принцип неопределённости на классических примерах
• Фракталы ▽
  • Фрактальная размерность
  • Фрактальные деревья
  • Применение фракталов
  • Комплексная размерность
• Гиперкуб
• Обучение и преподавание ▽
  • О репетиторстве
  • Типичные ошибки на экзаменах
  • Лёгкая подготовка к экзаменам
  • Как отвечать на экзамене
• Как я худел
• Личное ▽
  • Обо мне (как бы резюме)
  • Благодарности
  • Мои ошибки
  • Немного фотографий
  • Копирование этих материалов

Ещё когда я был студентом-первокурсником у меня с одним моим одногруппником вышел горячий спор.

Он говорил, что четырёхмерный куб представить нельзя ни в каком виде, а я уверял, что его можно представить достаточно отчётливо. Тогда я даже сделал из скрепок проекцию гиперкуба на наше трёхмерное пространство… Но давайте обо всём по-порядку.

Что такое гиперкуб и четырёхмерное пространство

В нашем привычном пространстве три измерения. С геометрической точки зрения это значит, что в нём можно указать три взаимно-перпендикулярных прямых. То есть для любой прямой можно найти вторую, перпендикулярную первой, а для пары можно найти третью прямую, перпендикулярную двум первым. Найти четвёртую прямую, перпендикулярную трём имеющимся, уже не удастся.

Четырёхмерное пространство отличается от нашего только тем, что в нём есть ещё одно дополнительное направление. Если у вас уже есть три взаимно перпендикулярные прямые, то вы можете найти четвёртую, такую, что она будет перпендикуляра всем трём.

Гиперкуб это просто куб в четырёхмерном пространстве.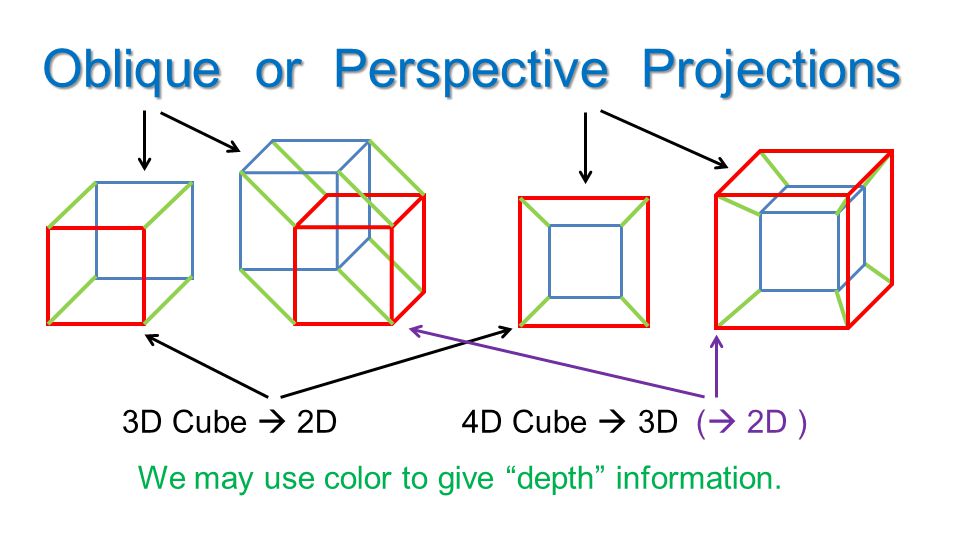

Можно ли представить четырёхмерное пространство и гиперкуб?

Этот вопрос сродни вопросу: «можно ли представить Тайную Вечерю, посмотрев на одноимённую картину (1495-1498) Леонардо да Винчи (1452-1519)?»

С одной стороны, вы конечно не представите то, что видел Иисус (он сидит лицом к зрителю), тем более вы не почувствуете запаха сада за окном и вкуса еды на столе, не услышите пения птиц… Вы не получите полного представления о происходившем в тот вечер, но нельзя сказать, что вы не узнаете ничего нового и что картина не представляет никакого интереса.

Аналогичная ситуация и с вопросом о гиперкубе. Полностью представить его нельзя, но можно приблизиться к пониманию, каков он.

Построение гиперкуба

0-мерный куб

Начнём с начала — с 0-мерного куба. Этот куб содержит 0 взаимно перпендикулярных граней, то есть это просто точка.

1-мерный куб

В одномерном пространстве у нас есть только одно направление. Сдвигаем точку в этом направление и получаем отрезок.

Это одномерный куб.

2-мерный куб

У нас появляется второе измерение, сдвигаем наш одномерный куб (отрезок) в направлении второго измерения и получаем квадрат.

Это куб в двумерном пространстве.

3-мерный куб

С появлением третьего измерения поступаем аналогично: сдвигаем квадрат и получаем обычный трёхмерный куб.

4-мерный куб (гиперкуб)

Теперь у нас появилось четвёртое измерение. То есть в нашем распоряжении имеется направление, перпендикулярное всем трём предыдущим. Воспользуемся им точно так же. Четырёхмерный куб будет выглядеть вот так.

Естественно, трёхмерный и четырёхмерный кубы нельзя изобразить на двумерной плоскости экрана. То, что нарисовал я — это проекции. О проекциях мы поговорим чуть позже, а пока немного голых фактов и цифр.

Количество вершин, рёбер, граней

Характеристики кубов различной размерности
размерность пространства	количество вершин	количество рёбер	количество граней
0 (точка)	1	0	0
1 (отрезок)	2	1	2 (точки)
2 (квадрат)	4	4	4 (отрезки)
3 (куб)	8	12	6 (квадраты)
4 (гиперкуб)	16	32	8 (кубы)
N (общая формула)	2N	N·2N-1	2·N

Обратите внимание, что гранью гиперкуба является наш обычный трёхмерный куб. Если внимательно посмотреть на рисунок гиперкуба, то можно действительно найти восемь кубов.

Проекции и зрение жителя четырёхмерного пространства

Несколько слов о зрении

Мы живём в трёхмерном мире, но видим мы его двумерным. Это связано с тем, что сетчатка наших глаз расположена в плоскости, имеющей только два измерения. Именно поэтому мы способны воспринимать двумерные картины и находить их похожими на реальность. (Конечно, благодаря аккомодации, глаз может оценить расстояние до объекта, но это уже побочное явление, связанное с оптикой, встроенной в наш глаз.)

Глаза жителя четырёхмерного пространства должны иметь трёхмерную сетчатку. Такое существо может сразу увидеть трёхмерную фигуру полностью: все её грани и внутренности. (Точно так же мы можем увидеть двумерную фигуру, все её грани и внутренности.)

Таким образом, с помощью наших органов зрения, мы не способны воспринять четырёхмерный куб так, как его воспринимал бы житель четырёхмерного пространства. Увы. Остаётся только уповать на мысленный взор и фантазию, которые, к счастью, не имеют физических ограничений.

Тем не менее, изображая гиперкуб на плоскости, я просто вынужден делать его проекцию на двумерное пространство. Учитывайте это обстоятельство, при изучении рисунков.

Пересечения рёбер

Естественно, ребра гиперкуба не пересекаются. Пересечения появляются только на рисунках. Впрочем, это не должно вызывать удивления, ведь рёбра обычного куба на рисунках тоже пересекаются.

Длины рёбер

Стоит отметить, что все грани и рёбра четырёхмерного куба равны. На рисунке они получаются не равными только потому, что расположены под разными углами к направлению взгляда. Однако можно развернуть гиперкуб так, что все проекции будут иметь одинаковую длину.

Кстати, на этом рисунке отчётливо видны восемь кубов, являющихся гранями гиперкуба.

Гиперкуб внутри пустой

В это трудно поверить, но между кубами, ограничивающими гиперкуб, заключено некоторое пространство (фрагмент четырёхмерного пространства).

Чтобы это лучше понять, давайте рассмотрим двумерную проекцию обычного трёхмерного куба (я специально сделал её несколько схематичной).

Можно ли по ней догадаться, что внутри куба есть некоторое пространство? Да, но только применив воображение. Глаз этого пространства не видит. Это происходит потому, что рёбра, расположенные в третьем измерении (которое нельзя изобразить на плоском рисунке), теперь превратились в отрезки, лежащие в плоскости рисунка. Они больше не обеспечивают объём.

Квадраты, ограничивающие пространство куба, наложились друг на друга. Но можно представить, что в исходной фигуре (трёхмерном кубе) эти квадраты располагались в разных плоскостях, а не один поверх другого в одной плоскости, как это получилось на рисунке.

Точно так же дело обстоит и с гиперкубом. Кубы-грани гиперкуба на самом деле не накладываются, как это кажется нам на проекции, а располагаются в четырёхмерном пространстве.

Развёртки

Итак, житель четырёхмерного пространства может увидеть трёхмерный объект одновременно со всех сторон. Можем ли мы одновременно со всех сторон увидеть трёхмерный куб? Глазом — нет. Но люди придумали способ, как изобразить на плоском рисунке все грани трёхмерного куба одновременно. Такое изображение называется развёрткой.

Развёртка трёхмерного куба

Как образуется развёртка трёхмерного куба все наверно знают. Этот процесс показан на анимации.

Для наглядности края граней куба сделаны полупрозрачными.

Следует отметить, что мы способны воспринять эту двумерную картинку только благодаря воображению. Если рассмотреть фазы разворачивания с чисто двумерной точки зрения, то процесс будет казаться странным и совсем не наглядным.

Он выглядит, как постепенное появление сперва очертаний искажённых квадратов, а потом их расползание на свои места с одновременным принятием необходимой формы.

Если смотреть на разворачивающийся куб в направлении одной из его граней (с этой точки зрения куб выглядит как квадрат), то процесс образования развёртки ещё менее нагляден. Всё выглядит как выползание квадратов из начального квадрата (не развёрнутого куба).

Но не наглядна развёртка только для глаз. Как раз благодаря воображению из неё можно почерпнуть много информации.

Развёртка четырёхмерного куба

Сделать анимированный процесс разворачивания гиперкуба хоть сколько нибудь наглядным просто невозможно. Но этот процесс можно представить. (Для этого надо посмотреть на него глазами четырёхмерного существа.)

Развёртка выглядит так.

Здесь видны все восемь кубов, ограничивающих гиперкуб.

Одинаковыми цветами покрашены грани, которые должны совместиться при сворачивании. Серыми оставлены грани для которых парных не видно. После свёртки самая верхняя грань верхнего куба должна совместиться с нижней гранью нижнего куба. (Аналогично сворачивается развёртка трёхмерного куба.)

Обратите внимание, что после свёртки все грани восьми кубиков придут в соприкосновение, замкнув гиперкуб. И наконец, представляя процесс свёртывания, не забывайте, что при свёртывании происходит не наложение кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области.

Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты фигурируют в очень многих его картинах. На картине «Распятие» (1954) используется развёртка гиперкуба.

Пространство-время и евклидово четырёхмерное пространство

Надеюсь, что вам удалось представить гиперкуб. Но удалось ли вам приблизиться к пониманию, как устроено четырёхмерное пространство-время в котором мы живём? Увы, не совсем.

Здесь мы говорили об евклидовом четырёхмерном пространстве, но пространство-время обладает совсем другими свойствами. В частности, при любых поворотах отрезки остаются всегда наклонены к оси времени либо под углом меньше 45 градусов, либо под углом больше 45 градусов.

Свойствам пространства времени я посвятил серию заметок.

---

---

Четырёхмерный гиперкуб. Программа Transformator 4D / Habr

В данной статье хотелось бы поговорить о четырехмерном гиперкубе (тессеракте), и его построение в программе Transformator 4D.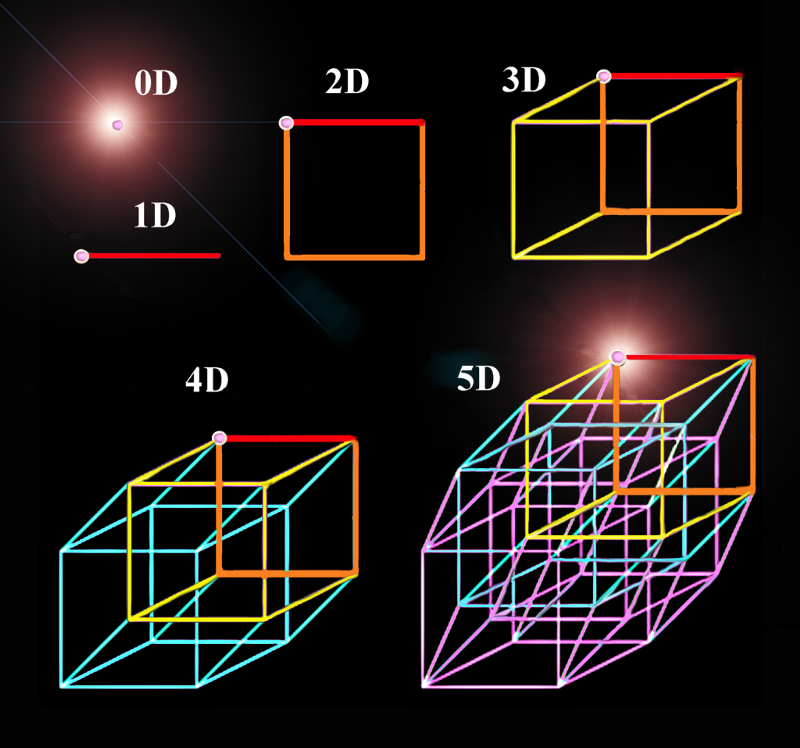

Как мы знаем из геометрии, квадрата – это правильный четырехугольник у которого все углы и стороны равны. Куб можно охарактеризовать следующим образом, это выпуклая фигура, обязательно замкнутая и состоящая из групп параллельных линий расположенных относительно друг друга на противоположных краях фигуры и, соединенных друг с другом под прямым углом. Следовательно гиперкуб — это n-мерная аналогия квадрата у которого n=2 и, куба у которого n=3.

Рассмотрим рисунок 1. На нем изображена точка, которая есть гиперкуб размерностью равной 0. Далее если сдвинуть точку на единицу длины, что приведет к получению отрезка единичной длины и как следствие гиперкуба размерностью единица. После чего сдвинуть отрезок на ту же единицу длины, но перпендикулярно в направлении исходного отрезка, и продолжить эту операцию до замыкания контура, то получится квадрат – гиперкуб размерностью в два. Если продолжить построение, то сдвигая квадрат на ту же единицу длины обязательно в направлении перпендикулярному плоскости квадрата, получим куб или гиперкуб размерностью 3. И наконец если сдвинуть куб на единицу длины в четвертом измерении то получим четырехмерный гиперкуб. Такое процесс можно повторять на n-е количество измерений.

Рис.1

В евклидовом пространстве тессеракт характеризуется как объемная оболочка состоящая из точек: +-1, +-1, +-1, +-1, что можно записать в виде:

Отсюда видно, что тессеракт ограничен 8-ю гиперплоскостями, пересечение которых с самим тессерактом задает его трехмерные грани, они же являются просто кубами, и в конечном итоге получаем:

• 8-мь трехмерных граней,
• 24-и двумерных,
• 32-а ребра,
• 16-ть вершин.

Программа Transformator 4D предназначена для создания модели, путем считывания аффинных преобразований и последующим их созданием.

Основой работы программы являются именно аффинные преобразования, это действия над объектом путем перемещения, масштабирования, поворота. Пользователь может сам составлять объекты, в формате файла txt, и анимировать его движение. Программа может выводить частные случаи аффинных преобразований в пространстве, и проекции для любого заданного тела.

Как задавать фигуры

В директории с программой создается папка FIGURES. Каждая фигура задается при помощи двух файлов: первый FigureX.txt, где находятся координаты вершин, второй FigureXm.txt, где находится матрица смежности этих вершин. Х – номер фигуры.

Характеристика файла FigureX.txt:

Координаты первой вершины по Х, находятся в первой строке.
Координаты второй вершины по У, находятся во второй строке.
и т.д. Последняя строка «х» — конец данных.

Характеристика файла FigureXm: Матрица смежности, показывает номера вершин из первого файла.

При запуске программа требует файл acrTrans2FA.txt. Файл описывает четырехмерную фигуру и аффинные преобразования в отдельности для каждого полигона.

По сути можно построить объект отдельные части которого подвергаются разным преобразованиям, и каждую субмодель представить отдельным цветом.

После указания каждого полигона нужно указать аффинные преобразования этого полигона.

Пример: Сборка развертки куба на основе построения квадрата.

Рис. 2

1 Замкнутые полигоны
0 0 0 1 Координаты вектора проецирования
6 Шесть полигонов
4 4 точки в первом полигоне
1 1 0 Цвет полигона №1

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

0 Аффинных преобразований отсутствуют — квадрат №1

4 4 точки — квадрат №2
0.5 0.5 0.5 Цвет полигона №2

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

2 Два преобразования
2 1 -1 0 0 0 Смещение на -1 по х
6 1 0 -1 0 0 0 0 Разворот по оси zx

4 4 точки в квадрате №3
0. 1 0.1 0.1 Цвет полигона 3

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4
2 Два преобразования
6 1 0 1 0 0 0 0 Разворот вокруг y от x к z
2 1 1 0 0 0 Смещение на 1 по x

4 Квадрат №4
0.6 0.1 0.7 Цвет полигона 4

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

2 Два преобразования
2 1 0 -1 0 0 Смещаем вниз по y
6 1 0 0 0 -1 0 0 Перемещение вокруг x от z к y

4 Квадрат №5
1 0 0 Цвет полигона 5

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

2 Два преобразования
6 1 0 0 0 1 0 0 Перемещение вокруг x от y к z
2 1 0 1 0 0 Смещаем вверх по y

4 Квадрат №6
0.25 0.5 0.5 Цвет полигона №6

0 0 0 0 Точка 1
1 0 0 0 Точка 2
1 1 0 0 Точка 3
0 1 0 0 Точка 4

4 Четыре преобразования
2 1 0 -1 0 0 Смещаем вниз по y
6 1 0 0 0 -1 0 0 Перемещение вокруг x от z к y
2 1 0 -1 0 0 Смещение вниз для квадрата №6
6 1 0 0 0 -1 0 0 Вращение относительно нижнего ребра четвертого квадрата.

Квадрат №6: описывает два поворота, так как одно из его ребер является общим с квадратом №4, поэтому изначально вращается квадрат №4, после происходит смещение на 1 вниз, и далее вращение вокруг этого же ребра.

Выглядит это так:

Рис.3

Как задать описание тессеракта:

Рис.4

Тессеракт можно развернуть в восемь кубов, так же как куб можно развернуть в шесть квадратов. Развертка тессеракта называется сетью. Для гиперкуба существует 261 вариант сетей, ниже показан самый распространенный.

Исходя из основ сборки куба, также можно написать программу сборки тессеракта или обратного.

Интересно знать

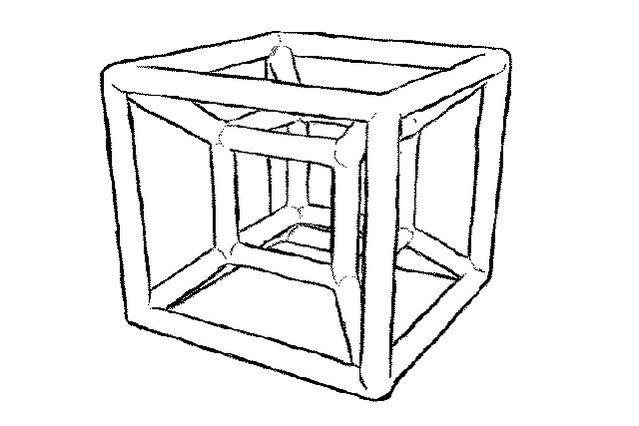
В фильме «Куб 2: Гиперкуб» — восемь незнакомых людей просыпаются в комнатах, имеющих форму куба. Комнаты находятся внутри четырёхмерного гиперкуба. Комнаты постоянно перемещаются путём «квантовой телепортации», и если перелезть в соседнюю комнату, то вернуться в прежнюю уже маловероятно. В гиперкубе пересекаются параллельные миры, время в некоторых комнатах течёт по-разному, а некоторые комнаты являются смертельными ловушками.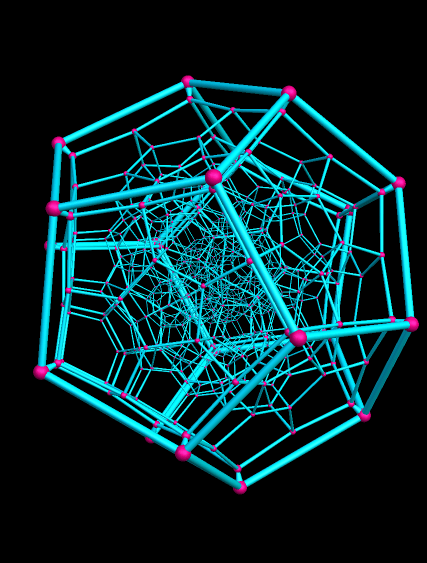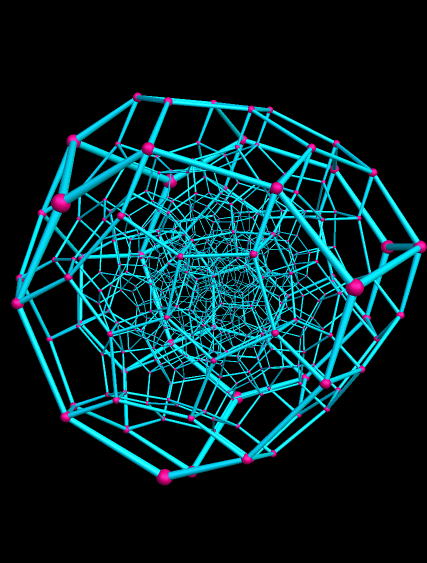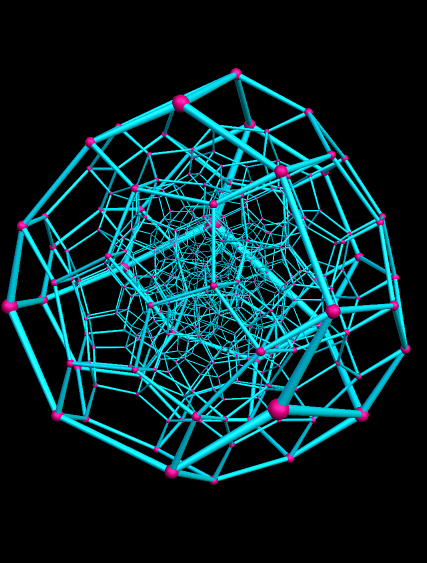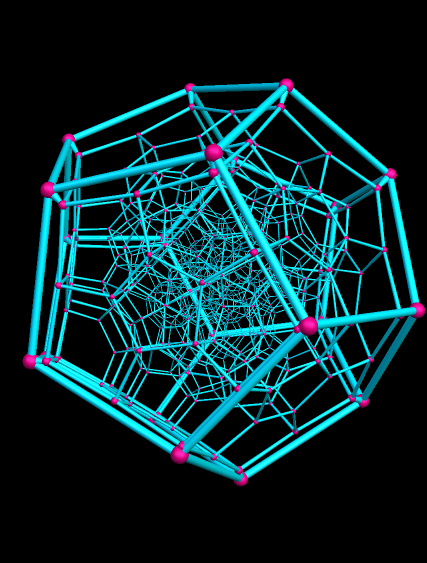

Используемый источник: damateur.narod.ru

Brilliant Math & Science Wiki

Аррон Кау внес

Содержание

• Введение
• Свойства тессерактов
• Визуализация тессерактов
• Смотрите также

На изображении ниже мы видим одну попытку представить схему гиперкуба, хотя изображение обманчиво в том смысле, что относительные размеры и углы на этом изображении искажены. Каждый четырехугольник на изображении ниже, образованный четырьмя вершинами гиперкуба, является квадратом (хотя на диаграмме они не выглядят квадратами!) Точно так же каждая пара прямых, которые встречаются в вершине, находятся под прямым углом друг к другу ( как и следовало ожидать в квадрате или кубе). Невозможно идеально представить гиперкуб в двух измерениях или даже построить его в трех измерениях.

Квадрат представляет собой двумерную замкнутую фигуру с линиями одинаковой длины, пересекающимися под прямым углом. Куб — это трехмерная фигура с линиями одинаковой длины, пересекающимися под прямым углом. Для квадрата две линии встречаются в каждой вершине (угле). Для куба, поскольку мы добавили еще одно измерение, у нас есть три линии, пересекающиеся в каждой вершине.

Тессеракт представляет собой четырехмерную замкнутую фигуру с линиями одинаковой длины, которые пересекаются друг с другом под прямым углом. Поскольку мы добавили еще одно измерение, четыре линии сходятся в каждой вершине под прямым углом. Как и в случае с кубом, каждая двумерная грань тессеракта представляет собой квадрат. На самом деле тессеракт имеет трехмерные «грани», каждая из которых представляет собой куб.

Вы можете определить свойства тессеракта, экстраполируя идею квадрата и куба (см. задачи ниже). Однако они также перечислены здесь за кнопкой:

. Гиперкуб обладает следующими свойствами:

• 16 вершин (0D: точки)
• 32 ребра (1D: линии)
• 24 грани (2D: квадраты)
• 8 ячеек (3D: кубики)

20 8 12 16

Сколько углов имеет гиперкуб (четырехмерный куб)?

Сколько двумерных граней имеет тессеракт (четырехмерный куб)?

Примечание: Грань — это плоская двумерная поверхность, являющаяся частью границы многогранного объекта.

Трудно визуализировать объекты в более высоких измерениях. Выше мы видели пару различных представлений выше. Вот еще один, в котором более наглядно показано свойство, заключающееся в том, что все строки в тессеракте имеют одинаковую длину. Хотя это изображение помогает нам увидеть, что все двумерные грани тессеракта являются квадратами, на этом рисунке труднее увидеть, что все трехмерные ячейки являются кубами:

Каждое отдельное представление помогает нам развить некоторую интуицию относительно взаимосвязей в форме. Возможны многие другие представления, каждое со своими компромиссами.

Выберите один или несколько

Ф я г л С ЧАС Дж Д

Если вы возьмете твердый четырехмерный гиперкуб и разрежете его одной плоской трехмерной гиперплоскостью, какое поперечное сечение может быть , а не ?

* Квадрат
* Гиперплоскость

Цитировать как: Тессеракт. Brilliant.org . Извлекаются из https://brilliant.org/wiki/tesseract/

Четыре измерения

Четыре измерения

HPS 0410

Эйнштейн для всех

---

Назад на страницу основного курса

Джон Д. Нортон
Кафедра истории и философии науки
Университет Питтсбурга

• Одномерный интервал
• Двумерный квадрат
• Трехмерный куб
• Четырехмерный куб: тессеракт
• Стереовидение
• Сводная таблица
• Вместительный вызов
• Запутанный вызов
• Использование цветов для визуализации дополнительного измерения
• Что вы должны знать

Мы уже видели, что нет ничего страшного таинственно о добавлении одного измерения к пространству, чтобы сформировать пространство-время. Тем не менее трудно устоять перед затянувшимся беспокойство по поводу идеи четырехмерного пространства-времени. проблема не в время часть четырехмерного пространства-времени; это это четыре . Легко представить себе три оси трехмерного мерное пространство: вверх-вниз, поперек и задом наперед. Но куда нам поставить четвертую ось, чтобы сделать четырехмерное пространство?

Моя нынешняя цель — показать вам, что на самом деле ничего нет. все таинственное в четырех измерениях пространства-времени. Для этого я брошу временная часть полностью. Я просто рассмотрю четырехмерный космос; то есть пространство точно такое же, как наше трехмерное пространство, но с одно дополнительное измерение. Каково это?

Без всяких усилий я могу визуализировать трехмерное пространство — и вы тоже можете. Что бы это быть как жить в трехмерном кубе? Чтобы его попросили визуализировать это как просят дышать или моргать. Это легко. Там мы сидим в куб с шестью квадратными стенками и восемью углами. Наш разум позволяет мы парим внутри.

Могу ли я представить, каково было бы жить в четырехмерный аналог куба, четырехмерный куб или «тессеракт»? Я не могу представить это с таким же легким непосредственность. Сомневаюсь, что и вы сможете. Но это только о единственное, что мы не можем сделать. В противном случае мы можем определить все свойства тессеракта и то, что это будет нравится жить в одном. Для этого существует множество техник. я покажет вам один ниже. Он включает в себя продвижение через последовательность измерений, экстраполируя естественные выводы в каждом шагнуть в четвертое измерение. Как только вы видели, как это делается для особого случая тессеракта у вас не будет проблем применяя его к другим случаям.

Дверь в четвертое измерение открывается.

Одномерный интервал

Одномерный аналог куба — интервал. Это формируется путем взятия безразмерной точки и перетаскивания ее на определенное расстояние. Это расстояние может быть 2 дюйма или 3 фута или что-то еще. Давайте позвоним расстояние «Л».

Интервал имеет длину L. Он ограничен двумя точками как его грани — две точки на обоих концах интервала.

Двумерный квадрат

Двумерным аналогом куба является квадрат. Это образованный перетаскиванием одномерного интервала на расстояние L в второе измерение.

Квадрат имеет площадь L ² . Он ограничен гранями на 4 стороны. Грани — это интервалы длины L. Мы знаем, что их четыре. их, поскольку его двумерные оси должны быть закрыты с обоих концов гранями.

Таким образом, у нас есть 2 измерения x 2 грани каждое = 4 грани. грани вместе образуют периметр длиной 4xL.

Трехмерный куб

Чтобы сформировать куб, мы берем квадрат и перетаскиваем его на расстояние L в третьем измерении.

Объем куба L ³ . Он ограничен гранями на 6 сторон. Грани представляют собой квадраты площадью L ² . Мы знаем, что есть 6 из них, так как его трехмерные оси должны быть закрыты с обоих концов лица.

Итак, у нас есть 3 измерения x 2 грани в каждой = 6 граней. грани вместе образуют поверхность площадью 6xL ² . Рисование изображение трехмерного куба на двумерной поверхности одинаково легко. Берем две его грани — два квадрата — и соединяем углы.

Есть несколько способов сделать рисунок, который соответствует взгляду на куб под разными углами. На рисунке показано два способа сделать это. Первый дает косой обзор; второй смотрит по одной из осей.

Четырехмерный куб: тессеракт

Пока я надеюсь, что вы нашли наши конструкции полностью безупречный. Следующий шаг в четыре измерения можно сделать одинаково механически. Мы просто систематически повторяем каждый шаг выше. Единственный разница в том, что на этот раз мы не можем легко сформировать ментальную картину что мы строим. Но мы можем знать все его свойства!

Чтобы сформировать тессеракт, мы берем куб и перетаскиваем его расстояние L в четвертом измерении . Мы не можем точно представить как это выглядит, но это примерно так:

Тессеракт имеет объем L ⁴ . Он ограничен грани с 8 сторон. Грани представляют собой кубы объема L ³ . Мы знаем их 8, так как его четыре оси должны быть ограничены любой конец гранями — две кубические грани на ось. Еще раз, мы не можем визуализируйте все четыре из этих закрытых измерений. Мы можем в лучшем случае визуализировать три направления перпендикулярны друг другу. Затем мы каким-то образом добавим в четвертый (красный):

Итак, у нас есть 4 измерения по 2 грани в каждой = 8 граней. грани вместе образуют «поверхность» (на самом деле трехмерный объем) размером 8xL ³ в объеме. Рисование изображения четырехмерного тессеракта в трехмерном размерное пространство прямолинейно. Мы берем два его лица — два кубики — и соедините углы.

Есть несколько способов сделать рисунок, который соответствует взгляду на тессеракт под разными углами. Фигура показывает два способа сделать это. Первый дает косой обзор; второй смотрит по одной из осей.

Итак, теперь мы, кажется, знаем все, что нужно знать о тессеракт! Мы знаем его объем в четырехмерном пространстве, как он выражается вместе из восьми кубов как поверхностей и даже каков объем его поверхность (8xL ³ ).

Стереовидение

«Чертежи» тессеракта плохо видны. Это потому, что они действительно должны быть трехмерными моделями в трехмерное пространство. Итак, что у нас есть выше, это два объемный чертежи трехмерных моделей четырехмерного тессеракт. Неудивительно, что он становится грязным!

Изображения ниже представляют собой стереопары. Если вы знакомы с тем, как их просматривать, вы увидите, что они дают вам хороший стереофонический вид трехмерной модели. Если это новое для вас, они берут практика, чтобы увидеть. Вам нужно расслабить свой взгляд, пока ваш левый глаз не смотрит на левое изображение и правый глаз смотрит на правое изображение.

Но как научиться этому? мне проще всего начать, если я сижу далеко от экрана и смотрю вдаль над верхней частью экрана. Я вижу два несколько размытых изображения на край моего поля зрения. Пока я не сосредотачиваюсь на них, они начинают дрейфовать вместе. Это то движение, которое вам нужно. Чем больше они дрейфуют вместе тем лучше. Я стараюсь усилить дрейф, насколько это возможно, пока осторожно перемещая свой взгляд к изображениям. Цель состоит в том, чтобы получить два изображения для слияния. Когда они это делают, я продолжаю смотреть на объединенные изображения, улучшается фокусировка и появляется полный трехмерный стереоэффект резко. Эффект поразителен и стоит небольших усилий.

Эту пару легче сплавить:

и этот немного сложнее:

Сводная таблица

Мы можем подытожить развитие свойств tesseract следующим образом:

Размер	Рисунок	Лицо	Том	Номер лиц	Том поверхность/периметр
1	интервал	точка	л	1×2=2	два баллы
2	квадрат	интервал	л 2	2×2=4	4 л
3	куб	квадрат	л 3	3×2=6	6 л 2
4	тессеракт	куб	л 4	4×2=8	8 л 3

Вместительный вызов

Если бы вы жили в тессеракте, вы могли бы выбрать жить на своей трехмерной поверхности, как двухмерный человек могли бы выбрать жить в 6 квадратных комнатах, которые образуют двухмерный поверхность куба. Таким образом, ваш дом будет состоять из восьми кубов, образующих поверхность. из тессеракта. Представьте себе, что есть двери, где когда-либо две из эти кубики встречаются. Если вы находитесь в одной из этих комнат, сколько дверей будет Понимаете? Как бы выглядела следующая комната, если бы вы прошли через одну из двери? Через сколько дверей нужно пройти, чтобы добраться до самой дальней комната? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо окна снаружи тессеракта? Как насчет окон внутрь? тессеракт?

Некоторые из этих вопросов непростые. Чтобы ответить на них, перейдите вернемся к простому случаю трехмерного куба с гранями, состоящими из квадраты. Задайте аналогичные вопросы там и просто экстраполируйте ответы на тессеракт.

Запутанный вызов

Доступ к четвертому измерению делает возможным многое иначе это было бы совершенно невозможно. Чтобы увидеть, как это работает, мы будем использовать стратегия обдумывания процесса в трехм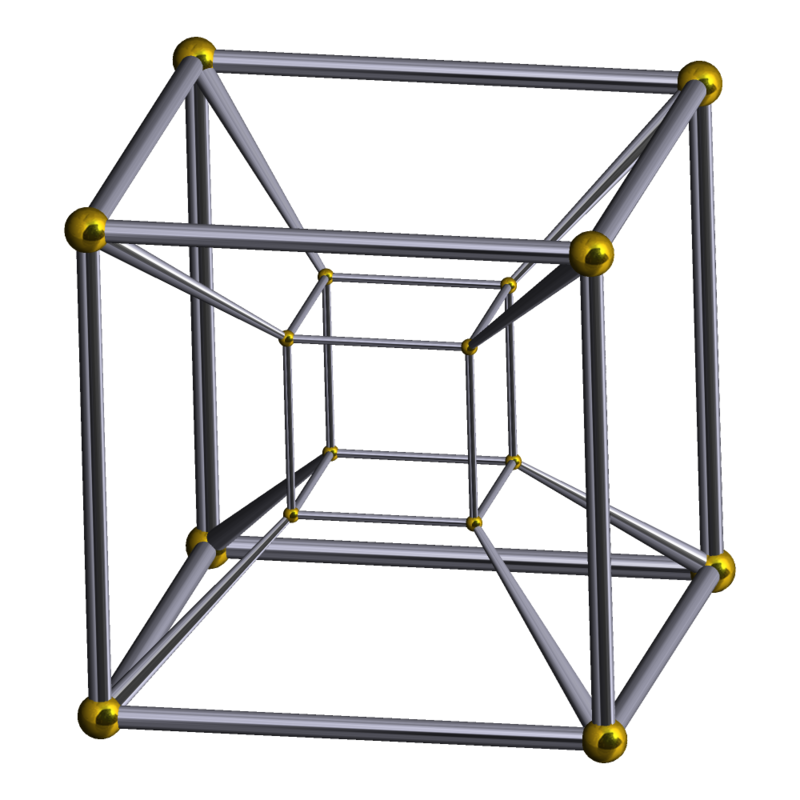ерном пространстве. Затем мы воспроизвели его в четырехмерном пространстве.

Рассмотрим монету, лежащую в рамке на столе.

Монета не может быть удалена из рамки в пределах ограничивает двумерную поверхность стола. Теперь вспомните что у нас есть доступ к третьему измерению. Монета легко удалить, просто подняв его в третье измерение, высота над столом. После этого мы можем свободно перемещать монету по своему усмотрению в более высокую слой, а затем опуститься обратно на столешницу за пределами рамы.

При подъеме следует обратить внимание на то, что движение вообще не двигает монету в двух горизонтальных направлениях двух объемное пространство. Таким образом, движение никогда не приближает его к кадру и там нет опасности столкновения с рамой.

Теперь повторите этот анализ для своего аналог в одном более высоком измерении, мрамор запертым в трехмерном ящике.

Мрамор можно удалить в точно так же, «подняв» его, на этот раз в четвертое измерение. Как и монета в рамке, ключ следует отметить, что при этом подъемном движении шарик положение в трех пространственных направлениях ящика без изменений. Мрамор никогда не приближается стены и нет опасности столкновения с ними. Как только оно поднимается в новое трехмерное пространство, оно можно свободно перемещать в этом пространстве и опускать обратно в исходное трехмерное пространство, но теперь за пределы коробка.

Теперь, наконец, рассмотрим два зацепленных колец в некотором трехмерном пространстве. Можем мы разделить их, используя доступ к четвертому измерению?

Это можно сделать точно так же процесс подъема одного из колец в четвертое измерение. Как прежде обратите внимание, что подъем не перемещает кольцо ни в одном из три направления трехмерного пространства, удерживающие первоначально связанные кольца. Так что движения рисков нет столкновения перемещаемого кольца с другим. Подъем просто поднимает перемещенное кольцо на новый трехмерный слой из четырех размерное пространство, в котором нет ни одной части другого кольца.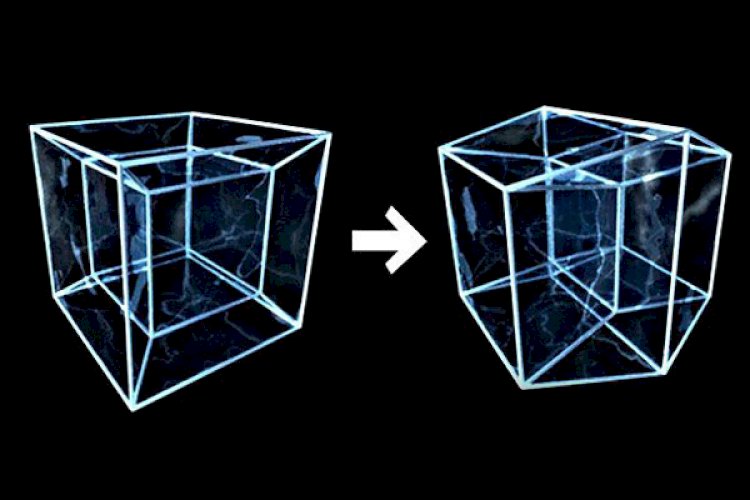 перемещенное кольцо может быть свободно перемещено в этот новый слой, и если мы с удовольствием опустился обратно в исходное трехмерное пространство в совсем другое место.

А теперь самое сложное. Мы знакомы в нашем трехмерное пространство с завязыванием узлов на веревке. Некоторые узлы просто кажущиеся клубки, которые могут довольно легко разойтись. Остальные настоящие и можно расстегнуть, только продев конец веревки в петлю. Так примите это за настоящий узел: тот, который не может быть развязаны любыми манипуляциями с веревкой, если мы не сможем ухватиться за заканчивается. (Представьте, если хотите, что каждый из них прикреплен к стене и нельзя удалить.)

Задача состоит в том, чтобы убедить сами понимаете, что в четырехмерном пространстве на веревках нет настоящих узлов. космос. Основная помощь, которая вам понадобится, — это манипуляция, описанная выше. связанные кольца. Для начала представьте, как бы вы использовали четвертый измерение, чтобы развязать какой-нибудь простой узел, который вы легко можете себе представить.

Использование цветов для визуализации дополнительных размер

Общая идея «поднятия» объекта в четвертое измерение все еще кажется неуловимым? Если да, то вот техника для визуализация этого может просто помочь. Хитрость заключается в том, чтобы представить, что различия в положении в дополнительном измерении пространства может быть представлено различия цветов.

Вот как это работает, когда мы начинаем с двухмерного пространства и подняться в третье измерение. Объекты в оригинале два мерное пространство черное. Когда мы поднимаемся через третий измерения, они последовательно приобретают синий цвет, зеленый и красный.

Теперь давайте применим цветной слой. трюк к более раннему примеру подъема монеты из рамки. монета начинается в том же двухмерном пространстве, что и рамка. Мы поднимаем это в третье измерение в более высокое пространственный слой, который мы закодировали красным цветом. В этом высшем слой, монета может свободно перемещаться влево/вправо и вперед/назад без пересекающие рамку. Мы перемещаем его вправо, пока он не пройдет над рамой. Затем опускаем обратно вниз снаружи.

А теперь представьте, что мы не можем воспринимать третье измерение напрямую. Вот как мы представить побег монеты. Он начинается внутри кадра в пространство кадра. Затем он поднимается из рамы в третье измерение. В этот момент на это указывает призрачный красная монета. Его пространственное положение слева/справа и направление вперед/назад не изменилось. Все, что изменилось, это его высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево или справа, или спереди и сзади, в этом красном слое уже не пересекает рамку и может двигаться прямо над ней. мы этого не увидим однако перемещайтесь по кадру. Насколько нам известно, это будет просто пройди через это. Движение монеты в этом трехмерном побеге иллюстрируется призрачным красным монета.

Этот последний анализ монеты в кадр является шаблоном для работы с реальный случай шарика, заключенного в трехмерную коробку. Если шарик движется в любом из трех известных измерений (вверх/вниз, влево/вправо и вперед/назад), его движение пересекает стены ящик, и он не может убежать. Итак, мы поднимаем шарик в четвертый измерение, не меняя своего положения в трех привычных размеры. На рисунке это показано тем, что мрамор становится призрачным. красный. В красном поле шарик может двигаться вверх/вниз, слева/справа и спереди/сзади, не пересекая стенки коробки. Затем мрамор перемещается так, что проходит над одной из стен. Это затем опустили из красного пространства обратно к исходным трем мерное пространство коробки, но уже вне стен.

То же самое анализ относится к связанным кольцам. Одно кольцо снято из трехмерного пространства исходной установки. В этом красное пространство, кольцо может свободно двигаться, не пересекаясь с другим звенеть. Мы отодвигаем его подальше от другого кольца, а затем опускаем обратно. в исходное трехмерное пространство. Теперь он не связан с другое кольцо.

Что следует знать

• Свойства квадратов, кубов и тессерактов.