Как перевести десятичное число в двоичную систему счисления. Какие существуют алгоритмы перевода чисел между системами счисления. Как выполнять арифметические операции в разных системах счисления.
Основные понятия систем счисления
Система счисления — это способ записи чисел с помощью определенного набора символов (цифр) и правил их использования. Выделяют два основных типа систем счисления:
- Позиционные — значение цифры зависит от ее позиции в записи числа (например, десятичная, двоичная)
- Непозиционные — значение цифры не зависит от ее позиции (например, римская система)
В позиционных системах счисления важную роль играет основание системы — количество уникальных цифр, используемых для записи чисел. Наиболее распространенные основания:
- 2 — двоичная система (цифры 0 и 1)
- 8 — восьмеричная система (цифры от 0 до 7)
- 10 — десятичная система (цифры от 0 до 9)
- 16 — шестнадцатеричная система (цифры 0-9 и буквы A-F)
Алгоритм перевода целых чисел из десятичной системы
Для перевода целого десятичного числа в систему счисления с основанием N используется метод последовательного деления:
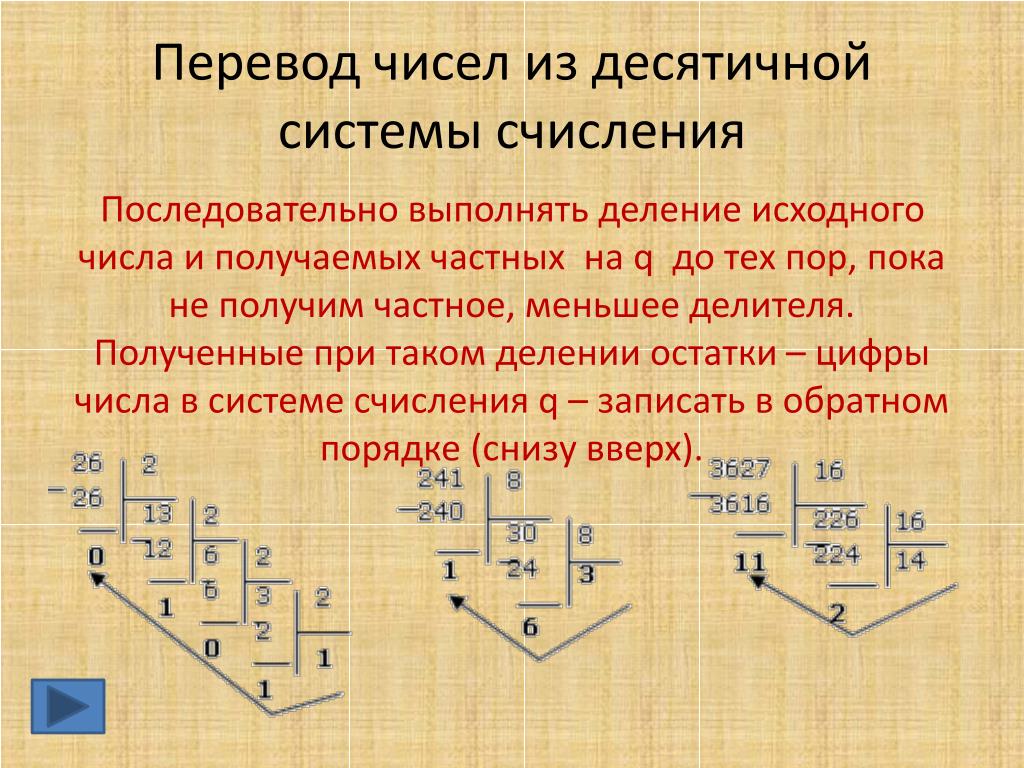
- Разделить число на N
- Записать остаток от деления
- Если частное не равно нулю, повторить шаги 1-2 для частного
- Полученные остатки записать в обратном порядке
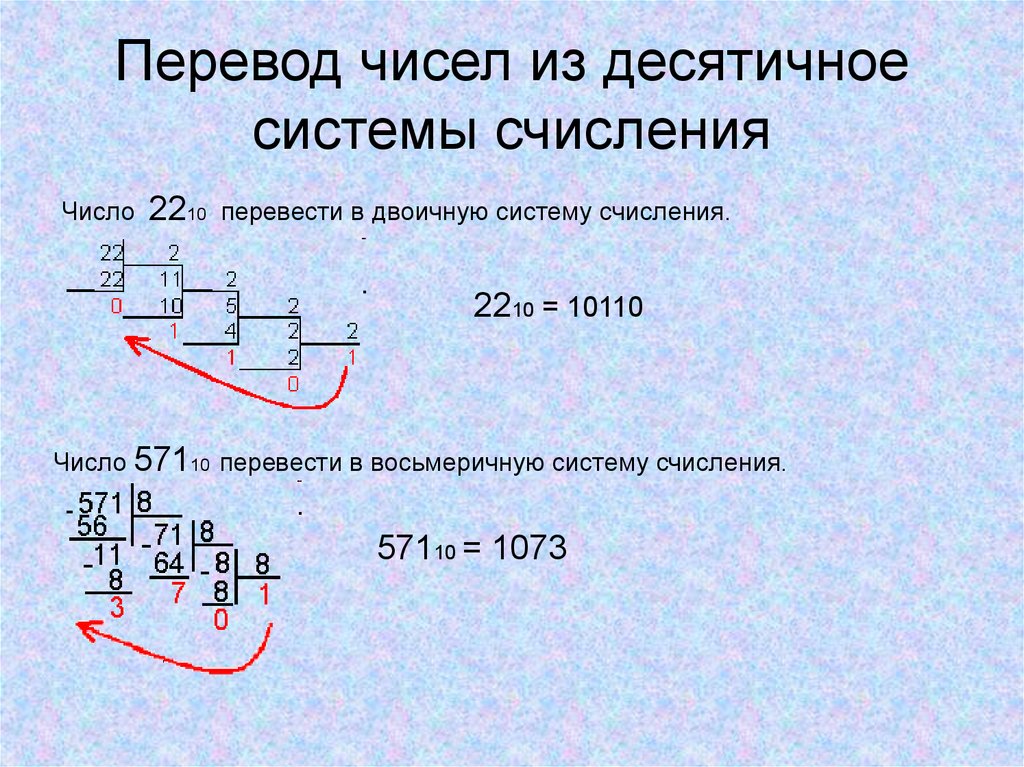
Рассмотрим пример перевода числа 75 в двоичную систему:
75 : 2 = 37 (остаток 1) 37 : 2 = 18 (остаток 1) 18 : 2 = 9 (остаток 0) 9 : 2 = 4 (остаток 1) 4 : 2 = 2 (остаток 0) 2 : 2 = 1 (остаток 0) 1 : 2 = 0 (остаток 1) Результат: 75(10) = 1001011(2)
Перевод дробных чисел
Для перевода правильной десятичной дроби в систему с основанием N используется метод умножения:
- Умножить дробь на N
- Отделить целую часть
- Если дробная часть не равна нулю, повторить шаги 1-2 для нее
- Записать полученные целые части
Пример перевода 0,625 в двоичную систему:
0,625 * 2 = 1,25 (1) 0,25 * 2 = 0,5 (0) 0,5 * 2 = 1,0 (1) Результат: 0,625(10) = 0,101(2)
Особенности перевода в различные системы счисления
Перевод в двоичную систему
При переводе в двоичную систему используются только цифры 0 и 1. Это делает двоичную систему очень удобной для представления информации в компьютерных системах, где данные кодируются с помощью двух состояний (есть сигнал/нет сигнала).

Перевод в восьмеричную систему
Восьмеричная система использует цифры от 0 до 7. Удобство ее применения заключается в том, что каждая восьмеричная цифра может быть представлена тремя двоичными разрядами.
Перевод в шестнадцатеричную систему
В шестнадцатеричной системе используются цифры от 0 до 9 и буквы A, B, C, D, E, F. Каждая шестнадцатеричная цифра может быть представлена четырьмя двоичными разрядами, что делает эту систему удобной для работы с компьютерной памятью.
Арифметические операции в различных системах счисления
Выполнение арифметических операций в недесятичных системах счисления имеет свои особенности. Рассмотрим основные правила на примере двоичной системы.
Сложение в двоичной системе
При сложении двоичных чисел необходимо помнить правила:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10 (перенос в следующий разряд)
Пример:
1011 + 1101 ------ 11000
Вычитание в двоичной системе
При вычитании используются следующие правила:
- 0 — 0 = 0
- 1 — 0 = 1
- 1 — 1 = 0
- 0 — 1 = 1 (с заемом из старшего разряда)
Пример:

1011 - 0101 ------ 0110
Применение систем счисления в информатике и программировании
Различные системы счисления широко используются в информатике и программировании:
- Двоичная система является основой для представления и обработки информации в компьютерах
- Восьмеричная и шестнадцатеричная системы часто применяются для компактной записи двоичных кодов
- Шестнадцатеричная система используется для представления цветов в веб-дизайне (например, #FF0000 — красный цвет)
- В программировании часто используются константы в различных системах счисления (например, 0b1010 — двоичное число, 0x1A — шестнадцатеричное)
Инструменты для работы с системами счисления
Для упрощения работы с различными системами счисления существует ряд полезных инструментов:
- Встроенный калькулятор в операционных системах (например, в Windows есть режим «Программист»)
- Онлайн-конвертеры систем счисления
- Специализированные калькуляторы для работы с двоичной и шестнадцатеричной системами
- Функции для перевода чисел между системами счисления в языках программирования (например, bin(), hex(), int() в Python)
Заключение
Понимание принципов работы различных систем счисления и умение переводить числа между ними является важным навыком для специалистов в области информационных технологий. Эти знания позволяют лучше понимать принципы работы компьютерных систем, эффективнее работать с данными и решать различные задачи в программировании и цифровой обработке информации.

Системы счисления (стр. 2 из 3)
Перевод целых чисел
1. основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе счисления;
2. последовательно выполнять деление данного числа и получаемых неполных частых на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
3. полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4. составить число в новой системе счисления, записывая его, начиная с последнего частного.
Пример 1. Перевести число
в двоичную систему. Для обозначения цифр используем символику:
Перевод дробных чисел.
1. основание новой системы счисления выразить в десятичной системе и все последующие действия производить в десятичной системе счисления;
2. последовательно умножать данное число и полученные дробные части произведений на основание новой системы до тех пор, пока дробная часть не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
3. полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4. составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Пример 4. Перевести десятичное число 315,1875 в восьмеричную и шестнадцатеричную системы счисления.
Из рассмотренных выше примеров следует:
.
Задачи
№23
Перевести целые числа из десятичной системы счисления в троичную:
1. 523; 65; 7000; 2307; 325
2. 12; 524; 76; 121; 56.
№24
Перевести целые числа из десятичной системы счисления в восьмеричную:
1. 856; 664; 5012; 6435; 78;
2. 214; 89; 998; 653; 111.
214; 89; 998; 653; 111.
№25
Перевести десятичные дроби в двоичную систему счисления. В двоичной записи числа сохранить шесть знаков.
1. 0,654; 0,321; 0,6135; 0,9876;
2. 0,55; 0,333; 0,1213; 0,453.
№26
Перевести десятичные дроби в шестнадцатеричную систему счисления. В новой записи дроби сохранить шесть знаков
1. 0,745; 0,101; 0,8453; 0,3451;
2. 0,8455; 0,225; 01234; 0,455
№27
Перевести смешанные десятичные числа в троичную и пятеричную системы счисления, оставить пять знаков в дробной части нового числа:
1. 40,5; 34,25; 124,44;
2. 78,333; 225,52; 90,99.
№28
Перевести смешанные десятичные числа в двоичную и восьмеричную системы счисления, оставив пять знаков в дробной части нового числа:
1. 21,5; 432,54; 678,333;
2. 12,25; 97,444; 7896,2.
№29
Перевести из десятичной системы счисления следующие числа:
1. 345 —
, 0,125 —
, 45,65 —
;
2. 675 —
675 —
, 0,333 —
, 23,15.
№30
Перевести из десятичной системы счисления следующие числа:
1. 1,25 —
, 675 —
, 0,355 —
;
2. 890 —
, 0,675 —
, 12,35 —
№31
Перевести из десятичной системы счисления следующие числа:
1. 425 —
, 0,425 —
, 98,45 —
;
2. 0,55 —
, 765 —
, 765,75 —
.
№32
Перевести из десятичной системы счисления следующие числа:
1. 98 —
, 0,545 —
, 87,325 —
;
2. 0,775 —
0,775 —
, 907 —
, 566,225 —
Системы счисления, используемые в ЭВМ (с основанием
)
Для того чтобы целое двоичное число записать в системе счисления с основанием
(4,8,16 и т.д.), нужно:
1. данное двоичное число разбить справа налево на группы по n цифр в каждой;
2. если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов;
3. рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой системе счисления с основанием
.
Для того чтобы дробное двоичное число записать в системе счисления с основанием
, нужно:
1. данное двоичное число разбить слева направо на группы по n цифр в каждой;
2. если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов;
3. рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой системе счисления с основанием
рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой системе счисления с основанием
.
Для того чтобы произвольное двоичное число записать в системе счисления с основанием
, нужно:
1. данное двоичное число разбить слева и справа (целую и дробную части) на группы по n цифр в каждой;
2. если в последних правой и левой группах окажется меньше n разрядов, то их нужно дополнить нулями до нужного числа разрядов;
3. рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой системе счисления с основанием
.
Для того чтобы произвольное число, записанное в системе счисления с основанием
, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления.
Применительно к компьютерной информации часто используются системы счисления с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).
Пример 5. Перевести число
в двоичную систему.
Для решения задачи воспользуемся приведенной ниже двоично-шестнадцатеричной таблицей.
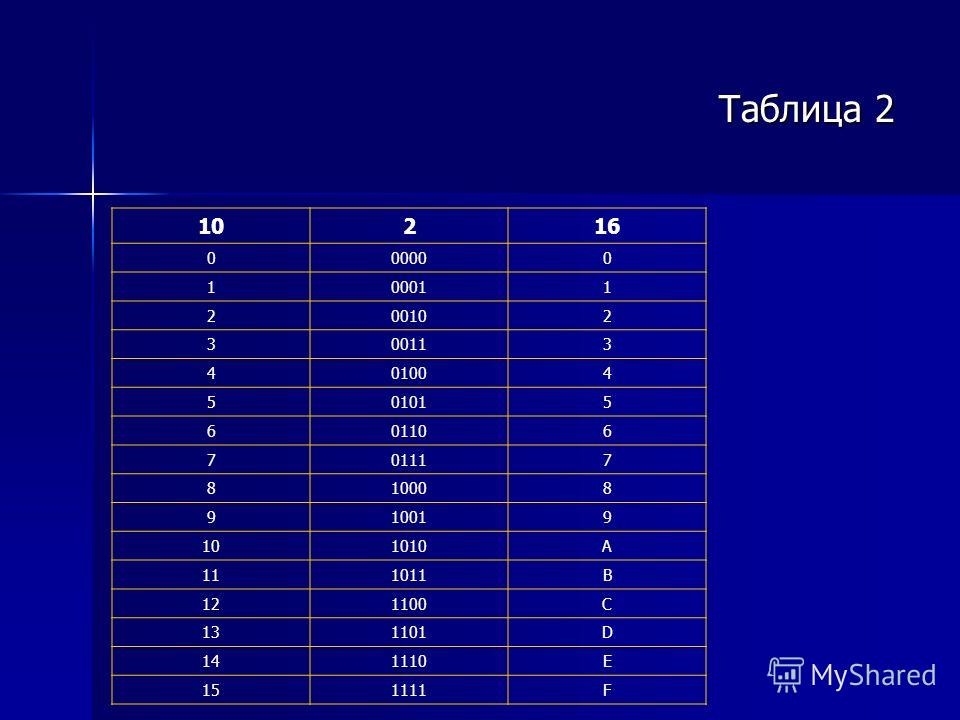
Двоично-шестнадцатеричная таблица
| 16 | 2 | 16 | 2 |
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | A | 1010 |
| 3 | 0011 | B | 1011 |
| 4 | 0100 | C | 1100 |
| 5 | 0101 | D | 1101 |
| 6 | 0110 | E | 1110 |
| 7 | 0111 | F | 1111 |
В одном столбце таблицы помещены шестнадцатеричные цифры, напротив, в соседнем столбце – равные им двоичные числа. Причем все двоичные числа записаны в четырехзначном виде (там, где знаков меньше четырех, слева добавлены нули).
А теперь проделаем следующее: каждую цифру в шестнадцатеричном числе 15FC заменим на соответствующую ей в таблице четверку двоичных знаков. Иначе говоря, перекодируем число 15FC по таблице в двоичную форму. Получается:
0001 0101 1111 1100
Если отбросить нули слева (в любой системе счисления они не влияют на значения числа), то получим искомое двоичное число. Таким образом:
В справедливости этого равенства можно убедиться, производя тот же перевод через десятичную систему.
Пример 6. Перевести двоичное число 110111101011101111 в шестнадцатеричную систему.
Разделим данное число на группы по четыре цифры, начиная справа. Если в крайней левой группе окажется меньше четырех цифр, то дополним ее нулями.
0011 0111 1010 1110 1111
А теперь, глядя на двоично-шестнадцатеричную таблицу, заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру.
3 7 А E F
Следовательно:
Пример 7. Перевести смешанное число
в шестнадцатеричную систему.
Практическое занятие «Представление чисел в компьютере»
Похожие презентации:
Пиксельная картинка
Информационная безопасность. Методы защиты информации
Электронная цифровая подпись (ЭЦП)
Этапы доказательной медицины в работе с Pico. Первый этап
История развития компьютерной техники
От печатной книги до интернет-книги
Краткая инструкция по CIS – 10 шагов
Информационные технологии в медицине
Информационные войны
Моя будущая профессия. Программист
1. Практическое занятие. «Представление чисел в компьютере»
2. Повторение
OO
O
O
O
O
O
O
Что такое системы счисления?
Что такое основание системы счисления?
Какие системы счисления используются в ПК?
Какой алфавит и основание имеет двоичная
система счисления?
Какой алфавит и основание имеет десятичная
система счисления?
Как перевести число из двоичной системы
счисления в десятичную?
Как перевести число из десятичной системы
счисления в двоичную?
Каковы правила сложения двоичных чисел.
O Методические указания.
O В ЭВМ в целях упрощения выполнения
арифметических операций применяют
специальные коды для представления
чисел. Использование кодов позволяет
свести операцию вычитания чисел к
арифметическому сложению кодов этих
чисел. Применяются прямой, обратный и
дополнительный коды чисел. Прямой код
используется для хранения чисел в
запоминающем устройстве ЭВМ. Обратный
и дополнительный коды используются для
сложения, что упрощает устройство
арифметического блока ЭВМ
O Прямой код. Прямой код двоичного
числа совпадает по изображению с
записью самого числа. Значение
знакового разряда для положительных
чисел равно 0, а для отрицательных
чисел 1.
O Обратный код. Обратный код для
положительного числа совпадает с
прямым кодом. Для отрицательного
числа все цифры числа заменяются на
противоположные (1 на 0, 0 на 1), а в
знаковый разряд заносится единица.

O Дополнительный код. Дополнительный код
положительного числа совпадает с прямым
кодом. Для отрицательного числа
дополнительный код образуется путем
получения обратного кода и добавлением к
младшему разряду единицы.
O Например, в однобайтовом формате числа 27 и
-27 имеют вид:
Числ
о
Прямой
код
Обратный
код
Дополнительный
код
27
00011011
00011011
00011011
-27
10011011
11100100
11100101
Пример 1. Найти прямой, обратный и дополнительный
код представления числа 13 в однобайтном формате.
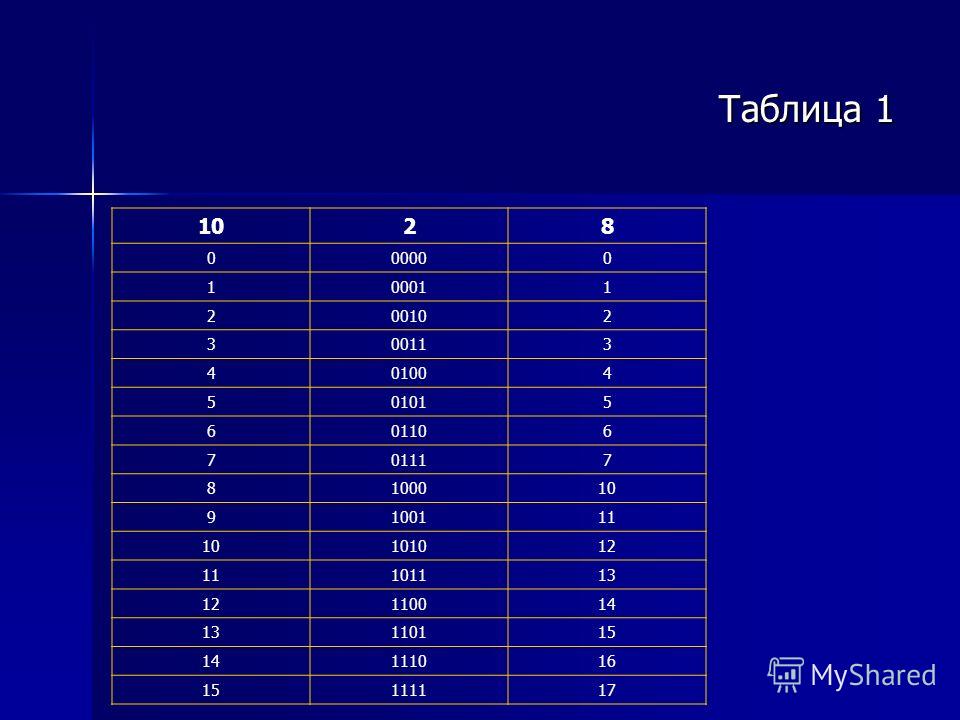
O 1 шаг: Переведем число 13 из десятичной системы
счисления в двоичную.
13 2
12 6
1 6
0
2
3
2
1
13 = 11012
2
1
O 2 шаг: Для представления числа в компьютере
выделен 1 байт. Старший бит занимает знак числа –
0. Сам код числа должен занимать 7 бит. Таким
образом прямой код числа 13
0 0 0 0 1 1 0 1
Пример 2. Найти прямой, обратный и дополнительный
код представления числа -23 в однобайтовом формате.

O 1 шаг: Переведем число -23 из десятичной системы
счисления в двоичную. Получим
-2310=-101112
O 2 шаг: Прямой код числа в однобайтовом формате,
имеет вид
1 0 0 1 0 1 1 1
O 3 шаг: Найдем обратный код числа -23, заменив все
цифры числа на противоположные (1 на 0, 0 на 1), а
в знаковый разряд заносится единица. Имеем,
1 1 1 0 1 0 0 0
O 4 шаг: Найдем дополнительный код
числа -23, добавив 1 к младшему
разряду обратного кода.
1 1 1 0 1 0 0 1
Выполнение
практической работы.
1. Выписать алфавиты 2-ичной, 5-ричной, 8-ричной, 16-ричной
систем счисления.
2. Перевести числа в десятичную систему счисления.
O
O
O
O
O
O
O
O
O
O
O
Самостоятельная работа.
Задание 1. Запишите числа в беззнаковом коде (формат 1
байт):
а) 31;
б) 163; в) 65; г) 128.
Задание 2. Найдите десятичные представления чисел,
записанных в беззнаковом коде: а) 0 1011000; б) 1 0011011; в) 0
1101001; г) 1 1000000.

Задание 3. Записать число в прямом, обратном и
дополнительном кодах (формат 1 байт):
а) 11010; б) 11101; в) -101001; г) -1001110.
Задание 4. Запишите числа в прямом коде (формат 1 байт):
а) 31;
б) -63; в) 65; г) -122.
Задание 5. Запишите числа в обратном и дополнительном
кодах (формат 1 байт):
а) 9;
б) -15; в) -127; г) -120.
Задание 6. Найдите десятичные представления чисел,
записанных в дополнительном коде: а) 1 1111000;
б) 1
0011011; в) 1 1101001;
г) 1 0000000.
Задание 7. Найдите десятичные представления чисел,
записанных в обратном коде:
а) 1 1101000;
б) 1 0011111;
в) 1 0101011;
г) 1 0000000.
Домашнее задание.
Задание 1
Перевести целые числа из десятичной системы счисления в
двоичную, восьмеричную и шестнадцатеричную системы:
а) 856; б) 664; в) 5012; г) 6435; д) 78.
Задание 2
Перевести десятичные дроби в двоичную и восьмеричную системы

а) 21,5; б) 432,54; в) 678,333.
Задание 3
Составить таблицы сложения и умножения в двоичной системе
счисления и выполнить вычисления:
а) 1110 + 101; б) 10101 — 11; в) 101 • 11; г) 1110 / 10.
Задание 4
Представить числа в двоичном виде в восьмибитовой
ячейке в формате
а) 5; б) 17; в) 64; г) 255.
Задание 5
Представить числа в двоичном виде в восьмибитовой
ячейке в формате целого со знаком.
a) 56; б) -56; в) 127; г) -127.
Задание 6 *
Представить вещественные числа в четырёхбайтовой
ячейке памяти в формате с плавающей точкой.
a) 0,5; б) 25,12; в) -25,12; г) -3456,1.
English Русский Правила
КР_3_Перевод чисел в др сс
Чайковский филиал
Пермский Государственный Технический Университет
Кафедра Информационных технологий
Практическая работа
«Перевод десятичных чисел в другие системы счисления»
по дисциплине информатика
г. Чайковский
Чайковский
2002
Практическая работа «Перевод десятичных чисел в другие системы счисления» по дисциплине информатика составила ст. преподаватель кафедры Информационных технологий Невоструева Т.В.
Практическая работа «работа «Перевод десятичных чисел в другие системы счисления» по дисциплине информатика обсуждены на заседании кафедры Информационных технологий «______» ______________ 2002 г.
Одобрено учебно-методическим отделом _______________________
______________________________________ «____» _______2002 г.
Директор учебно-методического отдела ________________________
Перевод десятичных чисел в другие системы счисления
Перевод целых чисел.
1) Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе счисления;
2) последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4) составить число в новой системе
счисления, записывая его, начиная с
последнего частного.
Пример 1. Перевести число 3710 в двоичную систему. Для обозначения цифр в записи числа используем символику: а5а4а3а2а,а0
Отсюда: 3710 = 1001012
Пример 2. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы:
Отсюда следует: 31510 = 4738 = 13В16. Напомним, что 1110 = В16.
Перевод дробных чисел.
1) Основание новой системы счисления выразить в десятичной системе и все последующие действия производить в десятичной системе счисления;
2) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
3) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4) составить дробную
часть числа в новой системе счисления,
начиная с целой части первого произведения.
Пример 3. Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы.
0 1875 0 1875 0 1875
х 2 х 8 х 16
0 3750 1 5000 1 1250
х 2 х 8 1 875
0 7500 4 0000 3 0000
х 2
1 5000
х 2
1 0000
Здесь вертикальная черта отделяет целые части чисел от дробных частей.
Отсюда: 0,187510 = 0,00112 = 0,148 = 0,316.
Перевод
смешанных чисел,
содержащих целую и дробную части,
осуществляется в два этапа. Целая и
дробная части исходного числа переводятся
отдельно по соответствующим алгоритмам.
В итоговой записи числа в новой системе
счисления целая часть отделяется от
дробной запятой (точкой).
Пример 4. Перевести десятичное число 315,187564* в восьмеричную и в шестнадцатеричную системы счисления. Из рассмотренных выше примеров следует:
315,187510 = 473,148 = 13В,316.
Вариант 1
1. Перевести целые числа из десятичной системы, счисления в троичную:
523; 65; 7000; 2307; 325.
2. Перевести целые числа из десятичной системы счисления в восьмеричную:
214; 89; 998; 653; 111.
3. Перевести десятичные дроби в двоичную систему счисления. В двоичной записи числа сохранить шесть знаков.
0,654; 0,321; 0,6135; 0,9876.
4. Перевести десятичные дроби в шестнадцатеричную систему счисления. В новой записи дроби сохранить шесть знаков.
0,8455; 0,225; 0,1234; 0,455.
5. Перевести смешанные десятичные числа в троичную и пятеричную системы счисления, оставив пять знаков в дробной части нового числа:
40,5; 34,25; 124,44.
6. Перевести смешанные десятичные числа в двоичную и восьмеричную системы счисления, оставив пять знаков в дробной части нового числа:
12,25; 97,444; 7896,2.
7. Перевести из десятичной системы счисления следующие числа:
675 -> А12, 0,333 -> А3, 23,15 -> А5.
8. Перевести из десятичной системы счисления следующие числа:
1,25 -> А16, 675 -> А7, 0,355 -> А4;
9. Перевести из десятичной системы счисления следующие числа:
425 -> А6, 0,425 -> А12, 98,45 -> А3.
10. Перевести из десятичной системы счисления следующие числа:
98 -> А2, 0,545 -> А16 , 87,325 -> А8.
Вариант 2
-
Перевести целые числа из десятичной системы, счисления в троичную:
12; 524; 76; 121;
56.
2. Перевести целые числа из десятичной системы счисления в восьмеричную:
856; 664; 5012; 6435; 78.
3. Перевести десятичные дроби в двоичную систему счисления. В двоичной записи числа сохранить шесть знаков.
0,555; 0,333; 0,1213; 0,453.
4. Перевести десятичные дроби в шестнадцатеричную систему счисления. В новой записи дроби сохранить шесть знаков.
0,745; 0,101; 0,8453; 0,3451.
5. Перевести смешанные десятичные числа в троичную и пятеричную системы счисления, оставив пять знаков в дробной части нового числа:
78,333; 225,52; 90,99.
6. Перевести смешанные десятичные числа в двоичную и восьмеричную системы счисления, оставив пять знаков в дробной части нового числа:
21,5; 432,54; 678,333.
7. Перевести из десятичной системы счисления следующие числа:
1)345->
А5,
0,125 ->А8,
45,65->А4.
8. Перевести из десятичной системы счисления следующие числа:
890 -> А6, 0,675 -> А8, 12,35 -> А7.
9. Перевести из десятичной системы счисления следующие числа:
0,55 -> А8, 765 -> А3, 765,75 -> А4.
10. Перевести из десятичной системы счисления следующие числа:
0,755 -> А5, 907 -> А6, 566,225 -> А16.
1
Презентация к уроку по теме «Системы счисления» презентация, доклад, проект
TheSlide.ru
- Регистрация |
- Вход
- Загрузить
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Презентация к уроку по теме «Системы счисления» из раздела Информатика. Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 32 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!
Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 32 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!
Системы счисления
Пупкова Вера Петровна
учитель информатики
МКОУ СОШ «Образовательный центр» г.Зуевка
Система счисления
1.Это способ изображения чисел и соответствующие ему правила действия над числами.
2.Это способ записи чисел с помощью заданного набора цифр и знаков.
Все системы счисления
Позиционные
Непозиционные
Непозиционная С.С.
В таких с.с. от положения знака в записи числа не зависит величина, которую он обозначает
Пользовались египтяне, древние греки, римляне и другие народы.
Непозиционная С.С.
I=1
V=5
X=10
L=50
C=100
D=500
M=1000
Непозиционная С.С.
CCXXXII
Складывается из двух сотен, трех десятков и двух единиц и равно 232.
Непозиционная С.С.
Правила записи:
Цифры записываются слева направо в порядке убывания и их значения складываются.
Если слева записана меньшая цифра, а справа большая, то их значения вычитаются.
VI=5+1=6 IV=5-1=4
Непозиционная С.С.
Были более или менее пригодны для выполнения сложения и вычитания, но непригодны для выполнения умножения и деления
Позиционная С.С.
Величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Основание позиционной С.С. – количество используемых цифр
Ак рк +Ак-1рк-1 + … +А1 р + А0 р0
р0=1
Где р – основание с.с.
а – цифры с.с
к – число целых разрядов
Позиционная С.С.
2749
2 *103 + 7*102 + 4*101+9*100
2000+700+40+9=2749
384,9506
3*102 +8*10 + 4+ 9*10-1+5*10-2+6*10-4=
300+80+4+0,9+0,05+0,0006=384,9506
Преимущества десятичной системы счисления не математические, а зоологические. Если бы у нас на руках было не десять пальцев , а восемь, то человечество пользовалось восьмиричной системой.
Н.Н. Лузин
математик
Позиционная С.С.
Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n10 к десяти арабским цифрам добавляют буквы.
Позиционная С. С.
С.
Вот примеры алфавитов нескольких систем:
Основание системы, к которой относится число обозначается подстрочным индексом:
1011012, 36718, 3В8Е16
Позиционная С.С.
Перевод чисел из одной с.с. в другую
1123=1 *32+1*31+2*30=9+3+2=14
1011012=1*25+0*24+1*23+1*22+0*21+1*20
Обратный перевод: 1510=8+4+2+1=1*22+1*22+1*21+1=11112
Перевод чисел из одной с.с. в другую
Как перевести 15710= ?2
Сложение в двоичной с.с.
В основе сложения чисел в двоичной системе счисления лежит таблица сложения одноразрядных двоичных чисел.
Сложение в двоичной с.с.
Важно обратить внимание на то, что при сложении двух единиц производится перенос в старший разряд.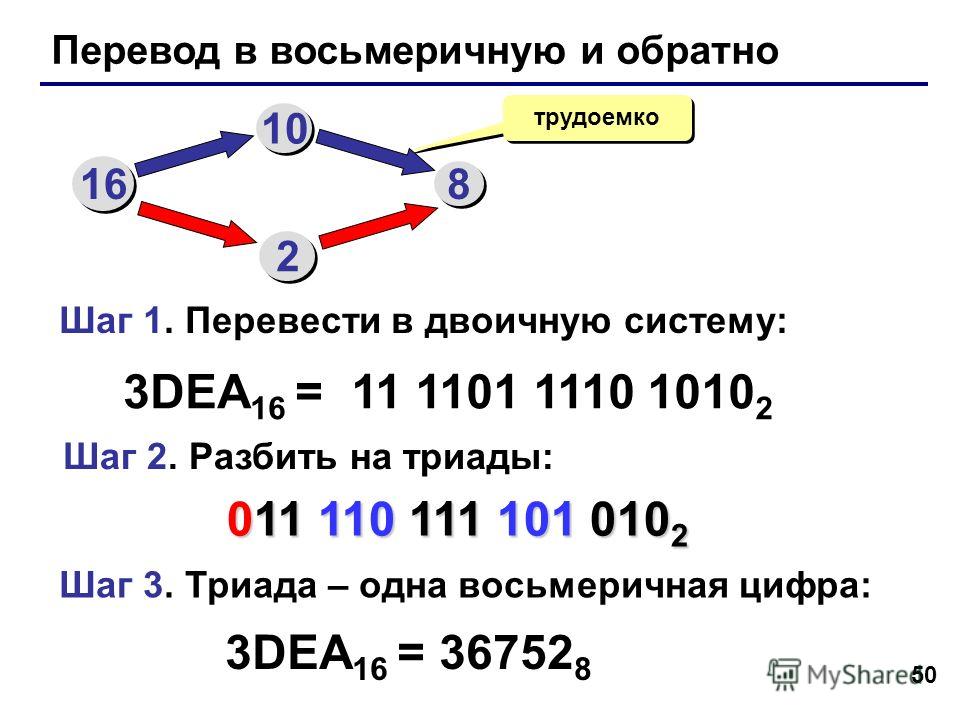
В качестве примера сложим в столбик двоичные числа 1102 и 112:
10012
Проверим правильность вычислений
1102=1*22+1*21+0*20=610
112=1*21+1*20=310
10012=1*23+0*22+0*21+1*20=910
610+310=910
Сложение выполнено верно.
Вычитание в двоичной с.с.
В основе вычитания двоичных чисел лежит таблица вычитания одноразрядных двоичных чисел.
При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда
Вычитание в двоичной с.с.
Для примера производим вычитание двоичных чисел 1102 и 112:
112
Умножение чисел в двоичной с.с.
В основе умножения лежит таблица умножения одноразрядных двоичных чисел.
Умножение чисел в двоичной с.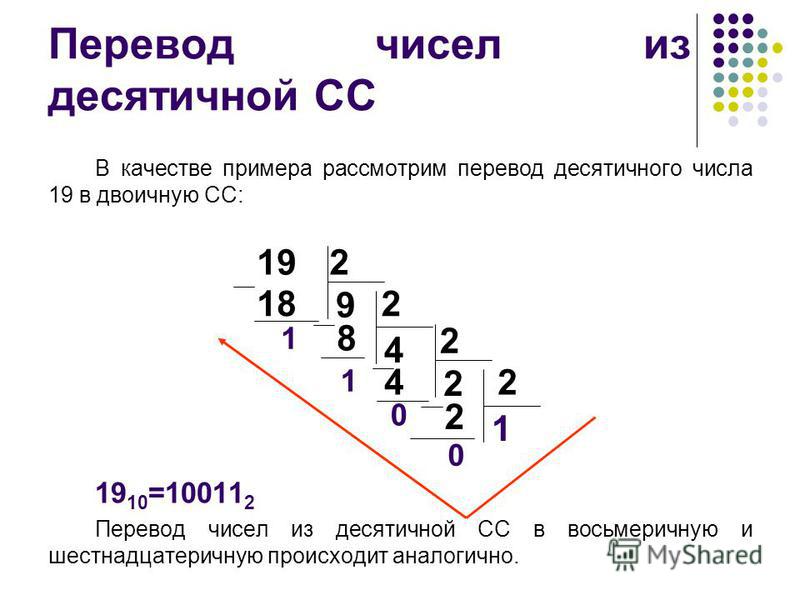 с.
с.
Рассмотрим пример умножения двоичных чисел 1102 и 112:
110
110
100102
Деление чисел в двоичной с.с.
Выполняется подобно операции деления в десятичной с.с.
Разделим двоичное число 1102 и 112:
1102
1
02
11
0
Задания
Чему равны в десятичной с.с. следующие числа:XI, IX, LX, CLX, MDCXLVIII.
Запишите римскими цифрами числа: 13; 99; 666; 444; 1692
Задания
3. Переведите числа из одной системы счисления в другую:
5610=?2 11112=?10
23С16=?10 5610=?8
5610=?5 1788=?10
1235=?10 2328=?10
2А,416=?10
Ответы:
5610=1110002 11112=1510
23С16=57210 5610=708
5610=2115 1748=12410
1235=3810 2328=15410
2А416=67610
Использование приложения «Калькулятор».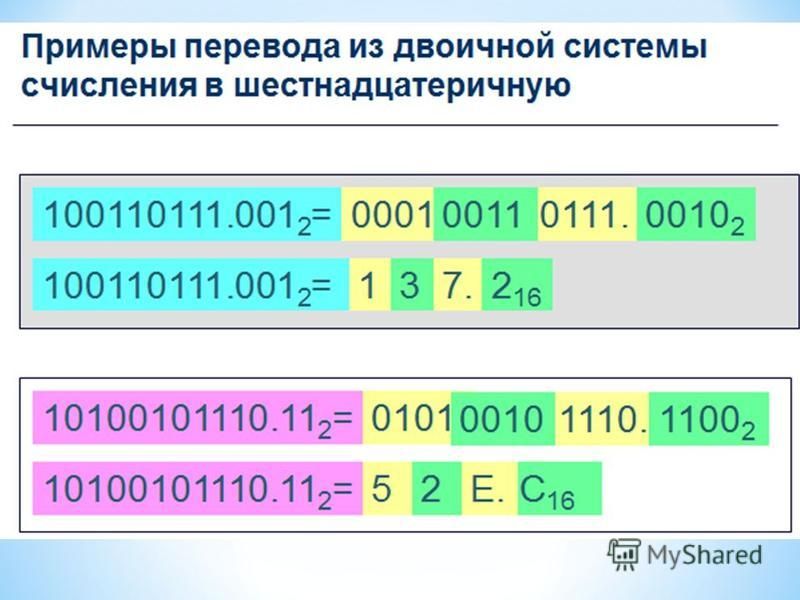
Скачать презентацию
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое TheSlide.ru?
Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.
Для правообладателей
Теория информации — Физическая энциклопедия
ТЕОРИЯ ИНФОРМАЦИИ -наука
о статистич. процессах передачи информации в техн., природных и социальных
системах. Осн. понятия Т.н.- мера кол-ва информации, пропускная способность
канала связи, эфф. кодирование сообщений — были введены в 40-х гг. 20 в. К.
Шенноном [1 ]. Т.н. является по существу статистич. теорией связи, или теорией
передачи информации, однако общий характер её положений позволяет исследовать
также процессы получения, обработки и хранения информации.
20 в. К.
Шенноном [1 ]. Т.н. является по существу статистич. теорией связи, или теорией
передачи информации, однако общий характер её положений позволяет исследовать
также процессы получения, обработки и хранения информации.
Т. и. тесно связана с теорией
кодирования, в к-рой рассматриваются общие проблемы установления соответствия
между сообщениями и сигналами ,представляющими эти сообщения (см.
также Кодирование информации ),а также с теорией обработки сигналов,
в к-рую входит квантование и восстановление квантованных сигналов, а также корреляц.
и спектральный анализы сигналов.
Методы Т. и. использовались
с разной степенью плодотворности во мн. прикладных областях, включая информатику,
языкознание, криптографию, теорию управления, обработку изображений, генетику,
психологию, экономику, организацию производства, однако осн. значение они имеют
для теории систем связи. Возникновение Т. и. стимулировало также исследования
в области теории вероятностей.
Т. и. рассматривает понятие
«информации» только с количеств. стороны, безотносительно к её ценности
и даже смыслу. При таком подходе страница машинописного текста максимально содержит
всегда примерно одинаковое кол-во информации, определяемое только числом знаков
и пробелов (т. е. символов) на странице и не зависящее от того, что именно на
ней напечатано, включая случай бессмысленного, хаотического набора символов.
Для моделирования систем связи такой подход правомерен, поскольку они предназначены
для безошибочной передачи по каналу связи информации, представленной любым набором
символов. В тех же случаях, когда существен учёт ценности и смысла информации,
количеств. подход неприменим. Это обстоятельство налагает существенные ограничения
на области возможных приложений Т. и. Неучёт его привёл на ранних этапах развития
к переоценке прикладной значи-
Осн. структурная схема
системы связи, рассматриваемая в Т.и., приведена на рис. 1. Информацию в виде
сообщений создаёт и с т о ч н и к с о о б щ е н и й. Сообщения представляют
собой слова или наборы слов, записанные б у к в а м и нек-рого алфавита. Источниками
сообщений могут быть человеческая речь, тексты на любых естеств. или формальных
языках, данные систем сбора и обработки информации, а также нек-рые математич.
модели -вероятностные процессы, создающие последовательности букв. П е р е д
а т ч и к преобразует передаваемое сообщение в сигнал, соответствующий физ.
природе к а н а л а с в я з и. Канал связи — это среда для передачи сигнала
от передатчика к приёмнику. При прохождении сигнала по каналу на него могут
воздействовать п о м е х и, вносящие искажения в значения информац. параметров
сигнала. П р и ё м н и к восстанавливает по принятому в общем случае с искажениями
сигналу исходное сообщение. Восстановленное сообщение поступает а д р е с а
т у — нек-рому лицу или техн. устройству.
1. Информацию в виде
сообщений создаёт и с т о ч н и к с о о б щ е н и й. Сообщения представляют
собой слова или наборы слов, записанные б у к в а м и нек-рого алфавита. Источниками
сообщений могут быть человеческая речь, тексты на любых естеств. или формальных
языках, данные систем сбора и обработки информации, а также нек-рые математич.
модели -вероятностные процессы, создающие последовательности букв. П е р е д
а т ч и к преобразует передаваемое сообщение в сигнал, соответствующий физ.
природе к а н а л а с в я з и. Канал связи — это среда для передачи сигнала
от передатчика к приёмнику. При прохождении сигнала по каналу на него могут
воздействовать п о м е х и, вносящие искажения в значения информац. параметров
сигнала. П р и ё м н и к восстанавливает по принятому в общем случае с искажениями
сигналу исходное сообщение. Восстановленное сообщение поступает а д р е с а
т у — нек-рому лицу или техн. устройству.
Источники сообщений, рассматриваемые
в теории информации, имеют статистич. характер, т. е. появление каждого из возможных
сообщений (полный набор к-рых предполагается заранее известным) определяется
соответствующей априорной вероятностью. Согласно Шеннону [1 ], считается, что
чем больше априорная вероятность данного сообщения, тем меньше неопределённости
относительно его действительного появления и, следовательно, тем меньше информации
оно несёт. Если вероятность появления сообщения-единица, т. е. его появление
достоверно, то неопределённости нет и считается, что сообщение не несёт информации.
характер, т. е. появление каждого из возможных
сообщений (полный набор к-рых предполагается заранее известным) определяется
соответствующей априорной вероятностью. Согласно Шеннону [1 ], считается, что
чем больше априорная вероятность данного сообщения, тем меньше неопределённости
относительно его действительного появления и, следовательно, тем меньше информации
оно несёт. Если вероятность появления сообщения-единица, т. е. его появление
достоверно, то неопределённости нет и считается, что сообщение не несёт информации.
Для оценки кол-ва информации
в сообщении в Т. и, используется логарифмич. мера, введённая Р. Хартли [2],
вероятностная интерпретация к-рой была дана в работах Шеннона [1 ]. Если вероятность
появления сообщения x есть p (x), причем 0 <р (х) <1, то к о л и ч е с т в о и н ф о рм а ц и и I(x),
содержащееся в сообщении, определяется ф-лой:
Ф-ла (1) определяет кол-во
информации с точностью до основания логарифма, т.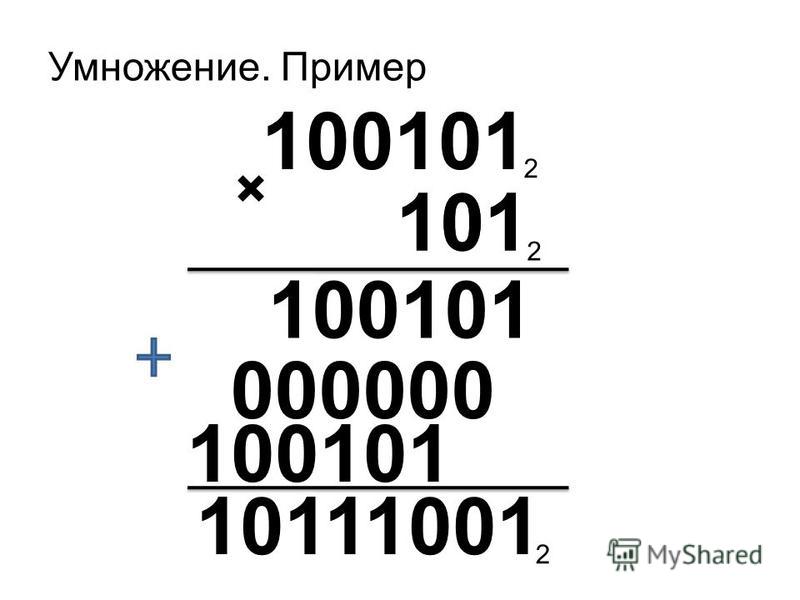 е. с точностью до пост. множителя.
Как правило, в качестве основания логарифма выбирается число 2 и единицей
кол-ва информации является б и т, что соответствует используемой в вычислит.
технике двоичной системе
счисления. При любом основании логарифма I(x)>=0, I(x)=0
при р(х)=1 и
при p(x)->0 (рис,
2).
е. с точностью до пост. множителя.
Как правило, в качестве основания логарифма выбирается число 2 и единицей
кол-ва информации является б и т, что соответствует используемой в вычислит.
технике двоичной системе
счисления. При любом основании логарифма I(x)>=0, I(x)=0
при р(х)=1 и
при p(x)->0 (рис,
2).
Если x1
и х2 — сообщения от двух независимых источников
с вероятностями появления p(x1)и p(x2), то вероятность их совместного появления r(x1, x2)=p(x1).p(x2)
а соответствующее кол-во информации
Это аддитивное свойство
логарифмич. меры служит основанием
для выбора ее в качестве меры кол-ва информации, т. к. соответствует интуитивным
представлениям о суммировании кол-ва информации, содержащегося в независимых
сообщениях.
Для сообщений x1,…,
xn, создаваемых источником с вероятностями p1…,pn,
причём
Шеннон ввёл ср. меру
кол-ва информации усреднением по множеству сообщений
Логарифм здесь, как и в
ф-ле (1), обычно берётся по основанию 2, Ф-ция Н, характеризующая информац.
свойства источника сообщений, наз. э н т р о п и е й, т. к. по форме она совпадает
с энтропией в статистич. физике, характеризующей априорную неопределённость
нахождения статистич. системы в состояниях x1…,xn,
имеющих вероятности p1 . ..,pn. Очевидна
прямая аналогия ф-лы (1) для кол-ва информации в сообщении и ф-лы Больцмана
для физ. энтропии S:
где k-постоянная
Больцмана, W—термодинамическая вероятность . В самой Т. и. и её
приложениях эта аналогия с физикой не играет, однако, существенной роли.
В самой Т. и. и её
приложениях эта аналогия с физикой не играет, однако, существенной роли.
Если в ф-ле (2) лишь одна
из вероятностей равна единице, а остальные-нули, неопределённости в появлении
сообщений нет и Н=0. Если сообщения равновероятны: p1=…=pn=1/n, и неопределённость в том, какое из них появится, максимальна, то H=log
n. Это значение энтропии является максимальным и равно в этом случае
кол-ву информации, получаемому от каждого отд. сообщения.
Для источника, создающего
два сообщения х1 и х2, к-рые
можно закодировать в двоичном коде как 0 и 1 соответственно, при вероятностях
сообщений p и q= 1 — p
График энтропии для этого
случая приведён на рис. 3.
Энтропия максимальная,
когда априорная неопределённость
максимальна, т. е. при p,q = 1/2. При этом Н=1 бит, что
соответствует одному двоичному символу (букве), используемому
в кодах сообщений.
е. при p,q = 1/2. При этом Н=1 бит, что
соответствует одному двоичному символу (букве), используемому
в кодах сообщений.
Если источник создаёт четыре
сообщения x1, x2, x3,
x4, то их можно закодировать в двоичном коде так: 00, 01, 10
и 11. При p1 = … = p4 =1/4 энтропия максимальна,
H=2 бит, что соответствует двум двоичным символам, используемым
для кодирования сообщений. Вообще для источника, создающего n сообщений,
макс. значение энтропии H=log2n, что соответствует
мин. числу двоичных символов в кодовых словах одинаковой длины, образующих р
а в н о м е р н ы е к о д ы и необходимых для кодирования
n равновероятных сообщений.
Если сообщения не являются
равновероятными, то для экономии ср. времени на их передачу по каналу связи
предпочтительно использование н е р а в н о м е р н ы х к од о в, образованных
более короткими кодовыми словами для более вероятных сообщений и более длинными
— для менее вероятных сообщений. Для n кодовых слов, имеющих l1…,ln
символов, средняя длина слова (сообщения) определяется ф-лой
Для n кодовых слов, имеющих l1…,ln
символов, средняя длина слова (сообщения) определяется ф-лой
где pi — вероятности появления соответств. слов (сообщений). Энтропия задаёт ниж.
границу для L, т.е. L>=H. Уменьшение L, т. е. приближение
L к H и как следствие уменьшение ср. времени передачи сообщений,
возможно за счёт применения
процедур э ф ф е к т и в н о г о к о д и р о в ан и я. Эффективность кодирования
характеризуется величиной h = H/L, а величина m=1-h наз.
и з б ы т о ч н ос т ь ю. Эфф, кодирование, обеспечивающее мин. значение избыточности,
можно осуществить с помощью кодов Шеннона, Р. Фано, Д, Хаффмена [1,3] (в случае
m = 0 код наз. о п т и м а л ь н ы м).
Код Хаффмена строится след.
образом. Сообщения (число к-рых конечно) располагаются в таблице в столбец в
порядке убывания их вероятностей. Два последних сообщения объединяются в одно
с суммарной вероятностью, и далее по тому же правилу строится след. столбец
таблицы. Затем в полученном столбце два последних сообщения вновь объединяются
в одно с суммарной вероятностью, строится новый столбец таблицы и т. д. Процесс
продолжается до тех пор, пока в последнем построенном столбце не останется двух
сообщений. Верхнему из них приписывается кодовое слово 0, нижнему — 1. Далее
рассматривается предпоследний столбец, в к-ром для объединявшихся сообщений
на втором месте кодового слова ставится 0 для верх. сообщения и 1-для нижнего.
Если сообщения не объединялись, то они сохраняют кодовые слова предыдущего
столбца. Процесс кодирования продолжается до тех пор, пока кодовые слова не
будут приписаны всем исходным сообщениям в первом столбце.
Два последних сообщения объединяются в одно
с суммарной вероятностью, и далее по тому же правилу строится след. столбец
таблицы. Затем в полученном столбце два последних сообщения вновь объединяются
в одно с суммарной вероятностью, строится новый столбец таблицы и т. д. Процесс
продолжается до тех пор, пока в последнем построенном столбце не останется двух
сообщений. Верхнему из них приписывается кодовое слово 0, нижнему — 1. Далее
рассматривается предпоследний столбец, в к-ром для объединявшихся сообщений
на втором месте кодового слова ставится 0 для верх. сообщения и 1-для нижнего.
Если сообщения не объединялись, то они сохраняют кодовые слова предыдущего
столбца. Процесс кодирования продолжается до тех пор, пока кодовые слова не
будут приписаны всем исходным сообщениям в первом столбце.
Пусть, напр., источник
создаёт четыре сообщения x1, х2, х3,
х4 с вероятностями p1= 1/2,
р2= 1/4, p3=р4= 1/8. Процесс построения кода Хаффмена для этого случая — объединение сообщений
и кодирование — показан в табл. 1 и табл. 2 соответственно. Для построенных
кодовых слов сообщений 0, 10, 110, 111 ср. длина слова L=
1/2 · 1 + 1/4 · 2 +1/8 · 3 + 1/8 · 3 = 7/4, что
равно значению энтропии для рассматриваемого источника: Н= — l/2 log21/2-
l/4 log21/4- l/8 log21/8— l/8 log21/8 = 7/4.
Избыточность кодирования m =0, эффективность h =1, т. е. построенный
код — оптимальный. Использование эфф. кодирования, однако, допустимо только
при полной гарантии отсутствия ошибок при кодировании и декодировании сообщений,
т.к. в этом случае ошибка в восстановлении одного сообщения может повлечь появление
ошибок при восстановлении многих последующих сообщений.
Процесс построения кода Хаффмена для этого случая — объединение сообщений
и кодирование — показан в табл. 1 и табл. 2 соответственно. Для построенных
кодовых слов сообщений 0, 10, 110, 111 ср. длина слова L=
1/2 · 1 + 1/4 · 2 +1/8 · 3 + 1/8 · 3 = 7/4, что
равно значению энтропии для рассматриваемого источника: Н= — l/2 log21/2-
l/4 log21/4- l/8 log21/8— l/8 log21/8 = 7/4.
Избыточность кодирования m =0, эффективность h =1, т. е. построенный
код — оптимальный. Использование эфф. кодирования, однако, допустимо только
при полной гарантии отсутствия ошибок при кодировании и декодировании сообщений,
т.к. в этом случае ошибка в восстановлении одного сообщения может повлечь появление
ошибок при восстановлении многих последующих сообщений.
К наиб. важным проблемам
Т. и. относится согласование информац. свойств источника сообщений и канала
связи. П р о п у с к н а я с п о с о б н о с т ь канала связи С определяется
как макс. кол-во информации, к-рое способен передать канал в единицу времени.
Единицей измерения
пропускной способности канала связи является 1 бит/с.
П р о п у с к н а я с п о с о б н о с т ь канала связи С определяется
как макс. кол-во информации, к-рое способен передать канал в единицу времени.
Единицей измерения
пропускной способности канала связи является 1 бит/с.
Пусть источник создаёт сообщения в виде слов, записываемых буквами алфавита Am={а1 …, ат}. При вероятностях появления этих букв p1,…, рт на одну букву приходятся в ср. бит информации. О с н о в н а я т е о р е м а Ш е н н о н а д л я к а н а л а с в я з и б е з ш у м а формулируется след. образом.
Пусть источник сообщений
характеризуется энтропией H (бит/буква), а канал связи имеет пропускную
способность С (бит/с). Тогда можно закодировать сообщения так, чтобы передавать
символы по каналу связи со ср. скоростью С/H—e (буква/с),
где e — сколь угодно малое число. Передавать буквы со ср. скоростью,
превышающей С/H, невозможно. Достижение верх. границы для скорости передачи,
указываемой теоремой Шеннона, осуществляется за счёт применения процедур эфф.
кодирования.
Передавать буквы со ср. скоростью,
превышающей С/H, невозможно. Достижение верх. границы для скорости передачи,
указываемой теоремой Шеннона, осуществляется за счёт применения процедур эфф.
кодирования.
При передаче сигналов по
каналам связи на них возможно действие разл. помех, шумов, к-рые могут привести
к искажениям восстанавливаемых сообщений. Пусть, как и ранее, источник сообщений
создаёт слова, записываемые буквами алфавита Am = {a1, ...,
ат} при вероятностях их появления р1…,
рт. Пусть далее вследствие действия помех слова, восстанавливаемые
приёмником, оказываются записанными в алфавите Bn =
{b1…, bn}, к-рый, в частности, может совпадать
с алфавитом источника, причём вероятности появления букв алфавита Вп равны r1,…, rn. Тогда кол-во информации
на выходе канала связи относительно его входа, приходящееся на одну передаваемую
букву, определяется след. ф-лой:
Тогда кол-во информации
на выходе канала связи относительно его входа, приходящееся на одну передаваемую
букву, определяется след. ф-лой:
где рij (i=l,…,
n; j=1,…, m)- вероятности совместного появления букв
входного и выходного алфавитов.
Пропускная способность
канала связи с шумами Сш определяется как макс. кол-во информации
I(Вn, Ат), к-рое можно передать по каналу связи
за 1 с. Максимум находится для всех возможных источников, к-рые могут быть использованы
на входе данного канала связи.
Т е о р е м а Ш е н н о
н д л я к а н а л а с в я з и с ш
у м а м и формулируется след. образом.
Пусть H1-ср.
кол-во информации, создаваемое источником в единицу времени, т, е. производительность
источника сообщений, измеряемая в бит/с. Пусть далее Сш —
пропускная способность канала с шумом, тоже измеряемая в бит/с. Тогда если Н1
=<Сш, то такой системы кодирования не существует.
Тогда если Н1
=<Сш, то такой системы кодирования не существует.
Пропускная способность
канала с шумом существенно зависит от действующих на сигналы помех. Рассмотрим
двоичный симметричный канал, передающий двоичные буквы 0 и 1 с вероятностью
правильной передачи e и искажающий их с вероятностью d
=1 — e. Пропускная способность такого канала при передаче одной
буквы в секунду определяется ф-лой
График зависимости Сш
от d приведён на рис. 4. Если e
= d = 1/2, т.е. если вероятность правильной передачи буквы равна
вероятности её искажения, то пропускная способность канала с шумом Сш
= 0.
Теорема Шеннона для канала
с шумом не указывает конкретного способа борьбы с помехами. Простейший способ
борьбы с помехами, состоящий в многократном повторении сообщений, неэффективен,
т. к. требует больших затрат времени на передачу. Большую эффективность обеспечивает
применение кодов, позволяющих обнаруживать и исправлять ошибки передачи. П о
м е х оу с т о й ч и в о с т ь кодирования при этом обеспечивается спец, введением
избыточности, т, е, введением в сообщение добавочных символов, к-рые используются
для обнаружения и исправления ошибок в принятом сообщении. К числу кодов, обнаруживающих
и исправляющих ошибки, относятся к о д ы Х э м м и н г а (см. Кодирование
информации).
к. требует больших затрат времени на передачу. Большую эффективность обеспечивает
применение кодов, позволяющих обнаруживать и исправлять ошибки передачи. П о
м е х оу с т о й ч и в о с т ь кодирования при этом обеспечивается спец, введением
избыточности, т, е, введением в сообщение добавочных символов, к-рые используются
для обнаружения и исправления ошибок в принятом сообщении. К числу кодов, обнаруживающих
и исправляющих ошибки, относятся к о д ы Х э м м и н г а (см. Кодирование
информации).
Лит.: 1) Шеннон К., Работы по теории информации и кибернетике, пер. с англ., М., 1963; 2} Хартли Р., Передача информации, [пер. с англ.], в сб.: Теория информации и ее приложения, М., 1959; 3) Стратонович Р. Л., Теория информации, М., 1975; 4) Поплавский Р. П., Термодинамика информационных процессов, М., 1981; 5) Николис Д. С., Динамика иерархических систем, пер. с англ., М., 1989. В, И. Капалин.
Предметный указатель >>
Перевод десятичных чисел в другие системы счисления — Студопедия.
 Нет
Нет Перевод целых чисел.
1) Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе счисления;
2) последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4) составить число в новой системе счисления, записывая его начиная с последнего остатка.
Пример. Перевести число 3710 в двоичную систему. Для обозначения цифр в записи числа используем символику: a5a4a3a2a1a0
Отсюда: 3710 – 1001012
Пример. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы:
Отсюда следует: 31510=473 8= 13B16.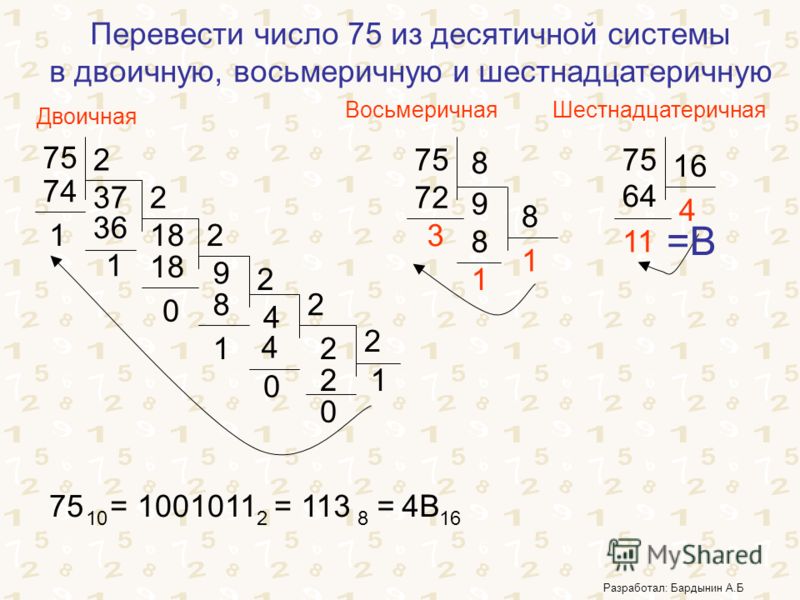
Напомним, что 1110 = В16
Перевод дробных чисел.
1) Основание новой системы счисления выразить в десятичной системе и все последующие действия производить в десятичной системе счисления;
2) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
3) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Пример 3. Перевести десятичную дробь 0,1876 в двоичную, восьмеричную и шестнадцатеричную системы.
Здесь вертикальная черта отделяет целые части чисел от дробных частей.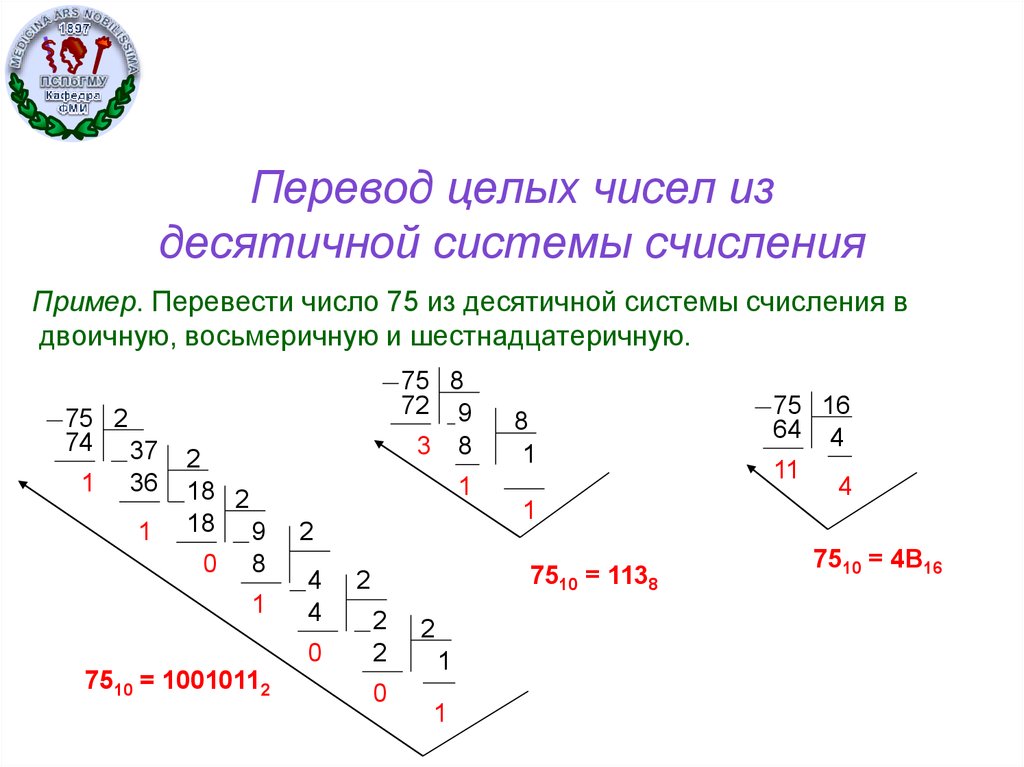
Отсюда:
0,187510= 0,00112= 0,148 =0,316.
Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Системы счисления, используемые в ЭВМ (с основанием 2n)
Для того чтобы целое двоичное число записать в системе счисления с основанием q=2n (4, 8, 16 и т.д.), нужно:
1) данное двоичное число разбить справа налево на группы по n цифр в каждой;
2) если в последней левой группе окажется меньше п разрядов, то ее надо дополнить слева нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.
Для того чтобы дробное двоичное число записать в системе счисления с основанием q = 2n, нужно:
1) данное двоичное число разбить слева направо на группы по n цифр в каждой;
2) если в последней правой группе окажется меньше п разрядов, то ее надо дополнить справа нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления q=2n.
Для того чтобы произвольное двоичное число записать в системе счисления с основанием q = 2n, нужно:
1) данное двоичное число разбить слева и справа (целую и дробную части) на группы по n цифр в каждой;
2) если в последних правой и левой группах окажется меньше п разрядов, то их надо дополнить справа и слева нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления q=2n.
Для того чтобы произвольное число записанное в системе счисления с основанием q =2n, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n- разрядным эквивалентом в двоичной системе счисления.
Применительно к компьютерной информации часто используются системы с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).
Пример. Перевести число 15FC16 в двоичную систему. Для решения задачи воспользуемся приведенной ниже двоично-шестнадцатеричной таблицей [2].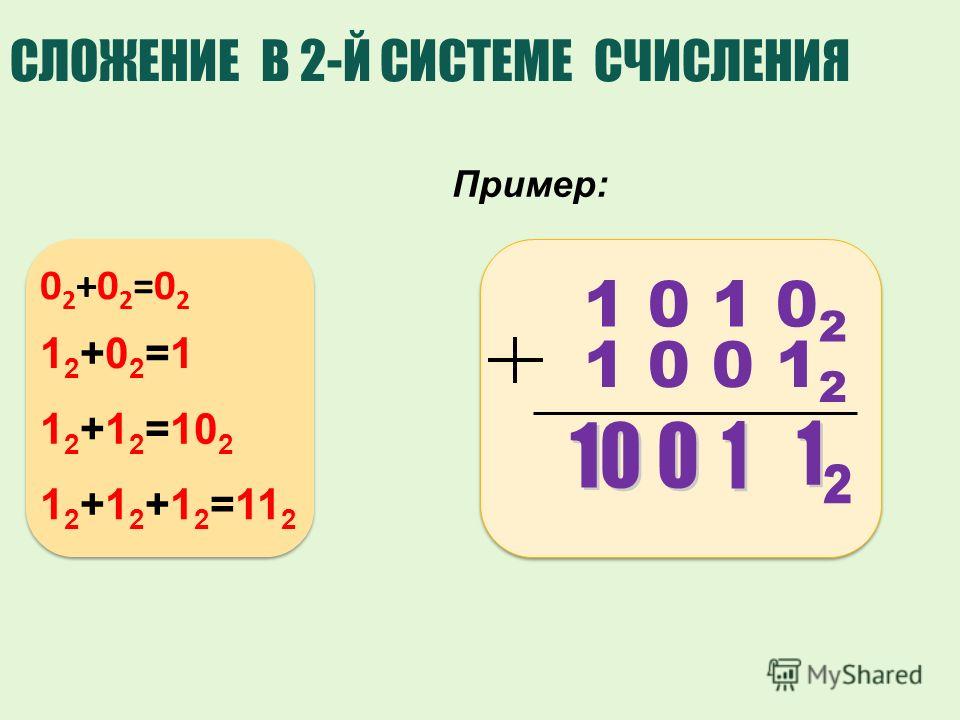
Каждую цифру в шестнадцатеричном числе 15FC заменим на соответствующую ей в таблице четверку двоичных знаков. Иначе говоря, перекодируем число 15FC по таблице в двоичную форму. Получается:
0001 0101 1111 1100.
Если отбросить нули слева (в любой системе счисления они не влияют на значение целого числа), то получим искомое двоичное число. Таким образом;
15FC16 = 10101111111002
В справедливости этого равенства можно убедиться, производя тот же перевод через десятичную систему.
Пример. Перевести двоичное число 110111101011101111 в шестнадцатеричную систему.
Решение.
Разделим данное число на группы по четыре цифры, начиная справа. Если в крайней левой группе окажется меньше четырех цифр, то дополним ее нулями.
0011 0111 1010 1110 1111.
А теперь, глядя на двоично-шестнадцатеричную таблицу, заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру.
3 7 А Е F
Следовательно:
1101111010111011112= 37АЕF16
Связь между двоичной и восьмеричной системами устанавливается аналогично. В этом случае используется двоично-восьмеричная таблица [2].
В этом случае используется двоично-восьмеричная таблица [2].
Пример. Перевести смешанное число 1011101,101112 восьмеричную систему.
Решение.
Группы по три двоичных знака выделяются от запятой как влево так и вправо. Затем производится перекодировка по таблице:
1011101,101112 => 001 011 101, 101 110 => 135,568.
7.3. Задание на лабораторную работу
Задания распределяются в зависимости от выданного преподавателем mn-кода. Для заданий 1…4: если m — число нечетное, то ваш вариант 1, если четное — вариант 2.
Задание 1.Перевести из десятичной системы счисления в двоичную, в восьмеричную и шестнадцатеричную (в новой записи дробей сохранить шесть знаков)
Вариант 1 Вариант 2
1) 856; 664; 5012; 6435; 78 1) 214; 89; 998; 653; 111
2) 0,745; 0,101; 0,8453; 0,3451 2) 0,8455; 0,225; 0,1234; 0,455
3) 40,5; 34,25; 124,44 3) 78,333; 225,52; 90,99
4) число состоящее из m*n в целой части и m+n в дробной
(для всех вариантов)
Задание 2. Перевести двоичные числа в восьмеричную, шестнадцатеричную и десятичную.
Перевести двоичные числа в восьмеричную, шестнадцатеричную и десятичную.
Вариант 1 Вариант 2
1) 110000110101;1010101; 1)0,1001111100000; ,1100010;
2) 0,1010011100100; 0,1111110001 2) 11100001011001; 1000010101
3) 100010,011101; 1111000000,101; 3) 101111,011; 100000111,00111;
4) число состоящее из m последовательностей <10> в целой части
и n последовательностей <101> в дробной (для всех вариантов)
Задание 3.Перевести восьмеричные числа в двоичную, десятичную и шестнадцатиричную
Вариант 1 Вариант 2
1) 256; 0,345; 24,025; 0,25 1) 657; 76,025; 0,344; 345,77
2) 774; 765,25; 0,5432; 654,763 2) 665; 546,76; 0,7654; 432,347
3) число состоящее из (m-2) в целой части и (n-2) в дробной (для всех вариантов)
Задание 4. Перевести шестнадцатеричные числа в двоичную, восьмеричную и десятичную
Перевести шестнадцатеричные числа в двоичную, восьмеричную и десятичную
Вариант 1 Вариант 2
1) 1AC7; 0,2D1; 2F,D8C; F0C,FF 1) FACC; 0,FFD; FDA,12F; DDFF,A
2) A45; 24A,9F; 0,FDD5; F12,045 2) A24,F9; 54A; 0,DFD3; 21D,567
3) число состоящее из (m+6) в целой части и (n+5) в дробной (для всех вариантов)
Задание 5.Опишите k-ричную систему счисления. Постройте двоично- k-ричную таблицу, таблицы сложения и умножения.
7.4. Требования к содержанию отчета
1. Цель лабораторной работы.
2. Задание на лабораторную работу. Mn – код.
3. Результаты решения задач своего варианта.
4. Выводы по полученным результатам.
7.5. Контрольные вопросы
1. Дать определение системы счисления. Пояснить различия между позиционными и непозиционными системами счисления.
2. Перевод целых чисел из десятичной в другие системы счисления.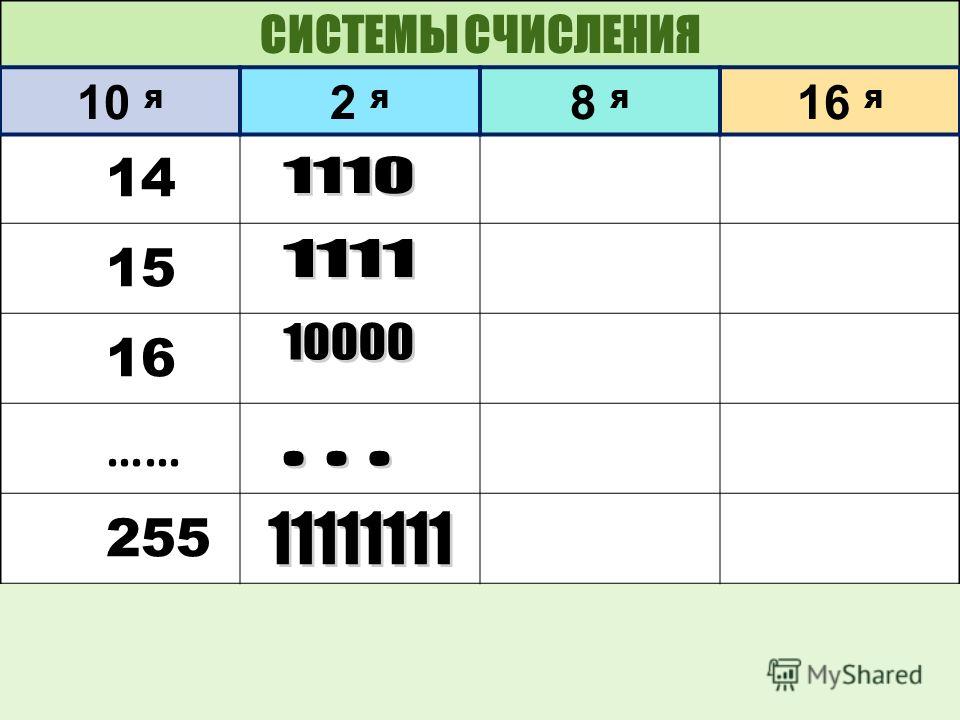
3. Перевод дробных чисел из десятичной в другие системы счисления.
4. Перевод смешанных чисел из десятичной в другие системы счисления.
5. Перевод целых чисел из других систем счисления в десятичную.
6. Перевод дробных чисел из других систем счисления в десятичную.
7. Перевод смешанных чисел из других систем счисления в десятичную.
8. Перевод чисел из двоичной в систему счисления с основанием 2n и обратно.
Лабораторная работа №8
«ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ»
8.1. Цель работы
Освоение приемов представления символьной, числовой, графической и звуковой информации в памяти ЭВМ
8.2. Методические указания [2]
преобразовать восьмеричное число 5012 в двоичное
Как записать 5012 в двоичное (основание 2)?
5012 равно 101000001010 в двоичной форме
|
||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования восьмеричной базы.
Здесь вы можете найти ответ на такие вопросы, как: преобразовать восьмеричное число 5012 в двоичное или преобразовать восьмеричное в двоичное.
Калькулятор преобразования восьмеричной базы.
Здесь вы можете найти ответ на такие вопросы, как: преобразовать восьмеричное число 5012 в двоичное или преобразовать восьмеричное в двоичное.
| Декабрь | Шестнадцатеричный | Октябрь | Бункер | |||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |||||
| 1 | 1 | 1 | 1 | |||||
| 2 | 2 | 2 | 10 | |||||
| 3 | 3 | 3 | 11 | |||||
| 4 | 4 | 4 | 100 | |||||
| 5 | 5 | 5 | 101 | |||||
| 6 | 6 | 99107 | 6 | 6 | 99999999988 60009 | 6 | 99999 11076 | 999|
| 8 | 6 | 99|||||||
| 6 | 999110||||||||
| 7 | 7 | 7 | 111 | |||||
| 8 | 8 | 10 | 1000 | |||||
| 9 | 9 | 11 | 1001 | |||||
| 10 | A | 12 | 1010 | |||||
| 11 | B | 13 | 1011 | |||||
| 12 | C | 14 | 11009 | |||||
| 13 | 11009 | |||||||
| 13 | 0008 D | 15 | 1101 | |||||
| 14 | E | 16 | 1110 | |||||
| 15 | F | 17 | 1111 |
| Dec | Hex | Октябрь | BIN | |
|---|---|---|---|---|
| 16 | 10 | 20 | 10000 | |
| 17 | 11 | 21 | 10001 | |
| 18 | 10001 | |||
| 18 | ||||
| 18 | 10001 | |||
| 18 | 0009 | 12 | 22 | 10010 |
| 19 | 13 | 23 | 10011 | |
| 20 | 14 | 24 | 10100 | |
| 21 | 15 | 25 | 10101 | |
| 22 | 16 | 26 | 10110 | |
| 23 | 17 | 27 | 100009 | |
| 24 | 18 | 100009 | ||
| 24 | 18 | 100009 | ||
| 24 | 18 | 100009 | ||
| 24 | 18 | 0009 | 30 | 11000 |
| 25 | 19 | 31 | 11001 | |
| 26 | 1A | 32 | 11010 | |
| 27 | 1B | 33 | 11011 | |
| 28 | 1C | 34 | 11100 | |
| 29 | 1D | 35 | 11101 | |
| 30 | 1 EE | 369 | ||
| 30 0009 | 1E | 369 | ||
| 30 | 1E | |||
| 30 | 10009 | 11110 | ||
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | ||
|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | ||
| 33 | 21 | 41 | 100001 | ||
| 34 | 22 | 42 | 100010 | ||
| 35 | 23 | 1000109 | |||
| 35 | 23 | 0009 | 43 | 100011 | |
| 36 | 24 | 44 | 100100 | ||
| 37 | 25 | 45 | 100101 | ||
| 38 | 26 | 46 | 100110 | ||
| 39 | 27 | 47 | 100111 | ||
| 40 | 28 | 50 | 101000 | ||
| 41 | 29 2009 | 51 | |||
| 410009 | 29 | 51 | 101001 | ||
| 42 | 2A | 52 | 101010 | ||
| 43 | 2B | 53 | 101011 | ||
| 44 | 2C | 54 | 101100 | ||
| 45 | 2d | 55 | 101101 | ||
| 46 | 2E | 56 | 101110 | ||
| 47 | 2F | 57 | 11111192F | 57 | 101111111111111111111111111111111111111111111111111111111111111119. 0009 0009 |
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 48 | 30 | 60 | 110000 | |||
| 49 | 31 | 61 | 110001 | |||
| 50 | 32 | 62 | 110010 | |||
| 51 | 33 | 63 | 110011 | |||
| 52 | 34 | 64 | 9110100 | |||
| 53 | 35 | 65 | 110101 | |||
| 54 | 36 | 66 | 110110 | |||
| 55 | 37 | 67 | 110111 | |||
| 56 | 38 | 70 | 111000 | |||
| 57 | 39 | 71 | 111001 | |||
| 3A | 72 | 1110 | 3A | 72 | 1110111111110 | |
| 59 | 3B | 73 | 111011 | |||
| 60 | 3C | 74 | 111100 | |||
| 61 | 3D | 75 | 111101 | |||
| 62 | 3E | 76 | 111110 | |||
| 63 | 3F | 77 | 111111 |
 0070
0070
| DEC | HEX | Октябрь | BIN | |
|---|---|---|---|---|
| 80999 | 50 9. 0009 0009 | 120 | 1010000 | |
| 81 | 51 | 121 | 1010001 | |
| 82 | 52 | 122 | 1010010 | |
| 83 | 53 | 123 | 1010011 | |
| 84 | 54 | 124 | 1010100 | |
| 85 | 55 | 125 | 1010101 | |
| 86 | 56 | 10009126 | 1010110 | |
| 87 | 57 | 127 | 1010111 | |
| 88 | 58 | 130 | 1011000 | |
| 89 | 59 | 131 | 1011001 | |
| 90 | 5A | 132 | 1011010 | |
| 91 | 5B | 133 | 1011011 | |
| 5C | 0009 | 134 | 1011100 | |
| 93 | 5D | 135 | 1011101 | |
| 94 | 5E | 136 | 1011110 | |
| 95 | 5F | 137 | 1011111 |
| DEC | HEX | Октябрь | BIN |
|---|---|---|---|
| 96 | 60 | 140 | |
| 0008 97 | 61 | 141 | 1100001 |
| 98 | 62 | 142 | 1100010 |
| 99 | 63 | 143 | 1100011 |
| 100 | 64 | 144 | 1100100 |
| 101 | 65 | 145 | 1100101 |
| 102 | 66 | 146 | 1100110 |
| 146 | 1100110 | ||
| 0008 103 | 67 | 147 | 1100111 |
| 104 | 68 | 150 | 1101000 |
| 105 | 69 | 151 | 1101001 |
| 106 | 6A | 152 | 1101010 |
| 107 | 6B | 153 | 1101011 |
| 108 | 6C | 154 | 1101100 | 154 | 1101100 | 0007 | 109 | 6D | 155 | 1101101 |
| 110 | 6E | 156 | 1101110 |
| 111 | 6F | 157 | 1101111 |
| Dec | HEX | октября | BIN |
|---|---|---|---|
| 112 | 70 | 160 | 1110000 |
| 113 | 71 | 161 | 1110001 |
| 114 | 72 | 162 | 1110010 |
| 115 | 73 | 163 | 1110011 |
| 116 | 74 | 164 | 1110100 |
| 117 | 75 | 165 | 1110101 |
| 118 | 76 | 166 | 1110110 |
| 119 | 167 | 0009 | 1110111 |
| 120 | 78 | 170 | 1111000 |
| 121 | 79 | 171 | 1111001 |
| 122 | 7A | 172 | 1111010 |
| 123 | 7B | 173 | 1111011 |
| 124 | 7C | 174 | 1111100 |
| 125 | 7D | 175 | 1111101 |
| 126 | 7E | 176 | 1111110 |
| 127 | 7F | 177 | 1111111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 128 | 80 | 200 | 10000000 | ||||
| 129 | 81 | 201 | 10000001 | ||||
| 130 | 10000001 | ||||||
| 130 | 000982 | 202 | 10000010 | ||||
| 131 | 83 | 203 | 10000011 | ||||
| 132 | 84 | 204 | 10000100 | ||||
| 133 | 85 | 205 | 10000101 | ||||
| 134 | 86 | 206 | 10000110 | ||||
| 135 | 207 | 10000119 | |||||
| 10000111 | |||||||
| 136 | 88 | 210 | 10001000 | ||||
| 137 | 89 | 211 | 10001001 | ||||
| 138 | 8A | 212 | 10001010 | ||||
| 139 | 8B | 213 | 10001011 | ||||
| 140 | 8C | 214 | 10001100 | ||||
| 141 | 8d | 215 | 10001101 | 215 | 10001101 | 0010 | |
| 142 | 8E | 216 | 10001110 | ||||
| 143 | 8F | 217 | 10001111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 144 | 90 | 220 | 10010000 | |
| 145 | 91 | 221 | 10010001 | |
| 146 | 9 | |||
| 1469 | 92 9000222 | 10010010 | ||
| 147 | 93 | 223 | 10010011 | |
| 148 | 94 | 224 | 10010100 | |
| 149 | 95 | 225 | 10010101 | |
| 150 | 96 | 226 | 10010110 | |
| 151 | 97 | 227 | 10010111 | |
| 152 | ||||
| 152 | 8 | 230 | 10011000 | |
| 153 | 99 | 231 | 10011001 | |
| 154 | 9A | 232 | 10011010 | |
| 155 | 9B | 233 | 10011011 | |
| 156 | 9C | 234 | 10011100 | |
| 157 | 9D | 235 | 10011101 | |
| 158 | 10011101 | |||
| 158 | 00099E | 236 | 10011110 | |
| 159 | 9F | 237 | 10011111 |
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 160 | A0 | 240 | 10100000 | |||
| 161 | A1 | 241 | 10100001 | |||
| 162 | A2 | 242 | 10100010 | 0009 | ||
| 163 | A3 | 243 | 10100011 | |||
| 164 | A4 | 244 | 10100100 | |||
| 165 | A5 | 245 | 10100101 | |||
| 166 | A6 | 246 | 10100110 | |||
| 167 | A7 | 247 | 10100111 | |||
| 168 | A8 | 250 | 168 | A8 | 250 | 0008 10101000 |
| 169 | A9 | 251 | 10101001 | |||
| 170 | AA | 252 | 10101010 | |||
| 171 | AB | 253 | 10101011 | |||
| 172 | AC | 254 | 10101100 | |||
| 173 | г. н.э.0009 н.э.0009 | 10101110 | ||||
| 175 | AF | 257 | 10101111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 176 | B0 | 260 | 10110000 | |
| 177 | B1 | 261 | 10110001 | |
| 178 | B2 | 262 | 10110010 | |
| 179 262 | ||||
| 179 | B3 | 263 | 10110011 | |
| 180 | B4 | 264 | 10110100 | |
| 181 | B5 | 265 | 10110101 | |
| 182 | B6 | 266 | 10110110 | |
| 183 | B7 | 267 | 10110111 | |
| 184 | B8 | 270 | 10111000 | 270 | 1011000 | 10111000 | 9000
| 185 | B9 | 271 | 10111001 | |
| 186 | BA | 272 | 10111010 | |
| 187 | BB | 273 | 10111011 | |
| 188 | BC | 274 | 10111100 | |
| 189 | BD | 275 | 10111101 | |
| 190 | BE | 276 | 10111110 | 0009 |
| 191 | BF | 277 | 10111111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 192 | C0 | 300 | 11000000 |
| 193 | C1 | 301 | 11000001 |
| 194 | C2 | 302 | 11000010 |
C3 10009 | 303 | 11000011 | |
| 196 | C4 | 304 | 11000100 |
| 197 | C5 | 305 | 11000101 |
| 198 | C6 | 306 | 11000110 |
| 199 | C7 | 307 | 11000111 |
| 200 | C8 | 310 | 11001000 |
| 201 | C9 | 311 | 11001001 |
| 202 | CA | 312 | 11001010 |
| 203 | CB | 313 | 11001011 |
| 204 | CC | 314 | 11001100 |
| 205 | CD | 315 | 11001101 |
| 206 | CE | 316 | 11001110 |
| 11001110 | |||
| 0008 207 | CF | 317 | 11001111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 208 | D0 | 320 | 11010000 |
| 209 | D1 | 321 | 11010001 |
| 210 | D2 | 322 | 11010010 |
| 211 | D3 | 323 | |
| 11010011 | |||
| 212 | D4 | 324 | 11010100 |
| 213 | D5 | 325 | 11010101 |
| 214 | D6 | 326 | 11010110 |
| 215 | D7 | 327 | 11010111 |
| 216 | D8 | 330 | 11011000 |
| 217 | D9 | ||
| 217 | D9 | 9000331 | 11011001 |
| 218 | DA | 332 | 11011010 |
| 219 | DB | 333 | 11011011 |
| 220 | DC | 334 | 11011100 |
| 221 | DD | 335 | 11011101 |
| 222 | DE | 336 | 1101110 |
| 223 | DF | ||
| 223 | DF | 0009337 | 11011111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 224 | E0 | 340 | 11100000 | ||||
| 225 | E1 | 341 | 11100001 | ||||
| 226 | E2 | 342 | 11100010 | ||||
| 227 | E3 | 343 | 1100011 | 343 | 1100011 | 9000||
| 228 | E4 | 344 | 11100100 | ||||
| 229 | E5 | 345 | 11100101 | ||||
| 230 | E6 | 346 | 11100110 | ||||
| 231 | E7 | 347 | 11100111 | ||||
| 232 | E8 | 350 | 11101000 | ||||
| 233 | 351 | 11101001 | 351 | 11101001 | 0009 | ||
| 234 | EA | 352 | 11101010 | ||||
| 235 | EB | 353 | 11101011 | ||||
| 236 | EC | 354 | 11101100 | ||||
| 237 | ED | 355 | 11101101 | ||||
| 238 | EE | 356 | 11101110 | ||||
| 239 | EF | 357 | 0008 11101111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 240 | F0 | 360 | 11110000 | ||||
| 241 | F1 | 361 | 11110001 | ||||
| 242 | F2 | 362 | 11110010 | ||||
| 243 | F3 | 363 | 11110011 | ||||
| 244 | F4 | 364 | 11110100 | ||||
| 245 | F5 | 365 | 11110101 | ||||
| 246 | F6 | 366 | 11110110 | ||||
| 247 | F7 | 367 | 11110111 | ||||
| 248 | F8 | 370 | 11111000 | ||||
| 249 | F9 | 371 | 11111001 | ||||
| 371 | 11111001 | ||||||
| 0008 250 | FA | 372 | 11111010 | ||||
| 251 | FB | 373 | 11111011 | ||||
| 252 | FC | 374 | 11111100 | ||||
| 253 | FD | 375 | 11111101 | ||||
| 254 | FE | 376 | 11111110 | ||||
| 255 | FF | 377 | 11111111199 | FF | 377 | 11111111111199 | 0010 |
Преобразователь базы чисел
Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
- 182 decimal to binary
- 3008 decimal to hexadecimal
- 3650 octal to decimal
- 4400 octal to hexadecimal
- 1984 decimal to binary
- 143 decimal to hexadecimal
- 202 octal to binary
- 14592 десятичный в шестнадцатеричный
- 62000 восьмеричный в шестнадцатеричный
десятичный 10025 в двоичном | работа, решение
Как записать 10025 в двоичном виде?
10025 записывается как 10011100101001 в двоичном формате
Преобразование из/в десятичное в двоичное. Преобразование десятичных чисел. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: Десятичное число 10025 в двоичном формате | работа, решение или преобразование десятичных чисел в двоичные. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.
Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.
С помощью этого конвертера вы можете получить ответы на такие вопросы, как:
- Что такое 10025 в двоичном формате?
- Что такое 10025 в шестнадцатеричном формате?
- Что такое 10025 в восьмеричной системе?
- Как преобразовать число 10025 в двоичное?
- Как преобразовать число 10025 в двоичное? И так далее.

Преобразование десятичной системы в двоичную, включая шестнадцатеричную и восьмеричную
| Декабрь | Hex | Oct | Bin | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ||||||||
| 1 | 1 | 1 | 1 | ||||||||
| 2 | 2 | 2 | 10 | ||||||||
| 3 | 3 | 3 | 11 | ||||||||
| 4 | 4 | 4 | 100 | ||||||||
| 5 | 5 | 5 | 9000 995 | 5 | 101999 | 5 | 5 | 9000 9995 | 5 | 99995 | 5 9000 |
| 6 | 6 | 6 | 110 | ||||||||
| 7 | 7 | 7 | 111 | ||||||||
| 8 | 8 | 10 | 1000 | ||||||||
| 9 | 9 | 11 | 1001 | ||||||||
| 10 | A | 12 | 1010 | ||||||||
| B | 13 | 1011 | |||||||||
| 12 | C | 1011 | |||||||||
| 12 | C | 1011 | |||||||||
| 12 | C | 1011 | |||||||||
| 12 | C | 1011 | |||||||||
| 12 | C | 1011 | |||||||||
| 12 | C | 1011 | |||||||||
| 12 | C | 000914 | 1100 | ||||||||
| 13 | D | 15 | 1101 | ||||||||
| 14 | E | 16 | 1110 | ||||||||
| 15 | F | 17 | 1111 |
| DEC | HEX | октября | BIN | ||||
|---|---|---|---|---|---|---|---|
| 16 | 10 | 20 | 10000 | ||||
| 10000 | |||||||
| 10000 | |||||||
| 10000 | |||||||
| 10000 | |||||||
| 21 | 10001 | ||||||
| 18 | 12 | 22 | 10010 | ||||
| 19 | 13 | 23 | 10011 | ||||
| 20 | 14 | 24 | 10100 | ||||
| 21 | 15 | 25 | 10101 | ||||
| 22 | 16 | 26 | 10110 | ||||
| 23 | 17 | 27 | |||||
| 23 | 17 | 27 | |||||
| 10111 | |||||||
| 24 | 18 | 30 | 11000 | ||||
| 25 | 19 | 31 | 11001 | ||||
| 26 | 1A | 32 | 11010 | ||||
| 27 | 1B | 33 | 11011 | ||||
| 28 | 1C | 34 | 11100 | ||||
| 29 | 1D | 35 | 1D | 35 | 11101 | 0009||
| 30 | 1E | 36 | 11110 | ||||
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | |||||
|---|---|---|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | |||||
| 33 | 21 | 41 | 100001 | |||||
| 34 | 22 | 42 | 100010 | |||||
| 35 | 23 | 43 | 100011 | |||||
| 36 | 24 | 44 | 100100 | |||||
| 37 | 25 | 45 | 100101 | |||||
| 38 | 26 | 46 | 100110 | |||||
| 39 | 27 | 47 | 100111 | |||||
| 40 | 28 | 50 | 101000 | 28 | 50 0009 | 101000 | 0009 | |
| 41 | 29 | 51 | 101001 | |||||
| 42 | 2A | 52 | 101010 | |||||
| 43 | 2B | 53 | 101011 | |||||
| 44 | 2C | 54 | 101100 | |||||
| 45 | 2d | 55 | 101101 | |||||
| 46 | 2E | 56 | 101110 | 20007 | 47 | 2F | 57 | 101111 |
| Dec | Hex | Oct | Bin | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 48 | 30 | 60 | 110000 | ||||||
| 49 | 31 | 61 | 110001 | ||||||
| 50 | 32 | 62 | 110010 | ||||||
| 51 | 33 | 63 | 110011 | 33 | 63 | 1 | 0009|||
| 52 | 34 | 64 | 110100 | ||||||
| 53 | 35 | 65 | 110101 | ||||||
| 54 | 36 | 66 | 110110 | ||||||
| 55 | 37 | 67 | 110111 | ||||||
| 56 | 38 | 70 | 111000 | ||||||
| 57 | 39 | 71 | 111001 | 71 | 111001 | 71999998 11001 | 9000 | ||
| 58 | 3A | 72 | 111010 | ||||||
| 59 | 3B | 73 | 111011 | ||||||
| 60 | 3C | 74 | 111100 | ||||||
| 61 | 3D | 75 | 111101 | ||||||
| 62 | 3E | 76 | 111110 | ||||||
| 63 | 3f | 111111999 |
- 34363 to binary
- 100101010000010 to decimal
- 1110101110101110 to decimal
- 35329 to binary
- 57812 to binary
- 1000001011111000 to decimal
- 32733 to binary
- 48657 to binary
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, мы не даем никаких гарантий в отношении этой информации. 93 байта
93 байта
| Decimal (SI Standard) | Binary (IEC Standard) | ||
|---|---|---|---|
| 1 Kilobit = 10 3 or 1000 Bits | 1 Kilobyte = 10 3 or 1000 Bytes | 1 Kibibit = 2 10 или 1024 бита | 1 кибибайт = 2 10 или 1024 байт |
| 1 Мегабит = 10 6 или 1000 2 бит | 1 Megabyte = 10 70008 1 Megabyt 20 or 1024 2 Bits | 1 Mebibyte = 2 20 or 1024 2 Bytes | |
| 1 Gigabit = 10 9 or 1000 3 Bits | 1 Gigabyte = 10 9 or 1000 3 Bytes | 1 Gibibit = 2 30 or 1024 3 Bits | 1 Gibibyte = 2 30 or 1024 3 Bytes |
| 1 Terabit = 10 12 or 1000 4 Bits | 1 Terabyte = 10 12 or 1000 4 Bytes | 1 Tebibit = 2 40 or 1024 4 Bits | 1 Tebibyte = 2 40 or 1024 4 Bytes |
| 1 Petabit = 10 15 or 1000 5 Bits | 1 Petabyte = 10 15 or 1000 5 Bytes | 1 Pebibit = 2 50 or 1024 5 Bits | 1 Pebibyte = 2 50 or 1024 5 Bytes |
| 1 Exabit = 10 18 or 1000 6 Bits | 1 Exabyte = 10 18 or 1000 6 Bytes | 1 Exbibit = 2 60 or 1024 6 Bits | 1 Exbibyte = 2 60 or 1024 6 Bytes |
| 1 Zettabit = 10 21 or 1000 7 Bits | 1 Zettabyte = 10 21 or 1000 7 Bytes | 1 Zebibit = 2 70 or 1024 7 Bits | 1 Zebibyte = 2 70 or 1024 7 Bytes |
| 1 Yottabit = 10 24 or 1000 8 Bits | 1 Yottabyte = 10 24 or 1000 8 Bytes | 1 Yobibit = 2 80 or 1024 8 Bits | 1 йобибайт = 2 80 или 1024 8 байт |
Введите байт — и нажмите Enter
Из Бит (b) NibbleByte (B)-килобит (kbit) кибибит (kibit)килобайт (kB) кибибайт (kiB)-мегабит (Mbit) мебибит (Mibit) мегабайт (MB) мебибайт (MiB)-гигабит (Gbit) гибибит (Gibit) )Гигабайт (ГБ)-Терабит (Тбит)Тебибит (Тибит)Терабайт (ТБ)Тебибайт (ТиБ)-Петабит (Пбит)Пебибит (Пибит)Петабайт (ПБ)Пебибайт (ПиБ)-Экзабит (Эбит)Эксбибит (Эйбит)Экзабайт ( EB )Exbibyte ( EiB )-Zettabit ( Zbit )Zebibit ( Zibit )Zettabyte ( ZB )Zebibyte ( ZiB )-Yottabit ( Ybit )Yobibit ( Yibit )Yottabyte ( YB )Yobibyte ( YiB )
К Бит ( б ) Полубайт-килобит ( кбит ) Кибибит ( кибит ) килобайт ( кБ ) кибибайт ( киби )-мегабит ( Мбит ) мебибит ( мибит ) мегабайт ( МБ ) мегабайт ( МиБ )- гигабит ( Гбит ) гибибит ( гибит ) гигабайт ( ГБ)Гибибайт (ГиБ)-Терабит (Тбит)Тебибит (Тибит)Терабайт (ТБ)Тебибайт (ТиБ)-Петабит (Пбит)Пебибит (Пибит)Петабайт (ПБ)Пебибайт (ПиБ)-Экзабит (Эбит)Эксбибит (Эйбит)Экзабайт (EB)Exbibyte (EiB)-Zettabit (Zbit)Zebibit (Zibit)Zettabyte (ZB)Zebibyte (ZiB)-Yottabit (Ybit)Yobibit (Yibit)Yottabyte (YB)Yobibyte (YiB)
РЕЗУЛЬТАТ : 01251015203040 Десятичные числа
5012 байт = 0,0000046677887439727783203125 ГиБ
Копировать
Рассчитывается как → 5012 x (8) / (8×1024 3 ) = 5012 x 0,000000000
Ваши недавние конверсии
Быстрые ссылки: { Swap } » Байты в гигабиты » Байты в гигабиты » Байты в гигабайты ● ГБ vs ГиБ
РЕКЛАМА
Источники гравитационных волн с экстремальным соотношением масс: массовая сегрегация и захваты после двойного приливного разрушения | Ежемесячные уведомления Королевского астрономического общества
Фильтр поиска панели навигации Ежемесячные уведомления Королевского астрономического обществаЭтот выпускЖурналы РАНАстрономия и астрофизикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Ежемесячные уведомления Королевского астрономического обществаЭтот выпускЖурналы РАНАстрономия и астрофизикаКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Получить доступ
Яэль Раве,
Яэль Раве
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Хагай Б Перец
Хагай Б. Перец
Перец
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Ежемесячные уведомления Королевского астрономического общества , том 501, выпуск 4, март 2021 г., страницы 5012–5020, https://doi.org/10.1093/mnras/staa4001
Опубликовано:
6 900 309 26 декабря 269 История статьиПолучено:
26 ноября 2020 г.
Получена редакция:
22 декабря 2020 г.
Принято:
22 декабря 2020 г.
Опубликовано:
26 декабря 2020 г.
Фильтр поиска панели навигации Ежемесячные уведомления Королевского астрономического обществаЭтот выпускЖурналы РАНАстрономия и астрофизикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Ежемесячные уведомления Королевского астрономического обществаЭтот выпускЖурналы РАНАстрономия и астрофизикаКнигиЖурналыOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Гравитационно-волновые (ГВ) спирали компактных объектов звездной массы на сверхмассивную черную дыру (СМЧД) являются одними из наиболее многообещающих источников ГВ, обнаруживаемых космическими ГВ следующего поколения. -детекторы. Интенсивность и характеристики таких источников спирали с экстремальным соотношением масс (EMRI) весьма неопределенны. Они определяются динамикой звезд вблизи ГЧД и скоростью, с которой компактные объекты сближаются с ГДД. Здесь мы рассматриваем слабо и сильно сегрегированные по массе ядерные скопления, а также эволюцию звезд, захваченных на орбиты с большим эксцентриситетом после разрушения двойных звезд ГЧД. Мы используем подход Монте-Карло для моделирования диффузии как захваченных объектов, так и компактных объектов, прошедших релаксационные процессы двух тел. Мы рассчитываем частоту GW-вдохов, возникающих в результате релаксации объектов, и характеризуем свойства EMRI. Мы корректируем предыдущие исследования и показываем, что источники, управляемые релаксацией, создают источники ГВ с более низким эксцентриситетом, чем было обнаружено ранее, и обеспечиваем подробное распределение эксцентриситета EMRI в режимах слабой и сильной массовой сегрегации. Мы также показываем, что захваченные звезды с двойным разрушением могут вводить ГВ-источники с низким эксцентриситетом звездных ЧД EMRI в сегрегированных по массе скоплениях.
-детекторы. Интенсивность и характеристики таких источников спирали с экстремальным соотношением масс (EMRI) весьма неопределенны. Они определяются динамикой звезд вблизи ГЧД и скоростью, с которой компактные объекты сближаются с ГДД. Здесь мы рассматриваем слабо и сильно сегрегированные по массе ядерные скопления, а также эволюцию звезд, захваченных на орбиты с большим эксцентриситетом после разрушения двойных звезд ГЧД. Мы используем подход Монте-Карло для моделирования диффузии как захваченных объектов, так и компактных объектов, прошедших релаксационные процессы двух тел. Мы рассчитываем частоту GW-вдохов, возникающих в результате релаксации объектов, и характеризуем свойства EMRI. Мы корректируем предыдущие исследования и показываем, что источники, управляемые релаксацией, создают источники ГВ с более низким эксцентриситетом, чем было обнаружено ранее, и обеспечиваем подробное распределение эксцентриситета EMRI в режимах слабой и сильной массовой сегрегации. Мы также показываем, что захваченные звезды с двойным разрушением могут вводить ГВ-источники с низким эксцентриситетом звездных ЧД EMRI в сегрегированных по массе скоплениях.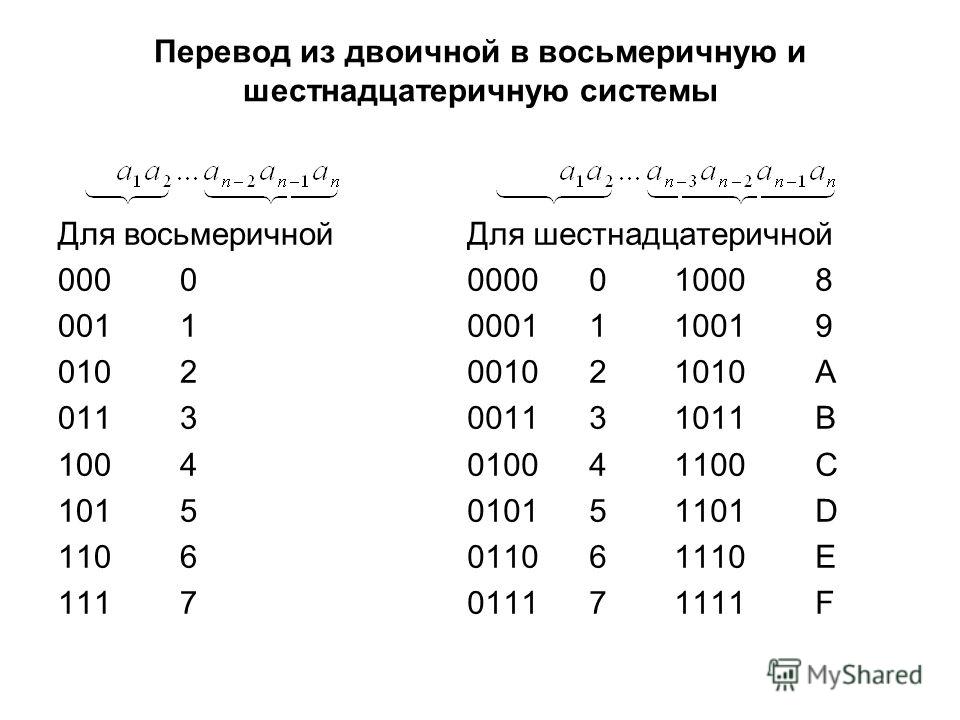 Однако эксцентриситеты источников ГВ из канала захвата сильно зависят от релаксационных процессов и значительно выше, чем предполагалось ранее. Мы обнаружили, что как скорость, так и распределение эксцентриситета EMRI могут исследовать динамику вблизи ГЧД и вклад захваченных звезд, характеризовать функцию масс звездных компактных объектов и проверять, имеют ли место слабые или сильные процессы масс-сегрегации вблизи ГЧД.
Однако эксцентриситеты источников ГВ из канала захвата сильно зависят от релаксационных процессов и значительно выше, чем предполагалось ранее. Мы обнаружили, что как скорость, так и распределение эксцентриситета EMRI могут исследовать динамику вблизи ГЧД и вклад захваченных звезд, характеризовать функцию масс звездных компактных объектов и проверять, имеют ли место слабые или сильные процессы масс-сегрегации вблизи ГЧД.
физика черных дыр, гравитационные волны, методы: численные, двойные системы: общие, Галактика: центр, Галактика: кинематика и динамика
© 2020 Автор(ы) Опубликовано Oxford University Press от имени Королевского астрономического общества Автор(ы) Опубликовано Oxford University Press от имени Королевского астрономического общества
Раздел выпуска:
Статья
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Войти через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Стоимость подписки и заказ этого журнала
Варианты покупки книг и журналов в Oxford Academic
Краткосрочный доступ
Чтобы приобрести краткосрочный доступ, войдите в свою учетную запись Oxford Academic выше.
У вас еще нет учетной записи Oxford Academic? регистр
Источники гравитационных волн с экстремальным соотношением масс: массовая сегрегация и захваты после двойного приливного разрушения — 24-часовой доступ
ЕВРО €14,00
12 фунтов стерлингов
16 долларов США.
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Оповещение о текущей проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Система астрофизических данных
Резюме объявленийСсылки на статьи по телефону
-
Последний
-
Самые читаемые
-
Самые цитируемые
Исследование корреляции между оптическим потоком и вариациями поляризации в BL Lac объектах
Газофазная спектроскопия фотостабильных ионов ПАУ в среднем и дальнем инфракрасном диапазоне
Структура фазового пространства в окрестности вертикальных ляпуновских орбит вокруг L 1, 2 в модели галактики с перемычкой
Истории слияния и сборки галактик, подобных Млечному Пути и M31, с TNG50: выживание диска в результате слияний
Порывы встречного ветра: неопределенности в прямом обнаружении темной материи
Реклама
5012 (номер)
5,012 ( пять тысяч двенадцать ) — четное четырехзначное составное число, расположенное между числами 5011 и 5013.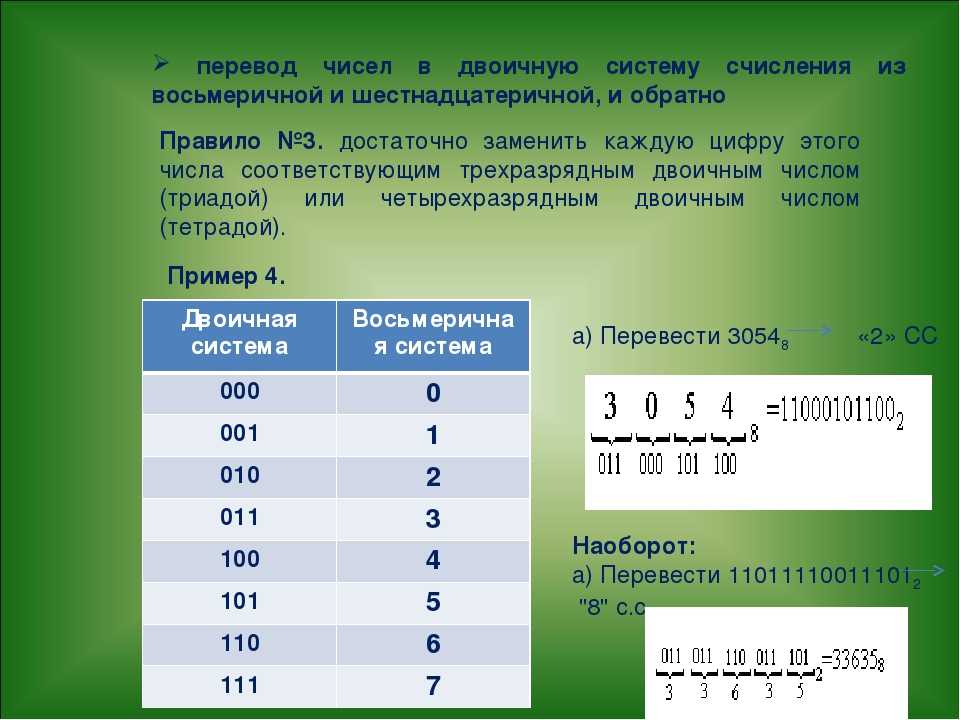 В научной записи оно записывается как 5,012 × 10 3 .
Сумма его цифр равна 8. Всего у него 4 простых делителя и 12 положительных делителей.
Существует 2136 натуральных чисел (до 5012), взаимно простых с 5012.
В научной записи оно записывается как 5,012 × 10 3 .
Сумма его цифр равна 8. Всего у него 4 простых делителя и 12 положительных делителей.
Существует 2136 натуральных чисел (до 5012), взаимно простых с 5012.
- Прайм? №
- Числовая четность Четное
- Длина номера 4
- Сумма цифр 8
- Цифровой корень 8
| Краткое наименование | 5 тысяч 12 |
|---|---|
| Полное имя | пять тысяч двенадцать |
| Научное обозначение | 5,012 × 10 3 |
|---|---|
| Техническое обозначение | 5,012 × 10 3 |
Простые множители 2 2 × 7 × 179
Составное число
| ω(n) | Отличительные факторы | 3 | Общее количество различных простых множителей |
|---|---|---|---|
| Ом(n) | Всего факторов | 4 | Общее количество простых множителей |
| рад(н) | Радикальный | 2506 | Произведение различных простых чисел |
| λ(n) | Лиувилль Лямбда | 1 | Возвращает четность Ω(n), такую что λ(n) = (-1) Ω(n) |
| мк(н) | Мебиус Мю | 0 | Возвращает:
|
| Л(н) | Функция Мангольдта | 0 | Возвращает log(p), если n является степенью p k любого простого числа p (для любого k >= 1), в противном случае возвращает 0 |
Разложение числа 5012 на простые множители равно 2 2 × 7 × 179. Поскольку у него всего 4 простых делителя, 5012 — составное число.
Поскольку у него всего 4 простых делителя, 5012 — составное число.
1, 2, 4, 7, 14, 28, 179, 358, 716, 1253, 2506, 5012
12 делителей
| Четный делитель | 8 |
|---|---|
| Нечетные делители | 4 |
| 4k+1 делителей | 2 |
| 4k+3 делителя | 2 |
| τ(n) | Всего делителей | 12 | Общее количество положительных делителей n |
|---|---|---|---|
| σ(n) | Сумма делителей | 10080 | Сумма всех положительных делителей n |
| с(н) | Аликвотная сумма | 5068 | Сумма собственных положительных делителей n |
| А(н) | Среднее арифметическое | 840 | Возвращает сумму делителей (σ(n)) деленную на общее количество делителей (τ(n)) |
| Г(н) | Среднее геометрическое | 70. 795480081711 795480081711 |
Возвращает корень n из произведения n делителей |
| Н(н) | Среднее гармоническое | 5,9666666666667 | Возвращает общее количество делителей (τ(n)), деленное на сумму обратных величин каждого делителя |
Число 5012 можно разделить на 12 положительных делителей (из них 8 четных и 4 нечетных). Сумма этих делителей (считая 5012) равна 10080, среднее 840.
1 ф (п) п
| φ(n) | Эйлер Тотиент | 2136 | Общее количество натуральных чисел не больше n, взаимно простых с n |
|---|---|---|---|
| λ(n) | Кармайкл Лямбда | 534 | Наименьшее положительное число такое, что λ(n) ≡ 1 (mod n) для всех чисел, взаимно простых с n |
| п(н) | Прайм Пи | ≈ 674 | Общее количество простых чисел меньше или равно n |
| р 2 (н) | Сумма 2 квадратов | 0 | Количество способов n представить в виде суммы двух квадратов |
Существует 2136 натуральных чисел (меньше 5012), взаимно простых с 5012. И существует примерно 674 простых числа, меньших или равных 5012.
И существует примерно 674 простых числа, меньших или равных 5012.
| м | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| п мод м | 0 | 2 | 0 | 2 | 2 | 0 | 4 | 8 |
Число 5012 делится на 2, 4 и 7.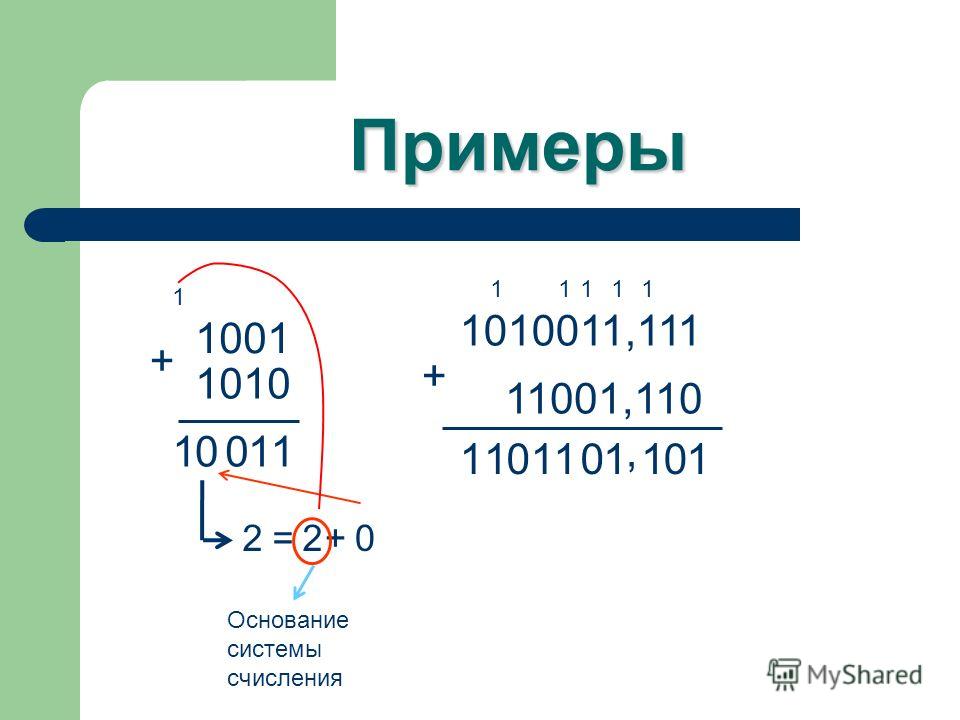
Арифметическими функциями
- Арифметика
- Изобилие
Выражается через конкретные суммы
- Вежливый
- Негипотенуза
| Основание | Система | Значение |
|---|---|---|
| 2 | Двоичный | 1001110010100 |
| 3 | Тернарный | 20212122 |
| 4 | Четвертичный | 1032110 |
| 5 | Квинарий | 130022 |
| 6 | Сенар | 35112 |
| 8 | Восьмеричный | 11624 |
| 10 | Десятичный | 5012 |
| 12 | Двенадцатеричный | 2а98 |
| 16 | Шестнадцатеричный | 1394 |
| 20 | Десятичное число | ок |
| 36 | База36 | 3 на 8 |
Умножение
п × у| n×2 | 10024 |
|---|---|
| n×3 | 15036 |
| n×4 | 20048 |
| n×5 | 25060 |
Отдел
n÷y| н÷2 | 2506.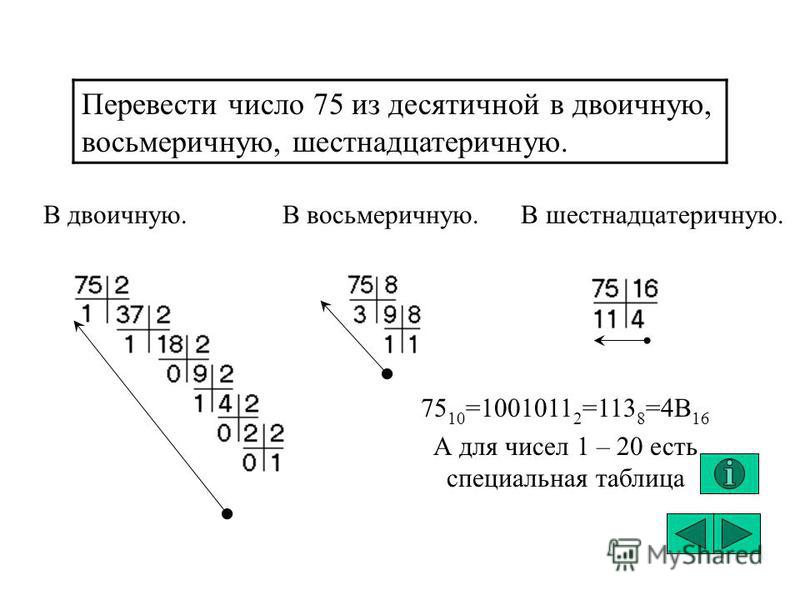 000 000 |
|---|---|
| н÷3 | 1670.666 |
| н÷4 | 1253.000 |
| н÷5 | 1002.400 |
Возведение в степень
п д| п 2 | 25120144 |
|---|---|
| п 3 | 125 | 1728
| п 4 | 631021634580736 |
| п 5 | 3162680432518648832 |
N-й корень
г √n| 2 √n | 70. 795480081711 795480081711 |
|---|---|
| 3 √n | 17.113428345063 |
| 4 √n | 8.4140049965347 |
| 5 √n | 5.4 7343897 |
Круг
Радиус = n| Диаметр | 10024 | |
|---|---|---|
| Окружность | 31491.324759584 | |
| Зона | 78 | 9.847518 |
Сфера
Радиус = n| Том | 527377741807,68 |
|---|---|
| Площадь поверхности | 315669039.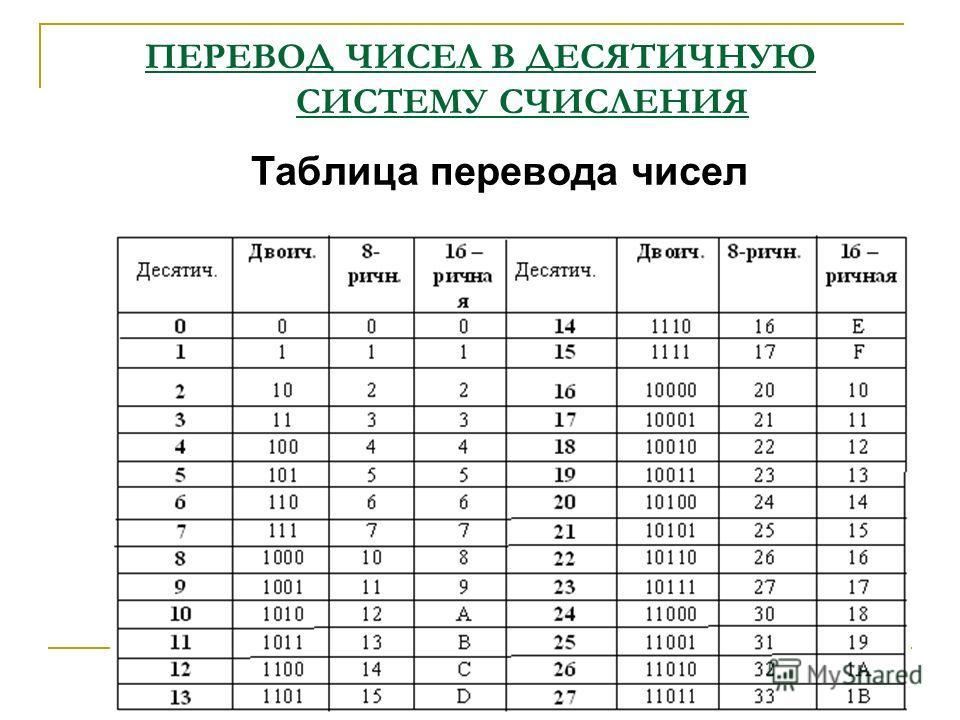 39007 39007 |
| Окружность | 31491.324759584 |
Квадрат
Длина = n| Периметр | 20048 |
|---|---|
| Зона | 25120144 |
| Диагональ | 7088.038374614 |
Куб
Длина = n| Площадь поверхности | 150720864 |
|---|---|
| Том | 125 | 1728
| Пространственная диагональ | 8681. 0386475352 0386475352 |
Равносторонний треугольник
Длина = n| Периметр | 15036 | |
|---|---|---|
| Зона | 10877341.425362 | |
| Высота над уровнем моря | 4340.51 | 676 |
Треугольная пирамида
Длина = n| Площадь поверхности | 43509365.701446 |
|---|---|
| Том | 14837712053.986 |
| Высота | 4092.2808636098 |
| мд5 | f0873a91b499e265ff6d78ff6e8985а0 |
|---|---|
| ша1 | 18кровать246387fe27024e1fca0df7bf105b1d |
| ша256 | ддд180а4466685b23ed9fee26d0d9cb5f081608808cceaa9cf74a9ece83a5bf4 |
| ша512 | 7eb02472d0984e1e41f8be55db1580f628f1e61ca0caaf490ab0ce4226cf14f72bf4b27f95a57eb5470005269d39c5bd52c4a50c5d0f4de309fb28da9d9d2a6d |
| римед-160 | 6bd32ee4a07ca0c5b97971357850fe88b0121796 |
Как писать, произносить по буквам 5012 английскими словами
- Главная
- Как писать, произносить по буквам 5012 английскими словами
5012 на английском языке, правописание для 5012 на английском языке, число слов для 5012
пять тысяч двенадцать
Поиск по заклинанию
Номер
Поделиться
Факты о числе 5012
Как записать число 5012 в валюте Правописание?
- AUD => пять тысяч двенадцать австралийских долларов
- лв.
 => пять тысяч двенадцать левов
=> пять тысяч двенадцать левов - BWP => пять тысяч двенадцать пул
- CAD => пять тысяч двенадцать канадских долларов
- GBP => пять тысяч двенадцать фунтов стерлингов
- CNY => пять тысяч двенадцать китайских юаней
- CHF => пять тысяч двенадцать швейцарских франков
- CZK => пять тысяч двенадцать чешских крон
- EEK => пять тысяч двенадцать крон
- евро => пять тысяч двенадцать евро
- GHS => пять тысяч двенадцать ганских седи
- GMD => пять тысяч двенадцать даласи
- HKD => пять тысяч двенадцать гонконгских долларов
- HRK => пять тысяч двенадцать кун
- HUF => пять тысяч двенадцать форинтов
- INR => пять тысяч двенадцать индийских рупий
- JMD => пять тысяч двенадцать ямайских долларов
- JPY => пять тысяч двенадцать японских иен
- KES => пять тысяч двенадцать кенийских шиллингов
- LRD => пять тысяч двенадцать либерийских долларов
- LSL => пять тысяч двенадцать малоти
- LTL => пять тысяч двенадцать литов
- LVL => пять тысяч двенадцать латов
- MGA => пять тысяч двенадцать ариариев
- MUR => пять тысяч двенадцать маврикийских рупий
- MXN => пять тысяч двенадцать мексиканских песо
- MWK => пять тысяч двенадцать малавийских квач
- NAD => пять тысяч двенадцать долларов Намибии
- NGN => пять тысяч двенадцать найр
- NZD => пять тысяч двенадцать новозеландских долларов
- PGK => пять тысяч двенадцать кина
- PHP => пять тысяч двенадцать филиппинских песо
- PKR => пять тысяч двенадцать пакистанских рупий
- PLN => пять тысяч двенадцать злотых
- RON => пять тысяч двенадцать румынских леев
- RSD => пять тысяч двенадцать сербских динаров
- RUB => пять тысяч двенадцать российских рублей
- RWF => пять тысяч двенадцать руандийских франков
- SDG => пять тысяч двенадцать суданских фунтов
- SGD => пять тысяч двенадцать сингапурских долларов
- SLL => пять тысяч двенадцать леоне
- SZL => пять тысяч двенадцать эмалангени
- THB => пять тысяч двенадцать бат
- TRY => пять тысяч двенадцать турецких лир
- TTD => пять тысяч двенадцать долларов Тринидада и Тобаго
- TZS => пять тысяч двенадцать танзанийских шиллингов
- UAH => пять тысяч двенадцать гривен
- UGX => пять тысяч двенадцать угандийских шиллингов
- USD => пять тысяч двенадцать долларов США
- ZMK => пять тысяч двенадцать замбийских квач
- ZMK => пять тысяч двенадцать замбийских квач
- ZWL => пять тысяч двенадцать долларов Зимбабве
Является ли 5012 простым числом?
Нет. Это не простое число…
Это не простое число…
Простые множители 5012 / Простые множители 5012?
Определенное уравнение для факторизации числа 5012: 179 * 7 * 2 * 2
Простые делители числа 5012: 179 *7 *2
Является ли 5012 составным числом?
5012 — составное число, потому что оно имеет больше делителей, чем 1 и само себя.
Является ли 5012 четным числом?
Да. Это четное число
Является ли 5012 нечетным числом?
Нет. Это нечетное число.
Научное обозначение 5012
5.012 × 10 3
Squares and roots of 5012
300 squared ( 5012
2 )25120144
300 cubed ( 5012
3 )1251728
Square Root Of 5012 ?
Квадратный корень из 5012 = 70,795480081711
Кубический корень из 5012?
Кубический корень из трех ∛5012 = 17,113428345063
Рекреационная математика с 5012
Число десятичных цифр равно
4
The sum of 5012’s digits
8
Backwards of 5012
2105
5012 x Pi
15745. 662379792
662379792
5012 x log
e8.5195016
5012 x log
103,7000110623221
5012 секунд конвертированы в дни, часы, минуты и секунды
0 дней 01 час 23 мин 32 с
Основания 5012
Как записать 5012 в двоичном формате?
1001110010100 2
Как записать 5012 в шестнадцатеричном формате?
1394 16
Как записать 5012 в восьмеричных числах?
11624 8
Length
5012 kilometre =
5012000 meter
501200000 Centimetre
5012000000 Millimetre
5012000000000 Micrometer
5.012E+15 Nanometer
3114.311452 Mile
5481188.1554981 Yard
16443564.466494 Foot
197322773.59793 Inch
2706.2626616563 Nautical mile
5012 Metre =
5.012 kilometre
501200 Centimetre
5012000 Millimetre
5012000000 Micrometer
5012000000000 Nanometer
3.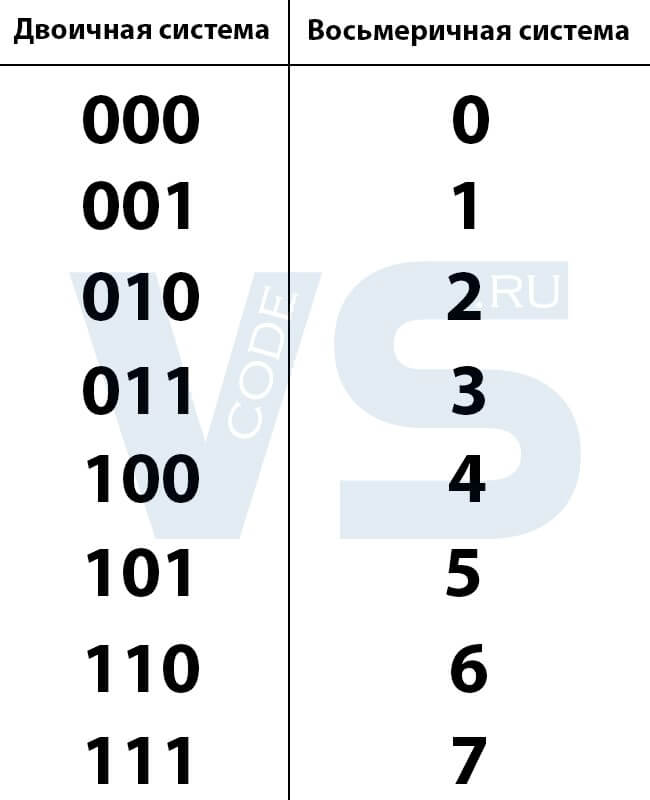

 , Страницы 5012–5020, https://doi.org/10.1093/mnras/staa4001
, Страницы 5012–5020, https://doi.org/10.1093/mnras/staa4001 