6 мкф в ф. Единицы измерения емкости конденсаторов: перевод и маркировка

Как перевести микрофарады в фарады. Как расшифровать маркировку конденсаторов. Какие бывают единицы измерения емкости конденсаторов. Как правильно читать номиналы конденсаторов.

Основные единицы измерения емкости конденсаторов

Емкость конденсатора измеряется в фарадах (Ф). Однако фарад — это очень большая единица, поэтому на практике чаще используются дольные единицы:

• Микрофарад (мкФ) — 10^-6 Ф
• Нанофарад (нФ) — 10^-9 Ф
• Пикофарад (пФ) — 10^-12 Ф

Как правило, емкость конденсаторов в электронных схемах варьируется от нескольких пикофарад до сотен микрофарад. Более крупные конденсаторы емкостью в миллифарады и фарады используются значительно реже.

Перевод единиц измерения емкости конденсаторов

Для перевода между единицами измерения емкости используются следующие соотношения:

• 1 Ф = 1 000 000 мкФ
• 1 мкФ = 1000 нФ
• 1 нФ = 1000 пФ

Таким образом, чтобы перевести, например, микрофарады в фарады, нужно разделить значение на 1 000 000. И наоборот, для перевода фарадов в микрофарады нужно умножить на 1 000 000.

Примеры перевода единиц емкости

Рассмотрим несколько примеров перевода между разными единицами измерения емкости конденсаторов:

1. 0,000001 Ф = 1 мкФ
2. 4700 пФ = 4,7 нФ
3. 0,1 мкФ = 100 нФ
4. 10 нФ = 0,01 мкФ
5. 1000000 пФ = 1000 нФ = 1 мкФ

Маркировка емкости на конденсаторах

На корпусе конденсатора обычно наносится маркировка, указывающая его номинальную емкость. Однако способ маркировки может отличаться в зависимости от типа конденсатора и производителя. Рассмотрим основные варианты:

Полная маркировка емкости

В этом случае на конденсаторе указывается числовое значение емкости и единица измерения, например:

• 100pF — 100 пикофарад
• 10nF — 10 нанофарад
• 1uF — 1 микрофарад

Кодированная маркировка

Для экономии места на малогабаритных конденсаторах часто используется кодированная маркировка. В этом случае емкость указывается в виде трехзначного числа, где:

• Первые две цифры — значащие цифры емкости
• Третья цифра — множитель (степень 10)

Единица измерения по умолчанию — пикофарады. Например:

• 104 = 10 * 10^4 пФ = 100 нФ = 0,1 мкФ
• 223 = 22 * 10^3 пФ = 22 нФ
• 471 = 47 * 10^1 пФ = 470 пФ

Как правильно читать номиналы конденсаторов?

Чтобы правильно определить емкость конденсатора по маркировке, нужно учитывать следующие моменты:

1. Определить тип маркировки — полная или кодированная
2. Для кодированной маркировки расшифровать числовой код
3. Обратить внимание на единицы измерения (пФ, нФ, мкФ)
4. При необходимости перевести в нужные единицы

Важно помнить, что реальная емкость конденсатора может отличаться от номинальной в пределах допуска, который также часто указывается на корпусе.

Влияние температуры на емкость конденсаторов

Емкость конденсатора может изменяться в зависимости от температуры окружающей среды. Это изменение характеризуется температурным коэффициентом емкости (ТКЕ). Различают следующие типы конденсаторов по характеру зависимости емкости от температуры:

• Конденсаторы с положительным ТКЕ — емкость увеличивается с ростом температуры
• Конденсаторы с отрицательным ТКЕ — емкость уменьшается с ростом температуры
• Конденсаторы с нулевым ТКЕ — емкость практически не зависит от температуры

При выборе конденсатора для конкретного применения важно учитывать его температурные характеристики, особенно если устройство будет эксплуатироваться в широком диапазоне температур.

Допуски емкости конденсаторов

Реальная емкость конденсатора может отличаться от номинального значения в пределах определенного допуска. Допуск обычно указывается на корпусе конденсатора в виде буквенного обозначения или процентного значения. Наиболее распространенные значения допусков:

• ±5% (J)
• ±10% (K)
• ±20% (M)

Например, конденсатор с номинальной емкостью 100 нФ и допуском ±10% может иметь фактическую емкость от 90 до 110 нФ. Для большинства применений такой разброс вполне приемлем, но в некоторых случаях (например, в прецизионных измерительных приборах) могут потребоваться конденсаторы с более жестким допуском.

Выбор конденсатора для конкретного применения

При выборе конденсатора для использования в электронной схеме необходимо учитывать несколько ключевых параметров:

1. Емкость — должна соответствовать расчетному значению для данной схемы
2. Рабочее напряжение — должно быть выше максимального напряжения в схеме
3. Тип диэлектрика — влияет на стабильность параметров и допустимые условия эксплуатации
4. Допуск — выбирается исходя из требуемой точности
5. Температурный коэффициент — важен для схем, работающих в широком диапазоне температур
6. Габариты — должны соответствовать доступному пространству на плате

Правильный выбор конденсатора обеспечивает надежную работу электронного устройства в заданных условиях эксплуатации.

Перевод мкф в ф

Расчет конденсаторов для пуска двигателя от однофазной. Перевод единиц емкости. Онлайн калькулятор для элекрический расчетов, тут вы можете расчитать диаметр плавкой вставки для предохранителей, подобрать резистор для светодиодов, расчитать сечения и диаметр проводов, расчитать конденсаторы для пуска электродвигателя от однофазной сети, определить величину тока. Скачать программу для определение. Для малогабаритных конденсаторов и резисторов кроме полной маркировки часто используют кодированное. Программу для определения маркировки конденсаторов можно скачать тут.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Кодовая и цветовая маркировка конденсаторов
• Таблица перевода единиц измерения в единицы СИ
• МкФ в фарад
• Маркировка конденсаторов, перевод величин и обозначения (пФ, нФ, мкФ)
• Фарад (F), электрическая ёмкость
• Перевод фарад (F) в микрофарады (µF)
• Маркировка конденсаторов
• Как перевести Фарады в Ампер*часы?
• Таблица значений конденсаторов, маркировка
• Конденсаторы – параметры и маркировка, перевод велечин эмкости. Единица измерения конденсаторов

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 100 Микрофарад РАЗНОЙ ЕМКОСТИ

Кодовая и цветовая маркировка конденсаторов

Mikrofarad, m rus. Конденсатор — электр. Конденсатор электрический — прибор, служащий для скопления на поверхности небольшого объема вещества большого количества электричества без значительного повышения при этом напряжения электричества в теле.

Брокгауза и И. Конденсатор, электрический — прибор, служащий для скопления на поверхности небольшого объема вещества большого количества электричества без значительного повышения при этом напряжения электричества в теле. Фарадея М.

В Международной системе единиц: единица измерения электрической ёмкости. Фарадея Названа по имени М. Мы используем куки для наилучшего представления нашего сайта.

Продолжая использовать данный сайт, вы соглашаетесь с этим. Перевод: с русского на английский с английского на русский. Толкование Перевод. Ефрона Конденсатор, электрический — прибор, служащий для скопления на поверхности небольшого объема вещества большого количества электричества без значительного повышения при этом напряжения электричества в теле.

Экспорт словарей на сайты , сделанные на PHP,. Пометить текст и поделиться Искать во всех словарях Искать в переводах Искать в Интернете.

Таблица перевода единиц измерения в единицы СИ

Раздел недели: Символы и обозначения оборудования на чертежах и схемах Техническая информация тут. Перевод единиц измерения величин Таблицы числовых значений Алфавиты, номиналы, единицы тут Математический справочник Физический справочник Химический справочник Материалы Рабочие среды Оборудование Инженерное ремесло Инженерные системы Технологии и чертежи Личная жизнь инженеров Калькуляторы. Поставщики оборудования. Полезные ссылки. 6 пФ).

МкФ в фарад

Конденсаторы являются второй, по распространенности и степени использования, после резисторов, деталью в электронных схемах. Действительно, в любом электронном устройстве, будь то мультивибратор на 2 транзисторах или материнская плата компьютера, во всех них находят применение эти радиоэлементы. Конденсатор обладает свойством накапливать заряд и впоследствии отдавать его. Простейший конденсатор представляет собой 2 пластины, разделенные тонким слоем диэлектрика. Емкостное сопротивление конденсатора зависит от его емкости и частоты тока. Конденсатор проводит переменный ток и не пропускает постоянный. Емкость конденсатора тем больше, чем больше площадь пластин обкладок конденсатора, и тем больше, чем тоньше слой диэлектрика между ними. Емкости параллельно соединенных конденсаторов складываются. Емкости последовательно соединенных конденсаторов считаются по формуле, приведенной на рисунке ниже:.

Маркировка конденсаторов, перевод величин и обозначения (пФ, нФ, мкФ)

Конденсатором обычно называют устройство, которое обладает способностью накапливать электрический заряд. Конструктивно конденсатор представляет собой два проводника, разделенных диэлектриком. Единицей электрической емкости конденсатора в системе СИ является фарада. Сокращенно обозначается буквой Ф.

Mikrofarad, m rus. Конденсатор — электр.

Фарад (F), электрическая ёмкость

Конденсаторы — это электрические накопители заряда, электронные пассивные компоненты, применяющиеся во всех электронных, радиотехнических конструкциях. Различные типы конденсаторов отличаются между собой конструктивным диэлектриком, что сказывается на области их применения, и схематическим предписанием в те или иные конструктивные приложения. При выборе и покупке компонента необходимо учитывать его основные характеристики, такие как, емкость, рабочее напряжение и тип конденсатора, а так же, конструктивное исполнение, выводной или чип-конденсатор, элемент поверхностного монтажа. Именно чип-конденсаторы являются лидерами производства таких компаний, как Epcos и Murata , совершенствующие конструктивные новации микроэлектроники.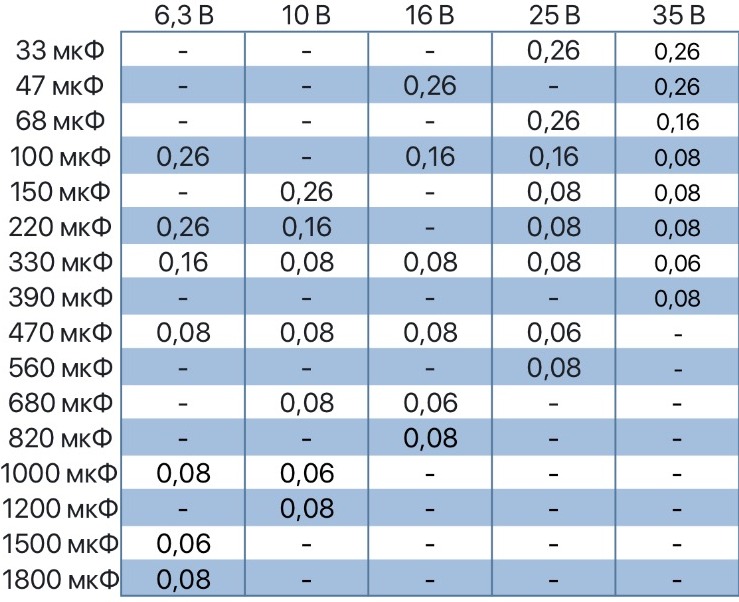 Работоспособность электродвигателей и компрессоров промышленных и бытовых установок всецело зависит от качественных пусковых конденсаторов. Ассортимент металлопленочных конденсаторов, широко применяемых в импульсных схемах, и, пользующихся огромной популярностью у аудиоманов, низкочастотных усилителях, представлен известными российскими и зарубежными производителями.

Перевод фарад (F) в микрофарады (µF)

Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор. Калькулятор справочный портал. Избранные сервисы. Кликните, чтобы добавить в избранные сервисы.

Маркировка конденсаторов, перевод величин и обозначения (пФ, нФ, мкФ). Полезная информация начинающим радиолюбителям по маркировке.

Маркировка конденсаторов

Во время работы над разделом о конденсаторах я подумал, что было бы полезно объяснить, почему один тип конденсаторов может быть заменен другим. Это важный вопрос, так как существует множество факторов температурные характеристики, тип корпуса и так далее , которые делают тот или иной тип конденсаторов электролитический, керамический и пр. В статье будут рассмотрены популярные типы конденсаторов, их достоинства и особенности, а также области применения.

Как перевести Фарады в Ампер*часы?

При сборке самодельных электронных схем поневоле сталкиваешься с подбором необходимых конденсаторов. Притом, для сборки устройства можно использовать конденсаторы уже бывшие в употреблении и поработавшие какое-то время в радиоэлектронной аппаратуре. Естественно, перед вторичным использованием необходимо проверить конденсаторы , особенно электролитические , которые сильнее подвержены старению. При подборе конденсаторов постоянной ёмкости необходимо разбираться в маркировке этих радиоэлементов, иначе при ошибке собранное устройство либо откажется работать правильно, либо вообще не заработает. Встаёт вопрос, как прочитать маркировку конденсатора?

Микрофарад англ. В советское время эта единица называлась микрофарада.

Таблица значений конденсаторов, маркировка

Информация содержит все, необходимые для подбора компонентов и проведения инженерных расчетов, параметры, а также цоколевку корпусов, типовые схемы включения и рекомендации по использованию радиоэлементов. Допуски Температурный коэффициент емкости ТКЕ Конденсаторы с ненормируемым ТКЕ Конденсаторы с линейной зависимостью от температуры Конденсаторы с нелинейной зависимостью от температуры Кодовая маркировка Кодовая маркировка электролитических конденсаторов для поверхностного монтажа Маркировка пленочных конденсаторов для поверхностного монтажа фирмы «HITACHI». В соответствии с требованиями Публикаций 62 и IEC для конденсаторов установлены следующие допуски и их кодировка:. Реальное значение конденсатора с маркировкой J 0. Второй цвет может быть представлен цветом корпуса.

Конденсаторы – параметры и маркировка, перевод велечин эмкости. Единица измерения конденсаторов

Говоря о ёмкости, мы чаще всего подразумеваем вместительность. То есть, если рассматривать ёмкость какого либо сосуда, то здесь мы под ёмкостью понимаем количество литров вещества, которое он может вместить. Или, например, количество килограммов конкретного вещества.

Примеры решения задач — Студопедия

Поделись  

 

Пример 1

Три конденсатора, имеющие электроёмкости С₁ = 1 мкФ, C₂ = 3 мкФ, С

3 = 6 мкФ, соединены последовательно и подключены к источнику с напряжением U = 120 B. Найти напряжение на третьем конденсаторе.

 

 

Дано: C1 = 1 мкФ = 10-6 Ф С2 = 3 мкФ =  Ф С3 = 6 мкФ =  Ф U = 120 В

U3-?

Решение

 

                                           

Общую электроёмкость определим из формулы

 Ф.

Общий заряд  Q  равен каждому из зарядов Q₁, Q₂ и Q₃:

 Кл.

Тогда Q₃ =  Кл.

Напряжение на третьем конденсаторе U₃ =  В.

Ответ: U₃ = 13,3 B.

 

Пример 2

К конденсатору электроемкостью С₁ = 200 пФ, заряженному до напряжения U₁ = 100 В и отключенному от источника, подключили параллельно незаряженный конденсатор электроемкостью С₂ = 300 пФ. Какое общее напряжение установится на обоих конденсаторах?

 

Дано: С1 = 200 пФ =  Ф С2 = 300 пФ =  Ф U1 = 100 В

U -?

Решение

По закону сохранения электрического заряда

Q_нач = Q_конеч или ,

где .

Тогда .

 В.

Ответ: U = 40 В.

 

Пример 3

Плоский воздушный конденсатор подключен к источнику напряжения U = 50 В. Какой заряд пройдёт по цепи, если пластины конденсатора сблизить до расстояния, втрое меньше первоначального, и заполнить конденсатор диэлектриком с

ε = 4? Начальная электроемкость воздушного конденсатора 0,6 мкФ.

 

Дано: U = 50 В ε = 4 C = 0,6 мкФ = 0,6.10-6 Ф d2 = 1/3.d1

Δq -?

Решение

Заряд Δq, прошедший по цепи,

Δq = q_кон. – q_нач..

Начальный заряд q_нач. = С^.U, конечный заряд q_кон = С₁^.U.

Электроемкость плоского конденсатора:

а) начальная ,

б) конечная .

Сравнивая выражения «а» и «б», получим .

         Тогда

Ответ: Δq = 3,3^.10^-4 Кл.

 

Пример 4

Два конденсатора электроемкостями С₁=3 нФ и С₂=6 нФ соединены параллельно, а последовательно к ним подключен конденсатор С₃=8 нФ. Заряд на конденсаторе С₁ равен q₁=12000 нКл. Найти заряды и напряжения на остальных конденсаторах.

 

Дано: С1 = 3 нФ = 3.10-9 Ф С2 = 6 нФ = 6.10-9  Ф С3 = 8 нФ = 8.10-9 Ф q1 = 12000 нКл = 12.10-7 Кл

q2, q3, U2, U3 — ?

Решение

Из определения электроемкости конденсатора напряжение U₁ на первом конденсаторе

В.

Поскольку 1-й и 2-й конденсаторы соединены параллельно, то   U₁ = U₂. Следовательно, U₂ = 400 В. Общая электроемкость 2-х параллельно соединенных конденсаторов С₁ и С₂

 Ф.

Общий заряд конденсаторов С₁ и С₂: q_1,2 = C_1,2^.U₁ = 2^.10^-9.400 = 8^.10^-7 Кл. При последовательном соединении q_1,2 = q₃, тогда q₃ = 8^.10^-7 Кл.

Напряжение  В.

Заряд 2-го конденсатора q₂ = C₂^.U₂ = 6^.10^-9.400 = 2.4^.10^-6 Кл.

Ответ: q₂ = 2.4^.10^-6 Кл; q₃ = 8^.10^-7 Кл; U₂ = 400 В; U₃ = 100 В.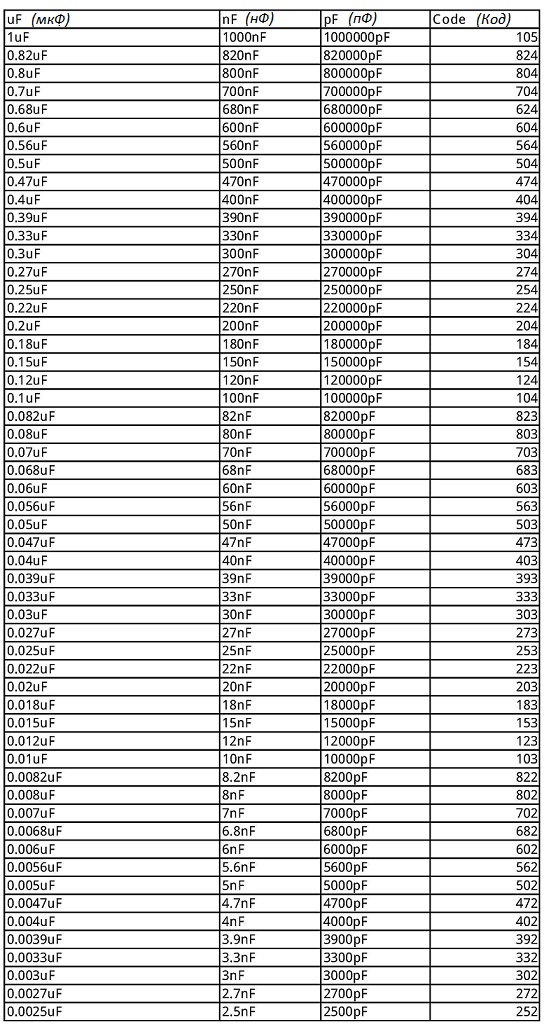

 

Пример 5

Плоский воздушный конденсатор электроемкостью С₁=4·10^-8 Ф, имеющий заряд q₁=8^.10^-6 Кл, соединен параллельно с таким же конденсатором, но заполненным диэлектриком с ε=6, заряженным до напряжения U₂=100 В. Найти количество теплоты, выделившееся в проводах при соединении конденсаторов.

 

Дано: С1 = 4.10-8 Ф q1 = 8.10-6 Кл ε = 6 U2 = 100 В

Q -?

Решение

Искомое количество теплоты равно разности энергий конденсаторов до их соединения и после соединения: 

Q = W₁ + W₂ — W₃,

где  – энергия 1-го конденсатора до соединения;  — энергия 2-го конденсатора до соединения;

Заряд q₂ 2-го конденсатора до соединения

q₂ = C₂^. U₂ = ε^.C₁^.U₂ = 6^.4^.10^-8.100 = 2,4^.10^-5 Кл.

После соединения конденсаторов общий заряд q = q₁ + q₂ (по закону сохранения заряда).

Общая электроемкость С = С₁ + С₂, тогда  . Получим

 Дж.

Ответ: Q = 1.9^.10^-3 Дж.

Пример 6

К пластинам плоского конденсатора, находящимся на расстоянии d = 5 мм, приложено напряжение 120 В. К одной из пластин прилегает пластина из слюды (ε = 7) толщиной d₁=2 мм. Найти плотность энергии электрического поля в слое слюды и воздушном слое конденсатора.

 

Дано: d = 5 мм = 5 · 10-3 м U = 120 В d1 = 2 мм = 2 · 10-3 м ε = 7

w1, w2 -?

Решение

 

 

Двухслойный плоский конденсатор можно заменить эквивалентной системой двух последовательно соединенных конденсаторов с расстояниями между пластинами, равными толщине слоев, поэтому будем рассматривать систему «б» вместо системы «а» (см. рисунок).

Плотность электрического поля w₁ и w₂ в слое слюды и воздуха конденсатора:

Напряженность Е₁ и Е₂ электрического поля в слюде и воздушном промежутке:

.

        Для напряжений U₁ и U₂ в двух слоях имеем систему уравнений

 

где уравнение (2) означает, что при последовательном соединении конденсаторов равны их заряды.

 тогда .

Подставим в уравнение (1), получим

,

отсюда

 В.

В.

 Дж/м³.

 Дж/м³.

Ответ: w₁ = 8.4^.10^-4 Дж/м³, w₂ = 5.9^.10^-3 Дж/м³.

 

Задачи для решения

 

C1 C2 C3

3. 1. Расстояние между пластинами плоского конденсатора равно       1,2 мм, площадь пластин – 40 см². В пространстве между пластинами конденсатора находятся два слоя диэлектриков: слой парафина толщиной  0,8 мм и слой стекла толщиной 0,2 мм. Какой заряд находится на конденсаторе, если разность потенциалов между его пластинами равна       100 В?

3.2. Четыре конденсатора С₁ =       = 2 мкФ, С₂ = 3 мкФ, С₃ = 6 мкФ и С₄ =      = 4 мкФ соединены между собой так, как показано на рисунке. Определить заряды конденсаторов и разности потенциалов между их обкладками, если разность потенциалов между точками А и В равна 500 В.

3.3. Расстояние между пластинами плоского воздушного конденсатора равно 2 мм, площадь пластин – 60 см². Конденсатор заряжен до разности потенциалов 150 В и отключён от батареи. Какая разность потенциалов будет между пластинами конденсатора после их раздвигания до расстояния 3 мм?

3. 4. Четыре конденсатора С₁ = 25 мкФ,     С₂ = 5 мкФ, С₃ = 45 мкФ и С₄ = 15 мкФ соединены между собой так, как показано на рисунке. Разность потенциалов на обкладках каждого конденсатора С₁ равна 20 В. Найти заряды и разности потенциалов на обкладках каждого конденсатора, а также общий заряд и разность потенциалов на всей батарее конденсаторов.

 

3.5. Четыре конденсатора С₁ = 0,1 мкФ, С₂ = 0,5 мкФ, С₃ = 0,2 мкФ и С₄ = 0,3 мкФ соединены между собой так, как показано на рисунке. Определить заряды конденсаторов и разности потенциалов между их обкладками, если разность потенциалов между точками А и В равна 400 В.

3.6. Четыре конденсатора С₁ = 30 пФ, C₂ = 10 пФ, С₃ = 55 пФ и С₄ =     5 пФ соединены между собой так, как показано на рисунке. Заряд на конденсаторе С₄ равен 0,5 нКл. Найти заряды и разности потенциалов на обкладках каждого конденсатора, а также общий заряд и разность по­тенциалов на всей батарее конденса­торов.

3.7. Расстояние между пластинами плоского воздушного конденсато­ра равно 3 мм, площадь пластин – 30 см². Конденсатор подключен кбатарее с ЭДС, равной 250 В. На сколько изменится заряд конденсатора, если в него вдвинуть параллельно его обкладкам стеклянную пластинку такой же плошали толщиной 1 мм?

3.8 Расстояние между пластинами плоского воздушного конденсато­ра равно 3,2 мм, площадь пластин – 48 см². Конденсатор подключен к батарее с ЭДС, равной 200 В. Найти изменение заряда конденсатора в результате раздвигания его пластин до расстояния 4,8 мм.

3.9.Пять конденсаторов C₁ = 4 мкФ, C₂ = 2 мкФ, С₃ = 5 мкФ, С₄ = 10 мкФ и C₅ = 7 мкФ соединены между собой так, как показано на рисунке. Разность потенциалов на обкладках конденсатора C₂ равна 50 В. Найти заряды и разности по­тенциалов на обкладках каждого кон­денсатора, а также общий заряд и разность потенциалов на всей бата­рее конденсаторов.

3.10. Расстояние между пластинами плоского воздушного конденсатора равно 3 мм, площадь пластин – 20 см². В пространстве между пластинами находится слой парафина толщиной 1 мм. Конденсатор подключен к батарее с ЭДС, равной 120 В. На сколько изменится заряд конденсатора, если из него вынуть парафин?

3.11. Расстояние между пластинами плоского воздушного конденса­тора равно 3,6 мм, площадь пластин – 72 см². Конденсатор подклю­чен к батарее с ЭДС, равной 50 В. Найти изменение заряда конденсатора в результате сближения его пластин до расстояния 1,2 мм.

3.12. Расстояние между пластинами плоского воздушного кон­денсатора равно 1,2 мм, площадь пластин – 48 см². В пространстве между пластинами находятся 2 слоя диэлектриков: слой стекла толщиной 0,4 мм и слой парафина толщиной 0,6 мм. Разность потенциалов между пластинами конденсатора равна 300 В. Найти: электрическое смещение, напряженность поля и падение потенциала в каждом слое.

3.13. Четыре конденсатора С₁ = 30 пФ, C₂ = 12 пФ, С₃ = 10 пФ и      C₄ = 40 пФ соединены между собой так, как показано на рисунке. Определить заряды конденсаторов и разности потенциалов между их обкладками, если разность потен­циалов между точками А и В равна 300 В.

3.14. К уединенному конденсатору емкостью 0,1 мкФ, заряженному до разности потенциалов, равной 400 В, присоединили параллельно вто­рой незаряженный конденсатор электроемкостью 0,3 мкФ. Как и на сколь­ко изменится разность потенциалов на первом конденсаторе?

3.15. Расстояние между пластинами плоского конденсатора равно 5 мм, площадь пластин – 24 см². В пространстве между пластинами конденсатора находится слой парафина толщиной 2 мм. Конденсатор заря­жен до разности потенциалов 300 В и отключен от батареи. Какая раз­ность потенциалов будет между обкладками конденсатора после выдвиже­ния из него слоя парафина? Для парафина e = 2.

3.16. Пять конденсаторов С₁ = 2 пФ, C₂= 3 пФ, С₃= 4 пФ, С₄ = 6 пФ и С₅ = 8 пФ соединены ме­жду собой так, как показано на рисунке. Определить заряды конденсаторов и разности потенциалов между их обкладками, если разность потен­циалов между точками А и В равна 500 В.

3.17. Расстояние между пластинами плоского воздушного конден­сатора равно 1 мм. Поверхностная плотность заряда на пластинах кон­денсатора равна 2 мкКл/м². Найти изменение разности потенциалов между пластинами конденсатора в результате их раздвигания до расстояния 1,6 мм.

3.18. К уединённому заряженному конденсатору электроемкостью    0,1 мкФ, имеющему заряд, равный 500 мкКл, присоединили параллельно второй незаряженный конденсатор электроёмкостью 2,4 мкФ. Найти заряд на втором конденсаторе.

C2          C3

3.19. Расстояние между пластинами плоского воздушного конденсатора равно 3,4 мм, площадь пластин – 34 см². Конденсатор подключён к батарее с ЭДС, равной 50 В. На сколько изменится заряд конденсатора, если в него вдвинуть параллельно его обкладкам металлическую пластинку такой же площади с толщиной, равной 1,4 мм?

3.20. Четыре конденсатора С₁ = 30 пФ, С₂ = 12 пФ, С₃ = 10 пФ и     С₄ = 40 пФ соединены между собой так, как показано на рисунке. Раз­ность потенциалов на обкладках конденсатора С₄ = 200 В. Найти заряды и разности потенциалов на обкладках каждого конденсатора, а также общий заряд и разность потен­циалов на всей батареи конденсаторов.

3.21. Расстояние между пластинами плоского воздушного конденсатора равно 2,4 мм. Поверхностная плотность заряда на пластинах конденсатора – 3 мкКл/м². Найти изменение разности потенциалов между пластинами конденсатора в результате утечки половины заряда конденса­тора.

3.22. К уединенному заряженному конденсатору электроемкостью
20 пФ, имеющему заряд, равный 200 нКл, присоединили параллельно вто­рой незаряженный конденсатор электроемкостью 80 пФ. Как и на сколько изменится заряд на первом конденсаторе?

3.23. Расстояние между пластинами плоского воздушного конденсатора равно 4,9 мм, площадь пластин – 36 см². В пространстве между обкладками параллельно им расположена металлическая пластинка такой же площади толщиной 1,2 мм. Конденсатор подключен к батарее с ЭДС, равной 140 В. На сколько изменится заряд конденсатора, если из него вынуть эту пластинку?

3.24. Расстояние между пластинами плоского воздушного конденсатора равно 4,8 мм, площадь пластин – 36 см². В пространстве между пластинами находится слой диэлектрика толщиной 1 мм с e₁ = 4. Конденсатор заряжен до разности потенциалов 200 В и отключен от батареи. На сколь­ко изменились электрическое смещение, напряженность поля и падение потенциала в каждом слое после погружения конденсатора в масло (e₂ = 2,2) ?

3.25. К уединенному конденсатору электроемкостью 0,6 мкФ, заряженному до разности потенциалов 300 В, присоединили параллельно вто­рой конденсатор электроемкостью 0,4 мкФ, заряженный до разности потенциалов 150 В. Найти изменение заряда на втором конденсаторе после его присоединения.

3.26. Определить энергию поля уединённой металлической сферы радиусом 0,2 м, имеющей заряд 2 мкКл.

3.27. К плоскому воздушному конденсатору, площадь каждой пластины которого 0,1 м² и расстояние между пластинами 2 мм, приложено нап­ряжение 300 В. Найти энергию конденсатора.

3.28. Плоский конденсатор с площадью пластин 0,02 м² каждая и расстоянием 1 мм между пластинами заполнен диэлектриком с e = 4. Най­ти энергию электрического поля в конденсаторе, если его зарядили до 200 нКл.

3.29. Конденсатор ёмкостью 20 мкФ, заряженный до разности потенциалов 60 В и отключенный от источника, соединяют параллельно с незаряженным конденсатором емкостью 10 мкФ. Найти энергию второго конденсатора после соединения его с первым.

3.30. Тонкая металлическая сфера, находящаяся в вакууме, имеет потенциал 400 В и поверхностную плотность заряда 2 мкКл/м² . Опреде­лить энергию сферы.

3.31. Пластины плоского конденсатора площадью 4 см² каждая притягиваются друг к другу с силой 0,002 Н. Пространство между пластинами заполнено слюдой (e = 6). Найти объемную плотность энергии электрического поля в конденсаторе.

3.32. Разность потенциалов между пластинами плоского воздушного конденсатора площадью 20 см² каждая равна 200 В. Поверхностная плотность заряда на пластинах – 4 мкКл/м². Найти энергию конденсатора.

3.33. Расстояние между пластинами плоского воздушного конденсатора 1 см, площадь каждой пластины 20 см², напряжение между пластинами 400 В. После отключения источника напряжения пластины сдвигают до расстояния 0,2 см. Найти энергию конденсатора до и после сближения пластин.

3.34. Между пластинами плоского конденсатора, находящимися на расстоянии 0,1 см друг от друга, площадью 4 см² каждая помешена пластинка из слюды (e = 6), полностью заполняющая пространство между пластинами. На конденсатор подано напряжение 500 В. Найти paботу, которую нужно совершить, чтобы вынуть диэлектрик из конденсатора, не отключая источник напряжения.

3.35. Плоский конденсатор заполнен диэлектриком с e = 6 и заряжен до некоторой разности потенциалов. Его энергия при этом равна 0,4 мДж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Найти работу, совершённую при вынимании диэлектрика.

3.36. Две параллельные бесконечно длинные заряженные нити с линейной плотностью заряда 0,2 мкКл/м и 0,6 мкКл/м соответственно находятся на расстоянии 0,2 м друг от друга. Найти плотность энергии электрического поля в точке, расположенной посредине между нитями.

3.37. Напряжение 600 В на батарее из 5 последовательно соединен­ных конденсаторов емкостью 40 мкФ каждый поддерживают постоянным. При этом один из конденсаторов пробивается. Определить: а) изменение энергии батареи; б) работу источника напряжения.

3.38. Два конденсатора, емкости которых 600 пФ и 1000 пФ, соединены последовательно. Батарею заряжают до напряжения 2000 В. Затем конденсаторы, не разряжая, соединяют параллельно. Определить работу разряда, происходящего при переключении.

3.39. Между пластинами плоского конденсатора площадью 500 см² находится металлическая пластинка такой же площади. Расстояние между обкладками конденсатора 5 см, толщина пластинки 1 см. Какую работу нужно совершить, чтобы извлечь эту пластинку из конденсатора, если он подключен к источнику, дающему напряжение 100 В?

3.40. Конденсаторы емкостями C₁ = 1 мкФ, С₂ = 2 мкФ и С₃ = 3 мкФ включены в цепь с напряжением 120 В. Определить энергию каждого кон­денсатора в случаях: а) последовательного их включения; б) параллель­ного включения.

3.41. Конденсатор электроёмкостью 3 мкФ был заряжен до разности потенциалов 40 В. После отключения от источника напряжения конденса­тор был соединён параллельно с другим незаряженным конденсатором электроёмкостью 5 мкФ. Определить работу происходящего разряда.

3.42. Конденсатор емкости 200 мкФ соединен последовательно с конденсатором переменной емкости. Батарея конденсаторов подключена к источнику напряжения U=120 В. На какую величину изменится энергия первого конденсатора, если ёмкость второго увеличить с 200 мкФ до
600 мкФ?

3.43. Бесконечная равномерно заряженная плоскость имеет поверхностную плотность заряда 40 мкКл/м². Определить энергию электрического поля, заключённого внутри цилиндра высотой 0,2 м и площадью каждого основания 0,01 м², если цилиндр не пересекается плоскостью.

3.44. Плоский конденсатор с площадью пластин 5 см² и рас­стоянием   2 см между ними находится под напряженном 200 В. К одной из пластин прилегает пластинка слюды (e = 6) толщиной 1 см. Найти энер­гию электрического поля в пластинке слюды.

3.45. Имеется плоский воздушный конденсатор с площадью обкладок 400 см² каждая. Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от 1 см до 3 см, если поддер­живать постоянным: а) заряд конденсатора, равный 0,2 мкКл; б) напря­жение на конденсаторе, равное 60 В.

3.46. Заряд 0,6 мкКл равномерно распределен по объему шара радиусом 0,2 м. Найти плотность энергии электрического поля в точках, расположенных на расстояниях 0,1 м и 0,3 м от центра шара. Диэлектрическую проницаемость шара и окружающей среды принять за единицу.

3.47. Определить энергию электрического поля вне мысленно проведенной сферы, в центре которой находится точечный заряд 0,3 мкКл. Радиус сферы равен 0,1 м.

3.48. Два последовательно соединённых конденсатора подключены к источнику напряжения 180 В. При этом отношение энергий конденсаторов равно 3. Найти напряжение на каждом конденсаторе.

3.49. На сколько уменьшится энергия заряженного металлического шара радиусом 9 см, имеющего заряд 10 мкКл, если его опустить в масло     (e = 2,5)?

3.50. На сколько изменится энергия батареи трех последовательно соединенных конденсаторов емкостью 12 мкФ каждый, если увеличить напряжение на батарее от 120 до 200 В?

3.51. Между пластинами накоротко замкнутого плоского кон­денсатора поместили металлическую пластину с равномерно распределен­ным зарядом Q. Пластину медленно перемещают параллельно самой себе на расстояние х. Какой заряд прохо­дит при этом во внешней цепи кон­денсатора, если расстояние между пластинами равно d?

3.52. Между пластинами накоротко замкнутого плоского конденсато­ра находится точечный заряд Q. Площадь пластин бесконечно велика, расстояние между ними равно d. Первоначально заряд находится на расстоянии d/3 от левой пластины. Какой заряд пройдет по проводнику, замыкающему пластины конденсатора, при перемещении заряда Q в новое по­ложение на расстоянии d/З от правой пластины?

3. 53. Два одинаковых металлических диска диаметром 12 см расположены параллельно друг к другу и разделены парафинированной бума­гой толщиной 0,02 см. Диски сдвинуты так, что центр одного из них находится против края другого. Определить электроемкость такой системы. Для парафина e = 2.

3.54. Определить электроемкость конденсатора, состоящего из ша­рика диаметром 1 см и большой проводящей пластинки, отстоящей на расстоянии 20 см от центра шарика. Считать, что заряд на поверхности шарика распределен равномерно.

3.55. Конденсатор электроёмкостью 1 мкФ, заряженный до напряжения 110 В, подключили параллельно к концам системы из двух последовательно соединенных незаряженных конденсаторов, емкости которых 2 мкФ и 3 мкФ. Какой заряд протечет при этом по соединительным проводам?

3.56. Два плоских конденсатора емкостью 0,6 мкФ каждый, соединенные параллельно и заряженные до напряжения 80 В, отсоединяют от источника. Пластины одного из конденсаторов могут двигаться свободно навстречу друг другу. Найти их скорость в момент, когда зазор между пластинами конденсатора уменьшится в два раза. Масса каждой пластины   20 мг. Силой тяжести пренебречь.

3.57. Система состоит из двух концентрических тонких металли­ческих оболочек радиусами 1 см и 2 см с соответствующими зарядами 0,2 мкКл и 0,4 мкКл. Найти собственные энергии каждой оболочки, энер­гию W₁₂ взаимодействия оболочек и полную электрическую энергию W сис­темы.

3.58. Заряд 0,5 мкКл распределен равномерно по объему шара радиусом 0,1 м. Полагая диэлектрическую проницаемость равной единице, найти: а) собственную электростатическую энергию шара, б) отношение энергии поля, запасенной внутри шара, к энергия поля, заключенной в окружающем пространстве.

3.59. Точечный заряд 3 мкКл находится в центре шарового слоя из однородного изотропного диэлектрика с проницаемостью e = 3. Внутрен­ний радиус слоя 25 см, внешний 50 см. Найти электростатическую энергию, заключенную в диэлектрическом слое.

3.60. Имеется сферическая оболочка, заряженная равномерно зарядом 4 мкКл. В центре ее расположен точечный заряд 2 мкКл. Найти работу электрических сил этой системы при расширении оболочки – увеличении ее радиуса от 0,25 до 0,5 м.

 

 

4. ЗАКОНЫ ПОСТОЯННОГО ЭЛЕКТРИЧЕСКОГО ТОКА

 

Основные формулы

 

Сила тока J по определению

,

где dQ – электрический заряд, проходящий через сечение проводника за время dt.

Плотность j тока при равномерном распределении тока по сечению проводника

где J – сила тока в проводнике; S – площадь сечения проводника.

Закон Ома для участка цепи, не содержащего источника тока

где U – напряжение на проводнике, R – сопротивление проводника.

Для однородного проводника

где ρ – удельное сопротивление материала проводника; l – длина проводника с площадью сечения S.

Закон Ома для участка цепи, содержащего источник тока,

,

где φ₁, φ₂ – потенциалы начала и конца участка;  – электродвижущая сила источника тока, которая берется со знаком «+», если ток встречает вначале отрицательный полюс источника, и со знаком «-», если ток встречает первым положительный полюс. R, r – внешнее и внутреннее сопротивления потока тока.

Закон Ома для замкнутой цепи

.

Напряжение на зажимах источника тока

.

Ток короткого замыкания

.

Сопротивление R_посл при последовательном соединении проводников

.

Сопротивление R_пар при последовательном соединении проводников определяется из равенства

,

где  – сопротивление проводника с номером «i».

Работа А тока

,

где t – время прохождения тока через произвольное сечение проводника, не содержащего источника тока.

Мощность Р тока

.

Закон Джоуля-Ленца

 при J = const,

где J – сила постоянного тока, проходящего по проводнику сопротивлением R за время t; Q – количество теплоты, выделяющееся в этом проводнике за время t.

Закон Ома в дифференциальной форме

,

где  – удельная электропроводность;  – напряженность электрического поля внутри проводника;  – плотность тока.

Удельная электропроводность

,

где Q – заряд иона; n – концентрация ионов;  и  – подвижности положительных и отрицательных ионов.

 



Конвертировать Единицы измерения / Конвертер единиц

Преобразуемое значение:

Калькулятор классических единиц измерения:

Категория измерения:Поглощенная дозаУскорениеКоличество веществаУголПлощадьБайты/БитыЕмкостьКаталитическая активностьВыброс CO2Скорость работы компьютера area productDose length productDynamic viscosityElectric chargeElectric conductanceElectric currentElectric dipole momentElectrical elastanceElectrical resistanceEnergyEquivalent doseFabric weight (Textiles)Font size (CSS)ForceFrequencyFuel consumptionIlluminanceImpulseInductanceIonizing radiation doseKinematic viscosityLuminanceLuminous energyLuminous fluxLuminous intensityMagnetic fieldMagnetic field strengthMagnetic fluxMagnetomotive forceMass / WeightMass flow rateMolar concentrationMolar massMolar volumeMusical intervalNumeral systemsOil equivalentParts-Per . .. МощностьДавлениеДоза радиацииРадиоактивный ityСкорость вращенияSI-префиксыТвердый уголУровень звукаПоверхностное натяжениеТемператураИзмерение тканиВремяКрутящий моментСкоростьНапряжениеОбъемОбъемный расход   

Преобразуемое значение:

Исходная единица измерения: Ангстрем [Å]Астрономическая единица [AU]Аттометр [am]Длина кабеляСантиметр [см]Цепь [ch]Кубит (британский)Декаметр [dam]Дециметр [дм]FathomFemtometre [ fm]Фут [фут]ФурлонгГигаметр [Гм]Гектометр [чм]Дюйм [дюйм]Километр [км]Световые дниСветовые часыСветовые минутыСветовые секундыСветовые годыСсылкаМегаметр [Мм]Метр [м]Метрическая миляМикрометр [мкм] Мил — Тысяча миль (международная) [ми ]Миля (США)Миллиметр [мм]Нанометр [нм]Морская миляПарсек [ПК]ПершПиметр [pm]Планковая длинаПолюсКварталРимская миляСтатутная миляTwipX Единица — ЗигбанЯрды

Целевая единица: Ангстрем [Å] Астрономическая единица [AU] Аттометр [am] Длина кабеля Сантиметр [cm] Цепь [ch] Кубит (британский) Декаметр [dam] Дециметр [dm] Fathom Femtometre [fm] Foot [ft] Furlong Gigameter [Gm ]Гектометр [чм]Дюйм [дюйм]Километр [км]Световые дниСветовые часыСветовые минутыСветовые секундыСветовые годыСсылкаМегаметр [Мм]Метр [м]Метрическая миляМикрометр [мкм]Мил — ТысячаМиль (международная) [мили]Миля (США)Миллиметр [мм] Нанометр [нм]Морская миляПарсек [пк]ПершПиметр [пм]Планковая длинаПолюсКварталРимская миляСтатутная миляTwipX Единица — ЗигбанЯрды

Преобразование единиц измерения совсем не тривиально: Миллиметр, сантиметр, дециметр, метр, километр, мили, морской мили, футы, ярды, дюймы, локти, парсекы и световые годы. Со всеми эти измерения расстояний могут быть рассчитаны. И это даже не близкие ко всем возможным измерениям , вернее только самые распространенные те. В случае площадей (квадратный метр, квадратный километр, площадь, гектар, Морган, акр среди прочего), температуры (градусы Цельсия, Кельвина, по Фаренгейту), скорость (м/с, км/ч, мили/ч, узлы, мах), вес (сотни вес, килограмм, метрическая тонна, тонна США, имперская тонна, фунт и др.) и объемы (кубический метр, гектолитр, имперский галлон жидкости, галлон США жидкость, сухой галлон США, баррель среди прочего) не намного лучше. К полный хаос большинство из этих единицы также имеют подразделения и выше единиц (-> милли, санти, деци и др.). Короче: Хаос, в котором никто действительно, кажется, не видит ясно без помощи справки и различные формы помощи. Калькулятор для преобразования единиц измерения , подобный этому, идеально подходит для преобразования единиц измерения .

Преобразование — калькулятор в преобразование единиц измерения . Поддерживает огромное количество измерение единицы .

Преобразователь микрофарад в фарад

Введите значение

Введите значение

Вывод

Вывод

Сколько фарад в микрофараде?

---

Ответ: один микрофарад равен 0,000001 фарад. Воспользуйтесь нашим онлайн-калькулятором перевода единиц измерения, чтобы перевести единицы из микрофарад в фарады. Просто введите значение 1 в Agate Line и посмотрите результат в Farad.

Как преобразовать микрофарады в фарады (мкФ в Ф)

---

Используя наш инструмент преобразования микрофарад в фарад, вы знаете, что один микрофарад эквивалентен 0,000001 фарад. Следовательно, чтобы преобразовать микрофарады в фарады, нам просто нужно умножить число на 0,000001. Для этого мы будем использовать очень простую формулу преобразования микрофарад в фарады. См. приведенный ниже пример расчета.

Перевести 1 микрофарад в фарад ⇒ 1 микрофарад = 1 × 0,000001 = 0,000001 фарад

Что такое микрофарад?

---

Микрофарад — единица измерения электростатической емкости. Конденсатор в один микрофарад создает между своими пластинами разность потенциалов в один микровольт, когда он накапливает электрический заряд в один микрокулон. Микрофарад — единица электростатической емкости, дольная по отношению к фараде. Один микрофарад равен 0,000001 фарад.

Что такое символ микрофарада?

---

Обозначение микрофарад — мкФ. Это означает, что вы также можете записать один микрофарад как 1 мкФ.

Что такое Фарада Единица измерения?

---

Фарад — единица измерения электростатической емкости. Конденсатор в один фарад создает разность потенциалов в один вольт между своими пластинами, когда он накапливает электрический заряд в один кулон.

Что такое символ Фарада?

---

Фарад обозначается символом F. Это означает, что один фарад можно также записать как 1 F.

Таблица преобразования микрофарад в фарад

---

Микрофарад [мкФ]	Farad [F]
1	0.000001
2	0.000002
3	0.000003
4	0.000004
5	0.000005
6	0.000006
7	0.000007
8	0.000008
9	0.000009
10	0.00001
100	0.0001
1000	0.001

Microfarad to Other Units Conversion Chart

---

Microfarad [μF]	Output
1 микрофарад в фарадах равен	0,000001
1 микрофарад в экзафарадах равен	1e-24
1 Микрофарада в Петафараде равен	1E-21
1 Микрофарада в терафараде равен	1E-18
1 Микрофарад в GIGAFARADARADARAD. Похожие записи 21.11.2024 0 Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании 19.11.2024 0 Новорожденный какает слизью: причины появления слизи в кале грудничка 19.11.2024 0 Гемангиома у новорожденных: причины, виды, лечение и профилактика Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт