Как представляются целые числа в памяти компьютера. Что такое прямой код числа. Как получить обратный код двоичного числа. Для чего нужен дополнительный код и как его вычислить. Преимущества использования дополнительного кода в вычислительной технике.
Представление чисел в памяти компьютера
В памяти компьютера все числа представляются в двоичной системе счисления. Для кодирования целых чисел используется несколько способов:
- Прямой код
- Обратный код
- Дополнительный код
Каждый из этих способов имеет свои особенности и применяется для решения определенных задач. Рассмотрим подробнее каждый из них.
Что такое прямой код числа
Прямой код — это самый простой способ представления целых чисел в двоичной системе. Он имеет следующий формат:
- Старший бит отводится под знак числа (0 — для положительных, 1 — для отрицательных)
- Остальные биты содержат абсолютное значение числа в двоичной системе
Например, число 5 в 8-битном прямом коде будет выглядеть так:
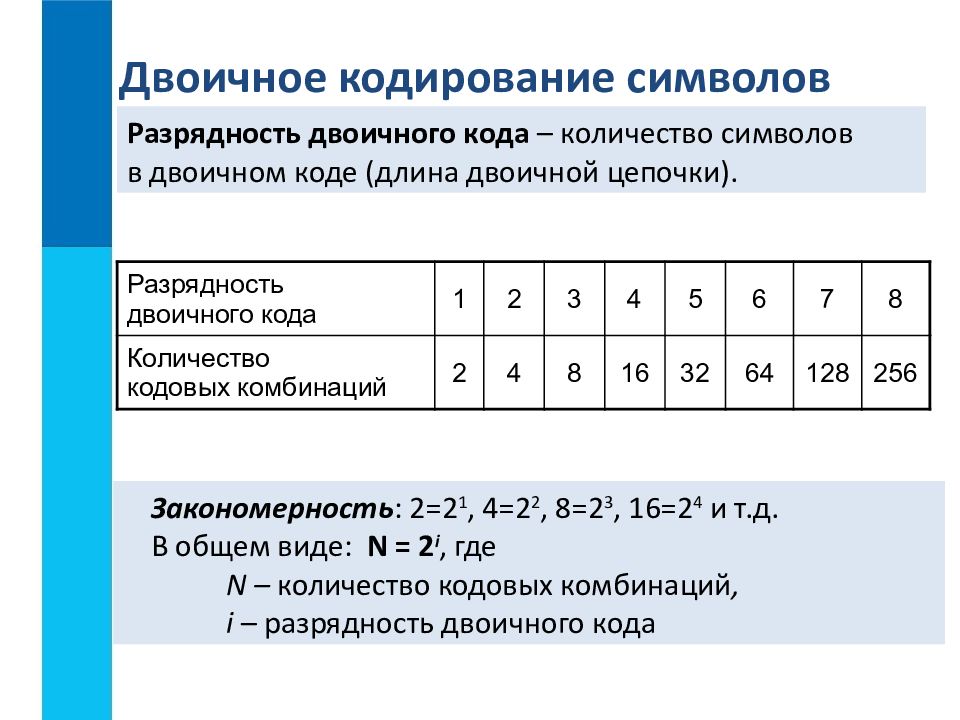
00000101
А число -5 в прямом коде:
10000101
Прямой код удобен тем, что положительные числа представляются в нем так же, как и в обычной двоичной системе. Однако при выполнении арифметических операций с отрицательными числами возникают сложности.
Особенности обратного кода
Обратный код позволяет упростить вычитание чисел, сведя его к операции сложения. Для положительных чисел обратный код совпадает с прямым. Для отрицательных чисел он формируется по следующим правилам:
- Старший бит устанавливается в 1 (признак отрицательного числа)
- Все остальные биты инвертируются (0 заменяется на 1 и наоборот)
Например, число -5 в 8-битном обратном коде будет выглядеть так:
11111010
Обратный код упрощает некоторые вычисления, но имеет недостаток — два представления нуля (положительный и отрицательный). Это усложняет проверку на равенство нулю.
Преимущества дополнительного кода
Дополнительный код является наиболее распространенным способом представления целых чисел в современных компьютерах. Он обладает следующими преимуществами:
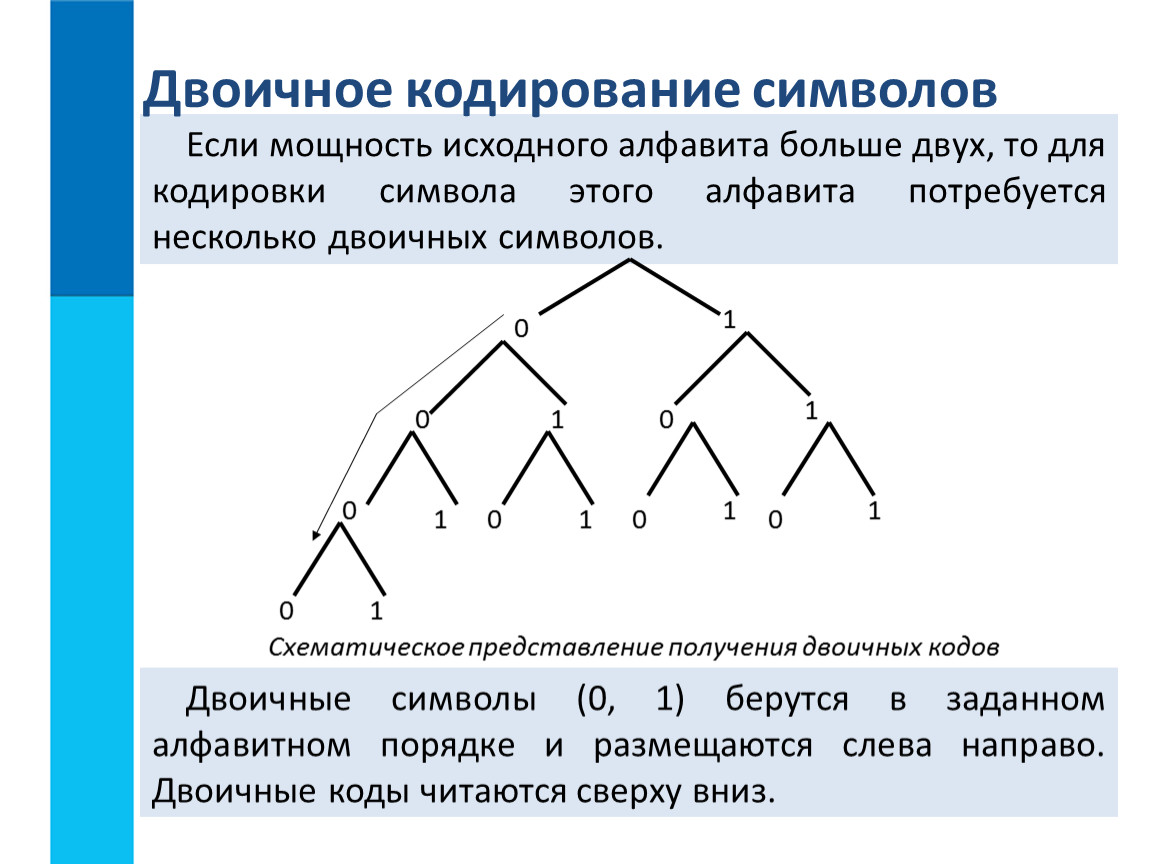
- Позволяет заменить вычитание на сложение
- Имеет единственное представление нуля
- Упрощает реализацию арифметических операций
Для положительных чисел дополнительный код совпадает с прямым. Для отрицательных чисел он формируется в два этапа:
- Вычисляется обратный код числа
- К результату прибавляется 1
Рассмотрим пример получения дополнительного кода для числа -5:
Прямой код: 10000101 Обратный код: 11111010 Добавляем 1: 11111011
Таким образом, число -5 в 8-битном дополнительном коде будет представлено как 11111011.
Диапазон представления чисел
При использовании дополнительного кода для n-разрядных чисел диапазон представления будет следующим:
- От -2^(n-1) до 2^(n-1) — 1
Например, для 8-битных чисел диапазон составит от -128 до 127.
Какой максимальный диапазон чисел можно представить в 16-битном дополнительном коде? Для 16-разрядных чисел диапазон будет от -32768 до 32767.
Выполнение арифметических операций
Одним из главных преимуществ дополнительного кода является простота выполнения арифметических операций. Рассмотрим несколько примеров:

Сложение чисел
При сложении чисел в дополнительном коде необходимо просто сложить их двоичные представления, отбросив перенос из старшего разряда. Например, сложим числа 5 и -3:
00000101 (5) + 11111101 (-3) -------- 00000010 (2)
Как видим, результат верный — получилось число 2.
Вычитание чисел
Вычитание сводится к сложению с отрицательным числом. Например, вычтем из 5 число 3:
00000101 (5) + 11111101 (-3) -------- 00000010 (2)
Результат снова верный — 5 — 3 = 2.
Применение дополнительного кода в технике
Дополнительный код широко используется в современных компьютерах и микропроцессорах для представления целых чисел. Это обусловлено следующими факторами:
- Упрощение арифметических схем процессора
- Экономия оборудования за счет универсальности операций
- Повышение скорости вычислений
Практически все современные процессоры работают с целыми числами в дополнительном коде. Это позволяет оптимизировать их архитектуру и повысить производительность.
Ограничения дополнительного кода
Несмотря на множество преимуществ, дополнительный код имеет некоторые ограничения:

- Асимметричный диапазон представления чисел
- Сложность понимания для начинающих программистов
- Необходимость дополнительных проверок при изменении знака числа
Кроме того, в некоторых специфических форматах (например, с плавающей запятой) преимущества дополнительного кода не так очевидны.
Заключение
Дополнительный код является эффективным способом представления целых чисел в компьютерах. Он позволяет упростить выполнение арифметических операций и оптимизировать архитектуру процессоров. Несмотря на некоторые ограничения, дополнительный код остается стандартом де-факто в современной вычислительной технике.
Понимание принципов работы с дополнительным кодом важно для программистов, работающих на низком уровне, а также для всех, кто интересуется устройством компьютеров и микропроцессоров. Это знание позволяет лучше понимать принципы работы вычислительной техники и создавать более эффективные программы.
Системы счисления по основанию 2, 8, 10, 16. Представление целых неотрицательных и отрицательных чисел в ЭВМ. Прямой, обратный и дополнительный коды. Примеры прямого, обратного и дополнительного кодов восьмибитового положительного и отрицательного целого числа. Запишите в десятичной с.с. целое число по его дополнительному коду.
Вопрос 8 (Системы счисления по основанию 2, 8, 10, 16. Представление целых неотрицательных и отрицательных чисел в ЭВМ. Прямой, обратный и дополнительный коды. Примеры прямого, обратного и дополнительного кодов восьмибитового положительного и отрицательного целого числа. Запишите в десятичной с.с. целое число по его дополнительному коду.) Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр). Существуют системы позиционные и непозиционные. Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. Десятичная система счисления Эта система пришла в Европу из Индии, где она появилась не позднее VI века н. э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системесчисления особую роль играют число 10 и его степени; 10, 100, 1000 и т. д. Крайняя правая цифра числа показывает число единиц, вторая справа — число десятков, следующая — число сотен и т. д. Причина наибольшей распространенностидесятичной системы счисления состоит в том, что первым счетным аппаратом человека являлись его руки. Число пальцев и стало отправным пунктом для системы счета. Двоичная система счисления В этой системе всего две цифры — 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Крайняя правая цифра числа показывает число единиц, следующая цифра — число двоек, следующая — число четверок и т. д. Двоичная система счисления позволяет закодировать любое натуральное число — представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически. Восьмеричная система счисления В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает — как и в десятичном числе — просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т. д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — цифровая часть содержит двоичную запись числа, в знаковом разряде содержится 0. Например, для k = 8:
преобразования числа декабря до 6-разрядное двоичное число
Я ищу, чтобы преобразовать dec-число в 6-битное двоичное число.. bin() работает нормально, но пропускает ведущие нули, которые важны.
например:
- 0 = 000000
- 1 = 000001
- 2 = 000010
и т. д. … с самым большим разрешенным числом dec-63.
python binary binПоделиться Источник Richard 07 октября 2011 в 13:26
2 ответа
8
Либо то, что сказал Мэтт в комментарии ( bin(63)[2:].zfill(6)), либо используйте строки формата в Python 2.6+:
'{0:06b}'.format(63)
Вы можете опустить первый ноль в Python 2.7+, так как вы можете неявно нумеровать группы.
Поделиться agf 07 октября 2011 в 13:30
0
Или просто:
n2=[2**x for x in xrange(0, 7)]
n2.reverse()
def getx(x):
ret = ''
for z in n2:
if x >= z:
x -= z
ret += '1'
else:
ret += '0'
return ret
Поделиться Balazs Kanyo 07 октября 2011 в 14:01
Похожие вопросы:
Преобразование десятичного числа в двоичное число на Fortran
Я хочу написать программу, которая преобразует десятичное число в двоичное и дает размер этого двоичного числа. У меня есть следующий код: program bin implicit none integer i, count, bin(100), dec…
Пользовательская функция для преобразования целого числа decimal в двоичное (до 20 цифр) в MATLAB
Мне нужно написать пользовательскую функцию MATLAB, которая преобразует целые числа, записанные в двоичной форме, в форму decimal. Назовите функцию d = binaTOint (b), где входной аргумент b-вектор с…
Как конвертировать числа (декабря) в двоичном (номер ОГРН) и от ящика до декабря?
Как преобразовать десятичное число в двоичное число с фиксированными битами
Я хочу преобразовать числа от 0 до 15 Вот так: 0000 0001 0010 0011 . . . 1111 Проблема в том, что когда мы преобразуем 2 в двоичное число, оно дает только 10 в двоичном виде, но я хочу преобразовать…
Десятичное число в двоичное для большого числа (>2253483438943167)
У меня есть приложение VB.Net, которое проходит через ряд процессов для декодирования строки, одна из проблем заключается в том, что я нашел функцию, которая преобразует двоичное число в десятичное…
Является ли приведение целого числа со знаком к двоичному числу с плавающей запятой дешевле, чем обратная операция?
Я знаю из таких статей, как Почему вы никогда не должны бросать поплавки в ints и многих других, подобных этому, что бросать поплавок в подписанный int дорого. Я также знаю, что некоторые…
Разница между 8-разрядное число в мало-endian и 8-разрядное число в обратном порядке байтов
В чем разница между 8-разрядное число в мало-endian и 8-разрядное число в обратном порядке байтов на Intel 64?
Доказать или опровергнуть: асимптотически быстрее возвести в квадрат n-разрядное целое число, чем умножить два n-разрядных целых числа
Доказать или опровергнуть: асимптотически быстрее возвести в квадрат n-разрядное целое число, чем умножить два n-разрядных целых числа.
Как получить отрицательное двоичное число из положительного числа
Учитывая положительное число, я пытаюсь напечатать строку, которая представляет его отрицательное двоичное число. Я делаю что-то вроде этого: def NegativeBinary(number): number_below = number — 1…
преобразование числа decimal в двоичное число
Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
☰
Прямой код
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Операция сложения положительного числа и отрицательного числа, представленного в прямом коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.
- Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего. При этом первый (знаковый) разряд в операции не участвует.
_ 000 0111 000 0101 ------------- 000 0010 - После выполнения операции учитывается первый разряд. Результат операции 1 000 0010, или -210.
Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Формирование дополнительного кода числа -7.
Прямой код : 1 000 0111
Инверсия : 1 111 1000
Добавление единицы: 1 111 1001 - Операция сложения.
0 000 0101 + 1 111 1001 -------------- 1 111 1110 - Проверка результата путем преобразования к прямому коду.
Дополнительный код: 1 111 1110
Вычитание единицы : 1 111 1101
Инверсия : 1 000 0010 (или -210)
Двоичная система счисления | Digital Music Academy
Если в десятичной системе счисления числа записываются с помощью десяти различных символов (от 0 до 9), то в двоичной системе — с помощью всего двух символов: 0 и 1. Такая система необходима для всех устройств, в которых информация представлена в виде последовательностей двух возможных состояний носителя, а это практически вся современная вычислительная техника.
Так же, как в десятичной системе разряды являются степенями основания 10, в двоичной системе разряды являются степенями основания 2:
| 10 000 000 000 | 1 000 000 000 | 100 000 000 | 10 000 000 | 1 000 000 | 100 000 | 10 000 | 1000 | 100 | 10 | 1 |
| 1010 | 109 | 108 | 107 | 106 | 105 | 104 | 103 | 102 | 101 | 100 |
| 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 210 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
При этом значением числа будет сумма значений всех разрядов. Например, переведем в привычный десятичный вид двоичное число 110001:
1 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 49
Или то же самое чуть иначе:
1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 49
Или так:
Биты и байты
В современных вычислительных системах информация представлена не в виде непрерывного потока двоичных символов (условных нолей и единиц), а за единицу информации, как правило, принимается байт (byte).
Байт состоит из восьми битов (т.е. это восьмиразрядное двоичное число), соответственно, он имеет 256 (28) возможных значений.
Именно поэтому стандартные варианты разрядности кратны восьми. Например, для операционных систем это 32 или 64 разряда (или бита), а для цифрового звука: 8, 16, 24 и 32.
Важно не запутаться в трех основных значениях, которые определяются разрядностью числа: количество возможных значений, максимальное значение и значение старшего бита/разряда.
Например, для 8-разрядного числа количество возможных значений = 256 (0 — 255), максимальное значение = 255, а значение старшего бита = 128.
Дополнительный код двоичного числа — Студопедия
Обратный код
Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения над натуральными числами. Ранее метод использовался в механических калькуляторах (арифмометрах). В настоящее время используется в основном в современных компьютерах.
Обратный n-разрядный двоичный код положительного целого числа состоит из одноразрядного кода знака (двоичной цифры 0), за которым следует n − 1-разрядное двоичное представление модуля числа (обратный код положительного числа совпадает с прямым кодом).
Пример. Двоичное представление числа 5 есть 101. Обратный 10-разрядный двоичный код числа +5 записывается как 0000000101.
Обратный n-разрядный двоичный код отрицательного целого числа состоит из одноразрядного кода знака (двоичной цифры 1), за которым следует n − 1-разрядное двоичное число, представляющее собой инвертированное n − 1-разрядное представление модуля числа. Следует отметить, что для изменения знака числа достаточно проинвертировать все его разряды не обращая внимания знаковый ли это разряд или информационные.
Пример. Двоичное представление числа 5 есть 101, его 10-разрядное двоичное представление — 0000000101. Обратный 10-разрядный двоичный код числа −5 есть 1111111010.
Для преобразования отрицательного числа в положительное тоже применяется операция инвертирования. Этим обратные коды удобны в применении.[1] В качестве недостатка следует отметить, что в обратных двоичных кодах имеются два кода числа 0: «положительный нуль» 0000000000 и «отрицательный нуль» 1111111111 (приведены 10-разрядные обратные коды). Это приводит к некоторому усложнению операции суммирования. Поэтому в дальнейшем перешли к дополнительным кодам записи знаковых целых чисел.
n-разрядный обратный код позволяет представить числа от − 2n − 1 + 1 до + 2n − 1 − 1.
Дополнительный код — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение), либо вычитанием числа из нуля.
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1.
Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2N для N-битного дополнения до 2).
Представление числа в дополнительном коде
При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно 27 − 1, что равно 127.
Преобразование дополнительного кода
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
· Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
· Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Дополнительный код для десятичных чисел
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
Преимущества и недостатки
Преимущества
· Один и тот же регистр может хранить как n-битовое положительное число, так и (n−1)-битовое число со знаком, с общими для обоих форматов операциями сложения, вычитания и левого сдвига.
· Более удобная упаковка чисел в битовые поля.
· Отсутствие числа «минус ноль».
Недостатки
· Дополнительный код неочевиден для новичков.
· В сложных форматах (таких, как плавающая запятая или двоично-десятичный код) большинство преимуществ аннулируются.
Дополнительный код (представление числа) — это… Что такое Дополнительный код (представление числа)?
Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение), либо вычитанием числа из нуля.
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]
Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2N для N-битного дополнения до 2).
Представление отрицательного числа в дополнительном коде
При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно , что равно 127.
Примеры:
| Десятичное представление |
Код двоичного представления (8 бит) | ||
|---|---|---|---|
| прямой | обратный | дополнительный | |
| 127 | 01111111 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | — |
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| -4 | 10000100 | 11111011 | 11111100 |
| -5 | 10000101 | 11111010 | 11111011 |
| -6 | 10000110 | 11111001 | 11111010 |
| -7 | 10000111 | 11111000 | 11111001 |
| -8 | 10001000 | 11110111 | 11111000 |
| -9 | 10001001 | 11110110 | 11110111 |
| -10 | 10001010 | 11110101 | 11110110 |
| -11 | 10001011 | 11110100 | 11110101 |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | — | — | 10000000 |
Дополнительный код для десятичных чисел
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):
| 10-ричная система счисления («обычная» запись) |
10-ричная система счисления, дополнительный код |
|---|---|
| … | … |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| … | … |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| … | … |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
| … | … |
Преобразование в дополнительный код
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
- Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
- Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:
101
Инвертируем все разряды числа, получая таким образом обратный код:
010
Добавим к результату 1
011
Допишем слева знаковый единичный разряд
1011
Для обратного преобразования используется тот же алгоритм. А именно:
1011
Инвертируем все разряды числа, получая таким образом обратный код:
0100
Добавим к результату 1 и проверим, сложив с дополнительным кодом
0101 + 1011 = 10000, пятый разряд выбрасывается.
p-адические числа
В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ричная система счисления, то число, противоположное 1000… (1) равно 4444…. (−1).
Реализация алгоритма преобразования в обратный код (для 8-битных чисел)
Pascal
if a<0 then a:=((not a) or 128) + 1;
C/C++
if (a < 0) a = ( (~(-a))|128 ) + 1;
Преимущества и недостатки
Преимущества
- Один и тот же регистр может хранить как n-битовое положительное число, так и (n−1)-битовое число со знаком, с общими для обоих форматов операциями сложения, вычитания и левого сдвига.
- Более удобная упаковка чисел в битовые поля.
- Отсутствие числа «минус ноль».
Недостатки
- Дополнительный код неочевиден для новичков.
- В сложных форматах (таких, как плавающая запятая или двоично-десятичный код) большинство преимуществ аннулируются.
- Модуль наибольшего числа не равен модулю наименьшего числа. Пример: знаковое целое 8-битовое. Максимальное число: 12710 == 7F16 == 011111112. Минимальное число: -12810 == 8016,дополнительный код == 100000002,дополнительный код. Соответственно, не для любого числа существует противоположное. Операция изменения знака может потребовать дополнительной проверки.
- Сравнение. В отличие от сложения, числа в дополнительном коде нельзя сравнивать, как беззнаковые, или вычитать без расширения разрядности. Один из методов состоит в сравнении как беззнаковые исходных чисел с инвертированным знаковым битом.
Пример программного преобразования
Если происходит чтение данных из файла или области памяти, где они хранятся в двоичном дополнительном коде (например, файл WAVE), может оказаться необходимым преобразовать байты. Если данные хранятся в 8 битах, необходимо, чтобы значения 128-255 были отрицательными. b2) — c; //Результат остаётся 121, потому что знаковый разряд — нуль.
См. также
Литература
- Behrooz Parhami 2.3. Complement Representation, 2.4. Two’s- and 1’s-complement numbers // Computer Arithmetic: Algorithms and Hardware Designs. — New York: Oxford University Press, 2000. — P. 22-27. — 510 p. — ISBN 0-19-512583-5
- Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. — К.: Вища школа, 1987. — 375 с.
Ссылки
- ↑ К.Г.Жуков «Справочное руководство пользователя Fixed-Point Blockset» 1.2. Понятие прямого, обратного и дополнительного кодов, Определение 3. Архивировано из первоисточника 23 июня 2012.
Преобразование чисел в различные системы счисления
Система чисел является систематическим способом представления чисел символьными символами и использует базовое значение для удобной группировки чисел в сжатой форме. Самая распространенная система числов — десятичная, которая имеет базовое значение 10, и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Однако существуют и другие числовые системы, которые могут быть более эффективными для определенной цели. Например, так как на компьютерах используется логическое значение для вычислений и операций, для выполнения вычислений и операций используется двоичная числовая система, которая имеет базовое значение 2.
Microsoft Office Excel есть несколько функций, которые можно использовать для преобразования чисел в числовые системы и из них:
|
Система номеров |
Базовое значение |
Набор символьных знаков |
|
Двоичный |
2 |
0,1 |
|
Восьмеричном |
8 |
0, 1, 2, 3, 4, 5, 6, 7 |
|
Действительное. |
10 |
0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 |
|
Шестнадцатеричный |
16 |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Преобразование двоичного числа в десятичное
Для этого используйте функцию ДВ.В.Е.
|
Преобразование двоичного числа в hexadecimal
Для этого используйте функцию ДВ.В.EX.
|
Преобразование двоичного числа в восьмую
Для этого используйте функцию ДВ.В.ВЕХ.
|
Преобразует десятичное число в двоичное.
Для этого используйте функцию DEC2BIN.
|
Преобразование десятичных числовом восьмерикое
Для этого используйте функцию DEC2HEX.
|
Преобразование десятичных числовых в восьмеричных
Для этого используйте функцию DEC2OCT.
|
Преобразование hexadecimal number в двоичное
Для этого используйте функцию HEX2BIN.
|
Преобразование hexadecimal number в десятичной
Для этого используйте функцию HEX2DEC.
|
Преобразование hexadecimal number в восьмую
Для этого используйте функцию HEX2OCT.
|
Преобразование восьмого числа в двоичное
Для этого используйте функцию ВОСЬМ.В.ДВ.
|
Преобразование восьмериального числа в десятичной
Для этого используйте функцию ВОСЬМ.В.Е.
|
Преобразование восьмого числа в hexadecimal
Для этого используйте функцию ВОСЬМ.В.EX.
|
двоичный код | 8-битные числа
Переключить навигацию Бинарный код- Дом
- 8 бит
- 16 бит
| Двоичный | Десятичное |
|---|---|
| 00000001 | 1 |
| 00000010 | 2 |
| 00000011 | 3 |
| 00000100 | 4 |
| 00000101 | 5 |
| 00000110 | 6 |
| 00000111 | 7 |
| 00001000 | 8 |
| 00001001 | 9 |
| 00001010 | 10 |
| 00001011 | 11 |
| 00001100 | 12 |
| 00001101 | 13 |
| 00001110 | 14 |
| 00001111 | 15 |
| 00010000 | 16 |
| 00010001 | 17 |
| 00010010 | 18 |
| 00010011 | 19 |
| 00010100 | 20 |
| 00010101 | 21 |
| 00010110 | 22 |
| 00010111 | 23 |
| 00011000 | 24 |
| 00011001 | 25 |
| 00011010 | 26 |
| 00011011 | 27 |
| 00011100 | 28 |
| 00011101 | 29 |
| 00011110 | 30 |
| 00011111 | 31 |
| 00100000 | 32 |
| 00100001 | 33 |
| 00100010 | 34 |
| 00100011 | 35 |
| 00100100 | 36 |
| 00100101 | 37 |
| 00100110 | 38 |
| 00100111 | 39 |
| 00101000 | 40 |
| 00101001 | 41 |
| 00101010 | 42 |
| 00101011 | 43 |
| 00101100 | 44 |
| 00101101 | 45 |
| 00101110 | 46 |
| 00101111 | 47 |
| 00110000 | 48 |
| 00110001 | 49 |
| 00110010 | 50 |
- 1
- 2
- 3
- 4
- 5
- 6
- »
Система Base-2 и 8-битный байт
Причина, по которой компьютеры используют систему base-2, заключается в том, что она значительно упрощает их реализацию с помощью современных электронных технологий.Вы можете подключить и построить компьютеры, которые работают по системе base-10, но сейчас они будут чертовски дорогими. С другой стороны, компьютеры base-2 относительно дешевы.
Итак, компьютеры используют двоичные числа и, следовательно, используют двоичных цифр вместо десятичных цифр. Слово бит является сокращением слов «Двоичная цифраIT». В то время как десятичные цифры имеют 10 возможных значений в диапазоне от 0 до 9, биты имеют только два возможных значения: 0 и 1. Следовательно, двоичное число состоит только из 0 и 1, например: 1011.0) = 8 + 0 + 2 + 1 = 11
Вы можете видеть, что в двоичных числах каждый бит содержит значение возрастающей степени 2. Это значительно упрощает подсчет в двоичном формате. Начиная с нуля и до 20, счет в десятичном и двоичном формате выглядит следующим образом:
0 = 0 1 = 1 2 = 10 3 = 11 4 = 100 5 = 101 6 = 110 7 = 111 8 = 1000 9 = 1001 10 = 1010 11 = 1011 12 = 1100 13 = 1101 14 = 1110 15 = 1111 16 = 10000 17 = 10001 18 = 10010 19 = 10011 20 = 10100
Если посмотреть на эту последовательность, 0 и 1 одинаковы для десятичной и двоичной систем счисления.Под цифрой 2 вы видите, что перенос происходит первым в двоичной системе. Если бит равен 1, и вы добавляете к нему 1, бит становится 0, а следующий бит становится 1. При переходе от 15 к 16 этот эффект проходит через 4 бита, превращая 1111 в 10000.
Биты редко встречаются. один в компьютерах. Они почти всегда объединяются в 8-битные коллекции, и эти коллекции называются байтами . Почему в байте 8 бит? Аналогичный вопрос: «Почему в дюжине 12 яиц?» 8-битный байт — это то, к чему люди пришли путем проб и ошибок в течение последних 50 лет.
С 8 битами в байте вы можете представить 256 значений в диапазоне от 0 до 255, как показано здесь:
0 = 00000000 1 = 00000001 2 = 00000010 ... 254 = 11111110 255 = 11111111
В статье Как работают компакт-диски вы узнаете, что на компакт-диске используется 2 байта или 16 бит на выборку. Это дает каждому образцу диапазон от 0 до 65 535, например:
0 = 0000000000000000
1 = 0000000000000001
2 = 0000000000000010
...
65534 = 1111111111111110
65535 = 1111111111111111 Далее мы рассмотрим один из способов использования байтов.
Двоичное слово — обзор
III Коды постоянного веса
A код постоянного веса (CW) с параметрами n , d , w представляет собой набор C двоичных слов длиной n , все имеют вес w , так что расстояние между любыми двумя кодовыми словами составляет по меньшей мере d . Все нетривиальные ( n , d , w ) коды CW имеют d ≤ 2 w . Пусть A ( n , d , w ) будет наибольшим количеством кодовых слов в любом коде CW с этими параметрами.Тогда классическая проблема состоит в том, чтобы определить это число или найти наилучшие верхние и нижние границы для A ( n , d , w ).
Двоичные коды CW нашли применение в задачах синхронизации, в таких областях, как системы связи с множественным доступом с оптическим разделением каналов (CDMA), связь с расширенным спектром со скачкообразной перестройкой частоты, модельное радио, проектирование сигналов радаров и гидролокаторов, а также построение последовательностей протоколов. для многопользовательского канала коллизий без обратной связи.Коды с постоянным весом по сравнению с другими алфавитами привлекли некоторое внимание, но пока что было немного приложений. Мы будем обсуждать только двоичные коды CW.
Коды с постоянным весом были тщательно изучены, и хорошей ссылкой является MacWilliams and Sloane (1977). Эрик Рейнс и Нил Слоан ведут таблицу наиболее известных нижних границ для A ( n , d , w ) на веб-сайте: http://www.research.att.com/njas/ коды / Andw /. Мы представим обзор этой темы с акцентом на связи с дизайном.
Поскольку сумма любых двух двоичных слов с одинаковым весом всегда имеет четный вес, мы имеем A ( n , 2δ — 1, w ) = A ( n , 2δ, w ). С этого момента мы будем считать, что расстояние d четное. У нас также есть A ( n , d , w ) = A ( n , d , n — w ), так как если два слова находятся на расстоянии d отдельно, так же их дополнения.Это означает, что нужно рассматривать только случай w ≤ n /2.
Связь между кодами CW и дизайном очевидна. С точки зрения наборов, код CW — это просто набор из w подмножеств из набора n , где пересечение любых двух подмножеств w содержит не более t = w − d2 элементов. Эквивалентно, CW-код — это частичная система Штейнера Sw − d2 + 1, w, n. Тогда мы имеем
A (n, d, w) ≤n (n − 1)… (n − w + d / 2) w (w − 1)… (d / 2)
с равенством тогда и только тогда, когда система Штейнера S (w − d2 + 1, w, n) существует.
Интерес к кодам CW также связан с проблемой поиска линейных (или нелинейных) кодов ( n , M , d ) максимального размера M . Очевидно, что A ( n , d , w ) — это верхняя граница количества слов с заданным весом в таком максимальном коде. И наоборот, такие коды (или их смежные классы) могут давать нижние границы для A ( n , d , w ). В частности, более сильная версия границы Хэмминга (приведенная в разделе о совершенных кодах) была первоначально доказана с использованием A ( n , 2 t + 2,2 t + 1).
A ( n , 2 t + 2,2 t + 1) — это просто количество блоков в максимальном частичном S ( t + 1,2 t + 1 , n ) конструкция или упаковка. Если C — это код с исправлением ошибок t , то для любого c ∈ C количество блоков в соседней упаковке ∣ NS ( c ) ∣ ≤ A ( n , 2 т + 2,2 т + 1).Количество слов, которые находятся на расстоянии t + 1 от c , но не на расстоянии t от любого другого кодового слова, равно
(nt + 1) — (2t + 1t + 1) | NS (c) | ≥ ( nt + 1) — (2t + 1t + 1) A (2t + 2,2t + 1).
Каждое такое слово находится на расстоянии t + 1 от не более ⌊ n / t + 1⌋ других кодовых слов. Таким образом, суммируя по всем c ∈ C , каждое такое слово считается не более этого числа раз. Это дает более сильную версию границы Хэмминга:
| C | ((∑i = 0t (ni)) + (nt + 1) — (2t + 1t + 1) A (n, 2t + 2,2t + 1 ) ⌊N / (t + 1) ⌋) ≤2n.
Коды с постоянным весом не могут быть линейными, поскольку это означало бы, что нулевой вектор был в коде, но можно иметь код, в котором все ненулевые слова имеют одинаковый вес. Эти коды иногда называют линейными эквидистантными кодами . Двойник кода Хэмминга (также называемый симплексным кодом ) является примером такого кода. Фактически было доказано, что единственные такие коды формируются путем взятия нескольких копий симплексного кода. Доказательства того, что все такие коды являются обобщенными симплексными кодами, явно вытекают из теории кодирования (Bonisoli, 1983), а также неявно из результатов по планам и системам множеств (Teirlinck, 1980).Существует тесная связь между линейными эквидистантными кодами и конечной геометрией. Слова симплексного кода соответствуют гиперплоскостям проективного пространства [более GF (2)] так же, как слова веса 3 в коде Хэмминга соответствуют строкам в этом проективном пространстве. [Информацию о связях между кодами и конечной геометрией см. В Black and Mullin (1976).]
Другой вариант кодов CW — это оптические ортогональные коды (OOC), которые были применены в оптических системах связи CDMA.Вкратце, ( n , w , t a , t b ) OOC является кодом CW, C , длиной n и массой w такой, что для любого c = ( c 0 , c 1 ,…, c n −1 ) ∈ C , и каждый y ∈ C , c ≠ y и каждый i ≢ 0 (mod n ),
(1) ∑j = 0n − 1cjcj + i≤ta,
и
(2) ∑j = 0n −1cjyj + i≤tc.
Уравнение (1) является свойством автокорреляции, а уравнение. (2) — свойство взаимной корреляции. Большинство исследований сосредоточено на случае, когда t a = t c = t , и в этом случае мы ссылаемся на ( n , w , t ) OOC. Опять же, можно изменить эти свойства в терминах (частичных) конструкций или упаковок. В этом случае OOC представляет собой набор из w подмножеств целых чисел (mod n ), так что для подмножеств c , b ∈ C ,
(3) c + i∩c + j≤tai ≠ j,
и
(4) c + i∩b + j≤tc.
Здесь c + i = { x + i (mod n ) ∣ x ∈ c }.
Код OOC эквивалентен циклическому расчету или упаковке. Код или упаковка называется циклической, если каждый циклический сдвиг кодового слова (или блока) является другим кодовым словом. Набор всех циклических сдвигов кодового слова называется орбитой . Представителя с этой орбиты часто называют базовым блоком. OOC ( n , w , t ) OOC представляет собой набор базовых блоков для циклической (частичной) конструкции или упаковки S ( t + 1, w , n ) (при условии т < ш ).И наоборот, при такой циклической частичной конструкции или упаковке S ( t + 1, w , n ) можно сформировать ( n , w , t ) OOC, взяв один репрезентативный блок или кодовое слово с каждой орбиты.
Десятичный преобразователь в двоичный
Из Двоичный, Десятичный, Шестнадцатеричный,
К Двоичный, Десятичный, Шестнадцатеричный,
= Конвертировать × Сброс Поменять местами Двоичное дополнение до 2 со знакомГруппировка цифр
Шаги вычисления от десятичного к двоичному
Разделите на 2 по основанию 2, чтобы получить цифры из остатка:
| Деление на 2 |
Частное | Остаток (цифры) |
Бит # |
|---|
Преобразование двоичного числа в десятичное ►
Как преобразовать десятичное число в двоичное
Шагов преобразования:
- Разделите число на 2.
- Получить целое частное для следующей итерации.
- Получите остаток от двоичной цифры.
- Повторяйте эти шаги, пока частное не станет равным 0.
Пример # 1
Преобразование 13 10 в двоичное:
| Деление на 2 |
Частное | остаток | Бит # |
|---|---|---|---|
| 13/2 | 6 | 1 | 0 |
| 6/2 | 3 | 0 | 1 |
| 3/2 | 1 | 1 | 2 |
| 1/2 | 0 | 1 | 3 |
Итак 13 10 = 1101 2
Пример # 2
Преобразовать 174 10 в двоичное:
| Деление на 2 |
Частное | остаток | Бит # |
|---|---|---|---|
| 174/2 | 87 | 0 | 0 |
| 87/2 | 43 | 1 | 1 |
| 43/2 | 21 | 1 | 2 |
| 21/2 | 10 | 1 | 3 |
| 10/2 | 5 | 0 | 4 |
| 5/2 | 2 | 1 | 5 |
| 2/2 | 1 | 0 | 6 |
| 1/2 | 0 | 1 | 7 |
Итак 174 10 = 10101110 2
Таблица преобразования десятичных чисел в двоичные
| Десятичное число Число |
Двоичный Число |
Hex Число |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
| 17 | 10001 | 11 |
| 18 | 10010 | 12 |
| 19 | 10011 | 13 |
| 20 | 10100 | 14 |
| 21 | 10101 | 15 |
| 22 | 10110 | 16 |
| 23 | 10111 | 17 |
| 24 | 11000 | 18 |
| 25 | 11001 | 19 |
| 26 | 11010 | 1A |
| 27 | 11011 | 1Б |
| 28 | 11100 | 1С |
| 29 | 11101 | 1D |
| 30 | 11110 | 1E |
| 31 | 11111 | 1 этаж |
| 32 | 100000 | 20 |
| 64 | 1000000 | 40 |
| 128 | 10000000 | 80 |
| 256 | 100000000 | 100 |
См. Также
Напишите, как улучшить эту страницу
ПРЕОБРАЗОВАНИЕ НОМЕРА
БЫСТРЫЕ СТОЛЫ
Этот веб-сайт использует файлы cookie для улучшения вашего опыта, анализа трафика и отображения рекламы.Учить больше8-битное двоичное число | Поиск контактной информации
Результаты листинга 8-битное двоичное число
Введение в SMS PDU и текстовый формат
1 час назад Gsmfavorites.com Просмотреть все
Режим PDU предлагает отправить двоичную информацию в 7 бит или 8-битный формат . Это полезно, если вам нужно отправить сжатые данные, двоичных данных или вы хотите создать свою собственную кодировку символов в потоке двоичных битов .(91 означает международный формат телефонного номера ) 72 38 01 00 10 F5. Сервисный центр номер (в десятичных полуоктетах
Веб-сайт: https://www.gsmfavorites.com/documents/sms/pdutext/
Категория : Телефон, базы данных Показать еще
Созданная схема представляет собой 8-битный сумматор 8-битный…
Just Now Cs.uic.edu Просмотреть все
Созданная схема представляет собой сумматор 8 — бит .Сумматор 8 — бит добавляет два 8 — бит двоичных входов, и результат выдается на выходе. Чтобы создать сумматор Full 8 – бит , я мог бы использовать восемь сумматоров Full 1– бит и подключить их. Таким образом, младший бит справа будет произведен путем добавления первых двух битов, затем он будет выполнен (если
Веб-сайт: https://www.cs.uic.edu/~i266 /hwk6/37.pdf
Категория : Номер телефона Подробнее
Система Base2 и 8-битный байт HowStuffWorks
5 часов назад Компьютер.howstuffworks.com Просмотреть все
Таким образом, компьютеры используют двоичных чисел и, следовательно, используют двоичных цифр вместо десятичных цифр. Слово бит является сокращением слов « двоичных цифр». В то время как десятичные цифры имеют 10 возможных значений от 0 до 9, биты имеют только два возможных значения: 0 и 1. Таким образом, двоичное число состоит только из нулей и единиц, например: 1011.
Веб-сайт: https: // компьютер.howstuffworks.com/bytes1.htm
Категория : Компьютер Показать еще
Умножение двух 8-битных двоичных чисел YouTube
3 часа назад Youtube.com Просмотреть все
ALP и моделирование Умножение двух 8-битных двоичных чисел в MIDE-51 или Keil-51 Следите за нами и ставьте лайки на нашей странице FB WikiNotehttps: //www.facebook.com/the
Автор: WikiNote
Просмотры: 1.4K
Веб-сайт: https://www.youtube.com/watch?v=snTM10iBDy8
Категория : Номер телефона Показать еще
Конвертер из десятичного в двоичный Двоичный шестнадцатеричный преобразователь
2 часа назад Binaryhexconverter.com Просмотреть все
Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел . Считывание двоичного числа проще, чем кажется: это позиционная система; следовательно, каждая цифра в двоичном числе возводится в степень двойки, начиная с крайнего правого числа с 2 0.В двоичной системе каждая двоичная цифра относится к 1 битам . От десятичного до двоичного
Веб-сайт: https://www.binaryhexconverter.com/decimal-to-binary-converter
Категория : Номер телефона Показать еще
Двоичный калькулятор 40 9373 903 назад Calculator.net Просмотреть все
При работе с двоичным кодом поначалу может показаться запутанным, понимание того, что каждое двоичное значение представляет собой 2 n, так же, как каждое десятичное место представляет 10 n, должно помочь уточнить.Возьмем, к примеру, номер 8 . В десятичной системе , число , 8 располагается в первом десятичном разряде слева от десятичной точки, что означает место 10 0. По сути это означает:
Веб-сайт: https://www.calculator.net/binary-calculator.html
Категория : Номер телефона Показать больше
Преобразование десятичных чисел в 8-битные двоичные YouTube
3 часа назад Youtube.com Просмотреть все
Это видео демонстрирует математические вычисления, необходимые для преобразования десятичного (с основанием 10) числа в беззнаковое 8 — -битное двоичное число .
Веб-сайт: https://www.youtube.com/watch?v=fMo6Tz5wY_E
Категория : Номер телефона Показать еще
Двоичный номер обзор Темы ScienceDirect
2 часа назад Sciens com Просмотреть все
Ячейка памяти 8 — бит может иметь номер от 0 до 255. Иногда полезно представить отрицательные числа в C. используется для знака.0 положительный, а 1 отрицательный. Остальные двоичных позиций находятся в так называемом формате с дополнением до 2.
Веб-сайт: https://www.sciencedirect.com/topics/engineering/binary-number
Категория : Сотовый телефон Показать еще
8Bit Binary Converter Princeton University
6 часов назад Cs .princeton.edu Просмотреть все
8 — Bit Binary Converter Mon Sep 24 08:15:43 EDT 2018 Эта простая программа Javascript показывает 8 — бит значений в десятичном, шестнадцатеричном формате, двоичном , и ASCII.Вы можете ввести значение в любом из окон номер , и когда вы нажмете возврат / ввод, оно будет отображаться во всех окнах. Вы также можете увеличивать и уменьшать отображаемое значение.
Веб-сайт: https://www.cs.princeton.edu/courses/archive/fall18/cos109/bc.html
Категория : Номер телефона Показать еще
8-битные вычисления Википедия
5 часов назад En.wikipedia.org Просмотреть всеПодробности.8-битный регистр может хранить 2 8 различных значений. Диапазон целочисленных значений, которые могут быть сохранены в 8 битах, зависит от используемого целочисленного представления. В двух наиболее распространенных представлениях диапазон от 0 до 255 (2 8 — 1) для представления в виде двоичного числа и от −128 (−1 × 2 7) до 127 (2 7 — 1) для представления. как дополнение до двух.
Веб-сайт: https://en.wikipedia.org/wiki/8-bit_computing
Категория : Номер телефона Показать еще
Номер Системная инженерия Информационные технологии
8 часов назад Пользователь.15 = -32768 (для 2-байтового 16- -битного числа ) и т. Д. -125 = -128 + 3 10000011 Пример. Найдите двоичное представление десятичного числа 1341.
Веб-сайт: https://user.eng.umd.edu/~nsw/chbe250/number.htm
Категория : Техническая поддержка Показать еще
Примеры сложения двоичного числа EightBit
8 часов назад Sandbox.mc.edu Просмотреть все
Вот несколько примеров сложения двоичного кода , выполненного для восьми- битов беззнаковых чисел .Здесь нет никакого глубокого трюка — просто заполните каждое число до восьми бит и заставьте сумму также уместиться. Если он не подходит, это считается «переполнением» и будет сопровождаться одним битом …
Веб-сайт: http://sandbox.mc.edu/~bennet/cs110/pm/add8. html
Категория : Номер телефона Показать еще
Таблица двоичных чисел / список чисел от 0 до 100…
8 часов назад Преобразовать двоичный.com Просмотреть все
🎓 Что означает двоичных чисел ? В математике и цифровой электронике двоичное число — это число , выраженное в системе счисления с основанием 2 или двоичной системе счисления , в которой используются только два символа: обычно «0» (ноль) и «1» (один ). Система счисления с основанием 2 — это позиционная система счисления с основанием 2. Каждая цифра обозначается как бит .
Веб-сайт: https: //www.convertbinary.com / numbers /
Категория : Электроника Показать еще
Как преобразовать 8 в двоичное десятичное
Just Now Decimal.info Просмотреть все
8 /2 = 4 с 0 остатком 4 / 2 = 2 с остатком 0 2/2 = 1 с остатком 0 1/2 = 0 с остатком 1 Затем, когда мы сложим остатки в обратном порядке, мы получим ответ. Десятичное число 8 преобразовано в двоичное , таким образом: 1000 Итак, что мы сделали на странице, было преобразовать A 10 в B 2, где A — это десятичное число 8 , а B — это
Веб-сайт: https: // десятичный.info / Decimal-to-Binary / how-to-convert-8-to-binary.html
Категория : Номер телефона Показать еще
Двоичные числа Формулы преобразования и…
5 часов назад Helpwithpcs. com Просмотреть все
Вот пример двоичного числа : 10011100 Как вы можете видеть, это просто набор нулей и единиц, всего 8 цифр, которые делают это 8-битным двоичным числом . Бит — это сокращение от B inary Dig it, и каждая цифра классифицируется как бит . бит в крайнем правом углу, в данном случае 0, известен как младший значащий бит (LSB).
Веб-сайт: https://www.helpwithpcs.com/hardware/binary-numbers.php
Категория : Номер телефона Показать больше
Игра с двоичными числами Cisco [Binary Blitz]. Penjee’s
5 часов назад Games.penjee.com Просмотреть все
Игра Cisco с двоичным числом была возвращена с нашей адаптацией.Узнайте, как преобразовать в двоичную форму в десятичную и наоборот с помощью этого быстро развивающегося «Легко выучить, трудно…
Веб-сайт: https://games.penjee.com/binary-numbers-game/
Категория : Телефонный номер Показать еще
8-битный преобразователь двоичных чисел Изображения
9 часов назад Imageslink.org Просмотреть все
Двоичный изображений — RIT ›Самые популярные изображения Новые изображения на www.rit.edu . Размещено: (3 дня назад) Цветные изображения: 24- бит RGB u Цветные изображения также необходимо кодировать u Глубина бит в цветном изображении определяет число цветов, которые могут быть назначены данному пикселю.u Одним из распространенных форматов является изображение 24– бит RGB с тремя плоскостями 8, – бит, ; Красный, зеленый и синий; 16,7 млн цветов =…
Веб-сайт: https://www.imageslink.org/image/8-bit-binary-number-converter-images
Категория : Номер телефона Показать еще
Полубайт — это группа из 8 бит истинно или ложно
6 часов назад Holisticworldherald.com Просмотреть все
На процессорах x86 / x64 байт равен 8 бит, и есть 256 возможных двоичных состояний в 8 биты от 0 до 255.2 ** 4 = 16 (2 в степени числа битов). При работе с группами битов полезно определить, какой бит группы имеет наименьшее значение, а какой бит имеет наибольшее или наибольшее значение.
Веб-сайт: https://holisticworldherald.com/f0uun/cecbad-nibble-is-a-group-of-8-bits-true-or-false
Категория : Номер телефона Подробнее
Глава 2: Основные концепции
9 часов назад Пользователи.ece.utexas.edu Просмотреть все
Этот метод работает, потому что в 8 — -битный двоичный код , прибавление 256 к числу не изменяет значение. Например, 256-100 имеет такое же значение 8 — битов в двоичном формате , что и –100. Контрольный пункт 2.16: Дайте представление -54 в 8 — бит, двоичный, и шестнадцатеричный. Контрольный пункт 2.17. Почему вы не можете представить номер 150 с помощью 8 …
Веб-сайт: https: // users.ece.utexas.edu/~valvano/Volume1/E-Book/C2_FundamentalConcepts.htm
Категория : Номер телефона Показать еще
Представление номеров Swarthmore College
9 часов назад Просмотреть все Swarthmore.edu
Нижний индекс 2 обозначает двоичное число . Каждая цифра в двоичном числе называется битом . Число 1010110 представлено 7 битами. Любое число может быть разбито таким образом, найдя все степени двойки, которые в сумме дают число , о котором идет речь (в данном случае 2 6, 2 4, 2 2 и 2 1).Вы можете видеть, что это в точности аналогично десятичной деконструкции числа числа 125, которая была сделана ранее.
Веб-сайт: https://www.swarthmore.edu/NatSci/echeeve1/Ref/BinaryMath/NumSys.html
Категория : Номер телефона Показать еще
Узнайте, как написать свое имя Двоичный код
3 часа назад Sciencefriday.com Просмотреть все
Просмотрите ключ ниже и попробуйте написать что-нибудь, используя двоичный код UTF- 8.Попробуйте свое имя! Найдите 8 — бит двоичную кодовую последовательность для каждой буквы вашего имени, записывая ее с небольшим промежутком между каждым набором из 8 бит. Например, если ваше имя начинается с буквы A, ваша первая буква будет 01000001.
Веб-сайт: https://www.sciencefriday.com/educational-resources/write-your-name-in-binary-code /
Категория : Номер телефона Показать еще
Двоичные чехлы для телефонов iPhone и Android TeePublic
3 часа назад Teepublic.com Просмотреть все
Есть те, кто понимает Binary , и те, кто не понимает Phone Case. пользователя ArtisticNinja. 25 долларов. Основной тег. Бинарный телефон Чехол. Описание. Есть мир, в котором все состоит из 0 и 1. Это ботаническое дерево для всех программистов и разработчиков. Теги: программа, код, разработчик, программист, 0.
Сайт: https://www.teepublic.com/phone-case/binary
Категория : Телефон Показать еще
Двоичный Список номеров
6 часов назад Numbergenerator.org Просмотреть все
Случайный Номер телефона Generator; Множественные наборы и комбинации; Список случайных комбинаций 3 битовых двоичных чисел список 4 битовых двоичных чисел список 5 битовых двоичных чисел список 6 битовых двоичных чисел список 7 битовых двоичных чисел список 8 битовых двоичных чисел список 9 битовых двоичных чисел Список 10 двоичных чисел Список 11 двоичных чисел Список 12 двоичных чисел
Веб-сайт: https: // numbergenerator.org / binarynumberslists
Категория : Номер телефона Показать еще
Управление выходными контактами с использованием 8-битного числа Синтаксис и…
1 час назад Forum.arduino.cc Просмотреть все
Я хотел бы знать, как управлять восемью выходными контактами, используя двоичное число 8 — бит (т. е. 00001100 включит выходы 2 и 3). На самом деле было бы даже лучше, если бы я мог управлять ими с помощью десятичного числа (0-255) — в зависимости от состояния потенциометра.Но они должны вывести двоичное значение : мой проект включает считывание аналогового датчика (в конечном итоге это будут последовательные данные, поступающие
Веб-сайт: https://forum.arduino.cc/t/control-output-pins- using-8-bit-number / 46017
Категория : Базы данных Показать еще
Преобразователь десятичных чисел в двоичные RapidTables.com
5 часов назад Rapidtables.com Просмотреть все
Bit # Binary в десятичное преобразование Как преобразовать десятичное в двоичное Шаги преобразования: разделите число на 2.Получите целое частное для следующей итерации. Получите остаток от двоичной цифры . Повторяйте шаги до тех пор, пока частное не станет равным 0. Пример №1. Преобразование 13 10 в двоичное значение :
Веб-сайт: https://www.rapidtables.com/convert/number/decimal-to-binary.html
Категория : Номер телефона Показать еще
Кодирование Хранить 2 4-битных числа в 1 8-битном числе…
4 часа назад Stackoverflow.com Просмотреть все
Я впервые задумываюсь о двоичных числах . Мне интересно, есть ли способ закодировать 2 4- битных чисел (т.е. шестнадцатеричные числа ) в 1 8 — битное число . Итак, если бы у меня были и 5 в качестве шестнадцатеричного числа , это были бы 10 и 5. Может быть, есть способ сохранить это в 1 8-битном номере таким образом, чтобы вы могли получить его из 8 — бит номер обратно в его
Веб-сайт: https: // stackoverflow.com / questions / 51219155 / store-2-4-bit-numbers-in-1-8-bit-number
Категория : Номер телефона Показать еще
Как преобразовать десятичные значения 125 и 128 в 8…
7 часов назад Quora.com Просмотреть все
Ответ (1 из 3): Двоичный работает с разрядами, как и с десятичными, за исключением того, что значение разряда 1 равно 1, а следующая цифра — 2 вместо 10, 4 вместо 100, 8 вместо 1000 и т. Д.Полномочия двух. Но проблема указана не полностью, так как не указано, что двоичный представляет
Веб-сайт: https://www.quora.com/How-do-I-convert-the-decimal-values-125- и -128-в-8-битный двоичный
Категория : Номер телефона Показать еще
Номер в 8-битные двоичные изображения
5 часов назад Imageslink.org Просмотреть все
Размещено: (3 дня назад) 13 февраля 2021 г. 83; 8-битное двоичное число может представлять собой максимум десятичное 255 = двоичное 11111111.Вычисляется следующим образом: 1 * 128 + 1 * 64 + 1 * 32 + 1 * 16 + 1 * 8 + 1 * 4 + 1 * 2 + 1 + 1 = десятичное 255. Вот еще 8-битное двоичное число — 01101011. Чтобы преобразовать его в десятичную форму, запишем число в столбец чисел выше, как показано ниже:
Веб-сайт: https://www.imageslink.org/image/number-to-8-bit -binary
Категория : Номер телефона Показать еще
Двоичная система счисления (определение, от десятичного к двоичному)
5 часов назад Byjus.com Просмотреть все
Двоичная система чисел является одним из четырех типов системы чисел . В компьютерных приложениях, где двоичных чисел представлены только двумя символами или цифрами, то есть 0 (ноль) и 1 (один). Здесь двоичных чисел выражены в системе счисления с основанием 2. Например, (101) 2 — это двоичное число . Каждая цифра в этой системе называется бит .
Веб-сайт: https: // byjus.com / maths / binary-number-system /
Категория : Компьютер Подробнее
Разработка и объяснение 8-битного двоичного сумматора с использованием IC 7483.
1 час назад Ques10.com Просмотреть все
Дизайн и объяснение 8-битного двоичного сумматора с использованием IC 7483. IC 7483 представляет собой 4 -битный параллельный сумматор , который состоит из четырех соединенных между собой полных сумматоров вместе со схемой упреждающего переноса. Схема выводов IC 7483 показана выше. Это 16-контактная микросхема.Входами IC являются A, B и C в 0, а выходами — S и C выход 3.
Веб-сайт: https://www.ques10.com/p/6212/design-and-explain-8- bit-binary-adder-using-ic-7-1 /
Категория : Номер телефона Показать еще
ASCII Wikipedia
5 часов назад En.wikipedia.org Просмотреть все
ASCII (/ ˈ æ sk iː / ASS-kee): 6, сокращенно от American Standard Code for Information Interchange, является стандартом кодировки символов для электронной связи.Коды ASCII представляют текст в компьютерах, телекоммуникационном оборудовании и других устройствах. Большинство современных схем кодирования символов основаны на ASCII, хотя они поддерживают множество дополнительных символов.
Веб-сайт: https://en.wikipedia.org/wiki/Ascii
Категория : Номер поддержки, Электроника Показать еще
Преобразователь двоичного числа в десятичный Преобразователь двоичного числа в шестнадцатеричный
2 часа назад Двоичный преобразователь в шестнадцатеричный .com Просмотреть все
Чтобы преобразовать двоичное число в десятичное, могут помочь базовые знания о том, как читать двоичное число .Как упоминалось выше, в позиционной системе двоичного каждый бит ( двоичный цифр) является степенью 2. Это означает, что каждое двоичное число может быть представлено в виде степеней…
Веб-сайт: https : //www.binaryhexconverter.com/binary-to-decimal-converter
Категория : Номер телефона Показать еще
Тип фильтра: За все время (49 результатов) Последние 24 часа Прошлая неделя Прошлый месяц
Пожалуйста, оставьте здесь свои комментарии:
Tech Stuff — Hexadecimal, Decimal и Binary
Основной единицей, используемой в компьютерном мире, является байт (a.k.a октет), байт (или октет) имеет 8 бит (также известный как двоичные цифры). Большинство современных систем используют число, кратное байту, таким образом, 16-разрядная система состоит из 2 байтов (2 x 8 = 16), 32-разрядная система имеет 4 байта (4 x 8 = 32), а 64-разрядная система имеет 8 байтов (8 x 8 = 64). Термин слово , как и в описании 32-битного слова, в значительной степени исчез из технической лексики.
Содержимое любого байта, например, в ячейке памяти или в сети, может быть выражено во многих системах нумерации .Чаще всего используются системы счисления: , десятичное, , шестнадцатеричное, , шестнадцатеричное, и двоичное, , :
| Система нумерации | База | Диапазон | Банкноты |
| Десятичное | база 10 | 0 — 1,2,3 … | Самая распространенная система нумерации — доллары, метрика и т. Д. Байт (8 бит) имеет 256 возможных значений в диапазоне 0 — 255 |
| двоичный | база 2 | 0–1 | Базовый уровень, на котором работает электронная схема в компьютере — один бит. |
| Шестнадцатеричный | база 16 | 0-9, A-F | Каждый шестнадцатеричный символ представляет 4 бита (от 0 до 15 в десятичной системе), что называется полубайтом (маленький байт — честно!). Байт (или октет) составляет 8 бит, поэтому всегда представлен двумя шестнадцатеричными символами в диапазоне от 00 до FF. |
Историческая справка: Когда-то давно, когда мир и даже автор этой страницы были молоды, компьютеры были построены с использованием 12-битных, 24-битных и даже 36-битных слов (это имело определенный смысл тогда как раз сегодня выглядит странно).Каждый из этих размеров слова делится на 3 и использует восьмеричную систему нумерации (основание 8). Каждый 3-битный элемент содержит 8 значений в диапазоне от 0 до 7. Таким образом, ячейка памяти с 12-битным двоичным значением 000.001.100.111 будет записана в восьмеричном виде как 0147.
Нумерация бит
При работе с двоичным кодом каждый бит в байте (октете) может потребоваться идентифицировать с помощью метода, называемого нумерацией битов. Нумерация битов может сильно сбивать с толку, поскольку различные стандартные органы принимают разные соглашения.Следующие ниже действительные и используемые правила нумерации битов , соглашения для описания 8-битного байта (октета).
| Содержимое памяти | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Условные обозначения нумерации бит | ||||||||
| Основание слева направо 0 (IETF) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Основание слева направо 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Основание справа налево 1 (ITU) | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Мощность 2 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Всегда проверяйте, какое соглашение используется в любой спецификации.Мы смирились с неизбежным и используем стандарт Left to right base 0 (IETF) , поскольку благодаря Интернету он широко используется и, надеюсь, столь же широко понимается. Обоснование этого стандарта IETF состоит в том, что он также недвусмысленно представляет то, что называется сетевым порядком , то есть бит 0 сначала идет в сеть, бит 1 — секунду и так далее. Биты также имеют тенденцию выходить из сети в том же порядке, в котором они поступали. Использование сетевого порядка необходимо, поскольку внутреннее (машинное) представление данных может сильно различаться (вся эта чушь с прямым порядком байтов и прямым порядком байтов), но когда данные загружаются в сеть, они должны быть в согласованном порядке, который может использоваться любая система, независимо от ее внутреннего представления, которая хочет использовать данные.
Наконец, при работе с двоичным кодом вы часто будете сталкиваться с терминами наиболее значимый бит (s) (MSB) и наименее значимый бит (s) (LSB). MSB всегда находится слева, а LSB — справа. Таким образом, при использовании нумерации битов IETF MSB — это бит 0, а LSB — бит 7, тогда как при использовании битовой нумерации ITU MSB — это бит 8, а LSB — бит 1. Совершенно ясно, не так ли?
8-битный байт (октет) Таблица преобразования:
Преобразование десятичного числа IPv4 в шестнадцатеричное
| Десятичное | Шестнадцатеричный | двоичный | десятичный | Шестнадцатеричный | двоичный |
| 0 | 00 | 0000 0000 | 128 | 80 | 1000 0000 |
| 1 | 01 | 0000 0001 | 129 | 81 | 1000 0001 |
| 2 | 02 | 0000 0010 | 130 | 82 | 1000 0010 |
| 3 | 03 | 0000 0011 | 131 | 83 | 1000 0011 |
| 4 | 04 | 0000 0100 | 132 | 84 | 1000 0100 |
| 5 | 05 | 0000 0101 | 133 | 85 | 1000 0101 |
| 6 | 06 | 0000 0110 | 134 | 86 | 1000 0110 |
| 7 | 07 | 0000 0111 | 135 | 87 | 1000 0111 |
| 8 | 08 | 0000 1000 | 136 | 88 | 1000 1000 |
| 9 | 09 | 0000 1001 | 137 | 89 | 1000 1001 |
| 10 | 0A | 0000 1010 | 138 | 8A | 1000 1010 |
| 11 | 0Б | 0000 1011 | 139 | 8Б | 1000 1011 |
| 12 | 0C | 0000 1100 | 140 | 8C | 1000 1100 |
| 13 | 0D | 0000 1101 | 141 | 8D | 1000 1101 |
| 14 | 0E | 0000 1110 | 142 | 8E | 1000 1110 |
| 15 | 0F | 0000 1111 | 143 | 8F | 1000 1111 |
| 16 | 10 | 0001 0000 | 144 | 90 | 1001 0000 |
| 17 | 11 | 0001 0001 | 145 | 91 | 1001 0001 |
| 18 | 12 | 0001 0010 | 146 | 92 | 1001 0010 |
| 19 | 13 | 0001 0011 | 147 | 93 | 1001 0011 |
| 20 | 14 | 0001 0100 | 148 | 94 | 1001 0100 |
| 21 | 15 | 0001 0101 | 149 | 95 | 1001 0101 |
| 22 | 16 | 0001 0110 | 150 | 96 | 1001 0110 |
| 23 | 17 | 0001 0111 | 151 | 97 | 1001 0111 |
| 24 | 18 | 0001 1000 | 152 | 98 | 1001 1000 |
| 25 | 19 | 0001 1001 | 153 | 99 | 1001 1001 |
| 26 | 1A | 0001 1010 | 154 | 9A | 1001 1010 |
| 27 | 1Б | 0001 1011 | 155 | 9Б | 1001 1011 |
| 28 | 1С | 0001 1100 | 156 | 9C | 1001 1100 |
| 29 | 1D | 0001 1101 | 157 | 9D | 1001 1101 |
| 30 | 1E | 0001 1110 | 158 | 9E | 1001 1110 |
| 31 | 1 этаж | 0001 1111 | 159 | 9F | 1001 1111 |
| 32 | 20 | 0010 0000 | 160 | A0 | 1010 0000 |
| 33 | 21 | 0010 0001 | 161 | A1 | 1010 0001 |
| 34 | 22 | 0010 0010 | 162 | A2 | 1010 0010 |
| 35 | 23 | 0010 0011 | 163 | A3 | 1010 0011 |
| 36 | 24 | 0010 0100 | 164 | A4 | 1010 0100 |
| 37 | 25 | 0010 0101 | 165 | A5 | 1010 0101 |
| 38 | 26 | 0010 0110 | 166 | A6 | 1010 0110 |
| 39 | 27 | 0010 0111 | 167 | A7 | 1010 0111 |
| 40 | 28 | 0010 1000 | 168 | A8 | 1010 1000 |
| 41 | 29 | 0010 1001 | 169 | A9 | 1010 1001 |
| 42 | 2A | 0010 1010 | 170 | AA | 1010 1010 |
| 43 | 2Б | 0010 1011 | 171 | AB | 1010 1011 |
| 44 | 2C | 0010 1100 | 172 | AC | 1010 1100 |
| 45 | 2D | 0010 1101 | 173 | н.э. | 1010 1101 |
| 46 | 2E | 0010 1110 | 174 | AE | 1010 1110 |
| 47 | 2F | 0010 1111 | 175 | AF | 1010 1111 |
| 48 | 30 | 0011 0000 | 176 | B0 | 1011 0000 |
| 49 | 31 | 0011 0001 | 177 | B1 | 1011 0001 |
| 50 | 32 | 0011 0010 | 178 | B2 | 1011 0010 |
| 51 | 33 | 0011 0011 | 179 | B3 | 1011 0011 |
| 52 | 34 | 0011 0100 | 180 | B4 | 1011 0100 |
| 53 | 35 | 0011 0101 | 181 | B5 | 1011 0101 |
| 54 | 36 | 0011 0110 | 182 | B6 | 1011 0110 |
| 55 | 37 | 0011 0111 | 183 | B7 | 1011 0111 |
| 56 | 38 | 0011 1000 | 184 | B8 | 1011 1000 |
| 57 | 39 | 0011 1001 | 185 | B9 | 1011 1001 |
| 58 | 3A | 0011 1010 | 186 | BA | 1011 1010 |
| 59 | 3B | 0011 1011 | 187 | BB | 1011 1011 |
| 60 | 3C | 0011 1100 | 188 | г. до н.э. | 1011 1100 |
| 61 | 3D | 0011 1101 | 189 | BD | 1011 1101 |
| 62 | 3E | 0011 1110 | 190 | BE | 1011 1110 |
| 63 | 3F | 0011 1111 | 191 | BF | 1011 1111 |
| 64 | 40 | 0100 0000 | 192 | C0 | 1100 0000 |
| 65 | 41 | 0100 0001 | 193 | C1 | 1100 0001 |
| 66 | 42 | 0100 0010 | 194 | C2 | 1100 0010 |
| 67 | 43 | 0100 0011 | 195 | C3 | 1100 0011 |
| 68 | 44 | 0100 0100 | 196 | C4 | 1100 0100 |
| 69 | 45 | 0100 0101 | 197 | C5 | 1100 0101 |
| 70 | 46 | 0100 0110 | 198 | C6 | 1100 0110 |
| 71 | 47 | 1100 0111 | 199 | C7 | 1100 0111 |
| 72 | 48 | 0100 1000 | 200 | C8 | 1100 1000 |
| 73 | 49 | 0100 1001 | 201 | C9 | 1100 1001 |
| 74 | 4A | 0100 1010 | 202 | CA | 1100 1010 |
| 75 | 4B | 0100 1011 | 203 | CB | 1100 1011 |
| 76 | 4C | 0100 1100 | 204 | CC | 1100 1100 |
| 77 | 4D | 0100 1101 | 205 | CD | 1100 1101 |
| 78 | 4E | 0100 1110 | 206 | CE | 1100 1110 |
| 79 | 4F | 1100 1111 | 207 | CF | 1100 1111 |
| 80 | 50 | 0101 0000 | 208 | D0 | 1101 0000 |
| 81 | 51 | 0101 0001 | 209 | D1 | 1101 0001 |
| 82 | 52 | 0101 0010 | 210 | D2 | 1101 0010 |
| 83 | 53 | 0101 0011 | 211 | D3 | 1101 0011 |
| 84 | 54 | 0101 0100 | 212 | D4 | 1101 0100 |
| 85 | 55 | 0101 0101 | 213 | D5 | 1101 0101 |
| 86 | 56 | 0101 0110 | 214 | D6 | 1101 0110 |
| 87 | 57 | 1101 0111 | 9002 215D7 | 1101 0111 | |
| 88 | 58 | 0101 1000 | 216 | D8 | 1101 1000 |
| 89 | 59 | 0101 1001 | 217 | D9 | 1101 1001 |
| 90 | 5A | 0101 1010 | 9002 218DA | 1101 1010 | |
| 91 | 5Б | 0100 1011 | 219 | DB | 1101 1011 |
| 92 | 5C | 0101 1100 | 220 | DC | 1101 1100 |
| 93 | 5D | 0101 1101 | 221 | DD | 1101 1101 |
| 94 | 5E | 0101 1110 | 222 | DE | 1101 1110 |
| 95 | 5F | 1101 1111 | 223 | DF | 1101 1111 |
| 96 | 60 | 0110 0000 | 224 | E0 | 1110 0000 |
| 97 | 61 | 0110 0001 | 225 | E1 | 1110 0001 |
| 98 | 62 | 0110 0010 | 226 | E2 | 1110 0010 |
| 99 | 63 | 0110 0011 | 227 | E3 | 1110 0011 |
| 100 | 64 | 0110 0100 | 228 | E4 | 1110 0100 |
| 101 | 65 | 0110 0101 | 229 | E5 | 1110 0101 |
| 102 | 66 | 0110 0110 | 230 | E6 | 1110 0110 |
| 103 | 67 | 1110 0111 | 231 | E7 | 1110 0111 |
| 104 | 68 | 0110 1000 | 232 | E8 | 1110 1000 |
| 105 | 69 | 0110 1001 | 233 | E9 | 1110 1001 |
| 106 | 6A | 0110 1010 | 234 | EA | 1110 1010 |
| 107 | 6Б | 0110 1011 | 235 | EB | 1110 1011 |
| 108 | 6C | 0110 1100 | 236 | EC | 1110 1100 |
| 109 | 6D | 0110 1101 | 237 | ED | 1110 1101 |
| 110 | 6E | 0110 1110 | 238 | EE | 1110 1110 |
| 111 | 6F | 1110 1111 | 239 | EF | 1110 1111 |
| 112 | 70 | 0111 0000 | 240 | F0 | 1111 0000 |
| 113 | 71 | 0111 0001 | 241 | F1 | 1111 0001 |
| 114 | 72 | 0111 0010 | 242 | F2 | 1111 0010 |
| 115 | 73 | 0111 0011 | 243 | F3 | 1111 0011 |
| 116 | 74 | 0111 0100 | 244 | F4 | 1111 0100 |
| 117 | 75 | 0111 0101 | 245 | F5 | 1111 0101 |
| 118 | 76 | 0111 0110 | 246 | F6 | 1111 0110 |
| 119 | 77 | 1111 0111 | 247 | F7 | 1111 0111 |
| 120 | 78 | 0111 1000 | 248 | F8 | 1111 1000 |
| 121 | 79 | 0111 1001 | 249 | F9 | 1111 1001 |
| 122 | 7A | 0111 1010 | 250 | FA | 1111 1010 |
| 123 | 7B | 0111 1011 | 251 | FB | 1111 1011 |
| 124 | 7C | 0111 1100 | 252 | FC | 1111 1100 |
| 125 | 7D | 0111 1101 | 253 | FD | 1111 1101 |
| 126 | 7E | 0111 1110 | 254 | FE | 1111 1110 |
| 127 | 7F | 0111 1111 | 255 | FF | 1111 1111 |
Преобразование десятичного в шестнадцатеричный формат IPv4
Чтобы преобразовать десятичный IPv4-адрес с точками в шестнадцатеричный, возьмите каждое десятичное значение, разделенное точками, и преобразуйте его с помощью шестнадцатеричного калькулятора (стандартный калькулятор Windows в научном или программистском режиме выполнит эту работу).Это даст:
IP-адрес в десятичном формате с точками = 192.168.0.5 Десятичное 192 = Шестнадцатеричное = C0 Десятичный 168 = Шестнадцатеричный = A8 Десятичный 0 = Шестнадцатеричный = 00 Десятичный 5 = Шестнадцатеричный = 05 IP-адрес в шестнадцатеричном формате с точками = C0.A8.00.05
Проблемы, комментарии, предложения, исправления (включая битые ссылки) или что-то добавить? Найдите время в напряженной жизни, чтобы «написать нам» (вверху экрана), веб-мастеру (внизу) или получить информационную поддержку на zytrax. У вас будет теплое внутреннее сияние до конца дня.
8-битных двоичных примеров сложения
восьмибитных двоичных примеров сложенияПримеры восьмибитного двоичного сложения
Вот несколько примеров бинарного сложения, выполненного на восьмибитный беззнаковый числа. Здесь нет глубокого трюка — просто заполните каждый число до восьми бит, а также принудительно подогнать сумму. Если это так не подходит, это считается «переполнением» и будет сопровождаться одним битом, выполненным из 128-е место, «вынос». С беззнаковым числа, переполнение и перенос всегда происходят вместе, хотя это не верно для двух дополнений. • 1011 + 10010
= 11101:
Без переполнения.Сумма верная. | • 1010110 + 110100
= 10001010:
Без переполнения.Сумма верная. |
• 11001011 + 1011010
= 100100101:
Переполнение.Унос отбрасывается, и сумма неверна | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
• 1010001 + 11001
= 1101010:
Без переполнения .Сумма верная. | • 110001 + 11100100
= 100010101:
Перелив.Унос отбрасывается, и сумма неверна |
• 10011011 + 1001010
= 11100101:
Нет переполнения. |

