Ачх полосового фильтра: по виду их амплитудно-частотных характеристик — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Содержание

по виду их амплитудно-частотных характеристик

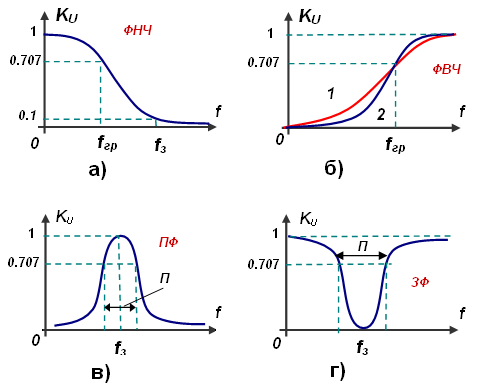
Рассмотрим основные типы фильтров, классифицируемых по виду амплитудно-частотных характеристик.

Фильтры нижних частот.

Для фильтров нижних частот (ФНЧ) характерно то, что входные сигналы низких частот, начиная с постоянных сигналов, передаются на выход, а сигналы высоких частот задерживаются.

Приведем примеры амплитудно-частотных характеристик фильтров нижних частот. На рис. 2.52, а показана характеристика идеального (не реализуемого на практике) фильтра (ее иногда называют характеристикой типа «кирпичная стена»). На других рисунках представлены характеристики реальных фильтров.

Полоса пропускания лежит в пределах от нулевой частоты до частоты среза ω_с. Обычно частоту среза определяют как частоту, на которой величина А(ω) равна 0,707 от максимального значения (т. е. меньше максимального значения на 3 дБ).

Васильев Дмитрий Петрович

Профессор электротехники СПбГПУ

Задать вопрос

Полоса задерживания (подавления) начинается от частоты задерживания ωз и продолжается до бесконечности. В ряде случаев частоту задерживания определяют как частоту, на которой величина А(ω) меньше максимального значения на 40 дБ (т. е. меньше в 100 раз).

Между полосами пропускания и задерживания у реальных фильтров расположена переходная полоса. У идеального фильтра переходная полоса отсутствует.

Фильтры верхних частот.

Фильтр верхних частот характерен тем, что он пропускает сигналы верхних и задерживает сигналы нижних частот.

Частотные характеристики фильтров верхних частот, как и характеристики фильтров нижних частот, многообразны в своих деталях.

Изобразим для иллюстрации две характеристики: идеальную, нереализуемую (рис. 2.53, а), и одну из типичных реальных (рис. 2.53, б). Через ω_си ω_з обозначены частоты среза и задерживания.

Полосовые фильтры (полосно-пропускающие).

Абрамян Евгений Павлович

Доцент кафедры электротехники СПбГПУ

Задать вопрос

Полосовой фильтр пропускает сигналы одной полосы частот, расположенной в некоторой внутренней части оси частот. Сигналы с частотами вне этой полосы фильтр задерживает.

Изобразим амплитудно-частотную характеристику для идеального (нереализуемого) фильтра (рис. 2.54, а) и одну из типичных реальных характеристик (рис. 2.54, б).

Через ω_с1 и ω_с2 обозначены две частоты среза, ω₀ — средняя частота. Она определяется выражением

ω₀ = √ (ω_с1 · ω_с2)

Режекторные фильтры (полосно-заграждающие).

Режекторные фильтры не пропускают (задерживают) сигналы, лежащие в некоторой полосе частот, и пропускают сигналы с другими частотами. Изобразим амплитудно-частотную характеристику для идеального (нереализуемого) фильтра (рис. 2.55, а) и одну из типичных реальных характеристик (рис. 2.55, б).

Всепропускающие фильтры (фазовые корректоры).

Эти фильтры пропускают сигналы любой частоты. Построим соответствующую амплитудно-частотную характеристику (рис. 2.56).

Такие фильтры используются в некоторой электронной системе для того, чтобы изменить с той или иной целью фазочастотную характеристику всей системы.

Исходя из приведенного математического описания фильтров, нетрудно сделать вывод, что ход амплитудно-частотной характеристики на достаточном удалении от полосы пропускания прямо определяется порядком фильтра.

Васильев Дмитрий Петрович

Профессор электротехники СПбГПУ

Задать вопрос

Этот факт хорошо иллюстрируют амплитудно-частотные характеристики, выполненные в логарифмическом масштабе. Рассмотрим указанные характеристики для некоторых фильтров различного порядка, имеющих одинаковые коэффициенты усиления на нулевой частоте, равные 100 (рис. 2.57).

Из математического описания следует, что на достаточном расстоянии от полосы пропускания наклон характеристики равен − 20n дБ/дек, где n — порядок фильтра. Наклон − 20 дБ/дек означает, что увеличение частоты в 10 раз приводит к уменьшению коэффициента усиления в 10 раз, а наклон − 40 дБ/дек означает, что увеличение частоты в 10 раз приводит к уменьшению коэффициента усиления в 100 раз.

Из изложенного следует, что если необходимо обеспечить более быстрое изменение коэффициента усиления на удалении от полосы пропускания, то следует увеличить порядок фильтра (но при этом схема фильтра усложняется).

Russian HamRadio — Справочное пособие по высокочастотной схемотехнике. Глава 1.3. ВЧ-фильтры.

Глава 1.3. ВЧ — фильтры.
Высокочастотные избирательные устройства (ВЧ-фильтры) выполняются, как правило, на основе L/C реализаций низкочастотных, высокочастотных и полосовых фильтров. Ниже мы обсудим реализацию подобных устройств при аппроксимации их характеристик полиномами Чебышева, Баттерворта (степенными) и эллиптическими (Кауэра) функциями.
Общее представление об амплитудно-частотных характеристиках фильтров можно получить, рассматривая рис. 1.36. Слева на рисунке изображена амплитудно-частотная характеристика (АЧХ) фильтра низкой частоты (ФНЧ) с полосой пропускания от 0 Гц до граничной частоты f
_c, выше которой, вплоть до бесконечности, расположена полоса задержания. В середине рисунка расположена АЧХ полосового фильтра (ПФ), полоса пропускания которого заключена между нижней f_c и верхней f_c граничными частотами, полоса задержания этого фильтра расположена от 0 Гц до f_c и от f_c до бесконечности. Справа на рисунке показана АЧХ фильтра высокой частоты (ФВЧ), полоса пропускания которого лежит от граничной частоты f_c до бесконечности, а полоса задержания расположена ниже f_c до нулевой частоты.
Более детально АЧХ изображена на рис. 1.37. Приведенные диапазоны допусков для функций Чебышева и Баттерворта справедливы для ФНЧ, ФВЧ и ПФ с учетом того, что они изображены в координатах нормированной расстройки Ω , причем значению Ω
= 1 соответствуют частота f_c для ФНЧ и ФВЧ и частоты f_c и f_c для ПФ.
При Ω
< 1 расположена полоса пропускания, а при Ј1>1-полоса задержания. Значение Ω = 0 соответствует нулевой частоте для ФНЧ, бесконечным частотам для ФВЧ и средней геометрической частоте f_mg для ПФ.
Величина Ω
_s соответствует граничной частоте f_c, на которой достигается заданное значение затухания A_s. В пределах полосы пропускания фильтра задается неравномерность характеристики А_Ь
Теперь поговорим о фильтрах нижних и высоких частот. На рис. 1.38 изображены схемы основных структур, частотные характеристики которых описываются функциями. Рис. 1.36. Общие определения амплитудно-частотных характеристик низкочастотных, полосовых и высокочастотных фильтров

Рис. 1.37. Типовые амплитудно-частотные характеристики НЧ- и ВЧ-фильтров 3-го порядка, выполненных на L/C-элементах.

Данные фильтры достаточно эффективно используются на практике.

Рис. 1.38. Типовые схемы фильтров Чебышева и Баттерворта. Фильтры с характеристикой Чебышева обладают сравнительно более высоким отношением затраты/эффективность.
Чебышева и Баттерворта. Эти схемы соответствуют фильтрам третьего порядка (п = 3).
В данном случае крутизна спада характеристики в полосе задержания составляет 18 дБ/октаву и обусловлена совместным влиянием каждого элемента, образующего фильтр (6 дБ/октаву).

Сопротивления R
₁и R₂ представляют собой источник сигнала и нагрузку соответственно.

Для типичных нечетных значений п они равноценны, так что можно допустить любое их расположение относительно входных клемм фильтра.

На практике из-за меньшего значения собственного затухания Аi предпочитают П-образные ФНЧ и Т-образные ФВЧ, как содержащие меньшее число индуктивностей.
Результирующие избирательные свойства фильтров в зависимости от типа (Чебышева и т.д.) и порядка приведены на рис. 1.39 и 1.40.
Эти рисунки служат для выбора оптимального аппроксимирующего полинома Чебышева или Баттерворта.
По оси абсцисс откладывается значение Ω
_s, нормированное к величине Ω = 1 = f_c, где f_c— граничная частота ФНЧ и ФВЧ.
При проектировании ФНЧ используют непосредственно Ω > 1, а в случае проектирования ФВЧ необходимо использовать обратную величину -1/ Ω
.

Чтобы определить конкретные номиналы L/C, исходят из схем и расчетных формул, изображенных на рис. 1.41, при этом в расчетах используют в качестве исходных данных тип аппроксимирующей функции, порядок фильтра, значение граничной частоты и соответствующие коэффициенты К_т, приведенные в табл. 1.2.
Рис. 1.39. Зависимость характеристик избирательности фильтров Чебышева 3, 5, 7 и 9-го порядка для различных значений А_р
.

Порядок расчета следующий:
а) по формулам (рис. 1.41, внизу слева) определяют базовые значения L
_B и С_B исходя из значений f_c и R;
б) вычисляют окончательные значения С
_n и L_n, основываясь на значениях коэффициентов К_т, взятых из табл. 1.2 и зависящих от порядка n фильтра.
Нумерация элементов С
₁ L_l C_n, L_n на рис. 1.41 соответствует третьему столбцу в табл. 1.2. Задается требуемое значение A_s (в дБ), соответствующее Ω _s, а так как частотная характеристика фильтров этого типа в области выше Ω_s сильно изрезана, то применение для расчета номограмм нецелесообразно.
Соответствующая информация об обсуждаемых здесь функциях, необходимая при проектировании, приведена в зависимости от п в табл. 1.3-1.5.
Эти таблицы содержат также значения К_т и Ω_Шn, нормированные к частоте
L.

Рис. 1.40. Характеристики избирательности фильтров Баттерворта 3, 5, 7 и 9-го порядков.
Используя аналогичный порядок расчета, следует проектировать и эллиптические фильтры
^}, типичные АЧХ которых изображены на рис. 1.42, а принципиальные схемы и расчетные формулы на рис. 1.43.

Рис. 1.41. Эквивалентные схемы и формулы для расчета ФВЧ и ФНЧ с характеристиками Чебышева и Баттерворта.

Значения коэффициентов К_т для ФНЧ и ФВЧ приведены в табл. 1.2.

Таблица
1.2. Коэффициенты, используемые при расчете ФВЧ и ФНЧ 3, 5, 7 и 9-го порядков с различными характеристиками Чебышева и Баттерворта (к рис. 1.41)
Сводка практически используемых основных параметров фильтров приведена в табл. 1.6, где указаны минимально допустимые значения собственной добротности индуктивностей Q_ШL на частоте f_c и максимальные допуски (в %) для номиналов элементов фильтра.
Предполагается также, что собственная добротность конденсаторов Q_Шc по меньшей мере в 10 раз превышает добротность катушек индуктивности Q_ШL , т.е. Q_ШC > |10 Q_ШL , что является основным практическим требованием.
Катушки с оптимальной добротностью можно реализовать только при нагрузочных сопротивлениях фильтра (R_x = R₂), находящихся в пределах от 25 до 200 Ом, что, вообще говоря, не является значительным ограничением.

Значения обоих R должны отличаться не более чем на 5% от номинальной величины.
Следует отметить, что описанные фильтры будут обладать требуемыми параметрами только в случае тщательного выполнения всех требований.

Рис. 1.42. Типовые характеристики эллиптических фильтров.

По сравнению с другими фильтрами, обладающими характеристиками с аналогичными параметрами п и А_р, эллиптические фильтры имеют лучшее отношение затраты/эффективность.

Рис. 1.43. Эквивалентные схемы и формулы для расчета эллиптических ФНЧ и ФВЧ (коэффициенты К_т
для ФНЧ и ФВЧ приведены в табл. 1.3-1.5).

Таблица 1.4. Коэффициенты, используемые при расчете различных эллиптических ФВЧ и ФНЧ 7-го порядка (к рис. 1.43).

Следует отметить, что описанные фильтры будут обладать требуемыми параметрами только в случае тщательного выполнения всех требований и предположений, положенных в основу.

Кроме того, можно приближенно считать, что для значений fc порядка 3-6 октав действительное значение собственного затухания Аi , составляет Ар плюс 0,2-0,3 дБ на каждую индуктивность фильтра, а при значениях полосы пропускания, отличных от вышеуказанного диапазона, величина Аi должна считаться несколько большей. расчeтов.
Таблица
1.5. Коэффициенты, используемые при расчете различных эллиптических ФВЧ и ФНЧ 9-го порядка (с рис. 1.43). Таблица 1.6. Типичные для фильтров значения ненагруженной собственной добротности катушек индуктивности и соответствующие диапазоны допусков*

Теперь скажем несколько слов о полосовых фильтрах. Мы будем различать два типа таких фильтров: узкополосные и широкополосные.
Для первых отношение полосы пропускания Вр к средней геометрической частоте fmg меньше или равно 10%, а для вторых- больше 10%. Узкополосные полосовые фильтры можно относительно просто реализовать на основе сравнительно высокодобротных элементов только при аппроксимации их характеристики функциями Баттерворта.
В дальнейшем речь пойдет об интегральных структурах 2-го и 3-го порядков, т.е. с двумя-тремя контурами.
В табл. 1.7 представлены элементарные соотношения для расчета частотно-зависимых параметров фильтров. Вообще, трехконтурные структуры- оказываются предпочтительными, особенно с неравномерностью А_р = 0,1 дБ и чебышевской характеристикой. Базовыми будут ФНЧ 3-го порядка П- и Т-конфигураций, изображенные на рис. 1.38 слева.
Если В_р< 30%, используют П — звенья, а если В
р от 30% до 70% — Т- и П — звенья; при еще больших значениях относительной полосы пропускания рекомендуется реализовывать полосовой фильтр в виде каскадно соединенных фильтров низких и высоких частот.
Таблица 1.7. Элементарные формулы для расчета частотных параметров полосовых фильтров (ПФ).

Рис. 1.44. Номограмма для определения оптимальных значений резонансного сопротивления в зависимости от ширины полосы пропускания для чебышевских и баттервортовских полосовых фильтров 3-го порядка в интегральном исполнении (см. также рис. 1.45).

Рис. 1.45. Синтез схем полосовых фильтров в интегральном исполнении с характеристиками Чебышева и Баттерворта 3-го порядка (см. рис. 1.44 и табл. 1.8).
Избирательные свойства фильтров зависят от их типа, что следует из рис. 1.39 и 1.40; для п = 3 нормированная расстройка П_ХД_Х вычисляется по формуле, приведенной в табл. 1.7. На рис. 1.44, 1.45 и в табл. 1.8 представлена типовая методика проектирования. При использовании приведенного метода и расчетных формул следует обращать особое внимание на соотношения между В
р, Q_ШL и |А_Р + А_i|. На рис. 1.46 сконцентрированы данные, важные с практической точки зрения и полезные в ходе проектирования; следует отметить, что при расчете полосовых фильтров с Чебышевской характеристикой, имеющих узкую полосу пропускания В_р, можно получить практически нереализуемые значения собственной добротности катушек индуктивности Q_ШL .
Избежать этой трудности можно, если при расчетах использовать практически достижимые значения Q_ШL , полученные в результате измерений или оценочных расчетов. В этом случае достаточно считать, что значение Q_ШL равно удвоенной добротности фильтра Q
_F. В результате этого предположения значение А_i будет более высоким. В качестве примера возьмем схему, часто применяемую в узкополосных ВЧ — усилителях, а именно П-образную схему с двумя параллельными колебательными контурами в интегральном исполнении. Соответствующая методика проектирования этого полосового фильтра с характеристикой Баттерворта второго порядка приведена на рис. 1.47 и в табл. 1.9, а его избирательные свойства иллюстрируются на рис. 1.48 и 1.40 (n = 2).

Следует отметить, что три или два колебательных контура полосового фильтра должны рассчитываться независимо от величины В_р на основе значения частоты f
_mg.
Корректное значение В_р получается в результате совместного включения колебательных контуров и шунтирования их сопротивлениями
R_iи R₂.
Для полосового фильтра 3-го порядка ВР_п3 необходимо иметь в виду, что значения граничных частот f
_cl и f_c2определяются внешними колебательными контурами, а величина А_р зависит от внутреннего контура, соединяющего внешние. Таблица 1.8. Метод расчета схем, приведенных на рис. 1.45. Наряду с нижеприведенными формулами при проектировании используются значения А_р, соответствующие ФНЧ 3-го порядка.

Рис. 1.46. Практически достижимые параметры полосовых фильтров в интегральном исполнении с характеристиками Чебышева и Баттерворта 3-го порядка (ВР-Т„
₃ и ВР В„₃)

Рис. 1.47. Схема интегрального полосового фильтра (ПФ) 2-го порядка с характеристикой Баттерворта (ВР-В„
₂).

Рис. 1.48. Зависимость вносимого затухания от отношения ненагруженной добротности катушек к добротности фильтра для интегральных ПФ с характеристикой Баттерворта 1, 2 и 3-го порядков.

Таблица 1.9. Метод расчета схемы, приведенной на рис. 1.47, с характеристикой Баттерворта.

Рис. 1.49. Основное представление АЧХ при каскадировании интегральных ПФ с характеристикой Баттерворта (см. табл. 1.10).

В случае, если к избирательным свойствам полосовых фильтров Баттерворта (ПФ-Б) с А_р = 3 дБ предъявляют особые требования, т. е. хотят, чтобы неравномерность спектра полезного сигнала А_р составляла, как и для полосовых фильтров Чебышева (ПФ-Ч), десятые доли децибела, тогда величина В_р+ фильтров Баттерворта будет больше, чем ширина спектра сигнала.
Эта зависимость подтверждается характеристиками, приведенными на рис. 1.49. О требуемой величине В_р+ для полосовых фильтров, образованных каскадным включением звеньев Баттерворта 2-го и 3-го порядков, можно судить на основе данных табл. 1.10. В этой таблице приведены также величины В_р+ для двух каскадно включенных полосовых фильтров Баттерворта, для каждого из которых А_р = 3 дБ; при этом предполагается, что развязка между каскадами А_х составляет не менее 10 дБ.

Что касается проектирования широкополосных (В_р > 70%) полосовых фильтров из ФНЧ и ФВЧ, то можно рекомендовать использовать методы, изложенные ранее. В данном случае оба фильтра независимо друг от друга формируют склоны частотной характеристики полосового фильтра и могут непосредственно каскадироваться. Также можно соединять интегральные полосовые фильтры с ФНЧ и ФВЧ.

Таблица 1.10. Значения В_р для каскадно включенных полосовых фильтров Баттерворта (к рис. 1.49).

Рис. 1.50. Схема полосового диплексера и формулы для его расчета.
В заключение рассмотрим так называемые диплексеры. Если необходимо соединить друг с другом две функциональные цепи, одна из которых является широкополосной, а другая, наоборот, обладает узкой полосой пропускания, то это можно сделать посредством специальной согласующей цепи, представляющей собой полосовой фильтр с характеристикой Баттерворта и образованный элементами L, С и R. Типичным примером устройства такого рода является цепь связи между диодным кольцевым смесителем и предусилителем ПЧ в приемнике. Оптимальная структура подобного устройства и соответствующие расчетные формулы приведены на рис. 1.50. Рекомендуется использовать колебательные контуры с одинаковыми полосами В_р (по уровню-3 дБ). Для получения минимального значения aj необходимо применять индуктивности с максимально возможным значением Q_ШL

Исследование полосового ARC-фильтра
Для того, чтобы правильно понять данную статью, а также для понимания поднятой здесь темы, следует для начала разобраться:
Что такое электрический фильтр?

Что такое ARC-фильтр?

Чем полосовой фильтр отличается от других видов?

Пойдем по порядку. Электрический фильтр – это четырёхполюсник, который пропускает один диапазон частот, который мы хотим оставить неизменным, и заглушает другой диапазон, который не требуется в результате.
ARC-фильтр или по-другому активный – это электрический фильтр в конструкции которого присутствует один или несколько реактивных элементы, например: транзистор или операционный усилитель.
Наиболее частыми в использовании являются фильтры: нижних частот, верхних частот и полосовые фильтры. Фильтр нижних частот – фильтр, пропускающий частотный спектр сигнала ниже некоторый частоты и заглушающий частоты выше. Фильтр верхних частот наоборот, пропускает верхние частоты и заглушает частоты ниже заданной. Полосовой фильтр является неким «гибридом» фильтра нижних и верхних частот, так как он пропускает только определенную полосу частот и заглушающий все частоты выше и ниже полосы пропускания
Любой полосовой фильтр имеет несколько основных параметров, определяющих его характеристики:
Полоса пропускания (полоса с наименьшим затуханием сигнала, при проходе через фильтр)

Полоса затухания (полоса, в которой сигналы максимально возможно ослабляются)

Коэффициент усиления (параметр, показывающий во сколько раз сигнал будет усилен или ослаблен в полосе пропускания).

Принцип работы полосового ARC-фильтра основан на изменении коэффициента усиления в зависимости от частоты входного сигнала. Основной в фильтре является RC-цепочка, включенная в цепь обратной связи, которая при изменении частоты влияет на коэффициент усиления.
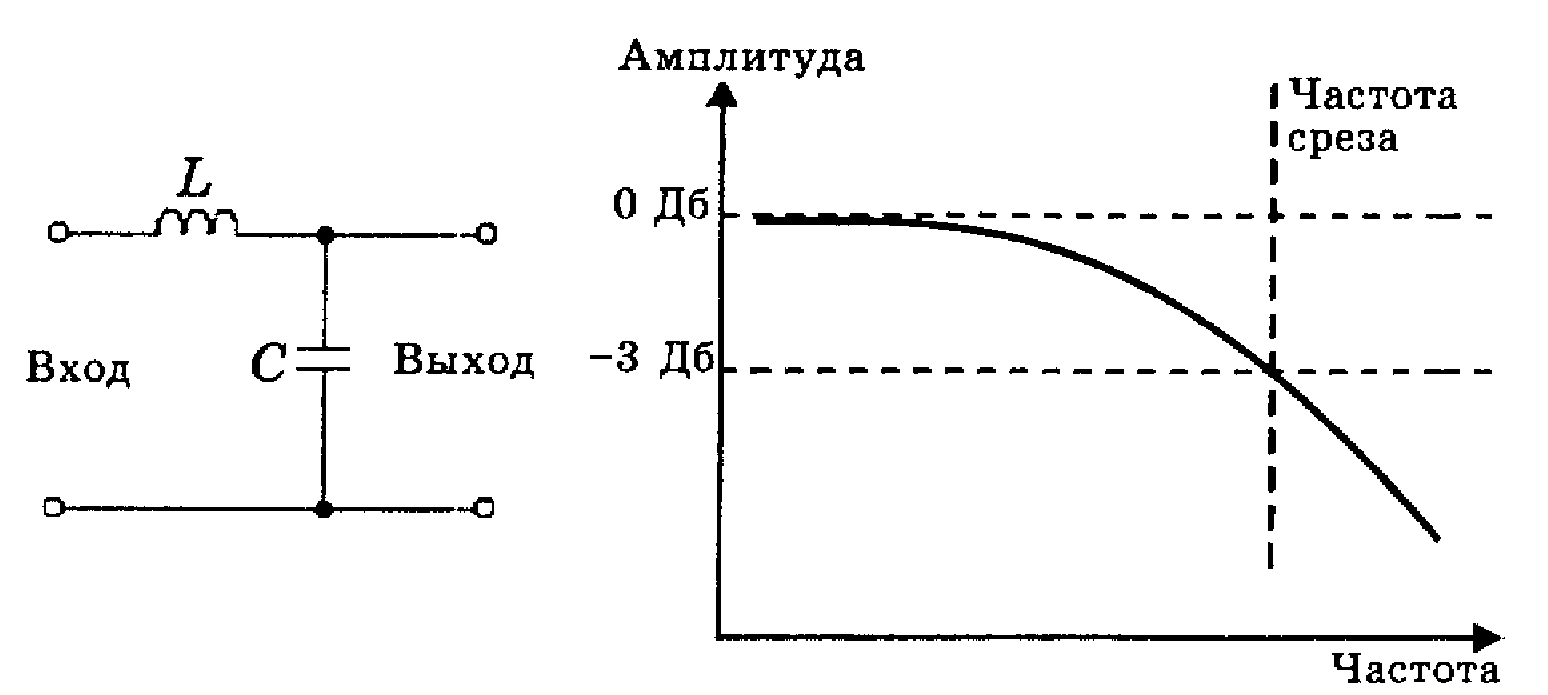
Рис. 1. АЧХ полосового фильтра
На рис. 1 представлена модель амплитудно-частотной характеристики активного полосового фильтра.
Разобравшись в теоретических нюансах работы активного полосового фильтра, можно перейти к расчетам элементов, входящих в состав фильтра.
Исходные данные
За исходные данные были взяты два конденсатора с одинаковыми ёмкостями С=С₁=С₂=3300 пФ, частота квазирезонанса (это центральная частота RC фильтра, не являющегося резонансной цепью) была взята равной f_x=2633 Гц, так как именно эта частота позволяет получить более качественную амплитудно-частотную характеристику. За входное напряжение был взят стандартный аккумулятор, разность потенциалов на концах которого равно U=5 В.
Далее требовалось выбрать добротность нашего контура, а также коэффициент усиления фильтра. Для выбора было использовано условие, что коэффициент усиления (К) должен быть меньше двух квадратов добротности (Q) контура, то есть: K<2⋅Q². Исходя из условия мы получили, что добротность контура равна Q=40, а коэффициент усиления K=220 дБ.
Следующим этапом было рассчитать резистивные элементы. В состав нашего фильтра входит пять резистивных элементов, которые требуется рассчитать, учитывая исходные данные, выбранные выше.
Первым, что требовалось сделать, это рассчитать циклическую частоту квазирезонанса:
ω₀=2πf_x=2π⋅2633=16500 рад/с
Далее нам достаточно данных, чтобы произвести расчет первых трех резисторов
кОм
Ом
МОм
Частоту пятого резистивного элемента обычно выбирают случайным образом от одного до нескольких десятков КОм. Выбор пал на 20 кОм., соответственно R₅ = 20 кОм.
Для расчета последнего – четвертого резистора требуется для начала выбрать точку смещения, в нашем случае равную E₀=2,2 В, тогда:
кОм
Последним этапом расчетов является расчет полосы пропускания
рад/с
Переводим полученное значение в Герцы
Гц
На этом расчеты окончены и теперь следует проверить выбранные начальные условия. Для этого подставляем полученные значения в соответствующие формулы
Проверка коэффициента усиления:
дБ
Проверка циклической частоты квазирезонанса:
рад/с
Проверка частоты квазирезонанса:
Гц
Проверка добротности:
Как видно из всех проверок, погрешность каждого параметра не превышает 3%, что является меньше допустимой погрешности в 5%.
Построим схему этого фильтра (рис. 2) в программной оболочке Micro-Cap 11 и получим АЧХ этого фильтра (рис. 3)
Рис. 2. Схема полосового ARC фильтра в программной оболочке Micro-Cap 11
Рис. 3. АЧХ разработанного полосового ARC фильтра
Теперь соберем реальную модель фильтра по рассчитанным выше данным, на базе микроконтроллера Arduino UNO (рис. 4), и также построим его АЧХ в линейном масштабе (рис. 5), для чего напишем программу на языке Python.
Рис. 4. Реальная модель ARC фильтра
Рис. 5. АЧХ реальной модели ARC фильтра в линейном масштабе
Для сборки фильтра потребовались нижеперечисленные элементы:
Конденсатор керамический выводной, К10-17Б имп. 3300пФ X7R,10%,0805 (2 шт.)

Резистор углеродистый CF-25 (С1-4) 0.25 Вт, 240 Ом – 1,5 МОм, 5% (5 шт.)

Двухканальный операционный усилитель малой мощности LM258N (1 шт.)

Аккумулятор 5 В (1 шт.)

В заключении стоит выделить ряд выводов:
В реальном фильтре невозможно добиться параметров как в идеальном, но можно максимально к ним приблизиться

Реализовать данный активный полосовой фильтр можно на любом типе операционного усилителя, что говорит о простоте и легкости его реализации

Для измерения выходного сигнала желательно встроить в схему детектор/демодулятор на германиевом транзисторе и RC-цепочке, чтобы замерять не отсчеты высокочастотной синусоиды, а выпрямленный сигнал

Реальный фильтр неспособен полностью задержать частоты за границами желаемого диапазона частот, в результате имеется область у границ заданного диапазона, где сигнал только частично ослабляется. Эта область называется крутизной спада фильтра, и измеряется в дБ затухания на октаву.

Схема активного полосового фильтра » Вот схема!

Для достижения высококачественного воспроизведения звука частотная полоса аппаратуры должна соответствовать частотной полосе фонограммы. Кроме того имеются многие источники помех, лежащих в высокочастотной и низкочастотной части спектра настолько сильные, что некоторое сужение полосы пропускания аудиотракта оказывает существенное улучшение восприятия, поскольку эти помехи оказываются за пределами полосы.
Для подавления побочных сигналов могут быть использованы активные RC-фильтры на основе операционных усилителей. Большое разделение в частотах среза ФНЧ и ФВЧ позволяет построить комбинированный полосовой фильтр второго порядка, используя всего один операционный усилитель (рисунок 1).
Для упрощения подбора номиналов частотозадающих элементов удобно применять равнокомпонентный фильтр Саллена-Ки. При этом номиналы элементов схемы попарно равны (С1=С2, R1=R2, С3=С4, R3=R4).
Последовательное соединение двух таких фильтров при сравнительной простоте обеспечивает крутизну спада АЧХ 24 дб на октаву, что в большинстве случаев более чем достаточно.
Из множества фильтров с равномерной АЧХ, наибольшей равномерностью в полосе пропускания и наибольшим затуханием за её пределами обладают фильтры с максимально плоской АЧХ. Для этого в схеме полосового фильтра (рисунок 2) используются два звена второго порядка с расчетными эквивалентными добротностями для А2 = 1,306, и для A3 — 0,541.
На ОУ А1 выполнен входной предварительный усилитель (его усиление, а следовательно и весь коэффициент передачи в полосе, можно установить подбором R3. для указанного на схеме R3 коэффициент передачи равен 10. если нужно 1, R3 = 27 ком)
При указанных на схеме элементах фильтр имеет характеристику, показанную на рисунке 3. Если требуется расширить полосу до 20гц…20кгц. номиналы резисторов R4.R5.R10.R14 должны быть по 1.8 ком, номиналы R6.R9.R13.R15 должны быть по 56 ком, емкости С2,С3,С7,С11 — по 0.15 мкф, емкости С4.С6.С10.С12 — по 4400 пф.
Если требуется вычистить канал, предназначенный только для передачи речи, например СВ радиостанции или диктофона, требуется полоса 300 Гц…3кпд, для этой полосы данные будут такие: R4.R5.R10.R14 — по 6,8 ком, R6.R9.R13.R15 — по 22 ком, емкости С2.С3.С7.С11 — по 0.022 мкф, емкости С4,С6,С10,С12 — по 6800 пф Отклонение реальных величин компонентов не должно быть более 5%. иначе может появиться всплеск или провал в характеристике.
Операционные усилители могут быть любые, например К140УД6. В данной схеме питание однополярное, и для обеспечения нормальной работы ОУ используется делитель R11R12 обеспечивающий среднюю точку. Если питание двуполярное эта цепь отсутствует, выводы 4 ОУ соединяются с минусом питания, а точки U/2 — с общим проводом.
Схемотехника: Лабораторный практикум, страница 6
Комбинации фильтров нижних и верхних частот позволяют создавать полосовые фильтры, с помощью которых из всего спектра частот пропускается только определенная область частот (полоса). Схемы простейших пассивных полосовых фильтров приведены на рис. 1.8.
Рис. 1.8. Простейшие полосовые фильтры:
а) RC-CR фильтр; б) фильтр Вина
АЧХ полосового фильтра характеризуется центральной частотой пропускания f₀, верхней и нижней граничными частотами пропускания f_ви f_н, соответственно, рис. 1.9.
Можно показать, что центральная частота для обоих фильтров, приведенных на рис. 1.8 равна:
.
Вывод выражений для АЧХ и ФЧХ полосовых фильтров предлагается сделать самостоятельно. Для самопроверки приведем лишь выраже-
Рис. 1.9. АЧХ и ФЧХ фильтра Вина
ние для передаточной функции, совпадающее для обоих фильтров, изображенных на рис. 1.8:
.
1.2. Задание на проведение исследований
1. Получите у преподавателя комплект из двух резисторов и двух конденсаторов.
2. По заданию преподавателя поочередно соберите схему однозвенного и двухзвенного ФВЧ или ФНЧ, а также одну из схем полосового фильтра.
3. С помощью генератора специальных сигналов и цифрового осциллографа снимите АЧХ и ФЧХ каждого из фильтров. Для этого установите на выходе генератора напряжение синусоидальной формы с неизменной амплитудой и изменяйте частоту сигнала в пределах не менее ± 1 декады от расчетного значения граничной частоты f_гр или центральной частоты f₀ фильтра. Для измерений отношения амплитуд и соотношения фаз входного и выходного сигналов используйте осциллограф в двухлучевом режиме, подавая на один из его входов напряжение, приложенное к фильтру, а на другой – выходное напряжение фильтра. Фазовый сдвиг между двумя сигналами одной и той же частоты рассчитывается через измеренный с помощью осциллографа временной сдвиг по формуле: (см. рис. 1.2).
4. При измерении параметров полосовых фильтров особенно важно зафиксировать частоту и коэффициент передачи, соответствующие нулевому фазовому сдвигу между входным и выходным напряжениями.
1.3. Содержание отчета
Отчет должен содержать схемы исследуемых фильтров, теоретический расчет выражений для АЧХ и ФЧХ исследованных фильтров, графики АЧХ и ФЧХ фильтров, полученные экспериментально и теоретически, выводы по проведенным исследованиям.
1.4. Вопросы для самопроверки
1. Какому уровню в абсолютном выражении и в дБ соответствует положение граничных частот на частотной зависимости коэффициента передачи фильтра?
2. Почему RC – фильтры не изменяют частоту и форму исходного сигнала?
3. Чем отличаются характеристики ФВЧ и ФНЧ?
4. Как повысить крутизну склона передаточной характеристики фильтра?
5. В чем преимущества изображения передаточной характеристики фильтра в представлении Боде?
Лабораторная работа №2
Исследование МАЛОМОЩНЫХ транзисторных
усилителей
Цели работы – научиться задавать режим по постоянному току транзисторного усилителя, сравнить термостабильность, входное и выходное сопротивления и коэффициент усиления по напряжению трех распространенных схем усилительных каскадов на транзисторах в режиме усиления малых сигналов.
Филин — Производство Фильтров
Центральная (номинальная) частота частота полосового фильтра, равная среднему арифметическому между верхней и нижней частотой полосы пропускания фильтра.
Ширина полосы пропускания Рисунок 1. Полоса пропускания фильтра.
характеристика полосового фильтра, равная разности частот верхней и нижней границ полосы пропускания. Определяется по какому-либо уровню, например, по уровню 3 дБ, или 1 дБ. На рисунке 1 показаны полосы пропускания фильтра по уровням 0,5 и 3 дБ.
Допустимая мощность сигнала на входе максимальная мощность сигнала, подаваемая на вход. Причиной ограничения подаваемой мощности является то, что при большой мощности сигнала некоторые пассивные элементы могут вести себя нелинейно. Также может произойти пробой устройства.
Коэффициент стоячей волны по напряжению по входу и выходу (КСВН) мера согласованности комплексных сопротивлений подключаемой 50-омной нагрузки с фильтром. Стандартом в радиотехнической отрасли является согласование на 50 Ом. Все устройства, представленные в каталоге согласованы на это значение.
Гарантированное затухание на частотах Рисунок 2.
Гарантированное затухание фильтра.
величина, выражаемая в децибелах и характеризующая степень уменьшения мощности сигнала на данных частотах, при прохождении через фильтр. На рисунке 2 показаны области частот фильтра, с гарантированным затуханием 60 дБ и 30 дБ. Обычно пишется абсолютное знгачение [дБ], может быть указано относительно потерь на центральной частоте [дБн].
Допустимая мощность сигнала на входе максимальная мощность сигнала, подаваемая на вход. Причиной ограничения подаваемой мощности является то, что при большой мощности сигнала некоторые пассивные элементы могут вести себя нелинейно. Также может произойти пробой устройства.
Прямоугольность фильтра отношение ширины полосы заграждения фильтра по одному заданному уровню (например, 30 дБ) к ширине полосы пропускания по другому заданному уровню (например, 3 дБ)
Пример определения прямоугольности фильтра:
прямоугольность @-0,5дБ @-30дБ =(46,23-26,35)/(40,5-29,5)=1.80;
прямоугольность @-0,5дБ @-60дБ =(53,29-23,36)/(40,5-29,5)=2.72.

Порядок фильтра число независимых резонансных контуров в системе. В системах на сосредоточенных элементах порядок фильтра определяется числом LC контуров, в устройствах на коаксиально-керамических резонаторах – числом резонаторов.
Частота среза по уровню 3 дБ верхняя для фильтра нижних частот или нижняя для фильтра верхних частот частота, на которой величина ослабления равна 3 дБ.
Неравномерность S21 в полосе пропускания отношение максимального значения АЧХ фильтра к минимальному значению в заданном диапазоне полосы пропускания, выраженное в дБ.
Групповое время запаздывания (ГВЗ) характеристика, показывающая величину временной задержки при прохождении сигнала определенной частоты через фильтр.
Неравномерность ГВЗ (НГВЗ) разность максимального и минимального ГВЗ в полосе пропускания. Пример вычисления НГВЗ показан на риснке 3.
Фазочастотная характеристика (ФЧХ) Рисунок 3. НГВЗ фильтра.
характеристика, показывающая величину набега фазы при прохождении сигнала определенной частоты через фильтр. Пример ФЧХ показан на риснке 4.
Отклонение фазочастотной характеристики от линейного закона разность максимального и минимального линеаризованного ФЧХ в полосе частот. Пример вычисления показан на рисунке 5
Рисунок 4. ФЧХ фильтра. Рисунок 5. Отклонение ФЧХ от личнейного
закона при задержке 126 нс.
Активные и пассивные электрические фильтры

Фильтр — устройство, которое передает сигналы в определенной области частот и препятствует прохождению сигналов вне этой области. Идеальный фильтр имеет постоянную и отличную от нуля передаточную характеристику в необходимом диапазоне частот (полоса пропускания или прозрачности) и нулевую в остальном диапазоне (полоса подавления или затухания).
Применение фильтров имеет очень большую потребность в радио и телеаппаратуре, в которой осуществляется настройка каналов на определённой частоте с помощью фильтрования принимаемых сигналов. Помимо радиотехники, фильтры применяются в аналого-цифровом и цифро-аналоговом преобразовании сигналов, а также в различных электронных системах, с целью фильтрации помех.
Одна из классификаций электрических фильтров — классификация по типам элементов, используемых для схемотехнической реализации: активные, пассивные фильтры, LC, RC-фильтры, фильтры на переключаемых конденсаторах и т. д. Пассивные фильтры (Рисунок 1) имеют в своем составе только пассивные элементы такие, как резисторы, индуктивности, конденсаторы. Данный тип фильтров не требует источника питания для функционирования и не усиливает мощность выходного сигнала (в отличие от активного фильтра). В активном фильтре (Рисунок 2) используется один или несколько активных компонентов: транзистор или операционный усилитель.
Рис. 1. Схема пассивного фильтра нижних частот
Рис. 2. Схемы активного фильтра нижних частот на операционном усилителе: а) первого б) второгопорядка
Порядок фильтра определяет максимальное количество нулей и полюсов передаточной функции фильтра. Что бы увеличить крутизну амплитудно-частотной характеристики необходимо увеличить порядок фильтра, но стоит отметить, что при увеличении порядка увеличивается и количество реактивных элементов (конденсаторов, резисторов) что в свою очередь усложняет сам фильтр и увеличивает его чувствительность к разбросу параметров его компонентов.
В идеальном случае разработчику хотелось бы получить амплитудно-частотную характеристику (АЧХ) имеющую резкий переход между полосой пропускания и подавления (Рисунок 3). Применяя пассивные элементы фильтрации, увеличение крутизны перехода характеристики АЧХ добиваются применением фильтров более высокого порядка, данных подход требует больших расчетов и более точной настройки. Однако применение активных фильтров основным элементом, которых является операционный усилитель с обратной связью, позволяет получить крутой спад характеристики АЧХ, затрачивая значительно меньше усилий и средств во время разработки и при изготовлении.
Рис. 3. АЧХ фильтра нижних частот а) первого порядка, спад 20 dB на декаду; б) второго порядка, спад 40 dB на декаду
Помимо классификации фильтров по типам элементов, на которых они построены, фильтры классифицируются и по виду амплитудно-частотной характеристики:
– Фильтр высоких частот (ФВЧ) — подавляет амплитуды гармонического сигнала ниже частоты среза (Рисунок 4).
– Фильтр низких частот (ФНЧ) — подавляет амплитуды гармонического сигнала выше частоты среза (Рисунок 2).
– Полосовой фильтр — подавляет амплитуды гармонического сигнала выше и ниже определенной полосы (Рисунок 6).
– Полосно-заграждающий фильтр — подавляет амплитуды гармонического сигнала в определенном диапазоне частот, т. е. фильтр, подавляющий колебания определенной полосы и пропускающий колебания, выходящие за границы этой полосы.
Рис. 4. Схема активного фильтра верхних частот первого порядка
Рис. 5. АЧХ фильтра верхних частот а) первого порядка, спад 20 dB на декаду; б) второго порядка, спад 40 dB на декаду
Рис. 6. Схема активного полосового фильтра
Рис. 7. АЧХ активного полосового фильтра
Рис. 8. Пропорционально-интегрирующий фильтр низких частот
Пропорционально-Интегриующий фильтра на ОУ (ПИ-фильтр), также является активным фильтром. ПИ-фильтр сравнивает средние значения двух входных сигналов за период частоты, резисторы R1 и R2 определяют масштабный коэффициент сравнения. Произведение C1*R1 (постоянная времени интегратора Ти) определяет интегрирующий эффект фильтра, резистор R3 обеспечивает устойчивость схемы ФАПЧ, а отношение R3 к R1 определяет пропорциональный коэффициент фильтра Кп.
Заключение
Фильтрация сигналов является важной функцией в аналоговых и аналого-цифровых устройствах, в зависимости от поставленных задач используется тот или иной тип схемотехнической реализации фильтра. В данной статье были рассмотрены несколько разновидностей электрических фильтров и их амплитудно-частотная характеристика. Широкое применение фильтров встречается в электротехнике, радиотехнике и электронике.
Активные фильтры часто применяются в геофизических, медицинских устройствах, а также в различных устройствах связи. Обычно фильтр такого типа представляет собой соединение цепей второго-первого порядка. Благодаря этому упрощается расчет и настройка данного фильтра.
Литература:
Изюмов Н. М. — Радиорелейная связь, Рипол Классик, 2013
Кеоун Д. — OrCAD Pspice. Анализ электрических цепей, Litres, 2014
Мелешин В. — Транзисторная преобразовательная техника, Litres, 2016
Тимошенков В. П., А. А. Миндеева — Элементная база систем связи, учебное пособие, 2015
Миндеева А. А. — Элементная база аналоговых схем, учебное пособие, 2012
У.Титце, К.Шенк — Полупроводниковая схемотехника, 2010 г.
M. Williamsen, «Notch-Filter Design», Audio Electronics, Jan. 2000
W. Jung, «Bootstrapped IC Substrate Lowers Distortion in JFET Op Amps», Analog Devices AN232
H. Zumbahlen, «Passive and Active Filtering», Analog Devices AN281
P. Toomey & W. Hunt, «AD7528 Dual 8-Bit CMOS DAC», Analog Devices AN318
http://www.dsplib.ru/content/filters/ch3/ch3.html
http://radio-hobby.org/modules/news/article.php?storyid=1162
Полосовой фильтр
— Учебное пособие по пассивному RC-фильтру
Полосовые фильтры
могут использоваться для выделения или фильтрации определенных частот, лежащих в определенной полосе или диапазоне частот. Частоту среза или точку c в простом пассивном RC-фильтре можно точно контролировать, используя всего один резистор, последовательно соединенный с неполяризованным конденсатором, и в зависимости от того, каким образом они подключены, мы видели, что либо низкочастотный фильтр или получается фильтр высоких частот.
Одно из простых применений для этих типов пассивных фильтров — в приложениях или схемах аудиоусилителей, таких как фильтры кроссовера громкоговорителей или регуляторы тембра предварительного усилителя.Иногда необходимо пропустить только определенный диапазон частот, который не начинается с 0 Гц (DC) и не заканчивается в какой-то верхней высокочастотной точке, но находится в пределах определенного диапазона или полосы частот, узких или широких.
Соединяя или «каскадируя» вместе одну схему фильтра нижних частот со схемой фильтра верхних частот , мы можем создать другой тип пассивного RC-фильтра, который пропускает выбранный диапазон или «полосу» частот, которая может быть узкой. или широкий при ослаблении всех тех, которые находятся за пределами этого диапазона.Этот новый тип устройства пассивных фильтров производит частотно-селективный фильтр, известный как полосовой фильтр или для краткости BPF .
Цепь полосового фильтра
В отличие от фильтра нижних частот, который пропускает только сигналы низкочастотного диапазона, или фильтра верхних частот, который пропускает сигналы более высокого частотного диапазона, полосовой фильтр пропускает сигналы в определенной «полосе» или «разбросе» частот без искажение входного сигнала или введение дополнительных шумов.Эта полоса частот может быть любой ширины и обычно известна как фильтры , полоса пропускания .
Полоса пропускания обычно определяется как частотный диапазон, который существует между двумя заданными точками отсечки частоты (ƒc), которые на 3 дБ ниже максимального центрального или резонансного пика при ослаблении или ослаблении других точек за пределами этих двух точек.
Тогда для широко распространенных частот мы можем просто определить термин «полоса пропускания», BW как разницу между нижней частотой среза (ƒc _LOWER) и верхней частотой среза (ƒc _HIGHER) точками.Другими словами, BW = ƒ _H — ƒ _L. Очевидно, что для правильной работы полосового фильтра частота среза фильтра низких частот должна быть выше, чем частота среза фильтра высоких частот.
«Идеальный» полосовой фильтр также может использоваться для выделения или фильтрации определенных частот, которые лежат в определенной полосе частот, например, шумоподавления. Полосовые фильтры обычно известны как фильтры второго порядка (двухполюсные), потому что в их схемотехнике есть «два» реактивных компонента — конденсаторы.Один конденсатор в цепи нижних частот и другой конденсатор в цепи верхних частот.
Частотная характеристика полосового фильтра 2-го порядка
График Боде или кривая частотной характеристики выше показывают характеристики полосового фильтра. Здесь сигнал ослабляется на низких частотах, а выходная мощность увеличивается с наклоном +20 дБ / декада (6 дБ / октава), пока частота не достигнет «нижней точки отсечки» ƒ _L. На этой частоте выходное напряжение снова 1 / √2 = 70.7% значения входного сигнала или -3 дБ (20 * log (V _OUT / V _IN)) входа.
Выходной сигнал продолжает работать с максимальным усилением, пока не достигнет точки «верхней границы» ƒ _H, где выходной сигнал уменьшается со скоростью -20 дБ / декада (6 дБ / октава), ослабляя любые высокочастотные сигналы. Точка максимального выходного усиления обычно представляет собой среднее геометрическое значение двух -3 дБ между нижней и верхней точками отсечки и называется значением «центральной частоты» или «резонансного пика» ƒr.Это среднее геометрическое значение рассчитывается как ƒr ² = _{(ВЕРХНИЙ)} x ƒ _{(НИЖНИЙ)}.
Полосовой фильтр считается фильтром второго порядка (двухполюсным), поскольку он имеет «два» реактивных компонента в структуре схемы, тогда фазовый угол будет вдвое больше, чем у ранее замеченных фильтров первого порядка, т. Е. , 180 ^o . Фазовый угол выходного сигнала LEADS входного сигнала +90 ^o до центральной или резонансной частоты, или точки, в которой он становится «нулевым» градусом (0 ^o) или «синфазным». », А затем изменяется на LAG входной сигнал на -90 ^или по мере увеличения выходной частоты.
Верхняя и нижняя точки отсечки частот для полосового фильтра могут быть найдены по той же формуле, что и для фильтров нижних и верхних частот, например.
Тогда ясно, что шириной полосы пропускания фильтра можно управлять путем расположения двух точек частоты среза двух фильтров.
Пример №1 полосового фильтра
.
Полосовой фильтр второго порядка должен быть сконструирован с использованием RC-компонентов, которые позволят пропускать только диапазон частот выше 1 кГц (1000 Гц) и ниже 30 кГц (30 000 Гц).Предполагая, что оба резистора имеют номиналы 10 кОм, рассчитайте номиналы двух необходимых конденсаторов.
Ступень фильтра высоких частот
Величина конденсатора C1, необходимая для обеспечения частоты отсечки ƒ _L, равной 1 кГц при номинале резистора 10 кОм, рассчитывается как:
Тогда значения R1 и C1, необходимые для каскада высоких частот, чтобы получить частоту отсечки 1,0 кГц, равны: R1 = 10 кОм и ближайшему предпочтительному значению C1 = 15 нФ.
Ступень фильтра нижних частот
Величина конденсатора C2, необходимая для обеспечения частоты отсечки ƒ _H, равной 30 кГц при номинале резистора 10 кОм, рассчитывается как:
Значения R2 и C2, необходимые для каскада нижних частот, чтобы получить частоту отсечки 30 кГц, равны R = 10 кОм и C = 530 пФ. Однако ближайшее предпочтительное значение расчетной емкости конденсатора 530 пФ составляет 560 пФ, поэтому вместо него используется это значение.
Со значениями сопротивлений R1 и R2, заданными как 10 кОм, и двумя значениями конденсаторов C1 и C2, найденными для обоих фильтров верхних и нижних частот, как 15 нФ и 560 пФ соответственно, тогда схема для нашего простого пассивного диапазона Пропускной фильтр представлен как.
Завершенная схема полосового фильтра
Полосовой фильтр Резонансная частота
Мы также можем вычислить «резонансную» или «центральную частоту» (ƒr) точку полосового фильтра, если выходное усиление находится на максимальном или пиковом значении. Это пиковое значение не является средним арифметическим верхних и нижних пороговых значений -3 дБ, как можно было бы ожидать, а фактически является «геометрическим» или средним значением. Это среднее геометрическое значение рассчитывается как ƒr ² = ƒc _{(ВЕРХНИЙ)} x ƒc _{(НИЖНИЙ)}, например:
Уравнение центральной частоты
Где ƒ _r — резонансная или центральная частота
ƒ _L — нижняя точка отсечки -3 дБ
ƒ _H — верхняя точка отсечки -3 дБ
, а в нашем простом примере выше вычисленные частоты среза оказались равными _L = 1060 Гц и _H = 28 420 Гц с использованием значений фильтра.
Затем, подставив эти значения в приведенное выше уравнение, получаем центральную резонансную частоту:
Сводная информация о полосовом фильтре
Простой пассивный полосовой фильтр может быть изготовлен путем каскадного соединения одного фильтра нижних частот с фильтром верхних частот . Диапазон частот в герцах между нижней и верхней точкой отсечки -3 дБ RC-комбинации известен как «Полоса пропускания» фильтров.
Ширина или частотный диапазон полосы пропускания фильтров может быть очень малым и избирательным или очень широким и неселективным, в зависимости от используемых значений R и C.
Центральная точка или точка резонансной частоты — это среднее геометрическое значение нижней и верхней точек отсечки. На этой центральной частоте выходной сигнал максимален, а фазовый сдвиг выходного сигнала такой же, как и у входного сигнала.
Амплитуда выходного сигнала от полосового фильтра или любого пассивного RC-фильтра, если на то пошло, всегда будет меньше, чем у входного сигнала. Другими словами, пассивный фильтр также является аттенюатором, дающим коэффициент усиления по напряжению менее 1 (Unity).Чтобы обеспечить выходной сигнал с коэффициентом усиления по напряжению больше единицы, требуется некоторая форма усиления в рамках конструкции схемы.
Пассивный полосовой фильтр классифицируется как фильтр второго порядка, поскольку в его конструкции есть два реактивных компонента — конденсаторы. Он состоит из двух одиночных цепей RC-фильтров, каждая из которых является фильтром первого порядка.
Если несколько фильтров соединены каскадом вместе, результирующая схема будет известна как фильтр «n ^{-го порядка}», где «n» обозначает количество отдельных реактивных компонентов и, следовательно, полюсов в схеме фильтра.Например, фильтры могут иметь порядок 2 ^nd, порядок 4 ^th, порядок 10 ^th и т. Д.
Чем выше порядок фильтров, тем круче будет наклон в n раз -20 дБ / декаду. Однако значение одного конденсатора, полученное путем объединения двух или более отдельных конденсаторов, по-прежнему является одним конденсатором.
В нашем примере выше показана кривая выходной частотной характеристики для «идеального» полосового фильтра с постоянным усилением в полосе пропускания и нулевым усилением в полосах заграждения.На практике частотная характеристика этой схемы полосового фильтра не будет такой же, как входное реактивное сопротивление схемы верхних частот, влияющее на частотную характеристику схемы нижних частот (компоненты, подключенные последовательно или параллельно), и наоборот. Один из способов преодоления этого — обеспечить некоторую форму гальванической развязки между двумя цепями фильтра, как показано ниже.
Буферизация отдельных ступеней фильтрации
Одним из способов объединения усиления и фильтрации в одной схеме было бы использование операционного усилителя или операционного усилителя, примеры которых приведены в разделе «Операционные усилители».В следующем уроке мы рассмотрим схемы фильтров, в конструкции которых используется операционный усилитель, чтобы не только вносить усиление, но и обеспечивать изоляцию между каскадами. Эти типы фильтров обычно известны как Активные фильтры .
Активный полосовой фильтр — полосовой фильтр операционного усилителя
Для фильтра нижних частот эта полоса пропускания начинается с 0 Гц или постоянного тока и продолжается до указанной точки частоты среза на -3 дБ ниже максимального усиления полосы пропускания.Точно так же для фильтра верхних частот полоса пропускания начинается с этой частоты среза -3 дБ и продолжается до бесконечности или максимального коэффициента усиления без обратной связи для активного фильтра.
Однако активный полосовой фильтр немного отличается тем, что это схема частотно-селективного фильтра, используемая в электронных системах для разделения сигнала на одной конкретной частоте или диапазона сигналов, которые лежат в определенной «полосе» частот. от сигналов на всех других частотах. Эта полоса или диапазон частот устанавливается между двумя точками отсечки или угловой частоты, обозначенными «более низкая частота» (ƒ _L) и «более высокая частота» (ƒ _H), при этом любые сигналы за пределами этих двух точек ослабляются. .
Простой активный полосовой фильтр можно легко создать путем каскадного соединения одного фильтра нижних частот с одним фильтром верхних частот, как показано.
Частота среза или среза фильтра нижних частот (LPF) выше, чем частота среза фильтра верхних частот (HPF), и разница между частотами в точке -3 дБ будет определять «полосу пропускания» полосовой фильтр при ослаблении любых сигналов за пределами этих точек.Один из способов сделать очень простой активный полосовой фильтр — это подключить базовые пассивные фильтры верхних и нижних частот, которые мы рассмотрели ранее, к усилительной схеме операционного усилителя, как показано.
Схема активного полосового фильтра
Это каскадное объединение отдельных пассивных фильтров нижних и верхних частот дает схему фильтра с низкой добротностью, которая имеет широкую полосу пропускания. Первым каскадом фильтра будет каскад верхних частот, который использует конденсатор для блокировки любого смещения постоянного тока от источника.Эта конструкция имеет преимущество создания относительно плоской асимметричной частотной характеристики полосы пропускания, при этом одна половина представляет собой характеристику нижних частот, а другая половина — характеристику верхних частот, как показано.
Верхняя угловая точка (_H), а также нижняя точка отсечки угловой частоты (ƒ _L) рассчитываются так же, как и раньше, в стандартных схемах фильтра нижних и верхних частот первого порядка. Очевидно, что между двумя точками отсечки требуется разумное разделение, чтобы предотвратить любое взаимодействие между ступенями низких и высоких частот.Усилитель также обеспечивает изоляцию между двумя каскадами и определяет общий коэффициент усиления схемы по напряжению.
Полоса пропускания фильтра — это разница между этими верхними и нижними точками -3 дБ. Например, предположим, что у нас есть полосовой фильтр, чьи точки отсечки -3 дБ установлены на 200 Гц и 600 Гц. Тогда полоса пропускания фильтра будет задана как: Полоса пропускания (BW) = 600 — 200 = 400 Гц.
Нормализованная частотная характеристика и фазовый сдвиг для активного полосового фильтра будут следующими.
Частотная характеристика активной полосы пропускания
Хотя вышеупомянутая схема пассивного настроенного фильтра будет работать как полосовой фильтр, полоса пропускания (полоса пропускания) может быть довольно широкой, и это может быть проблемой, если мы хотим изолировать небольшую полосу частот. Активный полосовой фильтр также можно сделать с помощью инвертирующего операционного усилителя.
Итак, изменив расположение резисторов и конденсаторов в фильтре, мы можем создать гораздо лучшую схему фильтра, как показано ниже.Для активного полосового фильтра нижняя точка отсечки -3 дБ задается как _C1, а верхняя точка отсечки -3 дБ задается как _C2.
Цепь инвертирующего полосового фильтра
Полосовой фильтр этого типа имеет гораздо более узкую полосу пропускания. Центральная частота и полоса пропускания фильтра связаны со значениями R1, R2, C1 и C2. Выходной сигнал фильтра снова берется с выхода операционного усилителя.
Активный полосовой фильтр с множественной обратной связью
Мы можем улучшить полосовой отклик вышеупомянутой схемы, снова переставив компоненты, чтобы получить полосовой фильтр с множественной обратной связью с бесконечным усилением (IGMF). Этот тип конструкции с активной полосой пропускания создает «настроенную» схему, основанную на активном фильтре с отрицательной обратной связью, что придает ему высокую «добротность» (до 25) амплитудной характеристики и крутой спад по обе стороны от его центральной частоты. Поскольку частотная характеристика контура аналогична резонансному контуру, эта центральная частота называется резонансной частотой (r).Рассмотрим схему ниже.
Активный фильтр с множественной обратной связью с бесконечным усилением
Эта схема активного полосового фильтра использует полное усиление операционного усилителя с множественной отрицательной обратной связью, подаваемой через резистор R ₂ и конденсатор C ₂. Тогда мы можем определить характеристики фильтра IGMF следующим образом:
Мы можем видеть, что соотношение между резисторами R ₁ и R ₂ определяет полосу пропускания «добротности» и частоту, на которой возникает максимальная амплитуда, коэффициент усиления схемы будет равен -2Q. ².Затем, по мере увеличения усиления, увеличивается и избирательность. Другими словами, высокий коэффициент усиления — высокая избирательность.
Активный полосовой фильтр, пример №1
Активный полосовой фильтр с коэффициентом усиления Av по напряжению, равным единице (1), и резонансной частотой, r, равной 1 кГц, построен с использованием схемы фильтра с множественной обратной связью с бесконечным коэффициентом усиления. Рассчитайте значения компонентов, необходимых для реализации схемы.
Во-первых, мы можем определить значения двух резисторов R ₁ и R ₂, необходимые для активного фильтра, используя коэффициент усиления схемы, чтобы найти Q следующим образом.
Тогда мы можем видеть, что значение Q = 0,7071 дает соотношение резисторов, R ₂ — удвоенное значение резистора R ₁. Затем мы можем выбрать любое подходящее значение сопротивлений, чтобы получить требуемое соотношение двух. Тогда резистор R ₁ = 10 кОм и R ₂ = 20 кОм.
Центральная или резонансная частота равна 1 кГц. Используя полученные новые значения резисторов, мы можем определить номинал требуемых конденсаторов, предполагая, что C = C ₁ = C ₂.
Ближайшее стандартное значение — 10 нФ.
Точка резонансной частоты
Фактическая форма кривой частотной характеристики для любого пассивного или активного полосового фильтра будет зависеть от характеристик схемы фильтра, при этом приведенная выше кривая определяется как «идеальная» характеристика полосы пропускания. Активный полосовой фильтр — это фильтр типа 2-го порядка , потому что он имеет «два» реактивных компонента (два конденсатора) в своей схемной конструкции.
В результате этих двух реактивных компонентов фильтр будет иметь пиковый отклик или резонансную частоту (r) на его «центральной частоте», ƒc. Центральная частота обычно рассчитывается как среднее геометрическое из двух частот -3 дБ между верхней и нижней точками отсечки с резонансной частотой (точкой колебания), задаваемой как:
Где:
ƒ _r — резонансная или центральная частота
ƒ _L — нижняя точка отсечки -3 дБ
ƒ _H — верхняя точка отсечки -3 дБ
, а в нашем простом примере в тексте выше нижняя и верхняя точки отсечки -3 дБ находятся на частотах 200 Гц и 600 Гц соответственно, тогда резонансная центральная частота активного полосового фильтра будет:
«Q» или фактор качества
В схеме полосового фильтра общая ширина фактической полосы пропускания между верхними и нижними угловыми точками -3 дБ фильтра определяет коэффициент качества или Q-точку схемы.Этот коэффициент Q является мерой того, насколько «селективным» или «неселективным» является полосовой фильтр по отношению к заданному диапазону частот. Чем ниже значение Q-фактора, тем шире полоса пропускания фильтра, и, следовательно, чем выше Q-фактор, тем уже и «селективнее» фильтр.
Коэффициент качества , Q фильтра, иногда обозначается греческим символом Alpha , (α) и известен как частота альфа-пика , где:
Поскольку добротность активного полосового фильтра (система второго порядка) связана с «резкостью» отклика фильтра вокруг его центральной резонансной частоты (ƒr), его также можно рассматривать как «коэффициент демпфирования» или «демпфирование». Коэффициент », потому что чем больше демпфирование у фильтра, тем более плоский его отклик, и аналогично, чем меньше демпфирование у фильтра, тем резче его отклик.Коэффициент демпфирования задается греческим символом Xi , (ξ) где:
«Q» полосового фильтра представляет собой отношение резонансной частоты , (ƒr) к полосе пропускания , (BW) между верхней и нижней частотами -3 дБ и выражается как:
Итак, для нашего простого примера, приведенного выше, если полоса пропускания (BW) составляет 400 Гц, то есть ƒ _H — ƒ _L, а центральная резонансная частота, _r составляет 346 Гц.Тогда добротность полосового фильтра « Q » будет иметь следующий вид:
346 Гц / 400 Гц = 0,865 . Обратите внимание, что Q — это соотношение, в нем нет единиц измерения.
При анализе активных фильтров обычно рассматривается нормализованная схема, которая дает «идеальную» частотную характеристику, имеющую прямоугольную форму, и переход между полосой пропускания и полосой заграждения, который имеет резкий или очень крутой спад. Однако эти идеальные отклики невозможны в реальном мире, поэтому мы используем приближения, чтобы получить наилучшую возможную частотную характеристику для типа фильтра, который мы пытаемся разработать.
Вероятно, наиболее известным приближением фильтра для этого является фильтр Баттерворта или фильтр с максимально плоским откликом. В следующем уроке мы рассмотрим фильтры более высокого порядка и воспользуемся приближениями Баттерворта для создания фильтров, которые имеют максимально ровную частотную характеристику в полосе пропускания и плавный переход или скорость спада.
Что такое полосовой фильтр? Нарисуйте и объясните частотную характеристику полосового фильтра
.
Полосовой фильтр
Иногда желательно пропустить только определенный диапазон частот, который не начинается с 0 Гц (DC) и не заканчивается в какой-то верхней высокочастотной точке, но находится в определенном диапазоне или полосе частот, узких или широких, и ослабляет другие частоты по обе стороны от этой полосы пропускания.
Эта полоса пропускания называется полосой пропускания фильтра.
Это может быть достигнуто путем каскадирования фильтра нижних частот, способного передавать все частоты до частоты среза f _L, на фильтр верхних частот, способный передавать все частоты выше частоты среза f _H, с f _H> f _L.
Разработанная таким образом система будет способна передавать частоты между f _L и f _H и ослаблять все другие частоты ниже f _L и выше f _H, и этот новый тип устройства пассивных фильтров широко известен как Полосовой фильтр или BPF .
Схема полосового фильтра R-C показана на рис. ниже:
Полоса пропускания или полоса пропускания этого фильтра определяется выражением:
Ширина полосы = f _H — f _L
Значения f _L и f _H задаются следующими уравнениями:
Частотная характеристика полосового фильтра
График Боде или кривая частотной характеристики полосового фильтра показаны на рисунке выше.
Здесь сигнал ослабляется на низких частотах, а выходная мощность увеличивается с наклоном +20 дБ / декада (6 дБ / октава), пока частота не достигнет точки «нижней границы» ƒ _L. На этой частоте выходное напряжение снова составляет 1 / √2 = 70,7% значения входного сигнала или -3 дБ (20 log (Vout / Vin)) входного.
Выходной сигнал продолжает работать с максимальным усилением, пока не достигнет точки «верхней границы» ƒ _H, где выходной сигнал уменьшается со скоростью -20 дБ / декада (6 дБ / октава), ослабляя любые высокочастотные сигналы.
Точка максимального выходного усиления обычно представляет собой среднее геометрическое значение двух -3 дБ между нижней и верхней точкой отсечки и называется значением «центральной частоты» или «резонансного пика» ƒr. Это среднее геометрическое значение рассчитывается как r ² = ƒ _H x ƒ _L.
Полосовой фильтр считается фильтром второго порядка (двухполюсным), поскольку он имеет «два» реактивных компонента в структуре схемы, тогда фазовый угол будет вдвое больше, чем у ранее замеченных фильтров первого порядка, т. Е. , 180 ^o .Фазовый угол выходного сигнала LEADS входного сигнала + 90 ^o до центральной или резонансной частоты, или точки, в которой он становится «нулевым» градусом (0 ^o) или «в -phase », а затем изменяется на LAG входной сигнал на -90 ^o по мере увеличения выходной частоты.
Sasmita
Привет! Я Сасмита. В ElectronicsPost.com я преследую свою любовь к преподаванию.Я магистр электроники и телекоммуникаций. И, если вы действительно хотите узнать обо мне больше, посетите мою страницу «О нас». Узнать больше
Полосовой фильтр
: что это такое? (Схема, конструкция и передаточная функция)
Что такое полосовой фильтр?
Полосовой фильтр (также известный как BPF или полосовой фильтр) определяется как устройство, которое разрешает использование частот в определенном частотном диапазоне и отклоняет (ослабляет) частоты за пределами этого диапазона.
Фильтр нижних частот используется для изоляции сигналов с частотами выше частоты среза. Точно так же фильтр верхних частот используется для изоляции сигналов с частотами ниже частоты среза.
Посредством каскадного соединения фильтра высоких и низких частот создается еще один фильтр, который позволяет передавать сигнал с определенным частотным диапазоном или полосой и ослаблять сигналы, частоты которых находятся за пределами этого диапазона. Этот тип фильтра известен как полосовой фильтр .
Полосовой фильтр имеет две частоты среза. Первая частота среза — от фильтра высоких частот. Это определит верхний предел частоты полосы, который известен как верхняя частота среза (fc-high). Вторая частота среза — от фильтра нижних частот. Это определит нижний предел частоты полосы, который известен как нижняя частота среза (fc-low).
Схема полосового фильтра
Полосовой фильтр представляет собой комбинацию фильтров нижних и верхних частот.Поэтому принципиальная схема содержит схему фильтров верхних и нижних частот. Принципиальная схема пассивного полосового RC-фильтра показана на рисунке ниже. Принципиальная схема полосового фильтра
Первая половина принципиальной схемы представляет собой пассивный RC-фильтр верхних частот. Этот фильтр пропускает сигналы с частотами выше нижней частоты среза (fc-low). И ослабьте сигналы с частотами ниже (fc-low).
Вторая половина принципиальной схемы представляет собой пассивный RC-фильтр нижних частот.Этот фильтр пропускает сигналы с частотами ниже верхней частоты среза (fc-high). И он будет ослаблять сигналы с частотами выше, чем (fc-high).
Полоса или область частот, в которой полосовой фильтр пропускает сигнал, известная как полоса пропускания. Полоса пропускания — это разница между верхним и нижним значением частоты среза.
Типы полосовых фильтров
Существует много типов схем полосовых фильтров.Давайте подробно объясним основные типы схем фильтров.
Активный полосовой фильтр
Активный полосовой фильтр представляет собой каскадное соединение фильтра верхних и нижних частот с усилительным компонентом, как показано на рисунке ниже. Блок-схема активного полосового фильтра
Принципиальная схема активной полосы Пропускной фильтр разделен на три части. Первая часть предназначена для фильтра высоких частот. Затем операционный усилитель используется для усиления. Последняя часть схемы — это фильтр нижних частот.На рисунке ниже показана принципиальная схема активного полосового фильтра. Принципиальная схема активного полосового фильтра
Пассивный полосовой фильтр
В пассивном фильтре используются только такие пассивные компоненты, как резисторы, конденсаторы и катушки индуктивности. Поэтому в пассивном полосовом фильтре также используются пассивные компоненты, и он не использует операционный усилитель для усиления. Таким образом, как и в случае активного полосового фильтра, в пассивном полосовом фильтре отсутствует усилительная часть.
Пассивный полосовой фильтр представляет собой комбинацию пассивных фильтров верхних частот и пассивных фильтров нижних частот.Следовательно, принципиальная схема также содержит схемы фильтров верхних и нижних частот. Принципиальная схема пассивного полосового фильтра
Первая половина схемы предназначена для пассивного фильтра верхних частот. А вторая половина — для пассивного фильтра нижних частот.
Полосовой фильтр RLC
Как следует из названия, этот полосовой фильтр содержит только резистор, катушку индуктивности и конденсатор. Это также пассивный полосовой фильтр.
В соответствии с подключением RLC существует две конфигурации схемы полосового фильтра RLC.В первой конфигурации последовательный LC-контур включен последовательно с нагрузочным резистором. И вторая конфигурация — параллельная LC-цепь, подключенная параллельно с нагрузочным резистором. Принципиальная схема полосового фильтра RLC
Полоса пропускания для последовательного и параллельного полосового фильтра RLC показана в уравнениях ниже.
Полоса пропускания для последовательного RLC-фильтра
Уравнение угловой частоты одинаково для обеих конфигураций, и уравнение:
Полоса пропускания для параллельного RLC-фильтра
Широкополосный фильтр
В зависимости от размера полосы пропускания, его можно разделить на широкий полосовой фильтр и узкий полосовой фильтр.Если добротность меньше 10, фильтр известен как широкополосный фильтр. Как следует из названия, ширина полосы пропускания широкая для широкополосного фильтра.
В этом типе фильтра фильтры верхних и нижних частот представляют собой разные секции, как мы видели в пассивном полосовом фильтре. Здесь оба фильтра пассивны.
Другая компоновка схемы может быть выполнена с использованием активного фильтра верхних частот и активного фильтра нижних частот. Принципиальная схема этого фильтра показана на рисунке ниже, где первая половина предназначена для активного фильтра верхних частот, а вторая половина — для активного фильтра нижних частот.Принципиальная схема широкополосного фильтра
Из-за различных частей фильтров легко спроектировать схему для широкого диапазона полосы пропускания.
Узкополосный фильтр
Полосовой фильтр с добротностью больше десяти. Полоса пропускания этого фильтра узкая. Следовательно, он позволяет передавать сигнал с небольшим диапазоном частот. У него есть множественная обратная связь. В этом полосовом фильтре используется только один операционный усилитель.
Этот полосовой фильтр также известен как фильтр с множественной обратной связью, поскольку существует два пути обратной связи.
В этом полосовом фильтре операционный усилитель используется в неинвертирующем режиме. Принципиальная схема полосового фильтра показана на рисунке ниже. Принципиальная схема узкополосного фильтра
На рисунке ниже показано различие частотной характеристики между широкополосным и узкополосным фильтром.
Частотная характеристика широкополосного и узкополосного фильтра
Передаточная функция полосового фильтра
Передаточная функция полосового фильтра первого порядка
Полосовой фильтр первого порядка невозможен, поскольку он имеет минимум два энергосберегающих элемента (конденсатор или индуктор).Таким образом, передаточная функция полосового фильтра второго порядка выводится следующим образом.
Передаточная функция полосового фильтра второго порядка
Передаточная функция полосового фильтра второго порядка показана и выведена ниже.
Передаточная функция полосового фильтра
(1)
Где,
Для полосового фильтра должно выполняться следующее условие:
Частота среза полосового фильтра
Полоса пропускания фильтр представляет собой комбинацию двух фильтров.Следовательно, он имеет две частоты среза. Одна частота среза получается из фильтра верхних частот и обозначается как F _c-high. Фильтр пропускает сигнал с частотами выше F _c-high. Значение F _c-high рассчитывается по приведенной ниже формуле.
Вторая частота среза получается из фильтра нижних частот и обозначается как F _c-low. Фильтр пропускает сигнал с частотами ниже, чем у F _c-low.Значение F _c-low рассчитывается по приведенной ниже формуле.
Фильтр работает между частотами F _c-high и F _c-low. Диапазон между этими частотами известен как полоса пропускания. Следовательно, полоса пропускания определяется следующим уравнением.
Частота среза фильтра верхних частот определяет нижнее значение полосы пропускания, а частота среза фильтра нижних частот определяет более высокое значение полосы пропускания.
График Боде полосового фильтра или частотная характеристика
На приведенном выше рисунке показан график Боде или частотная характеристика и фазовый график полосового фильтра. Фильтр пропускает сигнал, частота которого находится между полосой пропускания.
Фильтр будет ослаблять сигналы с частотой ниже, чем частота среза фильтра высоких частот. И пока сигнал не достигнет FL, выходной сигнал увеличивается со скоростью +20 дБ / декада, как и фильтр высоких частот.
После этого выходной сигнал будет работать с максимальным усилением до тех пор, пока не достигнет частоты среза фильтра нижних частот или в точке F _H. Затем выходной сигнал будет уменьшаться со скоростью -20 дБ / декада, как и у фильтра нижних частот.
Полосовой фильтр является фильтром второго порядка, поскольку на принципиальной схеме он имеет два реактивных компонента. Следовательно, разность фаз вдвое больше, чем у фильтра первого порядка, и она составляет 180 °.
До центральной частоты выходной сигнал опережает входной сигнал на 90 °.На центральной частоте выходной сигнал синфазен с входным. Следовательно, разность фаз равна 0˚.
После центральной частоты выходной сигнал отстает от входного на 90 °.
Идеальный полосовой фильтр
Идеальный полосовой фильтр позволяет получать сигнал с точностью от F _{до L}, подобной переходной характеристике. Сигнал разрешен ровно на F _L с крутизной 0 дБ / декада. И он резко ослабляет сигналы с частотой выше F _H.
Частотная характеристика идеального полосового фильтра показана на рисунке ниже. Этот тип ответа не может привести к фактическому полосовому фильтру.
Уравнение полосового фильтра
Когда частота сигнала находится в диапазоне ширины полосы, фильтр пропускает сигнал с входным сопротивлением. И выход равен нулю, когда частота сигнала выходит за пределы полосы пропускания.
Для полосового фильтра;
(2)
Применение полосового фильтра
Полосовой фильтр применяется следующим образом:
Полосовые фильтры широко используются в схемах звуковых усилителей.Например, динамик используется для воспроизведения только желаемого диапазона частот и игнорирования остальных частот.
Используется оптика, такая как ЛАЗЕР, ЛИДАРЫ и т. Д.
Эти фильтры используются в системе связи для выбора сигналов с определенной полосой пропускания.
Используется при обработке аудиосигнала.
Он также используется для оптимизации отношения сигнал / шум и чувствительности приемника.
Пример конструкции полосового фильтра
Теперь вы знакомы с полосовым фильтром.Давайте разработаем фильтр для определенной полосы пропускания. Мы сделаем фильтр, который пропускает сигналы с частотами в диапазоне от 80 Гц до 800 Гц.
F1 = 80 Гц
F2 = 800 Гц
В этом примере мы сделаем простой пассивный RC-фильтр для заданного диапазона частот. Итак, нам нужно вычислить значение R1, C1, R2 и C2.
Принципиальная схема пассивного полосового фильтра
Аналогично,
Мы должны принять значение сопротивления или емкости.Здесь мы примем значение C1 и C2. Для простых расчетов мы примем одно и то же значение для C1 и C2, которое составляет 10 ^-6 F. И вычислим значение сопротивления в соответствии с этим значением C1, C2 и F1, F2.
Следовательно,
Аналогично,
Теперь у нас есть все значения, и по этим значениям мы можем создать фильтр, который разрешает сигналы с определенной полосой пропускания.
Полосовой фильтр — обзор
4.3.4.1 ВЧ-фильтры
Полосовой фильтр, состоящий из дискретных компонентов, по сути, представляет собой резонансный контур, подобный тому, который показан на рис. 4.23. Показанный там идеальный резонатор без потерь пропускает только резонансную частоту, но реальные схемы имеют конечные потери, характеризуемые, как мы отметили ранее, добротностью Q . Потери заставляют резонансный контур пропускать через него конечную полосу частот; ширина полосы обратно пропорциональна Q (рисунок 4.33). (Обратите внимание, что выходная частотная характеристика, показанная на рисунке, для удобства нормирована на 1 Ом; другое значение изменит положение пика, но не ширину полосы.) Как показано в правой половине рисунка, коэффициент качества также определяет ширина полосы пропускания фильтра. Фильтры с узкой полосой пропускания должны иметь очень высокий Q: например, полосовой фильтр RF для диапазона ISM 902–928 МГц должен иметь полосу пропускания порядка 3% от центральной частоты, требуя Q не менее 30.На практике для создания хорошего фильтра требуется значительно более высокое значение Q: фильтр должен иметь довольно ровную передачу в полосе пропускания и резкий переход к очень низкой передаче в полосах задерживания , а не пиковое поведение, показанное на рисунке. Задачи очень серьезные. Например, в США базовые станции сотовых телефонов работают в полосе частот от 869 до 894 МГц (и могут передавать на уровнях мощности 100 Вт и более!). Чтобы обеспечить подавление сигнала на частоте 893 МГц на 40 или 50 дБ при приеме сигнала на частоте 903 МГц с минимальными потерями, нам потребуется добротность в несколько сотен.Встроенные фильтры, построенные с использованием катушек индуктивности и конденсаторов в процессах Si CMOS, обычно ограничиваются добротностью около 10, в основном из-за потерь в катушках индуктивности. Дискретные компоненты предлагают добротность до 20–30 на этих частотах, но сложные фильтры со многими элементами, построенными с использованием дискретных компонентов, станут физически большими и не подходят для частот ГГц.
Рисунок 4.33. Простой фильтр, использующий параллельный резонансный контур и полосовые характеристики.
С другой стороны, если все, что нужно, — это отклонить излучение второй и третьей гармоник от передатчика (т.е.е. для пропускания передачи на частоте 915 МГц, но отклонения 1830 МГц) вполне достаточно дискретных фильтров с Q около 10.
Для обеспечения фильтрации с выбором полосы требуются более совершенные технологии с высокой добротностью, малым физическим размером и низкой стоимостью. Существует несколько методов получения фильтров с высоким коэффициентом качества и небольшими размерами на микроволновых частотах. Многие из этих подходов зависят от того факта, что акустические (механические) колебания распространяются намного медленнее, чем электромагнитные волны, поэтому резонансная структура, содержащая одну или несколько длин волн звука, может быть намного меньше, чем аналогичное устройство, использующее электромагнитные резонансы.
Важным примером технологии электромеханических фильтров является устройство на поверхностных акустических волнах (SAW). (Читатель может вспомнить, что мы упоминали RFID-метки на основе ПАВ в главе 2; в них используется технология, аналогичная технологии фильтров на ПАВ для создания закодированных с задержкой отражений.) Фильтры на ПАВ достигают сотен добротностей, доступны в корпусах для поверхностного монтажа, и может без повреждений пропускать сотни милливатт. Фильтры на ПАВ относительно дороги (от 0,50 до 10 долларов).Упакованные фильтры имеют площадь порядка 1 см, что достаточно велико, чтобы количество фильтров необходимо было минимизировать как для экономии места на плате, так и для минимизации затрат. Пакеты со шкалой для микросхем с площадью всего в несколько квадратных миллиметров недавно стали доступны, что позволяет устанавливать фильтры с небольшими потерями в площади. Резонансная частота SAW-фильтра в некоторой степени зависит от температуры; кварцевые фильтры в этом отношении лучше, чем большинство других пьезоэлектрических материалов, но их производство дороже.
Упрощенная структура фильтра на ПАВ показана на рисунке 4.34. Устройство построено на пьезоэлектрической подложке, такой как кварц, LiNbO ₄ или ZnO. Электрические преобразователи состоят из слоя проводящего металла, такого как алюминий, нанесенного и нанесенного на поверхность пьезоэлектрика с использованием методов, аналогичных тем, которые используются при изготовлении интегральных схем.
Рисунок 4.34. Упрощенный фильтр поверхностных акустических волн.
Входной преобразователь состоит из примерно 100 встречно-штыревых пальцев, управляемых с переменной полярностью от источника ВЧ.Между каждой парой пальцев внутри пьезоэлектрического материала образуется электрическое поле, вызывающее зависящую от времени деформацию, которая создает акустическую волну. Для входной частоты, такой, что расстояние между пальцами составляет половину длины акустической волны, будет происходить резонансное усиление волны по мере ее распространения вдоль преобразователя, поскольку каждая чередующаяся область деформации будет находиться в фазе с волной и увеличивать смещение. . Результирующая сильная акустическая волна распространяется к меньшему выходному преобразователю, где акустическая деформация индуцирует электрическое поле между электродами, что приводит к выходному напряжению.Срез пьезоэлектрика часто разрезают под углом к оси распространения, так что акустическая энергия, которая не преобразуется обратно в электрическую, отражается от краев подложки под нечетным углом и рассеивается, прежде чем она может помешать желаемой работе. фильтра. Поскольку акустическая волна распространяется примерно в 10 000 раз медленнее, чем электромагнитное излучение, длины волн для микроволновых частот составляют порядка 1 микрона, что позволяет создавать компактные конструкции фильтров с высокой добротностью.
Характеристики довольно типичного полосового (или подавляющего изображение) фильтра показаны на рисунке 4.35 как зависимость передачи в дБ через фильтр от частоты. В диапазоне ISM потери через фильтр составляют всего около 2,3 дБ ± 0,3 дБ: эта передача известна как вносимые потери , поскольку это потери в полосе из-за вставки фильтра в схему. Низкие вносимые потери важны как при передаче, так и при приеме, хотя, поскольку фильтры передачи обычно должны обеспечивать только подавление гармоник, фильтр на ПАВ может не понадобиться.Вносимые потери фильтра передачи напрямую связаны с мощностью сигнала, поэтому фильтры с потерями означают более крупные усилители мощности передачи, которые стоят дороже и потребляют больше энергии постоянного тока. На приемной стороне потери в фильтре по существу равны его коэффициенту шума, и, поскольку фильтр обычно размещается перед малошумящим усилителем или смесителем, коэффициент шума фильтра должен добавляться непосредственно к коэффициенту шума приемника.
Рисунок 4.35. Зависимость передачи от частоты для типичного SAW-фильтра с центром в диапазоне ISM США, показывающая определения вносимых потерь, коэффициента формы и подавления внеполосных сигналов.
Другими важными свойствами фильтра являются резкость, с которой передача обрывается, когда частота выходит за границы диапазона, и передача (желательно небольшая, поэтому подавление) внеполосных сигналов. Полоса пропускания в этом случае при уменьшении передачи на 3 дБ по сравнению с центральной частотой составляет около 41 МГц, что значительно шире, чем полоса ISM 28 МГц: сигналы на 6–7 МГц за пределами полосы будут иметь небольшое подавление. После этого передача падает довольно быстро: коэффициент формы , отношение полосы пропускания при подавлении 20 дБ к подавлению 3 дБ, составляет примерно 1.4. Подавление сигналов далеко от краев полосы частот, таких как полоса частот восходящего канала сотового телефона 824–849 МГц, составляет 40 дБ или лучше. Однако этот фильтр обеспечивает подавление только около 3 дБ на верхнем конце полосы частот нисходящей линии связи сотовой связи. Соседняя базовая станция сотовой связи, работающая на верхнем краю полосы частот, не будет отклонена фильтром выбора полосы, а должна быть удалена после преобразования основной полосы частот. Такой мешающий сигнал может объединяться с другими мешающими сигналами (такими как другие считыватели RFID) из-за искажения третьего порядка во внешнем интерфейсе приемника, чтобы создавать помехи на частоте считывателя, которые не могут быть отфильтрованы.Как следствие, радиочастотной фильтрации может оказаться недостаточно для защиты считывающего устройства от источников помех, и вместо этого необходимо обеспечить хорошую линейность в смесителе и (если используется) радиочастотном усилителе.
Другие коммерчески доступные технологии фильтрации включают устройства объемной акустической волны (BAW), в которых используется тонкий слой пьезоэлектрического материала и которые могут обрабатывать более высокие плотности мощности, чем фильтры на ПАВ, и диэлектрические резонаторные фильтры, в которых используются электрические резонансы диэлектрика с высоким содержанием диэлектрика. -постоянный блок.
Полосовой фильтр Частотная характеристика
Используя те же принципы и процедуры в случае фильтров нижних и верхних частот , можно получить частотную характеристику полосового фильтра для конкретных типов схем.Такой фильтр пропускает вход на выход на частотах в определенном диапазоне. Анализ простого полосового фильтра второго порядка (т. {2}} LC} \ begin {matrix} {} & (2) \\\ end {matrix} \]
Уравнение 2 разложить на множители
\ [\ frac {{{V} _ {0}}} {{{V} _ {i}}} (j \ omega) = \ frac {jA \ omega} {(j \ omega / {{\ omega) } _ {1}} + 1) + (j \ omega / {{\ omega} _ {2}} + 1)} \ begin {matrix} {} & (3) \\\ end {matrix} \]
Где ω ₁ и ω ₂ — две частоты, которые определяют полосу пропускания (или полосу пропускания ) фильтра, то есть диапазон частот, через который фильтр «пропускает» вход сигнал — и — константа, полученная в результате разложения.
Непосредственное наблюдение, которое мы можем сделать, состоит в том, что если частота сигнала ω равна нулю, характеристика фильтра равна нулю, поскольку при ω = 0 полное сопротивление конденсатора 1/ jωC становится бесконечным . Таким образом, конденсатор действует как разомкнутая цепь , и выходное напряжение равно нулю. {2}} \ right]}} \\ & \ angle H (j \ omega) = \ frac { \ pi} {2} — \ arctan \ frac {\ omega} {{{\ omega} _ {1}}} — \ arctan \ frac {\ omega} {{{\ omega} _ {2}}} \\ \ end {align} & {} & (5) \\\ end {matrix} \]
Графики амплитуды и фазы для частотной характеристики полосового фильтра , рисунок 1, показаны на , рисунок 2, .Эти графики были нормализованы, чтобы иметь полосу пропускания фильтра с центром на частоте ω = 1 рад / с.
Графики частотной характеристики , рис. 2 предполагают, что в некотором смысле полосовой фильтр действует как комбинация высокочастотного и низкочастотного фильтров. Как показано в предыдущих случаях, должно быть очевидно, что можно настроить отклик фильтра по желанию, просто выбрав соответствующие значения для L, C и R .
Рисунок 2 Частотная характеристика полосового фильтра RLC
Резонанс и полоса пропускания
Отклик фильтров второго порядка можно объяснить в более общем виде, переписав функцию частотной характеристики полосового фильтра второго порядка из , рис. {2}} + (1 / Q {{\ omega} _ {n}}) j \ omega +1} & {} & {} \\\ end {matrix} \]
со следующими определениями:
\ [\ begin {matrix} {{\ omega} _ {n}} = \ sqrt {\ frac {1} {LC}} = натуральный \ begin {matrix} или \ begin {matrix} резонансный \ begin {matrix} частота \\\ end {matrix} \\\ end {matrix} \\\ end {matrix} & {} & {} \\ Q = \ frac {1} {2 \ zeta} = \ frac {1} {{ {\ omega} _ {n}} CR} = {{\ omega} _ {n}} \ frac {L} {R} = \ frac {1} {R} \ sqrt {\ frac {L} {C} } = качество \ text {} фактор & {} & (7) \\\ zeta = \ frac {1} {2Q} = \ frac {R} {2} \ sqrt {\ frac {C} {L}} = демпфирование \ text {} ratio & {} & {} \\\ end {matrix} \]
На рисунке 3 показана нормализованная частотная характеристика (амплитуда и фаза) полосового фильтра второго порядка для ω _n = 1 и различных значений Q (и ζ).Пик, отображаемый в частотной характеристике около частоты ω _n , называется резонансным пиком , а ω _n является резонансной частотой .
Обратите внимание, что по мере увеличения добротности Q резкость резонанса увеличивается, и фильтр становится все более селективным (т. Е. Он имеет возможность отфильтровывать большинство частотных компонентов входных сигналов, за исключением узкая полоса вокруг резонансной частоты).
Одним из показателей избирательности полосового фильтра является его полоса пропускания . Концепцию полосы пропускания можно легко визуализировать на графике , рис. 3 (a ), нарисовав горизонтальную линию поперек графика (мы решили нарисовать ее при значении отношения амплитуд 0,707 по причинам, которые будут объяснены в ближайшее время). Частотный диапазон между точками (амплитуды) частотной характеристики, пересекающими эту горизонтальную линию, определяется как полоса пропускания половинной мощности фильтра.{1} / {} _ {\ sqrt {2}} $ в выходном напряжении или токе соответствует уменьшению мощности в ½ раза.
Таким образом, мы называем частоты, на которых происходит пересечение линии 0,707 с частотной характеристикой, частотами половинной мощности . Другое полезное определение полосы пропускания B выглядит следующим образом. Обратите внимание, что фильтр высоких частот Q имеет узкую полосу пропускания, а фильтр низких частот Q имеет широкую полосу пропускания.
\ [B = \ frac {{{\ omega} _ {n}}} {Q} \ begin {matrix} {} & Ban {{d} _ {{}}} width & \ begin {matrix} {} & (8) \\\ end {matrix} \\\ end {matrix} \]
Рисунок 3 (a) Нормализованная амплитуда отклика полосового фильтра второго порядка; (б) нормализованная фазовая характеристика полосового фильтра второго порядка
Фазовая характеристика активных фильтров
Введение
В первой статье этой серии, ¹ я исследовал взаимосвязь фазы фильтра с топологией реализации фильтра.Во второй статье, ², я исследовал фазовый сдвиг передаточной функции фильтра для низких и высоких частот. В этой статье мы сосредоточимся на полосе пропускания. Хотя фильтры предназначены в первую очередь для их амплитудной характеристики, фазовая характеристика может быть важна в некоторых приложениях.
Для целей обзора передаточная функция активного фильтра фактически представляет собой каскад передаточной функции фильтра и передаточной функции усилителя (см. Рисунок 1).
Рисунок 1. Фильтр как каскад двух передаточных функций.
Полосовая передаточная функция
Изменение числителя ФНЧ прототипа на
преобразует фильтр в полосовую функцию. Это приведет к обнулению передаточной функции. Член s в числителе дает нам ноль, а член s в числителе дает нам полюс. Ноль даст ответ нарастающей с частотой, в то время как полюс даст отклик с понижением частоты.
Тогда передаточная функция полосового фильтра второго порядка равна:
ω0 здесь частота (F ₀ = 2 π ω0), на которой усиление фильтра достигает пика.
H ₀ — коэффициент усиления схемы (пик Q) и определяется как:
, где H — коэффициент усиления реализации фильтра.
Q имеет особое значение для полосы пропускания. Это избирательность фильтра. Это определяется как:
, где FL и FH — частоты, на которых отклик составляет –3 дБ от максимума.
Полоса пропускания (BW) фильтра описывается как:
Можно показать, что резонансная частота (F ₀) является средним геометрическим для F _L и F _H, что означает, что F ₀ появится на полпути между F _L и F _H в логарифмической шкале.
Также обратите внимание, что границы полосы пропускания всегда будут симметричными относительно F ₀ в логарифмической шкале.
Амплитудный отклик полосового фильтра на различные значения Q показан на рисунке 2. На этом рисунке усиление на центральной частоте нормировано на 1 (0 дБ).
Рис. 2. Нормированная амплитудная характеристика полосового фильтра.
Опять же, эта статья в первую очередь касается фазовой характеристики, но полезно иметь представление об амплитудной характеристике фильтра.
Здесь уместно сделать предостережение. Полосовые фильтры можно определить двумя разными способами. Узкополосный случай — это классическое определение, которое мы показали выше. Однако в некоторых случаях, если высокие и низкие частоты среза сильно разнесены, полосовой фильтр состоит из отдельных секций высоких и низких частот. Широкое разделение в данном контексте означает разделение по крайней мере на две октавы (× 4 по частоте). Это широкополосный случай. В данной статье нас в первую очередь интересует случай узкополосной связи.Для широкополосного случая оцените фильтр как отдельные секции высоких и низких частот.
Хотя полосовой фильтр может быть определен в терминах стандартных откликов, таких как Баттерворт, Бессель или Чебышев, они также обычно определяются их Q и F ₀.
Фазовая характеристика полосового фильтра:
Обратите внимание, что однополюсного полосового фильтра не существует.
Рисунок 3. Нормированный фазовый отклик полосового фильтра.
Рисунок 3 оценивает уравнение 6 от двух десятков ниже центральной частоты до двух десятков выше центральной частоты.Центральная частота имеет фазовый сдвиг 0 °. Центральная частота равна 1, а Q — 0,707. Это тот же Q, который использовался в предыдущей статье, хотя в этой статье мы использовали α. Помните, что α = 1 / Q.
Осмотр показывает, что форма этой кривой в основном такая же, как у нижних частот (и верхних частот, если на то пошло). Однако в этом случае фазовый сдвиг составляет от 90 ° ниже центральной частоты до 0 ° на центральной частоте до –90 ° выше центральной частоты.
На рисунке 4 мы исследуем фазовую характеристику полосового фильтра с изменяющейся добротностью.Если мы посмотрим на передаточную функцию, мы увидим, что изменение фазы может происходить в относительно большом частотном диапазоне, и что диапазон изменения обратно пропорционален добротности схемы. Опять же, осмотр показывает, что кривые имеют ту же форму, что и кривые для низких (и высоких) характеристик, только с другим диапазоном.
Рисунок 4. Нормализованная фазовая характеристика полосового фильтра с изменяющейся добротностью.
Передаточная функция усилителя
В предыдущих частях было показано, что передаточная функция в основном аналогична однополюсному фильтру.Хотя фазовый сдвиг усилителя обычно не учитывается, он может повлиять на общий коэффициент передачи композитного фильтра. AD822 был произвольно выбран для использования в моделировании фильтров в этой статье. Он был выбран частично, чтобы минимизировать влияние на передаточную функцию фильтра. Это связано с тем, что фазовый сдвиг усилителя значительно выше по частоте, чем граничная частота самого фильтра. Передаточная функция AD822 показана на рисунке 5, который является информацией, взятой непосредственно из таблицы данных.
Рисунок 5. Коэффициент усиления и фаза графика Боде AD822.
Пример 1: 2-полюсный полосовой фильтр 1 кГц с Q = 20
Первым примером будет фильтр, изначально спроектированный как полосовой. Мы произвольно выбираем центральную частоту 1 кГц и добротность 20. Поскольку добротность находится на более высокой стороне, мы будем использовать конфигурацию с двойным полосовым усилителем (DABP). Опять же, это произвольный выбор.
Мы используем расчетные уравнения из справочника 1. Результирующая схема показана на рисунке 6:
. Рисунок 6.1 кГц, Q = 20 полосовой фильтр DABP.
В этой статье нас в первую очередь интересует фаза, но я считаю полезным изучить амплитудную характеристику.
Рисунок 7. 1 кГц, Q = 20 Амплитудная характеристика полосового фильтра DABP.
Мы видим фазовую характеристику на рисунке 8:
. Рисунок 8. 1 кГц, Q = 20 Фазовая характеристика полосового фильтра DABP.
Обратите внимание, что конфигурация DABP не инвертирующая. Рисунок 8 соответствует рисунку 3.
Пример 2: Преобразование Чебышева ФНЧ в полосовой фильтр, 1 кГц, 3 полюса 0,5 дБ
Теория фильтра
основана на прототипе фильтра нижних частот, который затем может быть преобразован в другие формы.В этом примере прототипом, который будет использоваться, является 3-полюсный фильтр Чебышева, 1 кГц, 0,5 дБ. Был выбран фильтр Чебышева, потому что он будет более четко показать, если ответы будут неправильными. Например, рябь в полосе пропускания не совпадала. В этом случае фильтр Баттерворта, вероятно, был бы слишком снисходительным. 3-полюсный фильтр был выбран таким образом, чтобы пара полюсов и одиночный полюс были преобразованы.
Расположение полюсов для прототипа LP (из ссылки 1):
Стадия α β Факс ₀ α
1 0.2683 0,8753 1.0688 0,5861
2 0,5366 0,6265
Первая стадия — это пара полюсов, а вторая стадия — однополюсная. Обратите внимание на неудачное соглашение об использовании α для двух совершенно разных параметров. Значения α и β слева — это положения полюсов в плоскости s.Это значения, которые используются в алгоритмах преобразования. Значение α справа равно 1 / Q, что и хотят видеть уравнения конструкции физических фильтров.
Прототип нижних частот преобразован в полосовой фильтр. Строка уравнения, указанная в ссылке 1, используется для преобразования. Каждый полюс фильтра-прототипа превратится в пару полюсов. Следовательно, 3-полюсный прототип при преобразовании будет иметь шесть полюсов (3-полюсные пары). Кроме того, в начале координат будет шесть нулей.Однополюсной полосы пропускания не существует.
Частью процесса преобразования является определение ширины полосы 3 дБ результирующего фильтра. В этом случае эта полоса будет установлена на 500 Гц. По результатам трансформации выход:
Стадия F0 Q A0
1 804,5 7,63 3.49
2 1243 7,63 3,49
3 1000 3,73 1
На практике может быть полезно поместить секцию с низким коэффициентом усиления и добротностью первой в строке, чтобы максимально улучшить обработку уровня сигнала. Причина требования к усилению для первых двух каскадов заключается в том, что их центральные частоты будут ослаблены относительно центральной частоты всего фильтра (то есть они будут на юбке других секций).
Поскольку результирующие Q являются умеренными (менее 20), будет выбрана топология множественной обратной связи. Расчетные уравнения для полосового фильтра с множественной обратной связью из ссылки 1 используются для разработки фильтра. На рисунке 9 показана схема самого фильтра.
Рисунок 9. 6-полюсный полосовой фильтр Чебышева, 1 кГц, 0,5 дБ.
На рисунке 10 мы смотрим на фазовый сдвиг всего фильтра. График показывает фазовый сдвиг только первой секции (Секция 1), первых двух секций вместе (Секция 2) и всего фильтра (Секция 3).Они показывают фазовый сдвиг «реальных» секций фильтра, включая фазовый сдвиг усилителя и инверсию топологии фильтра.
На рисунке 10 следует отметить несколько деталей. Во-первых, фазовая характеристика является кумулятивной. В первом разделе показано изменение фазы на 180 ° (фазовый сдвиг функции фильтра без учета фазового сдвига топологии фильтра). Вторая часть показывает изменение фазы на 360 ° из-за наличия двух частей, по 180 ° от каждой из двух частей.Помните, что 360 ° = 0 °. И третья часть показывает сдвиг фазы 540 °, по 180 ° от каждой из секций. Также обратите внимание, что на частотах выше 10 кГц мы начинаем видеть небольшой спад фазы из-за отклика усилителя. Мы видим, что спад снова является кумулятивным, увеличиваясь для каждого раздела.
Рис. 10. Фазовая характеристика 6-полюсного полосового фильтра Чебышева, 1 кГц, 0,5 дБ.
На рисунке 11 мы видим амплитудную характеристику всего фильтра.
Рисунок 11. Амплитудная характеристика 6-полюсного датчика с частотой 1 кГц, 0.Полосовой фильтр Чебышева 5 дБ.
Вывод
В данной статье рассматривается фазовый сдвиг полосовых фильтров. В предыдущих статьях этой серии мы исследовали фазовый сдвиг в зависимости от топологии фильтра и для топологий верхних и нижних частот. В следующих статьях мы рассмотрим режекторные и всепроходные фильтры. В заключительной части мы свяжем все это воедино и исследуем, как фазовый сдвиг влияет на переходную характеристику фильтра, глядя на групповую задержку, импульсную характеристику и переходную характеристику, и что это означает для сигнала.
Примечания:
¹ Хэнк Зумбахлен. «Фазовые отношения в активных фильтрах». Аналоговый диалог , Volume 41, Number 4, 2007.
² Хэнк Зумбахлен. «Фазовый отклик в активных фильтрах, часть 2, низкочастотные и высокочастотные характеристики». Аналоговый диалог , Volume 43, Number 3, 2009.
использованная литература
Daryanani, G. Принципы синтеза и проектирования активных сетей n.John Wiley & Sons, 1976.
Грэм Дж., Дж. Тоби и Л. Хелсман. Разработка и применение операционных усилителей . McGraw-Hill, 1971.
Van Valkenburg, Mac. Конструкция аналогового фильтра . Холт, Райнхарт и Уинстон, 1982.
Уильямс, Артур Б. Справочник по проектированию электронных фильтров . McGraw-Hill, 1981.
Zumbahlen, Hank. Базовая линейная конструкция . Гл. 8. Analog Devices, Inc., 2006.
Zumbahlen, Hank. «Глава 5: Аналоговые фильтры.« Handboo по применению операционных усилителей k. Newnes-Elsevier, 2006.
Zumbahlen, Hank. Handboo Linear Circuit Design Handboo k. Newnes-Elsevier, 2008.
Zumbahlen, Hank.« Фазовые отношения в активных фильтрах ».

по виду их амплитудно-частотных характеристик

Фильтры нижних частот.

Фильтры верхних частот.

Полосовые фильтры (полосно-пропускающие).

Режекторные фильтры (полосно-заграждающие).

Всепропускающие фильтры (фазовые корректоры).

Russian HamRadio — Справочное пособие по высокочастотной схемотехнике. Глава 1.3. ВЧ-фильтры.

Исследование полосового ARC-фильтра

Схема активного полосового фильтра » Вот схема!

Схемотехника: Лабораторный практикум, страница 6

ние для передаточной функции, совпадающее для обоих фильтров, изображенных на рис. 1.8:

.

1.2. Задание на проведение исследований

Исследование МАЛОМОЩНЫХ транзисторных

усилителей

Филин — Производство Фильтров

Активные и пассивные электрические фильтры

— Учебное пособие по пассивному RC-фильтру

Цепь полосового фильтра

Частотная характеристика полосового фильтра 2-го порядка

.

Ступень фильтра высоких частот

Ступень фильтра нижних частот

Завершенная схема полосового фильтра

Полосовой фильтр Резонансная частота

Уравнение центральной частоты

Буферизация отдельных ступеней фильтрации

Активный полосовой фильтр — полосовой фильтр операционного усилителя

Схема активного полосового фильтра

Частотная характеристика активной полосы пропускания

Цепь инвертирующего полосового фильтра

Активный полосовой фильтр с множественной обратной связью

Активный фильтр с множественной обратной связью с бесконечным усилением

Активный полосовой фильтр, пример №1

Точка резонансной частоты

«Q» или фактор качества

Что такое полосовой фильтр? Нарисуйте и объясните частотную характеристику полосового фильтра

Полосовой фильтр

Частотная характеристика полосового фильтра

Sasmita

: что это такое? (Схема, конструкция и передаточная функция)

Что такое полосовой фильтр?

Схема полосового фильтра

Типы полосовых фильтров

Активный полосовой фильтр

Пассивный полосовой фильтр

Полосовой фильтр RLC

Широкополосный фильтр

Узкополосный фильтр

Передаточная функция полосового фильтра

Передаточная функция полосового фильтра первого порядка

Передаточная функция полосового фильтра второго порядка

Частота среза полосового фильтра

График Боде полосового фильтра или частотная характеристика

Идеальный полосовой фильтр

Уравнение полосового фильтра

Пример конструкции полосового фильтра

Полосовой фильтр — обзор

4.3.4.1 ВЧ-фильтры

Полосовой фильтр Частотная характеристика

Фазовая характеристика активных фильтров

Введение

Полосовая передаточная функция

Передаточная функция усилителя

Пример 1: 2-полюсный полосовой фильтр 1 кГц с Q = 20

Пример 2: Преобразование Чебышева ФНЧ в полосовой фильтр, 1 кГц, 3 полюса 0,5 дБ

Вывод

Примечания:

использованная литература

Похожие записи

Coocox: CooCox. Текущее состояние дел. / CoIDE / Pluslab

Приборы для измерения давления жидкости: Манометр — из чего состоит? Виды и типы

Регулируемая индуктивность: Регулируемая катушка индуктивности на кольцевом сердечнике

Добавить комментарий Отменить ответ