Что такое активная, реактивная и полная мощность в цепи переменного тока. Как рассчитываются эти виды мощности. Какая между ними связь. В чем измеряются активная, реактивная и полная мощность. Как определяется коэффициент мощности.
Виды мощности в цепи переменного тока
В цепи переменного тока выделяют три основных вида мощности:
- Активная мощность (P)
- Реактивная мощность (Q)
- Полная мощность (S)
Каждый из этих видов мощности характеризует определенные процессы, происходящие в электрической цепи. Рассмотрим их подробнее.
Активная мощность: характеристика и формула расчета
Активная мощность P — это мощность, которая необратимо преобразуется в другие виды энергии (тепловую, механическую и т.д.). Именно активная мощность выполняет полезную работу в электрической цепи.
Активная мощность измеряется в ваттах (Вт) и рассчитывается по формуле:
P = U * I * cos φ
где:
- U — действующее значение напряжения
- I — действующее значение тока
- cos φ — коэффициент мощности
Реактивная мощность: особенности и расчет
Реактивная мощность Q характеризует энергию, которая циркулирует между источником и нагрузкой, не совершая полезной работы. Она связана с созданием электромагнитных полей в индуктивных и емкостных элементах цепи.

Реактивная мощность измеряется в вольт-амперах реактивных (ВАр) и рассчитывается по формуле:
Q = U * I * sin φ
где φ — угол сдвига фаз между током и напряжением.
Полная мощность: определение и формула
Полная мощность S представляет собой геометрическую сумму активной и реактивной мощностей. Она характеризует общую нагрузку на электрическую сеть.
Полная мощность измеряется в вольт-амперах (ВА) и рассчитывается по формуле:
S = U * I
Также полную мощность можно выразить через активную и реактивную:
S = √(P² + Q²)
Взаимосвязь между видами мощности
Между активной, реактивной и полной мощностью существует четкая взаимосвязь, которую можно представить в виде так называемого «треугольника мощностей»:
- Гипотенуза треугольника — полная мощность S
- Катеты — активная P и реактивная Q мощности
- Угол между S и P — φ (угол сдвига фаз)
Из этого треугольника следуют соотношения:
- P = S * cos φ
- Q = S * sin φ
- tg φ = Q / P
Коэффициент мощности: значение и расчет
Коэффициент мощности (cos φ) показывает, какую часть полной мощности составляет активная мощность. Он является важной характеристикой эффективности использования электроэнергии.

Коэффициент мощности рассчитывается по формуле:
cos φ = P / S
Чем ближе значение cos φ к единице, тем эффективнее используется электроэнергия в цепи.
Практическое применение понятий мощности
Понимание различных видов мощности и их взаимосвязи важно для:
- Правильного выбора электрооборудования
- Расчета нагрузок на электрические сети
- Оценки эффективности использования электроэнергии
- Компенсации реактивной мощности для повышения энергоэффективности
Измерение мощности в электрических цепях
Для измерения различных видов мощности используются специальные приборы:
- Ваттметры — для измерения активной мощности
- Варметры — для измерения реактивной мощности
- Измерители коэффициента мощности
- Многофункциональные измерители мощности, способные определять все виды мощности и другие параметры электрической сети
Влияние характера нагрузки на мощность
Характер нагрузки в электрической цепи существенно влияет на соотношение различных видов мощности:
- Активная нагрузка (например, лампы накаливания, нагревательные приборы) потребляет только активную мощность
- Индуктивная нагрузка (электродвигатели, трансформаторы) потребляет как активную, так и реактивную мощность
- Емкостная нагрузка (конденсаторы) также потребляет оба вида мощности, но реактивная мощность имеет противоположный знак по сравнению с индуктивной нагрузкой
Способы улучшения коэффициента мощности
Низкий коэффициент мощности приводит к неэффективному использованию электроэнергии. Для его повышения применяются следующие методы:

- Установка компенсирующих устройств (например, конденсаторных батарей)
- Замена недогруженных двигателей на двигатели меньшей мощности
- Применение синхронных двигателей вместо асинхронных
- Использование оборудования с встроенными корректорами коэффициента мощности
Особенности расчета мощности в трехфазных цепях
В трехфазных цепях расчет мощности имеет свои особенности:
- Активная мощность трехфазной цепи: P = √3 * Uл * Iл * cos φ
- Реактивная мощность: Q = √3 * Uл * Iл * sin φ
- Полная мощность: S = √3 * U
где Uл и Iл — линейные напряжение и ток соответственно.
Мощность в цепях с несинусоидальными токами и напряжениями
В реальных электрических сетях часто присутствуют гармонические искажения, что влияет на расчет мощности:
- Появляется понятие мощности искажения D
- Полная мощность в этом случае: S = √(P² + Q² + D²)
- Вводится понятие коэффициента искажения мощности
Учет этих факторов важен для точного анализа энергопотребления в современных электрических системах.
Мощность переменного тока — виды, формула, примеры вычисления » Kupuk.net
Показатель мощности переменного тока характеризует темп передачи или видоизменения электроэнергии. Мощность — величина, полученная от произведения силы тока и напряжения на выбранном участке цепи. В Международной СИ применяется обозначение Ватт (интернациональное — W, в России — Вт).
Общее понятие
Электрическое напряжение определяется как отношение работы поля по переброске пробного заряда из одной заданной точки в другую к размеру потенциала. При дислокации единичного резерва выполняется работа, которая равняется напряжению на искомом участке. Общая мощность получают умножением работы электрического поля для единичного заряда на число потенциалов за определенную единицу времени.
В переменной электрической цепи выделяется 3 вида мощности:
- активный P;
- реактивный Q;
- полного типа S.
В цепи переменного электричества формула для расчета постоянного тока применяется только для вычисления мгновенной мощности. Этот показатель претерпевает изменения во времени и почти не имеет практического смысла для всех остальных расчетов. Среднезначимый показатель мощности требует временной интеграции. Мгновенная мощность объединяется в течение определенного промежутка для расчета величины в магистрали с периодическим изменением силы переменного потока и синусоидального напряжения.
Этот показатель претерпевает изменения во времени и почти не имеет практического смысла для всех остальных расчетов. Среднезначимый показатель мощности требует временной интеграции. Мгновенная мощность объединяется в течение определенного промежутка для расчета величины в магистрали с периодическим изменением силы переменного потока и синусоидального напряжения.
Применяется концепция комплексных чисел для связывания всех трех видов мощности. Это понятие обозначает, что в переменной цепи нагрузка выражается подобным числом так, что активная разновидность представляется действительной составляющей. Реактивный показатель выступает мнимым показателем, а полная мощность показывается в форме модуля. В этих расчетах принимает участие угол сдвига фаз φ, который является аргументом баланса мощностей в цепи переменного тока.
Активная мощность
Активная скорость преобразования выражается также через взаимное отношение силы потока, напряжения к значению активной составляющей сопротивления. В магистрали синусоидального и несинусоидального движения электронов активная нагрузка приравнивается к сумме аналогичных значений на отдельных участках.
В магистрали синусоидального и несинусоидального движения электронов активная нагрузка приравнивается к сумме аналогичных значений на отдельных участках.
Для определения среднего периодического размера используется активная мощность переменного тока, формула расчета P = U . I . cos φ (косинус), где:
Средний показатель мгновенной скорости преобразования в однофазной цепи берется в виде среднеквадратичного значения тока и напряжения с определенным углом сдвига. В цепях несинусоидального электричества мощность приравнивается к сумме соответствующих показателей отдельных перемещений. С помощью активной мощности характеризуется интенсивность необратимого видоизменения электроэнергии в другие разновидности, например, электромагнитную или тепловую.
Проходящая мощность используется в качестве активной в концепции длинных магистралей для анализа электромагнитных течений, протяженность которых сопоставляется с размерностью волны. Искомое значение рассчитывается как разница между понижающейся и отражающейся мощностями. От свойств коэффициента углового смещения зависят полученные показатели отрицательной или положительной нагрузки активного типа.
Искомое значение рассчитывается как разница между понижающейся и отражающейся мощностями. От свойств коэффициента углового смещения зависят полученные показатели отрицательной или положительной нагрузки активного типа.
Реактивная характеристика
Для обозначения применяется дополнительно единица вольт-ампер реактивный (вар). В русских аналогах используется вар, а международные специалисты применяют var. В РФ единица допускается для электротехнических расчетов в форме внесистемного значения.
Нахождение производится по формуле P = U . I . sin φ (синус), где:
При диапазоне показателя от 0 до 90º (ток отстает от напряжения, а нагрузка носит активно-индуктивный вид) синус φ будет иметь положительное значение. При угловом сдвиге от 0 до -90º (поток электронов опережает нагрузку, мощность отличается активно-емкостным свойством) константа всегда показывает отрицательный знак. Реактивная мощность характеризует напряженность, которая возникает в электромеханических приборах и цепях при изменении энергетических волн поля в магистрали переменного синусоидального потока.
При угловом сдвиге от 0 до -90º (поток электронов опережает нагрузку, мощность отличается активно-емкостным свойством) константа всегда показывает отрицательный знак. Реактивная мощность характеризует напряженность, которая возникает в электромеханических приборах и цепях при изменении энергетических волн поля в магистрали переменного синусоидального потока.
В физическом смысле реактивная нагрузка показывает энергию, которая перекачивается от источника тока на конденсаторы, индукторы, двигательные обмотки, а впоследствии возвращается к источнику за один колебательный период. Реактивная мощность не принимает участия в работе электротока. В случае положительной характеристики устройство потребляет, а нагрузка с отрицательным знаком говорит о производстве энергии.
Это обстоятельство рассматривается в условном контексте, т. к. почти все энергопотребляющие приборы, например, двигатели асинхронной работы, а также полезная нагрузка, подаваемая через трансформатор, относятся к активно-индуктивным видам. Синхронные двигатели электростанций одновременно производят и потребляют энергию в зависимости от максимальной величины электротока возбуждения в роторных обмотках. Эта особенность применяется для координации уровня нагрузки в магистрали в электротехнике.
Синхронные двигатели электростанций одновременно производят и потребляют энергию в зависимости от максимальной величины электротока возбуждения в роторных обмотках. Эта особенность применяется для координации уровня нагрузки в магистрали в электротехнике.
С помощью современных преобразователей производится компенсация реактивной нагрузки во избежание перегрузок и для увеличения коэффициента мощности электроустановок. Приборы более точно оценивают размер энергии, которая поступает в обратном направлении от индуктора к источнику переменного тока.
Полная нагрузка
Показатель используется в физике для описания потребляемой мощности, которая прилагается к подводящим агрегатам электросети с использованием резисторов. Суммируются параметры ЭДС распределительных щитков, кабелей, проводов, ЛЭП, трансформаторов.
Полную нагрузку можно рассчитать по формуле S = U . I, где:
I, где:
Параметр темпа преобразований зависит от характеристик применяемого тока, а не от свойств фактически использованной нагрузки. По этой причине полная мощность распределительных электрощитов и трансформаторных агрегатов измеряется в вольт-амперах, а значение ватт к ней не применяется.
Работа в различных условиях
Модуль комплексного показателя интенсивности передвижения равняется показателю полной нагрузки. Действительная составляющая часть приравнивается к активной силе, а мнимая считается реактивным видом. Имеет место положительный или отрицательный знак, что зависит от интенсивности загруженности цепи. Комплексная мощность должна соответствовать сопряженному электрическому сопротивлению. Положительная нагрузка характеризуется соотношением Р > 0, а знак минус проявляется в случае Р < 0.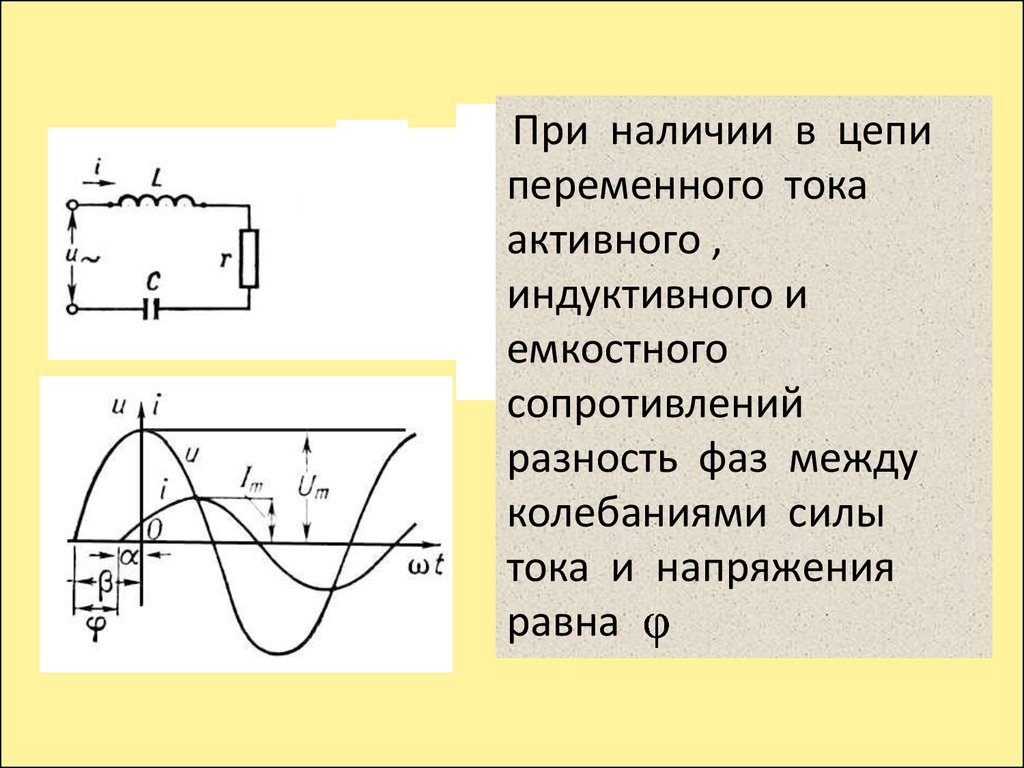
Измерение мощностных характеристик переменного потока электронов проводится при пропускании равного по значению тока по фазным проводникам. Показатели силы течения заряженных частиц с применением нулевого проводника имеют ничтожную размерность. Равномерная или симметричная фазовая нагрузка в трехфазной магистрали зависит от величины протекающих токов. Неравномерная или несимметричная нагрузка зависит от прохождения потока по нейтральным или нулевым кабелям. Общий мощностной уровень находится суммированием.
Если присутствует фазовый сдвиг между напряжением и силой тока, то он совпадает с углом смещения между векторными радиусами показателей электротока. В условиях переменного напряжения совпадение векторных радиусов тока и вольтажа отмечается только при отсутствии в цепи конденсаторов и катушек индукции. Установка индукторов не мешает совпадению фазных значений. При этом происходит векторное вращение равной интенсивности. График смещения внутреннего угла остается постоянным.
Если в магистрали происходит сдвиг напряжения и переменного тока, то мощностные показатели представляются значением с отрицательным знаком, так как калькулятор перемножает положительные и отрицательные величины. Продолжительность периодов зависит от уровня смещения фаз. При этом длительность отрицательных нагрузок определяет характеристики сдвига. При расчетах используются показатели сопротивления, которые знакомы из физического закона Ома.
Коэффициент скорости преобразования
Мощностной коэффициент является показателем потребления тока при присутствии реактивного компонента и искажающей нагрузки. Значение коэффициента отличается от понятия косинуса сдвигаемого угла. Второе понятие характеризуется смещением протекающего переменного тока, напряжения и используется только при синусоидальном токе и силе равного значения.
Коэффициент равняется отношению расходуемой нагрузки к ее полному значению. При этом работа совершается за счет активного вида преобразования. При синусоидальном токе и вольтаже полная нагрузка находится в виде суммы реактивной и активной форм. Активная нагрузка приравнивается к усредненному произведению силы тока и напряжения и не может быть выше произведения аналогичных среднеквадратических размерностей. Мощностной коэффициент показывается в диапазоне от 0 до 1 или ставится в процентах от 0 до 100.
При математическом расчете числовой множитель интерпретируется в качестве косинуса угла между токовыми векторами и направлением приложения вольтажа. Поэтому при синусоидальных характеристиках размерность коэффициента может совпадать с косинусом угла. Если применяется только синусоидальный вольтаж, а ток используется несинусоидальный с нагрузкой без реактивного компонента, то числовой переходник равняется части нагрузки при первых искажениях потребительского тока.
Если реактивный элемент присутствует в нагрузке, то, помимо мощностного коэффициента, указывается характер работы (емкостно-активный или индуктивно-активный).
Коэффициент в этих случаях отличается и является отстающим или опережающим значением.
Практическое применение и коррекция
Если к розетке с синусоидальным напряжением 50 Гц и 230 В подсоединить нагрузку с опережением или отставанием тока от напряжения на какую-то угловую величину, то на активной внутренней катушке будет создаваться увеличенная мощность. Это значит, что при работе в таких условиях выделяется много тепла, и электростанция отводит его в увеличенном количестве, по сравнению с применением активной нагрузки.
Коэффициенты полезного действия и мощности отличаются друг от друга. Мощностной показатель не влияет на потребление приемника, подключенного к сети, но изменяет энергетические потери в подводных проводах и местах выработки энергии или ее преобразования. В доме электросчетчик не реагирует на проявление мощности, так как оплачивается только та энергия, за счет которой работают приборы.
КПД влияет на потребляемую активную нагрузку.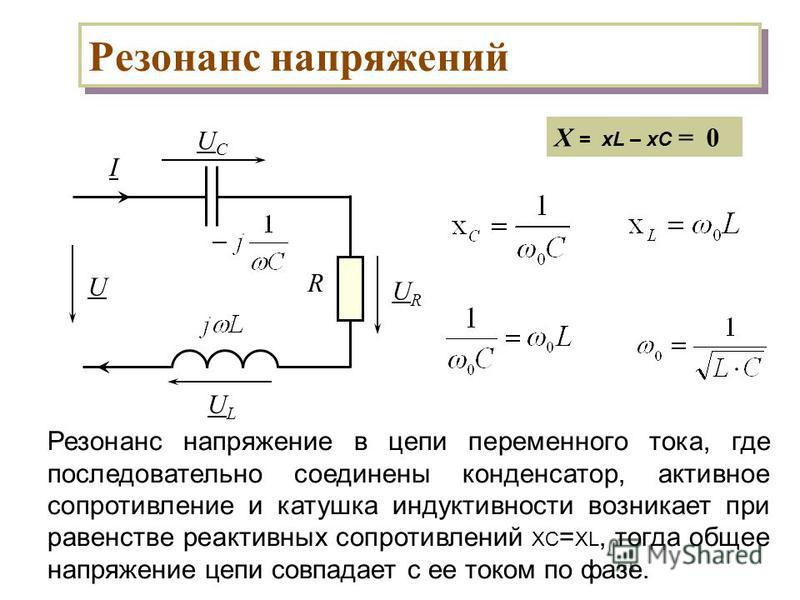 Например, энергосберегающая лампа потребляет в полтора раза больше электричества, чем аналогичный прибор накаливания. Это говорит о высоком коэффициенте полезного действия у первой лампы. Но показатель нагрузки может быть низким и высоким в обоих вариантах.
Например, энергосберегающая лампа потребляет в полтора раза больше электричества, чем аналогичный прибор накаливания. Это говорит о высоком коэффициенте полезного действия у первой лампы. Но показатель нагрузки может быть низким и высоким в обоих вариантах.
Коррекция заключается в приведении потребления прибора с низким мощностным коэффициентом к стандартным показателям при питании от силовой цепи переменного тока. Технически это осуществляется применением действенной схемы на входном устройстве, которая помогает равномерно использовать фазную мощность и исключает перегрузку нулевого провода. При этом снижаются всплески потребительского тока на верхушке синусоиды питающего вольтажа.
Реактивная нагрузка корректируется при включении в магистраль элемента с обратным действием. Например, в двигателе переменного тока для компенсации действия ставится конденсатор параллельно питающей линии. Применяется система активного или пассивного корректора при изменении используемого тока во время колебательного периода подпитывающего напряжения для преобразования коэффициента. Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.
Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.
Выберите продукцию из спискаНормирующие преобразователи измерительные …НПСИ-ТП нормирующий преобразователь сигналов термопар и напряжения …НПСИ-237-ТП нормирующий преобразователь сигналов термопар и напряжения, IP65 …НПСИ-ТС нормирующий преобразователь сигналов термосопротивлений …НПСИ-237-ТС нормирующий преобразователь сигналов термосопротивлений, IP65 …НПСИ-150-ТП1 нормирующий преобразователь сигналов термопар и напряжения …НПСИ-150-ТС1 нормирующий преобразователь сигналов термометров сопротивления …НПСИ-110-ТП1 нормирующий преобразователь сигналов термопар и напряжения …НПСИ-110-ТС1 нормирующий преобразователь сигналов термометров сопротивления . |
активная, реактивная, полная (P, Q, S), коэффициент мощности (PF)
Из письма клиента:
Подскажите, ради Бога, почему мощность ИБП указывается в Вольт-Амперах, а не в привычных для всех киловаттах. Это сильно напрягает. Ведь все уже давно привыкли к киловаттам. Да и мощность всех приборов в основном указана в кВт.
Алексей. 21 июнь 2007
В технических характеристиках любого ИБП указаны полная мощность [кВА] и активная мощность [кВт] – они характеризуют нагрузочную способность ИБП. Пример, см. фотографии ниже:
Мощность не всех приборов указана в Вт, например:
- Мощность трансформаторов указывается в ВА:
http://www. mstator.ru/products/sonstige/powertransf (трансформаторы ТП: см приложение)
mstator.ru/products/sonstige/powertransf (трансформаторы ТП: см приложение)
http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ: см приложение) - Мощность конденсаторов указывается в Варах:
http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39: см приложение)
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК: см приложение) - Примеры других нагрузок — см. приложения ниже.
Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.
Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность и реактивная мощность точно характеризуют нагрузку.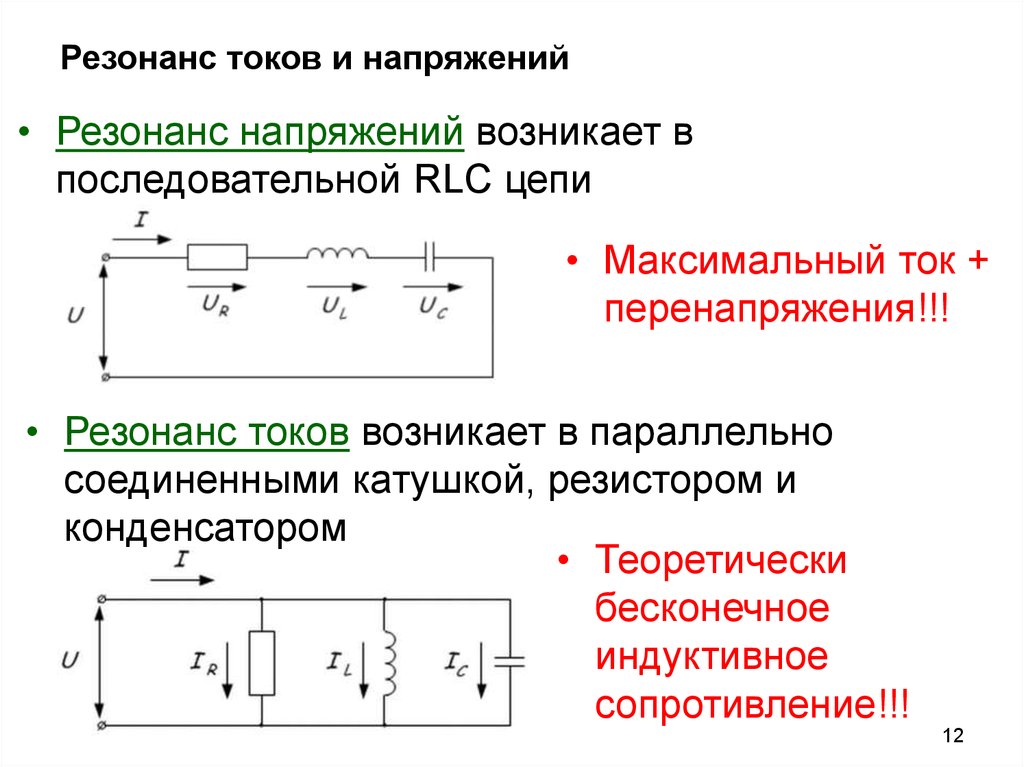
Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности. Все эти 4 параметра:
- Активная мощность: обозначение P, единица измерения: Ватт
- Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
- Полная мощность: обозначение S, единица измерения: ВА (Вольт Ампер)
- Коэффициент мощности: обозначение k или cosФ
Эти параметры связаны соотношениями: S*S=P*P+Q*Q, cosФ=k=P/S
Также cosФ называется коэффициентом мощности (Power Factor – PF)
Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.
Например, электромоторы, лампы (разрядные) — в тех. данных указаны P[кВт] и cosФ:
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР: см. приложение)
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ: см. приложение)
(примеры технических данных разных нагрузок см. приложение ниже)
То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.
Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
– при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
См. учебники по электротехнике, например:
1. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.
2. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.
3. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
Так же см. AC power, Power factor, Electrical resistance, Reactance http://en.wikipedia.org
(перевод: http://electron287.narod.ru/pages/page1.html)
Приложение
Пример 1: мощность трансформаторов и автотрансформаторов указывается в ВА (Вольт·Амперах)
Трансформаторы питания номинальной выходной мощностью 25-60 ВА
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП)
http://metz.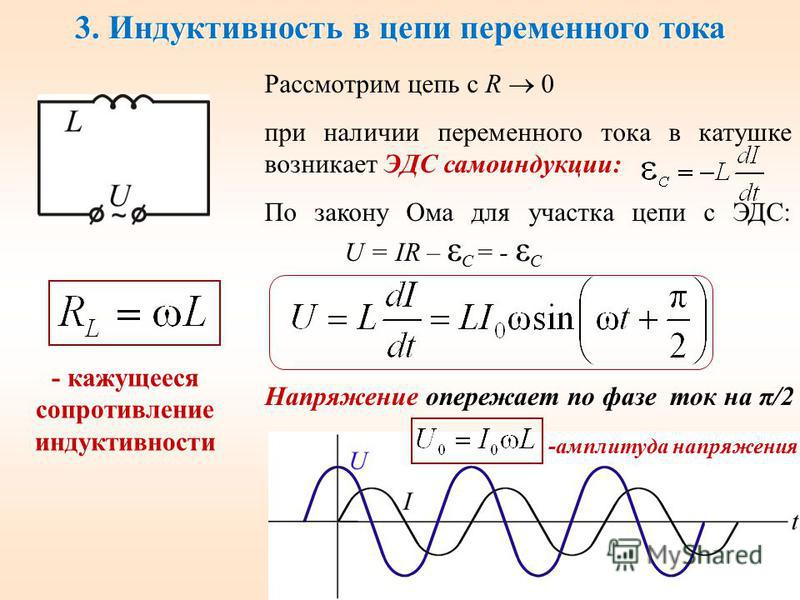 by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)
by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)
| АОСН-2-220-82 | |
| Латр 1.25 | АОСН-4-220-82 |
| Латр 2.5 | АОСН-8-220-82 |
| АОСН-20-220 | |
| АОМН-40-220 | |
http://www.gstransformers.com/products/voltage-regulators.html (ЛАТР / лабораторные автотрансформаторы TDGC2)
Пример 2: мощность конденсаторов указывается в Варах (Вольт·Амперах реактивных)
http://www. elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)
elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК)
Пример 3: технические данные электромоторов содержат активную мощность (кВт) и cosФ
Для таких нагрузок как электромоторы, лампы (разрядные), компьютерные блоки питания, комбинированные нагрузки и др. — в технических данных указаны P [кВт] и cosФ (активная мощность и коэффициент мощности) или S [кВА] и cosФ (полная мощность и коэффициент мощности).
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР)
http://www.weiku.com/products/10359463/Stainless_Steel_cutting_machine.html
(комбинированная нагрузка – станок плазменной резки стали / Inverter Plasma cutter LGK160 (IGBT)
Технические данные разрядных ламп содержат активную мощность (кВт) и cosФ
http://www. mscom.ru/katalog.php?num=38 (лампы ДРЛ)
mscom.ru/katalog.php?num=38 (лампы ДРЛ)
http://www.silverstonetek.com.tw/product.php?pid=365&area=en (блок питания ПК)
Дополнение 1
Если нагрузка имеет высокий коэффициент мощности (0.8 … 1.0), то её свойства приближаются к активной нагрузке. Такая нагрузка является идеальной как для сетевой линии, так и для источников электроэнергии, т.к. не порождает реактивных токов и мощностей в системе.
Если нагрузка имеет низкий коэффициент мощности (менее 0.8 … 1.0), то в линии питания циркулируют большие реактивные токи (и мощности). Это паразитное явление приводит к повышению потерь в проводах линии (нагрев и др.), нарушению режима работы источников (генераторов) и трансформаторов сети, а также др. проблемам.
Поэтому во многих странах приняты стандарты нормирующие коэффициент мощности оборудования.
Дополнение 2
Оборудование однонагрузочное (например, БП ПК) и многосоставное комбинированное (например, фрезерный промышленный станок, имеющий в составе несколько моторов, ПК, освещение и др. ) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.
) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.
Дополнение 3. Важное замечание относительно коэффициента мощности ИБП и стабилизаторов напряжения
Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8.
В стабилизаторах напряжения дело обстоит иначе. Для стабилизатора коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
Дополнение 4
Наглядные примеры чистой активной и чистой реактивных нагрузок:
- К сети переменного тока 220 VAC подключена лампа накаливания 100 Вт – везде в цепи есть ток проводимости (через проводники проводов и вольфрамовый волосок лампы). Характеристики нагрузки (лампы): мощность S=P~=100 ВА=100 Вт, PF=1 => вся электрическая мощность активная, а значит она целиком поглащается в лампе и превращается в мощность тепла и света.
- К сети переменного тока 220 VAC подключен неполярный конденсатор 7 мкФ – в цепи проводов есть ток проводимости, внутри конденсатора идёт ток смещения (через диэлектрик).
 Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Дополнение 5
Для обозначения преобладающего реактивного сопротивления (индуктивного либо ёмкостного) коэффициенту мощности приписывается знак:
+ (плюс) – если суммарное реактивное сопротивление является индуктивным (пример: PF=+0.5). Фаза тока отстаёт от фазы напряжения на угол Ф.
— (минус) – если суммарное реактивное сопротивление является ёмкостным (пример: PF=-0,5). Фаза тока опережает фазу напряжения на угол Ф.
Дополнение 6
В различных областях техники мощность может быть либо полезной, либо паразитной НЕЗАВИСИМО от того активная она или реактивная. Например, необходимо различать активную полезную мощность рассеиваемую на рабочей нагрузке и активную паразитную мощность рассеиваемую в линии электропередачи. Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.
Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.
Дополнительные вопросы
Вопрос 1:
Почему во всех учебниках электротехники при расчете цепей переменного тока используют мнимые числа / величины (например, реактивная мощность, реактивное сопротивление и др.), которые не существуют в реальности?
Ответ:
Да, все отдельные величины в окружающем мире – действительные. В том числе температура, реактивное сопротивление, и т. д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].
д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].
Замечание:
Раньше в физике использовались только одиночные величины и при расчете все математические величины соответствовали реальным величинам окружающего мира. Например, расстояние равно скорость умножить на время (S=v*t). Затем с развитием физики, то есть по мере изучения более сложных объектов (свет, волны, переменный электрический ток, атом, космос и др.) появилось такое большое количество физических величин, что рассчитывать каждую в отдельности стало невозможно. Это проблема не только ручного вычисления, но и проблема составления программ для ЭВМ. Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:
Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:
- Полное сопротивление (импеданс) Z=R+iX
- Полная мощность S=P+iQ
- Диэлектрическая проницаемость e=e’+ie»
- Магнитная проницаемость m=m’+im»
- и др.
Вопрос 2:
На странице http://en.wikipedia.org/wiki/Ac_power показаны S P Q Ф на комплексной, то есть мнимой / несуществующей плоскости. Какое отношение это все имеет к реальности?
Ответ:
Проводить расчеты с реальными синусоидами сложно, поэтому для упрощения вычислений используют векторное (комплексное) представление как на рис. выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.
выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.
Вопрос 3:
Обычными токовыми клещами и мультиметром измерен ток нагрузки 10 A, и напряжение на нагрузке 225 В. Перемножаем и получаем мощность нагрузки в Вт: 10 A · 225В = 2250 Вт.
Ответ:
Вы получили (рассчитали) полную мощность нагрузки 2250 ВА. Поэтому ваш ответ будет справедлив только, если ваша нагрузка чисто активная, тогда действительно Вольт·Ампер равен Ватту. Для всех других типов нагрузок (например электромотор) – нет. Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:
Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:
См. дополнительную литературу, например:
[1]. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.
[2]. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.
[3]. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
[4]. AC power, Power factor, Electrical resistance, Reactance
http://en.wikipedia.org (перевод: http://electron287.narod.ru/pages/page1.html)
[5]. Теория и расчёт трансформаторов малой мощности Ю.Н.Стародубцев / РадиоСофт Москва 2005 г. / rev d25d5r4feb2013
[6]. Международная система единиц, СИ, см напр. ГОСТ 8.417-2002. ЕДИНИЦЫ ВЕЛИЧИН
Отличия кВА от кВт
«В чем отличия кВА от кВт?» — этот вопрос — один из наиболее популярных. Его часто задают покупатели ИБП. Продавцы ИБП (которым, собственно, и задают это вопрос) отвечают на него по-разному и почти всегда неправильно. Попробуем разобраться, как рассчитывают мощность в электрической цепи.
Его часто задают покупатели ИБП. Продавцы ИБП (которым, собственно, и задают это вопрос) отвечают на него по-разному и почти всегда неправильно. Попробуем разобраться, как рассчитывают мощность в электрической цепи.
В цепи постоянного тока дело обстоит довольно просто. Электрический ток, поступая из источника постоянного тока в нагрузку, производит в ней полезную (или бесполезную) работу по перемещению зарядов в направлении электрического поля. Рассчитать мощность в такой цепи очень просто: нужно умножить ток на падение напряжения на нагрузке:
P[Ватт] = I[Ампер] × U[Вольт]
В цепи переменного тока, с которой нам приходится иметь дело, рассматривая работу ИБП, все немного по-другому.
Для переменного тока вводится понятие мгновенной мощности — это произведение мгновенных значений переменных напряжения и тока. Активная мощность (средняя по времени мощность, выделяемая в нагрузке) — она измеряется в ваттах — равна среднему за период значению мгновенной мощности.
Если напряжение имеет синусоидальную форму, и нагрузка в цепи активная (или, иначе говоря, омическая — например, лампы накаливания), то активная мощность равна произведению действующих значений напряжения и тока. Т.е. она рассчитывается примерно так же, как и мощность в цепи постоянного тока:
P[Ватт] = Uдейств × Iдейств.
Рис. 1. Мгновенная мощность в цепи переменного тока
- а) синусоидальный ток в
активной нагрузке; - б) синусоидальный ток в
нагрузке с реактивной составляющей; - в) несинусоидальный ток.
На рис.1. видно, что в этом случае напряжение и ток всегда имеют одинаковый знак (становятся положительными и отрицательными одновременно). Поэтому мгновенная мощность всегда положительна. Физически это означает, что в любой момент времени мощность выделяется в нагрузке. Иначе говоря, так же как в цепи постоянного тока, заряды всегда движутся в направлении действия электрического поля.
Если напряжение и ток имеют синусоидальную форму, но нагрузка имеет емкостную или индуктивную (реактивную) составляющую, то ток опережает по фазе напряжение или отстает от него. В этом случае мощность, выделяемая в нагрузке, уменьшается.
На рисунке б) видно, что из-за фазового сдвига, в некоторые моменты времени, напряжение и ток имеют противоположные знаки. В это время мгновенная мощность оказывается отрицательной и уменьшает среднюю за период мгновенную мощность. Электротехник скажет, что в эти моменты времени ток течет из нагрузки в источник тока. С точки зрения физика, в эти моменты времени заряды по инерции движутся против сил электрического поля.
Формула для средней за период мощности для случая нагрузки с реактивной составляющей несколько изменяется. В ней появляется коэффициент мощности. Для синусоидальных напряжения и тока он численно равен знакомому со средней школы «косинусу фи»:
P[Ватт] = Uдейств × Iдейств × Cos (fi).
Здесь: fi — угол сдвига фаз между напряжением и током.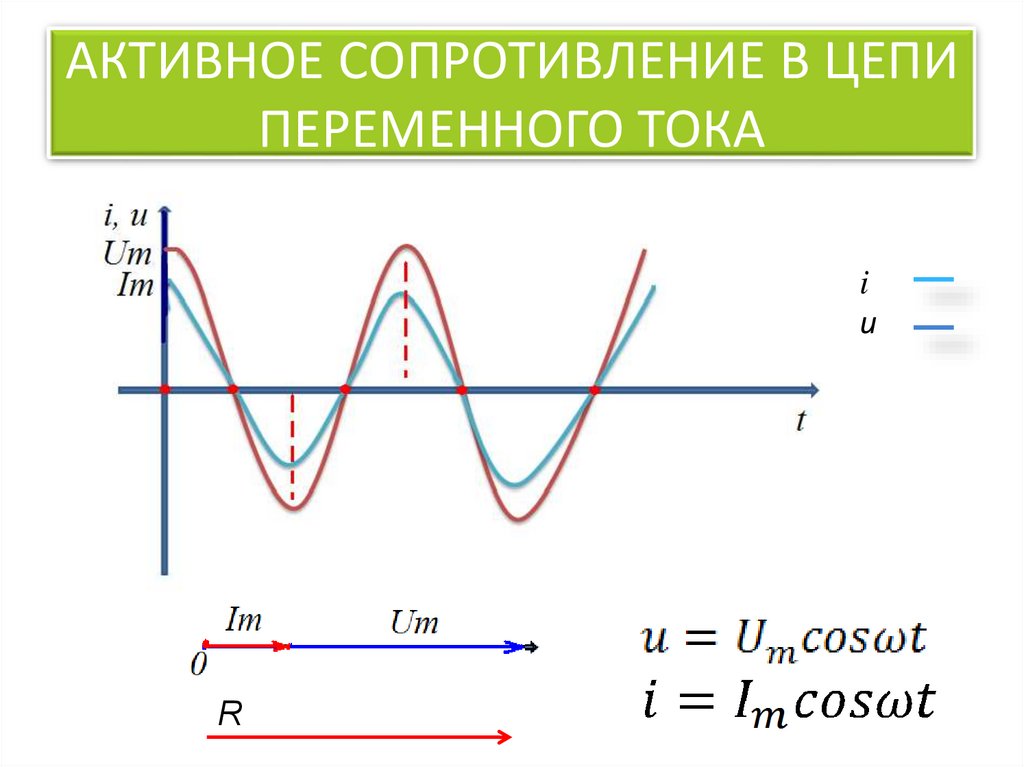
Произведение действующих значений напряжения и тока называется полной мощностью цепи переменного тока и измеряется в вольт-амперах (ВА). Полная мощность всегда больше или равна активной (выделяемой в нагрузке) мощности.
Если нагрузкой является компьютер, то дело обстоит еще немного сложнее. Ток, потребляемый компьютером, имеет несинусоидальную форму (см. рис. 30в). Мощность, выделяемая в нагрузке, при такой форме тока также меньше, чем произведение действующих значений напряжения и тока. На рис. 30в видно, что при некоторых значениях напряжения (когда напряжение мало) компьютер не потребляет тока. Мгновенная мощность в эти моменты времени равна нулю — напряжение как бы «пропадает зря», не производя работы.
Активная (выделяемая в нагрузке) мощность для случая нелинейной нагрузки выражается формулой:
P[Ватт] = Uдейств × Iдейств × К,
где: К — коэффициент мощности.
Ток «компьютерной» нагрузки как правило несколько опережает напряжение. Но сдвиг фаз очень невелик (10-30 градусов), поэтому коэффициент мощности для компьютера не равен косинусу угла фазового сдвига, а значительно меньше.
Если посчитать среднюю за период мощность импульсного блока питания и разделить на произведение действующих значений напряжения и тока, то получившийся коэффициент мощности будет примерно равен 0.6-0.8.
По данным фирмы American Power Conversion коэффициент мощности равен 0.6 для персональных компьютеров и 0.7 для мини компьютеров. На самом деле, коэффициент мощности компьютерной нагрузки связан с коэффициентом амплитуды тока и, даже для одного и того же импульсного блока питания, зависит от того, насколько блок питания использует свою номинальную мощность. Так, если импульсный блок питания нагружен слабо (к нему подключено мало потребителей — дисководов, процессоров и т.д.), то коэффициент амплитуды увеличивается, а коэффициент мощности уменьшается.
В зависимости от устройства ИБП, ток в разных местах его схемы зависит либо от активной мощности нагрузки (например, ток, отбираемый от аккумуляторов), либо от ее полной мощности (например, ток на выходе ИБП). Поэтому, как правило, производители ИБП указывают два значения максимальной мощности нагрузки, которая может быть подключена к ИБП: полную мощность в вольт-амперах и активную мощность в ваттах. В принципе, в каждом конкретном случае (для каждого сочетания ИБП + нагрузка) можно определить, какой из пределов (в ваттах или вольт-амперах) является критичным. Но это может сделать только специалист, зная, как устроен ИБП и как устроена нагрузка. Общего рецепта здесь дать нельзя — слишком много вариантов (разные типы и схемы ИБП, разные сдвиги фаз и коэффициенты амплитуды нагрузки и т.д.). Поэтому подбирая ИБП, покупатель должен просто учитывать оба ограничения. Т.е. и активная, и полная мощность его оборудования должны быть меньше заявленных производителем ИБП максимальных значений. Обычно, для надежной работы ИБП, берут еще и запас примерно в 30%.
В принципе, в каждом конкретном случае (для каждого сочетания ИБП + нагрузка) можно определить, какой из пределов (в ваттах или вольт-амперах) является критичным. Но это может сделать только специалист, зная, как устроен ИБП и как устроена нагрузка. Общего рецепта здесь дать нельзя — слишком много вариантов (разные типы и схемы ИБП, разные сдвиги фаз и коэффициенты амплитуды нагрузки и т.д.). Поэтому подбирая ИБП, покупатель должен просто учитывать оба ограничения. Т.е. и активная, и полная мощность его оборудования должны быть меньше заявленных производителем ИБП максимальных значений. Обычно, для надежной работы ИБП, берут еще и запас примерно в 30%.
Категории нагрузок реле переменного и постоянного тока
Категории нагрузок реле
| Категория нагрузки | Типичные примеры нагрузок |
| АС-1 | Активные нагрузки или нагрузки с незначительной индуктивностью |
| АС-2 | Коллекторные электродвигатели, включение и выключение |
| АС-3 | Асинхронные электродвигатели с КЗ ротором, включение, выключение при вращающемся роторе |
| АС-4 | Асинхронные электродвигатели с КЗ ротором, включение и выключение при вращающемся роторе |
| АС-5а | Включение люминесцентных ламп или ламп с электронным управлением разрядом |
| АС-5б | Включение ламп накаливания |
| АС-6а | Включение и отключение трансформаторов |
| АС-6б | Включение батарей конденсаторов |
| АС-7а | Небольшие индуктивные нагрузки в оборудовании для бытовой электротехники |
| АС-7б | Включение и отключение электродвигателей бытовой электротехники |
| АС-8а | Герметичные компрессоры холодильников с ручным сбросом после возникновения перегрузки |
| АС-8б | Герметичные компрессоры холодильников с автоматическим сбросом и перезапуском после возникновения перегрузки |
| АС-12 |
Управление резистивными нагрузками и полупроводниковыми приборами при применении опторазвязок для гальванической изоляции |
| АС-13 | Управление резистивными нагрузками и полупроводниковыми приборами при применении трансформаторов для гальванической изоляции |
| АС-14 | Управление небольшими электромагнитами и контакторами |
| АС-15 | Управление электромагнитами переменного тока |
| АС-20 | Коммутация при отсутствии тока нагрузки |
| АС-21 | Управление резистивными нагрузками с небольшими перегрузками при переходных процессах |
| АС-22 | Управление резистивно-индуктивными нагрузками, включая небольшие перегрузки при переходных процессах |
| АС-23 | Коммутация электродвигателей или других мощных индуктивных нагрузок |
| Категория нагрузки | Типичные примеры нагрузок |
| А | Защитные схемы без требований к кратковременному току перегрузки |
| В | Защитные схемы с нормированным кратковременным током перегрузки |
| Категория нагрузки | Типичные примеры нагрузок |
| DC-1 | Активные нагрузки или нагрузки с незначительной индуктивностью |
| DC-3 | Шунтовые электродвигатели, включение, выключение при вращающемся роторе, динамическое торможение |
| DC-5 | Электродвигатели, включение, выключение при вращающемся роторе, динамическое торможение |
| DC-6 | Включение ламп накаливания |
| DC-12 |
Управление резистивными нагрузками и полупроводниковыми приборами при применении опторазвязок для гальванической изоляции |
| DC-13 | Управление электромагнитами |
| DC-14 | Управление электромагнитными нагрузками со встроенными ограничительными резисторами |
| DC-20 | Коммутация при отсутствии тока нагрузки |
| DC-21 | Управление резистивными нагрузками с небольшими перегрузками при переходных процессах |
| DC-22 |
Управление резистивно-индуктивными нагрузками, включая небольшие перегрузки при переходных процессах (например, шунтовые электродвигатели) |
| DC-23 | Коммутация электродвигателей или других мощных индуктивных нагрузок |
У нас вы можете приобрести различные виды реле лучшего качества от проверенных производителей.
Также на нашем сайте есть компенсатор реактивной мощности в Москве в магазине компании АТ-Электросистемы, который отличается высоким качеством и недорогими ценами.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
В большинстве случаев электрические цепи содержат как активное, так и реактивное сопротивления. u = Uм ⋅ sin ωt, то ток в цепи i = Iм ⋅ sin(ωt — φ). Мгновенная мощность цепи p = u ⋅ i = Uмsinωt ⋅ Iм ⋅ sin(ωt — φ) = Uм ⋅ Iм [sinωt ⋅ sin (ωt — φ)] = UI [2 sinωt ⋅ sin (ωt — φ)]. Выражение, стоящее в квадратных скобках, можно на основа-кии тригонометрической формулы представить как разность косинусов [cos φ — cos (2ωt — φ)]. Таким образом, p = UI [cos φ — cos (2ωt — φ)] = UI ⋅ cos φ — UI cos (2ωt — φ). Среднее значение мгновенной мощности за период равно UI ⋅ cos φ, так как среднее значение cos (2ωt — φ) за период равно нулю. Следовательно, активная мощность цепей переменного тока определяется в общем случае формулой Р = UI ⋅ cos φ. Множитель cos φ называют коэффициентом мощности. Учитывая, что U = I ⋅ z, а соs φ = r/z, получаем P = I ⋅ z ⋅ I ⋅ r/z = I2r. Активная мощность измеряется в ваттах (вт) или в киловаттах (квт). Произведение Р ⋅ t называется активной энергией и измеряется в вт⋅сек или в квт⋅ч: 1 квт⋅ч = 3600 вт⋅сек (дж). Активная энергия, потребляемая электрической цепью, полностью преобразуется в тепло в активном сопротивлении этой цепи и обратно к источнику не возвращается. Если величины сторон треугольника сопротивлений (рис. 165, а) умножить на величину I2 (рис. 165, б), то получим треугольник мощностей (рис. 165, в). Все стороны этого треугольника, показанного отдельно на рис. 166, представляют собой мощности. Катет, прилегающий к углу φ, представляет собой известную нам активную мощность Р: P = I2 ⋅ r = UI ⋅ cos φ. Активная мощность в цепях переменного тока преобразуется в тепло. В двигателях переменного тока большая часть активной мощности превращается в механическую мощность, остальная часть также преобразуется в тепло. Катет, лежащий против угла φ, есть реактивная мощность Q: Q = I2x = UI ⋅ sin φ. Реактивная мощность обусловлена наличием магнитных и электрических полей в электрических цепях. Как уже указывалось, реактивная мощность характеризует интенсивность обмена энергией между источником, с одной стороны, и магнитными и электрическими полями — с другой. Реактивная мощность измеряется в вольт-амперах реактивных (вар) или киловольт-амперах реактивных (квар). Гипотенуза треугольника мощностей представляет собой полную мощность S: S = I2z = UI, или S = √(P2 + Q2). Она измеряется в вольт-амперах (ва) или киловольт-амперах (ква). Величина полной мощности, равная произведению U⋅I, определяет основные габариты (наибольшие размеры) генераторов и трансформаторов. Таким образом, чем больше значения U и I, на которые рассчитываются генераторы и трансформаторы, тем больше должны быть их размеры. Рассмотрим электрическую цепь, показанную на рис. 167, в которую входят индуктивное и активное сопротивления и измерительные приборы — амперметр, вольтметр и ваттметр. Об устройстве ваттметра будет подробно рассказано далее (см. главу одиннадцатую). 1. Если подключить эту цепь к постоянному напряжению U = 120 в, то, поскольку индуктивное сопротивление xL при постоянном токе будет равно нулю, в цепи остается одно активное сопротивление r и тогда I = U/r = 120/24 = 5 a. Амперметр покажет ток 5 а. Мощность Р = IU = 5 ⋅ 120 = 600 вт, или P = I2r = 25 ⋅ 24 = 600 вт. Ваттметр покажет 600 вт. Показание ваттметра, включенного в цепь постоянного тока, равно произведению показаний вольтметра и амперметра. 2. Подключим ту же цепь к переменному напряжению U = 120 в. В этом случае z = √(r2 + xL2) = √(242 + 182) = √900 = 30 ом. Ток в цепи I = U/z = 120/30 = 4 a. Амперметр покажет ток 4 а. Подсчитаем мощность, идущую на нагрев: Р = I2r = 42 ⋅ 24 = 384 вт. Действительно, активная мощность, потребляемая цепью, равна P = U ⋅ I ⋅ cos φ = 120 ⋅ 4 24/30 = 384 вт. Показание ваттметра в этом случае будет 384 вт. Полная мощность S = U ⋅ I = 120 ⋅ 4 = 480 ва. Следовательно, генератор, питающий эту цепь, отдает полную мощность S = 480 ва. Отсюда видно, что цепь переменного тока, содержащая наряду с активным сопротивлением индуктивное, из всей получаемой ею энергии только часть расходует на тепло. А остальная часть — реактивная энергия — то поступает в цепь от генератора и запасается в магнитном поле катушки, то возвращается обратно генератору.
§ 75. Коэффициент мощности («косинус фи») Коэффициентом мощности, или «косинусом фи» (cos φ), цепи называется отношение активной мощности к полной мощности.
или cos φ = P/S = P/UI = P/√(P2 + Q2). В общем случае активная мощность меньше полной мощности, т. е. у этой дроби числитель меньше знаменателя, и поэтому коэффициент мощности меньше единицы. Только в случае чисто активной нагрузки, когда вся мощность является активной, числитель и знаменатель этой дроби равны между собой, и поэтому коэффициент мощности равен единице. Чем большую часть полной мощности составляет активная мощность, тем меньше числитель отличается от знаменателя дроби и тем ближе коэффициент мощности к единице. Величину cos φ можно косвенно определить по показаниям ваттметра, вольтметра и амперметра: cos φ = P/UI. Коэффициент мощности можно также измерить особым прибором — фазометром. Пример 14. Амперметр показывает ток 10 а, вольтметр — 120 в, ваттметр — 1 квт. Определить cos φ потребителя: S = IU = 10 ⋅ 120 = 1200 ва, cos φ = P/S = 1000/1200 = 0,83. Пример 15. Определить активную мощность, отдаваемую генератором однофазного переменного тока в сеть, если вольтметр на щите генератора показывает 220 в, амперметр — 20 а и фазометр — 0,8: Р = IU cos φ = 20 ⋅ 220 ⋅ 0,8 = 3520 вт = 3,52 квт. Полная мощность S = IU = 20 ⋅ 220 = 4400 ва = 4,4 ква. Пример 16. Вольтметр, установленный на щитке электродвигателя, показывает 120 в, амперметр — 450 а, ваттметр — 50 квт. Определить z, r, xL, S, cos φ, Q: z = U/I = 120/450 = 0,267 ом. Так как Р = I2 ⋅ r, то r = Р/I2 = 50000/4502 = 0/247 ом; xL = √(z2 — r2) = √(0,2672 — 0,2472) = √0,01 = 0,1 ом; S = IU = 450 ⋅ 120 = 54000 ва = 54 ква; cos φ = Р/S = 50000/54000 = 0,927; Q = √(S2 — Р2) = √(540002 — 500002) = √416000000 = 20396 вар = 20,396 квар. Из построения треугольников сопротивлений, напряжений и мощностей для определенной цепи видно, что эти треугольники подобны один другому, так как их стороны пропорциональны. Пример 17. Определить z, xL, U, Uа, UL, S, Р, Q, если I = 6 а, r = 3 ом, cos φ = 0,8 и ток отстает по фазе от напряжения. Из треугольника сопротивлений известно, что cos φ = r/z, отсюда z = r/cos φ = 3/0,8 = 3,75 ом; U = I ⋅ z = 6 ⋅ 3,75 = 22,5 в; xL = √(z2 — r2) = √(3,752 — 32) = √(14,06 — 9) = √5,06 = 2,24 ом; Uа = Ir = 6 ⋅ 3 = 18 в; UL = IxL = 6 ⋅ 2,24 = 13,45 в; S = IU = 6 ⋅ 22,5 = 135 ва, или P = I2r = 36 ⋅ 3 = 108 вт; Р = IU cos φ = 6 ⋅ 22,5 ⋅ 0,8 = 108 вт; Q = IUL = 6 ⋅ 13,45 = 81 вар, или Q = √(S2 — P2) = √(1352 — 1082) = √6561 = 81 вар, или Q = I2xL = 62 ⋅ 2,24 = 81 вар. Основными потребителями электрической энергии являются электрические двигатели, машины и электронагревательные устройства. Все они потребляют активную мощность, которую преобразуют в механическую работу и тепло. Электрические двигатели потребляют также реактивную мощность. Последняя, как известно, совершает колебательное движение от источника к двигателю и обратно. У ламп и электрических печей сопротивления S = Р и cos φ = 1. У электрических двигателей S = √(P2 + Q2) и cos φ меньше 1. При неизменной передаваемой активной мощности Р величина нагрузочного тока обратно пропорциональна значению cos φ: I = P/U⋅cosφ Это означает, что при тех же значениях активной мощности Р и напряжения U нагрузочный ток электрических двигателей больше, чем у электрических ламп. Если, например, коэффициент мощности электрического двигателя равен 0,5, то он потребляет в 2 раза больший ток, чем электрическая печь сопротивления той же мощности Р. Потери мощности на нагрев проводов линии пропорциональны квадрату тока (ΔР = I2r). Таким образом, при cos φ = 0,5 потери мощности в линии, по которой энергия передается потребителям, больше в 4 раза, чем при cos φ = 1. Кроме того, генераторы и трансформаторы будут загружены током в 2 раза больше и в этом случае требуется примерно в 2 раза большее сечение проводов для обмоток. Отсюда видно, какое важное значение имеет величина cos φ в электроэнергетических установках. Для повышения коэффициента мощности промышленных установок, на которых преобладающая часть потребителей — электрические двигатели, параллельно им включают конденсаторы, т. е. добиваются резонанса токов, при котором cos φ близок к 1.
Задачи для самостоятельного решения 1. Определить частоту переменного тока, получаемого от генератора с 24 полюсами, при 250 оборотах ротора в минуту. 2. Двадцатиполюсный генератор переменного тока дает ток частоты 50 гц. Определить число оборотов ротора генератора в минуту. 3. Определить число полюсов генератора переменного тока, если скорость вращения ротора генератора равна 300 об/мин, а частота 50 гц. 4. Катушка включена в сеть однофазного переменного тока напряжением 120 в; э.д.с. самоиндукции равна 100 в. Чему равно активное падение напряжения? 5. Что покажет вольтметр, включенный на зажимы обмотки электромагнита, если индуктивное сопротивление обмотки равно 6 ом, активное сопротивление 8 ом, а ток, протекающий по виткам обмотки, равен 5 а? 6. Когда катушку включили в сеть постоянного тока напряжением 120 в, амперметр показал ток 4 а; когда ту же катушку включили в сеть переменного тока напряжением 380 в, амперметр показал 5 а. Определить полное, активное и индуктивное сопротивления катушки. 7. Два проводника с активным сопротивлением 6 и 5 ом и индуктивным сопротивлением 3 и 8 ом включены последовательно. Какое напряжение нужно приложить, чтобы в цепи проходил ток 4 а? 8. По проводнику с активным сопротивлением 7 ом и индуктивным сопротивлением 5 ом проходит ток 6 а. 9. Однофазный электродвигатель, включенный в сеть 120 в, потребляет ток 2 а. Коэффициент мощности двигателя 0,85. Определить активную и полную мощности, забираемые двигателем из сети, 10. На распределительном щите установлены три прибора: амперметр, вольтметр и ваттметр. Показание амперметра 40 а, вольтметра 110 в, ваттметра 4 квт. Определить z, r, xL, S, cos φ, Q, UL, Ua, если известно, что нагрузка имеет индуктивный характер. 11. Определить ток, потребляемый однофазным двигателем мощностью 5 квт, если он включен в сеть 120 в, а его коэффициент мощности равен 0,8. 12. На электростанции установлен генератор однофазного переменного тока мощностью 200 ква, напряжением 100 в. Определить активную мощность, отдаваемую генератором в сеть, при коэффициентах мощности 1; 0,8; 0,6; 0,4; 0,2. Найти также величину нагрузочного тока при этих значениях cos φ. 13. Через индукционную катушку с cos φ = 0,3 проходит переменный ток в 10 а. Ваттметр, измеряющий мощность катушки, показал 250 вт. Определить напряжение на зажимах катушки, ее полное, активное и индуктивное сопротивления. 14. Индуктивная катушка включена в сеть постоянного тока напряжением 12 в и потребляет ток 8 а. Тот же ток катушка потребляет при включении в сеть переменного тока напряжением 20 в. Определить активное, индуктивное и полное сопротивления катушки; полную, активную и реактивную мощности. 15. Показания приборов: амперметра — 20 а, вольтметра — 120 в, фазометра — 0,8. Определить S, p, Q, z, r, xL, UL, Ua. 16. Полезная мощность на валу однофазного двигателя 10 л. с., к.п.д. двигателя 85%, cos φ = 0,8, напряжение 220 в. Определить мощность генератора, питающего этот двигатель, если энергия передается по линии длиной 50 м, выполненной медным проводом сечением 16 мм2. Индуктивным сопротивлением проводов линии можно пренебречь. 17. Показания приборов: амперметра — 8 а, вольтметра — 220 в, активное сопротивление катушки равно 15 ом. Определить Р, S, Q, z, xL, cos φ, UL, Ua потребителя. 18. На паспорте однофазного двигателя написано: U = 120 в, I = 5 а, cos φ = 0,8. Определить активное, индуктивное и полное сопротивления обмотки двигателя. 19. В сеть однофазного тока включена катушка с сердечником из мягкой стали. В цепь катушки включены приборы: вольтметр, амперметр и ваттметр. Показание амперметра 5 а, вольтметра 120 в и ваттметра 200 вт. Активное сопротивление катушки 2 ом. Определить коэффициент мощности катушки, величину э.д.с. самоиндукции, потерю мощности в обмотке катушки, а также в сердечнике. 20. Дроссельная катушка (т. е. катушка со стальным сердечником) с коэффициентом мощности 0,2, включенная в сеть 60 в, потребляет ток 3 а. Активное сопротивление катушки 2 ом. Определить величину э.д.с., индуктируемой в катушке, потерю мощности в обмотке и в сердечнике.
Контрольные вопросы 1. Как получается переменный ток? 2. Дайте определения основным параметрам переменного тока и напишите выражения (формулы): · Переменный ток · Мгновенное значение переменного · Действующее значение переменного тока · Период · Частота · Угловая скорость · Сдвиг по фазе 3. Как определить частоту, если известно число полюсов и скорость вращения ротора генератора переменного тока? 4. Охарактеризуйте основные параметры электрической цепи переменного тока при включении в нее катушки индуктивности, емкости и резистора. 5. Что называется коэффициентом мощности? 6. Как измерить активную и полную мощности переменного тока? 7. Каким путем можно повысить «косинус фи» до 1? 8. Что называется резонансом напряжений? Перечислите основные характеристики резонанса напряжения. 9. Что называется резонансом токов? Перечислите основные характеристики резонанса тока.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
видов электрической нагрузки | Резистивная, индуктивная и емкостная нагрузка
Типы электрической нагрузки | Резистивная, индуктивная и емкостная нагрузка
https://www.theelectricalguy.in/wp-content/uploads/2020/08/Electrical-Load-1024×576.jpg
1024
576
Гаурав Дж. Гаурав Дж.
https://secure.gravatar.com/avatar/87a2d2e0182faacb2e003da0504ad293?s=96&d=mm&r=g
Гаурав Дж.
https://secure.gravatar.com/avatar/87a2d2e0182faacb2e003da0504ad293?s=96&d=mm&r=g
Если мы посмотрим на характер электрических нагрузок, то мы можем разделить их на 3 типа. В этом руководстве вы подробно разберетесь с резистивной, индуктивной и емкостной нагрузкой. Также выделю одно из очень распространенных заблуждений о том или ином типе нагрузки. Итак, начнем.
Рекомендуем прочитать перед тем, как двигаться дальше
Активная, реактивная и полная мощность
Что такое электрическая нагрузка?
Во-первых, давайте разберемся, что такое электрическая нагрузка? Проще говоря, все, что потребляет электроэнергию, называется электрической нагрузкой . Таким образом, это включает в себя лампочки, компьютеры, холодильник и т. Д., Все они потребляют электроэнергию, и, следовательно, мы можем называть их электрической нагрузкой. Теперь, если мы посмотрим на природу такой нагрузки, мы можем разделить их на три разных типа. И это так.
Д., Все они потребляют электроэнергию, и, следовательно, мы можем называть их электрической нагрузкой. Теперь, если мы посмотрим на природу такой нагрузки, мы можем разделить их на три разных типа. И это так.
- Резистивная нагрузка
- Индуктивная нагрузка и
- Емкостная нагрузка
Резистивная нагрузка
Давайте сначала разберемся с резистивной нагрузкой. Нагрузка, потребляющая только активную мощность, называется резистивной нагрузкой. И если вы посмотрите на кривые напряжения и тока такой нагрузки, вы обнаружите, что напряжение и ток идеально совпадают по фазе друг с другом.
Теперь, когда я говорю, что они идеально совпадают по фазе, это означает, что оба сигнала достигают своего пикового значения одновременно. Они также достигают нулевого значения в то же время. Один пример показан выше.
Так как этот тип нагрузки потребляет только активную мощность, мощность течет от Источника только к нагрузке. Мощность не будет течь от нагрузки к источнику. Да, в некоторых случаях мощность также передается от нагрузки к источнику, что я объяснил в своем видео об активной реактивной и полной мощности.
Да, в некоторых случаях мощность также передается от нагрузки к источнику, что я объяснил в своем видео об активной реактивной и полной мощности.
Поскольку такие нагрузки потребляют только активную мощность, коэффициент мощности таких нагрузок равен Единице! И это очень хороший знак. Если вы хотите подробно узнать коэффициент мощности, вы можете просмотреть мой полный плейлист на Power Factor.
Пример активной нагрузки
Пример активной нагрузки:
- Освещение
- Обогреватели
Или любые другие нагрузки, состоящие только из нагревательных элементов. Это примеры резистивной нагрузки.
Свойства резистивной нагрузки
Давайте посмотрим, каковы свойства резистивной нагрузки
- Эта нагрузка потребляет только активную мощность
- Кривые напряжения и тока таких нагрузок идеально совпадают по фазе друг с другом.
- Коэффициент мощности такой нагрузки равен единице
- Мощность всегда течет от источника к нагрузке
Индуктивная нагрузка
Теперь давайте разберемся с индуктивными нагрузками.
Нагрузка, потребляющая только реактивную мощность, называется индуктивной нагрузкой . И если вы посмотрите на кривые напряжения и тока такой нагрузки, вы обнаружите, что напряжение и ток не совпадают по фазе друг с другом на 90 градусов.
Теперь, когда я говорю, что они не совпадают по фазе, это означает, что обе формы волны достигают своего пикового значения в разное время. Они также достигают нулевого значения в разное время. Если вы посмотрите на форму волны, вы обнаружите, что напряжение опережает ток. Мы также можем сказать, что ток отстает от напряжения.
Поскольку такой тип нагрузки потребляет только реактивную мощность, мощность может течь от источника к нагрузке или даже от нагрузки к источнику. Далее, коэффициент мощности таких нагрузок не равен единице! Коэффициент мощности таких нагрузок носит отстающий характер. А это не очень хороший знак.
Пример индуктивной нагрузки
Давайте рассмотрим несколько примеров индуктивной нагрузки.
Электродвигатель
Вентиляторы
Стиральная машина или все, что имеет двигатель внутри.
Кроме того, реакторы, используемые в энергосистеме, являются примером индуктивной нагрузки.
Свойства индуктивной нагрузки
Давайте посмотрим, каковы свойства индуктивной нагрузки.
- Эта нагрузка потребляет только реактивную мощность.
- Коэффициент мощности такой нагрузки отстает
- Переток мощности от источника к нагрузке и от нагрузки к источнику
Этот тип нагрузки не является легкой нагрузкой, как резистивная нагрузка. Они создают много проблем в системе. Но, конечно, они одинаково важны. Так как ток отстает от напряжения на 90 градусов в таком типе нагрузок, что затрудняет переключение такой нагрузки. Как известно, автоматический выключатель размыкается при нулевом токе. Если вы посмотрите на кривые тока и напряжения такой нагрузки, вы обнаружите, что когда ток равен нулю, напряжение максимально.
Следовательно, когда выключатель размыкается при нулевом токе, напряжение на контакте выключателя максимальное. Принимая во внимание, что в случае резистивной нагрузки и ток, и напряжение становятся равными нулю одновременно. Поэтому переключение такого типа индуктивных нагрузок имеет решающее значение.
Принимая во внимание, что в случае резистивной нагрузки и ток, и напряжение становятся равными нулю одновременно. Поэтому переключение такого типа индуктивных нагрузок имеет решающее значение.
Такой тип нагрузки также сильно влияет на коэффициент мощности системы. И, следовательно, счета за электроэнергию растут.
Емкостная нагрузка
Емкостная нагрузка аналогична индуктивной нагрузке. В емкостных нагрузках ток и напряжение также не совпадают по фазе. Разница лишь в том, что при емкостной нагрузке ток опережает напряжение на 90 град. В то время как при индуктивной нагрузке ток отстает от напряжения на 90 град.
Неверное представление о емкостной нагрузке
Теперь поговорим о заблуждении, о котором я говорил в начале этого видео.
Как правило, емкостные нагрузки не существуют в автономном формате. Конденсаторные батареи устанавливаются для улучшения коэффициента мощности нагрузки или системы. Их работа заключается в обеспечении реактивной мощности.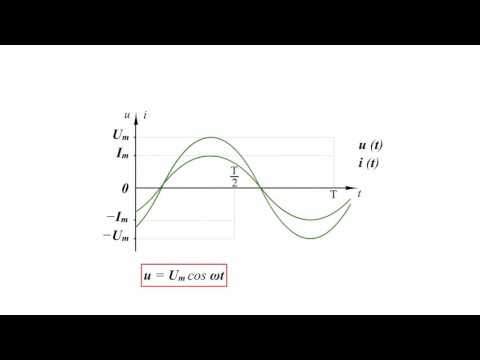 Поэтому мы не можем называть конденсаторные батареи емкостной нагрузкой. Потому что нагрузка — это то, что поглощает энергию. Я видел во многих местах в Интернете, что люди называют конденсаторную батарею емкостной нагрузкой. Ну, я думаю, конденсаторная батарея обеспечивает реактивную мощность и, следовательно, ее нельзя классифицировать как емкостную нагрузку./
Поэтому мы не можем называть конденсаторные батареи емкостной нагрузкой. Потому что нагрузка — это то, что поглощает энергию. Я видел во многих местах в Интернете, что люди называют конденсаторную батарею емкостной нагрузкой. Ну, я думаю, конденсаторная батарея обеспечивает реактивную мощность и, следовательно, ее нельзя классифицировать как емкостную нагрузку./
Допустим, у меня есть генератор переменного тока на 230 В и подключенная к нему батарея конденсаторов. Реактивное сопротивление конденсаторной батареи 23 Ом. Следовательно, ток, потребляемый системой, будет равен 10 А.
Теперь, если вы подключите счетчик реактивной мощности, который используется для расчета реактивной мощности, между генератором и батареей конденсаторов, он даст отрицательные показания. Минус 2300 ВАР или 2,3 кВАр. Таким образом, это отрицательное значение указывает на то, что мощность фактически течет от конденсаторной батареи к генератору. / Следовательно, мы не можем называть конденсаторную батарею емкостной нагрузкой.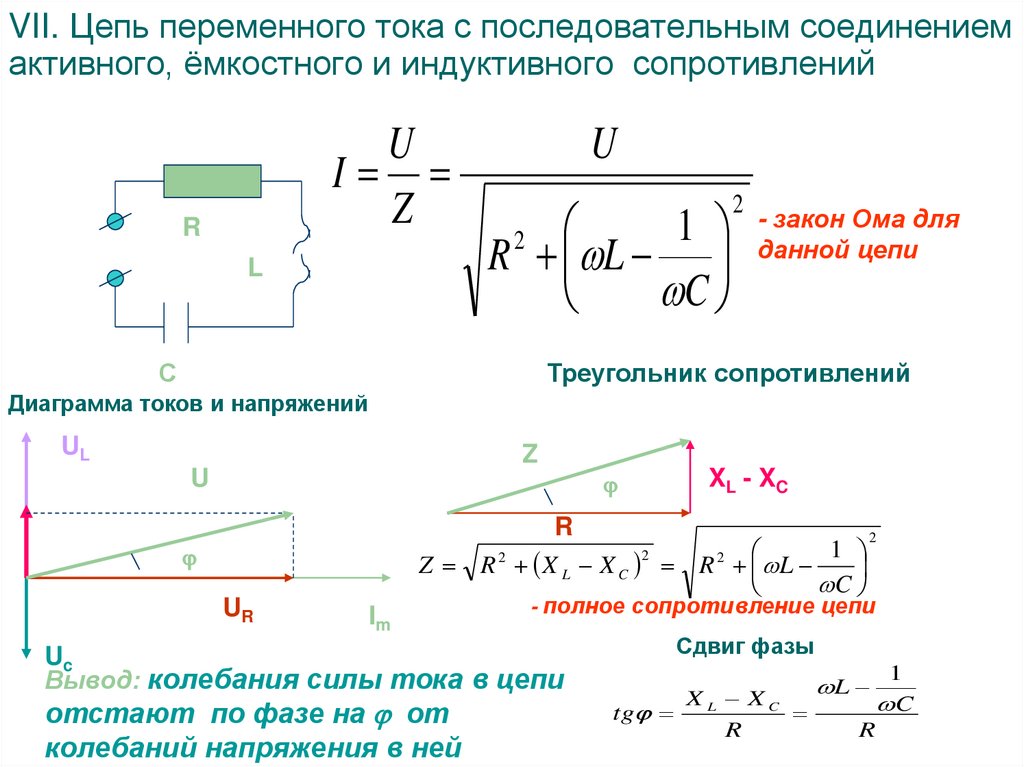 По сути, нет такой вещи, которую можно было бы классифицировать как емкостную нагрузку.
По сути, нет такой вещи, которую можно было бы классифицировать как емкостную нагрузку.
Вот и все о типах электрической нагрузки. Эту тему запросил один из моих подписчиков. Надеюсь, вы сегодня узнали что-то новое.
КОРРЕКЦИЯ КОЭФФИЦИЕНТА МОЩНОСТИ – Прикладное промышленное электричество
Рассмотрим цепь для однофазной системы питания переменного тока, в которой источник переменного напряжения 120 В, 60 Гц подает питание на резистивную нагрузку: (рисунок ниже)
Источник переменного тока питает чисто резистивную нагрузку.
[латекс]Z =60 + j0 \Omega \textbf{ или } 60\Omega \angle \text{ 0°}[/latex]
[латекс]\begin{align} I &= \frac{E}{Z} \\ &= \frac{120V}{60Ω} \\ &= \mathbf{2A} \end{align}[ /латекс]
В этом примере ток нагрузки будет 2 ампера, среднеквадратичное значение. Мощность, рассеиваемая на нагрузке, составит 240 Вт. Поскольку эта нагрузка является чисто резистивной (без реактивного сопротивления), ток совпадает по фазе с напряжением, и расчеты выглядят аналогично эквивалентной цепи постоянного тока. Если бы мы построили кривые напряжения, тока и мощности для этой схемы, это выглядело бы так, как показано на рисунке ниже.
Если бы мы построили кривые напряжения, тока и мощности для этой схемы, это выглядело бы так, как показано на рисунке ниже.
Обратите внимание, что для этой резистивной цепи сигнал мощности всегда положителен, а не отрицателен. Это означает, что мощность всегда рассеивается резистивной нагрузкой и никогда не возвращается к источнику, как это происходит с реактивной нагрузкой. Если бы источником был механический генератор, для вращения вала потребовалось бы 240 ватт механической энергии (около 1/3 лошадиной силы).
Также обратите внимание, что форма сигнала мощности не соответствует частоте напряжения или тока! Скорее, его частота удваивает формы сигнала напряжения или тока. Эта другая частота запрещает нам выражать мощность в цепи переменного тока, используя ту же сложную (прямоугольную или полярную) запись, которая используется для напряжения, тока и импеданса, потому что эта форма математического символизма подразумевает неизменные соотношения фаз. Когда частоты не совпадают, фазовые соотношения постоянно меняются.
Когда частоты не совпадают, фазовые соотношения постоянно меняются.
Как ни странно, лучший способ приступить к расчетам мощности переменного тока — использовать scalar обозначения и для обработки любых соответствующих фазовых соотношений с тригонометрией.
Цепь переменного тока с чисто реактивной нагрузкой
Для сравнения рассмотрим простую цепь переменного тока с чисто реактивной нагрузкой на рисунке ниже.
Цепь переменного тока с чисто реактивной (индуктивной) нагрузкой.
[латекс]X_L = 60,319 \Омега[/латекс]
[латекс]Z = 0+j60,319 \Омега \текст{ или } 60,319 Ом \угол \текст{ 90°}[/латекс]
[латекс]\begin{align}I &= \frac{E}{Z}\\ &= \frac{120V}{60.319\Omega}\\ & \mathbf{= 1.989A} \end{align}[/latex]
Рисунок 7.2 Мощность не рассеивается при чисто реактивной нагрузке. Хотя она попеременно поглощается из источника и возвращается к нему.
Обратите внимание, что мощность меняется одинаково между положительными и отрицательными циклами. (Рисунок выше) Это означает, что мощность попеременно поглощается и возвращается к источнику. Если бы источником был механический генератор, для вращения вала не потребовалось бы (практически) никакой чистой механической энергии, потому что нагрузка не использовала бы энергию. Вал генератора будет легко вращаться, а индуктор не будет нагреваться, как резистор.
(Рисунок выше) Это означает, что мощность попеременно поглощается и возвращается к источнику. Если бы источником был механический генератор, для вращения вала не потребовалось бы (практически) никакой чистой механической энергии, потому что нагрузка не использовала бы энергию. Вал генератора будет легко вращаться, а индуктор не будет нагреваться, как резистор.
Цепь переменного тока с резистивной и чисто реактивной нагрузкой
Теперь давайте рассмотрим цепь переменного тока с нагрузкой, состоящей как из индуктивности, так и из сопротивления на рисунке ниже. Схема
с реактивным сопротивлением и сопротивлением.
[латекс]X_L = 60,319 \Омега[/латекс]
[латекс]Z_L = 0+j60,319\Омега[/латекс] или [латекс]60,319\Омега \угол 90°[/латекс]
[латекс]Z_R = 60+j0\Омега[/латекс] или [латекс]60\Омега\угол 0°[/латекс]
[латекс]Z_{\text{всего}} = 60+ j60,319\Omega[/латекс] или [латекс]85,078\Омега \угол 45,152°[/латекс]
[латекс]\text{I} = \frac{E}{Z_{\text{total}}} = \frac{120V}{85,078 \Omega} = \mathbf{1,410A}[/latex]
При частоте 60 Гц 160 мГн индуктивности дают нам 60,319 Ом индуктивного сопротивления. Это реактивное сопротивление в сочетании с сопротивлением 60 Ом образует полное сопротивление нагрузки 60 + j60,319 Ом, или 85,078 Ом ∠ 45,152 o . Если нас не интересуют фазовые углы (которыми мы не занимаемся в данный момент), мы можем рассчитать ток в цепи, взяв полярную величину источника напряжения (120 вольт) и разделив ее на полярную величину импеданса. (85,078 Ом). При напряжении источника питания 120 вольт RMS ток нагрузки составляет 1,410 ампер. Это цифра, которую показал бы амперметр среднеквадратичного значения, если бы он был соединен последовательно с резистором и катушкой индуктивности.
Это реактивное сопротивление в сочетании с сопротивлением 60 Ом образует полное сопротивление нагрузки 60 + j60,319 Ом, или 85,078 Ом ∠ 45,152 o . Если нас не интересуют фазовые углы (которыми мы не занимаемся в данный момент), мы можем рассчитать ток в цепи, взяв полярную величину источника напряжения (120 вольт) и разделив ее на полярную величину импеданса. (85,078 Ом). При напряжении источника питания 120 вольт RMS ток нагрузки составляет 1,410 ампер. Это цифра, которую показал бы амперметр среднеквадратичного значения, если бы он был соединен последовательно с резистором и катушкой индуктивности.
Мы уже знаем, что реактивные компоненты рассеивают нулевую мощность, поскольку они в равной степени поглощают мощность от остальной части цепи и возвращают ее обратно. Следовательно, любое индуктивное сопротивление в этой нагрузке также будет рассеивать нулевую мощность. Единственное, что здесь остается для рассеивания мощности, — это резистивная часть импеданса нагрузки.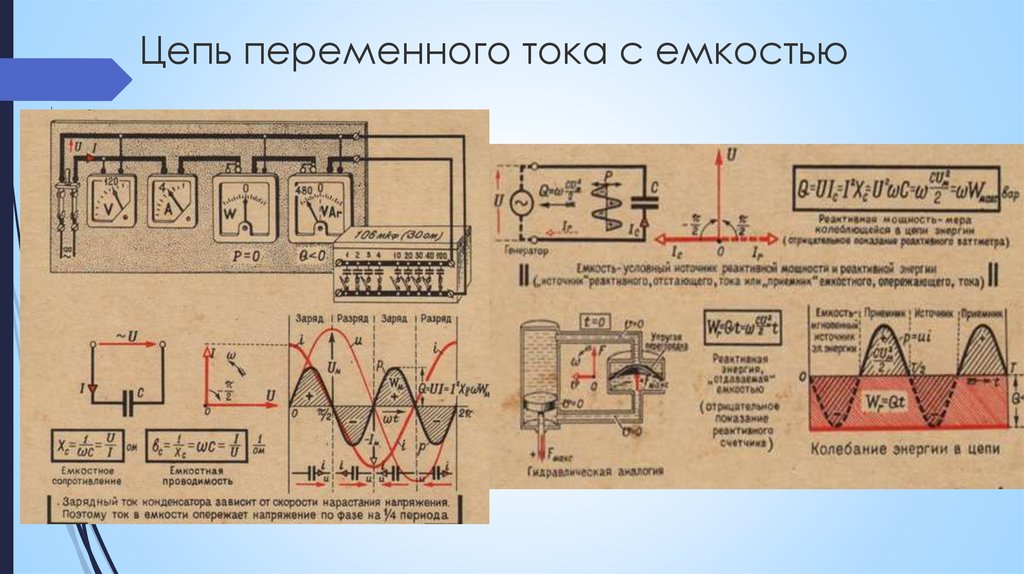 Если мы посмотрим на график формы сигнала напряжения, тока и общей мощности для этой схемы, мы увидим, как эта комбинация работает на рисунке ниже.
Если мы посмотрим на график формы сигнала напряжения, тока и общей мощности для этой схемы, мы увидим, как эта комбинация работает на рисунке ниже.
Как и в любой реактивной цепи, мгновенные значения мощности чередуются с положительными и отрицательными значениями с течением времени. В чисто реактивной цепи чередование положительной и отрицательной мощности делится поровну, что приводит к нулевому рассеиванию полезной мощности. Однако в цепях со смешанным сопротивлением и реактивным сопротивлением, подобных этой, форма сигнала мощности по-прежнему будет чередоваться между положительной и отрицательной, но количество положительной мощности будет превышать количество отрицательной мощности. Другими словами, комбинированная индуктивная/резистивная нагрузка потребляет больше энергии, чем возвращается к источнику.
Глядя на график формы сигнала для мощности, должно быть очевидно, что волна проводит больше времени на положительной стороне центральной линии, чем на отрицательной, что указывает на то, что нагрузка поглощает больше мощности, чем возвращается в цепь. Тот небольшой возврат мощности, который происходит, происходит из-за реактивного сопротивления; дисбаланс положительной и отрицательной мощности возникает из-за сопротивления, поскольку оно рассеивает энергию вне цепи (обычно в виде тепла). Если бы источником был механический генератор, количество механической энергии, необходимой для вращения вала, было бы суммой мощности, усредненной между положительным и отрицательным циклами мощности.
Математическое представление мощности в цепи переменного тока представляет собой сложную задачу, поскольку волна мощности не имеет той же частоты, что и напряжение или ток. Кроме того, фазовый угол для мощности означает нечто совершенно отличное от фазового угла для напряжения или тока. В то время как угол для напряжения или тока представляет собой относительный сдвиг во времени между двумя волнами, фазовый угол для мощности представляет собой отношение между рассеиваемой и возвращаемой мощностью. Из-за того, что мощность переменного тока отличается от напряжения или тока переменного тока, на самом деле проще получить значения мощности, вычислив с помощью скаляр количеств напряжения, тока, сопротивления и реактивного сопротивления, чем пытаться вывести его из вектора или комплексных величин напряжения, тока и импеданса, с которыми мы работали до сих пор.
В то время как угол для напряжения или тока представляет собой относительный сдвиг во времени между двумя волнами, фазовый угол для мощности представляет собой отношение между рассеиваемой и возвращаемой мощностью. Из-за того, что мощность переменного тока отличается от напряжения или тока переменного тока, на самом деле проще получить значения мощности, вычислив с помощью скаляр количеств напряжения, тока, сопротивления и реактивного сопротивления, чем пытаться вывести его из вектора или комплексных величин напряжения, тока и импеданса, с которыми мы работали до сих пор.
- В чисто резистивной цепи вся мощность цепи рассеивается резистором(ами). Напряжение и ток находятся в фазе друг с другом.
- В чисто реактивной цепи мощность цепи не рассеивается нагрузкой. Вместо этого мощность попеременно поглощается и возвращается к источнику переменного тока. Напряжение и ток 90° не совпадают по фазе друг с другом.
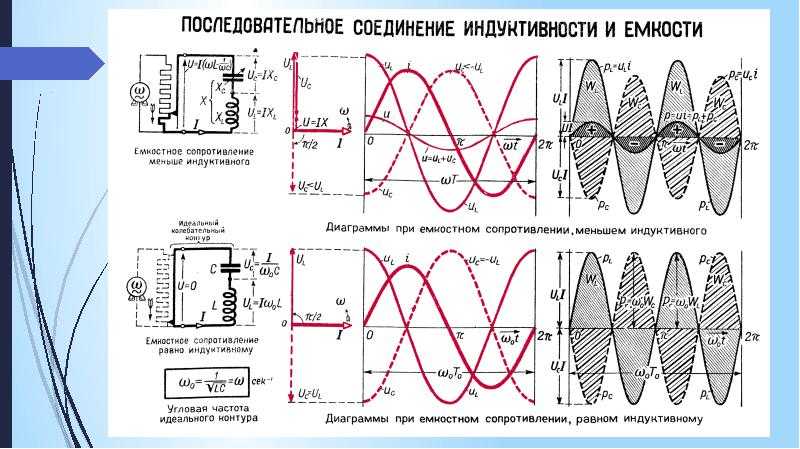
- В цепи, состоящей из смешанных сопротивлений и реактивных сопротивлений, будет больше мощности, рассеиваемой нагрузкой(ями), чем возвращаемой, но некоторая мощность определенно будет рассеиваться, а некоторая часть будет просто поглощаться и возвращаться. Напряжение и ток в такой цепи будут сдвинуты по фазе на величину где-то между 0° и 90°.
Реактивная мощность
Мы знаем, что реактивные нагрузки, такие как катушки индуктивности и конденсаторы, рассеивают нулевую мощность, но тот факт, что они понижают напряжение и потребляют ток, создает обманчивое впечатление, что они на самом деле 9от 0019 до рассеивать мощность. Эта «фантомная мощность» называется реактивной мощностью и измеряется в единицах измерения Вольт-Ампер-реактивная (ВАР), а не в ваттах. Математический символ реактивной мощности — (к сожалению) заглавная буква Q.
Истинная сила
Фактическое количество энергии, используемой или рассеиваемой в цепи, называется истинной мощностью и измеряется в ваттах (как всегда обозначается заглавной буквой P).
Полная мощность
Комбинация реактивной мощности и активной мощности называется полной мощностью и является произведением напряжения и тока в цепи без учета фазового угла. Полная мощность измеряется в единицах вольт-ампер (ВА) и обозначается заглавной буквой S.
Расчет реактивной, истинной или полной мощности
Как правило, истинная мощность является функцией рассеивающих элементов цепи, обычно сопротивлений (R). Реактивная мощность зависит от реактивного сопротивления цепи (X). Полная мощность является функцией полного сопротивления цепи (Z). Поскольку мы имеем дело со скалярными величинами для расчета мощности, любые сложные начальные величины, такие как напряжение, ток и импеданс, должны быть представлены их полярных величин , а не действительными или мнимыми прямоугольными компонентами. Например, если я вычисляю истинную мощность по току и сопротивлению, я должен использовать для тока полярную величину, а не просто «реальную» или «мнимую» часть тока. Если я вычисляю полную мощность по напряжению и импедансу, обе эти ранее сложные величины должны быть приведены к их полярным величинам для скалярной арифметики.
Если я вычисляю полную мощность по напряжению и импедансу, обе эти ранее сложные величины должны быть приведены к их полярным величинам для скалярной арифметики.
Уравнения с использованием скалярных величин
Существует несколько уравнений мощности, связывающих три типа мощности с сопротивлением, реактивным сопротивлением и импедансом (все используют скалярные величины): 92}{Z} \end{align}[/latex]
Измеряется в единицах Вольт-Ампер (ВА)
Обратите внимание, что для расчета истинной и реактивной мощности используется по два уравнения. Для расчета кажущейся мощности доступны три уравнения, P=IE используется только для этой цели. Изучите следующие схемы и посмотрите, как взаимодействуют эти три типа мощности: чисто резистивная нагрузка, чисто реактивная нагрузка и резистивная/реактивная нагрузка. 92Z= 169,256 ВА[/latex]
Истинная мощность, реактивная мощность и полная мощность для резистивной/реактивной нагрузки.
Треугольник власти
Эти три вида мощности — действительная, реактивная и полная — соотносятся друг с другом в тригонометрической форме.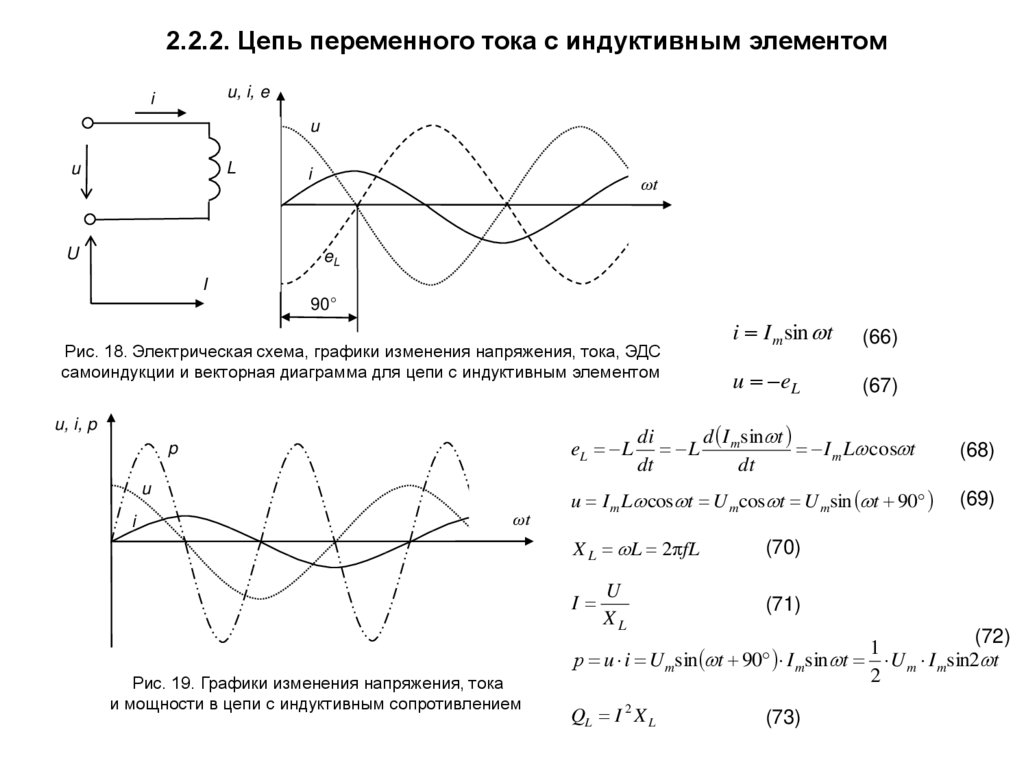 Мы называем это степенным треугольником : (рисунок ниже).
Мы называем это степенным треугольником : (рисунок ниже).
Используя законы тригонометрии, мы можем найти длину любой стороны (количество любой степени), зная длины двух других сторон или длину одной стороны и угол.
- Мощность, рассеиваемая нагрузкой, называется истинной мощностью . Истинная мощность обозначается буквой P и измеряется в ваттах (Вт).
- Мощность, просто поглощаемая и возвращаемая в нагрузку из-за ее реактивных свойств, называется реактивной мощностью . Реактивная мощность обозначается буквой Q и измеряется в единицах вольт-ампер-реактивная (ВАр).
- Суммарная мощность в цепи переменного тока, как рассеиваемая, так и поглощаемая/возвращаемая, обозначается как полная мощность . Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).
- Эти три вида власти тригонометрически связаны друг с другом.
 В прямоугольном треугольнике P = смежная длина, Q = противоположная длина и S = длина гипотенузы. Противоположный угол равен фазовому углу импеданса цепи (Z).
В прямоугольном треугольнике P = смежная длина, Q = противоположная длина и S = длина гипотенузы. Противоположный угол равен фазовому углу импеданса цепи (Z).
Как упоминалось ранее, угол этого «треугольника мощности» графически показывает отношение между количеством рассеянного (или потребляемая ) мощность и количество поглощаемой/возвращаемой мощности. Он также оказывается тем же углом, что и импеданс цепи в полярной форме. Выраженное в виде дроби, это отношение между истинной мощностью и кажущейся мощностью называется коэффициентом мощности для этой схемы. Поскольку истинная мощность и кажущаяся мощность образуют смежную и гипотенузную стороны прямоугольного треугольника соответственно, коэффициент коэффициента мощности также равен косинусу этого фазового угла. Используя значения из последнего примера схемы:
Коэффициент мощности
[латекс]\tag{7.4} PF =\frac{P}{S} = \frac{IECosθ}{IE} =Cosθ[/latex]
[латекс]Коэффициент мощности =\frac{119,365 Вт}{169,256 ВА}[/латекс]
[латекс]Коэффициент мощности =0,705[/латекс]
[латекс]\mathbf{Cos 45,152° = 0,705}[/ латекс]
Следует отметить, что коэффициент мощности, как и все измерения отношения, представляет собой безразмерную величину .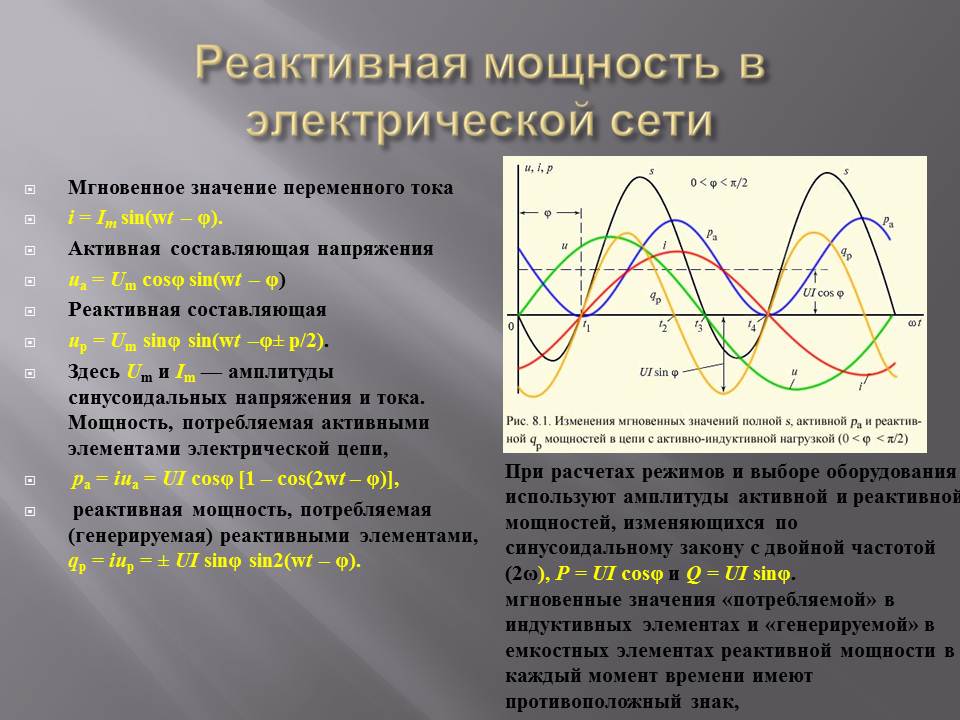
Значения коэффициента мощности
Для чисто резистивной цепи коэффициент мощности равен 1 (идеальный), поскольку реактивная мощность равна нулю. Здесь треугольник мощности будет выглядеть как горизонтальная линия, потому что противоположная сторона (реактивная мощность) будет иметь нулевую длину.
Для чисто индуктивной цепи коэффициент мощности равен нулю, поскольку реальная мощность равна нулю. Здесь треугольник мощности будет выглядеть как вертикальная линия, потому что смежная сторона (истинная мощность) будет иметь нулевую длину.
То же самое можно сказать и о чисто емкостной схеме. Если в цепи нет диссипативных (резистивных) составляющих, то истинная мощность должна быть равна нулю, что делает любую мощность в цепи чисто реактивной. Треугольник мощности для чисто емкостной цепи снова будет вертикальной линией (указывающей вниз, а не вверх, как это было для чисто индуктивной цепи).
Важность коэффициента мощности
Коэффициент мощности может быть важным аспектом, который следует учитывать в цепи переменного тока, поскольку любой коэффициент мощности меньше 1 означает, что проводка цепи должна пропускать больший ток, чем это было бы необходимо при нулевом реактивном сопротивлении в цепи. для подачи такого же количества (истинной) мощности на резистивную нагрузку. Если бы схема из нашего последнего примера была чисто резистивной, мы смогли бы отдать в нагрузку полные 169,256 Вт при том же токе 1,410 А, а не всего лишь 119 А.0,365 Вт, которые он в настоящее время рассеивает при той же величине тока. Плохой коэффициент мощности делает систему подачи энергии неэффективной.
для подачи такого же количества (истинной) мощности на резистивную нагрузку. Если бы схема из нашего последнего примера была чисто резистивной, мы смогли бы отдать в нагрузку полные 169,256 Вт при том же токе 1,410 А, а не всего лишь 119 А.0,365 Вт, которые он в настоящее время рассеивает при той же величине тока. Плохой коэффициент мощности делает систему подачи энергии неэффективной.
Плохой коэффициент мощности
Плохой коэффициент мощности можно скорректировать, как это ни парадоксально, добавив в цепь еще одну нагрузку, потребляющую равную и противоположную реактивную мощность, чтобы нейтрализовать влияние индуктивного реактивного сопротивления нагрузки. Индуктивное сопротивление может быть компенсировано только емкостным сопротивлением, поэтому мы должны добавить конденсатор 9.0020 параллельно нашей примерной схеме в качестве дополнительной нагрузки. Эффект этих двух противоположных реактивных сопротивлений, включенных параллельно, заключается в том, чтобы сделать общий импеданс цепи равным ее общему сопротивлению (чтобы фазовый угол импеданса стал равным или, по крайней мере, ближе к нулю).
Поскольку мы знаем, что (нескорректированная) реактивная мощность составляет 119,998 ВАР (индуктивная), нам нужно рассчитать правильный размер конденсатора, чтобы произвести такое же количество (емкостной) реактивной мощности. Поскольку этот конденсатор будет подключен непосредственно параллельно источнику (с известным напряжением), мы будем использовать формулу мощности, которая начинается с напряжения и реактивного сопротивления: 92}{119,998VAR}[/latex]
[latex]X= 120,002 Ом[/latex]
[latex]X_C= \frac{1}{2πfC}[/latex]
Решение для C:
[латекс]C= \frac{1}{2πfX_C}[/latex]
[латекс]C= \frac{1}{2π(60 Гц)(120,002 Ом}[/latex]
[латекс]C= 22,105 мкФ[/латекс]
Давайте возьмем округленное значение емкости конденсатора 22 мкФ и посмотрим, что произойдет с нашей схемой: (рисунок ниже)
[латекс]Z_{\text{всего}} = Z_C//(Z_L—Z_R ) [/латекс]
[латекс] Z _ {\ текст {всего}} = (120,57 Ом -92Z = 119,366 ВА[/latex]
Коэффициент мощности схемы в целом значительно улучшен. Основной ток был уменьшен с 1,41 А до 994,7 мА, а мощность, рассеиваемая на нагрузочном резисторе, осталась неизменной и составила 119,365 Вт. Коэффициент мощности намного ближе к 1:
Основной ток был уменьшен с 1,41 А до 994,7 мА, а мощность, рассеиваемая на нагрузочном резисторе, осталась неизменной и составила 119,365 Вт. Коэффициент мощности намного ближе к 1:
[латекс]PF =\frac{P}{S}[/latex]
[латекс]PF =\frac{119,365 Вт}{119,366 ВА}[/latex]
[латекс]PF =0,9999887[/латекс]
[латекс]\text{Импеданс (полярный) угол}= 0,272°[/латекс]
Поскольку угол импеданса по-прежнему является положительным числом, мы знаем, что схема в целом по-прежнему является более индуктивной, чем емкостной. Если бы наши усилия по коррекции коэффициента мощности были совершенно точными, мы бы получили угол импеданса, равный нулю, или чисто резистивный. Если бы мы добавили слишком большой конденсатор параллельно, мы бы получили отрицательный угол импеданса, что указывает на то, что цепь была скорее емкостной, чем индуктивной.
Следует отметить, что слишком большая емкость в цепи переменного тока приведет к низкому коэффициенту мощности точно так же, как и слишком большая индуктивность. Вы должны быть осторожны, чтобы не сделать чрезмерную коррекцию при добавлении емкости в цепь переменного тока. Вы также должны быть очень осторожно использовать подходящие конденсаторы для работы (соответствующие напряжению энергосистемы и случайным скачкам напряжения от ударов молнии, для непрерывной работы переменного тока и способные выдерживать ожидаемые уровни тока).
Вы должны быть осторожны, чтобы не сделать чрезмерную коррекцию при добавлении емкости в цепь переменного тока. Вы также должны быть очень осторожно использовать подходящие конденсаторы для работы (соответствующие напряжению энергосистемы и случайным скачкам напряжения от ударов молнии, для непрерывной работы переменного тока и способные выдерживать ожидаемые уровни тока).
Если цепь преимущественно индуктивная, мы говорим, что ее коэффициент мощности равен 9.0019 отстает от (поскольку волна тока в цепи отстает от волны приложенного напряжения). И наоборот, если цепь преимущественно емкостная, мы говорим, что ее коэффициент мощности равен , опережая . Таким образом, схема нашего примера начиналась с коэффициента мощности 0,705 отставания и была скорректирована до коэффициента мощности 0,999 отставания.
Низкий коэффициент мощности в цепи переменного тока может быть «скорректирован» или восстановлен до значения, близкого к 1, путем добавления параллельного реактивного сопротивления, противоположного влиянию реактивного сопротивления нагрузки. Если реактивное сопротивление нагрузки имеет индуктивный характер (что почти всегда будет), параллельный 9Емкость 0019 — это то, что необходимо для коррекции низкого коэффициента мощности.
Если реактивное сопротивление нагрузки имеет индуктивный характер (что почти всегда будет), параллельный 9Емкость 0019 — это то, что необходимо для коррекции низкого коэффициента мощности.
Когда возникает необходимость внести поправку на плохой коэффициент мощности в системе питания переменного тока, вы, вероятно, не сможете позволить себе роскошь знать точное значение индуктивности нагрузки в генри для использования в расчетах. Возможно, вам посчастливится иметь прибор, называемый измерителем коэффициента мощности, который скажет вам, что такое коэффициент мощности (число от 0 до 1) и полную мощность (которую можно вычислить, взяв показания вольтметра в вольтах и умножив на показания амперметра в амперах). В менее благоприятных обстоятельствах вам, возможно, придется использовать осциллограф для сравнения форм сигналов напряжения и тока, измерения фазового сдвига в градусах и расчета коэффициента мощности по косинусу этого фазового сдвига. Скорее всего, у вас будет доступ к ваттметру для измерения истинной мощности, показания которого вы сможете сравнить с расчетом полной мощности (из умножения измерений общего напряжения и полного тока). По значениям истинной и полной мощности можно определить реактивную мощность и коэффициент мощности.
По значениям истинной и полной мощности можно определить реактивную мощность и коэффициент мощности.
Давайте решим пример задачи, чтобы увидеть, как это работает: (Рисунок ниже)
Как рассчитать полную мощность в кВА
Сначала нам нужно рассчитать полную мощность в кВА. Мы можем сделать это, умножив напряжение нагрузки на ток нагрузки:
[латекс]S=IE[/латекс]
[латекс]S=(9,615 А)(240 В)[/латекс]
[латекс]S=2,308 кВА[/latex]
Как мы видим, 2,308 кВА — это гораздо большая цифра, чем 1,5 кВт, что говорит нам о том, что коэффициент мощности в этой схеме довольно плохой (существенно меньше 1). Теперь вычислим коэффициент мощности этой нагрузки, разделив действительную мощность на кажущуюся мощность:
[латекс]PF =\frac{P}{S}[/latex]
[латекс]PF =\frac{1,5 кВт}{2,308 кВА}[/latex]
[латекс]PF =0,65[/ латекс]
Используя это значение коэффициента мощности, мы можем нарисовать треугольник мощности и определить реактивную мощность этой нагрузки: (Рисунок ниже) Реактивная мощность может быть рассчитана из фактической мощности и полной мощности.
Как использовать теорему Пифагора для определения неизвестной величины треугольника
Чтобы определить неизвестную (реактивную мощность) величину треугольника, мы используем теорему Пифагора «наоборот», учитывая длину гипотенузы (кажущуюся мощность) и длину соседняя сторона (истинная сила): 92)[/latex]
[latex]Q=1,754 квар[/latex]
Как скорректировать коэффициент мощности с помощью конденсатора
Если этой нагрузкой является электродвигатель или любая другая промышленная нагрузка переменного тока, она имеют запаздывающий (индуктивный) коэффициент мощности, а это значит, что нам придется скорректировать его с помощью конденсатора соответствующего размера, включенного параллельно. Теперь, когда мы знаем количество реактивной мощности (1,754 кВАр), мы можем рассчитать размер конденсатора, необходимого для противодействия ее эффектам: 92}{1,754 квар}[/латекс]
[латекс]X= 32,845 Ом[/латекс]
[латекс]X_C= \frac{1}{2πfC}[/латекс]
Решение для C:
[латекс]C= \frac{1}{2πfX_C}[/latex]
[латекс]C= \frac{1}{2π(60 Гц)(32,845 Ом}[/latex]
[латекс]C= 80,761 мкФ[/латекс]
Округлив этот ответ до 80 мкФ, мы можем поместить этот размер конденсатора в цепь и вычислить результаты: (рисунок ниже)
Конденсатор 80 мкФ будет иметь емкостное сопротивление 33,157 Ом, что дает ток 7,238 А и соответствующую реактивную мощность 1,737 кВАр (для конденсатора только ). Поскольку ток конденсатора на 180 o не совпадает по фазе с индуктивным вкладом нагрузки в потребляемый ток, реактивная мощность конденсатора будет напрямую вычитаться из реактивной мощности нагрузки, в результате чего:
Поскольку ток конденсатора на 180 o не совпадает по фазе с индуктивным вкладом нагрузки в потребляемый ток, реактивная мощность конденсатора будет напрямую вычитаться из реактивной мощности нагрузки, в результате чего:
[latex]X_L — X_C = X[/latex ]
[latex]1,754 квар — 1,737 квар = 16,519 вар[/latex]
Эта коррекция, конечно, не изменит количество реальной мощности, потребляемой нагрузкой, но приведет к существенному снижению полная мощность и общий ток, потребляемый от источника 240 В: (рисунок ниже) 92[/латекс]
[латекс]S=1,50009 кВА[/латекс]
Узнайте о мощности в цепи переменного тока
Мощность в цепи переменного тока. Определение
В электрической цепи мощность, рассеиваемая электрическим элементом, определяется выражением
P=VI,P = VI,P=VI, где V — напряжение, через которое подключена цепь, а I — ток, проходящий через цепь. В цепи переменного тока ток и напряжение зависят от времени, поэтому мощность в цепи переменного тока является мгновенной, что равно p(t)=i(t). v(t)p\left( t \right) = i\left( t \right).v\left( t \right)p(t)=i(t).v(t), что также зависит от времени. Единицей электрической мощности является ватт.
v(t)p\left( t \right) = i\left( t \right).v\left( t \right)p(t)=i(t).v(t), что также зависит от времени. Единицей электрической мощности является ватт.
Обзор мощности в цепи переменного тока
В цепи переменного тока напряжение и ток имеют синусоидальную форму, поэтому мощность также является синусоидальной. Это связано с тем, что цепь переменного тока состоит из резистора, катушки индуктивности и конденсатора. Катушка индуктивности и конденсатор могут изменять направление потока энергии. Итак, согласно этому, сила имеет две составляющие; один — активная мощность, также известная как реальная мощность, а другой — реактивная мощность. Активная мощность – это та, которая потребляется электрической цепью, а реактивная мощность – это та, которая накапливается и возвращается к источнику в обратном порядке.
Мощность, рассеиваемая цепью переменного тока, может быть рассчитана как средняя мощность, потребляемая цепью, и мощность, возвращаемая обратно к источнику. Средняя мощность, рассеиваемая цепью переменного тока, представляет собой мгновенную мощность, которая определяется как произведение мгновенного напряжения и тока. Из приведенной ниже цифры средняя мощность цепи переменного тока равна средней мощности одного цикла.
Средняя мощность, рассеиваемая цепью переменного тока, представляет собой мгновенную мощность, которая определяется как произведение мгновенного напряжения и тока. Из приведенной ниже цифры средняя мощность цепи переменного тока равна средней мощности одного цикла.
Есть вопрос по этой теме?
Что вы узнаете:
- Мощность в цепи переменного тока Определение
- Обзор мощности в цепи переменного тока
- Коэффициент мощности
- Расчет мощности в цепи переменного тока
- Расчет мощности для различных типов нагрузки емкостная составляющая. Из-за индуктивной и емкостной составляющих ток и напряжение не совпадают по фазе. Если индуктивная составляющая больше, то ток отстает от напряжения, а если больше емкостная составляющая, то ток опережает напряжение.
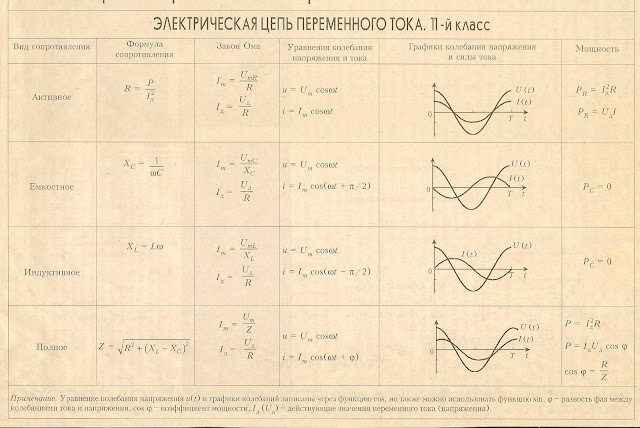 Угол между током и напряжением известен как угол вектора, а косинус угла вектора — это коэффициент мощности.
Угол между током и напряжением известен как угол вектора, а косинус угла вектора — это коэффициент мощности. Мощность Коэффициент = ∣cosφ∣{\rm{Мощность}}\;{\rm{Коэффициент}}= \left| {\cos \varphi} \right|PowerFactor=∣cosφ∣
Где PF – коэффициент мощности, φ\varphiφ – фазовый угол. Таким образом, из приведенных выше деталей можно сделать вывод, что коэффициент мощности всегда будет находиться в диапазоне от 0 до 1. Для чисто резистивной нагрузки он будет равен 1, тогда как для чисто индуктивной нагрузки он будет равен нулю.
Расчет мощности в цепи переменного тока
Мощность в цепи переменного тока представляет собой мгновенную мощность, поскольку переменный ток и напряжение также имеют синусоидальный характер, как показано на рисунке ниже.
P=V×IP = V \times IP=V×I
где \left( {\omega t + {\theta _v}}\right)\;{\rm{and}}\;I = {\mathop{\rm I}\nolimits} _m}\sin\left({ \omega t +{\theta _i}} \right)V=Vmsin(ωt+θv)andI=Imsin(ωt+θi)
P=[Vmsin(ωt+θv)]×Imsin (ωt+θi)P = \left[ {{V_m}\sin \left({\omega t + {\theta_v}} \right)} \right] \times {I_m}\sin \left({\omega t + {\theta_i}}\right)P=[Vmsin(ωt+θv)]×Imsin(ωt+θi)
Следовательно,
P=VmIm[Sin(ωt+θv)sin(ωt+θi)]P = {V_m}{I_m}\left[ {{\mathop{\rm Sin}\nolimits}\left( {\omega t + {\theta _v}} \right)\sin \left( {\omega t + {\theta _i}} \right)}\right]P=VmIm[Sin(ωt+θv )sin(ωt+θi)]
Применяя тригонометрическое тождество:
sinA×sinB=12(cos(A−B)−cos(A+B))\sin A \times \ sin B = \ frac {1} {2} \ left ( {\ cos \ left ( {A — B} \ right) — \ cos \ left ( {A + B} \ right)} \ right) sinA × sinB = 21(cos(A−B)−cos(A+B))
Теперь θ=θv−θi\theta= {\theta _v} — {\theta _i}θ=θv−θi разность фаз между током и напряжением.
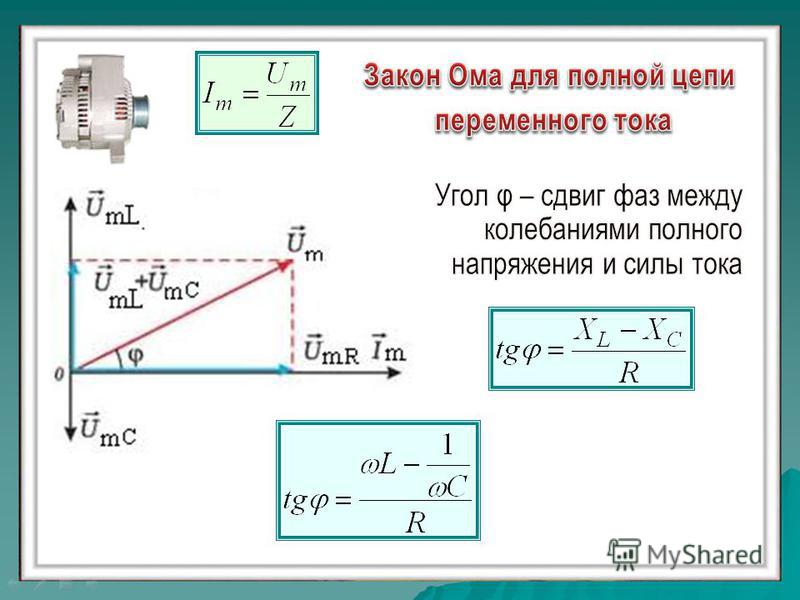
Итак,
P=(VmIm)12(cosθ−cos(2ωt+θ))P = \left( {{V_m}{I_m}} \right)\frac{1}{2}\ влево ({\ cos \ theta — \ cos \ left ( {2 \ omega t + \ theta } \ right)} \ right) P = (VmIm) 21(cosθ−cos(2ωt+θ))
Ас;
(VmIm)/2=Vm2×Im2=Vrms×Irms\left( {{V_m}{I_m}} \right)/2 =\frac{{{V_m}}}{{\sqrt 2 }} \times \frac{{{I_m}}}{{\sqrt 2 }} = {V_{rms}} \times{I_{rms}}(VmIm)/2=2Vm×2Im =Vrms×Irms
Где, Vrms{V_{rms}}Vrms – среднеквадратичное значение напряжения Irms{I_{rms}}Irms – среднеквадратичное значение тока. Мощность здесь мгновенная мощность, которую трудно рассчитать, так как она будет меняться со временем. Для устранения этой проблемы рассчитывается средняя мощность. Это среднее значение мгновенной мощности за один цикл.
Расчет мощности для различных типов нагрузки
1) Чисто резистивная нагрузка: Как показано на рисунке ниже, угол сдвига фаз между током и напряжением равен нулю, поэтому мощность определяется как:
P=VIcosφP =VI\cos \varphiP=VIcosφ
As,
φ=0, so cosφ=1\varphi=0,\;{\rm{so}}\;{\rm{cos}}\varphi {\rm{=1}}φ=0,socosφ=1
P=VIP =VIP=VI
2) Чисто индуктивная нагрузка: Как показано на рисунке ниже, фазовый угол между током и напряжением равен 90 градусов, то есть ток отстает от напряжения на 90 градусов, поэтому мощность определяется как: =90,\;{\rm{so}}\;{\rm{cos}}\varphi \;{\rm{=}}\;{\rm{0}}φ=90,socosφ=0
3) Чисто емкостная нагрузка: как показано на рисунке ниже, фаза и между током и напряжением составляют 90 градусов, т.
 е. напряжение отстает от тока на 90 градусов, поэтому мощность определяется как:
е. напряжение отстает от тока на 90 градусов, поэтому мощность определяется как: P=VIsinφP = VI\sin\ varphiP=VIsinφ
Как,
φ=-90, so cosφ = −1\varphi=-90,\;{\rm{so}}\;{\rm{cos}}\varphi \;{\rm{ = }}\;{ \rm{ — 1}}φ=−90,socosφ=−1
P=−VIP=- VIP=−VI
Продолжать учиться
Что изучать дальше на основе учебной программы колледжа
Power FactorAverage Power
Использование Формула фазового угла для понимания подачи мощности
Ключевые выводы
-
Подача энергии в системе переменного тока зависит от фазового угла между напряжением и током.
-
Фазовый угол также зависит от импеданса цепи, который вызывает изменение фазы.
-
При наличии разности фаз между напряжением и током реальная мощность, подаваемая на нагрузку, может быть довольно низкой.
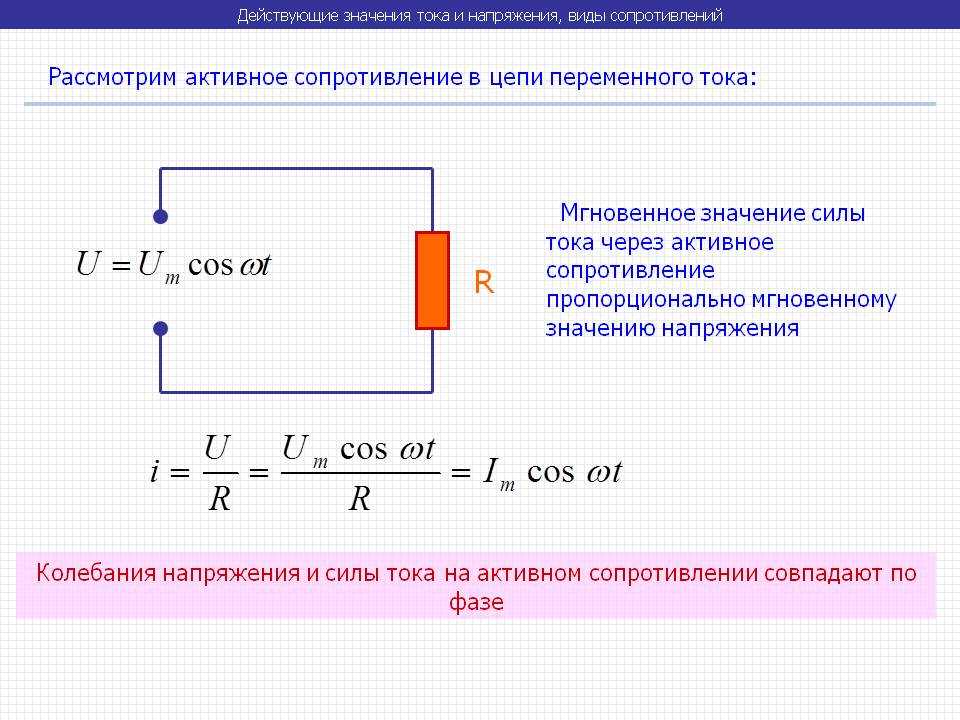 Вы можете определить, когда это произойдет, посмотрев на графики для вашей схемы.
Вы можете определить, когда это произойдет, посмотрев на графики для вашей схемы.
Поддерживайте высокий коэффициент мощности при работе с 3-фазным питанием в ваших системах переменного тока.
Работа с подачей энергии может быть опасной и сложной, особенно когда мы рассматриваем реактивное сопротивление в практических цепях переменного тока. Обеспечение реальной подачи мощности на резистивную нагрузку зависит от поддержания высокого коэффициента мощности в ваших цепях, что в свою очередь требует поддержания фазового угла в вашей системе близким к нулю. Время от времени вам нужно будет проверять угол сдвига фаз между напряжением и током в реактивной цепи, чтобы обеспечить достаточную подачу мощности на элемент нагрузки.
Просто взглянув на разницу во времени между подаваемым напряжением и током на вашем компоненте нагрузки, вы можете определить фазовый угол, определяющий реальную подачу мощности.
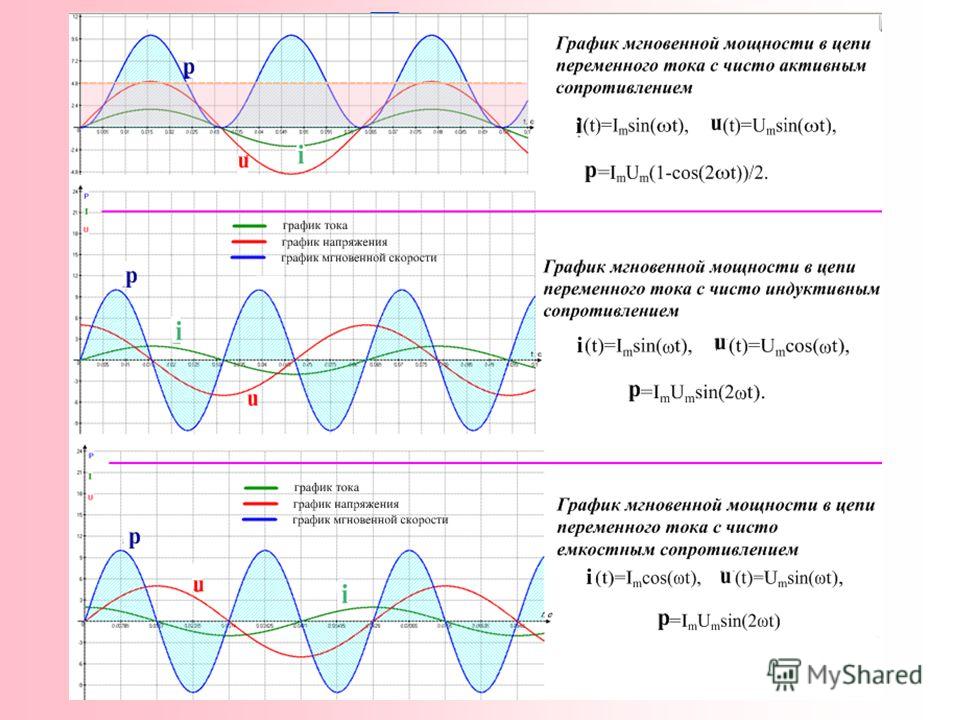 Затем вы можете использовать формулу фазового угла для реальной и полной мощности, чтобы определить коэффициент мощности в вашей системе. Затем вы можете определить, потребуется ли коррекция коэффициента мощности, которая будет зависеть от входного напряжения и мощности в системе.
Затем вы можете использовать формулу фазового угла для реальной и полной мощности, чтобы определить коэффициент мощности в вашей системе. Затем вы можете определить, потребуется ли коррекция коэффициента мощности, которая будет зависеть от входного напряжения и мощности в системе. Формула фазового угла
Фазовый угол цепи зависит от разности фаз между напряжением и током в цепи. Предполагая, что у нас есть простая система LTI, состоящая только из резисторов, конденсаторов и катушек индуктивности, вы можете определить простое соотношение фазового угла между напряжением и током в каждом элементе схемы.
Разность фаз в различных цепях RLC графически показана на изображении ниже, где мы видим, что напряжение и ток смещены друг относительно друга во временной области. Здесь реактивное сопротивление элементов C и L создает разность фаз между напряжением и током. Эта разность фаз станет важной позже, когда вы захотите рассчитать реальную мощность, подаваемую на компонент нагрузки.

Комплексные напряжения и токи в различных цепях, а также их разности фаз.
Фазовый угол можно определить, просто взглянув на разницу во времени между кривыми напряжения и тока. Это равно разнице во времени между соседними пиками тока и напряжения, деленной на 180 градусов. В качестве альтернативы, если вы знаете импеданс в вашей цепи переменного тока, вы можете рассчитать разницу фаз, которую вы увидите между напряжением и током:
Формула фазового угла в терминах импеданса.
Обратите внимание, что это относится к цепям LTI, где фаза является постоянной величиной (т. е. не зависит от напряжения или тока). Для обычной сети RLC фазовый угол может быть функцией частоты, даже если цепь представляет собой систему LTI. Теперь, когда у нас есть четкое определение разности фаз в цепи переменного тока, мы можем определить реальную мощность, подаваемую на компонент нагрузки в цепи переменного тока.
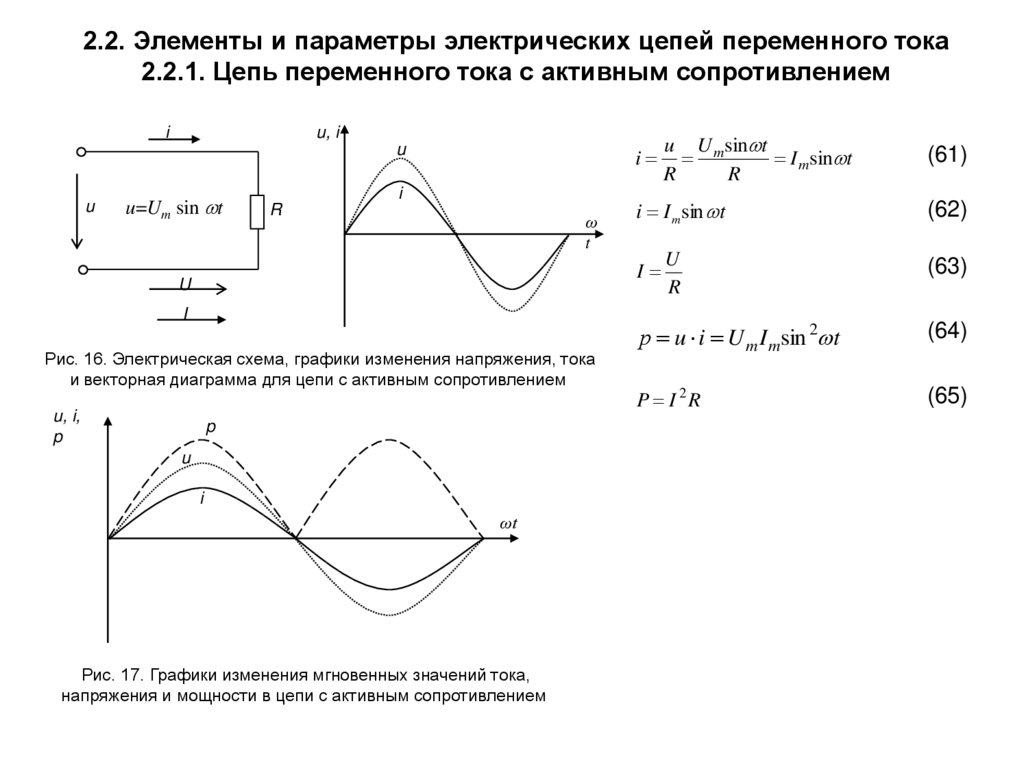
Отдаваемая мощность и фазовый угол
Когда ток и напряжение имеют некоторую разность фаз между собой, мощность в цепи представляется комплексным числом S. Действительная и мнимая части комплексной мощности представляют реальную отдаваемую мощность и реактивную мощность соответственно. Следующая формула определяет комплексную мощность S, которая выражается через комплексное сопротивление Z.
Комплексная мощность через комплексное сопротивление.
Обратите внимание, что резистивные части цепи всегда рассеивают активную мощность, как мы сейчас увидим, а реактивные части получают только реактивную мощность. Физически реактивная мощность представляет собой мощность, ограниченную реактивным элементом в цепи (т. е. элементами L и C). Напротив, реальная мощность рассеивается в виде тепла в резистивных элементах.
Если вы знаете фазовый угол из импеданса или временной разницы между током и напряжением, то вы можете рассчитать реальную мощность, подаваемую на нагрузку.
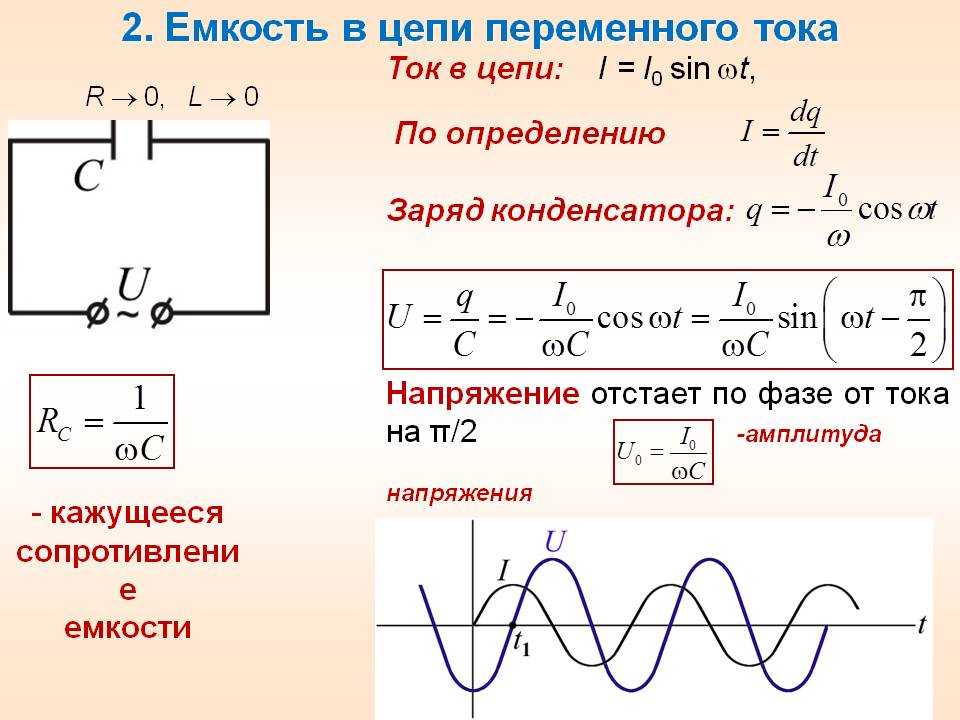 Это определяется ниже с точки зрения величины S и фазового угла:
Это определяется ниже с точки зрения величины S и фазового угла: Фактическая мощность, подаваемая на компонент нагрузки.
Чтобы рассчитать реактивную мощность, просто замените косинус на синус в приведенном выше уравнении. Обратите внимание на знак фазового угла в этом расчете, так как он покажет вам, когда мощность ограничивается реактивными элементами, а когда она рассеивается в резистивных элементах. Это различие между кажущейся мощностью и реальной мощностью становится более ясным, когда мы исследуем распределение тока и напряжения в последовательной цепи RLC, как показано на рисунке ниже.
Распределение напряжения и тока в последовательной цепи RLC.
На этом изображении напряжение тока и катушки индуктивности не совпадают по фазе друг с другом, поэтому общая реактивная мощность в LC-ветви цепи равна нулю. Другими словами, элементы C и L имеют противоположное реактивное поведение в разные моменты времени; один элемент генерирует реактивную мощность, а другой ограничивает ее.

Фазовый угол от активной и реактивной мощности
Другой важной величиной является кажущаяся мощность |S|, которая учитывает активную и реактивную мощности вместе без фазовой постоянной. В другом случае вы можете уже знать реальную мощность Re[S] и кажущуюся мощность |S|, и вам нужно найти фазовый угол. Отношение этих двух величин известно как коэффициент мощности, который очень важен в регулируемых системах преобразования переменного тока в постоянный. Коэффициент мощности определяется по фазовому углу следующим образом:
Определение коэффициента мощности по фазовому углу.
В идеале коэффициент мощности системы преобразования мощности должен быть равен 1. Поскольку реальные схемы регуляторов имеют коэффициент мощности где-то около ~0,7, схема PFC обычно добавляется на этапе выпрямления AC-DC, чтобы обеспечить коэффициент мощности как можно ближе к 1. Вычисление фазового угла говорит вам, как вам нужно будет компенсировать низкий коэффициент мощности при проектировании ваших цепей.

После того, как вы использовали формулу фазового угла и определили, какой уровень коррекции коэффициента мощности вам нужен, вы можете создать макет платы с помощью лучшего программного обеспечения для компоновки и проектирования печатных плат с полным набором инструментов проектирования. Allegro PCB Editor включает в себя функции, необходимые для компоновки плат для любого приложения, включая системы преобразования энергии переменного тока. Затем вы можете использовать инструменты анализа Cadence для моделирования и анализа поведения вашей силовой электроники.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты.
 Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на LinkedIn Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостейСпасибо!
Активная мощность, реактивная мощность, полная мощность и роль коэффициента мощности
Что такое сила?
Различные термины мощности в системах электроснабжения включают активную, реактивную и полную мощность, и все они приводят к введению эффективности «коэффициента мощности» в цепи переменного тока. Цепи переменного тока передают энергию резистивным и реактивным нагрузкам, а в случае чисто резистивных нагрузок энергия рассеивается так же, как постоянный ток рассеивает энергию в резисторе.
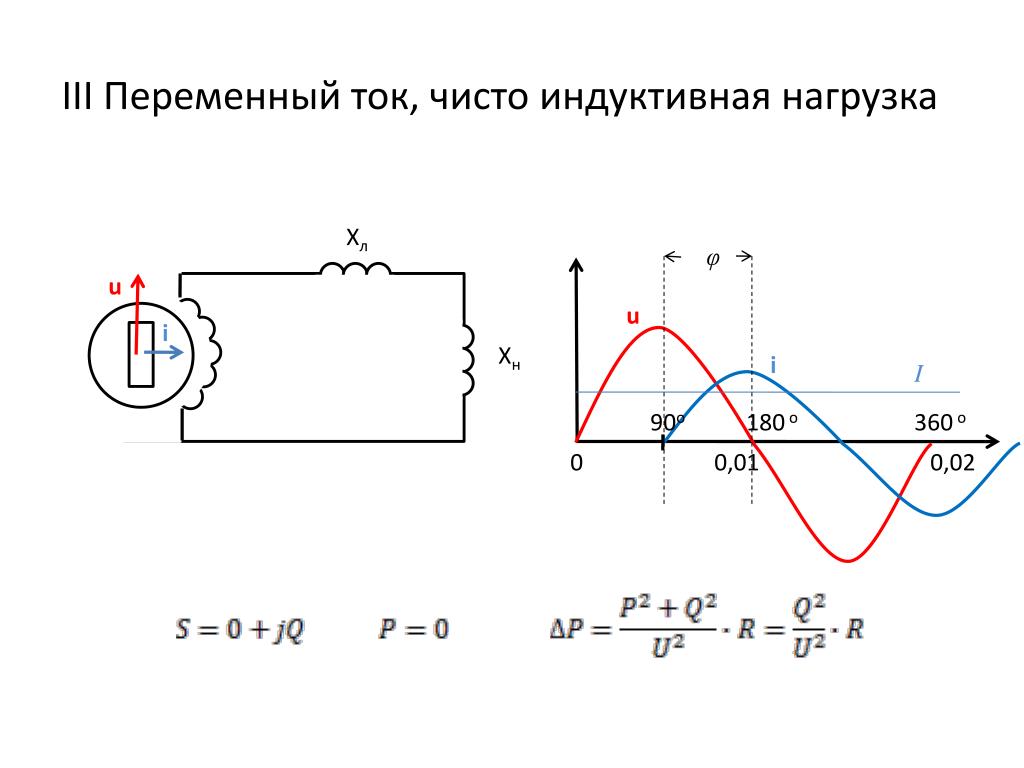
Электроэнергия – это скорость, с которой энергия передается в часть электрической цепи или от нее. В электрической цепи мощность равна разности напряжений на элементе, умноженной на ток \(V \times I\). Мощность измеряется в ваттах \(1Вт=1Дж\)/\(с\) 92}{R}$$
Эти уравнения получены из закона Ома, который равен \(V = I\times R\), где V = напряжение или разность потенциалов в цепи, I = ток и R = сопротивление в цепи .
Рис. 1. Измерение переменного тока является основным компонентом проверки выработки и рассеивания мощности при больших нагрузках. Изображение предоставлено CanvaМгновенная мощность
Мгновенная мощность означает мощность в любой момент времени или мощность в любой заданный момент времени и может быть записана как:
$$P (t) = V (t) \times I (t)$$
В цепи постоянного тока мощность, необходимая для напряжения V, чтобы вызвать ток I через цепь, равна V, умноженному на I.
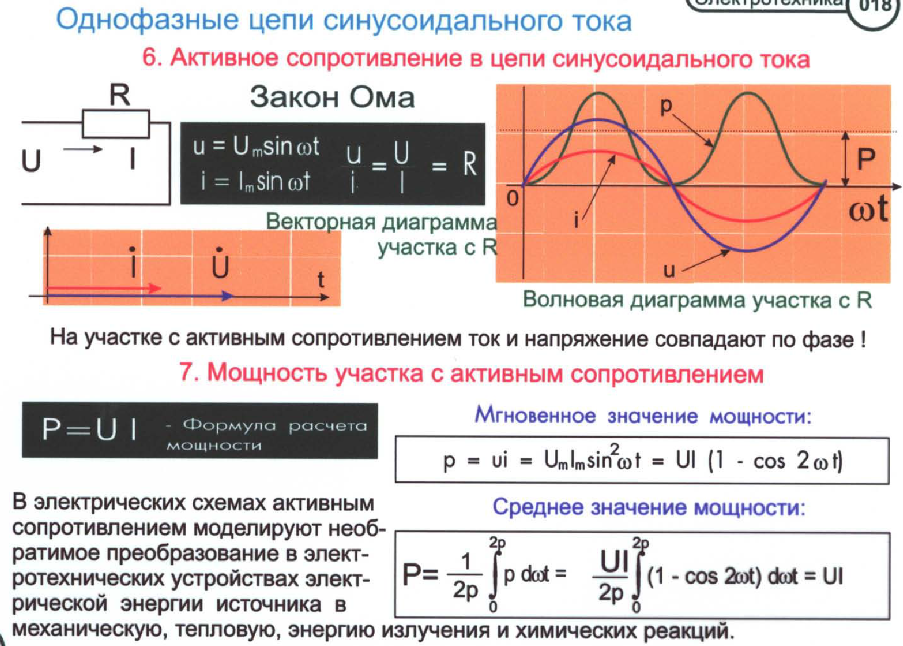 Точно так же, если через цепь проходит переменный ток, мощность, требуемая в каждый момент времени, равна значению напряжения в этот момент, умноженному на ток в тот же момент. На практике нагрузки представляют собой комбинацию резистивных, индуктивных и емкостных элементов на стороне потребителя.
Точно так же, если через цепь проходит переменный ток, мощность, требуемая в каждый момент времени, равна значению напряжения в этот момент, умноженному на ток в тот же момент. На практике нагрузки представляют собой комбинацию резистивных, индуктивных и емкостных элементов на стороне потребителя. Есть три типа нагрузок
1. Резистивная нагрузка: где V и I находятся в фазе, а мощность всегда положительна, как тормозные резисторы, нагреватели и лампочки.
2. Индуктивная нагрузка: ток отстает от напряжения, как двигатели, вентиляторы и трансформаторы.
3. Емкостная нагрузка: ток опережает напряжение (несколько примеров чисто емкостных нагрузок).
Разность фаз между током и напряжением оказывает важное влияние на подаваемую мощность, поскольку мгновенное напряжение, соответствующее любому конкретному мгновенному току, зависит от угла между ними. Поэтому в цепях переменного тока мощность обычно нельзя получить простым перемножением действующих напряжений и действующих ампер, как это делалось в случае постоянного тока.
 Необходимо учитывать влияние на мощность разности фаз между током и напряжением.
Необходимо учитывать влияние на мощность разности фаз между током и напряжением. Типы мощности:
1. Активная мощность (кВт, МВт, ГВт)
2. Реактивная мощность (кВАр, МВАР)
3. Полная мощность (кВА, МВА)
На рис. 2 показан известный пример понять разницу между тремя силами. Стакан, наполненный коктейлем, представляет собой истинную мощность, а пенистая пена наверху — реактивную мощность, а сумма активной и реактивной — кажущуюся мощность в системе.
Рисунок 2. Известная аналогия для описания активной, реактивной и полной мощностиАктивная мощность или реальная мощность
Активную мощность часто называют реальной, действительной, истинной или полезной мощностью. В цепях постоянного тока мощность — это просто произведение напряжения на нагрузке на ток, протекающий через нее, потому что в цепях постоянного тока нет фазового угла между напряжением и током, поэтому в цепях постоянного тока нет коэффициента мощности.
 Другими словами, напряжение и ток находятся в фазе друг с другом, что означает, что напряжение и ток начинаются в одно и то же время, достигают пика, а затем снова одновременно касаются нуля.
Другими словами, напряжение и ток находятся в фазе друг с другом, что означает, что напряжение и ток начинаются в одно и то же время, достигают пика, а затем снова одновременно касаются нуля. $$P = V \times I~для~цепей~постоянного~$$
В то время как в цепях переменного тока существует угол сдвига фаз между напряжением и током, выраженный добавленной составляющей \(cos \theta\).
В однофазной цепи переменного тока активная мощность:
$$P=V \times I\times cos\theta$$
В трехфазной цепи переменного тока:
$$P = \sqrt{3 } \times V \times I\times cos\theta$$
На рисунке 3 ток и напряжение находятся в фазе друг с другом, образуя угол +90 градусов в то же время, и положительное напряжение, умноженное на положительный ток, генерирует положительную мощность . Когда и ток, и напряжение отрицательны, мощность все еще положительна, поэтому в обоих случаях мощность всегда положительна, это называется активной мощностью. Кривая мощности будет лежать полностью над горизонтальной осью и отражает, что вся проделанная работа положительна.

Рис. 3. Ток и напряжение совпадают по фазе друг с другом
Рисунок 4. Активная мощность течет от источника к нагрузкеХарактеристики активной мощности:
- Активная мощность всегда положительна и не меняет своего направления, всегда течет от источника к нагрузке.
- Обозначается буквой P и измеряется в ваттах (кВт, МВт, ГВт).
- Измерьте с помощью ваттметра.
- Активная энергия производит тепло, механическую энергию и свет.
Реактивная мощность
Реактивная мощность возникает в цепях переменного тока, когда напряжение и ток не совпадают по фазе. Его единицей измерения является ВАР (реактивное напряжение в амперах). В реальном мире нагрузки представляют собой комбинацию резистивных, индуктивных и емкостных элементов, и невозможно определить характер нагрузки (малая/большая, бытовая/промышленная индуктивная/емкостная).
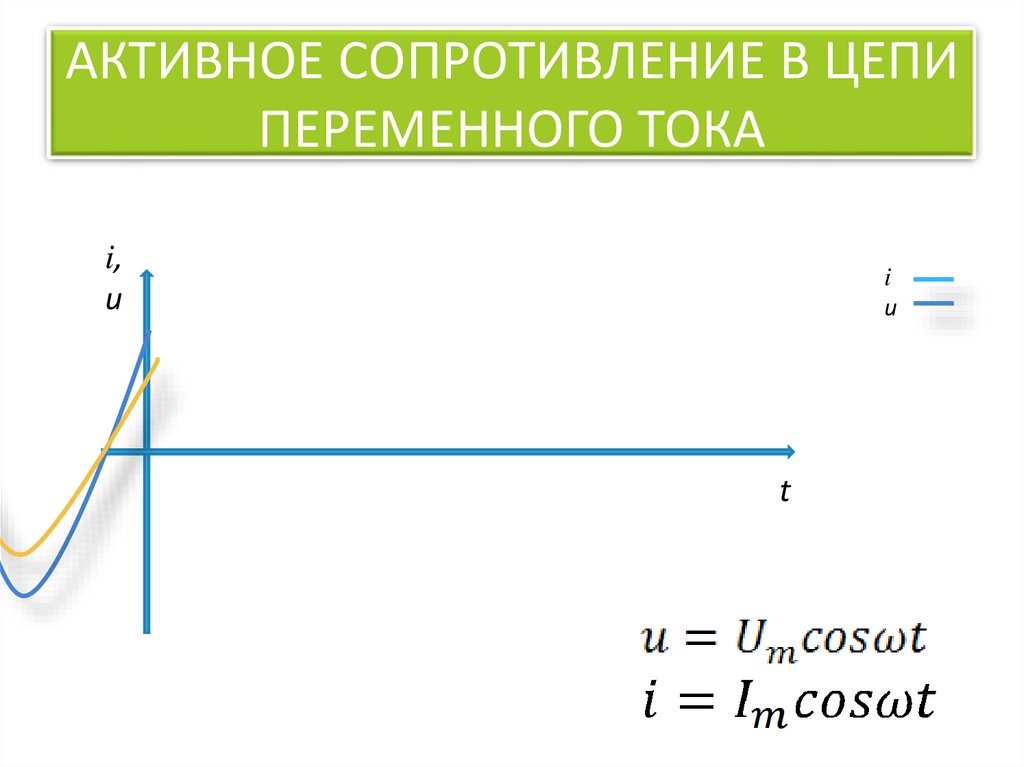 Существует два типа реактивного сопротивления:
Существует два типа реактивного сопротивления: - Емкостное реактивное сопротивление (отрицательное)
- Индуктивное сопротивление (положительное)
Мощность может быть положительной и отрицательной. Когда мощность течет от источника к нагрузке, она положительна, а мощность течет от нагрузки к источнику, тогда это называется отрицательной мощностью. Как правило, реактивная мощность определяется только для цепей переменного тока и постоянно колеблется между источником и нагрузкой и обозначается буквой Q, как на рис. 5.
Рис. 5. Потоки реактивной мощности от источника к нагрузке и обратно к источникуРеактивная мощность (Q)
Характеристики реактивной мощности:
- Периодически меняет свое направление, бывает как положительным, так и отрицательным.
- Подается буквой «Q» и измеряется в вар, квар, мвар
- Измерено с помощью вар-метра.
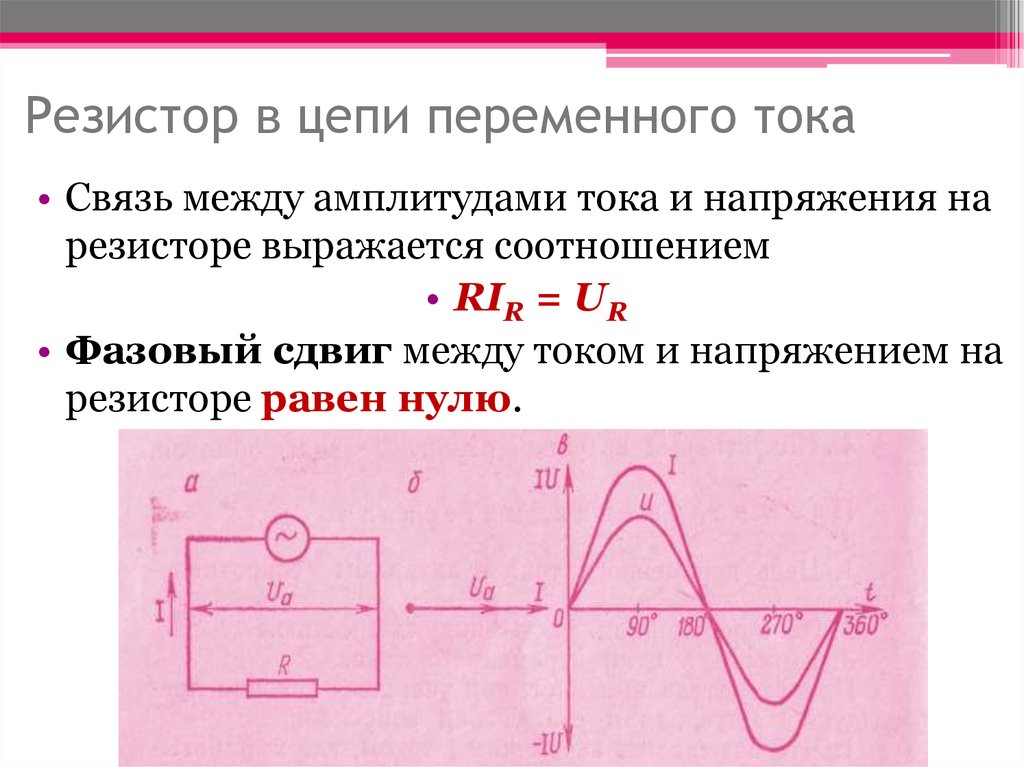
- Трансформаторы и асинхронные двигатели используют реактивную мощность для создания магнитного поля.
Трансформаторам также требуется реактивная мощность для создания магнитного поля в первичной обмотке и наведения напряжения во вторичной обмотке. Следовательно, если реактивная мощность недостаточна, трансформатор не будет преобразовывать напряжения, и двигатель не будет вращаться. Синхронные генераторы переменного тока также генерируют или поглощают реактивную мощность в зависимости от возбуждения постоянным током его обмотки возбуждения. Когда генератор перевозбужден, он вырабатывает реактивную мощность и поглощает реактивную мощность, когда генератор недовозбужден.
Полная мощность
Эта мощность представляет собой комбинацию активной и реактивной мощности и выражается в вольт-амперах или киловольт-амперах (кВА).
Фактически, большинство нагрузок в нашей повседневной жизни (электрический вентилятор, электрический утюг, асинхронный двигатель) представляют собой комбинацию резистивных и индуктивных нагрузок.
 Резистивная нагрузка потребляет активную мощность, а индуктивная нагрузка потребляет реактивную мощность, а общая мощность, отдаваемая источником, представляет собой комбинацию активной и реактивной мощности, называемой полной мощностью. 92$$
Резистивная нагрузка потребляет активную мощность, а индуктивная нагрузка потребляет реактивную мощность, а общая мощность, отдаваемая источником, представляет собой комбинацию активной и реактивной мощности, называемой полной мощностью. 92$$ Где S = Полная мощность, измеренная в кВА, Q = Реактивная мощность в кВАр и P = Активная мощность в кВт
Характеристики реактивной мощности
- Полная мощность представляет собой сумму активной и реактивной мощности.
- Подарено буквой «С»
- Измеряется в ВА, кВА и МВА
Треугольник власти
Отношение между полномочиями может быть представлено в виде векторов, называемых «треугольником власти». Активная мощность представлена в виде горизонтального вектора, тогда как реактивная мощность показана в виде вертикального вектора, а полная мощность соединяет активный и реактивный векторы. Если угол «θ» между активной и полной мощностью увеличивается, реактивная мощность увеличивается.
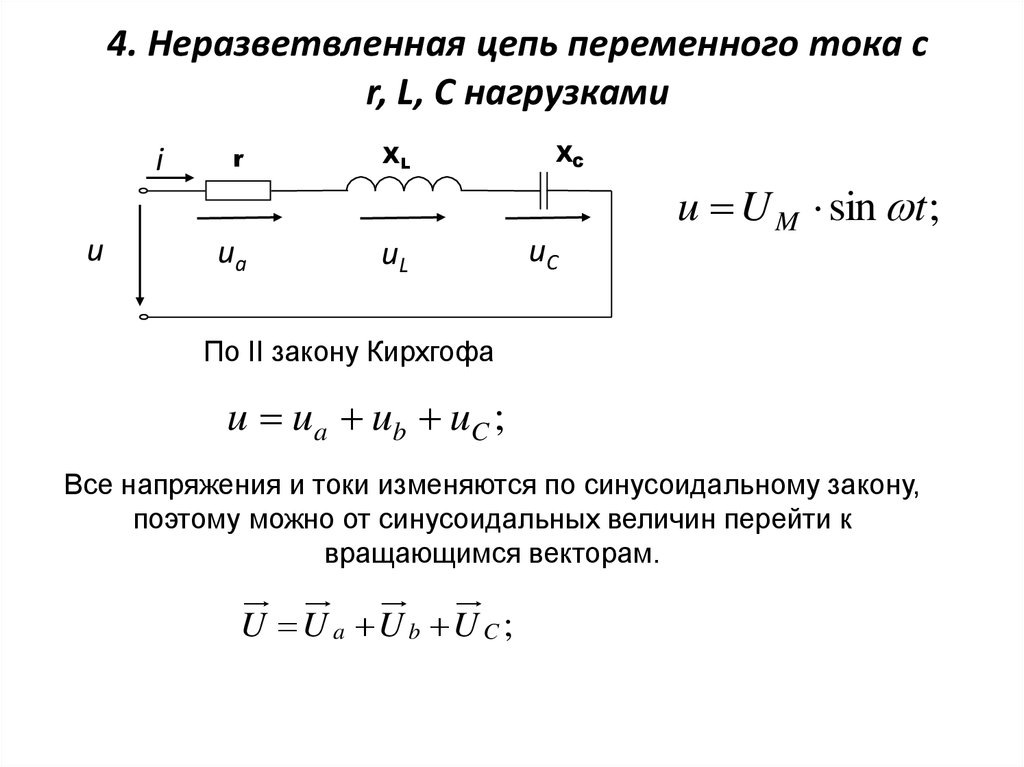
Рис. 6. Треугольник мощности описывает соотношение между активной, реактивной и полной мощностью.Коэффициент мощности
Коэффициент мощности является важным понятием в электрической системе, и хороший коэффициент мощности определяет качество конструкции и эффективное использование источника питания в электрической системе. Он показывает отношение активной мощности к полной мощности и представляет собой просто отношение активной (действительной) мощности в ваттах к полной мощности в вольт-амперах.
$$Power~Factor = \frac{Активная~мощность}{Полная~мощность}$$
Коэффициент мощности 1,0 называется «единичным коэффициентом мощности» или 100-процентным коэффициентом мощности, что означает, что ток и напряжение находится «в фазе». Невозможно получить 100% коэффициент мощности на всех участках энергосистемы. В линиях передачи необходим высокий коэффициент мощности, который снижает потери при передаче, а также способствует эффективной работе двигателя с индуктивной нагрузкой и предотвращению перегрева.
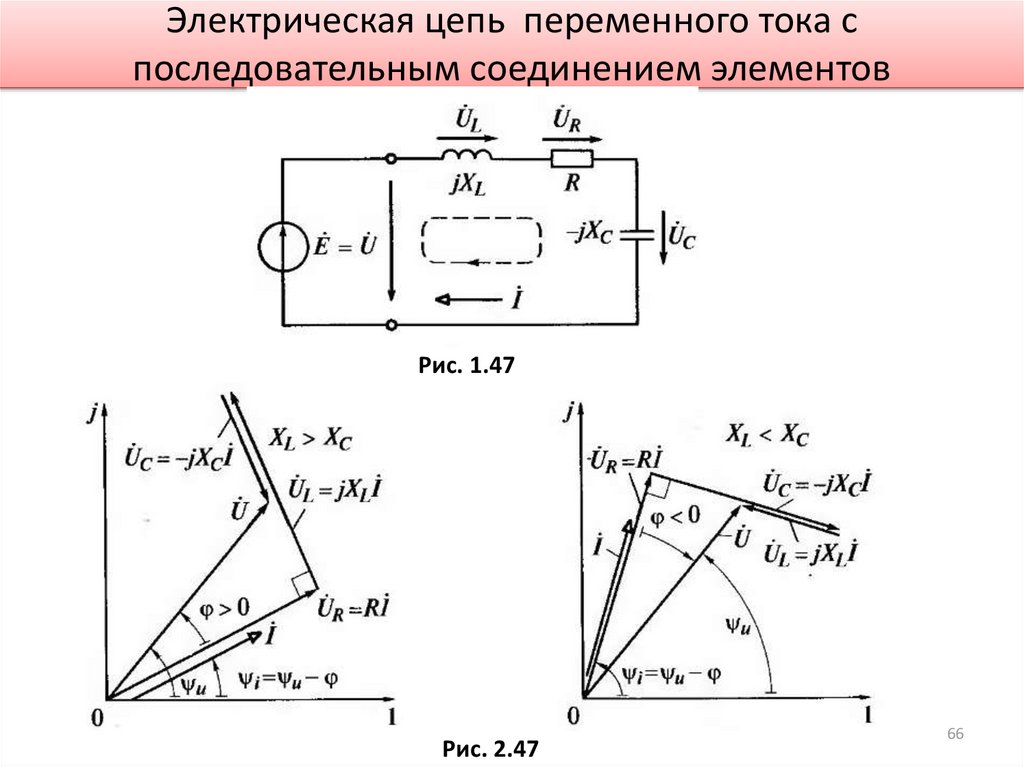
Вопрос: что на самом деле показывает коэффициент мощности? Предположим, что коэффициент мощности равен 0,8. Это означает, что из 100 % система потребляет 80 % активной мощности и 20 % реактивной мощности. Это значение коэффициента мощности, который указывает общее количество активной мощности в системе. Коэффициент мощности является важным термином в энергосистеме переменного тока, если напряжение и мощность системы постоянны, то коэффициент мощности обратно пропорционален.
$$Line~Current \propto \frac{1}{Power~Factor}$$
Выражение трехфазной мощности записывается как:
$$P = \sqrt{3} \times V \times I \times cos\theta$$
Следовательно,
$$I = \frac{P}{\sqrt{3} \times V \times cos\theta}$$
Здесь множители \(P\), \(\sqrt{3}\) и \(V\) взяты за константы, поэтому ток обратно пропорционален \(cos \theta\), т.е. \(I \propto 1\) / \(cos \theta\ ). Это означает, что если коэффициент мощности системы низкий, ток системы становится большим.

Недостатки низкого коэффициента мощности в системе
- Если коэффициент мощности системы ниже, ток системы становится большим.
- Большая номинальная мощность оборудования в кВА: генераторы переменного тока, трансформаторы и распределительные устройства оцениваются в кВА, поскольку мы знаем, что \(кВА=кВт\)/\(cos \theta\), что означает, что если вам нужна желаемая мощность в кВт от машина, KVA машины должна быть выше. Следовательно, чтобы увеличить пропускную способность машины по току, поперечное сечение проводящих частей машины должно быть увеличено, что делает машину больше, тяжелее и дороже.
- Больший размер проводника: При низком коэффициенте мощности для передачи того же количества мощности требуется проводник большего сечения. Это связано с тем, что в условиях низкого коэффициента мощности требуется больший ток для удовлетворения потребности потребителя в полезной мощности.
- Большие потери в меди: Поскольку мы уже знаем, что ток обратно пропорционален коэффициенту мощности, поэтому, если коэффициент мощности энергосистемы низкий, ток будет увеличиваться.
 2 \times R\), что приводит к снижению эффективности системы.
2 \times R\), что приводит к снижению эффективности системы. - Низкий отстающий коэффициент мощности вызывает высокое падение напряжения в генераторах переменного тока и трансформаторах.
Отставание коэффициента мощности от опережения
В системе электросети реактивная мощность может быть увеличена или уменьшена с помощью системного возбуждения. Если возбуждение увеличивается, это означает увеличение потока и, следовательно, увеличение реактивной мощности. Когда реактивная мощность увеличивается, коэффициент мощности отстает (уменьшается). Отстающая нагрузка потребляет реактивную мощность, а генератор подает реактивную мощность в систему.
Рис. 7. Визуализация «ведущего» коэффициента мощности.Давайте посмотрим на другой способ, когда напряжение уменьшается, возбуждение уменьшается, что означает уменьшение потока и, следовательно, уменьшение реактивной мощности и, следовательно, увеличение коэффициента мощности.
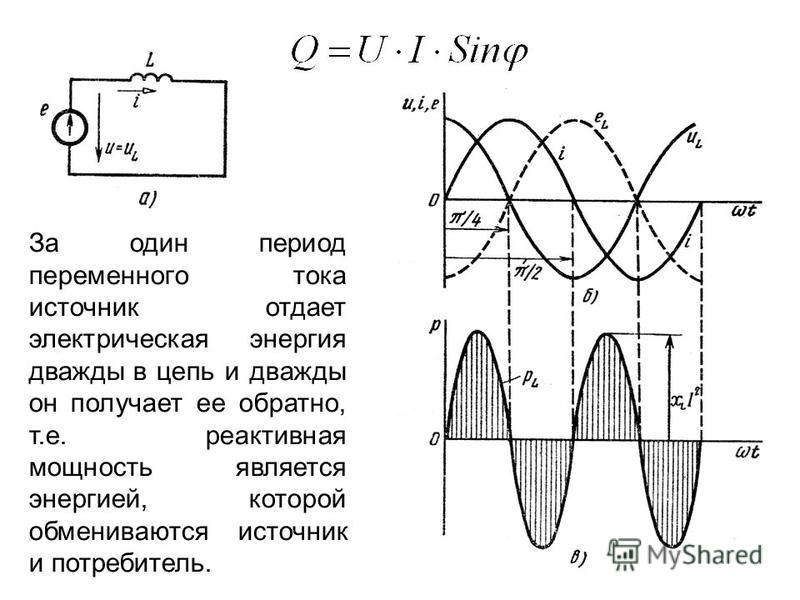 Генератор потребляет реактивную мощность от нагрузки. Эта реактивная мощность используется для создания магнитного поля, необходимого генератору для правильной работы. Таким образом, мы можем сказать, что возбужденная синхронизирующая машина действует как конденсатор, а возбужденная синхронизирующая машина действует как индуктор.
Генератор потребляет реактивную мощность от нагрузки. Эта реактивная мощность используется для создания магнитного поля, необходимого генератору для правильной работы. Таким образом, мы можем сказать, что возбужденная синхронизирующая машина действует как конденсатор, а возбужденная синхронизирующая машина действует как индуктор. Стало практикой говорить, что коэффициент мощности отстает, когда ток отстает от напряжения питания, и опережает, когда ток опережает напряжение питания.
Влияние коэффициента мощности на систему
Активная мощность — это полезная мощность, которая выполняет некоторую реальную работу в цепи переменного тока, тогда как реактивная мощность — это неполезная мощность, которая течет туда и обратно (в обоих направлениях от источника к нагрузке), но производит электрическую энергию. или магнитный поток. Полная мощность – это полная мощность в системе, представляющая собой комбинацию активной и реактивной мощностей и измеряемая в кварах. Крупные промышленные типы оборудования, такие как рейтинг трансформаторов, упоминаются в KVA.
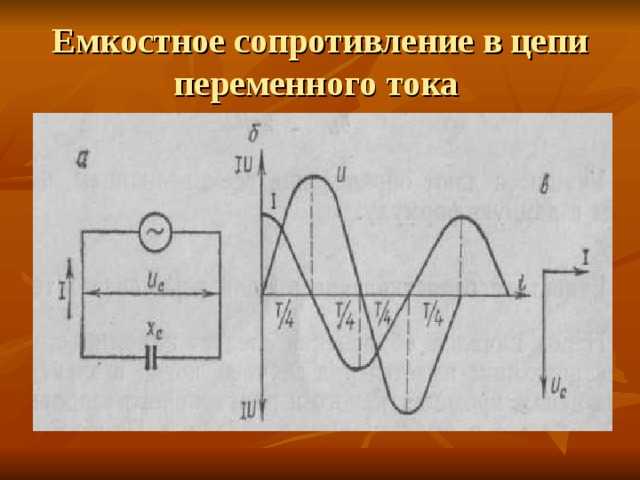 Чем ниже коэффициент мощности, тем больше размер источника для выработки этой мощности, что приводит к стоимости производства и передачи электроэнергии.
Чем ниже коэффициент мощности, тем больше размер источника для выработки этой мощности, что приводит к стоимости производства и передачи электроэнергии. Понимание коэффициента мощности | www.electriceasy.com
Энергия нужна и используется во всем мире. С точки зрения удобства, эффективности и экономии, лучше всего, чтобы мы генерировали, передавали и распространяли его в электрической форме до того, как он будет преобразован в требуемую форму с помощью подходящего оборудования. По тем же соображениям экономии и эффективности мы используем переменный ток, а не постоянный. Практически мы производим, передаем и распределяем энергию почти исключительно в форме переменного тока. Постоянный ток используется либо в приложениях постоянного тока (машины постоянного тока и электронные схемы), либо в линиях передачи постоянного тока высокого напряжения.
Везде, где используется мощность переменного тока, возникает вопрос коэффициента мощности.

Коэффициент мощности
- Определяется как ‘ косинус угла между напряжением и током ‘.
- В цепи переменного тока напряжение и ток идеально совпадают по фазе.
- Но на практике между ними существует разность фаз.
- Косинус этой разности фаз называется коэффициентом мощности.
- Его можно определить и математически представить следующим образом:
Из рис. (а) выше, можно четко отметить, что существует разность фаз угла ɸ между вектором напряжения и вектором тока.
Коэффициент мощности = cosɸНа рис. (b) называется Power Triangle
Здесь VI sinɸ = реактивная мощность (в ВАр)
VI cosɸ = активная мощность (в ваттах)
VI = полная мощность (в ВА)
PF = cosɸ = активная мощность ( Вт) / Полная мощность (ВА)На рис. (c) называется Треугольник импеданса
Здесь R = сопротивление, X = реактивное сопротивление, Z = импеданс отставание, опережение или единство.
Отстающий коэффициент мощности
- Когда ток отстает от напряжения, коэффициент мощности цепи называется «отстающим»
- Когда цепь индуктивная, коэффициент мощности отстает.
- Нагрузки, такие как асинхронные двигатели, катушки, лампы и т. д., являются индуктивными и имеют отстающий pf.
Опережающий коэффициент мощности
- Когда ток опережает напряжение (или напряжение отстает от тока), коэффициент мощности цепи называется опережающим.
- Когда цепь емкостная, коэффициент мощности опережает.
- Емкостные нагрузки, такие как синхронные конденсаторы, батареи конденсаторов и т. д., потребляют опережающий ток. Такие схемы имеют опережающий коэффициент мощности.
Unity Power Factor
- Коэффициент мощности равен единице (т.е. 1) для идеальных цепей.
- Когда ток и напряжение совпадают по фазе, PF = 1
- Коэффициент мощности не может быть больше единицы.
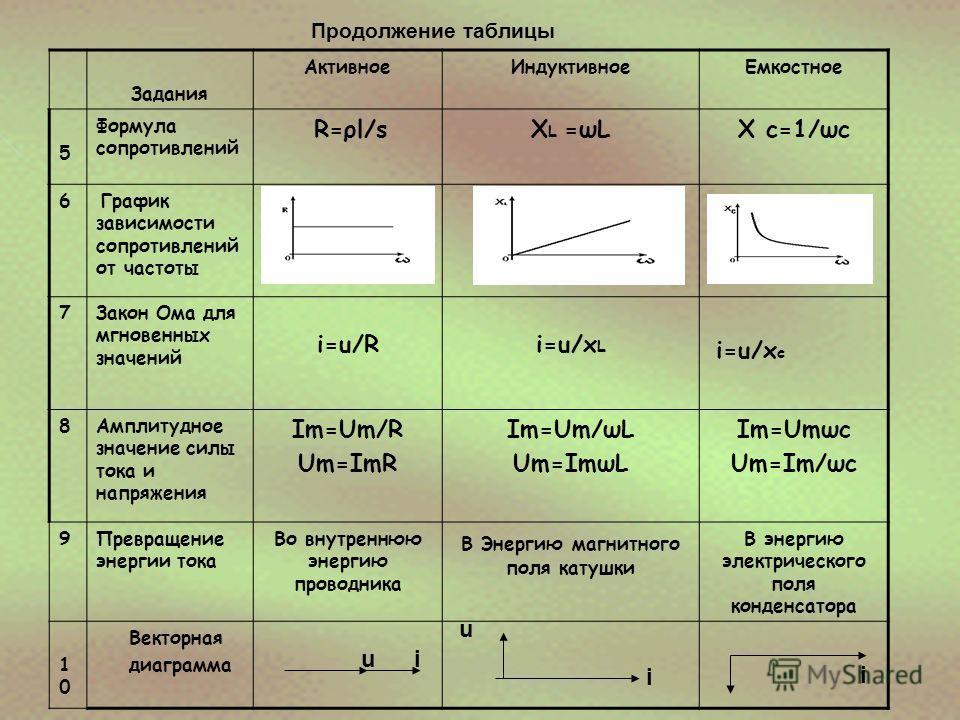
- На практике оно должно быть как можно ближе к единице.
Если коэффициент мощности низкий, возникают следующие проблемы:
Влияние низкого коэффициента мощности
- Ток нагрузки
Мощность в цепи переменного тока может быть выражена как: P = VI cosɸ
Следовательно, cosɸ = P / VI
I ∝ 1 / cosɸ
Аналогичное соотношение может быть получено для 3 фаз схема тоже. Мы видим, что ток обратно пропорционален pf.Например, предположим, что мы хотим передать мощность 10 кВА при 100 В
Если PF = 1,
I = P / (V cosɸ) = 10000 / (100 x 1) = 100 А
Если PF = 0,8 ,
I = P / (V cosɸ) = 10000 / (100 x 0,8) = 125 A
Следовательно, потребляемый ток выше при низком коэффициенте мощности. - Потери: Как указано выше, при низком коэффициенте мощности потребляемый ток велик. Следовательно, потери в меди (потери I 2 R) также будут высокими.
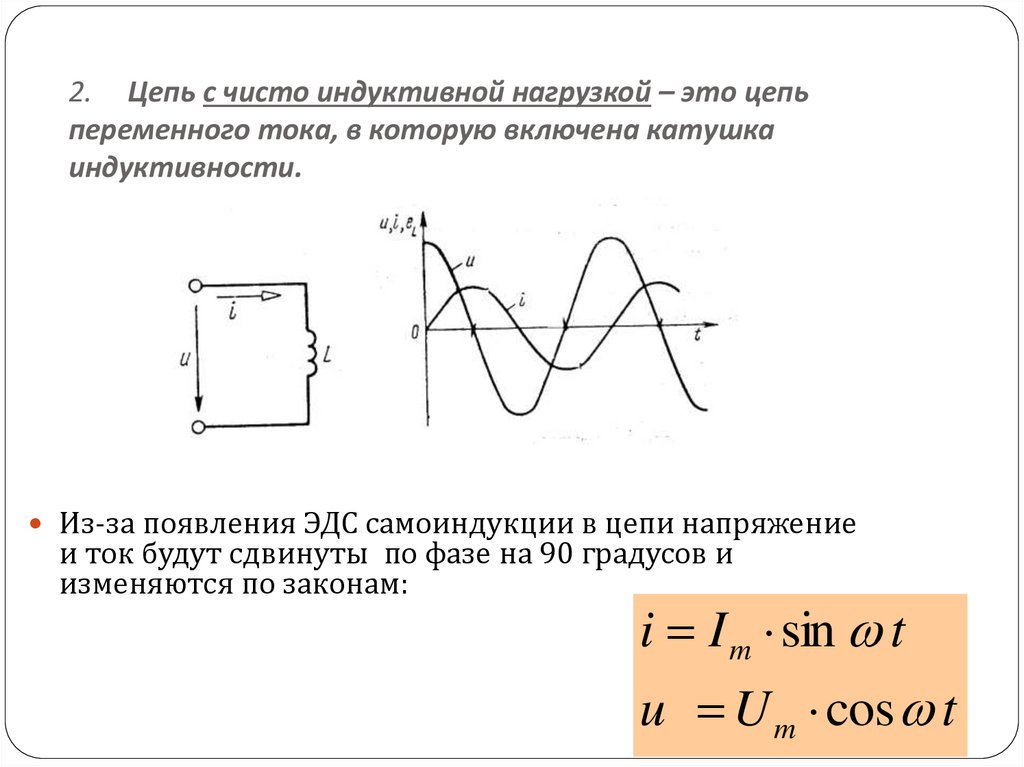 Это снижает эффективность оборудования.
Это снижает эффективность оборудования. - Перегрев оборудования: I 2 R потери выделяют тепло (закон Джоуля). Следовательно, повышение температуры будет относительно большим при низком коэффициенте мощности, что еще больше увеличит нагрузку на изоляцию.
- Размер проводника: Низкий коэффициент мощности приводит к более высокому току нагрузки. Если ток нагрузки увеличивается, размер требуемого проводника также увеличивается. Это еще больше увеличит стоимость проводника.
- кВА мощность машины: Машины не рассчитываются в кВт при производстве, потому что коэффициент мощности источника неизвестен. Вместо этого они оцениваются в кВА.
Согласно определению, Cosɸ = Активная мощность (кВт) / Полная мощность (кВА)
Следовательно, номинальная мощность в кВА = 1 / cosɸ
Следовательно, для низкого коэффициента мощности необходимо оборудование с большей номинальной мощностью в кВА. Но больший рейтинг кВА означает больший размер оборудования.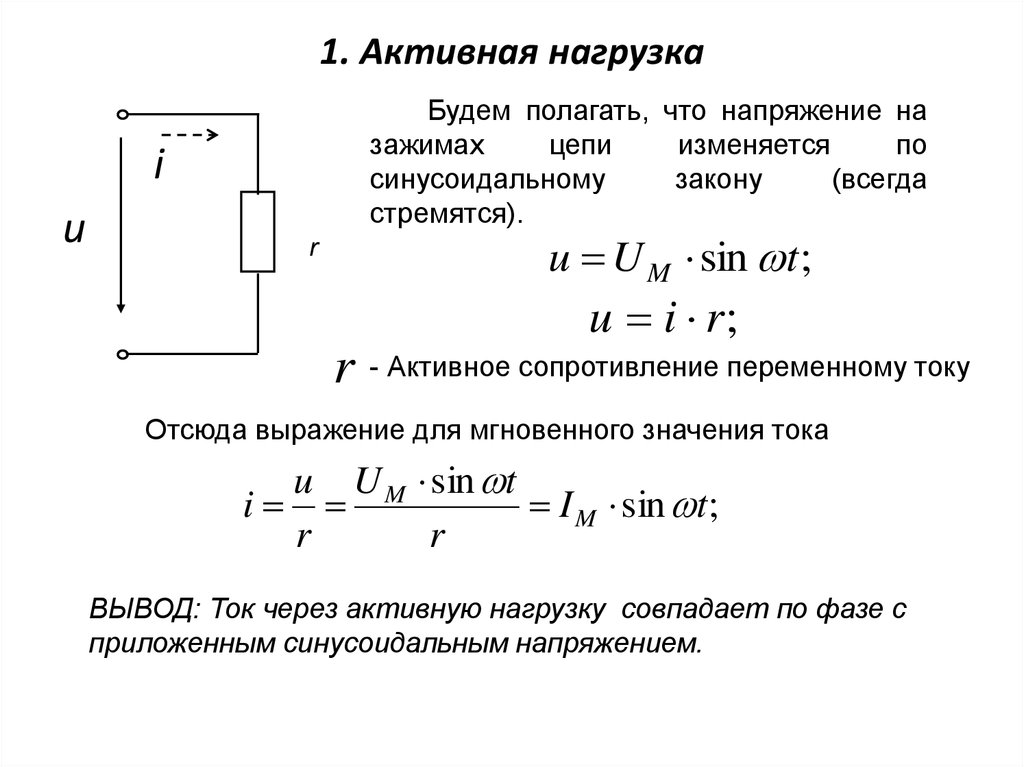 Если размер увеличивается, стоимость также увеличивается.
Если размер увеличивается, стоимость также увеличивается. - Регулирование напряжения: Определяется как разница между передающим и принимающим конечным напряжением на единицу передающего конечного напряжения. Когда мощность передается от одного конца к другому, напряжение падает по нескольким причинам. Это падение напряжения должно находиться в допустимых пределах.
P = VI cosɸ , поэтому I ∝ 1 / V
При низком коэффициенте мощности ток будет больше и, следовательно, падение напряжения будет больше. Следовательно, регулирование напряжения при низком коэффициенте мощности плохое. - Активная и реактивная мощность (мощность передачи): Активная и реактивная мощности передаются по линии вместе. Активная мощность необходима для питания нагрузки. Реактивная мощность необходима для поддержания напряжения в линии. Но если реактивная мощность больше, то передаваемая активная мощность уменьшается. При низком коэффициенте мощности активная мощность мала, поскольку cosɸ = активная мощность (Вт) / полная мощность (ВА).

-

 ..НПСИ-250/500-УВ1 преобразователь сигналов термопар, термосопротивлений и потенциометров…НПСИ-250/500-УВ1.2 преобразователь сигналов термопар, термосопротивлений и потенциометров, разветвитель «1 в 2» …НПСИ-230-ПМ10 нормирующий преобразователь сигналов потенциометров …НПСИ-200-ГРТП модули гальванической развязки токовой петли…НПСИ-200-ГР1/ГР2 модули гальванической развязки токового сигнала (4…20) мА…НПСИ-200-ГР1.2 модуль разветвления 1 в 2 и гальванической развязки сигнала (4…20) мА…НПСИ-ДНТВ нормирующий преобразователь действующих значений напряжения и тока…НПСИ-ДНТН нормирующий преобразователь действующих значений напряжения и тока …НПСИ-200-ДН/ДТ нормирующие преобразователи действующих значений напряжения и тока…НПСИ-МС1 преобразователь мощности, напряжения, тока, коэффициента мощности…НПСИ-500-МС3 измерительный преобразователь параметров трёхфазной сети с RS-485 и USB …НПСИ-500-МС1 измерительный преобразователь параметров однофазной сети с RS-485 и USB …НПСИ-УНТ нормирующий измерительный преобразователь унифицированных сигналов с сигнализацией.
..НПСИ-250/500-УВ1 преобразователь сигналов термопар, термосопротивлений и потенциометров…НПСИ-250/500-УВ1.2 преобразователь сигналов термопар, термосопротивлений и потенциометров, разветвитель «1 в 2» …НПСИ-230-ПМ10 нормирующий преобразователь сигналов потенциометров …НПСИ-200-ГРТП модули гальванической развязки токовой петли…НПСИ-200-ГР1/ГР2 модули гальванической развязки токового сигнала (4…20) мА…НПСИ-200-ГР1.2 модуль разветвления 1 в 2 и гальванической развязки сигнала (4…20) мА…НПСИ-ДНТВ нормирующий преобразователь действующих значений напряжения и тока…НПСИ-ДНТН нормирующий преобразователь действующих значений напряжения и тока …НПСИ-200-ДН/ДТ нормирующие преобразователи действующих значений напряжения и тока…НПСИ-МС1 преобразователь мощности, напряжения, тока, коэффициента мощности…НПСИ-500-МС3 измерительный преобразователь параметров трёхфазной сети с RS-485 и USB …НПСИ-500-МС1 измерительный преобразователь параметров однофазной сети с RS-485 и USB …НПСИ-УНТ нормирующий измерительный преобразователь унифицированных сигналов с сигнализацией. Выраженные симптомы появляются, когда опухоль…
Выраженные симптомы появляются, когда опухоль…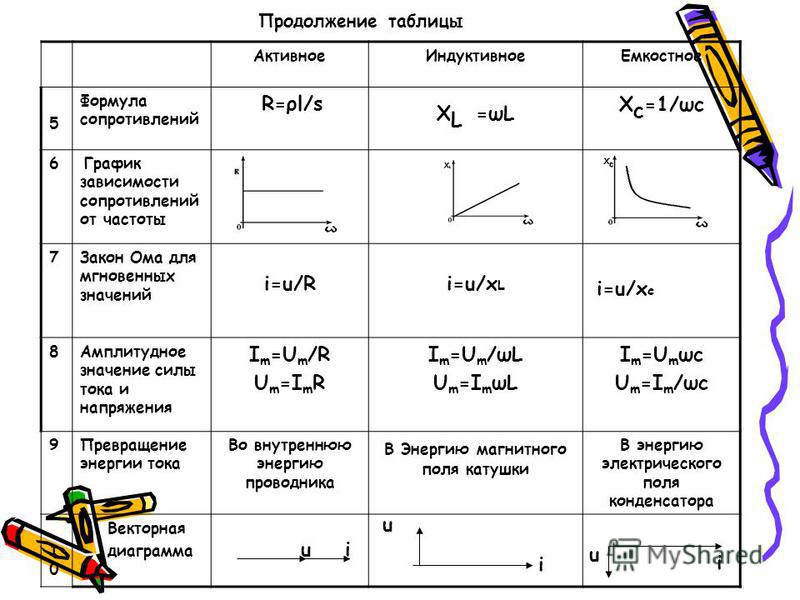 К такого рода цепям относятся, в частности, двигатели переменного тока, трансформаторы и другие устройства. В этих цепях между напряжением U и током I существует сдвиг фаз φ. Если к цепи приложено синусоидальное напряжение
К такого рода цепям относятся, в частности, двигатели переменного тока, трансформаторы и другие устройства. В этих цепях между напряжением U и током I существует сдвиг фаз φ. Если к цепи приложено синусоидальное напряжение

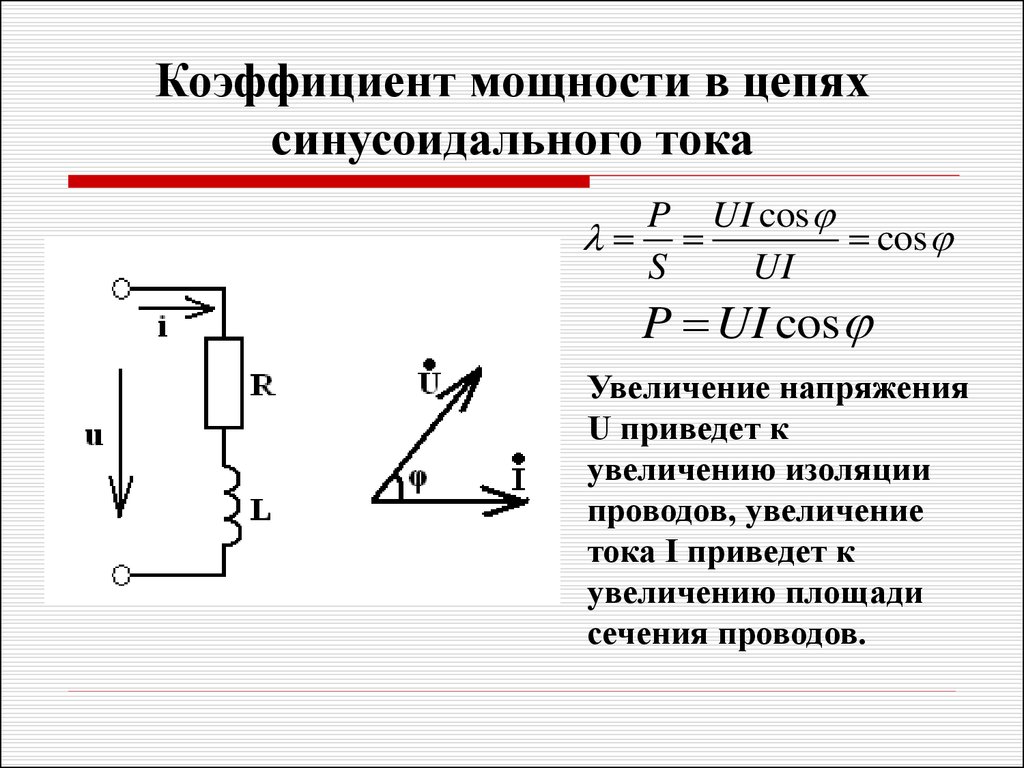 В самом деле, величина тока I определяет необходимое по условиям нагрева сечение проводов генераторов и трансформаторов, а число витков обмоток, их изоляция, а также размеры магнитопроводов пропорциональны величине напряжения U.
В самом деле, величина тока I определяет необходимое по условиям нагрева сечение проводов генераторов и трансформаторов, а число витков обмоток, их изоляция, а также размеры магнитопроводов пропорциональны величине напряжения U.
 Но в самой цепи только активная мощность Р = 384 вт безвозвратно преобразуется в тепло.
Но в самой цепи только активная мощность Р = 384 вт безвозвратно преобразуется в тепло.

 Из каждого треугольника можно найти «косинус фи» цепи, как показано на рис. 168. Этим можно воспользоваться для решения самых разнообразных задач.
Из каждого треугольника можно найти «косинус фи» цепи, как показано на рис. 168. Этим можно воспользоваться для решения самых разнообразных задач.
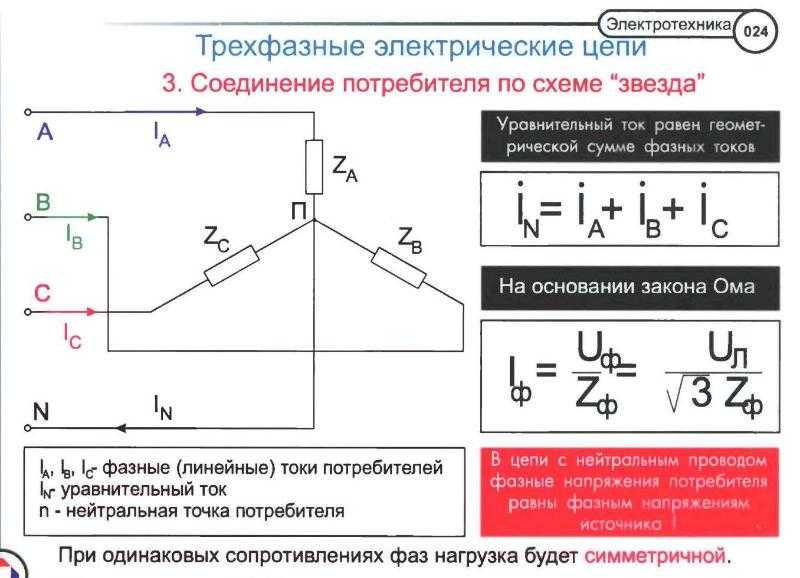

 Параллельно первому проводнику включен второй проводник с сопротивлением r = 2 ом и хL = 4 ом. Определить ток во втором проводнике.
Параллельно первому проводнику включен второй проводник с сопротивлением r = 2 ом и хL = 4 ом. Определить ток во втором проводнике.



