Активная составляющая тока: Недопустимое название — Радио Вики

Активные и реактивные составляющие токов и напряжений

 

При расчете электрических цепей переменного тока реальные элементы цепи (при­емники, источники) заменяются эквивалентными схемами замещения, состоящими из ком­бинации идеальных схемных элементов R, L и С.

Пусть некоторый приемник энергии носит в целом активно-индуктив­ный характер (например, электродвигатель). Такой приемник может быть пред­ставлен двумя простей­шими схемами замещения, состоящими из 2-х схемных элементов R и L: а) последовательной (рис. 51а) и б) параллельной (рис. 51б):

 

Обе схемы будут эквивалентны друг другу при условии равенства пара­метров ре­жима на входе: , .

Для последовательной схемы (рис. 51а) справедливы соотношения:

,

.

Для параллельной схемы (рис. 51б) справедливы соотношения:

,

.

Сравнивая правые части уравнений для U и I

, получим соотношения между пара­метрами эквивалентных схем:

, , , .

Из анализа полученных уравнений следует сделать вывод, что в общем случае и и соответственно и , как это имеет место для цепей постоян­ного тока.

Математически любой вектор можно представить состоящим из суммы нескольких векторов или составляющих.

Последовательной схеме замещения соответствует представление век­тора напряже­ния в виде суммы двух составляющих: активной составляющей U_а, совпадающей с векто­ром тока I, и реактивной составляющей U_р, перпенди­кулярной к вектору тока (рис. 52а):

 

 

 

Из геометрии рис. 52а следуют соотношения: , , . Треугольник, составленный из векто­ров , , получил назва­ние треугольника напряжений.

Если стороны треугольника напряжений разделить на ток I, то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются полное сопротивление Z, активное сопротивление R и реактивное сопро­тивление X. Треугольник со сторонами Z, R, X называется треугольником со­противлений (рис. 52б). Из треугольника сопротивлений следуют соотношения: R=Z×cosφ, X=Z×sinφ, , .

Параллельной схеме замещения соответствует представление вектора тока в виде суммы двух составляющих: активной составляющей I_а, совпадаю­щей с вектором напряже­ния U, и реактивной составляющей I_р, перпендикуляр­ной к вектору U (рис. 53а):

 

Из геометрии рисунка следуют соотношения:

, , .

Треугольник, составленный из векторов получил название треугольника токов.

Если стороны треугольника токов разделить на напряжение U, то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются проводимости: пол­ная – Y, активная — G, реактивная – B (рис. 53б). Тре­угольник со сторонами Y, G, B называется треугольником проводимостей. Из треугольника проводимостей следуют соотношения:

, , , .

Разложение напряжений и токов на активные и реактивные составляющие является математическим приемом и применяется на практике для расчета не­сложных цепей пере­менного тока.

 

10. Передача энергии от активного двухполюсника (источника) к пас­сивному двухполюснику (приемнику)

 

Двухполюсником называется устройство или часть схемы (цепи) с двумя выводами (полюсами). Если внутри двухполюсника содержатся источники энергии, то он называется активным (A), в противном случае – пассивным (П).

Энергетические характеристики передачи энергии от активного двухпо­люсника (источника) к пассивному двухполюснику (приемнику) на переменном токе зависят от со­отношения параметров приемника и источника между собой (рис. 54)

 

 

По закону Ома ток в схеме равен:

.

Активная мощность приемника:

.

Активная мощность источника: P_E=E×I.

При постоянных параметрах источника энергии активная мощность приемника за­висит от его параметров: . Исследуем эту функцию на максимум при измене­нии отдельных параметров.

Условие первое: X₂

= var, R₂=const:

или .

Максимум мощности приемника имеет место при условии равен­ства реактив­ных сопротивлений приемника и источника по модулю и противо­положности их по знаку, например, если реактивное сопротивление источника носит индуктивный характер, то реак­тивное сопротивление приемника должно быть емкостным, и наоборот.

Условие второе: R₂ = var, X₂ = const.

или .

Максимум мощности приемника имеет место при равенстве активных сопротивле­ний приемника и источника.

Абсолютный максимум мощности приемника наблюдается при выпол­нении обоих условий и равен:

.

В режиме максимума потребляемой мощности работают приемники в ли­ниях связи.

Коэффициент полезного действия передачи энергии от источника к при­емнику равен отношению активных мощностей и не зависит от величины их реактивных сопротивлений.

В режиме абсолютного максимума мощности приемника КПД составляет только 0,5. Линии электропередачи (ЛЭП) работают с КПД h = 0,90÷0,95, что соот­ветствует соотношению активных сопротивлений приемника и источника (ге­нератора + ЛЭП) R₂/R₁=10÷20.

На графической диаграмме рис. 2 показаны энергетические характери­стики передачи энергии при R₂= var, Х₂=const в функции тока: P₂, h = f(I).

 

 

Узнать еще:

ПОВЫШЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ

⇐ ПредыдущаяСтр 8 из 14Следующая ⇒

Итак, только активная составляющая тока определяет преобразование электроэнергии в другие виды энергии, т. е. позволяет количественно оценить совершаемую работу. Реактивная же составляющая тока никакой работы не производит. Однако при ее наличии увеличивается полный ток.

Рис. 8.5. Электрическая цепь с параллельным включением конденсатора
для повышения коэффициента мощности:
а ¾ схема; б ¾ векторная диаграмма токов

Представим электроприемник, потребляющий активную и индуктивную составляющие тока, схемой последовательного соединения элементов R_пр и L_пр (рис. 8.5, а). На векторной диаграмме (рис. 8.5, б) вектор тока приемника составляет с вектором напряжения угол j_пр, причем

В отсутствие емкости С, включенной параллельно с приемником , ток в линии передачи равен току приемника. Если в проводах линии передачи (сопротивление которых R) протекает ток , то теряемая в них мощность Р_п.л =RI².

Так как в данном случае

I_л = I_пр = P_пр / (Uсos

j_пр),

то при постоянной мощности приемника и постоянном питающем напряжении (Р_пр = const и U = const) с уменьшением коэффициента мощности Сos j_пр увеличиваются ток, в линии, а следовательно, и потеря мощности

P_{п. л} = (P²_пр R/U²) (1/cosj_пр).

Таким образом, для уменьшения потерь мощности в передающих устройствах необходимо увеличивать коэффициент мощности приемников электроэнергии.

Каждому промышленному предприятию задают то средневзвешенное значение коэффициента мощности (реактивной мощности), которое должно быть обеспечено. Получению заданного коэффициента мощности способствует правильный выбор электрооборудования. Однако при этом всегда необходимо принимать дополнительные меры, например, использовать батареи конденсаторов и т. д.

Конденсаторы емкостью С включают параллельно электроприемнику (рис. 8.5, а). Ток конденсатора является практически чисто реактивным, опережающим напряжение на угол p/2 (рис. 8.5, б). Этот ток компенсирует реактивную индуктивную составляющую тока приемника, в результате чего общая реактивная составляющая тока уменьшается.

При емкости конденсатора, равной С, и токе ток в линии , или I_л <I_пр.

Угол сдвига фаз jмежду напряжением и током уменьшился, а коэффициент мощности увеличился (cоs j₂ >cоs j_пр).

С увеличением емкости конденсатора ток I_С = В_СU = w CU увеличивается так, что при некотором значении емкости С_рез можно получить равенство I_С = I_L (режим

резонанса токов). В этом случае реактивная составляющая тока приемника I_L полностью компенсируется и ток в линии достигает минимального значения, равного активной составляющей тока приемника I_а.пр (рис. 8.5, б). При дальнейшем увеличении емкости конденсаторов I_С > I_L и реактивная составляющая тока в линии, а, следовательно, и полный ток в ней увеличиваются. Наступает режим перекомпенсации, когда реактивная составляющая тока в линии носит емкостной характер.

На рис. 8.6 показано, как изменяется ток I_л при изменении емкости С конденсатора при Р_пр = const и U = const. Сначала с ростом С ток I_л уменьшается, достигая минимума в режиме резонанса токов, а затем снова начинает увеличиваться. Коэффициент мощности изменяется в обратном порядке, достигая максимума при полной компенсации (cos = 1 при I

С = I_L). Следует помнить, что при подключении конденсаторов потребляемая реактивная индуктивная мощность электроприемника остается неизменной, но ее источником становится батарея конденсаторов, установленная вблизи приемника. В результате в линии передачи реактивные токи уменьшаются.

Рис. 8.6. Зависимость тока в линии и коэффициента мощности от емкости конденсаторов:
I ¾ область недокомпенсации, II ¾ область перекомпенсации

Для обеспечения заданного значения коэффициента мощности необходимо устанавливать конденсаторы определенной мощности или емкости. Если электроприемники имеют мощность Р = const и cоsj_пр, то они потребляют из сети реактивную индуктивную мощность Q_пр = P tgj_пр. При заданном значении cоsj₂, которое должно обеспечить предприятие (cоsj₂ > cоsj_пр), потребляемая реактивная мощность Q₂ = P tgj₂.

Разность реактивных мощностей Q_пр — Q₂ компенсируется емкостной реактивной мощностью конденсаторов

Q_c = Q_пр — Q₂ = Р(tgj_пр — tgj₂). (8.8)

Реактивную мощность конденсаторов можно также определить не формуле:

Q_c = B_CU² = w CU². (8.9)

Приравнивая правые части уравнений (8.8) и (8.9), получим

C = P (tgj_пр — tgj₂) / (2pfU²).

При этом емкость выражается в фарадах, если мощность выражена в ваттах, а напряжение ¾ в вольтах.

Для полной компенсации (j₂ = 0) необходимо, чтобы С = Ptgj_пр / (2pfU²).

Таким образом, на лекции рассмотрены вопросы, характеризующие мощность в однофазной цепи синусоидального тока, ее вариации, коэффициент мощности и способы его повышения.

 

Рекомендация:

Для самоконтроля полученных знаний выполните тренировочные задания
из набора объектов к текущему параграфу

 

Рекомендуемые страницы:

Активная и реактивная составляющие тока в асинхронном двигателе

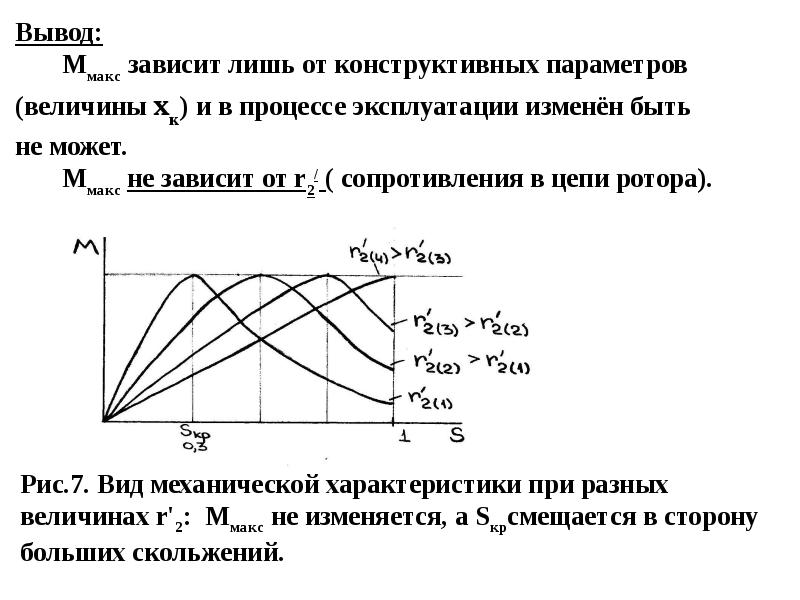
Рис.11.1 Механическая и электромеханическая характеристики асинхронного двигателя.

Уменьшение момента после достижения критического скольжения (Рис.11.1) объясняется тем, что в создании момента АД участвует только активная составляющая тока. Активная составляющая тока при уменьшении скорости уменьшается и доходит до минимального значения при остановке ротора .

А ток при неподвижном роторе имеет максимальное значение индуктивной составляющей (индуктивное сопротивление ротора максимальное при , когда ротор неподвижен).

В однородном магнитном поле на проводник с током действует электромагнитная сила . Эта формула справедлива, когда магнитное поле и проводник длиной с током движутся в пространстве с одинаковой скоростью и взаимно неподвижны.

Рассмотрим появление активной и реактивной составляющей тока в асинхронном двигателе[гер 343] .

Если прямолинейный проводник с синусоидальным током

находится в пульсирующем с той же частотой магнитном поле с индукцией ,и углом сдвига фаз магнитной индукции и тока равным углу ( ):

Электромагнитная сила, действующая на проводник с током, периодически изменяется с двойной частотой:

Постоянная (средняя) составляющая электромагнитной силы:

Постоянная составляющая электромагнитной силы зависит от сдвига по фазе (угол ) синусоидальных тока и магнитной индукции, а ток зависит от действующих значений и .

В электрических машинах переменного тока ЭДС обмотки ротора совпадает по фазе с магнитной индукцией поля статора . Поэтому угол сдвига фаз между ЭДС ( ) и током обмотки ротора равен углу ( ), углу сдвига фаз магнитной индукции и тока.

Следовательно в формуле (2.5) произведение определяет значение проекции вектора на вектор , другими словами равно активной составляющей тока ротора.

Из вышеизложенного следует, чтопостоянная (средняя) составляющая электромагнитной силы , действующая на проводник с синусоидальным током, находящимся в пульсирующем с той же частотой магнитном поле статора асинхронного двигателя, пропорциональна активной составляющей тока ротора .

=

Момент асинхронного двигателя, как и любой электрической машины, пропорционален магнитному потоку Ф и активной составляющей тока ротора [чил 80]

где конструктивнаяпостоянная асинхронного двигателя;

угол сдвига фаз между ЭДС ( ) и током обмотки ротора.

Непропорциональность между моментом асинхронного двигателя и током статора при пуске ( пусковой момент меньше максимального при пусковом токе достигающем максимального значения) объясняется значительным снижением магнитного потока двигателя, а также уменьшением коэффициента мощности цепи ротора при пуске, за счёт максимального значения индуктивного сопротивления ротора[чил 80].

При изменении нагрузки на валу двигателя [гер392] от нуля до номинальной значение скольжения увеличивается (от значения при холостом ходе) примерно до . При этом сохраняется неравенство

<< и = ,

т.е. активная составляющая тока ротора пропорциональна скольжению (при ).

При увеличении нагрузки скольжение так же возрастает и растёт ЭДС ротора = , растёт ток ротора в соответствии с (2.5), асимптотически стремясь к некоторому предельному значению, а с ростом уменьшается (причём на рабочем участке механической характеристики уменьшается очень мало, рис.11.1 участок DB), асимптотически стремясь к нулю при .

Магнитный поток двигателя также уменьшается при возрастании тока из-за падения напряжения на сопротивлениях обмотки статора [чил81]. Все эти процессы и обуславливают отсутствие пропорциональности между током и моментом двигателя.

А реактивная составляющая тока ротора

с двойной частотой и ротор, имея большую инерцию не успевает проворачиваться два раза при частоте 50Гц. Двойная частота 100Гц. Если бы ротор был тонким проводником он бы успевал проворачиваться [гер344]. Поэтому при анализе установившихся режимов нужно учитывать только постоянную (средную) составляющую электромагнитной силы .

мощность переменного тока

читать далее…

А с учетом того, что разность фазных напряжений (это то, что в скобках) равна соответствующему линейному, т.е. Ua — Uc = Uac, Uв — Uc = Uвс, можно записать, что мгновенная мощность равна
P = UacIa + UвсIв. Этому будет соответствовать первая схема включения из приведенных ниже.

Можно выразить ток Iа. Получим: Iа = — (Iв + Iс) и, соответственно, P = — Ua(Iв + Ic) + UвIв + UcIc = -UaIв — UаIс + UвIв + UcIc = (Uс — Uа)Iс + (Uв — Uа)Iв
А с учетом того, что разность фазных напряжений (это то, что в скобках) равна соответствующему линейному, т.е. Uс — Uа = Uса, Uв — Uа = Uва, можно записать, что мгновенная мощность равна P = UсаIс + UваIв. Этому будет соответствовать вторая схема включения из приведенных ниже.

Можно выразить ток Iв. Получим: Iв = — (Iс + Iа) и, соответственно, P = UaIа — Uв(Iс +Iа) + UcIc = UaIа — UвIс — UвIа + UcIc = (Uа — Uв)Iа + (Uс — Uв)Iс
А с учетом того, что разность фазных напряжений (это то, что в скобках) равна соответствующему линейному, т.е. Uа — Uв = Uав, Uс — Uв = Uсв, можно записать, что мгновенная мощность равна P = UавIа + UсвIс. Этому будет соответствовать третья схема включения из приведенных ниже.
Применять можно любую. Но только в трехпроводной сети. На практике это использование для измерения потребленной электроэнергии двух трансформаторов тока.

Возможные схемы включения двух ваттметров при измерении мощности в 3-х фазной 3-х проводной сети

На основании вышеприведенного получаем, что мгновенная мощность трехфазной трехпроводной сети равна сумме двух произведений мгновенных значений линейных напряжений и токов. Сумма средних значений этих двух произведений, т.е. активная мощность системы, может быть измерена двумя ваттметрами. Для первой схемы включения это
P = P1 + P2 = UcaIacos(φu — φi) + UвсIвcos(φu — φi), где φu — φi — угол сдвига фаз между соответствующими линейным напряжением и током.
При правильном включении ваттметров положительные направления линейных напряжений и токов должны совпадать с направлением от «начала» к «концу» цепи напряжения и цепи тока ваттметров. Так, у первого ваттметра в первой схеме нужно соединить «начало» (вывод, отмеченный звездочкой *) цепи напряжения с проводом А, а «конец» этой цепи — с проводом С.
Распределение измеряемой мощности трехфазной системы между показаниями двух ваттметров зависит главным образом от углов сдвига фаз между линейными напряжениями и токами. Проследим эту зависимость на векторной диаграмме в случае симметричного проемника, фазы которого соединены звездой.

Векторная диаграмма напряжений и токов при симметричной нагрузке

Углы сдвига фаз между соответствующими фазными напряжением и током одинаковые и равны аргументу φ комплексного сопротивления фазы приемника. Из диаграммы следует, что при симметричном приемнике углы сдвига между векторами Uас и Iа (линейным током и линейным напряжением измеряемых ваттметром параметров), Uвс и Iв соответственно равны φ — 30° и φ + 30° . Действующие значения линейных напряжений и токов при симметричном приемнике соответственно одинаковы, т.е. Uвс = Uac = Uл; Ia = Iв = Iл.
Таким образом, сумма показаний двух ваттметров, равна мощности симметричной трехфазной трехпроводной сети, т.е.
P = P1 + P2 = UлIлcos(φ — 30°) + UлIлcos(φ + 30°). Из выражения следует, что при симметричном приемнике показания ваттметров Р1 и Р2 будут равны только при φ = 0. Если φ > 60°, то показание второго ваттметра будет отрицательным, т.е. сумма показаний у них алгебраическая.
Ну, а для измерения в трехфазных системах с нейтральным проводом (4-х проводной) самым простым является метод трех ваттметров. На практике это применение счетчика с тремя трансформаторами тока. При таком подключении каждый измеряет мошность одной фазы и активная мощность такой сети равна
Р = Р1 + Р2 + Р3.

Определение тока холостого хода трансформатора

Электротехника Определение тока холостого хода трансформатора

просмотров — 828

Ток первичной обмотки трансформатора, возникающий при холостом ходе при номинальном синусоидальном напряжении и номинальной частоте, принято называть током холостого хода.

При расчет тока холостого хода трансформатора отдельно определяют его активную и реактивную составляющие.

Активная составляющая тока холостого хода вызывается наличием потерь холостого хода. Активная составляющая тока, А,

I_х.а = Р_х / (mU_ф),

где Р_х – потери холостого хода, Вт; U_ф – фазное напряжение первичной обмотки, В.

Обычно определяют не абсолютное значение тока холостого хода и его составляющих, а их относительное значение по отношению к номинальному току трансформатора i_оа, i_0р, i_о, выражая их в процентах номинального тока.

Тогда активная составляющая, %,

,

или

i_оа = Р_х /(10S),

где S – мощность трансформатора, кВ· А; Р_х – потери холостого хода, Вт.

Расчет реактивной составляющей тока холостого хода усложняется наличием в магнитной цепи трансформатора немагнитных зазоров. При этом расчете магнитная система трансформатора разбивается на четыре участка – стержни, ярма, за исключением углов магнитной системы, углы и зазоры. Для каждого из этих участков подсчитывается требуемая намагничивающая мощность, суммируемая затем по всœей магнитной системе. Также как и потери, реактивная составляющая тока холостого хода зависит от базовых магнитных свойств стали магнитной системы и ряда конструктивных и технологических факторов, оказывающих на эту составляющую существенно большое влияние, чем на потери.

Немагнитные зазоры в шихтованной магнитной системе имеют особую форму – в месте зазора стыки пластин чередуются со сквозными пластинами. Магнитный поток вместе стыка проходит частично через зазор между пластинами и частично – через сосœеднюю сквозную пластину. Индукция в сквозных пластинах в зоне, лежащей против стыков, увеличивается. Вместе с этим происходит местное увеличение потерь и реактивной составляющей тока холостого хода, однако общая намагничивающая мощность для зазора оказывается существенно меньшей, чем при стыке частей стыковой магнитной системы.

В практике расчета намагничивающая мощность для зазоров шихтованных магнитных систем, собираемых из пластин горячекатаной или холоднокатаной стали, определяется для условного немагнитного зазора, по площади сечения стали в данном стыке, ᴛ.ᴇ. по активному сечению стержня или ярма, и по удельной намагничивающей мощности, отнесенной к единице площади активного сечения, q_з, В∙А/м², и определяемой экспериментально для каждой марки стали.

Удельные намагничивающие мощности для стали марок 3404 и 3405 приведены в табл.26.

Таблица 26. Полная удельная намагничивающая мощность в стали q и в зоне шихтованного стыка q₃ для холоднокатаной стали марок 3404 и 3405 толщиной 0,35 и 0,30 мм при различных индукциях и f = 50 Гц

В, Тл	Марка стали и ее толщина	qз, В∙А/м2
3404, 0,35 мм	3404, 0,30 мм	3405, 0,35 мм	3405, 0,30 мм
1,30 1,32 1,34 1,36 1,38   1,40 1,42 1,44 1,46 1,48   1,50 1,52 1,54 1,56 1,58   1,60 1,62 1,64 1,66 1,68   1,70 1,72 1,74 1,76 1,78   1,80 1,82 1,84 1,86 1,88	0,900 0,932 0,964 0,996 1,028   1,060 1,114 1,168 1,222 1,276   1,330 1,408 1,486 1,575 1,675   1,775 1,958 2,131 2,556 3,028   3,400 4,480 5,560 7,180 9,340   11,500 20,240 28,980 37,720 46,460	0,870 0,904 0,938 0,972 1,006   1,040 1,089 1,139 1,188 1,238   1,289 1,360 1,431 1,511 1,600   1,688 1,850 2,012 2,289 2,681   3,073 4,013 4,953 6,364 8,247   10,130 17,670 25,210 32,750 40,290	0,860 0,892 0,924 0,956 0,988   1,020 1,065 1,110 1,156 1,210   1,246 1,311 1,376 1,447 1,524   1,602 1,748 1,894 2,123 2,435   2,747 3,547 4,347 5,551 7,161   8,770 15,110 21,450 27,790 34,130	0,850 0,880 0,910 0,940 0,970   1,000 1,041 1,082 1,123 1,161   1,205 1,263 1,321 1,383 1,449   1,526 1,645 1,775 1,956 2,188   2,420 3,080 3,740 4,736 6,068   7,400 12,540 17,680 22,820 27,960

При экспериментальных исследованиях стали удельная намагничивающая мощность, отнесенная к 1 кг стали или к 1 м² площади зазора q, может определяться как полная мощность или как ее реактивная составляющая. В табл. 26 приведены значения полной удельной намагничивающей мощности.

Полная намагничивающая мощность трансформатора, В∙А, для магнитной системы может быть определœена из следующего выражения:

Q_x = Q_x.c + Q_x.я + Q_x.з = q_cG_c + q_яG_я + ∑n_зq_зП_з,

Где q_c и q_я – удельные намагничивающие мощности для стержня и ярма, определяемые по табл.26 для холоднокатаной стали в зависимости от соответствующих индукций, В∙А/кг; G_c и G_я – масса стали в стержнях и ярмах, кг; n_з – число немагнитных зазоров (стыков) в магнитной системе; q_з – удельная намагничивающая мощность, В∙А/м², для немагнитных зазоров, определяемая для индукции в стержне по табл.26; П_з площадь зазора, ᴛ.ᴇ. активное сечение стержня или ярма, м².

При расчете тока холостого хода для плоской стержневой шихтованной магнитной системы, собранной из пластин холоднокатаной анизотропной стали, также как и при расчете потерь холостого хода, приходиться считаться с факторами конструктивными – форма стыков стержней и ярм, форма сечения ярма, способ прессовки стержней и ярм – и технологическими – резка рулонов стали на пластины, удаление заусенцев, отжиг пластин, покрытие их лаком, прессовка магнитной системы при сборке и перешихтовка верхнего ярма при установке обмоток.

От воздействия этих факторов реактивная составляющая тока холостого хода увеличивается при несовпадении линий магнитной индукции и прокатки стали, а также в результате механических воздействий при заготовке пластин и сборке остова. Отжиг пластин ведет к уменьшению реактивной составляющей тока холостого хода. На токе холостого хода влияние этих факторов сказывается более резко, чем на потерях.

Полный фазный ток холостого хода, А,

I_x = Q_x/(mU_ф).

Относительное значение тока холостого в процентах номинального тока

i₀ = Q_x/10S.

Активная составляющая тока холостого хода, фазное значение, А,

I_x.а = Р_х/(mU_ф)

и в процентах номинального тока

i_оа = Р_х/(10S).

Реактивная составляющая тока холостого хода, А,

I_x.р =

и в процентах номинального тока

i_op =

Полученное значение тока холостого хода должно быть сверено с предельно допустимым значением по ГОСТ, техническим условиям или заданию на расчет трансформатора. Отклонение расчетного значения тока холостого хода от заданного гарантийного не следует допускать более чем на половину допуска разрешенного ГОСТ (по ГОСТ 11677-85 разрешенный допуск +30%).

При расчете тока холостого хода по намагничивающей мощности определяется среднее значение, тока холостого хода для всœех стержней трансформатора. В симметричных магнитных системах, к примеру однофазных, или пространственных, это среднее значение будет совпадать с действительным значением тока холостого хода для каждого стержня.

В несимметричной магнитной системе ток холостого хода в обмотке среднего стержня меньше, чем в обмотках крайних стержней. Током холостого хода трансформатора в этом случае считается среднее значение токов трех фаз.

Читайте также

— Определение тока холостого хода трансформатора

Ток первичной обмотки трансформатора, возникающий при холостом ходе при номинальном синусоидальном напряжении и номинальной частоте, называется током холостого хода. При расчет тока холостого хода трансформатора отдельно определяют его активную и реактивную… [читать подробенее]

Барданов А.И. Вектор мгновенной реактивной мощности в трехфазных несимметричных сетях

Барданов Алексей Игоревич
Национальный Минерально-Сырьевой Университет «Горный», г.Санкт-Петербург
кафедра электротехники, электромеханики, электроэнергетики

Bardanov Alexey Igorevich
St.Petersburg National Mining-Resorses University
department of electrical engineering, electro mechanic, electrical energy

Библиографическая ссылка на статью:
Барданов А.И. Вектор мгновенной реактивной мощности в трехфазных несимметричных сетях // Современные научные исследования и инновации. 2015. № 9. Ч. 1 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2015/09/57392 (дата обращения: 24.04.2021).

Известно, что реактивная мощность трехфазной системы сложная величина, которая зависит от характера нагрузки, симметрии, наличия или отсутствия нулевого провода, уровня искажений в токе и питающем напряжении. Понятие реактивной мощности однозначно определено для симметричных систем в синусоидальном режиме. Однако такой режим, практически не встречается.

Для построения эффективных систем управления потоками мощности требуется точно определить причины возникновения неактивных токов для выбора средств компенсации. В качестве основы для анализа токов реальных систем можно использовать теорию мгновенных мощностей [1,2,3].

Основы были заложены Фризе в 1936 г.[4]. Было предложено рассматривать ток в цепи как сумму активного и неактивного токов в функции от времени, но на момент разработки теория Фризе не нашла применения и в течение 60 лет оставалась неизвестной, пока в конце прошлого столетия ее не начали использовать для управления активными фильтрами.

,	(1)
где: – активная составляющая тока,  – неактивная составляющая тока.

Активная составляющая тока , согласно теории, пропорциональна активной мощности и в фазе с напряжением, что значит, что неактивная составляющая тока  полезной работы не выполняет и является причиной дополнительных потерь в линии.

Для трехфазной цепи можно представить напряжение и ток трехкомпонентными векторами, координаты которых пропорциональны токам и напряжениям в фазах, а скалярное произведение равно сумме мгновенных мощностей трех фаз:

,	(2)
где:  – фазные токи,  – орты системы координат.
,	(3)
где:  – фазные напряжения.
,	(4)
где: p – мгновенная мощность системы.

Как и в теории Фризе ток системы делится на две составляющие: векторы активного и неактивного тока. Активная составляющая является проекцией вектора тока на вектор напряжения, неактивная составляющая находится к вектору напряжения под прямым углом, образуя с активной составляющей и вектором тока прямоугольный треугольник:

,	(5)
где:  – вектор активного тока системы,  – вектор неактивного тока системы.

Неактивная составляющая в любой момент времени определяется помощью вектора мгновенной реактивной мощности (МРМ), который в свою очередь определяется как векторное произведение векторов тока и напряжения системы:

,	(6)
где: q – вектор МРМ системы.

 

Рассмотрим два случая активной трехфазной несимметричной нагрузки с нулевым проводом и без него.

Рисунок 1 – Годографы векторов напряжения и тока трехфазной системы с нулевым проводом и координаты вектора мгновенной реактивной мощности при активной несимметричной нагрузке

Рисунок 1 отражает изменение координат векторов напряжения и тока системы во времени, представлены годографы векторов за три четверти периода, чтобы лучше показать положение векторов в пространстве друг относительно друга. Изменение вектора мгновенной реактивной мощности можно проследить по изменению его координат во времени (на рисунке справа). Видно, что координаты изменяются по синусоидальному закону, и каждая имеет постоянную составляющую, отличную от нуля. Уравнение координаты вектора МРМ по оси а:

,	(7)

где:  – постоянная составляющая координаты вектора мгновенной реактивной мощности по оси а,– амплитуда переменной составляющей координаты вектора по оси а,  – круговая частота вектора напряжения,  – начальная фаза переменной составляющей координаты вектора.

В векторе МРМ можно выделить постоянную несимметричную составляющую:

,	(8)

где:  – постоянная несимметричная составляющая вектора мгновенной реактивной мощности,  – постоянная составляющая координаты вектора по оси b,  – постоянная составляющая координаты вектора по оси c.

В системе без нулевого провода вектор МРМ меняет свое поведение (рис.2).

Рисунок 2 – Годографы векторов мгновенных напряжений и токов трехфазной системы без нулевого провода и координаты вектора мгновенной реактивной мощности при активной несимметричной нагрузке

Вектор симметрично изменяется по синусоидальному закону и не имеет постоянной составляющей. В этом случае векторы тока и напряжения вращаются постоянно в одной плоскости.

Интересна для анализа система с чисто индуктивной нагрузкой (рис.3).

 

Рисунок 3 – Годографы векторов мгновенных напряжений и токов трехфазной системы с нулевым проводом и координаты вектора мгновенной реактивной мощности при индуктивной несимметричной нагрузке

Вектор тока за период описывает эллипс в плоскости отличной от плоскости вектора напряжения. При этом координаты вектора МРМ имеют постоянную и переменную составляющие. Постоянная составляющая в отличие от предыдущего случая значительно смещена в седьмой октант.

Рисунок 4 демонстрирует поведение вектора МРМ при отсутствии нулевого провода. Вектор имеет симметричную постоянную составляющую и переменную, изменяющуюся по синусоидальному закону.

 

Рисунок 4 – Годографы векторов мгновенных напряжений и токов трехфазной системы без нулевого провода и координаты вектора мгновенной реактивной мощности при индуктивной несимметричной нагрузке

Исходя из полученных результатов вектор МРМ, можно разделить, на три составляющие: симметричную постоянную ,  несимметричную постоянную , появляющуюся в случае наличия нулевого провода и переменную составляющую .

,

(9)

Сравнивая поведение вектора в симметричных[5] и несимметричных системах, можно сделать вывод о том, что симметричная постоянная составляющая вектора пропорциональна реактивной мощности системы. При наличии нулевого провода в несимметричной системе появляется постоянная несимметричная составляющая вектора МРМ.

Подводя итог вышесказанному, нужно отметить, что анализ вектора МРМ в несимметричных системах возможен. Вектор, а значит и неактивный ток трехфазной систем имеет составляющие: симметричные и несимметричные, постоянные и изменяющиеся во времени, появляющиеся в зависимости от нагрузки. Несимметричная постоянная составляющая вектора появляется только в несимметричных системах с нулевым проводом, в то время как симметричная постоянная составляющая появляется всегда при наличии реактивной нагрузки.

Библиографический список

1. H. Akagi, Y. Kanazawa, A. Nabae, “Instantaneous reactive power compensator’s comprising switching device without energy storage components,” IEEE Trans. Ind. Applications,vol. .IA-20, May/June 1984, pp. 625-630.
2. H. Akagi, H. Kim “” IEEE International Conference on Power Electronics and Drive Systems, PEDS’99, July 1999, Hong Kong.
3. Жеменов Г.Г. Ильина О.В. «Теория мощности Фризе и современные теории мощности» Электротехника и электромеханика №6, 2007 с.63-65
4. S. Frize, “Active and Apparent power in non-sinusoidal systems”. Przeglad Electrot (In Poland), no 7, 1931, p.p. 193-203.
5. Шклярский А.Я., Барданов А.И. «Анализ вектора мгновенной Реактивной мощности трехфазной сети при различной симметричной нагрузке», Естественные и технические науки №3, М.:Спутник, 2015. с.127-131

---

Количество просмотров публикации: Please wait

Все статьи автора «Алексей Барданов»

О разложении полной мгновенной мощности в цепи синусоидального тока на мгновенную активную и мгновенную реактивную мощности Текст научной статьи по специальности «Электротехника, электронная техника, информационные технологии»

УДК 621.311.16 ББК 31.280.7

А С. СЕРЕБРЯКОВ, В.Л. ОСОКИН

О РАЗЛОЖЕНИИ ПОЛНОЙ МГНОВЕННОЙ МОЩНОСТИ В ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА НА МГНОВЕННУЮ АКТИВНУЮ И МГНОВЕННУЮ РЕАКТИВНУЮ МОЩНОСТИ

Ключевые слова: полная мгновенная мощность, активная мгновенная мощность, реактивная мгновенная мощность, активно-индуктивная нагрузка, интегральные значения мощностей, ваттметры активной и реактивной мощности, компенсации реактивной мощности.

Рассмотрены особенности систем электроснабжения переменного тока, в которых для оценки их энергоэффективности необходимо учитывать не только активную, но реактивную мощность, для передачи которой по проводам затрачивается определенная часть активной мощности. Отмечено, что дефицит реактивной мощности приводит к снижению уровня напряжения в электрической сети и может нарушить статическую устойчивость электрической системы. Следовательно, источники питания должны вырабатывать не только активную, но и реактивную мощность для питания приемников, имеющих реактивные элементы. Поскольку передача реактивной мощности по сети экономически невыгодна из-за потерь в линии электропередачи, то более целесообразным является выработка ее непосредственно в местах потребления с помощью местных источников реактивной мощности — установок емкостной компенсации реактивной мощности. В этом случае обменная часть электромагнитной энергии становится равной нулю. Она не потребляется от источника энергии и не возвращается к нему. Емкостной и индуктивный элементы обмениваются реактивной энергией между собой. По сети в этом случае передается только энергия, которая преобразуется в полезную работу. С введением в систему управления энергетическими процессами цифровых технологий необходимо обосновать основные теоретические положения для оптимального управления режимами энергопотребления и компенсации реактивной мощности. В статье приводятся теоретические положенияЛ которые могут лечь в основу автоматизированных цифровых систем управления энергопотреблением. Приведены выражения и волновые диаграммы для мгновенных значений активной, реактивной и полной мощностей в цепи синусоидального тока с активно-индуктивной нагрузкой, состоящей из последовательного или параллельного соединения резистора и индуктивной катушки. Показано, как изменятся волновые диаграммы мгновенных значений мощностей в случае компенсации реактивной мощности с помощью поперечной емкостной компенсации, т.е. включением параллельно нагрузке конденсатора. В обоих случаях реактивная мощность на входе цепи становится равной нулю, а полная мощность — равной активной мощности. Однако кривые мгновенных значений активных мощностей в указанных случаях имеют разные фазы, что необходимо учитывать при разработке и эксплуатации цифровых систем автоматического регулирования устройств компенсации реактивной мощности.

Основной задачей электрических сетей является электроснабжение потребителей, т.е. обеспечение их электроэнергией. Поэтому основными важными для практики величинами, характеризующими эффективность работы электрических систем, являются мощность и энергия. По значению мощности оценивают работу системы электроснабжения в каждом отдельном рабочем режиме, а по значению потребленной энергии — работу системы за длитель-

ный период времени. Особенностью систем электроснабжения переменного тока является то обстоятельство, что для оценки их энергоэффективности необходимо учитывать не только активную, но и так называемую реактивную мощность. Активной мощностью Р в электрической цепи при периодических процессах называют среднее значение полной мгновенной мощности 5 за один период, или среднее значение мгновенной активной мощности р за один период. Разность полной мгновенной мощности 5 и активной мгновенной мощностир является мгновенной реактивной мощностью д.

Задачи исследования. Дефицит реактивной мощности приводит к снижению уровня напряжения в электрической сети и в ряде случаев может нарушить статическую устойчивость электрической системы. С введением в систему управления энергетическими процессами цифровых технологий необходимо обосновать основные теоретические положения для оптимального управления режимами энергопотребления. Ниже приводятся положения, которые могут лечь в основу разработки автоматизированных систем управления энергопотреблением.

Методы исследования. Полную мгновенную мощность в цепях синусоидального тока можно представить как сумму мгновенной активной мощности р и мгновенной реактивной мощности д [3, 10]. Например, для цепи, содержащей последовательно соединенные сосредоточенные элементы, обладающие активным сопротивлением Я, индуктивностью Ь и емкостью С, по которой протекает синусоидальный ток г, результирующее напряжение, приложенное к цепи:

и = иЯ + иь + иС = Яг + Ь—— + иС . (1)

М

Выражение для полной мгновенной мощности 5, подводимой к цепи, будет выглядеть как

. п2 Т.—г иС 5 = и ■ г = и„1 + ит1 + ил = Яг + Ьг—+и „С- —

= Яг 2 + & &

2

22

Ьг

2

— +—

Ж

Си’С

(2)

= я— 2 + & (у ) + (У ) = Ря + Чь + Чс , т М

. „ ЖиС т —— где г = С- — ток в цепи; иь = ь — и иС — напряжения на индуктивной катушке и конденсаторе, соответственно; рЯ = иЯг — мгновенная активная мощность в активном сопротивлении; чь = иьг и дС = иСг — мгновенные реактивные мощности в индуктивной катушке и конденсаторе, соответственно.

В выражениях (1) и (2) ток, напряжения и мощности являются функциями времени Мгновенная активная мощность, которая потребляется в активном сопротивлении Я, выраженная по закону Джоуля — Ленца как рЯ = Я ■ — , всегда положительная. Она характеризует необратимый процесс поглощения энергии.

Мгновенные реактивные мощности qL в индуктивной катушке и в конденсаторе, в которых электроэнергия запасается и затем снова возвращается к источнику энергии, будут положительными в том случае, когда энергия в них запасается, т.е. возрастает, и отрицательными, когда энергия убывает. Таким образом, мгновенные реактивные мощности qL в индуктивной катушке и дс определяют скорость поступления энергии в магнитное поле катушки и электрическое поле конденсатора и скорость возвращения энергии из этих полей.

На рис. 1 в качестве примера приведены расчетные формулы в интегрированном пакете Mathcad для расчета рассмотренных выше мгновенных мощностей в цепи синусоидального тока с активно-индуктивной нагрузкой, состоящей из последовательного соединения резистора Я = 4 Ом и индуктивной катушки с индуктивным сопротивлением X = 3 Ом [11]. Полное сопротивление цепи + X = 5 Ом. Действующее значение питающего напряжения и = 100 В, частота / = 50 Гц. Начальная фаза напряжения принята равной нулю. Фазовый угол нагрузки равен ф = 36,87° = 0,644 рад. На этот угол синусоида тока 1 отстает от синусоиды напряжения и. Там же приведены формулы для расчета интегральных значений мощностей Р, Q, 5.

Мгновенные мощности прн активно индуктнвной нагрузке

U := 100 u(t) := u-/2siii! lOOirt! R := 4 X := 3 Z := -JR2 + X2 = 5

i R » ip := acos| —

cosiip) = 0.8

U

siii(ip) = 0.6 I:= —= 20

Л

t:= 0,0.0001. 0.02 111(t) := 10072-sill ЮОтгГ—|

2 ;

i(t) := и-л/2-smilOOTrt-ip) I := 1

AM

0.02

i(tr dt = 20

,41.02

p(t) := R-ift)1 *(t) :=u(r)-i(r)

q(t) := * <lt

L-i(t)

(jl(t) := ul(t)-i(t)

P :=

Q:=

Q:=

P := 1

ОЛ2′ 1

0.02 1

0.02 J

0.02 J

i4).02

p (t) (lt= 1.6 X 10

s(t) (It = 1.6 X 10

0

4)02 0

r0.02

q(t) (lt= 6.182 x 10

-13

4l(t) (lt= 1.2 X 10

0

й := ТТ1 =2×10 Р := Ясо5(1р) = 1.6 х 10 (} := = 1.2 х 10

Рис. 1. Формулы для расчета мгновенных и интегральных значений мощностей в цепи с последовательно включенной активно-индуктивной нагрузкой

Для расчета интегрального значения активной мощности P = 1600 Вт взят принцип действия ваттметра индукционной системы, усредняющего мощность за один период питающего напряжения. Из рис. 1 видно, что средняя за период мощность, т.е. активная мощность, на зажимах всей цепи равна средней за период мощности на участке с активным сопротивлением R.

Для расчета интегрального значения реактивной мощности Q = 1200 вар, так же, как и в реальных ваттметрах реактивной мощности, взято напряжение u1, сдвинутое в сторону отставания от питающего напряжения u на угол 90°

и В й й

1 — 1. В этом случае мгновенное значение измеряемой реактивной мощности

обозначено на рис. 1 как q1. Интегральное значение реактивной мощности без сдвига напряжения (интегрирование мгновенной реактивной мощности q за один период), как видно из рис. 1, равно нулю (Q = 6,182 • 10-13 ~ 0) [2, 8].

Научная новизна. На рис. 2 приведены зависимости мгновенных значений мощности, полученные по формулам, приведенным на рис. 1. Заметим, что такие же значения мгновенных мощностей можно получить при последовательном соединении элементов R и L, разложив питающее напряжение на

две составляющие — активную ua = и 42 • cos9 • sin(100rc • t — ф), совпадающую

по фазе с током i в цепи, и реактивную составляющую

up = U-v/2 • sin ф- sin(100rc-1 + 90°-ф), опережающую по фазе ток i на 90°

(рис. 3). Первая составляющая — это мгновенное значение напряжения на резисторе, а вторая — на индуктивной катушке. Ток же i в обоих элементах при последовательном их включении одинаковый. Его амплитуда составляет

20/2 = 28,2 А. В этом случае две составляющие напряжения дают две составляющие p и q мгновенной мощности s. Активная мощность p и ток i одновременно проходят через нуль. Отметим, что интегральное значение активной мощности Р получается одинаковым как при интегрировании мгновенной активной мощности p(t), так и при интегрировании полной мгновенной мощности s(t), что подтверждает рис. 1.

Как видно из рис. 2, кривые мгновенной активной мощности p и мгновенной полной мощности s являются несинусоидальными функциями времени. Они обе содержат синусоидальные составляющие двойной частоты и постоянные составляющие. Амплитуды синусоидальных составляющих этих кривых различны, а постоянные составляющие одинаковые и равны P. Поэтому их интегральные значения равны их постоянным составляющим — активной мощности P. Значение активной мощности P можно определить из

s + s ■ 3600 — 400

кривых s и p следующим образом: P = -=-= 1600 Вт,

2 2

p 3200 или P = =-= 1600 Вт .

В

300 250 200 150 100 50 0

-50 -100 -150

Рис. 2. Зависимости мгновенных значений мощности от времени, полученные по формулам, приведенным на рис. 1

Кривая мгновенной реактивной мощности q представляет собой синусоидальную величину. Поэтому ее интегральное значение за период равно нулю. Амплитуда колебаний мгновенной реактивной мощности q равна значению реактивной мощности Q. Пульсирующий характер мгновенных мощностей дает полную энергетическую характеристику процесса передачи электрической энергии.

На рис. 2 начало синусоиды реактивной мощности q совпадает с началом синусоиды тока, или концом ее полупериода. Из представленных на рис. 2 кривых мгновенных значений мощностей реактивную мощность Q можно определить через амплитудное значение мгновенной реактивной мощности qmax или через максимальное smax и минимальное (отрицательное) smin значения полной мощности s следующим образом:

Q = qmax = |q mini = 1200 Бар

или Q = V*max ‘(_smm ) = V3600 • 400 = 1200 вар. и коэффициент реактивной мощ-

S smax — smm

___ „4. Q 2 V smax ‘ (—smm)

ности как tg ф = — = —1-.

P s + s

max mm

Если же двухполюсник с активно-индуктивной нагрузкой представлен не как последовательное, а как параллельное соединение элементов, то в этом случае следует брать две составляющие тока и одно общее напряжение (рис. 3). Активная составляющая тока совпадает по фазе с напряжением и определяется по формуле

ia (t) = /V2 • cosfo) • sin(100re-1). (3)

Рис. 3. Векторная диаграмма напряжений и токов при активно-индуктивной нагрузке для последовательного и параллельного соединения элементов

%

Реактивная составляющая тока отстает от напряжения на угол — и определяется по формуле

Iр (1) = /л/2 • 8ш(ф) • 81п[^100% • X — (4)

Мгновенные значения мощностей в этом случае определяются по формулам

р (X) = и (X) • 1а (X), (5)

q(t) = иЦ) • 1р (0, (6)

s(t) = и(Х) • 1(Х). (7)

Две составляющие р и q полной мощности 5 = р + q определяются двумя составляющими общего тока I. Мгновенные значения мощностей, рассчитанные по формулам (5)-(7), приведены на рис. 4 [3]. Здесь же показаны кривые напряжения и и тока I. Начало синусоиды реактивной мощности q совпадает с максимальным и минимальным значениями питающего напряжения и.

В

зоо

250 200 150 100 50 0

-50 -100 -150

Рис. 4. Зависимости мгновенных значений мощности от времени, полученные по формулам (5)-(7) при параллельном соединении элементов

Сравнивая осциллограммы на рис. 2 и рис. 4, можно заключить, что мгновенные значения полной мощности s, поступающей на вход схемы, в обоих случаях одинаковые, так как одинаковы амплитудные значения и начальные фазы напряжения u и тока i на входе в обеих схемах. Однако кривые мгновенных значений активной мощности p и реактивной мощности q в обоих рассматриваемых случаях имеют разные фазы, хотя амплитудные значения их в обоих случаях одинаковы: Q = 1200 вар, Р = 1600 Вт. Но при этом постоянная составляющая реактивной мощности q, так же, как и ранее, равна нулю, а постоянная составляющая активной мощности p равна половине максимального значения этой мощности, или амплитудному значению ее синусной составляющей.

На прохождение реактивного тока по проводам затрачивается определенная часть активной мощности, так как потери мощности пропорциональны квадрату полного тока. Кроме того, реактивный ток вызывает дополнительное снижение напряжения в точке потребления энергии. Таким образом, с одной стороны, реактивный ток и реактивная мощность являются нежелательными величинами. С другой стороны, они помимо нашего желания необходимы для нормальной работы большинства потребителей электрической энергии, имеющих в своем составе реактивные (индуктивные) элементы. Следовательно, источники питания должны вырабатывать не только активную, но и реактивную мощность для питания приемников, имеющих реактивные элементы.

Передача реактивной мощности по сети экономически невыгодна из-за потерь в линии электропередачи. Более целесообразным является выработка ее непосредственно в местах потребления с помощью местных источников реактивной мощности, например, конденсаторных установок. Такие установки называют установками поперечной емкостной компенсации реактивной мощности. В этом случае полупериоды запасания и возврата электромагнитной энергии индуктивностью и емкостью сдвинуты на 180°, т.е. они находятся в проти-вофазе. Поэтому при наличии рядом двух различных потребителей — индук-

тивности и емкости с равными реактивными сопротивлениями — суммарная обменная часть электромагнитной энергии становится равной нулю. Она не потребляется от источника энергии и не возвращается к нему./2со8ф = 22,6 А. Пунктирными линиями на рис. 5 показаны мощности р и q до компенсации. Потребляемая из сети реактивная мощность Q становится равной нулю, а полная мощность 5 становится равной активной мощности р.

Рис. 5. Зависимости мгновенных значений мощностей от времени при компенсации реактивной мощности последовательно соединенных активного сопротивления и катушки индуктивности

На рис. 6 приведены кривые мгновенных мощностей при компенсации реактивной мощности и параллельном включении активного сопротивления и катушки индуктивности. Индуктивная мощность q в схеме до компенсации на рис. 6 показана пунктирной линией.

В обоих случаях кривые мгновенных значений полных мощностей 5 совпадают. Обе схемы потребляют только активную мощность, т.е. Р = Б и Q = 0. При этом активные мощности, потребляемые активным сопротивлением Я, на рис. 5 и 6 имеют разные фазы.

Сумма мгновенных реактивных мощностей равна нулю. В обоих случаях для компенсации реактивной мощности емкость компенсирующего конденсатора теоретически подбирают так, чтобы ток в нем был бы равен реактивной составляющей в соответствии с формулой (4):

C =-1-, (8)

2я — f -U sin ф

где f — частота питающего напряжения; U, I — действующие значения питающего напряжения и тока нагрузки, соответственно; ф — фазовый параметр нагрузки.

На практике коэффициент мощности повышают не до значения единицы, а до значения 0,95, вводя некоторую расстройку резонанса, для того, чтобы избежать нежелательных перенапряжений при коммутационных процессах.

в

зов 250 200 150 100 50 О

-50 -100

о 0.005 0.01 0.015 С

Рис. 6. Зависимости мгновенных значений мощностей от времени при компенсации реактивной мощности параллельно соединенных активного сопротивления и катушки индуктивности

Выводы. Мгновенная мощность в цепях синусоидального тока определяется в общем случае несинусоидальной функцией времени, содержащей две составляющие — синусоидальную функцию и постоянную составляющую. Именно две величины — амплитуда синусоидальной составляющей и значение постоянной составляющей — дают полную характеристику протекающего в электрической цепи процесса с энергетической точки зрения.

Приведенные соотношения могут быть полезны при разработке и эксплуатации цифровых систем автоматического регулирования устройств компенсации реактивной мощности1, а также при разработке информационно-

1 ГОСТ Р 52425- 2005 (МЭК 62053-23: 2003). Аппаратура для измерения электрической энергии переменного тока. Частные требования. Часть 23. Статические счетчики реактивной энергии. М.: Стандартинформ, 2006; ГОСТ Р 52320-2005 (МЭК 6205211:2003). Аппаратура для измерения электрической энергии переменного тока. Общие требования. Испытания и условия испытаний. Часть 11. Счетчики электрической энергии. М.: Стандартинформ, 2005.; ГОСТ Р 54149-2010. Национальный стандарт Российской Федерации. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. М.: Стандартинформ, 2010.

измерительной техники и при оптимизации управления качеством электрической энергии и оценки электромагнитной совместимости электротехнических средств [4-6, 9, 12, 14].

Литература

1. Железко Ю.С. Компенсация реактивной мощности и повышение качества электроэнергии. М.: Энергоатомиздат, 1985. 216 с.

2. Железко Ю.С. Потери электроэнергии. Реактивная мощность. Качество электроэнергии. М.: ЭНАС, 2009. 459 с.

3. Зевеке Г.В. Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. 3-е изд., испр. М.; Л.: Энергия, 1965. 753 с.

4. ЗиновьевГ.С. Силовая электроника. 5-е изд., испр. и доп. М.: Юрайт, 2012. 667 с.

5. Кармашев В.С. Электромагнитная совместимость технических средств. Справочник. М.: НОРТ, 2001. 401 с.

6. Карташев И.И., Зуев Н.Н. Качество электроэнергии в системах электроснабжения. Способы его контроля и обеспечения. М.: Изд-во МЭИ, 2000. 120 с.

7. Ковалев И.Н. Выбор компенсирующих устройств при проектировании электрических сетей. М.: Энергоатомиздат, 1990. 200 с.

8. МельниковН.А. Реактивная мощность в электрических сетях. М.: Энергия, 1975. 128 с.

9. Повышение эффективности использования электроэнергии в системах электротехнологии / Б.П. Борисов, Г.Я. Вагин, А.Б. Лоскутов, Ф.К. Шидловский и др. Киев: Наукова думка, 1990. 252 с.

10. Серебряков А.С., Осокин В.Л. Моделирование в пакете Mathcad переходных процессов в активно-емкостных цепях при переменном питающем напряжении и дискретном изменении параметров элементов // Вестник ВИЭСХ. 2016. № 4(25). С. 13-21.

11. Серебряков А.С., Шумейко В.В. Mathcad и решение задач электротехники. М.: Маршрут, 2005. 240 с.

12. Управление качества электроэнергии / И.И. Карташев, В.Н. Тульский, Р.Г. Шамонов и др.; под ред. Ю.В. Шарова. М.: Изд-во МЭИ, 2006. 320 с.

13. Электрические системы. Т. 2. Электрические сети / под ред. В.А. Веникова. М.: Высш. шк., 1971. 440 с.

14. Электромагнитная совместимость в электроэнергетике и электротехнике / А.Ф. Дьяков, Б.К. Максимов, Р.К. Борисов и др.; под ред. А.Ф. Дьякова. М.: Энергоатомиздат, 2003. 768 с.

СЕРЕБРЯКОВ АЛЕКСАНДР СЕРГЕЕВИЧ — доктор технических наук, профессор кафедры электрификации и автоматизации, Нижегородский государственный инженерно-экономический университет, Россия, Княгинино ([email protected]).

ОСОКИН ВЛАДИМИР ЛЕОНИДОВИЧ — кандидат технических наук, доцент, заведующий кафедрой электрификации и автоматизации, Нижегородский государственный инженерно-экономический университет, Россия, Княгинино ([email protected]).

Ä. SEREBRYAKOV, V. OSOKIN EXPANSION OF FULL INSTANTANEOUS POWER IN CIRCUIT OF SINUSOIDAL CURRENT ON INSTANTANEOUS ACTIVE AND INSTANTANEOUS REACTIVE POWER Key words: full instantaneous power, instantaneous active power, instantaneous reactive power, active-inductive load, integral value of the capacity, power meter of active and reactive power, compensation of reactive power.

The features of AC power supply systems are considered, it is necessary to take into account not only active, but reactive power to assess their energy efficiency for the transmission of which a certain part of the active power is spent on the wires. It is noted that the lack of reactive power leads to a decrease in the voltage level in the electrical network and can disrupt the static stability of the electrical system. Consequently, the power sources must produce not only active, but also reactive power for power receivers with reactive elements.

Since the transmission of reactive power over the network is economically unprofitable due to losses in the power line, it is more expedient to develop it directly in the places of consumption with the help of local sources of reactive power — installations for capacitive compensation of reactive power. In this case, the exchange part of the electromagnetic energy becomes zero. It is not consumed from or returned to the energy source. Capacitive and inductive elements exchange reactive energy with each other. In this case, only energy is transmitted through the network, which is converted into useful work. With the introduction of digital technologies into the energy process control system, it is necessary to substantiate the basic theoretical provisions for optimal control of energy consumption modes and reactive power compensation. The article presents the theoretical provisions that can form the basis of automated digital energy management systems. Expressions and wave diagrams for instantaneous values of active, reactive and full powers in a circuit of a sinusoidal current with an active-inductive load consisting of a series or parallel connection of a resistor and an inductive coil are given. It is shown how the wave diagrams of instantaneous power values will change in the case of reactive power compensation by means of transverse capacitive compensation, i.e. by switching the capacitor in parallel with the load. In both cases, the reactive power at the input of the circuit becomes zero, and the total power becomes equal to the active power. However, the curves of the instantaneous values of the active power in these cases have different phases, which must be taken into account in the development and operation of digital systems of automatic control of reactive power compensation devices.

References

1. Zhelezko Yu.S. Kompensatsiya reaktivnoy moshchnosti i povysheniye kachestva elektro-energii [Reactive power compensation and power quality improvement]. Moscow, Energoatomizdat Publ., 1985, 216 p.

2. Zhelezko Yu.S. Poteri elektroenergii. Reaktivnaya moshchnost. Kachestvo elektroenergii [Power loss. Reactive power. Power quality]. Moscow, ENAS Publ., 2009, 459 p.

3. Zeveke G.V. Ionkin P.A.. Netushil A.V.. Strakhov S.V. Osnovy teorii tsepey. 3-e izd., ispr. [Basics of circuit theory. 3rd ed.]. Moscow, Leningrad, Energiya Publ., 1965, 753 p.

4. Zinovyev G.S. Silovaya elektronika. 5-e izd.. ispr. i dop. [Power electronics. 5th ed.]. Moscow, Yurayt Publ., 2012, 667 p.

5. Karmashev V.S. Elektromagnitnaya sovmestimost tekhnicheskikh sredstv. Spravochnik [Electromagnetic compatibility of technical means]. Moscow, NORT Publ., 2001, 401 p.

6. Kartashev I.I.. Zuyev N.N. Kachestvo elektroenergii v sistemakh elektrosnabzheniya. Spo-soby ego kontrolya i obespecheniya [Power quality in power supply systems. Methods of its control and maintenance]. Moscow, MEI Publ., 2000, 120 p.

7. Kovalev I.N. Vybor kompensiruyushchikh ustroystvpriproyektirovanii elektricheskikh se-tey [Selection of compensating devices in the design of electrical networks]. Moscow, Energoatomizdat Publ., 1990, 200 p.

8. Melnikov N.A. Reaktivnaya moshchnost v elektricheskikh setyakh [Reactive power in electrical networks]. Moscow, Energiya Publ., 1975, 128 p.

9. Borisov B.P., Vagin G.Ya., Loskutov A.B., Shidlovskii F.K. et al. Povysheniye effektivnosti ispolzovaniya elektroenergii v sistemakh elektrotekhnologii [Increase of efficiency of use of the electric power in systems of electrotechnology]. Kiev, Naukova dumka Publ., 1990, 252 p.

10. Serebryakov A.S., Osokin V.L. Modelirovaniye v pakete Mathcadperekhodnykh protsessov v aktivno-emkostnykh tsepyakh pri peremennom pitayushchem napryazhenii i diskretnom izmenenii

parametrov elementov [Modeling in the Mathcad transient processes in active-inductive circuits with AC supply voltage and the discrete change in parameters of elements]. Vestnik VIESKh, 2016, no. 4(25), pp. 13-21.

11. Serebryakov A.S., Shumeyko V.V. Mathcad i resheniye zadach elektrotekhniki [Mathcad and the solution of problems in electrical engineering]. Moscow, Marshrut Publ., 2005, 240 p.

12. Sharov Yu.V., ed., Kartashev I.I., Tulskiy V.N., Shamonov R.G. et al. Upravleniye kachestva elektroenergii [Power quality management]. Moscow, MEI Publ., 2006, 320 p.

13. Venikov V.A., ed. Elektricheskiye sistemy. T. 2. Elektricheskiye seti [Electrical system. Vol. 2. Electric network]. Moscow, Vysshaya shkola Publ., 1971, 440 p.

14. Diakov A.F., ed., Diakov A.F., Maksimov B.K., Borisov R.K. et al. Elektromagnitnaya sovmestimost v elektroenergetike i elektrotekhnike [Electromagnetic compatibility in power and electrical engineering]. Moscow, Energoatomizdat Publ., 2003, 768 p.

SEREBRYAKOV ALEKSANDR — Doctor of Technical Sciences, Professor of Electrification and Automatization Department, Nizhny Novgorod State Engineering and Economic University, Russia, Knyaginino ([email protected]).

OSOKIN VLADIMIR — Candidate of Technical Sciences, Associate Professor, Head of Electrification and Automatization Department, Nizhny Novgorod State Engineering and Economic University, Russia, Knyaginino ([email protected]).

Формат цитирования: Серебряков А. С., Осокин В.Л. О разложении полной мгновенной мощности в цепи синусоидального тока на мгновенную активную и мгновенную реактивную мощности // Вестник Чувашского университета. — 2019. — № 1. — С. 134-145.

активных и пассивных компонентов — в чем разница между ними? — Компоненты ES

Два типа электронных устройств

Электронные элементы, составляющие цепь, соединяются вместе проводниками, образуя законченную цепь.

• Активные компоненты

• Пассивные компоненты

Активные компоненты

Активный компонент — это электронный компонент, который подает энергию в цепь.

Общие примеры активных компонентов включают:

• Источники напряжения

• Источники тока

• Генераторы (например, генераторы переменного тока и генераторы постоянного тока)

• Все типы транзисторов (например, транзисторы с биполярным переходом, МОП-транзисторы, полевые транзисторы и полевые транзисторы)

• Диоды (например, стабилитроны, фотодиоды, диоды Шоттки и светодиоды)

Источники напряжения

Источник напряжения является примером активного компонента в цепи.Когда ток уходит от положительной клеммы источника напряжения, в цепь подается энергия. Согласно определению активного элемента, аккумулятор также можно рассматривать как активный элемент, поскольку он непрерывно подает энергию в схему во время разряда.

Источники тока

Источник тока также считается активным компонентом. Ток, подаваемый в цепь от идеального источника тока, не зависит от напряжения в цепи. Поскольку источник тока управляет потоком заряда в цепи, он классифицируется как активный элемент.

Транзисторы

Транзисторы, хотя и не так очевидны, как источник тока или напряжения, также являются активным компонентом схемы. Это связано с тем, что транзисторы могут усиливать мощность сигнала (см. Нашу статью о транзисторах в качестве усилителя, если вы хотите точно знать, как).

Пассивные компоненты

Пассивный компонент — это электронный компонент, который может только получать энергию, которую он может рассеивать, поглощать или накапливать в электрическом поле или магнитном поле.Пассивным элементам для работы не требуется электричество.

Как следует из названия «пассивный» — пассивные устройства не обеспечивают усиления или усиления. Пассивные компоненты не могут усиливать, генерировать колебания или генерировать электрический сигнал.

Типичные примеры пассивных компонентов включают:

• Резисторы

• Катушки индуктивности

• Конденсаторы

• Трансформаторы

Резисторы

Резистор не может быть пассивным, поскольку он не может быть пассивным элементом. энергия в цепь.Вместо этого резисторы могут получать только энергию, которую они могут рассеивать в виде тепла, пока через них протекает ток.

Катушки индуктивности

Катушка индуктивности также считается пассивным элементом схемы, поскольку она может накапливать в ней энергию в виде магнитного поля и передавать эту энергию в цепь, но не непрерывно. Способность индуктора к поглощению и передаче энергии ограничена и носит временный характер. Поэтому индуктор принят как пассивный элемент схемы .

Конденсаторы

Конденсатор считается пассивным элементом, поскольку он может накапливать в нем энергию в виде электрического поля. Энергетическая способность конденсатора ограничена и нестационарна — он фактически не подает энергию, а накапливает ее для дальнейшего использования.

Таким образом, он не считается активным компонентом, так как энергия не подается и не усиливается.

Трансформаторы

Трансформатор также является пассивным электронным компонентом. Хотя это может показаться удивительным, поскольку для повышения уровня напряжения часто используются трансформаторы — помните, что мощность остается постоянной.

Когда трансформаторы повышают (или понижают) напряжение, мощность и энергия на первичной и вторичной стороне остаются неизменными. Поскольку энергия фактически не усиливается, трансформатор классифицируется как пассивный элемент.

Источник: El; ectrical 4U.com

Различия между активными и пассивными компонентами

Все электронные компоненты можно условно разделить на два класса, а именно Активные компоненты и Пассивные компоненты. Эти компоненты диаметрально отличаются друг от друга по своим функциональным свойствам и принципу действия.В этой статье мы узнаем о различных типах активных и пассивных компонентов, а также рассмотрим разницу между активными и пассивными устройствами . Но, прежде чем понять, насколько они отличаются друг от друга, важно понять, что означает каждый компонент и как они работают, поэтому давайте начнем с активных компонентов.

Что такое активные компоненты?

Активные компоненты — это устройства , которые могут усиливать электрический сигнал и вырабатывать энергию .Любой характеристический активный компонент будет содержать генератор, транзистор или интегральную схему. Активный компонент в устройствах работает как цепь переменного тока. Это помогает устройству увеличить мощность и напряжение. Этот компонент может выполнять свои операции, потому что он питается от источника электричества. Все активные компоненты требуют некоторого источника энергии, который обычно извлекается из цепи постоянного тока.

Пример активных компонентов

Активные компоненты по своим характеристикам полагаются на внешние источники для своей работы.У них есть возможность увеличить и добавить больше мощности в схему. Ниже приведены различных типов активных компонентов .

Транзисторы:

Транзисторы

используются для усиления тока, принимая небольшое напряжение энергии и давая больший выход энергии. Это полупроводниковое устройство является одним из наиболее важных компонентов, которые можно найти во многих схемах. Самыми популярными и часто используемыми транзисторами являются BC547, 2N2222 и BC557.Они могут быть индивидуальными или упакованными вместе в зависимости от конструкции устройства. Чаще всего используются транзисторы. Они имеют множество функций, включая регулирование напряжения, усиление, регулировку сигналов и т. Д.

Выпрямители с кремниевым управлением (SCR):

Выпрямители с кремниевым управлением

или для краткости тиристоры — это тип переключателя силовой электроники. Он имеет три терминала, которые называются анодом, катодом и затвором.По умолчанию переключатель разомкнут, и ток между клеммами анода и катода SCR не течет. Когда на вывод затвора подается небольшой ток, переключатель замыкается, и между выводами анода и катода может проходить большой ток. Использование тиристора / SCR очень похоже на тиристор BJT (транзистор). Переключаемая нагрузка подключается между анодом и катодом, и тиристор можно включать или выключать, подав ток затвора на штырь затвора тиристоров.Самыми популярными и часто используемыми тиристорами являются 2N2324 и 2N1595.

Что такое пассивные компоненты?

Пассивные компоненты не могут управлять электрическим током , используя второй электрический сигнал. Некоторыми важными пассивными компонентами являются конденсаторы, резисторы, катушки индуктивности и трансформаторы. Пассивным компонентам не требуется энергия для работы, исключая цепь переменного тока. В отличие от активного компонента, они не могут увеличить мощность сигнала, а также не могут его усилить.Есть в основном два типа пассивных компонентов, а именно .

С потерями или рассеиванием : Они не могут поглощать мощность от внешней цепи. Резисторы являются примером пассивных компонентов с потерями.

Lossless : у них нет входного или выходного потока чистого уровня. Несколько примеров компонентов без потерь — это индукторы, трансформаторы и гираторы.

Большинство пассивных компонентов состоят из двух терминалов и обычно называются двухпортовыми терминалами .Обычно они соблюдают стандарты взаимности. Примерами двухпортовой сети являются транзисторы и электронные фильтры. В некоторых пассивных компонентах также используется схемная архитектура, такая как резисторы, катушки индуктивности, источники напряжения и тока.

Примеры пассивных компонентов С другой стороны, пассивные компоненты

не требуют для работы какого-либо внешнего источника энергии. Они рассеивают энергию внутри цепи. Ниже приведены наиболее распространенные пассивные компоненты.

Конденсаторы:

Конденсаторы могут накапливать энергию в электрическом поле, расположенном между пластинами. Они обычно используются в электронных схемах для хранения. Их также можно использовать в схемах фильтров для различения высокочастотных и низкочастотных сигналов. Конденсаторы в основном можно разделить на керамические конденсаторы, электролитические конденсаторы, майларовые конденсаторы и конденсаторы с рейтингом X. Вы также можете прочитать эту статью о конденсаторах, чтобы понять основы конденсатора, его типы и области применения.

Резисторы:

Как следует из названия, их работа заключается в сопротивлении или противодействии течению тока. Они предназначены для управления прохождением электрического тока в цепи, автоматически понижая напряжение в устройстве. Вы также можете прочитать эту статью о резисторах, чтобы понять основы резисторов, их типы и области применения.

Катушки индуктивности:

Их также можно использовать для хранения энергии и доставки заряда.В пределах параметров цепи индукторы имеют очень высокий импеданс на переменном токе и очень маленький импеданс на постоянном токе. Катушки индуктивности очень часто встречаются в цепях питания, таких как преобразователи переменного / постоянного тока, цепи SMPS и т. Д. Вы также можете прочитать эту статью о индукторах, чтобы понять основы индукторов, их типы и применения.

Диоды:

Диоды — это крошечные активные компоненты, которые используются для направления потока энергии в пределах схемы.Функция диода чрезвычайно важна, потому что он контролирует поток энергии, предотвращая повреждения, которые могут быть вызваны плохим потоком энергии. Наиболее популярными и часто используемыми диодами являются выпрямительный диод 1N4007, стабилитрон 1N4732A 4,7 В и диод Шоттки 1N5817. Вы можете прочитать эту статью о диодах, чтобы узнать больше об основах диодов, их типах, характеристиках и т. Д.

Различия между активными и пассивными компонентами

Теперь, когда мы разобрались с активными и пассивными устройствами и их типами, давайте проведем сравнение между активными и пассивными компонентами на основе определенных параметров, как определено ниже

1) Источник энергии — Активным компонентам требуется дополнительный источник энергии.В случае пассивных компонентов для их работы не требуется дополнительных источников энергии. Резистор работает сам по себе, не требуя определенного напряжения.

2) Энергия: Активные компоненты производят энергию в виде напряжения или тока, но пассивные компоненты — это те устройства, которые накапливают энергию, например, конденсатор, хранят ее энергию в виде электрического поля, а индуктор хранит свою энергию в виде магнитное поле.

3) Линейность : Пассивные компоненты линейны, а активные компоненты нелинейны.Это означает, что в пассивном компоненте, таком как резистор, падение напряжения на нем будет линейно относительно его значения сопротивления в соответствии с законом Ома. В транзисторе или других активных компонентах выходной коэффициент усиления не будет линейным.

4) Прирост мощности: Активные компоненты могут обеспечивать прирост мощности, тогда как в случае пассивных компонентов возможность усиления мощности отсутствует.

5) Управление током : Активный компонент, как следует из названия, может легко управлять потоком тока.Та же задача не может быть выполнена пассивным компонентом.

6) Внешний источник : Активным компонентам, как было показано ранее, требуется дополнительный источник для управления и поддержки их операций, но в случае пассивных компонентов внешний источник не требуется.

Введение в электронные компоненты: активные и пассивные компоненты

ОСНОВНЫЕ ЗНАНИЯ — ЭЛЕКТРОННЫЕ КОМПОНЕНТЫ Введение в электронные компоненты: активные и пассивные компоненты.пассивные компоненты

Одним из ключевых факторов, который отличает типы электронных компонентов друг от друга, является то, являются ли они активными или пассивными. Однако многие люди не уверены, что именно влечет за собой эта разница. Эта статья здесь, чтобы помочь.

Связанные компании

Активные и пассивные компоненты систем силовой электроники.

Ключевое различие между активными и пассивными компонентами.

Электронные компоненты делятся на активные и пассивные в зависимости от функций, которые они могут выполнять.Короче говоря, активные компоненты могут, вообще говоря, вводить мощность в цепь и способны электрически контролировать и усиливать поток электрического тока, в то время как пассивные компоненты не могут.

В отличие от активных компонентов, пассивные компоненты либо потребляют, либо накапливают энергию. Простой способ проверить, активен ли компонент, — это измерить разницу между его входными и выходными сигналами. Если есть спад мощности, компонент пассивный. Если сигнал усилен, он активен.

Основной доклад на PCIM Digital Days 2021

Не пропустите ключевой доклад «Новое поколение упаковки модулей силовой электроники» от Ханнеса Штара, руководителя группы по технологиям — R&D, AT&S на PCIM Digital Days с 3 по 7 мая 2021 года.

Откройте для себя всю программу!

Все электронные схемы должны содержать хотя бы один активный компонент, а большинство электронных устройств содержат как активные, так и пассивные компоненты.

Активные компоненты и их функции

Активным компонентам требуется источник энергии, обычно в виде постоянного тока, для выполнения своей конкретной функции.Они могут каким-то образом управлять потоком электричества. Большинство активных компонентов состоят из полупроводниковых устройств, таких как диоды, транзисторы и интегральные схемы.

• Транзистор: В основном используется для усиления электрических сигналов или в качестве переключающих устройств

• Диод: Позволяет электричеству течь только в одном направлении

• Интегральная схема (микросхемы или микрочипы): несколько сложных схем на печатной плате; используется для выполнения всевозможных задач; все еще считается компонентом, несмотря на то, что он состоит из многих других компонентов

• Устройства отображения , такие как ЖК-дисплеи, светодиоды и ЭЛТ-дисплеи

• Источники питания , такие как батареи и другие источники переменного или постоянного тока DC)

Пассивные компоненты и их функции

Пассивные компоненты могут влиять на поток электричества, проходящий через них.Например, они могут сопротивляться его потоку, накапливать энергию для дальнейшего использования или создавать индуктивность. Однако сами они не могут контролировать или усиливать электричество.

Наиболее распространенные компоненты и их функции:

• Резистор: Сопротивляет прохождению электрического тока в цепи; используется для понижения напряжения

• Конденсатор: Накапливает электрическую энергию электростатически в электрическом поле (так называемая «зарядка») и может высвобождать ее позже при необходимости

• Индуктор: Сохраняет электрическую энергию в магнитном поле ; позволяет протекать через него постоянному току (DC), но не переменному (AC)

• Преобразователь: Преобразует входной сигнал из одного типа энергии в другой; датчики — это тип преобразователя, который преобразует физическое воздействие / входной сигнал в электрический сигнал

Типичные области применения активных и пассивных компонентов

Эти крошечные электронные элементы окружают нас в повседневной жизни.Они спрятаны внутри фонарей, звуковых систем, компьютеров, телефонов, автомобилей и многого другого. По определению, активные компоненты можно найти в каждом электронном устройстве, поэтому у них есть бесчисленное множество вариантов использования. Классические примеры включают любые устройства с вычислительной мощностью (интегральные схемы), устройства со встроенным аккумулятором или дисплеем и светодиодные фонари (светоизлучающие диоды).

Когда дело доходит до пассивных компонентов, лампы накаливания являются прекрасным примером преобразователей в действии — они преобразуют электрическую энергию в световую и тепловую.Громкоговорители используют преобразователи для преобразования электрического входного сигнала в механический выход, заставляя конусы внутри динамиков вибрировать, тем самым генерируя звуковые волны, которые мы можем слышать. Датчики — это еще один тип преобразователей, которые давно используются в научных исследованиях и становятся все более и более повсеместными благодаря «умелости» бесчисленных устройств и машин.

Другие варианты использования пассивных компонентов включают микроволновые и радиочастотные приложения, такие как системы удаленного доступа без ключа, в которых используются индукторы.Антенны также являются пассивными и используются в радиоприемниках, устройствах GPS, спутниках, беспроводных модемах и маршрутизаторах, общественном транспорте и т. Д.

Следуйте за нами в LinkedIn

Вам понравилось читать эту статью? Тогда подпишитесь на нас в LinkedIn и будьте в курсе последних событий в отрасли, продуктов и приложений, инструментов и программного обеспечения, а также исследований и разработок.

Следуйте за нами здесь!

(ID: 46300364)

Основное различие между активными и пассивными компонентами

Основное различие между активными и пассивными компонентами

Наиболее распространенные активные и пассивные (очень простое объяснение с примерами)

Активные компоненты:
Те устройства или компоненты, которые требуются Внешний источник их работы называется активными компонентами.
Например: Диод, транзисторы, SCR и т. Д.
Объяснение и пример: Как мы знаем, диод является активным компонентом. Поэтому для его работы требуется внешний источник.
Потому что, если мы подключим диод в цепь, а затем подключим эту цепь к напряжению питания, то диод не будет проводить ток, пока напряжение питания не достигнет 0,3 (в случае германия) или 0,7 В (в случае кремния). ). Думаю, вы поняли 🙂

Пассивные компоненты:

Те устройства или компоненты, которые не требуют внешнего источника для своей работы, называются пассивными компонентами.
Например, : резистор, конденсатор, индуктор и т. Д.

Объяснение и пример: Пассивные компоненты не требуют внешнего источника для своей работы.
Как и диод, резистору не требуется 0,3-0,7 В. То есть, когда мы подключаем резистор к напряжению питания, он начинает работать автоматически без использования определенного напряжения. Если вы поняли приведенное выше утверждение об активных компонентах, то вы легко получите этот пример.:) Другими словами:

Активные компоненты:
Те устройства или компоненты, которые производят энергию в виде напряжения или тока, называются активными компонентами
Например: диоды, транзисторы, SCR и т. Д. …

Пассивные компоненты:
Те устройства или компоненты, которые хранят или поддерживают энергию в форме напряжения или тока, известны как пассивные компоненты
Например, : резистор, конденсатор, индуктор и т. Д.…

Очень простыми словами;
Активные компоненты: энергия Донор
Пассивные компоненты: энергия Приемник
Также пассивных компонентов относятся к линейной категории, а активные компоненты — к нелинейной.

Вы также можете прочитать:

Разница между активными и пассивными компонентами

Пишем о разнице между активными и пассивными компонентами. Важнейшим фактором, который отличает типы электронных компонентов друг от друга, является то, являются ли они активными или пассивными. Тем не менее, многие люди не уверены, в чем именно заключается эта разница. Здесь мы хотим прояснить эти концепции. Итак, мы представим активные и пассивные элементы. Затем мы поговорим об их различиях.

Активные элементы

Прежде чем обращать внимание на разницу между активным и пассивным компонентами, давайте представим активный компонент. Активные элементы в схеме — это компоненты, которые обеспечивают питание или энергию для схемы, отбирая мощность из внешнего источника, а также способность обеспечивать сохранение энергии в течение неограниченного периода времени до наличия внешнего источника.

Поскольку активные элементы обеспечивают питание цепи, в которой они применяются, они работают как генераторы.Более того, эти компоненты могут управлять током в цепи.

Такие элементы, как транзистор, диод, операционный усилитель и т. Д., Идентифицируются как активные компоненты в любой схеме. Давайте посмотрим на краткое обсуждение этих упомянутых компонентов:

Диод

Диоды — это в основном полупроводниковые материалы, которые состоят из полупроводниковых материалов p- и n-типа. Диод — это двухполюсное оборудование.

Диод — это активный компонент, используемый для направления тока, протекающего в цепи, просто обеспечивая проводимость в одном направлении.

Символ диода (ссылка: vivadifferences.com)

Транзистор

Транзистор — это 3-х оконечное оборудование, отображающее усиливающее действие. Как мы объяснили, активные компоненты используют питание от внешнего источника и подают его в цепь, к которой они подключены.

Аналогичным образом транзистор усиливает влияние тока в цепи.

Транзисторы в основном классифицируются как BJT и FET.

Символ транзистора (ссылка: vivadifferences.com)

Все, что нужно знать об активных компонентах

Теперь мы хотим представить важные советы об активных компонентах, чтобы лучше понять разницу между активными и пассивными компонентами.

1. Активный компонент — это часть оборудования, которая может усиливать выходной сигнал электронной схемы в большей степени, чем входной сигнал.
2. Активным компонентам требуется внешний источник питания для обеспечения энергией цепи.
3. Эти компоненты однонаправленные
4. Они работают как источник тепла и, следовательно, могут обеспечивать увеличение мощности.
5. Активные компоненты производят или передают мощность или энергию в форме тока или напряжения.
6. Когда активные компоненты присутствуют в какой-либо цепи, они демонстрируют некоторый уровень контроля над током, протекающим в цепи.
7. Активные компоненты действуют как генераторы из-за их способности обеспечивать мощность.
8. Активные компоненты не могут накапливать энергию.
9. Активные компоненты относятся к категории нелинейных.
10. Активные компоненты поставляют энергию или мощность в цепь.
11. Активные компоненты широко применяются в персональных компьютерах (ПК).
12. Они могут усиливать сигнал за счет усиления более одного.

Пассивные элементы

Чтобы провести различие между активными и пассивными компонентами, давайте теперь представим пассивный компонент. Пассивные элементы в цепи — это компоненты, которые не могут производить энергию в цепи, в которой они работают.Однако они могут накапливать или потреблять мощность, присутствующую в цепи.

Кроме того, пассивные элементы не требуют внешнего электрического питания для своей работы. Кроме того, пассивные компоненты могут быть подключены в цепи в обоих направлениях из-за их двунаправленности. Благодаря своей способности накапливать и потреблять энергию, они работают как аттенюаторы. Пассивными компонентами являются катушка индуктивности, резистор, конденсатор и т. Д. Давайте взглянем на краткое описание этих компонентов.

Резистор

Резисторы

— это пассивные элементы, которые обладают способностью ограничивать ток, протекающий в цепи, когда они применяются в любой цепи.

Величина, которая взвешивает величину ограничения, создаваемого резисторами, называется сопротивлением. Сопротивление имеет единицы Ом .

Сопротивление конкретного резистора рассчитывается по формуле:

R = \ frac {V} {I} [\ katex]

где

«В» — падение напряжения на резисторе, а

В — падение напряжения на резисторе.

«I» обозначает ток, протекающий через этот конкретный резистор.

Конденсатор

Конденсатор — это устройство, которое накапливает электрические заряды, протекающие по нему, на двух емкостных пластинах.

Количество заряда, собираемого конденсатором, определяется как емкость, которая имеет единицу фарад .

Емкость конденсатора определяется как:

C = \ frac {Q} {V} [\ katex]

где

«Q» описывает собранный платеж, а

«В» выражает напряжение на пластинах конкретного конденсатора.

Индуктор

Катушки индуктивности — это элементы, которые могут накапливать энергию. Однако индукторы хранят энергию в виде магнитного поля, в отличие от конденсаторов.

Пока ток течет по цепи, энергия накапливается в витках катушки. Индуктивность — это единица, используемая для оценки магнитного поля, хранящегося в катушке, и ее единицей является Генри.

Индуктивность рассчитывается по:

L = \ frac {\ phi} {I} [\ katex]

где

«𝜙» — это флюсовая связь

и

«I» обозначает ток, протекающий в катушке индуктивности.

Все, что нужно знать о пассивных компонентах

Здесь мы хотим представить основные моменты, касающиеся пассивных компонентов, чтобы лучше понять разницу между активными и пассивными компонентами.

1. Пассивные компоненты — это инструменты, которые управляют или изменяют выходной сигнал электронной схемы, не выполняя активной функции в своей работе.
2. Пассивным компонентам не требуется внешний источник питания, поскольку они не могут подавать питание и могут просто сохранять или передавать мощность, доступную в цепи.
3. Эти компоненты являются двунаправленными по своей природе.
4. Пассивные компоненты служат радиатором и, следовательно, не могут обеспечить выигрыш в мощности.
5. Пассивные компоненты используют или собирают энергию в виде тока или напряжения.
6. Пассивные компоненты действительно не предназначены для управления током, протекающим в цепи.
7. Пассивные компоненты работают как аттенюаторы из-за их способности к поглощению.
8. Пассивные компоненты могут собирать и накапливать энергию (в случае конденсатора и катушки индуктивности).
9. Пассивные компоненты относятся к линейной категории.
10. Пассивные элементы используют энергию или мощность в цепи.
11. Пассивные компоненты широко используются в MP3-плеерах, стиральных машинах и т. Д.
12. Эти компоненты не могут усиливать сигнал из-за того, что коэффициент усиления меньше единицы.

Ключевые различия между активными и пассивными компонентами

Теперь, чтобы пояснить разницу между активными и пассивными компонентами, в таблице ниже представлены двенадцать различий между активными и пассивными компонентами.

ОСНОВА СРАВНЕНИЯ	АКТИВНЫЕ КОМПОНЕНТЫ	ПАССИВНЫЕ КОМПОНЕНТЫ
Описание	Активный компонент — это оборудование, которое может усилить выходной сигнал электронной схемы в количестве, превышающем входной сигнал	Пассивные компоненты — это инструменты, которые управляют или изменяют выходной сигнал электронной схемы, не выполняя при этом активную функцию
Внешний источник питания	Активным компонентам требуется внешний источник питания для обеспечения энергией цепи	Пассивным компонентам не требуется внешний источник питания, поскольку они не могут подавать питание и могут просто сохранять или передавать мощность, доступную в цепи
Природа	Эти компоненты однонаправленные	Эти компоненты являются двунаправленными по своей природе
Функциональность	Они работают как источник тепла и, следовательно, могут обеспечивать увеличение мощности	Пассивные компоненты служат радиатором и, следовательно, не могут обеспечить выигрыш в мощности
Мощность	Активные компоненты вырабатывают или передают мощность или энергию в виде тока или напряжения	Пассивные компоненты используют или собирают энергию в виде тока или напряжения
Текущее управление потоком	Когда активные компоненты присутствуют в любой цепи, они показывают некоторый уровень контроля над током, протекающим в цепи	Пассивные компоненты действительно не предназначены для управления током, протекающим в цепи
Функция	Активные компоненты действуют как генераторы из-за своей способности обеспечивать мощность	Пассивные компоненты работают как аттенюаторы из-за их способности к поглощению
Накопитель энергии	Активные компоненты не могут накапливать энергию	Пассивные компоненты могут накапливать и накапливать энергию
Категория	Активные компоненты относятся к категории нелинейных	Пассивные компоненты относятся к линейной категории
Контур	Активные компоненты поставляют энергию или мощность в цепь	Пассивные элементы используют энергию или мощность в цепи
Заявка	Активные компоненты широко применяются в персональных компьютерах (ПК)	Пассивные компоненты широко используются в MP3-плеерах, стиральных машинах и т. Д.
Усиление сигнала	Они могут усиливать сигнал за счет усиления более одного.	Эти компоненты не могут усиливать сигнал из-за коэффициента усиления меньше единицы.

Определение реактивной мощности — Руководство по электрическому монтажу

Для большинства электрических нагрузок, таких как двигатели, ток I отстает от напряжения V на угол φ.

Если токи и напряжения являются идеально синусоидальными сигналами , для представления может использоваться векторная диаграмма.

На этой векторной диаграмме вектор тока можно разделить на две составляющие: одна в фазе с вектором напряжения (компонент I _a ), другая в квадратуре (отставание на 90 градусов) с вектором напряжения (компонент I _r). ). См. Рис. L1.

I _a называется активной составляющей тока.

I _r называется реактивной составляющей тока.

Рис. L1 — Векторная диаграмма токов

Предыдущая диаграмма, составленная для токов, также применима к мощности путем умножения каждого тока на общее напряжение V.См. Рис. L2.

Таким образом, мы определяем:

• Полная мощность : S = V x I (кВА)
• Активная мощность : P = V x Ia (кВт)
• Реактивная мощность : Q = V x Ir (квар)

Рис. L2 — Векторная диаграмма мощности

На этой диаграмме мы видим, что:

• Коэффициент мощности : P / S = cos φ

Эта формула применима для синусоидального напряжения и тока. Вот почему коэффициент мощности затем обозначается как «Коэффициент мощности смещения» .{2}}

Коэффициент мощности, близкий к единице, означает, что полная мощность S минимальна. Это означает, что номинальные параметры электрического оборудования минимальны для передачи данной активной мощности P на нагрузку. Тогда реактивная мощность мала по сравнению с активной. мощность.

Низкое значение коэффициента мощности указывает на противоположное состояние.

Полезные формулы (для сбалансированных и почти сбалансированных нагрузок в 4-проводных системах):

• Активная мощность P (в кВт)
  • Однофазный (1 фаза и нейтраль): P = V.I.cos φ
  • Однофазный (между фазами): P = U.I.cos φ
  • Трехфазный (3 провода или 3 провода + нейтраль): P = √3.U.I.cos φ
• Реактивная мощность Q (в квар)
  • Однофазный (1 фаза и нейтраль): Q = V.I.sin φ
  • Однофазный (между фазами): Q = U.I.sin φ
  • Трехфазный (3 провода или 3 провода + нейтраль): Q = √3.U.I.sin φ
• Полная мощность S (в кВА)
  • Однофазный (1 фаза и нейтраль): S = V.Я
  • Однофазный (между фазами): S = U.I
  • Трехфазный (3 провода или 3 провода + нейтраль): S = √3.U.I

где:

В = Напряжение между фазой и нейтралью
U = Напряжение между фазами
I = Линейный ток
φ = Фазовый угол между векторами V и I.

Пример расчета мощности (см.

Рис. L3)

Рис. L3 — Пример расчета активной и реактивной мощности

Тип цепи		Полная мощность S (кВА)	Активная мощность P (кВт)	Реактивная мощность Q (квар)
Однофазный (фаза и нейтраль)		S = VI	P = VI cos φ	Q = VI sin φ
Однофазный (между фазами)		S = UI	P = UI cos φ	Q = UI sin φ
Пример: нагрузка 5 кВт, cos φ = 0.5		10 кВА	5 кВт	8,7 квар
Трехфазное 3-проводное или 3-проводное + нейтраль		S = 3 {\ displaystyle {\ sqrt {3}}} пользовательского интерфейса	P = 3 {\ displaystyle {\ sqrt {3}}} UI cos φ	Q = 3 {\ displaystyle {\ sqrt {3}}} грех пользовательского интерфейса φ
Пример	Двигатель Pn = 51 кВт	65 кВА	56 кВт	33 квар
	cos φ = 0,86
	ρ = 0.91 (КПД двигателя)

Расчеты для трехфазного примера, приведенного выше, следующие:

Pn = поставленная мощность на валу = 51 кВт

P = потребляемая активная мощность

P = Pnρ = 510,91 = 56 кВт {\ displaystyle P = {\ frac {Pn} {\ rho}} = {\ frac {51} {0.91}} = 56 \, кВт}

S = полная мощность

S = Pcosφ = 560,86 = 65 кВА {\ displaystyle S = {\ frac {P} {cos \ varphi}} = {\ frac {56} {0.86}} = 65 \, кВА}

Таким образом, при обращении к рис. L16 или использовании карманного калькулятора значение tan φ, соответствующее cos φ, равному 0.{2}}} = 33 \, квар}

Рис. L4 — Расчетная диаграмма мощности

Реактивный компонент

— обзор

Операционный усилитель интегратора (фильтр «полюс-ноль»)

Прежде чем мы перейдем к пассивным сетям, включающим два реактивных компонента , давайте рассмотрим интересный активный RC- фильтр на основе (первого порядка). Для обсуждения здесь выбран , «интегратор», потому что он является фундаментальным строительным блоком любой «компенсационной сети».”

Инвертирующий операционный усилитель, представленный на рис. 12.5, имеет только конденсатор в цепи обратной связи. Мы знаем, что в условиях постоянного постоянного тока все конденсаторы по существу «выходят из поля зрения». Таким образом, в нашем случае мы остаемся с без отрицательной обратной связи на всех на постоянном токе — и, следовательно, с бесконечным усилением постоянного тока (хотя на практике реальные операционные усилители ограничивают его очень высоким, но конечным значением). Но что еще более удивительно, это не мешает нам знать точное усиление на более высоких частотах.Если мы вычислим передаточную функцию этой схемы, мы увидим, что что-то «особенное» снова происходит в точке f = 1 / (2 π × RC). Однако, в отличие от пассивного RC-фильтра, эта точка не является ни точкой излома, ни полюсом, ни положением нуля. Это точка, в которой коэффициент усиления равен y (0 дБ). Обозначим эту частоту как «fp0».

Рисунок 12.5. Интегратор (полюс в нуле) операционного усилителя и некоторые связанные математики.

Обратите внимание, что пока, как показано на Рисунок 12.5, интегратор — это только каскад. Таким образом, в данном конкретном случае «fp0» совпадает с наблюдаемой частотой кроссовера «fcross». Но в целом этого не будет. В общем, в этой главе «fp0» будет относиться к частоте кроссовера, которую каскад интегратора произвел бы , если бы он присутствовал только .

Обратите внимание, что интегратор имеет однополюсный датчик на «нулевой частоте», хотя 0 не может отображаться в логарифмической шкале. Мы, , всегда стремимся ввести этот полюс в нуле, потому что без него система имела бы довольно низкое усиление по постоянному току (низкочастотное). Интегратор — это самый простой способ получить как можно большее усиление по постоянному току. Наличие высокого усиления по постоянному току — это способ добиться хорошего установившегося регулирования в любом преобразователе мощности. Это также показано на рисунке 12.3 (помечено как «DC shift»). Высокое усиление постоянного тока уменьшит сдвиг постоянного тока.

На правой стороне рисунка 12.4 мы намеренно сделали граф геометрически квадратом формы. С этой целью мы назначили равное количество делений сетки на двух осях, то есть оси масштабируются и пропорциональны одинаково.Кроме того, мы нанесли 20 × log ( f ) на ось y (вместо просто log ( f )). Сделав таким образом оси x и y идентичными во всех отношениях, мы понимаем, почему наклон называется «-1» — он действительно падает ровно на 45 ° (теперь мы видим это и визуально).

Мы пользуемся этой возможностью, чтобы показать, как выполнить простую математику в логической плоскости. Это показано в нижней части рисунка 12.5. Мы вывели одно конкретное полезное соотношение между произвольной точкой «А» и частотой кроссовера «fcross.