Активное реактивное сопротивление. Реактивное сопротивление: формула расчета, виды и применение в электротехнике — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое реактивное сопротивление. Как рассчитать реактивное сопротивление катушки индуктивности и конденсатора. Какие бывают виды реактивного сопротивления. Как применяется реактивное сопротивление в электротехнике.

Содержание

Понятие реактивного сопротивления в электротехнике

Реактивное сопротивление — это величина, характеризующая сопротивление, которое оказывают переменному электрическому току в цепи индуктивные и емкостные элементы. В отличие от активного сопротивления, реактивное сопротивление не приводит к необратимому преобразованию электрической энергии в тепло.

Реактивное сопротивление обозначается буквой X и измеряется в омах (Ом). Различают два основных вида реактивного сопротивления:

Индуктивное сопротивление XL — создается катушками индуктивности
Емкостное сопротивление XC — создается конденсаторами

Чем отличается реактивное сопротивление от активного? Основные отличия заключаются в следующем:

Реактивное сопротивление зависит от частоты тока, а активное — нет

На реактивном сопротивлении энергия не рассеивается в виде тепла
Реактивное сопротивление может быть как положительным, так и отрицательным

Формула для расчета реактивного сопротивления

Для расчета реактивного сопротивления используются следующие формулы:

Индуктивное сопротивление:

XL = ωL = 2πfL

где:

XL — индуктивное сопротивление (Ом)
ω — угловая частота (рад/с)
f — частота переменного тока (Гц)
L — индуктивность катушки (Гн)

Емкостное сопротивление:

XC = 1 / (ωC) = 1 / (2πfC)

где:

XC — емкостное сопротивление (Ом)
C — емкость конденсатора (Ф)

Общее реактивное сопротивление цепи равно разности индуктивного и емкостного сопротивлений:

X = XL — XC

Виды реактивного сопротивления

В электротехнике различают следующие основные виды реактивного сопротивления:

1. Индуктивное сопротивление

Индуктивное сопротивление создается катушками индуктивности. При протекании через них переменного тока возникает ЭДС самоиндукции, препятствующая изменению тока. Индуктивное сопротивление прямо пропорционально частоте тока и индуктивности катушки.

2. Емкостное сопротивление

Емкостное сопротивление создается конденсаторами. При изменении напряжения на обкладках конденсатора возникает ток смещения, препятствующий изменению напряжения. Емкостное сопротивление обратно пропорционально частоте тока и емкости конденсатора.

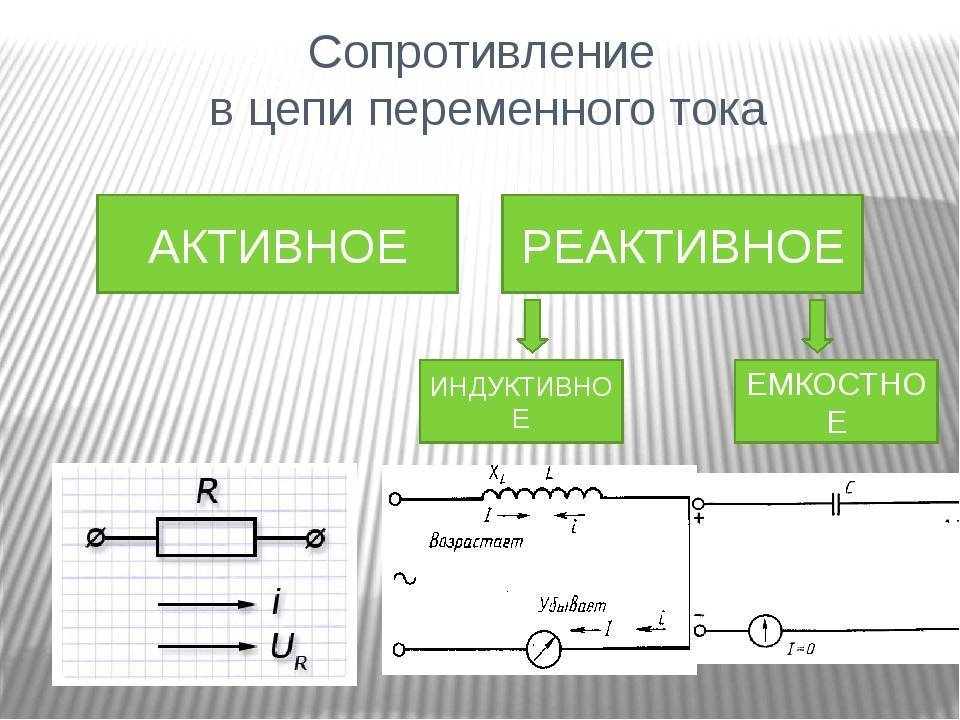
3. Полное реактивное сопротивление

Полное реактивное сопротивление цепи равно алгебраической сумме индуктивного и емкостного сопротивлений. При этом индуктивное сопротивление считается положительным, а емкостное — отрицательным.

Применение реактивного сопротивления в электротехнике

Реактивное сопротивление находит широкое применение в различных областях электротехники:

1. Фильтрация сигналов

Реактивные элементы используются для создания фильтров высоких и низких частот, полосовых и режекторных фильтров. Они позволяют выделять или подавлять определенные частотные составляющие сигналов.

2. Компенсация реактивной мощности

Конденсаторные батареи применяются для компенсации индуктивной составляющей нагрузки и повышения коэффициента мощности в электрических сетях.

3. Создание колебательных контуров

Сочетание индуктивности и емкости позволяет создавать резонансные LC-контуры, используемые в радиотехнике для настройки на определенные частоты.

4. Сглаживание пульсаций

Индуктивно-емкостные фильтры применяются в выпрямителях для сглаживания пульсаций выпрямленного напряжения.

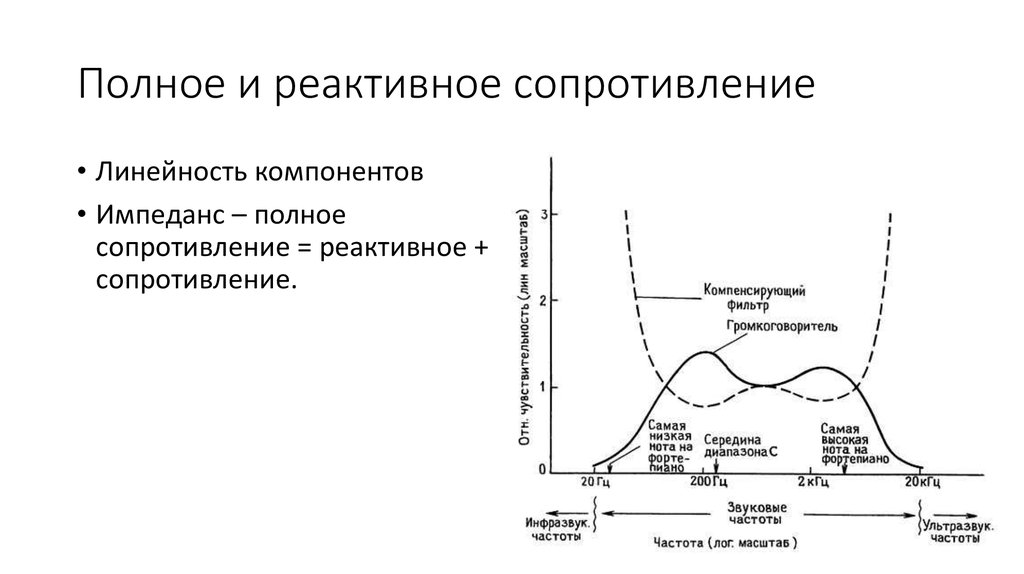
Зависимость реактивного сопротивления от частоты

Одной из ключевых особенностей реактивного сопротивления является его зависимость от частоты переменного тока. Как эта зависимость проявляется для разных элементов?

Катушка индуктивности:

Для катушки индуктивности реактивное сопротивление увеличивается с ростом частоты:

На постоянном токе (f = 0) XL = 0
При увеличении частоты XL растет линейно
На высоких частотах катушка становится практически изолятором

Конденсатор:

Для конденсатора реактивное сопротивление уменьшается с ростом частоты:

На постоянном токе XC стремится к бесконечности
При увеличении частоты XC уменьшается обратно пропорционально
На высоких частотах конденсатор становится практически проводником

Эта частотная зависимость позволяет использовать реактивные элементы для фильтрации сигналов и создания частотно-избирательных цепей.

Особенности измерения реактивного сопротивления

Измерение реактивного сопротивления имеет ряд особенностей по сравнению с измерением активного сопротивления:

Необходимо учитывать частоту измерительного сигнала

Измерение проводится на переменном токе
Требуется определение не только модуля, но и знака сопротивления
Используются специальные измерительные приборы — измерители иммитанса

При измерениях важно соблюдать следующие правила:

Выбирать частоту измерительного сигнала, соответствующую рабочей частоте исследуемого элемента
Учитывать паразитные параметры измерительной схемы
Использовать четырехпроводную схему подключения для исключения влияния соединительных проводов

Точное измерение реактивного сопротивления позволяет правильно рассчитывать и проектировать электрические цепи с реактивными элементами.

Реактивное сопротивление в цепях переменного тока

В цепях переменного тока реактивное сопротивление играет важную роль, влияя на ток, напряжение и мощность. Основные особенности:

Реактивное сопротивление вызывает сдвиг фаз между током и напряжением
На реактивных элементах происходит накопление энергии электромагнитного поля

Появляется реактивная мощность, которая не совершает полезной работы

Как реактивное сопротивление влияет на параметры цепи переменного тока?

Уменьшает действующее значение тока
Снижает коэффициент мощности
Увеличивает полную мощность
Вызывает дополнительные потери в линиях электропередачи

Для улучшения характеристик электрических цепей стремятся минимизировать реактивную составляющую с помощью компенсирующих устройств.

Формула расчета реактивного сопротивления, калькулятор расчетов

В цепь переменного электрического тока входят активные (содержащие внутренние источники энергии) и пассивные элементы (потребители энергии). К пассивным элементам относят резисторы и реактивные устройства.

Пассивные элементы

Виды пассивных элементов

В электротехнике рассматривают два типа резисторов: активное и реактивное сопротивление. Активным – обладают приборы, в которых энергия электрического тока преобразуется в тепловую. В физике оно обозначается символом R. Единица измерения – Ом.

Рассчитать его можно, используя закон Ома:

R = U/I.

Этой формулой можно пользоваться для расчёта по мгновенным значениям тока и напряжения, максимальным или действующим.

Реактивные устройства энергию не рассеивают, а накапливают. К ним относятся:

катушка индуктивности;
конденсатор.

Реактивное сопротивление обозначается символом Х. Единица измерения – Ом.

Катушка индуктивности

Представляет собой проводник, выполненный в форме спирали, винта или винтоспирали. Благодаря высокой инерционности, прибор используют в схемах, которые применяются для уменьшения пульсаций в цепях переменного тока и колебательных контурах, для создания магнитного поля и т.д. Если она имеет большую длину при небольшом диаметре, то катушку называют соленоидом.

Схема включения

Для вычисления падения напряжения (U) на концах катушки используют формулу:

U = –L·DI/Dt, где:

L – индуктивность прибора, измеряется в Гн (генри),
DI – изменение силы тока (измеряется в амперах) за промежуток времени Dt (измеряется в секундах).

Внимание! При любом изменении тока в проводнике возникает ЭДС самоиндукции, которая препятствует этому изменению.

Вследствие этого в катушке возникает сопротивление, которое называется индуктивным.

В электротехнике обозначается ХL и рассчитывается по формуле:

ХL = w · L,

где w – угловая частота, измеряется в рад/с.

Угловая частота является характеристикой гармоничного колебания. Связана с частотой f (количество полных колебаний в секунду). Частота измеряется в колебаниях в секунду (1/с):

w = 2 · p · f.

Если в схеме используется несколько катушек, то при их последовательном соединении общее ХL для всей системы будет равно:

XL = XL1 + XL2 + …

В случае параллельного соединения:

1/XL = 1/XL1 + 1/XL2 + …

Закон Ома для такого соединения имеет вид:

XL=UL/I,

где UL – падение напряжения.

Помимо индуктивного, устройство обладает и активным R.

Электрический импеданс в этом случае равен:

Z = XL + R.

Емкостной элемент

В проводниках и обмотке катушки, кроме индуктивного и активного сопротивлений, присутствует и емкостное, которое обусловлено наличием ёмкости в этих приборах. Кроме резистора и катушки, в схему может быть включен конденсатор, который состоит из двух металлических пластин, между которыми размещён слой диэлектрика.

К сведению. Электрический ток протекает за счёт того, что в устройстве проходят процессы заряда и разряда пластин.

Схема подключения

При максимальном заряде на пластинах прибора:

U = max, I = 0.

За счёт того, что резистивное устройство может накапливать энергию, его используют в приборах, которые стабилизируют напряжение в цепи.

Возможность накапливать заряд характеризуется ёмкостью.

Реактивное сопротивление конденсатора (ХС) можно рассчитать по формуле:

XC = 1/(w·C), где:

w – угловая частота,
С – ёмкость конденсатора.

Единица измерения ёмкости – Ф (фарада).

Учитывая, что угловая частота связана с циклической частотой, расчет значения реактивного сопротивления конденсатора можно выполнить по формуле:

XC=1/(2·p·f·C).

Если в цепи последовательно соединены несколько устройств, то общее XС системы будет равно:

XС = XС1 + XС2 + …

Если соединение объектов параллельное, то:

1/XC = 1/XC1 + 1/XC2+…

Закон Ома для этого случая записывается следующим образом:

XC = UC/I,

где UС – падение напряжения на конденсаторе.

Расчёт цепи

При последовательном соединении I = const в любой точке и, согласно закону Ома, его можно рассчитать по формуле:

I = U/R,

где Z – электрический импеданс.

Последовательное соединение элементов

Напряжение на устройствах рассчитывается следующим образом:

UR = I · R, UL = I · XL, UC = I · XC.

Вектор индуктивной составляющей напряжения направлен в противоположную сторону от вектора емкостной составляющей, поэтому:

UX = UL – UC,

следовательно, согласно расчётам:

X = XL – XC.

Внимание! Для вычисления значения импеданса можно воспользоваться «треугольником сопротивлений», в котором гипотенузой является значение Z, а катетами – значения X и R.

Треугольник сопротивлений

Если в цепь подключены и конденсатор, и катушка индуктивности, то, согласно теореме Пифагора, гипотенуза (Z) будет равна:

Так как X = XL – XC, то:

При решении электротехнических задач часто импеданс записывают в виде комплексного числа, в котором действительная часть соответствует значению активной составляющей, а мнимая – реактивной. Таким образом, выражение для импеданса в общем виде имеет вид:

Z = R + X·i,

где i – мнимая единица.

Для онлайн расчёта реактивного сопротивления можно использовать программу – калькулятор, которую можно найти в сети Интернет. Подобных сервисов достаточно много, поэтому вам не составит труда подобрать удобный для вас калькулятор.

Онлайн калькулятор для расчёта емкостных и индуктивных характеристик

Благодаря таким Интернет сервисам, можно быстро выполнить нужный расчёт.

Видео

Оцените статью:

Что такое реактивное сопротивление 🚩 активные и реактивные сопротивления кабелей 🚩 Естественные науки

Реактивным сопротивлением называется величина типа сопротивления, которая показывает соотношение тока и напряжения на реактивной (индуктивной, емкостной) нагрузке, не связанное с количеством потребляемой электрической энергии. Реактивное сопротивление характерно лишь для цепей переменного тока. Обозначается величина символом X, а ее единицей измерения является ом.

В отличие от активного сопротивления реактивное может быть как с положительным, так и отрицательным знаком, который соответствует тому знаку, которым сопровождается сдвиг фазы между напряжением и током. Если ток отстает от напряжения, он положителен, а если опережает, то отрицателен.

Реактивное сопротивление может быть двух видов: индуктивного и емкостного. Первый из них характерен для соленоидов, трансформаторов, обмотки электродвигателя или генератора), а второй — для конденсаторов. Для определения соотношения между током и напряжением необходимо знать величину не только реактивного, но и активного сопротивления, оказываемого проводником переменному току, проходящему на нему. Первое из них дает лишь ограниченные физические данные об электрической цепи или электрическом устройстве.

Реактивное сопротивление создается за счет потери реактивной мощности – силы, затрачиваемой на создание магнитного поля в электрической цепи. Уменьшение реактивной мощности, вызывающее реактивное сопротивление, достигается за счет подключения к трансформатору устройства с активным сопротивлением.

Например, конденсатор, подключаемый к цепи переменного тока, успевает накапливать лишь ограниченный заряд перед изменением знака разности потенциалов на противоположный. Таким образом, ток не успевает упасть до нулевой отметки так, как в цепи постоянного тока. При низкой частоте в конденсаторе будет аккумулироваться меньший заряд, отчего конденсатор меньше противодействует внешнему току. Это создает реактивное сопротивление.

Бывают случаи, когда цепь имеет реактивные элементы, однако результирующее реактивное сопротивление в ней равно нулю Нулевая величина реактивного сопротивления подразумевает совпадение тока и напряжения по фазе, но если реактивное сопротивление больше или меньше нуля, между напряжением и током возникает разность фаз. Например, в RLC-цепи резонанс происходит в том случае, если реактивные импедансы ZL и ZC взаимоуничтожаются. При этом импеданс имеет равную нулю фазу.

Реактивное сопротивление — Википедия. Что такое Реактивное сопротивление

Реакти́вное сопротивле́ние (реактанс) — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).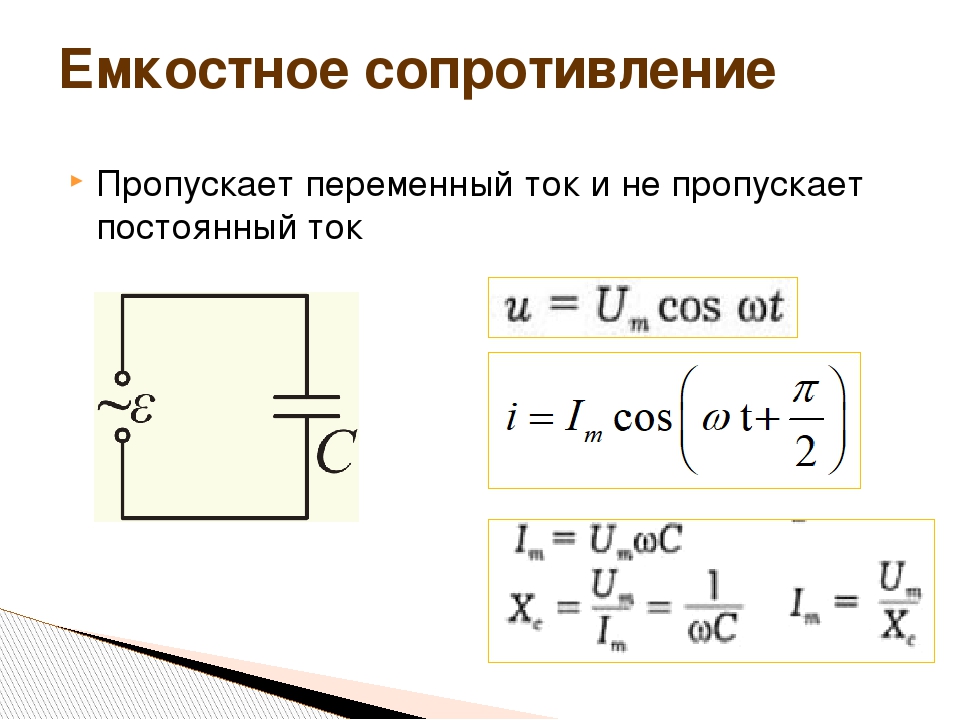

Реактивное сопротивление определяет мнимую часть полного сопротивления (импеданса):

Z=R+jX{\displaystyle Z=R+jX}, где Z{\displaystyle Z} — полное сопротивление или импеданс, R{\displaystyle R} — величина активного сопротивления, X{\displaystyle X} — величина реактивного сопротивления, j{\displaystyle j} — мнимая единица.

В зависимости от знака величины X{\displaystyle X} какого-либо элемента электрической цепи говорят о трёх случаях:

X>0{\displaystyle X>0} — элемент проявляет свойства индуктивности.
X=0{\displaystyle X=0} — элемент имеет чисто активное сопротивление.
X<0{\displaystyle X<0} — элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

X=XL−XC{\displaystyle X=X_{L}-X_{C}}

Индуктивное сопротивление (XL{\displaystyle X_{L}}) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующую изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности L{\displaystyle L} элемента и угловой частоты ω{\displaystyle \omega } протекающего тока:

XL=ωL=2πfL{\displaystyle X_{L}=\omega L=2\pi fL}

Ёмкостное сопротивление (XC{\displaystyle X_{C}}). Величина ёмкостного сопротивления зависит от ёмкости элемента C{\displaystyle C} и также частоты протекающего тока f{\displaystyle f}:

XC=1ωC=12πfC{\displaystyle X_{C}={\frac {1}{\omega C}}={\frac {1}{2\pi fC}}}

Здесь ω{\displaystyle \omega } — циклическая частота, равная 2πf{\displaystyle 2\pi f}.

См. также

Реактивное акустическое сопротивление
Активное сопротивление
Реактивное сопротивление (психология)

Примечания

Это заготовка статьи по физике. Вы можете помочь проекту, дополнив её.

В этой статье не хватает ссылок на источники информации.Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 19 июня 2018 года.

Что такое сопротивление и реактивность?

Сопротивление трансформатора определяется как внутреннее сопротивление первичной и вторичной обмоток. В реальном трансформаторе первичная и вторичная обмотки имеют некоторое сопротивление, представленное R ₁ и R ₂, а реактивные сопротивления — X ₁ и X ₂. Пусть K — коэффициент трансформации.

Чтобы упростить вычисления, сопротивления и реактивные сопротивления могут быть перенесены на любую сторону, что означает, что либо все первичные члены относятся к вторичной стороне, либо все вторичные члены относятся к первичной стороне.

Резистивные и реактивные падения на первичной и вторичной стороне представлены следующим образом:

Падение сопротивления на вторичной стороне = I ₂ R ₂
Реактивное падение на вторичной стороне = I ₂ X ₂
Падение сопротивления на первичной стороне = I ₁ R ₁
Реактивное падение на первичной стороне = I ₁ X ₁

Первичная сторона относительно вторичной

Поскольку коэффициент трансформации равен K, падение сопротивления и реактивности первичной обмотки по отношению к вторичной стороне будет K раз, т.е.е., K I ₁ R ₁ и K I ₁ X ₁ соответственно. Если I ₁ подставить равным KI ₂, тогда у нас будет сопротивление первичной обмотки, а падение реактивной мощности, относящееся к вторичной стороне, равно K ² I ₂ R ₁ и K ² I ₂ X ₁ соответственно.

Суммарное сопротивление трансформатора

Суммарное реактивное падение в трансформаторе

Термины
обозначают эквивалентное сопротивление и реактивное сопротивление трансформатора относительно вторичной обмотки.

Где
Таким образом,

Из векторной диаграммы, показанной выше, уравнение может быть сформировано как
, где V ₂ — вторичное напряжение на клеммах, а I ₂ — вторичный ток, отстающий от напряжения на клеммах V ₂ на угол ϕ.

Поскольку член
очень мал и им пренебрегают по сравнению с термином

Теперь уравнение принимает вид

Где V ₁ — напряжение, приложенное к первичной обмотке

Если нагрузка на вторичной стороне трансформатора является чисто резистивной, тогда ϕ = 0 и уравнение (1) принимает вид
Если нагрузка на вторичной стороне трансформатора является емкостной, то ϕ следует принимать как отрицательное, и уравнение ( 1) становится

Следовательно, это будет напряжение нагрузки.

эффективное реактивное сопротивление — определение — английский

Примеры предложений с «эффективным реактивным сопротивлением», память переводов

патент-wipoAn индуктор (X, 20) (реактор) последовательно соединен с двумя соединенными встречно-встречно тиристорами (24, 26), которые контролировать период проводимости и, следовательно, эффективное реактивное сопротивление катушки индуктивности (21) .patents-wipo Работа инвертора (115) в этом режиме управления напряжением приводит к увеличению потока мощности, когда компенсирующее напряжение подается под углом 180 ° по фазе с напряжение на эффективном реактивном сопротивлении линии передачи.Патенты-wipo Когда компенсирующее напряжение вводится в фазе с напряжением на эффективном реактивном сопротивлении линии передачи, поток мощности сначала уменьшается от нескомпенсированного значения и может быть уменьшен до нуля, когда компенсирующее напряжение равно напряжению на эффективном реактивном сопротивлении линии передачи без Компенсация.

patents-wipo Система переключения МЭД предназначена для эффективного понижения отношения реактивного сопротивления к сопротивлению МЭД во время перегрузки по току, чтобы во время короткого замыкания эффективное отношение реактивного сопротивления к сопротивлению на выходе Система переключения МЭД ниже отношения реактивного сопротивления к сопротивлению предохранителя EPS.Патенты-wipo Каждый конденсатор выбирается таким образом, чтобы иметь реактивное сопротивление, которое эффективно нейтрализует индуктивное реактивное сопротивление части сегмента контура, предшествующего соответствующему последовательному конденсатору. springer Введение в представленный документ предлагает критический обзор наиболее важных публикаций, касающихся эффекта насыщения реактивное сопротивление утечки.patents-wipo Метод включает эффективное снижение отношения реактивного сопротивления к сопротивлению МЭД путем контролируемого изменения рабочего состояния переключающего устройства во время повреждения.Патенты-WIPO Первый тракт обратной связи также содержит конденсатор (7), который компенсирует неблагоприятные эффекты реактивного сопротивления в цепи, вызванные емкостью фотодиода (3) и переменного резистора (8), чтобы оптимизировать частотные характеристики the amp.

springerAnalysis четко указывает на параллельный, косвенный отрицательный эффект, вызванный тем, что участники демонстрируют реактивное сопротивление как следствие повторения. амперы и коэффициент мощности при указанном значении тока или напряжения и частоты.В смесителе также есть компенсационная катушка индуктивности (56), подключенная между первым и вторым узлами (50, 52), для подавления эффекта емкостного реактивного сопротивления на частоте сигнала гетеродина. WikiMatrix: на более высоких частотах реактивное сопротивление падает, и конденсатор эффективно функционирует как короткое замыкание. WikiMatrix Импеданс, вызванный этими двумя эффектами, в совокупности называется реактивным сопротивлением и образует мнимую часть комплексного импеданса, тогда как сопротивление формирует реальную часть. пружина На потери влияют параметры демпфера — в основном его реактивные сопротивления и омические сопротивления.Патенты-wipo С этой целью изменения параметров управления применяются или генерируются с помощью PFC (20) и включают изменения в управляющем входе u, управляющем усилии e (вводимое последовательное напряжение, вставленное последовательное реактивное сопротивление) или управляющий эффект q ( поток энергии, передача активной мощности, фазовый сдвиг, ток) .WikiMatrix Как правило, ближние поля оказывают сильное влияние на собственные источники, вызывая повышенную «нагрузку» (снижение электрического реактивного сопротивления) в источнике или передатчике всякий раз, когда энергия отбирается из электромагнитное поле приемником.Giga-frenImpedance Суммарное противодействие протеканию тока в цепи переменного тока. Импеданс может состоять из сопротивления или сопротивления и реактивного сопротивления. Patents-wipo Одновременно с измерением, по крайней мере, реактивного тока в цепи нагрузки, эффективное напряжение на нагрузке увеличивается за счет увеличения фазового угла полуволны напряжения до тех пор, пока не появится ток достигает заданного порога. пружина Линеаризованная модель, основанная на малых смещениях, используется в анализе устойчивости для исследования влияния изменения параметров машины, таких как сопротивления статора и ротора, реактивные сопротивления утечки и т. д.на участках устойчивости двигателя. patents-wipo Роторная индукционная машина с намотанными первичной (11-13) и вторичной обмотками (17-19) с резистивными средствами (55-57), соединенными последовательно с вторичными обмотками, и индуктивными реактивными средствами (51 -53), подключенного к упомянутым резистивным средствам, причем средства индуктивного реактивного сопротивления (51-53) и резистивные средства (55-57), выбранные для обеспечения эффективного сопротивления, которое регулирует ток во вторичных обмотках генератора, посредством чего достигается номинальный ток генератора. при максимальном скольжении для диапазона желаемой выходной мощности.Патенты-wipo В зависимости от увеличения напряжения катушка реактивного сопротивления (DR) подключается к цепи управления электронных переключателей (S2) схемы инвертора через тиристор (12), который управляется увеличением напряжения и который влияет на ослабляется, если тиристор (12) находится под напряжением, указанное состояние переключения сохраняется до устранения причины отказа. patents-wipo Входное постоянное напряжение передается на первичную обмотку катушки реактивного сопротивления через индуктор (L1) и конденсатор ( C1) расположен параллельно контактному промежутку переключающего транзистора, указанная катушка индуктивности (L1) и указанный конденсатор (C1) создают последовательный резонансный контур, который действует в фазе включения и выключения переключающего транзистора.

Показаны страницы 1. Найдено 23 предложения с фразой эффективное реактивное сопротивление.Найдено за 5 мс.Накопители переводов создаются человеком, но выравниваются с помощью компьютера, что может вызвать ошибки. Найдено за 1 мс.Накопители переводов создаются человеком, но выравниваются с помощью компьютера, что может вызвать ошибки. Они поступают из многих источников и не проверяются. Имейте в виду.

Автоматизация бизнеса с открытым исходным кодом | Activiti

Помощь предприятиям в решении задач автоматизации проблемы в распределенных, масштабируемых и экономичных инфраструктуры.

Учить больше

Последние новости: Выпущен Activiti Cloud 7.1.0.M6!

Activiti — это ведущий облегченный, ориентированный на Java движок BPMN с открытым исходным кодом, поддерживающий реальные потребности в автоматизации процессов. Activiti Cloud теперь представляет собой платформу автоматизации бизнеса нового поколения, предлагающую набор стандартных облачных строительных блоков, предназначенных для работы в распределенных инфраструктурах.

Стандартные блоки для облачных вычислений

Пакет среды выполнения

Неизменяемые, масштабируемые и безболезненные среды выполнения процессов и решений, разработанные для интегрироваться с вашей облачной инфраструктурой.

Аудиторская служба

Масштабируемая, независимая от хранилища и расширяемая служба аудита.

Служба запросов

Масштабируемая, независимая от хранилища и расширяемая служба запросов.

Соединители Cloud

Упрощенная система для системного взаимодействия, которое может масштабироваться в распределенном среды.

Служба приложений

Уровень агрегирования распределенных и масштабируемых приложений.

Служба уведомлений

Облачный безопасный WebSocket и обработка подписки как часть Интеграция с GraphQL.

Сообщество Activiti

Activiti Cloud CI / CD Demo

Ознакомьтесь с нашей демонстрацией CI / CD на основе Kubernetes, включая практические советы по совершенствованию практики DevOps в вашей организации.

Activiti Cloud Обзор и BluePrint

Узнайте об использовании Activiti Cloud в этом видео.Ознакомьтесь с обновлениями дорожной карты, чтобы узнать, чем мы заняты.

Начать с Activiti

Следуйте нашему руководству по быстрому запуску, чтобы запустить приложение Activiti Cloud за 3 простых шага в установку Kubernetes.

Попробуй сейчас .