Что такое активное сопротивление в цепи переменного тока. Как оно влияет на параметры цепи. Какие факторы определяют величину активного сопротивления. Как рассчитать активное сопротивление в цепи переменного тока.
Что представляет собой активное сопротивление в цепи переменного тока
Активное сопротивление в цепи переменного тока — это элемент цепи, в котором происходит необратимое преобразование электрической энергии в другие виды энергии, чаще всего в тепловую. К активным сопротивлениям относятся:
- Резисторы
- Лампы накаливания
- Нагревательные элементы
- Омическое сопротивление проводников
В отличие от реактивных элементов (катушек индуктивности и конденсаторов), активное сопротивление не создает сдвига фаз между током и напряжением в цепи переменного тока.
Основные характеристики активного сопротивления в цепи переменного тока
Активное сопротивление в цепи переменного тока характеризуется следующими ключевыми особенностями:
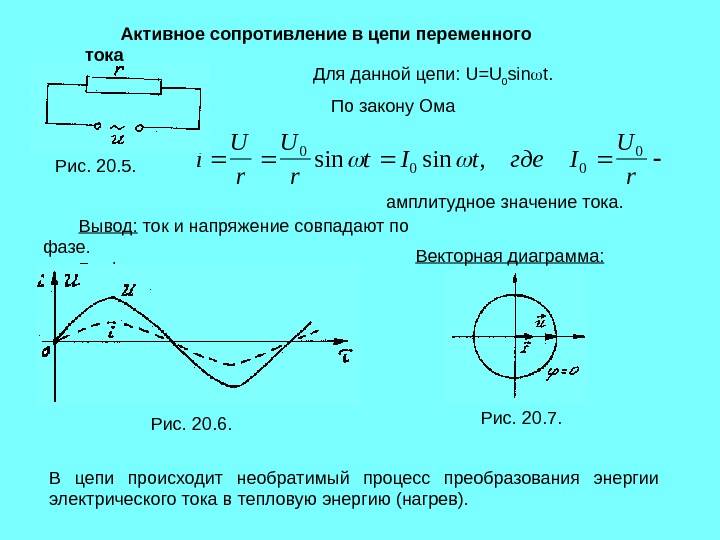
- Ток и напряжение на активном сопротивлении совпадают по фазе
- Мгновенная мощность всегда положительна
- Средняя мощность за период равна произведению действующих значений тока и напряжения
- Закон Ома справедлив для действующих значений тока и напряжения
- Активное сопротивление не зависит от частоты переменного тока
Факторы, влияющие на величину активного сопротивления
На величину активного сопротивления в цепи переменного тока оказывают влияние следующие факторы:
- Материал проводника — удельное сопротивление материала определяет базовое значение сопротивления.
- Геометрические размеры — длина и площадь поперечного сечения проводника.
- Температура — с ростом температуры сопротивление металлов увеличивается.
- Частота тока — на высоких частотах проявляется скин-эффект, приводящий к росту сопротивления.
- Наличие ферромагнитных материалов — вызывают дополнительные потери на гистерезис и вихревые токи.
Расчет активного сопротивления в цепи переменного тока
Для расчета активного сопротивления в цепи переменного тока используются следующие формулы:

- R = ρ * l / S, где ρ — удельное сопротивление, l — длина, S — площадь сечения проводника
- R = U / I, где U и I — действующие значения напряжения и тока
- R = P / I^2, где P — активная мощность, I — действующее значение тока
При высоких частотах необходимо учитывать поверхностный эффект, приводящий к увеличению сопротивления:
R = R_0 * sqrt(f / f_0), где R_0 — сопротивление на постоянном токе, f — частота переменного тока, f_0 — частота, при которой глубина проникновения тока равна радиусу проводника.
Влияние активного сопротивления на параметры цепи переменного тока
Активное сопротивление оказывает следующее влияние на параметры цепи переменного тока:
- Вызывает падение напряжения, пропорциональное протекающему току
- Ограничивает максимальный ток в цепи
- Приводит к выделению тепловой энергии
- Снижает добротность колебательных контуров
- Вызывает затухание колебаний в RLC-цепях
Измерение активного сопротивления в цепях переменного тока
Для измерения активного сопротивления в цепях переменного тока применяются следующие методы:

- Вольтметра-амперметра — измеряются напряжение и ток, сопротивление рассчитывается по закону Ома
- Мостовой — используются мосты переменного тока
- Резонансный — основан на измерении параметров резонансного контура
- Ваттметра — измеряется активная мощность и ток
При измерениях на высоких частотах необходимо учитывать паразитные емкости и индуктивности схемы измерения.
Способы снижения активного сопротивления в цепях переменного тока
Для снижения активного сопротивления в цепях переменного тока применяются следующие способы:
- Использование проводников с низким удельным сопротивлением (медь, серебро)
- Увеличение площади поперечного сечения проводников
- Применение многожильных проводов (литцендрат) для уменьшения скин-эффекта
- Охлаждение проводников для снижения температурной составляющей сопротивления
- Использование сверхпроводящих материалов
Особенности активного сопротивления на высоких частотах
На высоких частотах активное сопротивление проводников имеет ряд особенностей:
- Проявляется скин-эффект, приводящий к вытеснению тока к поверхности проводника
- Возрастают потери на излучение электромагнитной энергии
- Усиливаются диэлектрические потери в изоляции
- Увеличиваются потери на вихревые токи в ферромагнитных материалах
Для учета этих эффектов используются специальные высокочастотные сопротивления и методы расчета цепей.

Активное сопротивление цепи переменного тока
Активным или ваттным сопротивлением называется всякое сопротивление, поглощающее электрическую энергию или вернее превращающее ее в другой вид энергии, например в тепловую, световую или химическую.
Потери энергии, а, следовательно, и активное сопротивление в электрической цепи при переменном токе всегда больше потерь энергии в этой же цепи при постоянном токе. Причина этого заключается в том, что в цепях переменного тока потери энергии обусловлены не только обычным омическим сопротивлением проводников, но и многими другими причинами.
Рассмотрим некоторые из этих.
Так, например, наличие конденсатора в цепи переменного тока связано с дополнительными потерями энергии в результате периодического (с частотой переменного тока) изменения поляризации диэлектрика или, попросту говоря, в результате непрерывного переворачивания взад и вперед молекулярных парных зарядов. При этом происходит нагревание диэлектрика, т. е. электрическая энергия превращается в тепловую. Эти потери энергии называются диэлектрическими потерями.
Кроме диэлектрических потерь, как уже говорилось раньше, происходят потери энергии из-за утечки тока вследствие несовершенства изоляции между пластинами конденсаторов. Эти потери называются потерями утечки.
Вокруг всякого переменного тока существует переменное магнитное поле. Следовательно, во всех окружающих железных предметах происходит непрерывное переворачивание молекулярных магнитиков в такт с частотой переменного тока. В результате железные предметы, находящиеся в поле переменного тока, нагреваются, т. е электрическая энергия превращается в тепловую. Эти потери называются потерями на гистерезис.
Благодаря электромагнитной индукции переменный электрический ток наводит в близлежащих замкнутых электрических цепях индукционные токи, что связано с нагреванием этих цепей, т. е. с дополнительными потерями энергии.
Кроме того, такие же индукционные круговые токи возникают не только в замкнутых электрических цепях, но и в близлежащих металлических предметах и нагревают их. Эти токи называются токами Фуко. Возникновение токов Фуко также сопряжено с потерями электрической энергии.
Токи Фуко не всегда являются вредными. Например, на принципе токов Фуко основана защита радиоприборов медными или алюминиевыми экранами от переменных магнитных полей высокой частоты.
Наконец, при очень высоких частотах цепь переменного тока может излучать электромагнитные волны (радиоволны), что связано с потерями на излучение.
Наличие всех этих потерь увеличивает активное сопротивление цепи переменному току.
Опыт показывает, что при высоких частотах и омическое сопротивление проводника оказывается значительно большим, чем при постоянном токе.
Для объяснения этого явления увеличим мысленно сечение проводника (рис. 1) и посмотрим, что происходит в нем при прохождении по нему переменного тока. Вдоль проводника взад и вперед с частотой переменного тока движется огромное количество электронов.
Рисунок 1. Поверхностный эффект, как фактрор увеличения активного сопротивления в цепи переменного тока. Ток вытесняется магнитным полем на поверхность проводника (а), поэтому у поверхности проводника плотность тока больше, чем внутри проводника (б).
До сих пор нам было известно, что движущийся по проводнику переменный поток электронов создает вокруг него переменное магнитное поле. Теперь же, когда мы заглянем внутрь проводника, мы увидим, что магнитное поле имеется и внутри проводника. Это вызвано тем, что каждый электрон при движении создает вокруг себя магнитное поле, а так как часть электронов движется вблизи оси проводника, то они создают магнитное поле не только во вне, но и внутри проводника.
Продолжая присматриваться к происходящему внутри проводника, мы заметим, что наиболее быстро движутся электроны, находящиеся у поверхности проводника, а по мере приближения к середине проводника амплитуда (размах) колебаний электронов становится все меньше и меньше.
Почему же электроны колеблются с различными амплитудами в разных точках сечения проводника?
Это явление также имеет свое объяснение. Вспомним, что при всяком изменении скорости движения электрона на него действует ЭДС самоиндукции, противодействующая этому изменению. Вспомним также, что ЭДС самоиндукции зависит от числа магнитных силовых линий вокруг движущегося электрона. Чем большим числом магнитных силовых линий охватывается электрон, тем труднее ему совершать колебательное движение.
Теперь становится ясным, почему электроны, находящиеся у поверхности проводника, колеблются с большой амплитудой, а электроны, находящиеся глубоко внутри проводника, — с малой. Ведь первые охватываются только теми магнитными силовыми линиями, которые расположены вне проводника, а вторые охватываются и внешними и внутренними магнитными силовыми линиями.
Таким образом, плотность переменного тока получается большей у поверхности проводника и меньшей внутри его.
На рис. 1,б плотность тока характеризуется количеством красных точек. Как видим, наибольшая плотность тока получается около самой поверхности проводника.
При очень высоких частотах противодействие ЭДС самоиндукции внутри проводника становится настолько сильным, что все электроны движутся только по поверхности проводника. Это явление и называется поверхностным эффектом. Так как активное сопротивление проводника зависит от его сечения, а полезным сечением при токе высокой частоты оказывается только тонкий наружный слой проводника, то вполне понятно, что его активное сопротивление увеличивается с повышением частоты переменного тока.
Для уменьшения поверхностного эффекта проводники, по которым протекают токи высокой частоты, делают трубчатыми и покрывают их слоем хорошо проводящего металла, например серебра.
В целях борьбы с явлением поверхностного эффекта применяют также провода специальной конструкции, так называемый литцендрат.
Такой проводник свивают из отдельных тонких медных жилок, имеющих эмалевую изоляцию, причем скрутка жилок производится таким образом, чтобы каждая из них проходила поочередно то внутри проводника, то снаружи его.
Явление поверхностного эффекта особенно сильно сказывается в железных проводах, в которых вследствие большой магнитной проницаемости железа внутренний магнитный поток оказывается особенно большим и поэтому явление поверхностного эффекта становится очень заметным даже при сравнительно низких (звуковых) частотах.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Переменный ток получил весьма широкое применение в связи с тем, что он имеет ряд преимуществ перед постоянным током, основным из которых является возможность преобразования—трансформации напряжения.
Строго говоря, всякий ток, изменяющийся с течением времени по величине и по направлению, является переменным. Однако под термином переменный ток принято понимать такой ток, величина и направление которого изменяются периодически.
Источником переменного тока служат генераторы, принцип действия которых основан на использовании явления электромагнитной индукции при движении проводников в магнитном поле (см. «Радио» № 6, 1962 г.). Источником переменного тока высоких радиочастот служат ламповые, транзисторные, параметрические и другие генераторы. Простейшим способом получить переменный ток можно, вращая проводник, согнутый в виде рамки, между полюсами магнита (рис. 1). При вращении рамки ее участки а—б и в—г пересекают линии магнитного поля и в них индуктируется ЭДС, величина которой зависит от интенсивности магнитного поля, пересекаемого проводником, и от скорости движения проводника. Направление ЭДС можно определить, пользуясь правилом правой руки.
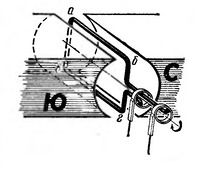
На рис. 2 показаны несколько характерных положений рамки в магнитном поле и график ЭДС. Как видно из рис. 2,б, ЭДС изменяется периодически по гармоническому закону.
Период и частота. Весь этот цикл изменений соответствует одному периоду Т. Число таких изменений, происходящих в течение одной секунды, называется частотой и обозначается буквой f. Между продолжительностью одного периода Т, измеряемого в секундах, и частотой существует следующее соотношение:
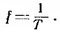 Частота определяется количеством циклов переменной ЭДС или тока, происходящих в одну секунду, и выражается в герцах (Гц) или его производных — килогерцах, мегагерцах, гигагерцах.
Частота определяется количеством циклов переменной ЭДС или тока, происходящих в одну секунду, и выражается в герцах (Гц) или его производных — килогерцах, мегагерцах, гигагерцах.Частота переменного тока в нашей осветительной сети составляет 50 Гц.
Если считать магнитное поле, в котором вращается рамка, однородным, то магнитный поток Ф через рамку можно определить, как произведение напряженности магнитного поля Н на площадь рамки S и на синус угла φ между плоскостью витка и направлением поля:
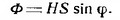 Если рамка вращается равномерно и совершает полный оборот за время Т, то за одну секунду она повернется на угол 2π/Т радиан (угол в радианах измеряется по длине дуги; угол в радианах равен числу 0,0175, умноженному на значение угла в градусах; таким образом 1 радиан=57,3°).
Если рамка вращается равномерно и совершает полный оборот за время Т, то за одну секунду она повернется на угол 2π/Т радиан (угол в радианах измеряется по длине дуги; угол в радианах равен числу 0,0175, умноженному на значение угла в градусах; таким образом 1 радиан=57,3°).Если отсчитывать время от момента, когда рамка расположена параллельно линиям поля, то значение угла в некоторый момент времени t будет равно φ = 2π/Т. Частота вращения рамки, то есть число ее оборотов в секунду f=1/Т, а угловая скорость ω=2πf=2π/T, следовательно φ=ωt. Закон изменения магнитного потока с течением времени можно выразить иначе, как
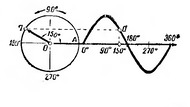
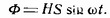 График ЭДС для равномерно вращающейся рамки имеет вид синусоиды.
График ЭДС для равномерно вращающейся рамки имеет вид синусоиды.Наряду с изображением переменного тока (или ЭДС) в виде синусоиды широко применяется также векторное изображение (рис. 3). Величину, имеющую определенное значение и направление, можно представить в виде отрезка прямой линии со стрелкой на конце. Стрелка указывает направление вектора, а проекция отрезка, измеренного в определенном масштабе, дает величину тока (ЭДС). Все фазы изменения переменного синусоидального тока за один период можно изобразить при помощи векторов. Угол поворота вектора определяет его фазу, которой соответствует определенное мгновенное значение силы тока. О положении вектора в данный момент можно судить по угловой скорости его вращения и по времени, которое прошло от начала вращения, то есть начала периода.
Мгновенным значением ЭДС и тока называются значения этих величин для любого момента времени и обозначаются строчными буквами е, i. Мгновенные величины синусоидальных ЭДС и токов изменяются со временем по следующему закону:
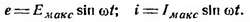 Амплитудным значением или амплитудой переменного тока или ЭДС называется максимальное значение, которое достигает ток или ЭДС два раза за один оборот рамки.
Амплитудным значением или амплитудой переменного тока или ЭДС называется максимальное значение, которое достигает ток или ЭДС два раза за один оборот рамки.Действующее значение или эффективное значение переменного тока определяют по тепловому эффекту. Действующим значением переменного тока I называют величину, равную значению постоянного тока, который, проходя по проводнику, в течение некоторого времени выделяет такое же количество тепла, какое выделяет данный переменный ток за это же время. Действующее значение меньше амплитудного значения, и связано с ним следующими соотношениями:
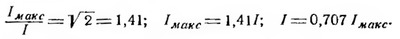 Среднее значение переменного тока есть некоторое значение постоянного тока, равноценного данному переменному току по количеству электричества, протекающего через поперечное сечение провода. Для нахождения среднего значения тока надо построить прямоугольник равновеликой площади, очерченной синусоидой.
Среднее значение переменного тока есть некоторое значение постоянного тока, равноценного данному переменному току по количеству электричества, протекающего через поперечное сечение провода. Для нахождения среднего значения тока надо построить прямоугольник равновеликой площади, очерченной синусоидой.Среднее значение тока или напряжения можно вычислить, исходя из амплитудного или действующего значения тока. Для одного полупериода синусоидального переменного тока:
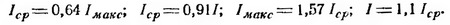 Соотношения для напряжений имеют такой же вид.
Соотношения для напряжений имеют такой же вид.АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Сопротивление, потребляющее мощность, называется активным, а сопротивления, которые не потребляют мощность,— реактивными.
Активное сопротивление переменному току кроме сопротивления,зависящего от материала проводника, может быть обусловлено потерями энергии в диэлектрике (изоляции проводника), потерями в магнитных материалах, потерями на вихревые токи и пр. Особенно сильно могут сказываться эти потери на высоких частотах.
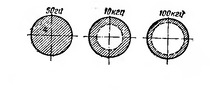 В цепи переменного тока высокой частоты ток по сечению провода распределяется неравномерно и идет главным образом по тонкому поверхностному слою провода, не проникая в его середину (рис. 4). Поэтому активное сопротивление проводника в цепи переменного тока несколько больше сопротивления этого же проводника при постоянном токе. Объясняется это возникновением индукционных токов (токов Фуко), что вызывает поверхностный (скин) эффект. Если переменный ток течет по цилиндрическому проводнику, то в момент увеличения тока индуктируемые токи будут направлены у поверхности проводника в направлении основного тока, а у оси проводника — навстречу току. В результате внутри проводника ток уменьшится, а у поверхности увеличится. Таким образом, вследствие возникновения индукционных токов плотность тока по сечению проводника будет распределяться неравномерно. При большой частоте тока поверхностный эффект сказывается сильнее и плотность тока вблизи оси проводника практически оказывается равной нулю. Происходит как бы «вытеснение» высокочастотных токов к поверхности проводника. В связи с тем, что внутренние части проводника для переменных токов высокой частоты оказываются бесполезными, в целях экономии цветного металла их делают полыми или биметаллическими. Так, например, часто провода для воздушных телефонных линий изготовляют из стали, нанося на нее поверхностный слой из меди.
В цепи переменного тока высокой частоты ток по сечению провода распределяется неравномерно и идет главным образом по тонкому поверхностному слою провода, не проникая в его середину (рис. 4). Поэтому активное сопротивление проводника в цепи переменного тока несколько больше сопротивления этого же проводника при постоянном токе. Объясняется это возникновением индукционных токов (токов Фуко), что вызывает поверхностный (скин) эффект. Если переменный ток течет по цилиндрическому проводнику, то в момент увеличения тока индуктируемые токи будут направлены у поверхности проводника в направлении основного тока, а у оси проводника — навстречу току. В результате внутри проводника ток уменьшится, а у поверхности увеличится. Таким образом, вследствие возникновения индукционных токов плотность тока по сечению проводника будет распределяться неравномерно. При большой частоте тока поверхностный эффект сказывается сильнее и плотность тока вблизи оси проводника практически оказывается равной нулю. Происходит как бы «вытеснение» высокочастотных токов к поверхности проводника. В связи с тем, что внутренние части проводника для переменных токов высокой частоты оказываются бесполезными, в целях экономии цветного металла их делают полыми или биметаллическими. Так, например, часто провода для воздушных телефонных линий изготовляют из стали, нанося на нее поверхностный слой из меди.Чем выше частота тока, больше диаметр провода, больше магнитная проницаемость и меньше удельное сопротивление материала проводника, тем сильнее поверхностный эффект и тем на меньшую глубину проникают токи в провод.
Глубину проникновения высокочастотного тока в проводник можно приближенно подсчитать по формуле:
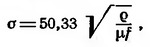
где σ — удельное сопротивление материала, ом мм;
μ — относительная магнитная проницаемость материала,
f — частота, Гц.
Для прямого медного провода круглого сечения формула имеет еще более простой вид:
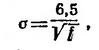
где f — частота, Гц.
Сопротивление медного провода при высоких частотах на один сантиметр длины провода можно приближенно подсчитать по формуле:
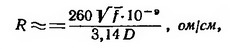
где f — частота, Гц, D — диаметр проводника, см.
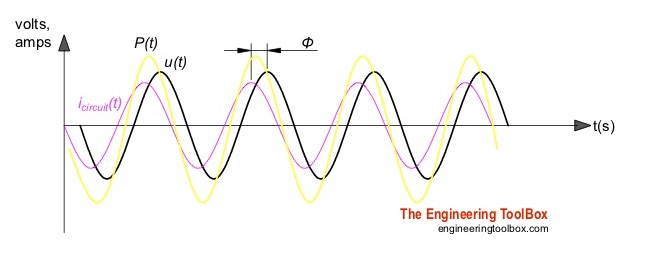
Если подключить активное сопротивление к источнику переменного синусоидального напряжения (рис. 5), то для коротких моментов времени ток можно считать постоянным и определять его величину по формуле закона Ома. Построив график тока (по точкам 1,2, 3, 4, 5, 6, 7, 8) в цепи переменного тока с активным сопротивлением можно убедиться в том, что амплитудные и нулевые значения напряжения и тока совпадают по времени и по направлению (рис. 6). Такое совпадение двух периодически изменяющихся величин называется совпадением по фазе.
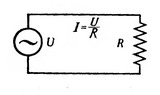
Закон Ома для цепи переменного тока с активным сопротивлением справедлив не только для мгновенных значений, но также и для действующих и амплитудных значений тока и напряжения.
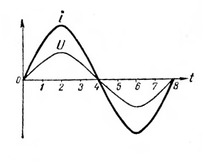 Общее сопротивление нескольких активных сопротивлений в цепи переменного тока подсчитывается так же, как и для цепей постоянного тока.
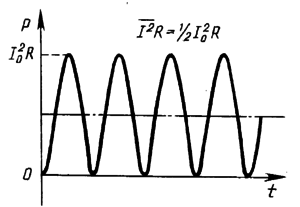
Общее сопротивление нескольких активных сопротивлений в цепи переменного тока подсчитывается так же, как и для цепей постоянного тока.Мгновенное значение мощности, затрачиваемой в цепи переменного тока с активным сопротивлением, периодически меняется, так как она равна произведению соответствующих значений токов и напряжений. Для получения средней мощности за период необходимо суммировать мгновенные значения мощности. Средняя мощность за период равна произведению действующих значений тока и напряжения.
Эта мощность называется также активной мощностью и характеризует ту работу, которую совершает переменный ток. Измеряется активная мощность в ваттах (Вт).
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ ИСТОРИИ И ГОСУДАРСТВЕННОГО УПРАВЛЕНИЯ
Кафедра общей физики
КОНТРОЛЬНАЯ РАБОТА
вариант №13
по дисциплине: Электроника и электротехника
тема:Активное сопротивление в цепи переменного тока
Выполнил:
Студент 3 курса заочной
формы обучения
Направление подготовки/специальность ТБ 31-16«Техносферная безопасность»
__________/ И.Х. Мухамадьянов
Преподаватель: Доцент кафедры
_______________ АльмухаметовР.Ф.
УФА 2018
Содержание
1.Введение……………………………………………………………..3
2.Активное сопротивление в цепи переменного тока………………5
3.Список использованной литературы………………………………16
2
Введение
Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.
Электронная теория так объясняет сущность электрического сопротивления металлических проводников. Свободные электроны при движении по проводнику бесчисленное количество раз встречают на своем пути атомы и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Электроны испытывают как бы сопротивление своему движению. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Точно тем же объясняется сопротивление жидких проводников и газов прохождению электрического тока. Однако не следует забывать, что в этих веществах не электроны, а заряженные частицы молекул встречают сопротивление при своем движении.
Сопротивление обозначается латинскими буквами R или r.
За единицу электрического сопротивления принят ом.
Ом есть сопротивление столба ртути высотой 106,3 см с поперечным сечением 1 мм2 при температуре 0° С.
Если, например, электрическое сопротивление проводника составляет 4 ом, то записывается это так: R = 4 ом или r = 4ом.
Для измерения сопротивлений большой величины принята единица, называемая мегомом. Один мегом равен одному миллиону ом.
Чем больше сопротивление проводника, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем легче электрическому току пройти через этот проводник.
Следовательно, для характеристики проводника (с точки зрения прохождения через него электрического тока) можно рассматривать не
3
только его сопротивление, но и величину, обратную сопротивлению и называемую, проводимостью.
Электрической проводимостью называется способность материала пропускать через себя электрический ток.
Так как проводимость есть величина, обратная сопротивлению, то и выражается она как 1/R,обозначается проводимость латинской буквой g.
Сопротивление различных проводников зависит от материала, из которого они изготовлены. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Удельное сопротивление обозначается буквой греческого алфавитар. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 0,017, т. е. медный проводник длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,017 ом. Удельное сопротивление алюминия равно 0,03, удельное сопротивление железа — 0,12, удельное сопротивление константана — 0,48, удельное сопротивление нихрома — 1-1,1.
Сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление.
Сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.
4
Активное сопротивление в цепи переменного тока
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
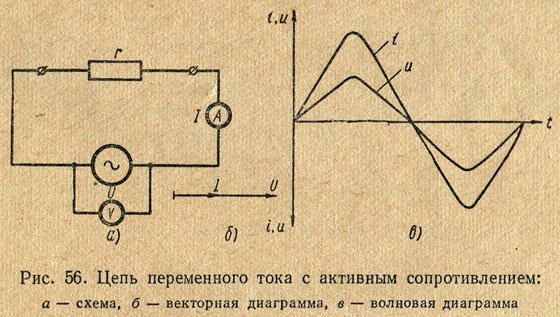
Рассмотрим цепь переменного тока (рис. 56), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
5
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отложим в выбранном масштабе по горизонтали вектор напряжения . Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (φ = 0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
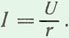
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
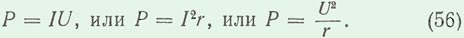
Пример. К цепи переменного тока с активным сопротивлением r = 55 ом подключен генератор, максимальное значение напряжения которого
Um = 310,2 в.
Определить:
1) показание вольтметра, подключенного к зажимам генератора;
2) показание амперметра, включенного в цепь;
3) среднее значение мощности, потребляемой сопротивлением.
Решение. Известно, что электроизмерительные приборы, включенные в цепь переменного тока, измеряют действующие значения. Поэтому показание вольтметра, измеряющего напряжение,
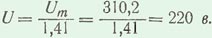
6
Показание амперметра, измеряющего действующее значение тока,
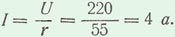
Среднее значение активной мощности, потребляемой сопротивлением, Р = I U = 220 · 4 = 880 вт или Р = I2 r = 42 · 55 = 16 · 55 = 880 вт.
7
Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как
u = Um sin ωt, то изменение тока i также идет по синусоиде:
i = Im sin ωt
ПриэтомIm = Um/R
Так что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.
8
Если взять равенство Im = Um / R и каждую из его частей разделить на √2, то в итоге получится ни что иное, как закон Ома, применимый для той цепи, которая рассматривается: I = U/R.
Таким образом, получается, что это основополагающий закон для той цепи, которая имеет в своем составе только активное сопротивление, с точки зрения математики имеет такую же форму, что и для цепи тока постоянного. 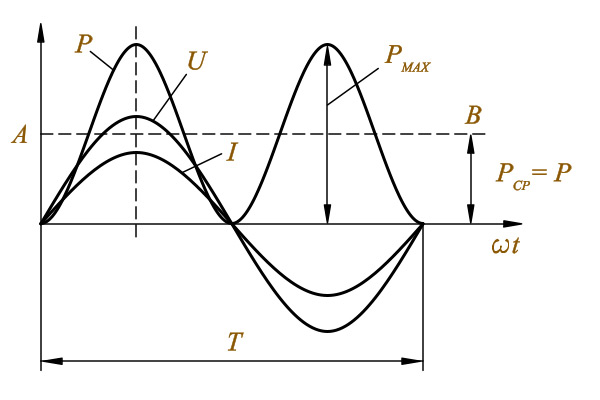
Электрическая мощность
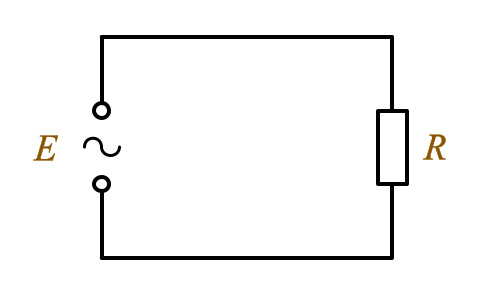
Такой показатель, как электрическая мощность P для цепи, имеющей в своем составе активное сопротивление, равняется произведению мгновенного значения напряжения U на мгновенное значение силы тока i в любой момент времени. Из этого следует, что в цепях переменного тока, в отличие от цепей тока постоянного, мгновенная мощность P – величина непостоянная, а ее изменение происходит по кривой. Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения U и силы тока i перемножить при разных углах ωt. Мощность изменяется по отношению к изменению тока с двойной частотой ωt.
9
Это означает, что половине периода изменения напряжения и тока соответствует один период изменения мощности. Следует заметить, что абсолютно все значения, которые может принимать мощность, являются положительными величинами. С точки зрения физики это означает, что от источника к приемнику передается энергия. Своих максимальных значений мощность достигает тогда, когда ωt = 270° и ωt = 90°.
В практическом отношении о той энергии W, которую создает электрический ток, принято судить по средней мощности, выражаемой формулой Рср = Р, а не по мощности максимальной. Ее можно определить, перемножив на время протекания тока среднее значение мощности W = Pt.
Относительно линии АБ, соответствующей среднему значению мощности P, кривая мгновенной мощности симметрична. По этой причине
P = Pmax / 2 = UI
Если использовать закон Ома, то можно выразить активную мощность в следующем виде:
P = I2R или P = U2/R.
Специалисты в области электротехники ту среднюю мощность, которую потребляет активное сопротивление, чаще всего именуют или просто мощностью, или активной мощностью, а для ее обозначения используется буква P.
10
Поверхностный эффект
Необходимо особо отметить такую особенность проводников, включенных в сеть переменного тока: их активное сопротивление во всех случаях оказывается больше, чем если бы они были включены в сеть тока постоянного. Причина этого состоит в том, что переменный ток не протекает равномерно распределяясь по всему поперечному сечению проводника, как ведёт себя постоянный ток, а выводится на его поверхность. Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.
То, что переменный ток распределяется по сечению проводника неравномерно, объясняется действием электродвижущей силы самоиндукции. Она индуцируется в проводнике тем магнитным полем, которое создается током, проходящим по нему. Необходимо заметить, что действие этого магнитного поля распространяется не только на окружающее проводник пространство, но и на внутреннюю его часть. По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности. Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.
Электродвижущая сила самоиндукции является существенным препятствием для изменения тока, и поэтому он будет следовать преимущественно по поверхностным слоям проводника. Необходимо также отметить, что сопротивление активных проводников в цепях переменного тока существенно зависит от частоты: чем она больше, тем выше ЭДС самоиндукции, и поэтому ток в большей степени подвергается вытеснению на поверхность.
11
Активным или ваттным сопротивлением называется всякое сопротивление, поглощающее электрическую энергию или вернее превращающее ее в другой вид энергии, например в тепловую, световую или химическую.
Потери энергии, а, следовательно, и активное сопротивление в электрической цепи при переменном токе всегда больше потерь энергии в этой же цепи при постоянном токе. Причина этого заключается в том, что в цепях переменного тока потери энергии обусловлены не только обычным омическим сопротивлением проводников, но и многими другими причинами.
Рассмотрим некоторые из этих.
Так, например, наличие конденсатора в цепи переменного тока связано с дополнительными потерями энергии в результате периодического (с частотой переменного тока) изменения поляризации диэлектрика или, попросту говоря, в результате непрерывного переворачивания взад и вперед молекулярных парных зарядов. При этом происходит нагревание диэлектрика, т. е. электрическая энергия превращается в тепловую. Эти потери энергии называются диэлектрическими потерями.
Кроме диэлектрических потерь, как уже говорилось раньше, происходят потери энергии из-за утечки тока вследствие несовершенства изоляции между пластинами конденсаторов. Эти потери называются потерями утечки.
Вокруг всякого переменного тока существует переменное магнитное поле. Следовательно, во всех окружающих железных предметах происходит непрерывное переворачивание молекулярных магнитиков в такт с частотой переменного тока. В результате железные предметы, находящиеся в поле переменного тока, нагреваются, т. е электрическая энергия превращается в тепловую. Эти потери называются потерями на гистерезис.
Благодаря электромагнитной индукции переменный электрический ток наводит в близлежащих замкнутых электрических цепях индукционные токи, что связано с нагреванием этих цепей, т. е. с дополнительными потерями энергии.
12
Кроме того, такие же индукционные круговые токи возникают не только в замкнутых электрических цепях, но и в близлежащих металлических предметах и нагревают их. Эти токи называются токами Фуко. Возникновение токов Фуко также сопряжено с потерями электрической энергии.
Токи Фуко не всегда являются вредными. Например, на принципе токов Фуко основана защита радиоприборов медными или алюминиевыми экранами от переменных магнитных полей высокой частоты.
Наконец, при очень высоких частотах цепь переменного тока может излучать электромагнитные волны (радиоволны), что связано с потерями на излучение.
Наличие всех этих потерь увеличивает активное сопротивление цепи переменному току.
Опыт показывает, что при высоких частотах и омическое сопротивление проводника оказывается значительно большим, чем при постоянном токе.
Для объяснения этого явления увеличим мысленно сечение проводника (и посмотрим, что происходит в нем при прохождении по нему переменного тока. Вдоль проводника взад и вперед с частотой переменного тока движется огромное количество электронов.
Активное сопротивление цепи переменного тока
Поверхностный эффект, как фактор увеличения активного сопротивления в цепи переменного тока. Ток вытесняется магнитным полем на поверхность проводника (а), поэтому у поверхности проводника плотность тока больше, чем внутри проводника (б).
До сих пор нам было известно, что движущийся по проводнику переменный поток электронов создает вокруг него переменное магнитное поле. Теперь же, когда мы заглянем внутрь проводника, мы увидим, что магнитное поле имеется и внутри проводника. Это вызвано тем, что каждый
13
1электрон при движении создает вокруг себя магнитное поле, а так как часть электронов движется вблизи оси проводника, то они создают магнитное поле не только во вне, но и внутри проводника.
Продолжая присматриваться к происходящему внутри проводника, мы заметим, что наиболее быстро движутся электроны, находящиеся у поверхности проводника, а по мере приближения к середине проводника амплитуда (размах) колебаний электронов становится все меньше и меньше.
Почему же электроны колеблются с различными амплитудами в разных точках сечения проводника?
Это явление также имеет свое объяснение. Вспомним, что при всяком изменении скорости движения электрона на него действует ЭДС самоиндукции, противодействующая этому изменению. Вспомним также, что ЭДС самоиндукции зависит от числа магнитных силовых линий вокруг движущегося электрона. Чем большим числом магнитных силовых линий охватывается электрон, тем труднее ему совершать колебательное движение.
Теперь становится ясным, почему электроны, находящиеся у поверхности проводника, колеблются с большой амплитудой, а электроны, находящиеся глубоко внутри проводника, — с малой. Ведь первые охватываются только теми магнитными силовыми линиями, которые расположены вне проводника, а вторые охватываются и внешними и внутренними магнитными силовыми линиями.
Таким образом, плотность переменного тока получается большей у поверхности проводника и меньшей внутри его.
При очень высоких частотах противодействие ЭДС самоиндукции внутри проводника становится настолько сильным, что все электроны движутся только по поверхности проводника. Это явление и называется поверхностным эффектом. Так как активное сопротивление проводника зависит от его сечения, а полезным сечением при токе высокой частоты оказывается только тонкий наружный слой проводника, то вполне понятно, что его активное сопротивление увеличивается с повышением частоты
14
переменного тока.
Для уменьшения поверхностного эффекта проводники, по которым протекают токи высокой частоты, делают трубчатыми и покрывают их слоем хорошо проводящего металла, например серебра.
В целях борьбы с явлением поверхностного эффекта применяют также провода специальной конструкции, так называемый литцендрат.
литцендрат
Такой проводник свивают из отдельных тонких медных жилок, имеющих эмалевую изоляцию, причем скрутка жилок производится таким образом, чтобы каждая из них проходила поочередно то внутри проводника, то снаружи его.
Явление поверхностного эффекта особенно сильно сказывается в железных проводах, в которых вследствие большой магнитной проницаемости железа внутренний магнитный поток оказывается особенно большим и поэтому явление поверхностного эффекта становится очень заметным даже при сравнительно низких (звуковых) частотах.
15
КОНТРОЛЬНАЯ РАБОТА
вариант №13
по дисциплине: Электроника и электротехника
тема: Активное сопротивление в цепи переменного тока
Выполнил:
Студент 3 курса заочной
формы обучения
Направление подготовки/специальность ТБ 31-16 «Техносферная безопасность»
__________/ И.Х. Мухамадьянов
Преподаватель: Доцент кафедры
_______________ Альмухаметов Р.Ф.
УФА 2018
Содержание
1. Введение……………………………………………………………..3
2. Активное сопротивление в цепи переменного тока………………5
3. Список использованной литературы………………………………16
2
Введение
Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.
Электронная теория так объясняет сущность электрического сопротивления металлических проводников. Свободные электроны при движении по проводнику бесчисленное количество раз встречают на своем пути атомы и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Электроны испытывают как бы сопротивление своему движению. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Точно тем же объясняется сопротивление жидких проводников и газов прохождению электрического тока. Однако не следует забывать, что в этих веществах не электроны, а заряженные частицы молекул встречают сопротивление при своем движении.
Сопротивление обозначается латинскими буквами R или r.
За единицу электрического сопротивления принят ом.
Ом есть сопротивление столба ртути высотой 106,3 см с поперечным сечением 1 мм2 при температуре 0° С.
Если, например, электрическое сопротивление проводника составляет 4 ом, то записывается это так: R = 4 ом или r = 4ом.
Для измерения сопротивлений большой величины принята единица, называемая мегомом. Один мегом равен одному миллиону ом.
Чем больше сопротивление проводника, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем легче электрическому току пройти через этот проводник.
Следовательно, для характеристики проводника (с точки зрения прохождения через него электрического тока) можно рассматривать не
3
только его сопротивление, но и величину, обратную сопротивлению и называемую, проводимостью.
Электрической проводимостью называется способность материала пропускать через себя электрический ток.
Так как проводимость есть величина, обратная сопротивлению, то и выражается она как 1/R, обозначается проводимость латинской буквой g.
Сопротивление различных проводников зависит от материала, из которого они изготовлены. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Удельное сопротивление обозначается буквой греческого алфавитар. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 0,017, т. е. медный проводник длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,017 ом. Удельное сопротивление алюминия равно 0,03, удельное сопротивление железа — 0,12, удельное сопротивление константана — 0,48, удельное сопротивление нихрома — 1-1,1.
Сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление.
Сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.
4
Активное сопротивление в цепи переменного тока
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
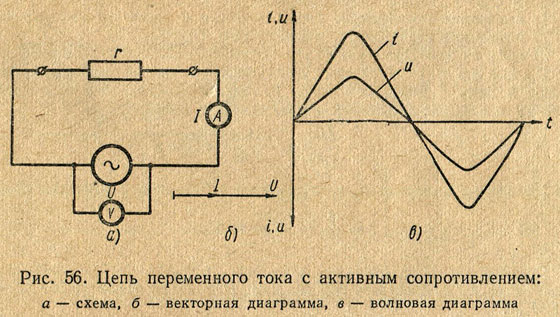
Рассмотрим цепь переменного тока (рис. 56), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
5
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отложим в выбранном масштабе по горизонтали вектор напряжения . Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (φ = 0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
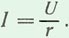
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
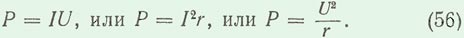
Пример. К цепи переменного тока с активным сопротивлением r = 55 ом подключен генератор, максимальное значение напряжения которого
Um = 310,2 в.
Определить:
1) показание вольтметра, подключенного к зажимам генератора;
2) показание амперметра, включенного в цепь;
3) среднее значение мощности, потребляемой сопротивлением.
Решение. Известно, что электроизмерительные приборы, включенные в цепь переменного тока, измеряют действующие значения. Поэтому показание вольтметра, измеряющего напряжение,
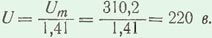
6
Показание амперметра, измеряющего действующее значение тока,
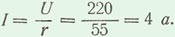
Среднее значение активной мощности, потребляемой сопротивлением, Р = I U = 220 · 4 = 880 вт или Р = I2 r = 42 · 55 = 16 · 55 = 880 вт.
7
Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как
u = Um sin ωt, то изменение тока i также идет по синусоиде:
i = Im sin ωt
При этом Im = Um/R
Так что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.
8
Если взять равенство Im = Um / R и каждую из его частей разделить на √2, то в итоге получится ни что иное, как закон Ома, применимый для той цепи, которая рассматривается: I = U/R.
Таким образом, получается, что это основополагающий закон для той цепи, которая имеет в своем составе только активное сопротивление, с точки зрения математики имеет такую же форму, что и для цепи тока постоянного. 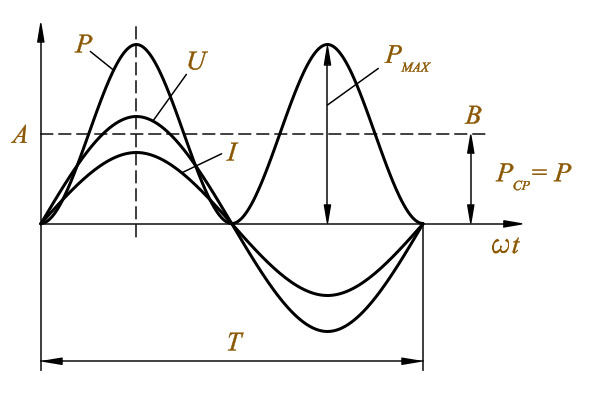
Электрическая мощность
Такой показатель, как электрическая мощность P для цепи, имеющей в своем составе активное сопротивление, равняется произведению мгновенного значения напряжения U на мгновенное значение силы тока i в любой момент времени. Из этого следует, что в цепях переменного тока, в отличие от цепей тока постоянного, мгновенная мощность P – величина непостоянная, а ее изменение происходит по кривой. Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения U и силы тока i перемножить при разных углах ωt. Мощность изменяется по отношению к изменению тока с двойной частотой ωt.
9
Это означает, что половине периода изменения напряжения и тока соответствует один период изменения мощности. Следует заметить, что абсолютно все значения, которые может принимать мощность, являются положительными величинами. С точки зрения физики это означает, что от источника к приемнику передается энергия. Своих максимальных значений мощность достигает тогда, когда ωt = 270° и ωt = 90°.
В практическом отношении о той энергии W, которую создает электрический ток, принято судить по средней мощности, выражаемой формулой Рср = Р, а не по мощности максимальной. Ее можно определить, перемножив на время протекания тока среднее значение мощности W = Pt.
Относительно линии АБ, соответствующей среднему значению мощности P, кривая мгновенной мощности симметрична. По этой причине
P = Pmax / 2 = UI
Если использовать закон Ома, то можно выразить активную мощность в следующем виде:
P = I2R или P = U2/R.
Специалисты в области электротехники ту среднюю мощность, которую потребляет активное сопротивление, чаще всего именуют или просто мощностью, или активной мощностью, а для ее обозначения используется буква P.
10
Поверхностный эффект
Необходимо особо отметить такую особенность проводников, включенных в сеть переменного тока: их активное сопротивление во всех случаях оказывается больше, чем если бы они были включены в сеть тока постоянного. Причина этого состоит в том, что переменный ток не протекает равномерно распределяясь по всему поперечному сечению проводника, как ведёт себя постоянный ток, а выводится на его поверхность. Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.
То, что переменный ток распределяется по сечению проводника неравномерно, объясняется действием электродвижущей силы самоиндукции. Она индуцируется в проводнике тем магнитным полем, которое создается током, проходящим по нему. Необходимо заметить, что действие этого магнитного поля распространяется не только на окружающее проводник пространство, но и на внутреннюю его часть. По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности. Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.
Электродвижущая сила самоиндукции является существенным препятствием для изменения тока, и поэтому он будет следовать преимущественно по поверхностным слоям проводника. Необходимо также отметить, что сопротивление активных проводников в цепях переменного тока существенно зависит от частоты: чем она больше, тем выше ЭДС самоиндукции, и поэтому ток в большей степени подвергается вытеснению на поверхность.
11
Активным или ваттным сопротивлением называется всякое сопротивление, поглощающее электрическую энергию или вернее превращающее ее в другой вид энергии, например в тепловую, световую или химическую.
Потери энергии, а, следовательно, и активное сопротивление в электрической цепи при переменном токе всегда больше потерь энергии в этой же цепи при постоянном токе. Причина этого заключается в том, что в цепях переменного тока потери энергии обусловлены не только обычным омическим сопротивлением проводников, но и многими другими причинами.
Рассмотрим некоторые из этих.
Так, например, наличие конденсатора в цепи переменного тока связано с дополнительными потерями энергии в результате периодического (с частотой переменного тока) изменения поляризации диэлектрика или, попросту говоря, в результате непрерывного переворачивания взад и вперед молекулярных парных зарядов. При этом происходит нагревание диэлектрика, т. е. электрическая энергия превращается в тепловую. Эти потери энергии называются диэлектрическими потерями.
Кроме диэлектрических потерь, как уже говорилось раньше, происходят потери энергии из-за утечки тока вследствие несовершенства изоляции между пластинами конденсаторов. Эти потери называются потерями утечки.
Вокруг всякого переменного тока существует переменное магнитное поле. Следовательно, во всех окружающих железных предметах происходит непрерывное переворачивание молекулярных магнитиков в такт с частотой переменного тока. В результате железные предметы, находящиеся в поле переменного тока, нагреваются, т. е электрическая энергия превращается в тепловую. Эти потери называются потерями на гистерезис.
Благодаря электромагнитной индукции переменный электрический ток наводит в близлежащих замкнутых электрических цепях индукционные токи, что связано с нагреванием этих цепей, т. е. с дополнительными потерями энергии.
12
Кроме того, такие же индукционные круговые токи возникают не только в замкнутых электрических цепях, но и в близлежащих металлических предметах и нагревают их. Эти токи называются токами Фуко. Возникновение токов Фуко также сопряжено с потерями электрической энергии.
Токи Фуко не всегда являются вредными. Например, на принципе токов Фуко основана защита радиоприборов медными или алюминиевыми экранами от переменных магнитных полей высокой частоты.
Наконец, при очень высоких частотах цепь переменного тока может излучать электромагнитные волны (радиоволны), что связано с потерями на излучение.
Наличие всех этих потерь увеличивает активное сопротивление цепи переменному току.
Опыт показывает, что при высоких частотах и омическое сопротивление проводника оказывается значительно большим, чем при постоянном токе.
Для объяснения этого явления увеличим мысленно сечение проводника (и посмотрим, что происходит в нем при прохождении по нему переменного тока. Вдоль проводника взад и вперед с частотой переменного тока движется огромное количество электронов.
Активное сопротивление цепи переменного тока
Поверхностный эффект, как фактор увеличения активного сопротивления в цепи переменного тока. Ток вытесняется магнитным полем на поверхность проводника (а), поэтому у поверхности проводника плотность тока больше, чем внутри проводника (б).
До сих пор нам было известно, что движущийся по проводнику переменный поток электронов создает вокруг него переменное магнитное поле. Теперь же, когда мы заглянем внутрь проводника, мы увидим, что магнитное поле имеется и внутри проводника. Это вызвано тем, что каждый
13
1электрон при движении создает вокруг себя магнитное поле, а так как часть электронов движется вблизи оси проводника, то они создают магнитное поле не только во вне, но и внутри проводника.
Продолжая присматриваться к происходящему внутри проводника, мы заметим, что наиболее быстро движутся электроны, находящиеся у поверхности проводника, а по мере приближения к середине проводника амплитуда (размах) колебаний электронов становится все меньше и меньше.
Почему же электроны колеблются с различными амплитудами в разных точках сечения проводника?
Это явление также имеет свое объяснение. Вспомним, что при всяком изменении скорости движения электрона на него действует ЭДС самоиндукции, противодействующая этому изменению. Вспомним также, что ЭДС самоиндукции зависит от числа магнитных силовых линий вокруг движущегося электрона. Чем большим числом магнитных силовых линий охватывается электрон, тем труднее ему совершать колебательное движение.
Теперь становится ясным, почему электроны, находящиеся у поверхности проводника, колеблются с большой амплитудой, а электроны, находящиеся глубоко внутри проводника, — с малой. Ведь первые охватываются только теми магнитными силовыми линиями, которые расположены вне проводника, а вторые охватываются и внешними и внутренними магнитными силовыми линиями.
Таким образом, плотность переменного тока получается большей у поверхности проводника и меньшей внутри его.
При очень высоких частотах противодействие ЭДС самоиндукции внутри проводника становится настолько сильным, что все электроны движутся только по поверхности проводника. Это явление и называется поверхностным эффектом. Так как активное сопротивление проводника зависит от его сечения, а полезным сечением при токе высокой частоты оказывается только тонкий наружный слой проводника, то вполне понятно, что его активное сопротивление увеличивается с повышением частоты
14
переменного тока.
Для уменьшения поверхностного эффекта проводники, по которым протекают токи высокой частоты, делают трубчатыми и покрывают их слоем хорошо проводящего металла, например серебра.
В целях борьбы с явлением поверхностного эффекта применяют также провода специальной конструкции, так называемый литцендрат.
литцендрат
Такой проводник свивают из отдельных тонких медных жилок, имеющих эмалевую изоляцию, причем скрутка жилок производится таким образом, чтобы каждая из них проходила поочередно то внутри проводника, то снаружи его.
Явление поверхностного эффекта особенно сильно сказывается в железных проводах, в которых вследствие большой магнитной проницаемости железа внутренний магнитный поток оказывается особенно большим и поэтому явление поверхностного эффекта становится очень заметным даже при сравнительно низких (звуковых) частотах.
15
Ток и напряжение. При включении в цепь переменного тока активного сопротивления R (рис. 175, а) напряжение и источника создает в цепи ток i. Если напряжение и изменяется по синусоидальному закону u = Uт sin ?t, то ток i также изменяется синусоидально:
i = Iт sin ?t
При этом
Iт = Uт / R
Таким образом, ток и напряжение изменяются по одному и тому же закону; они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 175,б). Следовательно, при включении в цепь переменного тока активного сопротивления ток и напряжение совпадают по фазе (рис. 175, в).

Если обе части равенства Iт = Uт / R разделить на ?2, то получим выражение закона Ома для рассматриваемой цепи для действующих значений напряжения и тока:
I = U / R
Следовательно, для цепи переменного тока, содержащей только активное сопротивление, этот закон имеет такую же математическую форму, как и для цепи постоянного тока.
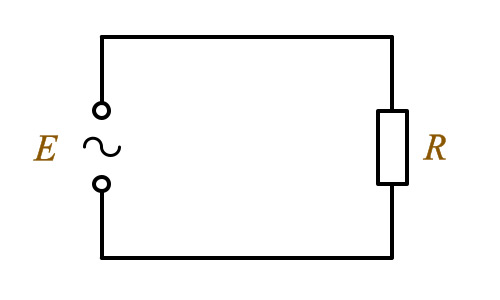
Электрическая мощность. Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения и. Следовательно, мгновенная мощность р не является постоянной величиной, как при постоянном токе, а изменяется по кривой (см. рис. 175,б). Эту кривую можно также получить графически, перемножая ординаты кривых силы тока i и напряжения и при различных углах ?t. Изменение мощности происходит с двойной частотой ?t по отношению к изменению тока и напряжения, т. е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности являются положительными. Физически положительное значение мощности означает, что энергия передается от источника электрической энергии к приемнику. Максимальное значение мощности при ?t = 90° и ?t = 270°
Pmax = UтIт = 2UI
Рис. 175. Схема включения в цепь переменного тока активного сопротивления (а), кривые тока i, напряжения и, мощности р (б) и векторная диаграмма (в)
Практически об энергии W, создаваемой электрическим током, судят не по максимальной мощности, а по средней мощности Рср = Р, так как эта энергия может быть выражена как произведение среднего значения мощности Р на время протекания тока:
W = Pt.
Кривая мгновенной мощности симметрична относительно линии АБ, которая соответствует среднему значению мощности Р. Поэтому
P = Pmax / 2 = UI
Используя формулу (67) закона Ома, активную мощность можно выразить также в виде P = I2R или P=U2/R.
В электротехнике среднюю мощность, потребляемую активным сопротивлением, обычно называют активной мощностью, или просто мощностью, и обозначают буквой Р.
Поверхностный эффект. Следует отметить, что активное сопротивление проводников в цепи переменного тока всегда больше их сопротивления в цепи постоянного тока. Переменный ток i не протекает равномерно по всему поперечному сечению проводника, как постоянный ток i, а вытесняется на его поверхность (рис. 176, а). Поэтому полезное сечение проводника как бы уменьшается и сопротивление его при переменном токе возрастает. Это явление носит название поверхностного эффекта. Неравномерное распределение переменного тока по поперечному сечению проводника объясняется действием э. д. с. самоиндукции, индуцированной в проводнике магнитным полем, которое создается проходящим по проводнику током I. Это магнитное поле действует не только в пространстве, окружающем проводник (внешний поток Ф2), но и внутри самого проводника (внутренний поток Ф2) (рис. 176,б). Поэтому слои проводника, расположенные ближе к его центру, будут охватываться большим магнитным потоком, чем слои, расположенные ближе к его поверхности, и э. д. с. самоиндукции, индуцированная во внутренних слоях, будет большей, чем во внешних. Поскольку э. д. с. самоиндукции препятствует изменению
Рис. 176. Схема протекания постоянного I и переменного i токов по проводнику (а) и возникновение поверхностного эффекта (б)
Рис. 177. Схема термообработки деталей токами высокой частоты: 1 — высокочастотный индуктор; 2 — закаливаемая деталь; 3 — разогретый слой
тока, последний будет стремиться пройти там, где э. д. с. самоиндукции имеет наименьшее значение, т. е. пройдет преимущественно по поверхностным слоям проводника. В результате этого плотность тока У в поверхностных слоях будет больше, чем во внутренних. Чем больше частота тока, тем больше э. д. с. самоиндукции индуцируется во внутренних слоях проводника и тем в большей степени ток вытесняется на поверхность.
При частоте 50 Гц увеличение сопротивления медных и алюминиевых проводников при малом их диаметре практически ничтожно, и сопротивление таких проводников в цепях переменного и постоянного тока можно считать одинаковым. Но для медных и алюминиевых проводников диаметром свыше 10 мм, а для стальных проводников при еще меньших диаметрах необходимо при расчетах учитывать влияние поверхностного эффекта на их активное сопротивление.
При токах высокой частоты, принятых в радиотехнике, телевидении и различных высокочастотных установках, с целью лучшего использования металла проводников их обычно изготовляют полыми.
На свойстве переменного тока высокой частоты протекать, главным образом, по поверхности проводников основаны различные методы высокочастотной закалки и термообработки. Например, при высокочастотной термообработке деталей вихревыми токами (рис. 177) эти токи индуцируются в основном в поверхностном слое металла. Они быстро разогревают поверхностные слои обрабатываемой детали, раньше, чем ее внутренняя часть успеет заметно нагреться за счет теплопроводности металла.

Активное сопротивление
Определение 1
Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:
\[I\left(t\right)=I_m{sin \left(\omega t\right)\ \left(1\right).\ }\]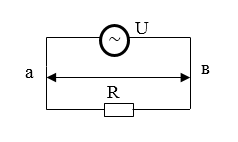
Рисунок 1.
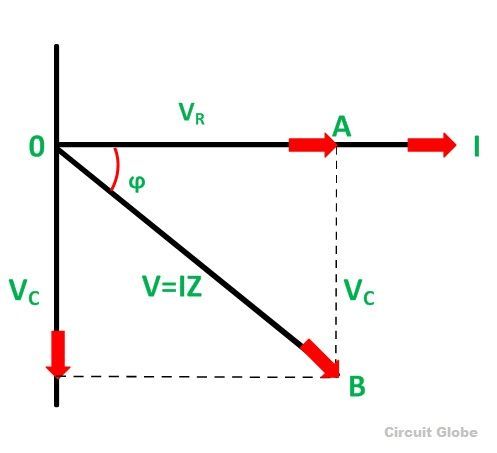
Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:
\[U=IR=I_m{Rsin \left(\omega t\right)\ \left(2\right),\ }\]где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:
\[U_m=RI_m\left(3\right),\]где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.
Ёмкостное сопротивление
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.
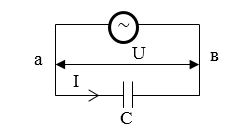
Рисунок 2.
Мы можем использовать следующие соотношения:
Готовые работы на аналогичную тему
Если $I(t)$ определена уравнением (1), то заряд выражен как:
где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:
Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $\frac{\pi }{2}.$ Амплитуда напряжения на емкости равна:
Величину $X_C=\frac{1}{\omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=\infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.
Индуктивное сопротивление
Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.
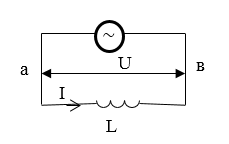
Рисунок 3.
Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:
По условию $R=0. \mathcal E$ самоиндукции можно выразить как:
Из выражений (8), (9) следует, что:
Амплитуда напряжения в данном случае равна:
где $X_L-\ $индуктивное сопротивление (кажущееся сопротивление индуктивности).
Закон Ома для цепей переменного тока
Определение 2
Выражение вида:
\[I_m=\frac{U_m}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}\left(12\right).\]где
\[Z=\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}(13)\]называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.
Пример 1
Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $\nu$.
Решение:
Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.
Амплитудное значение силы тока выражается «законом Ома для переменного тока»:
\[I_m=\frac{U_m}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}\left(1.1\right)\]оно связано с действующим значением силы тока как:
\[I=\frac{I_m}{\sqrt{2}}\left(1.2\right).\]В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:
\[U=\frac{U_m}{\sqrt{2}}\to U_m=\sqrt{2}U\left(1.3\right).\]Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:
\[I=\frac{1}{\sqrt{2}}\frac{\sqrt{2}U}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}=\frac{U}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}=\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},\]где $\omega =2\pi \nu .$
Ответ: $I=\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.$
Пример 2
Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).
Решение:
Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой:
\[U_L=I\omega L=2 \pi \nu L\frac{U}{\sqrt{R^2+{\left(2 \pi \nu L-\frac{1}{2 \pi \nu C}\right)}^2}}.\]Напряжение на активном сопротивлении ($U_R$) равно:
\[U_R=IR=\frac{UR}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.\]Напряжение на конденсаторе ($U_C$) определяется как:
\[U_C=\frac{I}{C2 \pi \nu}=\frac{1}{C2 \pi \nu}\frac{U}{\sqrt{R^2+{\left(2 \pi \nu L-\frac{1}{2 \pi \nu C}\right)}^2}}.\]Ответ: $U_L=2\pi \nu L\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},\ U_R=\frac{UR}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},U_C=\frac{1}{C2\pi \nu }\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.$
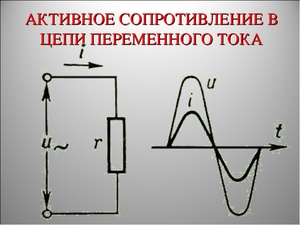 Для проектирования электронных устройств следует рассчитывать различные параметры, одним из которых является электропроводимость или сопротивление проводника. Для цепей, питающихся постоянным током, вычислить его несложно. Но в цепях переменного тока (ПТ) существуют совсем другие соотношения. Для расчета активного сопротивления необходимо ознакомиться с основными формулами, а также альтернативными способами его вычисления.
Для проектирования электронных устройств следует рассчитывать различные параметры, одним из которых является электропроводимость или сопротивление проводника. Для цепей, питающихся постоянным током, вычислить его несложно. Но в цепях переменного тока (ПТ) существуют совсем другие соотношения. Для расчета активного сопротивления необходимо ознакомиться с основными формулами, а также альтернативными способами его вычисления.
Основные сведения об электропроводимости
Каждое вещество проводит ток по-разному. Все зависит от электронной конфигурации, которую можно получить из таблицы Д. И. Менделеева. Электронная конфигурация показывает основной параметр, от которого зависит величина сопротивления R, — количество свободных электронов (Nсэ). Вещество состоит из атомов, которые образуют кристаллическую решетку (КР). Не все электроны прочно удерживаются ядром.
Классификация веществ
В веществах присутствует несколько электронов (Э), которые имеют очень слабую силу взаимодействия с ядром. Кроме того, в металлах, кроме обыкновенных Э, есть определенное Nсэ. При приложении незначительной сторонней энергии происходит отрыв электронов от ядер атомов, и это приводит к образованию ионов. Металл остается незаряженным, так как отрицательный заряд всех Э равен положительному заряду элементарных частиц (ЭЧ), входящих в состав ядер. Ядро состоит из нуклонов, а именно:
- протонов — положительно заряженных ЭЧ;
- нейтронов — нейтральные ЭЦ.
Свободные Э движутся хаотично, однако среди них есть такие, которые летят близко к поверхности металла, и они не могут вылететь из вещества, так как их удерживает сила притяжения ионов и ядер. Исходя из Nсэ, можно разделить любое вещество на 3 группы по проводимости:
- Проводники.
- Полупроводники.
- Диэлектрики.
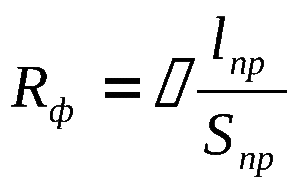 К проводникам (П) относятся вещества, обладающие большим Nсэ. К ним относятся металлы, электролитические растворы и ионизированные газы. В металлах свободными носителями заряда (СНЗ) являются свободные Э, в электролитах и ионизированных газах — ионы, под действием электрического поля движение СНЗ становится упорядоченным, в результате которого образуется электрический ток (ЭТ).
К проводникам (П) относятся вещества, обладающие большим Nсэ. К ним относятся металлы, электролитические растворы и ионизированные газы. В металлах свободными носителями заряда (СНЗ) являются свободные Э, в электролитах и ионизированных газах — ионы, под действием электрического поля движение СНЗ становится упорядоченным, в результате которого образуется электрический ток (ЭТ).
В полупроводниках Nсэ зависит от различных внешних факторов, при действии которых происходит освобождение некоторых Э от действия силы притяжения ядра — силы Кулона при взаимодействии 2 и более частиц. Место, которое покинул Э, называется дыркой. Движение дырок и Э является противоположным, и при этом возникает ЭТ. К веществам полупроводникового типа относятся следующие: кремний (Si), германий (Ge), селен (Se) и т. д.
К группе диэлектриков или изоляторов относятся вещества, которые вообще не обладают СНЗ, а следовательно, они не проводят электрический ток вообще. При некоторых условиях диэлектрик может стать отличным от П тока, например, если будет покрыт каплями электропроводящей жидкости. Этот момент является очень важным для избежания выхода аппаратуры из строя или поражения ЭТ. При протекании по П ЭТ оказывает тепловое действие на него. Это свойство обусловлено тем, что Э взаимодействуют с узлами КР, и кинетическая энергия Э превращается в тепловую.
В результате происходит снижение скорости Э, а затем ее полное восстановление при воздействии электромагнитного поля. Этот процесс повторяется большое количество раз и называется электрическим сопротивлением, которое обозначается для цепей постоянного тока R, а для цепей переменного тока (ПТ) существует полное сопротивление — Z. Измеряется R и Z в Ом.
Зависимость от различных параметров
R является величиной, зависящей от многих факторов. Эти факторы можно разделить на группы:
- Физические свойства: длина, площадь поперечного сечения (S) и деформация.
- Внешняя среда: температура.
- Электрические: I, U, e (электродвижущая сила — ЭДС).
R рассчитывается по закону Ома: I = U / R. Формулировка этого закона следующая: I, протекающий на участке цепи, прямо пропорционален U и обратно пропорционален R выбранного участка.
Формулировка для всей цепи: I, протекающий по всей цепи, прямо пропорционален ЭДС и обратно пропорционален R всего участка с учетом внутреннего сопротивления источника питания (ИП). Формула имеет вид: I = e / (R + Rип). Из соотношений для полной и участка цепи можно получить R:
- R = U / I.
- R = (e / I) — Rип.
 Тип вещества определяется коэффициентом удельного сопротивления p, который берется из справочника. Однако следует учесть, что в справочнике приведено его значение при температуре +20 градусов. Кроме того, существует и удельная проводимость, которая обратно пропорциональна p. Она обозначается σ и равна: p = 1 / σ.
Тип вещества определяется коэффициентом удельного сопротивления p, который берется из справочника. Однако следует учесть, что в справочнике приведено его значение при температуре +20 градусов. Кроме того, существует и удельная проводимость, которая обратно пропорциональна p. Она обозначается σ и равна: p = 1 / σ.

При меньшей величине S Э протекают через П и взаимодействия с КР учащаются, что иллюстрирует зависимость R от S. Для вычисления S необходимо воспользоваться справочной литературой или интернетом. Если учесть, что проводник является плоскостью, то необходимо разрезать его при помощи другой плоскости (стереометрия).
При разрезе получается плоская фигура в виде квадрата, окружности, эллипса, прямоугольника или треугольника. Затем необходимо вычислить S этой фигуры. Если П состоит из определенного количества жил, то нужно измерить S одной жилы, а затем умножить на количество жил.
R зависит прямо пропорционально от длины П (L): чем больше длина, тем больше взаимодействий совершает Э при движении. Исходя из всех зависимостей можно выразить R формулами:
- R = p * L / S.
- R = L / (σ * S).
Эти соотношения справедливы при температуре +20 градусов, но для проведения точных расчетов этого недостаточно. Некоторые сверхчувствительные элементы могут работать некорректно из-за низких значений I.
Значение p зависит от t и выражается следующим соотношением: p = p20 * [1 + a * (t — 20)]. В этом соотношении присутствуют следующие величины:
- p — удельное сопротивление, полученное при вычислении.
- p20 — величина удельного сопротивления, взятого из справочной литературы при температуре (температура +20 градусов по Цельсию).
- Температурный коэффициент a, который берется из справочной литературы. Для металлов он всегда больше 1, а для электролитических растворов — меньше.
- Температура П при конкретных условиях эксплуатации, температурная шкала по Цельсию — t.
Кроме того, p зависит еще и от уровня деформации КР. Деформация бывает упругой и пластической. При упругой происходит увеличение p, а при пластической — уменьшение. Это связано с условиями деформаций, а также со степенью затрудненности движения Э. Конечная формула при учете основных факторов примет следующий вид: R = p20 * [1 + a * (t — 20)] * L / S.
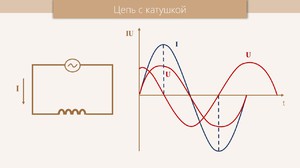
Соотношения для переменного тока
 Для того чтобы разобраться в некоторых терминах, например, какое сопротивление называется активным, и что оно из себя представляет, необходимо применить формулу полного сопротивления: sqr (Z) = sqr® +sqr (Xc-Xl). Сопротивление переменного тока является полным и состоит из активного R, индуктивного (Хl) и емкостного (Xc).
Для того чтобы разобраться в некоторых терминах, например, какое сопротивление называется активным, и что оно из себя представляет, необходимо применить формулу полного сопротивления: sqr (Z) = sqr® +sqr (Xc-Xl). Сопротивление переменного тока является полным и состоит из активного R, индуктивного (Хl) и емкостного (Xc).
Формула сопротивления
Сопротивление называется активным, если на участке или в полной цепи нет индуктивности или емкости. Для расчета необходимо измерить амплитудные значения тока и напряжения. Для этих целей применяются вольтметр и амперметр для переменного тока и напряжения. Однако минусом таких измерений является получение не амплитудных, а действующих значений. Амплитудные значения высчитываются по формулам:
- Для U: Um = 1,4142 * Ud.
- Для I: Im = 1,4142 * Id.
Исходя из этих соотношений формула активного сопротивления вычисляется по формуле: R = Um / Im. Активное сопротивление зависит еще и от Um и Im.
Простые способы измерения
 Не всегда требуются точные расчеты R, и для этих целей применяется прибор, называющиеся омметром. С ростом научного прогресса на рынке появились комбинированные приборы — мультиметры. Они имеют много функций, но основной из них является измерение значений I, R и U. Существуют также и специализированные приборы для измерения больших значений R, которые называются мегаомметрами. Мегаомметр применяется для измерения R уровня изоляции между жилами кабеля.
Не всегда требуются точные расчеты R, и для этих целей применяется прибор, называющиеся омметром. С ростом научного прогресса на рынке появились комбинированные приборы — мультиметры. Они имеют много функций, но основной из них является измерение значений I, R и U. Существуют также и специализированные приборы для измерения больших значений R, которые называются мегаомметрами. Мегаомметр применяется для измерения R уровня изоляции между жилами кабеля.
Омметр применяется и для поиска неисправностей в электроцепях, а также позволяет определить радиодеталь на предмет исправности. Для измерения значений R, а также для выявления неисправностей, необходимо соблюдать правила электробезопасности и обесточить участок цепи. Нужно разрядить и конденсаторы, так как их заряд может вывести из строя прибор, который находится в режиме измерения R.
Таким образом, активным сопротивлением в цепи переменного тока является любая нагрузка, не являющаяся емкостной или индуктивной, и зависящей от температуры, вида деформации, типа вещества, Um, Im, длины и S проводника.
активной, реактивной и полной мощности
Требуемое электропитание в электрической цепи зависит от
- активной мощности — потребляемой мощности реального электрического сопротивления в цепи
- реактивной мощности — мнимой индуктивной и емкостной потребляемой мощности в цепи
Требуемый источник питания называется полной мощностью и представляет собой комплексное значение, которое может быть выражено в соотношении пифагорейского треугольника, как показано на рисунке ниже.
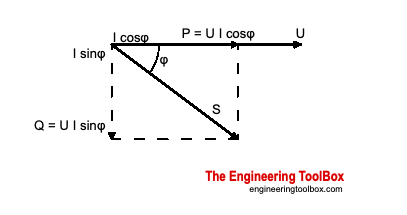
Кажущаяся мощность — S
Кажущаяся мощность — это мощность, подаваемая в электрическую цепь — как правило, от поставщика питания в сеть — для покрытия реальной и реактивной потребляемой мощности в нагрузках.
Кажущаяся мощность может быть рассчитана как
S = (Q 2 + P 2 ) 1/2 (1)
, где
S = полная мощность в цепи ( вольт-ампер, ВА)
Q = потребляемая реактивная мощность в нагрузке (вольт-ампер реактивная, ВАР)
P = потребляемая активная мощность в нагрузке (Вт, Вт)
Видимая мощность измеряется в вольт-амперах (ВА) — напряжение системы переменного тока, умноженное на текущий ток.Кажущаяся мощность является комплексным значением и векторной суммой активной и реактивной мощности, как показано на рисунке выше.
Однофазный ток
S = UI (2a)
, где
U = электрический потенциал (В)
I = ток (A)
Трехфазный ток
S = 3 1/2 UI
= 1.732 U I (2b)
Активная мощность — P
Активная — или реальная или истинная — мощность выполняет фактическую работу в нагрузке. Активная мощность измеряется в Вт (Вт) и представляет собой мощность, потребляемую электрическим сопротивлением.
Однофазный ток
P = UI cos φ
= UI PF (3a)
, где
φ = фазовый угол между электрическим потенциалом (напряжением) и током
PF = cos φ
= коэффициент мощности
Трехфазный ток
P = 3 1/2 UI cos φ
= 1.732 U I PF (3b)
Постоянный ток
P = U I (3c)
Реактивная мощность — Q
Реактивная мощность — это мнимая или сложная мощность в емкостной или индуктивной нагрузке. Реактивная мощность представляет собой обмен энергией между источником питания и реактивными нагрузками, при котором полезная мощность не увеличивается и не теряется. Чистая средняя реактивная мощность равна нулю. Реактивная мощность накапливается и разряжается асинхронными двигателями, трансформаторами, соленоидами и конденсаторами.
Реактивная мощность должна быть сведена к минимуму, поскольку она увеличивает общий ток, протекающий в электрической цепи, не оказывая никакой нагрузки на нагрузку. Увеличенные реактивные токи обеспечивают только невосстановимые потери мощности из-за сопротивления линии электропередачи.
Увеличение реактивной и полной мощности уменьшит коэффициент мощности — PF .
Реактивная индуктивная мощность измеряется в вольт-амперных реактивных (VAR).
Однофазный ток
Q = UI sin φ
= UI PF (4a)
, где
φ = фазовый угол
Трехфазный ток
Q = 3 1/2 UI sin φ
= 1.732 UI PF (4b)
.Цепь переменного тока— напряжение, ток и мощность
В цепи переменного тока — переменный ток генерируется синусоидальным источником напряжения
Напряжение
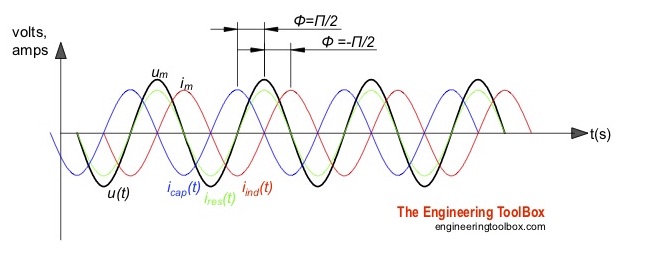
Токи в цепях с чистыми резистивными, емкостными или индуктивными нагрузками.
Мгновенное напряжение в синусоидальной цепи переменного тока может быть выражено в форме во временной области как
u (t) = U макс. cos (ω t + θ) (1)
, где
u (t) = напряжение в цепи в момент времени t (В)
U max = максимальное напряжение на амплитуде синусоидальной волны (В)
t = время (с)
ω = 2 π f
= угловая частота синусоидальной волны (рад / с)
f = частота (Гц, 1 / с)
θ = сдвиг фазы синусоидальной волны (рад)
В качестве альтернативы мгновенное напряжение может быть выражено в форме частотной области (или вектор) как
U = U (jω) = U макс. e jθ (1а)
, где
U (jω) = U = комплексное напряжение (В)
Вектор представляет собой комплексное число, выраженное в полярной форме, состоящее из величины, равной амплитуде пика синусоидального сигнала и фазы угол равен фазовому сдвигу синусоидального сигнала относительно косинусоидального сигнала.
Обратите внимание, что конкретная угловая частота — ω — явно не используется в выражении вектора.
Ток
Моментальный ток может быть выражен в форме во временной области как
i (t) = I м cos (ω t + θ) (2)
, где
i (t) = ток в момент времени t (A)
I макс = максимальный ток с амплитудой синусоидальной волны (A)
Токи в цепях с резистивные чистые , емкостные или индуктивные нагрузки указаны на рисунке выше.Ток в «реальной» цепи с резистивной, индуктивной емкостью и указан на рисунке ниже.
Моментальный ток в цепи переменного тока может альтернативно быть выражен в форме частотной области (или фазора) как
I = I (jω) = I макс. e jθ (2a)
, где
I = I (jω) = комплексный ток (A)
Частота
Обратите внимание, что частота большинства систем переменного тока фиксирована — как 60 Гц в Северной Америке и 50 Гц в большей части остального мира.
Угловая частота для Северной Америки составляет
ω = 2 π 60
= 377 рад / с
Угловая частота для большей части остального мира составляет
ω = 2 π 50
= 314 рад / с
Резистивная нагрузка
Напряжение на резистивной нагрузке в системе переменного тока может быть выражено как
U = RI (4)
где
R = сопротивление (Ом)
Для резистивной нагрузки в цепи переменного тока напряжение составляет в фазе с током.
Индуктивная нагрузка
Напряжение индуктивной нагрузки в системе переменного тока можно выразить как
U = j ω LI (5)
, где
L = индуктивность (Генри)
Для индуктивной нагрузки ток в цепи переменного тока составляет π / 2 (90 o ) фазы после напряжения (или напряжения до тока).
Емкостная нагрузка
Напряжение индуктивной нагрузки в системе переменного тока можно выразить как
U = 1 / (j ω C) I (6)
, где
C = емкость (Фарад)
Для емкостной нагрузки ток в цепи переменного тока опережает напряжение на π / 2 (90 o ) фаза .
В реальной электрической цепи существует комбинация резистивных, емкостных и индуктивных нагрузок с фазовым сдвигом напряжения / тока в диапазоне — π / 2 <= φ <= π / 2 , как показано на рисунке. рисунок ниже.
Ток в «реальной» цепи с комбинацией резистивных, индуктивных и емкостных нагрузок. φ — фазовый угол между током и напряжением.
Импеданс
Закон Ома для комплексного переменного тока может быть выражен как
U z = I z Z (7)
где
U z = падение напряжения на нагрузке (вольт, В)
I z = ток через нагрузку (ампер, А)
Z = полное сопротивление нагрузки (Ом, Ом)
Полное сопротивление в цепи переменного тока можно рассматривать как сложное сопротивление.Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения.
Импедансы в серии
Результирующий импеданс для последовательных импедансов может быть выражен как
Z = Z 1 + Z 2 (7b)
Импедансы параллельно
Результирующее сопротивление параллельно параллельно может быть выражено как
1 / Z = 1 / Z 1 + 1 / Z 2 (7c)
Пропускная способность
Пропускная способность — это инвертированный импеданс
Y = 1 / Z (8)
, где
Y = допустимое сопротивление (1 / Ом)
RMS или эффективное напряжение
Среднеквадратичное значение является действующим значением синусоидального напряжения или тока.
RMS — среднеквадратичное значение — или эффективное напряжение можно выразить как
U среднеквадратичное значение = U eff
= U max / (2) 1/2
= 0,707 U макс. (9)
, где
U среднеквадратичное значение = U эфф
= среднеквадратичное напряжение (В)
U макс. = максимальное напряжение (амплитуда) синусоидального источника напряжения (В)
RMS — среднеквадратичное значение — или эффективный ток может быть выражен как
I среднеквадратичное значение = I эфф
= I макс. / (2) 1/2
= 0.707 I макс (10)
, где
I среднеквадратичное значение = I эфф
= среднеквадратичный ток (A)
I макс = максимальный ток (амплитуда) синусоидального источника напряжения (A)
Вольтметры и амперметры переменного тока показывают среднеквадратическое значение напряжения или тока — или 0,707 от максимальных пиковых значений. Максимальные пиковые значения 1.41 раз значения вольтметра.
Пример
- для системы 230В U среднеквадратичное значение = 230 В и U макс = 324 В
- для системы 120 В U среднеквадратичное значение = 120 В и U макс. = 169 В
Трехфазное напряжение переменного тока — линия к линии и линия к нейтрали
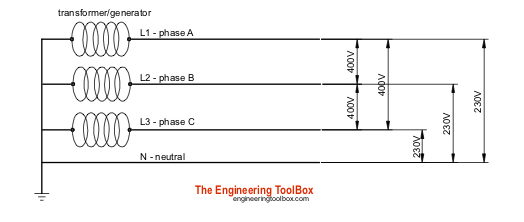
В трехфазной системе переменного тока напряжение может подаваться между линиями и нейтралью (потенциал фазы), или между линиями (потенциал линии).Результирующие напряжения для двух распространенных систем — европейской 400 / 230В и североамериканской системы 208 / 120В указаны для одного периода на рисунках ниже.
400 В / 230 В переменного тока
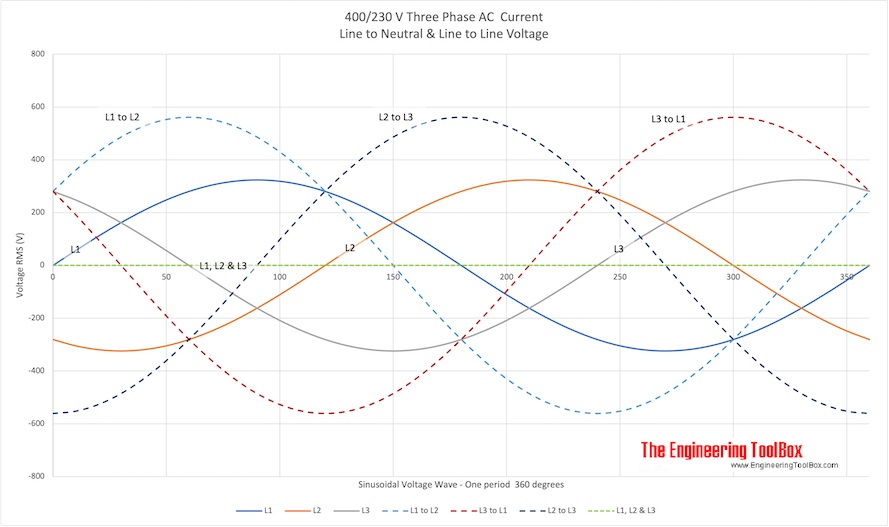
print 400/230 В Трехфазная схема
- L1, L2 и L3 представляют собой три фазы, соединяющие с нейтральными потенциалами — фазовые потенциалы
- L1 — L2, L1 до L3 и от L2 до L3 представляют собой трехфазные линейные потенциалы — линейных потенциалов
- L2, L2 и L3 — результирующий потенциал трехфазных фаз в сбалансированной цепи — результирующий потенциал = 0
Величина линейных потенциалов равна 3 1/2 (1.73) величина фазового потенциала.
U среднеквадратичное значение, линия = 1,73 U среднеквадратичное значение, фаза (11)
208 В / 120 В переменного тока
печать 208/120 В трехфазная диаграмма
Мощность
Активно — или реально или верно — мощность, которая фактически выполняет работу в цепи — может быть рассчитана как
P = U среднеквадратичное значение I среднеквадратичное значение cos φ (12)
где
P = активная действительная мощность (Вт)
φ = фазовый угол между током и напряжением (рад, градусы)
Cos φ также называется коэффициентом мощности.
Реактивная мощность в цепи может быть рассчитана как
Q = U среднеквадратичное значение I среднеквадратичное значение sin φ (13)
Q = реактивная мощность (VAR)
.Цепь с чистым сопротивлением RОм, соединенная последовательно с чистым конденсатором с емкостью С Фарад, известна как RC Series Circuit. Подается синусоидальное напряжение, и ток I течет через сопротивление (R) и емкость (C) цепи.
Схема серии RC показана на рисунке ниже:
 Где
Где
- В R — напряжение на сопротивлении R
- В C — напряжение на конденсаторе C
- В — общее напряжение на цепи серии RC
Содержание:
Phasor Diagram RC серии Схема
Фазовая диаграмма цепей серии RC показана ниже:
Шаги для построения векторной диаграммы
Следующие шаги используются для построения векторной диаграммы цепи RC серии
- Взять ток I (р.M.S., значение) в качестве опорного вектора
- Падение напряжения в сопротивлении VR = IR берется в фазе с вектором тока
- Падение напряжения в емкостном реактивном сопротивлении VC = IXC отводится на 90 градусов позади вектора тока, а токоподводы — на 90 градусов (в чистой емкостной цепи)
- Сумма векторов двух падений напряжения равна приложенному напряжению V (значение r.m.s).
Сейчас
V R = I R и V C = IX C
, где X C = I / 2πfC
В прямоугольном треугольнике OAB,
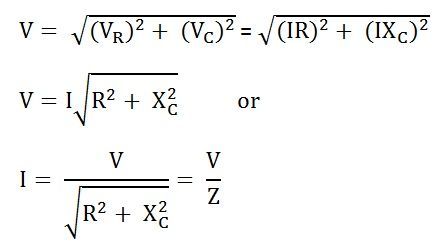
Где,
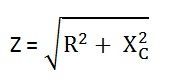
Z — полное сопротивление, предлагаемое потоку переменного тока последовательной цепью RC, и называется сопротивлением схемы .Измеряется в омах (Ω).
Фазовый угол
Из приведенной выше векторной диаграммы ясно, что ток в цепи опережает приложенное напряжение на угол ϕ, и этот угол называется фазовым углом .
Мощность в цепи RC серии
Если переменное напряжение, подаваемое на цепь, задается уравнением
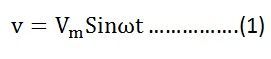
Затем
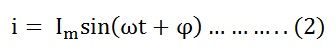
Следовательно, мгновенная мощность определяется как p = vi
Помещение значения v и i из уравнения (1) и (2) в p = vi
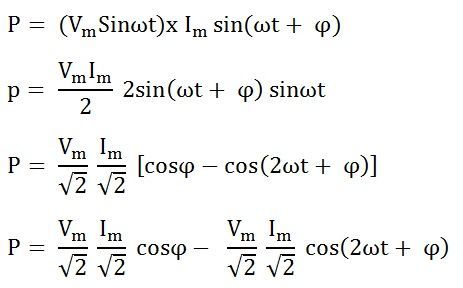
Средняя мощность, потребляемая в цепи за полный цикл, определяется как:
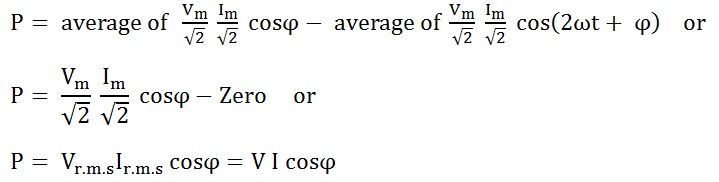
Где cosϕ называется коэффициентом мощности схемы.
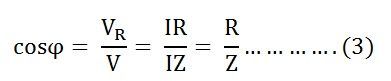
С учетом значения V и cosϕ из уравнения (3) значение мощности будет
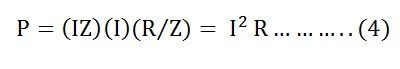
Из уравнения (4) ясно, что мощность фактически потребляется только сопротивлением, и конденсатор не потребляет никакой энергии в цепи.
Форма волны и кривая мощности цепи серии RC
Форма волны и кривая мощности RC-цепи показаны ниже:
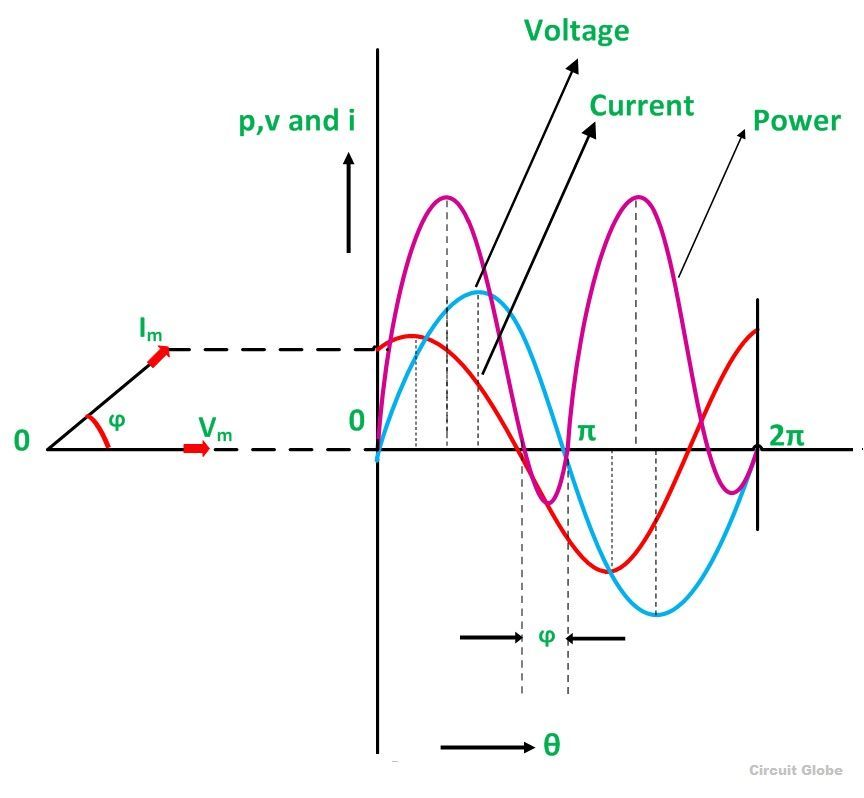 Различные точки на кривой мощности получены из произведения мгновенного значения напряжения и тока.
Различные точки на кривой мощности получены из произведения мгновенного значения напряжения и тока.
Мощность отрицательна между углом (180 ° — ϕ) и 180 ° и между (360 ° — ϕ) и 360 °, а в остальной части цикла мощность является положительной. Поскольку площадь под положительными петлями больше, чем под отрицательными, то чистая мощность за полный цикл составляет положительных .
,являются неотъемлемой частью практически всех технологических достижений, которые происходят сегодня в нашей жизни. Телевидение, радио, телефоны и компьютеры сразу приходят на ум, но электроника также используется в автомобилях, кухонных приборах, медицинском оборудовании и промышленных контролях. В основе этих устройств лежат активные компоненты или компоненты схемы, которые электронно управляют потоком электронов, например, полупроводники.Однако эти устройства не могли бы функционировать без гораздо более простых пассивных компонентов, которые предшествуют полупроводникам на многие десятилетия. В отличие от активных компонентов, пассивные компоненты, такие как резисторы, конденсаторы и индукторы, не могут контролировать поток электронов с помощью электронных сигналов.
Resistance
Как следует из названия, резистор — это электронный компонент, который сопротивляется потоку электрического тока в цепи.
В металлах, таких как серебро или медь, которые имеют высокую электропроводность и, следовательно, низкое удельное сопротивление, электроны могут свободно переходить от одного атома к другому с небольшим сопротивлением.
Электрическое сопротивление элемента схемы определяется как отношение приложенного напряжения к электрическому току, который течет через него, согласно HyperPhysics, сайту физических ресурсов, размещенному на кафедре физики и астрономии в Университете штата Джорджия. Стандартной единицей сопротивления является Ом, названный в честь немецкого физика Георга Симона Ома. Он определяется как сопротивление в цепи с током 1 ампер при 1 вольт. Сопротивление можно рассчитать по закону Ома, согласно которому сопротивление равно напряжению, деленному на ток, или R = V / I (чаще записывается как V = IR), где R — сопротивление, V — напряжение, а I — ток.
Резисторы обычно классифицируются как фиксированные или переменные. Резисторы с фиксированным значением — это простые пассивные компоненты, которые всегда имеют одинаковое сопротивление в пределах своих предписанных пределов тока и напряжения. Они доступны в широком диапазоне значений сопротивления, от менее 1 Ом до нескольких миллионов Ом.
Переменные резисторы — это простые электромеханические устройства, такие как регуляторы громкости и диммеры, которые изменяют эффективную длину или эффективную температуру резистора при повороте ручки или перемещении ползункового регулятора.
Пример индуктора из медного провода, установленного на печатной плате. (Фото предоставлено: Shutterstock)Индуктивность
Индуктор — это электронный компонент, состоящий из катушки с проводом, через который проходит электрический ток, создающий магнитное поле. Единицей индуктивности является Генри (H), названный в честь Джозефа Генри, американского физика, который открыл индуктивность независимо примерно в то же время, что и английский физик Майкл Фарадей. Один генри — это величина индуктивности, которая требуется для индукции 1 вольт электродвижущей силы (электрического давления от источника энергии), когда ток изменяется со скоростью 1 ампера в секунду.
Одним из важных применений индукторов в активных цепях является то, что они имеют тенденцию блокировать высокочастотные сигналы, позволяя проходить колебаниям низких частот. Обратите внимание, что это противоположная функция конденсаторов. Объединение двух компонентов в цепи может избирательно фильтровать или генерировать колебания практически любой желаемой частоты.
С появлением интегральных микросхем, таких как микросхемы, катушки индуктивности становятся все менее распространенными, поскольку трехмерные катушки чрезвычайно сложно изготовить в 2D-печатных платах.По этой причине, по словам Майкла Дубсона, профессора физики из Университета Колорадо в Боулдере, микросхемы спроектированы без индукторов и вместо них используют конденсаторы, чтобы достичь практически одинаковых результатов.
Несколько примеров конденсаторов. Конденсаторы хранят электрический заряд. (Фото предоставлено Питером Матисом, Университет Колорадо)Емкость
Емкость — это способность устройства накапливать электрический заряд, и поэтому электронный компонент, который накапливает электрический заряд, называется конденсатором.Самый ранний пример конденсатора — лейденский сосуд. Это устройство было изобретено для хранения статического электрического заряда на проводящей фольге, которая выстилала стеклянную банку внутри и снаружи.
Самый простой конденсатор состоит из двух плоских проводящих пластин, разделенных небольшим зазором. Разность потенциалов, или напряжение, между пластинами пропорциональна разнице в количестве заряда на пластинах. Это выражается как Q = CV, где Q — заряд, V — напряжение, а C — емкость.
Емкость конденсатора — это количество заряда, которое он может хранить на единицу напряжения. Единицей измерения емкости является Фарад (F), названный по имени Фарадея, и определяется как способность хранить 1 кулон заряда с приложенным потенциалом 1 вольт. Один кулон (C) — это количество заряда, передаваемого током в 1 ампер за 1 секунду.
Чтобы максимизировать эффективность, пластины конденсаторов уложены слоями или намотаны в катушках с очень небольшим воздушным зазором между ними. Диэлектрические материалы — изоляционные материалы, которые частично блокируют электрическое поле между пластинами — часто используются в воздушном зазоре.Это позволяет пластинам хранить больше заряда без искрения и замыкания.
Конденсаторы часто встречаются в активных электронных цепях, которые используют колеблющиеся электрические сигналы, такие как в радио и аудиооборудовании. Они могут заряжаться и разряжаться практически мгновенно, что позволяет использовать их для создания или фильтрации определенных частот в цепях. Колеблющийся сигнал может заряжать одну пластину конденсатора, в то время как другая пластина разряжается, а затем, когда ток меняется на противоположный, он заряжает другую пластину, пока разряжается первая пластина.
Как правило, более высокие частоты могут проходить через конденсатор, тогда как более низкие частоты блокируются. Размер конденсатора определяет частоту среза, для которой сигналы блокируются или пропускаются. Конденсаторы в комбинации могут использоваться для фильтрации выбранных частот в указанном диапазоне.
Суперконденсаторы изготавливаются с использованием нанотехнологий для создания сверхтонких слоев материалов, таких как графен, для достижения емкости, в 10-100 раз превышающей емкость обычных конденсаторов такого же размера; но они имеют намного более медленное время отклика, чем обычные диэлектрические конденсаторы, поэтому их нельзя использовать в активных цепях.С другой стороны, они могут иногда использоваться в качестве источника питания в определенных приложениях, например в микросхемах памяти компьютера, для предотвращения потери данных при отключении основного питания.
Конденсаторы также являются важными компонентами устройств синхронизации, таких как разработанные компанией SiTime, базирующейся в Калифорнии. Эти устройства используются в самых разных приложениях, от мобильных телефонов до скоростных поездов и торговли на фондовом рынке. Известный как MEMS (микроэлектромеханические системы), крошечное устройство синхронизации полагается на конденсаторы для правильной работы.«Если резонатор [колебательный компонент в устройстве синхронизации] не имеет подходящего конденсатора и емкости нагрузки, схема синхронизации не будет запускаться надежно, а в некоторых случаях она вообще прекращает колебаться», — сказал Пиюш Севалия, исполнительный директор. вице-президент по маркетингу в SiTime.
Дополнительные ресурсы:
Эта статья была обновлена 16 января 2019 года автором Live Science Рэйчел Росс.
,