Как работает активное и реактивное сопротивление в цепи переменного тока. Какие виды сопротивлений существуют. Как рассчитать полное сопротивление цепи переменного тока. Какие эффекты оказывают разные типы сопротивлений на электрический ток.
Виды сопротивлений в цепи переменного тока
В цепях переменного тока различают три основных вида сопротивлений:
- Активное сопротивление (R)
- Индуктивное сопротивление (XL)
- Емкостное сопротивление (XC)
Каждый из этих видов сопротивлений оказывает свое специфическое влияние на протекание переменного тока в электрической цепи. Рассмотрим их подробнее.
Активное сопротивление в цепи переменного тока
Активное сопротивление R — это сопротивление проводника, измеренное при прохождении по нему переменного тока. Оно обусловлено преобразованием электрической энергии в тепловую.
Особенности активного сопротивления:
- Не зависит от частоты переменного тока
- Приводит к нагреву проводника
- Вызывает потери энергии в цепи
- Напряжение и ток на активном сопротивлении совпадают по фазе
Как активное сопротивление влияет на переменный ток?
Активное сопротивление оказывает одинаковое противодействие протеканию тока независимо от его направления и частоты. При этом происходит необратимое преобразование электрической энергии в тепловую.
Индуктивное сопротивление в цепи переменного тока
Индуктивное сопротивление XL обусловлено наличием в цепи катушек индуктивности. Оно возникает из-за явления самоиндукции в проводниках с током.
Ключевые свойства индуктивного сопротивления:
- Прямо пропорционально частоте переменного тока
- Вызывает отставание тока от напряжения по фазе на 90°
- Не приводит к потерям энергии
- При постоянном токе равно нулю
Как рассчитать индуктивное сопротивление?
Индуктивное сопротивление катушки рассчитывается по формуле:
XL = 2πfL
где f — частота переменного тока, L — индуктивность катушки.
Емкостное сопротивление в цепи переменного тока
Емкостное сопротивление XC создается конденсаторами в цепи переменного тока. Оно обусловлено периодической зарядкой и разрядкой конденсатора.
Характерные особенности емкостного сопротивления:
- Обратно пропорционально частоте переменного тока
- Вызывает опережение тока относительно напряжения на 90°
- Не приводит к потерям энергии
- При постоянном токе стремится к бесконечности
Формула для расчета емкостного сопротивления
Емкостное сопротивление конденсатора вычисляется по формуле:
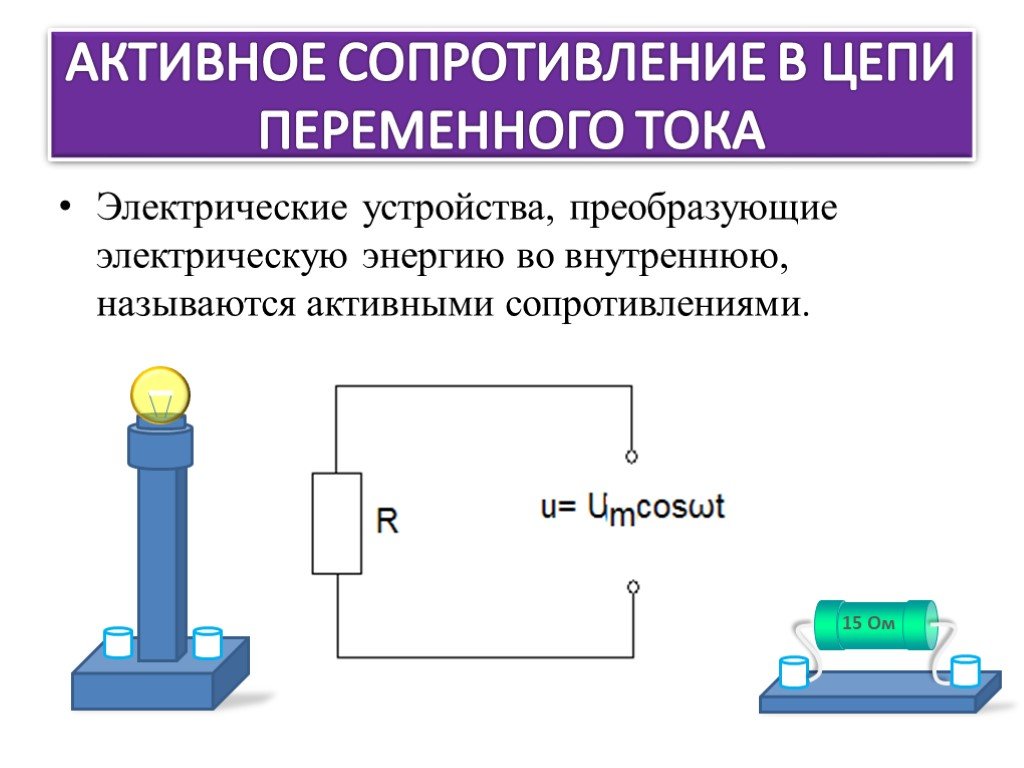
XC = 1 / (2πfC)
где f — частота переменного тока, C — емкость конденсатора.
Полное сопротивление цепи переменного тока
Полное сопротивление Z цепи переменного тока включает в себя все виды сопротивлений:
Z = √(R² + (XL — XC)²)
где R — активное сопротивление, XL — индуктивное сопротивление, XC — емкостное сопротивление.
Как рассчитать полное сопротивление цепи?
- Определить активное сопротивление R
- Рассчитать индуктивное сопротивление XL
- Вычислить емкостное сопротивление XC
- Подставить полученные значения в формулу полного сопротивления
Влияние разных видов сопротивлений на электрический ток
Каждый вид сопротивления оказывает специфическое воздействие на протекающий в цепи переменный ток:
- Активное сопротивление уменьшает амплитуду тока
- Индуктивное сопротивление вызывает отставание тока от напряжения
- Емкостное сопротивление приводит к опережению тока относительно напряжения
Как сопротивления влияют на мощность в цепи?
Влияние разных видов сопротивлений на мощность в цепи переменного тока:
- Активное сопротивление — вызывает активную мощность и потери энергии
- Индуктивное и емкостное — создают реактивную мощность без потерь энергии
Практическое применение знаний о сопротивлениях в электротехнике
Понимание особенностей разных видов сопротивлений важно для:
- Расчета и проектирования электрических цепей
- Анализа работы электрооборудования
- Повышения энергоэффективности электроустановок
- Правильного выбора элементов электрических схем
Где используются знания о сопротивлениях на практике?
Знания о сопротивлениях в цепях переменного тока применяются в следующих областях:
- Проектирование систем электроснабжения
- Разработка электронной аппаратуры
- Настройка и ремонт электрооборудования
- Оптимизация работы электрических машин и приборов
Заключение
Понимание природы и особенностей различных видов сопротивлений в цепях переменного тока крайне важно для специалистов в области электротехники и электроники. Эти знания позволяют грамотно проектировать, анализировать и оптимизировать работу электрических цепей и оборудования.
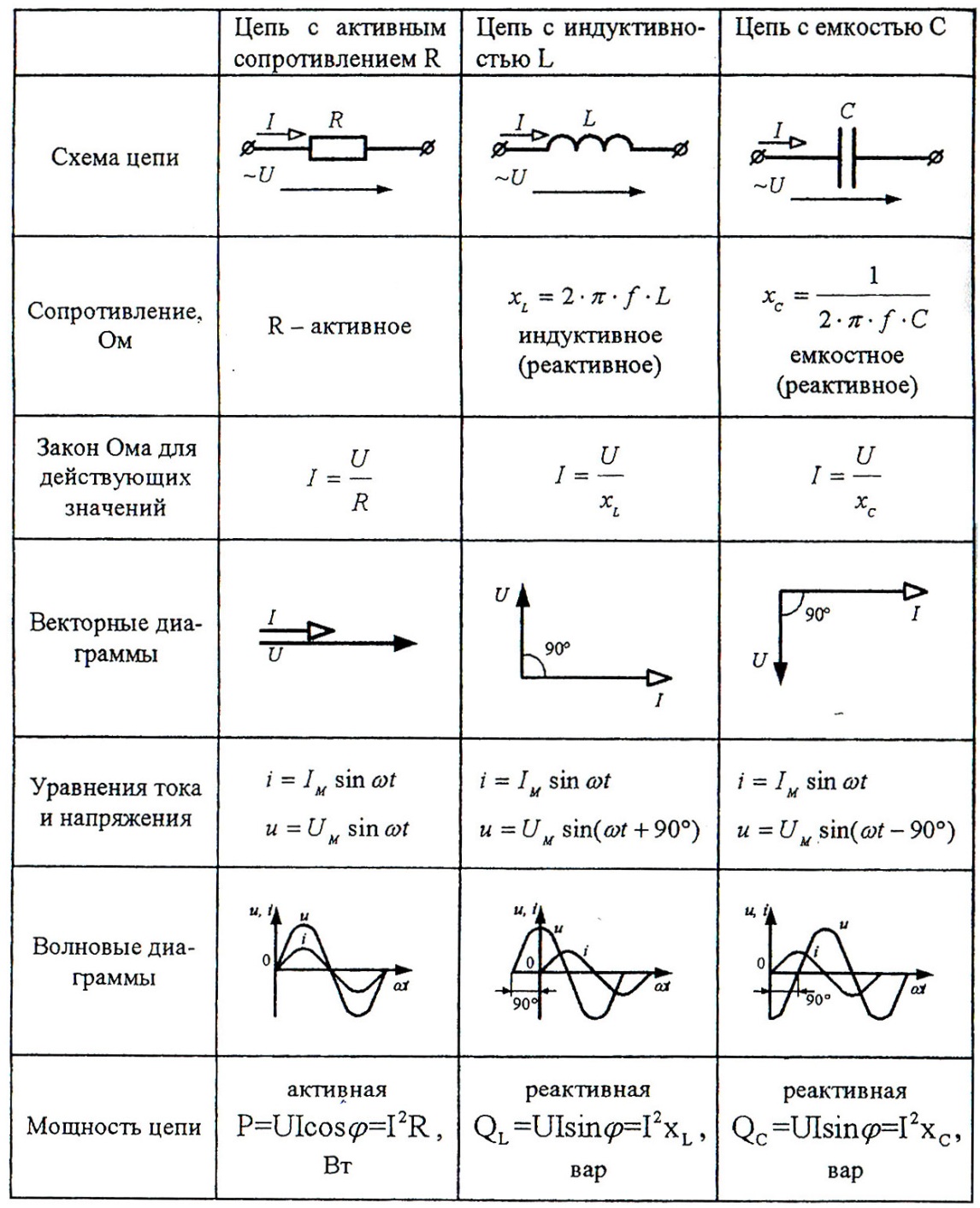
§ 52. Активное сопротивление в цепи переменного тока
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
Рассмотрим
цепь переменного тока (рис. 53), в которую
включено активное сопротивление. В
такой цепи под действием переменного
напряжения протекает переменный ток.
Изменение тока в Цепи, согласно закону
Ома, зависит только от изменения
напряжения, подключенного к ее
зажимам. Когда напряжение равно нулю,
ток в цепи также равен нулю. По мере
увеличения напряжения ток в Цепи
возрастает и при максимальном значении
напряжения ток становится наибольшим.
При уменьшении напряжения ток убывает.
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (=0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
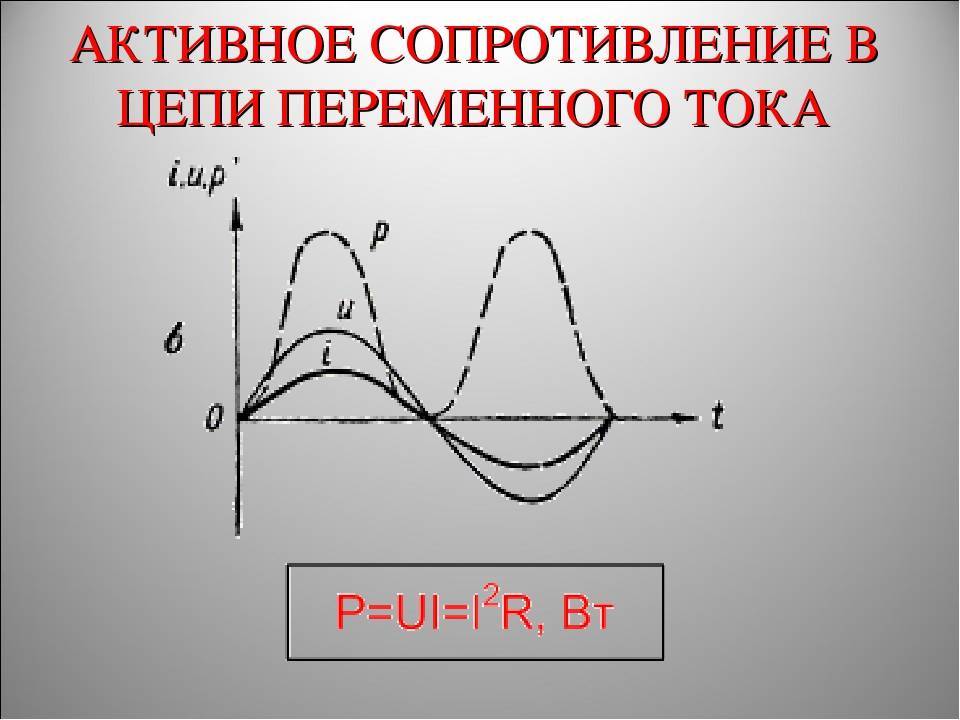
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
Пример.
К цепи переменного тока
с активным сопротивлением
r=55
ом подключен генератор,
максимальное значение напряжения
которого Um=310,2
в.
Определить:
показание вольтметра, подключенного к зажимам генератора;
показание амперметра, включенного в цепь;
среднее значение мощности, потребляемой сопротивлением.
Решение. Известно, что электроизмерительные приборы, включенные в цепь переменного тока, измеряют действующие значения. Поэтому показание вольтметра, измеряющего напряжение,
Показание амперметра, измеряющего действующее значение тока,
Среднее значение активной мощности, потребляемой сопротивлением, Р=220х4 = 880 вт или Р=I2r=42×55=16×55=880 вт.
Прохождение
электрического тока по проводнику или
катушки сопровождается появлением
магнитного поля.
Рассмотрим электрическую
цепь переменного тока (рис. 54,а), в которую
включена катушка индуктивности, имеющая
небольшое количество витком проволоки
сравнительно большого сечения, активное
сопротивления которой можно считать
практически равным нулю.
Под действием э.д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции
(55)
где L — индуктивность катушки,
— скорость изменения тока в ней.
Электродвижущая
сила самоиндукции, согласно правилу
Ленца, всегда противодействует
причине, вызывающей ее. Так как э. д. с.
самоиндукции всегда противодействует
изменениям переменного тока, вызываемым
э.д.с. генератора, то она препятствует
прохождению переменного тока.
При
расчетах это учитывается по индуктивному
сопротивлению, которое обозначается
ХL
и измеряется
в омах. Таким образом, индуктивное сопротивление катушки ХL зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э.д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ) и от индуктивности катушки L:
где XL, — индуктивное сопротивление, ом,
ώ — угловая частота переменного тока, рад/сек,
L — индуктивность катушки, гн.
Так как угловая частота переменного тока , то индуктивное сопротивление
где, f—-частота переменного тока, гц.
Пример. Катушка, обладающая индуктивностью L=0,5 гн, присоединена к источнику переменного тока, частота которого f=50 гц. Определить:
1) индуктивное сопротивление катушки при частоте f=50 гц;
2)
индуктивное сопротивление этой катушки
переменному току, частота которого
f=800
гц.
Решение. Индуктивное сопротивление переменному току при f=50 гц
При частоте тока f=800 гц
Приведенный
пример показывает, что индуктивное
сопротивление катушки повышается с
увеличением частоты переменного тока,
протекающего по ней. По мере уменьшения
частоты тока индуктивное сопротивление
убывает. Для постоянного тока, когда
ток в катушке не изменяется и магнитный
поток не пересекает ее витки, э.д.
с. самоиндукции не возникает, индуктивное
сопротивлений катушки Х
Выясним, как изменяется э. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток.
Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.
На
графике (рис.
54, в) переменный ток показан
в виде синусоиды (сплошная линия). В
первую четверть периода сила тока
возрастает от нулевого до максимального
значения. Электродвижущая сила
самоиндукции ес,
согласно правилу Ленца, препятствует
увеличению тока в цепи. Поэтому на
графике (пунктирной линией) показано,
что ес
в это время имеет отрицательное значение.
Во вторую четверть периода сила тока
в катушке убывает до нуля. В это время
э.д.с. самоиндукции изменяет свое
направление и увеличивается препятствуя
убыванию силы тока. В третью четверть
периода том изменяет свое направление
и постепенно увеличивается до
максимального значения; э. д. с.
самоиндукции имеет положительное
значение и далее, когда сила тока
убывает, э. д. с. самоиндукции опять
меняет свое направление и вновь
препятствует уменьшению силы тока
в цепи.
Из
сказанного следует, что ток в цепи и э.
д. с. самоиндукции не совпадают по фазе.
Ток опережает э.д.с. самоиндукции по
фазе на четверть периода или на угол
= 90°.
Необходимо также иметь в виду,
что в цепи с индуктивностью, не содержащей
г, в каждый момент времени электродвижущая
сила самоиндукции направлена навстречу
напряжению генератора U.
В связи с этим напряжения и э. д. с.
самоиндукции ес
также сдвинуты по фазе друг относительно
друга на 180°.
Из изложенного следует, что в цепи переменного тока, содержащей только индуктивность, ток отстает от напряжения, вырабатываемого генератором, на угол ==90о (на четверть периода) и опережает э.д.с. самоиндукции на 90°. Можно также сказать, что в индуктивной цепи напряжение опережает по фазе ток на 90°.
Построим векторную диаграмму тока и напряжения для цеь переменного тока с индуктивным сопротивлением. Для этого отложим вектор тока I по горизонтали в выбранном нами масштаба (рис. 54,6.)
Чтобы
на векторной диаграмме показать, что
напряжение опережает по фазе ток на
угол = 90°, откладываем вектор
напряжения вверх под углом 90°.
Закон
Ома для цепи с индуктивностью можно
выразить так:
Следует подчеркнуть, что имеется существенное отличие между индуктивным и активным сопротивлением переменному току.
Когда к генератору переменного тока подключена активная нагрузка, то энергия безвозвратно потребляется активным сопротивлением.
Если же к источнику переменного тока присоединено индуктивное сопротивление r= 0, то его энергия, пока сила тока возрастает, расходуется на возбуждение магнитного поля. Изменение этого поля вызывает возникновение э. д. с. самоиндукции. При уменьшении силы тока энергия, запасенная в магнитном поле, вследствие возникающей при этом э.д.с. самоиндукции возвращается обратно генератору.
В первую четверть периода сила тока в цепи с индуктивностью возрастает и энергия источника тока накапливается в магнитном поле. В это время э.д.с. самоиндукции направлена против напряжения.
Когда
сила тока достигнет максимального
значения и начинает во второй четверти
периода убывать, то э.
д.с. самоиндукции,
изменив свое направление, стремится
поддержать ток в цепи. Под действием
э.д.с. самоиндукции энергия магнитного
поля возвращается к источнику энергии
— генератору. Генератор в это время
работает в режиме двигателя, преобразуя
электрическую энергию в механическую.
В третью четверть периода сила тока в цепи под действием э. д. с. генератора увеличивается, и при этом ток протекает в противоположном направлении. В это время энергия генератора вновь накапливается в магнитном поле индуктивности.
В четвертую четверть периода сила тока в цепи убывает, а накопленная в магнитном поле энергия при воздействии э.д.с. самоиндукции вновь возвращается генератору.
Таким
образом, в первую и третью четверть
каждого периода генератор переменного
тока расходует свою энергию в цепи с
индуктивностью на создание магнитного
поля, а во вторую и четвертую четверть
каждого периода энергия, запасенная в
магнитном поле катушки в результате
возникающей э.
д. с. самоиндукции,
возвращается обратно генератору.
Из этого следует, что индуктивная нагрузка в отличие от активной в среднем не потребляет энергию, которую вырабатывает генератор, а в цепи с индуктивностью происходит «перекачивание» энергии от генератора в индуктивную нагрузку и обратно, т, е. возникают колебания энергии.
Из сказанного следует, что индуктивное сопротивление является Реактивным. В цепи, содержащей реактивное сопротивление, происходят колебания энергии от генератора к нагрузке и обратно.
|
Сопротивления в цепи переменного тока Категория: Сварка металлов Сопротивления в цепи переменного тока В цепях переменного тока различают активное, индуктивное и емкостное сопротивления. Под активным сопротивлением R понимается сопротивление проводника, измеренное при црохождении по нему переменного тока. В любой электрической цепи переменного тока вокруг проводников с током возникает магнитное поле, следовательно электрическая цепь всегда обладает индуктивностью. Если переменное напряжение приложить к катушке индуктивности, ток в цепи будет меньше в сравнении с тем током, который бы протекал при наличии одного активного сопротивления катушки. ЭДС самоиндукции катушки противодействует периодическим изменениям переменного тока, т. Индуктивное сопротивление XL при постоянном токе равно нулю. По этой причине недопустима ошибочная подача постоянного напряжения на электрические машины и аппараты переменного тока — в этом случае в их обмотках возникает очень большой постоянный ток, разрушающий их своим тепловым действием. Рис. 1. Взаимоиндукция Рис. 8. Совпадение (а) и сдвиг (б) по фазе синусоидальных напряжений и токов Индуктивность электрической цепи вызывает сдвиг по фазе между приложенным переменным напряжением и током, вызванным этим напряжением. В цепи с чистой индуктивностью (идеальный частный случай) ток отстает на четверть периода (90°) от приложенного напряжения. Электрический ток возникает под действием электрического поля, поэтому всякая электрическая цепь обладает некоторой емкостью С. Способность накапливать электрические заряды с одновременным повышением потенциала до определенного уровня называется электрической емкостью. Для получения необходимых емкостей применяют электрические конденсаторы. В некоторых случаях влияние емкостей на режим цепи незначительно и его можно не учитывать. Если к электрической цепи, замкнутой на емкость, приложить постоянное напряжение, то ток возникает только в момент включения и прекращается, когда емкость заряжается до напряжения источника. Переменное напряжение, приложенное к этой же цепи, изменяется периодически и вместе с ним периодически изменяется заряд емкости. Переменный ток создает переменный ток заряда и разряда. Конденсаторы различной емкости вызывают в цепи разные токи заряда и разряда. Конденсатор можно рассматривать как некоторое сопротивление переменному току, т: е. включенный в цепь переменного тока он вносит в нее дополнительное емкостное сопротивление, измеряемое в омах. Таким образом, индуктивность и емкость вносят дополнительные сопротивления в цепь переменного тока и вызывают сдвиг по фазе между приложенным напряжением и током, возникающим под действием этого напряжения. Причем индуктивность и емкость вызывают фазовые сдвиги противоположного направления, т. е. как бы компенсируют друг друга. Индуктивное XL и емкостное Хс сопротивления являются условными величинами, их возникновение обусловлено реакцией цепи на изменения тока и напряжения в ней, поэтому оба эти сопротивления называются реактивными. Индуктивное и емкостное сопротивления называют еще безваттными сопротивлениями, т. к. на их преодоление никакой мощности не затрачивается. На индуктивном сопротивлении XL энергия источника расходуется на создание только ЭДС самоиндукции, т. е. превращается в энергию магнитного поля — происходит попеременный обмен энергией между источником тока и магнитным полем катушки.
Реклама:Читать далее:Мощности в цепях переменного тока
Статьи по теме:
Главная → Справочник → Статьи → Блог → Форум |
Сопротивление проводника, измеренное при постоянном токе, называется омическим. В одной и той же электрической цепи активное сопротивление больше омического. При низких частотах переменного тока разница между активным и омическим сопротивлением проводника мала и ее можно не учитывать. В цепи переменного тока с активным сопротивлением (идеальный частный случай) напряжение и вызванный им ток совпадают по фазе, т. е. кривые напряжения и тока одновременно проходят через нулевые и амплитудные значения. На векторной диаграмме этой цепи векторы напряжения и тока совпадают по направлению.
е. в катушке возникает дополнительное препятствие (кроме активного сопротивления) прохождению по ней переменного тока. Противодействие катушки индуктивности переменному току, измеряемое в омах, условно назвали индуктивным сопротивлением. Индуктивное сопротивление пропорционально индуктивности цепи и частоте переменного тока. Коэффициент обусловлен круговым движением, связанным с периодом синусоидальной волны тока (напряжения). 
Чем больше переменный ток, тем меньше емкостное сопротивление конденсатора . Емкостное сопротивление цепи обратно пропорционально емкости конденсатора и частоте переменного тока.
На емкостном сопротивлении Хс энергия источника расходуется на создание электрического поля — происходит попеременный обмен энергией между источником тока и электрическим полем конденсатора.Поведение резистора при переменном токе
Поведение резистора при переменном токе
Для обычных токов и частот резистор ведет себя как диссипативный элемент, преобразующий электрическую энергию в тепло. |
Индекс Цепи переменного тока | |||||||||||||||
Емкость и импеданс в цепи переменного тока | Блог Advanced PCB DesignКлючевые выводы
Конденсаторы являются чрезвычайно распространенными компонентами практически в каждой электронной схеме. Область электроники содержит различные параметры, которые измеряют, помогают и влияют на функциональность и производительность каждого электронного устройства. Одним из важнейших параметров является импеданс в цепи переменного тока. В процессе проектирования необходимо точно оценивать импеданс, вызванный различными компонентами, чтобы принимать обоснованные проектные решения. Кроме того, такие параметры, как емкость и импеданс, должны оставаться в допустимых проектных пределах, иначе даже точные конструкции могут не обеспечить желаемую функциональность. Что такое емкость?Ниже приведено полезное определение емкости:
Теперь, когда мы определили емкость, давайте посмотрим на роль конденсатора в цепи переменного тока. Функция конденсатора в цепи переменного тока Конденсаторы представляют собой пассивные электронные компоненты, обеспечивающие накопление энергии в виде электростатического поля. Инженеры-электрики используют конденсаторы для улучшения коэффициента мощности в цепи переменного тока. Например, цепь переменного тока, питающая индуктивные нагрузки, такие как двигатель, приводит к запаздывающему току. Добавление конденсатора помогает компенсировать отстающий ток и приближает коэффициент мощности к единице. Коррекция коэффициента мощности повышает эффективность использования энергии и снижает счета за электроэнергию. Конденсаторы в фильтрах нижних частот В конструкции печатных плат конденсаторы часто используются в фильтрах нижних или верхних частот. Это связано с тем, что импеданс конденсатора зависит от частоты сигнала переменного тока, проходящего через него.
RC-фильтр нижних частот. Источник На приведенной выше диаграмме показан RC-фильтр нижних частот. Конденсатор зашунтирован на землю. Таким образом, высокочастотные сигналы направляются на землю. Это предотвращает попадание высокочастотного шума выше частоты среза на нагрузку. Частота среза RC-фильтра нижних частот определяется следующим уравнением.
Вы можете лучше понять поведение фильтра по его передаточной функции с помощью следующего преобразования Лапласа.
Конденсаторы в фильтрах верхних частот При этом конденсатор подключается последовательно с входным сигналом, образуя фильтр верхних частот. Судя по приведенной ниже диаграмме, конденсатор блокирует передачу постоянного тока или низкочастотных сигналов на нагрузку.
RC-фильтр верхних частот. Источник Частота среза фильтра верхних частот RC следующая:
Передаточная функция RC-фильтра верхних частот определяется следующим уравнением.
Емкость конденсатора.
Анатомия конденсатора. Конденсатор состоит из двух проводящих пластин, разделенных изолирующим материалом, называемым диэлектриком. Емкость конденсатора прямо пропорциональна площади поверхности его пластины и обратно пропорциональна расстоянию между пластинами. Емкость также зависит от диэлектрической проницаемости вещества, разделяющего эти пластины. Емкость выражается следующим уравнением:
Где C — емкость, q — электрический заряд, а V — дифференциальный потенциал на проводящих пластинах. Теперь, когда мы лучше понимаем емкость, давайте взглянем на импеданс в цепи переменного тока. Понимание импеданса в цепи переменного токаПолное сопротивление — это активное сопротивление электрической цепи или компонента переменному току, возникающее в результате комбинированного воздействия реактивного сопротивления и омического сопротивления. Другими словами, импеданс — это просто расширение принципов сопротивления в цепях переменного тока. Мы также определяем его как любое препятствие или меру противодействия электрического тока потоку энергии при подаче напряжения. Более техническое определение — это противопоставление электрической цепи потоку переменного тока одной частоты. Таким образом, это комбинация реактивного сопротивления и сопротивления, которую мы измеряем в омах, обозначая ее символом Z. Однако реактивное сопротивление (X) выражает сопротивление компонента переменному току, тогда как полное сопротивление (Z) представляет собой сумму реактивное сопротивление. Z = R + jX Здесь комплексное сопротивление равно Z. Обозначаем сопротивление как R (реальный аспект). Мы представляем реактивное сопротивление как X (воображаемый аспект). Имейте в виду, что реактивное сопротивление может быть как отрицательным, так и положительным, тогда как сопротивление всегда положительное. Кроме того, реактивное сопротивление накапливает энергию в магнитном или электрическом поле, а сопротивление внутри цепи рассеивает энергию в виде тепла. Теперь, когда мы изучили импеданс в цепи переменного тока, давайте посмотрим, как рассчитать импеданс конденсатора. Как рассчитать импеданс конденсатора Конденсатор создает в цепи определенный уровень емкости. Функционально конденсатор обеспечивает временное хранение электрической энергии в виде электрического потенциала, при котором ток конденсатора опережает его напряжение на 90°. Z C = -jX CXC — емкостное реактивное сопротивление, характеризующее, какое сопротивление будет иметь конденсатор на определенной частоте. Вышеприведенное уравнение можно расширить следующим образом: Z C = 1/j ω CЗдесь полное сопротивление конденсатора равно ZC. Угловая частота составляет ω, которая мы рассчитываем: ω = 2πfМы представляем частоту сигнала в виде F и капитанного параметра C. . сопротивление идеального конденсатора равно нулю. Однако реактивное сопротивление и импеданс реального конденсатора отрицательны для всех значений емкости и частоты. Эффективное сопротивление (абсолютное значение) конденсатора зависит и уменьшается с частотой. Из приведенных выше уравнений видно, что реактивное сопротивление конденсатора обратно пропорционально емкости и частоте. Следовательно, более высокая емкость и более высокая частота приводят к более низкому реактивному сопротивлению. Это позволяет использовать конденсаторы с другими компонентами в конструкциях фильтров нижних или верхних частот и блокирует избирательные частоты. Хотя емкость в цепи переменного тока легко различима, параметр импеданса в цепи переменного тока требует тщательного анализа цепи. Имея это в виду, получение более глубокого понимания взаимосвязи между емкостью и импедансом имеет первостепенное значение. Правильное использование конденсаторов и уверенность в том, что их влияние на импеданс в цепи переменного тока предсказуемо и приемлемо, требует хорошего программного обеспечения для проектирования и анализа печатных плат. Если вы хотите узнать больше о том, как у Cadence есть решение для вас, поговорите с нашей командой экспертов или подпишитесь на наш канал YouTube. Похожие записи
|
Он не зависит от направления тока и частоты. Поэтому мы говорим, что импеданс резистора по переменному току равен его сопротивлению постоянному току. Однако это предполагает, что вы используете среднеквадратичные или эффективные значения тока и напряжения в случае переменного тока. 
Также бывают случаи, когда требуется преобразование одного параметра в эквивалент другого. Более того, преобразование таких параметров, как емкость, в импеданс необходимо при выполнении подробного анализа цепи переменного тока. Поэтому очень важно, чтобы разработчики понимали взаимосвязь между емкостью и импедансом в цепях переменного тока. 
Конденсатор заряжается, когда переменный ток достигает своего пика в цепи переменного тока, и разряжается, когда переменный ток уменьшается. Такое поведение позволяет конденсатору действовать как временное хранилище, в котором ток опережает напряжение на 90 градусов.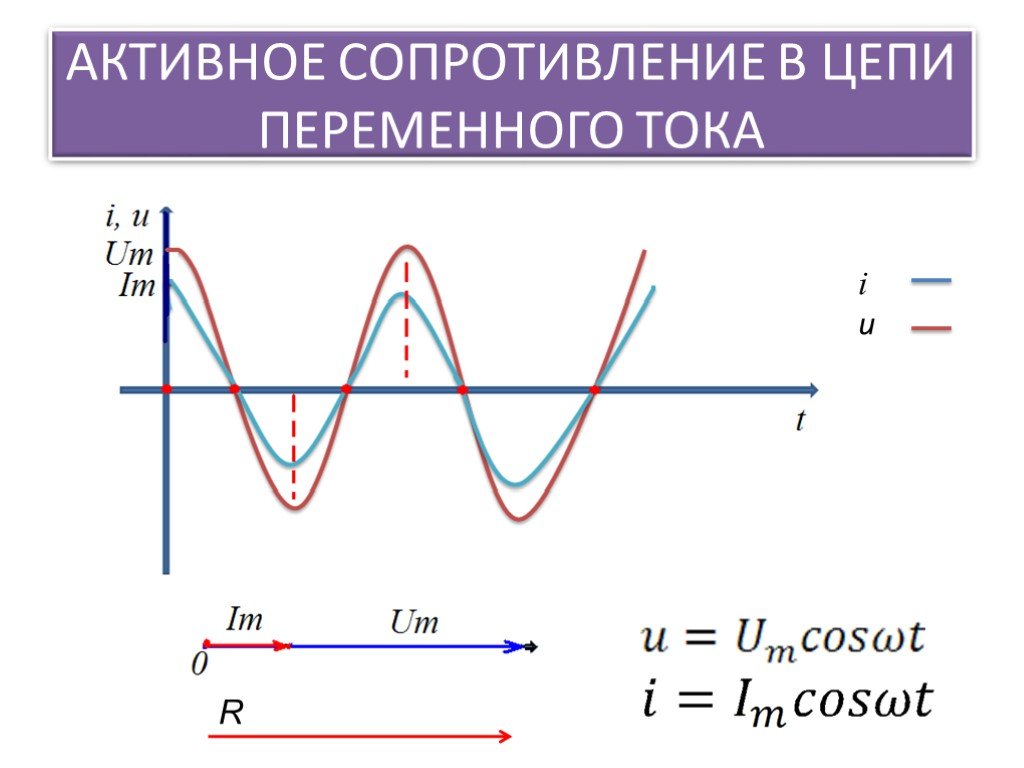 
Конденсатор обычно блокирует низкочастотные сигналы, пропуская более высокочастотные сигналы. 
Допускаются только сигналы выше частоты среза. 
Мы показываем его как комплексное число, используя следующую формулу: 
Формула импеданса конденсатора выглядит следующим образом: 