Активное сопротивление в цепи переменного тока это. Активное сопротивление в цепи переменного тока: особенности и характеристики

Что такое активное сопротивление в цепи переменного тока. Как оно влияет на параметры цепи. Какие особенности имеет активное сопротивление по сравнению с реактивным. Как рассчитать активное сопротивление в цепи переменного тока.

Понятие активного сопротивления в цепи переменного тока

Активное сопротивление в цепи переменного тока — это элемент электрической цепи, который преобразует электрическую энергию в другие виды энергии, например, в тепловую. Основные особенности активного сопротивления:

• На активном сопротивлении происходит необратимое преобразование электрической энергии в тепловую
• Ток и напряжение на активном сопротивлении совпадают по фазе
• Величина активного сопротивления не зависит от частоты переменного тока
• Активное сопротивление измеряется в Омах

Таким образом, активное сопротивление в цепи переменного тока аналогично обычному омическому сопротивлению в цепи постоянного тока. Оно характеризует способность элемента цепи преобразовывать электрическую энергию в тепловую.

Отличие активного сопротивления от реактивного

В чем заключается основное отличие активного сопротивления от реактивного в цепи переменного тока?

• Активное сопротивление вызывает необратимые потери энергии, а реактивное — обратимый обмен энергией между цепью и магнитным/электрическим полем
• На активном сопротивлении ток и напряжение совпадают по фазе, а на реактивном — сдвинуты на 90°
• Активное сопротивление не зависит от частоты, а реактивное — зависит
• Активное сопротивление всегда положительно, а реактивное может быть как положительным, так и отрицательным

Таким образом, активное и реактивное сопротивления играют разную роль в цепи переменного тока и по-разному влияют на ее параметры.

Формула активного сопротивления в цепи переменного тока

Как рассчитать активное сопротивление в цепи переменного тока? Для этого используется следующая формула:

R = U / I

где:

• R — активное сопротивление, Ом
• U — действующее значение напряжения, В
• I — действующее значение силы тока, А

Данная формула аналогична закону Ома для участка цепи. Важно отметить, что для расчета используются действующие (эффективные) значения тока и напряжения.

Влияние активного сопротивления на параметры цепи переменного тока

Как активное сопротивление влияет на основные параметры цепи переменного тока?

• Уменьшает амплитуду колебаний тока
• Вызывает выделение тепла в проводниках
• Приводит к потерям электрической энергии
• Не вызывает сдвига фаз между током и напряжением
• Определяет активную мощность в цепи

Таким образом, активное сопротивление играет важную роль в цепях переменного тока, влияя на основные характеристики и энергетические процессы.

Особенности активного сопротивления в различных элементах цепи

Активное сопротивление присуще различным элементам электрических цепей. Каковы его особенности в разных компонентах?

• В проводниках — определяется удельным сопротивлением материала и геометрическими размерами
• В резисторах — является основным параметром и специально задается при изготовлении
• В катушках индуктивности — обусловлено сопротивлением провода обмотки
• В конденсаторах — связано с потерями в диэлектрике
• В полупроводниковых приборах — зависит от типа прибора и режима работы

Понимание особенностей активного сопротивления в разных элементах позволяет правильно учитывать его влияние при расчете и проектировании электрических цепей.

Методы измерения активного сопротивления в цепи переменного тока

Какими способами можно измерить активное сопротивление в цепи переменного тока?

• Метод вольтметра-амперметра — измеряются действующие значения тока и напряжения
• Мостовой метод — используются мосты переменного тока
• Резонансный метод — основан на явлении резонанса напряжений
• Метод ваттметра — измеряется активная мощность
• Цифровые измерительные приборы — позволяют напрямую измерять активное сопротивление

Выбор метода измерения зависит от требуемой точности, диапазона измеряемых сопротивлений и особенностей исследуемой цепи.

Практическое применение активного сопротивления в электротехнике

Где на практике используется активное сопротивление в цепях переменного тока?

• Нагревательные элементы — преобразуют электрическую энергию в тепловую
• Осветительные приборы — лампы накаливания, светодиоды
• Измерительные приборы — шунты, добавочные сопротивления
• Балластные резисторы — для ограничения тока
• Демпфирующие цепи — для гашения колебаний

Таким образом, активное сопротивление широко применяется в различных областях электротехники и электроники для решения практических задач.

Урок 8. переменный электрический ток — Физика — 11 класс

Физика, 11 класс

Урок 8. Переменный электрический ток

Перечень вопросов, рассматриваемых на уроке:

1) Свойства переменного тока;

2) Понятия активного сопротивления, индуктивного и ёмкостного сопротивления;

3) Особенности переменного электрического тока на участке цепи с резистором;

4) Определение понятий: переменный электрический ток, активное сопротивление, индуктивное сопротивление, ёмкостное сопротивление.

Глоссарий по теме

Переменный электрический ток — это ток, периодически изменяющийся со временем.

Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю называют активным сопротивлением.

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Величину Х_C, обратную произведению ωC циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.

Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Сейчас невозможно представить себе нашу цивилизацию без электричества. Телевизоры, холодильники, компьютеры – вся бытовая техника работает на нем. Основным источником энергии является переменный ток.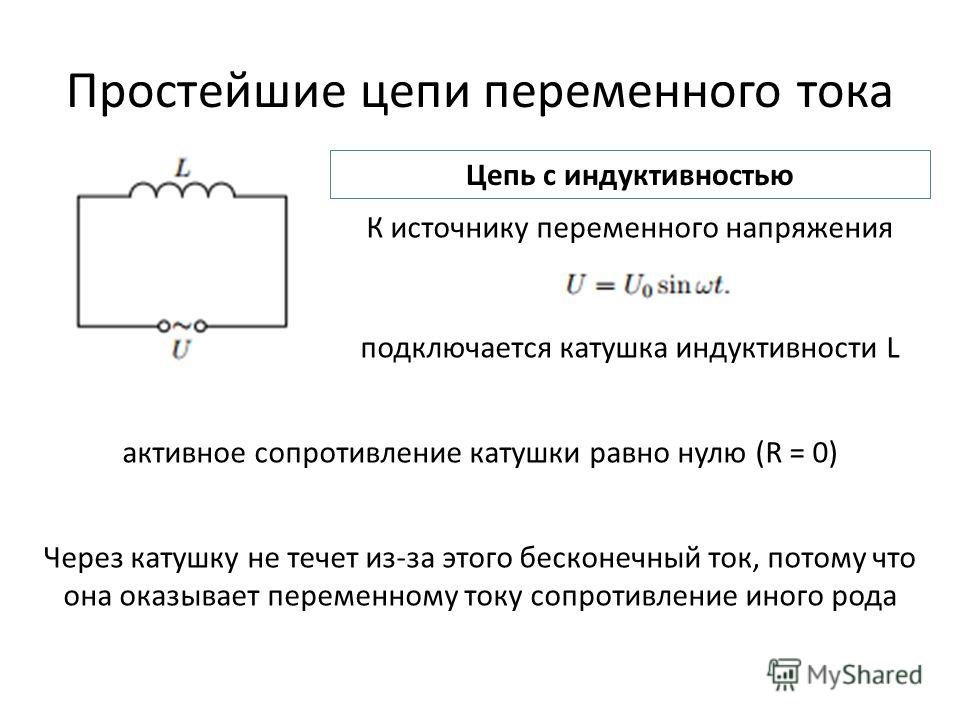

Электрический ток, питающий розетки в наших домах, является переменным А что это такое? Каковы его характеристики? Чем же переменный ток отличается от постоянного? Об этом мы поговорим на данном уроке.

В известном опыте Фарадея при движении полосового магнита относительно катушки появлялся ток, что фиксировалось стрелкой гальванометра, соединенного с катушкой. Если магнит привести колебательное движение относительно катушки, то стрелка гальванометра будет отклоняться то в одну сторону, то в другую – в зависимости от направления движения магнита. Это означает, что возникающий в катушке ток меняет свое направление. Такой ток называют переменным.

Электрический ток, периодически меняющийся со временем по модулю и направлению, называется переменным током.

Переменный электрический ток представляет собой электромагнитные вынужденные колебания. Переменный ток в отличие от постоянного имеет период, амплитуду и частоту.

Сила тока и напряжение меняются со временем по гармоническому закону, такой ток называется синусоидальным. В основном используется синусоидальный ток. Колебания тока можно наблюдать с помощью осциллографа.

Если напряжение на концах цепи будет меняться по гармоническому закону, то и напряженность внутри проводника будет так же меняться гармонически. Эти гармонические изменения напряженности поля, в свою очередь вызывают гармонические колебания упорядоченного движения свободных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи, в ней с очень большой скоростью распространяется электрическое поле. Сила переменного тока практически во всех сечениях проводника одинакова потому, что время распространения электромагнитного поля превышает период колебаний.

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока. Сопротивление проводника, в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным. При изменении напряжения на концах цепи по гармоническому закону, точно так же меняется напряженность электрического поля и в цепи появляется переменный ток.

При наличии такого сопротивления колебания силы тока и напряжения совпадают по фазе в любой момент времени.

𝒾 — мгновенное значение силы тока;

ℐ_m— амплитудное значение силы тока.

– колебания напряжения на концах цепи.

Колебания ЭДС индукции определяются формулами:

При совпадении фазы колебаний силы тока и напряжения мгновенная мощность равна произведению мгновенных значений силы тока и напряжения. Среднее значение мощности равно половине произведения квадрата амплитуды силы тока и активного сопротивления.

Часто к параметрам и характеристикам переменного тока относят действующие значения. Напряжение, ток или ЭДС, которая действует в цепи в каждый момент времени — мгновенное значение (помечают строчными буквами — і, u, e). Однако оценивать переменный ток, совершенную им работу, создаваемое тепло сложно рассчитывать по мгновенному значению, так как оно постоянно меняется. Поэтому применяют действующее, которое характеризует силу постоянного тока, выделяющего за время прохождения по проводнику столько же тепла, сколько это делает переменный.

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

U_m — амплитудное значение напряжения.

Действующие значения силы тока и напряжения:

Электрическая аппаратура в цепях переменного тока показывает именно действующие значения измеряемых величин.

Конденсатор включенный в электрическую цепь оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.

Величину Х_C, обратную произведению циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току.

Если включить в электрическую цепь катушку индуктивности, то она будет влиять на прохождение тока в цепи, т.е. оказывать сопротивление току. Это можно объяснить явлением самоиндукции.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

X_L= ωL

Если частота равна нулю, то индуктивное сопротивление тоже равно нулю.

При увеличении напряжения в цепи переменного тока сила тока будет увеличиваться так же, как и при постоянном токе. В цепи переменного тока содержащем активное сопротивление, конденсатор и катушка индуктивности будет оказываться сопротивление току. Сопротивление оказывает и катушка индуктивности, и конденсатор, и резистор. При расчёте общего сопротивления всё это надо учитывать. Основываясь на этом закон Ома для переменного тока формулируется следующим образом: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Если цепь содержит активное сопротивление, катушку и конденсатор соединенные последовательно, то полное сопротивление равно

Закон Ома для электрической цепи переменного тока записывается имеет вид:

Преимущество применения переменного тока заключается в том, что он передаётся потребителю с меньшими потерями.

В электрической цепи постоянного тока зная напряжение на зажимах потребителя и протекающий ток можем легко определить потребляемую мощность, умножив величину тока на напряжение.   В цепи переменного тока мощность равна произведению напряжения на силу тока и на коэффициент мощности.

Мощность цепи переменного тока

P=IU cosφ

Величина cosφ – называется коэффициентом мощности

Коэффициент мощности показывает какая часть энергии преобразуется в другие виды. Коэффициент мощности находят с помощью фазометров. Уменьшение коэффициента мощности приводит к увеличению тепловых потерь. Для повышения коэффициента мощности электродвигателей параллельно им подключают конденсаторы. Конденсатор и катушка индуктивности в цепи переменного тока создают противоположные сдвиги фаз. При одновременном включении конденсатора и катушки индуктивности происходит взаимная компенсация сдвига фаз и повышение коэффициента мощности. Повышение коэффициента мощности является важной народнохозяйственной задачей.

Разбор типовых тренировочных заданий

1. Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80 sin 25πt. Определите время одного оборота рамки.

Дано: e=80 sin 25πt.

Найти: T.

Решение:

Колебания ЭДС индукции в цепи переменного тока происходят по гармоническому закону

Согласно данным нашей задачи:

Время одного оборота, т.е. период связан с циклической частотой формулой:

Подставляем числовые данные:

Ответ: T = 0,08 c.

2. Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?

Дано:

ν=50 Гц,

R=1 кОм=1000 Ом,

C=1 мкФ=10^-6 Ф,

U=220 В.

Найти: I_m

Решение:

Напишем закон Ома для переменного тока:

I=U/Z

Для амплитудных значений силы тока и напряжения, мы можем записать I_m=U_m/Z?

Полное сопротивление цепи равно:

Подставляя числовые данные находим полное сопротивление Z≈3300 Ом. Так как действующее значение напряжения равно:

то после вычислений получаем I_m ≈0,09 Ом.

Ответ: I_m ≈0,09 Ом.

2. Установите соответствие между физической величиной и прибором для измерения.

Физические величины	Физические приборы
Сила тока	Омметр
Напряжение	Вольтметр
Сопротивление	Амперметр
Мощность	Ваттметр

Правильный ответ:

Физические величины	Физические приборы
Сила тока	Амперметр
Напряжение	Вольтметр
Сопротивление	Омметр
Мощность	Ваттметр

Формула активного сопротивления в цепи переменного тока

В электротехнике активное сопротивление в цепи переменного тока, так же как и реактивная нагрузка, относится к разряду труднодоступных для понимания тем.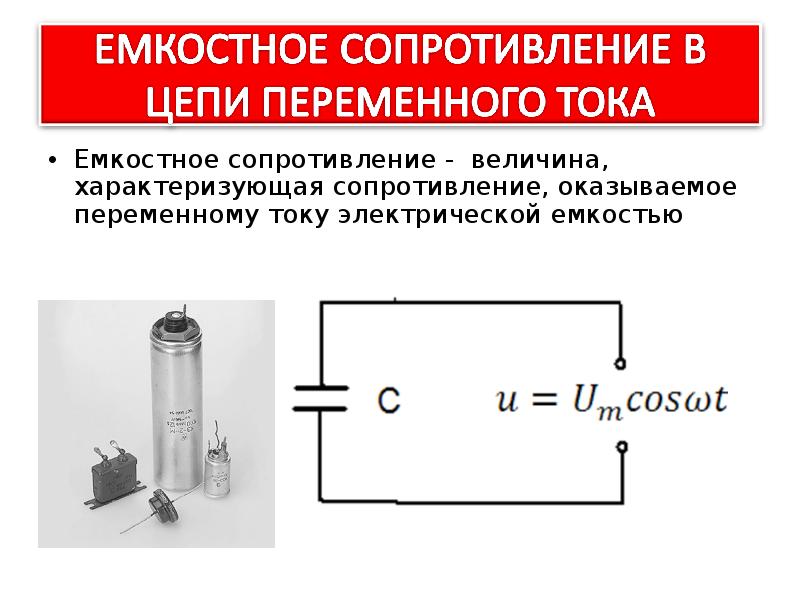 Только немногие специалисты могут понятно объяснить, какие процессы происходят на участке электрической схемы. Для начала понимания нужно обратиться к словарю и узнать, что означает слово «активный». Это деятельный, инициативный и энергичный элемент или объект. В электротехнике под сопротивлением с активным свойством понимают элемент, способный потреблять электроэнергию и превращать ее в иной вид энергии (свет, тепло или химические реакции). Специалисты его называют еще ваттным сопротивлением. К активным элементам в электрической схеме тока с переменной характеристикой относят различные накаливаемые элементы и, конечно же, лампы с нитью накаливания. Графически активное сопротивление рисуют в виде резистора.

Графическое обозначение элемента с активным свойством в электротехнике

Сопротивление с активным свойством в цепи с переменной характеристикой

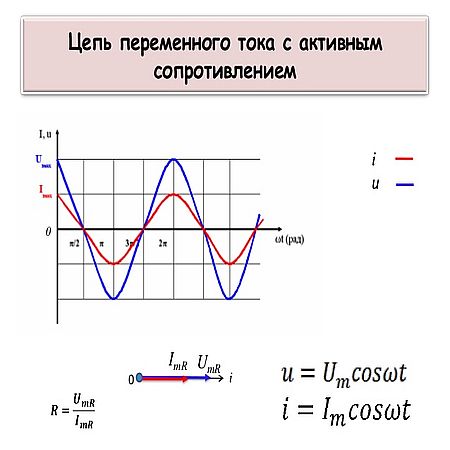
Если в цепь с переменной характеристикой тока подключить активную нагрузку, то по проводнику начнет протекать электрический ток по синусоидальной траектории. Это происходит за счет видоизменения напряжения по синусоиде:

u = Um sin ωt.

Отсюда и силу тока можно выразить формулой:

i = Im sin ωt,

где максимальная амплитуда силы тока считается по формуле:

Im =Um/R.

Важно знать! Сила тока в цепи с переменной характеристикой переменяется по тому закону, что и напряжение. То есть прохождение нулевой отметки у них происходит синхронно, так же как и достижение пиковой вершины.

Графика видоизменения силы тока и напряжения

Из графика видно, что за счет идеального активного в цепи сопротивления ток и напряжение совмещаются по фазе. Если в формуле:

i = Im sin ωt

каждую сторону поделить на √2, то получим формулу, выражающую закон Ома:

I=U/R.

Отсюда следует вывод, что для электрической схемы с переменной характеристикой, имеющей активное сопротивление, основополагающим законом является закон Ома.

Характеристики потерь

Причиной потерь с активной нагрузкой в схеме с переменной характеристикой тока являются:

1. Омическое сопротивление самого материала проводника;
2. Кроме этого, нельзя не обращать внимания на другие причины, как, например, наличие конденсатора (в электротехнике под ним можно подразумевать, например, кабель в изоляции).В такой схеме энергия теряется за счет постоянно изменяющего поляризацию диэлектрика такой изоляции. Это происходит за счет систематического «переворачивания» парных зарядов молекул, в свою очередь, приводящее к нагреву диэлектрического слоя. Такие потери в электротехнике называют диэлектрическими утечками;
3. Кроме диэлектрических потерь в конденсаторном элементе, в схеме переменного тока присутствует потеря утечки. Она возникает за счет несовершенства материала изоляции;
4. Также нельзя исключать потери на гистерезис, за счет постоянного присутствия переменного магнитного поля. Это приводит к нагреванию металлических частей схемы, так как наличествует систематическое переворачивание в такт с частотой переменного тока магнитиков;
5. Токи Фуко также порождают высокие утраты в электрической цепи с переменной характеристикой. Они представляют собой индуктивные круговые токи и подвергают нагреванию все элементы схемы.

Присутствие всех перечисленных потерь значительно увеличивает активное сопротивление в схеме с переменным током.

Мощность в схеме с активной нагрузкой

Когда схема функционирует на переменном напряжении и токе, то напряженность преобразования электрической энергии в иной вид энергии изменяется. Отсюда получается, что такое изменение меняет мощность. Из формулы:

p  = Umsinωt * Imsinωt = UmImsin2ωt

следует, что мгновенная мощность равноправна произведению мгновенного напряжения на мгновенную составляющую силы тока.

Генерация активной составляющей мощности

После тригонометрических переустройств видим, что мгновенная мощность одинакова по сумме с мгновенной и постоянной составляющими:

р = Р + р’, где Р = UmIm√2.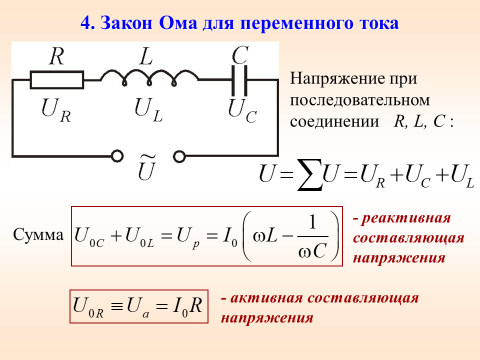

Важно знать! Под понятием активная мощность следует понимать, что она представляет собой среднее арифметическое мгновенных составляющих за определенный период времени.

На простом языке активная мощность – это положительная характеристика электрической схемы с переменным током. Она относится к разряду основных свойств в ходе выбора электрических нагрузок и учета потребления электрической энергии.

Взгляд на эффект с поверхностным влиянием

Активное сопротивление электрической цепи, функционирующей от переменного напряжения, постоянно больше от сопротивления с активной функцией в цепи постоянного напряжения. Основанием этому является то, что переменный ток по равноправному уровню разделяется по всей поперечной плоскости проводника. От этого полезная плоскость значительно убавляется, а сопротивление растет. Этот физический процесс называется эффектом поверхностного действия.

При поверхностном эффекте заряженные частицы в основном двигаются по внешней оболочке проводника, так как поверхность проводника становится полезным сечением. С увеличением частоты электроны двигаются, максимально приближаясь к внешним границам. Для понижения данного явления изготавливают провода специального устройства. Их делают с трубчатыми жилами или покрывают жилы металлами, имеющими идеальную проводимость. Схемы с серебряными выводами очень хорошо знакомы многим специалистам.

Понижение поверхностного эффекта

На практике для повышения активной мощности в электрических схемах применяют специальные устройства и технологии, позволяющие снизить потери и уменьшить реактивную характеристику мощности. Самыми распространенными являются компенсирующие конденсаторные установки, а в быту – это индивидуальные блоки питания. Также перед созданием электрической сети в проекты закладываются проводники с наибольшей проводимостью и требуемым от нагрузок сечением. Кроме этого, в сложных схемах немаловажным является равномерное распределение активных нагрузок потребителей.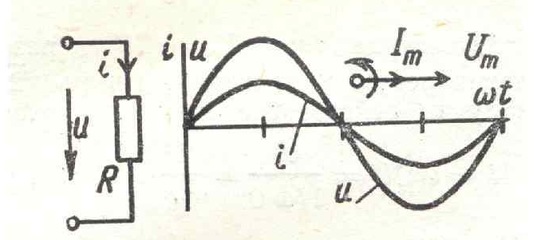

Видео

Оцените статью:

Переменный электрический ток. Активное, индуктивное, ёмкостное сопротивления.

Переменный электрический ток

Электромагнитные колебания, как и механические, бывают двух типов: свободные и вынужденные.

Свободные электромагнитные колебания, всегда колебания затухающие. Поэтому на практике они почти не используются. В то время, как вынужденные колебания используются везде и повсеместно. Ежедневно мы с вами можем наблюдать эти колебания.

Все наши квартиры освещены с помощью переменного тока. Переменный ток есть не что иное, как вынужденные электромагнитные колебания. Сила тока и напряжение будут меняться с течением времени согласно гармоническому закону. Колебания, например, напряжения можно обнаружить, если подать напряжение из розетки, на осциллограф.

На экране осциллографа появится синусоида. Можно вычислить частоту переменного тока. Она будет равняться частоте электромагнитных колебаний. Стандартная частота для промышленного переменного тока принята равной 50 Гц. То есть за 1 секунду направление тока в розетке меняется 50 раз.

Изменение напряжения на концах цепи будет вызывать за собой изменение силы тока в цепи колебательного контура. Следует всё же понимать, что изменение электрического поля во всей цепи не происходит мгновенно. Но так как это время, значительно меньше, чем период колебания напряжения на концах цепи, то обычно считают, что электрическое поле в цепи сразу же меняется, как меняется напряжение на концах цепи.

Переменное напряжение создается генераторами на электростанциях. Простейшим генератором можно рассматривать проволочную рамку, которая вращается в однородном магнитном поле. 

Магнитный поток, пронизывающий контур, будет постоянно меняться и будет пропорционален косинусу угла между вектором магнитной индукции и нормалью к рамке. Если рамка вращается равномерно, то угол будет пропорционален времени.

Следовательно, магнитный поток будет изменяться по гармоническому закону:

Ф = BScos(ωt)

Скорость изменения магнитного потока, взятая с обратным знаком, согласно закону ЭМИ, будет равняться ЭДС индукции.

E_i = -Ф’ = E_msin(ωt).

Если к рамке подключить колебательный контур, то угловая скорость вращения рамки определит частот колебаний напряжения на различных участках цепи и силы тока. В дальнейшем мы будем рассматривать только вынужденные электромагнитные колебания.

Они описываются следующими формулами:

u = U_msin(ωt),

u = U_mcos(ωt)

Здесь U_m – амплитуда колебаний напряжения. Напряжение и сила тока меняются с одинаковой частой ω. Но колебания напряжения не всегда будут совпадать с колебаниями силы тока, поэтому лучше использовать более общую формулу:

I = I_msin(ωt +φ), где I_m — амплитуда колебаний силы тока, а φ – сдвиг фаз между колебаниями силы тока и напряжения.

 Активное сопротивление

Рассмотрим следующую цепь.

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

U = U_mcos(ωt).

Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.

I = u/R = U_mcos(ωt)/R = I_mcos(ωt).

Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.

Действующее значение силы тока

Амплитуда силы тока определяется по следующей формуле:

I_m = U_m/R.

Среднее значение квадрата силы тока за период вычисляется по следующей формуле:

i² = (I_m)²/2.

Здесь I_m есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока. 

Для обозначения действующего значения силы тока используется буква I. То есть в виде формулы это будет выглядеть следующим образом:

I = √(i²) = I_m/√2.

Действующее значение силы переменного тока будет равно силе такого постоянного тока, при котором за одинаковый промежуток времени в рассматриваемом проводнике будет выделяться столько же теплоты, сколько и при переменном токе. Для определения действующего значения напряжения используется следующая формула.

U = √(u²) = U_m/√2.

Теперь подставим действующие значения силы тока и напряжения, в выражение I_m = U_m/R. Получим:

I = U/R.

Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения. 

Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

Для вычисления средней мощности используется следующая формула:

P = I²R = UI.

Отметим, что измерительные приборы (амперметры и вольтметры переменного тока) регистрируют именно действующие значения. Кроме того, номинальные значения напряжений и токов бытовых приборов также указываются как действующие значения. Так стандартное напряжение в цепи − 220 вольт есть действующее значение, а амплитудное значение этого напряжения равно

При изучении постоянного тока мы узнали, что он не может проходить в цепи, в которой есть конденсатор. Так как конденсатор — это две пластины, разделенные слоем диэлектрика. Для цепи постоянного тока конденсатор будет, как разрыв в цепи. Если конденсатор пропускает постоянный ток, значит, он неисправен.

В отличии от постоянного переменный ток может идти и через цепь, в которой присутствует конденсатор.

Рассмотрим, как будет меняться сила тока в цепи, содержащей конденсатор, с течением времени. При этом будем пренебрегать сопротивлением соединяющих проводов и обкладок конденсатора.

рисунок

Напряжение на конденсаторе будет равняться напряжению на концах цепи. Значит, мы можем приравнять эти две величины.

u = φ₁-φ₂ = q/C,   u = U_mcos(ωt).

Имеем:

q/C = U_mcos(ωt).

Выражаем заряд:

q = CU_mcos(ωt).

Видим, что заряд будет изменяться по гармоническому закону. Сила тока — это скорость изменения заряда. Значит, если возьмем производную от заряда, получим выражение для силы тока.

I = q’ = U_mCωcos(ωt+π/2).

Разность фаз между колебаниями силы тока и заряда, а также напряжения, получилась равной π/2. Получается, что колебания силы тока опережают по фазе колебания напряжения на π/2. Это представлено на рисунке.

Из уравнения колебаний силы тока получаем выражение для амплитуды силы тока:

I_m = U_mCω.

Введем следующее обозначение:

Xc = 1/(Cω).

Запишем следующее выражение закона Ома, используя Xc и действующие значения силы тока и напряжения:

I = U/Xc.

Xc — величина, называемая емкостным сопротивлением.

Индуктивность в цепи переменного тока будет влиять на силу переменного тока.

Рассмотрим цепь, в которой есть только катушка индуктивности. При этом значение сопротивления катушки и соединительных проводов пренебрежимо мало. 

рисунок

Выясним, как будут связаны напряжение на катушке с ЭДС самоиндукции в ней. При сопротивлении катушки равном нулю, напряженность электрического поля внутри проводника тоже будет равна нулю. Равенство нулю напряженности возможно.

Напряженности электрического поля создаваемого зарядами Eк будет соответствовать такая же по модулю и противоположно направленная напряженность вихревого электрического поля, которое появится вследствие изменения магнитного поля.

Следовательно, ЭДС самоиндукции e_i будет равна по модулю и противоположна по знаку удельной работе кулоновского поля.

Следовательно:  e_i = -u.

Сила тока будет изменяться по гармоническому закону: I = I_m sin(ωt).

ЭДС самоиндукции будет равна:  Ei = -Li’ = -Lω I_m cos(ωt).

Следовательно, напряжение будет равно:  U = Lω I_m cos(ωt) = Lω I_m sin(ωt+ π/2).

Отсюда значение действующего напряжения будет равняться U_m = Lω I_m. Видим, что между колебаниями тока и напряжения получилась разность фаз равная π/2. Следовательно, колебания силы тока отстают от колебания напряжения на π/2. Это наглядно представлено на следующем рисунке.

рисунок

I_m = U_m/(ωL). Введем обозначение XL = ωL. Эта величина называется индуктивное сопротивление.

Что такое активное сопротивление переменного тока?

Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.

Активное сопротивление в цепи переменного тока.

Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т. е. имеют место явления индуктивности. Ток возникает под действием электрического поля на заряды, следовательно, проводник должен обладать емкостью, так как в диэлектрической среде вокруг него возникает поток смещения.

Однако в ряде случаев относительная роль двух из трех параметров  R, L, С в электрической цепи практически незначительна. Это позволяет рассматривать подобную цепь как обладающую только сопротивлением, или только индуктивностью, или только емкостью. Мы рассмотрим поочередно условия в трех таких простейших цепях переменного тока.

В цепи, содержащей только сопротивление г, синусоидальное напряжени u = U_m sin ?t источника электроэнергии создает ток:

i = u : r = (U_m : r ) sin ?t

Так как сопротивление r от времени не зависит, то в этой цепи ток совпадает по фазе с напряжением (рис. 1) и изменяется также синусоидально:

i = I_m sin ?t

здесь:

I_m = U_m : r

Рисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.

Разделив последнее выражение на , получим формулу закона Ома для действующих значений напряжения и тока:

I = U : r

Как видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.

В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.). Оно может существенно отличаться от сопротивления r при постоянном токе. Сопротивление для постоянного тока называют омическим, чтобы отличить его от активного сопротивления для переменного тока.

Различие между активным и омическим сопротивлениями обуславливается рядом причин. Одна из них – поверхностный эффект, частичное вытеснение переменного тока в поверхностные слои проводника. Чем больше частота переменного тока, тем это вытеснение значительнее. Из-за поверхностного эффекта сопротивление r оказывается уже существенно большим, чем вычисленное по формуле:

r = ? (l : S)

Поверхностный эффект создается тем, что переменное магнитное поле индуктирует во внешних слоях проводника меньшую ЭДС самоиндукции, чем во внутренней его части. Особенно сильно поверхностный эффект увеличивает активное сопротивление стальных проводов. На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв.мм).

Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.

Переменный ток в цепи с активным сопротивлением. Цепь переменного тока с активным сопротивлением

Для простоты пренебрегаем. К зажимам цепи приложено синусоидальное напряжение

u = U m × sin ωt .

В цепи, представленной на рисунке 1, приложенное внешнее напряжение уравновешивается в сопротивлении r , которое называется активным падением напряжения и обозначается U a .

U a = I × r .

Мгновенное значение мощности в рассматриваемой цепи равно произведению мгновенных значений напряжения и тока:

p = u × i .

На рисунке 3 дана кривая мгновенной мощности за один . Из чертежа видно, что мощность не является постоянной величиной, она пульсирует с двойной .

Рисунок 3. Кривая мгновенной мощности цепи с активным сопротивлением

Среднее за период значение мощности или просто средняя мощность обозначается буквой P и может быть определена по формуле, доказательство которой мы не приводим:

P = U × I × cos φ ,

где угол φ — угол между напряжением и током.

Средняя мощность называется также активной мощностью. Данная формула справедлива для любых цепей переменного тока.

Для цепи с активным сопротивлением напряжение и ток совпадают по фазе. Поэтому угол φ равен нулю, а cos φ = 1. Для активной мощности получим:

P = U × I

P = I 2 × r ,

то есть формула мощности для цепи переменного тока с активным сопротивлением такая же, как формула мощности для цепи постоянного тока. Активным сопротивлением обладают все проводники. В цепи переменного тока практически только одним активным сопротивлением обладают нити ламп накаливания, спирали электронагревательных приборов и реостатов, дуговые лампы, специальные бифилярные обмотки и прямолинейные проводники небольшой длины.

1 Пульсацией называется изменение численного значения величины при постоянстве ее знака.

Рассмотрим цепь (фиг. 140), состоящую из сопротивления г. Влиянием индуктивности и емкости для простоты пренебрегаем.

К зажимам цепи приложено синусоидальное напряжение

Как следует из последнего выражения, вид закона Ома для цепи переменного тока, содержащей сопротивление, тот же, что для цепи постоянного тока. Кроме того, из закона Ома вид-на пропорциональность между мгновенным значением напряжения и мгновенным значением тока. Отсюда следует, что в цепи переменного тока, содержащей сопротивление г, напряжение и ток совпадают по фазе. На фиг. 141 даны кривые напряжения и тока и векторная диаграмма для рассматриваемой цепи, причем длины векторов обозначают действующие значения напряжения и тока. Сопротивление проводников переменному току несколько больше их сопротивления постоянному току. Это объясняется поверхностным эффектом, сущность которого изложена в 87. Поэтому сопротивление проводников переменному току называют активным. Обозначается оно также буквой r.

В цепи, представленной на фиг. 140, приложенное внешнее напряжение уравновешивается падением напряжения в сопротивлении r, которое называется активным падением напряжения и обозначается U a

Мгновенное значение мощности в рассматриваемой цепи равно произведению мгновенных значений напряжения и тока:

На фиг.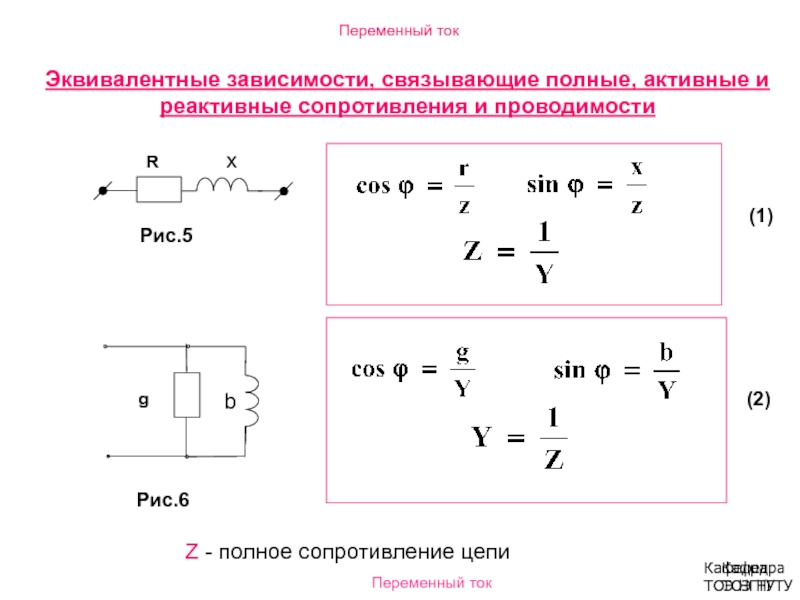 142 дана кривая мгновенной мощности за один период. Из чертежа видно, что мощность не является постоянной величиной, она пульсирует с двойной частотой.

Среднее за период значение мощности или просто средняя мощность обозначается буквой Р и может быть определена по формуле, доказательство которой мы не приводим:

Где — угол сдвига фаз между напряжением и током.

Средняя мощность называется также активной мощностью. Данная формула активной мощности справедлива для любых цепей переменного тока.

Для цепи с активным сопротивлением напряжение и ток совпадают по фазе. Поэтому угол равен нулю, a cos=1. Для активной мощности получим:

Т. е. формула мощности для цепи переменного тока с активным сопротивлением такая же, как формула мощности для цепи постоянного тока. Активным сопротивлением обладают все проводники. В цепи переменного тока практически только одним активным сопротивлением обладают нити ламп накаливания, спирали электронагревательных приборов и реостатов, дуговые лампы, специальные бифилярные обмотки и прямолинейные проводники небольшой длины.

Если цепь переменного тока содержит только резистор R (лампа накаливания, электронагревательный прибор и т. д.), к которому приложено переменное синусоидальное напряжение и (рис. 1-5, а):

то ток i в цепи будет определяться значением этого сопротивления:

где — амплитуда тока; при этом ток i и напряжение и совпадают по фазе. Обе эти величины, как видно, можно изобразить на временной (рис. 1-5, б) и векторной (1-5, в) диаграммах. Теперь установим, как изменяется мощность в любой момент времени — мгновенная мощность, характеризующая собой скорость преобразования электрической энергии в другие виды энергии в данный момент времени

где IU — произведение действующих значений тока и напряжения.

Из полученного следует, что мощность в течение периода остается положительной и пульсирует с удвоенной частотой. Графически это можно представить так, как показано на рисунке 1-6. В этом случае электрическая энергия превращается необратимо, например, в теплоту независимо от направления тока в цепи.

Кроме мгновенного значения мощности различают еще среднюю мощность за период:

но так как второй интеграл равен нулю, то окончательно имеем:

Средняя за период мощность переменного тока называется активной мощностью, а соответствующее ей сопротивление — активным.

Средняя мощность и активное сопротивление связаны с безвозвратным преобразованием электрической энергии в другие виды энергии. Активное сопротивление электрической цепи не сводится только к

сопротивлению проводников, в которых электрическая энергия превращается в теплоту. Это понятие значительно шире, так как средняя мощность электрической цепи равна сумме мощностей всех видов энергии, полученной из электрической, на всех участках цепи (теплота, механическая и др.).

Из полученных соотношений следует, что

которое является математической записью закона Ома для цепи переменного тока с активным сопротивлением.

Вынужденные Электромагнитные Колебания

Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника. Внешним источником ЭДС в электрических цепях являются генераторы переменного тока, работающие на электростанциях.

Принцип действия генератора переменного тока легко показать при рассмотрении вращающейся рамки провода в магнитном поле.

В однородное магнитное поле с индукцией В помещаем прямоугольную рамку, образованную проводниками (abсd).

Пусть плоскость рамки перпендикулярна индукции магнитного поля В и ее площадь равна S.

Магнитный поток в момент времени t 0 = 0 будет равен Ф = В*8.

При равномерном вращении рамки вокруг оси OO 1 с угловой скоростью w магнитный поток, пронизывающий рамку, будет изменяться с течением времени по закону:

Изменение магнитного потока возбуждает в рамке ЭДС индукцию, равную

где Е 0 = ВSw — амплитуда ЭДС.

Если с помощью контактных колец и скользящих по ним щеток соединить концы рамки с электрической цепью, то под действием ЭДС индукции, изменяющейся со временем по гармоническому закону, в электрической цепи возникнут вынужденные гармонические колебания силы тока — переменный ток .

На практике синусоидальная ЭДС возбуждается не путем вращения рамки в магнитном поле, а путем вращения магнита или электромагнита (ротора) внутри статора — неподвижных обмоток, навитых на сердечники из магнитомягкого материала. В этих обмотках находится переменная ЭДС, что позволяет избежать снятия напряжения с помощью контактных колец.

Переменный Ток

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока.

Если индуктивность проводника настолько мала, что при включении его в цепь переменного тока индукционными полями можно пренебречь по сравнению с внешним электрическим полем, то движение электрических зарядов в проводнике определяется действием только внешнего электрического поля, напряженность которого пропорциональна напряжению на концах проводника.

При изменении напряжения по гармоническому закону U = U m cos wt напряженность электрического поля в проводнике изменяется по такому же закону.

Под действием переменного электрического поля в проводнике возникает переменный электрический ток, частота и фаза колебаний которого совпадает с частотой и фазой колебаний напряжения:

где i — мгновенное значение силы тока, I m — амплитудное значение силы тока.

Колебания силы тока в цепи являются вынужденными электрическими колебаниями, возникающими под действием приложенного переменного напряжения.

Амплитуда силы тока равна:

При совпадении фаз колебаний силы тока и напряжения мгновенная мощность переменного тока равна:

Среднее значение квадрата косинуса за период равно 0,5. В результате средняя мощность за период

Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = PR), вводится понятие действующих значений силы тока и напряжения. Из равенства мощностей получим

Действующим значением силы тока называют величину, в корень из 2 раз меньшую ее амплитудного значения:

Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока.

Действующее значение переменного напряжения в корень из 2 раз меньше его амплитудного значения:

Средняя мощность переменного тока при совпадении фаз колебаний силы тока и напряжения равна произведению действующих значений силы тока и напряжения:

Сопротивление элемента электрической цепи, в которой происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением . Активное сопротивление участка цепи можно определить как частное от деления средней мощности на квадрат действующего значения силы тока:

Активным сопротивлением R называется физическая величина, равная отношению мощности к квадрату силы тока , что получается из выражения для мощности . При небольших частотах практически не зависит от частоты и совпадает с электрическим сопротивлением проводника.

Пусть в цепь переменного тока включена катушка. Тогда при изменении силы тока по закону в катушке возникает ЭДС самоиндукции . Т.к. электрическое сопротивление катушки равно нулю, то ЭДС равна минус напряжению на концах катушки, созданному внешним генератором (??? Каким еще генератором???) . Следовательно, изменение силы тока вызывает изменение напряжения, но со сдвигом по фазе . Произведение является амплитудой колебаний напряжение, т.е. . Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний тока называется индуктивным сопротивлением .

Пусть в цепи находится конденсатор. При его включение он четверть периода заряжается, потом столько же разряжается, потом то же самое, но со сменой полярности. При изменении напряжения на конденсаторе по гармоническому закону заряд на его обкладках равен . Ток в цепи возникает при изменении заряда: , аналогично случаю с катушкой амплитуда колебаний силы тока равна . Величина, равная отношению амплитуды к силе тока, называется емкостным сопротивлением .

АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. Сопротивление R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются. Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону: u = U m cos t. Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома : В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой P = I 2 R. (4.18) На протяжении очень малого интервала времени переменный ток можно считать практически постоянным. Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой P = i 2 R. (4.19) Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t Действующие значения силы тока и напряжения . Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I: Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока: Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем Это закон Ома для участка цепи переменного тока с резистором.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры ивольтметры переменного тока.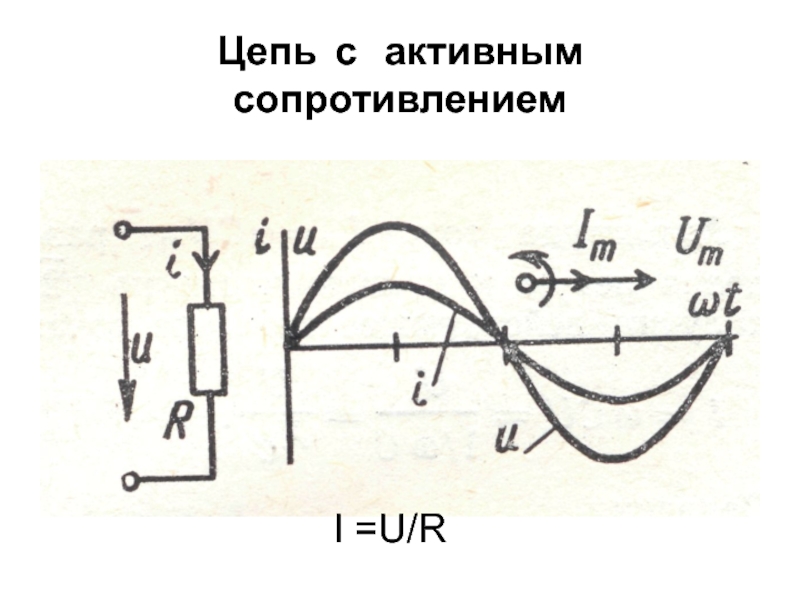

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока: P = I 2 R = UI. Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

Переменный ток оценивается его действием, эквивалентной действия постоянного тока. Активным сопротивлением называют такое сопротивление проводника, в котором электрическая энергия необратимо превращается во внутреннюю. Пусть напряжение в цепи переменного тока изменяется по гармоничным законом. Под действием переменного электрического поля в проводнике возникает переменный ток, частота и фаза колебаний которого совпадает с частотой и фазой колебания напряжения. Амплитудное значение силы тока равна отношению амплитудного значения напряжения к сопротивлению проводника. Мощность тока равна произведению силы тока и напряжения. Тогда активное сопротивление можно определить как отношение мощности переменного тока на участке цепи к квадрату действующей силы тока. Действующим значением силы тока называется сила постоянного тока, благодаря которой в проводнике выделяется за одинаковое время такое же количество теплоты, что и переменным током. Найти действующее значение силы тока можно как отношение амплитудного значения силы тока до квадратного корня из двух. Действующее значение напряжения также в корень из двух меньше его амплитудного значения.

При изучении вынужденных механических колебаний мы ознакомились с явлением резонанса . Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы. Если трение мало, то амплитуда установившихся вынужденных колебаний при резонансе резко увеличивается. Совпадение вида уравнений для описания механических и электромагнитных колебаний (позволяет сделать заключение о возможности резонанса также и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.

При механических колебаниях резонанс выражен отчетливо при малых значениях коэфициента трения . В электрической цепи роль коэффициента трения выполняет ее активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока но внутреннюю энергию проводника (проводник нагревается). Поэтому резонанс в электрическом колебательном кон-lype должен быть выражен отчетливо при малом активном сопротивлении R.

Мы с вами уже знаем, что если активное сопротивление мало, то собственная циклическая частота колебаний в контуре определяется формулой Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру, равна собственной частоте колебательного контура: Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внегннего переменного напряжения с собственной частотой колебательного контура.

Амплитуда силы тока при резонансе. Как и в случае механического резонанса, при резонансе в колебательном контуре создаются оптимальные условия для поступления энергии от внешнего источника в контур. Мощность в контуре максимальна в том случае, когда сила тока совпадает по фазе с напряжением. Здесь наблюдается полная аналогия с механическими колебаниями: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).

Не сразу после включения внешнего переменного напряжения в цепи устанавливается резонансное значение силы тока. Амплитуда колебаний силы тока нарастает постепенно — до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией , поступающей в контур за это же время:

Отсюда амплитуда установившихся колебаний силы тока при резонансе определяется уравнением При R 0 резонансное значение силы тока неограниченно возрастает: (I m) рез .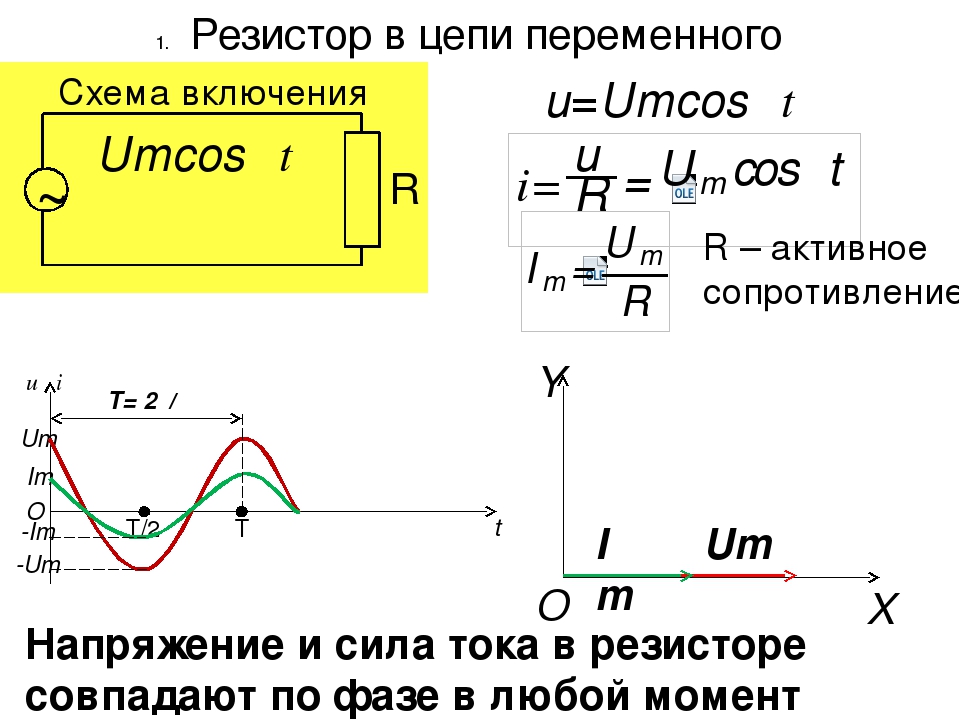 Наоборот, с увеличением R максимальное значение силы тока уменьшается, и при больших R говорить о резонансе уже не имеет смысла. Зависимость амплитуды силы тока от частоты при различных сопротивлениях (R 1 Одновременно с увеличением силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Эти напряжения при ма.пом активном сопротивлении во много раз превышают внешнее напряжение.

Использование резонанса в радиосвязи. Явление электрического резонанса широко используется при осуществлении радиосвязи. Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур (рис. 4.20). Вследствие электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока тех же частот. Но только при резонансе колебания силы тока в контуре и напряжения в нем будут значительными, т. е. из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте. Настройка контура на нужную частоту обычно осуществляется путем изменения емкости конденсатора . В этом обычно состоит настройка радиоприемника на определенную радиостанцию. Необходимость учета возможности резонанса в электрической цепи. В некоторых случаях резонанс в электрической цепи может принести большой вред. Если цепь не рассчитана на работу в условиях резонанса, то его возникновеие может привести к аварии.

Чрезмерно большие токи могут перегреть провода. Большие напряжения приводят к пробою изоляции.

Такого рода аварии нередко случались еще сравнительно недавно, когда плохо представляли себе законы электрических колебаний и не умели правильно рассчитывать электрические цепи .

При вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний. На явлении резонанса основана вся радиосвязь.

Изучение цепей переменного тока с активным, емкостным и индуктивным сопротивлениями происходит в следующей логической последовательности: сначала дается понятие о том или ином виде сопротивлений в цепи переменного тока (сравнение с его поведением в цепи постоянного тока), затем фазовые соотношения, формула соответствующего сопротивления, преобразования энергии в цепи, содержащей только активное, емкостное или индуктивное сопротивление. Последовательность изучения сопротивлений в цепи переменного тока может быть и несколько иной. Понятие действующего значения силы тока и напряжения можно ввести так: вначале выводят выражение для расчета мгновенных значений мощности на активном сопротивлении, отсюда находят среднее значение мощности за период и выясняют, что есть среднее значение квадрата силы тока за период. Вводят определение: корень квадратный из этой величины называют действующим значением переменного тока. Название связано с тем, что при прохождении такого тока по участку с активным сопротивлением выделяется мощность

Такая же мощность выделяется в цепи постоянного тока, величина которого равна действующему значению переменного тока. Итак, действующим значением переменного тока является такое значение постоянного тока, которое в резисторе R выделяет такое же количество теплоты, что и переменный ток. Очень важно отметить, что шкалы электроизмерительных приборов, для измерения переменных с

илы тока и напряжения градуируют именно в действующих значениях этих величин. Рассмотрение цепи переменного тока со смешанным сопротивлением начинают с эксперимента — измеряют напряжение на каждом из последовательно включенных элементов цепи (лампе, катушке и батарее конденсаторов), подключенных к источнику переменного напряжения. Обращают внимание на следующие опытные факты: 1. Общее напряжение не равно сумме напряжений на отдельных участках, как это имело место для цепей постоянного тока. 2. Напряжение на участке, включающем в себя катушку и конденсатор, равно не сумме, а разности напряжений на каждом из них в отдельности. Объяснить этот результат можно предложить самим учащимся; им известно, что на индуктивности напряжение опережает ток на π/2, а на электроемкости отстает от него на ту же величину. Так как мгновенное значение силы тока в цепи всюду одно и то же, то ясно, что колебания напряжения на индуктивности и электроемкости происходят со сдвигом фаз, равным π, т. е. их фазы противоположны. 3. Полное сопротивление цепи меньше суммы всех включенных в нее сопротивлений (активного, индуктивного и емкостного). Учащихся нужно убедить, что чем меньше сдвиг фаз между током и напряжением, тем большую часть мощности, подводимой к цепи, используют полезно, необратимо превращая в другие виды энергии. Далее рассматривают устройство и работу трансформатора. На примере однофазного трансформатора показывают его действие (повышение и понижение напряжения) и устройство. Вначале рассматривают режим холостого хода, а затем нагруженного трансформатора. В качестве нагрузки целесообразно использовать реостат, так как им проще изменять нагрузку. Показывают, что при увеличении нагрузки возрастает сила тока как во вторичной, так и в первичной обмотке трансформатора. Учащимся предлагают самим с энергетических позиций объяснить возрастание силы тока в первичной цепи (увеличение потребления энергии на нагрузке естественно должно сопровождаться увеличением потребления энергии первичной обмоткой от генератора). Для изучения электромагнитных колебаний широко используется школьный прибор- звуковой генератор школьный ГЗШ. Он перекрывает диапазон генерируемых частот синусоидальных колебаний от 20 до 20000 Гц с диапазонами: «X1» (от 20 до 200 Гц), «X10» (от 200 до 2000 Гц), «X100» (от 2000 до 20000 Гц), питается от сети переменного тока напряжением 220 В. На лицевую панель генератора выведены тумблёр включения генератора в сеть, сигнальная лампочка, переключатель поддиапазонов на три фиксированных положения, отмеченных «X1», «X10», «X100», диск с неравномерной шкалой деления (от 20 до 200) ручка переменного резистора, позволяющая менять амплитуду выходного сигнала, выходные зажимы, рассчитанные на подключение цепей с разным сопротивлением (5, 600, 5000 Ом). Если для опытов необходимы частоты 20 – 200 Гц, то переключатель устанавливают в положение «X1» если 200 – 2000 Гц – в положение «X10», а для частот 2000 – 20000 Гц используют положение «X100». Плавную регулировку частоты осуществляют поворотом диска. Так же широко используются выпрямители ВУП-1 и ВУП-2 ВУП-2 предназначен для обеспечения питанием демонстрационных установок в опытах по электричеству. Технические данные: Прибор позволяет получить на выходных зажимах: выпрямленное напряжение 350В при максимальной силе тока 220мА; постоянное отфильтрованное напряжение 250В при максимальной нагрузке 50мА; регулируемое напряжение от 0 до 250В постоянного тока до 50мА; регулируемое напряжение от 0 до +100В и от 0 до-100В постоянного тока до 10мА; напряжение 6.3В переменного тока до 3А. Еще один источник питания без которого практически невозможно осуществлять многие опыты по электричеству РНШ. Регулятор напряжения школьный предназначен для плавного регулирования напряжения однофазного переменного тока с частотой 50 Гц, при проведении лабораторных и демонстрационных опытов в физических кабинетах школ. Прибор присоединяется к сети выводным шнуром. Прибор можно включить в сеть напряжением 127 и 220В. Рабочее напряжение снимается с зажимов, обозначенных «Выходное напряжение». В целях правильной эксплуатации регулятора напряжения в паспорте прибора приведена таблица допустимых значений электрической мощности нагрузки регулятора при разных напряжениях, подаваемых на нагрузку, и при сетевых напряжениях 127 и 220В. Установленный в регуляторе напряжения вольтметр имеет неравномерную шкалу. Достоверный отсчет можно вести только при 50В. В случае необходимости снимать с регулятора более низкие напряжения нужно параллельно выходным зажимам подключать дополнительный вольтметр с соответствующим пределом измерения. Регулятор напряжения может быть использован как для повышения, так и для понижения напряжений переменного тока, при разных демонстрационных и лабораторных опытах Для наглядного отображения электромагнитных колебаний применяют школьные осциллографы ОДШ-2 и ОЭШ-70. Наиболее широко при­меняют осциллографы для исследования периодических процессов, а также для изучения вольтамперных характеристик диода и трио­да, петли гистерезиса и др. В простейшем случае осциллограф состоит из четырех блоков: блока электронно-лучевой трубки ЭЛТ, генератора развертки ГР, усилителя исследуемого сигнала УС и блока питания БП. Основным элементом первого блока является электронно-лучевая трубка, на экране которой формируется картина исследуемого сиг­нала (осциллограмма). Нить накала НН подогревает ка­тод К, с поверхности которого вылетают элект­роны. Электроны, пролетев через отверстия уп­равляющего электрода, фокусирующего ци­линдра ФЦ и анода А, а также между пласти­нами XX и УУ, попадают на экран и вызывают его свечение. Изменением разности потенциалов между катодом и управляющим электродом мож­но менять число электронов в пучке, а это по­зволяет регулировать яркость изображения на экране. Чем больше по модулю отрицательный потенциал на управляющем электроде относи­тельно катода, тем меньше электронов пройдет через управляющий электрод и достигнет анода. Осциллограф снабжен ручкой «яркость» для уп­равления потоком электронов в пучке. Электрическое поле между фокусирующим цилиндром и анодом способно фокусировать рас­ходящийся электронный пучок. Обычно на передней стенке смонтированы выключатель сети, сигнальная лампочка, за­жимы «Вход У», «Вход X» и делитель входного сигнала. На боко­вую панель выведены ручки управления электронным пучком, «Синхронизация», «Внутр. — от сети — внешн.», «Уси­ление», ручки развертки, «Диапазоны 0, 30, 150, 500 Гц, 2, 8, 16 кГц», «Частота плавно», а также ручки усиления сигнала «Уси­ление У», «Усиление X». Осциллограф ОДШ-2 отличается от ОЭШ-70 конструктивно и внешним оформлением. На переднюю панель выведен не только экран электронно-лучевой трубки, но и основные ручки уп­равления. Верхний ряд ручек предназначен для управления элек­тронным пучком: «Яркость», «Фокус», «Вверх-вниз», «Влево-вправо». Во втором ряду сверху смонтированы ручки управления уси­лителем «Усиление У» и делитель напряжения 1:1, 1:10, 1:30, 1:1OO, 1:1000, а также выключатель сети с сигнальной лампоч­кой. В третьем ряду сверху расположены ручки и кнопки генера­тора развертки: «Частота плавно», «Вкл. 1, 2, 3, 4», «Усиление X». Кнопочный переключатель позволяет менять пилообразное напря­жение частотой от 20 Гц до 20 кГц. Генератор развертки рабо­тает только при нажатой кнопке «Вкл». В нижнем ряду располо­жены зажимы «Вход У», «Вход X», «Внешн. синхр», кнопки син­хронизации «Внешн.», «Внутр.» и ручка синхронизации. На боковую панель осциллографа ОДШ-2 выведены ручки уп­равления двухканальным коммутатором с двумя входами. Комму­татор позволяет наблюдать на экране осциллографа одновремен­но сигналы от двух источников переменного тока. Если частоты источников одинаковы, то по полученным осциллограммам мож­но судить о сдвиге фаз поданных сигналов. Например, на один вход можно подать сигнал, пропорциональный напряжению на конденсаторе, а на другой — пропорциональный силе тока, текущего через конденсатор. Тогда на экране осциллографа можно наблю­дать две синусоиды, сдвинутые по фазе на 90°. Применяя комму­татор, можно сравнивать частоту исследуемого сигнала со стан­дартной частотой, если эти сигналы отличаются по частоте. На задней стенке осциллографов ОДШ-2 и ОЭШ-70 смонтиро­ваны гнезда, позволяющие подавать исследуемый сигнал непосред­ственно на пластины электронно-лучевой трубки. Возможность подавать исследуемый сигнал непосредственно на пластины позво­ляет применить осциллограф и для цепей постоянного тока. По­давая сигнал постоянного напряжения на пластины XX (или УУ) при отключенной развертке, можно наблюдать смещение светя­щейся точки по горизонтали (или вертикали), причем отклонение этой точки пропорционально приложенному напряжению. Следо­вательно, осциллограф можно применить как вольтметр с боль­шим внутренним сопротивлением. Для усиления электромагнитных колебаний применяют усилители низкой частоты. Усилитель низкой частоты– электронный прибор. Предназначенный для усиления электрических колебаний звуковой частоты от 20 Гц до 20 кГц. Обычно усилитель состоит из нескольких блоков: предварительного усилителя напряжения, усилителя мощности, согласующего выходного трансформатора и блока питания. Для школ выпускаются усилители разной конструкции и отличающиеся по внешнему виду. Усилитель УНЧ-3на лицевой панели имеет ручку регулятора громкости и сигнальную лампочку. Ручкой регулятора громкости производят также включение и выключение сети. В крайнем левом положении ручки при повороте против часовой стрелки прибор отключен. Включение осуществляют поворотом ручки по часовой стрелке после щелчка. Так как усилитель собран на электронных лампах, то он начинает работать после их прогрева. На боковой стенке смонтированы три входных гнезда: для подключения М – микрофона, АД – адаптера, Л – линии. Нижние гнёзда соединены с корпусом прибора. На задней стенке имеются две пары гнёзд: Гр – для подключения громкоговорителя (низкоомный выход) и Л – высокоомный выход. Здесь же имеются вывод сетевого шнура с вилкой и октальная панель, в которую вставлена специальная вилка с предохранителем (на 0,5 А) для сети с напряжением 220 В. Вилку можно устанавливать в двух положениях: «220 В» и «127 В». Усилитель УНЧ-5 собран на транзисторах. На лицевой панели усилителя смонтирован выключатель сети с индикаторной лампочкой, гнезда выхода, гнезда входа для микрофона и звукоснимателя, разъем для подключения микрофона, ручки регулировки тембра по низкой и высокой частоте, ручка регулировки уровня сигнала, индикатор перегрузки. На задней стенке имеются вывод сетевого шнура с вилкой и предохранитель (на 0,5 А). На вход усилителя могут подаваться сигналы не только с микрофона и звукоснимателя, но и от других датчиков электрических колебаний напряжением от нескольких милливольт до вольт (сигналы с элементов цепи переменного тока, звукового генератора и т.д.). К выходу усилителя можно подключить не только громкоговоритель, но и другие приборы: осциллограф, измерительные приборы переменного тока, головные телефоны и пр. Потребляемая усилителем мощность не более 40 Вт, выходная – около 5 Вт. Запрещается при эксплуатации усилителя менять предохранитель, разбирать и ремонтировать прибор, включенный в сеть. Усилитель на вертикальной панели входит в комплект демонстрационных приборов по радиотехнике. Слева смонтированы универсальные зажимы входа усилителя. Первая лампа работает в режиме усиления напряжения, вторая – как усилитель мощности. В анодную цепь второй лампы включен согласующий трансформатор, вторичная обмотка которого соединена с зажимами низкого и высокого выходного напряжения. Три нижних зажима служат для подключения питания от ВУП –2, на два нижних зажима подаётся напряжение переменного тока 6,3 В для питания накала ламп, а на средний и третий снизу – напряжение постоянного тока 250 В для анодной цепи ламп, причём на третий снизу зажим подаётся положительный потенциал. Подключение блока питания и сборку установок с усилителем на панели запрещается выполнять при включённом в сеть выпрямителе ВУП-2. В демонстрационных установках предпочтение следует отдавать усилителю УНЧ-5.

Формула активного сопротивления в цепи переменного тока

Различные факторы играют важную роль для вычисления потерь в линиях транспортировки электрической энергии. Для постоянного тока вполне хватает стандартных данных об омическом сопротивлении. А вот для цепей переменной разновидности необходимо учитывать активное и индуктивное сопротивление в сочетании с емкостной проводимостью токопроводников.

Можно воспользоваться для вычислений специальными таблицами. В них представлены с большой точностью различные варианты для выполнения расчетов в сетях переменного тока. Но, чтобы быстро разобраться в специфике представленных характеристик, желательно знать природу подобного явления и его основные характеристики.

Особенности активного сопротивления

Важно! Это явление наблюдается исключительно в ситуациях с переменным током. Только он способен образовывать в кабелях оба вида противодействия.

Величина активного сопротивления обусловлена эффектом поверхностного типа. Наблюдается процесс своеобразного перемещения тока от центра к поверхности проводника. Сечение кабеля используется не полностью, а возникающее противодействие будет значительно превышать аналогичный омический показатель.

Обратим внимание на такой момент:

1. Поверхностный эффект имеет незначительную величину в линиях из металлов, относящихся к категории цветных. Активное сопротивление приравнивают к омическому и считают его при условной температуре в +20°С, без учета фактических показателей окружающей среды. В справочниках имеются данные определения для использования в основном выражении R=r0l, с учетом того, что r0 – это номинальное значение искомой величины для 1 км провода, а l – его фактическая протяженность.
2. А вот в стальных изделиях данный показатель намного выше. Обязательно потребуется брать во внимание, зависящее от сечения явление перемагничивания и влияние таких компонентов, как вихревые токи. На практике обычно при больших нагрузках пользуются справочными данными. При этом, само явление ослабевает в проводниках многопроволочного типа.

Индуктивное сопротивление

Созданное в ходе передачи энергии переменное магнитное поле становится источником реактивного сопротивления подобного вида. Индуктивный вариант в основном зависит от характеристик проходящего тока, диаметра и расстояния между проводами.

Само сопротивление обычно классифицируют следующим образом:

• зависящее от параметров тока и материала — внутреннее;
• обусловленное геометрическими особенностями линии — внешнее. В этом случае данный показатель будет постоянной величиной, не зависящей от каких-либо других факторов.

Заводы по производству кабельной продукции всегда указывают в своих каталогах информацию об индуктивном сопротивлении.

Данный параметр обычно определяется следующим выражением:

в котором индуктивный показатель для 1 км провода – , а L – протяженность.

Х километрового участка рассчитывается по следующей формуле:

Где: Dср – расстояние среднее по центральной оси имеющихся проводов, мм; d – диаметр рабочего токопроводника, мм; μт –относительная магнитная проницаемость.

Принцип действия индуктивного сопротивления линий

Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.

Емкостная проводимость

Одним из эксплуатационных показателей остается данный параметр, обозначающий емкость между проводниками и землей, а также аналогичный показатель между самими токопроводниками.

Можно увидеть прямую зависимость рабочей емкости от уменьшения расстояния между кабелями и их сечения. Следовательно, для линий низкого напряжения данная величина всегда будет больше, чем для высокого.

Попытка применить именно подобный способ для самостоятельного выполнения будет весьма непростой задачей, ведь в нем применяются и различные конструктивные нюансы типа геометрических характеристик, и диэлектрическая проницаемость изоляционного слоя, и многие другие вводные. Следовательно, оптимальным решением будет информация из таблиц, составленных производителями для конкретной марки кабеля. В каталогах все данные приведены с учетом номинального напряжения для каждой модификации.

Данный показатель будет объективным только при полностью обесточенных приемниках электричества.

Большое значение обозначенная емкость в любой рассматриваемой конструкции имеет для точного выполнения предварительных расчетов для устройств компонентов защиты и элементов заземления.

Для кабельных магистралей:

Источник: https://uelektrika.ru/osnovy-yelektrotekhniki/aktivnoe-i-induktivnoe-soprotivleni/

Активное сопротивление: формула, от чего зависит, в чем измеряется реактивное сопротивление

Сопротивлением в электротехнике называют такую величину, которая характеризует противодействие отдельность части электрической сети или ее элементов электрическому току.

Это основано на том, что сопротивление изменяет электрическую энергию и конвертирует ее в другие типы.

Например, в сетях с переменных электротоком происходят необратимые изменения энергии и ее передача между участниками этой электроцепи.

Сопротивление как физическую величину трудно переоценить, так как она является одной из ключевых характеристик электричества в сети и прямо или пропорционально определяет силу тока и напряжение. Этот материал познакомит с такими понятиями как: активное сопротивление и реактивное сопротивление в цепи переменного тока, как проявляется зависимость активного сопротивления от частоты.

Векторное изображение полного импеданса

Какое сопротивление называется реактивным, какое активным

Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.

Типы рассматриваемой величины и формулы ее расчета

Реактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии. Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.

Течение переменного электротока не зависит от типа сопротивляемости элементов и всей сети

Какие отличия

Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.

Индуктивная величина и ее формулы

Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть.

Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.

Комплексная сопротивляемость отдельного элетроэлемента сети R

В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.

Активная сопротивляемость в цепи переменного синусоидального тока

От чего зависит активное сопротивление

Активное электросопротивление зависит от сечения проводника. Это значит, что полезным сечением при электротоке с высокой частотой будет только тонкий наружный слой проводника. Из этого исходит также то, что активностное электросопротивление только возрастает с увеличением частоты электротока переменного типа.

Для того чтобы уменьшить поверхностный эффект проводника, по которому течет электроток высокой частоты, его изготавливают трубчатым и покрывают напылением металла, хорошо проводящего электрический ток, например, серебром.

Схема косвенного метода амперметра, вольтметра и ваттметра

В чем измеряется реактивное сопротивление

Само по себе, явление реактанса характерно только для цепей с электрическим током переменного типа. Обозначается оно латинской буквой «X» и измеряется в Омах.

В отличие от активностного варианта, реактанс может иметь как положительное, так и отрицательное значение. Знак «+» или «-» соответствует знаку, по которому сдвигается фаза электротока и напряжения.

Знак положительный, когда ток отстает от напряжения и отрицателен, когда кот опережает напряжение.

Важно! Абсолютно чистое реактивное электросопротивление имеет сдвиг фазы на ± 180/2. То есть, фаза «двигается» на π/2.

Примером активной сопротивляемости — линия электропередач

Как правильно измерять сопротивление

При работе с радиоаппаратурой иногда требуется измерять не только активностное, но и реактивное электросопротивление (индуктивность и емкость). Для измерений применяют косвенный метод использования мультиметра, а более точные значения получают при мостовом методе.

Активом сопротивляемости может выступать любой резистор

Косвенный метод наиболее прост в своей реализации, так как не требует дополнительных схем включения. Одна требуется наличие трех отдельных приборов: амперметра, вольтметра и ваттметра.

Если измерить напряжение и силу электротока в цепи, то можно получить полное электросопротивление: Z=U*I  После измерения активностной мощности P, можно получить величину активного сопротивления отдельного элемента: R= P/I².

Обмотка трансформатора — один из примеров актива по превращению электроэнергии

Области проявления

Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.

Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя.

Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление.

Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.

Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.

Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.

Индукция ЭДС может наблюдаться в дросселе

Таким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.

Источник: https://rusenergetics.ru/polezno-znat/aktivnoe-soprotivlenie

Активное сопротивление. Действующие значения силы тока и напряжения — Класс!ная физика

«Физика — 11 класс»

Активное сопротивление

Сила тока в цепи с резистором

Есть цепь, состоящая из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R.

Сопротивление R называется активным сопротивлением, т.к. при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.

• Напряжение на зажимах цепи меняется по гармоническому закону:
• u = Um cos ωt
• Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. По закону Ома мгновенное значение силы тока:

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством

Мощность в цепи с резистором

В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются. При прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет меняться во времени.

1. Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
2. Р = I2R
3. Мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
4. Р = i2R

График зависимости мгновенной мощности от времени (рис.а):

Согласно графику (рис.б) среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в формуле для среднего значения мощности за период.

Действующие значения силы тока и напряжения

Среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично:

Закон Ома для участка цепи переменного тока с резистором в действующих значениях:

В случае электрических колебаний важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

• Действующие значения непосредственно определяют среднее значение мощности Р переменного тока:
• р = I2R = UI.
• Итак: Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
• Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Следующая страница «Конденсатор в цепи переменного тока» Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре.

Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление.

Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы

Источник: http://class-fizika.ru/11_27.html

Цепь переменного тока с активным сопротивлением

Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как u = Um sin ωt, то изменение тока i также идет по синусоиде:

Активное сопротивление

i = Im sin ωt

При этом

Так что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.

Мощность, ток, напряжение

Если взять равенство Im = Um / R и каждую из его частей разделить на √2, то в итоге получится ни что иное, как закон Ома, применимый для той цепи, которая рассматривается: I = U/R.

Таким образом, получается, что это основополагающий закон для той цепи, которая имеет в своем составе только активное сопротивление, с точки зрения математики имеет такую же форму, что и для цепи тока постоянного.

Такой показатель, как электрическая мощность P для цепи, имеющей в своем составе активное сопротивление, равняется произведению мгновенного значения напряжения U на мгновенное значение силы тока i в любой момент времени.

Из этого следует, что в цепях переменного тока, в отличие от цепей тока постоянного, мгновенная мощность P – величина непостоянная, а ее изменение происходит по кривой. Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения U и силы тока i перемножить при разных углах ωt.

Мощность изменяется по отношению к изменению тока с двойной частотой ωt. Это означает, что половине периода изменения напряжения и тока соответствует один период изменения мощности. Следует заметить, что абсолютно все значения, которые может принимать мощность, являются положительными величинами.

С точки зрения физики это означает, что от источника к приемнику передается энергия. Своих максимальных значений мощность достигает тогда, когда ωt = 270° и ωt = 90°.

В практическом отношении о той энергии W, которую создает электрический ток, принято судить по средней мощности, выражаемой формулой Рср = Р, а не по мощности максимальной. Ее можно определить, перемножив на время протекания тока среднее значение мощности W = Pt.

• Относительно линии АБ, соответствующей среднему значению мощности P, кривая мгновенной мощности симметрична. По этой причине
• P = Pmax / 2 = UI
• Если использовать закон Ома, то можно выразить активную мощность в следующем виде:
• P = I2R или P = U2/R.
• Специалисты в области электротехники ту среднюю мощность, которую потребляет активное сопротивление, чаще всего именуют или просто мощностью, или активной мощностью, а для ее обозначения используется буква P.

Необходимо особо отметить такую особенность проводников, включенных в сеть переменного тока: их активное сопротивление во всех случаях оказывается больше, чем если бы они были включены в сеть тока постоянного.

Причина этого состоит в том, что переменный ток не протекает равномерно распределяясь по всему поперечному сечению проводника, как ведёт себя постоянный ток, а выводится на его поверхность.

Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.

То, что переменный ток распределяется по сечению проводника неравномерно, объясняется действием электродвижущей силы самоиндукции. Она индуцируется в проводнике тем магнитным полем, которое создается током, проходящим по нему.

Необходимо заметить, что действие этого магнитного поля распространяется не только на окружающее проводник пространство, но и на внутреннюю его часть. По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности.

Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.

Электродвижущая сила самоиндукции является существенным препятствием для изменения тока, и поэтому он будет следовать преимущественно по поверхностным слоям проводника.

Необходимо также отметить, что сопротивление активных проводников в цепях переменного тока существенно зависит от частоты: чем она больше, тем выше ЭДС самоиндукции, и поэтому ток в большей степени подвергается вытеснению на поверхность.

Источник: http://selectelement.ru/basic-concepts/ac-active-resistance.php

Активное и реактивное сопротивление

В электротехнике понятие сопротивления представляет собой величину, за счет которой определенная часть цепи может противодействовать электрическому току. Она образуется за счет изменения и перехода электроэнергии в другое энергетическое состояние.

Данное явление присуще только переменному току, когда в сети образуется активное и реактивное сопротивление, выражающееся в необратимом изменении энергии или передаче этой энергии между отдельными компонентами электрической цепи.

В случае необратимых изменений электроэнергии сопротивление будет считаться активным, а при наличии обменных процессов – реактивным.

Основные различия между активным и реактивным сопротивлением

Когда электрический ток проходит через элементы с активным сопротивлением, происходят необратимые потери выделяемой мощности. Типичным примером служит электрическая плита, где в процессе работы происходят необратимые превращения электричества в тепловую энергию. То же самое происходит с резистором, в котором тепло выделяется, но обратно в электроэнергию не превращается.

Реактивное сопротивление возникает в тех случаях, когда переменный ток проходит через так называемые реактивные элементы, обладающие индуктивностью и емкостью.

Первое свойство характерно для катушки индуктивности без учета активного сопротивления ее обмотки. В данном случае причиной появления реактивного сопротивления считается ЭДС самоиндукции.

В зависимости от частоты тока, при ее возрастании, наблюдается и одновременный рост сопротивления, что отражается в формуле xl = wL.

Закон Ома для участка цепи

Реактивное сопротивление конденсатора зависит от емкости. Оно будет уменьшаться при увеличении частоты тока, поэтому данное свойство широко используется в электронике для выполнения регулировочных функций. В этом случае для расчетов используется формула xc = 1/wC.

В графике это выражение выглядит в виде треугольника сопротивлений, где реактивное и активное сопротивление соответствуют катетам, а полное сопротивление или импеданс – гипотенузе.

Индуктивное сопротивление

Реактивное сопротивление подразделяется на два основных вида – индуктивное и емкостное.

При рассмотрении первого варианта следует отметить возникновение в индуктивной обмотке магнитного поля под действием переменного тока.

В результате, в ней образуется ЭДС самоиндукции, направленной против движения тока при его росте, и по ходу движения при его уменьшении.

Таким образом, при всех изменениях тока и наличии взаимосвязей, ЭДС оказывает на него противоположное действие и приводит к созданию индуктивного сопротивления катушки.

Под влиянием ЭДС самоиндукции энергия магнитного поля обмотки возвращается в электрическую цепь. То есть, между источником питания и обмоткой происходит своеобразный обмен энергией. Это дает основание полагать, что катушка индуктивности обладает реактивным сопротивлением.

В качестве типичного примера можно рассмотреть действие реактивного сопротивления в трансформаторе. Данное устройство имеет общий магнитопровод, с расположенными на нем двумя обмотками или более, имеющими общую зависимость. На одну из них поступает электроэнергия из внешнего источника, а из другой выходит уже трансформированный ток.

Под действием первичного тока, проходящего по катушке, в магнитопроводе и вокруг него происходит наведение магнитного потока. В результате пересечения витков вторичной обмотки, в ней формируется вторичный ток.

При невозможности создания идеальной конструкции трансформатора, магнитный поток будет частично уходить в окружающую среду, что приведет к возникновению потерь.

От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.

Конденсатор в цепи переменного тока

Емкостное сопротивление

В цепи, содержащей емкость и источник переменного тока происходят изменения заряда. Такой емкостью обладают конденсаторы, обладающие максимальной энергией при полном заряде. Напряжение емкости создает сопротивление, противодействующее течению переменного тока, которое считается реактивным. В результате взаимодействия, конденсатор и источник тока постоянно обмениваются энергией.

В конструкцию конденсатора входят токопроводящие пластины в количестве двух и более штук, разделенных слоями диэлектрика. Такое разделение не позволяет постоянному току проходить через конденсатор. Переменный ток может проходить через емкостное устройство, отклоняясь при этом от своей первоначальной величины.

Изменения переменного тока происходят под влиянием емкостного сопротивления. Чтобы лучше понять схему работы, найдем и рассмотрим принцип действия данного явления. Переменное напряжение, приложенное к конденсатору, изменяется в форме синусоиды.

Под его воздействием на обкладках наблюдается всплеск, одновременно здесь накапливаются заряды электроэнергии с противоположными знаками. Их общее количество ограничено емкостью устройства и его габаритами.

Чем выше емкость устройства, тем больше времени требуется на зарядку.

В момент изменения полупериода колебания, напряжение на обкладках конденсатора меняет свою полярность на противоположное значение, потенциалы также изменяются, а заряды пластин перезаряжаются.

За счет этого удается создать течение первичного тока и находить способ противодействовать его прохождению, при уменьшении величины и сдвиге угла.

Зарядка обкладок позволяет току, проходящему через конденсатор, опережать напряжение на 90.

Компенсация реактивной мощности

С помощью электрических сетей осуществляется передача электроэнергии на значительные расстояния.

В большинстве случаев она используется для питания электродвигателей, имеющих высокое индуктивное сопротивление и большое количество резистивных элементов. К потребителям поступает полная мощность, которая делится на активную и реактивную.

В первом случае с помощью активной мощности совершается полезная работа, а во втором – происходит нагрев трансформаторных обмоток и электродвигателей.

Сколько миллиампер в ампере

Под действием реактивной составляющей, возникающей на индуктивных сопротивлениях, существенно понижается качество электроэнергии. Противостоять ее вредному воздействию помогает комплекс мероприятий по компенсации с использованием конденсаторных батарей. За счет емкостного сопротивления удается понизить косинус угла φ.

Компенсирующие устройства применяются на подстанциях, от которых электричество поступает к проблемным потребителям. Этот способ дает положительные результаты не только в промышленности, но и на бытовых объектах, снижая нагрузку на оборудование.

Источник: https://electric-220.ru/news/aktivnoe_i_reaktivnoe_soprotivlenie/2017-12-23-1414

Активное сопротивление в цепи переменного тока

Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R. Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону

u = Umsinωt

Найдём ток и мощность в цепи.

Ток в цепи переменного тока с активным сопротивлением

По закону Ома найдем выражение для мгновенного тока:

где Im = Um/R — амплитуда тока

Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).

Действующий ток найдем, разделив амплитуду на √ 2:

Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.

 Мгновенная мощность в цепи переменного тока с активным сопротивлением

При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p  = Umsinωt * Imsinωt = UmImsin2ωt

Из тригонометрии найдём 

Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t.

 Зависимость мощности от времени — периодическая кривая (рис. 13.2).

Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:

Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:

р = Р + р’

Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.

Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.

Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.

Активная мощность для цепи переменного тока с активным сопротивлением

Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.

Активная мощность — среднее арифметическое мгновенной мощности за период.

Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).

• Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
• В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
• P = UI
• Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
• P = UI = I2R = U2R

С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].

Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:

Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.

Источник: https://electrikam.com/aktivnoe-soprotivlenie-v-cepi-peremennogo-toka/

Активное и реактивное сопротивление. Треугольник сопротивлений

Активное и реактивное сопротивление — сопротивлением в электротехнике называется величина, которая характеризует противодействие части цепи электрическому току. Это сопротивление образовано путем изменения электрической энергии в другие типы энергии. В сетях переменного тока имеется необратимое изменение энергии и передача энергии между участниками электрической цепи.

При необратимом изменении электроэнергии компонента цепи в другие типы энергии, сопротивление элемента является активным. При осуществлении обменного процесса электроэнергией между компонентом цепи и источником, то сопротивление реактивное.

В электрической плите электроэнергия необратимо преобразуется в тепло, вследствие этого электроплита имеет активное сопротивление, так же как и элементы, преобразующие электричество в свет, механическое движение и т.д.

В индуктивной обмотке переменный ток образует магнитное поле. Под воздействием переменного тока в обмотке образуется ЭДС самоиндукции, которая направлена навстречу току при его увеличении, и по ходу тока при его уменьшении. Поэтому, ЭДС оказывает противоположное действие изменению тока, создавая индуктивное сопротивление катушки.

С помощью ЭДС самоиндукции осуществляется возвращение энергии магнитного поля обмотки в электрическую цепь. В итоге обмотка индуктивности и источник питания производят обмен энергией. Это можно сравнить с маятником, который при колебаниях преобразует потенциальную и кинетическую энергию. Отсюда следует, что сопротивление индуктивной катушки имеет реактивное сопротивление.

Самоиндукция не образуется в цепи постоянного тока, и индуктивное сопротивление отсутствует. В цепи емкости и источника переменного тока изменяется заряд, значит между емкостью и источником тока протекает переменный ток. При полном заряде конденсатора его энергия наибольшая.

В цепи напряжение емкости создает противодействие течению тока своим сопротивлением, и называется реактивным. Между конденсатором и источником происходит обмен энергией.

После полной зарядки емкости постоянным током напряжение его поля выравнивает напряжение источника, поэтому ток равен нулю.

Конденсатор и катушка в цепи переменного тока работают некоторое время в качестве потребителя энергии, когда накапливают заряд. И также работают в качестве генератора при возвращении энергии обратно в цепь.

Если сказать простыми словами, то активное и реактивное сопротивление – это противодействие току снижения напряжения на элементе схемы. Величина снижения напряжения на активном сопротивлении имеет всегда встречное направление, а на реактивной составляющей – попутно току или навстречу, создавая сопротивление изменению тока

Настоящие элементы цепи на практике имеют все три вида сопротивления сразу. Но иногда можно пренебречь некоторыми из них ввиду незначительных величин. Например, емкость имеет только емкостное сопротивление (при пренебрежении потерь энергии), лампы освещения имеют только активное (омическое) сопротивление, а обмотки трансформатора и электромотора – индуктивное и активное.

Активное сопротивление

В цепи действия напряжения и тока, создает противодействие, снижения напряжения на активном сопротивлении. Падение напряжения, созданное током и оказывающее противодействие ему, равно активному сопротивлению.

При протекании тока по компонентам с активным сопротивлением, снижение мощности становится необратимым. Можно рассмотреть резистор, на котором выделяется тепло. Выделенное тепло не превращается обратно в электроэнергию. Активное сопротивление, также может иметь линия передачи электроэнергии, соединительные кабели, проводники, катушки трансформаторов, обмотки электромотора и т.д.

• Отличительным признаком элементов цепи, которые обладают только активной составляющей сопротивления, является совпадение напряжения и тока по фазе. Это сопротивление вычисляется по формуле:
• R = U/I, где R – сопротивление элемента, U – напряжение на нем, I – сила тока, протекающего через элемент цепи.
• На активное сопротивление влияют свойства и параметры проводника: температура, поперечное сечение, материал, длина.

Реактивное сопротивление

Тип сопротивления, определяющий соотношение напряжения и тока на емкостной и индуктивной нагрузке, не обусловленное количеством израсходованной электроэнергии, называется реактивным сопротивлением. Оно имеет место только при переменном токе, и может иметь отрицательное и положительное значение, в зависимости от направления сдвига фаз тока и напряжения. При отставании тока от напряжения величина реактивной составляющей сопротивления имеет положительное значение, а если отстает напряжение от тока, то реактивное сопротивление имеет знак минус.

Активное и реактивное сопротивление, свойства и разновидности

Рассмотрим два вида этого сопротивления: емкостное и индуктивное. Для трансформаторов, соленоидов, обмоток генераторов и моторов характерно индуктивное сопротивление. Емкостный вид сопротивления имеют конденсаторы. Чтобы определить соотношение напряжения и тока, нужно знать значение обоих видов сопротивления, которое оказывает проводник.

Реактивное сопротивление образуется при помощи снижения реактивной мощности, затраченной на образование магнитного поля в цепи. Снижение реактивной мощности создается путем подключения к трансформатору прибора с активным сопротивлением.

Конденсатор, подключенный в цепь, успевает накопить только ограниченную часть заряда перед изменением полярности напряжения на противоположный. Поэтому ток не снижается до нуля, так как при постоянном токе. Чем ниже частота тока, тем меньше заряда накопит конденсатор, и будет меньше создавать противодействие току, что образует реактивное сопротивление.

Иногда цепь имеет реактивные компоненты, но в результате реактивная составляющая равна нулю. Это подразумевает равенство фазного напряжения и тока. В случае отличия от нуля реактивного сопротивления, между током и напряжением образуется разность фаз.

Катушка имеет индуктивное сопротивлением в схеме цепи переменного тока. В идеальном виде ее активное сопротивление не учитывают. Индуктивное сопротивление образуется с помощью ЭДС самоиндукции. При повышении частоты тока возрастает и индуктивное сопротивление.

На индуктивное сопротивление катушки оказывает влияние индуктивность обмотки и частота в сети.

Конденсатор образует реактивное сопротивление из-за наличия емкости. При возрастании частоты в сети его емкостное противодействие (сопротивление) снижается. Это дает возможность активно его применять в электронной промышленности в виде шунта с изменяемой величиной.

Треугольник сопротивлений

Схема цепи, подключенной к переменному току, имеет полное сопротивление, которое можно определить в виде суммы квадратов реактивного и активного сопротивлений.

Если изобразить это выражение в виде графика, то получится треугольник сопротивлений. Он образуется, если рассчитать последовательную цепь всех трех видов сопротивлений.

По этому треугольному графику можно увидеть, что катеты представляют собой активное и реактивное сопротивление, а гипотенуза является полным сопротивлением.

Похожие темы:

Источник: https://electrosam.ru/glavnaja/jelektrotehnika/aktivnoe-i-reaktivnoe-soprotivlenie/

Простейшие цепи переменного тока — Электротехника — Учебные материалы — Каталог статей

Список всех статей на технические темы

Простая электротехника все статьи

Сначала читаем статью «Переменный ток — краткие сведения»

 

Все электротехнические устройства состоят из сопротивлений индуктивностей и емкостей

 

 

Соотношение индуктивности емкости в цепи переменного тока принципиально определяют свойства цепи переменного тока.

 

Активное сопротивление R — это такой элемент электрической цепи, который оказывает сопротивление току с выделением тепла. Ведет себя одинаково в цепях постоянного и переменного тока, хотя величина сопротивления несколько отличается, это придется учитывать в точных расчетах.

 

 

Индуктивность L –это такой элемент электрической цепи, который состоит из витков провода и при протекании тока создает магнитное поле, это магнитное поле противодействует изменениям тока.

 

 

При протекании постоянного тока индуктивность ведет себя как проволока и не считается сопротивлением. Сопротивлением она является только для переменного тока, чем больше частота переменного тока, тем больше сопротивление индуктивности.

 

Емкость C – это такой элемент электрической цепи, который накапливает заряд, и проводит ток, только пока заряжается, или разряжается, поэтому в цепях постоянного тока, тока не проводит, а в цепях переменного тока все время заряжается – разряжается и, значит, проводит ток. Сопротивление емкости переменному току тем меньше, чем выше частота переменного тока.

 

 

Емкость и индуктивность взаимно противоположные по свойствам элементы, значит, они могут снижать взаимное влияние в цепях переменного тока или совсем отключать друг друга. Емкость и индуктивность оказывают сопротивление переменному току, но не могут выделить тепла, поэтому на них не происходит прямых потерь мощности.

Активное сопротивление R в цепи переменного тока

 

Что нам интересно знать про простейшую электрическую цепь содержащую R ?

 

  

 

Какой ток протекает в ней, какое напряжение на ней действует? и какая мощность может быть получена.

 

    

 

 

 

 

Здесь изображены две синусоиды, которые нельзя сравнивать и говорить какая больше, какая меньше. Они разные для удобства рассмотрения. Красная синусоида изображает переменное напряжение, а синяя синусоида изображает переменный ток

 

Если через активное R сопротивление протекает переменный синусоидальный ток, то на нем действует переменное синусоидальное напряжение. Ток и напряжение имеют одинаковую частоту и совпадают по фазе.

 

Мощность на активном сопротивлении определяется как произведение тока и напряжения. Действующая мощность будет равна произведению действующего значения тока на действующее значение напряжения.

 

 

Черные полуволны показывают, что мощность выделяемая в цепи на активном сопротивление изменяется также по синусоидальному закону,

Только знак остается все время положительным, это значит, что поток мощности однонаправлен. Мощность получается как произведение каждой точки синусоиды тока на каждую точку синусоиды напряжения в один и тот же момент. Плюс напряжения на плюс тока даст нам плюс мощности. Минус напряжения на минус тока даст нам плюс мощности.

Это значит, что при протекании тока через активное сопротивление R, электрическая мощность приводит к выделению тепла.

 

P=UI U = Uа√2 ; I = Iа√2 P = UаIа/2

 

Средняя мощность за период равна постоянной составляющей мощности

Uа Iа/2

 

Физический смысл этого явления состоит в том, что активное сопротивление потребляет энергию от источника, выделяет энергию в виде тепла. Электрическая мощность, которая превращается в тепло, называется активной мощностью и обозначается, как и в цепях постоянного тока, буквой P

 

Активными сопротивлениями в цепях переменного тока являются нагревательные и осветительные приборы, а также резисторы в сигнальных схемах, кроме того, как активные сопротивления проявляют себя все устройства, на которых выделяется полезная мощность в любом виде. Например, электрический мотор, звуковые динамики и т. п.

 

Индуктивное сопротивление в цепи переменного тока

 

X_L = ωL     

 

Чтобы сделать сосредоточенную индуктивность, кусок проволоки сматывают в катушку

Если к цепи с индуктивностью подключить переменное синусоидальное напряжение, то в ней должен протекать переменный синусоидальный ток.

Что же происходит в цепи с индуктивностью при протекании переменного тока.

Оказывается, ток и напряжение действуют не одновременно,

то есть, сдвинуты по фазе

 

На активном сопротивлении R, появление напряжения сразу – в тот же момент,  вызывает появление тока, и они действуют в одной фазе.

На индуктивности так не получается.

Если напряжение от источника начинает нарастать, то ток за ним не успевает.

Почему? В индуктивности изменение тока, приводит к появлению ЭДС самоиндукции, а эта ЭДС направлена на встречу изменения тока. Напряжение растет, и ток хочет расти, но ЭДС самоиндукции препятствует нарастанию тока. Это примерно также, как сила инерции мешает разогнать тележку, когда мы сдвигаем ее с места.

Ток преодолевает сопротивление направленной навстречу ему ЭДС самоиндукции, и начинает нарастать, но это происходит, когда напряжение уже достигло максимального значения. Ток, наконец, достигает максимального значения, но напряжение в этот момент уже снизилось до нуля. Так и повторяется – ток все время отстает от напряжения на 90⁰ то есть на π/2. Значит, фаза тока отрицательна и составляет  — π/2 

 

Откуда берется эта ЭДС самоиндукции, и почему она не мешает в цепи с сопротивлением  R. Это связано с тем, что катушка индуктивности, в отличие от сопротивления R, создает сильное магнитное поле, благодаря большому количеству витков. Магнитное поле не может мгновенно изменяться, оно и рождает внутри провода ЭДС, которая препятствует изменению тока.

 

Более подробно об ЭДС самоиндукции смотри в статье  Начальные представления об электромагнетизме

 

 

Красная синусоида напряжения пресекает ноль каждый раз раньше зеленой синусоиды тока на π/2 

     

 

 

Вывод: В цепи с индуктивностью напряжение впереди тока на 90°.

 

Любое сопротивление ограничивает ток, но бывает активное сопротивление, бывает реактивное..

R — активное сопротивление — на нем выделяется тепло

X — реактивное сопротивление на нем  не выделятся тепло

 

X_L – сопротивление индуктивности

X_L – сопротивление индуктивности L является реактивным, оно равно X_L =ωL, то есть, оно прямо пропорционально частоте ω и индуктивности L, чем больше индуктивность, тем больше реактивное сопротивление и чем выше частота тем больше реактивное сопротивление.

Индуктивность тем сильнее ограничивает ток, чем выше частота тока.

Индуктивность пропускает переменный ток тем лучше, чем меньше индуктивность и чем меньше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток индуктивность пропускает без всякого сопротивления

 

 

Мощность на индуктивности

Мощность определяется как произведение тока на напряжение. Для каждого момента времени точка синусоиды тока умножается на точку синусоиды напряжения и получается точка синусоида мощности. Синусоида мощности получается двунаправленной, положительные полупериоды сменяются отрицательными, значит, мощность пол периода выделяется и пол периода поглощается. Это значит, что индуктивность L полпериода накапливает энергию в магнитном поле, а затем полпериода возвращает ее в источник.

 

 

Частота синусоиды мощности вдвое больше частоты тока и напряжения.

На индуктивности не получается выделение тепла, и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на индуктивности, называется реактивной и обозначается не Р, а другой буквой – Q_L

 

 

 

Емкость в цепи переменного тока

 

X_C =1/ ωc  

 

При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться. Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.

 

 

   

 

 

 

Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.

Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.

То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2

 

X_C — сопротивление емкости

X_C — сопротивление емкости является реактивным, оно равно X_C =1/ ωc, то есть оно обратно пропорционально частоте и емкости, чем больше емкость, тем меньше реактивное сопротивление и чем выше частота тем меньше меньше реактивное сопротивление.

Емкость пропускает переменный ток тем лучше, чем больше емкость и чем выше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток емкость вообще не пропускает.

Конденсатор часто ставят в участки цепей, в которых не должен проходить постоянный ток

 

 

Мощность в цепи с емкостью

 

Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.

 

 

 

Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник.  Частота синусоиды мощности вдвое больше частоты тока и напряжения.

Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.

 

Реактивные сопротивления

 

Индуктивность и емкость проявляют себя в электрических цепях как сопротивления.

 

X_C – реактивное сопротивление емкости

X_{L — реактивное сопротивление индуктивности}

Формулы сопротивлений позволяют их использовать для расчета задач по закону Ома для участка цепи.

 

Формула X_C =1/ ωc показывает, что сопротивление емкости зависит от частоты ω. Это означает, что емкость по-разному пропускает ток низкой и высокой частоты.

Емкость пропускает переменный ток тем лучше, чем выше частота.

Емкость вообще не пропускает постоянный ток, и это ее важнейшее свойство. Одно из главных применений емкости (конденсатора) состоит в том, что его ставят в те ветви схем, где запрещено протекание постоянного тока.

 

Формула X_L = ωL _{показывает, что сопротивление индуктивности зависит от частоты. Это означает, что индуктивность по-разному пропускает ток низкой и ток высокой частоты.}

Индуктивность хуже пропускает переменный ток высокой частоты

Чем больше частота. Тем труднее проходит переменный ток. Катушка индуктивности используется для ограничения переменного тока.

Конденсатор и катушка являются противоположностями.

Конденсатор пропускает переменный ток и не пропускает постоянный

Катушка пропускает постоянный ток и не пропускает переменный

 

 

 

Такие цепи содержат сопротивление R, индуктивность L, и ёмкость C.

Реальное сопротивление цепи, содержащей одновременно R, L и C, зависит от величины каждого элемента цепи, и от частоты переменного тока, который протекает в этой цепи.

Расчет цепей переменного тока по аналогии с расчетом цепей постоянного тока невозможен, потому, что необходимо учитывать фазовый сдвиг между током и напряжением.

Можно упростить цепи, если какой-то  элемент: R, L или  C пренебрежительно мал.

 

 

Задачи на переменный ток решаются методом векторных диаграмм.

Ток и напряжение являются векторными величинами.Их изображают как вращающиеся радиус -векторы, в этом смысле они отличаются от векторов сил и скоростей в механике, но правила сложения и вычитания векторов аналогичны.

 

 

Метод векторных диаграмм

 

Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.

 

В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает  изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.

 

Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.

 

Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.

 

Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.

 

 

Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.

Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.

Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.

На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.

 

Векторная диаграмма напряжений представляет собой векторный треугольник напряжений

 

Последовательное соединение L R.

 

Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.

 

 

Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.

Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,

Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.

 

Векторная диаграмма строится так.

 

 

Выберем фазу общего тока равной 0, вектор тока откладывается как горизонтальный вектор слева на право. Далее строим векторную диаграмму напряжений. Сначала откладывается вектор напряжения на сопротивлении R. Этот вектор, пойдет горизонтально, так как его фаза совпадает с фазой тока. Затем строят вектор напряжения на индуктивности L. Его надо откладывать под углом 90

⁰ вверх, это потому, что напряжение на индуктивности впереди на 90⁰.

Второй вектор переносится из центра вращения. Прикладываем его к концу вектора напряжения на активном сопротивлении. Таковы правила сложения векторов.

Теперь остается построить вектор полного напряжения на обоих элементах. Это вектор суммы, он, как известно, строится из начала первого вектора  к концу второго.

Получился прямоугольный треугольник. Любую сторону этого треугольника можно найти по теореме Пифагора.

Острый угол этого треугольника и есть реальный сдвиг фаз в этой цепи между током и общим напряжением. Он обязательно меньше 90 градусов, потому что только на идеально индуктивности он составляет 90 градусов. Активное сопротивление обязательно уменьшает сдвиг фаз.

 

Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление, обозначается Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и X_L

 

Z², = Rа² + X²_L

 

В цепи L R, в отличие от цепи только с L, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.

Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и Q_L

 

S² = Р^{2 +} Q²_L

 

Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников.

 

 

Последовательное соединение RC

Конденсаторы очень часто включают последовательно с сопротивлениями, но если даже специального сопротивления нет, любой конденсатор обладает определённой величиной активного сопротивления, которую необходимо учитывать в точных расчетах. Есть понятие «добротность» конденсатора, которая проявляет  активную составляющую его сопротивления

 

 

При последовательном соединении, через все элементы цепи протекает один ток, который называем – общий.

Сначала откладываем вектор тока, фазу которого принимаем равной нулю. Вектор напряжения на активном сопротивлении, откладываем в том же направлении, так как на активном сопротивлении ток и напряжение совпадают по фазе.

К концу вектора напряжения на активном сопротивлении прикладываем начало вектора напряжения на емкости. Фаза напряжения на емкости отстает от фазы напряжения на активном сопротивлении на 90 градусов, а вектор отстающего напряжения откладывается вниз.

 

Векторная диаграмма напряжений представляет собой прямоугольный треугольник, который позволяет определить все составляющие по теореме Пифагора.

Активное сопротивление R включенное в цепь с катушкой или конденсатором уменьшает угол сдвига фаз.

Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление обозначается буквой Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и X_С

 

Z ² = Rа² + X²_С

 

В цепи L C, в отличие от цепи только с C, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.

 

Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и Q_С

 

S² = Р^{2 +} Q²_С

 

Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников

 

Параллельное соединение RL

 

 

При параллельном соединении RL одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через катушку отстает по фазе от напряжения. на 90⁰. Общий ток отстает от напряжения меньше чем на 90⁰.

Для цепей с параллельным соединением элементов, гораздо удобнее использовать не сопротивления (активные и реактивные) а их обратные величины, которые называются проводимости. Вместо  r используется g, вместо   X_L используется b_L, вместо Xc используется b_c 

 

 

 

 

Параллельное соединение RC

 

При параллельном соединении RС одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через конденсатор опережает по фазе от напряжения. на 90⁰. Общий ток опережает напряжение меньше чем на 90⁰

 

 

 

Значение Cos φ

 

Cos φ в практической электротехнике имеет очень важное значение. Реальные нагрузки, типа электромоторов и трансформаторов, имеют большую индуктивную составляющую сопротивления, то есть, фактически, представляют собой цепи RL. Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P).

 

Из формулы видно, что чем меньше Cos φ (Чем больше угол сдвига фаз), тем меньшую часть активная мощность составляет от полной мощности .

Только активная мощность является полезной, если источник затрачивает полную мощность, а от нагрузки мы можем получить только активную мощность, значит, Cos φ имеет смысл электротехнического КПД или коэффициента мощности.

В идеале источник должен отдавать такую мощность, которую будет потреблять нагрузка. Реальные устройства неизбежно содержат индуктивности (катушки, обмотки, и т.п.), значит, источник вынужден отдавать полную мощность, которая значительно больше, активной.

Проектирование устройств и электрических цепей должно иметь целью получить значение Cos φ как можно ближе к единице, то есть влияние индуктивности надо свести к минимуму. Плохие значения Cos φ приводят к большим неоправданным затратам электроэнергии.

 

Цепи RLC

 

Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.

В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.

 

RLC последовательно

 

 

Как будет выглядеть векторная диаграмма в общем случае?

 

 

 

При последовательном соединении сопротивлений на каждом сопротивлении действует своя часть напряжения. На большем сопротивлении будет большая часть напряжения.

На первой векторной диаграмме видно, что напряжение на конденсаторе U_c больше, чем на катушке U_L тогда суммарный вектор общего напряжения направлен вниз, и видно, xnj угол сдвига фаз отрицательный. На второй диаграмме видно, что напряжение на конденсаторе U_c, значительно меньше, чем U_L , и вектор общего напряжения оказался направленным вверх, угол сдвига фаз стал положительным.

В первом случае цепь имеет емкостный характер, во втором индуктивный.

На определенной частоте наступает равенство Uc = Ul, такое явление называется резонанс напряжений

 

Условие резонанса  X_L = X_C

 

При резонансе напряжений Общее сопротивление цепи становится минимально, а ток становится максимальным, что может быть опасно для источника и требует надежной защиты.

 

 

RLC параллельно

 

 

 

 

 

Векторные диаграммы токов при параллельном соединении

 

 

При параллельно соединении элементов RLC напряжение на всех элементах действует одно и то же, а токи разные, чем меньше сопротивление ветви, тем больше ток. В первом случае ток катушки значительно больше тока конденсатора. Вектор общего тока направлен вниз. Во втором случае ток катушки значительно меньше тока конденсатора и вектор тока направлен вверх.

В первом случае цепь имеет индуктивный характер, во втором емкостный

На определенной частоте наступает равенство токов I_c = I_L  такое явление называется резонанс токов.

При резонансе токов сопротивление цепи становится максимальным и ток уменьшается до величины, которая определяется сопротивлением R, которое остается в цепи.

 

Условия резонанса

Резонанс широко применяется в радиотехнических и различных электронных схемах.

XL = XC

 

 

Устройства для переменного тока и устройства для постоянного тока

Устройства. Которые включаются электрические цепи

Лампочки

Нагреватели

Электромоторы

Электроинструмент

Бытовые приборы

Электроника

И т. п.

 

Лампочки и нагреватели работают одинаково в цепях переменного и постоянного тока. В некоторых случаях разница может быть заметной, так как активное сопротивление в цепи постоянного тока (омическое) может отличаться от сопротивления в цепи переменного тока.

Электромоторы и электроинструмент рассчитанный на переменный ток, при подключении в цепь постоянного тока скорее всего сгорят, так как, у них пропадает индуктивное сопротивление и ток сильно возрастает.

Если моторы, и инструмент рассчитанные на постоянный ток, включены на переменный ток, они сильно потеряют мощность, так как появившееся индуктивное сопротивление и сильно ограничит потребляемый ток.

Активная, реактивная и полная мощность в цепях переменного тока

Активная мощность:

Если активное сопротивление (например, нагревательный элемент) подключено к цепи переменного тока, результирующие напряжение и ток совпадают по фазе (синяя и красная кривые на схеме ниже). Умножение связанных пар мгновенных значений напряжения и тока дает мгновенную мощность (зеленая кривая).

Такая кривая мощности всегда положительна, потому что для активного сопротивления напряжение и ток всегда либо положительные, либо отрицательные.Положительная мощность передается от генератора к потребителю. Зеленые зоны отображают выполненную активную работу. Поскольку мощность имеет частоту в два раза превышающую частоту напряжения или тока, не может быть нанесено вместе с током и напряжением на нормальную векторную диаграмму.

Мощность переменного тока p ( t ) имеет пиковое значение p ₀ = u ₀ · i ₀ и может быть преобразовано путем приравнивания областей под кривой в эквивалентную мощность постоянного тока , или активная мощность P .Активная мощность для активного сопротивления составляет половину пиковой мощности, т.е.

Другими словами:

Активная мощность активного сопротивления является произведением среднеквадратичного напряжения и среднеквадратичного тока.

Реактивная мощность:

Если чистое реактивное сопротивление, т. Е. Емкостное или индуктивное сопротивление, подключено к цепи переменного тока, сдвиг фазы j между током и напряжением составляет 90 °, ток опережает напряжение в случае емкости и отстает от напряжения в случай индуктивности (как показано на схеме ниже).Кривая мощности здесь симметрична относительно оси времени, так что положительная и отрицательная (серые) области компенсируют друг друга, и в целом активная мощность не потребляется. Отрицательные значения означают, что мощность возвращается от потребителя к генератору. В течение одного периода энергия дважды возвращается от катушки (потребителя) к генератору. Общая энергия постоянно колеблется между генератором и потребителем. В результате получается чистая потребляемая реактивная мощность индуктивного или емкостного характера в зависимости от используемого компонента.Реактивная мощность обозначается Q и выражается в единицах Var .

Полная мощность:

Если нагрузка, включающая компоненты активного и реактивного сопротивления, подключена к переменному напряжению, возникают компоненты активной и реактивной мощности. Схема ниже демонстрирует это в случае индуктивной нагрузки, ток и напряжение которой сдвинуты по фазе на 60 °. Кривая мощности здесь в основном расположена выше оси времени.Серые области частично компенсируют друг друга и представляют компонент реактивной мощности, а зеленые области представляют активную мощность (или выполненную активную работу).

Умножение измеренных значений напряжения и сдвинутого по фазе тока дает здесь полную мощность S , которая выражается в вольт-амперах (ВА):

Кажущаяся мощность — это , а не мера преобразования электрической энергии в цепи, вместо этого она служит просто вычисляемой переменной, состоящей из активной и реактивной мощности.Соответственно, активная мощность P , показанная измерителем мощности (ваттметром) при наличии фазового сдвига между током и напряжением, всегда меньше, чем кажущаяся мощность S , вычисленная из среднеквадратичных значений тока и напряжения.

Активное сопротивление в цепи переменного тока

Электрическая цепь предполагает наличие в своем составе ряда различных компонентов. Конденсаторы и элементы индуктивности включены в схему для получения разного эффекта.Сопротивления присутствуют в виде отдельных элементов-резисторов и резисторов соединения проводов. С физикой влияние компонента схемы на законы протекания электрических явлений было изучено достаточно тщательно и мало отличается от природы протекания электрического тока, будь то под влиянием переменного или постоянного напряжения.

Сопротивление в цепи переменного тока работает так же, как и в режиме постоянного напряжения потока. Другое дело — элементы емкости и индуктивности.Если в подсхеме, в которую включен конденсатор, отсутствует постоянная составляющая тока, то на индуктивность она никак не влияет. Прохождение постоянного тока в индуктивности влияет только на активное сопротивление катушки.

Совершенно иная ситуация в описании электрических процессов в цепи переменного тока. Конденсаторы становятся проводниками, а индукторы (дроссель, трансформатор и т. Д.) Находят индуктивное сопротивление, которое, в свою очередь, играет гораздо более важную роль, а сопротивление часто просто не принимается во внимание.

Но, тем не менее, необходимость точных расчетов требует учитывать эту составляющую. Чтобы начать понимать, как активное сопротивление катушки сочетается с индуктивным, следует в целом рассматривать устройство как стандартный индуктор.

Являясь составной частью электрической цепи, данное устройство не что иное, как биполярный элемент множества электрических, электромеханических и электронных систем и устройств. В качестве основного параметра используется значение самоиндукции.Это, в свою очередь, зависит только от геометрических размеров и материалов изготовления. На величину индуктивности не влияет ни сила тока, ни напряжение. Использование индукторов в фильтрах для подавления помех, их использование позволяет добиться сглаживания, также катушка может накапливать энергию, что широко используется при проектировании резонансных цепей.

Чтобы проанализировать, какое влияние оказывает сопротивление работе дроссельной заслонки, вы должны рассмотреть цепь переменного тока с одним элементом, которым является индуктор.Рассчитывая активное и индуктивное сопротивление, казалось бы, самый простой способ вычислить общие значения — это сумма их модулей.

Но с такими количествами дело обстоит не так просто, как могло бы показаться. Опуская теоретическое обоснование, опишите использование на практике метода суммирования активного и индуктивного сопротивлений.

Чтобы найти общий балл, постройте прямоугольный треугольник. Одна сторона — это сопротивление, а другая — индуктивная. Гипотенуза будет равна сопротивлению цепи, которое согласно определению равно квадратному корню из суммы квадратов активного и индуктивного сопротивлений.

Выполненные таким образом расчеты дают более точную информацию о процессах, происходящих в цепи переменного тока, элементами которой являются индукторы. В формуле закона Ома есть возможность использовать величину импеданса. В будущем следует отметить, что значительное сопротивление по сравнению с индуктивным может влиять на фазовый сдвиг между током и напряжением. Поэтому при изготовлении катушек индуктивности широко используется конструкция сердечника, которая дает значительные преимущества по индуктивному сопротивлению.

Резисторы в цепях переменного тока | Мощность, напряжение и ток переменного тока

Введение

При постоянном токе (DC) поток электрического заряда является однонаправленным. В постоянном токе напряжение и ток поддерживают постоянную полярность и направление. Источником постоянного тока является аккумулятор. С другой стороны, при переменном токе (AC) поток электрического заряда периодически меняет направление на противоположное. В переменном токе напряжение меняет полярность с положительной на отрицательную и наоборот с течением времени.Это изменение полярности напряжения происходит из-за изменения направления тока. AC — это источник питания, используемый для питания домашних хозяйств, офисов, промышленных предприятий и т. Д. Несмотря на то, что синусоида является наиболее распространенной формой питания переменного тока, некоторые приложения используют различные формы волны, такие как треугольная волна, прямоугольная волна и пилообразная волна.

Наиболее распространенной формой питания переменного тока является синусоидальная волна. Математическая функция, описывающая типичное переменное напряжение, равна

В (t) = VMax sin ωt.

В (t) — напряжение в зависимости от времени.Напряжение меняется со временем.

t — переменное время в секундах.

VMax — пиковое значение, которого синусоидальная волна может достигать как в положительном, так и в отрицательном направлении. Для положительного цикла это VMax, а для отрицательного — -VMax.

ω — угловая частота. ω = 2πf.

f — частота синусоидальной волны.

В цепях постоянного тока расчет тока, напряжения и мощности выполняется по закону Ома. Здесь предполагается, что полярности напряжения и тока постоянны.

В случае чисто резистивных цепей переменного тока значениями индуктивности и емкости можно пренебречь. Следовательно, расчет тока, напряжения и мощности будет следовать тем же принципам закона Ома и законов цепи Кирхгофа. Разница заключается в использовании мгновенного значения от пика до пика или среднеквадратичного значения.

Резистор с питанием постоянного и переменного тока

Резистор — это пассивное устройство. Он не потребляет и не производит энергии. Энергия здесь — это электрическая энергия. Но резистор рассеивает электрическую энергию в виде тепла.

Резистор с источником питания постоянного тока указан ниже

В резистивных цепях постоянного тока сопротивление, которое представляет собой отношение напряжения к току, является линейным.

Резистор с источником питания переменного тока указан ниже

В цепях переменного тока отношение напряжения к току в основном зависит от частоты питания f и сдвига фаз φ. Следовательно, термин импеданс используется в цепях переменного тока для обозначения сопротивления, поскольку оно обладает как величиной, так и фазой, в отличие от сопротивления в цепях постоянного тока, где оно имеет только величину.Символ сопротивления — Z.

Фазовое соотношение V-I в чисто резистивной цепи переменного тока

Значение сопротивления резистора в цепях переменного и постоянного тока одинаково независимо от частоты напряжения питания переменного тока. Изменение направления тока в сети переменного тока не влияет на поведение резисторов. Таким образом, ток в резисторе будет расти и падать в зависимости от напряжения, когда он растет и падает.

Напряжение и ток в резистивной цепи переменного тока достигают максимума, затем падают до нуля и одновременно достигают минимума.Говорят, что они находятся «в фазе», поскольку они поднимаются и опускаются в одно и то же время.

Рассмотрим следующую цепь переменного тока.

Здесь ток I (t) = IMax sin ωt.

Напряжение V (t) = VMax sin ωt. => V (t) = IMax R sin ωt.

Поскольку схема является чисто резистивной, влияние индуктивности и емкости незначительно, а разность фаз равна 0.

Следовательно, соотношение между напряжением и током в резисторе, который является частью резистивной цепи переменного тока, составляет

Мгновенные значения токов и напряжений «синфазны» по оси x кривой.Они поднимаются и опускаются одновременно и достигают своих максимальных и минимальных значений точно в одно и то же время. Это означает, что их фазовый угол равен θ = 00. Векторная диаграмма, представляющая этот фазовый угол, вместе со сравнением максимальных и минимальных значений напряжения и тока, показана ниже.

Расчет мощности, напряжения и тока переменного тока

Мгновенные значения тока и напряжения в резистивной цепи переменного тока можно использовать для определения сопротивления в его омической форме с помощью закона Ома.

Рассмотрим следующую резистивную схему с питанием переменного тока.

Пусть напряжение питания V (t) = VMax sin ωt, подключенное к резистору R.

Пусть мгновенное напряжение на резисторе будет V _R .

Пусть I _R будет мгновенным током, протекающим через резистор.

Поскольку приведенная выше схема является чисто резистивной по своей природе, можно применить принципы Ома.

Согласно закону Ома, напряжение на резисторе в момент t составляет

В _R = В _Макс sin ωt.

Аналогично, ток, протекающий через резистор в момент t, может быть определен с использованием закона Ома как

I _R = V _R / R

Но V _R = V _Max sin ωt.

Следовательно, I _R = (V _Max * sin ωt) / R

Но значение V _Max / R есть не что иное, как максимальный ток в цепи, обозначенный I _Max ..

Следовательно I _R = I _Макс sin ωt.

В чисто резистивной последовательной цепи переменного тока полное напряжение цепи равно сумме напряжений отдельных резисторов, потому что все отдельные напряжения синфазны в чисто резистивной цепи. Аналогичным образом, полный ток в чисто резистивной параллельной цепи Цепь переменного тока — это сумма токов отдельных ветвей всех параллельных резистивных ветвей.
Для расчета мощности в цепи переменного тока важную роль играет коэффициент мощности. Коэффициент мощности определяется как косинус фазового угла между током и напряжением.Фазовый угол обозначается символом φ.

Если P — активная мощность в цепи, измеренная в ваттах, а S — полная мощность цепи, измеренная в вольтах-амперах, соотношение между реальной мощностью и полной мощностью определяется выражением

P = S Cos φ.

В случае чисто резистивных цепей переменного тока фазовый угол между током и напряжением составляет 0 ⁰ . Следовательно, φ = 0 ⁰ . Следовательно, коэффициент мощности Cos φ равен Cos 0 ⁰ = 1.

Следовательно, активная мощность равна полной мощности, которая является произведением напряжения и тока.
В чисто резистивных цепях переменного тока мощность в любой момент в цепи может быть определена путем вычисления произведения напряжения и тока в этот момент.

Мощность, потребляемая вышеуказанной схемой, может быть рассчитана с использованием

P = V _RMS * I _RMS * Cos φ.

Поскольку φ = 0 ⁰ в этом случае мощность составляет

P = V _RMS * I _RMS

Мощность в чистом сопротивлении

В случае чисто резистивных цепей переменного тока мощность, потребляемая схемой, является просто произведением напряжения и тока, поскольку между током и напряжением нет фазового угла.

Форма сигнала мощности для чисто резистивной цепи переменного тока показана ниже.

Форма сигнала мощности состоит из серии положительных импульсов. Это потому, что, когда и напряжение, и ток положительны в первом полупериоде, их произведение, которое является мощностью, также положительно. А когда во втором полупериоде и напряжение, и ток отрицательны, их производительная мощность снова становится положительной (-V x -I = + P). Следовательно, значение мощности всегда больше или равно нулю.

Из приведенного выше сигнала видно, что мощность возрастает по мере увеличения как напряжения, так и тока и достигает своего максимума, когда и напряжение, и ток достигают своего максимума. Затем он падает до нуля, когда напряжение и ток падают до нуля. При изменении полярности напряжения и тока значение мощности снова возрастает и достигает максимума, когда напряжение и ток достигают своего отрицательного пика. Когда напряжение и ток падают до нуля, значение мощности падает до нуля.

В случае чисто резистивной цепи с источником питания переменного тока RMS рассеиваемая мощность такая же, как и в случае резистора, подключенного к источнику питания постоянного тока.

P = VRMS * IRMS = I2RMS * R = V2RMS / R.

VRMS и IRMS — это действующие значения напряжения и тока соответственно.

P — мощность в ваттах.

R — сопротивление в Ом (Ом)

Для сравнения эффектов нагрева, вызванных переменным и постоянным током, постоянный ток следует сравнивать со среднеквадратичным значением переменного тока, но не с максимальным или пиковым током IMAX¬.

Резисторы в цепях переменного тока Примеры

Пример 1

Рассмотрим следующую схему.

Нагревательный элемент резистивного типа подключается к источнику переменного тока напряжением 240 В. Мощность, потребляемая нагревательным элементом, составляет 1,2 КВт. Значение его сопротивления можно рассчитать как

Ток, протекающий через нагревательный элемент, равен

I = P / V

P = 1,2 КВт = 1200 Вт.

В = 240 В.

Следовательно, I = 1200/240 = 5 А.

Значение сопротивления нагревательного элемента можно рассчитать по закону Ома как

R = V / I

R = 240/5 = 48 Ом.

Пример 2

Рассмотрим следующую схему.

Резистор сопротивлением 47 Ом подключен к источнику питания 120 В.

Значения тока, протекающего через резистор, и мощность, потребляемая резистором, могут быть рассчитаны как

Можно рассчитать ток, протекающий через резистор используя закон Ома

I = V / R

I = 120/47 = 2,55 ампер.

Мощность, потребляемая резистором, составляет

P = I2 * R = V2 / R

P = 1202/47 = 306 Вт.

Часть 11: Питание в цепях переменного тока

11,1 переменного / постоянного тока

Мощность — это скорость выполнения работы или расходования энергии (раздел 3.1). Электрическая единица энергии — ватт (Вт), а один ватт — это расход энергии со скоростью один джоуль в секунду. В цепи постоянного тока мощность, рассеиваемая в резистивной цепи, равна:

где:
P = мощность (Вт)
U = разность потенциалов (PD) (В)
I = ток (A)
R = сопротивление (Ом)

В цепях переменного тока мгновенные значения напряжения, тока и, следовательно, мощности постоянно меняются.Однако в любой момент мы еще можем сказать, что:

где:
p = мгновенная мощность (Вт)
v = мгновенное напряжение (В)
i = мгновенное значение тока (A)

Среднеквадратичные значения (U, I и P) могут быть легко использованы в цепях переменного тока с одним сопротивлением, однако, когда речь идет о емкости и индуктивности, ситуация усложняется. Помните, что среднеквадратичные значения определены таким образом, что действующий ток 1 А переменного тока будет вызывать такой же нагревательный эффект в резисторе, что и 1 А постоянного тока.

11.2 Питание в цепи переменного тока сопротивления

Для резистивной цепи ток и напряжение совпадают по фазе, и мощность в любой момент можно найти, умножив напряжение на ток в этот момент. На рисунке 11.1 показаны волны напряжения, тока и мощности, и ясно, что когда напряжение положительное, ток и мощность положительны. Кроме того, когда напряжение отрицательное, ток и, следовательно, снова положительный. Из-за этого синфазного отношения среднеквадратичные значения могут использоваться в уравнении мощности постоянного тока:

Многие электрические нагрузки, такие как обогреватели, утюги, чайники и лампы накаливания, могут считаться полностью резистивными.

Пример

Погружной нагреватель мощностью 3 кВт подключен к источнику переменного тока 240 В. Рассчитайте ток.

Рисунок 11.1: Мощность в резистивной цепи переменного тока. Обратите внимание, что v, i и p не отображаются в одном масштабе.

11.3 Питание в емкостной цепи переменного тока

На рисунке 11.2 представлена ​​волновая диаграмма цепи конденсатора переменного тока и показан ток, опережающий напряжение на 90 °. В первой четверти цикла и v, и i положительны, поэтому мощность также положительна (поскольку p = vi, в любой момент).Во второй четверти цикла v остается положительным, тогда как i стало отрицательным, поэтому p отрицательно. В третьем квадранте и i , и v отрицательны, а значит, p положительны. Наконец, в четвертом квадранте i положительно, а v все еще отрицательно, что приводит к отрицательному значению p . Таким образом, волна мощности представляет собой серию идентичных положительных и отрицательных импульсов, среднее значение которых за полупериод напряжения равно нулю, также обратите внимание, что ее частота в два раза превышает частоту напряжения.

Рисунок 11.2: Мощность в емкостной цепи переменного тока. Обратите внимание, что v, i и p не отображаются в одном масштабе.

В течение первой и третьей четверти цикла мощность является положительной, что означает, что питание подается схемой для зарядки конденсатора. Во второй и четвертой четвертьциклах конденсатор разряжается и, таким образом, передает накопленную в нем энергию (раздел 7.6) обратно в схему, таким образом, p имеет отрицательное значение. Хотя отрицательная мощность может показаться странной концепцией, знаки «минус» или «плюс» просто указывают направление, в котором течет мощность.Поскольку при таком обмене энергией не происходит рассеивание средней мощности, нагрев не происходит, и мощность не теряется (по крайней мере, для идеального конденсатора, который не имеет утечки тока).

Поскольку у нас есть напряжение и ток, но нет рассеиваемой мощности, выражение P = IV (с использованием среднеквадратичного значения) больше не действует. Произведение тока и напряжения в этом случае называется реактивной мощности или реактивных вольт-ампер и измеряется в вольтамперах (VA _r ). (Реактивная мощность — это вовсе не мощность, и название немного обманчиво).Ток, протекающий через конденсатор (не имеющий сопротивления), не вызывает нагрева и называется реактивным током .

Пример

Конденсатор

10 мкФ подключается к источнику питания 240 В, 50 Гц. Рассчитайте реактивный ток и реактивные вольтамперы.

11.4 Питание в индуктивной цепи переменного тока

Рисунок 11.3 содержит волновую диаграмму индуктивной цепи переменного тока и показывает отставание тока от напряжения на 90 °. В ситуации, аналогичной той, что была обнаружена для мощности в конденсаторах, мощность в индуктивной цепи состоит из положительных и отрицательных импульсов.Среднее значение этих импульсов за полупериод равно нулю, и поэтому нагрев не происходит (для идеального индуктора, хотя на практике провод, образующий катушку, будет иметь сопротивление). В этом случае отрицательная мощность возникает из-за энергии, которая была сохранена в магнитном поле и возвращена в цепь.

Рисунок 11.3: Мощность в индуктивной цепи переменного тока. Обратите внимание, что v, i и p не отображаются в одном масштабе.

11,5 Мощность в резистивных и емкостных цепях (RC-цепи)

В цепи, состоящей из последовательно соединенных сопротивления и емкостного реактивного сопротивления, напряжение и ток будут иметь относительный фазовый угол от 0 ° до 90 °, в зависимости от отношения сопротивления к реактивному сопротивлению (раздел 9.3). На рисунке 11.4 показана волновая диаграмма такой цепи, где ток опережает напряжение на °. Поскольку энергия рассеивается в резисторе, в цепь возвращается меньше энергии, чем в чисто емкостной цепи, а отрицательные импульсы значительно меньше. Таким образом, из источника поступает полезная мощность, которая будет рассеиваться в виде тепла. Однако рассеиваемая энергия будет меньше, чем рассеиваемая в чисто резистивной цепи, потому что ток не совпадает по фазе с напряжением.

На рисунке 11.4 показана векторная диаграмма, соответствующая волновой диаграмме, показанной на рисунке 11.3.

Рисунок 11.4: Мощность в резистивной и емкостной цепи переменного тока. Обратите внимание, что v, i и p не отображаются в одном масштабе.

Рисунок 11.5: Векторная диаграмма для резистивной и емкостной цепи переменного тока

Вектор тока можно разделить на две составляющие тока; они фактически не выходят, но, как показано в разделе 8.1, векторные величины могут быть разделены на компоненты для упрощения суммирования.I _P — это синфазная или активная составляющая тока , синфазная с напряжением, это та часть тока, которая считается причиной рассеивания тепла. В то время как квадратура или реактивный компонент I _Q опережает напряжение на 90 ° и считается частью тока, которая заставляет энергию накапливаться, а затем возвращаться в схему, но не вызывает нагрева. На рисунке 11.5 напряжение питания (U) взято за эталон, поэтому в RC-цепи ток питания (I) опережает его на °.

Из рисунка 11.5 видно, что, поскольку I _P синфазен с U, мощность, рассеиваемая в резистивной части схемы, определяется выражением:

Но из рисунка 11.5:

Cos известен как коэффициент мощности цепи. Поскольку этот результат был получен из векторной диаграммы, он применим только к синусоидальным волнам, и в таких случаях средняя мощность = среднеквадратичное напряжение × среднеквадратичный ток × косинус фазового угла между напряжением и током.

Часто бывает полезно вычислить фазовый угол цепи по сопротивлению, реактивному сопротивлению и импедансу цепи.Из раздела 10.1:

Мы также можем видеть, что, поскольку мощность рассеивается только в резистивной части схемы, отсюда следует, что:

Обратите внимание, что в приведенных выше уравнениях не смешиваются ток и напряжение (в отличие от P = UI), поэтому нет проблем с разностью фаз. По этой причине потери мощности в проводах и кабелях, по которым идет питание переменного тока, рассчитываются с использованием P = I ² R.

Пример

Цепь, подключенная к источнику переменного тока 240 В, имеет сопротивление 28.8 Ом последовательно с конденсатором с реактивным сопротивлением 38,4 Ом. Рассчитайте (i) ток в цепи, (ii) фазовый угол цепи и (iii) рассеиваемую мощность.

(я) ток цепи:

(ii) фазовый угол цепи:

текущее опережающее напряжение, потому что это RC-цепь.

(iii) рассеиваемая мощность:

или:

11.6 Мощность в резистивных и индуктивных цепях

Когда сопротивление и индуктивное реактивное сопротивление соединены последовательно, ток отстает от напряжения питания на угол  °, который будет изменяться от почти 0 ° до почти 90 °.На рисунке 11.6 показана волновая диаграмма такой схемы. Как и в RC-цепи, количество энергии, забираемой из источника питания, больше, чем энергия, возвращаемая в цепь индуктором, и потребляется чистая энергия. Средняя потребляемая мощность (P) показана на рисунке 11.6.

Рисунок 11.6: Мощность в резистивной и индуктивной цепи переменного тока. Обратите внимание, что v, i и p не отображаются в одном масштабе.

На рисунке 11.7 показана векторная диаграмма, соответствующая волновой диаграмме на рисунке 11.6. Опять же, поскольку I и U не совпадают по фазе, P = IU недействительно, однако снова потребляемая мощность может быть найдена из:

Это уравнение справедливо только для синусоидальных волн.

Рисунок 11.7: Векторная диаграмма для резистивной и индуктивной цепи переменного тока.

Из раздела 10.1 и рисунка 11.7 можно вывести следующие отношения:

11.7 Питание в цепях общего ряда (цепи RCL)

Эти схемы следуют тем же правилам, что и схемы RC и RL, поскольку мощность все еще рассеивается только в резистивной части схемы.Следовательно:

Пример

Дроссель с индуктивностью 0,318 Гн, сопротивлением 30 Ом, соединен последовательно с емкостью 53 мкФ через источник питания 24 В, 50 Гц. Рассчитайте рассеиваемую мощность.

Это та же схема, что и в примере в разделе 10.3, где было вычислено, что ток цепи составляет 0,48 А,  = 54,1 ° (cos  = 0,6) и V _R = 14,4 В.

Два альтернативных метода:

или:

Базовая электротехника

Обзор R, X и Z (сопротивление, реактивное сопротивление и импеданс) | Реактивное сопротивление и импеданс — R, L и C

Прежде чем мы начнем исследовать влияние резисторов, катушек индуктивности и конденсаторов, соединенных вместе в одних и тех же цепях переменного тока, давайте кратко рассмотрим некоторые основные термины и факты.

Сопротивление

Это по сути трение против тока. В той или иной степени он присутствует во всех проводниках (кроме проводов super !), Особенно в резисторах. Когда переменный ток проходит через сопротивление, возникает падение напряжения, синфазное с током. Сопротивление математически обозначается буквой «R» и измеряется в омах (Ом).

Реактивное сопротивление

Это по сути инерция против тока.Он присутствует везде, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току, соответственно; но особенно в конденсаторах и катушках индуктивности.

Когда переменный ток проходит через чистое реактивное сопротивление, возникает падение напряжения, которое на 90 ° не совпадает по фазе с током. Реактивное сопротивление математически обозначается буквой «X» и измеряется в омах (Ом).

Импеданс

Это исчерпывающее выражение любых форм противодействия протеканию тока, включая как сопротивление, так и реактивное сопротивление.Он присутствует во всех схемах и во всех компонентах.

Когда переменный ток проходит через полное сопротивление, возникает падение напряжения, которое находится где-то между 0 ° и 90 ° по фазе с током. Импеданс математически обозначается буквой «Z» и измеряется в единицах Ом (Ом) в сложной форме.

Идеальные резисторы обладают сопротивлением, но не реактивным сопротивлением. Идеальные катушки индуктивности и идеальные конденсаторы обладают реактивным сопротивлением, но не имеют сопротивления. Все компоненты обладают импедансом, и из-за этого универсального качества имеет смысл перевести все значения компонентов (сопротивление, индуктивность, емкость) в общие термины импеданса в качестве первого шага при анализе цепи переменного тока.

Идеальный резистор, индуктор и конденсатор.

Фазовый угол импеданса для любого компонента — это фазовый сдвиг между напряжением на этом компоненте и током через этот компонент.

Для идеального резистора падение напряжения и ток всегда находятся в фазе , поэтому угол импеданса резистора считается равным 0 °. Для идеального индуктора падение напряжения всегда опережает ток на 90 °, поэтому фазовый угол импеданса индуктора равен + 90 °.

Для идеального конденсатора падение напряжения всегда отстает от тока на 90 °, поэтому считается, что фазовый угол импеданса конденсатора составляет -90 °.

Полное сопротивление переменного тока ведет себя аналогично сопротивлению в цепях постоянного тока: они добавляются последовательно и уменьшаются параллельно. Пересмотренная версия закона Ома, основанная на импедансе, а не на сопротивлении, выглядит так:

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Что такое сопротивление постоянному и переменному току?

Обновлено 28 декабря 2020 г.

Автор: S.Hussain Ather

Когда электростанции подают электроэнергию в здания и домашние хозяйства, они посылают ее на большие расстояния в виде постоянного тока (DC). Но бытовая техника и электроника обычно используют переменный ток.

Преобразование между двумя формами может показать вам, как сопротивления для разных форм электричества отличаются друг от друга и как они используются на практике. Вы можете придумать уравнения постоянного и переменного тока, чтобы описать разницу в сопротивлении постоянному и переменному току.

В то время как мощность постоянного тока течет в одном направлении в электрической цепи, ток от источников переменного тока чередуется между прямым и обратным направлениями через равные промежутки времени. Эта модуляция описывает, как изменяется переменный ток, и принимает форму синусоидальной волны.

Это различие также означает, что вы можете описать мощность переменного тока с помощью измерения времени, которое вы можете преобразовать в пространственное измерение, чтобы показать вам, как напряжение изменяется в разных областях самой цепи. Используя основные элементы схемы с источником питания переменного тока, можно математически описать сопротивление.

Сопротивление постоянному току и переменному току

Для цепей переменного тока обрабатывайте источник питания синусоидальной волной наряду с законом Ома ,

В = IR

для напряжения В, , тока I и сопротивление R , но используйте сопротивление Z вместо R.

Сопротивление цепи переменного тока можно определить так же, как и для цепи постоянного тока: разделив напряжение на ток.В случае цепи переменного тока сопротивление называется импедансом и может принимать другие формы для различных элементов схемы, таких как индуктивное сопротивление и емкостное сопротивление, измерение сопротивления катушек индуктивности и конденсаторов соответственно. Индукторы создают магнитные поля для хранения энергии в ответ на ток, в то время как конденсаторы накапливают заряд в цепях.

Вы можете представить электрический ток через сопротивление переменному току

I = I_m \ sin {(\ omega t + \ theta)}

для максимального значения тока Im , как разность фаз θ , угловая частота контура ω и время t .Разность фаз — это измерение угла самой синусоидальной волны, которое показывает, насколько ток не совпадает по фазе с напряжением. Если ток и напряжение совпадают по фазе друг с другом, то фазовый угол будет равен 0 °.

Частота — это функция от того, сколько синусоидальных волн прошло через одну точку за одну секунду. Угловая частота — это частота, умноженная на 2π, чтобы учесть радиальный характер источника питания. Умножьте это уравнение для тока на сопротивление, чтобы получить напряжение.2}

для индуктивного сопротивления X _L , емкостного сопротивления X _C для определения полного сопротивления Z по переменному току. Это позволяет вам измерять полное сопротивление между катушками индуктивности и конденсаторами в переменном токе. схемы. Вы также можете использовать уравнения X _L = 2πfL и X _C = 1 / 2πfC , чтобы сравнить эти значения сопротивления с индуктивностью L и емкостью C для индуктивность в Генри и емкость в Фарадах.

Уравнения для цепей постоянного и переменного тока

Хотя уравнения для цепей переменного и постоянного тока принимают разные формы, они оба основываются на одних и тех же принципах. Учебное пособие по цепям постоянного и переменного тока может продемонстрировать это. Цепи постоянного тока имеют нулевую частоту, потому что, если бы вы наблюдали за источником питания для цепи постоянного тока, не было бы никакой формы волны или угла, под которым вы могли бы измерить, сколько волн пройдет заданную точку. Цепи переменного тока показывают эти волны с гребнями, впадинами и амплитудами, которые позволяют использовать частоту для их описания.

Сравнение уравнений постоянного тока и цепей может показать разные выражения для напряжения, тока и сопротивления, но лежащие в основе теории, которые управляют этими уравнениями, одинаковы. Различия в уравнениях цепи постоянного и переменного тока обусловлены природой самих элементов схемы.

Вы используете закон Ома V = IR в обоих случаях и суммируете ток, напряжение и сопротивление между разными типами цепей одинаково для цепей постоянного и переменного тока. Это означает суммирование падений напряжения вокруг замкнутого контура, равное нулю, и вычисление тока, который входит в каждый узел или точку в электрической цепи, как равного выходящему току, но для цепей переменного тока вы используете векторы.

Учебное пособие по схемам постоянного и переменного тока

Если у вас была параллельная цепь RLC, то есть цепь переменного тока с резистором, индуктором (L) и конденсатором, расположенными параллельно друг другу и параллельно источнику питания, вы бы рассчитали ток, напряжение и сопротивление (или, в данном случае, импеданс) так же, как и для цепи постоянного тока.

Суммарный ток от источника питания должен быть равен векторной сумме тока, протекающего через каждую из трех ветвей.2

для тока питания I _S , тока резистора I _R , тока индуктора I _L и тока конденсатора I _C . Это контрастирует с версией ситуации для цепи постоянного тока, которая будет

I_S = I_R + I_L + I_C

Поскольку падение напряжения на ветвях остается постоянным в параллельных цепях, мы можем рассчитать напряжения на каждой ветви в параллельной цепи RLC как R = V / I _R , X _L = V / I _L и X _C = V / I _C .2}

Это значение 1 / Z также называется проводимостью для цепи переменного тока. Напротив, падение напряжения на ветвях для соответствующей схемы с источником питания постоянного тока будет равно напряжению источника питания В, .

Для последовательной цепи RLC, цепи переменного тока с последовательно соединенными резистором, катушкой индуктивности и конденсатором, вы можете использовать те же методы. Вы можете рассчитать напряжение, ток и сопротивление, используя те же принципы установки тока на входе и выходе из узлов и точек как равные друг другу, суммируя падения напряжения на замкнутых контурах как равные нулю.

Ток в цепи будет одинаковым для всех элементов и будет определяться током для источника переменного тока I = I _m x sin (ωt) . Напряжение, с другой стороны, можно суммировать по контуру как В _с — В _R — В _L — В _C = 0 для В _R для напряжение питания В _S , напряжение резистора В _R , напряжение индуктора В _L и напряжение конденсатора В _C .

Для соответствующей цепи постоянного тока ток будет просто В / R , как задано законом Ома, и напряжение также будет В _с — В _R — В _L — В _C = 0 для каждого компонента в серии. Разница между сценариями постоянного и переменного тока заключается в том, что для постоянного тока вы можете измерить напряжение резистора как IR , напряжение катушки индуктивности как LdI / dt и напряжение конденсатора как QC (для заряда C и емкость Q) , напряжения для цепи переменного тока будут V _R = IR, VL = IX _L sin (ωt + 90 ° ) и VC = IX _C sin (ωt — 90 ° ). Это показывает, как в цепях RLC переменного тока индуктор впереди источника напряжения на 90 °, а конденсатор сзади на 90 °.

AC Ток в цепи с активным сопротивлением. Цепь переменного тока с активным сопротивлением

Для простоты пренебрегаем. На зажимы цепи подается синусоидальное напряжение

ед. = U M. × sin Ом. т. .

В схеме, показанной на рисунке 1, приложенное внешнее напряжение сбалансировано сопротивлением Ом. обозначает активное падение напряжения А обозначает U. a.

У. а =. I. × р. .

Мгновенная мощность в рассматриваемой цепи равна произведению мгновенных значений напряжения и тока:

ф. = ед. × и. .

На рисунке 3 показана кривая мгновенной мощности для одного. Из рисунка видно, что мощность не является постоянной величиной, она пульсирует с удвоением.

Рисунок 3. Кривая мгновенной мощности с активным сопротивлением

Среднее значение за период мощности или просто средняя мощность обозначается буквой P. и может быть определена по формуле, доказательство которой мы и делаем не дают:

P. = U. × I. × cos. φ ,

где угол φ — угол между напряжением и током.

Средняя мощность также называется активной мощностью.Эта формула действительна для любых цепей. переменный ток.

Для цепи с активным сопротивлением напряжение и ток совпадают по фазе. Следовательно, угол φ равен нулю, а COS φ = 1. По активной мощности получаем:

П. = U. × I.

P. = I. 2 × р. ,

то есть формула мощности для цепи переменного тока с активным сопротивлением такая же, как формула мощности для цепи постоянного тока.Все проводники имеют активное сопротивление. В цепи переменного тока нити ламп накаливания, спирали электронагревательных приборов и ризостатов, дуговые лампы, специальные бифилярные окна и прямые проводники небольшой длины обладают одним активным сопротивлением.

1 пульсацией называется изменение числового значения величины при неизменности ее знака.

Рассмотрим цепь (фиг. 140), состоящую из сопротивления под влиянием индуктивности и емкости для простоты пренебрежения.

На зажимы цепи подается синусоидальное напряжение

Как следует из последнего выражения, тип закона ОМА для цепи переменного тока, содержащей сопротивление, такой же, как и для цепи постоянного тока. Кроме того, из закона Ома, пропорциональность между мгновенным значением напряжения и мгновенным значением тока. Отсюда следует, что в цепи переменного тока, содержащей сопротивление r, напряжение и ток совпадают по фазам. ИНЖИР. 141 Имеются кривые напряжения и тока и векторная диаграмма для рассматриваемой цепочки, а длины векторов обозначают активные значения и значения тока.Сопротивление проводов переменного тока несколько больше, чем их сопротивление постоянному току. Объясняется это поверхностным эффектом, суть которого изложена в 87. Поэтому сопротивление проводников переменного тока называется активным. Он также обозначается буквой R.

В цепочке, показанной на фиг. 140, приложенное внешнее напряжение уравновешивается падением напряжения на сопротивлении R, которое называется активным падением напряжения и обозначается u a

Мгновенная мощность в рассматриваемой цепи равна произведению мгновенного значения напряжения и тока:

РИС.142 Кривая мгновенной мощности Dana за один период. Из рисунка видно, что мощность не является постоянной величиной, она пульсирует с удвоенной частотой.

Среднее значение мощности за период или просто средняя мощность обозначается буквой P и может быть определена по формуле, доказательства которой мы не приводим:

Где — угол сдвига фаз между напряжением и Текущий.

Средняя мощность также называется активной мощностью. Эта формула для активной мощности действительна для любых цепей переменного тока.

Для цепи с активным сопротивлением напряжение и ток совпадают по фазе. Следовательно, угол равен нулю, A cos = 1. Для активной мощности получаем:

То есть формула мощности для цепи переменного тока с активным сопротивлением такая же, как формула мощности для цепи постоянного тока. Все проводники имеют активное сопротивление. В цепи переменного тока нити ламп накаливания, спирали электронагревательных приборов и ризостатов, дуговые лампы, специальные бифилярные окна и прямые проводники небольшой длины обладают одним активным сопротивлением.

Если цепь переменного тока содержит только R (лампа накаливания, электронагреватель и т. Д.), К которому приложено переменное синусоидальное напряжение и (рис. 1-5, а):

этот ток i в цепи будет определяться величиной этого сопротивления:

где — амплитуда тока; При этом ток I и напряжение и совпадают по фазе. Обе эти величины, как видно, могут быть изображены на временной (рис. 1-5, б) и векторной (1-5, в) диаграммах.Теперь установите, как мощность изменяется в любой момент времени — мгновенная мощность, характеризующая скорость преобразования электрической энергии в другие виды энергии в данный момент

, где IU — произведение значений текущего тока и напряжения.

Из этого следует, что мощность в течение периода остается положительной и пульсирует с двойной частотой. Графически это можно представить, как показано на рисунке 1-6. В этом случае электрическая энергия превращается в необратимую, например, в тепловую, независимо от направления тока в цепи.

Помимо мгновенной мощности, выделяется средняя мощность за период:

, но поскольку второй интеграл равен нулю, то окончательно получается:

Средняя за период мощность переменного тока называется активной мощностью, и соответствующее сопротивление является активным.

Средняя мощность и активное сопротивление связаны с безвозвратным преобразованием электрической энергии в другие виды энергии.Активное сопротивление электрической цепи не опускается только до

.

сопротивление проводников, в которых электрическая энергия превращается в тепло. Это понятие значительно шире, поскольку средняя мощность электрической цепи равна сумме мощностей всех видов энергии, получаемой от электрической на всех частях цепи (тепловой, механической и т. Д.).

Из полученных соотношений следует, что

является математической записью закона Ома для цепи переменного тока с активным сопротивлением.

Вынужденные электромагнитные колебания

Вынужденные электромагнитные колебания Рассчитайте периодические изменения силы тока и напряжения в электрической цепи, возникающие под действием переменной EDC от внешнего источника. Внешним источником EDC в электрических цепях являются генераторы переменного тока, работающие на электростанциях.

Принцип работы генератора переменного тока легко показать, если рассмотреть вращающуюся проволочную рамку в магнитном поле.

В однородном магнитном поле с индукцией на месте прямоугольная рамка, образованная проводниками (ABSD).

Пусть плоскость рамки перпендикулярна индукции магнитного поля B и ее площадь равна S.

Магнитный поток в момент времени t 0 = 0 будет равен F = B * 8.

С При равномерном вращении рамки вокруг оси OO 1 с угловой скоростью w магнитный поток, проникающий в рамку, будет изменяться во времени по закону:

Изменение магнитного потока возбуждает в кадре ЭДС индукцию, равную

где E 0 = ASW — амплитуда ЭДС.

Если соединить концы рамы в электрическую цепь с помощью контактных колец и скольжения по ней, то под действием индукции EDC, изменяющейся во времени по гармоническому закону, в электрической цепи возникнут вынужденные гармонические колебания. в силе тока — переменного тока .

На практике синусоидальная ЭДС возбуждается не вращением корпуса в магнитном поле, а вращением магнита или электромагнита (ротора) внутри статора — неподвижных обмоток, наложенных на сердечники из магнитного материала.В этих обмотках присутствует переменная ЭДС, позволяющая избежать снятия напряжения с помощью контактных колец.

Переменный ток

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока.

Если индуктивность проводника настолько мала, что при его включении в цепь переменного тока можно пренебречь полями индукции по сравнению с внешним электрическим полем, движение электрических зарядов в проводнике определяется действием только внешнего электрического поля, напряжение которого пропорционально напряжению на концах проводника.

При изменении напряжения по гармоническому закону U = u M COS WT напряженность электрического поля в проводнике изменяется по такому же закону.

Под действием переменного электрического поля в проводнике возникает переменный электрический ток, частота и фаза колебаний которого совпадает с частотой и фазой колебаний напряжения:

где i — мгновенное значение ток, IM — амплитудное значение тока.

Колебания тока в цепях — это внутренние электрические колебания, возникающие под действием приложенного напряжения.

Амплитуда тока равна:

При совпадении фаз колебаний силы тока и напряжения мгновенная мощность переменного тока равна:

Среднее значение квадрата косинуса за период 0,5 . В результате средняя мощность за период

Для того, чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (P = PR), понятие значений тока силы тока и напряжения.Из равенства мощностей получаем

Текущее значение текущего значения называется значением, в корне 2-кратного меньшего значения амплитуды:

Активное значение текущего значения равно степени такой постоянный ток, при котором средняя мощность, выделяемая в проводнике в цепи переменного тока, равна мощности, выделенной в том же проводнике в цепи постоянного тока.

Активное значение переменного напряжения в корне в 2 раза меньше его амплитудного значения:

Средняя мощность переменного тока при совпадении фаз колебаний силы тока и напряжения равна произведению значений тока \ силы тока и напряжения:

Сопротивление элемента электрической цепи, в котором происходит преобразование электрической энергии во внутреннюю, называется активным сопротивлением .Активное сопротивление участка цепи можно определить как частное от деления средней мощности на квадрат текущего значения тока:

Активное сопротивление R — это физическая величина, равная отношению мощности к квадрату. текущей силы, которая получается из выражения для мощности. На малых частотах он практически не зависит от частоты и совпадает с электрическим сопротивлением проводника.

Предположим, что катушка включена в цепь переменного тока.Затем при изменении тока в катушке по закону возникает ЭДС самоиндукции. Поскольку электрическое сопротивление катушек равно нулю, то ЭДС минус напряжение на концах катушки, создаваемое внешним генератором (??? Что еще такое генератор ???). Следовательно, изменение тока вызывает изменение напряжения, но со сдвигом фазы. Произведение представляет собой амплитуду колебаний напряжения, т.е. Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний тока называется индуктивным сопротивлением.

Пусть конденсатор будет в цепи. При его включении заряжает четверть периода, потом кренит столько же, но со сменой полярности. При изменении напряжения на конденсаторе гармонического закона заряд на его пластинах равен. Ток в цепочке возникает при изменении заряда: аналогично случаю с катушкой амплитуда колебаний силы тока равна. Величина, равная отношению амплитуды к силе тока, называется емкостным сопротивлением.

Активное сопротивление. Текущие значения тока и напряжения Перейдем к более подробному рассмотрению процессов, происходящих в цепи, подключенной к источнику переменного напряжения.

Сила тока в номинале резистора. Пусть схема состоит из соединительных проводов и нагрузок с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эта величина, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будет называться активным сопротивлением. Сопротивление R называется активным, потому что при наличии нагрузки с этим сопротивлением схема поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются. Предположим, что напряжение на зажимах цепи изменяется по гармоническому закону: u = u m cos t. Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ом : В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения (рис.4.11), а амплитуда силы тока определяется равенством

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (В = 50 Гц) ток и напряжение изменяются относительно быстро. Следовательно, при пропускании тока по проводнику, например, по нити лампочки, количество выделенной энергии также будет быстро меняться со временем. Но мы не замечаем этих быстрых изменений.

Как правило, нам необходимо знать среднюю мощность тока на участке цепи за большой промежуток времени, включая множество периодов.Для этого достаточно найти среднюю мощность за один период. Под средней за период мощностью переменного тока понимают отношение общей энергии , поступающей в цепочку за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется по формуле P = i 2 R. (4.18) на очень малом временном интервале переменный ток можно считать практически постоянным. Следовательно, мгновенная интенсивность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется по формуле P = i 2 R.(4.19) Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставив выражение (4.16) для силы тока и используя известное математическое соотношение. График мгновенной мощности времени изображен на рис. 4.12, а. По графику (рис. 4.12, б.), За тот же восьмой период, когда мощность в любой момент больше, чем. Но для следующей восьмой части периода при COS 2T Текущие значения тока и напряжения . Из формулы (4.21) видно, что величина является средней за период текущего значения силы тока:

Значение, равное квадратному корню из среднего значения силы тока тока, называется текущее значение силы неизменяемого тока. Активный эффект силы непреходящего тока обозначен I: Фактическая мощность переменного тока , равная мощности такого постоянного тока, в котором такое же количество выделено в проводнике теплый Что касается переменного тока во время в то же время.

Активное значение переменного напряжения определяется аналогично текущему значению тока: заменяя амплитудные значения тока и напряжения на текущие значения по формуле (4.17), получаем этот ока-закон для Участок цепи переменного тока с резистором.

Как и в случае с механическими колебаниями, в случае с электрическими колебаниями нас обычно не интересуют значения тока, напряжения и других величин в каждый момент времени.Важны общие характеристики колебаний, такие как амплитуда, период, частота, текущие значения тока и напряжения, средняя мощность. Это действующие значения силы тока и напряжения регистрируют амперметры и вольтметров переменного тока.

Кроме того, действующие значения более удобны, чем мгновенные значения, тем более что они напрямую определяются средним значением мощности ПК: P = I. 2 R = UI. Колебания тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется текущими значениями тока и напряжения.

переменного тока оценивается по его действию, эквивалентному действию постоянного тока. Активное сопротивление Это сопротивление проводника, при котором электрическая энергия необратимо превращается во внутреннюю. Пусть напряжение в цепи переменного тока изменяется по гармоничному закону. Под действием переменного электрического поля в проводнике возникает переменный ток, частота и фаза колебаний которого совпадает с частотой и фазой колебаний напряжения.Амплитудное значение силы тока равно отношению амплитуды напряжения к сопротивлению проводника. Текущая мощность равна произведению силы тока и напряжения. Тогда активное сопротивление можно определить как отношение мощности переменного тока на участке цепи к квадрату текущего тока. Активное значение мощности Ток называется силой постоянного тока, благодаря которой в проводнике выделяется такое же количество тепла, как и у переменного тока. Найдите активное значение текущего значения как отношение амплитудного значения текущей силы к квадратному корню из двух.Действующее напряжение также в два раза меньше его амплитудного значения.

При изучении вынужденных механических колебаний мы познакомились с явлением резонанс . Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы. Если трение невелико, то амплитуда устанавливаемых вынужденных колебаний при резонансе резко возрастает. Совпадение типа уравнений для описания механических и электромагнитных колебаний (позволяет сделать вывод о возможности резонанса и в электрической цепи, если эта цепь представляет собой колебательный контур с определенной частотой колебаний.

При механических колебаниях резонанс ярко выражен при малых значениях коэффициента трения. В электрической цепи роль коэффициента трения выполняет его активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к преобразованию энергии тока, а вот внутренняя энергия проводника (проводник нагревается вверх). Следовательно, резонанс в электрическом колебательном кон-Лайпе должен четко выражаться при небольшом активном сопротивлении R.

Мы уже знаем, что если активного сопротивления недостаточно, собственная циклическая частота колебаний в цепи определяется по формуле Сила тока вынужденных колебаний Она должна достигать максимальных значений при частоте переменного тока. приложенное к контуру напряжение равно частоте его собственного колебательного контура: Резонанс в электрическом колебательном контуре Явление резкого увеличения амплитуды вынужденных колебаний силы тока называется совпадением частоты входного переменное напряжение с собственной частотой колебательного контура.

Амплитуда силы тока при резонансе. Как и в случае механического резонанса, при резонансе в колебательном контуре создаются оптимальные условия для перетока энергии от внешнего источника в контуре. Мощность в цепи максимальна в том случае, когда текущий ток совпадает с фазой напряжения. Здесь полная аналогия с механическими колебаниями: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает с фазой по скорости (аналог силы тока).

Не сразу после включения внешнего переменного напряжения в цепи устанавливается резонансное значение тока. Амплитуда колебаний силы тока увеличивается постепенно — до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравнится с энергией , поступающей в контур за то же время:

Отсюда амплитуда установленных колебаний тока Сила во время резонанса определяется уравнением. При R 0 резонансное значение тока постоянно увеличивается: (im) срез.Напротив, с увеличением R максимальное значение тока для тока уменьшается, а при больших Rs говорить о резонансе уже не имеет смысла. Зависимость амплитуды силы тока от частоты при разных сопротивлениях (R 1 Одновременно с увеличением тока для резонанса резко возрастают напряжения на конденсаторе и индукторе индуктивности. Эти напряжения с ма.По активного сопротивления многократно выше, чем внешнее напряжение.

Использование резонанса в радиосвязи. Явление электрического резонанса широко используется при реализации радиосвязи. Радиоволны от различных передающих станций возбуждаются переменными частотами в антенне радио, поскольку каждая передающая радиостанция работает на своей частоте. Индуктивность антенны связана с колебательным контуром (рис. 4.20). Из-за электромагнитной индукции в контурной катушке возникают переменные соответствующих частот и вынужденные колебания силы тока той же частоты.Но только при резонансе колебания силы тока в цепи и напряжения в ней будут значительными, т.е.из колебаний различной частоты, возбуждаемых в антенне, схема выделяет только те частоты, частота которых равна его собственной частоте. Настройка контура на нужную частоту обычно осуществляется заменой емкости , конденсатора . Обычно это заключается в настройке радио на определенную радиостанцию. Необходимо учитывать возможность возникновения резонанса в электрической цепи.В некоторых случаях резонанс в электрической цепи может принести большой вред. Если цепь не предназначена для работы в резонансе, то ее возникновение может привести к аварии.

Чрезмерно большие токи могут привести к перегреву проводов. Большие напряжения приводят к нарушению изоляции.

Такого рода аварии часто случались даже сравнительно недавно, когда законы электрических колебаний были плохо представлены и не умели правильно считать на электрических цепях .

При вынужденных электромагнитных колебаниях возможен резонанс — резкое увеличение амплитуд колебаний тока и колебаний напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний. На явлении резонанса основана вся радиосвязь.

Исследование цепей переменного тока с активным, емкостным и индуктивным сопротивлением происходит в следующей логической последовательности: сначала понятие того или иного сопротивления в цепи переменного тока (сравнение с его поведением в цепи постоянного тока), затем соотношения фаз, формула соответствующего сопротивления, преобразование энергии в цепи, содержащей только активное, емкостное или индуктивное сопротивление.Последовательность удельного сопротивления в цепи переменного тока может быть несколько иной. Понятие активного значения силы тока и напряжения можно вводить следующим образом: Сначала отображается выражение для расчета мгновенных значений мощности активного сопротивления, отсюда найдите среднее значение мощности за период и узнайте То есть есть среднее значение тока для текущего за период. Определение: квадратный корень из этого значения называется активным значением AC.Название связано с тем, что при прохождении тока через область с активным сопротивлением выделяется мощность

Такая же мощность выделяется в цепи постоянного тока, значение которой равно активному значению переменного тока. Таким образом, активное значение переменного тока — это значение постоянного тока, который в резисторе R выделяет то же количество тепла, что и переменный ток. Очень важно отметить, что шкалы электрических инструментов, для измерения переменных с

, ток и напряжение ils градуируются в допустимых значениях этих значений.Рассмотрение схемы переменного тока со смешанным сопротивлением начинается с эксперимента — измеряется напряжение на каждом из последовательно включенных элементов цепи (лампа, катушка и конденсаторная батарея), подключенных к источнику напряжения. Обратите внимание на следующие факты: 1. Общее напряжение не равно величине напряжений в определенных областях, как это было в цепях постоянного тока. 2. Напряжение на участке, содержащем катушку и конденсатор — это не сумма, а разница напряжений на каждом из них в отдельности.Объяснить этот результат могут сами студенты; Они знают, что по индуктивности напряжение опережает ток на π / 2, а электрическая емкость за ним на такую ​​же величину. Поскольку мгновенное значение силы тока в цепи везде и одинаково, понятно, что колебания напряжения на индуктивности и электрической емкости происходят со сдвигом фаз, равным π, то есть их фазы противоположны. 3. Полное сопротивление цепи меньше суммы всех включенных в нее сопротивлений (активных, индуктивных и емкостных).Студентов нужно убедить, что чем меньше фазовый сдвиг между током и напряжением, большая часть энергии, подаваемой в цепь, полезна, необратимо превращаясь в другие виды энергии. Далее рассмотрим устройство и работу трансформатора. На примере однофазного трансформатора показано его действие (повышение и понижение напряжения) и устройство. Сначала нет холостого режима, а потом уже нагруженный трансформатор. В качестве нагрузки желательно использовать ритейл, так как им легче поменять нагрузку.Покажите, что с увеличением нагрузки увеличивается ток как во вторичной, так и в первичной обмотке трансформатора. Студенты предлагают себя с позиций энергетики, чтобы объяснить увеличение силы тока в первичной цепи (увеличение потребления энергии на нагрузке, естественно, должно сопровождаться увеличением потребления энергии первичной обмоткой от генератора). Для исследования электромагнитных колебаний широко используется школьный приборный генератор Школьный ГЗШ.Он перекрывает диапазон генерируемых частот синусоидальных колебаний от 20 до 20000 Гц с диапазонами: «X1» (от 20 до 200 Гц), «X10» (от 200 до 2000 Гц), «X100» (от 2000 до 20000 Гц). питается от сети переменного тока напряжением 220 В на лицевой панели генератора в сеть включен в сеть, сигнальная лампа, переключатель поддиапазона в трех фиксированных положениях с маркировкой «x1», «x10», «x100», диск с неравномерная шкала деления (от 20 до 200) Ручка переменного резистора, позволяющая изменять амплитуду выходного сигнала, выходные зажимы рассчитаны на подключение цепей с разным сопротивлением (5, 600, 5000 Ом).Если для экспериментов требуется частота 20-200 Гц, переключатель устанавливают в положение «x1», если 200-2000 Гц — в положение «X10», а для частот 2000-20000 Гц используйте положение «X100». Плавная регулировка частоты осуществляется поворотом диска. Также широко применяемые выпрямители PPE-1 и PSU-2 WEUP-2 предназначены для питания демонстрационных установок в электрических экспериментах. Технические данные: Устройство позволяет получить на выходах клещи: выпрямленное напряжение 350В с максимальной силой тока 220мА; Постоянное фильтрованное напряжение 250 В при максимальной нагрузке 50 мА; регулируемое напряжение от 0 до 250 В постоянного тока до 50 мА; регулируемое напряжение от 0 до +100 В и от 0 до 100 В постоянного тока до 10 мА; Напряжение 6.3В переменного тока до 3а. Еще один источник питания, без которого практически невозможно проводить множество экспериментов по RNS-электричеству. Стабилизатор напряжения школьный предназначен для плавного регулирования однофазного переменного напряжения с частотой 50 Гц во время лабораторных и демонстрационных экспериментов в физических кабинетах школ. Устройство подключается к сети теневым шнуром. Устройство может быть включено в сеть напряжением 127 и 220В. Рабочее напряжение снимается с фиксаторов с указанием «выходного напряжения».Для правильной работы регулятора напряжения в паспорте прибора приведена таблица допустимых значений электрической нагрузки регулятора нагрузки при разных напряжениях, подаваемых на нагрузку, и при сетевых напряжениях 127 и 220В. Установленный в регуляторе напряжения вольтметр имеет неровную шкалу. Надежный счет можно провести только при 50 В. Если нужно снять с регулятора более низкие напряжения, необходимо параллельно выходным зажимам подключить дополнительный вольтметр с соответствующим пределом измерения.Стабилизатор напряжения может использоваться как для повышения, так и для понижения напряжений переменного тока, при различных демонстрационных и лабораторных экспериментах, школьные осциллографы ODS-2 и OES-70 используются для визуального отображения электромагнитных колебаний. Наиболее широко применяемые осциллографы для исследования периодических процессов, а также для исследования вольтаминных характеристик диода и триода, петель гистерезиса и др. В простейшем случае осциллограф состоит из четырех блоков: блока электронно-лучевой трубки ЭЛТ , генератор помола гр, усилитель СК и блок питания бп.Основным элементом первого блока является электронно-лучевая трубка, на экране которой формируется картина исследуемого сигнала (осциллограмма). Продукция NN нагревается катодом, с поверхности которого вылетают электроны. Электроны, пролетающие через отверстия управляющего электрода, фокусирующего цилиндр FC и анод A, а также между пластинами XX и UU, попадают на экран и вызывают его свечение. Изменяя разность потенциалов между катодом и управляющим электродом, вы можете изменять количество электронов в пучке, а это позволяет регулировать яркость изображения на экране.Чем больше отрицательный потенциал модуля на управляющем электроде относительно катода, тем меньше электронов пройдет через управляющий электрод и достигнет анода. Осциллограф оснащен ручкой регулировки яркости для управления потоком электронов в пучке. Электрическое поле между фокусирующим цилиндром и анодом способно фокусировать отправляемый электронный пучок. Обычно сетевой выключатель крепится на передней стенке, сигнальной лампе, «Входе», «входе X» и входном делителе.На боковой панели расположены ручки управления электронным лучом, «синхронизация», «внутренняя. — от сети — внешняя», «усиление», ручки развертки, «диапазоны 0, 30, 150, 500 Гц, 2, 8, 16 кГц» , «Частота плавно», а также ручка усиления «Усиление», «Усиление X». Осциллограф ODOS-2 отличается от OES-70 конструктивно и внешним оформлением. На лицевой панели выводится не только экран электронно-лучевой трубки, но также и основные ручки управления. Верхний ряд ручек предназначен для управления электронным лучом: «яркость», «фокус», «вверх-вниз», «влево-вправо».Во втором ряду сверху сверху монтируется «Усиление» и делитель напряжения 1: 1, 1:10, 1:30, 1: 10o, 1: 1000, а также сетевой выключатель с лампочкой. В третьем ряду расположены вершины и кнопки генератора разверток: «Частота плавно», «вкл. 1, 2, 3, 4», «Усиление X». Кнопочный переключатель позволяет изменять напряжение пиления с частотой от 20 Гц до 20 кГц. Генератор разверток работает только при нажатой кнопке «Вкл.». В нижнем ряду «Логин пользователя», «Вход X», «Внешний.Синхронизация », кнопки синхронизации« Внешняя. »,« Внутренний »и ручка синхронизации. На боковой панели осциллографа ОСОС-2 расположены ручки управления двухканальным переключателем с двумя входами. Переключатель позволяет наблюдать на экране осциллографа одновременно сигналы от двух источников переменного тока. источники одинаковые, то по полученным осциллограммам можно судить о фазовом сдвиге поданных сигналов.Например, на один вход может подаваться сигнал, пропорциональный напряжению на конденсаторе, а на другой — пропорциональная сила тока, протекающего через конденсатор.Затем на экране осциллографа можно наблюдать две синусоиды, сдвинутые по фазе на 90 °. Применяя переключатель, вы можете сравнить частоту тестового сигнала со стандартной частотой, если эти сигналы различаются по частоте. На задней стенке осциллографов ODS-2 и OES-70 установлены розетки, позволяющие подавать сигнал непосредственно на пластины электронно-лучевой пластины. Возможность подачи тестового сигнала прямо на пластину позволяет применять осциллограф и для цепей постоянного тока.Подав сигнал постоянного напряжения на пластину XX (или UU) при отключенной развертке, вы можете наблюдать точку смещения по горизонтали (или вертикали), и отклонение этой точки пропорционально приложенному напряжению. Следовательно, осциллограф можно использовать как вольтметр с большим внутренним сопротивлением. Для усиления электромагнитных колебаний используются усилители низкой частоты. Усилитель низкой частоты — электронное устройство. Предназначен для усиления электрических колебаний звуковой частоты от 20 Гц до 20 кГц.Обычно усилитель состоит из нескольких блоков: предварительного усилителя напряжения, усилителя мощности, согласующего выходного трансформатора и блока питания. Для школ выпускаются усилители разной конструкции и различающиеся по внешнему виду. Усилитель ANLC-3 на передней панели имеет ручку регулировки громкости и сигнальную лампочку. Ручка регулятора громкости тоже производится по сети и вне сети. В крайнем левом положении ручки при повороте устройства против часовой стрелки устройство отключено. Включение осуществляется поворотом ручки по часовой стрелке после щелчка.Поскольку усилитель собран на электронных лампах, он начинает работать после их прогрева. На боковой стенке смонтированы три входных гнезда: для подключения М — микрофон, переходник, l — линии. Нижнее гнездо подключается к корпусу прибора. На задней стенке две пары небрежности: GR — для подключения громкоговорителя (низковольтный выход) и l — высокоомный вывод. Также есть выход сетевого шнура с вилкой и восьмеричная панель, в которой специальная вилка с предохранителем (0.5 А) вставляется для сети с напряжением 220 В. Вилку можно установить в двух положениях: «220 В» и «127 В». Усилитель УНФ-5 собран на транзисторах. На передней панели усилителя сетевой переключатель со световым индикатором, выходное гнездо, входное гнездо для микрофона и звукоснимателя, разъем для подключения микрофона, ручка регулировки низких и высоких частот, ручка управления сигналом, индикатор перегрузки. . На задней стенке — вывод сетевого шнура с вилкой и предохранитель (0.5 А). На вход усилителя можно подавать сигналы не только с микрофона и звукоснимателя, но и с других датчиков электрических колебаний напряжением от нескольких милливольт до вольт (сигналы от элементов цепи переменного тока, звукового генератора и т. Д.). К выходу усилителя можно подключить не только динамик, но и другие устройства: осциллограф, измерители переменного тока, наушники и др. Потребляемая мощность не более 40 Вт, выходная — около 5 Вт.Запрещается во время работы усилителя менять предохранитель, разбирать и ремонтировать устройство, включенное в сеть. Усилитель на вертикальной панели входит в комплект демонстрационных устройств радиотехники. Слева установлены универсальные зажимы для входа усилителя. Первая лампа работает в режиме усиления по напряжению, вторая — как усилитель мощности. В анодной цепи второй лампы включен трансформатор грубой очистки, вторичная обмотка которого подключена к зажимам низкого и высокого выходного напряжения.Для подключения питания от ВЭУ2 используются три нижних зажима, напряжение переменного тока составляет 6,3 В для питания ламп, а напряжение постоянного тока 250 В для анодной цепи ламп, а на третьем дне лампы, поставляется. На зажим подается положительный потенциал. Подключение источника питания и сборку установок с усилителем на панели запрещается производить при включенном выпрямителе СИЗ-2. В демонстрационных установках следует отдавать предпочтение усилителю UNG-5.

.