Что такое активное сопротивление в цепи переменного тока. Как ведут себя индуктивное и емкостное сопротивление при прохождении переменного тока. Какие законы описывают поведение тока и напряжения в цепях с различными видами сопротивлений. Как рассчитать полное сопротивление цепи переменного тока.
Активное сопротивление в цепи переменного тока
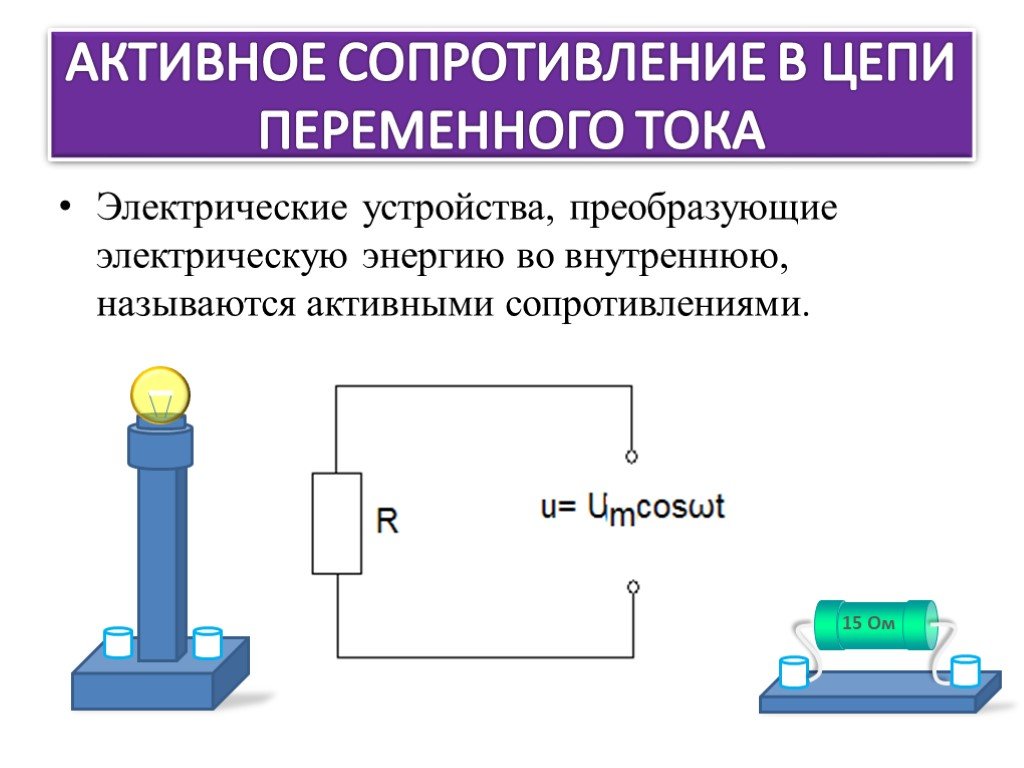
Активное сопротивление в цепи переменного тока обладает следующими ключевыми свойствами:
- Преобразует электрическую энергию в тепловую
- Не создает сдвига фаз между током и напряжением
- Описывается законом Ома: I = U / R, где I — действующее значение силы тока, U — действующее значение напряжения, R — активное сопротивление
- Мгновенные значения тока и напряжения связаны соотношением: i = u / R
Мощность, выделяемая на активном сопротивлении, рассчитывается по формуле:
P = I^2 * R = U^2 / R
Таким образом, активное сопротивление ведет себя в цепи переменного тока аналогично тому, как оно ведет себя в цепи постоянного тока.
Индуктивное сопротивление в цепи переменного тока
Индуктивное сопротивление обладает следующими особенностями:
- Создается катушкой индуктивности
- Вызывает отставание тока от напряжения по фазе на 90°
- Зависит от частоты тока: XL = ωL = 2πfL, где ω — циклическая частота, f — частота переменного тока, L — индуктивность катушки
- Описывается законом Ома: I = U / XL
Мгновенные значения тока и напряжения на индуктивности связаны соотношением:
u = L * di/dt
Это означает, что напряжение на индуктивности пропорционально скорости изменения тока.
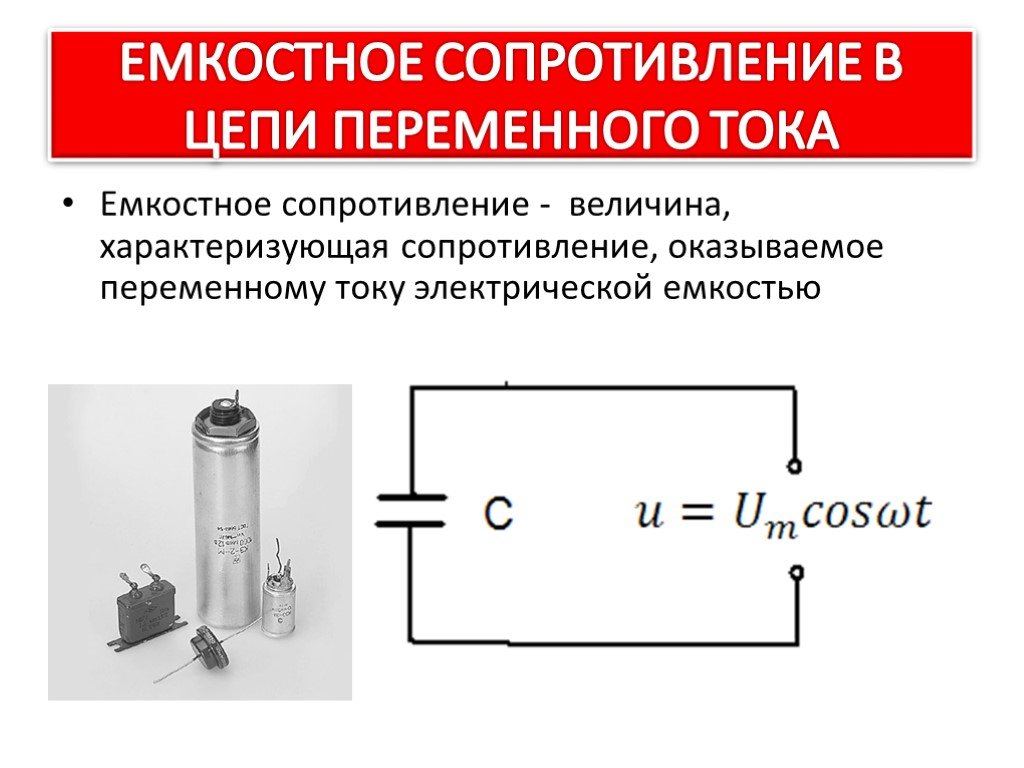
Емкостное сопротивление в цепи переменного тока
Емкостное сопротивление имеет следующие характерные свойства:
- Создается конденсатором
- Зависит от частоты тока обратно пропорционально: XC = 1 / (ωC) = 1 / (2πfC), где C — емкость конденсатора
- Описывается законом Ома: I = U / XC
Мгновенные значения тока и напряжения на емкости связаны соотношением:
i = C * du/dt
Это означает, что ток через емкость пропорционален скорости изменения напряжения на ней.
Полное сопротивление цепи переменного тока
В цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления, полное сопротивление (импеданс) рассчитывается по формуле:
Z = √(R^2 + (XL — XC)^2)
Где:
- Z — полное сопротивление цепи
- R — активное сопротивление
- XL — индуктивное сопротивление
- XC — емкостное сопротивление
Закон Ома для цепи переменного тока принимает вид:
I = U / Z
Где I и U — действующие значения тока и напряжения соответственно.
Резонанс в цепи переменного тока
Резонанс в цепи переменного тока наступает при равенстве индуктивного и емкостного сопротивлений:
XL = XC
Или:
ωL = 1 / (ωC)
Отсюда можно найти резонансную частоту:
ωрез = 1 / √(LC)
При резонансе полное сопротивление цепи становится равным активному сопротивлению, а ток достигает максимального значения.
Мощность в цепи переменного тока
В цепи переменного тока различают три вида мощности:
- Активная мощность: P = I^2 * R = U^2 / R
- Реактивная мощность: Q = I^2 * (XL — XC) = U^2 * (XL — XC) / Z^2
- Полная мощность: S = I * U = √(P^2 + Q^2)
Коэффициент мощности определяется как:
cos φ = P / S
Где φ — угол сдвига фаз между током и напряжением.
Применение различных видов сопротивлений в электротехнике
Различные виды сопротивлений находят широкое применение в электротехнике:
- Активное сопротивление используется в нагревательных приборах, лампах накаливания
- Индуктивное сопротивление применяется в дросселях, трансформаторах, электродвигателях
- Емкостное сопротивление используется в фильтрах, колебательных контурах, для компенсации реактивной мощности
Понимание свойств и особенностей различных видов сопротивлений позволяет эффективно проектировать и эксплуатировать электрические цепи и устройства.
Векторные диаграммы для цепей переменного тока
Векторные диаграммы являются удобным инструментом для анализа цепей переменного тока. Они позволяют наглядно представить соотношения между токами и напряжениями на различных элементах цепи.
Для цепи с активным сопротивлением вектор тока совпадает по направлению с вектором напряжения:
«` «`Для цепи с индуктивностью вектор тока отстает от вектора напряжения на 90°:
«` «`Для цепи с емкостью вектор тока опережает вектор напряжения на 90°:
«` «`Методы расчета цепей переменного тока
Для расчета цепей переменного тока используются различные методы:
- Метод комплексных амплитуд — позволяет применять законы Кирхгофа к комплексным значениям токов и напряжений
- Символический метод — использует алгебраические операции с комплексными числами
- Метод векторных диаграмм — наглядно представляет соотношения между токами и напряжениями
- Топографический метод — удобен для анализа сложных разветвленных цепей
Выбор метода расчета зависит от сложности цепи и поставленной задачи. Часто наиболее эффективным является комбинирование различных методов.
Курс физики (Грабовский Р.И.)
Курс физики (Грабовский Р.И.)
ОглавлениеПредисловиеВведение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 10. Силы упругости § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III.  Работа и энергия§ 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика § 35.  Основные положения молекулярно-кинетической теории§ 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 43. О числе степеней свободы. Внутренняя энергия газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50.  Внутреннее трение (вязкость)Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 53. Тепловое расширение твердых и жидких тел § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 65. Сжижение газов. Эффект Джоуля-Томсона § 66. Испарение и конденсация. Кипение § 67.  Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором§ 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле.  Поляризация диэлектриков§ 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции § 83. Конденсатор. Энергия электрического поля Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 91. Ток в жидкостях. Электролиз. Законы Фарадея § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток.  § 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 100. Действие магнитного поля на проводник с током. Определение ампера § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106.  Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока§ 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122.  Об интерференции света, отраженного от прозрачных пленок§ 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору).  Объяснение спектров излучения и поглощения водорода§ 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии |
Переменный электрический ток.
Активное, индуктивное, ёмкостное сопротивления.Переменный электрический ток Электромагнитные колебания, как и механические, бывают двух типов: свободные и вынужденные. Свободные электромагнитные колебания, всегда колебания затухающие. Поэтому на практике они почти не используются. В то время, как вынужденные колебания используются везде и повсеместно. Ежедневно мы с вами можем наблюдать эти колебания. Все наши квартиры освещены с помощью переменного тока. Переменный ток есть не что иное, как вынужденные электромагнитные колебания. Сила тока и напряжение будут меняться с течением времени согласно гармоническому закону. Колебания, например, напряжения можно обнаружить, если подать напряжение из розетки, на осциллограф. На экране
осциллографа появится синусоида. Можно вычислить частоту переменного тока. Она
будет равняться частоте электромагнитных колебаний. Стандартная частота для
промышленного переменного тока принята равной 50 Гц. Изменение напряжения на концах цепи будет вызывать за собой изменение силы тока в цепи колебательного контура. Следует всё же понимать, что изменение электрического поля во всей цепи не происходит мгновенно. Но так как это время, значительно меньше, чем период колебания напряжения на концах цепи, то обычно считают, что электрическое поле в цепи сразу же меняется, как меняется напряжение на концах цепи. Переменное напряжение создается генераторами на электростанциях. Простейшим генератором можно рассматривать проволочную рамку, которая вращается в однородном магнитном поле. Магнитный поток, пронизывающий контур, будет постоянно меняться и будет пропорционален косинусу угла между вектором магнитной индукции и нормалью к рамке. Если рамка вращается равномерно, то угол будет пропорционален времени. Следовательно, магнитный поток будет изменяться по гармоническому закону: Ф = BScos(ωt) Скорость
изменения магнитного потока, взятая с обратным знаком, согласно закону ЭМИ,
будет равняться ЭДС индукции. Ei = -Ф’ = Emsin(ωt). Если к рамке подключить колебательный контур, то угловая скорость вращения рамки определит частот колебаний напряжения на различных участках цепи и силы тока. В дальнейшем мы будем рассматривать только вынужденные электромагнитные колебания. Они описываются следующими формулами: u = Umsin(ωt), u = Umcos(ωt) Здесь Um – амплитуда колебаний напряжения. Напряжение и сила тока меняются с одинаковой частой ω. Но колебания напряжения не всегда будут совпадать с колебаниями силы тока, поэтому лучше использовать более общую формулу: I = Imsin(ωt +φ), где Im — амплитуда колебаний силы тока, а φ – сдвиг фаз между колебаниями силы тока и напряжения. Активное сопротивление Рассмотрим
следующую цепь. Она состоит из
источника переменного напряжения, соединительных проводов и некоторой нагрузки.
Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону: U = Umcos(ωt). Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения. I = u/R = Umcos(ωt)/R = Imcos(ωt). Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует. Действующее значение силы тока Амплитуда силы тока определяется по следующей формуле: Im = Um/R. Среднее значение квадрата силы тока за период вычисляется по следующей формуле: i2 =
(Im)2/2. Здесь Im есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока. Для обозначения действующего значения силы тока используется буква I. То есть в виде формулы это будет выглядеть следующим образом: I = √(i2) = Im/√2. Действующее значение силы переменного тока будет равно силе такого постоянного тока, при котором за одинаковый промежуток времени в рассматриваемом проводнике будет выделяться столько же теплоты, сколько и при переменном токе. Для определения действующего значения напряжения используется следующая формула. U = √(u2) = Um/√2. Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим: I = U/R. Данное выражение
является законом Ома для участка цепи с резистором, по которому течет
переменный ток. Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока. Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока. Для вычисления средней мощности используется следующая формула: P = I2R = UI. Отметим, что измерительные приборы (амперметры и вольтметры переменного тока) регистрируют именно действующие значения. Кроме того, номинальные значения напряжений и токов бытовых приборов также указываются как действующие значения. Так стандартное напряжение в цепи − 220 вольт есть действующее значение, а амплитудное значение этого напряжения равно При изучении
постоянного тока мы узнали, что он не может проходить в цепи, в которой есть
конденсатор. В отличии от
постоянного переменный ток может идти и через цепь, в которой присутствует
конденсатор. Рассмотрим, как будет меняться сила тока в цепи, содержащей конденсатор, с течением времени. При этом будем пренебрегать сопротивлением соединяющих проводов и обкладок конденсатора. рисунок Напряжение на конденсаторе будет равняться напряжению на концах цепи. Значит, мы можем приравнять эти две величины. u = φ1-φ2 = q/C, u = Umcos(ωt). Имеем: q/C = Umcos(ωt). Выражаем заряд: q = CUmcos(ωt). Видим, что заряд
будет изменяться по гармоническому закону. Сила тока — это скорость изменения
заряда. Значит, если возьмем производную от заряда, получим выражение для силы
тока. I = q’ = UmCωcos(ωt+π/2). Разность фаз между колебаниями силы тока и заряда, а также напряжения, получилась равной π/2. Получается, что колебания силы тока опережают по фазе колебания напряжения на π/2. Это представлено на рисунке. Из уравнения колебаний силы тока получаем выражение для амплитуды силы тока: Im = UmCω. Введем следующее обозначение: Xc = 1/(Cω). Запишем следующее выражение закона Ома, используя Xc и действующие значения силы тока и напряжения: I = U/Xc. Xc — величина, называемая емкостным сопротивлением. Индуктивность в
цепи переменного тока будет влиять на силу переменного тока. Рассмотрим цепь, в которой есть только катушка индуктивности. При этом значение сопротивления катушки и соединительных проводов пренебрежимо мало. рисунок Выясним, как
будут связаны напряжение на катушке с ЭДС самоиндукции в ней. При сопротивлении
катушки равном нулю, напряженность электрического поля внутри проводника тоже
будет равна нулю. Напряженности электрического поля создаваемого зарядами Eк будет соответствовать такая же по модулю и противоположно направленная напряженность вихревого электрического поля, которое появится вследствие изменения магнитного поля. Следовательно, ЭДС самоиндукции ei будет равна по модулю и противоположна по знаку удельной работе кулоновского поля. Следовательно: ei = -u. Сила тока будет изменяться по гармоническому закону: I = Im sin(ωt). ЭДС самоиндукции будет равна: Ei = -Li’ = -Lω Im cos(ωt). Следовательно, напряжение будет равно: U = Lω Im cos(ωt) = Lω Im sin(ωt+ π/2). Отсюда значение
действующего напряжения будет равняться Um = Lω Im. Видим, что между колебаниями
тока и напряжения получилась разность фаз равная π/2. Следовательно,
колебания силы тока отстают от колебания напряжения на π/2. рисунок Im = Um/(ωL). Введем обозначение XL = ωL. Эта величина называется индуктивное сопротивление. |
То есть за 1 секунду
направление тока в розетке меняется 50 раз.
Эту
нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным
сопротивлением.
Как и в случае механических колебаний, в переменном токе нас
мало будут интересовать значения силы тока, напряжении в какой-то отдельный
момент времени. Гораздо важнее будет знать общие характеристики колебаний —
такие, как амплитуда, частота, период, действующие значения силы тока и
напряжения. 
Так как конденсатор — это две пластины, разделенные слоем
диэлектрика. Для цепи постоянного тока конденсатор будет, как разрыв в цепи.
Если конденсатор пропускает постоянный ток, значит, он неисправен.
Равенство нулю напряженности возможно.
Это наглядно
представлено на следующем рисунке.Индуктивное реактивное сопротивление и емкостное реактивное сопротивление – определение и примеры решения
Дата последнего обновления: 06 апреля 2023 г. реактивное сопротивление, создаваемое емкостными элементами (конденсаторами). Мы можем обозначить его как. Емкостное реактивное сопротивление представляет собой противодействие напряжения на емкостном элементе, которое временно используется для накопления электрической энергии в виде электрического поля. Емкостное сопротивление создает разность фаз между током и напряжением.
В емкостной цепи напряжение опережает ток. Для идеальной емкостной цепи напряжение опережает ток. Благодаря емкостному реактивному сопротивлению, из-за которого коэффициент мощности системы или цепи опережает.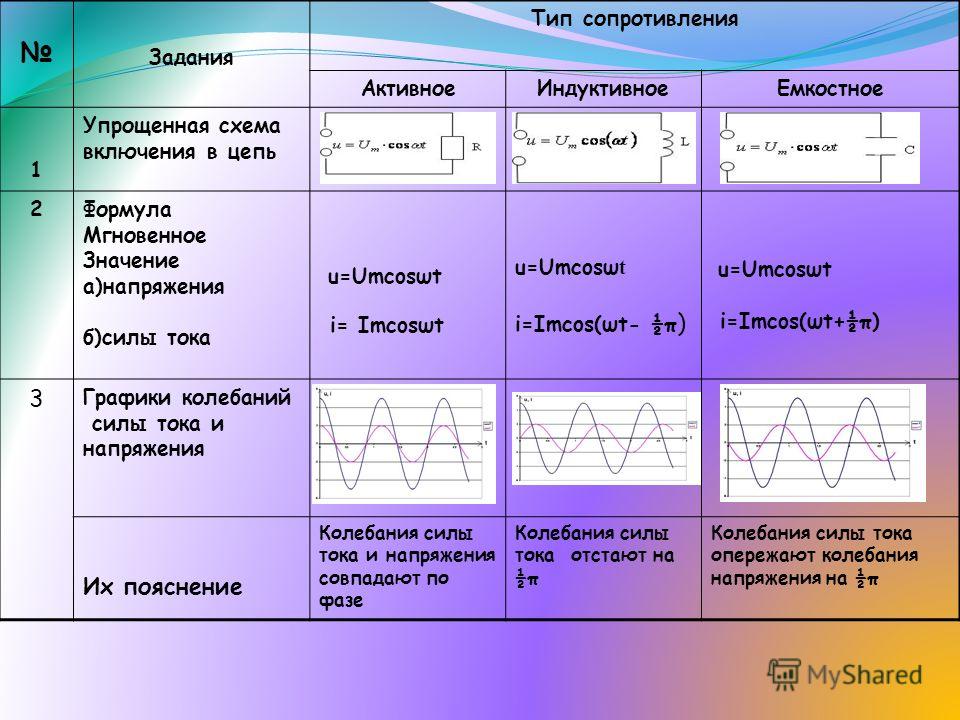
Ниже показана векторная диаграмма идеальной емкостной цепи.
(Изображение будет загружено в ближайшее время)
Разница между реактивным сопротивлением и сопротивлением
Реактивное сопротивление является составляющей импеданса, а сопротивление является постоянной составляющей сопротивления.
Значение реактивного сопротивления всегда представляет собой комплексное число, тогда как значение сопротивления должно быть действительным числом.
В чисто индуктивной или емкостной цепи сопротивление будет равно нулю, а в чисто резистивной цепи реактивное сопротивление будет равно нулю.
Из-за реактивного сопротивления будет изменяться как амплитуда, так и фаза тока.
Из-за сопротивления ток и напряжение всегда будут оставаться в фазе.Значение реактивного сопротивления зависит от частоты сети, тогда как значение сопротивления не зависит от частоты сети.
Для источника постоянного тока индуктивное сопротивление должно быть равно нулю, а емкостное сопротивление будет бесконечно. Для питания постоянным током сопротивление останется прежним.
Реактивные сопротивления обозначаются как и. Сопротивление обозначается как.
Коэффициент мощности в реактивном сопротивлении опережает или отстает из-за элемента реактивного сопротивления. В сопротивлении мощность равна единице, когда реактивное сопротивление равно нулю.
Из-за сопротивления ток и напряжение всегда будут оставаться в фазе.Решенные примеры Индуктивное реактивное сопротивление и емкостное реактивное сопротивление
Что такое реактивное электрическое сопротивление?
Электрическое реактивное сопротивление можно определить как поток, противоположный направлению тока в элементе цепи из-за его индуктивности и емкости.
Если реактивное сопротивление больше, то ток будет меньше при том же приложенном напряжении. Реактивное сопротивление, почти аналогичное электрическому сопротивлению, также имеет несколько отличий от него. Когда через электрическую цепь или элемент проходит переменный ток, изменяется как фаза, так и амплитуда тока. Кроме того, энергия запасается в элементе, содержащем реактивное сопротивление.
Таким образом, энергия высвобождается либо в форме электрического поля, либо в форме магнитного поля. Реактивное сопротивление в магнитном поле сопротивляется изменению тока, тогда как в электрическом поле реактивное сопротивление будет сопротивляться изменению напряжения. Если реактивное сопротивление высвобождает энергию в виде магнитного поля, оно называется индуктивным реактивным сопротивлением, тогда как если реактивное сопротивление высвобождает энергию в форме электрического поля, оно называется емкостным реактивным сопротивлением. С увеличением частоты емкостное сопротивление уменьшается, а индуктивное сопротивление увеличивается.
Идеальный резистор будет иметь нулевое реактивное сопротивление, тогда как идеальные катушки индуктивности и конденсаторы будут иметь нулевое сопротивление.
Что такое индуктивное сопротивление?
Индуктивное сопротивление – это реактивное сопротивление, создаваемое индуктивным элементом (индуктором). Его можно обозначить как. С помощью индуктивных элементов электрическая энергия может храниться в виде магнитного поля. Когда через цепь пропускают переменный ток, вокруг нее образуется магнитное поле, которое может изменяться под действием тока. Изменения в магнитном поле могут индуцировать другой электрический ток в той же цепи. Закон Ленца гласит, что направление этого тока противоположно основному току. Следовательно, мы можем сказать, что индуктивное сопротивление фактически препятствует изменению тока через элемент.
Протекание тока из-за индуктивного реактивного сопротивления приводит к задержке, которая может привести к созданию разности фаз между сигналами тока и напряжения.
Ток индуктивной цепи может отставать от напряжения. В идеальной индуктивной цепи ток отстает от напряжения на . Индуктивное сопротивление также является причиной отставания коэффициента мощности. Ниже показана векторная диаграмма идеальной индуктивной цепи.
(Изображение скоро будет загружено)
Векторная диаграмма идеальной индуктивной цепи
Когда учащиеся готовятся к ЕГЭ, вопросы могут быть сложными, но, безусловно, их можно решить. Помните, что будучи студентами, вы находитесь на пути к построению светлого будущего, поэтому о чем беспокоиться? Дайте экзаменам все возможное!
Чтобы помочь учащимся лучше учиться и стараться изо всех сил, Vedantu дает определения и решенные примеры, чтобы лучше всего проиллюстрировать тему индуктивного реактивного сопротивления и емкостного реактивного сопротивления. Этот ресурс особенно полезен, когда учащиеся хотят быстро ознакомиться с темами и решить свои сомнения относительно вопросов, которые могут быть заданы в JEE Mains.
Студенты должны знать, что каждая тема важна не только для экзамена, но и для их будущей карьеры.
Что такое электрическое, индуктивное и емкостное сопротивление?
1. Электрическое реактивное сопротивление – определяется как поток, который течет в направлении, противоположном течению тока в электрической цепи. Чем больше реактивное сопротивление, тем меньше ток будет для этого приложенного напряжения. Реактивное сопротивление ведет себя по-разному в магнитном и электрическом полях. В магнитном поле реактивное сопротивление будет сопротивляться изменению тока, в то время как оно сопротивляется изменению напряжения в электрическом поле.
2. Индуктивное реактивное сопротивление — Обозначается символом X L , создается за счет наличия индуктивного элемента, т.е. индуктора. Одним из применений индуктивного элемента является то, что его можно использовать для хранения электрической энергии в виде магнитного поля.
Конкретный закон, называемый законом Ленца, ясно гласит, что направление тока, создаваемого индуктивным реактивным сопротивлением, противоположно направлению основного тока. Это может привести к задержке мощности между формами сигналов напряжения и тока.
3. Емкостное реактивное сопротивление — Обозначается символом X C , создается за счет наличия емкостного элемента, т.е. конденсаторов. Емкостной элемент помогает хранить электрическую энергию в виде электрического поля, в отличие от индуктивного элемента. Емкостное реактивное сопротивление возникает из-за противоположности напряжения на конденсаторах. Это также создает отставание между током и напряжением. Идеальное отставание в индуктивной цепи и идеальное опережение напряжения по току в емкостной цепи равны 90 градусов.
23.11 Реактивное, индуктивное и емкостное сопротивление – College Physics
Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии
Резюме
- Зарисовка зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
- Рассчитать индуктивное и емкостное сопротивление.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.
Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рисунке 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление.
(б) График тока и напряжения на катушке индуктивности в зависимости от времени.График на рис. 2(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом: 9{\circ}}[/latex] фазовый угол.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС [латекс]{V= -L(\Delta I/ \Delta t)}[/латекс].
Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока [латекс]{I}[/латекс] через катушку индуктивности [латекс]{L}[/латекс] определяется версией закона Ома:
[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {X_L}}, [/ латекс]
, где [latex]{V}[/latex] — среднеквадратичное напряжение на катушке индуктивности, а [latex]{X_L}[/latex] определяется как 9.0003
[латекс]{X_L = 2 \pi fL},[/латекс]
с [latex]{f}[/latex] частотой источника переменного напряжения в герцах (анализ цепи с использованием правила цикла Кирхгофа и исчисления фактически дает это выражение). [латекс]{X_L}[/латекс] называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. [latex]{X_L}[/latex] имеет единицы измерения омы ([latex]{1 \;\textbf{H}=1 \;\Omega \cdot \;\text{s}}[/latex], так что частота, умноженная на индуктивность, имеет единицы (циклы / с) ([латекс] {\ Omega \ cdot \; \ text {s}} [/ латекс]) = [латекс] {\ Omega} [/латекс]), что соответствует его роль эффективного сопротивления.
Имеет смысл, что [латекс]{X_L}[/латекс] пропорционален [латексу]{L}[/латексу], поскольку чем больше индукция, тем больше его сопротивление изменению. Также разумно, что [латекс]{X_L}[/латекс] пропорционален частоте [латекс]{f}[/латекс], поскольку большая частота означает большее изменение тока. То есть [latex]{\Delta I/\Delta t}[/latex] велико для больших частот (большой [latex]{f}[/latex] , маленький [латекс] {\ Delta t} [/латекс]). Чем больше изменение, тем больше сопротивление индуктора.
Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока
(a) Рассчитайте индуктивное реактивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Индуктивное сопротивление находится непосредственно из выражения [латекс]{X_L = 2 \pi fL}[/латекс].
Как только [латекс]{X_L}[/латекс] найден на каждой частоте, можно использовать закон Ома, указанный в уравнении [латекс]{I=V/X_L}[/латекс], чтобы найти ток на каждой частоте. 94 \;\text{/s})(3,00 \;\text{мГн}) = 188 \;\Omega \;\text{at} 10 \;\text{кГц}}[/latex]
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении [latex]{I = V/X_L}[/latex], при условии, что приложенное среднеквадратичное значение напряжения составляет 120 В. Для первой частоты это дает
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_L}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {120 \;\text{V}}{1.13 \;\Omega}}[/latex] [латекс]{= 106 \;\text{A at} \; 60 \;\text{Гц}}.[/latex]
Аналогично, на частоте 10 кГц
[латекс] {I=}[/латекс] [латекс]{\ гидроразрыва {V} {X_L}}[/латекс] [латекс] {=}[/латекс] [латекс ] {\ frac {120 \; \ text {V}} {188 \; \ Omega}} [/latex] [латекс] {= 0,637 \; \ text {A at} \; 10 \;\text{кГц}}.
[/latex]
Обсуждение
Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис.
2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке a конденсатор полностью разряжен ([латекс]{Q = 0}[/латекс] на нем), и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение.
Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла: 9{\circ}}[/latex] фазовый угол.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока [латекс]{I}[/латекс] в цепи, содержащей только конденсатор [латекс]{С}[/латекс], определяется другим выражением вариант закона Ома будет
[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {X_C}}, [/ латекс]
, где [латекс]{V}[/латекс] — среднеквадратичное значение напряжения, а [латекс]{X_C}[/латекс] определяется (как и в случае с [латекс]{X_L}[/латекс], это выражение для [латекс]{ X_C}[/latex] результат анализа схемы с использованием правил и исчисления Кирхгофа) равно
[латекс] {X_C =} [/латекс] [латекс] {\ гидроразрыва {1} {2 \ pi fC}}, [/латекс]
, где [латекс]{X_C}[/латекс] называется емкостным реактивным сопротивлением, потому что конденсатор препятствует протеканию тока.
[latex]{X_C}[/latex] измеряется в омах (проверка оставлена читателю в качестве упражнения). [латекс]{X_C}[/латекс] обратно пропорциональна емкости [латекс]{С}[/латекс]; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Это также обратно пропорционально частоте [латекс]{ф}[/латекс]; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
Пример 2. Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Емкостное реактивное сопротивление находится непосредственно из выражения в [latex]{X_C = \frac{1}{2 \pi fC}}[/latex]. Как только [латекс]{X_C}[/латекс] найден на каждой частоте, можно использовать закон Ома, сформулированный как [латекс]{I = V/X_C}[/латекс], чтобы найти ток на каждой частоте.
4 \; \ text{/s}) (5,00 \; \ mu \ textbf {F} )}} \\[1em] & {3.18 \;\Omega \;\text{at} \; 10 \;\text{Гц}}. \end{массив}[/латекс]
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в [latex]{I = V/X_C}[/latex], при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первая частота, это дает
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_C}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ frac{120 \;\text{V}}{531 \;\Omega}}[/latex] [латекс]{= 0,226 \;\text{A at} \; 60 \;\text{Гц}}.[/latex]
Аналогично, при 10 кГц
[латекс]{I =}[/латекс] [латекс]{\ гидроразрыва {V} {X_C}}[/ латекс] [латекс] {=}[/ латекс] [латекс] {\ гидроразрыва {120 \; \ текст {V}} {3,18 \; \ Omega}} [/ латекс] [латекс] {= 37,7 \; \ текст {А в} \; 10 \;\text{кГц}}.[/latex]
Обсуждение
Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор.
На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), [латекс]{X_C}[/латекс] стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод).
Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .
В качестве напоминания рассмотрите рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Рис. 3. (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе. 9{\circ}}[/latex] фазовый угол.[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {X_L}}, [/ латекс]
, где [латекс]{В}[/латекс] — среднеквадратичное напряжение на катушке индуктивности.
[латекс]{X_L = 2 \pi fL},[/латекс]
с [latex]{f}[/latex] частотой источника переменного напряжения в герцах. 9{\circ}}[/latex] фазовый угол.
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_C}}, [/латекс]
, где [латекс]{В}[/латекс] — среднеквадратичное напряжение на конденсаторе.
[латекс] {X_C =} [/латекс] [латекс] {\ гидроразрыва {1} {2 \ pi fC}}. [/латекс]
Задачи и упражнения
1: При какой частоте индуктор на 30,0 мГн будет иметь реактивное сопротивление [латекс]{100 \;\Омега}[/латекс]
2: Какое значение индуктивности следует использовать, если [латекс]{20,0 \;\text{k} \Omega}[/latex] реактивное сопротивление необходимо при частоте 500 Гц?
3: Какую емкость следует использовать для получения реактивного сопротивления [латекс]{2,00 \;\textbf{M} \Omega}[/latex] на частоте 60,0 Гц?
4: При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление [латекс]{0,250 \;\Омега}[/латекс]?
5: (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В.
б) Какой будет сила тока на частоте 100 кГц?
6: (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору [латекс] {0,250 мкФ}[/латекс]? б) Какой будет сила тока на частоте 25,0 кГц?
7: Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, создает ток силой 2,00 А. Индуктивность какая?
8: Источник 20,0 Гц, 16,0 В производит ток 2,00 мА при подключении к конденсатору. Какова емкость?
9: (a) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какой минимальной индуктивностью он должен обладать, чтобы создавать [латекс]{2,00 \;\текст{к} \Омега}[/латекс] реактивное сопротивление для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?
10: Конденсатор на рис.
4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. а) Какая емкость необходима для получения реактивного сопротивления [латекс]{100 \;\text{k} \Омега}[/латекс] на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
11: Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекс]{10,0 \;\текст{м} \Омега}[/латекс] для сигнала 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
12: необоснованные результаты
При регистрации напряжений, вызванных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
13: Создайте свою собственную задачу
Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц.
