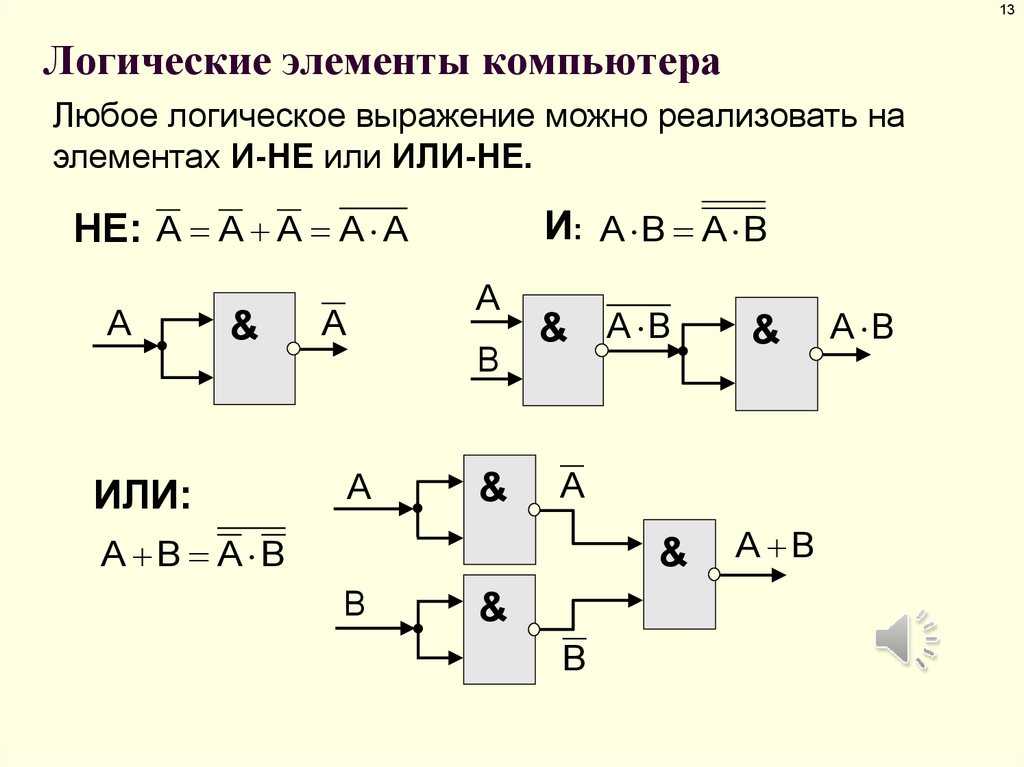
Что такое логические элементы. Какие виды логических элементов существуют. Как работают основные логические операции. Где применяются логические элементы в современной электронике.
Что такое логические элементы и для чего они нужны
Логические элементы — это базовые электронные устройства, предназначенные для обработки информации в цифровой форме. Они выполняют простейшие логические операции над входными сигналами и формируют выходной сигнал в соответствии с заданной логической функцией.
Основное назначение логических элементов — реализация булевых функций и построение более сложных цифровых устройств. Они являются фундаментальными «кирпичиками», из которых строятся все современные цифровые системы — от простейших электронных схем до мощных компьютеров.
Основные виды логических элементов
Существует несколько базовых видов логических элементов, выполняющих различные логические операции:
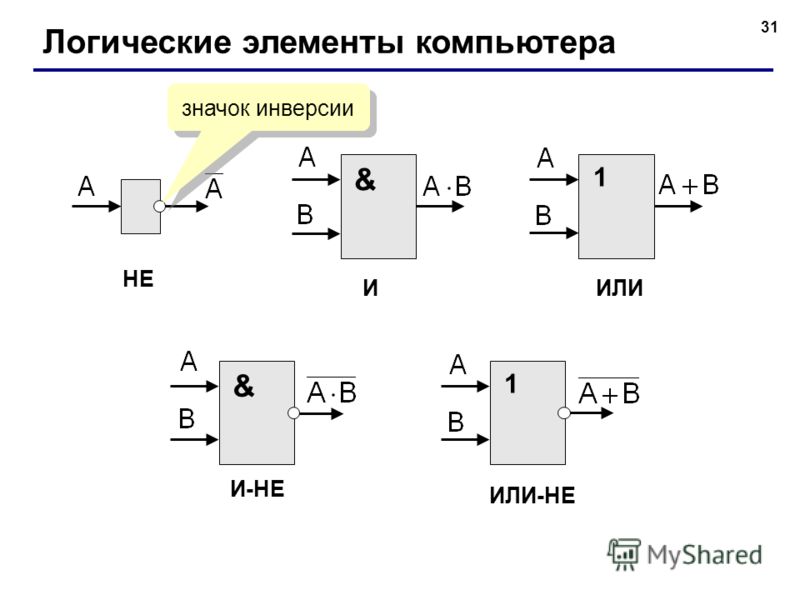
- НЕ (инвертор) — выполняет операцию отрицания
- И (конъюнкция) — реализует логическое умножение
- ИЛИ (дизъюнкция) — выполняет логическое сложение
- И-НЕ — инверсия конъюнкции
- ИЛИ-НЕ — инверсия дизъюнкции
- Исключающее ИЛИ — сложение по модулю 2
Комбинируя эти базовые элементы, можно реализовать любую логическую функцию и построить сложные цифровые устройства.

Принцип работы основных логических элементов
Рассмотрим принцип работы трех наиболее распространенных логических элементов:
Элемент НЕ (инвертор)
Инвертор имеет один вход и один выход. Его задача — инвертировать входной сигнал, то есть преобразовывать логический 0 в 1, а 1 в 0.
Таблица истинности элемента НЕ:
| Вход | Выход |
|---|---|
| 0 | 1 |
| 1 | 0 |
Элемент И (конъюнкция)
Элемент И имеет два или более входов и один выход. Выходной сигнал равен 1 только в том случае, если на всех входах присутствует 1. В остальных случаях на выходе будет 0.
Таблица истинности двухвходового элемента И:
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Элемент ИЛИ (дизъюнкция)
Элемент ИЛИ также имеет два или более входов и один выход. Выходной сигнал равен 1, если хотя бы на одном из входов присутствует 1. Только если на всех входах 0, на выходе будет 0.
Таблица истинности двухвходового элемента ИЛИ:

| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Физическая реализация логических элементов
Логические элементы могут быть реализованы различными способами:
- Механические (на основе переключателей и реле)
- Электронные (на основе транзисторов и диодов)
- Оптические (на основе оптических переключателей)
- Пневматические и гидравлические (в специализированных системах)
Наиболее распространенной является электронная реализация на основе полупроводниковых приборов. Современные интегральные микросхемы содержат миллионы логических элементов на одном кристалле.
Основные типы электронных логических элементов
В современной электронике используются следующие основные типы логических элементов:
- ТТЛ (транзисторно-транзисторная логика)
- КМОП (комплементарная металл-оксид-полупроводниковая логика)
- ЭСЛ (эмиттерно-связанная логика)
Каждый тип имеет свои особенности и области применения. Наиболее распространенными сегодня являются элементы КМОП, обладающие низким энергопотреблением и высокой степенью интеграции.
Применение логических элементов в современной электронике
Логические элементы являются основой для построения практически всех цифровых устройств:
- Процессоры и микроконтроллеры
- Оперативная и постоянная память
- Программируемые логические интегральные схемы (ПЛИС)
- Цифровые сигнальные процессоры
- Шифраторы и дешифраторы
- Мультиплексоры и демультиплексоры
- Триггеры, регистры, счетчики
Логические элементы используются во всех областях современной электроники — от бытовой техники до систем управления космическими аппаратами.
Преимущества и недостатки различных типов логических элементов
Рассмотрим основные достоинства и недостатки наиболее распространенных типов логических элементов:
ТТЛ (транзисторно-транзисторная логика)
Преимущества ТТЛ:
- Высокое быстродействие
- Хорошая помехоустойчивость
- Совместимость с большинством других типов логики
Недостатки ТТЛ:
- Относительно высокое энергопотребление
- Ограниченная степень интеграции
КМОП (комплементарная металл-оксид-полупроводниковая логика)
Преимущества КМОП:

- Очень низкое энергопотребление в статическом режиме
- Высокая степень интеграции
- Широкий диапазон напряжений питания
Недостатки КМОП:
- Меньшее быстродействие по сравнению с ТТЛ
- Чувствительность к статическому электричеству
ЭСЛ (эмиттерно-связанная логика)
Преимущества ЭСЛ:
- Самое высокое быстродействие среди биполярных логик
- Малые задержки переключения
Недостатки ЭСЛ:
- Очень высокое энергопотребление
- Сложность схемотехники
- Низкая степень интеграции
Перспективы развития логических элементов
Современные тенденции в развитии логических элементов связаны с переходом к наноэлектронике и поиском новых физических принципов для создания логических устройств. Основные направления исследований включают:
- Квантовые логические элементы
- Спинтронные устройства
- Молекулярная электроника
- Оптические логические элементы
- Биологические вычислительные системы
Эти новые технологии могут привести к созданию сверхбыстродействующих и сверхминиатюрных логических устройств, способных обрабатывать информацию на совершенно новом уровне.

Заключение
Логические элементы являются фундаментальной основой современной цифровой электроники. Они позволяют реализовывать сложнейшие алгоритмы обработки информации, лежащие в основе работы всех компьютерных систем. Несмотря на кажущуюся простоту, эти базовые «кирпичики» цифровой логики продолжают развиваться, открывая новые горизонты в области информационных технологий.
Логические элементы | это… Что такое Логические элементы?
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно логических функций и соответствующих им логических элементов, где — основание системы счисления, — число входов (аргументов), — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).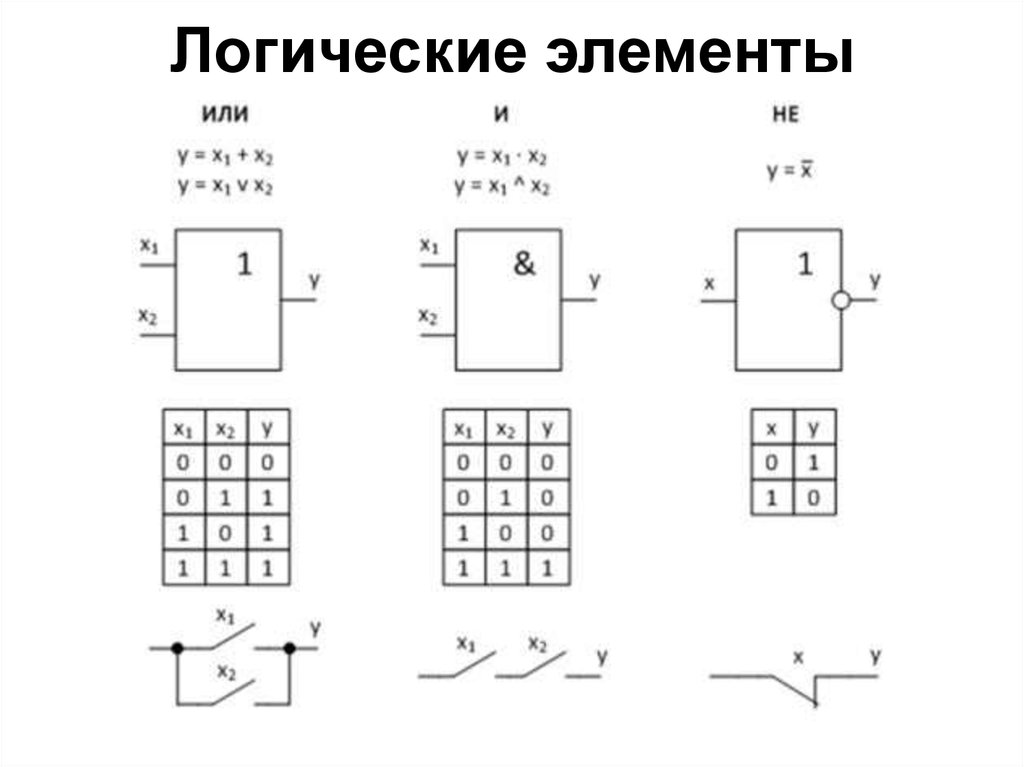
|
Содержание
|
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
Инвертор, НЕ
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе «0»,
- «0» тогда и только тогда, когда на входе «1»
Повторение, ДА
Повторитель (буфер,) ДА
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков.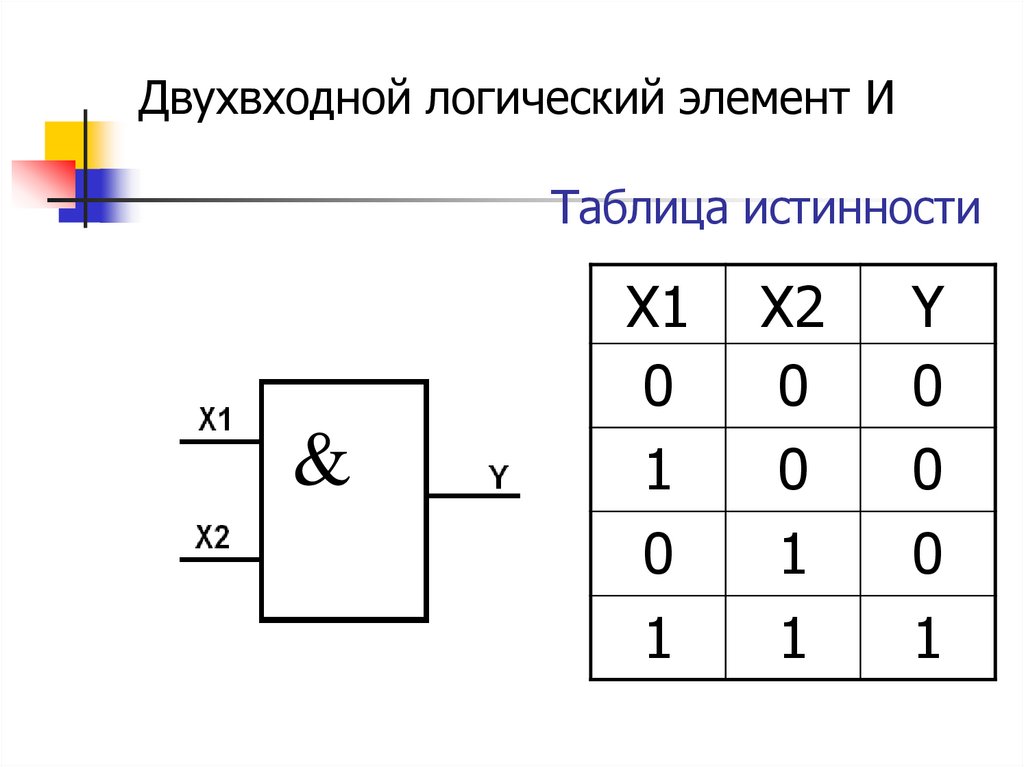 Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)
2И
| ٨ | ||
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
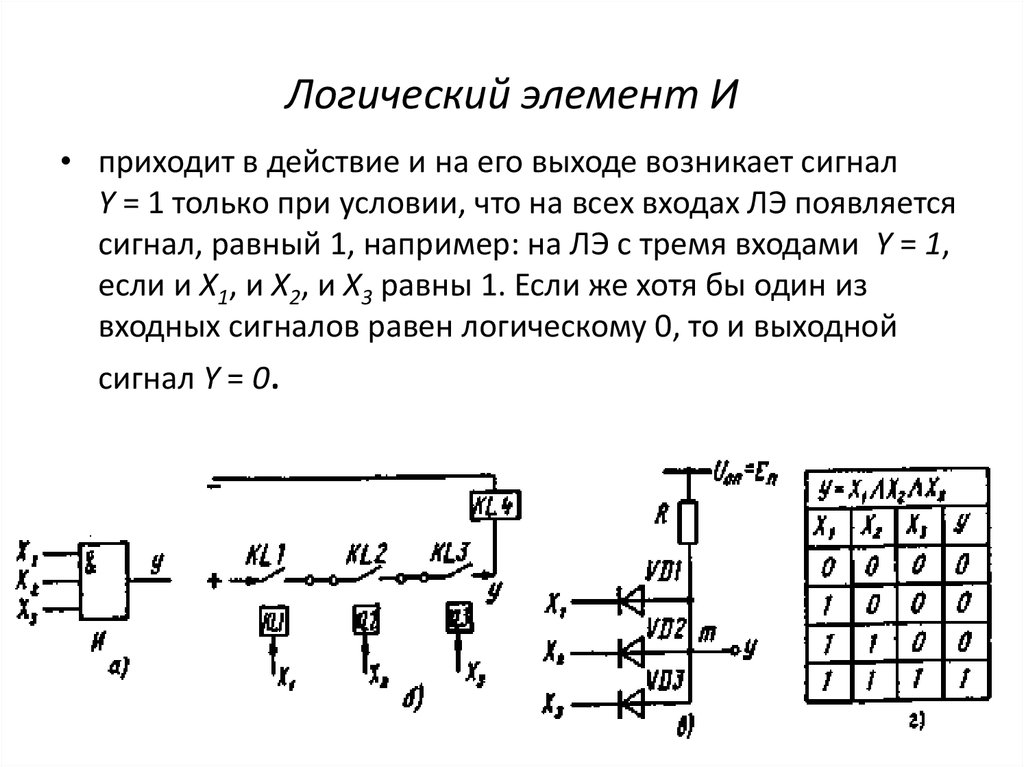
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Дизъюнкция (логическое сложение).
 Операция 2ИЛИ. Функция max(A,B)
Операция 2ИЛИ. Функция max(A,B) 2ИЛИ
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)
2И-НЕ
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции.
 Операция 2ИЛИ-НЕ (стрелка Пирса)
Операция 2ИЛИ-НЕ (стрелка Пирса) 2ИЛИ-НЕ
| ↓ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
ИСКЛ-ИЛИ-НЕ
| ↔ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует четное количество,
- «0» тогда и только тогда, когда на входе действует нечетное количество
Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность).
 Инверсия равнозначности.
Инверсия равнозначности. ИСКЛ-ИЛИ
В англоязычной литературе 2XOR.
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент.
 Запрет импликации по B. Инверсия импликации от A к B
Запрет импликации по B. Инверсия импликации от A к B | 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации логических элементов
Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
- ТТЛШ (то же с диодами Шоттки)
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
- КМОП (логика на основе комплементарных ключей на МОП транзисторах)
- ЭСЛ (эмиттерно-связанная логика)
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады.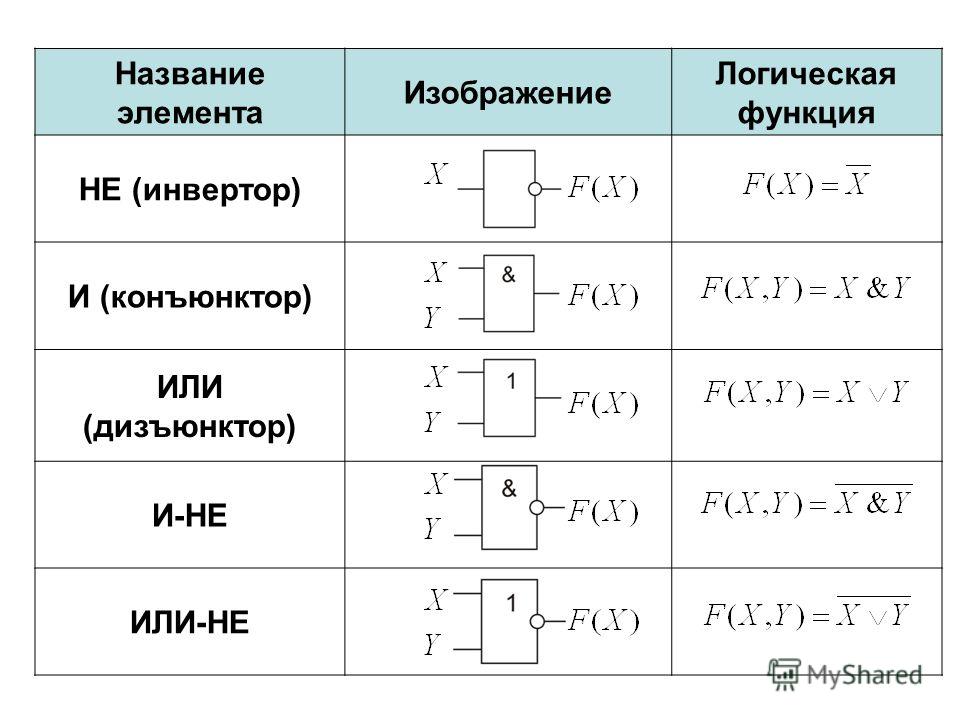 Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155.
Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
- Сумматор
- Полусумматор
- Делитель
- Шифратор
- Дешифратор
- Мультиплексор
- Демультиплексор
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
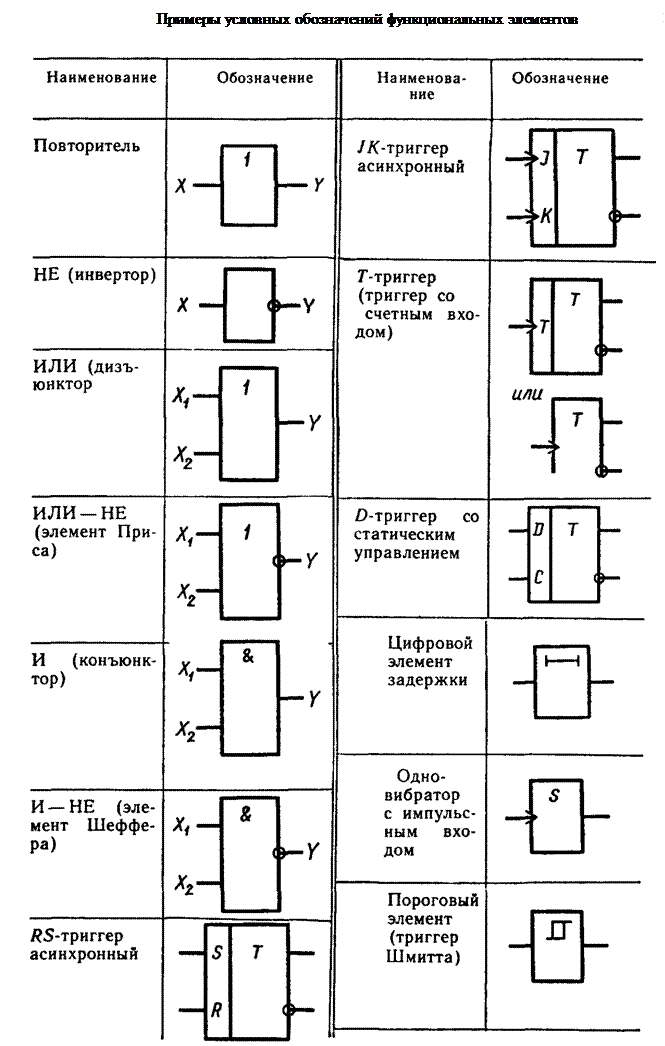
- Триггер
- Счётчик импульсов
- Регистр
- Венъюнктор
- Секвентор
См. также
- Битовые операции
- Булева функция
- Двоичная логика
- Комбинационная логика
- Секвенциальная логика
- Двухуровневый элемент
Ссылки
- Элементы и узлы цифровых электронных приборов. Логические элементы.
Литература
- Новиков Ю. В. Введение в цифровую схемотехнику. Курс лекций. — М.: Интернет-университет информационных технологий, 2006. — ISBN 5-94774-600-Х
Логические элементы | это… Что такое Логические элементы?
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно логических функций и соответствующих им логических элементов, где — основание системы счисления, — число входов (аргументов), — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
|
Содержание
|
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т.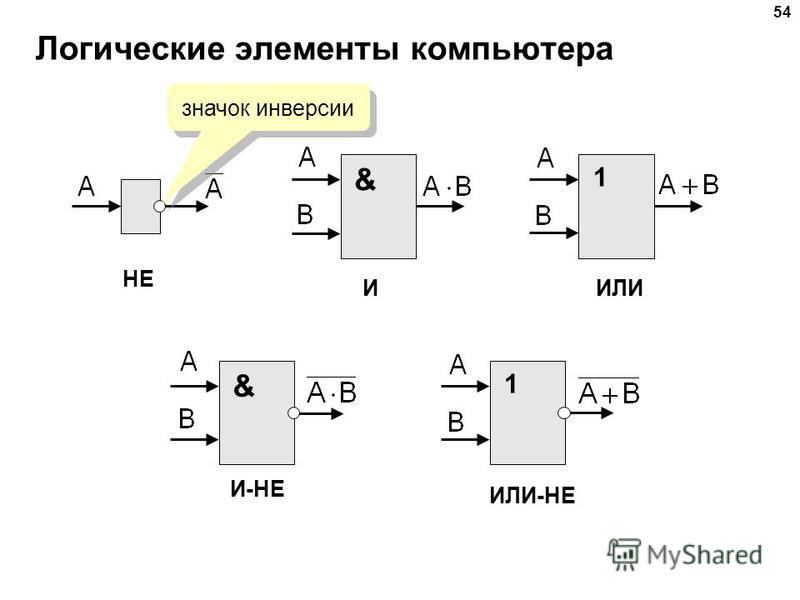 д.
д.
Из возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
Инвертор, НЕ
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе «0»,
- «0» тогда и только тогда, когда на входе «1»
Повторение, ДА
Повторитель (буфер,) ДА
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.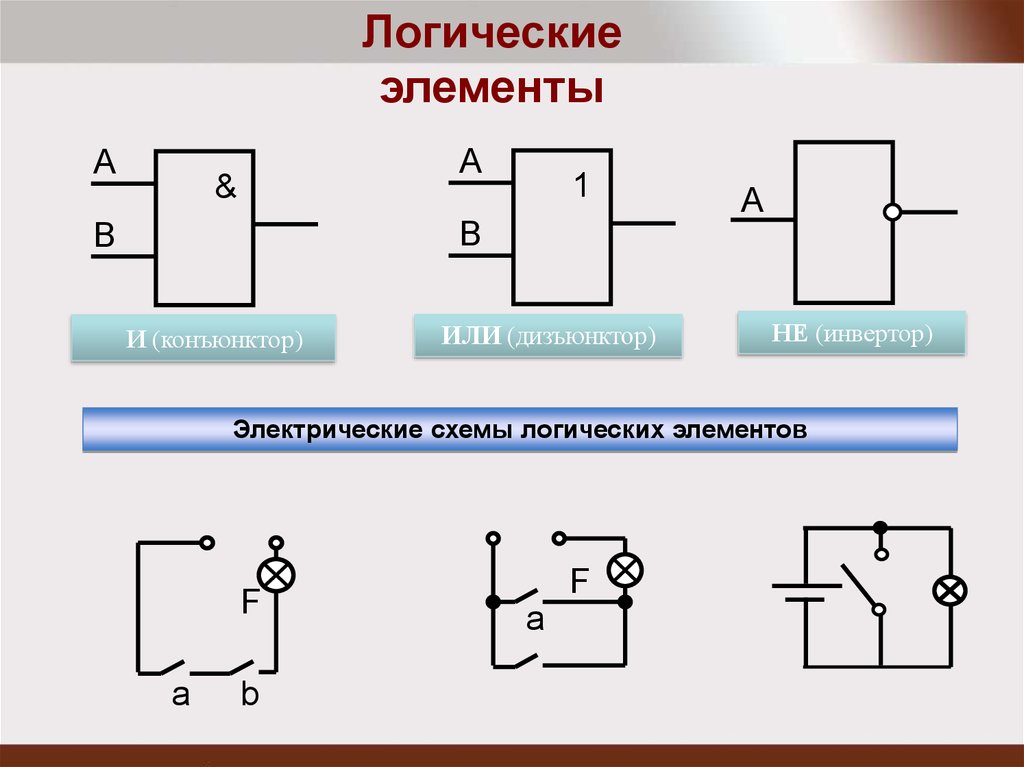
Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
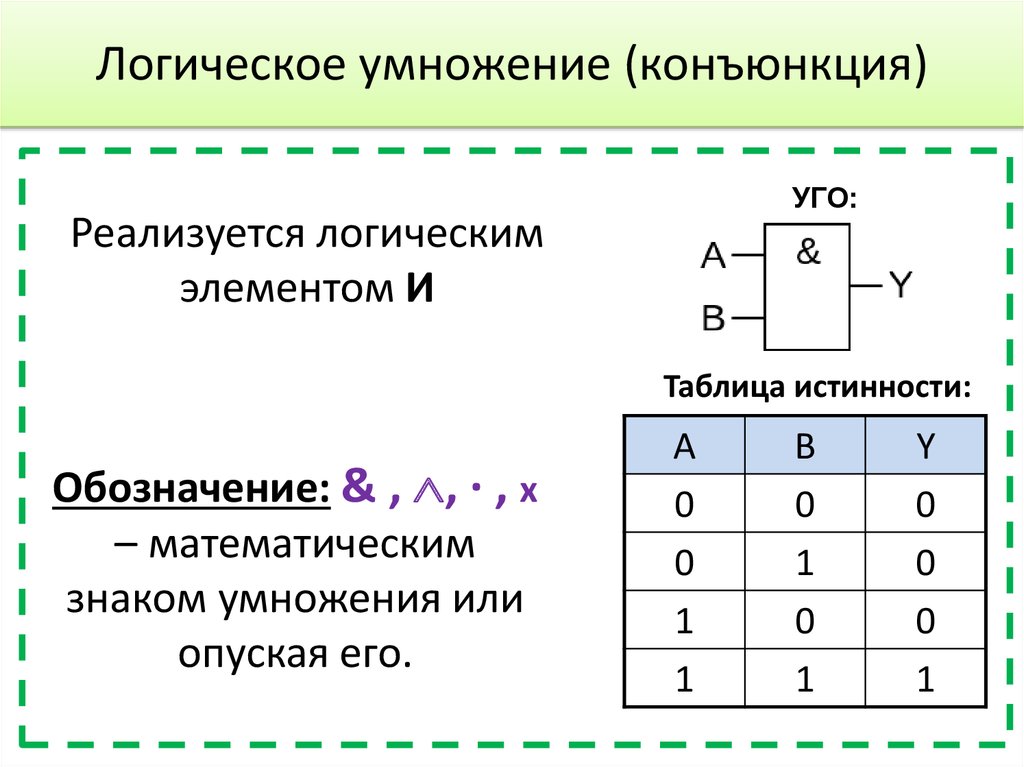
Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)
2И
| ٨ | ||
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)
2ИЛИ
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции.
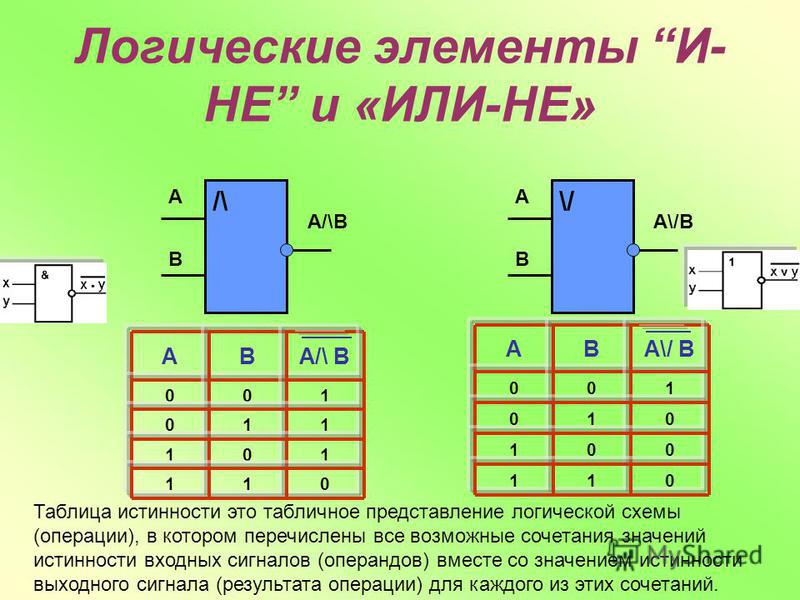 Операция 2И-НЕ (штрих Шеффера)
Операция 2И-НЕ (штрих Шеффера) 2И-НЕ
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)
2ИЛИ-НЕ
| ↓ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
ИСКЛ-ИЛИ-НЕ
| ↔ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует четное количество,
- «0» тогда и только тогда, когда на входе действует нечетное количество
Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность).
 Инверсия равнозначности.
Инверсия равнозначности. ИСКЛ-ИЛИ
В англоязычной литературе 2XOR.
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент.
 Запрет импликации по B. Инверсия импликации от A к B
Запрет импликации по B. Инверсия импликации от A к B | 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1.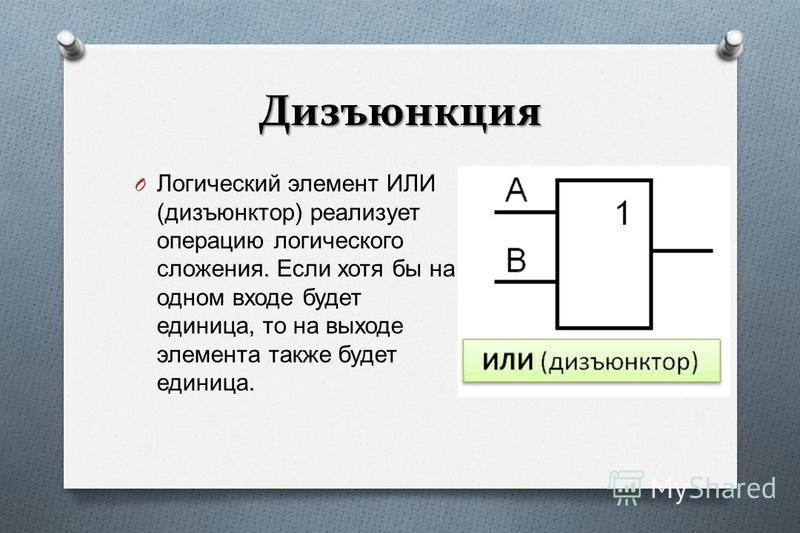 Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации логических элементов
Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
- ТТЛШ (то же с диодами Шоттки)
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
- КМОП (логика на основе комплементарных ключей на МОП транзисторах)
- ЭСЛ (эмиттерно-связанная логика)
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155.
Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт).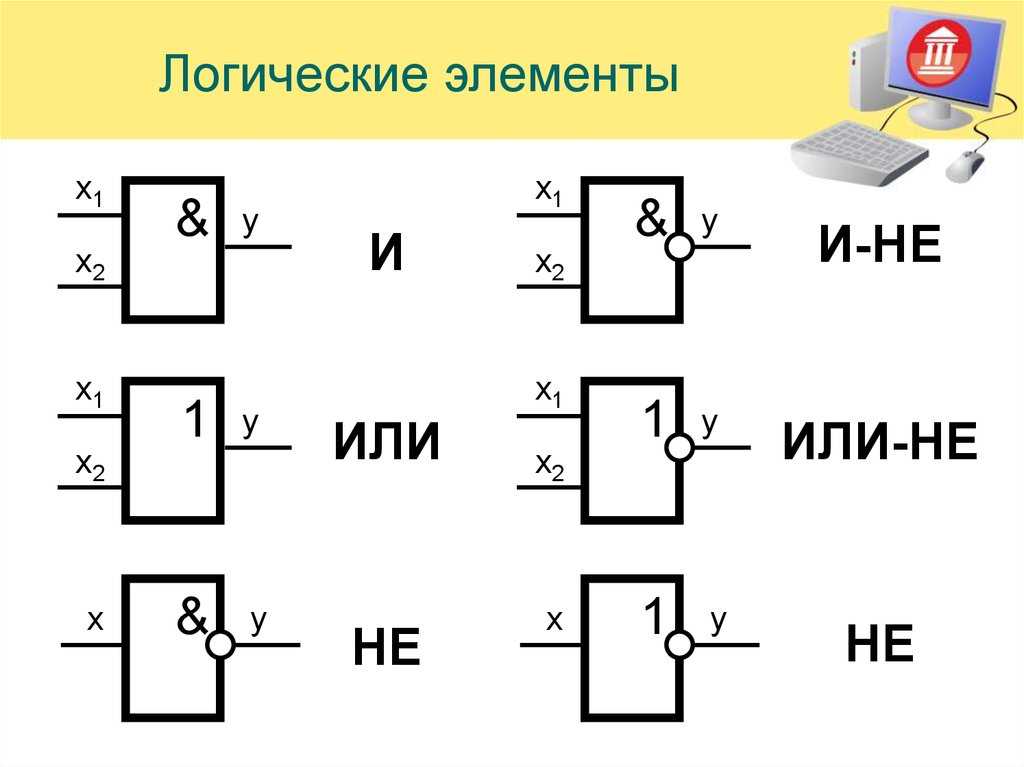 Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
- Сумматор
- Полусумматор
- Делитель
- Шифратор
- Дешифратор
- Мультиплексор
- Демультиплексор
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
- Триггер
- Счётчик импульсов
- Регистр
- Венъюнктор
- Секвентор
См. также
- Битовые операции
- Булева функция
- Двоичная логика
- Комбинационная логика
- Секвенциальная логика
- Двухуровневый элемент
Ссылки
- Элементы и узлы цифровых электронных приборов. Логические элементы.
Литература
- Новиков Ю. В. Введение в цифровую схемотехнику. Курс лекций. — М.: Интернет-университет информационных технологий, 2006. — ISBN 5-94774-600-Х
Статья о логике+элемент в The Free Dictionary
Логика+элемент | Статья о логике+элемент от The Free DictionaryЛогика+элемент | Статья о логике+элемент The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
Возможно, Вы имели в виду:
Пожалуйста, попробуйте слова по отдельности:
логика элемент
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.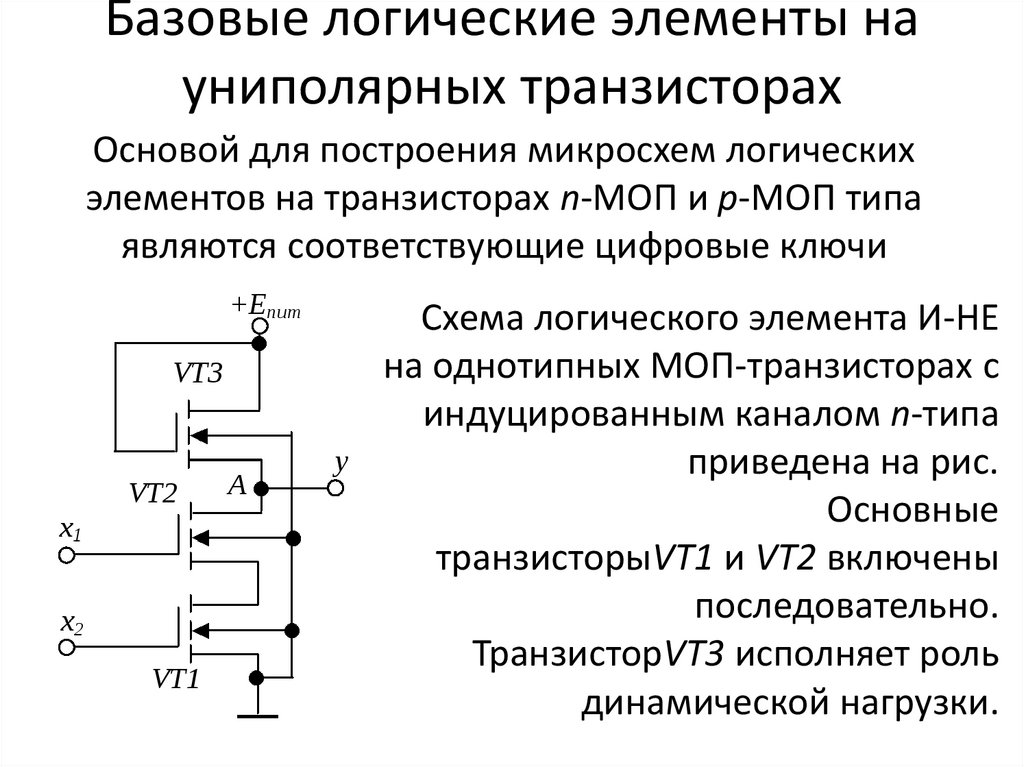
Полный браузер ?
- ▲
- логическая секция
- логический секвенсор
- Логическое моделирование
- Логические очки
- Анализатор логического состояния
- Студия логики
- логические колебания
- логический переключатель
- Логический синтез
- Логический синтез
- Логический синтез
- Логический синтез
- Логический синтез
- Логическая система
- Логическая система
- Функциональный тест логической системы
- Логические системы
- Логические системы
- Разработка логических технологий
- Теоретик логики
- Теория логики
- Логический транковый радиомодем
- Логический транковый радиомодем
- логический блок
- Группа пользователей логики
- логическая переменная
- Логика разобьет вам сердце
- логическое слово
- Логические Работы
- Логический ноль
- логика+элемент
- Логика, алгебра и степени истины
- Логика, домены и языки программирования
- Логика, Закон
- логика, многозначная
- логика, многозначная
- Логика, методология и философия науки
- Логический, Модальный
- Логический, Модальный
- Логика, рациональность и взаимодействие
- логико-арифметический блок
- Логический синтез и преобразование программ
- Логическое переключение
- логическое прерывание
- Логически развитая модель принятия решений
- логический принтер
- Логическая система
- Логическая система
- Логические системы
- Логические системы
- Логика/альтернативный пуск
- Логика/альтернативный пуск
- Логика/альтернативный пуск
- Логический/логический канал
- Логика
- Логика
- Логика Бизнес Консалтинг
- Компьютерный центр Logica & Management
- Логика Нова
- LogicaCMG
- логический
- ▼
Сайт: Следовать:
Делиться:
Открыть / Закрыть
определение логики+элемент в The Free Dictionary
Логика+элемент — определение логика+элемент в The Free DictionaryЛогика+элемент — определение логики+элемент в The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.

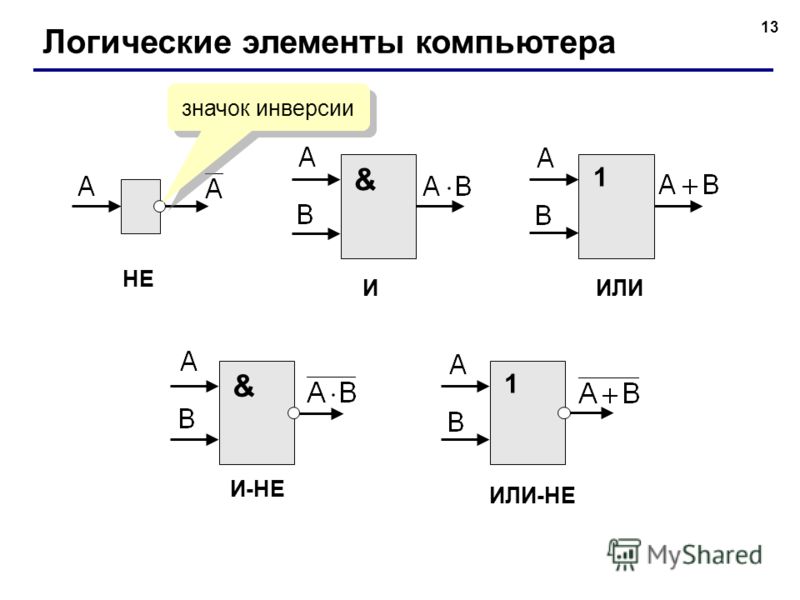 1 Инвертор
1 Инвертор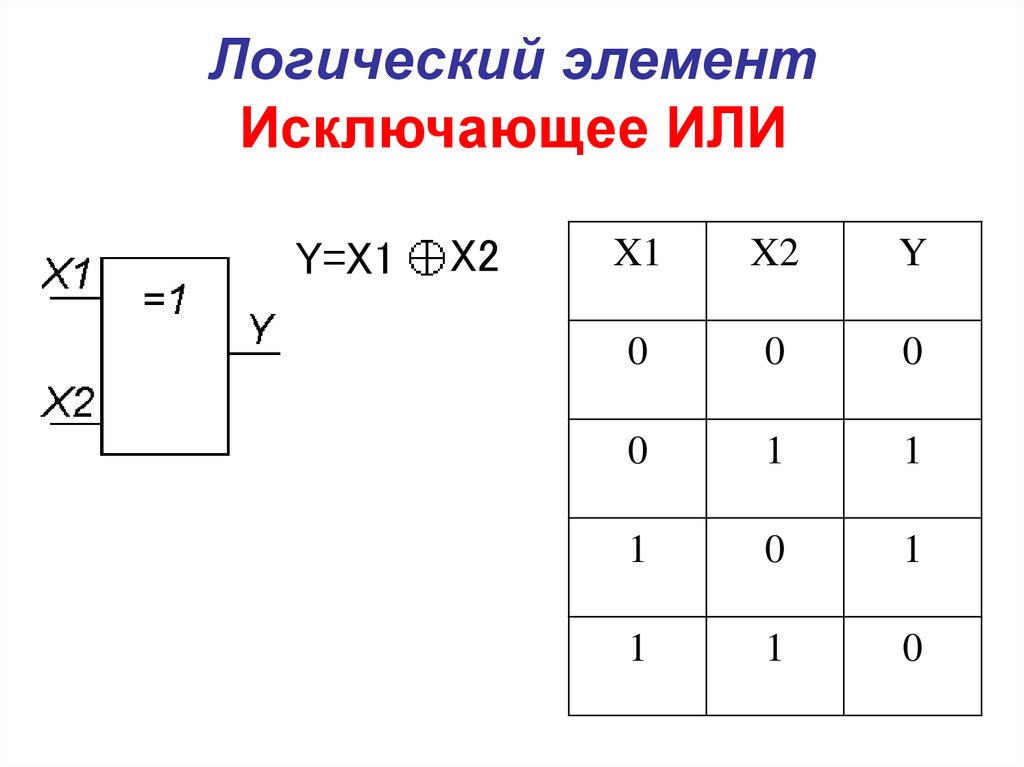 8 Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.
8 Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.