Как рассчитать общее сопротивление при последовательном и параллельном соединении резисторов. Какие формулы используются для расчета токов и напряжений в цепях с различными соединениями резисторов. Чем отличаются последовательное и параллельное соединение.
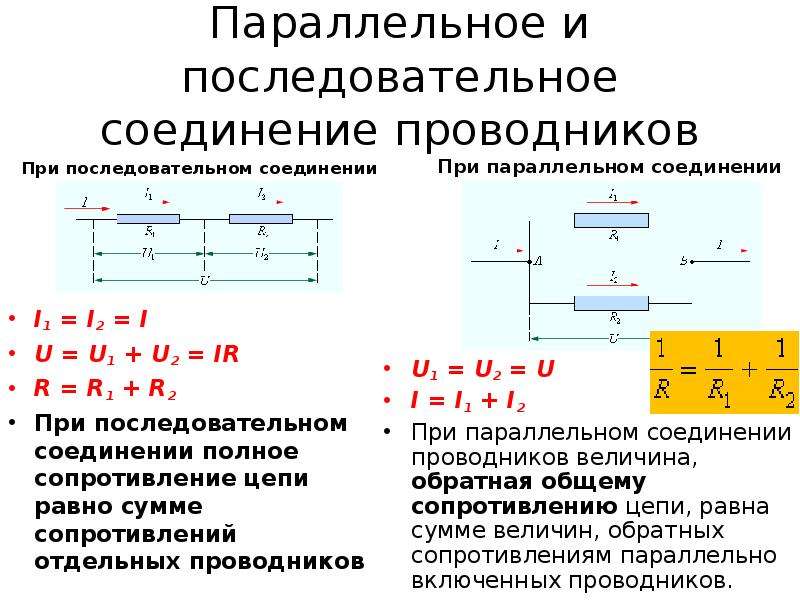
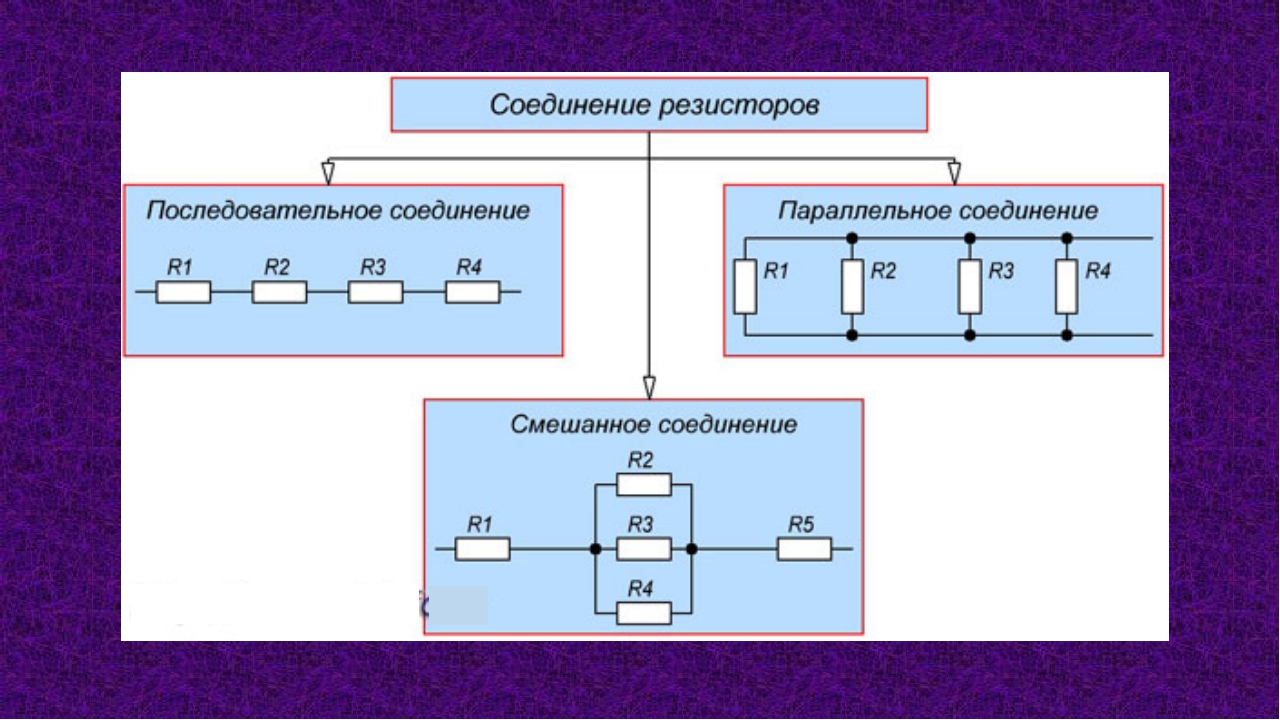
Последовательное соединение резисторов
При последовательном соединении резисторы подключаются один за другим, образуя единую цепочку. Основные характеристики такого соединения:
- Общий ток, протекающий через все резисторы, одинаков
- Общее напряжение равно сумме падений напряжения на каждом резисторе
- Общее сопротивление равно сумме сопротивлений всех резисторов
Формула для расчета общего сопротивления при последовательном соединении:
Rобщ = R1 + R2 + … + Rn
Где Rобщ — общее сопротивление, R1, R2, Rn — сопротивления отдельных резисторов.
Параллельное соединение резисторов
При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Основные характеристики:

- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток равен сумме токов через каждый резистор
- Общее сопротивление всегда меньше сопротивления любого из параллельно соединенных резисторов
Формула для расчета общего сопротивления при параллельном соединении:
1/Rобщ = 1/R1 + 1/R2 + … + 1/Rn
Где Rобщ — общее сопротивление, R1, R2, Rn — сопротивления отдельных резисторов.
Сравнение последовательного и параллельного соединения
Основные отличия двух видов соединения резисторов:
| Параметр | Последовательное | Параллельное |
|---|---|---|
| Общее сопротивление | Увеличивается | Уменьшается |
| Ток | Одинаков на всех участках | Делится между резисторами |
| Напряжение | Делится между резисторами | Одинаково на всех резисторах |
Применение различных соединений резисторов
Выбор типа соединения резисторов зависит от конкретной задачи:
- Последовательное соединение применяется для увеличения общего сопротивления цепи и деления напряжения
- Параллельное соединение используется для уменьшения общего сопротивления и деления тока
- Смешанное соединение позволяет получить более сложные соотношения токов и напряжений
Правильный выбор схемы соединения резисторов позволяет оптимально распределить токи и напряжения в электрической цепи.
Расчет параметров цепи с различными соединениями резисторов
При анализе электрических цепей с резисторами необходимо уметь рассчитывать основные параметры — токи, напряжения и мощности. Рассмотрим порядок расчета для разных типов соединений.
Расчет цепи с последовательным соединением резисторов
Дано: резисторы R1 = 100 Ом, R2 = 200 Ом, R3 = 300 Ом соединены последовательно. Напряжение источника U = 12 В.
Порядок расчета:
- Находим общее сопротивление: Rобщ = R1 + R2 + R3 = 100 + 200 + 300 = 600 Ом
- Рассчитываем общий ток: I = U / Rобщ = 12 В / 600 Ом = 0.02 А
- Определяем падение напряжения на каждом резисторе:
- U1 = I * R1 = 0.02 А * 100 Ом = 2 В
- U2 = I * R2 = 0.02 А * 200 Ом = 4 В
- U3 = I * R3 = 0.02 А * 300 Ом = 6 В
- Проверяем: U1 + U2 + U3 = 2 + 4 + 6 = 12 В (равно напряжению источника)
Расчет цепи с параллельным соединением резисторов
Дано: резисторы R1 = 30 Ом, R2 = 60 Ом, R3 = 90 Ом соединены параллельно. Напряжение источника U = 12 В.
Порядок расчета:
- Находим общее сопротивление: 1/Rобщ = 1/30 + 1/60 + 1/90. R общ ≈ 16.36 Ом
- Рассчитываем общий ток: I = U / Rобщ = 12 В / 16.36 Ом ≈ 0.733 А
- Определяем токи через каждый резистор:
- I1 = U / R1 = 12 В / 30 Ом = 0.4 А
- I2 = U / R2 = 12 В / 60 Ом = 0.2 А
- I3 = U / R3 = 12 В / 90 Ом ≈ 0.133 А
- Проверяем: I1 + I2 + I3 = 0.4 + 0.2 + 0.133 ≈ 0.733 А (равно общему току)
Практическое применение расчетов соединений резисторов
Умение рассчитывать параметры цепей с различными соединениями резисторов необходимо при:
- Проектировании электронных устройств
- Анализе работы существующих схем
- Подборе номиналов резисторов для получения нужных параметров цепи
- Диагностике неисправностей в электрических цепях
Например, последовательное соединение резисторов часто используется для создания делителей напряжения, а параллельное — для точной подгонки сопротивления или увеличения мощности рассеивания.
Особенности смешанного соединения резисторов
На практике часто встречаются схемы, где присутствуют как последовательные, так и параллельные участки — смешанное соединение резисторов. Расчет таких цепей производится поэтапно:
- Цепь разбивается на участки с однотипным соединением
- Рассчитываются параметры каждого участка по соответствующим формулам
- Полученные результаты используются для расчета всей цепи
Важно помнить, что в сложных цепях со смешанным соединением необходимо правильно определять эквивалентные сопротивления участков для корректного расчета токов и напряжений.
Вопросы для самопроверки
Для закрепления материала попробуйте ответить на следующие вопросы:
- Как изменится общее сопротивление цепи, если два одинаковых резистора соединить последовательно? А если параллельно?
- В каком случае общий ток будет больше — при последовательном или параллельном соединении одинаковых резисторов?
- Как распределяется напряжение между резисторами при их последовательном соединении?
- Почему при параллельном соединении общее сопротивление всегда меньше сопротивления любого из резисторов?
- В каких случаях целесообразно использовать смешанное соединение резисторов?
Правильные ответы на эти вопросы помогут вам лучше понять принципы работы различных соединений резисторов и их применение в электрических цепях.
Параллельное соединение резисторов определение — Морской флот
Как правильно соединять резисторы?
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы.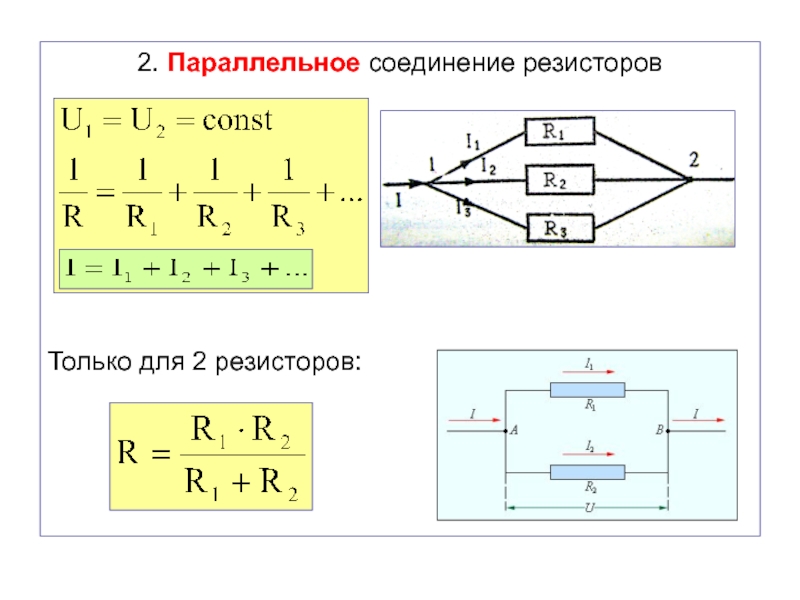 Выглядит она вот так:
Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.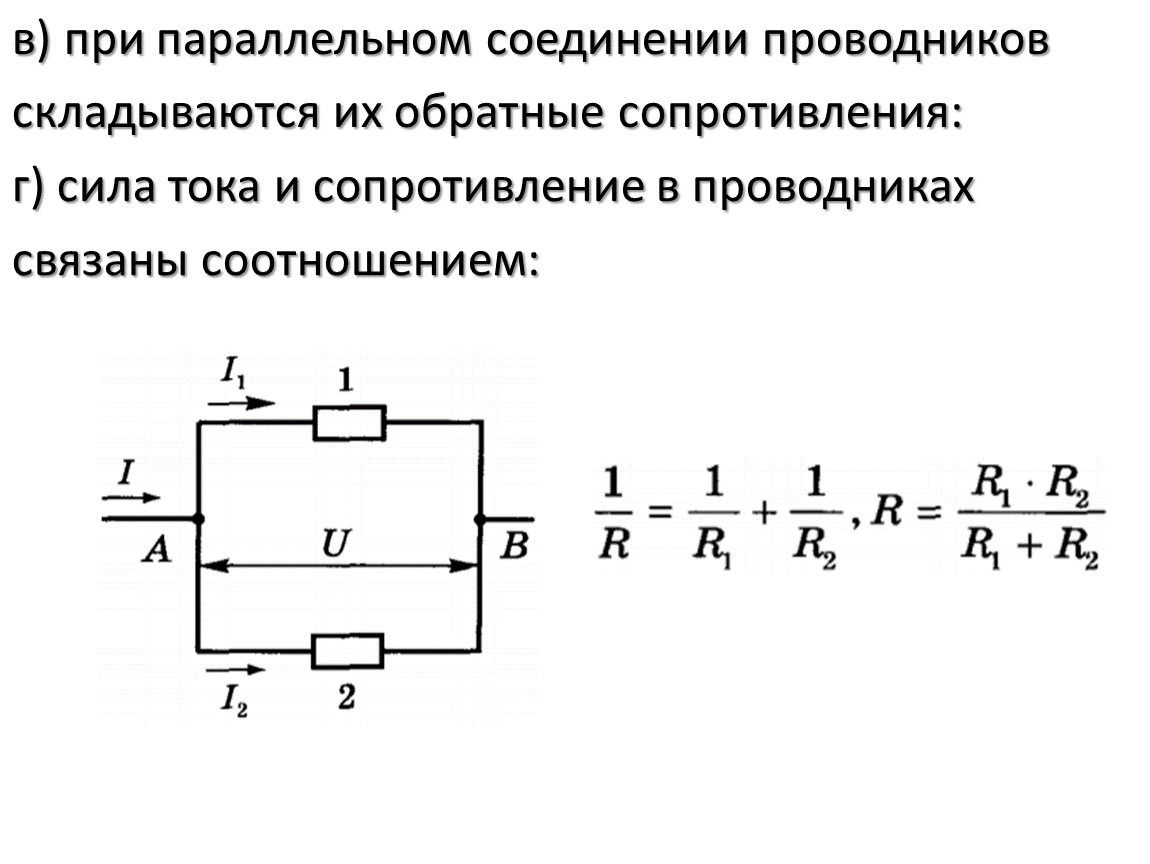
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока.
Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn).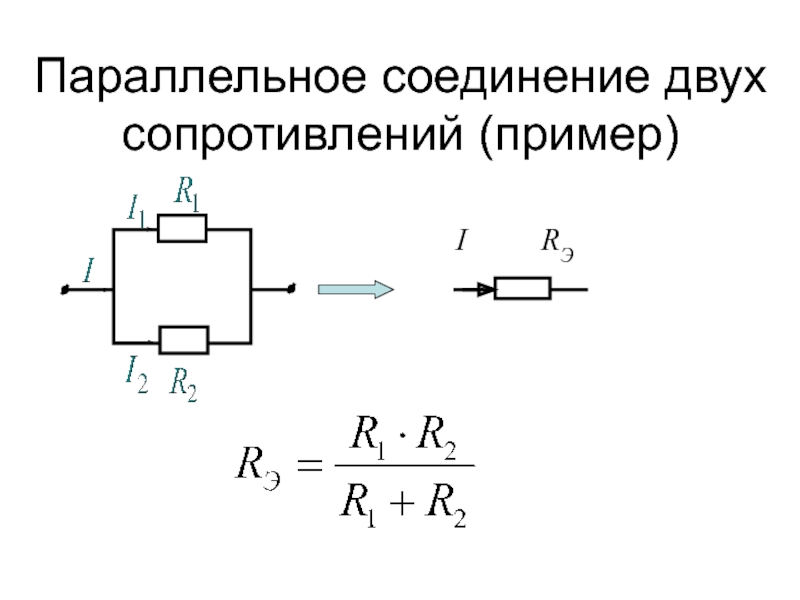 Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
Электрическое сопротивление характеризует свойство проводника препятствовать прохождению через него электрического тока. У каждого материала есть свое удельное сопротивление. Это табличная величина, и условно она считается постоянной.
Условно, потому что во многом эта характеристика зависит от внешних условий, например температуры. Сопротивление же какого-либо конкретного элемента (мы будем говорить о резисторах) складывается из многих факторов, например, из геометрических параметров, а когда речь идет о цепи переменного тока, то в расчеты включают также индуктивное и емкостное сопротивление, но об этом мы расскажем позже. Пока же — немного теории.
Закон Ома
В 1826 году немецкий физик Георг Ом на основе своих опытов вывел закон, согласно которому сила тока на участке цепи прямо пропорциональна напряжению, которое к нему приложено, и обратно пропорциональна сопротивлению участка. Из школьного курса мы знаем этот закон:
I=U/R
Позже он был сформулирован и для полной цепи:
I=ε/(R+r)
Где ε — ЭДС источника, R — сопротивление цепи, а r — сопротивление источника.
Мощность прибора
Электрический заряд при своем перемещении совершает работу. Может быть, это незаметно глазу, но вот пощупать результат этой работы можно: электроприборы у нас греются, а иногда нагрев — это цель, а не побочное явление. Не верите — ну, электроплитки, ТЭНы, утюги как раз это свойство и эксплуатируют. Правда, руками это проверять не советую.
Мощностью у нас называют работу, совершенную за единицу времени. Попробуем вычислить мощность электроприбора, включенного в цепь.2/R
Последовательное и параллельное соединение
В реальной жизни мы редко имеем дело с одним проводником и одним источником. Достаточно взглянуть в любую принципиальную электрическую схему, например, такую простенькую:
(это схема микроволновки «Электроника»)
можно увидеть, что элементы в схеме соединены по-разному, но мы покажем вам базовые закономерности, которые работают в цепях.
Правила Кирхгофа
Если взять замкнутую электрическую цепь, по которой течет заряд, то можно определенно сказать: он никуда не денется. Сумма всех зарядов, которые текут в одной цепи, всегда одинакова. Это называется законом сохранения заряда, частным случаем общего закона сохранения (как говорится, если в одном месте что-то убудет, в другом непременно прибудет).
Отсюда мы и выводим тот факт, что в каждом узле цепи сумма токов равна нулю. То есть, если ток «приходит» в точку по ветке и «уходит» по двум — значит, первый равен сумме второго и третьего.
На этой картинке мы видим, что I1+I4=I2+I3
Это называется первым правилом Кирхгофа.
Если наша цепь не будет содержать узлов, значит, ток в ней будет величиной постоянной, а элементы, один за другим поставленные в цепь, будут давать падение напряжения. При этом общее напряжение в цепи останется тем же. Отсюда вытекает второе правило Кирхгофа: сумма напряжений на участках цепи будет равна ЭДС источников тока, входящий в эту цепь. Если у нас источник один, то будет верно равенство:
ε=U1+U2+U3+…+Un
Сумма падений напряжения будет, таким образом, нулевой.
В ситуациях, когда мы имеем дело с переменным током, падение будет наблюдаться на участках с конденсаторами и катушками — в цепях переменного тока у них появляется сопротивление (об этом позже).
Теперь, когда мы познакомились с теоретической частью, можем перейти к более приближенному к суровой реальности вопросу, а именно — расчету последовательного и параллельного соединения резисторов.
Примеры расчетов
Рассчитаем параметры цепей с разным типом соединения.
Как мы видим из рисунка, резисторы соединены один за другим, последовательным способом.2/R
Исходя из вышеперечисленных закономерностей, вы сможете рассчитывать самые причудливые соединения резисторов, можете попрактиковаться, взяв в библиотеке задачник.
Типы резисторов
Как уже было сказано ранее, элемент, который ставится в цепь для нагрузки, называется резистором. Ставят его для разных целей, главным образом для того, чтобы изменить тот или иной параметр на участке цепи. Например, понизить напряжение или силу тока, чтобы деталь, стоящая за резистором, не сгорела.
Предприятиями выпускается большой ассортимент таких изделий, и их можно по-разному классифицировать. Номинально резистор имеет то сопротивление, которое указано на нем, а по факту оно может зависеть от напряжения в сети (нелинейность), иметь разброс параметра (иногда до 20% доходит). По применяемой технологии резисторы можно разделить на:
- проволочные;
- композитные;
- металлофольговые;
- угольные;
- интегральные.
Фактическое сопротивление такого элемента может зависеть от температуры окружающей среды и даже от частоты, если мы имеем дело с переменным током. Дело в том, что часть ассортимента резисторов выполнены по проволочной технологии, то есть фактически они представляют собой мини-катушку. При малых частотах (50 Гц) это в расчет не берется, а вот на высоких (мегагерцы) паразитная индуктивность и индуктивное сопротивление может сказаться на работе схемы. Поэтому при выборе резистора для работы с высокочастотными схемами внимательно смотрите. по какой технологии он сделан. Отдайте предпочтение тонкослойным и композиционным изделиям.
Помимо этого, большое распространение получили переменные резисторы, значение сопротивления которых можно регулировать. Делается это чаще всего отверткой. Необходимость в таких изделиях продиктована разбросом параметров у обычных резисторов, а подстроечный вариант позволяет регулировать сопротивление.
Все вышесказанное актуально для цепей постоянного тока и переменного при невысоких частотах, и все это — при нормальных условиях внешней среды. Расчеты цепей при нарушении этих условий нуждаются в дополнительной корректировке: это связано с ограниченностью действия закона Ома. С чем связаны ограничения? Вот несколько примеров:
- при сверхнизких температурах многие проводники проявляют такое интересное явление, как сверхпроводимость;
- также сопротивление может разниться при нагревании;
- неприменим закон Ома для описания электрического тока в газах;
- наконец, обычный резистор можно просто пробить высоким напряжением.
Все это прекрасно работает. Не верите — можете поэкспериментировать у себя дома или провести замеры тестером. Например, изучить елочную гирлянду или показания счетчиков при включенных электроприборах (напомню, что в гирлянде лампочки соединены последовательно, а розетки в доме — параллельно). Удачи!
Что такое последовательное и параллельное соединение. Параллельное соединение резисторов. Калькулятор для расчета. Параметры цепи при параллельном соединении
Содержание:Резистор представляет собой устройство, обладающее устойчивым, стабильным значением сопротивления. Это позволяет выполнять регулировку параметров на любых участках электрической цепи. Существуют различные виды соединений, в том числе и смешанное соединение резисторов. От использования того или иного способа в конкретной схеме, напрямую зависит падение напряжений и распределение токов в цепи. Вариант смешанного соединения состоит из последовательного и параллельного подключения активных сопротивлений. Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы.
Последовательное соединение
Последовательная схема подключения предполагает расположение резисторов в схеме таким образом, что конец первого элемента соединяется с началом второго, а конец второго — с началом третьего и т.д. То есть все резисторы поочередно следуют друг за другом. Сила тока при последовательном соединении будет одинаковой в каждом элементе. В виде формулы это выглядит следующим образом: I общ = I 1 = I 2 , где I общ является общим током цепи, I 1 и I 2 — соответствуют токам 1-го и 2-го резистора.
В соответствии с законом Ома, напряжение источника питания будет равно сумме падений напряжения на каждом резисторе: U общ = U 1 + U 2 = I 1 r 1 + I 2 r 2 , в которой U общ — напряжение источника электроэнергии или самой сети; U 1 и U 2 — значение падений напряжения на 1-м и 2-м резисторах; r 1 и r 2 — сопротивления 1-го и 2-го резисторов. Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r 1 + r 2).
Таким образом, можно сделать вывод, что при последовательной схеме включения резисторов, электрический ток, протекающий через каждый из них равен общему значению тока во всей цепи. Напряжение на каждом резисторе будет разное, однако их общая сумма составит значение, равное общему напряжению всей электрической цепи. Общее сопротивление цепи также будет равно сумме сопротивлений каждого резистора, включенного в эту цепь.
Параметры цепи при параллельном соединении
Параллельное соединение представляет собой включение начальных выходов двух и более резисторов в единой точке, и концов этих же элементов в другой общей точке. Таким образом, фактически происходит соединение каждого резистора непосредственно с источником электроэнергии.
В результате, будет одинаковым с общим напряжением цепи: U общ = U 1 = U 2 . В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: I общ = I 1 + I 2 .
Для расчетов общего сопротивления используется формула: . Она используется при наличии в цепи только двух сопротивлений. В тех случаях, когда сопротивлений в цепи подключено три и более, применяется другая формула:
Таким образом, значение общего сопротивления электрической цепи будет меньше, чем самое минимальное сопротивление одного из резисторов, подключенных параллельно в эту цепь. На каждый элемент поступает напряжение, одинаковое с напряжением источника электроэнергии. Распределение тока будет прямо пропорциональным . Значение общего сопротивления резисторов, соединенных параллельно, не должно превышать минимального сопротивления какого-либо элемента.
Схема смешанного соединения резисторов
Схема смешанного соединения обладает свойствами схем резисторов. В этом случае элементы частично подключаются последовательно, а другая часть соединяется параллельно. На представленной схеме резисторы R 1 и R 2 включены последовательно, а резистор R 3 соединен параллельно с ними. В свою очередь резистор R 4 включается последовательно с предыдущей группой резисторов R 1 , R 2 и R 3 .
Расчет сопротивления для такой цепи сопряжен с определенными трудностями. Для того чтобы правильно выполнить расчеты используется метод преобразования. Он заключается в последовательном преобразовании сложной цепи в простейшую цепь за несколько этапов.
Если для примера вновь использовать представленную схему, то в самом начале определяется сопротивление R 12 резисторов R 1 и R 2 , включенных последовательно: R 12 = R 1 + R 2 . Далее, нужно определить сопротивление резисторов R 123 , включенных параллельно, по следующей формуле: R 123 =R 12 R 3 /(R 12 +R 3) = (R 1 +R 2)R 3 /(R 1 +R 2 +R 3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R 123 и сопротивления R 4 , включенного последовательно с ним: R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4 .
В заключение следует отметить, что смешанное соединение резисторов обладает положительными и отрицательными качествами последовательного и параллельного соединения. Это свойство успешно используется на практике в электрических схемах.
Здравствуйте, уважаемые читатели сайта . Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.
В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно , подбирают нужное сопротивление.
В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2 , их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений . Это условие справедливо для любого числа резисторов, где:
Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
Запомните . Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.
При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:
Если параллельно включены два резистора с сопротивлениями R1 и R2 , тогда основную формулу немного упрощаем и получаем:
При включении трех резисторов расчет общего сопротивления будет таким:
Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47 68 / (47 + 68) = 27,8 кОм.
При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10 15 33 / (15 33) + (10 33) + (10 15) = 5,07 Ом.
На заметку . При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.
Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.
Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Для параллельного соединения сопротивлений характерны следующие свойства:
Напряжения на зажимах всех сопротивлений одинаковы:
U 1 = U 2 = U 3 = U;
— проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:
1/R = 1/R 1 + 1/R 2 + 1/R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 /R 1 R 2 R 3 ,
где R — эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае R 1 , R 2 и R 3).
Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости. Следовательно, сопротивление параллельного разветвления из трёх резисторов:
R = R 1 R 2 R 3 /R 1 R 2 + R 2 R 3 + R 1 R 3 .
Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.
Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.
При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.
На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.
Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений R 1 и R 2 (см. рис.). Проводимость первой ветви равна 1/R 1 , проводимость второй ветви — 1/R 2 . Общая проводимость:
1/R = 1/R 1 + 1/R 2 .
Приведём к общему знаменателю:
1/R = R 2 + R 1 /R 1 R 2 ,
отсюда эквивалентное сопротивление
R = R 1 R 2 /R 1 + R 2 .
Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.
Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.
При параллельном соединении n равных сопротивлений R1 эквивалентное сопротивление их будет в n раз меньше, т.е.
R = R 1 /n.
На схеме, изображённой на последнем рисунке, включено пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R будет
R = R 1 /5 = 30/5 = 6 Ом.
Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:
I = I 1 + I 2 + I 3 .
Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то
U = I 1 R 1 и U = I 2 R 2 .
Левые части этих равенств одинаковы, следовательно, равны и правые части:
I 1 R 1 = I 2 R 2 ,
или
I 1 /I 2 = R 2 /R 1 ,
т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.
Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.
При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.
Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить общее сопротивление цепи R общ.
Решение. Rобщ = R 1 R 2 /R 1 + R 2 = 25 x 50 / 25 + 50 ≈ 16, 6 Ом.
Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1, 5 ампера и третьей I 3 = 2, 5 ампера. Определить общий ток цепи накала ламп усилителя I общ.
Решение. I общ = I 1 + I 2 + I 3 = 1 + 1, 5 + 2, 5 = 5 ампер.
Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.
Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R = 1/U , где R = 1 Ом
А мощность будет выделяться P = I * U , то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G , по аналогии с сопротивлением R и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I = U * G &
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Резистор — это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала. Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует. Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов. О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.
Последовательное соединение резисторов — это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи. При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам. Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.
На фотографии можно увидеть параллельное подключение резисторов.
Ниже представлена принципиальная схема параллельного соединения резисторов.
Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:
R(общ)=1/(1/R1+1/R2+1/R3+1/R n).
R1, R2, R3 и Rn — параллельно подключенные резисторы.
Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:
R(общ)=R1*R2/R1+R2.
R(общ) — общее сопротивление;
R1, R2 — параллельно подключенные резисторы.
В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:
R(общ) — общее сопротивление;
R — номинал параллельно подключенного резистора;
N — количество соединенных элементов.
Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.
Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:
R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.
Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью. В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением. Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.
Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.
При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.
Параллельное соединение резисторов – jelectro.ru
Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.
Общий вид
Особенности включения
Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.
Для такого включения типичны следующие особенности:
- Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
- Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.
В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.
Расчёт
Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).
Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:
I= U/R (одного из резисторов).
После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.
Типичные подключения
Пример №1
Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).
Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.
Из неё следует:
16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.
Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.
Пример №2
В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.
Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.
Пример
В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:
1/R = 1/200+1/220+1/470 = 0,0117;
R=1/0,0117 = 85,67Ом.
В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.
Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.
Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.
Расчёт комбинированных схем
Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.
Смешанная схема
В приведённом выше примере требуется посчитать суммарное значение номиналов цепи, состоящей из трех резисторов.
Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.
Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.
Для элементов из группы 2 значение общего сопротивления находится как сумма R2 и R3:
R (2+3) = R2 + R3.
Для получения окончательного результата приводим схему к виду, получаемому при параллельном соединении двух сопротивлений. После этого суммарное значение для всей схемы в целом вычисляется согласно уже рассмотренной ранее формуле.
В заключение отметим, что для проведения расчётных операций, относящихся к категории сложных соединений, можно воспользоваться теми же методиками. В их основу заложены всё те же закон Ома и правила Кирхгофа, известные ещё со школьной скамьи. Главное – это грамотно распорядиться всеми описанными выше формулами.
Видео
Оцените статью:Параллельное и последовательное соединение резисторов
В схемах используется параллельное, последовательное и смешанное подключение резисторов.
Необходимо помнить, что ток будет протекать по пути наименьшего сопротивления.
Последовательное соединение
При последовательном соединении общее сопротивление увеличивается. Общее сопротивление будет выше, чем сопротивление любого из резисторов.На всем участке цепи течет один и тот же ток, а общее сопротивление равно сумме всех сопротивлений. Для вычисления значения общего сопротивления необходимо к сопротивлению первого резистора прибавить сопротивление второго, третьего, четвертого резистора.
Rобщ = R1 + R2 + R3 + Rn
Например: R1 = 2 Om + R2 = 3 Om + R3 = 1 oM
Rобщ = 6 Om.
Другими словами:
При последовательном соединении резисторов их сопротивление складывается и общее сопротивление будет равно сумме R1 + R2 + R3…….
Параллельно сопротивление
При параллельном соединении общее сопротивление уменьшается. Общее сопротивление будет ниже, чем сопротивление любого из резисторов.При параллельном подключении резисторов, все немного интересней: Общее сопротивление всегда будет меньшим, чем значение наименьшего сопротивления в этой комбинации.
К каждому резистору при параллельном их соединении приложено одно и то же напряжение. А если сопротивлений резисторов в цепи при параллельном их соединении может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (в соответствии с законом Ома).
Для расчета общего сопротивления резисторов подключенных параллельно можно воспользоваться одной из следующих формул:
- Для нескольких параллельно соединенных резисторов с одинаковым номиналом:
\[ Rобщ = \frac{\color{red}R}{\color{blue}N} \]
\( Rобщ \) = общее сопротивление цепи или всех резисторов\( R \) = Номинал любого из резисторов
\( N \) = Количество резисторов в цепиПредположим мы имеем 2 резистора соединенных параллельно. Номинал каждого из которых равен 10 Ом.
\[ Rобщ = ? \]
Исходя из формулы:
\[ Rобщ = \frac{\color{red}Rлюбого из резисторов = 10 Om}{\color{blue}2} \]
\[ Rобщ = 5 \]
Для нескольких параллельно соединенных резисторов с разным номиналом:
\[ \frac{1}{\color{red}R} = \frac{1}{\color{red}R1} + \frac{1}{\color{red}R2} +…+ \frac{1}{\color{red}Rn} \]
Калькулятор параллельного соединения резисторов
Что происходит с мощностью при параллельном подключении. Параллельное соединение резисторов
Последовательное соединение сопротивлений
Возьмем три неизменных сопротивления R1, R2 и R3 и включим их в цепь так, чтоб конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений именуется поочередным. Разумеется, что ток в таковой цепи будет во всех ее точках один и тот же.
Рис 1 . Последовательное соединение сопротивлений
Как найти общее сопротивление цепи, если все включенные в нее поочередно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
либо
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив сейчас обе части равенства на I , будем совсем иметь R = R1 + R2 + R3
Таким макаром, мы сделали вывод, что при поочередном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на последующем примере. Возьмем три неизменных сопротивления, величины которых известны (к примеру, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их поочередно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример поочередного соединения 3-х сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим наружное сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во наружной цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким макаром, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Разъясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув сейчас ключ выключатель К, можно убедиться по устройствам, что наши подсчеты приблизительно верны.
Возьмем два неизменных сопротивления R1 и R2 и соединим их так, чтоб начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив потом точки а и б с источником тока, получим замкнутую электронную цепь. Такое соединение сопротивлений именуется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Любой из этих токов пойдет по собственной ветки до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким макаром, при параллельном соединении сопротивлений выходит разветвленная цепь. Поглядим, какое же будет соотношение меж токами в составленной нами цепи.
Включим амперметр меж положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив потом амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Означает, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем сейчас включать амперметр попеременно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветки амперметр покажет силу тока I1 , а во 2-ой — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Как следует, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее огромное практическое значение, носит заглавие закона разветвленной цепи .
Разглядим сейчас, каково будет соотношение меж токами в ветвях.
Включим меж точками а и б вольтметр и поглядим, что он нам покажет. Во-1-х, вольтметр покажет напряжение источника тока, потому что он подключен, как это видно из рис. 3 , конкретно к зажимам источника тока. Во-2-х, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, потому что он соединен с началом и концом каждого сопротивления.
Как следует, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Потому для каждой ветки можно написать: U1 = I1R1 и U2 = I2R2 , но потому что U1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветки будет во столько раз больше (либо меньше) тока во 2-ой ветки, во сколько раз сопротивление первой ветки меньше (либо больше) сопротивления 2-ой ветки.
Итак, мы пришли к принципиальному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, назад пропорциональные величинам сопротивлении параллельных веток. По другому говоря, чем больше сопротивление ветки, тем наименьший ток потечет через нее, и, напротив, чем меньше сопротивление ветки, тем больший ток потечет через эту ветвь.
Убедимся в корректности этой зависимости на последующем примере. Соберем схему, состоящую из 2-ух параллельно соединенных сопротивлений R1 и R 2, присоединенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем поначалу, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется назад пропорционально сопротивлениям.
Вправду, R1 == 10 Ом в два раза меньше R 2 = 20 Ом, при всем этом I1 = 300 мА в два раза больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через наименьшее сопротивление (R1 = 10 Ом), а наименьшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением воды по трубам. Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.
Рис. 4
Разглядим сейчас, чему будет равно общее сопротивление наружной цепи, состоящей из 2-ух параллельно соединенных сопротивлений.
Под этим общим сопротивлением наружной цепи нужно осознавать такое сопротивление, которым можно было бы поменять при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при всем этом тока до разветвления. Такое сопротивление именуется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и поглядим, чему будет равно эквивалентное сопротивление 2-ух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во наружной цепи (до точки разветвления), U — напряжение наружной цепи, R — сопротивление наружной цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветки I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления веток.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Потому что при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив сейчас обе части равенства на U , будем совсем иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью именуется величина, оборотная сопротивлению , мы можем сказать, что в приобретенной формуле 1 / R — проводимость наружной цепи; 1 / R1 проводимость первой ветки; 1 / R2- проводимость 2-ой ветки.
На основании этой формулы делаем вывод: при параллельном соединении проводимость наружной цепи равна сумме проводимостей отдельных веток.
Как следует, чтоб найти эквивалентное сопротивление включенных параллельно сопротивлений, нужно найти проводимость цепи и взять величину, ей оборотную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветки, а это означает, что эквивалентное сопротивление наружной цепи меньше меньшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли более ординарную цепь, состоящую из 2-ух веток. Но на практике могут повстречаться случаи, когда цепь состоит из 3-х и поболее параллельных веток. Как поступать в этих случаях?
Оказывается, все приобретенные нами соотношения остаются справедливыми и для цепи, состоящей из хоть какого числа параллельно соединенных сопротивлений.
Чтоб убедиться в этом, разглядим последующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ). R = 1 / 6 Как следует, эквивалентное сопротивление R = 6 Ом.
Таким макаром, эквивалентное сопротивление меньше меньшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Поглядим сейчас, вправду ли это сопротивление является эквивалентным, т. е. таким, которое могло бы поменять включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при всем этом силы тока до разветвления цепи.
Допустим, что напряжение наружной цепи, а как следует, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если заместо 3-х параллельно включенных узнаваемых нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как лицезреем, отысканное нами сопротивление R = 6 Ом вправду является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных устройствах, если собрать схему с взятыми нами сопротивлениями, измерить ток во наружной цепи (до разветвления), потом поменять параллельно включенные сопротивления одним сопротивлением 6 Ом и опять измерить ток. Показания амперметра и в том и в другом случае будут приблизительно схожими.
На практике могут повстречаться также параллельные соединения, для которых высчитать эквивалентное сопротивление можно проще, т. е. не определяя за ранее проводимостей, сходу отыскать сопротивление.
К примеру, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно конвертировать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении 2-ух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Содержание:Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
1. Находят эквивалентное сопротивление участков цепи с параллельным соединением резисторов. Рисунок 2. Последовательное соединение резисторов. Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов.
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Этот результат справедлив для любого числа параллельно включенных проводников.
На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений. Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения.
При последовательном соединении проводников сила тока во всех проводниках одинакова. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов. При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно.
Цепь разбивают на участки с только пареллельным или только последовательным соединением. Вычисляют общее сопротивление для каждого отдельного участка. Вычисляют общее сопротивление для всей цепи смешанного соединения. Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Если резисторы соединяются последоватеьно — складывать.
То есть при последовательном соединении резисторы подключатся друг за другом. На рисунке 4 показан простейший пример смешанного соединения резисторов. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.4. Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.
В результате вы научитесь с нуля не тольно разрабатывать собственные устройства, но и сопрягать с ними различную переферию! Узел — точка разветвления цепи, в которой соединяются не менее трёх проводников. Последовательное соединение резисторов применяется для увеличения сопротивления.
Напряжение при параллельном соединении
Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее. Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением.
Общее сопротивление Rобщ
Такое соединение сопротивлений называется последовательным. Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Точно так же для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
Это значит, что общее сопротивление цепи всегда будет ниже любого параллельно включенного резистора. 2. Если эти участки включают последовательно соединенные резисторы, то сначала вычисляют их сопротивление. Применяя закон Ома для участка цепи, можно доказать, что полное сопротивление при последовательном соединении равно сумме сопротивлений отдельных проводников.
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Знаете ли Вы,
что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, «мысленный эксперимент» фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей «мысленных экспериментов» является обман слушателя или читателя путем замены настоящего физического эксперимента его «куклой» — фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, «мысленными экспериментами» привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие «фантики» от настоящих ценностей.
Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: «Если факт не соответствует теории — измените факт» (В другом варианте » — Факт не соответствует теории? — Тем хуже для факта»).
Максимально, на что может претендовать «мысленный эксперимент» — это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Параллельное соединение сопротивлений
- Подробности
- Категория: Начинающим
При монтаже и ремонте всевозможной радиоэлектронной техники и аппаратуры, зачастую, приходится подыскивать резистор с необходимым сопротивлением. Бывают случаи когда нужного номинала не оказывается под рукой. Необходимое по номиналу сопротивление можно получить путем комбинациф параллельного либо последовательного соединения сопротивлений.
При параллельном соединении сопротивлений общее сопротивление будет меньше наименьщего из них, т.е. сопротивление при таком соединении уменьшается.
Схема параллельного соединения сопротивлений
Подсчет результирующего сопротивления производится по формуле:
Gоб=G1+G2+…+Gn;
где G-проводимость ветви.
G=1/R;
Существует простое правило, дающее, без всяких расчетов определить общее сопротивление:
при соединении двух сопротивлений с одинаковым сопротивлением, результирующее сопротивление будет в два раза меньше сопротивления каждого из резисторов, примененных в этой цепи.
В случае набора составного резистора из сопротивлений разного номинала, при параллельном соединении, общее сопротивление будет меньше наименьшего из входящих в эту цепь сопротивлений.
Параллельное соединение сопротивлений требует обязательной подборки резисторов по рассеиваемой мощности. Если один из резисторов будет меньшей мощности, то при работе схемы через него потечет больший ток. Это ведет к недопустимому перегреву, и как следствие, выходу из строя резистора.
Параллельное соединение сопротивлений, в основном, применяют при необходимости получить резистор большей мощности. Используют резисторы равные по мощности и с одинаковым сопротивлением. Полученный элемент имеет меньшее сопротивление, но с мощностью равной количеству применяемых резисторов.
Существует большое количество резисторов по типу используемых для их производства материалов. Поэтому необходимо подбирать резисторы, учитывая этот немаловажный фактор.
- < Назад
- Вперёд >
Добавить комментарий
Параллельное соединение резистора и конденсатора
Автор Aluarius На чтение 5 мин. Просмотров 3.4k. Опубликовано
Для чего предназначены резисторы и конденсаторы
Резисторы – одни из наиболее распространённых элементов в электронике. Их главное назначение – сопротивление течению тока и преобразовывать его в тепло. Главной характеристикой данных элементов является значение R.
Чем больше величина R, тем большая часть электроэнергии сможет рассеется в тепло. В схемах, которые питаются небольшим напряжением от 5 до 12 В, чаще всего используют резисторы имеющие величину R от 100 Ом до 100 кОм.
Конденсаторы – устройства, главная задача которых накапливать электрические заряды. Стоит отметить, что эту же функцию выполняет и аккумулятор, но в отличие от батареи конденсатор сразу же отдаёт весь накопившийся заряд. Величина, которую способно накопить устройство, называют «ёмкость».
Когда подсоединяется цепь к источнику электроэнергии: через конденсатор течет электрический ток. Сила тока в начале прохождения через устройство имеет наивысшее значение, в это же время напряжение станет низким.
После того, как устройство начнет накопление заряда, сила тока упадёт до нуля, а напряжение наоборот станет увеличиваться.
Особенности соединения резистора и конденсатора в цепи
Существует два типа соединения резисторов и конденсаторов: параллельное и последовательное.
Параллельное соединение резистора и конденсатора
Для того, чтобы осуществить параллельное соединение резистора и конденсатора, необходимо объединить все элементы цепи двумя узлами. Они не должны иметь связи с другими элементами.
При таком соединении, величина напряжения между обоими узлами станет падать, и оно станет равным для каждого элемента. А величина, которая обратна общему R, будет равняться сумме величин, которые обратны R всех проводников.
Когда осуществляется параллельное соединение резисторов, проводимость всех резисторов станет равняться проводимости цепи.
Если резистор соединить к заряженному конденсатору то вполне возможно короткое замыкание.
Последовательное соединение
Последовательное соединение – связка элементов между собой так, чтобы начальный участок цепи не имел ни одного узла. При таком соединении величина тока на проводниках станет равна между собой.
Когда осуществляется последовательное соединение всех элементов, то их общая ёмкость имеет формулу 1/Собщ = 1/С1 + 1/С2 + … + 1/Сn.
Как рассчитать импеданс в цепи
Импеданс – полное R тока, который обозначается Z. Этот параметр – отражение меняющегося во времени значения тока. Импеданс – векторная величина, которая состоит из двух значений: активное и реактивное сопротивление.
Активная часть импеданса, которая обозначается R – это мера степени, с которой материал будет противостоять движению электронов между атомными частицами. Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.
К материалам с минимальным сопротивлением можно отнести сталь, алюминий, золото. Самое большое значение R имеют стекло, слюда, полиэтилен и чаще всего их называют изоляторы или диэлектрики.
Стоит отметить! Активное R, имеет одно и тоже значение, как при последовательном, так и при параллельном соединении.
Если использовать резисторы в цепях синусоидального тока, то термин «импеданс» будет использоваться для обозначения сопротивления R=Z.
Практические расчеты импеданса чаще всего выполняются по следующей формуле:
Z = Um/Im.
Реактивное сопротивление обозначается X и является выражением степени, с которой электронный компонент схемы станет хранить или высвобождать электроэнергию, в то время, когда сила тока и значение напряжения станет колебаться при каждом цикле. Реактивное сопротивление выражается в числе Ом.
Энергия будет храниться и выделяться в двух типах:
- Магнитного поля. Реактивная часть является индуктивной.
- Электрического поля.
Как рассчитать время разряда и заряда конденсатора через резистор
Чтобы осуществить заряд устройства, нужно включить устройство в цепь и присоединить к зажимам генератора. Как вы уже знаете, генератор имеет внутреннее сопротивление.
Если резистор подключить к заряженному конденсатору то ключ будет замкнут и конденсатор начнёт зарядку до напряжения между обкладками, которая станет равна э.д.с генератора и равна Uc=E. При этом, обкладка которая соединена с положительным зажимом, получит положительный заряд, вторая же получит отрицательный заряд.
Чтобы обе обкладки устройства полностью зарядились, нужно, чтобы одни из них приобрела определенное количество электронов, а вторая столько же потеряла.
Зарядный ток в цепи будет протекать сотые доли секунды, пока величина напряжения на устройстве достигнет такой же уровня, что и на генераторе. В то время, пока конденсатор будет заряжаться, по всей цепи будет проходить зарядный ток. Вначале он будет иметь максимальную величину, т.к. величина напряжения станет равна 0.
По мере того как конденсатор станет заряжаться, величина R на нём будет падать.
Время процесса зарядки будет зависеть от следующих величин:
- Внутреннее сопротивление электрического генератора.
- Способность конденсатора принять количество тока.
Для того, чтобы разрядить устройство нужно отключить его от генератора переменного тока и присоединить к его обкладкам сопротивление. Дело в том, что на обкладках уже есть разность потенциалов, поэтому в цепи потечет ток.
Он будет проходить от одной обкладки через сопротивление к другой. Процесс разряда будет проходить до тех пор, пока обе обкладки не станут равны, т.е. пока напряжение между ними станет равно 0.
В самом начале, напряжение будет максимальным, сила тока – наибольшая. Как только начнется разрядка, напряжение и сила тока будут уменьшаться.
Продолжительность разряда устройства имеет зависимость от:
- Отношению заряда к разности потенциалов;
- Удельному электрическому сопротивлению.
Чем значение сопротивления выше, тем дольше будет происходить разряд конденсатора. Это можно объяснить тем, что при максимальном сопротивлении, сила тока небольшая, а величина заряда станет медленно уменьшаться.
Важно! Заряженный конденсатор не станет пропускать постоянный ток, потому что диэлектрик между его положительной и отрицательной обкладками будет размыкать цепь.
Для того, чтобы рассчитать время заряда и разряда на устройстве, лучше всего воспользоваться онлайн калькулятором.
Последовательные и параллельные резисторы— College Physics
Большинство схем имеет более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела для потока заряда называется сопротивлением. Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на (Рисунок). Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Резисторы серии
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно.Например, если ток течет через человека, держащего отвертку, в землю, то на (Рисунок) (a) может быть сопротивление вала отвертки, сопротивление ее ручки, сопротивление тела человека и сопротивление ее туфли.
(рисунок) показывает резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно.(Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы стать недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением. прибор, уменьшающий рабочий ток.)
Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).
Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения, в каждом резисторе на (Рисунок).
Согласно закону Ома падение напряжения на резисторе при протекании через него тока рассчитывается по формуле, где равно току в амперах (A), а — сопротивление в омах. Другой способ думать об этом — это напряжение, необходимое для протекания тока через сопротивление.
Таким образом, падение напряжения равно, что есть, а что есть. Сумма этих напряжений равна выходному напряжению источника; то есть
Это уравнение основано на сохранении энергии и сохранении заряда.Электрическая потенциальная энергия может быть описана уравнением, где — электрический заряд, а — напряжение. Таким образом, энергия, подаваемая источником, равна, а энергия, рассеиваемая резисторами, равна
.Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, . Плата отменяется, уступая, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
Обратите внимание, что для эквивалентного одиночного последовательного сопротивления мы имеем
Это означает, что полное или эквивалентное последовательное сопротивление трех резисторов составляет.
Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление последовательного соединения составляет
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на (Рисунок) равно, а сопротивления равны, и.а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
Стратегия и решение для (b)
Ток определяется по закону Ома.Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
Стратегия и решение для (c)
Напряжение — или падение — на резисторе определяется законом Ома. Ввод значения тока и значения первого сопротивления дает
.Аналогично
и
Обсуждение для (c)
Три капли добавляют к, как и прогнозировалось:
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, где — электрическая мощность.В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
Аналогично
и
Обсуждение для (d)
Мощность также можно рассчитать с помощью либо, где — падение напряжения на резисторе (а не полное напряжение источника). Получатся те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать, где — напряжение источника.Это дает
Обсуждение для (e)
По совпадению обратите внимание, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, что соответствует мощности, выдаваемой источником. То есть
Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Сопротивления серии добавить:
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
Параллельные резисторы
(рисунок) показывает резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. (Рисунок) (b).)
(a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления, давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны, и. Сохранение заряда подразумевает, что полный ток, производимый источником, является суммой этих токов:
Подстановка выражений для отдельных токов дает
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление параллельного соединения связано с отдельными сопротивлениями на
.Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений.(Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на (Рисунок) будут такими же, как и в ранее рассмотренном последовательном соединении:,, и. а) Каково полное сопротивление? (б) Найдите полный ток.(c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает
Таким образом,
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны инвертировать это, чтобы найти полное сопротивление. Это дает
Суммарное сопротивление с правильным количеством значащих цифр —
.Обсуждение для (а)
, как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление. Это дает
Обсуждение для (б)
Ток для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
Аналогично
и
Обсуждение для (c)
Общий ток складывается из отдельных токов:
Это соответствует сохранению заряда.
Стратегия и решение для (d)
Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Давайте использовать, так как каждый резистор получает полное напряжение. Таким образом,
Аналогично
и
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбор и ввод полного тока дает
Обсуждение для (e)
Общая мощность, рассеиваемая резисторами, также 179 Вт:
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики параллельных резисторов
- Параллельное сопротивление получается из любого отдельного сопротивления в комбинации, и оно меньше.
- Каждый резистор, включенный параллельно, имеет одинаковое полное напряжение источника. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
- Не каждый параллельный резистор получает полный ток; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они обычно встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного подключения можно свести к одному эквивалентному сопротивлению, используя методику, показанную на (Рисунок).Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто одно эквивалентное сопротивление.
Самая простая комбинация последовательного и параллельного сопротивления, показанная на (Рисунок), также является наиболее поучительной, поскольку она используется во многих приложениях.Например, это может быть сопротивление проводов от автомобильного аккумулятора к его электрическим устройствам, которые включены параллельно. и мог быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Расчет сопротивления, падения, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей(рисунок) показывает резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного.Мы можем считать сопротивление проводов, ведущих к и. (а) Найдите полное сопротивление. б) Что такое падение? (c) Найдите сквозной ток. (г) Какая мощность рассеивается?
Эти три резистора подключены к источнику напряжения так, что и включены параллельно друг другу, а эта комбинация — последовательно с.
Стратегия и решение для (а)
Чтобы найти полное сопротивление, отметим, что и находятся параллельно, а их комбинация — последовательно с.Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
.Сначала мы находим, используя уравнение для параллельных резисторов и вводя известные значения:
Инвертирование дает
Таким образом, общее сопротивление равно
.Обсуждение для (а)
Общее сопротивление этой комбинации является промежуточным между значениями чисто последовательного и чистого параллельного (и, соответственно), найденными для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение, отметим, что через него протекает полный ток.Таким образом, его падение составляет
.Мы должны найти, прежде чем сможем вычислить. Полный ток определяется по закону Ома для цепи. То есть
Вводя это в выражение выше, мы получаем
Обсуждение для (б)
Напряжение, приложенное к общему напряжению, и меньше его на величину. Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных и.
Стратегия и решение для (c)
Чтобы найти сквозной ток, мы должны сначала найти приложенное к нему напряжение.Мы называем это напряжением, потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное к обоим и уменьшается на величину, так что оно составляет
.Теперь ток через сопротивление определяется по закону Ома:
Обсуждение для (c)
Ток меньше, чем 2,00 А, которые протекали, когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.
Стратегия и решение для (d)
Рассеиваемая мощность равна
Обсуждение для (d)
Мощность меньше 24.0 Вт этот резистор рассеивает при параллельном подключении к источнику 12,0 В.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если протекает большой ток, провал в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет.Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на (Рисунок). Устройство, представленное значком, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение в проводах, представленных значком, уменьшая напряжение на лампочке (которая есть), которое затем заметно гаснет.
Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
|
Под последовательностью цепей понимается цепь, имеющая только один путь, по которому течет ток. В последовательной цепи все компоненты соединены таким образом, что при возникновении неисправности в цепи ток не будет течь через цепь.Ток в последовательной цепи одинаков во всей цепи. С другой стороны, параллельные цепи относятся к схеме с более чем одним путем, по которому протекает ток. В параллельной цепи все компоненты имеют различные ответвления для прохождения тока; таким образом, ток в цепи неодинаков. Прочтите данное руководство, чтобы узнать разницу между последовательными и параллельными цепями. Что такое последовательная цепь?Цепь называется последовательной, если ток одинаков во всех компонентах цепи.В последовательных цепях ток имеет только один путь. В последовательной цепи отношения между током и напряжением прямо противоположны отношениям в параллельной цепи. Ток через каждый элемент серии одинаков и равен току источника (Is). Напротив, напряжение на каждом последовательном элементе (V1, V2. V3) изменяется в соответствии с импедансом (в этом примере, сопротивлением) каждого элемента. Применяется закон Кирхгофа о напряжении (KVL), и напряжение, подаваемое источником (Vs), равно сумме индивидуальных падений напряжения на каждом последовательном элементе. Преимущество последовательных цепей
Недостаток последовательной цепи
Теперь рассмотрим пример последовательной схемы, чтобы понять концепцию. Найдите ток, протекающий через резисторы R1, R2 и R3. Учитывая R1 = 6 Ом R2 = 6 Ом R3 = 6 Ом А V = 36V Ответ: Применяя закон Ом в данной цепи, получаем В = ИК В = I (R1 + R2 + R3) I = В / (R1 + R2 + R3) I = 36 / (6 + 6 + 6) I = 36/18 I = 2 А Что такое параллельная цепь?Параллельная цепь — это цепь с двумя или более двумя путями прохождения тока.В параллельной цепи все компоненты имеют одинаковое напряжение. В параллельной цепи напряжение на каждом элементе одинаково и равно напряжению источника (Vs), а ток через каждый элемент (I1, I2, I3) изменяется в соответствии с импедансом (в данном примере сопротивление) каждого элемента. Применяется закон Кирхгофа (KCL) _, и общий ток, протекающий от источника (Is), равен сумме отдельных токов, протекающих через каждый параллельный элемент. Преимущество параллельных цепей
Недостаток параллельной цепи
Теперь рассмотрим пример параллельной схемы, чтобы понять концепцию. Найдите полное сопротивление между точками P и Q Ответ: Здесь сопротивление 2 Ом, подключенное параллельно с резистором 3 Ом, дает 6/5 Ом.Теперь резистор 6/5 Ом подключен последовательно с сопротивлением 5 и 4 Ом, поэтому общее сопротивление между точками P и Q = 6/5 + 5 + 4 = 10,2 Ом. Разница между последовательной и параллельной цепями
|
Сопротивления последовательно и сопротивления параллельно
Более одного электрического сопротивления могут быть подключены последовательно или параллельно, в дополнение к этому, более двух сопротивлений также могут быть подключены в комбинации последовательно и параллельно.Здесь мы будем обсуждать в основном последовательную и параллельную комбинацию.
Сопротивления в серии
Предположим, у вас есть три разных типа резисторов — R 1 , R 2 и R 3 — и вы соединяете их встык, как показано на рисунке ниже, тогда он будет называться как резисторы в серии . В случае последовательного соединения эквивалентное сопротивление комбинации складывается из суммы этих трех электрических сопротивлений.
Это означает, что сопротивление между точками A и D на рисунке ниже равно сумме трех отдельных сопротивлений.Ток входит в точку A комбинации, также уходит из точки D, поскольку в цепи нет другого параллельного пути.
Теперь предположим, что это ток I. Итак, этот ток я пропущу через сопротивление R 1 , R 2 и R 3 . Применяя закон Ома, можно найти, что падение напряжения на сопротивлениях будет V 1 = IR 1 , V 2 = IR 2 и V 3 = IR 3 . Теперь, если полное напряжение, приложенное к комбинации из последовательно соединенных сопротивлением , будет равно В.
Тогда очевидно
Так как сумма падений напряжения на отдельном сопротивлении не что иное, как равное приложенному напряжению на комбинации.
Теперь, если мы рассмотрим общую комбинацию сопротивлений как один резистор с величиной электрического сопротивления R, тогда, согласно закону Ома,
В = IR …………. (2)
Теперь сравним уравнение (1) и (2) получаем
Итак, приведенное выше доказательство показывает, что эквивалентное сопротивление комбинации последовательно соединенных сопротивлений равно сумме отдельных сопротивлений.Если бы было n сопротивлений вместо трех, эквивалентное сопротивление будет
Сопротивления параллельно
Скажем, у нас есть три резистора со значением сопротивления R 1 , R 2 и R 3 . Эти резисторы подключаются таким образом, что правая и левая клеммы каждого резистора соединяются вместе, как показано на рисунке ниже.
Эта комбинация называется параллельных сопротивлений . Если к этой комбинации приложить разность электрических потенциалов, то она будет потреблять ток I (скажем).
Поскольку этот ток пройдет три параллельных пути через эти три электрических сопротивления, ток будет разделен на три части. Скажем, токи I 1 , I 1 и I 1 проходят через резистор R 1 , R 2 и R 3 соответственно.
Где полный ток источника
Теперь, как видно из рисунка, каждое из сопротивлений , включенных параллельно , подключено к одному и тому же источнику напряжения, напряжение падает на каждом резисторе одинаково, и оно такое же, как напряжение питания V (скажем).
Следовательно, согласно закону Ома,
Теперь, если мы рассмотрим эквивалентное сопротивление комбинации R.
Затем
Теперь поместим значения I, I 1 , I 2 и I 3 в уравнении (1) получаем,
Вышеприведенное выражение представляет эквивалентное сопротивление резистора, включенного параллельно. Если бы было n сопротивлений, соединенных параллельно, вместо трех сопротивлений, выражение эквивалентного сопротивления было бы
Узнать о параллельных резисторах
Когда четыре резистора, R1, R2, R3 и R4, подключены параллельно, эквивалентное сопротивление определяется по формуле:
1Rparallel = 1R1 + 1R2 + 1R3 + 1R4 \ frac {1} {{{R_ {parallel}}}} = \ frac {1} {{{R_1}}} + \ frac { 1} {{{R_2}}} + \ frac {1} {{{R_3}}} + \ frac {1} {{{R_4}}} Rparallel 1 = R1 1 + R2 1 + R3 1 + R4 1
RparallelR_ {параллельно} Rparallel будет меньше, чем наименьший параллельный резистор, подключенный в цепи.
Например, четыре резистора, 2 Ом, 4 Ом, 16 Ом и 8 Ом, подключены параллельно, эквивалентное сопротивление определяется как:
1Rпараллельно = 12 + 14 + 116 + 18 = (8 + 4 + 1 + 2) 16 = 1516 = 0,94 Ом \ frac {1} {{{R_ {parallel}}}} = \ frac {1} {2} + \ frac {1} {4} + \ frac {1} {{16}} + \ frac {1} {8} = \ frac {{\ left ({8 + 4 + 1 + 2} \ right)}} {{16}} = \ frac {{15}} { {16}} = 0,94 \ Омега R, параллель 1 = 21 +41 + 161 +81 = 16 (8 + 4 + 1 + 2) = 1615 = 0,94 Ом
Если подключено n резисторов параллельно эквивалентное сопротивление определяется как:
1Rparallel = 1R1 + 1R2 +… + 1Rn \ frac {1} {{{R_ {parallel}}}} = \ frac {1} {{{R_1}}} + \ frac {1} {{{R_2}}} + … + \ frac {1} {{{R_n}}} Rparallel 1 = R1 1 + R2 1 + … + Rn 1
Rparallel = 1 [1R1 + 1R2 + … + 1Rn] { R_ {parallel}} = \ frac {1} {{\ left [{\ frac {1} {{{R_1}}}} + \ frac {1} {{{R_2}}} + … + \ frac { 1} {{{R_n}}}} \ right]}} Rparallel = [R1 1 + R2 1 + … + Rn 1] 1
Следовательно, в параллельной цепи эквивалентное сопротивление — это обратная сумма отдельных резисторов.
Давайте обсудим этот частный случай, когда два резистора включены параллельно.Предположим, что два резистора, R1R_1R1 и R2R_2R2, подключены параллельно, изображение будет выглядеть примерно так, как показано на рисунке.
Эквивалентное сопротивление определяется по формуле:
1Rparallel = 1R1 + 1R2 \ frac {1} {{{R_ {parallel}}}} = \ frac {1} {{{R_1}}} + \ frac {1} {{{R_2}}} Rparallel 1 = R1 1 + R2 1
Упрощение,
1Rparallel = R1 + R2R1R2 \ frac {1} {{{R_ {parallel}}}} = \ frac {{{R_1} + {R_2}}} {{{R_1} {R_2}}} Rparallel 1 = R1 R2 R1 + R2
Rparallel = R1R2R1 + R2 {R_ {parallel}} = \ frac {{{R_1} {R_2}}} {{{R_1} + {R_2}}} Rparallel = R1 + R2 R1 R2
Это выражение упрощает вычисление эквивалентного сопротивления, когда два резистора включены параллельно.
Например, когда резистор 4 Ом подключен к резистору 8 Ом параллельно, эквивалентное сопротивление комбинации будет:
Rparallel = R1R2R1 + R2 = 4 × 812 = 2,67 Ом {R_ {parallel}} = \ frac { {{R_1} {R_2}}} {{{R_1} + {R_2}}} = \ frac {{4 \ times 8}} {{12}} = 2,67 \ Omega Rparallel = R1 + R2 R1 R2 = 124 × 8 = 2,67 Ом
Предположим, что два параллельно соединенных резистора подобны, тогда:
R1 = R2 = RR_1 = R_2 = RR1 = R2 = R
И выражение для эквивалентного сопротивления дается следующим образом:
Rparallel = R1R2R1 + R2 = R × R2R = R2 {R_ {parallel}} = \ frac {{R_1} {R_2}}} {{{R_1} + {R_2}}} = \ frac {{R \ раз R}} {{2R}} = \ frac {R} {2} Rparallel = R1 + R2 R1 R2 = 2RR × R = 2R
Например, если два резистора 4 Ом при параллельном подключении эквивалентное сопротивление будет вдвое меньше, т.е.е., 2 Ом.
электрических цепей — Как определить, включены ли резисторы параллельно или последовательно?
электрические цепи — Как определить, включены ли резисторы параллельно или последовательно? — Обмен физическими стекамиСеть обмена стеком
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 36k раз
$ \ begingroup $В некоторых схемах легче увидеть, какие резисторы включены параллельно или последовательно.Однако, столкнувшись с более сложной схемой, я не могу понять, какие из них включены последовательно или параллельно. В настоящее время я столкнулся со следующей проблемой:
Мне поручено найти эквивалентное сопротивление; но я не знаю, как определить, какие из них параллельны или последовательно. Есть ли для этого особый способ?
Создан 04 ноя.
АльбертоАльберто3311 золотых знаков11 серебряных знаков33 бронзовых знака
$ \ endgroup $ 1 $ \ begingroup $Уловка состоит в том, чтобы посмотреть на узлы в цепи.Узел — это стык в цепи. Два резистора включены параллельно, если узлы на обоих концах резисторов одинаковы. Если одинаковый только один узел, они идут последовательно. Итак, R1 и R2 параллельны, а R3 — последовательно с R1 || R2.
Создан 04 ноя.
пользователь2355041,91499 серебряных знаков1010 бронзовых знаков
$ \ endgroup $ 2 $ \ begingroup $По сути, вы упрощаете, упрощаете, упрощаете.Например, ваши $ R_1 $ и $ R_2 $ просто параллельны, поэтому вы можете заменить их одним резистором. Затем, в зависимости от того, с каких клемм вы проводите измерения, объединенный резистор и $ R_3 $ будут подключены параллельно или последовательно.
Создан 04 ноя.
Дэниел ГрискомДэниел Гриском3,86344 золотых знака1616 серебряных знаков3333 бронзовых знака
$ \ endgroup $ 3 $ \ begingroup $Иногда может помочь небольшая визуализация — либо в качестве умственного упражнения, либо с использованием реальных объектов.Представьте резисторы как, скажем, мячи для пинг-понга, а провода — как эластичную нить (например, тросик). Выберите два любых терминала, потяните за них и посмотрите, что произойдет; повторите для другой пары и т. д. Вы обнаружите, что:
- Нижние выводы — это один и тот же узел, потому что на пути между ними нет резистора
- R1 и R2 подключены параллельно, потому что они будут располагаться бок о бок по крайней мере для одной пары клемм и никогда не будут совпадать друг с другом.
- R3 соединен последовательно с R1 / R2, потому что они будут соответствовать по крайней мере одной паре клемм, а R3 никогда не окажется рядом ни с R1, ни с R2.
Создан 17 мар.
Энтони Икс, Энтони Икс3,78111 золотой знак1515 серебряных знаков2424 бронзовых знака
$ \ endgroup $ $ \ begingroup $Самый простой способ определить последовательное и параллельное соединение — это сделать следующее: 1.Если один конец R1 подключен к одному концу R2, а другой конец R1 подключен к другому концу R2, то резисторы включены параллельно. R1 и R2 параллельны. 2. Если только 1 конец R2 подключен к 1 концу R3, а другой конец каждого резистора не подключен, то R3 включен последовательно с параллельной парой R2 и R1.
Создан 04 ноя.
Сделай сам1111 серебряный знак1111 бронзовых знаков
$ \ endgroup $ Очень активный вопрос .Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Physics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
резисторов в последовательном и параллельном соединении цепей
резисторов в последовательном и параллельном соединении
резисторы могут быть соединены отдельно друг от друга последовательно или только параллельно.Некоторые схемы резисторов состоят из комбинации последовательных и параллельных цепей для создания более сложных схем. Эти схемы обычно известны как схемы со смешанными резисторами. Несмотря на то, что в этих схемах объединены последовательные и параллельные цепи, метод расчета эквивалентного сопротивления не изменился. Основные правила отдельных сетей, такие как «одинаковый ток течет через последовательно подключенные резисторы» и «одинаковое напряжение на резисторах, подключенных параллельно», применимы к смешанным схемам.
Пример схемы смешанных резисторов показан ниже
Он состоит из четырех резисторов R1, R2, R3 и R4 в комбинации схем смешанных резисторов. Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.
Здесь последовательно соединены резисторы R2 и R3. Следовательно, применяя правило последовательно соединенных резисторов, эквивалентное сопротивление R2 и R3 дается как
R A = R2 + R3
Здесь RA — эквивалентное сопротивление R2 и R3
Теперь резисторы R2 и R3 могут заменить на одиночный резистор РА.Полученная схема показана ниже.
Теперь резисторы RA и R4 соединены параллельно. Следовательно, при применении правила параллельной комбинации резисторов эквивалентное сопротивление RA и R4 равно
R B = R A × R4 / (R A + R4)
Здесь RB — эквивалентное сопротивление RA. и R4
Теперь мы можем заменить резисторы RA и R4 одним резистором RB. После замены резисторов полученная схема показана ниже.
Теперь схема состоит всего из двух резисторов. Здесь также последовательно соединены резисторы R1 и RB. Следовательно, применяя правило последовательных резисторов, общее эквивалентное сопротивление цепи определяется как
R EQ = R1 + R B
Здесь R EQ — полное эквивалентное сопротивление цепи. Теперь резисторы R1 и R B можно заменить одним резистором R EQ .
Окончательная эквивалентная схема для вышеуказанной сложной схемы показана ниже.
Несмотря на то, что они выглядят сложными, схемы смешанных резисторов можно свести к простой схеме, состоящей только из одного источника напряжения и одного резистора, следуя простым правилам последовательного включения резисторов и параллельного включения резисторов.
Последовательные и параллельные резисторы Пример
Рассчитаем эквивалентное сопротивление для приведенной ниже цепи, состоящей из 7 резисторов R1 = 4 Ом, R2 = 4 Ом, R3 = 8 Ом, R4 = 10 Ом, R5 = 4 Ом, R6 = 2 Ом и R7 = 2 Ом. Напряжение питания 5 В.
Теперь резисторы R6 и R7 соединены последовательно. Если эквивалентное сопротивление последовательностей R6 и R7in равно Ra, тогда
Ra = R6 + R7 = 2 + 2 = 4 Ом
Результирующая цепь сокращается до показанной ниже.
В приведенной выше схеме резисторы Ra и R5 соединены параллельно. Следовательно, эквивалентное сопротивление Ra и R5 равно
R b = (R a × R 5 ) / (R a + R 5 ) = (4 × 4) / (4 + 4 ) = 2 Ом.
Далее упрощенная схема показана ниже.
В этой схеме резисторы R4 и R b соединены последовательно.
Rc = R4 + R b = 10 + 2 = 12 Ом.
Теперь мы можем заменить резисторы R4 и R b резистором Rc, как показано ниже.
В приведенной выше схеме резисторы R2 и R3 снова включены последовательно. Если Rd эквивалентно сопротивлению R2 и R3, тогда
Rd = R2 + R3 = 4 + 8 = 12 Ом.
Эквивалентная схема:
Здесь резисторы Rc и Rd соединены параллельно. Пусть Rp будет эквивалентным сопротивлением Rc и Rd, включенных параллельно. Тогда
R p = (R c × R d ) / (R c + R d ) = (12 × 12) / (12 + 12) = 6 Ом.
В результате получается схема
Здесь резисторы R1 и Rp соединены последовательно. Пусть R EQ будет эквивалентным сопротивлением этой комбинации.
Тогда
R EQ = R1 + Rp = 4 + 6 = 10 Ом.
Это эквивалентное сопротивление цепи. Следовательно, данную схему можно окончательно перерисовать как
Ток в цепи можно рассчитать по закону Ома
I = V / R EQ = 5/10 = 0,5 A
Сеть резисторов
Вычислим эквивалентное сопротивление для сложной резисторной схемы.
Схема ниже состоит из десяти резисторов от R1 до R10, соединенных последовательно и параллельно.
Значения сопротивления, указанные в цепи, указаны в Ом (Ом), а напряжение питания — в Вольтах (В).
Здесь последовательно соединены резисторы R9 и R10. Пусть R A — эквивалентное сопротивление этой комбинации.
Следовательно, R A = R9 + R10 = 3 + 3 = 6 Ом.
Схема после замены R9 и R10 на R A равна
В этой схеме резисторы R8 и R A соединены параллельно.Тогда эквивалентное сопротивление R8 и R A равно
R B = (R8 × R A ) / (R8 + R A ) = (6 × 6) / (6 + 6) = 3 Ω.
Теперь заменив R8 и R A на R B , мы получим следующую схему.
В этой схеме резисторы R7 и R B соединены последовательно.
R C = R7 + R B = 9 + 3 = 12 Ом.
Эквивалентная схема после замены R7 и R B на R C :
Понятно, что резисторы R6 и Rc соединены параллельно.Если R D является эквивалентным сопротивлением этой комбинации, тогда
R D = (R6 × Rc) / (R6 + Rc) = (12 × 12) / (12 + 12) = 6 Ом.
Схема с R¬D, заменяющим R6 и Rc:
Теперь резисторы R4 и RD соединены последовательно. Если RE эквивалентное сопротивление R4 и RD, тогда
R E = R4 + R D = 6 + 6 = 12 Ом.
Результирующая сокращенная схема после замены R4 и R D на R E составляет
В этой схеме резисторы R5 и R E соединены параллельно.
Пусть R F будет эквивалентным сопротивлением R5 и R E , включенных параллельно.
Тогда
R F = (R5 × R E ) / (R5 + R E ) = (12 × 12) / (12 + 12) = 6 Ом.
Упрощенная схема показана ниже.
Здесь резисторы R2 и R3 включены последовательно. Если RG является эквивалентом этой комбинации, то
R G = R2 + R3 = 4 + 2 = 6 Ом.
После замены R2 и R3 на RG схема преобразуется в
Резисторы RF и RG включены параллельно.
Пусть R T будет эквивалентом этой комбинации.
Тогда R T = (R F × R G ) / (R F + R G ) = (6 × 6) / (6 + 6) = 3 Ом.
Теперь резисторы R1 и RT включены последовательно. Если REQ — полное эквивалентное сопротивление цепи, то REQ = R1 + RT = 3 + 3 = 6 Ом.
Наконец, вышеуказанная сложная схема может быть перерисована следующим образом
Общий ток в цепи может быть рассчитан по закону Ома
I = V1 / R EQ = 6/6 = 1 A
Следовательно Резистивную цепь, состоящую из числа резисторов, соединенных в комбинации как последовательной, так и параллельной комбинаций, можно уменьшить, сначала определив простые параллельные ветви резистора и ветви последовательного резистора.Рассчитывается эквивалентное сопротивление этих простых ветвей, и ветви заменяются эквивалентным резистором. Этот процесс снижает сложность схемы. Продолжая этот процесс, мы можем заменить сложную резистивную цепь одним резистором.
Существуют некоторые сложные резистивные схемы, которые нельзя свести к простым схемам, просто применяя правила последовательных резистивных комбинаций и параллельных резистивных комбинаций. Такие схемы, как аттенюаторы T-Pad и некоторые сложные резистивные мостовые схемы являются примерами таких сложных резистивных схем.Чтобы упростить эти сложные резистивные схемы, следует придерживаться другого подхода.
Некоторые сложные резистивные цепи можно уменьшить, используя закон Кирхгофа по току и закон Кирхгофа по напряжению.
Найти токи и напряжения в сложной резистивной цепи, просто используя закон Ома, может быть невозможно. Для такого типа цепей будут полезны правила Кирхгофа для цепей.
Законы Кирхгофа для цепей основаны на концепции сохранения тока и энергии в цепи.Есть два закона Кирхгофа. Первый — это закон тока Кирхгофа, который касается тока в узле, а второй — закон напряжения Кирхгофа, который касается напряжения в замкнутой цепи.
Закон Кирхгофа о течениях гласит, что «ток, входящий в узел, равен току, выходящему из узла, потому что ему некуда идти, и ток не теряется в узле».
Проще говоря, закон Кирхгофа по току гласит, что сумма токов, входящих в узел, равна сумме токов, выходящих из цепи.
Закон Кирхгофа о напряжении гласит, что «полное напряжение в замкнутом контуре равно сумме всех падений напряжения в этом контуре».
Проще говоря, закон Кирхгофа по напряжению гласит, что направленная алгебраическая сумма напряжений в замкнутом контуре равна нулю.
С помощью этих двух законов можно рассчитать значения токов и напряжений в любой сложной цепи.
Тем не менее, у нас могут быть сложные резистивные схемы, в которых трудно определить эквивалентное сопротивление, в таких ситуациях мы будем использовать преобразование резисторов по схеме звезда-треугольник, чтобы упростить схемы резисторов.
параллельных резисторов
Электрические цепи используются в авиакосмической технике, от систем управления полетом до приборов в кабине и двигателей системы управления, чтобы аэродинамическая труба приборостроение и эксплуатация. Самая простая схема включает один резистор . и источник электрического потенциала или напряжения . Электроны проходят через схема вырабатывает тока электричества.Сопротивление, напряжение и ток связаны друг с другом соотношением Закон Ома. Обычно в практической схеме используется более одного резистора. При анализе сложной схемы мы часто можем группировать компоненты вместе и разработать схему замещения . При анализе схем с несколько резисторов, мы должны определить, подвержены ли резисторы какое-то напряжение или такой же ток. Несколько резисторов в параллельной цепи подвергаются одинаковому напряжению.Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем эквивалентную схему для резисторов параллельно.
На рисунке изображена схема, состоящая из источника питания и трех резисторов. подключены параллельно. Если обозначить сопротивление R , ток и , а напряжение В , то закон Ома гласит, что для каждого резистора в цепи:
V = i Rя = V / R
Если рассматривать каждый резистор по отдельности, каждый резистор имеет свой ток. ( i1 , i2 и i3 ), сопротивление ( R1 , R2 и R3 ), и напряжение ( V1 , V2 и V3 ).Поскольку резисторы подключены параллельно друг другу, напряжение на каждый резистор одинаковый:
V = V1 = V2 = V3Ток через каждый резистор определяется законом Ома:
i1 = V / R1i2 = V / R2
i3 = V / R3
Если обозначить пересечение проводов, соединяющих резисторы, как узла , В нашей схеме с тремя резисторами шесть узлов.На рисунке мы помечаем два узлы в правом верхнем углу схемы. В каждом узле ток, поступающий в узел должен равняться току, выходящему из узла, согласно закону Фарадея . Для узлов, расположенных выше и ниже резистора R2 , текущий ib вход в узел определяется:
ib = i2 + i3Аналогично для узлов выше и ниже резистора R1 , текущий ia вход в узел определяется:
ia = i1 + ib = i1 + i2 + i3Теперь мы знаем напряжение, сопротивление и ток в каждой части цепи.
Если бы мы построили эквивалентную схему, как показано в нижнем левом углу, мы бы имеют одинаковое напряжение В , такой же ток от источника питания ie = ia , и один эквивалентный резистор Re . Для нашей эквивалентной схемы закон Ома указывает, что:
ie = V / ReМы можем определить значение Re , используя небольшую алгебру:
V / Re = ie = i1 + i2 + i3V / Re = V / R1 + V / R2 + V / R3
1 / Re = 1 / R1 + 1 / R2 + 1 / R3
1 / Re = (R2 R3 + R1 R3 + R1 R2 / (R1 R2 R3)
Re = (R1 R2 R3) / (R2 R3 + R1 R3 + R1 R2).
Мы можем использовать эти знания о схеме параллельного резистора для анализа Мост Уитстона схема, которая используется для контроля температуры в аэродинамической трубе баланс сил используя электронные тензодатчики.
Навигация ..
- Руководство для начинающих Домашняя страница

