Что такое порядок фильтра в акустике. Какие бывают порядки фильтров в акустических системах. Как выбрать оптимальный порядок фильтра для кроссовера. Чем отличаются фильтры разных порядков.
Что такое порядок фильтра в акустических системах
Порядок фильтра в акустике — это характеристика, определяющая крутизну спада амплитудно-частотной характеристики (АЧХ) на границе полосы пропускания. Чем выше порядок, тем круче спад АЧХ за пределами полосы пропускания фильтра.
Основные типы порядков фильтров в акустических системах:
- Фильтры первого порядка — 6 дБ/октава
- Фильтры второго порядка — 12 дБ/октава
- Фильтры третьего порядка — 18 дБ/октава
- Фильтры четвертого порядка — 24 дБ/октава
Порядок фильтра определяет, насколько резко будут подавляться частоты за пределами полосы пропускания. Например, фильтр первого порядка ослабляет сигнал на 6 дБ при удвоении частоты, а фильтр четвертого порядка — на 24 дБ.
Особенности фильтров разных порядков
Рассмотрим основные особенности фильтров разных порядков:
Фильтры первого порядка (6 дБ/октава)
- Самая простая схема — один конденсатор и одна катушка
- Минимальные фазовые искажения
- Слабое подавление нежелательных частот
- Применяются в недорогих акустических системах
Фильтры второго порядка (12 дБ/октава)
- Более крутой спад АЧХ
- Лучшее подавление помех
- Небольшие фазовые искажения
- Оптимальны для большинства применений
Фильтры третьего порядка (18 дБ/октава)
- Еще более эффективное подавление помех
- Заметные фазовые искажения
- Сложная схема реализации
- Применяются в профессиональной акустике
Фильтры четвертого порядка (24 дБ/октава)
- Максимально крутой спад АЧХ
- Очень эффективное подавление помех
- Значительные фазовые искажения
- Сложная и дорогая схема
- Используются в высококачественных акустических системах
Как выбрать оптимальный порядок фильтра
При выборе порядка фильтра для акустической системы необходимо учитывать следующие факторы:
- Тип акустической системы (полочная, напольная, профессиональная и т.д.)
- Количество полос (2-х, 3-х полосная система)
- Характеристики используемых динамиков
- Требования к качеству звучания
- Стоимость реализации
Для большинства домашних акустических систем оптимальным выбором являются фильтры второго порядка (12 дБ/октава). Они обеспечивают хороший баланс между эффективностью фильтрации и простотой реализации.
Фильтры высоких порядков (3-го и 4-го) применяются в профессиональных системах, где требуется максимальное подавление помех между полосами. Однако они сложнее в реализации и вносят заметные фазовые искажения.
Влияние порядка фильтра на звучание акустической системы
Порядок фильтра оказывает существенное влияние на характер звучания акустической системы:
- Фильтры низких порядков (1-го и 2-го) обеспечивают более «прозрачное» и естественное звучание за счет минимальных фазовых искажений
- Фильтры высоких порядков (3-го и 4-го) дают более «четкое» разделение полос, но могут привести к окрашиванию звука
- Высокие порядки фильтров позволяют использовать динамики ближе к границам их рабочего диапазона
- Низкие порядки требуют более широкой полосы перекрытия между соседними полосами
При проектировании акустической системы важно найти оптимальный баланс между эффективностью фильтрации и качеством звучания.
Пассивные и активные фильтры в акустических системах
Фильтры в акустических системах могут быть реализованы как пассивным, так и активным способом:

Пассивные фильтры
- Состоят из пассивных компонентов — конденсаторов, катушек, резисторов
- Не требуют дополнительного питания
- Проще в реализации
- Имеют ограничения по крутизне спада АЧХ
- Вносят потери сигнала
Активные фильтры
- Используют активные компоненты — операционные усилители
- Требуют отдельного источника питания
- Позволяют реализовать фильтры высоких порядков
- Не вносят потерь сигнала
- Обеспечивают лучшие характеристики
Активные фильтры чаще применяются в профессиональных акустических системах, где требуется максимальное качество звучания. Пассивные фильтры распространены в бытовой акустике из-за простоты и низкой стоимости.
Примеры расчета фильтров разных порядков
Рассмотрим пример расчета пассивных фильтров разных порядков для частоты раздела 3 кГц и сопротивления нагрузки 8 Ом:
Фильтр первого порядка (6 дБ/октава)
- Фильтр нижних частот: L = 0.42 мГн
- Фильтр верхних частот: C = 6.6 мкФ
Фильтр второго порядка (12 дБ/октава)
- Фильтр нижних частот: L = 0.6 мГн, C = 4.7 мкФ
- Фильтр верхних частот: L = 0.3 мГн, C = 9.4 мкФ
Фильтр третьего порядка (18 дБ/октава)
- Фильтр нижних частот: L1 = 0.66 мГн, L2 = 0.22 мГн, C = 4.7 мкФ
- Фильтр верхних частот: C1 = 7.2 мкФ, C2 = 2.4 мкФ, L = 0.33 мГн
Как видно из примеров, с повышением порядка фильтра увеличивается количество компонентов и усложняется схема.
Современные тенденции в проектировании фильтров для акустических систем
В современном проектировании акустических систем наблюдаются следующие тенденции в области фильтров:
- Использование цифровых фильтров на основе DSP-процессоров
- Применение адаптивных фильтров, подстраивающихся под акустику помещения
- Комбинирование фильтров разных порядков для оптимизации звучания
- Использование нестандартных топологий фильтров (например, фильтры с асимметричными характеристиками)
- Применение активных кроссоверов с раздельным усилением полос
Эти технологии позволяют добиться еще более высокого качества звучания и гибкости настройки акустических систем.
Порядок — фильтр — Большая Энциклопедия Нефти и Газа, статья, страница 2
Порядок — фильтр
Cтраница 2
Кроме того, четность или нечетность порядка фильтра и наличие того или иного типа симметрии накладывают определенные ограничения на коэффициенты передачи фильтра на нулевой частоте и на частоте Найквиста. Эти ограничения легко получить из условий симметрии и формулы (4.7) для комплексного коэффициента передачи фильтра. Сочетание четности порядка фильтра и типа симметрии дает четыре типа симметричных фильтров, перечисленных в табл. 4.1 вместе с указанными ограничениями значений АЧХ. Приведенные в таблице номера типов часто используются в зарубежной литературе. [17]
Показатели качества фильтрации улучшаются при повышении
После выбора типа аппроксимации и уточнения порядка фильтра можно приступить ко второму этапу проектирования — выбору структуры, реализующей заданный аппроксимирующий полином. [19]
При этом следует учитывать, что повышение порядка фильтра п выше шестого нецелесообразно. [20]Выходными параметрами являются минимально необходимый для выполнения заданных требований порядок фильтра п и частота среза фильтра Wn. Эти параметры должны затем использоваться при вызове функции расчета фильтра. Возврат значения Wn избавляет пользователя от забот, связанных с тем, что при расчете разных фильтров понятие частоты среза имеет разный смысл. [21]
Рассмотренные выше функции расчета фильтров требуют задания в качестве входных параметров порядка фильтра и его частоты среза. При этом понятие частоты среза для фильтров разных типов определяется по-разному. [22]
Рассмотренные выше функции расчета фильтров требуют задания в качестве входных параметров порядка фильтра и его частоты среза. При этом понятие частоты среза для фильтров разных типов определяется по-разному. Серые области на рисунке демонстрируют допуски, в которые должна укладываться АЧХ фильтра в полосах пропускания и задерживания. [23]
Результаты показывают, что для фильтра Баттерворта требуется очень большой порядок, порядок фильтров Чебышева обоих типов более чем в пять раз меньше и, наконец, минимальный порядок требуется при синтезе эллиптического фильтра. [24]
При увеличении D полоса пропускания ФНЧ должна сужаться, что приводит к увеличению порядка фильтра, а, следовательно, количества необходимых для его реализации операций; здесь необходимо найти компромисс. Вы должны задать себе вопрос: Компенсирует ли уменьшение размера БПФ дополнительные операции понижающего преобразования частоты и фильтрации. Это определенно так, если выполнение БПФ большого размера невозможно на имеющейся аппаратуре или в программе. Если фаза составляющих сигнала не важна, для фильтрации можно использовать эффективный БИХ-фильтр. Если же фазовые искажения недопустимы, то можно использовать полифазные или полуполосные КИХ-фильтры. Если спектр сигнала очень узок по сравнению с частотой дискретизации fs1, и требуется большой коэффициент прореживания и сложный фильтр нижних частот, можно попробовать использовать комбинированный интегратор — гребенчатый фильтр. [26]
Можнр наметить, что острота этого минимума уменьшается с уменьшением ц 0 и увеличением порядка фильтра, а положение минимума смещается в сторону меньших глубин модуляции с ростом [ i0 и порядка фильтра. Процесс расплывания и смещения минимума и приводит, очевидно, при N — — оо к той зависимости ККИ от М, которая характерна для идеального фильтра НЧ. Тот факт, что при малых глубинах модуляции ККИ растет, можно объяснить тем, что в этом случае основной вклад в ККИ вносит составляющая с частотой ш 0, причем величина этой составляющей на выходе ФНЧ определяется исключительно величиной затухания ФНЧ на частоте о0, и, следовательно, уменьшается с увеличением порядка фильтра. [27]
Здесь со0 — частота среза, Т ( х) — полином Чебышева и-го порядка, п — порядок фильтра, е — параметр, определяющий величину пульсаций АЧХ в полосе пропускания. [28]
Здесь соо — частота среза, Т ( х) — полином Чебышева и-го порядка, п — порядок фильтра, е — параметр, определяющий величину пульсаций АЧХ в полосе задерживания. [29]
Поэтому после синтеза фильтра функцией firl следует проверить его АЧХ с помощью функции f reqz и при необходимости попробовать точнее подобрать порядок фильтра вручную. [30]
Страницы: 1 2 3 4 5
Порядок фильтра (кроссовера)
Порядок фильтра
Начиная от 6 дБ/окт, 12 дБ/окт и т.д.
Разберём.
дБ/окт — Децибел по простому Громкость
дБ/окт — Октава
На примере купольного среднечастотника рабочий диапазон которого в среднем является от 800 Гц и до 4000 Гц. покажу как это выглядит.
Мы говорим, столько то … децибел на октаву . Это сколько???
Показываю .
На одну октаву ниже от 800 Гц будет 400 Гц.
На одну Октаву выше от 4 кГц это 8 кГц.
Читаем про Октаву http://clippu.net/threads/Октава.850/
По остальным порядкам смотрим рисунок ниже.
Белая линия Первый порядок (фильтр первого порядка) 6 дБ/окт (от 90 дБ минус 6 = 84 дб) На частоте 400 Гц. громкость будет 84 децибела.
Зелёная Второй порядок (фильтр второго порядка) 12 дБ/окт (90 -12 = 78 дБ) На частоте 400 Гц. громкость будет 78 децибел.
Синяя Третий порядок (фильтр третьего порядка) 18 дБ/окт (90 — 18 = 72 дБ) На частоте 400 Гц громкость будет 72 децибел.
Чёрная Четвёртый порядок (фильтр четвёртого порядка) 24 дБ/окт (90 — 24 = 66 дБ) На частоте 400 Гц громкость будет 66 децибел.
Каждый следующий порядок будет тише на 6 децибел.
То же самое будет если отрезать фильтром всё, что выше 4 кГц. Спад будет такой же.
Это Мы рассматриваем идеальное поведение фильтра. Чисто в качестве общего развития. В жизни фильтра ведут себя немного по другому.
Фильтр Чебышева
Код:
http://ru.wikipedia.org/wiki/Фильтр_ЧебышеваФильтр Бесселя
Код:
http://ru.wikipedia.org/wiki/Фильтр_БесселяФильтр Линквица — Райли
Код:
http://ru.wikipedia.org/wiki/Фильтр_Линквица_—_РайлиИ т.д.
Таким образом график АЧХ с уже отфильтрованными нижними частотами фильтром 4 порядка (24 децибел на октаву) будет иметь следующий вид. То есть частота 400 Гц будет тише на 24 децибела по отношению к частоте 800 Гц.
Показываю на практике.
Частота 800 Гц с уровнем в 90 Дб
Красными стрелками указал уровень одного (левого) канала. Мы его примем за 100 %
Частота 400 Гц уровень минус 6 дБ (от частоты 800 Гц) — фильтр первого порядка.
Смотрим как уменьшается уровень громкости
Частота 400 Гц уровень минус 12 дБ (от частоты 800 Гц) — фильтр второго порядка.
Частота 400 Гц уровень минус 18 бД (от частоты 800 Гц) — фильтр третьего порядка.
Частота 400 Гц уровень минус 24 дБ (от частоты 800 Гц) — фильтр четвёртого порядка.
Кроссовер, порядки фильтров — на пальцах.
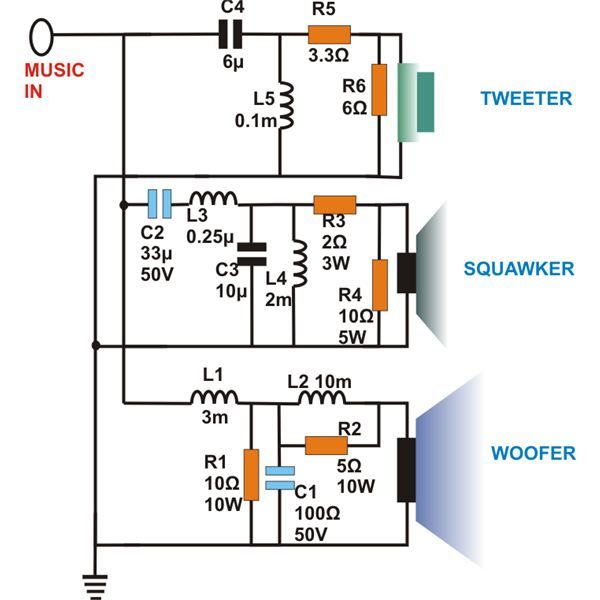
Сам когда-то искал, кроссы, порядок фильтров???)))Кроссоверы— это устройства в звуковых системах, которые создают нужные рабочие частотные диапазоны для динамиков. Динамики сконструированы таким образом, чтобы работать в определенном частотном диапазоне. Они не приемлют частоты, не входящие в эти рамки. Если на высокочастотный динамик (твитер) подать низкую частоту, то звуковая картина испортится, а если сигнал еще и мощный, то твитер «сгорит». Высокочастотные динамики должны работать только с высокими частотами, а низкочастотные динамики должны получить от общего звукового сигнала только низкочастотный диапазон. Оставшаяся средняя полоса достается среднечастотным динамикам (мидвуферы). Следовательно, задача кроссоверов заключается в разделении звукового сигнала на нужные (оптимальные) частотные полосы для соответствующих типов динамиков.
Проще говоря, кроссовер — это пара электрических фильтров. Допустим, кроссовер имеет частоту среза равную 1000 Гц. Это означает, что один из его фильтров срезает все частоты ниже 1000 Гц и пропускает только частоты выше 1000 Гц. Такой фильтр называют high-pass фильтром. Другой фильтр, пропускающий частоты ниже 1000 Гц называется low-pass,. Графически работа этого кроссовера представлена на рисунке 3. Точка пересечения двух кривых есть частота среза кроссовера равная 1000 Гц. В трехполосных кроссоверах присутствует еще и среднечастотный фильтр (band-pass), который пропускает только средний диапазон частот (приблизительно от 600 Гц до 5000 Гц.) На рисунке изображена частотная характеристика трехполосного кроссовера.
Порядок чувствительности — это отношение интенсивности выходного сигнала (dB) кроссовера к частоте входного сигнала при условии, что интенсивность входного сигнала постоянна. Обычно чувствительность (крутизну среза) характеризуют как отношение dB/octave. В силу многих математических причин чувствительность кроссоверов всегда кратна 6 децибелам на октаву (6 dB/octave). Кроссовер первого порядка имеет чувствительность 6 dB/octave. Кроссовер второго порядка имеет чувствительность 12 dB/octave, третьего порядка — 18 dB/octave, и чувствительность кроссоверов четвертого порядка равна 24 dB на октаву.
Рассмотрим low-pass фильтр третьего порядка с частотой среза равной 100 Гц. Как уже говорилось выше, этот кроссовер пропустит только частоты ниже 100 Гц, а частоты выше 100 Гц срежет. Срезание частот будет происходить следующим образом: все частоты выше 100 Гц будут терять на выходе из фильтра свою интенсивность кратно 18 dB в зависимости от октавы, в которую они входят. То есть, частота в 200 Гц (первая октава выше частоты среза) потеряет свою интенсивность на 18 Дб, интенсивность частоты в 400 Гц (вторая октава) упадет 36 Гц, а третья октава (800 Гц) ослабеет на 54 Дб. И так далее, все последующие октавы будут ослабевать кратно 18 Дб. Менее чувствительный low-pass фильтр первого порядка с частотой среза в 100 Гц будет делать тоже самое, только ненужные октавы будут ослабевать не на 18 Дб, а на 6 Дб.
Как видим, фильтры, из которых состоят кроссоверы, не могут сразу срезать ненужные частоты, а делают это постепенно, с разной чувствительностью в зависимости от своего порядка.
Кроссоверы первого порядка — это простейший пассивный кроссовер, который состоит из одного конденсатора, и одной катушки индуктивности. Конденсатор работает как high-pass фильтр для защиты твитера от ненужных низких и средних частот. Катушка используется как low-pass фильтр. Чувствительность кроссоверов первого порядка низкая — всего 6 Дб на октаву. Положительная черта этих кроссоверов -отсутствие фазового сдвига между твитером и другим динамиком.
Кроссоверы второго порядка. Их также называют кроссоверами Баттерворта, по имени создателяматематической модели этих кроссоверов. Конструктивно они состоят из одного конденсатора и катушки на твитере и одного конденсатора и катушки на низкочастотном динамике. Они обладают более высокой чувствительностью, равной 12 Дб на октаву, но дают фазовый сдвиг в 180 градусов, что означает несинхронный ход мембран твитера и другого динамика. Для устранения этой проблемы небходимо поменять полярность подключения проводов на твитере.
Кроссоверы третьего порядка. У таких кроссоверов на твитере ставится одна катушка и два конденсатора, тогда как на динамике низкой частоты наоборот. Чувствительность таких кроссоверов равна 18 Дб на октаву, и они имеют хорошие фазовые характеристики при любой полярности. Негативная черта кроссоверов III-го порядка — неприемлемость использования временных задержек для устранения проблем, связанных с динамиками не излучающими на одной и той же вертикальной плоскости.
Кроссоверы четвертого порядка. Кроссоверы Баттерворта четвертого порядка имеют высокую чувствительность равную 24 дБ на октаву, что резко уменьшает взаимовлияние динамиков в области разделения частот. Сдвиг по фазе составляет 360 градусов, что фактически означает его отсутствие. Однако величина фазового сдвига в данном случае непостоянна и может привести к неустойчивой работе кроссовера. Эти кроссоверы практически не применяются на практике.
Оптимизировать конструкцию кроссовера четвертого порядка удалось Линквицу и Рили. Данный кроссовер состоит из двух последовательно соединенных кроссоверов Баттерворта второго порядка для твитера, и тоже самое для басового динамика. Чувствительность их также равна 24 дБ на октаву, однако уровень выходного сигнала на каждом фильтре меньше на 6 дБ, чем уровень выходного сигнала кроссовера. Кроссовер Линквица-Рили не имет фазовых сдвигов и позволяет проводить временную коррекцию для динамиков, не работающих в одной физической плоскости. Эти кроссоверы по сравнению с другими конструкциями дают самые лучшие акустические характеристики.
Конструирование пассивных кроссоверов
Как говорилось выше, пассивный кроссовер состоит из конденсаторов и катушек индуктивности. Для того, чтобы собрать пассивный кроссовер первого порядка необходимо иметь один конденсатор и одну катушку индуктивности. Конденсатор устанавливается последовательно на твитер (high-pass filter), а катушка последовательно на вуфер (low-pass filter). Номинальные значения индуктивности для катушки ((H — микрогенри) и емкости ((F — микрофарады) приводятся в таблице в зависимости от желаемой частоты среза кроссовера и сопротивления динамиков.
Кроссовер I порядка (6 dB/octave)
К примеру, подберем емкость и индуктивность для кроссовера с частотой среза 4000 Гц при сопротивлении динамиков 4 Ом. Из вышеприведенной таблицы находим, что емкость конденсатора первого порядка должна быть равной 10 мФ, а индуктивность катушки 0.2 мГ.
Для определения номинальных значений компонентов для кроссовера второго порядка (12 дБ/октава) необходимо значения из этой же таблицы для конденсатора умножить на коэффициент равный 0.7, а значение для катушки индуктивности умножить на коэффициент 1.414. Надо помнить, что для кроссовера второго порядка необходимо два конденсатора и две катушки индуктивности. Составим кроссовер второго порядка для частоты среза 4000 Гц. Для определения значений для обоих конденсаторов умножаем значение из таблицы 10 мФ на коэффициент 0.7 и получим 7мФ. Далее, значение индуктивности 0.2 мГ умножим на коэффицент 1.414 и получим значение индуктивности для каждой катушки 0.28 мГ. Один из этих конденсаторов устанавливается последовательно на твитер, а второй параллельно на вуфер. Одна катушка параллельно на твитер, а вторая последовательно на вуфер.
Пассивные и активные кроссоверы
Отличие между эти двумя типами кроссоверов очень простое. Активный кроссовер требует подвода питания извне, а пассивный — нет. В силу этого активный кроссовер занимает место в звуковой системе до усилителя, обрабатывая звуковой сигнал с предусилителя головного устройства (допустим, автомагнитолы). Далее, после активного кроссовера устанавливаются два или три усилителя мощности. Один усилитель в этом случае не ставится, так как нет смысла разделенные активным кроссовером сигналы сводить в усилителе в единый сигнал. Разделенные сигналы надо усиливать по отдельности. Как видим, активные кроссоверы применяются в дорогих звуковых системах высокого качества.
Пассивные кроссоверы обрабатывают уже усиленный сигнал и устанавливаются перед динамиками. Возможности пассивных кроссоверов ограничены по сравнению с активными, однако их правильное применение может дать хорошие результаты при минимальных финансовых затратах. Пассивные кроссоверы хорошо себя зарекомендовали при требовании к порядку чувствительности менее 18 дБ на октаву. Выше этого предела хорошо работают только активные кроссоверы.
Пассивные кроссоверы в основном применяются для обработки сигнала твитеров и среднечастотных динамиков. Для низкочастотных динамиков эти кроссоверы применять можно, однако резко возрастает требование в качеству конденсаторов и катушек индуктивности, что приводит к их удорожанию и увеличению в размерах. Пассивные кроссоверы плохо переносят перегрузки. Пиковые интенсивности сигнала, поступающие от усилителя, могут менять частоту среза фильтров. Кроме того, перегруженный фильтр ослабляет звуковой сигнал (damping). Поэтому при выборе пассивных кроссоверов обращайте внимание на их способность выдерживать пиковые нагрузки, создаваемые усилителем.
Активные (или электронные) кроссоверы представляют из себя множество активных фильтров, которыми можно управлять и легко изменять частоту среза любого канала. Порядок чувствительности активных кроссоверов может быть любым, от 6 Дб до 72 Дб на октаву (и выше).В основном активные кроссоверы для автомобильных аудиосистем имеют чувствительность 24 Дб на октаву. При такой чувствительности обмен частотами между динамиками практически исключен. Звуковая картина получается очень качественной. Единственный недостаток активных кроссоверов, — это их дороговизна по сравнению с пассивными.
Фазовый сдвиг
Теперь поговорим о фазовых сдвигах, которые могут возникать в звуковых системах, использующих кроссоверы. Фазовый сдвиг — это неизбежное явление, являющееся следствием конструктивных особенностей high-pass, low-pass и band-pass фильтров.
Фаза — это временная связь двух сигналов. Измеряется фаза в градусах от 0 до 360. Если два одинаковых динамика излучают звуковые волны в противоположной фазе (фазовый сдвиг 180 градусов), то происходит ослабление звука. Проблема устраняется изменением полярности на одном из динамиков .
Когда акустическая система состоит их разных динамиков, работающих в различных частотных диапазонах (твитер и мидвуфер), то устранение фазового сдвига не всегда решается простой сменой «+» на «-«. Длина волны от твитера короче, чем от мидвуфера. Поэтому фронт высокочастотной волны может достигнуть слушателя позже (или раньше) фронта среднечастотной (или низкочастотной) волны. Эта временная задержка является следствием фазового сдвига. Оптимизировать звуковую картину в данном случае можно путем физического выравнивания двух динамиков относительно друг друга в вертикальной плоскости до момента улучшения звуковой картины. К примеру, при частоте волны 1000 Гц временная задержка в одну милисекунду устраняется сдвигом динамиков друг относительно друга на 30 см.
Настройка активного кроссовера
Самое важное в настройке кроссовера — это правильный выбор частоты среза. Если мы имеем трехполосный активный кроссовер, то значит перед нами стоит задача в определении двух точек (частот) среза. Первая точка определяет частоту среза для сабвуфера (low-pass) и начало среднечастотного диапазона для мидвуфера (high-pass). Вторая точка определяет частоту окончания среднего диапазона (low-pass) и отправную частоту высокочастотного диапазона для твитера (high-pass). Самое главное, при установке частот среза кроссовера помнить о частотных характеристиках динамика и не в коем случае не нагружать динамик частотами, которые не входят в его рабочий диапазон.
К примеру, если сабвуфер немного гремит или издает гул (неприятный резонанс корпуса автомобиля) значит он перегружен нежелательными для него средними частотами (выше 100 Гц). Перенесите частоту среза (low-pass) на отметку 75 Гц и/или установите, если возможно, чувствительность на 18 Дб или 24 Дб на октаву. Напомним, что увеличение порядка чувствительности кроссовера (величина dB/octave) более качественно срезает ненужные частоты, не давая им просачиваться через фильтр. Порядок чувствительности high-pass фильтров для мидвуфера можно оставить на 12 Дб/октава (для «мягких» среднечастотных динамиков). Подобная настройка активного кроссовера называется асимметричной.
В этой таблице приведены начальные величины частот среза для различных типов динамиков при настройке активных кроссоверов.
Полезные темы:
Кое-что о выборе порядка фильтра для АС…
Выбор порядка фильтра для будущей АС — довольно нетривиальная задача, зависящая от очень многих факторов. Под силу ли её решить начинающему колонкостроителю? Хватит ли для этого выбора одних лишь характеристик применяемых головок или нужно знать что-то еще? Попробуем немного разобраться в этом вопросе вместе. Начнем с идеальной АС (излучатели головок пренебрежимо малы, находятся в одной и той же точке пространства и обладают идеальными собственными АЧХ/ФЧХ и не имеют прочих ограничений) и постепенно будем приближаться к более реальной АС.
Хотя выше, я и обмолвился про начинающего колонкостроителя, однако, я предполагаю что все-таки базисный уровень подготовки у читающего эти строки все же имеется…
Для начала построим графики АЧХ/ФЧХ и переходных характеристик (далее ПХ) фильтров для идеальной АС.
Исследуем четыре популярных типа фильтров, с частотой раздела 2,5кГц (и сделаем сразу оговорку о том что это головки все-таки будут с идеальными собственными АЧХ/ФЧХ, а применяемые фильтры активные, т.к. с пассивными дело обстоит еще сложнее, а нам, для примера очень важна наглядность происходящего):
-
1-ый порядок. Обеспечивает плоскую АЧХ/ФЧХ и великолепную ПХ — меандр 1кГц действительно похож на прямоугольник.
-
2-ой порядок Линквица-Райли (далее 2ЛР). Плоская АЧХ получается только при переполюсовке одной из головок, если этого не сделать, то на частоте раздела будет наблюдаться глубокий (бесконечный) провал. Крутит фазу, но все еще обладает приемлемой ПХ.
-
3-ий порядок Баттерворта (далее 3БТВ). Плоская АЧХ обеспечивается вне зависимости от того как подключены головки. Если инвертировать полярность у одной из головок то улучшается характер ФЧХ и ПХ, которые почти повторяют вариант 2ЛР, если же не инвертировать, то получим следующий график.
-
4-ий порядок Линквица-Райли (далее 4ЛР). Плоская АЧХ. Не требует переполюсовки головок. Сильно искаженная ФЧХ и ПХ.
В этих идеальных условиях выбор, думаю, для всех очевиден — фильтр первого порядка.
Здесь и далее. Слева направо: 1-ый, 2ЛР, 3БТВ, 4ЛР.
Теперь усложним задачу, а точнее приблизим её немного ближе к реальности. Зададимся размерами самих излучателей и разнесем их по вертикали. Получим картину расположения головок для типичной 2-ух полосной АС полочного типа, с конусным НЧ/СЧ драйвером 6,5″ и купольным 1″ ВЧ динамиком. Расстояние от АС до слушателя зададим 1 м строго на оси ВЧ головки. И повторим расчеты фильтров для такого варианта расположения динамиков.
Довольно приличные изменения, не правда ли? Объясняется такое изменение тем, что разнесение головок в пространстве дало фазовую ошибку, а задание размеров излучателей вызвало изменения в характеристике направленности излучателей, причем, на частоте раздела она стала многолепестковой в вертикальной плоскости. Как видим, во всех случаях изменилась осевая АЧХ и соответственно ПХ фильтров. Как нетрудно заметить из графиков, чем ниже порядок фильтра, тем более радикальные изменения претерпела АЧХ/ФЧХ. Это объясняется тем, что чем ниже порядок, то тем хуже его фильтрующие свойства — две разнотипные головки совместно работают с большим перекрытием по полосе.
Если сверху показаны графики для наблюдателя, находящегося на удалении 1 м, строго на оси ВЧ головки. То что произойдет с АЧХ, если сместиться по вертикали от этой оси? Скажем, вверх на 15 и 30 градусов и вниз, на те же15 и 30 градусов. Обратите внимание, что расстояние до ВЧ при этом не меняется, в то время как расстояние до НЧ/СЧ будет все время различно. Даст ли это ошибку? Безусловно.
Вот такие вот замечательные кривули будут наблюдаться на внеосевых АЧХ. Видим что 1-ый порядок вновь не на высоте. Отдельно стОит отметить, что переполюсовка динамика при 3БТВ сильно меняет картину. Обратите внимание на различия четных и нечетных порядков. У четных порядков девиация АЧХ вызвала только лишь провалы на АЧХ, в то время как у нечетных порядков имеются как провалы, так и подъемы, которые будут восприниматься на слух гораздо заметнее. Такое различное поведение АЧХ объясняется тем, что четные порядки фильтров имеют симметричную диаграмму направленности на частоте раздела, когда главный лепесток смотрит почти перпендикулярно линии соединяющей акустические центры (о них чуточку позже) головок. Тогда как нечетные порядки отклоняют главный лепесток в сторону и не обеспечивают симметричную диаграмму направленности. Это наглядно видно по полярной диаграмме, график синего цвета.
Настало время для следующего шажка, еще больше приближающего наши графики к реальности — указать все координаты акустических центров головок (далее а.ц.). Грубо говоря, а.ц. это некая, воображаемая точка ДГ, откуда собственно зарождается звуковая волна, её импульс. Раз точка, значит она имеет 3 координаты в пространстве: dX, dY и dZ. И если первые две легко определяются (так, для круглой мембраны это будет её геометрический центр, если посмотреть на головку сверху), то с последней координатой все несколько сложнее… Но для упрощенных расчетов, обычно за dZ принимают место сопряжения каркаса звуковой катушки и мембраны. Очевидно, что у 1″ купольной головки и 6,5″ конусного излучателя, закрепленных на одной общей панели, эти точки будут различаться по расстоянию вглубь от этой панели. Для 1″ ВЧ обычно dZ принимают равным нулю. А для 6,5″ dZ примерно 2,5-3 cм (примем 2,5 cм). Т.к. осевые графики мы строим строго с оси ВЧ головки, то координаты её а.ц. принимаем как dX=0; dY=0; dZ=0. А координаты для НЧ/СЧ головки находим по отношению к а.ц. ВЧ. Таким образом, для НЧ/СЧ будем иметь dX=15; dY=0; dZ=2,5.
Получили следующую пачку кривых. Красота…! Особенно первый порядок. Правда тут следует отметить, что часть графиков принимает менее устрашающий вид при переполюсовке одной из головок, но я уже позволю себе не приводить эти графики, да и вообще задерживаться тут, т.к. самое время запустить мастер оптимизации и путем подбора номиналов, корректирующих цепей, а также полярности подключения головок попробовать свести головки…
После оптимизации… «Первым порядком» головки так и не удалось свести, только лишь после добавления двух корректирующих фильтров-подпорок ситуация с осевой АЧХ улучшилась. «Второй порядок» получилось свести только подключив головки в одной полярности и применив один фильтр-подпорку. «Третий порядок» свелся неплохо без применения дополнительных корректирующих цепей, причем при различных вариантах включения полярности, единственное что, при соблюдении одной полярности частота раздела оказалась вблизи заданных нами 2,5кГц, а во втором варианте она сместилась ближе к 3,8-4кГц (иначе не сводилось), потому второй вариант не привожу. «Четвертый порядок» так же свелся в двух вариантах включения полярности, при однополярном вблизи 2,8кГц, а при разной полярности включения около 5-5,5кГц. Привожу только первый вариант.
Как видно из этих графиков, основными механизмами для сведения оказались следующие приемы:
-
Разнос частот раздела
-
Применение корректирующих цепей
-
Ассиметричные порядки фильтров
-
Отход от классических аппроксимаций кривых
-
Смена полярности головок
Плюс, отдельно стоит отметить, что фазовую ошибку еще можно скомпенсировать путем каскадного включения всепропускающих фильтров, а также в случае цифровой фильтрации посредством DSP, но в данном примере это не применялось.
Наиболее удачный оказался вариант на основе бывшего 3БТВ. Для него и приведем внеосевые характеристики, полярную диаграмму, фазу каждой головки, а также график ГВЗ.
Ну и в завершении этого маленького исследования, я еще раз напоминаю что все эти расчеты были сделаны для идеальных ДГ и активных фильтров. Для реальных же головок, установленных в реальных ящиках и используя только лишь пассивное деление все будет еще веселее, поверьте мне на слово 🙂
Выводы? Это уж увольте, вы сами. Я преследовал своей целью дать лишь некую, пусть местами и сумбурную, но все-таки пищу для ваших самостоятельных размышлений 🙂
Ccылки по теме:
Фильтры — Никитин Константин. Автозвук.
Фильтры-2 — Никитин Константин. Автозвук.
Подробности из жизни кроссоверов. Часть 1 — Car&Music.
Подробности из жизни кроссоверов. Часть 2 — Car&Music.
Подробности из жизни кроссоверов. Часть 3 — Car&Music.
РадиоКот :: Констролим ФНЧ.
РадиоКот >Лаборатория >Аналоговые устройства >Констролим ФНЧ.
В нашем сабвуфере используется низкочастотный динамик, который может воспроизводить только определенную часть спектра сигнала — его низкочастотную часть — для того он и нужен. Поэтому, если мы будем скармливать ему весь спектр сигнала целиком, он будет плеваться и хрюкать, потому как не в состоянии все это воспроизвести. Таким образом, мы получим гору искажений вместо приличного звука. Чтобы от них избавиться, мы должны отрезать ту часть спектра сигнала, которую саб воспроизводить не может и не должен. Для этого есть у нас Фильтр Низких Частот. Ну, точнее, будет.
Мы не будем шарить по сайтам в Интернете и банально тырить уже готовые схемы — мы все посчитаем и спаяем сами. Тем более, что это не так уж и сложно, как кажется на первый взгляд.
Посоветовавшись с Котом, мы решили не вываливать сюда кучу формул, от которых у любого нормального человека волосы начинают шевелиться просто везде, а воспользоваться специальной программкой для расчета всяких разных фильтров. Программка называется Filter Wiz Pro. Запускаем.
Это её главное окошко, откуда все и начинается. Видите кнопочки с загадочными сочетаниями буков и синими полосками? Вот оно нам и надо.
Итак, програмулина может справляться со следующими фильтрами:
LP — LowPass — ФНЧ —Фильтр Низких Частот
HP — HighPass — ФВЧ — Фильтр Высоких Частот
BP — BandPass — Полосовой Фильтр
BS — BandStop — Режекторный Фильтр
USR — пользовательский тип фильтра — что хотите, что и считайте.
На данный момент нас интересует первая кнопка — LP. Нажимаем.
Слева — форма для заполнения исходных данных для фильтра. Справа — АЧХ (Будь здоров!) фильтра. Спасибо. Это я не чихал, это Кот не знает что такое АЧХ (Будь здоров!). Спасибо. Аплитудно-Частотная Характеристика позволяет нам наглядно увидеть каков будет уровень сигнала на той или иной частоте. Очень удобно, очень.
Хорошо, заводим начальные параметры.
Passband Attenuation — ослабление сигнала в полосе пропускания — оставляем 0,5 дБ, нехай подавится.
Stopband Attenuation — ослабление сигнала на частоте среза.
Passband Frequency — это частота, вернее полоса частот, которую наш фильтр должен пропускать; с этой частоты начнется ослабление сигнала. Обычно эта частота составляет от 100 до 300Гц, в зависимости от саба, помещения, акустики, с которой данный сабвуфер будет применяться. Ну, выберем например 150Гц.
Stopband Frequency — частота среза — частота, на которой реализуется максимальное ослабление сигнала. Выбираем 500Гц. Ниже объясню почему.
Overall Filter Gain — общее усиление фильтра — оставляем 0 дБ — наш фильтр не будет ни усиливать, ни ослаблять сигнал.
Теперь немножко теории, даже не теории, а просто хочется рассказать откуда растут ноги у всех этих частот среза и ослаблений сигнала.
Есть такое понятие у фильтров, как крутизна спада. Фактически, эта штука обозначает как быстро будет ослабляться сигнал в выбранной полосе частот.
И есть еще одно понятие для фильтров — это порядок фильтра. Порядок не в смысле «помой за собой посуду, свинья», а в смысле количества элементарных звеньев в фильтре (На каждое звено обычно приходится один конденсатор).
Смотрим на график, где обезображены АЧХ фильтров разных порядков.
Теперь, я надеюсь, понятно, что такое крутизна спада? Чем круче «горка» на графике уходит вниз, тем больше эта самая крутизна. И как видно, она здорово зависит от порядка фильтра. Наша задача состоит в том, чтобы получить фильтр с максимально возможной крутизной спада. Однако, по мере увеличения порядкового числа фильтра, увеличивается и сложность его схемного решения — попросту говоря — нужно до фига всяких железок. Поэтому на практике находят компромисс между крутизной фильтра и его сложностью.
Однако продолжим.
Жмем кнопку Calculate.
Хлоп — у нас появилась еще одна закладочка — Calculation results. Отправляемся туда.
Итак, у нас есть уже табличка с некоторыми результатами. Наверху — различные типы фильтров — Баттерворта, Чебышева, инвертированный Чебышева, Эллиптический и Бесселя. В колонке слева нас интересует три параметра — Order — Порядок, Circuit stages — количество узлов схемы и Passband ripple — неравномерность в полосе пропускания. Мы будем собирать фильтр Баттерворта — это самый распространенный фильтр, у него самая хорошая линейность и простые схемные решения.
По заданным нами исходным данным видно, что у нас получается фильтр 4-го порядка. В принципе, если по каким то причинам этого мало или наоборот много, меняя частоту среза и/или ослабление на частоте среза можно изменять порядок фильтра. Кстати, можно сразу задать порядок фильтра, поставив галочку Force Filter Order и указав необходимый порядок фильтра.
В общем, жмем Next.
На этой страничке нам предлагают полюбоваться на расчетную АЧХ выбранного фильтра.
Идем дальше.
Теперь надо выбрать смотехническое решение для будущего фильтра для двух узлов схемы — Stage1 и Stage2. Возможны 13 вариантов — на любой вкус и размер. Не мудрствуя лукаво выбираем самый первый — фильтр Саллена и Ки. Жмем кнопку Select и идем дальше.
Вот почти и все. Программа рассчитала за нас номиналы необходимых компонентов схемы нашего фильтра. Мы можем оставить все как есть, а можно немного изменить номиналы элементов и посмотреть как это отобразится на результирующей АЧХ, которую можно посмотреть на следующей странице.
Теперь осталось составить общую схему нашего фильтра и спаять его.
Схема будет выглядеть следующим образом:
В фильтре использован ОУ К1401УД2Б — это счетверенный операционный усилитель общего назначения. Очень удобная штука — микросхема одна, а операционников сразу четыре. Можно так же применить К1401УД2А или К1401УД1. В принципе, можно применить и другие операционные усилители, но в таком случае на плате будет уже не один корпус, а два или три.
На элементе DA1.1 собран буферный каскад. DA1.2 и DA1.3 — непосредственно сам фильтр 4-го порядка. Необычность номиналов резисторов R2-R5 объясняется тем, что у меня не было под рукой резисторов именно тех номиналов, которые получались по расчету и пришлось их составлять из последовательно включенных резисторов величиной 47 кОм. Питание фильтра должно быть стабилизированным.
Уфф… ну вроде все пока.
В следующей, заключительной части мы быстренько рассмотрим усилитель для всего этого безобразия и соединим все это воедино — фильтр, усилитель и ящик. Ну и разумеется посмотрим, как нам быть с питанием — кушать то все хотят.
|
Как вам эта статья? |
Заработало ли это устройство у вас? |
5.05. Типы фильтров
Активные фильтры и генераторы
При анализе фильтров и при расчете их параметров всегда используются некоторые стандартные термины и имеет смысл придерживаться их с самого начала.
Предположим, что требуется фильтр нижних частот с плоской характеристикой в полосе пропускания и резким переходом к полосе подавления. Окончательный же наклон характеристики в полосе задерживания всегда будет 6n дБ/октава, где n — число «полюсов». На каждый полюс необходим один конденсатор (или катушка индуктивности), поэтому требования к окончательной скорости спада частотной характеристики фильтра, грубо говоря, определяют его сложность.
Теперь предположим, что вы решили использовать 6-полюсный фильтр нижних частот. Вам гарантирован окончательный спад характеристики на высоких частотах 36 дБ/октава. В свою очередь теперь можно оптимизировать схему фильтра в смысле обеспечения максимально плоской характеристики в полосе пропускания за счет уменьшения крутизны перехода от полосы пропускания к полосе задерживания. С другой стороны, допуская некоторую неравномерность характеристики в полосе пропускания, можно добиться более крутого перехода от полосы пропускания к полосе задерживания. Третий критерий, который может оказаться важным, описывает способность фильтра пропускать сигналы со спектром, лежащим в полосе пропускания, без искажений их формы, вызываемых фазовыми сдвигами. Можно также интересоваться временем нарастания, выбросом и временем установления.
Известны методы проектирования фильтров, пригодные для оптимизации любой из этих характеристик или их комбинаций. Действительно разумный выбор фильтра происходит не так, как описано выше; как правило, сначала задаются требуемая равномерность характеристики в полосе пропускания и необходимое затухание на некоторой частоте вне полосы пропускания и другие параметры. После этого выбирается наиболее подходящая схема с количеством полюсов, достаточным для того, чтобы удовлетворялись все эти требования. В следующих нескольких разделах будут рассмотрены три наиболее популярных типа фильтров, а именно фильтр Баттерворта (максимально плоская характеристика в полосе пропускания), фильтр Чебышева (наиболее крутой переход от полосы пропускания к полосе подавления) и фильтр Бесселя (максимально плоская характеристика времени запаздывания). Любой из этих типов фильтров можно реализовать с помощью различных схем фильтров; некоторые из них мы обсудим позже Все они равным образом годятся для построения фильтров нижних и верхних частот и полосовых фильтров.
Фильтры Баттерворта и Чебышева. Фильтр Баттерворта обеспечивает наиболее плоскую характеристику в полосе пропускания, что достигается ценой плавности характеристики в переходной области т.е. между полосами пропускания и задерживания. Как будет показано дальше у него также плохая фазочастотная характеристика. Его амплитудно-частотная характеристика задается следующей формулой:
Uвых/Uвх = 1/[1 + (ƒ/ƒc)2n]1/2,
где n определяет порядок фильтра (число полюсов). Увеличение числа полюсов дает возможность сделать более плоским участок характеристики в полосе пропускания и увеличить крутизну спада от полосы пропускания к полосе подавления, как это показано на рис. 5.10.
Рис. 5.10 Нормированные характеристики фильтров нижних частот Баттерворта. Обратите внимание увеличение крутизны спада характеристики с увеличением порядка фильтра.
Выбирая фильтр Баттерворта, мы ради максимально плоской характеристики поступаемся всем остальным. Его характеристика идет горизонтально, начиная от нулевой частоты, перегиб ее начинается на частоте среза ƒс — эта частота обычно соответствует точке -3 дБ.
В большинстве применений самым существенным обстоятельством является то, что неравномерность характеристики в полосе пропускания не должна превышать некоторой определенной величины, скажем 1 дБ. Фильтр Чебышева отвечает этому требованию, при этом допускается некоторая неравномерность характерности во всей полосе пропускания, но при этом сильно увеличивается острота ее излома. Для фильтра Чебышева задают число полюсов и неравномерность в полосе пропускания. Допуская увеличение неравномерности в полосе пропускания, получаем более острый излом. Амплитудно-частотная характеристика этого фильтра задается следующим соотношением
Uвых/Uвх = 1/[1 + ε2Cn2(ƒ/ƒc)]1/2,
где Сn— полином Чебышева первого рода степени n, а ε — константа, определяющая неравномерность характеристики в полосе пропускания. Фильтр Чебышева, как и фильтр Баттерворта имеет фазочастотные характеристики, далекие от идеальных. На рис. 5.11 представлены для сравнения характеристики 6-полюсных фильтров нижних частот Чебышева и Баттерворта. Как легко заметить, и тот, и другой намного лучше 6-полюсного RC-фильтра.
Рис. 5.11. Сравнение характеристик некоторых обычно применяемых 6-полюсных фильтров нижних частот. Характеристики одних и тех же фильтров изображены и в логарифмическом (вверху), и в линейном (внизу) масштабе. 1 — фильтр Бесселя; 2 — фильтр Баттерворта; 3 — фильтр Чебышева (пульсации 0,5 дБ).
На самом деле фильтр Баттерворта с максимально плоской характеристикой в полосе пропускания не столь привлекателен, как это может показаться, поскольку в любом случае приходится мириться с некоторой неравномерностью в полосе пропускания (для фильтра Баттерворта это будет постепенное понижение характеристики при приближении к частоте ƒс, а для фильтра Чебышева-пульсации, распределенные по всей полосе пропускания). Кроме того, активные фильтры, построенные из элементов, номиналы которых имеют некоторый допуск, будут обладать характеристикой, отличающейся от расчетной, а это значит, что в действительности на характеристике фильтра Баттерворта всегда будет иметь место некоторая неравномерность в полосе пропускания. На рис. 5.12 проиллюстрировано влияние наиболее нежелательных отклонений значений емкости конденсатора и сопротивления резистора на характеристику фильтра.
Рис. 5.12. Влияние изменений параметров элементов на характеристику активного фильтра.
В свете вышеизложенного весьма рациональной структурой является фильтр Чебышева. Иногда его называют равноволновым фильтром, так как его характеристика в области перехода имеет большую крутизну за счет того, что по полосе пропускания распределено несколько равновеликих пульсаций, число которых возрастает вместе с порядком фильтра. Даже при сравнительно малых пульсациях (порядка 0,1 дБ) фильтр Чебышева обеспечивает намного большую крутизну характеристики в переходной области, чем фильтр Баттерворта. Чтобы выразить эту разницу количественно, предположим, что требуется фильтр с неравномерностью характеристики в полосе пропускания не более 0,1 дБ и затуханием 20 дБ на частоте, отличающейся на 25% от граничной частоты полосы пропускания. Расчет показывает, что в этом случае требуется 19-полюсный фильтр Баттерворта или всего лишь 8-полюсный фильтр Чебышева.
Мысль о том, что можно мириться с пульсациями характеристики в полосе пропускания ради увеличения крутизны переходного участка, доводится до своего логического завершения в идее так называемого эллиптического фильтра (или фильтра Кауэра), в котором допускаются пульсации характеристики как в полосе пропускания, так и в полосе задерживания ради обеспечения крутизны переходного участка даже большей, чем у характеристики фильтра Чебышева. С помощью ЭВМ можно сконструировать эллиптические фильтры так же просто, как и классические фильтры Чебышева и Баттерворта. На рис. 5.13 представлено графическое задание амплитудно-частотной характеристики фильтра. В этом случае (фильтр нижних частот) определяются допустимый диапазон коэффициента передачи фильтра (т.е. неравномерность) в полосе пропускания, минимальная частота, на которой характеристика покидает полосу пропускания, максимальная частота, где характеристика переходит в полосу задерживания, и минимальное затухание в полосе задерживания.
Рис. 5.13. Задание параметров частотной характеристики фильтра.
Фильтры Бесселя. Как было установлено ранее, амплитудно-частотная характеристика фильтра не дает о нем полной информации. Фильтр с плоской амплитудно-частотной характеристикой может иметь большие сдвиги фаз. В результате этого форма сигнала, спектр которого лежит в полосе пропускания, будет искажена при прохождении через фильтр. В ситуации, при которой форма сигнала имеет первостепенное значение, желательно иметь в распоряжении линейно-фазовый фильтр (фильтр с постоянным временем запаздывания). Предъявление к фильтру требования обеспечения линейного изменения сдвига фазы в зависимости от частоты эквивалентно требованию постоянства времени запаздывания для сигнала, спектр которого расположен в полосе пропускания, т. е. отсутствия искажений формы сигнала. Фильтр Бесселя (также называемый фильтром Томсона) имеет наиболее плоский участок кривой времени запаздывания в полосе пропускания, подобно тому как фильтр Баттерворта имеет наиболее плоскую амплитудно-частотную характеристику. Чтобы понять, какое улучшение во временной области дает фильтр Бесселя, посмотрите на рис. 5.14, где изображены нормированные по частоте графики времени запаздывания для 6-полюсных фильтров нижних частот Бесселя и Баттерворта. Плохая характеристика времени запаздывания фильтра Баттерворта обуславливает появление эффектов типа выброса при прохождении через фильтр импульсных сигналов. С другой же стороны, за постоянство времен запаздывания у фильтра Бесселя приходится расплачиваться тем, что его амплитудно-частотная характеристика имеет еще более пологий переходной участок между полосами пропускания и задерживания, чем даже у характеристики фильтра Баттерворта.
Рис. 5.14. Сравнение временных запаздываний для 6-полосных фильтров нижних частот Бесселя (1) и Баттерворта (2). Фильтр Бесселя благодаря своим превосходным свойствам во временной области дает наименьшее искажение формы сигнала.
Существует много различных способов проектирования фильтров, в которых делаются попытки улучшить рабочие параметры фильтра Бесселя во временной области, частично жертвуя постоянством времени запаздывания ради уменьшения времени нарастания и улучшения амплитудно-частотной характеристики. Фильтр Гаусса имеет почти столь же хорошие фазочастотные характеристики, как и фильтр Бесселя, но при улучшенной переходной характеристике. Другой интересный класс представляют собой фильтры, позволяющие добиться одинаковых по величине пульсаций кривой времени запаздывания в полосе пропускания (аналогично пульсациям амплитудно-частотной характеристики фильтра Чебышева) и обеспечивающие примерно одинаковое запаздывание для сигналов со спектром вплоть до полосы задерживания. Еще один подход к созданию фильтров с постоянным временем запаздывания — это применение всепропускающих фильтров, называемых иначе корректорами во временной области. Эти фильтры обладают постоянной амплитудно-частотной характеристикой, а сдвиг фазы может меняться согласно конкретным требованиям. Таким образом, их можно применять для выравнивания времени запаздывания любых фильтров, в частности фильтров Баттерворта и Чебышева.
Сравнение фильтров. Несмотря на ранее высказанные замечания о переходной характеристике фильтров Бесселя, он все же обладает очень хорошими свойствами во временной области по сравнению с фильтрами Баттерворта и Чебышева. Сам фильтр Чебышева при его весьма подходящей амплитудно-частотной характеристике имеет наихудшие параметры во временной области из всех этих трех типов фильтров. Фильтр Баттерворта дает компромисс между частотами и временными характеристиками. На рис. 5.15 дана информация по рабочим характеристикам этих трех типов фильтров во временной области, дополняющая приведенные ранее графики амплитудно-частотных характеристик. По этим данным можно сделать вывод, что в тех случаях, когда важны параметры фильтра во временной области, желательно применять фильтр Бесселя.
Рис. 5.15. Сравнение переходных процессов 6-полюсных фильтров нижних частот. Кривые нормированы приведением значения ослабления 3 дБ к частоте 1 Гц. 1 — фильтр Бесселя; 2 — фильтр Баттерворта; 3 — фильтр Чебышева (пульсации 0.5 дБ).
Схемы активных фильтров
Расчёт активных фильтров. Онлайн калькулятор.
И начнём мы с активных фильтров нижних частот (ФНЧ) и фильтров верхних частот (ФВЧ) 2-го и 3-го порядков имени товарищей Бесселя, Баттерворта и Пафнутия нашего Чебышева.
Эко нас понесло! Почему бы не удовлетвориться одним учёным мужем? К примеру, привычный с детства Баттерворт совсем не плох, к тому же широко известен в узких кругах.
Согласен, с какой стороны не возьми, Баттерворт — хорошая штука. Тут тебе и максимально гладкая АЧХ на частотах полосы пропускания, и
приличный спад характеристики в полосе подавления, однако…
Если на первый план выдвигается линейность фазо-частотной характеристики в полосе пропускания фильтра (например, в аудио-кроссоверах),
то пальма первенства в АЧХ-строении переходит к обратному многочлену профессора Фридриха Вильгельма Бесселя, ну а если ФЧХ нам
до фени, а в приоритете максимально крутой спад характеристики на частотах полосы подавления, то как ни крути, придётся с головой
окунуться в полиномы Пафнутия Львовича Чебышёва.
Фильтры построим на основе повторителей, они просты в расчётах, к тому же легко могут быть реализованы не только на операционных усилителях, но и на транзисторах.
А желающим спроектировать активный фильтр нижних частот 3-6-го порядка с перестраиваемой частотой среза, следует посетить страницу ссылка на страницу .
Рис.1
На Рис.1 приведены схемы активных фильтров нижних частот (ФНЧ) 2-го и 3-го порядка на ОУ и, для примера, реализация фильтра на биполярном транзисторе, отличающаяся от схем на операционниках только наличием двух резисторов, задающих необходимое напряжение смещения на базе.
Крутизна спада АЧХ этих фильтров в полосе подавления для Бесселя — около 5 дБ/октаву на каждый порядок фильтра, для
Баттерворта — 6 дБ/октаву и около 8 дБ/октаву для Чебышёва.
Коэффициент передачи в полосе пропускания К=1, а номиналы рассчитываются исходя из формул:
C1=КС1/(2π*F*R)   C2=КС2/(2π*F*R)   C3=КС3/(2π*F*R), где коэффициенты
КС1, КС2 и КС3 зависят как от порядка фильтра, так и от его принадлежности к той или иной фамилии.
К примеру для фильтров Баттерворта 2-го порядка КС1=1,114, КС2=0,707, а для фильтров Баттерворта 3-го порядка
КС1=1,393, КС2=3,549, КС3=0,202.
Критерии выбора величины сопротивления R, такие же, как и в пассивных фильтрах, она должна быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного сопротивления ОУ или ЭП (на практике 1-100 кОм).
РИСУЕМ ТАБЛИЦУ ДЛЯ АКТИВНЫХ ФНЧ БЕССЕЛЯ, БАТТЕРВОРТА И ЧЕБЫШЕВА
Плавно переходим к активным фильтрам верхних частот (ФВЧ) 2-го и 3-го порядка на ОУ (Рис.2). В транзисторной реализации резисторы, задающие напряжение смещения на базе, уже участвуют в формировании необходимой АЧХ фильтра, поэтому значение Rб1 ll Rб2 должно равняться значению резистора R2 в ФВЧ 2-го порядка, либо R3 в ФВЧ 3-го порядка.
Рис.2
Номиналы элементов рассчитываются исходя из следующих формул:
R1=КR1/(2π*F*C) R2=КR2/(2π*F*C) R3=КR3/(2π*F*C)
Rrб1llRrб2=R2 для фильтров 2-го порядка, либо Rrб1llRrб2=R3 для 3-го.
Для фильтров Баттерворта 2-го порядка КR1=0,707, КR2=1,414, а для фильтров Баттерворта 3-го порядка
КR1=0,717, КR2=0,282, КR3=4,950.
И опять же, изначально надо определиться с номиналом R1, исходя из принципов, описанных в предыдущих схемах.
ТАБЛИЦА ДЛЯ РАСЧЁТА АКТИВНЫХ ФВЧ БЕССЕЛЯ, БАТТЕРВОРТА И ЧЕБЫШЕВА
И наконец, мы подобрались к схеме полосового активного фильтра.
Здесь всё несколько сложнее, поскольку, при расчёте фильтра, помимо значения центральной частоты, нам не стоит забывать
и про такие немаловажные вещи, как коэффициент передачи фильтра в полосе пропускания, да и собственно ширину самой полосы
пропускания.
Формулы, для расчёта элементов:
C1=C2=C
R1=Q/(2πF*Kп*C)
R2=Q/((2πF*C*(2Q²-Kп))
R3=2Q/(2πF*C)
Q=F/Bпр, где
Q-добротность фильтра,
Впр-полоса пропускания по уровню -3дБ,
F-центральная частота фильтра,
Кп-коэффициент передачи фильтра в полосе пропускания.
Рис.3
В фильтре, приведённом на рисунке, не стоит слишком усердствовать с высокими значениями добротности и коэффициента передачи. Как показывает практика, и тот и другой параметр следует ограничить сверху на уровне 5-6 единиц.
Как всегда, начинаем с выбора номинала резистора R1, который как минимум в 10 раз должен быть выше выходного импеданса предыдущего каскада.
РИСУЕМ ТАБЛИЦУ ДЛЯ АКТИВНОГО ПЛОСОВОГО ФИЛЬТРА 2-го ПОРЯДКА
ВНИМАНИЕ!!! Для правильной работы этого фильтра должно соблюдаться условие К<2*Q². При несоблюдении этого условия, значение R2 в таблице примет отрицательное значение.
А что делать, если полученные значения элементов не попадают в стандартную сетку?
Не беда, нарисуем ещё одну таблицу, но до этого надо поиграться коэффициентом передачи фильтра в небольших пределах (например,
сделать не 1,5, а 1,45, или 1,55) до достижения значения R3 величины, попадающей в сетку. Номинал R1 мы уже выбрали, исходя из соображений
приемлемого входного импеданса.
Предположим, нам надо рассчитать фильтры для 10-полосного эквалайзера.
Фильтры у нас получаются октавные, стандартное значение добротности для них Q=1,41.
R1 выберем номиналом 30кОм, Кпер = 1,5. Произведём расчёт для частоты 1000 Гц.
Подставив эти цифры в верхнюю таблицу, получаем С=4987пФ, R2=18,173кОм, R3=90кОм.
Пошебуршав туда-сюда Кпер, понимаем, что для получения стандартного значения R3=91кОм, коэффициент передачи фильтра должен
быть равен 1,517, что для нашего случая вообще не принципиально, тем более, что это значение Кпер будет сопровождать все фильтры,
независимо от частоты.
Итак, подставляем в нижнюю таблицу R1=30кОм, R3=91кОм, R2=18кОм, стандартное значение ёмкости С=5100пФ и естественным образом
видим, что значение резонансной частоты у нас съехало до 975Гц.
Но у нас было с собой, а именно замечательное сопротивление R2, которое никак не влияет на Кпер, и весьма скромно — на добротность.
Покрутив номинал этого резистора, получаем — 16,7кОм, центральную частоту — 999Гц и добротность — 1.46. Всё, расчёт фильтра — завершён.
ЕЩЁ ТАБЛИЦА ДЛЯ АКТИВНОГО ПОЛОСОВОГО ФИЛЬТРА
Для желающих рассчитать параметры и элементы многополосных графических эквалайзеров следует посетить страницу ссылка на страницу , а на следующей странице мы рассмотрим универсальный перестраиваемый активный фильтр с регулировкой частоты и добротности.
11.4: Порядок фильтров и полюса
-
- Последнее обновление
- Сохранить как PDF
Скорость, с которой отклик фильтра попадает в полосу перехода, определяется порядком фильтра. Чем выше порядок фильтра, тем выше скорость его спада.Порядок фильтра задается как целое число и выводится из передаточной функции фильтра. Например, при прочих равных условиях фильтр четвертого порядка будет спадать в два раза быстрее, чем фильтр второго порядка, и в четыре раза быстрее, чем блок первого порядка. Порядок фильтра также указывает минимальное количество реактивных компонентов, которые потребуются фильтру. Например, для фильтра третьего порядка требуется по крайней мере три реактивных компонента: один конденсатор и две катушки индуктивности, два конденсатора и одна катушка индуктивности или, в случае активного фильтра, три конденсатора.С этим связано количество полюсов, которые использует фильтр. Часто можно услышать такие описания, как «четырехполюсный фильтр». Для большинства универсальных фильтров верхних или нижних частот термины «полюс» и «порядок» могут использоваться взаимозаменяемо и полностью описывать скорость спада. Для более сложных фильтров это не совсем так, и вы также можете услышать такие описания, как «шестиполюсный фильтр с двумя нулями». Поскольку эта глава представляет собой введение в фильтры, мы не будем подробно описывать работу этих более эзотерических типов.Достаточно сказать, что когда схема описывается как фильтр \ (N-го \) порядка, вы можете предположить, что это также \ (N \) -полюсный фильтр.
Можно сделать общее наблюдение, что скорость спада фильтра в конечном итоге приблизится к 6 дБ на октаву на полюс (20 дБ на декаду на полюс). Следовательно, фильтр третьего порядка (т. Е. Трехполюсный) в конечном итоге затухает со скоростью 18 дБ на октаву (60 дБ на декаду). Мы говорим «в конце концов», потому что реакция около частоты прерывания может быть несколько быстрее или медленнее, чем это значение.На рисунке \ (\ PageIndex {1} \) сравнивается влияние порядка на четырех идентичных в остальном фильтрах нижних частот. Обратите внимание, что фильтры более высокого порядка обеспечивают большее затухание на любой частоте за пределами точки излома. Как и в большинстве графиков отклика, на рисунке \ (\ PageIndex {1} \) используются децибелы вместо обычного усиления. Кроме того, эти фильтры показаны с единичным усилением в полосе пропускания, хотя это не обязательно. Фильтры высокого порядка используются, когда переходная полоса должна быть как можно более узкой. Нередко можно увидеть фильтры двенадцатого порядка и выше, используемые в специальных приложениях.Как вы можете догадаться, фильтры более высокого порядка сложнее и дороже в разработке и создании. Для многих типичных приложений обычно используются заказы от двух до шести.
Рисунок \ (\ PageIndex {1} \): Влияние порядка на фильтры нижних частот.
бесконечная импульсная характеристика — типовые заказы фильтров
Приложение само определяет требуемое качество фильтров в терминах спецификаций фильтра и требует обработки пропускной способности в терминах частоты дискретизации $ F_s $, выборок в секунду.
Фильтры высокого качества, как правило, имеют жесткие спецификации, и для этого потребуются высокие заказы для данного типа фильтра. Однако разные типы фильтров могут соответствовать сходным характеристикам в разном порядке.
Порядок фильтра и заданная частота данных (выборки) $ F_s $, в свою очередь, определяют требования к вычислительной мощности. Например, КИХ-фильтр порядка $ N $ будет выполнять $ N + 1 $ MAC (умножение и накопление) на типичную выходную выборку для длинных входных последовательностей; и если частота дискретизации данных составляет $ F_s $ выборок в секунду, это означает, что фильтр будет выполнять $ (N + 1) \ times F_s $ MACs в секунду.
Учитывая ЦП с тактовой частотой $ M $ Гц и эффективностью MAC $ L $ MAC на герц, ваш процессор должен обеспечивать $ M \ times L> (N + 1) \ times F_s $, исключая любые накладные расходы. индексация, цикл или операций памяти операций.
Это типичная реализация FIR в одноядерной однопоточной системе. Существует множество архитектур для реализации фильтров FIR / IIR на основе многоскоростных методов или распараллеливания на основе методов SIMD, которые могут повлиять на мощность обработки.
Наконец, как очень грубая цифра, для аудиоприложений с частотой 44,1 долл. США кГц КИХ-фильтр порядка менее 20 долл. США будет иметь в основном слабые свойства. Заказы на сумму от 20 до 90 долларов будут иметь (все более и более) умеренное качество, а заказы больше 128 могут иметь характеристики от хорошего до высокого, где высокое качество относится к большему контролю на спектральной форме частотной характеристики фильтра. Имейте в виду, что для реализации КИХ-фильтра с резким переходом и узкой полосой могут потребоваться тысячи ответвлений.
В позднем ответе на комментарии ниже можно сказать, что свертка КИХ-фильтра может быть значительно более эффективной за счет использования метода умножения в частотной области на основе БПФ. Мой ответ на данный момент касается реализации во временной области.
Практическое правило порядка фильтрации
Моим любимым «практическим правилом» для порядка КИХ-фильтра нижних частот является «практическое правило Фреда Харриса»:
$$ N = \ frac {f_s} {\ Delta f} \ cdot \ frac {\ rm Аттен_ {дБ}} {22} $
где
- $ \ Delta f $ — полоса перехода, в тех же единицах $ f_s $
- $ f_s $ — частота дискретизации фильтра
- $ \ rm Аттен_ {дБ} $ — целевое отклонение в дБ
Например, если у вас есть полоса перехода 100 Гц в системе с дискретизацией 1 кГц, и ваше требование подавления составляет 50 дБ в полосе заграждения, то порядок может быть приблизительно равен:
$$ N = \ frac {1 \ \ rm kHz} {100 \ \ rm Hz} \ cdot \ frac {50} {22} = 23 \ rm taps \ tag {округление в большую сторону} $
Спасибо, Фред Харрис!
Обратите внимание, что еще одна более подробная формула, которая учитывает колебания полосы пропускания, — это формула Кайзера, созданная Джеймсом Кайзером из Bell Labs, которую я включил в свой рисунок ниже.
Для большинства применений, которые я сделал, подход Фреда Харриса был просто прекрасен, поскольку с учетом определенного отклонения полученные фильтры, использующие традиционные алгоритмы проектирования фильтров, такие как Parks-McClellan и Remez, превзошли мои требования к пульсации полосы пропускания после выполнения требования отклонения. (Что я обычно делаю, так это оцениваю порядок, разрабатываю фильтр с этим порядком, проверяю результат и оттуда увеличиваю или уменьшаю порядок для точной настройки). Результаты оценок таковы: оценки и могут широко варьироваться в зависимости от общих проектных параметров и не должны рассматриваться как точное решение.
Для тех, кто знаком с проектированием фильтров с использованием оконных подходов, обзор товарного или прямоугольного окна (которое представляет собой простое усечение) показывает, почему для этого требуется нажатие $ f_s / \ Delta f $ (что то же самое, что и $ 2 \ pi / \ Delta \ omega $, если единицы для нормализованной частоты — радианы / отсчет, как это часто делается), чтобы завершить переходную полосу. См. Изображения ниже, которые помогают объяснить это.
На верхнем изображении ниже показано ожидаемое значение Sinc по частоте для прямоугольного окна во времени, в данном случае как беспричинный прямоугольный импульс с центром в $ t = 0 $.Затем это повторяется в дискретных формах как причинный сигнал, начиная с $ t = 0 $, как с дискретным преобразованием Фурье (DTFT), так и с дискретным преобразованием Фурье (DFT), где разница в том, что отсчеты во времени простираются до $ \ pm \ infty $ для DTFT, что приводит к непрерывной форме волны в частотной области. В обоих случаях результатом является функция Sinc с псевдонимом, которая является периодической в интервале $ f = [0, f_s) $, с ключевым моментом, что для $ N $ выборок во времени прямоугольной функции частотная характеристика будет иметь свой первый null при $ f = 1 / N $ (где $ f $ — нормализованная частота, а 1 — частота дискретизации).
На следующем изображении ниже показан подход с прямоугольным окном к дизайну фильтров (который я бы никогда не рекомендовал, но он информативен). Первый график в верхнем левом углу показывает целевую частотную характеристику для нашего фильтра как идеальную характеристику «кирпичной стены». Пожалуйста, не путайте это с «окном товарного вагона» (или «прямоугольным окном»), которое также имеет прямоугольную форму — окно находится во временной области!
Чтобы реализовать такой фильтр, мы могли бы использовать импульсную характеристику желаемой частотной характеристики в качестве коэффициентов в нашем FIR-фильтре (коэффициенты фильтра — это импульсная характеристика — подавайте импульс на входе и выходе, все коэффициенты !).Импульсная характеристика для прямоугольной частотной характеристики (кирпичная стена) — это обратная FT, которая является функцией Sinc во временной области, показанной в нижнем левом углу как «Требуемый импульсный отклик». Функция Sinc распространяется на плюс и минус бесконечность, поэтому для реализации такого фильтра нам понадобится бесконечно длинный фильтр, и у него будет бесконечно большая задержка. Очевидно, мы не можем этого сделать, поэтому мы усекаем коэффициенты до чего-то реализуемого. Чем длиннее фильтр, тем ближе мы приближаемся к идеальному отклику кирпичной стены, но также тем больше будет задержка (и тем больше ресурсов нам потребуется с точки зрения конструкции фильтра; больше ответвлений).
Усечение импульсной характеристики во временной области математически идентично умножению на прямоугольное окно во временной области. (Обратите внимание, что импульсный отклик также задерживается на половину длительности окна, чтобы система была причинной). Умножение во временной области эквивалентно свертке в частотной области. Частотная область (FT) импульсной характеристики до усечения является нашей первоначальной желаемой частотной характеристикой кирпичной стены. Частотная характеристика для прямоугольного окна является функцией Sinc в частотной области.
Итак, когда мы усекаем желаемый импульсный отклик (умножаем во времени на прямоугольное окно), мы сворачиваем желаемый частотный отклик с функцией Sinc, что приводит к приближению нашей целевой частотной характеристики, как показано в верхнем правом углу изображение ниже.
Ключевым выводом для функций Sinc в целом является то, что первый нуль — это $ 1 / T $, где $ T $ — длительность прямоугольной функции. Для системы с выборкой первый нуль будет в $ 2 \ pi / N $, где $ N $ представляет количество выборок для продолжительности прямоугольной функции.На изображениях для оси частот используется нормализованная частота в радианах (если это сбивает вас с толку, вы просто знаете, что $ 2 \ pi $ — это частота в радианах для частоты дискретизации). Таким образом, в процессе свертки резкий переход кирпичной стены расширяется и в этом случае переходит в 0 (наша $ \ Delta \ omega $) с частотой $ 2 \ pi / N $! Итак, здесь $$ N = 2 \ pi / \ Delta \ omega $$, и, конечно, фильтр плох с боковыми лепестками и т. Д. Обратите внимание на это: этот переход от функции Sinc является наиболее резким из возможных для данного количества нажатий; у него лучшее разрешение по частоте, но самый плохой динамический диапазон (подавление).Другие типологии окон (Blackman, Blackman-harris, Kaiser (моя любимая) и т. Д.) Значительно улучшают динамический диапазон, но всегда за счет перехода.
Итак, из вышеизложенного мы видим происхождение $ 2 \ pi / \ Delta \ omega $, которое используется в формулах аппроксимации, а также мы видим, почему существует дополнительный коэффициент умножения, увеличивающий количество ответвлений выше этого для типичного фильтра конструкции; прямоугольное окно даст нам наилучший возможный переход с $ N $ нажатиями, где $ N = 2 \ pi / \ Delta \ omega $, но имеет очень плохое отклонение.Больше касаний используется для сглаживания временного перехода дальше резкого перехода прямоугольного окна, обеспечивая большее отклонение за счет полосы пропускания перехода.
Дизайн фильтра Баттерворта с фильтром нижних частот Баттерворта
В приложениях, которые используют фильтры для формирования частотного спектра сигнала, например, в системах связи или управления, форма или ширина спада, также называемая «переходной полосой», для простого фильтра первого порядка может быть слишком длинной. или требуются широкие и поэтому активные фильтры, разработанные с более чем одним «порядком».Эти типы фильтров обычно известны как фильтры «высокого порядка» или «n th -order».
Сложность или тип фильтра определяется «порядком» фильтров и зависит от количества реактивных компонентов, таких как конденсаторы или катушки индуктивности, в его конструкции. Мы также знаем, что скорость спада и, следовательно, ширина полосы перехода зависит от порядкового номера фильтра и что для простого фильтра первого порядка стандартная скорость спада составляет 20 дБ / декаду или 6 дБ. / октава.
Тогда для фильтра, который имеет порядковый номер n -го , он будет иметь последующую скорость спада 20n дБ / декаду или 6n дБ / октаву. Таким образом, фильтр первого порядка имеет скорость спада 20 дБ / декаду (6 дБ / октаву), фильтр второго порядка имеет скорость спада 40 дБ / декаду (12 дБ / октаву), а фильтр четвертого порядка имеет скорость спада 80 дБ / декада (24 дБ / октава) и т. д. и т. д.
Фильтры высокого порядка, например третьего, четвертого и пятого порядка, обычно формируются путем каскадного объединения одиночных фильтров первого и второго порядка.
Например, два фильтра нижних частот второго порядка могут быть объединены каскадом для создания фильтра нижних частот четвертого порядка и так далее. Хотя порядок формирования фильтра не ограничен, по мере того, как порядок увеличивается, увеличиваются его размер и стоимость, а также снижается его точность.
Десятилетия и октавы
Последний комментарий о Decades и Octave . На шкале частот Декада — это десятикратное увеличение (умножение на 10) или десятикратное уменьшение (деление на 10).Например, от 2 до 20 Гц представляет одну декаду, а от 50 до 5000 Гц — две декады (от 50 до 500 Гц, а затем от 500 до 5000 Гц).
Октава — это удвоение (умножение на 2) или уменьшение вдвое (деление на 2) шкалы частот. Например, от 10 до 20 Гц представляет одну октаву, а от 2 до 16 Гц — это три октавы (от 2 до 4, от 4 до 8 и, наконец, от 8 до 16 Гц), каждый раз удваивая частоту. В любом случае, логарифмические шкалы широко используются в частотной области для обозначения значения частоты при работе с усилителями и фильтрами, поэтому важно их понимать.
Логарифмическая шкала частот
Поскольку резисторы, определяющие частоту, все равны, как и конденсаторы, определяющие частоту, частота среза или граничная частота ( C ) для фильтра первого, второго, третьего или даже четвертого порядка также должны быть одинаковыми. и находится с помощью нашего уже старого знакомого уравнения:
Как и фильтры первого и второго порядка, фильтры верхних частот третьего и четвертого порядков формируются путем простого обмена местами компонентов, определяющих частоту (резисторов и конденсаторов) в эквивалентном фильтре нижних частот.Фильтры высокого порядка можно разработать, следуя процедурам, которые мы видели ранее в руководствах по фильтрам низких частот и фильтрам высоких частот. Однако общий коэффициент усиления фильтров высокого порядка равен фиксированным , потому что все компоненты, определяющие частоту, равны.
Приближение фильтра
До сих пор мы рассматривали схемы фильтра нижних и верхних частот первого порядка, их результирующие частотные и фазовые характеристики. Идеальный фильтр дал бы нам характеристики максимального усиления и равномерности полосы пропускания, минимального затухания в полосе задерживания, а также очень крутой полосы пропускания для спада полосы задерживания (переходная полоса), и поэтому очевидно, что большое количество сетевых откликов будет удовлетворить эти требования.
Неудивительно, что в конструкции линейных аналоговых фильтров существует ряд «аппроксимирующих функций», которые используют математический подход для наилучшего приближения передаточной функции, необходимой нам для конструкции фильтров.
Такие конструкции известны как Elliptical , Butterworth , Chebyshev , Bessel , Cauer и многие другие. Из этих пяти «классических» функций аппроксимации линейного аналогового фильтра только фильтр Баттерворта и особенно фильтр Баттерворта нижних частот будет рассматриваться здесь как его наиболее часто используемая функция.
Конструкция фильтра Баттерворта нижних частот
Частотная характеристика аппроксимирующей функции фильтра Баттерворта также часто упоминается как «максимально ровная» (без пульсаций) характеристика, потому что полоса пропускания разработана так, чтобы иметь частотную характеристику, которая является настолько плоской, насколько это математически возможно, от 0 Гц (постоянный ток) до частоты среза -3 дБ без пульсаций. Более высокие частоты за пределами точки отсечки спадают до нуля в полосе заграждения при 20 дБ / декада или 6 дБ / октава.Это потому, что у него «коэффициент качества» «Q» всего 0,707.
Однако одним из основных недостатков фильтра Баттерворта является то, что он обеспечивает равномерность полосы пропускания за счет широкой переходной полосы, когда фильтр переключается с полосы пропускания на полосу заграждения. Также он имеет плохие фазовые характеристики. Идеальная частотная характеристика, называемая фильтром «кирпичной стены», и стандартные аппроксимации Баттерворта для различных порядков фильтров приведены ниже.
Идеальная частотная характеристика для фильтра Баттерворта
Обратите внимание, что чем выше порядок фильтра Баттерворта, тем больше количество каскадных каскадов в конструкции фильтра и тем ближе фильтр к идеальному отклику «кирпичной стены».
Однако на практике идеальная частотная характеристика Баттерворта недостижима, поскольку она создает чрезмерную пульсацию полосы пропускания.
Если обобщенное уравнение представляет фильтр Баттерворта «n-го» порядка, частотная характеристика задается как:
Где: n представляет порядок фильтрации, Omega ω равно 2πƒ, а Epsilon ε — максимальное усиление полосы пропускания (A max ). Если A max определен на частоте, равной угловой точке отсечки -3 дБ (ƒc), тогда ε будет равно единице, и, следовательно, ε 2 также будет равно единице.Однако, если теперь вы хотите определить A max при другом значении усиления напряжения, например 1 дБ или 1,1220 (1 дБ = 20 * logA max ), то новое значение epsilon, ε находится по:
|
Переставьте уравнение, чтобы получить:
Частотная характеристика фильтра может быть определена математически с помощью его передаточной функции со стандартной передаточной функцией напряжения H (jω), записанной как:
|
Примечание: (jω) также можно записать как (s) для обозначения S-домена . , а результирующая передаточная функция для фильтра нижних частот второго порядка задается как:
Нормализованные полиномы фильтра Баттерворта нижних частот
Чтобы помочь в разработке своих фильтров нижних частот, Баттерворт создал стандартные таблицы нормализованных полиномов нижних частот второго порядка с учетом значений коэффициента, которые соответствуют угловой частоте среза, равной 1 радиан / сек.
| n | Нормированные многочлены знаменателя в факторизованной форме |
| 1 | (1 + с) |
| 2 | (1 + 1.414 с + с 2 ) |
| 3 | (1 + с) (1 + с + с 2 ) |
| 4 | (1 + 0,765 с + с 2 ) (1 + 1,848 с + с 2 ) |
| 5 | (1 + с) (1 + 0,618 с + с 2 ) (1 + 1,618 с + с 2 ) |
| 6 | (1 + 0.518s + s 2 ) (1 + 1.414s + s 2 ) (1 + 1.932s + s 2 ) |
| 7 | (1 + с) (1 + 0,445 с + с 2 ) (1 + 1,247 с + с 2 ) (1 + 1,802 с + с 2 ) |
| 8 | (1 + 0,390 с + с 2 ) (1 + 1,111 с + с 2 ) (1 + 1,663 с + с 2 ) (1 + 1,962 с + с 2 ) |
| 9 | (1 + s) (1 + 0,347s + s 2 ) (1 + s + s 2 ) (1 + 1,532s + s 2 ) (1 + 1.879s + s 2 ) |
| 10 | (1 + 0.313 с + с 2 ) (1 + 0,908 с + с 2 ) (1 + 1,414 с + с 2 ) (1 + 1,782 с + с 2 ) (1 + 1,975 с + с 2 ) |
Конструкция фильтра — фильтр нижних частот Баттерворта
Найдите порядок активного фильтра нижних частот Баттерворта, технические характеристики которого следующие: A max = 0,5 дБ при частоте полосы пропускания (ωp) 200 рад / с (31,8 Гц) и A min = -20 дБ при частоте полосы заграждения (ωs) 800 рад / сек. Также разработайте подходящую схему фильтра Баттерворта, соответствующую этим требованиям.
Во-первых, максимальное усиление полосы пропускания A max = 0,5 дБ, что равно усилению 1,0593 , помните, что: 0,5 дБ = 20 * log (A) на частоте (ωp) 200 рад / с, поэтому значение эпсилон ε находится по формуле:
Во-вторых, минимальное усиление полосы задерживания A мин = -20 дБ, что равно усилению 10 (-20 дБ = 20 * log (A)) на частоте полосы задерживания (ωs) 800 рад / с или 127,3 Гц.
Подстановка значений в общее уравнение для частотной характеристики фильтров Баттерворта дает нам следующее:
Поскольку n всегда должно быть целым числом (целым числом), то следующее по величине значение равно 2.42 равно n = 3, поэтому «требуется фильтр третьего порядка», и для создания фильтра Баттерворта третьего порядка требуется каскад фильтра второго порядка, соединенный каскадом вместе с каскадом фильтра первого порядка.
Из приведенной выше таблицы нормализованных полиномов Баттерворта нижних частот коэффициент для фильтра третьего порядка задается как (1 + s) (1 + s + s 2 ), и это дает нам коэффициент усиления 3-A = 1, или A = 2. Поскольку A = 1 + (Rf / R1), выбор значения как для резистора обратной связи Rf, так и для резистора R1 дает нам значения 1 кОм и 1 кОм соответственно как: (1 кОм / 1 кОм) + 1 = 2.
Мы знаем, что граничная частота, точка -3 дБ (ω o ) может быть найдена по формуле 1 / CR, но нам нужно найти ω o из частоты полосы пропускания ω p , тогда ,
Итак, угловая частота среза равна 284 рад / с или 45,2 Гц (284 / 2π), и, используя знакомую формулу 1 / CR, мы можем найти значения резисторов и конденсаторов для нашей схемы третьего порядка.
Обратите внимание, что ближайшее предпочтительное значение к 0.352 мкФ будет 0,36 мкФ или 360 нФ.
Фильтр нижних частот Баттерворта третьего порядка
и, наконец, наша схема нижнего прохода третьего порядка Фильтр Баттерворта с частотой среза угла 284 рад / с или 45,2 Гц, максимальным усилением полосы пропускания 0,5 дБ и минимальным усилением полосы задерживания 20 дБ. следующее.
Итак, для нашего фильтра нижних частот Баттерворта 3-го порядка с угловой частотой 45,2 Гц, C = 360 нФ и R = 10 кОм
[Eeglablist] порядок фильтров
[Eeglablist] порядок фильтров Андреас Видманн widmann в уни-лейпциге.деЧт 15 июня 08:33:47 PDT 2017
Привет Джале, у каждого цифрового КИХ- или БИХ-фильтра есть порядок фильтров. Математически порядок - это задержка от входа до выхода. Поскольку мы фильтруем офлайн и обычно компенсируем любые задержки тем или иным способом, порядок фильтрации как таковой обычно не имеет значения. Однако порядок также определяет максимальную крутизну спада фильтра в частотной области. Чем выше порядок, тем круче спад между полосой пропускания и полосой задерживания.Для КИХ-фильтров ширина переходной полосы является более полезным понятием, чем спад. Полоса перехода с представляет собой разность частот между полосой пропускания и полосой задерживания и может быть вычислена из порядка для наиболее распространенных типов КИХ-фильтров. Чем выше порядок, тем уже полоса перехода. Обратите внимание, что нельзя напрямую сравнивать порядок фильтров БИХ и КИХ, поскольку они реализованы по-разному. Следует сравнить достаточно эффективную длительность импульсной характеристики. Существует также бесплатная полнотекстовая версия статьи, упомянутой Тариком, в которой представлены основные концепции: http: // home.uni-leipzig.de/~biocog/eprints/widmann_a2015jneuroscimeth350_34.pdf Надеюсь это поможет! Лучший, Андреас > Am 12.06.2017 um 08:34 schrieb Jaleh Mohammad alipoor: > > привет. > Я отфильтровал свои данные в диапазоне от 1 до 45 Гц, но мой профессор считает, что я должен применить порядок фильтрации к данным. Чудо, порядок фильтров - это вещь, связанная с шкалой времени, а фильтрация связана с частотой. как они связаны друг с другом? и как мы можем решить, какой порядок фильтрации подходит? что именно делает порядок фильтрации ?? > Я буду признателен за любую помощь (особенно в деталях!).> > большое спасибо > Жалех > _______________________________________________ > Страница Eeglablist: http://sccn.ucsd.edu/eeglab/eeglabmail.html > Чтобы отказаться от подписки, отправьте пустое письмо по адресу eeglablist-unsubscribe на sccn.ucsd.edu > Для режима дайджеста отправьте электронное письмо с темой "set digest mime" в eeglablist-request на sccn.ucsd.edu
Дополнительная информация о eeglablist список рассылки
Что такое фильтр 4-го порядка? — MVOrganizing
Что такое фильтр 4-го порядка?
Фильтр нижних частот четвертого порядка состоит из двух каскадных секций фильтра нижних частот второго порядка.Нет ограничений на порядок фильтра, который может быть сформирован; Чем больше порядок фильтра, тем больше его размер.
Какой порядок фильтров?
Максимальная задержка в выборках, используемая при создании каждой выходной выборки, называется порядком фильтра. В представлении разностного уравнения порядок больше и в уравнении (5.1). Например, указывает конкретный фильтр второго порядка.
В чем разница между фильтрами первого и второго порядка?
Основное различие между фильтром нижних частот 1-го и 2-го порядка состоит в том, что спад полосы заграждения будет в два раза больше, чем у фильтров 1-го порядка.➢ В конфигурации фильтра нижних частот второго порядка и конфигурации фильтра верхних частот второго порядка изменилось только положение резисторов и конденсаторов.
Как найти 3 дБ?
Частоту среза или точку -3 дБ можно найти по стандартной формуле ƒc = 1 / (2πRC). Фазовый угол выходного сигнала при ƒc и -45o для фильтра низких частот.
Что такое частота среза фильтра низких частот?
Частота среза фильтра нижних частот — это та частота, при которой выходное напряжение (нагрузочное) равно 70.7% от входного (исходного) напряжения. Выше частоты среза выходное напряжение ниже 70,7% входного, и наоборот.
Почему мы используем фильтр нижних частот?
Фильтры нижних частот используются для фильтрации шума в цепи. При прохождении через фильтр нижних частот большая часть шума удаляется, и получается чистый звук. • Фильтры нижних частот также используются в различных аудиоприложениях и иногда называются. фильтры высоких или высоких частот.
Как мне узнать, есть ли у меня высокий или низкий проход?
Ключевое различие между фильтром высоких частот и фильтром низких частот заключается в том, что схема фильтра высоких частот пропускает сигналы с частотой выше, чем частота среза, в то время как фильтр низких частот пропускает сигналы с частотой ниже, чем частота среза.
Как сделать фильтр низких частот для сабвуфера?
Усиление первой ступени можно отрегулировать с помощью POT R3. Выход первой ступени соединен с входом второй ступени через сеть фильтров, состоящую из компонентов R5, R6, R7, R8, C4 и C5. Второй операционный усилитель (IC1b) служит буфером, а отфильтрованный выход доступен на выводе 7 TLC062.
Как сделать фильтр нижних частот первого порядка?
Активный фильтр нижних частот первого порядка, инвертированная конфигурация Инвертирующий фильтр нижних частот разработан с использованием IC741, операционного усилителя с 8-контактной конфигурацией.В инвертирующем режиме выходной сигнал операционного усилителя сдвинут по фазе на 180 градусов с входным сигналом. Первоначально операционный усилитель должен быть запитан постоянным током.
Где используется LPF?
Активные фильтры нижних частот применяются в усилителях звука, эквалайзерах или акустических системах для направления низкочастотных басовых сигналов на большие басовые динамики или для уменьшения высокочастотного шума или искажения типа «шипение».
Поиск, просмотр и печать заказов · Справочный центр Shopify
Эта страница была напечатана 31 октября 2021 г.Чтобы посмотреть текущую версию, посетите https://help.shopify.com/en/manual/orders/search-view-print-orders.
По умолчанию все ваши заказы отображаются на странице Заказы . Вы можете настроить представления заказов или создать новые представления, которые включают фильтры, сортировку и расположение столбцов, которые помогут вам быстро получить доступ к группам заказов и расставить приоритеты в будущем.
Просмотр деталей из списка заказов
Когда вы наводите курсор на части списка заказов, вы можете быстро просмотреть детали заказа во всплывающих окнах.
Всплывающие окна доступны для следующих столбцов:
Например, вы можете щелкнуть имя клиента для получения такой информации, как местонахождение клиента, количество заказов и контактная информация.
Значки рядом с номерами заказов также предоставляют дополнительную информацию. Например, вы можете определить, есть ли примечания или комментарии к заказу или существует ли высокий риск мошенничества с заказом. Наведите курсор на значок, чтобы открыть всплывающее окно.
Порядок просмотров
Представления заказов создаются с сохраненными фильтрами, выбором столбцов, порядком столбцов и порядком сортировки.Представления заказов отображаются в виде вкладок в верхней части страницы Заказы . Вы можете настроить представления порядка, а также создавать, переименовывать или удалять представления. Если вы создаете новое представление заказа, оно добавляется в виде новой вкладки на странице Заказы .
Следующие ракурсы заказа являются ракурсами по умолчанию:
- Все
- Не выполнено
- Неоплаченный
- Закрыто
- Открыть
- Местная доставка также отображается, если для вашего магазина включена функция «Местоположение».
В любом ракурсе заказа, кроме Все , вы можете внести следующие изменения и сохранить их в текущем ракурсе или сохранить их как новый вид:
- выбрать фильтры
- показать или скрыть столбцы
- изменить порядок столбцов
- выберите критерии сортировки и порядок сортировки
- фильтр с настраиваемым условием поиска
- переименовать представление
- удалить представление
Хотя вы не можете изменить или удалить представление Все , вы можете создать новое представление, основанное на представлении Все .
Заказы, отображаемые в сохраненных представлениях, обновляются автоматически. Например, если вы сохранили фильтр для оплаченных заказов , то все оплаченные заказы автоматически добавляются в этот просмотр заказов.
Сохранить изменения в текущем ракурсе заказа
Вы можете сохранить изменения в любом представлении, кроме представления Все .
Примечание
Вы можете сохранять изменения в просмотрах заказов только с помощью администратора Shopify на настольном компьютере.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
Измените фильтры, столбцы или порядок сортировки.
-
Нажмите Сохранить .
Создание нового ракурса заказа
Вы создаете новые ракурсы заказа на основе существующих ракурсов заказа.
Вы можете изменить фильтры, столбцы и порядок сортировки до или после сохранения в новом представлении.
Примечание
Вы можете сохранять изменения в просмотрах заказов только с помощью администратора Shopify на настольном компьютере.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
В любом ракурсе заказа щелкните … , а затем выполните одно из следующих действий:
- Чтобы создать новый ракурс заказа на основе текущего ракурса, нажмите Сохранить как .
- Чтобы создать новый ракурс заказа на основе ракурса Все , щелкните Создать ракурс .
- Введите имя представления и щелкните Сохранить представление или Создать представление .
Удалить ракурс заказа
Вы не можете удалить представление заказа All , но можете удалить любые другие представления, которые вы не используете.
Если вы удалите представление по умолчанию и позже решите, что оно вам нужно, вы можете воссоздать его так же, как и любое новое представление. Для получения информации о настройках см. Настройки по умолчанию для представлений заказов.
Примечание
Вы можете сохранять изменения в просмотрах заказов только с помощью администратора Shopify на настольном компьютере.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
Щелкните вкладку просмотра заказа, которую вы хотите удалить.
-
Щелкните … , затем щелкните Удалить представление .
-
Чтобы подтвердить удаление, нажмите Удалить представление .
Фильтрация заказов
Из своего администратора Shopify вы можете использовать различные типы фильтров, чтобы изменять отображаемые заказы и выполнять массовые действия с несколькими заказами. Вы также можете фильтровать свои заказы с помощью настраиваемого поиска. Чтобы повторно использовать фильтры или комбинации фильтров, сохраните их как представления порядка.
С фильтрами заказов можно делать следующее:
Отфильтруйте заказы
Фильтры определяют, какие заказы отображаются в ракурсе заказов. Например, представление Все не имеет фильтров. По умолчанию в представлении Unfulfilled используется фильтр Fullfillment status со значением невыполнено, чтобы показать вам все невыполненные заказы вашего магазина.
При выборе фильтров их также можно комбинировать для просмотра заказов, соответствующих нескольким критериям.Например, вы можете комбинировать фильтры с низким уровнем риска, и , без оплаты, , чтобы просмотреть список заказов вашего магазина, которые являются одновременно неоплаченными и с низким уровнем риска.
Вы можете использовать следующие фильтры в вашем списке заказов:
- Способ доставки : местная доставка, местный самовывоз, доставка клиенту
- Статус : открыто, в архиве, отменено
- Статус платежа : санкционировано, оплачено, частично оплачено, частично возвращено, ожидает рассмотрения, возвращено, неоплачено, аннулировано
- Статус выполнения : выполнено, невыполнено, частично выполнено, запланировано, приостановлено
- Статус возврата : выполняется возврат, возвращен
- Tagged with : фильтровать по тегу индивидуального заказа
- Канал продаж : фильтр по активированным каналам продаж
- Статус отзыва и запроса : открыт, отправлен, выиграл, проиграл, любой
- Уровень риска : высокий, средний, низкий
- Дата : на последней неделе, в прошлом месяце, в последние 3 месяца, в прошлом году или по выбору
- Кредитная карта : последние 4 цифры кредитной карты
Примечание
Вы можете сохранять изменения в просмотрах заказов только с помощью администратора Shopify на настольном компьютере.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
В любом ракурсе заказа щелкните Фильтры .
-
Щелкните Выберите фильтр и выберите фильтр.
-
Щелкните Выберите значение и выберите или введите значение.
-
Чтобы добавить еще один фильтр, щелкните Добавить фильтр .
-
Необязательно: Сохраните изменения в представлении или сохраните изменения как новое представление.
-
В приложении Shopify перейдите к Заказы > Все заказы .
-
Коснитесь значка фильтра.
-
На экране Filters нажмите, чтобы выбрать каждый фильтр, который вы хотите добавить.
-
Чтобы удалить все фильтры с экрана «Фильтры», нажмите
xрядом с именем фильтра.
-
В приложении Shopify перейдите к Заказы > Все заказы .
-
Коснитесь значка фильтра.
-
На экране Filters нажмите, чтобы выбрать фильтры, которые вы хотите добавить.
-
Чтобы удалить все фильтры с экрана «Фильтры», нажмите
xрядом с именем фильтра.
Фильтрация заказов с использованием пользовательских терминов
Вы можете использовать строку поиска, чтобы отфильтровать свои заказы по индивидуальному запросу. Пользовательский термин может использоваться как фильтр сам по себе или в сочетании с фильтрами в существующих категориях.Например, вы можете фильтровать свои заказы, выполнив поиск по имени клиента, названию продукта, артикулу, номеру заказа или стране.
Если вы планируете повторно использовать настраиваемый поисковый запрос отдельно или в сочетании с другими фильтрами, сохраните его в представлении.
Примечание
Вы можете сохранять изменения в просмотрах заказов только с помощью администратора Shopify на настольном компьютере.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
В строке поиска Фильтр заказов введите пользовательский термин как
имя: значение. -
Необязательно: Сохраните изменения в представлении или сохраните изменения как новое представление.
-
В приложении Shopify перейдите к Заказы > Все заказы .
-
В строке поиска Фильтр заказов введите пользовательский термин как
имя: значение.
-
В приложении Shopify перейдите к Заказы > Все заказы .
-
В строке поиска Фильтр заказов введите пользовательский термин как
имя: значение.
Подсказка
Чтобы узнать о различных настраиваемых терминах, которые можно использовать, см. Поддерживаемые параметры фильтра .
Для дальнейшего уточнения результатов можно использовать операторы структурированного поиска. Чтобы узнать о различных операторах, которые можно использовать, обратитесь к синтаксису поиска .
Сохранить фильтры порядка в представлениях
См. Сохранение изменений в текущем представлении или Создание нового представления.
Фильтрация заказов по их местонахождению
Если у вашего магазина несколько адресов, вы можете отфильтровать заказы по местоположению.Местоположение устанавливается отдельно от других фильтров, которые вы можете сохранить в представлениях заказов. Когда вы меняете местоположение, новое местоположение применяется ко всем вашим представлениям.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
Щелкните переключатель местоположения в правом верхнем углу страницы.
-
Выберите подходящее место.
-
В приложении Shopify перейдите к Заказы > Все заказы .
-
Коснитесь переключателя местоположения.
-
Выберите подходящее место.
-
В приложении Shopify перейдите к Заказы > Все заказы .
-
Коснитесь переключателя местоположения.
-
Выберите подходящее место.
Показать, скрыть и изменить порядок столбцов
Чтобы оптимизировать каждый из просмотров вашего заказа, вы можете отображать, скрывать и переупорядочивать столбцы.Единственный столбец, который нельзя переупорядочить, — это Порядок, который всегда стоит первым.
Примечание
Вы можете сохранять изменения в просмотрах заказов только с помощью администратора Shopify на настольном компьютере.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
Щелкните Столбцы .
-
Установите флажок для столбцов, чтобы их отображать, или снимите флажок для столбцов, чтобы скрыть их.
-
В списке Столбцы щелкните маркер элемента
⠿, а затем перетащите его вверх, чтобы переместить столбец влево, или вниз, чтобы переместить столбец вправо.По мере внесения изменений список заказов обновляется. -
Сохраните изменения в представлении или сохраните изменения как новое представление.
Использовать массовые действия с просмотром заказа или фильтром
В любом представлении заказов вы можете выбрать некоторые или все заказы и выполнить массовые действия с ними. Вы можете выполнять массовые действия в любом представлении заказа с сохранением или без сохранения фильтров. Однако, если вы часто выполняете массовые действия, сохранение фильтров в представлении заказа может помочь вам работать быстрее.
Например, вы можете захотеть быстро собрать средства для всех заказов, ожидающих оплаты. Вы можете использовать массовые действия, чтобы вам не приходилось открывать каждый ордер и вручную собирать средства.
Примечание
Вы можете выполнять массовые действия только с помощью администратора Shopify на настольном компьютере.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
Щелкните вид заказа.
-
Выберите элементы, которые нужно отредактировать.
-
Щелкните действие или щелкните Дополнительные действия , а затем выберите действие из списка.
-
Если появится запрос, подтвердите свой выбор.
Распечатать заказ
Возможно, вы захотите изготовить печатную копию заказа для ваших собственных записей или включить ее в коробку при отправке покупателю.
Примечание
Если вы хотите распечатать с мобильного устройства или использовать индивидуальные счета-фактуры или упаковочные листы, вы можете загрузить Order Printer из Shopify App Store.
Шагов:
-
От администратора Shopify перейдите к Заказы .
-
На странице Заказы щелкните номер заказа, который нужно распечатать.
-
Щелкните Печать > Страница заказа печати .
-
В окне параметров печати выберите свой принтер и настройки и щелкните Печать .
Настройки по умолчанию для ракурсов заказа
В следующей таблице приводится описание представлений порядка по умолчанию.Если вы удалите представление порядка по умолчанию, вы можете использовать это описание, чтобы помочь вам воссоздать представление.
| Просмотр имени | Имя и значение фильтра | Колонны |
|---|---|---|
| Не выполнено |
|
|
| Без оплаты |
|
|
| Открыть |
|
|
| Закрыт |
|
|
| Доставка на месте |
|

