Что такое таблица истинности в логике. Как построить таблицу истинности для логической функции. Какие правила нужно соблюдать при составлении таблицы истинности. Для чего используются таблицы истинности в математике и информатике.
Что такое таблица истинности и для чего она используется
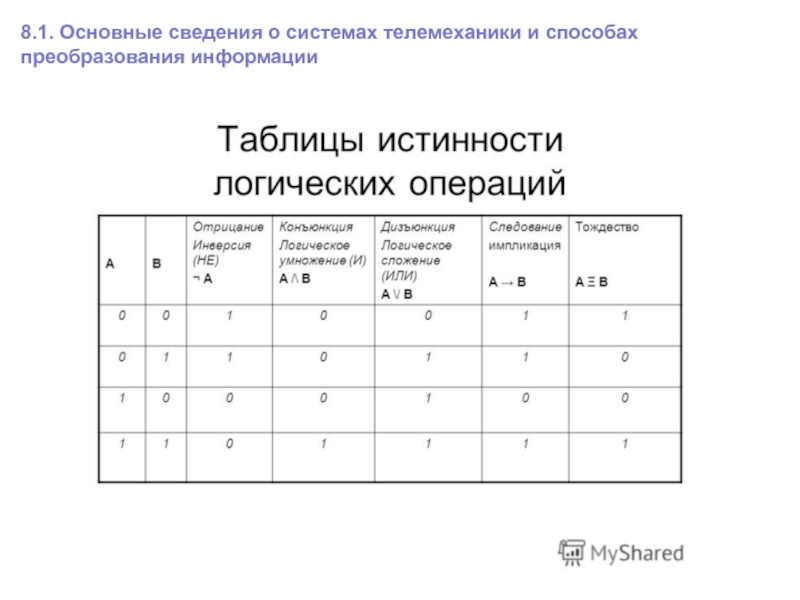
Таблица истинности — это математический инструмент, используемый в логике для определения истинности сложных логических выражений. Она наглядно показывает, какие значения (истина или ложь) принимает логическая функция при всех возможных комбинациях значений входящих в нее переменных.
Основные цели использования таблиц истинности:
- Проверка эквивалентности логических выражений
- Упрощение сложных логических функций
- Анализ работы логических схем
- Проектирование цифровых устройств
- Решение логических задач
Принципы построения таблиц истинности
При составлении таблицы истинности необходимо соблюдать следующие правила:
- Число строк таблицы равно 2^n, где n — количество переменных в функции
- Количество столбцов = число переменных + число логических операций
- В левой части таблицы записываются все возможные комбинации значений переменных
- В правой части вычисляются значения промежуточных операций и итоговой функции
Порядок построения таблицы истинности
1. Определить количество строк и столбцов таблицы
2. Заполнить заголовки столбцов переменными и операциями
3. Записать все комбинации значений переменных
4. Вычислить значения промежуточных операций
5. Определить итоговое значение функции для каждой строки
Примеры построения таблиц истинности
Пример 1: Функция двух переменных
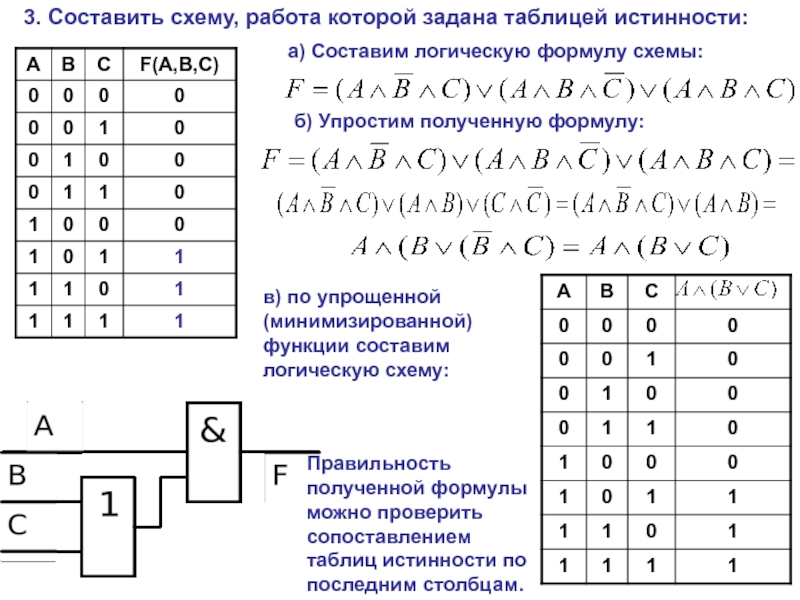
Построим таблицу истинности для функции F = A ∧ B (конъюнкция)
| A | B | F = A ∧ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Пример 2: Функция трех переменных
Составим таблицу истинности для функции F = (A ∨ B) ∧ ¬C
| A | B | C | A ∨ B | ¬C | F = (A ∨ B) ∧ ¬C |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Применение таблиц истинности в информатике и программировании
Таблицы истинности широко используются в информатике и программировании для следующих целей:
- Проектирование и анализ логических схем компьютеров
- Оптимизация булевых выражений в программном коде
- Разработка алгоритмов для решения логических задач
- Тестирование условных конструкций в программах
- Реализация логических операций в базах данных
Связь таблиц истинности с другими разделами математической логики
Таблицы истинности тесно связаны с другими концепциями математической логики:
- Булева алгебра — таблицы истинности используются для описания булевых функций
- Логические схемы — на основе таблиц истинности строятся схемы из логических элементов
- Карты Карно — графическое представление таблиц истинности для минимизации функций
- Логическое программирование — таблицы истинности применяются при разработке экспертных систем
Методы упрощения логических выражений с помощью таблиц истинности
Таблицы истинности позволяют упрощать сложные логические выражения:
- Построить таблицу истинности для исходного выражения
- Найти более простое выражение с такой же таблицей истинности
- Использовать законы булевой алгебры для преобразования выражения
- Применить метод карт Карно для минимизации функции
Упрощение логических выражений позволяет оптимизировать логические схемы и программный код.
Решение логических задач с использованием таблиц истинности
Таблицы истинности — эффективный инструмент для решения логических задач:
- Формализовать условие задачи в виде логического выражения
- Построить таблицу истинности для этого выражения
- Проанализировать полученную таблицу и сделать выводы
- При необходимости упростить выражение
Этот метод позволяет решать сложные логические головоломки и задачи на рассуждения.
Особенности построения таблиц истинности для сложных логических функций
При работе со сложными функциями необходимо учитывать следующие особенности:
- Число строк растет экспоненциально с увеличением количества переменных
- Важно правильно определить порядок выполнения операций
- Промежуточные вычисления лучше выполнять в отдельных столбцах
- Для больших таблиц удобно использовать компьютерные программы
- Сложные функции часто можно разбить на более простые подфункции
Таблицы истинности в преподавании математической логики
Таблицы истинности — важный инструмент в обучении основам математической логики:
- Наглядно демонстрируют работу логических операций
- Помогают понять принципы булевой алгебры
- Развивают навыки формализации логических рассуждений
- Позволяют практиковаться в решении логических задач
- Формируют базу для изучения более сложных разделов логики
Их изучение закладывает фундамент логического мышления, необходимого в математике, информатике и других науках.
Принципы построения таблиц истинности
Оглавление
Время чтения: 5 минут
535
Логическая функция одно из основополагающих понятий математической логики. Она зависит от логических переменных и принимает значения из множества, от которого находится в зависимости. Логические функции булевых переменных могут принимать только два значения – 1 или 0.
Понятие таблиц истинности
Задаваться логическая функция может числовым способом, словесным описанием, картами Карно, аналитическим выражением и с помощью таблиц истинности. В последнем случае все аргументы функции следует записать в левой части таблицы, а значения, которые им соответствуют, в правой.
Определения 1 — 2
Таблица истинности – это таблица, просто и наглядно показывающая, какие значения будут у логического выражения при всевозможных наборах переменных функции.
Равносильными именуют те логические выражения с совпадающими последними столбцами таблицы истинности.
Обозначают равносильные функции знаком «=».
Правила того, как следует проводить построение таблицы истинности
Несоблюдение хотя бы одного из них ведёт к очень грубой ошибке. Вот эти правила:
- Число строк таблицы должно совпадать с числом комбинаций всевозможных n логических переменных, то есть быть равным 2n;
- Количество столбцов таблицы должно равняться сумме числа логических переменных и числа логических операций;
- В построенный шаблон таблицы истинности должны вписываться все значения исходных переменных;
- Построение таблицы истинности выражения происходит по её столбцам, при этом обязательно учитываются правила логических операций.
Порядок действий при построении таблицы истинности для логических выражений
Порядок действий при построении таблицы истинности, какой бы ни была логическая функция, следующий:
- Определить, какое число строк и столбцов будет в будущей таблице. Делается подобное по формулам
X = n + m, Y = 2n+1.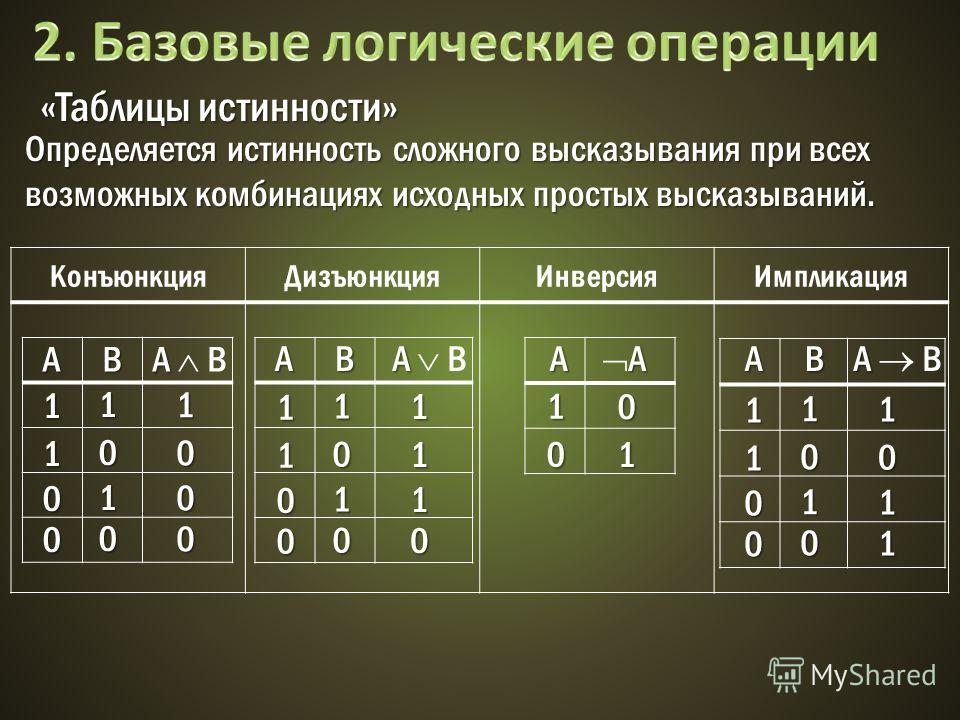
Где n – число переменных, m – чило логических операций. - Заполнить самую верхнюю строку таблицы переменными и логическими операциями, идя слева направо. При этом приоритетность логических операций следует учитывать обязательно, иначе получится совсем не то, что нужно;
- В первых столбцах перечислить всевозможные комбинации входных значений;
- Выполняя заданные логические операции, заполнить все оставшиеся ячейки;
Ответом следует считать последний заполненный столбец таблицы.
О порядке логических операций
Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.
После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.
Далее приведём несколько поучительных задач на построение таблиц истинности
Задачи 1 — 3
Сделать построение таблицы истинности для функции ((A→B) ∧ A) ↔ B
Решение:
- Определяем сколько будет у нас столбцов.
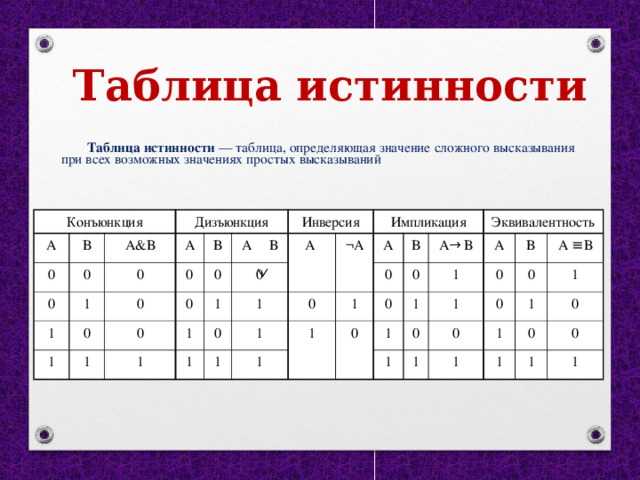
- Определяем, сколько будет у на строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2n+1 = 22 + 1= 5;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В двух первых столбцах записываем возможные значения переменных;
- В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
- В самом последнем из столбцов записываем итоговые значения функции.
- Определяем сколько будет у нас столбцов.
В результате всего этого у нас должно получиться:
Провести построение таблицы истинности функции (A ∨ B) ∧ – C
Решение:
- Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3. 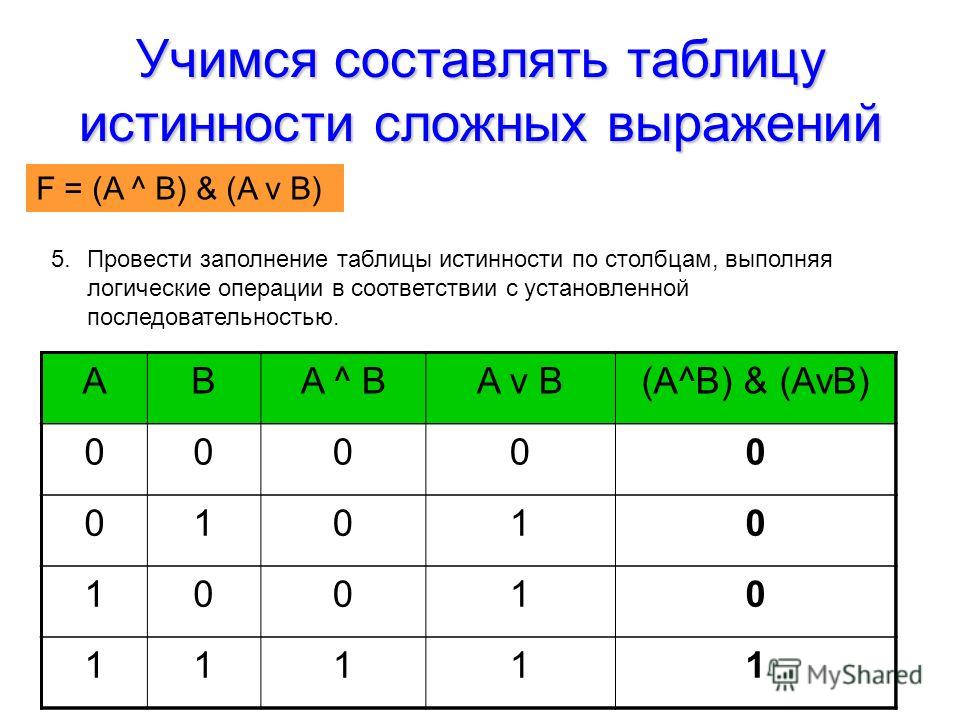Складываем то и другое: 3+3 = 5.
- Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 23 + 1= 9;
Складываем то и другое: 3+3 = 5.- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В два первые столбца вносим возможные значения наших переменных;
- В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
- В последнем столбце записываем итоговые значения функции.
В итоге получим таблицу:
Сделать таблицу истинности для
(A ∧ B ↔ B ∧ C) ∨ (C → A)
Функция посложнее и таблица получится значительно больше, чем предыдущая.
- Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
- Считаем строки. Их количество будет 23+1= 9;
- Заполняем первую строку таблицы;
- В первых столбцах записываем все допустимые значения наших переменных;
- В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
- В последний столбец пишем итоговые значения данной нам функции.
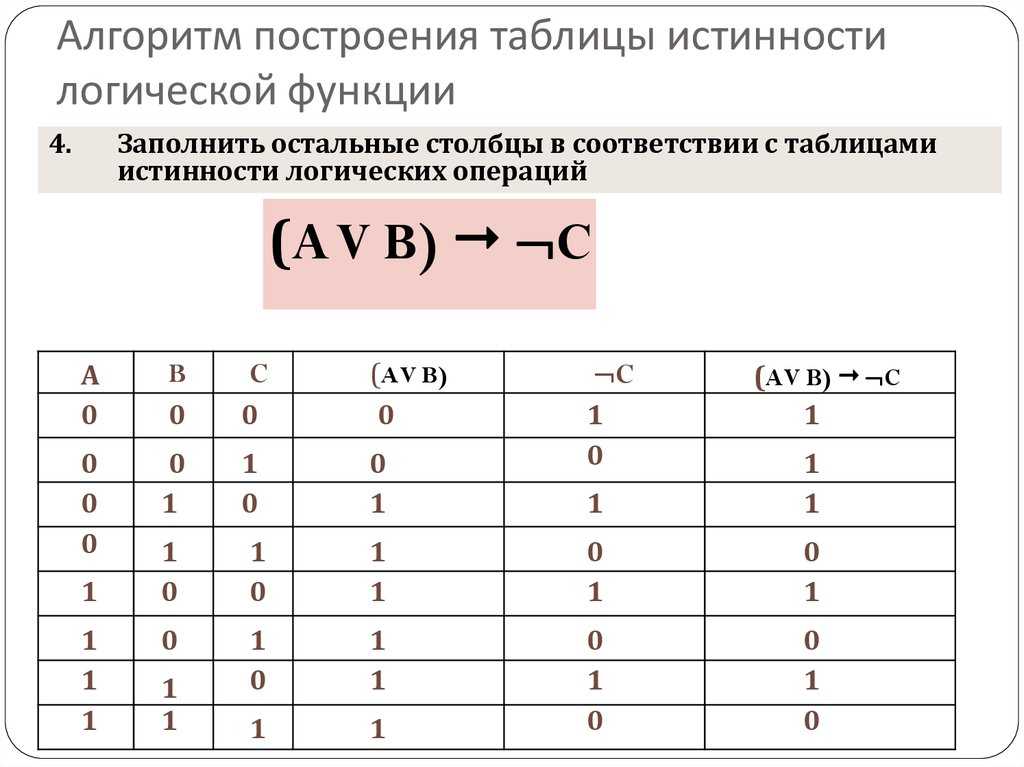
В итоге у нас получается таблица:
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Построения функции, если известна её таблица истинности
Совершенной дизъюнктивной нормальной формой считают такую нормальную форму, в которой отсутствуют одинаковые элементарные конъюкции и все конъюкции включают один и тот же набор переменных, куда каждая из них входит не более одного раза.
Алгоритм действий для получения СДНФ по таблице истинности:
- Отметьте в таблице строки, в которых значение функции равняется 1
- Выпишете для каждой отмеченной строки конъюкцию всех переменных. Если переменная равна 1, в конъюкцию следует включить саму эту переменную. Если переменная равняется 0, то её отрицание;
- Все полученные конъюкции свяжите в дизъюкцию.
Аналогичным образом определяется СКНФ
В строках, в последнем столбце которых функция равна 0, запишите дизъюкции всех переменных.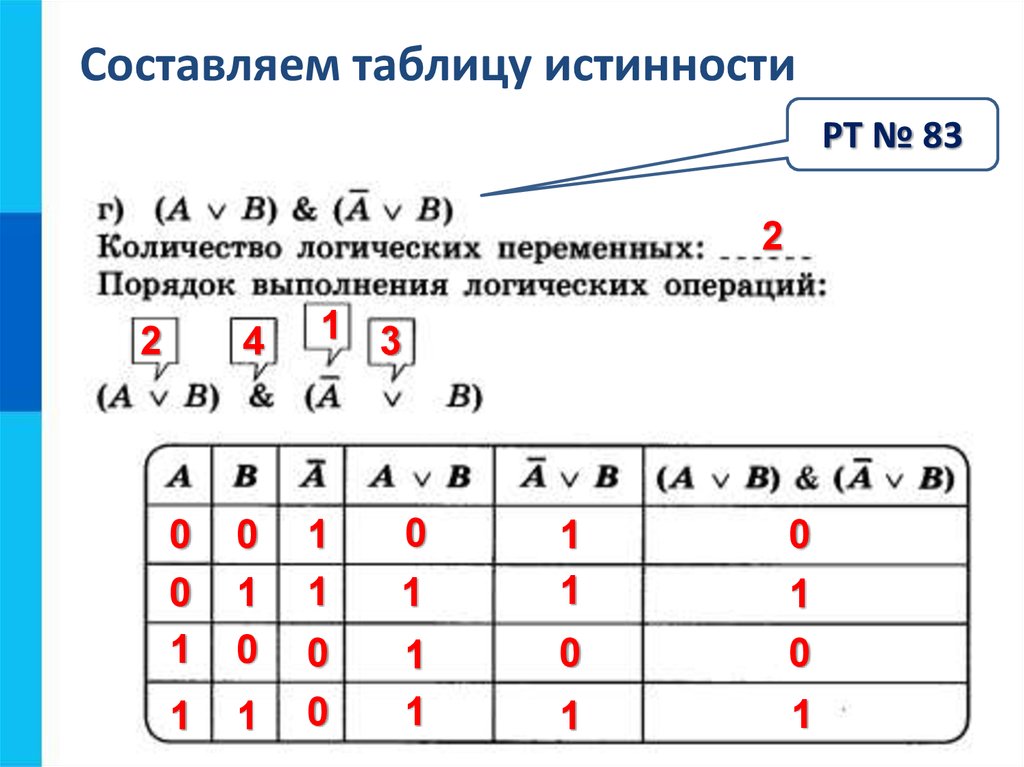
Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.
Правило + задача
СДНФ всегда равно СКНФ. СДНФ = СКНФ.
Дана таблица истинности:
Выделяем в ней цветом строку
Заполняем столбцы с СДНФ и с СКНФ
Записываем СДНФ
СДНФ = A & B
Записываем СКНФ
СКНФ = (A ∨ B) & (A ∨ B) & (A ∨ B)
Оценить статью (79 оценок):
Поделиться
Жанна Ивановна Конева — Магистр прикладной информатики
Популярные статьи
Выполнение любых работ по информатике
Page not found — Сайт skobelevserg!
- Главная
- Информатика
- Практикумы
- Подготовка к ОГЭ
- Рабочие программы
- Используемая литература
- Об авторах
Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.
- Главная
- Информатика
- 5 класс (ФГОС)
- Информация вокруг нас
- Компьютер — универсальная машина для работы с информацией
- Ввод информации в память компьютера
- Управление компьютером
- Хранение информации
- Передача информации
- Кодирование информации
- Текстовая информация
- Представление информации в виде таблиц
- Наглядные формы представления информации
- Компьютерная графика
- Обработка информации
- 6 класс (ФГОС)
- Объекты окружающего мира
- Компьютерные объекты
- Отношения объектов и их множеств
- Разновидности объектов и их классификация
- Системы объектов
- Персональный компьютер как система
- Как мы познаем окружающий мир
- Понятие как форма мышления
- Информационное моделирование
- Знаковые информационные модели
- Табличные информационные объекты
- Графики и диаграммы
- Схемы
- Что такое алгоритм
- Исполнители вокруг нас
- Формы записи алгоритмов
- Типы алгоритмов
- Управление исполнителем Чертежник
- Компьютерный практикум
- 7 класс (ФГОС)
- Информация и информационные процессы
- Компьютер универсальное устройство для работы с информацией
- Обработка графической информации
- Обработка текстовой информации
- Технология мультимедиа
- 8 класс (ФГОС)
- Математические основы информатики
- Основы алгоритмизации
- Начала программирования
- 9 класс (ФГОС)
- Моделирование и формализация
- Алгоритмизация и программирование
- Обработка числовой информации в электронных таблицах
- Коммуникационные технологии
- 10 класс (ФГОС)
- Информация и информационные процессы
- Компьютер и его программное обеспечение
- Представление информации в компьютере
- Элементы теории множеств и алгебры логики
- Современные технологии создания и обработки информационных объектов
- 11 класс (ФГОС)
- Обработка информации в электронных таблицах
- Алгоритмы и элементы программирования
- Информационное моделирование
- Сетевые информационные технологии
- Основы социальной информатики
- Практикумы
- Google формы
- Основы работы в Microsoft PowerPoint
- Создание анимации в презентациях
- Основы работы в Microsoft Word
- Основы работы в Microsoft Excel
- Создание простейшей базы данных
- Практикум по MS Excel
- Подготовка к ОГЭ
- Рабочие программы
- Используемая литература
- Об авторах
- Блоги
- Сайты
1.
3: Таблицы истинности и значение «~», «&» и «v»- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1657
Мы сказали, что «~А» означает не А, «А&В» означает А и В, а «АвВ» означает А или В во всеобъемлющем смысле. Это должно дать вам довольно хорошее представление о том, что означают связки «~», «&» и «v». Но логики должны быть максимально точными. Поэтому нам нужно уточнить, как мы должны понимать связки еще точнее. Более того, метод, который мы будем использовать для этого, окажется очень полезным для многих других вещей.
Чтобы получить представление, начнем с очень простого случая знака отрицания, ‘~’. Предложение «А» либо истинно, либо ложно.
Если «А» истинно, то «~А» ложно. Если «А» ложно, то «~А» истинно. И это все, что вам нужно знать о значении «~». Мы можем выразить это более кратко с помощью таблицы, называемой таблицей истинности :
Определение таблицы истинности ‘~’
| Чемодан | А | ~А |
| 1 | т | ф |
| 2 | ф | т |
В столбце под «А» перечислены все возможные случаи истинности и ложности «А». Мы делаем это, описывая случаи в терминах того, что мы называем истинными ценностями . Случай, в котором A истинно, описывается утверждением, что A имеет истинностное значение t. Случай, в котором A ложно, описывается утверждением, что A имеет истинностное значение f. Поскольку А может быть только истинным или ложным, у нас есть только эти два случая.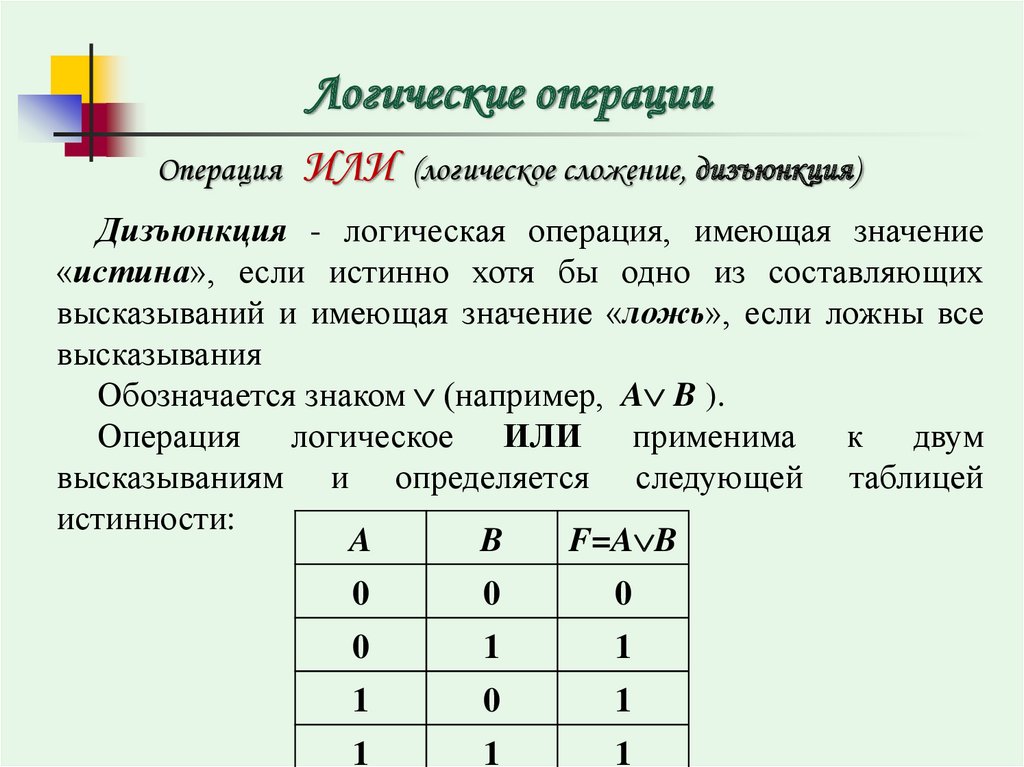
Мы объясняем, как понимать «~», говоря, каково истинное значение «~ A» в каждом случае. В случае 1 ‘~A’ имеет истинностное значение f; то есть ложно. В случае 2 ‘~A’ имеет истинностное значение t; то есть это правда. Хотя то, что мы сделали, кажется тривиальным в этом простом случае, очень скоро вы увидите, что таблицы истинности чрезвычайно полезны.
Давайте посмотрим, как использовать таблицы истинности для объяснения ‘&’. Союз состоит из двух атомарных предложений, поэтому нам нужно рассмотреть четыре случая:
| Чемодан | А | Б | АиБ |
| 1 | т | т | |
| 2 | т | ф | |
| 3 | ф | т | |
| 4 | ф | ф |
Когда «А» истинно, «В» может быть истинным или ложным.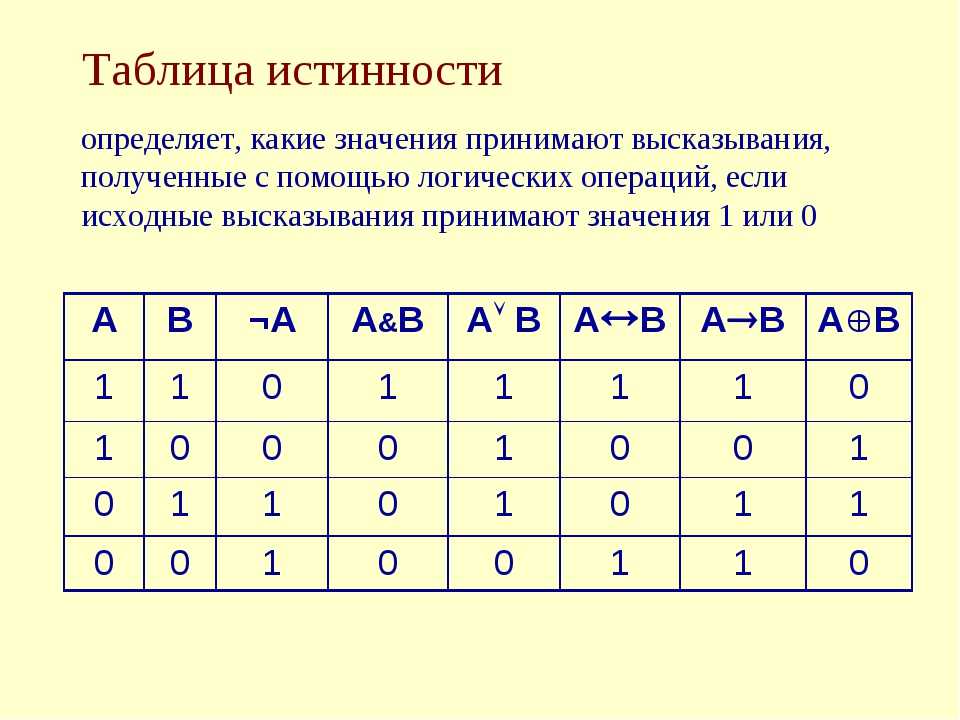
Когда «А» ложно, снова «В» может быть истинным или ложным. Приведенная выше таблица истинности дает все возможные комбинации значений истинности, которые могут иметь вместе «А» и «В».
Теперь мы уточняем, как следует понимать ‘&’, указав значение истинности для каждого случая для составного ‘A&B’:
Определение таблицы истинности ‘&’
| Чемодан | А | Б | АиБ |
| 1 | т | т | т |
| 2 | т | ф | ф |
| 3 | ф | т | ф |
| 4 | ф | ф | ф |
Другими словами, «А и В» истинны, когда истинны конъюнкты «А» и «В».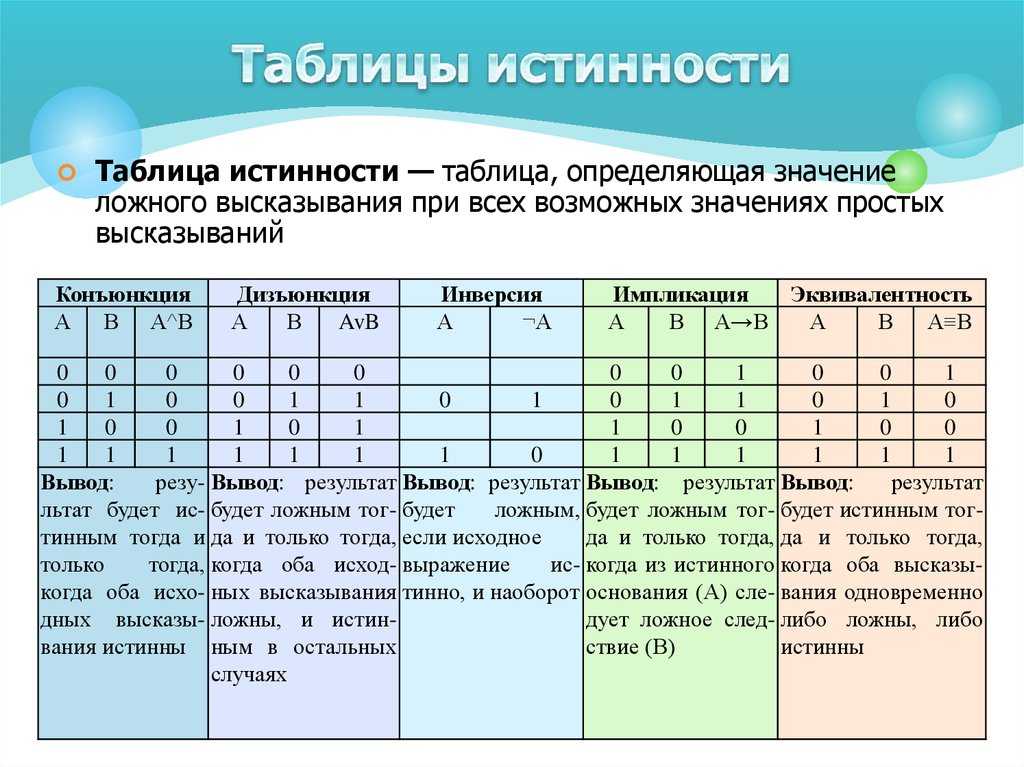
«А и В» ложны во всех остальных случаях, то есть когда один или оба конъюнкта ложны.
Несколько слов о порядке, в котором я перечислил дела. Если вам интересно, вы можете попробовать угадать рецепт, по которому я заказывала ящики. (Если вы попытаетесь, взгляните также на более сложный пример в разделе 1.5.) Но я не буду останавливаться на объяснениях, потому что все, что важно в порядке, это то, что мы не пропускаем ни одного случая, и все мы перечисляем их. в том же порядке, чтобы мы могли легко сравнить ответы. Так что просто перечислите случаи, как я.
Мы следуем тому же методу, определяя, как понимать «V». Дизъюнкция «AvB» истинна, когда истинны одна или обе дизъюнкции «А» и «В». «AvB» ложно только тогда, когда «A» и «B» оба ложны:
определение таблицы истинности ‘v’
| Чемодан | А | Б | АвБ |
| 1 | т | т | т |
| 2 | т | ф | т |
| 3 | ф | т | т |
| 4 | ф | ф | ф |
Мы определили связки ‘~’, ‘&’ и t’, используя таблицы истинности для специального случая букв предложения ‘A’ и ‘B’.
Но, очевидно, ничего не изменится, если мы будем использовать какую-то другую пару предложений, например «H» и «D».
В этом разделе основное внимание уделяется определениям таблицы истинности ‘~’, ‘&’ и ‘v’. Но попутно я ввел два вспомогательных понятия, с которыми вам нужно быть очень ясными. Во-первых, на Значение истинности Назначение значений истинности с по Буквы предложения , я имею в виду, грубо говоря, строку таблицы истинности, а Таблица истинности представляет собой список всех возможных назначений значений истинности для букв предложения в предложении:
Присвоение значений истинности набору атомарных букв предложений является спецификацией для каждой из букв предложения, следует ли считать букву (для этого присвоения) истинной или ложной. Слово Случай также будет использоваться для «присвоения значений истинности».
Таблица истинности для предложения — это спецификация всех возможных присвоений значений истинности буквам предложения, которые встречаются в предложении, и описание значения истинности предложения для каждого из этих назначений.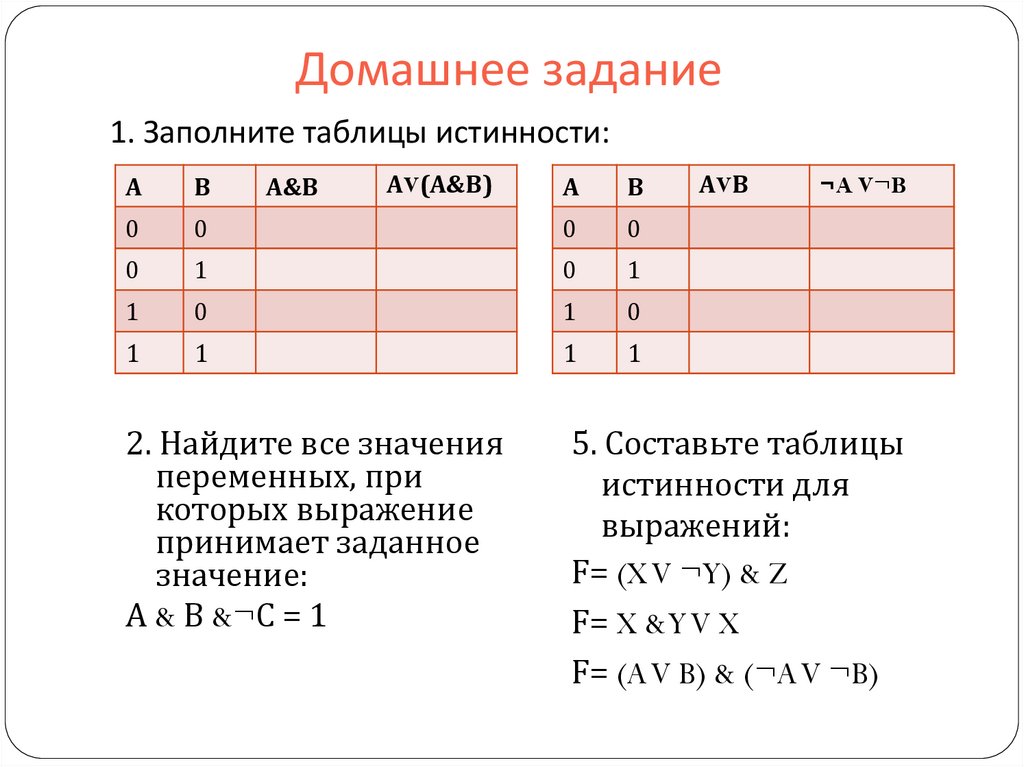
Пол Теллер (Калифорнийский университет в Дэвисе). Букварь был опубликован в 1989 году издательством Prentice Hall, после чего его приобрела компания Pearson Education. Компания Pearson Education разрешила прекратить выпуск учебника для начинающих и вернула авторские права профессору Теллеру, который с радостью сделает его бесплатным для использования в учебных и образовательных целях.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Теги
Таблица истинности | логика | Британика
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- В этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Компаньоны
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы. - Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
