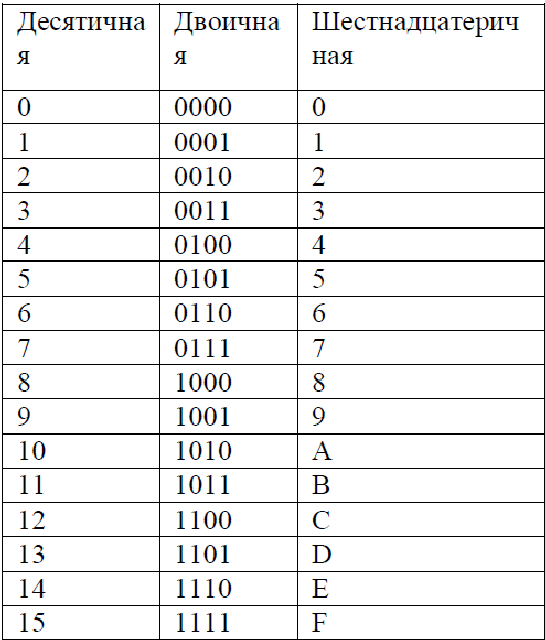
Что такое двоично-десятичная система счисления. Как она устроена. Каковы ее основные преимущества. Где применяется двоично-десятичная система счисления. Как выполняются арифметические операции в этой системе.
Основные принципы двоично-десятичной системы счисления
Двоично-десятичная система счисления (ДДС) представляет собой гибридную систему, сочетающую элементы двоичной и десятичной систем. Ее ключевые особенности:
- Каждая десятичная цифра от 0 до 9 кодируется четырьмя двоичными разрядами
- Используются только коды от 0000 до 1001, остальные комбинации (1010-1111) не применяются
- Числа записываются и обрабатываются поразрядно, как в десятичной системе
- Арифметические операции выполняются над 4-битными группами
Как это работает. Рассмотрим представление числа 394 в двоично-десятичном коде:
3 = 0011
9 = 1001
4 = 0100
Таким образом, число 394 в ДДС будет записано как 001110010100.
Преимущества двоично-десятичной системы счисления
Двоично-десятичная система имеет ряд важных преимуществ по сравнению с чисто двоичной или десятичной:
- Простота преобразования между десятичной и ДДС формами
- Отсутствие ошибок округления при представлении десятичных дробей
- Возможность выполнения арифметических операций с произвольной точностью
- Упрощение операций ввода-вывода в десятичном формате
Основной недостаток ДДС — большее количество разрядов для представления числа по сравнению с двоичной системой. Однако в ряде приложений преимущества ДДС перевешивают этот недостаток.
Области применения двоично-десятичной системы
Где чаще всего используется двоично-десятичная система счисления. Основные области применения:
- Финансовые и бухгалтерские приложения
- Калькуляторы и кассовые аппараты
- Системы с десятичным вводом-выводом данных
- Устройства точного измерения (электронные весы, счетчики и др.)
- Научные вычисления, требующие высокой точности
В этих областях важна безошибочность представления десятичных чисел и простота преобразования в привычный для человека формат.
Арифметические операции в двоично-десятичной системе
Как выполняются основные арифметические действия над числами в ДДС. Рассмотрим на примерах:

Сложение в двоично-десятичной системе
При сложении чисел в ДДС операция выполняется отдельно для каждой тетрады (4-битной группы). Если при сложении тетрад получается результат больше 9, производится коррекция:
0101 1000 (58)
+ 0111 0011 (73)
————
1 0100 1011
0110 0000 (коррекция)
————
1 0110 0001 (131)
Вычитание в двоично-десятичной системе
Вычитание также выполняется поразрядно. Если результат отрицательный, производится заем из старшего разряда:
1000 0101 (85)
————
0100 1110
0000 0110 (коррекция)
————
0100 1000 (48)
Преобразование между двоичной и двоично-десятичной системами
Как осуществляется перевод чисел между двоичной и двоично-десятичной системами счисления.
Из двоичной в ДДС
Алгоритм перевода:
- Разбить двоичное число на группы по 4 бита справа налево
- Если значение группы > 9, прибавить 6
- Повторять шаг 2, пока не будут обработаны все группы
Пример: 10110110 (двоичное) -> 1 0110 1100 (ДДС) = 9210
Из ДДС в двоичную
Обратное преобразование выполняется так:
- Разбить ДДС число на тетрады
- Если значение тетрады > 9, вычесть 3
- Объединить полученные двоичные группы
Пример: 1001 0010 (ДДС) -> 10010010 (двоичное) = 14610
Представление отрицательных чисел в ДДС
Как записываются отрицательные числа в двоично-десятичной системе счисления. Существует несколько способов:
- Знаковый разряд — добавление дополнительного бита для знака (0 — положительное, 1 — отрицательное)
- Дополнительный код — инвертирование цифр и добавление единицы
- Избыточный код — добавление фиксированного числа (например, 9) к каждой цифре
Пример представления числа -58 в ДДС со знаковым разрядом:
1 0101 1000
Здесь первый бит (1) указывает на отрицательное число, а остальные кодируют модуль числа 58.
Сравнение ДДС с другими системами счисления
Как двоично-десятичная система соотносится с чисто двоичной и десятичной системами счисления. Основные отличия:
| Характеристика | ДДС | Двоичная | Десятичная |
|---|---|---|---|
| Основание системы | 10 (в группах по 4 бита) | 2 | 10 |
| Количество цифр | 10 (0-9) | 2 (0-1) | 10 (0-9) |
| Эффективность хранения | Средняя | Высокая | Низкая |
| Простота преобразования в десятичную | Высокая | Низкая | Не требуется |
| Точность представления дробей | Высокая | Низкая | Высокая |
Реализация ДДС в цифровых устройствах
Как двоично-десятичная система реализуется в электронных схемах и микропроцессорах. Основные аспекты:

- Использование специализированных регистров для хранения ДДС чисел
- Применение корректирующих схем при выполнении арифметических операций
- Реализация операций сдвига и сравнения с учетом специфики ДДС
- Наличие аппаратных инструкций для работы с ДДС в некоторых процессорах
Например, многие микроконтроллеры имеют встроенные команды для преобразования между двоичным и ДДС форматами, а также для выполнения арифметических операций над ДДС числами.
Ограничения и недостатки двоично-десятичной системы
Какие проблемы возникают при использовании ДДС. Основные недостатки:
- Более низкая эффективность использования памяти по сравнению с двоичной системой
- Сложность реализации некоторых математических операций (например, умножения и деления)
- Ограниченный диапазон представления чисел при фиксированном количестве разрядов
- Необходимость дополнительных схем коррекции при выполнении арифметических операций
Несмотря на эти ограничения, в определенных областях преимущества ДДС перевешивают ее недостатки, что обуславливает ее широкое применение.

Двоично-десятичная система счисления
Понятие смешанной системы счисления
Среди систем счисления выделяют класс так называемых смешанных систем счисления.
Определение 1
Смешанной называется такая система счисления, в которой числа, заданные в некоторой системе счисления с основанием $P$ изображаются с помощью цифр другой системы счисления с основанием $Q$, где $Q
При этом в такой системе счисления во избежание разночтения для изображения каждой цифры системы с основанием $P$ отводится одинаковое количество разрядов системы с основанием $Q$, достаточное для представления любой цифры системы с основанием $P$.
Примером смешанной системы счисления является двоично-десятичная система.
Практическое обоснование использования двоично-десятичной системы счисления
Поскольку человек в своей практике широко использует десятичную систему счисления, а для компьютера свойственно оперирование двоичными числами и двоичной арифметикой, был введен в практику компромиссный вариант — система двоично-десятичной записи чисел, которая, как правило, используется там, где присутствует необходимость частого использования процедуры десятичного ввода-вывода (например, электронные часы, калькуляторы и т.д.). В подобных устройствах не всегда целесообразно применять универсальный микрокод перевода двоичных чисел в десятичные и обратно по причине малого объема программной памяти.
Готовые работы на аналогичную тему
Замечание 1
В некоторых типах ЭВМ в арифметико-логических устройствах (АЛУ) имеются специальные блоки десятичной арифметики, которые выполняют операции над числами, представленными в двоично-десятичном коде. Это позволяет в некоторых случаях существенно повысить производительность ЭВМ.
К примеру, в автоматизированной системе обработки данных используется большое количество чисел, а вычислений при этом немного. В подобном случае операции перевода чисел из одной системы в другую существенно превысили бы время выполнения операций по обработке информации. Микропроцессоры же используют чистые двоичные числа, однако при этом понимают и команды преобразования в двоично-десятичную запись. АЛУ AVR-микроконтроллера (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде, а именно:
-
считывает результаты преобразования АЦП;
-
в формате целых чисел или чисел с плавающей точкой выполняет обработку результатов измерения.
Однако окончательный результат при этом выводится на индикатор в десятичном формате, удобном для восприятия человеком.
Принципы построения двоично-десятичной системы счисления
При построении двоично-десятичной системы счисления для изображения каждой десятичной цифры в ней отводится $4$ двоичных разряда, поскольку максимальная десятичная цифра $9$ кодируется как $10012$.
Например: $925_{10} = 1001 0010 0101_{2-10}$.

Рисунок 1.
В данной записи последовательные четверки двоичных разрядов изображают цифры $9$, $2$ и $5$ десятичной записи соответственно.
Для записи числа в двоично-десятичной системе счисления его необходимо сначала представить в десятичной системе, а затем каждую, входящую в состав числа, десятичную цифру представить в двоичной системе. При этом для написания различных десятичных цифр в двоичной системе счисления требуется разное количество двоичных разрядов. Чтобы обойтись без применения каких-либо разделительных знаков, при двоичном изображении десятичной цифры всегда записывается 4 двоичных разряда. Группа из этих четырех разрядов называется тетрадой.
Хотя в двоично-десятичной записи используются только цифры $0$ и $1$, она отличается от двоичного изображения данного числа, так как десятичный эквивалент двоичного числа в несколько раз больше десятичного эквивалента двоично-десятичного числа.
Например:
$1001 0010 0101_{(2)} = 2341_{(10)}$,
$1001 0010 0101_{(2)} = 925_{(2-10)}$.
Такая запись довольно часто используется как промежуточный этап при переводе числа из десятичной системы в двоичную и обратно. Так как число $10$ не является точной степенью числа $2$, то используются не все $16$ тетрад (тетрады, изображающие числа от $A$ до $F$ отбрасываются, так как эти числа считаются запрещенными), алгоритмы же арифметических операций над многозначными числами в этом случае более сложные, чем в основных системах счисления. И, тем не менее, двоично-десятичная система счисления используется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах.
Чтобы откорректировать результаты арифметических операций над числами, представленными в двоично-десятичном коде, в микропроцессорной технике используются команды, которые преобразуют результаты операций в двоично-десятичную систему счисления. При этом используется следующее правило: при получении в результате операции (сложения или вычитания) в тетраде числа, большего, чем $9$, к этой тетраде прибавляют число $6$.
Например: $75+18=93$.
$+00011000$
$10001101 \ (8D)$
В младшей тетраде появилась запрещенная цифра $D$. Прибавим к младшей тетраде $6$ и получим:
$+00000110$
$10010011 \ (93)$
Как видим, несмотря на то, что сложение осуществлялось в двоичной системе счисления результат операции получился в двоично-десятичной.
Замечание 2
Поразрядное уравновешивание часто осуществляют на основе двоично-десятичной системы счисления. Применение двоичной и двоично-десятичной системы счисления наиболее целесообразно, поскольку в этом случае число тактов уравновешивания оказывается наименьшим среди прочих систем счисления. Заметим, что применение двоичного кода позволяет примерно на $20\%$ уменьшить время обработки компенсирующего напряжения по сравнению с двоично-десятичным.
Преимущества использования двоично-десятичной системы счисления
Преобразование чисел из десятичной системы в двоично-десятичную систему счисления не связано с вычислениями и его легко реализовать, используя при этом простейшие электронные схемы, так как преобразовывается небольшое количество (4) двоичных цифр. Обратное же преобразование происходит в ЭВМ автоматически с помощью особой программы перевода.
Применение двоично-десятичной системы счисления совместно с одной из основных систем счисления (двоичной) позволяет разрабатывать и создавать высокопроизводительные ЭВМ, так как использование блока десятичной арифметики в АЛУ исключает при решении задач необходимость программированного перевода чисел из одной системы счисления в другую.
Поскольку две двоично-десятичные цифры составляют $1$ байт, с помощью которого можно представить значения чисел от $0$ до $99$, а не от $0$ до $255$, как при использовании $8$-разрядного двоичного числа, то используя $1$ байт для преставления каждых двух десятичных цифр, можно формировать двоично-десятичные числа с любым требуемым числом десятичных разрядов.
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА — ТолВИКИ
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
Автор-составитель: Ерещенко Александр
Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000 и 9=1001. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).
Поскольку человеку наиболее привычны представление и арифметика в десятичной системе счисления, а для компьютера — двоичное представление и двоичная арифметика, была введена компромиссная система двоично-десятичной записи чисел. Такая система чаще всего применяется там, где существует необходимость частого использования процедуры десятичного ввода-вывода. (электронные часы, калькуляторы, АОНы, и т.д.). В таких устройсвах не всегда целесообразно предусматривать универсальный микрокод перевода двоичных чисел в десятичные и обратно по причине небольшого объема программной памяти.
Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например: 369110=0011 0110 1001 0001DEC:
Десятичное число 3 6 9 1 Двоично-десятичное число 0011 0110 1001 0001
Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Получим 1000 0000 0111 0010DEC = 807210:
Двоично-десятичное число 1000 0000 0111 0010 Десятичное число 8 0 7 2
Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Преобразование двоичных чисел в двоично-десятичные
Арифметико-логическое устройство AVR-микроконтроллеров (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде (в формате целых чисел или чисел с плавающей точкой) удобно выполнять обработку результатов измерения. Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком.
В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные.
1. Форматы представления десятичных чисел
В настоящее время распространены два формата представления десятичных чисел в микропроцессорах — упакованный двоично-десятичный код (BCD-Binary-Coded Decimal) и неупакованный десятичный код [1].
Упакованный BCD-код — это такое представление десятичного числа, когда каждая десятичная цифра представляется 4-х битным двоичным позиционным кодом 8-4-2-1. При этом байт содержит две десятичные цифры. Младшая десятичная цифра занимает правую тетраду (биты 3 : 0), старшая — левую тетраду (биты 7 : 4). Многоразрядные BCD-числа занимают несколько смежных байт. Если число является знаковым, то для представления знака в BCD-формате отводится старшая тетрада старшего байта. Для кодирования знака можно использовать шесть двоичных кодовых комбинаций, которые не используются для представления десятичных цифр. Это коды 1010-1111 (A-F в шестнадцатеричном представлении). Обычно для кодирования знака плюс применяют код 1100 (С), а для знака минус — 1101 (D).
Неупакованный десятичный код является подмножеством международной таблицы кодирования символов ASCII (Таблица 1). Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом. Таблица 1: ASCII-коды десятичных цифр
2. Преобразование целых 16-битных чисел в двоично-десятичные числа
На сайте www.atmel.com предлагается программа «bin2bcd16» для преобразования целых 16-битных двоичных чисел в двоично-десятичные упакованные числа. В данной статье рассматривается программа «bin16bcd5» (см. Приложение, Программа 1), написанная Терешкиным А. В. согласно алгоритму, изложенному в [1], и выполняющая ту же задачу. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая.
Алгоритм программы «bin16bcd5» заключается в следующем. Предположим, что имеется целое беззнаковое 16-битное число (диапазон от 0 до 65535). Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число 10000, сначала определить десятичную цифру десятков тысяч. Затем находится цифра тысяч последовательным вычитанием числа 1000 и т. д. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Программа «bin16ASCII5» (см. Приложение, Программа 2) преобразует целое двоичное 16-битное число в десятичное неупакованное число. При этом используется тот же алгоритм.
3. Преобразование двоичной дроби в двоично-десятичную дробь
Двоичная дробь, по определению, представляется следующим выражением:
0.A-1A-2 … A-m = A-1*2-1 + A-2*2-2 + … A-m*2-m
Из этого представления следует алгоритм преобразования (Рис. 2), который содержит m шагов. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2.
На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата. Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.
Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.
При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется. При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.
4. Преобразование чисел с плавающей точкой в двоично-десятичные числа
Представление чисел с плавающей точкой имеет следующий вид:
± M * 2 ± П
где М — двоичная мантисса числа, П — двоичный порядок числа.
Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел. Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных (а не десятичных) разрядов, на которое необходимо переместить эту точку влево или вправо.
Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля. Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти.
Тест
1. ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
2. Преобразование двоичных чисел в двоично-десятичные
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Двоично-десятичная система счисления — Студопедия.Нет
Двоично-десятичная система счисления широко используется в цифровых устройствах, когда основная часть операций связана не с обработкой и хранением вводимой информации, а с ее вводом и выводом на какие-либо индикаторы с десятичным представлением полученных результатов (микрокалькуляторы, кассовые аппараты и т. п.).
В двоично-десятичной системе счисления цифры от 0 до 9 представляют четырехразрядными двоичными комбинациями от 0001 до 1001, т.е. двоичными эквивалентами десяти первых шестнадцатеричных чисел. Преобразования из двоично-десятичной системы в десятичную систему и обратные преобразования выполняются путем прямой замены четырех двоичных цифр одной десятичной цифрой или обратной замены.
Пример.Преобразовать число 001101112-10 из двоично-десятичной системы в десятичную систему.
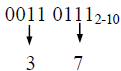 Ответ: 001101112-10 = 3710.
Ответ: 001101112-10 = 3710.
Две двоично-десятичные цифры составляют 1 байт. Таким образом, с помощью 1 байта можно представить значения от 0 до 99, а не от 0 до 255, как при использовании 8-разрядного двоичного кода. Используя 1 байт для представления каждых двух десятичных цифр, можно формировать двоично-десятичные числа с любым требуемым числом десятичных разрядов.
Так, если число 1000 0011 0010 0111 рассматривать как двоичное, то его десятичный эквивалент 1000 0011 0010 01112 = 3357510 в несколько раз больше десятичного эквивалента двоично-десятичного числа 1000 0011 0010 01112-10 = 832710.
Арифметические действия с нормализованными числами
Сложение и вычитание
К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.
Сначала производится подготовительная операция, называемая выравниванием порядков.
В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов.
После каждого сдвига порядок увеличивается на единицу, а освободившиеся старшие разряды заполняются нулями. В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.
В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево.
Нормализацией называется выбор такого значения порядка, при котором старший разряд мантиссы имеет значение 1. При нормализации возможны две ситуации:
− результат меньше 1/2, то есть старшие разряды мантиссы нулевые. Если при этом результат представлен в прямом коде, мантисса сдвигается влево до тех пор, пока первая значащая 1 не окажется в старшем разряде. Если же результат представлен в обратном или дополнительном коде (отрицательный), производится сдвиг влево до появления в старшем разряде первого значащего нуля. При каждом сдвиге значение порядка уменьшается на 1;
− результат больше 1, то есть разрядная сетка переполнена. В этом случае мантисса сдвигается вправо на один разряд с одновременным увеличением порядка на 1.
Правила выполнения основных арифметических операций справедливы для чисел любой позиционной системы счисления.
Примеры
1) Сложить десятичные нормализованные числа 0,536·106 и 0,284·103.
Разность порядков слагаемых здесь равна трём (6-3=3), поэтому перед сложением мантисса второго числа сдвигается на три разряда вправо:
| 0,536 ·106 0,000284 ·106 |
| 0,536284 ·106 |
2) Сложить двоичные нормализованные числа 0,11011·210 и 0,10111·2–1.
Разность порядков слагаемых здесь равна трем (102+12=112=310), поэтому перед сложением мантисса второго числа сдвигается на три разряда вправо:
| 0,11011 ·210 0,00010111·210 |
| 0,11101111·210 |
3) Сложить шестнадцатеричные нормализованные числа 0,1В5·163 и 0,34Е·16–1.
Разность порядков слагаемых здесь равна четырём (316+116=416=410), поэтому перед сложением мантисса второго числа сдвигается на четыре разряда вправо:
| 0,1В5 ·163 0,000034Е·163 |
| 0,1В5034Е·163 |
4) Выполнить вычитание двоичных нормализованных чисел 0,10101·210 и 0,11101·21.
Разность порядков уменьшаемого и вычитаемого здесь равна единице (102-12=12=110), поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:
| 0,10101 ·210 0,011101·210 |
| 0,001101·210 |
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0,1101·20.
4) Выполнить вычитание восьмеричных нормализованных чисел 0,125·83 и 0,32·8-2 Разность порядков уменьшаемого и вычитаемого здесь равна пяти (38+28=58=510), поэтому перед вычитанием мантисса второго числа сдвигается на пять разрядов вправо:
| 0,125 ·83 0,0000032 ·83 |
| 0,0147746 ·83 |
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на один разряд с соответствующим уменьшением порядка на одну единицу: 0,147746 ·82.
Умножение и деление
Для получения результата в данном случае производятся следующие действия, причем не важно, какое из двух данных чисел больше.
1. Мантиссы перемножаются или одна делится на другую;
2. Порядки при умножении складываются, а при делении вычитаются;
3. При необходимости мантисса результата нормализуется.
Примеры:
1). Выполнить умножение двоичных нормализованных чисел:
(0,11101 . 2101) . (0,1001 . 211) = (0,11101 . 0,1001) . 2(101+11) = 0,100000101 . 21000.
2). Выполнить умножение восьмеричных нормализованных чисел:
(0,765 . 84) . (0,537 . 85) = (0,765 . 0,537) . 8(4+5) = 0,527353 . 811.
3). Выполнить умножение шестнадцатеричных нормализованных чисел:
(0,А25 . 167) . (0,6С . 169) = (0,А25 . 0,6С) . 16(7+9) = 0,4479С . 1610.
4). Выполнить деление двоичных нормализованных чисел:
(0,100000101 . 21000) : (0,1001 . 211) = (0,100000101 : 0,1001) . 2(1000-11) = 0,11101 . 2101
5). Выполнить деление восьмеричных нормализованных чисел:
(0,527353 . 811) : (0,537 . 85) = (0,527353 :0,537) . 8(11-5) = 0,765 . 84
6). Выполнить деление шестнадцатеричных нормализованных чисел:
(0,4479С . 1610) :(0,6С . 169) = (0, 4479С :0,6С) . 16(10-9) = 0,А25 . 167.
Двоично-десятичная запись — число — Большая Энциклопедия Нефти и Газа, статья, страница 1
Двоично-десятичная запись — число
Cтраница 1
Двоично-десятичная запись чисел состоит в следующем. Каждая цифра десятичного числа записывается в виде четырехразрядного двоичного числа. Четверка двоичных цифр, изображающая десятичную цифру, называется тетрадой. Таким образом, двоично-десятичная запись числа отличается от его десятичной записи тем, что для изображения каждой цифры применяется не один знак, а четыре знака. [1]
Двоично-десятичную запись числа используют непосредственно или как промежуточную форму записи между обычной десятичной его записью и машинной двоичной. Вычислительная машина сама по специальной программе переводит двоично-десятичные числа в двоичные и обратно. [2]
Следует обратить внимание на то, что хотя в двоично-десятичной записи числа используются только цифры 0 и 1, эта запись отличается от записи данного числа в двоичной системе счисления. Как видно, эта запись отличается от записи этого же числа в смешанной двоично-десятичной системе. [3]
При переводе на цифровой вычислительной машине десятичных чисел в двоичные промежуточной является двоично-десятичная запись чисел. [4]
Здесь последовательные четверки ( тетрады) двоичных разрядов изображают цифры 9, 2 и Г записи числа в десятичной системе счисления. Следует обратить внимание, что хотя л двоично-десятичной записи числа и используются только цифры 0 и 1, эта запись отличается от двоичного изображения данного числа. [5]
При записи двоичного числа каждый разряд ячейки соответствует разряду числа, а при записи двоично-десятичного числа десятичный разряд представляется двоичной тетрадой. Следовательно, всего в ячейке может разместиться 9 разрядов двоично-десятичной записи числа. [6]
В некоторых электронных цифровых машинах принято представление чисел в двоично-десятичной системе счисления. В машинах, в которых принята двоичная система счисления, двоично-десятичная запись чисел применяется как промежуточная для ввода чисел в машину. [7]
При записи десятичных чисел с фиксированной запятой в ячейках памяти применяется двоично-десятичная запись числа. В двоично-десятичной записи числа каждая десятичная цифра представляется соответствующей ей двоичной тетрадой. [9]
При записи десятичных чисел с фиксированной запятой в ячейках памяти применяется двоично-десятичная запись числа. В двоично-десятичной записи числа каждая десятичная цифра представляется соответствующей ей двоичной тетрадой. [11]
В противном случае число х не может быть записано с хорошей точностью в виде правильной 9-разрядной десятичной дроби. Число х имеет двоичную запись, совпадающую с округленной двоично-десятичной записью числа х, иначе говоря, его можно считать результатом перевода. [12]
В противном случае число х не может быть записано с хорошей точностью в виде правильной 9-разрядной десятичной дроби. Число х9 имеет двоичную запись, совпадающую с округленной двоично-десятичной записью числа х, иначе говоря, его можно считать результатом перевода. [13]
В некоторых электронных цифровых машинах принято представление чисел в двоично-десятичной системе счисления. При этом арифметические действия над двоично-десятичными числами выполняются по специальным правилам. В машинах, в которых принята двоичная система счисления, двоично-десятичная запись чисел применяется как промежуточная для ввода чисел в машину. [14]
Двоично-десятичная запись чисел состоит в следующем. Каждая цифра десятичного чи
20.2 Двоично-десятичная система счисления Двоично-десятичная…
20.2 Двоично-десятичная система счисления
Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000 , 1=0001 , 2=0010 , 3=0011 , 4=0100 , 5=0101 , 6=0110 , 7=0111 , 8=1000 и 9=1001 . Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).
Поскольку человеку наиболее привычны представление и арифметика в десятичной системе счисления, а для компьютера — двоичное представление и двоичная арифметика, была введена компромиссная система двоично-десятичной записи чисел. Такая система чаще всего применяется там, где существует необходимость частого использования процедуры десятичного ввода-вывода. (электронные часы, калькуляторы, АОНы, и т.д.). В таких устройсвах не всегда целесообразно предусматривать универсальный микрокод перевода двоичных чисел в десятичные и обратно по причине небольшого объема программной памяти.
Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например:
369110=0011 0110 1001 0001DEC:
Десятичное число | 3 | 6 | 9 | 1 |
Двоично-десятичное число | 0011 | 0110 | 1001 | 0001 |
Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент.
Каждая группа из 4 бит преобразуется в её десятичный эквивалент.
Получим 1000 0000 0111 0010DEC = 807210:
Двоично-десятичное число | 1000 | 0000 | 0111 | 0010 |
Десятичное число | 8 | 0 | 7 | 2 |
Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
2.2.3. Двоично-десятичная система счисления
Эта система имеет основание S = 10, но каждая цифра изображается четырехразрядным двоичным числом, называемым тетрадой. Обычно данная система счисления используется в ЭВМ при вводе и выводе информации. Однако в некоторых типах ЭВМ в АЛУ имеются специальные блоки десятичной арифметики, выполняющие операции над числами в двоично-десятичном коде. Это позволяет в ряде случаев существенно повышать производительность ЭВМ.
Например, в автоматизированной системе обработки данных чисел много, а вычислений мало. В этом случае операции, связанные с переводом чисел из одной системы в другую, существенно превысили бы время выполнения операций по обработке информации.
Перевод чисел из десятичной системы в двоично-десятичную весьма прост и заключается в замене каждой цифры двоичной тетрадой.
Пример.
Записать десятичное число 572.38(10)в двоично-десятичной системе счисления.
Обратный перевод также прост: необходимо двоично-десятичное число разбить на тетрады от точки влево (для целой части) и вправо (для дробной), дописать необходимое число незначащих нулей, а затем каждую тетраду записать в виде десятичной цифры.
Пример.
Записать двоично-десятичное число 10010.010101(2-10)в десятичной системе счисления.
Перевод чисел из двоично-десятичной в двоичную систему осуществляется по общим правилам, описанным выше.
2.3. Восьмеричная система счисления
В восьмеричной системе счисления употребляются всего восемь цифр, т.е. эта система счисления имеет основание S = 8. В общем виде восьмеричное число выглядит следующим образом:
,
где .
Восьмеричная система счисления не нужна ЭВМ в отличие от двоичной системы. Она удобна как компактная форма записи чисел и используется программистами (например, в текстах программ для более краткой и удобной записи двоичных кодов команд, адресов и операндов). В восьмеричной системе счисления вес каждого разряда кратен восьми или одной восьмой, поэтому восьмиразрядное двоичное число позволяет выразить десятичные величины в пределах 0-255, а восьмеричное охватывает диапазон 0-99999999 (для двоичной это составляет 27 разрядов).
Поскольку 8=23, то каждый восьмеричный символ можно представить трехбитовым двоичным числом. Для перевода числа из двоичной системы счисления в восьмеричную необходимо разбить это число влево (для целой части) и вправо (для дробной) от точки (запятой) на группы по три разряда (триады) и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняются необходимым количеством незначащих нулей.
Пример.
Двоичное число 10101011111101(2)записать в восьмеричной системе счисления.
Пример.
Двоичное число 1011.0101(2) записать в восьмеричной системе счисления.
Перевод из восьмеричной системы счисления в двоичную осуществляется путем представления каждой цифры восьмеричного числа трехразрядным двоичным числом (триадой).
2.4. Шестнадцатеричная система счисления
Эта система счисления имеет основание S = 16. В общем виде шестнадцатеричное число выглядит следующим образом:
,
где .
Шестнадцатеричная система счисления позволяет еще короче записывать многоразрядные двоичные числа и, кроме того, сокращать запись 4-разрядного двоичного числа, т.е. полубайта, поскольку 16=24. Шестнадцатеричная система также применяется в текстах программ для более краткой и удобной записи двоичных чисел.
Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить это число влево и вправо от точки на тетрады и представить каждую тетраду цифрой в шестнадцатеричной системе счисления.
Пример.
Двоичное число 10101011111101(2)записать в шестнадцатеричной системе.
Пример.
Двоичное число 11101.01111(2)записать в шестнадцатеричной системе.
Для перевода числа из шестнадцатеричной системы счисления в двоичную, необходимо, наоборот, каждую цифру этого числа заменить тетрадой.
В заключение следует отметить, что перевод из одной системы счисления в другую произвольных чисел можно осуществлять по общим правилам, описанным в разделе “Двоичная система счисления”. Однако на практике переводы чисел из десятичной системы в рассмотренные системы счисления и обратно осуществляются через двоичную систему счисления.
Кроме того, следует помнить, что шестнадцатеричные и восьмеричные числа – это только способ представления больших двоичных чисел, которыми фактически оперирует процессор. При этом шестнадцатеричная система оказывается предпочтительнее, поскольку в современных ЭВМ процессоры манипулируют словами длиной 4, 8, 16, 32 или 64 бита, т.е. длиной слов, кратной 4. В восьмеричной же системе счисления предпочтительны слова, кратные 3 битам, например слова длиной 12 бит (как в PDP-8 фирмы DEC).
Десятичный преобразователь в двоичный
Из Двоичный Десятичный Шестнадцатеричный
Чтобы Двоичный Десятичный Шестнадцатеричный
Преобразование двоичного числа в десятичное ►
Как преобразовать десятичное число в двоичное
Шаг преобразования:
- Разделите число на 2.
- Получить целое частное для следующей итерации.
- Получить остаток от двоичной цифры.
- Повторяйте эти шаги до тех пор, пока частное не станет равным 0.
Пример # 1
Преобразование 13 10 в двоичное:
| Подразделение по 2 |
Частное | остаток | Бит # |
|---|---|---|---|
| 13/2 | 6 | 1 | 0 |
| 6/2 | 3 | 0 | 1 |
| 3/2 | 1 | 1 | 2 |
| 1/2 | 0 | 1 | 3 |
Итак 13 10 = 1101 2
Пример # 2
Преобразование 174 10 в двоичное:
| Подразделение по 2 |
Частное | остаток | Бит # |
|---|---|---|---|
| 174/2 | 87 | 0 | 0 |
| 87/2 | 43 | 1 | 1 |
| 43/2 | 21 | 1 | 2 |
| 21/2 | 10 | 1 | 3 |
| 10/2 | 5 | 0 | 4 |
| 5/2 | 2 | 1 | 5 |
| 2/2 | 1 | 0 | 6 |
| 1/2 | 0 | 1 | 7 |
Итак 174 10 = 10101110 2
Таблица преобразования десятичных чисел в двоичные
| Десятичное Число |
Двоичное Число |
Hex Число |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
| 17 | 10001 | 11 |
| 18 | 10010 | 12 |
| 19 | 10011 | 13 |
| 20 | 10100 | 14 |
| 21 | 10101 | 15 |
| 22 | 10110 | 16 |
| 23 | 10111 | 17 |
| 24 | 11000 | 18 |
| 25 | 11001 | 19 |
| 26 | 11010 | 1A |
| 27 | 11011 | 1Б |
| 28 | 11100 | 1С |
| 29 | 11101 | 1D |
| 30 | 11110 | 1E |
| 31 | 11111 | 1F |
| 32 | 100000 | 20 |
| 64 | 1000000 | 40 |
| 128 | 10000000 | 80 |
| 256 | 100000000 | 100 |
См. Также
Напишите, как улучшить эту страницу
ПРЕОБРАЗОВАНИЕ НОМЕРА
СТОЛЫ БЫСТРЫЙ
Этот веб-сайт использует файлы cookie для улучшения вашего опыта, анализа трафика и отображения рекламы.Выучить больше .Двоичный преобразователь в десятичный
Из Двоичный Десятичный Шестнадцатеричный
Чтобы Двоичный Десятичный Шестнадцатеричный
Преобразователь десятичной системы в двоичную ►
Как преобразовать двоичное в десятичное
Для двоичного числа с n цифрами:
d n-1 … d 3 d 2 d 1 d 0
Десятичное число равно сумме двоичных цифр (d n ), умноженной на их степень двойки (2 n ):
в десятичном виде = d 0 × 2 0 + d 1 × 2 1 + d 2 × 2 2 +…
Пример
Найдите десятичное значение 111001 2 :
| двоичное число: | 1 | 1 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|
| степень 2: | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
111001 2 = 1⋅2 5 + 1⋅2 4 + 1⋅2 3 + 0⋅2 2 + 0⋅2 1 + 1⋅2 0 = 57 10
Таблица преобразования двоичного числа в десятичное
| Двоичный Число |
Десятичное число Число |
Hex Число |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | А |
| 1011 | 11 | B |
| 1100 | 12 | С |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
| 10000 | 16 | 10 |
| 10001 | 17 | 11 |
| 10010 | 18 | 12 |
| 10011 | 19 | 13 |
| 10100 | 20 | 14 |
| 10101 | 21 | 15 |
| 10110 | 22 | 16 |
| 10111 | 23 | 17 |
| 11000 | 24 | 18 |
| 11001 | 25 | 19 |
| 11010 | 26 | 1A |
| 11011 | 27 | 1Б |
| 11100 | 28 | 1С |
| 11101 | 29 | 1D |
| 11110 | 30 | 1E |
| 11111 | 31 | 1 этаж |
| 100000 | 32 | 20 |
| 1000000 | 64 | 40 |
| 10000000 | 128 | 80 |
| 100000000 | 256 | 100 |
См. Также
.Конвертер десятичных чисел в двоичные онлайн
Этот онлайн-калькулятор может переводить числа из одной системы счисления в любую другую, показывая подробный курс решений. А калькулятор рассчитан на:
- Десятичное преобразование в двоичное ,
- Двоичное преобразование в десятичное ,
- Преобразование десятичного в шестнадцатеричное,
- Десятичное преобразование в двоичное метод ,
- Метод преобразования десятичной запятой в двоичную с плавающей запятой ,
- Преобразователь десятичных чисел в двоичные с шагом,
- Десятичная Дробь в двоичный преобразователь.
- Введите числа, которые необходимо перевести.
- Укажите его систему нумерации.
- Укажите в какую систему счисления переводите.
- Щелкните «Перевести».
- Нажмите «Показать прогресс решений», чтобы просмотреть подробные решения для путешествий.
Валютный перевод чисел имеет одно поле ввода. В это поле вы должны ввести номер, который хотите перевести.
После этого обязательно нужно указать, в какой записи вы его ввели.«Его система счисления» Для этого под полем ввода находится график.
Если вы не нашли свою систему, выберите «другое», и количество будет в поле ввода. В этом поле вы должны ввести базовую систему одним числом без пробелов.
Затем вы должны выбрать число, которое хотите перевести в какую-нибудь систему. Если вы снова не нашли нужную систему, вставьте ее в «другую».
После нажатия на «ПЕРЕВЕСТИ» результат появится в поле. Если вы хотите получить подробный курс решений, перейдите по соответствующей ссылке.
Перевод чисел в разных системах счисления
Система счисления — это набор символов (цифр) и правила их использования для представления чисел. Есть два типа систем счисления. Непозиционная система — некоторые буквы используются как цифры. Позиционная система — количественное значение числа зависит от его места в вводном номере. Положение фигуры называется разрядом. Номер ранга увеличивается справа налево. Количество различных цифр (символов), используемых в позиционной системе счисления для представления (записи) числа, называется основанием.
Однородная система — для каждой категории набор разрешенных символов (цифр) одинаков. В качестве примера мы используем десятичную систему счисления. Если записать число в однородной 10-й системе, то можно использовать в каждом разряде только одну цифру в диапазоне от 0 до 9, таким образом, допустимое число 450 (класс 1 st — 0, 2 nd — 5, 3 ряд — 4), а 4F5 — нет, так как буква F не входит в набор цифр от 0 до 9.
Почему нужно переносить номера из одной системы в другую?
При выполнении заданий на компьютере ввод исходных данных и вывод результатов расчетов обычно выполняется пользователем в привычной для него десятичной системе счисления.Однако, учитывая, что подавляющее большинство компьютеров используют двоичную систему счисления, возникает необходимость переводить числа из одной системы счисления в другую. Перевод чисел из q-one в десятичное происходит непосредственно из полиномиального выражения определенного числа.
Суть этого перевода — последовательное десятичное число и его частное деление на значение системы счисления q. Деление выполняется до тех пор, пока следующее частное не станет меньше основания q.Вычисленный остаток на последнем шаге — это самая старая (первая) цифра переданного номера. Результатом такого перевода числа в систему счисления q-one является запись последнего частного и всех остатков в обратном порядке.
Десятичная система счисления
Десятичная система счисления — это алфавит цифр, который состоит из десяти общеизвестных чисел и основания 10. Позиция цифры в номере называется разрядом. Ранг номера увеличивается справа налево, от младшего разряда к старшему.В десятичной системе цифра в крайней правой позиции (ранг) представляет количество единиц; сдвинутые цифры на одну позицию влево — число десятков, еще слева — сотни, тысячи и так далее. Соответственно у нас есть категория единиц, разряд десятков и так далее.
Может быть использован набор позиционных систем счисления, где основание больше или равно 2. Для преобразования чисел из десятичной системы счисления в двоичную систему счисления используйте так называемый «алгоритм замены», состоящий из следующих последовательностей:
- Разделите десятичное число A на 2.Частное Q запоминается для следующего шага, а остаток записывается как младший бит двоичного числа.
- Если частное Q не равно 0, возьмите его за новое делимое и повторите процедуру, описанную в шаге 1. Каждый новый остаток (0 или 1) записывается в битах двоичного числа в направлении от младшего разряда (минимум значащий бит) старшему.
- Алгоритм продолжается до тех пор, пока не получится частный Q = 0, а остаток a = 1, полученный в результате шагов 1 и 2.
Двоичная система счисления
Двоичная система счисления сейчас используется практически во всех цифровых устройствах. Компьютеры, контроллеры и другие вычислительные устройства выполняют вычисления точно в двоичном формате. Цифровые устройства записи и воспроизведения звука, фото и видео хранят и обрабатывают сигналы в двоичной системе счисления. При передаче информации по цифровым каналам связи используется модель двоичной системы. Система названа так потому, что ее основание системы счисления равно двум (2) или в двоичной системе счисления 102 — это означает, что для изображения числа используются только две цифры «0» и «1».
Двойка, записанная справа внизу от числа, в дальнейшем будет обозначать основание системы счисления. Для десятичной системы основание системы счисления обычно не указывается. Чтобы преобразовать двоичное число в десятичное, это число должно быть записано как произведение суммы степеней основ двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления является наиболее популярным средством записи компактных двоичных цифр.Он широко используется при проектировании и разработке цифровых технологий. Как следует из названия, основанием системы счисления является число 16 или 1016 в шестнадцатеричной системе счисления. Чтобы не было путаницы, при записи чисел в позиционных системах счисления, отличных от десятичной, справа внизу от основных чисел ввода необходимо указывать систему счисления.
Первые десять чисел взяты из десятичной системы (0, 1,…, 8, 9) и к ним добавлены шесть букв (a, b, c, d, e и f). В шестнадцатеричном числе 3f7c2 буквы «f» и «c» являются шестнадцатеричными цифрами.В конце шестнадцатеричного числа может приниматься буква h. Таким образом можно отличить шестнадцатеричные числа от других систем счисления.
.
Преобразование десятичного IP-адреса в двоичный и двоичный в десятичный
В этом руководстве объясняется, как преобразовать десятичный IP-адрес в двоичный IP-адрес и двоичный IP-адрес в десятичном IP-адресе, шаг за шагом с примерами. Изучите самый простой способ преобразования десятичной дроби IP-адрес и маска подсети в двоичном IP-адресе и маске подсети соответственно.
IP-адрес и маска подсети совместно обеспечивают числовую идентификацию интерфейса. Оба адреса всегда используются вместе.Без маски подсети IP-адрес является неоднозначным адресом, а без IP-адреса маска подсети — это просто число.
Оба адреса имеют длину 32 бита. Эти биты разделены на четыре части. Каждая часть известна как октет и содержит 8 бит. Октеты разделяются точками и записываются последовательно.
Для записи этих адресов используются два популярных обозначения: двоичное и десятичное.
В двоичной системе счисления все четыре октета записываются в двоичном формате.
Примеры IP-адреса в двоичной системе счисления: —
00001010.00001010.00001010.00001010 10101100.10101000.00000001.00000001 11000000.10101000.00000001.00000001
Примеры маски подсети в двоичной системе счисления: —
11111111.00000000.00000000.00000000 11111111.11111111.00000000.00000000 11111111.11111111.11111111.00000000
В десятичной системе счисления все четыре октета записываются в десятичном формате.В каждом октете используется десятичное эквивалентное значение битов.
Примеры IP-адресов в десятичной системе счисления: —
10.10.10.10 172.168.1.1 192.168.1.1
Примеры маски подсети в десятичной системе счисления: —
255.0.0.0 255.255.0.0 255.255.255.0
В реальной жизни вам редко нужно скрывать IP-адрес и маску подсети из десятичного формата в двоичный и наоборот. Но если вы готовитесь к какому-либо экзамену Cisco, я настоятельно рекомендую вам изучить это преобразование.Почти все экзамены Cisco включают вопросы об IP-адресах. Изучение этого преобразования поможет вам более эффективно решать вопросы, связанные с IP-адресацией.
Базовая стоимость и позиция
За исключением базового значения, двоичная система работает точно так же, как десятичная. Базовое значение — это цифры, которые используются для построения чисел в обеих системах. В двоичной системе две цифры (0 и 1) используются для построения чисел, а в десятичной системе десять цифр (0,1,2,3,4,5,6,7,8,9) используются для построения чисел. числа.
Чтобы преобразовать число из двоичного в десятичное и наоборот, мы должны изменить базовое значение. После изменения базового значения полученное число можно записать в новой системе.
Поскольку IP-адрес и маска подсети состоят из 32 битов и эти биты разделены на 4 октета, чтобы преобразовать эти адреса в двоичную форму из десятичной и наоборот, нам нужно только понимать числа, которые могут быть построены из октета или 8 бит.
Бит может быть включен или выключен.В двоичной системе на бит записывается как 1 и выкл бит записывается как 0 в числе. В десятичной системе, если бит включен, его значение позиции добавляется числом, а если бит выключен, его значение позиции пропускается в числе.
В следующей таблице перечислены значения позиции каждого бита в октете.
| Положение бита | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Значение положения | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Ключевые моменты
- Независимо от того, какую систему мы используем для записи октета, он всегда содержит все 8 бит.Биты всегда пишутся слева направо.
- Число, в котором все 8 битов отключены, записывается как 00000000 в двоичной системе. Это же число записывается как 0 (0 + 0 + 0 + 0 + 0 + 0 + 0 + 0) в десятичной системе.
- Число, в котором включены все 8 бит, записывается как 11111111 в двоичной системе. Это же число записывается как 255 (128 + 64 + 32 + 16 + 8 + 4 + 2 + 1) в десятичной системе.
Преобразование десятичного числа в двоичное
Чтобы преобразовать десятичное число в двоичное, выполните следующие действия: —
- Сравните значение позиции первого бита с заданным числом.Если данное число больше, чем значение позиции, напишите 0 в приблизительной области вашего рабочего листа. Если заданное число меньше или равно значению позиции, запишите значение позиции.
- Добавьте значение позиции второго бита во все, что вы написали на первом шаге, и сравните его со значением позиции второго бита. Если сумма больше, чем значение позиции, пропустите значение позиции. Если сумма меньше или равна значению позиции, сложите значение позиции в сумме.
- Повторяйте этот процесс до тех пор, пока не будут сравнены все 8 бит. Если сумма становится равной в любом бите, запишите все биты расширения как 0 .
| Операция | В десятичном формате | В двоичном формате |
| Добавить | Использовать значение позиции | Установить бит на 1 |
| Пропустить | Пропустить значение позиции | Установить бит на 0 |
Рассмотрим пример. Преобразуйте десятичное число 117 в двоичное.
- Десятичное число: 117
- Направление вычисления Слева направо
| Положение бита | значение положения | Сравнение | Десятичное значение | Десятичное значение | Двоичное значение | Двоичное значение |
| 1 | 128 | 128 больше 117 | Пропустить | 0 | Выкл. | 0 |
| 2 | 64 | 0 + 64 = 64 меньше 117 | Добавить | 64 | Вкл. | 1 |
| 3 | 32 | 0 + 64 + 32 = 96 меньше 117 | Добавить | 32 | На | 1 |
| 4 | 16 | 0 + 64 + 32 + 16 = 112 меньше 117 | Добавить | 16 | Вкл. | 1 |
| 5 | 8 | 0 + 64 + 32 + 16 + 8 = 120 больше 117 | Пропустить | 0 | Выкл. 9 0059 | 0 |
| 6 | 4 | 0 + 64 + 32 + 16 + 0 + 4 = 116 меньше 117 | Добавить | 4 | На | 1 |
| 7 | 2 | 0 + 64 + 32 + 16 + 0 + 4 + 2 = 118 больше, чем 117 | Пропустить | 0 | Выкл. | 0 |
| 8 | 1 | 0 + 64 + 32 + 16 + 0 + 4 + 0 + 1 = 117 эквивалентно 117 | Добавить | 1 | На | 1 |
После того, как вышеупомянутое сравнение сделано в черновой бумаге: —
- Чтобы записать данное число в десятичном формате, просуммируйте все значения десятичного поля и запишите результат.В этом примере это будет 0 + 64 + 32 + 16 + 0 + 4 + 0 + 1 = 117 .
- Чтобы записать данное число в двоичном формате, запишите все значения двоичного поля слева направо. В этом примере это будет 11110101 .
Преобразование двоичного числа в десятичное
Чтобы преобразовать двоичное число в десятичное, просуммируйте значения всех битов. Возьмем пример. Преобразуйте двоичное число 10101010 в десятичное число.
- Данное двоичное число — 10101010
- Направление вычисления Слева направо
| Положение бита | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| значение позиции | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| В двоичном формате | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Статус бита | Включен | Выкл. | Вкл. | Выкл. | Вкл. | Выкл. | Вкл. | Выкл. |
| Если состояние бита включено, используйте значение позиции в десятичном виде | 128 | 0 | 32 | 0 | 8 | 0 | 2 | 0 |
Двоичное число 10101010 равно числу 170 (128 + 0 + 32 + 0 + 8 + 0 + 2 + 0) в десятичной системе.
Практика для вас
- Выберите любое число от 0 до 255 и преобразуйте его в двоичную форму.
- Выберите любую комбинацию от 00000000 до 11111111 и преобразуйте ее в десятичное число.
Преобразование IP-адреса и маски подсети
Как мы знаем, IP-адрес и маска подсети состоят из 4 отдельных октетов, разделенных точками. Мы можем использовать вышеуказанные методы для индивидуального преобразования всех октетов. После преобразования всех четырех октетов мы можем снова объединить их, разделив их точками.
Вот и все для этого руководства. Если у вас есть какие-либо комментарии, предложения или отзывы об этом руководстве, напишите мне. Если вам нравится этот урок, не забудьте поделиться им в своей любимой социальной сети.
.
