Что такое действующее значение переменного напряжения. Как рассчитать действующее напряжение синусоидального тока. Какая связь между амплитудным и действующим напряжением. Почему действующее напряжение важно на практике.
Что такое действующее напряжение переменного тока
Действующее напряжение переменного тока — это такое эквивалентное постоянное напряжение, которое за период переменного тока выделяет на активном сопротивлении такое же количество тепла, что и данное переменное напряжение. Другими словами, это среднеквадратичное значение переменного напряжения.
Действующее напряжение является важной характеристикой переменного тока, так как:
- Позволяет сравнивать переменные напряжения разной формы
- Используется для расчета мощности и энергии в цепях переменного тока
- Его показывают измерительные приборы (вольтметры)
- Им оперируют при проектировании электрооборудования
Формула расчета действующего напряжения
Для синусоидального напряжения действующее значение связано с амплитудным следующим соотношением:
Uдейств = Um / √2 ≈ 0.707 Um
где Um — амплитудное значение напряжения.
Для напряжения произвольной формы действующее значение определяется как:
Uдейств = √(1/T ∫0T u2(t)dt)
где T — период, u(t) — мгновенное значение напряжения.
Соотношение между амплитудным и действующим напряжением
Для синусоидального напряжения связь между амплитудным и действующим значением описывается коэффициентом √2:
- Um = √2 * Uдейств ≈ 1.41 * Uдейств
- Uдейств = Um / √2 ≈ 0.707 * Um
Это соотношение справедливо только для синусоидального напряжения. Для других форм сигнала коэффициент может отличаться.
Почему используется действующее, а не амплитудное значение
Действующее значение напряжения используется чаще амплитудного по следующим причинам:
- Позволяет легко рассчитывать мощность и энергию
- Дает возможность сравнивать переменные и постоянные напряжения
- Его проще измерять на практике
- Оно характеризует реальный тепловой эффект переменного тока
Как измерить действующее напряжение
Существует несколько способов измерения действующего напряжения переменного тока:
- С помощью электромагнитных вольтметров
- Цифровыми мультиметрами
- Специальными измерителями True RMS
- Осциллографом с функцией измерения RMS
Большинство бытовых и промышленных вольтметров показывают именно действующее значение напряжения.
Применение действующего напряжения на практике
Понятие действующего напряжения широко используется в электротехнике:
- Номинальное напряжение сети 220 В — это действующее значение
- Мощность электроприборов указывается для действующего напряжения
- Расчет нагрева проводов ведется по действующему току
- Электросчетчики измеряют энергию по действующим значениям
Поэтому важно понимать физический смысл и уметь рассчитывать действующее напряжение для различных сигналов.
Действующее напряжение для разных форм сигнала
Соотношение между амплитудным и действующим напряжением зависит от формы сигнала:
- Синусоидальный: Uдейств = 0.707 * Um
- Прямоугольный: Uдейств = Um
- Треугольный: Uдейств = 0.577 * Um
- Пилообразный: Uдейств = 0.577 * Um
Для сложных несинусоидальных сигналов действующее значение рассчитывается по общей формуле интегрирования.
Влияние формы сигнала на измерения
Форма сигнала может влиять на точность измерения действующего напряжения:
- Большинство мультиметров калибровано на синусоидальный сигнал
- При измерении несинусоидальных напряжений возможны погрешности
- Для точных измерений используют приборы True RMS
- Осциллограф позволяет увидеть реальную форму сигнала
Поэтому при работе с несинусоидальными напряжениями важно учитывать особенности измерительных приборов.
Действующее и среднее значение напряжения
Действующее значение напряжения не следует путать со средним. Для синусоидального сигнала:
- Среднее значение за период равно нулю
- Среднее выпрямленное значение Uср = 0.637 * Um
- Действующее значение Uдейств = 0.707 * Um
Действующее значение всегда больше среднего выпрямленного. Это важно учитывать при расчетах и измерениях.
Заключение
Действующее напряжение является ключевой характеристикой переменного тока. Оно позволяет сравнивать разные сигналы, рассчитывать мощность и энергию. В большинстве практических применений оперируют именно действующими, а не амплитудными значениями напряжения и тока. Поэтому важно понимать физический смысл этой величины и уметь ее определять для различных форм сигнала.
Действующее значение напряжения
В проводниках переменного тока основные электродинамические показатели постоянно изменяются. Вследствие этого возникает вопрос: как можно адекватно оценить напряжение и силу тока в конкретной электроцепи? Так как моментальные и простые усредненные значения недостаточны для полной характеристики электротока, в электродинамике вводят такое понятие, как действующее значение тока.
- Что такое действующее значение напряжения
- Действующее значение тока
- Какие коэффициенты характеризуют переменное напряжение
- Параметры переменного тока
- Формула действующего значение тока
Что такое действующее значение напряжения
Изменение значений переменного тока обычно описывается синусоидальной линией с определенным периодом (Т) и амплитудой напряжения (Um). Кроме напряжения, электрический ток также характеризуется силой (I) и мощностью (P). Для постоянного электротока эти параметры складываются в простую формулу:P = U × I.
При имеющемся сопротивлении в цепи и с учетом закона Ома (I = U / R) мощность, расходуемую электропотребителем. Можно определить как отношение квадрата напряжения к сопротивлению:
P = U2 / R.
В случае же переменного тока не все так однозначно. С изменением напряжения изменяется и мощность — в каждый момент времени (t) значения отличаются друг от друга. В такой ситуации для оценки электротока удобнее всего использовать его мощностные и тепловые характеристики. Поэтому действующее значение переменного тока приравнивается к работе постоянного тока, производимой за временной промежуток одного периода переменного тока.
При существующей активной нагрузке, независящей от частоты тока и напряжения мгновенная мощность определяется по формуле:
P(t) = U(t) × I(t) = U2 / R
Введя амплитудное значение напряжения, и учитывая период синусоидальной функции, мгновенную мощность можно определить следующим образом:
P(t) = (Um × sin(2π × 1/T))2 / R
Однако этот параметр для переменного тока — не имеет особой важности.
Для практических расчетов обычно берут мощность, усредненную за период. Как раз этот показатель указывается на бытовых электроприборах.
Формула усредненной мощности:
Здесь же представлена формула расчета действующего напряжения.
В вышеприведенной формуле интегрирование квадратной величины с последующим извлечением корня дает понять, почему эффективная величина напряжения также носит название «среднеквадратичной». При этом интегральное выражение под корнем является усредненной мощностью, пропорциональной сопротивлению.
Относительно синусоиды напряжение это интегральное выражение упрощается до формулы:
Именно эти цифры показывают вольтметры, настроенные на измерение проводников переменного тока.
Действующее значение тока
Применив метод интегрирования к квадратам амплитудной силы тока и синусу круговой частоты и выведя среднеквадратичные величины, можно получить действующее значение силы тока:
org/ImageObject»>Сравнивая тепловые эффекты постоянного и переменного электротоков, взятые за одинаковый временной отрезок и при одинаковой активной нагрузке, можно обнаружить, что равенство тепловых характеристик проводников того и другого типа достигается в том случае, если сила линейного тока будет меньше максимальных силовых значений в цепи переменного тока в 1,414 раз.
Какие коэффициенты характеризуют переменное напряжение
Помимо базовых параметров переменного тока, в электротехнике принято производить измерения электросигналов, включая выходные напряжения выпрямителей и импульсы различной формы.
Амплитудное значение напряжения
Под амплитудным или пиковым напряжением подразумевают максимальный показатель U за один период синусоиды:
Um = max(|u(t)|)
Для измерения данного параметра обычно используют вольтметр импульсного типа или осциллограф.
Мгновенное значение тока
Параметр обозначает силу тока или напряжение в конкретный временной момент (u(t), i(t)). В зависимости от динамики электрического сигнала, для определения мгновенных значений могут применяться малоинерционные вольтметры, а также шлейфовые или электронно-лучевые осциллографы.
Среднее значение
Показатель является постоянной составляющей переменного тока. Для напряжения оно рассчитывается по следующей интегральной формуле:
Для синусоидного напряжения с симметричной формой среднее значение равно нулю. Это можно определить с помощью обычного вольтметра. В геометрическом виде это может быть выражено как отношение разности площадей с обеих сторон оси t к периоду. Под названием напряжения смещения величина часто применяется в радиоэлектронике и обозначает напряжение, прилагаемое к электроду для выработки конкретных параметров постоянного электротока.
Среднеквадратичное значение
Среднеквадратичные интегральные величины силы тока и напряжения используются достаточно часто, вследствие их удобства для практического определения электродинамических характеристик в реальных проводниках.
Они основываются на сравнении работы постоянного и переменного тока с активной нагрузкой и определенными величинами U и I.
К примеру, лампочка или обогреватель будут выполнять одинаковую работу по освещению или обогреву как в сети переменного тока со стандартным напряжением 220 В, так и в цепи постоянного тока, если на нее подать такое же напряжение.
Напряжение в электросети обычно выражают в среднеквадратичном исчислении. Большинство приборов, измеряющих силу тока и напряжение, спроектированы под действующие показатели. Отдельные типы амперметров и вольтметров способны показывать верные эффективные значения только для синусоидального тока. В универсальных устройствах, работающих с любыми формами электросигнала, измерение осуществляется с помощью термопреобразователя. При этом фиксируется температура нагревателя, создающего определенное сопротивление.
Кроме того, в измерительных приборах может быть реализован метод возведения в квадрат мгновенного значения, после чего величина усредняется по временному периоду, а затем выводится квадратный корень.
Средневыпрямленное значение
Величина определяется как взятое по модулю среднеарифметическое всех мгновенных значений напряжения. Для одного периода средневыпрямленная величина равна сумме площадей сверху и снизу оси времени. Хотя параметр не находит практического применения, именно он фиксируется по факту большинством измеряющих устройств магнитоэлектрического принципа действия, несмотря на то, что их шкалы имеют градацию для действительных значений. При этом эффективные и средневыпрямленные значения оказываются близки друг к другу только в случае синусоидального напряжения.
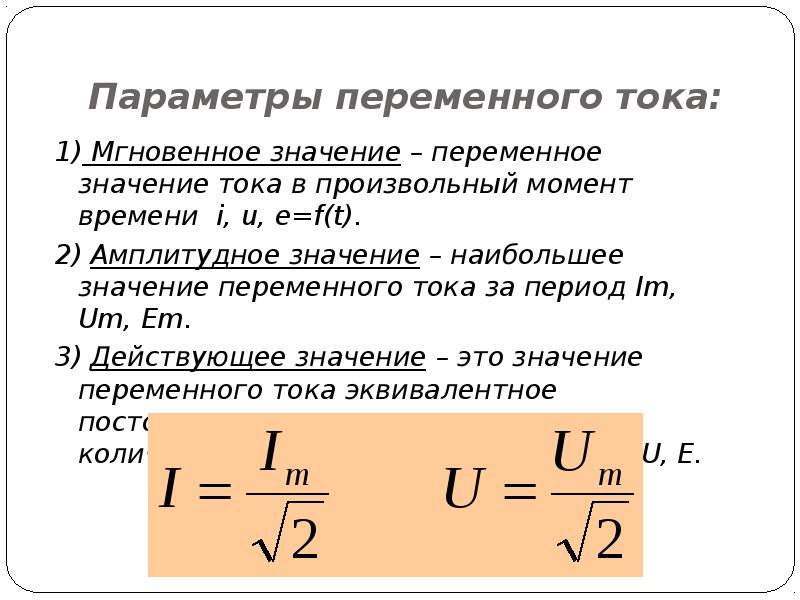
Параметры переменного тока
Синусоидальные гармоники являются типичной характеристикой переменного тока. В этом отношении по синусоиде происходит изменение электродвижущей силы и тока при определенной нагруженности цепи. При этом динамика ЭДС может быть описана следующими параметрами:
• Период — время, за которое электродинамические показатели изменяются по полному циклу. Он напрямую связан с частотой вращения роторного механизма генератора электротока.
• Частота — определяется как число периодов за одну единицу времени. Современные стандарты для электросетей предписывают частоту переменного тока в 50 герц. Это означает, что за 1 секунду ток меняет направление 50 раз, а один период длится 20 миллисекунд.
• Амплитуда — максимальная величина гармоники переменного тока. В строгом смысле параметр применим исключительно к синусоидальному изменению. С некоторыми допущениями амплитуда может быть определена и для других форм электросигнала. За один период электродвижущая сила дважды доходит до пиковых значений и обозначается как Em+ и Em- соответственно положению полупериодов.
• Угловая частота — скорость колебательного движения, измеряемая в радианах в секунду. При этом один период синусоиды приравнивается к значению 2π. Общая формула угловой частоты: ω = 2π / Т.
• Фаза колебаний — стадия синусоидальной волны, принимаемая как аргумент функции тока, которая отсчитывается от среднего нулевого значения. Величина фазы колебаний, используемая для определения синуса или косинуса фазового угла, описывается формулой φ = ωt.
Как в случае со среднеквадратичными значениями тока и напряжения, через основные характеристики определяется и среднее значение ЭДС, которое сводится к следующему выражению:
Формула действующего значение тока
Среднеквадратичные показатели переменного тока определяется как отношение амплитудного значения тока к корню из 2.
Схожим образом обозначаются эффективные значения напряжения и ЭДС.
Действительные значения синусоидального тока помогают производить практическую оценку и описание электроцепей. Несмотря на сложность составляющих понятий, эти величины сводятся к простым выражениям. Номинальное напряжение электрических сетей и приборов представляет собой как раз среднеквадратичное значение. Умножив указанный вольтаж на корень из 2, можно узнать амплитудное значение напряжения электроустройств.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.
Действующее значение тока. Действующее значение напряжения
- Details
- 08 March 2017
Господа, в прошлой статье мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока. Сегодня про него и поговорим!
Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да.
Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.
Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток.
Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.
Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда Аm и период Tпериод (ну или частота f). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период Tпериод нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз. Допустим, мы насчитали, что за один период Tпериод синусоидального тока выделится Q джоулей тепла.
А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время Tпериод выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?
Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье, закон изменения мощности переменного тока равен
Количество выделившейся энергии при работе тока за время Tпериод – соответственно, равно интегралу за время периода Tпериод:
Господа, теперь нам надо взять этот интеграл.
Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .
Итак, как его нам брать? Ну, величины Im2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:
Погнали считать!
Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.
Итак, имеем
Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!
Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю.
Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.
Итак, отбрасывая интеграл с косинусом, получаем
Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен
И, таким образом, получаем ответ
Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой Im в течении периода Tпериод. Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время Tпериод выделится то же самое количество энергии Q.
Поэтому мы можем записать
Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца. А мы тем временем выразим действующее значение тока Iдейств. из этого выражения, предварительно сократив все, что можно
Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.
Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения. При этом у нас зависимость мощности от времени примет вот такой вид
Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током.
Итак, действующее значение напряжения синусоидального тока равно
Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.
Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.
Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры, включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда.
Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать
Отсюда получаем
Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.
Рисунок 1 – Закон изменения напряжения в розетках
И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.
ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.
Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)
На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц.
Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна
Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.
На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla
Напряжение переменного тока — HomoFaciens
Новости Проект Технологии РобоСпатиум Способствовать Предметный указатель Скачать Ответы Игры Советы по покупкам Контакт
<<< Вихревой ток Собственная индуктивность >>>
Напряжение постоянного тока
В главе о напряжении мы рассматривали его как неизменную во времени величину.
В качестве причины возникновения напряжения мы упомянули разность потенциалов внутри электрического поля точечного заряда. В последующих главах об электрическом токе, сопротивлении и мощности мы также считали напряжение постоянной величиной на отдельных компонентах электрических сетей.
В главе об индукции мы видели, что напряжение, создаваемое с помощью постоянного магнита и контура проводника, действительно непостоянно. В этом случае напряжение называется
Напряжение переменного тока
Напряжение, полярность которого меняется через равные промежутки времени и среднее значение которого в течение одного промежутка времени равно нулю, называется напряжением переменного тока. Точная прогрессия кривой не имеет значения. Рисунок 1:
Прогресс трех кривых напряжения переменного тока с одинаковым периодом времени и пиковым напряжением:
Синяя кривая показывает синусоидальный ход, красная кривая образует треугольники с осью X (= треугольное напряжение), а зеленая кривая образует прямоугольники с осью X (= прямоугольное напряжение).
Кроме того, кривые симметричны , что означает, что если вы перевернете кривую вокруг оси X и переместите ее в течение половины периодического времени, развитие кривой будет идентично исходной кривой.
Терминология
Период — Период — это наименьший интервал времени или длины, на котором повторяются значения функции.Периодическое время — Периодическое время (T) отмечает наименьший возможный интервал времени, в течение которого значения функции повторяются.
[3.25]
T — периодическое время, n — целочисленное значение
Частота — Частота (f) описывает количество периодов в секунду. Единицей частоты является Герц (Гц), названный в честь немецкого физика Генриха Герца. Корреляция между частотой и периодическим временем определяется выражением:
[3.26]
f — Частота, T — периодическое время
Размах напряжения — Размах напряжения (U PP ) равен разнице между самым верхним положительным и отрицательным значением кривой.
Пиковое напряжение — Пиковое напряжение (U P ) — это максимальное значение напряжения, независимое от знака значения.
Действующее напряжение, среднеквадратичное значение (RMS) — Действующее напряжение (U eff ) представляет собой квадратный корень из среднего арифметического (среднего) квадратов значений кривой. Использование «трюка» для вычисления квадратного корня из квадратов устраняет отрицательный знак (квадратный корень из -1 2 дает +1).
Выражение условия, при котором среднее значение за один период времени становится равным нулю:
[3.27]
Где находится:T — периодическое время, т 1 — необязательный момент времени
Чтобы различать напряжение постоянного и переменного тока, для напряжения переменного тока используется символ U с тильдой в качестве индекса. U ˜ указывает напряжение переменного тока.
Рисунок 2:
Характерные параметры синусоидального переменного напряжения.
Для изменения напряжения (виртуального) эксперимента с катушкой индуктивности, движущейся вдоль постоянного магнита, мы получаем:
Рисунок 3:
Если бы мы возобновили эксперимент, как только он закончился, результатом тоже было бы переменное напряжение. Позже мы увидим, что подобная процедура выполняется внутри генератора.
В последующих главах мы увидим, как можно выпрямить переменное напряжение. Результат дает следующую кривую:
Рисунок 4:
Выпрямленное синусоидальное напряжение:
Согласно определению, это уже не переменное напряжение, хотя напряжение периодически изменяется. Ни одно значение не ниже нуля, что означает, что полярность не изменена. В главе о напряжении мы заметили, что напряжение — это энергия, используемая для перемещения заряженной частицы через две точки внутри электрического поля.
Используя другую базовую точку в качестве эталона, этот вид кривой снова дает нам переменное напряжение (пунктирная линия). Новая базовая линия делит кривую таким образом, что площади выше и ниже линии равны.
Переменный ток
Как упоминалось ранее несколько раз, появление напряжения вызывает электрический ток. Корреляция между напряжением переменного тока и соответствующим током, протекающим через различные линейные компоненты электрической сети, будет рассмотрена несколькими главами позже.<<< Вихревой ток Собственная индуктивность >>>
Новости Проект Технологии РобоСпатиум Способствовать Предметный указатель Архивы Скачать Ответы Игры Ссылки Советы по покупкам Контакт Выходные данные
Мощность в цепях переменного тока
Мощность в цепях переменного тока Как и в случае с мощностью постоянного тока, мгновенная электрическая мощность в цепи переменного тока определяется выражением P = VI, но эти величины непрерывно изменяются. , где φ — фазовый угол между током и напряжением, а где V и I — эффективные или среднеквадратичные значения напряжения и тока. Срок 9ампер.
| Индекс Цепи переменного тока | ||
|
Почти всегда требуемая мощность в цепи переменного тока — это средняя мощность, которая определяется как Как и в цепях постоянного тока, мгновенная электрическая мощность в цепи переменного тока определяется выражением P=VI, где V и I — мгновенные значения напряжения и тока.
и используя идентификатор триггера мощность становится: Усреднение этой мощности за полный цикл дает среднюю мощность. | Индекс Цепи переменного тока | ||
| Назад |
Обычно средняя мощность представляет собой интересующую мощность в цепях переменного тока. Поскольку выражение для мгновенной мощности непрерывно меняется со временем, среднее значение должно быть получено путем интегрирования. Усреднение по одному периоду T синусоидальной функции даст среднюю мощность.
| Индекс Цепи переменного тока | ||||||
| Назад |
Второй член в приведенном выше выражении для мощности в среднем равен нулю, поскольку он является нечетной функцией t. Среднее значение первого члена равно
