Действующие значения тока и напряжения это. Действующие значения тока и напряжения в цепях переменного тока: полное руководство

Что такое действующее значение тока и напряжения. Как рассчитать действующее значение синусоидального сигнала. Почему действующее значение важно для анализа цепей переменного тока. Какие формулы используются для нахождения действующих значений различных сигналов.

Что такое действующее значение тока и напряжения

Действующее значение переменного тока или напряжения — это такое значение постоянного тока или напряжения, которое выделяет на активном сопротивлении такое же количество тепла за период, что и данный переменный ток или напряжение.

Другими словами, действующее значение переменного тока численно равно такому постоянному току, который за период выделяет на сопротивлении такое же количество теплоты, что и данный переменный ток.

Почему важно знать действующее значение

Действующее значение является важной характеристикой переменного тока по нескольким причинам:

• Оно позволяет сравнивать эффективность переменного и постоянного токов
• Большинство измерительных приборов показывают именно действующее значение
• Номинальные значения электрооборудования обычно указываются в действующих значениях
• Расчет мощности и энергии в цепях переменного тока производится через действующие значения

Как рассчитать действующее значение синусоидального сигнала

Для синусоидального тока или напряжения действующее значение связано с амплитудным значением следующим соотношением:

I_д = I_m / √2 ≈ 0.707 * I_m

U_д = U_m / √2 ≈ 0.707 * U_m

где I_m и U_m — амплитудные значения тока и напряжения.

Действующее значение несинусоидальных сигналов

Для несинусоидальных периодических сигналов действующее значение определяется как квадратный корень из среднего значения квадрата сигнала за период:

I_д = √[(1/T) * ∫(0 до T) i²(t)dt]

где T — период сигнала, i(t) — мгновенное значение тока.

Формулы для расчета действующих значений различных сигналов

Для наиболее распространенных форм сигналов действующие значения могут быть рассчитаны по следующим формулам:

• Прямоугольный импульс: I_д = I_m * √D, где D — коэффициент заполнения
• Треугольный сигнал: I_д = I_m / √3 ≈ 0.577 * I_m
• Пилообразный сигнал: I_д = I_m / √3 ≈ 0.577 * I_m
• Трапецеидальный сигнал: I_д = I_m * √[(t1 + 3t2 + t3) / (3T)], где t1, t2, t3 — длительности участков сигнала

Как измерить действующее значение

Существует несколько способов измерения действующих значений тока и напряжения:

1. С помощью специальных измерительных приборов — вольтметров и амперметров действующего значения
2. Методом сравнения с постоянным током, дающим такой же тепловой эффект
3. Расчетным путем по известной форме сигнала
4. С помощью осциллографа, позволяющего определить форму сигнала

Большинство современных цифровых мультиметров показывают именно действующее значение переменного тока и напряжения.

Применение действующих значений в расчетах

Действующие значения широко используются при анализе и расчете цепей переменного тока. Некоторые примеры применения:

• Расчет активной мощности: P = I_д² * R
• Определение напряжения на участках цепи: U_д = I_д * Z
• Расчет потерь энергии в проводниках: W = I_д² * R * t
• Выбор сечения проводов по допустимому нагреву

Особенности действующих значений в трехфазных цепях

В трехфазных цепях действующие значения линейных и фазных токов и напряжений связаны следующими соотношениями:

• I_л = √3 * I_ф (при соединении звездой)
• U_л = √3 * U_ф (при соединении звездой)
• I_л = I_ф (при соединении треугольником)
• U_л
  = U_ф (при соединении треугольником)

где I_л, U_л — линейные ток и напряжение, I_ф, U_ф — фазные ток и напряжение.

Сравнение действующего, среднего и амплитудного значений

Для синусоидального сигнала существуют следующие соотношения между различными значениями:

• I_д = 0.707 * I_m
• I_ср = 0.637 * I_m
• I_д = 1.11 * I_ср

где I_д — действующее значение, I_m — амплитудное значение, I_ср — среднее за полупериод значение.

Действующие значения в импульсных источниках питания

В импульсных источниках питания действующие значения токов и напряжений играют важную роль:

• Определяют нагрев элементов
• Влияют на выбор компонентов
• Учитываются при расчете КПД
• Используются для оценки пульсаций выходного напряжения

Для расчета действующих значений в импульсных преобразователях обычно используют специализированное программное обеспечение.

Заключение

Действующие значения тока и напряжения являются важнейшими характеристиками в цепях переменного тока. Их знание необходимо для правильного анализа работы электрических цепей и устройств, расчета мощности и энергии, выбора элементов. Умение определять действующие значения для различных форм сигналов — важный навык для инженеров-электриков и электронщиков.

Действующее, среднеквадратичное, эффективное напряжение или ток, что это такое

Электрический ток — направленное (упорядоченное) движение частиц или квазичастиц — носителей электрического заряда.

Среднее значение переменного синусоидального напряжения или тока

Говоря о величине, изменяющейся по синусоидальному (гармоническому) закону, можно за половину периода определить ее среднее значение. Поскольку ток в сети у нас в подавляющем большинстве случаев синусоидальный, то для этого тока также легко может быть найдена средняя его величина (за половину периода), достаточно прибегнуть к операции интегрирования, установив пределы от 0 до Т/2. В результате получим:

Подставив Пи = 3,14, найдем среднюю, за половину периода, величину синусоидального тока в зависимости от его амплитуды. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:

Действующее значение тока I или напряжения U

Однако среднее значение не так широко применяется на практике, как действующее значение синусоидального тока или напряжения. Действующее значение синусоидально меняющейся во времени величины — есть среднеквадратичное, другими словами — эффективное ее значение.

Эффективное (или действующее) значение тока или напряжения находится так же, путем интегрирования, но уже по отношению к квадратам, и с последующим извлечением квадратного корня, причем пределы интегрирования теперь — целый период синусоидальной функции.

Итак, для тока будем иметь:

Подставив значение корня из 2, получим формулу для нахождения эффективного (действующего, среднеквадратичного) значения тока, напряжения, ЭДС — по отношению к амплитудному значению. Эту формулу можно встретить очень часто, ее используют всюду в расчетах, связанных с цепями переменного синусоидального тока:

С практической точки зрения, если сравнить тепловое действие тока переменного синусоидального с тепловым действием тока постоянного непрерывного, на протяжении одного и того же периода времени, на одной и той же активной нагрузке, то выяснится, что выделенная за период синусоидального переменного тока теплота окажется равна выделенной за это же время теплоте от тока постоянного, при условии, что величина постоянного тока будет меньше амплитуды тока переменного в корень из 2 раз:

Это значит, что действующее (эффективное, среднеквадратичное) значение синусоидального переменного тока численно равно такому значению постоянного тока, при котором тепловое действие (выделяемое количество теплоты) этого постоянного тока на активном сопротивлении за один период синусоиды равно тепловому действию данного синусоидального тока за тот же период.

Аналогичным образом находится действующее (эффективное, среднеквадратичное) значение синусоидального напряжения или синусоидальной ЭДС.

Подавляющее большинство современных портативных измерительных приборов, измеряя переменный ток или переменное напряжение, показывают именно действующее значение измеряемой величины, то есть среднеквадратичную величину, а не ее амплитуду и не среднее значение за полпериода.

Если других уточняющих настроек на приборе нет, а стоит значок ~I или ~U – измерены будут действующие значения тока и напряжения. Обозначения для конкретно амплитуды или конкретно действующего — Im (m — maximum – максимум, амплитуда) или Irms (rms — Root Mean Square – среднеквадратичное значение).

Ранее ЭлектроВести писали, что компания Tesla выпустила новое компактное зарядное устройство Wall Connector with 14-50 Plug, которое подключается непосредственно к розетке, благодаря чему ее без проблем можно возить с собой использовать по мере необходимости. Стоимость новинки составляет те же $500, что и для обычной настенной зарядки Wall Connector.

По материалам: electrik.info.

Как определяются действующие значения тока и напряжения — Dudom

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r .

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m

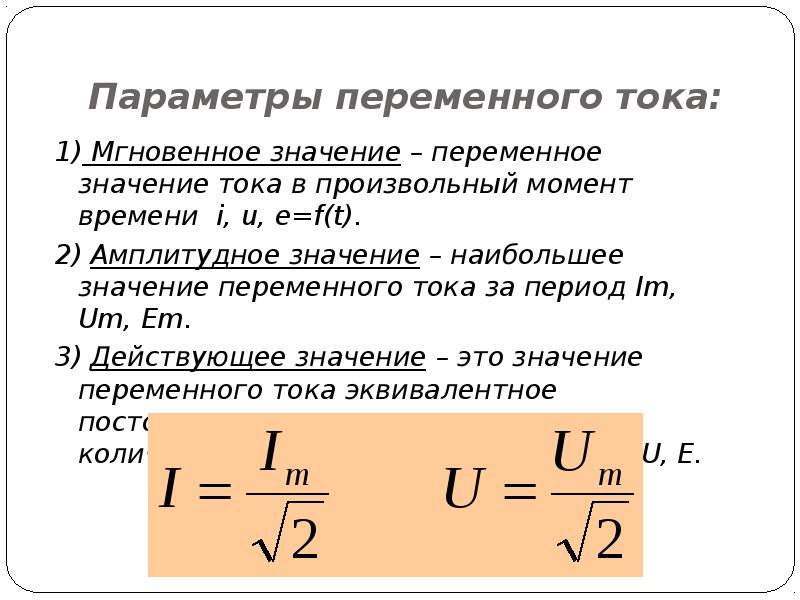
Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √ 2 E= Em / √ 2

Действующие значения переменных величин обозначаются прописными буквами без индексов ( I , U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. <2>dt>>.>

Содержание

Действующее значение в типичных случаях [ править | править код ]

Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.

Синусоида [ править | править код ]

I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , <displaystyle I=<frac <1><sqrt <2>>>cdot I_approx 0<,>707cdot I_,>

Прямоугольная форма [ править | править код ]

Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:

I = I m D , <displaystyle I=I_<sqrt >,>

В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):

I = I m 0 , 5 ≈ 0 , 707 ⋅ I m . <displaystyle I=I_<sqrt <0,5>>approx 0,707cdot I_.>

Для тока, имеющего форму двухполярного меандра:

I = I m . <displaystyle I=I_.>

Треугольная форма [ править | править код ]

Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):

I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . <displaystyle I=<frac <1><sqrt <3>>>cdot I_approx 0<,>577cdot I_.>

Трапециевидная форма [ править | править код ]

Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:

I = I m t 1 + 3 t 2 + t 3 3 T , <displaystyle I=I_<sqrt <frac +3t_<2>+t_<3>><3T>>>,> 1>

Дугообразная форма [ править | править код ]

Для тока имеющего форму дуги (половины окружности):

I = I m 2 3 ≈ 0,816 ⋅ I m . <displaystyle I=I_<sqrt <frac <2><3>>>approx 0<,>816cdot I_.>

Дополнительные сведения [ править | править код ]

В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).

Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания [1] .

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r .

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m

Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √ 2 E= Em / √ 2

Действующие значения переменных величин обозначаются прописными буквами без индексов ( I , U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.

Простая формула RMS Напряжение и ток Цепь переменного тока

Идея эффективного значения возникает из-за необходимости измерять эффективность источника напряжения или тока при подаче мощности на резистивную нагрузку. Здесь мы изучим термин среднеквадратичное напряжение и ток.

Эффективное значение периодического тока представляет собой постоянный ток, который передает на резистор ту же среднюю мощность, что и периодический ток.

Сначала обязательно прочитайте, что такое цепь переменного тока.

Существует несколько типов мощности в цепи переменного тока:

1. Максимальная средняя передаваемая мощность
2. Напряжение и ток RMS
3. Коэффициент мощности и полная мощность
4. Треугольник мощности и комплекс мощности
5. Сохранение мощности переменного тока

Вычислить среднеквадратичное значение напряжения и тока

На рис. (1) цепь (a) имеет переменный ток, а цепь (b) — постоянный ток. Наша цель — найти I _eff , которые передают на резистор R ту же мощность, что и синусоида и .

Рисунок 1. Найдите эффективного тока: (a) Схема переменного тока, (b) Цепь постоянного тока

Средняя мощность, поглощенная резистором в цепи AC, составляет

.

(1)

while the power absorbed by the resistor in the dc circuit is

(2)

Приравнивая выражения в уравнениях. (1) и (2) и решение для I _EFF , мы получаем

(3)

находится так же, как текущий; то есть

(4)

Это указывает на то, что эффективное значение является (квадратным) корнем из среднего (или среднего)0003 квадрат периодического сигнала.

Таким образом, действующее значение часто называют среднеквадратичным значением или среднеквадратичным значением для краткости; и мы пишем

(5)

Для любой периодической функции x (T) В целом значение RMS приводится

4444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444400444444444н. )

Действующее значение периодического сигнала является его среднеквадратичным (среднеквадратическим) значением.

Уравнение (6) утверждает, что для нахождения среднеквадратичного значения x(t) сначала нужно найти его квадрат x ² , а затем найти среднее значение, или

33

(7)

и квадратный корень (√) из этого среднего. Среднеквадратичное значение константы — это сама константа.

Для синусоиды i(t) =  I _м COS ωt, эффективное значение OR RMS составляет

(8)

Аналогично, для В (T) = 9003 V _M 9 9000. (9)

Имейте в виду, что уравнения (8) и (9) действительны только для синусоидальных сигналов.

Прежде чем двигаться дальше, вспомните все уравнения, которые у нас были в формулах мгновенной мощности и средней мощности.

The average power can be written in terms of the rms values ​​

(10)

Similarly, the average power absorbed by a resistor R can be written as

(11)

Когда задается синусоидальное напряжение или ток, это часто выражается в терминах его максимального (или пикового) значения или его среднеквадратичного значения, поскольку его среднее значение равно нулю.

Энергетика определяет векторные величины в терминах их среднеквадратичных значений, а не пиковых значений.

Например, 110 В, доступные в каждом домашнем хозяйстве, представляют собой среднеквадратичное значение напряжения от энергетической компании.

При анализе мощности удобно выражать напряжение и ток в их среднеквадратичных значениях.

Кроме того, аналоговые вольтметры и амперметры предназначены для непосредственного считывания среднеквадратичных значений напряжения и тока соответственно.

См. также: коэффициент мощности и полная мощность

Примеры среднеквадратичного значения

Для лучшего понимания рассмотрим примеры ниже:

1. Определите среднеквадратичное значение формы волны тока на рисунке (2). Если ток проходит через резистор сопротивлением 2 Ом, найти среднюю мощность, поглощаемую резистором.

Рисунок 2

Решение:
Период волны — T = 4. В течение периода, мы можем записаться.0005

Среднеквадратичное значение равно

Мощность, поглощаемая резистором 2 Ом, составляет

2. Форма волны показана на рисунке (3) — это полупериодная выпрямленная синусоида. Найдите среднеквадратичное значение и количество средней мощности, рассеиваемой на резисторе 10 Ом.

Рисунок 3

Решение:
Период напряжения.0005

Но sin ² t = ½(1 – cos 2 t ). Следовательно,

Средняя потребляемая мощность равна

 

Анализ генерации переменного тока: эффективные значения, угол сдвига фаз и частота

Анализ процесса выработки электроэнергии переменного тока и переменного тока, который мы используем почти во всех аспектах нашей жизни, необходим для лучше понять, как мощность переменного тока используется в современных технологиях.

Действующие значения

Выходное напряжение генератора переменного тока можно выразить двумя способами. Один из них — графически с использованием синусоиды (рис. 3). Второй способ — алгебраически по уравнению e = E _max sin ωt, которые будут рассмотрены далее в тексте.

Рисунок 3: Синусоида напряжения

Когда напряжение вырабатывается генератором переменного тока, результирующий ток изменяется пропорционально напряжению. Когда катушка генератора вращается на 360°, выходное напряжение проходит один полный цикл. За один цикл напряжение увеличивается от нуля до E в одном направлении, уменьшается до нуля, увеличивается до E _max в обратном направлении (отрицательное E _max ), а затем снова уменьшается до нуля. Значение Е _max возникает при 90° и называется пиковым напряжением. Время, за которое генератор совершает один цикл, называется периодом, а количество циклов в секунду называется частотой (измеряется в герцах).

Одним из способов обозначения напряжения или тока переменного тока является пиковое напряжение (E _p ) или пиковый ток (I _p ). Это максимальное напряжение или ток для синусоидальной волны переменного тока.

Другое значение, значение размаха (E _p-p или I _p ), представляет собой величину напряжения или диапазона тока, охватываемого синусоидой. Однако значение, наиболее часто используемое для переменного тока, является эффективным значением. Эффективное значение переменного тока — это количество переменного тока, которое производит такой же эффект нагрева, как и равное количество постоянного тока.

Проще говоря, эффективное значение одного ампера переменного тока будет выделять такое же количество тепла в проводнике за заданное время, как один ампер постоянного тока. Нагревательный эффект данного переменного тока пропорционален квадрату тока. Эффективное значение переменного тока можно рассчитать, возведя в квадрат все амплитуды синусоиды за один период, взяв среднее значение этих значений, а затем извлекая квадратный корень. Эффективное значение, являющееся корнем среднего (среднего) квадрата токов, известно как среднеквадратичное или среднеквадратичное значение. Чтобы понять значение эффективного тока, приложенного к синусоиде, обратитесь к рисунку 4.9.0005

Значения I нанесены на верхнюю кривую, а соответствующие значения I ² нанесены на нижнюю кривую. Кривая I ²  имеет вдвое большую частоту, чем I, и изменяется выше и ниже новой оси. Новая ось представляет собой среднее значение I ² , а квадратный корень из этого значения представляет собой среднеквадратичное или эффективное значение тока. Среднее значение равно ½ I _max ² . Тогда среднеквадратичное значение равно

Существует шесть основных уравнений, которые используются для преобразования значения переменного напряжения или тока в другое значение, как указано ниже.

• Среднее значение = пиковое значение x 0,637
• Эффективное значение (RMS) = пиковое значение x 0,707
• Пиковое значение = среднее значение x 1,57
• Эффективное значение (RMS) = среднее значение x 1,11
• Пиковое значение = эффективное значение (RMS) x 1,414
• Среднее значение = эффективное (RMS) x 0,9

Обычно встречающиеся значения тока (I) и напряжения (E) считаются среднеквадратичными значениями; поэтому индекс не используется.

Рисунок 4: Действующее значение тока

Другим полезным значением является среднее значение амплитуды в течение положительной половины цикла.

Уравнение ниже представляет собой математическое соотношение между I _av , I _max и I.

I _av = 0,637 av , E _max и E.

E _av = 0,637 E _max   = 0,9 E

Пример 1:

Пиковое значение напряжения в цепи переменного тока составляет 200 В. Каково среднеквадратичное значение напряжения?

E   =  0,707E _макс.

E = 0,707 x 200 = 141,4 В

Чему равно среднее значение силы тока в цепи?

I _ср = 0,637 I _макс

I _ср = 0,637 x 10 = 6,37 ампер

Фазовый угол

Фазовый угол — это доля периода в градусах, которая прошла с момента прохождения напряжения или тока через заданное значение. Заданное значение обычно равно нулю. Возвращаясь к рисунку 3, примем точку 1 за начальную точку или нулевую фазу. Фаза в точке 2 составляет 30°, в точке 3 — 60°, в точке 4 — 90° и так далее до точки 13, где фаза равна 360° или нулю. Чаще используется термин «разность фаз».

Рис. 5: Соотношение фаз

Разность фаз можно использовать для описания двух разных напряжений с одинаковой частотой, которые проходят через нулевые значения в одном направлении в разное время. На рис. 5 углы по оси обозначают фазы напряжений e ₁ и e ₂ в любой момент времени.

При 120° e ₁ проходит через нулевое значение, которое на 60° опережает e ₂   ( e ₂  равно нулю при 180°). Говорят, что напряжение e ₁ ведет e ₂ на 60 электрических градусов, или можно сказать, что e ₂ отстает от e ₁ на 60 электрических градусов.

Разность фаз также используется для сравнения двух разных токов или тока и напряжения. Если разность фаз между двумя токами, двумя напряжениями или напряжением и током составляет ноль градусов, говорят, что они «синфазны». Если разность фаз отличается от нуля, говорят, что они «не совпадают по фазе».

Расчет напряжения

Приведенное ниже уравнение представляет собой математическое представление напряжения, связанного с любой конкретной ориентацией катушки (индуктора).

E = E _MAX SINθ

, где

E = индуцированный EMF
E _MAX = максимальный индуцированный EMF
θ = угол от ссылки (градусы или Radian ЭДС индукции в катушке создает максимальную ЭДС 120 В, когда угол от точки отсчета составляет 45 °?

e = E _max sinθ

e= 120 В Sin (45)

e = 84,84 В

Максимальное индуцированное напряжение также можно назвать пиковым напряжением E _p . Если (t) — время, за которое катушка поворачивается на угол (θ), то угловая скорость (ω) катушки равна θ/t и выражается в радианах/сек.

Приведенное ниже уравнение является математическим представлением угловой скорости.

θ = ωt

где

ω = угловая скорость (радиан/сек)
t = время поворота на угол от точки отсчета (сек)
θ = угол от точки отсчета (радиан)

Используя законы подстановки, соотношение между наведенным напряжением и максимальным наведенным напряжением , а угловая скорость может быть выражена.

Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между индуцируемым напряжением, максимальным напряжением и угловой скоростью и равно выходной мощности генератора переменного тока.

e = E _max sin(ωt)

где
e = ЭДС индукции (вольты)
E _max = максимальная ЭДС индукции (вольты)
ω = угловая скорость (радиан/сек) t 9029 время поворота на угол от эталона (сек)

Расчет тока

Максимальный индуцированный ток рассчитывается аналогичным образом. Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между максимальным индуцированным током и угловой скоростью.

i = I _max sin(ωt)

где

i = ток индукции (ампер)
I _max = максимальный ток индукции (ампер)
ω = угловая скорость (радиан/с) 9091 t = время поворота на угол от точки отсчета (сек)

Расчет частоты

Частота переменного напряжения или тока может быть напрямую связана с угловой скоростью вращающейся катушки. Единицы угловой скорости — радианы в секунду, а 2π радиан — это полный оборот.

Радиан — это угол, опирающийся на дугу, равную радиусу окружности. Один радиан равен 57,3 градуса. Один цикл синусоидальной волны генерируется, когда катушка вращается на 2π радиан.

Приведенное ниже уравнение представляет собой математическое соотношение между частотой (f) и угловой скоростью (ω) в цепи переменного тока.

ω = 2πf

где

ω = угловая скорость (радиан/с)
f = частота (Гц)

Найдите: 1.