Как найти все делители числа онлайн. Что такое делители числа и для чего они нужны. Как работает калькулятор делителей. Примеры использования калькулятора для поиска делителей больших чисел.
Что такое делители числа и для чего они нужны
Делители числа — это числа, на которые данное число делится без остатка. Например, делителями числа 12 являются 1, 2, 3, 4, 6 и 12. Поиск делителей числа может потребоваться в различных ситуациях:
- При решении математических задач и уравнений
- Для оптимизации вычислений в программировании
- При анализе свойств чисел в теории чисел
- Для равномерного распределения ресурсов или объектов
Знание делителей числа позволяет лучше понять его свойства и структуру. Это может быть полезно в различных областях математики, информатики и прикладных задачах.
Как работает онлайн калькулятор делителей
Онлайн калькулятор делителей позволяет быстро найти все делители заданного числа. Принцип его работы следующий:
- Пользователь вводит число в поле ввода
- Алгоритм программы перебирает все числа от 1 до введенного числа
- Для каждого числа проверяется, делится ли введенное число на него без остатка
- Если деление происходит без остатка, число добавляется в список делителей
- После перебора всех чисел формируется итоговый список всех делителей
Такой подход позволяет быстро найти все делители даже для больших чисел. Калькулятор выполняет вычисления за доли секунды, избавляя пользователя от необходимости делать это вручную.
Примеры использования калькулятора делителей
Рассмотрим несколько примеров использования онлайн калькулятора для поиска делителей чисел:
Пример 1: Делители числа 24
Введем в калькулятор число 24. Результат:
Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24
Как видим, калькулятор быстро нашел все 8 делителей числа 24.
Пример 2: Делители простого числа 17
Введем простое число 17:
Делители числа 17: 1, 17У простого числа всего два делителя — единица и само число.
Пример 3: Делители большого числа
Попробуем найти делители числа 1234567:

Делители числа 1234567: 1, 127, 9721, 1234567
Даже для такого большого числа калькулятор мгновенно нашел все 4 делителя.
Преимущества использования онлайн калькулятора делителей
Использование онлайн калькулятора для поиска делителей имеет ряд преимуществ:
- Высокая скорость вычислений даже для больших чисел
- Отсутствие ошибок, свойственных ручным расчетам
- Возможность быстро проверить результаты своих вычислений
- Удобство использования с любого устройства с доступом в интернет
- Экономия времени при решении математических задач
Как найти делители числа вручную
Хотя онлайн калькулятор значительно упрощает поиск делителей, полезно также уметь находить их вручную. Алгоритм ручного поиска следующий:
- Начните с числа 1 — оно всегда является делителем
- Проверьте деление на 2, 3, 4 и так далее до половины исходного числа
- Если число делится без остатка, запишите его как делитель
- Для каждого найденного делителя запишите также результат деления исходного числа на этот делитель
- Не забудьте добавить само исходное число в конец списка делителей
Этот метод позволяет найти все делители, но может быть трудоемким для больших чисел. Поэтому для сложных случаев рекомендуется использовать онлайн калькулятор.

Интересные факты о делителях чисел
Делители чисел обладают некоторыми интересными математическими свойствами:
- Количество делителей всегда четное, кроме случая полных квадратов
- Сумма всех делителей числа всегда больше самого числа (кроме числа 1)
- Произведение всех делителей числа равно числу в степени половины количества его делителей
- Наибольший делитель числа, не равный самому числу, называется наибольшим собственным делителем
Изучение свойств делителей чисел — важная часть теории чисел и дискретной математики.
Применение знаний о делителях чисел
Знание делителей чисел находит применение во многих областях:
- В криптографии для создания и взлома шифров
- В компьютерных алгоритмах для оптимизации вычислений
- В теории графов для анализа структуры сетей
- В планировании для оптимального распределения ресурсов
- В теории музыки для создания гармоничных композиций
Понимание свойств делителей помогает решать сложные задачи в различных областях науки и техники.
Заключение
Онлайн калькулятор делителей — мощный инструмент для быстрого поиска всех делителей числа. Он значительно упрощает математические вычисления и позволяет сэкономить время при решении задач. Использование такого калькулятора особенно полезно при работе с большими числами или при необходимости часто находить делители в ходе решения задачи.

Тем не менее, важно также понимать принципы поиска делителей вручную и знать основные свойства делителей чисел. Это помогает развивать математическое мышление и лучше понимать структуру чисел.
Независимо от того, используете ли вы онлайн калькулятор или выполняете вычисления вручную, знание делителей чисел остается важным математическим навыком, применимым во многих областях науки и повседневной жизни.
Деление столбиком. Онлайн калькулятор | Математика
Как записывать деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело.
780 : 12 = 65.
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
9027 : 9 = 1003.
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
3000 : 6 = 500.
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340 : 23 = 58 (остаток 6).
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3 : 10 = 0 (остаток 3).
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить
.
Найти количество делителей числа | Рассчитай
Учеников часто просят найти количество делителей числа, но в действительности это полезно не только для учащихся. Подобные вычисления помогают быстро выяснить, как распределить значительный объём чего-то на несколько равных частей. К тому же можно узнать, сколько именно таких равных частей вообще может быть.
Заниматься поиском всех делителей числа в реальной жизни нередко приходится бухгалтерам и руководителям предприятий, когда они распределяют поступившую прибыль. Такие же расчёты очень полезны для самопроверки тем, кто постоянно имеет дело с разными вычислениями. Например, в строительстве при создании какого-нибудь проекта. Или же при проведении разных экспериментов, как теоретических, так и практических.
Такие же расчёты очень полезны для самопроверки тем, кто постоянно имеет дело с разными вычислениями. Например, в строительстве при создании какого-нибудь проекта. Или же при проведении разных экспериментов, как теоретических, так и практических.
А кому ещё нужно искать количество делителей числа?
С этими расчётами периодически сталкиваются студенты, особенно если для них математика не относится к профильным предметам. Такие вычисления делают, разумеется, и преподаватели при проверке работ. Им нередко приходится обрабатывать большое количество домашних заданий, контрольных, курсовых. И всего вычислений оказывается столько, что в них очень легко запутаться. В такой ситуации калькулятор поможет проверить себя.
Программа нужна далеко не только тем, кто не умеет находить делители самостоятельно. В первую очередь она помогает тем, кто сильно загружен и может пропустить ошибку просто из-за большого объёма работы.
Какие ещё математические калькуляторы на нашем сайте вам пригодятся?
На нашем сайте опубликовано множество математических программ, которые вам могут пригодиться. Например, калькулятор квадратных корней позволяет быстро извлечь корень квадратный из числа. Конечно, справится с такой задачей без особых проблем может большинство школьников. Однако задание усложняется, если речь идёт о большом числе. И ещё легче запутаться, когда за запятой оказывается много цифр. А благодаря калькулятору вы получите точный результат, причём быстро.
Например, калькулятор квадратных корней позволяет быстро извлечь корень квадратный из числа. Конечно, справится с такой задачей без особых проблем может большинство школьников. Однако задание усложняется, если речь идёт о большом числе. И ещё легче запутаться, когда за запятой оказывается много цифр. А благодаря калькулятору вы получите точный результат, причём быстро.
А вот разница в процентах поможет сравнить между собой 2 разные величины в ситуации, когда что-то меняется. Например, у предпринимателя может скакать от месяца к месяцу прибыль. Причём это вполне вероятно по разным точкам или по разным источникам поступления прибыли. В такой ситуации очень важно увидеть тенденцию, быстро сделать расчёты, чтобы понять, что предпринимать дальше.
Преимущество калькуляторов в том, что они позволяют не тратить время. Сделать множество расчётов можно буквально за несколько минут. И при этом программы были неоднократно проверены. В правильности расчётов можно не сомневаться.
Как найти общее количество делителей числа?
Воспользоваться калькулятором довольно просто. Для этого достаточно указать какое-то число, которое вас интересует. А потом – нажать на кнопку для расчёта. Но обратите внимание на то, что число в любом случае должно быть целым.
Для этого достаточно указать какое-то число, которое вас интересует. А потом – нажать на кнопку для расчёта. Но обратите внимание на то, что число в любом случае должно быть целым.
Результат появится наверху, на зелёном фоне. При этом вы увидите перечисление делителей, а также указание их общего количества. Данные можно сохранить в файл, скопировать (как саму информацию, так и ссылку на результат расчётов). Кроме того, сведения можно вывести на печать.
Также есть кнопка «запомнить». Благодаря ей вы увидите результат, когда зайдёте в очередной раз на сайт под своим аккаунтом.
Вычисления проводятся очень быстро. Ждать не придётся: результат появится мгновенно! При этом пользоваться калькулятором можно с любого устройства, вне зависимости от того, идёт ли речь о планшете или о смартфоне.Калькулятор НОД и НОК с решением онлайн
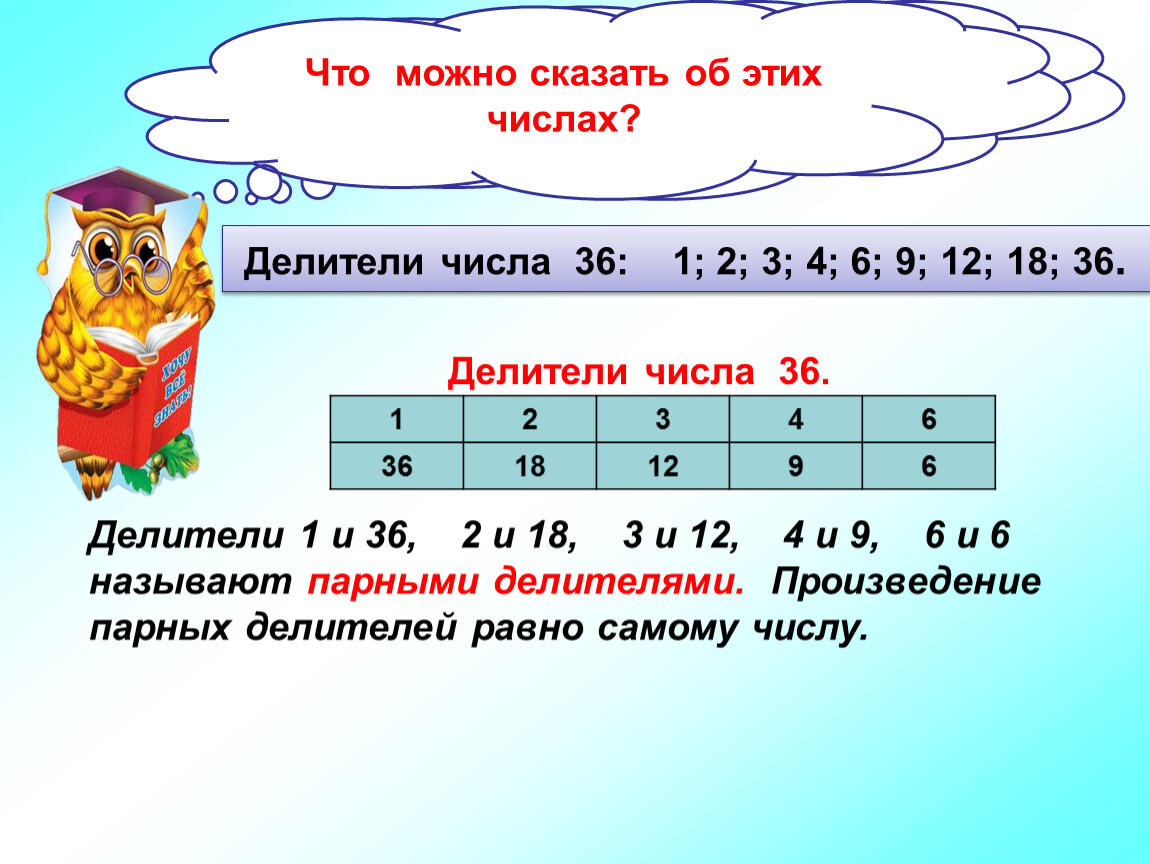
Найдем наибольший общий делитель НОД (36 ; 24)Этапы решения
Способ №1
1) Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением)
36 — составное число
24 — составное число
Разложим число 36 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
36 : 2 = 18 — делится на простое число 2
18 : 2 = 9 — делится на простое число 2
9 : 3 = 3 — делится на простое число 3.
Завершаем деление, так как 3 простое число
Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
24 : 2 = 12 — делится на простое число 2
12 : 2 = 6 — делится на простое число 2
6 : 2 = 3 — делится на простое число 2.
Завершаем деление, так как 3 простое число
2) Выделим синим цветом и выпишем общие множители
36 = 2 ⋅ 2 ⋅ 3 ⋅ 3
24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
Общие множители (36 ; 24) : 2, 2, 3
3) Теперь, чтобы найти НОД нужно перемножить общие множители
Ответ: НОД (36 ; 24) = 2 ∙ 2 ∙ 3 = 12
Способ №2
1) Найдем все возможные делители чисел (36 ; 24). Для этого поочередно разделим число 36 на делители от 1 до 36, число 24 на делители от 1 до 24. Если число делится без остатка, то делитель запишем в список делителей.
Для этого поочередно разделим число 36 на делители от 1 до 36, число 24 на делители от 1 до 24. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 36 выпишем все случаи, когда оно делится без остатка:
36 : 1 = 36;36 : 2 = 18;36 : 3 = 12;36 : 4 = 9;36 : 6 = 6;36 : 9 = 4;36 : 12 = 3;36 : 18 = 2;36 : 36 = 1;
Для числа 24 выпишем все случаи, когда оно делится без остатка:
24 : 1 = 24;24 : 2 = 12;24 : 3 = 8;24 : 4 = 6;24 : 6 = 4;24 : 8 = 3;24 : 12 = 2;24 : 24 = 1;
2) Выпишем все общие делители чисел (36 ; 24) и выделим зеленым цветом самы большой, это и будет наибольший общий делитель НОД чисел (36 ; 24)
Общие делители чисел (36 ; 24): 1, 2, 3, 4, 6, 12
Ответ: НОД (36 ; 24) = 12
Найдем наименьшее общее кратное НОК (52 ; 49)Этапы решения
Способ №1
1) Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением)
52 — составное число
49 — составное число
Разложим число 52 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
52 : 2 = 26 — делится на простое число 2
26 : 2 = 13 — делится на простое число 2.
Завершаем деление, так как 13 простое число
Разложим число 49 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
49 : 7 = 7 — делится на простое число 7.
Завершаем деление, так как 7 простое число
2) Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.
52 = 2 ∙ 2 ∙ 13
49 = 7 ∙ 7
3) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом
НОК (52 ; 49) = 2 ∙ 2 ∙ 13 ∙ 7 ∙ 7 = 2548
Способ №2
1) Найдем все возможные кратные чисел (52 ; 49). Для этого поочередно умножим число 52 на числа от 1 до 49, число 49 на числа от 1 до 52.
Для этого поочередно умножим число 52 на числа от 1 до 49, число 49 на числа от 1 до 52.
Выделим все кратные числа 52 зеленым цветом:
52 ∙ 1 = 52; 52 ∙ 2 = 104; 52 ∙ 3 = 156; 52 ∙ 4 = 208;
52 ∙ 5 = 260; 52 ∙ 6 = 312; 52 ∙ 7 = 364; 52 ∙ 8 = 416;
52 ∙ 9 = 468; 52 ∙ 10 = 520; 52 ∙ 11 = 572; 52 ∙ 12 = 624;
52 ∙ 13 = 676; 52 ∙ 14 = 728; 52 ∙ 15 = 780; 52 ∙ 16 = 832;
52 ∙ 17 = 884; 52 ∙ 18 = 936; 52 ∙ 19 = 988; 52 ∙ 20 = 1040;
52 ∙ 21 = 1092; 52 ∙ 22 = 1144; 52 ∙ 23 = 1196; 52 ∙ 24 = 1248;
52 ∙ 25 = 1300; 52 ∙ 26 = 1352; 52 ∙ 27 = 1404; 52 ∙ 28 = 1456;
52 ∙ 29 = 1508; 52 ∙ 30 = 1560; 52 ∙ 31 = 1612; 52 ∙ 32 = 1664;
52 ∙ 33 = 1716; 52 ∙ 34 = 1768; 52 ∙ 35 = 1820; 52 ∙ 36 = 1872;
52 ∙ 37 = 1924; 52 ∙ 38 = 1976; 52 ∙ 39 = 2028; 52 ∙ 40 = 2080;
52 ∙ 41 = 2132; 52 ∙ 42 = 2184; 52 ∙ 43 = 2236; 52 ∙ 44 = 2288;
52 ∙ 45 = 2340; 52 ∙ 46 = 2392; 52 ∙ 47 = 2444; 52 ∙ 48 = 2496;
52 ∙ 49 = 2548;
Выделим все кратные числа 49 зеленым цветом:
49 ∙ 1 = 49; 49 ∙ 2 = 98; 49 ∙ 3 = 147; 49 ∙ 4 = 196;
49 ∙ 5 = 245; 49 ∙ 6 = 294; 49 ∙ 7 = 343; 49 ∙ 8 = 392;
49 ∙ 9 = 441; 49 ∙ 10 = 490; 49 ∙ 11 = 539; 49 ∙ 12 = 588;
49 ∙ 13 = 637; 49 ∙ 14 = 686; 49 ∙ 15 = 735; 49 ∙ 16 = 784;
49 ∙ 17 = 833; 49 ∙ 18 = 882; 49 ∙ 19 = 931; 49 ∙ 20 = 980;
49 ∙ 21 = 1029; 49 ∙ 22 = 1078; 49 ∙ 23 = 1127; 49 ∙ 24 = 1176;
49 ∙ 25 = 1225; 49 ∙ 26 = 1274; 49 ∙ 27 = 1323; 49 ∙ 28 = 1372;
49 ∙ 29 = 1421; 49 ∙ 30 = 1470; 49 ∙ 31 = 1519; 49 ∙ 32 = 1568;
49 ∙ 33 = 1617; 49 ∙ 34 = 1666; 49 ∙ 35 = 1715; 49 ∙ 36 = 1764;
49 ∙ 37 = 1813; 49 ∙ 38 = 1862; 49 ∙ 39 = 1911; 49 ∙ 40 = 1960;
49 ∙ 41 = 2009; 49 ∙ 42 = 2058; 49 ∙ 43 = 2107; 49 ∙ 44 = 2156;
49 ∙ 45 = 2205; 49 ∙ 46 = 2254; 49 ∙ 47 = 2303; 49 ∙ 48 = 2352;
49 ∙ 49 = 2401; 49 ∙ 50 = 2450; 49 ∙ 51 = 2499; 49 ∙ 52 = 2548;
2) Выпишем все общие кратные чисел (52 ; 49) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (52 ; 49).
Общие кратные чисел (52 ; 49): 2548
Ответ: НОК (52 ; 49) = 2548
Калькулятор НОД и НОК по алгоритму Евклида
ТеорияНаибольший общий делитель (НОД) чисел a и b — это наибольшее число, на которое делятся без остатка числа a и b.
Среди всех способов нахождения наибольшего общего делителя для двух чисел алгоритм Евклида наиболее удобный и простой.
Нахождения НОД и НОК по алгоритму Евклида методом деления:
Как известно, деление с остатком целых чисел a — делимое и b — делитель, где b ≠ 0, подразумевает нахождение таких целых чисел q и r, что выполняется равенство:
a = b ∙ q + r, где
q — называется неполным частным,
r — остаток от деления, который не может быть отрицательным числом и по модулю не может быть больше делителя.
Суть метода состоит в том, что сначала выбираем наибольшее из двух чисел, для которых требуется найти НОД и делим большее число на меньшее. Если остаток от деления не равен нулю, делим делитель на остаток от деления, так продолжаем до тех пор, пока остаток от деления не будет равен нулю. Приведем примеры:
Приведем примеры:
Найдем НОД (36; 30), для этого сначала найдем остаток от деления 36 на 30
36 : 30 = 1 (остаток 6), так как 36 = 30 ∙ 1 + 6, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 30 на 6
30 : 6 = 5 (остаток 0) так как 30 = 6 ∙ 5 + 0, остаток от деления равен нулю, значит НОД равен предыдущему остатку от деление 6
Ответ: НОД (36; 30) = 6
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (36; 30) = (36 ∙ 30) : 6 = 180
Найдем НОД (176; 36), для этого сначала найдем остаток от деления 176 на 36
176 : 36 = 4 (остаток 32) так как 176 = 36 ∙ 4 + 32, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 36 на 32
36 : 32 = 1 (остаток 4) так как 36 = 32 ∙ 1 + 4, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 32 на 4
32 : 4 = 8 (остаток 0) так как 32 = 4 ∙ 8 + 0, остаток от деления равен нулю, значит НОД равен предыдущему остатку от деление 4
Ответ: НОД (176; 36) = 4
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (176; 36) = (176 ∙ 36) : 4 = 1584
Нахождения НОД и НОК по алгоритму Евклида методом вычитания:
Суть метода вычитания состоит в том, что необходимо из большего числа вычитать меньшее, если результат вычитания не равен нулю,
тогда уменьшаемое заменяем на получившуюся разность, если разность равна нулю, то НОД равен предыдущему значению разности. Приведем примеры:
Приведем примеры:
Найдем НОД (36; 30)
36 — 30 = 6
30 — 6 = 24
24 — 6 = 18
18 — 6 = 12
12 — 6 = 6
6 — 6 = 0
Ответ: НОД (36; 30) = 6
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (36; 30) = (36 ∙ 30) : 6 = 180
Найдем НОД (176; 36)
176 — 36 = 140
140 — 36 = 104
104 — 36 = 68
68 — 36 = 32
36 — 32 = 4
32 — 4 = 28
28 — 4 = 24
24 — 4 = 20
20 — 4 = 16
16 — 4 = 12
12 — 4 = 8
8 — 4 = 4
4 — 4 = 0
Ответ: НОД (176; 36) = 4
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (176; 36) = (176 ∙ 36) : 4 = 1584
Деление в столбик онлайн. Калькулятор наглядного деления.
Введите два числа: делимое и делитель.
Для простоты вычислений умножим делимое 1124.72 и делитель 6.8 на 100. Результат (частное) от этого не изменится. В результате пример сводится к делению следующих чисел:
1124.72÷6.8 = 112472÷680
| — | 1 | 1 | 2 | 4 | 7 | 2 | 6 | 8 | 0 | |
| 6 | 8 | 0 | 1 | 6 | 5 | . | 4 | |||
| — | 4 | 4 | 4 | 7 | ||||||
| 4 | 0 | 8 | 0 | |||||||
| — | 3 | 6 | 7 | 2 | ||||||
| 3 | 4 | 0 | 0 | |||||||
| — | 2 | 7 | 2 | 0 | ||||||
| 2 | 7 | 2 | 0 | |||||||
| 0 |
Окончательный ответ: 1124,72÷6,8 = 165. 4
4
Делители и кратные. Онлайн тренажер. — Kid-mama
Что такое делители и кратные?
Разберемся с понятиями делители и кратные.
1 Что такое делитель числа?
Запомните Делитель натурального числа а — это натуральное число, на которое а делится без остатка. |
Например:
число 3 является делителем числа 15, так как 15 : 3 = 5
числа 1, 2, 3, 4, 6, 12 являются делителями числа 12
число 4 не является делителем числа 10, так как 10 : 4 = 2,5
число 1 является делителем любого натурального числа.
Таким образом, самым маленьким делителем любого числа является 1, а самым большим делителем является само это число.
У любого числа имеется как минимум 2 делителя — 1 и само число.
2 делителя имеют все простые числа — так как они делятся только сами на себя. Это числа 2, 3, 5, 7, 11, 13, 17 и т.д.
У остальных (не простых) чисел имеется делителей больше, чем два.
Теперь разберемся с кратным
2 Что такое кратное числа?
| Кратное натурального числа а — это натуральное число, которое делится без остатка на а Любое натуральное число имеет бесконечное число кратных (поскольку числа бесконечны) |
Например:
числа 8, 16, 24, 32 — кратны числу 8
число 20 — кратное числа 5
Наименьшим кратным натурального числа является само это число.
Необходимо запомнить, как правильно употреблять слова делитель и кратное в речи:
Говорят:
—число пятнадцать кратно числу три
(или: пятнадцать кратно трем)
—число пятнадцать — кратное числа три
(или: пятнадцать — кратное трех)
—числа девять, пятнадцать, двенадцать — кратные трех.
Число кратно можно заменить словом делится
—сорок пять делится на пять
—сорок пять кратно девяти
Онлайн тренажер «Делители и кратные»
Тренажер построен в виде теста. В каждом задании необходимо выбрать правильный ответ и нажать кнопку «Готово». При правильном ответе происходит автоматический переход к следующему вопросу.
На весь экран
Делитель потенциала — Онлайн калькулятор
Делитель потенциала — это самый простой способ получения источника с более низкой ЭДС. от источника с более высокой э.д.с.
Выходное напряжение делителя потенциала можно рассчитать как
U out = U in R 2 / (R 1 + R 2 ) (1)
где
U out = выходное напряжение (В)
R = сопротивление (Ом, Ом)
U in = входное напряжение (В)
Пример — Делитель потенциала — Высокая потребляемая мощность
Выходное напряжение от делителя потенциала с двумя резисторами R 1 = 10 Ом и R 2 = 20 Ом и входное напряжение 12 В можно рассчитать как
U out = (12 В) (20 Ом) / ((10 Ом) + (20 Ом))
= 8 (В)
Ток через делитель потенциала R 1 и 900 рандов 11 2 (напр. выходной ток) можно рассчитать по закону Ома
выходной ток) можно рассчитать по закону Ома
I = U / R
= (12 В) / ((10 Ом) + (20 Ом))
= 0,4 А
можно рассчитать потребляемую мощность делителя
P = UI
= (12 В) (0,4 A)
= 4,8 Вт
Пример — Делитель потенциала — меньшее энергопотребление
Выходное напряжение от делителя потенциала с двумя резисторами R 1 = 1000 Ом и R 2 = 2000 Ом и входное напряжение 12 В можно рассчитать как
U out = (12 В) ( 2000 Ом) / ((1000 Ом) + (2000 Ом))
= 8 (В)
Ток через делитель потенциала R 1 и R 2 (пример.выходной ток) можно рассчитать по закону Ома
I = U / R
= (12 В) / ((1000 Ом) + (2000 Ом))
= 0,004 А
можно рассчитать потребляемую мощность делителя
P = UI
= (12 В) (0,004 A)
= 0,048 Вт
Потребляемую мощность в делителе потенциала можно уменьшить за счет увеличения сопротивления .
Делитель потенциала — Калькулятор
Входное напряжение (вольт)
резистор R 1 (Ом)
резистор R 2 (Ом)
Делитель потенциала Номограмма ниже
Номограмма использоваться для оценки потенциального делителя.
Загрузите и распечатайте Номограмму делителя потенциала!
Значения по умолчанию на приведенной ниже номограмме для U в = 12 В , R 2 = 47 Ом и U вне = 3,3 В . Так как сумма сопротивлений (R 1 + R 2 ) по номограмме составляет примерно 170 Ом — сопротивление R 1 можно рассчитать как
R 1 ≈ ( 170 Ом — 47 Ом)
≈ 123 Ом.
Калькулятор смешанных чисел
Использование калькулятора
Выполняет математические вычисления со смешанными числами (смешанными дробями), выполняя операции с дробями, целыми числами, целыми числами, смешанными числами, смешанными дробями и неправильными дробями. Калькулятор смешанных чисел может складывать, вычитать, умножать и делить смешанные числа и дроби.
Калькулятор смешанных чисел может складывать, вычитать, умножать и делить смешанные числа и дроби.
Калькулятор смешанных чисел (также называемых смешанными дробями):
Этот онлайн-калькулятор выполняет простые операции с целыми числами, целыми числами, смешанными числами, дробями и неправильными дробями путем сложения, вычитания, деления или умножения.Ответ предоставляется в сокращенной дроби и в смешанном числе, если таковой существует.
Введите смешанные числа, целые числа или дроби в следующих форматах:
- Смешанные числа: введите 1 1/2, что составляет полтора или 25 3/32, что составляет двадцать пять и три тридцать секунд. Сохраняйте ровно один пробел между целым числом и дробью и используйте косую черту для ввода дробей. Вы можете ввести до 3-х цифр для каждого целого числа, числителя или знаменателя (123 456/789).
- Целые числа: до 3 цифр.
- Дроби: введите 3/4, что составляет три четверти, или 3/100, что составляет три сотых.
 Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Сложение смешанных чисел с помощью формулы сложения дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу для сложения дробей:
a / b + c / d = (ad + bc) / bd - Уменьшить дроби и, если возможно, упростить
Формула сложения дробей
\ (\ dfrac {a} {b} + \ dfrac {c} {d} = \ dfrac {(a \ times d) + (b \ times c)} {b \ times d} \)
Пример
Сложить 1 2/6 и 2 1/4
\ (1 \ dfrac {2} {6} + 2 \ dfrac {1} {4} = \ dfrac {8} {6} + \ dfrac {9} {4} \)
\ (= \ dfrac {(8 \ times 4) + (9 \ times 6)} {6 \ times 4} \)
\ (= \ dfrac {32 + 54} {24} = \ dfrac {86} {24} = \ dfrac {43} {12} \)
\ (= 3 \ dfrac {7} {12} \)
1 2/6 + 2 1/4 = 8/6 + 9/4 = (8 * 4 + 9 * 6) / 6 * 4 = 86/24
Итак, мы получаем 86/24 и упрощаем до 3 7/12
Вычитание смешанных чисел по формуле вычитания дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу для вычитания дробей: a / b — c / d = (ad — bc) / bd
- Уменьшить дроби и, если возможно, упростить
Формула вычитания дробей
\ (\ dfrac {a} {b} — \ dfrac {c} {d} = \ dfrac {(a \ times d) — (b \ times c)} {b \ times d} \)
Пример
Вычтем 2 1/4 из 1 2/6
1 2/6 — 2 1/4 = 8/6 — 9/4 = (8 * 4 — 9 * 6) / 6 * 4 = -22/24
Уменьшите дробь, чтобы получить -11/12
Умножение смешанных чисел по формуле умножения дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу для умножения дробей: a / b * c / d = ac / bd
- Уменьшить дроби и, если возможно, упростить
Формула умножения дробей
\ (\ dfrac {a} {b} \ times \ dfrac {c} {d} = \ dfrac {a \ times c} {b \ times d} \)
Пример
умножить 1 2/6 на 2 1/4
1 2/6 * 2 1/4 = 8/6 * 9/4 = 8 * 9/6 * 4 = 72/24
Уменьшите дробь, чтобы получить 3/1, и упростите до 3
Разделение смешанных чисел по формуле деления на дроби
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу для деления дробей: a / b ÷ c / d = ad / bc
- Уменьшить дроби и, если возможно, упростить
Формула деления дробей
\ (\ dfrac {a} {b} \ div \ dfrac {c} {d} = \ dfrac {a \ times d} {b \ times c} \)
Пример
разделить 1 2/6 на 2 1/4
1 2/6 ÷ 2 1/4 = 8/6 ÷ 9/4 = 8 * 4/9 * 6 = 32/54
Уменьшите дробь, чтобы получить 16/27
Связанные калькуляторы
Для выполнения математических операций с простыми правильными или неправильными дробями используйте нашу
Калькулятор дробей. Этот калькулятор превращает неправильные дробные ответы в смешанные числа.
Этот калькулятор превращает неправильные дробные ответы в смешанные числа.
Если вы хотите упростить отдельную дробь до наименьших значений, используйте наш Упростите калькулятор дробей.
Для объяснения того, как множить числа, чтобы найти наибольший общий множитель (GCF), см. Калькулятор наибольшего общего коэффициента.
Если вы вручную упрощаете большие дроби, вы можете использовать Длинное деление с калькулятором остатков, чтобы найти целые числа и остатки.
Примечание:
Этот калькулятор выполняет расчет сокращения быстрее, чем другие, которые вы можете найти. Основная причина заключается в том, что код использует теорему Евклида для сокращения дробей, которую можно найти на Математический форум: LCD, LCM.
визуальных разделителей в пользовательских интерфейсах: типы и советы по дизайну
Продуманный дизайн производительности контента в веб-и мобильных пользовательских интерфейсах имеет большое значение для повышения полезности и удобства использования продукта. Наша сегодняшняя статья посвящена визуальным разделителям, элементам макета, которые помогают упорядочивать контент на экране и четко разделять его части. Давайте посмотрим, как работают визуальные разделители и какие из них популярны.
Наша сегодняшняя статья посвящена визуальным разделителям, элементам макета, которые помогают упорядочивать контент на экране и четко разделять его части. Давайте посмотрим, как работают визуальные разделители и какие из них популярны.
Что такое визуальный разделитель
Визуальный разделитель — это элемент макета, который помогает разделять фрагменты контента на четкие группы, разделы, параметры или части. Таким образом, он помогает дизайнеру организовать страницу в соответствии с типичными шаблонами визуального восприятия и сделать макет более понятным и понятным для пользователей.
Вместе с другими элементами на странице разделители играют большую роль в создании прочной визуальной иерархии. Например, с их помощью пользователи могут легче определять отношения контента, например, являются ли части контента одинаковыми, похожими или связанными; если один из них подчиняется другим и т. д.
Разделители также важны для удобства использования: во многих случаях они создают визуальные контейнеры, которые выглядят интерактивными или доступными, что особенно важно для мобильных интерфейсов.
Визуальные виды разделителей
Говоря о разделителях, мы можем проанализировать их в двух аспектах: их внешний вид и их функции.Начиная с визуальной части, существует пять основных и широко используемых методов разделения контента в пользовательских интерфейсах:
- линия
- цвет
- отрицательное пространство
- тени / объем
- рис.
Строки
Линии с незапамятных времен принадлежали к ведущим методам разделения частей контента как в печатной продукции, так и в цифровых интерфейсах. Их легко узнать в этой роли, поэтому пользователям не нужно дважды думать.
С другой стороны, этот тип кажется суперпростым и далеко не оригинальным. Поэтому довольно часто дизайнеры стремятся найти другие способы разделения контента. Более того, рекомендуется использовать строки только в том случае, если контент не может быть эффективно разделен другим способом. Слишком много линий может перегрузить экран визуальным шумом и создать ненужное визуальное напряжение.
На странице продукта для веб-сайта, посвященного безотходному образу жизни, горизонтальные линии используются в качестве визуальных разделителей, чтобы четко организовать различную информацию о продукте.
На веб-странице научной платформы используются горизонтальные линии для разделения различных блоков контента и упрощения сканирования их структуры.
На веб-сайте электронной коммерции чайного бренда используются разные уровни визуального разделения контента: от простой горизонтальной линии для разделения цены и элемента CTA до своего рода таблицы с нерегулярной сеткой для поиска информации о товаре, обычного вида таблицы для элементов в заголовке веб-сайта и цветовой контраст, чтобы отделить визуальное содержимое от текстового содержимого.
Негативное пространство
Негативное пространство (также известное как белое пространство) означает пустое пространство на экране вокруг и часто внутри элементов. Тем не менее, пустой не означает пассивный или потраченный впустую: как и любой другой элемент экрана, он работает, обеспечивая положительный пользовательский опыт. Негативное пространство — один из самых популярных видов визуальных разделителей, особенно в интерфейсах, построенных на идее минимализма и простоты. Приправленное знанием гештальных принципов визуального восприятия, например принципов близости и сходства, негативное пространство превращается в эффективный и элегантный визуальный разделитель, который также позволяет интерфейсу дышать и избегать беспорядка.
Тем не менее, пустой не означает пассивный или потраченный впустую: как и любой другой элемент экрана, он работает, обеспечивая положительный пользовательский опыт. Негативное пространство — один из самых популярных видов визуальных разделителей, особенно в интерфейсах, построенных на идее минимализма и простоты. Приправленное знанием гештальных принципов визуального восприятия, например принципов близости и сходства, негативное пространство превращается в эффективный и элегантный визуальный разделитель, который также позволяет интерфейсу дышать и избегать беспорядка.
Приложение-планировщик путешествий разделяет элементы в списке без каких-либо дополнительных визуальных элементов, только с помощью пробела.
Список статей в блоге о здоровье основан на типографской иерархии и отрицательном пространстве, чтобы они выглядели как четкий набор элементов, не отвлекая внимание от макета.
Цветовой контраст
Еще один эффективный вид визуального разделителя — это цветовой контраст. Выбор и комбинации цветов в дизайне пользовательского интерфейса обладают большим психологическим потенциалом: они могут усилить сообщение и содержание веб-сайта, создав соответствующее настроение.Контрастность — один из ключевых факторов, влияющих на возможность сканирования и визуальную иерархию страницы или экрана. При этом цветовой контраст может эффективно разделять различные варианты, элементы или интерактивные зоны, что означает работу в качестве визуального разделителя. Вот почему в последнее время так популярны разделенные экраны. Этим можно объяснить популярный подход к организации целевых страниц и одностраничных веб-сайтов по блокам контента, представленным на контрастном цветном фоне.
Выбор и комбинации цветов в дизайне пользовательского интерфейса обладают большим психологическим потенциалом: они могут усилить сообщение и содержание веб-сайта, создав соответствующее настроение.Контрастность — один из ключевых факторов, влияющих на возможность сканирования и визуальную иерархию страницы или экрана. При этом цветовой контраст может эффективно разделять различные варианты, элементы или интерактивные зоны, что означает работу в качестве визуального разделителя. Вот почему в последнее время так популярны разделенные экраны. Этим можно объяснить популярный подход к организации целевых страниц и одностраничных веб-сайтов по блокам контента, представленным на контрастном цветном фоне.
Концепция мобильного меню основана на цветовом контрасте, чтобы элементы были четко различимы.
Даже в таких пастельных элементах, как этот, очевидна сила цветового контраста: он помогает разделить страницу на главный раздел с помощью CTA и активного раздела меню. Также обратите внимание на вертикальные линии, используемые в качестве визуальных разделителей для пунктов меню: вместе со слегка видимыми изображениями здесь они также работают как ориентиры и помогают избежать иллюзии полноты на странице.
Также обратите внимание на вертикальные линии, используемые в качестве визуальных разделителей для пунктов меню: вместе со слегка видимыми изображениями здесь они также работают как ориентиры и помогают избежать иллюзии полноты на странице.
В дизайне веб-сайта для одеял GNO цветовой контраст помогает разделить длинную веб-страницу на удобоваримые и элегантные блоки контента.
Тени и объем
Тени и объем, которые обычно достигаются за счет эффекта визуального возвышения части контента, также могут эффективно работать как разделители. Они создают ощущение глубины и разделяют страницу на несколько слоев, что часто выглядит естественным и гармоничным для человеческого глаза. С другой стороны, он выглядит менее очевидным и заметным, чем линии, поэтому такой подход может быть полезен для достижения баланса и четкости отдельных элементов без излишнего визуального шума или отвлечения внимания.
На экране каталога, на котором представлены товары на складе, используются тени, что придает макету больше глубины и четко отделяет карточки друг от друга.
Мобильное приложение для покупки букетов по индивидуальному заказу также разделяет позиции в каталоге карточкой, выступающей на заднем плане. Таким образом, контент выглядит четким и интерактивным в интерфейсе, который выглядит легким и воздушным.
Изображения
Любые изображения представляют собой еще один эффективный визуальный разделитель.В этой роли они особенно популярны в интерфейсах с большим количеством текстового контента, например, в блогах, онлайн-СМИ и текстовых целевых страницах. Фотографии, иллюстрации, трехмерная графика, а также анимированные изображения помогают сбалансировать текстовое содержимое, повышают уровень читаемости и возможности сканирования, эффективно разделяют визуальные блоки, а также добавляют веселья и эмоциональной привлекательности.
На целевой странице отчета по криптовалюте используются запоминающиеся блоки трехмерной графики с анимированным призывом к действию «Узнать больше».Таким образом, тематические блоки также четко разделены.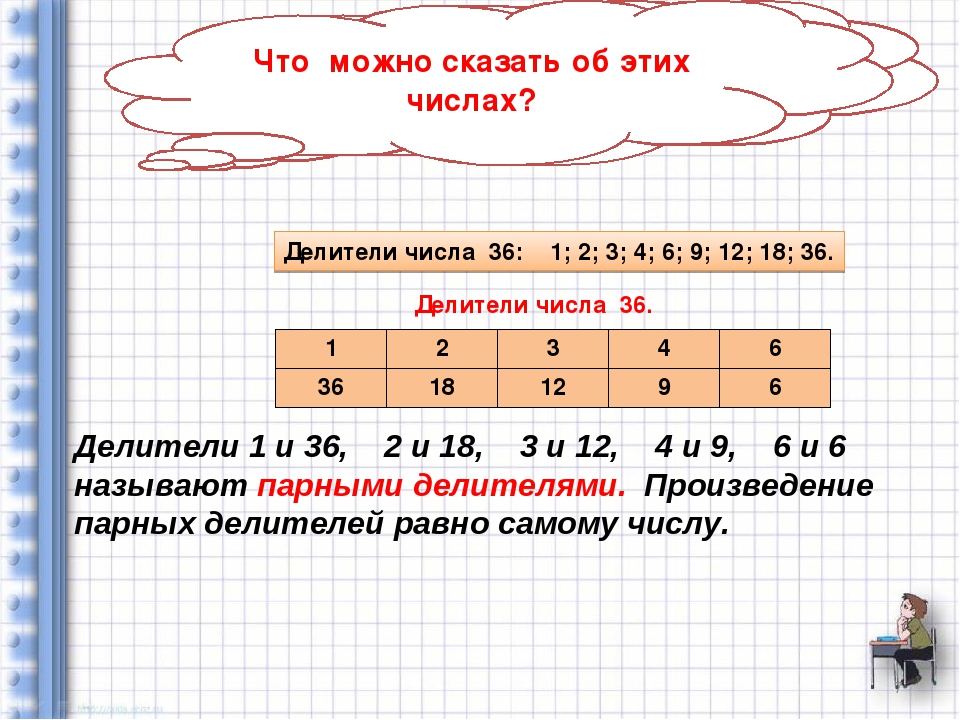
Экран меню для ресторанного приложения использует изображения как важный элемент разделения опций.
Функциональные типы
Функциональные типы визуальных разделителей зависят от уровней иерархии, на которых они работают.
Разделители под обрез
Разделители без полей — это те, которые разделяют разделы и занимают всю длину макета экрана.
Приложение «Галерея» использует горизонтальные линии как разделители в каталоге художников.
Приложение Perfect Recipe использует разделители без полей для разделения рецептов.
Финансовое приложение использует едва заметные разделители без полей для разделения статей в списке расходов.
Приложение «Кино» использует разделители без полей на экране оформления заказа.
Разделители вставные
Разделители-вкладыши разделяют элементы и элементы связанного содержимого, закрепленные элементами, которые выравниваются по заголовку панели приложения или подстраиваются под конкретный вид текстового содержимого на странице.
На сайте конструкции представлена деталь со спецификациями, в которой в качестве разделителей используются горизонтальные линии.
Разделители с подзаголовками
В некоторых случаях можно объединить разделители с подзаголовками для идентификации блока сгруппированного содержимого. В этом случае разделитель следует разместить над подзаголовком, чтобы сделать связь подзаголовка с контентом более очевидной.
Средний разделитель
Обычно это разделители, размещаемые где-то в середине макета, например, для разделения связанного содержимого, например цен на чеке.
На странице продукта для веб-сайта электронной коммерции, где продаются травы, есть средний разделитель, чтобы четко отделить интерактивную зону оформления заказа от текстового содержания, описывающего продукт.
Пункты для рассмотрения
Выбирая тип визуального разделителя для макета, который вы разрабатываете, вы должны учитывать два важных фактора.
Тонкость : разделители не должны привлекать внимание пользователей, не должны отвлекать пользователей от самого контента.Цель разделителя — поддержать и сделать макет чистым, а не привлекать внимание. Итак, сделайте заметное, но не раздражающее.
Средняя частота : как было упомянуто выше, слишком много визуальных разделителей, особенно если они представляют дополнительный элемент макета, как это делают линии, могут создавать визуальный шум и утомлять пользователей. Итак, обдумывая тип, подумайте дважды, а то и в семь раз больше. По возможности предпочитайте отрицательное пространство линиям; не переусердствуйте с цветами; стремитесь к гармонии и последовательности.
Как показывают приведенные выше примеры, дизайнеры стремятся найти эффективную комбинацию визуальных разделителей, которые эффективно организуют контент на веб-странице или экране мобильного устройства.
Полезные статьи
Вот набор статей о других аспектах и передовых методах проектирования пользовательского интерфейса.
Направленные сигналы в пользовательских интерфейсах
Как сделать пользовательский интерфейс читабельным
Основные типы кнопок в пользовательских интерфейсах
3C дизайна интерфейса: цвет, контраст, содержание
Негативное пространство в дизайне: практики и советы
Как сделать веб-интерфейс для сканирования
От нуля к герою: посмотрите на изображения героев в веб-дизайне
Светлый или Темный интерфейс? Советы по выбору подходящей цветовой схемы
Добро пожаловать, чтобы увидеть дизайн Tubik на Dribbble и Behance
.

