Дискретность отсчета. Точность измерений массы: дискретность и погрешность весов

Что такое дискретность весов и как она влияет на точность измерений. Чем отличается дискретность от погрешности весов. Как определяется класс точности весовых приборов. Какие факторы влияют на точность электронных весов.

Дискретность весов: что это такое и как она влияет на точность

Дискретность — это минимальное значение массы, которое способны отобразить весы. Другими словами, это цена деления шкалы весов. Чем меньше дискретность, тем точнее измерения может производить весовой прибор.

Например, если весы имеют дискретность 5 г, то они будут показывать массу с шагом в 5 г — 100 г, 105 г, 110 г и т.д. Даже если реальная масса предмета составляет 102 г, такие весы покажут либо 100 г, либо 105 г.

Дискретность обозначается буквой «d» и указывается в технических характеристиках весов. Для лабораторных и аналитических весов высокого класса точности дискретность может составлять 0,1 мг, 0,01 мг и даже 0,001 мг.

Погрешность весов: в чем отличие от дискретности

Погрешность весов — это максимально допустимое отклонение показаний прибора от истинного значения массы. Погрешность определяет, насколько точно весы способны измерить массу предмета.

Основное отличие погрешности от дискретности:

• Дискретность показывает минимальный шаг отображения массы
• Погрешность определяет точность самого измерения

Например, весы с дискретностью 1 г и погрешностью ±2 г при взвешивании предмета массой 100 г могут показать значение от 98 г до 102 г с шагом в 1 г.

Как определяется класс точности весов

Класс точности весов определяется на основе нескольких параметров:

• Цена поверочного деления (e) — расчетная величина для определения предельно допустимой погрешности
• Число поверочных делений (n) — отношение максимальной нагрузки к цене поверочного деления
• Значение минимальной нагрузки (Min)

Согласно ГОСТ OIML R-1-2011, выделяют 4 класса точности весов:

1. Специальный (I) — самый высокий класс точности
2. Высокий (II)
3. Средний (III)
4. Обычный (IIII)

Чем выше класс точности, тем меньше погрешность измерений способны обеспечить весы.

Факторы, влияющие на точность электронных весов

На точность измерений электронных весов могут влиять различные факторы:

• Качество и чувствительность тензодатчиков
• Стабильность электронных компонентов
• Температура окружающей среды
• Вибрации и сотрясения
• Электромагнитные помехи
• Неправильная калибровка

Для обеспечения максимальной точности важно соблюдать правила эксплуатации весов, регулярно проводить их калибровку и поверку.

Многодиапазонные весы: повышение точности при разных нагрузках

Многодиапазонные весы позволяют повысить точность измерений за счет изменения дискретности и погрешности в зависимости от массы груза. Такие весы имеют несколько диапазонов взвешивания с разными значениями дискретности:

• При малых нагрузках используется минимальная дискретность для максимальной точности
• С увеличением массы груза дискретность увеличивается

Это позволяет обеспечить высокую точность при малых массах и сохранить приемлемую точность при больших нагрузках.

Выбор весов с оптимальной точностью для разных задач

При выборе весов следует учитывать несколько факторов:

• Требуемая точность измерений
• Диапазон взвешиваемых масс
• Условия эксплуатации
• Стоимость оборудования

Для лабораторных исследований обычно требуются весы специального (I) или высокого (II) класса точности. Для складского учета и торговли часто достаточно весов среднего (III) класса.

Важно выбирать весы с оптимальным соотношением максимальной нагрузки, дискретности и погрешности для конкретных задач.

Калибровка и поверка весов: обеспечение стабильной точности

Для поддержания заявленной точности весы нуждаются в регулярном обслуживании:

• Калибровка — настройка весов для обеспечения точных показаний
• Поверка — официальная процедура подтверждения соответствия весов заявленным метрологическим характеристикам

Периодичность калибровки и поверки зависит от класса точности весов и интенсивности их использования. Для весов высокого класса точности рекомендуется проводить калибровку ежедневно, а поверку — не реже одного раза в год.

Современные технологии повышения точности весов

Производители весового оборудования постоянно работают над повышением точности измерений. Среди современных технологий можно выделить:

• Использование цифровых тензодатчиков
• Применение систем температурной компенсации
• Внедрение алгоритмов цифровой фильтрации сигнала
• Разработка специальных конструкций для снижения влияния вибраций

Эти технологии позволяют создавать высокоточные весы, способные обеспечивать стабильные результаты измерений даже в сложных условиях эксплуатации.

Дискретность, погрешность и класс точности лабораторных весов согласно ГОСТ – полезные материалы от A&D

Несмотря на развитие современных технологий, определить абсолютную массу предмета не представляется возможным, даже с помощью самых чувствительных приборов. Поэтому специалисты ввели понятие точности измерения, которая напрямую зависит от погрешности и дискретности измерений.

 

 

Все весовое оборудование, используемое в лаборатории, делится на 3 класса точности в соответствии с ГОСТ OIML R 1 2011.

 

Основными характеристиками являются пределы взвешивания (наименьший и наибольший), точность измерений, дискретность и погрешность измерения веса. Они указываются в сопроводительной документации, спецификациях к оборудованию. По поводу последних 3 параметров у неопытных пользователей часто возникают вопросы.

 

В статье ниже мы рассмотрим основные государственные стандарты, классификацию весового оборудование, важнейшие технические характеристики весов и их отражение в стандартах.

 

 

Государственные стандарты для лабораторных весов

Следует отметить, что для лабораторных весов действуют стандарты для весов, предназначенных для статического (не динамического) измерения массы в лабораториях и на предприятиях. Эти стандарты не действуют для весов специального назначения, аптекарских, масс-компараторов, а также для весов, измеряющие массу косвенно (не непрямую).

 

Итак, одним из первых стандартов, закрепляющих требования к лабораторным весам, является устаревший ГОСТ 24104-88 «Весы лабораторные общего назначения и образцовые» от 1988 г.

 

Далее, уже в РФ, в 2001 г. был принят новый ГОСТ 24104-2001 «Весы лабораторные», в котором стандарты для лабораторных весов были существенно изменены, а разделение оборудования на весы общего назначения и т.н. образцовые было убрано в принципе. В связи с этим, существенные изменения претерпели классы точности весов:

Класс точности согласно ГОСТ 24104-2001	Класс точности согласно ГОСТ 24104-88
I «Специальный»	1 класс, 2 класс, 3 класс (практически все)
II «Высокий»	4 класс
III «Средний»	Многие приборы из из ГОСТ 29329-92 «Весы для статического взвешивания».

Также были внесены следующие изменения:

 

• Введение новых характеристики (цена деления (дискретность) «d», наименьший предел взвешивания (НмПВ, Min), цена поверочного деления «e», число поверочных делений «n».
• В качестве обязательной характеристики устанавливаются тесты (0,5-часовой и 4-часовой)
• Реализована возможность эксплуатации многодиапазонных весов (приборов с несколькими НПВ). Конструктивно каждый диапазон рассматривается как отдельная модель весов с отдельными техническими характеристиками.

 

Срок действия данного ГОСТ закончился в 2010 г., и далее он был заменен на международный стандарт на весы ГОСТ OIML R 1 2011. Он не содержит существенных технических нововведений, был создан для соответствия мировым (международным) стандартам. Это стало важной вехой для производителей, поставляющих весовое оборудование на экспорт.

 

 

Пределы взвешивания

 

Эта характеристика, которая вызывает наименьшее количество вопросов у потребителя.

 

Верхний (наибольший) предел взвешивания (НПВ, Max) – это максимальное значение нагрузки (навески), которое может быть отображено на дисплее весов. Если масса образца больше этого значения, то результаты измерений не будут точными.

 

Нижний (наименьший) предел взвешивания (НмПВ, Min) – это величина массы, ниже которой погрешность измерений будет чрезмерной. Иными словами, дисплей весов не покажет никаких значений.

 

Нельзя путать НПВ с предельной нагрузкой (Lim). Если масса образца будет больше НПВ, то результат измерений не будет точным. А если масса больше Lim, то прибор сломается.

 

 

Дискретность (цена деления)

 

Дискретность – свойство измерений, обратное непрерывности. Это показатель, изменяющийся между 2 соседним делениями весоизмерительного оборудования (стабильными состояниями). Отсюда название – цена деления (обозначается «d»).

 

Цена деления – одна из ключевых характеристик стандартов для лабораторных весов. Чем она меньше, тем выше точность весоизмерения. К примеру, если на весы с дискретностью 5 г поставить гирю 3 кг, то на дисплее будет результат 3 кг. Если далее на платформу добавить груз 3.5г, то весы покажут результат взвешивания 3 кг и 5 г. Это вызвано дискретностью оборудования.

 

 

Цена поверочного деления (предельно допустимая погрешность)

Это расчетная величина, обозначаемая «e». Она не имеет физического воплощения в оборудовании, однако является важной, т.к. на ее основе определяется класс точности весов и проводится их поверка. Расчет цены поверочного деления производится следующим образом:

Для весов градуированных, без вспомогательного показывающего устройства	e = d, где d — это действительная цена деления шкалы;
Для весов градуированных, со вспомогательным показывающим устройством	e выбирается изготовителем;
Для весов неградуированных	e выбирается изготовителем.

 

Класс точности весов

Согласно действующему ГОСТ OIML R-1-2011, класс точности весов определяется исходя из значения поверочного интервала «e», числа поверочных интервалов «n», значения минимальной нагрузки «Min» (НмПВ).

 

Требования к лабораторным весам (весам для исследований) как правило, подразумевают под собой I «Специальный» или II «Высокий» класс точности. Также они широко применяются в медицинской, химической, фармацевтической отрасли.

 

Весы III класса (как правило, порционные, общего назначения) более востребованы в торговле, на предприятиях общественного питания и т.д.

 

 

Погрешность весов

 

Для расчета фактической погрешности весов следует использовать предельно допустимую погрешность весов, а также класс точности.

 

Даже у самых точных весов (I специального класса) есть погрешность, измеряемая в долях мг. Стандартизация погрешности позволяет преследовать следующие уели:

1. Введение общеиспользуемой системы сертификации весоизмерительного оборудования.
2. Разработка и внедрение единых технических требований к весам.
3. Возможность детального сравнения по классам точности от различных производителей.
4. Разработка и внедрение удобной для потребителя товарной номенклатуры.

 

 

Большой спектр оборудования является многодиапазонными весами, что позволяет увеличить точность (уменьшить погрешность) проводимых измерений. В этом случае характеристики каждого диапазона взвешивания рассматриваются отдельно.

 

Надеемся, данные материалы по стандартам для лабораторных весов помогут Вам сделать оптимальный выбор измерительного оборудования.

К списку новостей

Закажите бесплатную демонстрацию

или звоните+7 (495) 937-33-44

Наши менеджеры рады ответить
на все Ваши вопросы!

Точность весов. Дискретность и погрешность весов.

12.04.2021

Человечество всегда знало, что каждый материальный предмет имеет свою массу, однако, измерить точный вес объекта стало возможным лишь с изобретением весов. Введение различных мер массы, таких, как килограмм или фунт, тонна, грамм, миллиграмм. Следует отметить, что абсолютную массу предмета измерить невозможно, даже используя сверхчувствительные весовые приборы. Это связано с понятием «точность измерения», которое зависит от двух факторов: дискретности и погрешности.

Многие люди ошибочно считают, что эти понятия тождественны, однако, это не так. Дискретность и погрешность реализованы на разных весах по разному.

Что такое дискретность

Дискретность – это свойство, которое имеет значение, противоположное непрерывности, т.е. «прерывность». Дискретность – это значение, изменяющееся между несколькими различными стабильными состояниями. В качестве примера можно привести механические часы, в которых минутная стрелка перемещается скачкообразно, т.е. дискретно, на одну шестидесятую целой окружности циферблата. Дискретность обозначается как «d».

Понятие дискретности в электронных весах связано с шагом взвешивания и отображения массы. Так например, если на весы, обладающие дискретностью d=5 грамм, положить гирю массой в 1 килограмм, то они отобразят на дисплее массу, равную 1 кг. Если же к этому килограмму добавить гирьку массой 3 грамма, то такие весы отобразят на дисплее значение не в 1,003 кг, а в 1,005, поскольку шаг (и, соответственно, дискретность) таких весов равен 5 граммам.

Предельно допустимая погрешность

Предельно допустимая погрешность у весов обозначается величиной «e». Метрологически, такая величина называется «цена поверочного деления». Предельно допустимая погрешность должна быть не более определенной по нормативным документам. Она указывается заводом изготовителем при производстве весов.

Идеальным считается такое соотношение дискретности и цены деления, при котором соблюдается их равенство (d=e). Соотношение должно быть указано на том же шильдике весов, на котором указывается заводской номер.

В соответствующих ГОСТах (например ГОСТ EN: 45501 ), указывается соотношение максимально допустимой погрешности и цены поверочного деления «e» для каждого класса точности весов. Данные об этом соотношении, в обязательном порядке, указываются в приложениях к метрологическому сертификату, который можно найти в описании к типу средства измерения. Для лабораторных весов, такую погрешность указывают в «Руководстве по эксплуатации», которое поставляется вместе с весами.

Для повышения точности взвешивания малого веса, некоторые современные модели электронных весов оборудованы многодиапазонным режимом измерений. В этом режиме, весь диапазон допустимых взвешиваний, подразделяется на несколько. При этом, каждый диапазон имеет свои, отличные от других, значения дискретности и погрешности.

Кстати, высоких показателей дискретности, а следовательно и точности, не стоит ожидать от весов с большим значением НПВ (наибольший предел взвешивания). Поэтому, для точного взвешивания, лучше выбрать весы с наименьшими значениями «e», «d» и НПВ.

Читайте также

Детекторы высокого разрешения для ПЭТ-сканеров всего тела с использованием двустороннего считывания

Сохранить цитату в файл

Формат: Резюме (текст)PubMedPMIDAbstract (текст)CSV

Добавить в коллекции

• Создать новую коллекцию
• Добавить в существующую коллекцию

Назовите свою коллекцию:

Имя должно содержать менее 100 символов

Выберите коллекцию:

Не удалось загрузить вашу коллекцию из-за ошибки
Повторите попытку

Добавить в мою библиографию

• Моя библиография

Не удалось загрузить делегатов из-за ошибки
Повторите попытку

Ваш сохраненный поиск

Название сохраненного поиска:

Условия поиска:

Тестовые условия поиска

Электронная почта: (изменить)

Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый рабочий день

Который день? ВоскресеньеПонедельникВторникСредаЧетвергПятницаСуббота

Формат отчета: РезюмеРезюме (текст)АбстрактАбстракт (текст)PubMed

Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.

Отправить, даже если нет новых результатов

Необязательный текст в электронном письме:

Создайте файл для внешнего программного обеспечения для управления цитированием

. 2022 21 апреля; 9 (1): 29.

doi: 10.1186/s40658-022-00460-4.

Чжэн Лю ¹ , Мин Ню ¹ , Чжунхуа Куан ¹ , Нин Рен ¹ , Сан Ву ¹ , Лонхан Конг ¹ , Сяохуэй Ван ¹ , Зиру Санг ¹ , Криспин Уильямс ² , Юнфэн Ян ³

Принадлежности

• ¹ Исследовательский центр биомедицинской визуализации Пола С. Лаутербура, Шэньчжэньский институт передовых технологий, Китайская академия наук, Шэньчжэнь, 518055, Китай.
• ² Европейский центр ядерных исследований (ЦЕРН), Женева, Швейцария.
• ³ Исследовательский центр биомедицинской визуализации Пола С. Лаутербура, Шэньчжэньский институт передовых технологий, Китайская академия наук, Шэньчжэнь, 518055, Китай. [email protected].

• PMID: 35445890
• PMCID: PMC28
• DOI: 10.1186/с40658-022-00460-4

Бесплатная статья ЧВК

Чжэн Лю и др. EJNMMI физ. 2022 .

Бесплатная статья ЧВК

. 2022 21 апреля; 9 (1): 29.

doi: 10.1186/s40658-022-00460-4.

Авторы

Чжэн Лю ¹ , Мин Ню ¹ , Чжунхуа Куан ¹ , Нин Рен ¹ , Сан Ву ¹ , Лонхан Конг ¹ , Сяохуэй Ван ¹ , Зиру Санг ¹ , Криспин Уильямс ² , Юнфэн Ян ³

Принадлежности

• ¹ Исследовательский центр биомедицинской визуализации Пола С. Лаутербура, Шэньчжэньский институт передовых технологий, Китайская академия наук, Шэньчжэнь, 518055, Китай.
• ² Европейский центр ядерных исследований (ЦЕРН), Женева, Швейцария.
• ³ Исследовательский центр биомедицинской визуализации Пола С. Лаутербура, Шэньчжэньский институт передовых технологий, Китайская академия наук, Шэньчжэнь, 518055, Китай. [email protected].

• PMID: 35445890
• PMCID: PMC28
• DOI: 10.1186/с40658-022-00460-4

Абстрактный

Фон: Большинство современных сканеров позитронно-эмиссионной томографии (ПЭТ) всего тела используют детекторы с высоким временным разрешением для измерения времени пролета двух фотонов с энергией 511 кэВ, улучшая отношение сигнал/шум ПЭТ-изображений. Однако почти все современные ПЭТ-сканеры всего тела используют детекторы без возможности кодирования глубины; поэтому на их пространственное разрешение может влиять эффект параллакса.

Методы: В данной работе четыре глубинно-кодирующих детектора, состоящие из массивов LYSO с кристаллами 2,98 × 2,98 × 20 мм ³ , 2,98 × 2,98 × 30 мм ³ , 1,95 × 1,95 × 20 мм ³ и 1,95 × 1,95 × 1,95 × 1,95 × 30 мм ³ , × 30 мм ³ соответственно, считывались с обоих концов, с использованием кремниевых фотоумножителей (SiPM) размером 6 × 6 мм ² в массиве 4 × 4. Временные сигналы детекторов обрабатывались индивидуально с использованием сверхбыстрой специализированной интегральной схемы NINO (ASIC) для получения хорошего временного разрешения. 16 сигналов энергии массива SiPM считывались с использованием схемы суммирования строк и столбцов для получения четырех сигналов энергии с кодированием положения.

Полученные результаты: Четыре ПЭТ-детектора обеспечили хорошие гистограммы заливки, на которых можно было четко разглядеть все кристаллы, измеренное разрешение по энергии кристаллов составило 10,2, 12,1, 11,4 и 11,7% от полной ширины на полувысоте (FWHM) при средней глубине взаимодействия кристалла (DOI). разрешение 3,5, 3,9, 2,7 и 3,0 мм соответственно. Была измерена и скорректирована зависимость синхронизации каждого Si-ФЭУ от глубины, причем синхронизация двух Si-ФЭУ использовалась в качестве синхронизации двустороннего считывающего детектора. Четыре детектора обеспечили временные разрешения совпадений 180, 214, 239и 263 пс соответственно.

Выводы: Временное разрешение двухстороннего считывающего ПЭТ-детектора было примерно на 20% лучше, чем у одностороннего считывающего детектора, использующего ту же матрицу LYSO, матрицу SiPM и считывающую электронику. Детекторы, разработанные в этой работе, использовали длинные кристаллы с небольшим поперечным сечением и обеспечивали хорошие гистограммы потока, DOI, энергетическое и временное разрешение, что позволяет предположить, что их можно использовать для разработки ПЭТ-сканеров всего тела с высокой чувствительностью, однородным высоким пространственным разрешением, и высокое временное разрешение.

Ключевые слова: глубина взаимодействия; Высокое разрешение; ПЭТ-детектор; кремниевый фотоумножитель; Время полета.

© 2022. Автор(ы).

Заявление о конфликте интересов

Авторы заявляют, что у них нет конкурирующих интересов.

Цифры

Рис. 1

Фото четырех LYSO…

Рис. 1

Фотография четырех кристаллических массивов LYSO, оцененных в этой работе, кристалл…

рисунок 1

Фотография четырех кристаллических массивов LYSO, оцененных в этой работе, размеры кристаллов четырех массивов: (1) 2,98 × 2,98 × 20 мм ³ , (2) 2,98 × 2,98 × 30 мм ³ , (3) 1,95 × 1,95 × 20 мм ³ и (4) 1,95 × 1,95 × 30 мм ³

Рис. 2

a Механический дизайн, b фото…

Рис. 2

a Механическая конструкция, b фото световода с канавками, c…

Рис. 2

a Механическая конструкция, b фотография световода с канавками и c – d иллюстрация того, как перенос фотонов в краевых кристаллах и световод улучшает идентификацию краевых кристаллов

Рис. 3

(слева) Схема…

Рис. 3

(слева) Схема считывания сигнала 4×4 SiPM…

Рис. 3

(слева) Схема считывания сигнала массива КФУ 4 × 4, (справа) фото массива КФУ с платой считывания

Рис. 4

a Экспериментальная установка для…

Рис.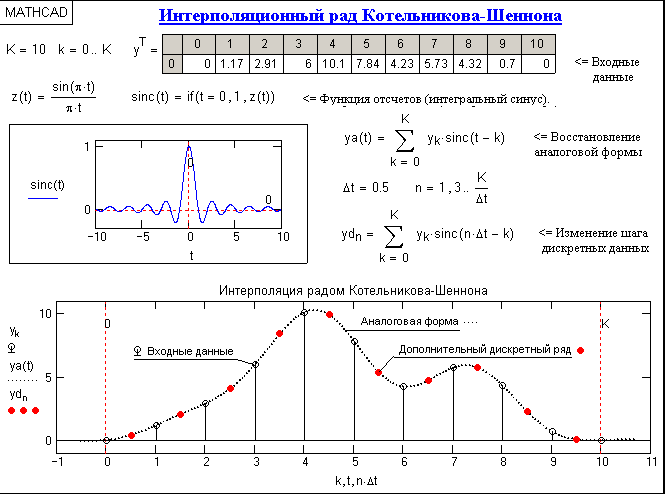 4

a Экспериментальная установка для измерения гистограммы паводка, энергетического и временного разрешения,…

Рис. 4

a Экспериментальная установка для измерения гистограммы наводнения, энергетического и временного разрешения, эталонный детектор, состоящий из 2 × 2 × 3 мм ³ Кристалл LYSO, считываемый с использованием 3 × 3 мм ² SiPM, b Экспериментальная установка для измерения разрешения DOI, эталонный детектор состоит из 40 × 20 × 1 мм ³ Плита LYSO считывается с помощью одноканального ФЭУ

Рис. 5

(Вверху) Гистограммы наводнений и (внизу)…

Рис. 5

(Вверху) Гистограммы наводнений и (внизу) линейные профили среднего ряда…

Рис.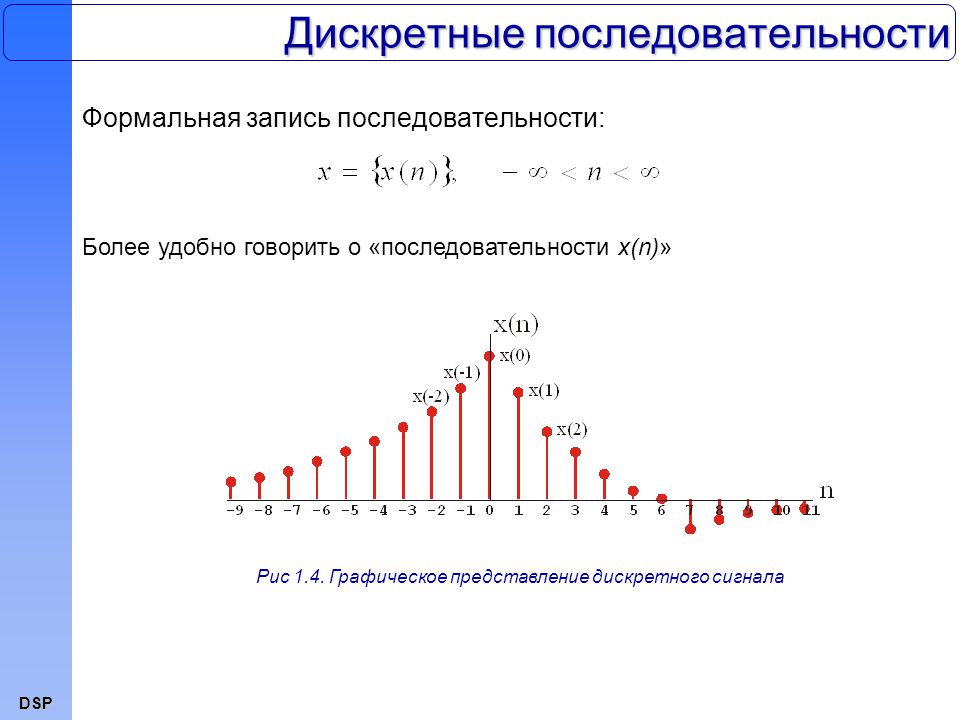 5

(Вверху) Гистограммы заливки и (внизу) линейные профили среднего ряда кристаллов детектора 3 с использованием 12 × 12 кристаллов LYSO 1,95 × 1,95 × 20 мм ³ измерил a без световода, b со стеклянным световодом толщиной 1 мм и c со световодом толщиной 1 мм с канавками

Рис. 6

(вверху) Гистограммы наводнений и (внизу)…

Рис. 6

(вверху) Гистограммы заливки и (внизу) линейчатые профили среднего ряда кристаллов…

Рис. 6

(вверху) Гистограммы заливки и (внизу) линейные профили среднего ряда кристаллов 4 детекторов, a детектор 1 с использованием массива 8 × 8 LYSO размером 2,98 ×2,98 × 20 мм ³ размер кристалла, b Детектор 2 с использованием матрицы лизов 8 × 8 составляет 2,98 × 2,98 × 30 мм ³ Размер кристалла, C Детектор 3 с использованием 12 × 12 матриц Lyso 1,95 × 1,95 × 20 мм ³ размер кристалла и D Detector 3 и D . 4 с использованием массива 12 × 12 LYSO 1,95 × 1,95 × 30 мм ³ размер кристалла. Гистограммы потока детекторов 1 и 2 измерены без световодов. Гистограммы потока детекторов 3 и 4 измерены с помощью световодов с канавками

.

Рис. 7

Энергетические спектры (…

Рис. 7

Энергетические спектры ( a ), среднего кристалла и б ан…

Рис. 7

Энергетические спектры ( a ), среднего кристалла и b краевого кристалла в кристаллической решетке 3 × 3 × 20 мм ³

Рис. 8

Амплитуды фотопиков (вверху) всех…

Рис.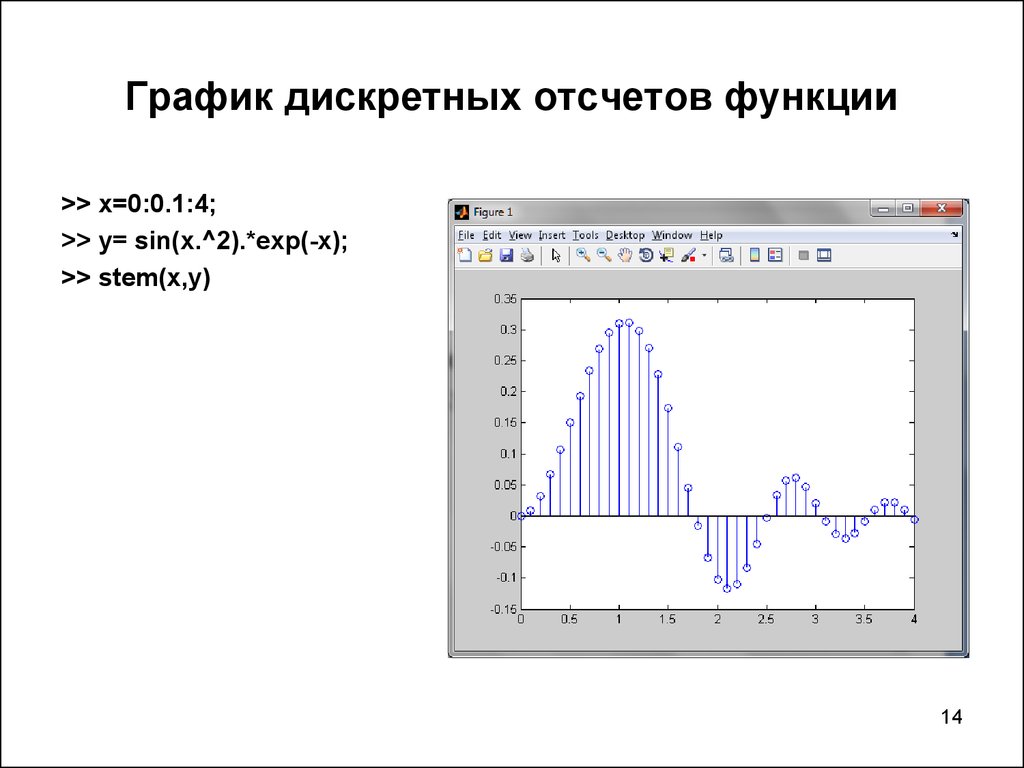 8

Амплитуды фотопиков (вверху) всех отдельных кристаллов четырех детекторов, измеренные с…

Рис. 8

Амплитуды фотопиков (вверху) всех отдельных кристаллов четырех детекторов, измеренные по амплитудным спектрам импульсов всех глубин, a детектор 1, b детектор 2, c детектор 3 и d детектор 4. Энергия разрешения (внизу) всех отдельных кристаллов четырех детекторов, измеренные по энергетическим спектрам всех глубин, e детектор 1, f детектор 2, g детектор 3 и h детектор 4

Рис. 9

Гистограммы коэффициента DOI…

Рис. 9

Гистограммы отношения DOI среднего кристалла в четырех детекторах, измеренные при…

Рис.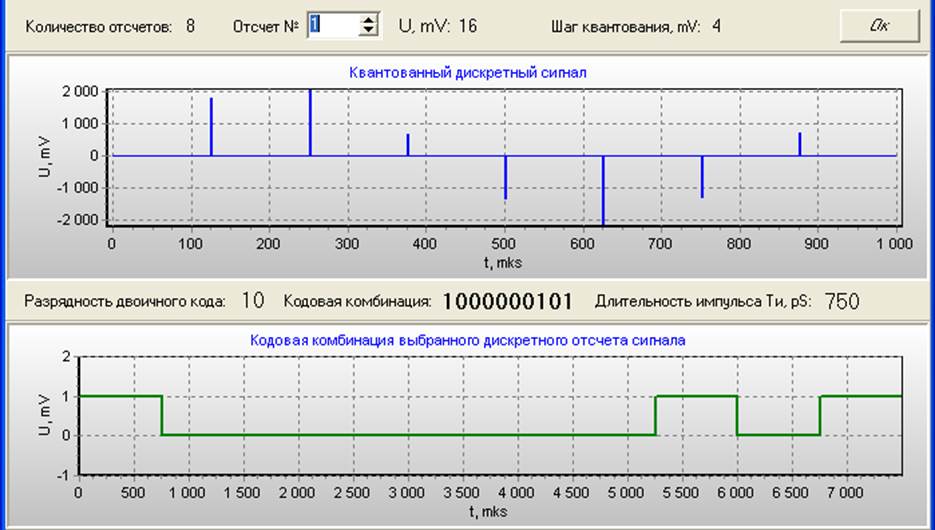 9

Гистограммы отношения DOI среднего кристалла в четырех детекторах, измеренные на разной глубине с шагом 4 мм, a детектор 1, b детектор 2, c детектор 3 и d детектор 4. Глубина, измеренная для детекторов 1 и 3, составляет 2, 6, 10, 14 и 18 мм от одного конца. Глубина, измеренная для детекторов 2 и 4, составляет 3, 7, 11, 15, 19, 13 и 27 мм от одного конца

Рис. 10

Разрешения DOI всех отдельных…

Рис. 10

Разрешение DOI всех отдельных кристаллов в a детектор 1, b детектор 2,…

Рис. 10 Разрешения

DOI всех отдельных кристаллов в a детектор 1, b детектор 2, c детектор 3 и d детектор 4

Рис. 11

Время (разница между…

Рис. 11

Время (разница между временем эталонного детектора и временем…

Рис. 11

Время (разница между временем эталонного детектора и временем измеренного детектора) в зависимости от отношения DOI, измеренного Si-ФЭУ 1, Si-ФЭУ 2 и среднего значения двух Si-ФЭУ для детектора 1, a до и b после зависимости временной коррекции от глубины

Рис. 12

a CTR детекторов…

Рис. 12

a CTR детекторов 1 и 3 как функция света…

Рис. 12

a CTR детекторов 1 и 3 в зависимости от толщины световода, b CTR пяти детекторов в зависимости от перенапряжения SiPM

Рис. 13

CTR всех отдельных кристаллов…

Рис. 13

CTR всех отдельных кристаллов четырех детекторов, a детектор 1, b…

Рис. 13

CTR всех отдельных кристаллов четырех детекторов, a детектор 1, b детектор 2, c детектор 3, d детектор 4

См. это изображение и информацию об авторских правах в PMC

Похожие статьи

• Разработка ПЭТ-детекторов мелких животных с кодированием глубины с использованием двустороннего считывания массивов пиксельных сцинтилляторов с SiPM.

  Куанг З., Сан З., Ван Х., Фу Х., Рен Н., Чжан Х., Чжэн Ю., Ян Ц., Ху З., Ду Дж., Лян Д., Лю Х., Чжэн Х., Ян Ю. Куанг Зи и др. мед. физ. 2018 фев; 45 (2): 613-621. doi: 10.1002/mp.12722. Epub 2017 30 декабря. мед. физ. 2018. PMID: 29222959

• Характеристики длинных прямоугольных полумонолитных сцинтилляционных ПЭТ-детекторов.

  Zhang X, Wang X, Ren N, Hu B, Ding B, Kuang Z, Wu S, Sang Z, Hu Z, Du J, Liang D, Liu X, Zheng H, Yang Y. Чжан X и др. мед. физ. 2019Апр; 46 (4): 1608-1619. doi: 10.1002/mp.13432. Epub 2019 20 февраля. мед. физ. 2019. PMID: 30723932

• ПЭТ-детекторы мелких животных со сверхвысоким разрешением и глубинным кодированием: использование кристаллических матриц GAGG и LYSO.

  Ню М., Лю З., Куан З., Ван Х., Рен Н., Санг З., Ву С., Конг Л., Сунь Т., Ху З., Ян Ю. Ниу М. и др. мед. физ. 2022 май; 49(5):3006-3020. doi: 10.1002/mp.15606. Epub 2022 28 марта. мед. физ. 2022. PMID: 35301730

• Производительность модуля ПЭТ-детектора с кодированием глубины с использованием разделения света и одностороннего считывания с SiPM.

  Куанг З., Ян Ц., Ван Х., Фу Х., Рен Н., Ву С., Чжан С., Чжао Б., Сан З., Ху З., Ду Дж., Лян Д., Лю Х., Чжэн Х., Ян Ю. Куанг Зи и др. физ.-мед. биол. 2019 10 апреля; 64 (8): 085012. doi: 10.1088/1361-6560/ab1152. физ.-мед. биол. 2019. PMID: 30893674

• Толстый полумонолитный сцинтилляционный детектор для клинических ПЭТ-сканеров.

  Zhang C, Wang X, Sun M, Kuang Z, Zhang X, Ren N, Wu S, Sang Z, Sun T, Hu Z, Yang Y, Liu Z. Чжан С и др. физ.-мед. биол. 2021 12 марта; 66 (6): 065023. дои: 10.1088/1361-6560/abe761. физ.-мед. биол. 2021. PMID: 33709958

Посмотреть все похожие статьи

Рекомендации

1. 1. Conti M. Сосредоточьтесь на времяпролетной ПЭТ: преимущества улучшенного временного разрешения. Eur J Nucl Med Mol Imaging. 2011;38(6):1147–1157. doi: 10.1007/s00259-010-1711-y. — DOI — пабмед
2. 1. Ванденберг С., Михайлова Э., Д’Хоэ Э., Молле П., Карп Дж. С. Последние разработки в области времяпролетной ПЭТ. EJNMMI физ. 2016;3(1):30. doi: 10.1186/s40658-016-0138-3. — DOI — ЧВК — пабмед
3. 1. Сурти С., Карп Дж.С. Обновленная информация о последних достижениях в области времяпролетной ПЭТ. Physica Medica-Eur J Med Phys. 2020; 80: 251–258. doi: 10.1016/j.ejmp.2020.10.031. — DOI — ЧВК — пабмед
4. 1. Шаарт Др. Физика и технология времяпролетных ПЭТ-детекторов. физ.-мед. биол. 2021;66(9):09TR01. doi: 10.1088/1361-6560/abee56. — DOI — пабмед
5. 1. Головин В., Савельев В. Новый тип лавинного фотоприемника с режимом Гейгера. Nucl Instrum Methods Phys Res Sect A-Accel Spectrom Dect Assoc Equip. 2004; 518 (1–2): 560–564. doi: 10.1016/j.nima.2003.11.085. — DOI

Грантовая поддержка

• 2020B1212060051/Ключевая лаборатория магнитно-резонансной и мультимодальной визуализации провинции Гуандун
• JCYJ20190807155418935/Программа фундаментальных исследований Шэньчжэня
• GJJSTD20180002 / Группа инноваций в области научных инструментов Китайской академии наук

Полнотекстовые ссылки

Спрингер Бесплатная статья ЧВК

Укажите

Формат: ААД АПА МДА НЛМ

Отправить по номеру

Разрешение дисплея измерения не учитывает точность

Опубликовано 22 февраля 2022 г. автором Weschler Instruments

Случайные пользователи цифровых приборов часто предполагают, что большее разрешение дисплея обеспечивает более точное измерение — что дополнительная цифра в показаниях увеличивает точность на десятилетие. Это бывает редко.

Разрешение — это наименьшее значение измеряемой величины, которое можно различить. В цифровом измерителе разрешение дисплея обычно представляет собой числовое значение, связанное с самой младшей значащей цифрой показаний. Примеры: 0,001 В на вольтметре, 0,1 мА на амперметре. На измерителях с несколькими диапазонами или функциями вместо того, чтобы указывать значение для каждого диапазона, разрешение часто выражается в виде количества отображаемых цифр.

Цифры Отображаемые значения

3 0-999 (1000 единиц)
4 0-9999 (10 000 единиц)
5 0-99999 (100 000 единиц)

 

Пользователь определяет разрешение для определенного диапазона на основе десятичной позиции. Например, младшая значащая цифра в диапазоне 10 В трехразрядного счетчика равна 0,01 В.

Часто счетчик не отображает весь диапазон от 0 до 9 в первой цифре. В этом случае для описания интервала измерения счетчика используется дробное число разрядов. Типичные значения:

Цифры Отображаемые значения

3½ 0-1999 (2000 единиц)
3¾ 0-3999 (4000 единиц)
4½ 0-19999 (20000 единиц)
4¾ 0-39999 (40000 единиц)

Этот дополнительный диапазон не изменяет разрешение. В том же диапазоне 3-разрядный измеритель имеет то же разрешение, что и 3½-разрядный измеритель. Младшая значащая цифра в диапазоне 20 В 3,5-разрядного счетчика по-прежнему составляет 0,01 В. Обратите внимание, что измеритель, который считывает положительные и отрицательные сигналы, такой как цифровой мультиметр, имеет удвоенное количество отсчетов дисплея. Опять же, разрешение не меняется.

Следует отметить два особых случая:
Некоторые счетчики не отображают все возможные значения младшей значащей цифры. Одним из примеров этого являются недорогие весы для ванны. В то время как показания имеют разрешение в десять фунтов, весы могут показывать приращения только в полфунта. Следовательно, разрешение составляет полфунта. Некоторые измерители температуры проявляют эту характеристику из-за способа линеаризации датчика.

Усреднение нескольких показаний может увеличить разрешение измерения сверх того, что отображается на дисплее. Для этого пользователь наблюдает за дисплеем и интерполирует дополнительную цифру разрешения на основе количества показаний двух соседних значений. Например: пять показаний 103 и пять показаний 104 интерполируются до значения 1035. Хотя визуально это трудно сделать, это можно легко сделать с помощью счетчиков, имеющих компьютерный интерфейс.

Точность показывает, насколько сильно измеренное значение отклоняется от истинного или идеального значения. В цифровом измерителе, в зависимости от формата спецификации точности, разрешение может влиять на точность. Если точность измерителя указана в процентах от полной шкалы или диапазона, то разрешение не влияет на точность. Если 3-разрядный и 4-разрядный счетчики имеют точность 1% от полной шкалы, они имеют одинаковую точность измерения на любом уровне. Дополнительное разрешение не обеспечивает лучшей точности. Измерители физических параметров, таких как давление, уровень и температура, часто указывают точность в процентах от диапазона.

Для электрических параметров, таких как напряжение, ток и сопротивление, точность цифрового измерителя обычно указывается в процентах от показаний плюс число отсчетов в младшей значащей цифре. Здесь дополнительное разрешение обеспечивает некоторое улучшение точности.

Пример: Точность счетчика составляет 0,1% от показаний плюс 2 такта. Для показания 10 В в диапазоне 10 В:

Показания дисплея % показания + счетчики Точность

3 цифры 10,00 10 мВ + 20 мВ 30 мВ
4 цифры 10,000 10 мВ + 2 мВ 12 мВ

Дополнительная цифра разрешения обеспечивает примерно в 2,5 раза более высокую точность.