Дискретные и непрерывные сигналы: ключевые отличия и особенности — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Чем отличаются непрерывные и дискретные сигналы. Как происходит дискретизация аналоговых сигналов. Какие преимущества у цифровых систем передачи данных. Где применяются аналоговые и цифровые сигналы в современных технологиях.

Содержание

Основные характеристики непрерывных и дискретных сигналов

Сигналы играют ключевую роль в передаче информации в современных системах связи и обработки данных. Существует два основных типа сигналов — непрерывные (аналоговые) и дискретные (цифровые). Рассмотрим их ключевые характеристики и отличия.

Непрерывные сигналы

Непрерывные или аналоговые сигналы имеют следующие особенности:

Определены в любой момент времени
Могут принимать любые значения в заданном диапазоне
Изменяются плавно, без резких скачков
Описываются непрерывными функциями
Встречаются в природе (звук, свет и т.д.)

Дискретные сигналы

Дискретные или цифровые сигналы характеризуются следующим:

Определены только в дискретные моменты времени
Принимают конечное число значений

Изменяются скачкообразно
Описываются последовательностями чисел
Получаются путем дискретизации аналоговых сигналов

Процесс дискретизации непрерывных сигналов

Для преобразования аналогового сигнала в цифровой используется процесс дискретизации, который включает следующие этапы:

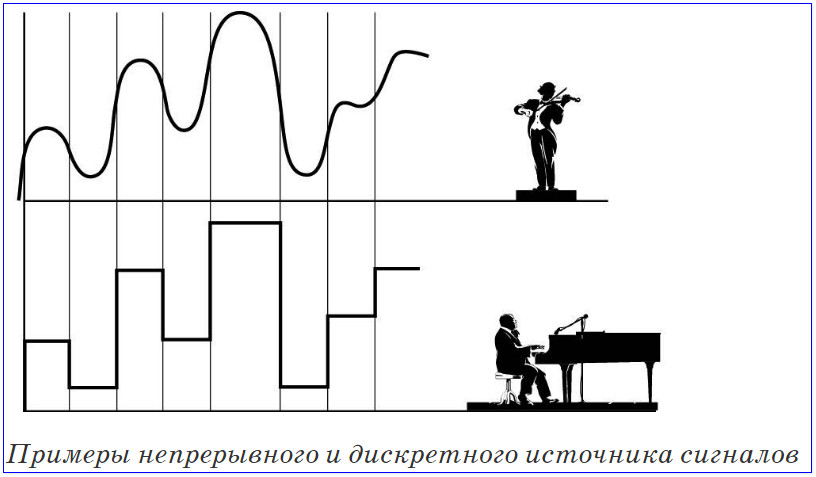
Выборка — измерение значений сигнала через равные промежутки времени
Квантование — округление измеренных значений до ближайших допустимых уровней
Кодирование — представление квантованных значений в двоичном коде

Ключевым параметром дискретизации является частота дискретизации — количество выборок в секунду. Согласно теореме Котельникова, для корректного восстановления сигнала частота дискретизации должна как минимум в два раза превышать максимальную частоту в спектре исходного сигнала.

Преимущества цифровых систем передачи данных

Системы связи на основе дискретных сигналов имеют ряд существенных преимуществ по сравнению с аналоговыми:

Высокая помехоустойчивость
Возможность сжатия и эффективного кодирования данных
Простота обработки на компьютерах
Отсутствие накапливающихся искажений при передаче
Возможность применения методов коррекции ошибок

Благодаря этим преимуществам цифровые технологии активно вытесняют аналоговые практически во всех сферах.

Области применения аналоговых и цифровых сигналов

Несмотря на повсеместное внедрение цифровых технологий, аналоговые сигналы продолжают использоваться в некоторых областях:

Применение аналоговых сигналов

Аудиотехника высокого класса
Аналоговое телевещание (уходящая технология)
Аналоговые датчики и измерительные приборы
Аналоговые системы радиосвязи

Применение цифровых сигналов

Мобильная связь
Цифровое телевидение
Интернет и компьютерные сети
Системы хранения и обработки данных
Цифровая аудио- и видеозапись

Таким образом, цифровые технологии доминируют в современных системах связи и обработки информации благодаря своим многочисленным преимуществам.

Методы преобразования аналоговых сигналов в цифровые

Для преобразования непрерывных сигналов в дискретную форму используются аналого-цифровые преобразователи (АЦП). Существует несколько основных типов АЦП:

АЦП последовательного приближения
Параллельные АЦП
Сигма-дельта АЦП
Конвейерные АЦП

Выбор конкретного типа АЦП зависит от требуемой скорости преобразования, разрядности и других параметров. Современные АЦП позволяют оцифровывать сигналы с частотой дискретизации до нескольких гигагерц и разрешением до 24 бит.

Особенности представления дискретных сигналов

При работе с дискретными сигналами важно учитывать следующие аспекты:

Временную дискретизацию — сигнал определен только в дискретные моменты времени
Квантование по уровню — сигнал принимает только конечное число значений
Цифровое кодирование — значения представляются двоичным кодом
Частоту дискретизации — определяет временное разрешение
Разрядность квантования — определяет точность представления значений

Правильный выбор этих параметров позволяет минимизировать погрешности дискретизации и обеспечить требуемое качество цифрового сигнала.

Спектры непрерывных и дискретных сигналов

Важной характеристикой сигналов является их спектральное представление. Спектры непрерывных и дискретных сигналов имеют ряд отличий:

Спектр непрерывного сигнала

Непрерывный во всей полосе частот
Может быть ограничен по ширине
Описывается непрерывной функцией

Спектр дискретного сигнала

Периодически повторяется
Ограничен частотой Найквиста (половина частоты дискретизации)

Описывается дискретной функцией

При дискретизации непрерывного сигнала его спектр трансформируется — появляются копии исходного спектра, смещенные на частоту дискретизации и ее гармоники. Это явление называется наложением спектров и может приводить к искажениям, если не соблюдается теорема Котельникова.

Заключение

Непрерывные и дискретные сигналы имеют принципиальные отличия в своих характеристиках и способах обработки. Переход от аналоговых к цифровым технологиям позволил создать более совершенные системы передачи и обработки информации. При этом важно понимать особенности дискретного представления сигналов, чтобы корректно их использовать и минимизировать возможные искажения. Грамотное применение методов цифровой обработки сигналов открывает широкие возможности для развития современных информационных технологий.

Чем отличается непрерывный сигнал от дискретного кратко

Что ты хочешь узнать?

Ответ

1.Непрерывный сигнал определен в каждый момент времени и принимает все значения в своей области значений. Дискретный сигнал определен либо только в определенные моменты времени (квантование по времени, решетчатая функция), либо его значение может принимать только определенные значения (квантование по уровню, ступенчатая функция).
2. Частота взятия отсчётов непрерывного по времени сигнала при его дискретизации. Чем выше частота дискретизации, тем более широкий спектр сигнала может быть представлен в дискретном сигнале.
3.
аудиоформаты без сжатия, такие как WAV, AIFF

аудиоформаты со сжатием без потерь(APE, FLAC)

аудиоформаты со сжатием с потерями(MP3)
4. Для того, чтобы закодировать видеоинформацию, следует пойти 3 этапа.

Первый этап – это подготовка видеоданных;

Второй этап – это сжатие видеоданных;

Третий этап – это квантование.

5. Видеофайл MPEG-4, Видеофайл Windows Media, файл Windows Video, файл Adobe Flash Media

Аналоговый сигнал (analogue signal) – непрерывный во времени поток данных (информации), имеющий изменяющиеся и принимающие любое возможное значение характеристики (напряжение, силы тока, мощности, давления звуковой волны и т.д.). Несмотря на большое количество недостатков и постепенное вытеснение цифровым аналогом, в таких областях, как телефония, звукозапись, телевидение, такой вид передачи информации сохраняет свою актуальность, благодаря относительной своей дешевизне и простоте генерирующего его оборудования.

История появления термина

Появление термина, обозначающего такой способ передачи данных, тесно связано с такими сферами, как вычислительная техника, телефония и звукозаписывающая индустрия, электрические измерения.

Вычислительная техника

В 40-х годах создаются первые вычислительные системы, предназначенные для сбора и обработки цифровой информации. В начале 80-х годов с появлением новых моделей компьютеров на базе процессоров Intel возможности вычислительной техники расширились. Именно в этот период появляется данный термин.

Звукозапись и телефония

Понятие непрерывного способа передачи данных изначально связано с телефонией. Непрерывные колебания поступают на динамик устройства, становятся электрическим аналогом, затем преобразуются в сигнал, подобный голосу.

Электрические измерения

Непрерывный поток воспроизводится приемным устройством пропорционально таким электрическим параметрам, как напряжение, сила тока. Именно с началом измерения указанных выше электрических величин связывают появление этого термина.

Общая информация

Энергия потока

Так как аналоговый сигнал – это непрерывный поток данных, то энергия его бесконечна. Однако в качестве значения данной характеристики обычно используют усредненную для определенного промежутка времени величину, так, к примеру, переменный электрический ток в телефонной сети, отвечающий за передачу голоса, имеет среднее напряжение 60 В.

Взаимное преобразование различных по природе потоков

Непрерывный поток данных преобразуется в дискретный (прерывистый). Достаточно воспользоваться импульсным блоком питания, который сформирует входное напряжение в виде дискретных ультразвуковых пачек. Преобразование проводится программой либо технически через микросхемы.

Отличия дискретного и цифрового сигналов

Один из способов передачи данных, описываемых в данной статье, – дискретный, имеющий сходные характеристики с аналоговым, но отличающийся от него тем, что он является прерывистым.

По сравнению с дискретным и аналоговым, цифровой сигнал, наоборот, характеризуется конкретными параметрами:

Строго определённой своими характеристиками длительностью;
Ярко выраженной амплитудой;
Наличием двух состояний: «0» либо «1».
Формированием из битов машинных слов, необходимых для дальнейшей обработки информации, ее представлении в доступном и понятном виде для пользователя.

Благодаря этим особенностям, цифровая передача и хранение информации в последнее время находят очень широкое применение в различных отраслях техники, электроники, связи.

Важно! Самое основное, чем отличается аналоговая информация от дискретной, – это прерывистость передачи последней при помощи соответствующего потока данных. Однако, несмотря на данное различие, дискретная информация не является цифровой, так как ее характеристики в процессе существования могут обладать как ограниченным, так и неограниченным диапазоном значений.

Виды сигналов

В зависимости от изменения характеристик во времени, все потоки подразделяются на следующие виды:

Аналоговые – непрерывные, имеющие большое количество значений;
Дискретные – прерывистые, с большим количеством значений;
Цифровые – прерывистые, имеющие 2 четко обозначенных основных значения.

Также, в зависимости от среды передачи и способа формирования, они бывают электрические, звуковые, оптические.

Для чего обрабатывается сигнал

Чтобы получить данные, содержащиеся в описанных выше потоках, их обрабатывают через процессы усиления, фильтрации, модуляции и демодуляции. Лишь после этого они будут представлены в понятном для пользователя виде и использованы по назначению.

Создание и формирование

Для создания непрерывного потока используют такое специальное оборудование, как генераторы. Собирают их, используя различные транзисторы (полевые и биполярные), трансформаторы.

Динамический диапазон

Важной характеристикой любой системы динамических измерений считается ее динамический диапазон. Четкого определения данного параметра для сигнала пока не существует, поэтому принято считать, что это соотношение наибольшего и наименьшего его значений, измеренных системой в определенный промежуток времени.

Для каждого потока важно, чтобы его динамический диапазон максимально соответствовал аналогичной характеристике системы либо устройства, предназначенного для преобразования, передачи и хранения его величин. От правильного подбора зависит, насколько точно будет передана и преобразована информация любого потока.

Аналоговый сигнал

Такой вид потока данных непрерывен во времени, его определение возможно в любой временной промежуток.

Цифровой сигнал

Такой поток представлен последовательностью конкретных цифровых значений, как правило, двух, которые принимают за логические «0» и «1» или «true» и «false».

Применение цифрового сигнала

Цифровой поток наиболее применим в современной электронике, при двоичной системе шифрования и кодирования данных.

Дискретный сигнал

В отличие от непрерывного, дискретный способ передачи данных имеет следующие особенности:

Может характеризоваться постоянным значением параметра, изменятся только по времени;
Изменяется уровень величины, но во времени остается постоянным;
Меняется как по значению величины, так и по временному параметру.

Сравнение цифрового и аналогового сигналов

Широко применяемые в современном мире аналоговый и цифровой сигналы имеют свои преимущества и недостатки.

К основным плюсам непрерывного потока информации относятся:

Простота формирования;
Небольшая стоимость оборудования для его получения и поддержания.

Недостатки такого вида передачи данных:

Содержание большого количества лишней информации, которую необходимо фильтровать;
Низкая помехоустойчивость, что сказывается на качестве воспроизводимой информации;
В передачу такого сигнала возможно нежелательное вмешательство с целью похищения передаваемой информации.

Прерывистый способ передачи данных имеет следующие преимущества:

Небольшое количество значений, помехоустойчивость;
Простота расшифровки на принимающем оборудовании;
Возможность кодировки больших объемов данных при их хранении и передаче на большие расстояния.

У прерывистого способа передачи и хранения информации имеется один серьезный недостаток – при серьезном уровне помех может произойти обрыв, первоначальный вид потока данных не сохранится. Для восстановления его параметров на момент обрыва приходится предусматривать дополнительные функции.

Аналоговый и цифровой сигналы и цифро-аналоговое преобразование

Современные системы, устройства позволяют проводить процессы взаимных преобразований. Так, при аналого-цифровом преобразовании (АЦП) проходит квантование аналогового потока данных в цифровой, после чего информация готова для передачи через цифровые каналы.

При процессе ЦАП цифровые коды на входе, наоборот, преобразуются в эквивалентный выходной аналоговый поток (ток, напряжение). Преобразователи широко используются для формирования сигналов в системах управления, аудио,-и видеоаппаратуре.

Таким образом, сигнал аналоговый – это хоть и уже утрачивающий свою актуальность, но достаточно широко применимый способ передачи данных. Хотя аналоговый сигнал и называют пережитком прошлого, его роль в современной телекоммуникационной технике, радиопередаче и телевещании еще до сих пор очень существенна.

Видео

Сигнал — это любая переменная содержащая какой-либо вид информации. Причем эту информацию можно передавать на расстояние, переносить на устройства хранения, выводить на экран и через динамики или совершать с ней подобные действия. Существующие аналоговый и цифровой кардинально отличаются природой происхождения, способом передачи и хранения.

p, blockquote 1,0,0,0,0 –>

p, blockquote 2,0,0,0,0 –>

Аналоговый сигнал

Это природный тип сигналов окружает нас повсеместно и постоянно. Звук, изображение, тактильные ощущения, запах, вкус и команды мозга. Все возникающие, во Вселенной без участия человека, сигналы являются аналоговыми.

p, blockquote 3,0,0,0,0 –>

В электронике, электротехнике и системах связи аналоговую передачу данных применяют со времени изобретения электричества. Характерной особенностью является непрерывность и плавность изменения параметров. Графически сеанс аналоговой связи можно описать как непрерывную кривую, соответствующую величине электрического напряжения в определённый момент времени. Линия изменяется плавно, разрывы возникают только при обрыве связи. В природе и электронике аналоговые данные генерируются и распространяются непрерывно. Отсутствие непрерывного сигнала означает тишину или черный экран.

p, blockquote 4,0,0,0,0 –>

В непрерывных системах связи аналогом звука, изображения и любых других данных является электрические или электромагнитные импульсы. Например, громкость и тембр голоса передаются от микрофона на динамик посредством электрического сигнала. Громкость зависит от величины, а тембр от частоты напряжения. Поэтому при голосовой связи сначала напряжение становится аналогом звука, а потом звук аналогом напряжения. Таким же образом происходит передача любых данных в аналоговых системах связи.

p, blockquote 5,0,0,0,0 –>

Что такое дискретный сигнал

В цифровой системе хранения и передачи данных, отсутствие сигнала, также является формой обмена информацией. В какой-то момент времени он равен нулю, в другой принимает какое-либо значение. Поэтому дискретным называют сигнал прерывный, отсюда и название discretus или разделённый. Аналоговые данные разбиваются на отдельные блоки, обрабатываются и передаются в виде цифрового кода.

p, blockquote 6,0,0,0,0 –>

p, blockquote 7,0,0,0,0 –>

Дискретность не подразумевает разрыв связи. В цифровых системах широко используется двоичная система обработки и обмена информацией. Двоичная подразумевает кодировку данных с помощью единицы и нулей. В доли секунды сигнал прерывисто принимает значение 1 или 0. Вместо непрерывной кривой имеем отдельные дискретные значения. Определенный набор нулей и единичек уже несёт в себе какую либо информацию. Примитивный набор это бит или двоичный разряд. Сам по себе он ничего не значит. Данные могут кодироваться только при объединении восьми битов в следующую по сложности комбинацию – байт. Чем больше объединённых байтов, тем больше и точнее можно описать передаваемую информацию.

p, blockquote 8,0,1,0,0 –>

На качество генерируемых данных влияет не только количество объединённых битов, но и скорость передачи. Непрерывная аналоговая кривая должна быть разбита на как много больше мини участков прерывного сигнала. Полученный таким образом звук и цвет будут соответствовать оригиналу. Качественный дискретный сигнал формирует точную копию аналогового. Например, звуковая дорожка MP3 закодированная со скоростью 320 000 бит в секунду (320 kbps) значительно лучше кодированной в 128 kbps. Дорожки скоростью меньше 128 слушать вообще невозможно.

p, blockquote 9,0,0,0,0 –>

Чем отличается непрерывный сигнал от дискретного

На первый взгляд отличия в сигналах можно не различить. Оба передаются в виде электрических импульсов по проводам или электромагнитными волнами в эфире. Преобразовываются в звук и изображение, выводятся на динамики и экран. Но разница существенна. Отличие аналогового сигнала от цифрового обусловлено особенностями обработки и передачи данных.

p, blockquote 10,0,0,0,0 –>

Аналоговые данные не кодируются и не шифруются, просто отображаются в электрические или электромагнитные импульсы. Приёмник преобразовывает импульсы в полном соответствии с полученным сигналом. Передаваемый и принимаемый импульс многогранен и характеризуются постоянным плавным изменением с течением времени. Величина и частота определяют параметры информации. Примером может быть соответствие определённого цвета экрана заданному напряжению. С течением времени цвета плавно меняются следуя изменению напряжения.

Казалось бы, природное происхождение, простота генерации, передачи и приёма благоприятствуют использованию аналогового сигнала. Но в дело вмешиваются электрические и электромагнитные помехи. Это могут быть электромагнитные наводки от электрических сетей, работающих механизмов, рельеф местности, грозы, бури на солнце, шумы создаваемые работой передающего и принимающего оборудования, прочие. Они изменяют плавную кривую. На приёмник информация поступает с изменениями. Шипение, хрипы и искаженное изображение обычная история для аналоговой связи.

p, blockquote 12,0,0,0,0 –>

Цифровая технология использует совсем иной принцип передачи. Аналоговые данные сначала кодируются и только потом передаются. Кодировка заключается в описании непрерывной кривой аналоговой информации. В каждый конкретный момент времени, передаваемый импульс имеет значение единицы или нуля, и определенная последовательность битов отображает всю полноту оригинальной картинки или звука.

Дискретный сигнал как азбука Морзе, только вместо точек и тире — чёткие биты. Ничего более, шумы и помехи им не мешают. Цифровой информации главное дойти до цели. Цифры без примесей передадут данные и без изменений перевоплотятся в звук и цвет. Но слабый сигнал может не донести полную картину. Как пример — пропадание слов или изображения полностью. Поэтому сотовые передатчики, устанавливают как можно ближе друг от друга, также используют повторители.

p, blockquote 14,0,0,0,0 –>

p, blockquote 15,0,0,0,0 –>

Примером непрерывных и дискретных сигналов могут служить старая проводная и новая сотовая связь. Через старые АТС иногда невозможно было разговаривать с соседним домом. Шумы и плохое усиление сигнала мешали слышать друг друга. Что бы вести полноценную беседу, приходилось громко кричать самому и прислушиваться к собеседнику. Другое дело сотовая связь основанная на цифровой технологии. Звук закодирован и хорошо передаётся на далёкие расстояния. Отчетливо слышно собеседника даже с другого континента.

p, blockquote 16,1,0,0,0 –>

Оба вида связи не лишены недостатков, а ключевыми отличиями являются:

p, blockquote 17,0,0,0,0 –>

Аналоговый подвержен помехам и поступает с искажениями. В то время как цифровой доходит полностью без искажений или отсутствует вовсе.
Принять или перехватить аналоговое вещание может любой приёмник такого принципа. Дискретная передача адресована конкретному адресату, кодируется и мало доступна к перехвату.
Объём передаваемых данных у аналоговой связи конечен, поэтому она практически исчерпала себя в передаче теле сигнала. Напротив с развитием технологии преобразования аналоговой информации в цифровой код растут объемы и качество трансляции. Например, главным отличием цифрового от аналогового телевидения является превосходное качество изображения.

Цифровая технология выигрывает по всем показателям. Споры идут только среди любителей музыки. Многие меломаны и звукорежиссеры утверждают, что могут различить аналоговый оригинал и цифровую копию. Однако большинство слушателей этого сделать не в состоянии. Да и с развитием цифровых систем аналоговые данные кодируются точнее. Оригинальное звучание и цифровая копия делаются практически неразличимым.

p, blockquote 18,0,0,0,0 –>

Как аналоговый сигнал преобразуется в цифровой и наоборот

Первой в цифровую форму преобразовали математическую, физическую и компьютерную информацию. Описать формулы и расчеты не составило труда. А вот для преображения аналоговой действительности в цифровые массивы уже потребовались специальные устройства. Ими стали аналого-цифровые преобразователи или сокращенно АЦП. Они предназначены для преобразования различных физических величин в цифровые коды. Обратное действие совершают устройства ЦАП.

p, blockquote 19,0,0,0,0 –>

Любые цифровые передатчики и приёмники оснащены такими преобразователями. Например, сотовому телефону, поступивший звук необходимо обработать и передать в оцифрованном виде. В то же время необходимо принять от другого абонента код, преобразовать и передать напряжение на динамик. Так же и с изображением на смартфонах и в телевизорах. В любом случае первоначальной информацией выступает напряжение.

p, blockquote 20,0,0,0,0 –>

p, blockquote 21,0,0,0,0 –>

Существует много видов АЦП, но самыми распространёнными являются следующие:

p, blockquote 22,0,0,0,0 –>

параллельного преобразования;
последовательного приближения;
дельта-сигма, с балансировкой заряда.

Преобразования в АЦП понятийно связаны с измерением и сравнением. Кодировка, это процесс сравнения полученных от источника данных с эталоном. То есть полученная аналоговая величина сравнивается с эталонной (с заданным напряжением). Эталоном выступает информация о конкретном цвете, звуке и т.п. Она соответствует заложенным в устройство представлениям о преобразуемом сигнале. Потом данные эталонной величины кодируются для передачи. Во время аналого-цифровой обработки физических превращений сигнала не происходит. С аналогового делается цифровой матрица (модель).

p, blockquote 23,0,0,0,0 –>

Упрощенно работу любого АЦП можно представить так:

p, blockquote 24,0,0,1,0 –>

Измерение через определенные интервалы времени амплитуды напряжения.
Сравнение с эталоном и формирование данных.
Отгрузка оцифрованных сведений об изменениях амплитуды на передатчик.

Качество передаваемой информации зависит от двух параметров — точности и частоты измерений. Чем точнее измеряется и зашифровывается входящее напряжение, тем качественней передаваемая информация. Поэтому, имеет большое значение, сколько бит может зашифровать преобразователь. Чем плотнее информационный поток, тем точней передача данных. Это выражается в красках экрана, контрастности картинки и чистоте звука. Следующим важным показателем является дискретизация, то есть частота измерений. Чем чаще, тем меньше провалов в измерениях и необходимости сглаживания. В совокупности, чем чаще и точнее преобразователь может измерять и обрабатывать полученное напряжение, тем он лучше.

p, blockquote 25,0,0,0,0 –>

Как выглядят спектры аналогового и дискретного сигнала

Изображение сигналов можно представить как две функции. На рисунке наглядно представлено, чем отличается непрерывный сигнал от дискретного. Напряжение исходного изменяется плавно, обработанного прерывисто. Спектр дискретного периодически ступенчато совпадает с непрерывным.

p, blockquote 26,0,0,0,0 –>

p, blockquote 27,0,0,0,0 –>

Изменения дискретного происходят резко, через определённый период времени. Уровень в цифровой системе зашифровывается и любую величину напряжения описывают двоичным кодом. От частоты измерений зависит сглаженность преобразования и оригинальность передаваемых данных. Чем точнее описан уровень сигнала и чем чаще проводится и обрабатывается измерение, тем точнее совпадает спектр начального и переданного сигналов.

p, blockquote 28,0,0,0,0 –>

p, blockquote 29,0,0,0,0 –>

Какие системы связи используют цифровой сигнал а какие аналоговый

Несмотря на архаичность аналоговая технология ещё используется для телефонной и радио связи. Многие проводные сети до сих пор остаются аналоговыми. В основном это традиционные телефонные линии местных операторов. Но, для магистральной передачи данных связи уже повсеместно используют цифровые каналы. Так же аналоговая технология применяется в простых и дешёвых переносных радиостанциях.

p, blockquote 30,0,0,0,0 –>

Во всех вновь создаваемых системах используют цифровую технологию обработки сигнала. Это оптоволоконные и проводные линии, сигнализация и телеметрия, военная и гражданская промышленная связь. И конечно же на цифровое вещание переходит телевидение. Аналоговый способ передачи данных исчерпал себя. На смену пришла новая высококачественная и защищенная связь.

p, blockquote 31,0,0,0,0 –>

Список книг помогающих разобраться в аналоговых и цифровых сигналах

Более подробно изучить и сравнить принципы обработки и передачи данных можно прочитав следующую литературу:

p, blockquote 32,0,0,0,0 –>

Сато Ю. Обработка сигналов. Первое знакомство. / Пер. с яп.; под ред. Ёсифуми Амэмия. — М: Изд-кий дом «Додэка-XXI», 2002. Книга даёт основы знаний о способах ЦОС. Адресована радиолюбителям, студентам и школьникам, только начинающим изучение систем передачи данных.
Введение в цифровую фильтрацию /под ред. Р. Богнера и А. Константинидиса; перевод с англ. — М: Изд-во «Мир», 1977. В этой книге популярно и доступно изложена информация о различных системах обработки данных. Сравниваются аналоговая и цифровая системы, описаны плюсы и минусы.
Основы цифровой обработки сигналов: Курс лекций /Авторы: А.И. Солонина, Д.А. Улахович, С.М. Арбузов, Е.Б. Соловьев, И.И. Гук. — СПб: Изд-во «БХВ-Петербург», 2005. Книга написана по курсу лекций для студентов ГУТ им. Бонч-Бруевича. Изложены теоретические основы обработки данных, описаны дискретные и цифровые системы разных способов преобразования. Предназначена для изучения в вузах и повышения квалификации специалистов.
Сергиенко А.Б. Цифровая обработка сигналов (второе издание) — СПб: Изд-во «Питер», 2006. Электронный учебно-методический комплекс по дисциплине «Цифровая обработка сигналов». Представлены курс лекций, лабораторный практикум и методические рекомендации по самостоятельной работе. Предназначена для преподавателей и самостоятельного изучения для студентов уровня подготовки бакалавр.
Лайонс Р. Цифровая обработка сигналов. 2-е изд. Пер. с англ. – М.: ООО «Бином-Пресс», 2006. Книга представляет подробную информацию о ЦОС. Написана понятным языком и снабжена большим количеством иллюстрации. Одна из самых простых и понятных книг на русском языке.

p, blockquote 33,0,0,0,1 –>

Старая добрая аналоговая связь быстро сдаёт позиции. Несмотря на модернизацию и улучшения, возможность обмена данными достигла предела. К тому же, остались старые болезни – искажения и шумы. В то же время цифровая связь лишена этих недостатков, и передаёт большие объёмы информации быстро, качественно, без ошибок.

Дискретные сигналы (Реферат) — TopRef.ru

Дискретные сигналы

А. Т. Бизин

Сибирская Государственная Академия телекоммуникаций и информатики

Новосибирск 1998 г.

Дискретизация непрерывных сигналов

Обработка сигналов на цифровых ЭВМ начинается с замены непрерывного сигнала X(t) на дискретную последовательность, для которой применяются такие обозначения

x(nT) , x(n) , x_n , {x₀ ; x₁ ; x₂ ; … } .

Дискретизация осуществляется электронным ключом (ЭК) через равные интервалы времени T (Рис. 1.1).

Дискретная последовательность аппроксимирует исходный сигнал X(t) в виде решетчатой функции X(nT). Частота переключения электронного ключа f_д и шаг дискретизации T связаны формулой

f_д = 1 / T . (1.1)

Дискретная последовательность или дискретный сигнал выражается через исходный непрерывный (аналоговый) сигнал следующим образом

x(nT) = x(t)d(t — nT) , (1.2)

где d(t) — дискретная d — функция (Рис. 1.2, а),

d(t — nT) — последовательность d — функций (Рис. 1.2, б).

Погрешность, возникающую при замене аналогового сигнала дискретным сигналом, удобно оценить сравнивая спектры этих сигналов.

Связь спектров дискретного и непрерывного сигналов.

Исходное выражение для спектра дискретного сигнала с учетом (1.2) запишется следующим образом

X(jw) =x(nT) e^-j^w^t dt =x(t)d(t — nT) e^-j^w^t dt .

Периодическую последовательность d — функций здесь можно разложить в ряд Фурье

d(t — nT) =,

где с учетом формулы связи спектров периодического и непериодического сигналов

, поскольку F_d(jw) = 1

После замены в исходном выражении периодической последовательности d — функций ее разложением в ряд Фурье получим

X(jw) =x(t)() e^-j^w^t dt =x(t)e^-j^w^t dt .

Учитывая здесь теорему смещения спектров, т.е. :

если f(t) ® F(jw), то f(t)® F[j(w ± w₀)] ,

последнее равенство можно представить в виде формулы, выражающей связь спектров дискретного X(jw) и аналогового X_a(jw) сигналов

X(jw) =X_a[j(w -)] . (1.3)

На основании формулы (1.3) с учетом поясняющих рисунков 1.3, а, б можно сделать следующие выводы :

Спектр дискретного сигнала состоит из суммы спектров исходного непрерывного сигнала, сдвинутых друг относительно друга по оси частот на величину равную частоте дискретизации w_д

Спектры аналогового и дискретного сигналов совпадают в диапазоне частот [-0,5w_д ; 0,5w_д], если удовлетворяется неравенство

w_в £ 0,5w_д , (1.4)

где w_в — верхняя частота спектра аналогового сигнала.

Равенство в (1.4) соответствует утверждению теоремы Котельникова о минимальной частоте w_д.

Смежные спектры X_a(jw) в (1.3) частично перекрываются, если условие (1.4) не выполняется (Рис 1.3, б). В этом случае спектр дискретного сигнала искажается по отношению к спектру аналогового сигнала. Эти искажения являются неустранимыми и называются ошибками наложения.

Аналоговый сигнал можно восстановить полностью по дискретному сигналу с помощью ФНЧ, частота среза которого w_с = 0,5w_д. Это утверждение основано но совпадении спектров дискретного сигнала на выходе ФНЧ и непрерывного сигнала. Сигнал восстанавливается без искажений, если выполняется условие (1.4). в противном случае сигнал восстанавливается с искажениями, обусловленными ошибками наложения.

Выбор частоты дискретизации осуществляется в соответствии с (1.4). если частота w_в не известна, то выбор из w_д определяется расчетом по формуле (1.1), в которой интервал T выбирается приближенно с таким расчетом, чтобы аналоговый сигнал восстанавливался без заметных искажений плавным соединением отсчетов дискретного сигнала.

Преобразование Фурье и Лапласа для дискретных сигналов.

Для дискретных сигналов формулы Фурье и Лапласа представляется возможным упростить. Действительно, поскольку

то после перехода к дискретной переменной пара преобразований Фурье принимает вид

Здесь применяются формулы одностороннего преобразования Фурье, так как начало отсчета совмещается с началом действия дискретного сигнала.

Формулы Фурье для дискретных сигналов применяются в нормированном виде, поэтому после замены X(nT) ® X(nT) / T преобразование Фурье принимает окончательный вид

(1.5)

Формулы Лапласа для дискретных сигналов получаются на основании (1.5) после обобщения частоты на всю плоскость комплексного переменного, то есть jw ® P = d + jw

(1.6)

Z — преобразование.

Эффективность частотного анализа дискретных сигналов существенно возрастает, если заменить преобразование Лапласа Z — преобразованием. В этом случае изображение сигнала X(p), которое представляет собой трансцендентную функцию переменной P = d + jw, заменяется Z — изображением сигнала X(Z), которое является рациональной функцией переменной Z = x + jy.

Формулы Z — преобразования получаются из формулы Лапласа (1.6) заменой переменных

e^pT = Z . (1.7)

Подстановка (1.7) и ее производной

dZ / dp = Te^pT

в (1.6) приводит к формулам прямого и обратного Z — преобразования

(1.8)

Точки на мнимой оси комплексного переменного p = d +jw, то есть точки p = jw, определяют реально частотные характеристики сигнала. Мнимой оси соответствует на плоскости Z единичная окружность, так как в этом случае согласно (1.7)

Z = e^j^w^T = (1.9)

Поэтому непрерывному росту переменной на мнимой оси плоскости p = d + jw, соответствует многократный обход единичной окружности на плоскости z = x + jy (Рис. 1.4). Этим фактом объясняется, в частности, то обстоятельство, что интегрирование в формуле обратного z — преобразования (1.8) осуществляется вдоль единичной окружности плоскости z взамен интегрирования вдоль прямой параллельной мнимой плоскости p.

Учитывая вышеизложенное и формулы (1.7), (1.9) можно утверждать, что левая полуплоскость переменного p = d + jw отображается на плоскость единичного круга переменного z = x + jy, правая полуплоскость — на плоскость z за пределами единичного круга.

Подстановка (1.9) в z — изображение сигнала приводит к спектру этого сигнала, подстановка (1.7) дает изображение по Лапласу.

Пример. Определить спектр и построить графики модуля и аргумента спектральной плотности сигнала x(nT) = {a ; b} (Рис. 1.5, а).

Решение.

Z — изображение сигнала согласно (1.8)

X(Z) =x(nT) Z^-n = x(0T) Z^-0 + x(1T) Z^-1 = a + bZ^-1

Отсюда подстановкой (1.9) определяем спектр сигнала

X(jw) = a + be^-j^w^T.

Графики модуля и аргумента спектральной плотности приведены на рисунке 1.6, а, б на интервале частот [0 ; w_д].

Вне интервала частот [0 ; w_д] частотные зависимости повторяются с периодом w_д.

Основные теоремы Z — преобразования.

Перечислим без доказательства теоремы z — преобразования, которые потребуются в последующих разделах.

1. Теорема линейности.

Если x(nT) = ax₁(nT) + bx₂(nT) ,

то X(Z) = a X₁(Z) + bX₂(Z).

Теорема запаздывания.

Если x(nT) = x₁(nT — QT) ,

то X(Z) = X₁(Z) Z^-Q.

Теорема о свертке сигналов.

Если X(nT) = x₁(kT) x₂(nT — kT) ,

то X(Z) = X₁(Z) X₂(Z).

Теорема об умножении сигналов.

Если x(nT) = x₁(nT) x₂(nT) ,

то X(Z) = X₁(V) X₂() V^-1 dV,

где V, Z — переменные на плоскости Z.

Теорема энергий (равенство Парсеваля).

x²(nT) =X(Z) X(Z^-1) Z^-1 dZ.

Z — преобразование дискретных сигналов имеет значение равное значению преобразования Лапласа непрерывных сигналов.

Дискретное преобразование Фурье.

Если сигнал ограничен во времени значением t_u, а его спектр — частотой w_в , то он полностью характеризуется конечным числом отсчетов N как во временной, так и в частотной областях (Рис. 1.7, а, б) :

N = t_u/T — во временной области, где T = 1/f_д ,

N = f_д/f₁ — в частотной области, где f₁ = 1/t_u .

Дискретному сигналу соответствует периодический спектр, дискретному спектру будет соответствовать периодический сигнал. В этом случае отсчеты X(nT) = {X₀ ; X₁ ; … X_N-1} являются коэффициентами ряда Фурье периодической последовательности X(jkw₁), период, который равен w_д. Соответственно, отчеты X(jkw₁) = {X₀ ; X₁ ; … X_N-1} являются коэффициентами ряда Фурье периодической последовательности X(nT), период, который равен t_u.

Связь отсчетов сигнала и спектра устанавливается формулами дискретного преобразования Фурье (ДПФ). Формулы ДПФ следуют из формул Фурье для дискретных сигналов (1.5), если непрерывную переменную w заменить дискретной переменной kw₁, то есть

w ® kw₁ , dw ® w₁.

После замены переменной в (1.5) получим

X(jkw₁) = x(nT),

x(nT) =X(jkw₁).

Отсюда после подстановки w₁ = w_д/N, T = 2p/w_д формулы ДПФ принимают окончательный вид

X(jkw₁) =x(nT)- прямое ДПФ ,

x(nT) =X(jkw₁)- обратное ДПФ (1.10)

Сигнал с ограниченным спектром имеет, строго говоря, бесконечную протяженность во времени и, соответственно бесконечное число отсчетов и непрерывный спектр. Спектр останется непрерывным, если число отсчетов сигнала ограничить конечным числом N. Формулы (1.10) в этом случае будут выражать связь между N отсчетами дискретного сигнала и N отсчетами его непрерывного спектра, который можно полностью восстановить по его отсчетам.

Пример. Определить отсчеты спектра сигнала на Рис. 1.5, а.

Здесь N = 2 поэтому X(jkw₁) =x(nT) e^-j^p^kn следовательно

X(j0w₁) =x(nT)e^-j0 = x(0T) + x(1T) = a + b

X(j1w₁) =x(nT)e^-j^pⁿ = x(0T) e^-j0 + x(1T) e^-j^p = a — b

график отсчетов спектра приведен на Рис. 1.5, б, где w₁ = w_д/N = 0,5w_д.

Сигнал с конечным числом отсчетов N имеет спектр, который повторяет с конечной погрешностью спектр сигнала с бесконечным числом отсчетов : спектры совпадают на отсчетных частотах kw₁ и отличаются на других частотах. Отличие спектров тем меньше, чем больше N. В самом деле, реальные сигналы обладают конечной энергией и, следовательно, начиная с некоторого номера отсчета остальными номерами можно пренебречь ввиду их малости, что не окажет заметного влияния на спектр сигнала.

Пример. Осуществить дискретизацию экспоненциального импульса X(t) = Ae^—^a^t = 1 e^-10t и сравнить спектры исходного и дискретного сигналов.

Решение.

График сигнала X(t) представлен на Рис. 1.8

Пусть T = 0,02с. В этом случае плавным соединением отсчетов сигнала (штриховая линия на Рис. 1.8) сигнал восстанавливается удовлетворительно хотя заметны искажения в окрестности точки t = 0, поэтому ошибки наложения будут некоторым образом влиять на спектральные характеристики.

Пусть t_u = 0,4с. В этом случае

N = t_u/T = 20.

Расчет спектра по формуле прямого ДПФ в точке w = 0 (k = 0) запишется так

X(j0w₁) = 1,0 + 0,8187 + 0,6703 + 05488 + 0,4493 + 0,368 + 0,3012 + 0,2466 + 0,2019 + 0,1653 + 0,1353 + 0,1108 + 0,09072 + 0,07427 + 0,06081 + 0,04979 + 0,04076 + 0,03337 + 0,02732 + 0,02237 = 5,41

Истинное значение спектра в точке w = 0 можно определить зная спектр аналогового экспоненциального импульса

X_a(jw) =, следовательно X_a(j0) == 0,1.

чтобы сравнить спектры дискретного и непрерывного сигналов, дискретный спектр необходимо денормировать умножением на T, так как формулы Фурье для дискретных сигналов применяются в нормированном виде. Поэтому

X(jow₁) = 5,41 T = 5,42×0,02 = 0,1082.

Таким образом совпадение спектров X_a(jw) и X(jw) в точке w = 0 вполне удовлетворительное. Некоторая неточность объясняется влиянием ошибок наложения.

Уместно заметить, что выбор шага дискретизации достаточно контролировать в точках максимальной крутизны исходной функции X(t). В рассмотренном примере такой точкой является момент времени t = 0.

В заключение отметим, что формулы ДПФ упрощают расчетные процедуры по взаимному преобразованию сигналов и их спектров, что особенно важно для технических систем, функционирующих В реальном масштабе времени. В этих случаях применяется алгоритм быстрого преобразования Фурье (БПФ), основанный на формулах ДПФ. Ускоренная процедура расчетов по алгоритму БПФ достигается за счет исключения повторных арифметических операций, характерных для расчетов по формулам ДПФ.

2. Непрерывные и дискретные сигналы. Дискретизация.

Основной задачей отрасли телекоммуникации является передача сигналов на расстоянии. Первыми передавались простые сигналы, такие как телеграф, посредством азбуки Морзе. Впоследствии, с развитием техники, сначала осуществлялась передача аналоговых (непрерывных) сигналов – звука и видео, а затем цифровых сигналов (к цифровым аудио и видео сигналам добавились данные).

Что же такое непрерывный сигнал? Очевидно, что непрерывный сигнал – это сигнал, изменяющийся во времени непрерывно. Например, звук. Упрощенно, звук – колебания воздуха. Посредством струн – голосовых связок и резонаторов – рта, зубов, языка мы способны создавать определенные колебания воздуха, которые улавливаются ухом и далее распознаются как речь. Эти колебания изменяются непрерывно, несмотря на то, что их интенсивность может изменяться довольно резко (например, когда человек кричит, а затем переходит на шепот). Аналогично создаются колебания различных музыкальных инструментов.

Хорошенько крикнув, мы способны передать звуковые колебания на несколько сот метров (эхо в горах). Однако чтобы передать музыку или речь на 20 километров, хорошенько крикнуть или «бзденькнуть» гитарной струной недостаточно. Здесь нам на помощь приходит микрофон, который преобразует непрерывное колебание воздуха (издаваемое, например, человеком или инструментом), в такой же непрерывный электрический ток, изменяющийся в соответствии с изменениями колебаний воздуха.

В случае аналоговой техники, этот непрерывный сигнал использовался для записи на магнитные ленты, пластинки и т.п. и для передачи на большие расстояния по проводам или радио эфиру. В случае же цифровой техники, этот сигнал, прежде чем использовать оцифровывают с помощью Аналого-цифрового преобразователя.

Рассмотрим процесс этого преобразования подробнее.

Итак, мы имеем некоторый непрерывно меняющийся во времени сигнал x(t):

Вцифровой технике только два конечных состояния – 0 и 1. И все данные представляются в виде последовательностей нулей и единиц. Поэтому возникает вопрос о преобразовании аналогового сигнала в такую последовательность. Так как же это осуществить?

Первый шаг – дискретизация. Дискретизация – переход от непрерывного сигнала x(t) к последовательности значений этого сигнала {x[n]}, взятых через определенный интервал времениT_д, называемый периодом дискретизации. Этот процесс отображает следующий рисунок:

Отличие непрерывного сигнала от дискретного состоит в том, непрерывный сигнал существует на всем отрезке времени t, а дискретный сигнал – только в моменты времениi*T_д. Таким образом, дискретный сигнал – по сути ряд (последовательность) значений. Связь элементов этого ряда с исходным сигналом простая:

x[i] =x(i*T_д), i=1,2…N.

Значения x[i] – называют отсчетами.

В цифровой обработке сигналов оперируют выборками сигналов. То есть накапливают определенное количество дискретных отсчетов в буфер. Как только накопится определенное количество, выборка отсчетов передается далее для обработки, и начинает накапливаться новая выборка. Количество отсчетов Nвыборки зависит от задач, типа сигнала и т.д.

Что касается периода дискретизации. Его необходимо выбирать таким, чтобы исходный сигнал можно было восстановить без потерь. Правило выбора минимального шага (периода) при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано в теореме Котельникова: «Любая непрерывная функция x(t), спектр которой ограничен частотой F_max полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал T_д = 1 \ 2F_max = π \ ω_max».

Page

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ПРАКТИЧЕСКАЯ ЧАСТЬ

1. ПЕРЕХОД ОТ НЕПРЕРЫВНОЙ СИСТЕМЫ К ЦИФРОВОЙ В ПРОСТРАНСТВЕ СОСТОЯНИЙ

2. ПЕРЕХОД ОТ НЕПРЕРЫВНОЙ СИСТЕМЫ К ЦИФРОВОЙ С ПОМОЩЬЮ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ

3. МОДЕЛИРОВАНИЕ И АНАЛИЗ ЦИФРОВЫХ СИСТЕМ В ПАКЕТЕ SIMULINK СИСТЕМЫ MATLAB

4. ПРЕОБРАЗОВАНИЕ ФОРМ ЛИНЕЙНЫХ МОДЕЛЕЙ ЦИФРОВЫХ СИСТЕМ

Контрольные вопросы

Лабораторная работа № 13

Моделирование и исследование

цифровых систем управления

Цель работы: проанализировать линейные стационарные системы управления с дискретным временем.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Любая система автоматического регулирования и управления представляет собой совокупность элементов, предназначенных для преобразования сигналов, поступающих на ее вход, чтобы обеспечить выполнение цели управления [4]. Если на вход всех элементов системы поступают сигналы, которые могут быть описаны непрерывными функциями времени, система называется непрерывной. Система, содержащая, по крайней мере, один элемент, выходным сигналом которого является дискретный сигнал, называется дискретной.

Дискретный сигнал – это такой сигнал, который определяется последовательностью значений а₀, а₁, а₂, ¼, а_n_,_¼_.Сигналы могут быть дискретными по уровню, по времени, а также одновременно по уровню и по времени.

В зависимости от способов получения дискретных сигналов может быть введена следующая классификация дискретных систем [4, 18]:

1) импульсная система – это система, в которой используются сигналы, дискретные по времени;

2) релейная система – это система, в которой используются сигналы, дискретные по уровню;

3) цифровая система – это система, в которой используются сигналы, дискретные как по времени, так и по уровню.

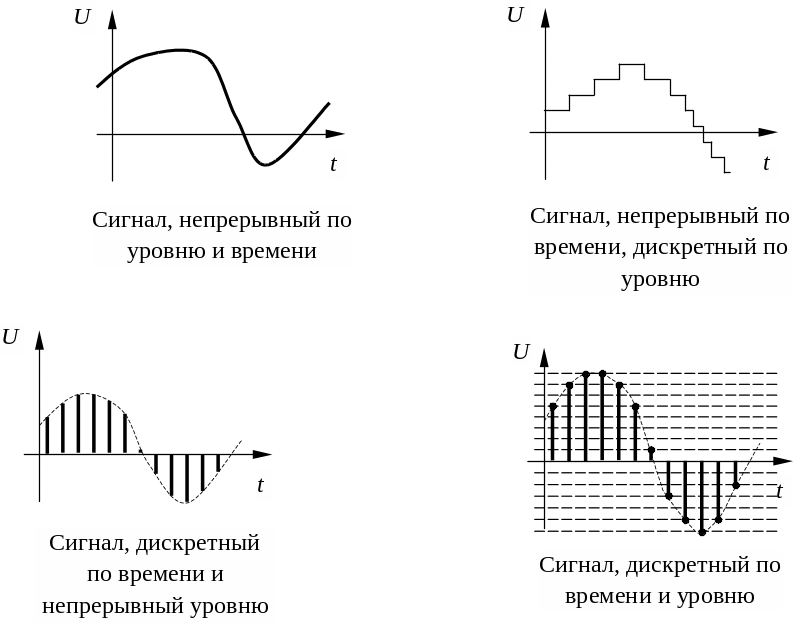
На рис. 13.1 показана идеализированная амплитудно-импульсная модуляция непрерывного сигнала на основе идеальных импульсов, ширина которых бесконечна малая, а высота равна значениям непрерывного сигнала в дискретные моменты времени. Если f(t) есть непрерывный сигнал, то выделение дискретных значений f(kT) называется квантованием сигнала f(t) по времени с постоянным шагом квантования или периодом дискретизации Т. В то же время f(kT) называют решетчатой функцией. Другим видом импульсной модуляции является широтно-импульсная модуляция, при которой амплитуда импульсов постоянная, а их ширина пропорциональна в некоторых пределах значениям f(kT). Еще возможна фазоимпульсная модуляция сигнала, которая осуществляется за счет смещения импульсов в пределах шага квантования Т. Величина смещения пропорциональна значениям f(kT).

Рис. 13.1. Идеальное квантование непрерывного сигнала по времени

Квантование (дискретизация) непрерывного сигнала по уровню с шагом h показано на рис. 13.2. Оно может быть получено, если преобразовать непрерывный сигнал с помощью многоступенчатого релейного устройства. Дискретный по уровню сигнал, представленный на рис. 13.2, может быть описан в соответствии с выражением [4]:

При квантовании по уровню в произвольные моменты времени выделяются значения непрерывного сигнала при достижении им фиксированных дискретных уровней [18]. Как отмечалось, квантование по уровню характерно для релейных систем автоматического управления, которые представляют собой достаточно большой класс динамических систем, в состав которых входят нелинейные звенья с разрывной характеристикой. Основными достоинствами релейных систем автоматического управления является их простота, связанная с ней высокая надежность, а также экономичность в расходе энергии питания. В то же время к ним не могут быть применены методы анализа и синтеза гладких систем.

Рис. 13.2. Квантование непрерывного сигнала по уровню

Характер квантования по уровню и по времени непрерывного сигнала показан на рис. 13.3. В этом случае непрерывный сигнал f(t) заменяется фиксированными дискретными (по уровню) значениями, ближайшими к значениям непрерывной функции f(t) в дискретные моменты времени 0, Т, 2Т, ¼ . Квантование по уровню и по времени осуществляется в цифровых системах управления при преобразовании непрерывных сигналов в цифровую форму или в коды. Если цифровое устройство оперирует с числовым представлением со значительным количеством разрядов (что характерно для современных компьютеров), то квантованием по уровню можно пренебречь. Тогда цифровую систему можно рассматривать как импульсную систему с амплитудно-импульсной модуляцией.

Рис. 13.3. Квантование сигнала по уровню и по времени

Цифровая система управления включает объект управления (обычно непрерывный объект или процесс), чувствительные элементы (или датчики), аналого-цифровой преобразователь (АЦП), цифровое вычислительное устройство (микропроцессор или компьютер) и цифроаналоговый преобразователь (ЦАП). Функциональная схема цифровой системы управления показана на рис. 13.4.

Разница между цифровым сигналом и дискретным сигналом

В электротехнике термины «дискретный сигнал» и «сигнал с дискретным временем» периодически используются для обозначения одного и того же, последний термин является более распространенным и более точным. Формулировка «сигнал с дискретным временем» в некоторой степени самоочевидна.

Многие инженеры и теоретики приравнивают и приравнивают цифровую обработку сигналов к обработке сигналов квантованных сигналов с дискретным временем. Однако есть свои тонкости. Информационно-теоретическую концепцию сигнала слишком трудно втиснуть в объяснение «простым словом», я предлагаю вам сначала изучить, что такое «цифровая форма волны». Форма волны не является сигналом, но может представлять сигнал в ваших конструкциях блоков обработки. Для новичка в исследованиях DSP знание, что такое цифровая форма волны, является практически полезным знанием с обещанием помочь вам своевременно пройти через тонкости информационно-теоретической концепции.

Цифровой сигнал — это напряжение или ток, который изменяется во времени между значениями, называемыми «логическими уровнями», эти уровни определяются дисциплиной «цифровая абстракция» ( http://ocw.mit.edu/courses/electrical-engineering-and-computer -Наука / 6-002-схема-и-электроника-весна-2007 / видео-лекция / 6002_l4.pdf). Изменяющиеся значения напряжения или тока не всегда попадают в пределы, установленные цифровыми правилами абстракции для значений сигналов на логических уровнях: при переключении между уровнями напряжение или ток, являясь непрерывной функцией, проходит «запрещенные» диапазоны. Та же дисциплина цифровой абстракции предписывает учитывать ограничения не только для значений логических уровней, но и для временных параметров, из которых очень важными являются время установки и удержания — защитные временные интервалы стабильности сигнала, окружающие край утверждения часов. Смотрите хороший учебник по цифровым сигналам в http://www.ni.com/white-paper/3299/en/ . Примечательно, что цифровые формы волны называются цифровыми сигналами в этом руководстве.

Иными словами, (относительно простыми) цифровая форма волны — это форма волны с уровнями логического сигнала и параметрами синхронизации, соответствующими правилам цифровой абстракции для данной схемы. То, что является законным цифровым сигналом для одного дизайна, может оказаться неподходящим для другого.

Непрерывное и дискретное. Непрерывные и дискретные процессы.

<<Назад | Содержание | Далее>>

В зависимости от того, меняются свойства приёмника информации под воздействием источника непрерывно (плавно) или дискретно (скачкообразно), воспринимаемый им сигнал имеет непрерывную или дискретную форму. Непрерывный сигнал может принимать бесконечное множество значений, а количество значений дискретного сигнала ограниченно.

Абсолютное большинство процессов в природе протекают с нашей точки зрения непрерывно (изменение напряжения, температуры, давления, скорости…). Непрерывно меняющиеся величины называют аналоговыми величинами, а соответствующие им сигналы – аналоговыми. Т.е. аналоговый сигнал означает непрерывный по значению сигнал.

Все модели реальных процессов в наших рассуждениях о них – дискретны. Мы наносим цифровую шкалу на столбик термометра, цифры на циферблат часов и т.д. Поэтому дискретные сигналы называют также цифровыми сигналами. Дискретны и все сигнальные (символьные) системы, созданные человечеством для обмена информацией, т.е. любая из них использует конечное число возможных значений.

Чтобы получить из непрерывного сигнала его дискретное представление необходимо измерять значение сигнала через равные промежутки времени, и соотносить полученный результат измерения с одним из возможных значений, составляющих дискретное множество.

Рис. 6. Представление непрерывного и дискретного сигналов.

<<Назад | Содержание | Далее>>

1.1 Дискретные и непрерывные сигналы. Цифровая обработка сигналов

Что такое непрерывный и дискретный сигнал времени? — Цвета-NewYork.com

Что такое непрерывный и дискретный сигнал времени?

Независимые переменные для сигнала могут быть непрерывными или дискретными. Сигнал считается непрерывным временным сигналом, если он определен по континууму независимой переменной. Сигнал считается дискретным по времени, если независимая переменная имеет только дискретные значения.

В чем разница между дискретным и цифровым сигналом?

Цифровой сигнал — сигнал непрерывный во времени, но дискретный по амплитуде.Дискретность по амплитуде означает, что сигнал не может иметь несколько значений амплитуды. Это может быть 1 или 0. Дискретный сигнал — сигнал дискретный по времени, но непрерывный по амплитуде.

Что такое определение «непрерывный сигнал»?

Непрерывный сигнал — это непрерывная функция времени, определенная на вещественной прямой R, обозначенной символом. s (t), t — время. Сигнал может быть комплексным. Непрерывный сигнал называется аналоговым. сигнал.

Что такое пример дискретного сигнала?

Напротив, дискретный сигнал имеет счетную область, как и натуральные числа.Другими примерами непрерывных сигналов являются синусоидальная волна, косинусная волна, треугольная волна и т. Д. Сигнал определяется в области, которая может быть или не быть конечной, и существует функциональное отображение из области в значение сигнала.

Возраст непрерывен или дискретен?

Возраст измеряется в единицах, которые, если достаточно точны, могут быть любым числом. Следовательно, набор, из которого они происходят, бесконечен. Например, кому-то может быть 22,32698457 или 22,32698459 лет. Мы могли бы быть бесконечно точными и использовать бесконечное количество десятичных знаков, таким образом делая возраст непрерывным.

Как узнать, являются ли ваши данные дискретными или непрерывными?

Дискретные данные — это числовой тип данных, который включает целые конкретные числа с конкретными и фиксированными значениями данных, определяемыми путем подсчета. Непрерывные данные включают комплексные числа и изменяющиеся значения данных, измеренные в течение определенного интервала времени.

Пол — дискретная или непрерывная переменная?

Я намеренно дал понять, что переменная либо дискретная, либо непрерывная…. Справочная таблица переменных: несколько примеров.

переменная	Тип переменной	Переменная шкала
Пол	Дискретный	Категориальный
Пол как двоичное кодирование 1/0	Дискретный	Категориальный
Верно / Неверно	Дискретный	Категориальный
Телефон	Дискретный	Номинал

Деньги непрерывны или дискретны?

Непрерывное распределение должно иметь бесконечное количество значений от 0 до $.00 и 0,01 доллара. У денег нет этого свойства — всегда есть неделимая единица наименьшей валюты. Таким образом, деньги — это дискретная величина.

Группа крови непрерывная или дискретная?

Группа крови не является дискретной случайной величиной, потому что она категориальна. Непрерывные случайные переменные имеют числовые значения, которые могут быть любым числом в интервале. Например, (точный) вес человека — это непрерывная случайная величина. Длина стопы также является непрерывной случайной величиной.

Стоимость — это дискретная или непрерывная переменная?

Стоимость технически является непрерывной переменной. Учтите, что что-то может стоить 0,01 доллара — бесконечность.

В чем разница между дискретной и непрерывной переменной?

Дискретная переменная — это переменная, значение которой получается путем подсчета. Непрерывная переменная — это переменная, значение которой получается путем измерения. Дискретная случайная величина X имеет счетное число возможных значений.

Почему деньги — это непрерывная переменная?

Однако деньги непрерывны, потому что они могут иметь много и любую ценность и иметь любую сумму, в значительной степени.Например, плати, тогда как она может иметь бесконечное значение.

Является ли занятость дискретной переменной?

Доход — непрерывная переменная. Размер домохозяйства и количество компьютеров — дискретные переменные. (*) Род занятий главы семьи и тип подключения к Интернету являются качественными переменными.

Почтовый индекс непрерывный или дискретный?

непрерывный дискретный атрибут Имеет только конечный или счетно бесконечный набор значений. Примеры из текста: почтовые индексы, счетчики или набор слов в коллекции документов, двоичные данные.

Является ли да или нет дискретной переменной?

Дискретные данные можно подразделить на три категории: двоичные, номинальные и порядковые. Двоичные данные: двоичные данные принимают только два возможных значения. Например, лампа горит или лампа выключена, ответ — истина или ложь, 0 или 1, да или нет и т. Д. Эти пять ответов упорядочены, так что это будет пример порядковых данных.

Процент — это дискретная переменная?

С технической точки зрения процентные данные являются дискретными, поскольку базовые данные, на основании которых рассчитываются проценты, являются дискретными.На практике процентные данные часто обрабатываются как непрерывные, потому что процентные данные могут принимать любое значение в континууме от нуля до 100%.

Скорость автомобиля непрерывна или дискретна?

Да, скорость — это обычная непрерывная переменная, а значение выбирается случайным образом. Мы знаем, что это непрерывно, потому что всегда есть другое возможное значение между любыми двумя значениями скорости.

Население дискретно или непрерывно?

Подсчет населения обычно называют дискретными или количественными данными.Почему плотность населения является непрерывным типом данных, если она обычно измеряется для агрегированных областей, таких как переписные участки или районы / кварталы (т. Е. Ее нельзя измерить в любой точке поверхности, такой как градиент или температура).

Какой набор данных дискретный?

Определение: набор данных называется дискретным, если значения, принадлежащие набору, являются различными и отдельными (несвязанные значения). Примеры: рост лошади (может быть любым значением в пределах диапазона роста лошади).Время на выполнение задачи (может быть измерено до долей секунды).

Могут ли данные быть как дискретными, так и непрерывными?

Дискретные данные — это информация, которая может принимать только определенные значения. Рост, вес, температура и длина — все это примеры непрерывных данных. …

Почему непрерывные данные лучше дискретных?

Но когда вы можете это получить, непрерывные данные — лучший вариант… .Некоторые заключительные преимущества непрерывных данных над дискретными.

Непрерывные данные	Дискретные данные
Выводы можно сделать с помощью нескольких точек данных — достоверный анализ можно выполнить с небольшими образцами.	Чтобы сделать эквивалентный вывод, необходимо больше точек данных (большая выборка).

Являются ли дискретные данные количественными или качественными?

Количественные разновидности: непрерывные данные и дискретные данные Существует два типа количественных данных, которые также называются числовыми данными: непрерывные и дискретные. Как правило, подсчеты являются дискретными, а измерения — непрерывными. Дискретные данные — это счет, который невозможно уточнить.

Могут ли качественные данные быть дискретными?

Качественные данные содержат категориальные переменные, а количественные данные содержат числовые переменные.Категориальные переменные бывают номинальными или порядковыми, тогда как числовые переменные могут быть дискретными или непрерывными.

В чем разница между качественными дискретными и непрерывными данными?

Качественные данные — это не числа. Они могут включать любимые блюда; религии; национальности; и т. д. Дискретные данные — это числа, которые могут принимать определенные, разделенные значения. Непрерывные данные — это числа, которые могут принимать всевозможные десятичные или дробные значения.

Температура тела дискретная или постоянная?

Температура является непрерывной переменной, так как имеет дробное значение.Например: сегодняшняя температура составляет 30,5 градусов Цельсия, здесь 30,5 не является дискретной переменной и, следовательно, является непрерывной переменной.

Лекция 18: Дискретная обработка сигналов непрерывного времени | Видео-лекции | Сигналы и системы

Связанные ресурсы

Дискретно-временная обработка сигналов непрерывного времени (PDF)

[ВОСПРОИЗВЕДЕНИЕ МУЗЫКИ]

ПРОФЕССОР: В прошлый раз мы начали обсуждение дискретной обработки сигналов непрерывного времени .И, как напоминание, позвольте мне повторить основное понятие. Идея заключалась в том, чтобы преобразовать сигнал с непрерывным временем в последовательность посредством операции, которую я представляю как преобразователь непрерывного времени в дискретное. И затем эта последовательность используется в качестве входных данных для соответствующей системы дискретного времени. И после соответствующей обработки в дискретном времени эта последовательность преобразуется обратно в сигнал непрерывного времени посредством операции, которую я обозначил как преобразователь дискретного времени в непрерывный.

Теперь, в прошлый раз на лекции, мы провели некоторый анализ, который связал для нас спектры на первом этапе этой операции.А именно в преобразовании сигнала непрерывного времени в последовательность. И позвольте мне, кстати, обратить ваше внимание на тот факт, что в реальном мире эта операция по существу реализуется тем, что вы обычно называете аналого-цифровым преобразователем, если на самом деле выполняется дискретная обработка. в цифровом виде. Теперь важно подчеркнуть, что это не совсем то, что делает аналого-цифровой преобразователь, но, по крайней мере, в некотором смысле, вы должны думать об этом отображении непрерывного времени в дискретное время почти так же, как можно было бы подумать. аналого-цифрового преобразователя.И тогда отображение в некотором смысле соответствует тому, что произошло бы с цифроаналоговым преобразователем.

Что ж, позвольте мне рассмотреть, что задействовано в преобразовании сигнала непрерывного времени в последовательность. И позвольте мне еще раз подчеркнуть, что эта операция в основном — в непрерывном преобразовании в дискретное время — представляет собой двухэтапный процесс. В первой части процесса непрерывный сигнал модулируется с помощью последовательности импульсов, период которой равен T.Итак, у нас есть импульсный сигнал непрерывного времени, который захватывает выборки исходного непрерывного сигнала.

Затем эта последовательность импульсов подвергается операции, которая, по сути, перемаркирует образцы так, чтобы значения выборки, области импульсов, были перемаркированы как значения последовательности. И результатом этого преобразования будет последовательность x из n. Таким образом, общий процесс — это процесс отбора проб, за которым следует то, что в данном блоке является просто процессом перемаркировки. И хотя, как я указал всего минуту назад, аналого-цифровой преобразователь, по сути, делает именно это.Аналого-цифровой преобразователь не обязательно выполняет эти два этапа, но, в частности, с точки зрения проведения анализа, особенно удобно рассматривать его как двухэтапный процесс.

В прошлый раз мы говорили о том, что означает преобразование непрерывного времени в дискретное как во временной области, так и в терминах спектров. И, в частности, во временной области мы начинаем с сигнала непрерывного времени, который затем дискретизируется с помощью последовательности импульсов и преобразуется в последовательность путем простого генерирования последовательности, значения которой являются областями импульсов.И я подчеркиваю тот факт, что это, по сути, соответствует нормализации оси времени, по сути, делением оси времени на заглавную T.

Итак, в частотной области у нас был спектр исходного сигнала, который, из-за процесса дискретизации, воспроизводится с целым числом кратным частоте дискретизации omega sub s, или на 2 пи больше заглавной T. И затем, преобразовывая импульсы в последовательность, мы по существу нормализуем ось частот, так что частота 2 пи над заглавной T переименовывается в 2 пи.И результирующий спектр дискретного времени выглядит так, как я здесь указываю. Что на самом деле является не чем иным, как масштабированием частоты, соответствующим соответствующему масштабированию времени. Таким образом, преобразование из спектра импульсной последовательности в спектр дискретного времени соответствует отображению, заданному заглавной омегой, равной малой омеге, умноженной на заглавную T.

И, что эквивалентно, это частота на 2 пи над заглавной T, что, конечно же, частота дискретизации, которая нормализуется до частоты 2 пи. Итак, в частотной области существует нормализация частоты, связанная с тем фактом, что этому спектру соответствует временная последовательность или последовательность дискретного времени, как я показал ранее, а последовательность дискретного времени связана с исходной непрерывной сигнал времени через временную нормализацию.Другими словами, эти значения последовательности являются просто выборками сигнала непрерывного времени с перенормированной временной осью.

Теперь то, что мы хотим рассмотреть — это преобразование из непрерывного времени в дискретное время — сейчас мы хотим рассмотреть общую систему, которая реализует не только преобразование, но и фильтрацию, а затем возвращается обратно. преобразования обратно в непрерывное время. Итак, давайте посмотрим на систему в целом. И, конечно, вся система, как я уже неоднократно подчеркивал в прошлом, состоит сначала из процесса выборки, преобразования в последовательность импульсов и последовательности импульсов.

Затем эта последовательность обрабатывается нашим фильтром дискретного времени. И после дискретной временной обработки результат преобразуется обратно в последовательность импульсов. Таким образом, эта результирующая последовательность процессов затем преобразуется обратно в последовательность импульсов. И затем, наконец, мы выполняем процесс удаления дискретизации, просто используя фильтр нижних частот с отсечкой, связанной с частотой дискретизации, которую мы использовали.

Теперь, как правило, в такой системе, которая реализует дискретную обработку сигналов непрерывного времени, нам нужно так или иначе гарантировать, что полоса пропускания входа достаточно ограничена, чтобы избежать наложения спектров. .Один из способов сделать это — заставить его тем или иным способом или просто знать, что наш сигнал удовлетворяет ограничению полосы пропускания. Хотя довольно типичная вещь, которую нужно сделать в дополнение к этому процессу выборки, — это включить то, что называется фильтром сглаживания. Другими словами, это фильтр, который будет ограничивать входную полосу по крайней мере на половину частоты дискретизации, так что мы можем быть уверены, что в этом процессе не будет наложения спектров. И важно подчеркнуть, что при таком виде обработки — дискретной обработке сигналов непрерывного времени — за исключением определенных особых ситуаций, очень важно избегать наложения спектров, потому что мы собираемся провести реконструкцию после того, как мы делаем выборку и обработку.

Хорошо, теперь это последовательность шагов во временной области. Давайте посмотрим, что происходит в результате этого в частотной области. Что ж, давайте выберем какой-нибудь тип простого репрезентативного спектра. И, конечно же, важно то, что выбранный нами спектр ограничен полосой или что есть фильтр сглаживания. И дело, конечно, не в форме.

И пока мы проходим через систему, это непрерывный временной спектр. После дискретизации этот спектр воспроизводится с кратной частотой дискретизации — целыми числами, кратными частоте дискретизации — и поэтому будет еще один здесь, другой здесь и так далее.А затем, при преобразовании в дискретную временную последовательность, происходит соответствующая нормализация частоты, так что частота дискретизации нормализуется до частоты 2 пи. Хорошо, теперь, в той точке, где мы находимся в системе, находится в этой точке, так что мы преобразовали в последовательность. Теперь мы хотим выполнить некоторую фильтрацию, а затем, после этой фильтрации, преобразовать обратно в сигнал непрерывного времени.

Хорошо, вот мы находимся у спектра, связанного с последовательностью. И теперь обработка, которую мы выполняем, — это линейная временная и вариантная фильтрация в дискретной временной области.И тогда это соответствует умножению этого спектра на частотную характеристику фильтра. И я выбрал определенную форму. И снова, для обсуждения важна не форма, а тот факт, например, что она имеет определенную частоту среза, которую мы будем отслеживать по мере проработки этого.

Итак, спектр y из n, выходной сигнал цифрового фильтра, является произведением этого спектра и преобразования Фурье или частотной характеристики цифрового фильтра.

Теперь, прорабатывая наш путь, мы собираемся взять выходной сигнал фильтра и отменить двухэтапный процесс. Итак, теперь мы хотим взять эту последовательность, преобразовать ее в последовательность импульсов, а затем взять эту последовательность импульсов и уменьшить дискретизацию через фильтр нижних частот. Итак, вот мы и подошли к выходу цифрового фильтра. Затем мы преобразуем это в импульсный поезд. Что ж, это действительно отменяет первоначальную нормализацию времени.

Итак, это означает, что мы отменяем нормализацию частоты.В частности, мы делим частотную ось на заглавную T. Принимая во внимание, что эта точка в y омеги была 2 пи, теперь она на 2 пи больше заглавной T. Это означает, что, эквивалентно, мы умножаем этот спектр на частотная характеристика цифрового фильтра, но теперь линейно масштабированная по частоте, так что то, что было частотой среза omega sub c, теперь является частотой среза omega sub c, деленной на заглавную T.

Итак, теперь следующий шаг в процесс — восстанавливающий фильтр нижних частот. И то, что он извлекает, является просто частью этого периодического спектра вокруг начала координат.И, наконец, спектр выходного сигнала всей системы будет спектром входного сигнала, умноженным на частотную характеристику, которая представляет собой частоту частотной характеристики цифрового фильтра, масштабированную путем деления этой частотной оси цифрового фильтра на заглавную T.

Хорошо, теперь мы можем спросить, у нас есть эта обработка — мы перешли в дискретное время, и мы вернулись к непрерывному времени, и теперь можно спросить, что эквивалентное, общее непрерывное время система это соответствует? Другими словами, если мы — это, конечно, система с непрерывным временем, это вход с непрерывным временем и выход с непрерывным временем — и тогда вся система в целом была бы такой, которая дала бы нам именно то, что нам нужно. тот же выходной спектр, что и у нас.Ну что это?

У нас есть выходной спектр, который является произведением входного спектра и частотной характеристики цифрового фильтра с масштабированием по частоте. Фактически, результирующий фильтр с непрерывным временем представляет собой просто цифровой фильтр с соответствующим масштабированием частоты. Другими словами, с частотной осью, разделенной на заглавную букву T. Итак, по-другому говоря, если мы покажем здесь частотную характеристику исходного цифрового фильтра, тогда соответствующий фильтр непрерывного времени будет таким, масштабированным по частоте.

И затем, из-за соответствующей фильтрации нижних частот и реконструкции, мы бы выбрали только один из этих периодов, в частности, часть вокруг начала координат. И существенным следствием этого является то, что соответствующий фильтр непрерывного времени задается этим. И эти два связаны просто линейным масштабированием оси частот. И обратите внимание, что там, где цифровой фильтр имеет частоту среза omega sub c, фильтр непрерывного времени имеет частоту среза omega sub c, деленную на заглавную T.

Итак, это линейное масштабирование частоты. И, кстати, пока отложим — и мы вернемся к этому моменту позже — наблюдение о том, что даже если частотная характеристика цифрового фильтра фиксирована, что мы могли бы предположить, изменяя частоту дискретизации, в Фактически, что мы можем сделать, так это повлиять на линейное масштабирование всего эквивалентного фильтра непрерывного времени.

Хорошо, это в значительной степени процесс и анализ, но чтобы выделить ряд проблем и подчеркнуть эти моменты, я бы хотел проиллюстрировать некоторые из них с помощью видеопленки, которая, по сути, изначально был разработан как часть другого курса — курса, полностью посвященного цифровой обработке сигналов, которая, по сути, представляет собой обработку в дискретном времени, независимо от того, связана она с сигналами непрерывного времени или нет.И сейчас я хотел бы сосредоточиться на некоторых деталях этой демонстрации.

В демонстрации я показываю конкретную импульсную характеристику, которая используется для цифрового фильтра или фильтра дискретного времени. И соответствующая частотная характеристика является частотной характеристикой дискретного фильтра нижних частот, как я указываю ниже. И частота среза этого фильтра — как я уже сказал, фильтр был разработан как фильтр дискретного времени с частотой среза пи более 5.

И позвольте мне просто обратить ваше внимание на то, что число «пи» больше 5 равно 10-м от 2-го числа «пи». Фактически, частота среза цифрового или дискретного фильтра составляет 10-ю часть от 2 пи. И, как я еще раз подчеркну в ближайшее время, помните, что при нормализации или ненормализации частоты 2 пи представляет, по сути, частоту дискретизации. Следствием этого является то, что частота среза на самом деле будет связана с 10-й частотой дискретизации. Но пока имейте в виду, что это просто десятая часть 2 пи.

Теперь, эквивалентная система с непрерывным временем, с точки зрения импульсной характеристики, конечно же, представляет собой ограниченную полосой интерполяцию импульсной характеристики, связанной с фильтром дискретного времени. А в частотной области частотная характеристика, соответственно, является масштабированной по времени, масштабированной по частоте версией частотной характеристики. Таким образом, на самом деле, в частотной области и во временной области, связанной с непрерывным сигналом, я указываю здесь связанную импульсную характеристику — ограниченную полосой интерполяцию импульсной характеристики дискретного времени и временной шкалы в факт.А частотная характеристика — после обсуждения, которое мы уже прошли — представляет собой масштабированную по частоте версию той, которая связана с цифровым фильтром.

Ну, первое, что я хочу посмотреть, это импульсная характеристика. И когда мы это сделаем, позвольте мне просто указать, что в реальной реализации все немного отличается от того, что связано с идеальным анализом. В частности, при преобразовании последовательности с дискретным временем в сигнал с непрерывным временем, тогда как такой способ рассмотрения удобен в контексте анализа, на самом деле способ, которым это делается, заключается в использовании более или менее стандартного цифрового сигнала. аналоговый преобразователь.

И то, что делает цифроаналоговый преобразователь, как я указывал в предыдущей лекции, — это преобразование последовательности не в последовательность импульсов, а, по сути, прохождение непосредственно через удержание нулевого порядка. Итак, обычно то, что выходит из цифроаналогового преобразователя, представляет собой ступенчатый сигнал, связанный с удержанием нулевого порядка. И затем результат этого фильтруется нижними частотами для реконструкции.

Итак, мы хотим рассмотреть эту реконструкцию, сначала только с импульсным входом.Итак, то, что мы увидим после фильтра нижних частот для импульсной характеристики, представляет собой плавную кривую, подобную этой. Но также, как часть демонстрации, что я сделаю, просто чтобы показать удержание нулевого порядка, — это временно отключить фильтр нижних частот, а затем снова вставить его. Итак, сначала давайте просто посмотрим на фильтр импульсивный ответ.

Здесь мы видим импульсную характеристику всей системы. И мы наблюдаем, во-первых, что это симметричный импульсный отклик. Другими словами, соответствует линейному фазовому фильтру.Мы также могли бы посмотреть на импульсную характеристику перед фильтром нижних частот с удаленной дискретизацией — давайте медленно снимем фильтр нижних частот с удаленной дискретизацией — и то, что мы наблюдаем, является, в основном, выходным сигналом цифроаналогового преобразователя.

Это, конечно же, лестница или товарный вагон, а не импульсный поезд. В реальном мире выходной сигнал цифро-аналогового преобразователя, как правило, представляет собой функцию типового вагона. Теперь мы можем снова вставить фильтр десэмплинга и заметить, что эффект фильтра десэмплинга заключается, в основном, в сглаживании грубых краев на выходе прямоугольной формы из цифро-аналогового преобразователя.

Хорошо, это импульсная характеристика системы. Теперь я хотел бы показать частотную характеристику системы. И, конечно же, чтобы измерить частотную характеристику, мы можем ввести в систему синусоидальную волну и посмотреть на синусоидальный выходной сигнал.

Итак, в частности, сейчас произойдет то, что с системой мы введем синусоиду непрерывного времени, которая будет дискретизирована, преобразована в последовательность. Дискретизированная синусоида с непрерывным временем является синусоидой с дискретным временем. Он проходит через цифровой фильтр и соответствующим образом ослабляется или усиливается.А затем выходной сигнал преобразуется обратно — и это опять же синусоидальный выходной сигнал, — который снова преобразуется в синусоиду с непрерывным временем. Теоретически, как я указываю здесь — но опять же, как мы только что видели, на самом деле, представленное удержанием нулевого порядка, за которым следует фильтр нижних частот. Итак, это общая операция с одной модификацией из диаграммы, которая у нас есть.

В этой конкретной диаграмме я включил фильтр сглаживания. Фактически в демонстрации нет фильтра сглаживания.Таким образом, на самом деле вход является синусоидальным входом, диапазон которого не ограничен фильтром сглаживания. Это только, конечно, с соответствующей полосой пропускания, если мы выберем синусоидальную частоту таким образом.

Итак, сглаживающего фильтра нет, а это система. И одним из следствий этого является то, что фактически, если мы развернем входную синусоиду только до половины частоты дискретизации, мы не увидим наложения спектров. Но если мы позволим этому пройти мимо, мы получим алиасинг.

Теперь, в демонстрации, частота дискретизации, выбранная для этой части демонстрации, составляет 20 килогерц.Это означает, что, основываясь на теореме выборки, пока входная частота ниже 10 килогерц, мы не получаем наложения спектров. Когда входная частота превышает 10 килогерц, эта более высокая частота переходит в более низкую частоту.

Таким образом, следствием этого является то, что, когда мы проходим обработку и демонстрируем частотную характеристику системы, то, что мы увидим на выходе, будет отсутствием наложения спектров, когда входной сигнал ниже 10 килогерц. По мере того, как входной сигнал превышает 10 килогерц — когда мы позволяем ему, что мы, в конечном итоге, сделаем при демонстрации — тогда, фактически, эта частота, как она, наконец, показана здесь, начнет снижаться до более низкой частоты.Другой способ думать об этом заключается в том, что, когда мы смотрим на частотную характеристику системы, когда мы смотрим на частотную характеристику цифрового фильтра, то, что мы изменяем, когда мы переходим от 0 до 10 килогерц на входной частоте, является этой частью частотной характеристики.

При переходе от 10 килогерц к 20 килогерцам мы увидим эту часть частотной характеристики. Другими словами, мы увидим, как это периодически тиражируется. Или, если мы посмотрим на соответствующую частотную характеристику в непрерывном времени, то на самом деле это означает, что таким образом увеличивается развертка от 0 до 10 килогерц.А затем колебание от 10 килогерц до 20 килогерц на входе, действительно из-за наложения спектров, отражается в цифровом фильтре, обращаясь к более низким частотам. Таким образом, фильтр непрерывного времени возвращается с 10 килогерц обратно к 0.

Хорошо, вот что мы увидим, и мы увидим это разными способами, как объяснено в демонстрации. Итак, теперь давайте посмотрим на частотную характеристику фильтра.

Теперь мы хотели бы проиллюстрировать частотную характеристику эквивалентного фильтра непрерывного времени.И мы можем сделать это, развернув фильтр с синусоидальным входом. Итак, то, что мы увидим в этой демонстрации, — это на верхней кривой входная синусоида, на нижней кривой — выходная синусоида с использованием частоты дискретизации 20 килогерц и развертки от 0 до 10 килогерц. Другими словами, развертка от 0 до пи, в терминах цифрового фильтра.

Итак, что мы будем наблюдать по мере увеличения входной частоты, так это то, что выходная синусоида будет иметь, по существу, постоянную амплитуду до частоты среза фильтра, а затем приблизительно нулевую амплитуду после.Итак, давайте теперь исследуем частотную характеристику фильтра. И есть частота среза фильтра.

Теперь мы можем наблюдать частотную характеристику фильтра несколькими другими способами. Один из способов, которым мы можем это наблюдать, — это также посмотреть на амплитуду выходной синусоиды как функцию частоты, а не как функцию времени. Итак, мы увидим это в левой области.

В то время как на правом осциллографе у нас будет такая же трасса, которую мы только что видели, а именно две трассы: верхняя трасса — это синусоида входов, нижняя трасса — выходная синусоида.И, помимо наблюдения за частотной характеристикой, давайте также послушаем синусоиду на выходе и понаблюдаем за ослаблением на выходе при переходе от полосы пропускания фильтра к полосе задерживания фильтра. Опять же, частота дискретизации 20 килогерц и диапазон развертки от 0 до 10 килогерц.

Теперь, конечно, мы находимся в полосе задерживания фильтра. Теперь, если мы увеличим диапазон развертки с 10 килогерц до 20 килогерц, так что диапазон развертки будет равен частоте дискретизации, по сути, что соответствует развертке цифрового фильтра от 0 до 2 пи.И в этом случае мы начнем видеть некоторую периодичность в частотной характеристике цифрового фильтра. Итак, давайте сделаем это сейчас с частотой дискретизации 20 килогерц и диапазоном развертки от 0 до 20 килогерц.

Теперь, когда мы приближаемся к 2 пи, мы возвращаемся к прошлой полосе. И, наконец, вернемся к развертке от 0 до 10 килогерц, так что мы снова переходим только от 0 до пи в отношении цифрового фильтра.

Теперь важное наблюдение заключается в том, что при фиксированной частоте среза цифрового или дискретного фильтра, как я указал здесь — и я напоминаю вам, что частота среза составляет 10-ю часть от 2 пи — с этим частота среза фиксированная, из-за нормализации, которую мы получаем, когда возвращаемся к фильтру с непрерывным временем, фактически, у нас есть частота среза, которая зависит от частоты дискретизации или от периода дискретизации.И, более конкретно, поскольку дискретный или цифровой фильтр или имеет частоту среза, которая составляет 10-ю часть от 2 пи, нормализация, как вы помните, состоит в том, что 2 пи на частоте дискретного времени соответствуют омега суб. s, частота дискретизации в непрерывном времени. Следствием этого является то, что эта частота среза, на самом деле, составляет 1/10 от — а не 2 пи теперь из-за нормализации — это 1/10 от частоты дискретизации.

Следовательно, при изменении частоты дискретизации произойдет то, что даже при фиксированной отсечке дискретного фильтра частота отсечки эквивалентного непрерывного фильтра изменится.Вот что я хочу продемонстрировать. Но позвольте мне еще раз подчеркнуть и попросить вас иметь в виду, что эта демонстрация выполняется без фильтра сглаживания.

И мы собираемся изменить частоту дискретизации, поэтому имейте в виду, что, когда мы будем смотреть на это , когда входная частота переходит половину частоты дискретизации — какую бы частоту дискретизации мы ни наблюдали — тогда из-за того, что нет фильтра сглаживания, мы получим сглаживание. Другими словами, частота и цифровой фильтр, или фильтр дискретного времени, когда мы увеличиваем входную частоту, будут двигаться вверх по частоте, пока мы не превысим половину частоты дискретизации, а затем по существу вернемся вниз по частоте.Следовательно, то, что мы получим, или то, что мы увидим, является периодическим повторением частотной характеристики, когда мы проскальзываем половину частоты дискретизации.

Хорошо, теперь давайте посмотрим на тот же цифровой фильтр, но на частотную характеристику, когда мы меняем частоту дискретизации. Теперь мы хотели бы продемонстрировать эффект изменения частоты дискретизации. И мы знаем, что эффективная частота среза фильтра связана с частотой дискретизации и для этого конкретного фильтра соответствует 10-й части частоты дискретизации.Следовательно, если мы удвоим частоту дискретизации, мы должны удвоить эффективную ширину полосы пропускания фильтра или удвоить частоту среза фильтра.

Итак, давайте сделаем это сейчас. Снова диапазон развертки от 0 до 10 килогерц, но частота дискретизации 40 килогерц. И мы должны заметить, что частота среза фильтра увеличилась вдвое до четырех килогерц. Теперь приступим к уменьшению частоты дискретизации фильтра. Итак, с 40 изменим частоту дискретизации на 20 килогерц. Мы должны увидеть уменьшение частоты среза вдвое.

Теперь мы можем пойти еще дальше. Мы можем снизить частоту дискретизации до 10 килогерц. И помните, что диапазон развертки составляет от 0 до 10 килогерц. Итак, теперь мы переместимся от 0 до 2 пи. Так что, когда мы приблизимся к 2 пи, мы снова увидим полосу пропускания. А теперь давайте еще больше снизим частоту дискретизации до 5 килогерц. Здесь мы находимся на 2 пи. А потом на 4pi.

Хорошо, это иллюстрирует эффект изменения частоты дискретизации. Теперь давайте завершим эту демонстрацию влияния частоты дискретизации на частоту среза фильтра, выполнив некоторую фильтрацию некоторого живого звука.В этом случае мы будем наблюдать за выходным звуковым сигналом как функцией времени на единичном осциллографе, а также послушаем вывод. Мы начнем с частоты дискретизации 40 килогерц, затем уменьшим ее до 20 килогерц, 10 килогерц, а затем 5 килогерц. И в каждом из этих случаев эффективная частота среза фильтра затем уменьшается вдвое с 4 килогерц, до 2 килогерц, до 1 килогерца, а затем до 500 циклов.

Итак, давайте начнем с частоты дискретизации 40 килогерц или эффективной частоты среза фильтра 4 килогерца.Теперь давайте уменьшим частоту дискретизации 20 килогерц или 2 килогерцовый фильтр. Затем частота дискретизации 10 килогерц. И, наконец, частота дискретизации 5 килогерц, соответствующая аналоговому фильтру, эквивалентному 500 циклам. Хорошо, теперь давайте, наконец, вернемся к более высокому качеству регтайма, изменив частоту дискретизации обратно на 40 килогерц.

Хорошо, что ж, надеюсь, то, что вы видели на демонстрации и в этой лекции, дает вам смысл и чувство анализа и использования фильтров дискретного времени для обработки сигналов непрерывного времени.И, как вы, возможно, знаете, и как я пытался указать ранее в прошлом, это, на самом деле, один очень важный — но не единственный — но один очень важный контекст, в котором используется дискретная фильтрация. . Фактически, это область, которая быстро развивается из-за того, что микропроцессоры, цифровая технология, компьютеры и т. Д. Предоставляют значительную гибкость при проведении цифровой обработки сигналов. А когда используется цифровая обработка, это, естественно, соответствует выполнению обработки и ее анализу в дискретное время.

Теперь, в следующей лекции мы продолжим рассмотрение другого аспекта — разработки другого аспекта — выборки. И, в частности, мы будем говорить о дискретизации сигналов дискретного времени. Как я там укажу, один из контекстов, в котором дискретное время выборки, по сути, играет важную роль, — это контекст, в котором мы обрабатываем сигналы непрерывного времени с использованием обработки дискретного времени. Фактически, один шаг, который мы могли бы сделать — в дополнение к шагам, о которых мы говорили здесь, — это дополнительный процесс выборки, следующий за любыми видами фильтрации, которую мы делаем.

Что ж, это обсуждение и тема, которой мы займемся в следующей лекции. Спасибо.

дискретных и непрерывных систем | Encyclopedia.com

дискретные и непрерывные системы Системы, с помощью которых сигналы записываются, передаются или отображаются, могут представлять данные в дискретной форме (например, в виде целых чисел) или в непрерывной форме (в виде «реальных» чисел). Важная классификация является результатом выбора дискретного или непрерывного представления амплитуды, а также дискретного или непрерывного представления времени, в которое возникла амплитуда.Аналоговые компьютеры используют физические величины, которые являются приближениями к непрерывным представлениям. Цифровые компьютеры требуют дискретных представлений как времени, так и амплитуды.

Вопрос о том, является ли сигнал (или его источник) внутренне дискретным или внутренне непрерывным, неразрешим: любой эксперимент для определения этого потребовал бы бесконечной полосы пропускания (или бесконечного времени) и бесконечного отношения сигнал / шум, и поэтому был бы невозможен в упражняться. Все, что находится под вопросом, — удобнее, полезнее или привлекательнее дискретное или непрерывное представление.

Сигналы, которые интуитивно кажутся непрерывными по времени или с непрерывной амплитудой, но для которых предпочтительно дискретное время или дискретно-амплитудное представление, называются квантованными по времени или квантованными по амплитуде . Временное квантование либо адекватно, либо неадекватно согласно критерию Найквиста. Квантованные по времени сигналы называются дискретизированными , а системы, которые их обрабатывают, называются системами дискретных данных . Квантование по амплитуде ухудшает отношение сигнал / шум, эффект, который можно описать как введение шума квантования.

Время и амплитуда должны быть квантованы для обработки цифровыми компьютерами (или другими цифровыми устройствами), которые работают с конечными скоростями с конечными объемами данных с конечной точностью. Те же физические ограничения действуют, хотя и по-другому, чтобы ограничить степень, в которой аналоговые компьютеры (или другие аналоговые устройства) могут приближаться к непрерывному представлению сигналов.

См. Также квантование.

урок2

Урок 2

Сигналы и системы с дискретным временем

Мы предполагаем, что мы получили сигнал дискретного времени из сигнала непрерывного времени с помощью выборки .Учитывая, что это непрерывный сигнал времени, это значение at. Сигнал с дискретным временем определяется только для целого числа. Итак, если мы получим выборку каждые секунды, где период выборки, мы получим:

Мы не обязательно будем предполагать, что это сигнал дискретной амплитуды . Сигнал с дискретным временем и дискретной амплитудой известен как цифровой сигнал . Вы увидите это на более поздних курсах связи. Хорошо известным примером цифрового сигнала является музыка на компакт-диске.

Обратите внимание, что сигнал с дискретным временем не нужно генерировать путем явной дискретизации сигнала с непрерывным временем. Некоторые сигналы по своей сути являются дискретными по времени, например, компьютерные битовые последовательности, а некоторые сигналы неявно дискретизируются, например, дневные значения DJIA или среднегодовые значения температуры.

Сигналы и системы дискретного времени

Помните о квадратных скобках!

Прочтите (просмотрите) пример интегрирования Эйлера в книге, но мы рассмотрим разностные уравнения в главе 10 и при обсуждении Z-преобразования.Интегрирование Эйлера аппроксимирует площадь под кривой суммой прямоугольных площадей.

Шаговая функция дискретного времени

Обратите внимание, что здесь единичный шаг определяется равным, в отличие от непрерывного времени.

Функция единичного шага со сдвигом во времени:

Импульсная функция дискретного времени

Здесь нетрудно определить импульс, как мы имели в непрерывном времени.

Сдвинутый единичный импульс:

Суммирование представляет собой аналог текущего интеграла в непрерывном времени в дискретном времени, а первая разность является аналогом производной.Согласно этим аналогиям, единичный импульс имеет по существу одинаковое поведение в дискретном и непрерывном времени, включая свойство просеивания.

Напомним, что сигналы с непрерывным временем могут быть представлены уравнением (которое может быть определено в регионах) или графиком. Сигналы с дискретным временем могут быть представлены этими способами, но также могут быть представлены в виде таблицы. Например:

Сегодняшняя лекция Сигналы непрерывного и дискретного времени Последовательность

Презентация на тему: «Сегодняшняя лекция Последовательность сигналов непрерывного и дискретного времени» — стенограмма презентации:

ins [data-ad-slot = «4502451947»] {display: none! important;}} @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}} @media (max-width: 800px) {# place_14 {width: 250px;}} @media (max-width: 500 пикселей) {# place_14 {width: 120px;}} ]]>

1 Сегодняшняя лекция Непрерывные и дискретные временные сигналы Последовательность
Различие между дискретными и цифровыми Примеры Последовательность Непрерывная и дискретная временные системы Обозначения Преобразование независимой оси Сдвиг во времени Разворот во времени Пример масштабирования по времени Синусоиды

2 Непрерывные сигналы
Значение сигнала существует в каждый момент времени Независимая переменная Независимая переменная

3 Дискретные временные сигналы
Значение сигнала существует только в равномерно распределенных дискретных точках времени Независимая переменная Независимая переменная

4 Дискретные временные сигналы
Зачем проводить дискретизацию Как дискретизировать Насколько близко расположены выборки Различие между дискретными и цифровыми сигналами Как обозначать дискретные сигналы Является ли изображение дискретным или непрерывным сигналом Изображение обычно считается непрерывной переменной. однако может использоваться для получения дискретного двумерного сигнала (дискретизированного изображения)

5 Непрерывные и дискретные сигналы
Сигнал непрерывного времени представлен заключением независимой переменной (времени) в круглые скобки (). Сигнал дискретного времени представлен заключением независимой переменной (индекса) в квадратные скобки []

6 Непрерывные и дискретные сигналы
Примеры непрерывных сигналов Речь, видео, изображение Изменение атмосферного давления, скорости ветра и температуры в зависимости от высоты Примеры дискретного сигнала Демографические данные, еженедельная позиция акций компании

7 Система с непрерывным и дискретным временем
Подобно сигналам, у нас есть системы с непрерывным и дискретным временем, а также системные системы

8 Система непрерывного и дискретного времени
Примеры систем непрерывного и дискретного времени Система возведения в квадрат Система дифференциатора Система накопления

9 Преобразования Преобразования независимой переменной Time Shift

10 Преобразования Обращение времени

11 Масштабирование времени преобразований

12 Пример преобразований

13 A — максимальная амплитуда синусоидального сигнала
Синусоидальные сигналы x (t) = A cos (ωt + Φ) A — максимальная амплитуда синусоидального сигнала ω — частота в радианах  — фазовый сдвиг

9780521854559: Непрерывные и дискретные временные сигналы и системы с CD-ROM — AbeBooks

Этот учебник представляет собой введение в фундаментальные концепции сигналов и систем с непрерывным (CT) и дискретным (DT) временем (DT), рассматривая их по отдельности в педагогической и автономной манере.Акцент делается на базовых принципах обработки сигналов, при этом лежащие в основе концепции иллюстрируются на практических примерах из обработки сигналов, мультимедийных коммуникаций и биоинформатики. После вводных глав текст разделен на две части. В части I рассматриваются теории, методы и приложения сигналов и систем CT, а в части II обсуждаются эти темы для DT, чтобы их можно было обучать независимо или вместе. К книге прилагается компакт-диск, содержащий код MATLAB, аудиоклипы, изображения, интерактивные программы и анимацию сигналов.Этот учебник, содержащий более 300 иллюстраций, 285 рабочих примеров и 385 домашних заданий, является идеальным введением в предмет для студентов, изучающих электротехнику и компьютерную инженерию. Дополнительные ресурсы, в том числе решения для инструкторов, доступны в Интернете по адресу www.cambridge.org/9780521854559.

«синопсис» может принадлежать другой редакции этого названия.

Описание книги :

Вводное пособие по фундаментальным понятиям сигналов и систем с непрерывным и дискретным временем, автономные для независимых или комбинированных подходов к обучению.Включает CD-ROM, содержащий код MATLAB и различные сигналы. Содержит рабочие примеры, домашние задания (решения для инструкторов онлайн) и обширные иллюстрации. Подходит для бакалавров в области электротехники и вычислительной техники.

Об авторе :

Мринал Мандал — доцент кафедры электротехники и вычислительной техники Университета Альберты, Эдмонтон, Канада.

Амир Асиф — доцент кафедры компьютерных наук и инженерии Йоркского университета, Тороното, Канада.

«Об этом заглавии» может принадлежать другой редакции этого заглавия.

сигналов в дискретном времени | CircuitBread

До сих пор мы рассматривали так называемые аналоговые сигналы и системы .Математически аналоговые сигналы — это функции, имеющие в качестве независимых переменных непрерывные величины, такие как пространство и время. Сигналы дискретного времени — это функции, определенные на целых числах; это последовательности. Один из фундаментальных результатов теории сигналов детализирует условия, при которых аналоговый сигнал может быть преобразован в сигнал с дискретным временем и получен без ошибок . Этот результат важен, потому что дискретными сигналами времени можно управлять с помощью систем, созданных как компьютерные программы.Последующие модули описывают, как практически вся обработка аналоговых сигналов может выполняться с помощью программного обеспечения.

Какими бы важными ни были такие результаты, сигналы с дискретным временем носят более общий характер и включают в себя сигналы, полученные из аналоговых сигналов и , которые таковыми не являются. Например, символы, образующие текстовый файл, образуют последовательность, которая также является сигналом дискретного времени. Мы также должны иметь дело с такими символически значимыми сигналами и системами.

Как и в случае с аналоговыми сигналами, мы ищем способы разложения сигналов дискретного времени с действительным знаком на более простые компоненты.Благодаря этому подходу, ведущему к лучшему пониманию структуры сигнала, мы можем использовать эту структуру для представления информации (создавать способы представления информации с помощью сигналов) и для извлечения информации (извлекать информацию, представленную таким образом). Для сигналов с символическими значениями используется другой подход: мы разрабатываем общее представление всех сигналов с символическим значением, чтобы объединить содержащуюся в них информацию. С точки зрения представления информации, наиболее важным вопросом становится эффективность как для сигналов с действительным, так и для символьных значений; Каков наиболее экономичный и компактный способ представления информации для последующего извлечения.

Сигналы с действительным и комплексным знаком

Сигнал с дискретным временем представлен символически как

, где

. Обычно мы рисуем сигналы с дискретным временем в виде основных графиков, чтобы подчеркнуть тот факт, что это функции, определенные только для целых чисел. Мы можем задержать сигнал с дискретным временем на целое число, как и с аналоговыми. Отсроченная единичная выборка имеет выражение

и равняется единице, когда

Косинусный сигнал в дискретном времени

Рис. 1. Косинусный сигнал в дискретном времени нанесен в виде основного графика.Вы можете найти формулу этого сигнала?

Комплексные экспоненты

Самым важным сигналом, конечно же, является комплексная экспоненциальная последовательность .

Синусоиды

Дискретные синусоиды имеют очевидную форму

. В отличие от аналоговых комплексных экспонент и синусоид, частота которых может быть любой действительной величиной, частоты их аналогов в дискретном времени дают уникальные формы волны только , когда

лежит в интервале

.Это свойство можно легко понять, заметив, что добавление целого числа к частоте комплексной экспоненты с дискретным временем не влияет на значение сигнала.

Этот вывод следует из того, что комплексная экспонента, вычисленная как целое число, кратное

равно единице.

Единичная выборка

Вторым по важности сигналом дискретного времени является единичная выборка , которая определена как

Единичная выборка

Рисунок 2. Единичная выборка.

Исследование графика дискретного сигнала, такого как график косинусоидального сигнала, показанного на рисунке, показывает, что все сигналы состоят из последовательности отсроченных и масштабированных единичных отсчетов.Поскольку значение последовательности для каждого целого числа

обозначается

, а единичная выборка, задержанная до

, записывается как

, мы можем разложить любой сигнал как сумму единичных отсчетов, задержанных в соответствующем месте, и масштабируется значением сигнала.

Этот вид разложения уникален для сигналов с дискретным временем и впоследствии окажется полезным.

Системы с дискретным временем могут воздействовать на сигналы с дискретным временем таким же образом, как и в аналоговых сигналах и системах.Из-за роли программного обеспечения в системах с дискретным временем можно представить и «сконструировать» гораздо больше различных систем с помощью программ, чем с помощью аналоговых сигналов. Фактически, особый класс аналоговых сигналов может быть преобразован в сигналы с дискретным временем, обработан с помощью программного обеспечения и преобразован обратно в аналоговый сигнал, и все это без появления ошибки. Для таких сигналов системы могут быть легко созданы в программном обеспечении с эквивалентными аналоговыми реализациями, которые сложно, если не невозможно, спроектировать.

Символьные сигналы

Другой интересный аспект сигналов с дискретным временем состоит в том, что их значения не обязательно должны быть действительными числами.У нас есть действительные сигналы с дискретным временем, такие как синусоида, но у нас также есть сигналы, которые обозначают последовательность символов, набранных на клавиатуре. Такие символы определенно не являются действительными числами, и как набор возможных значений сигналов они имеют небольшую математическую структуру, кроме того, что они являются членами набора. Более формально, каждый элемент символьного сигнала

принимает одно из значений

, которые составляют алфавит

.Эта техническая терминология не означает, что мы ограничиваем символы только членами английского или греческого алфавита. Они могут представлять символы клавиатуры, байты (8-битные величины), целые числа, передающие суточную температуру. Независимо от того, управляются ли они программным обеспечением или нет, системы с дискретным временем в конечном итоге состоят из цифровых схем, которые состоят из полностью аналоговых схемных элементов.

Основные характеристики непрерывных и дискретных сигналов

Непрерывные сигналы

Дискретные сигналы

Процесс дискретизации непрерывных сигналов

Преимущества цифровых систем передачи данных

Области применения аналоговых и цифровых сигналов

Применение аналоговых сигналов

Применение цифровых сигналов

Методы преобразования аналоговых сигналов в цифровые

Особенности представления дискретных сигналов

Спектры непрерывных и дискретных сигналов

Спектр непрерывного сигнала

Спектр дискретного сигнала

Заключение

Чем отличается непрерывный сигнал от дискретного кратко

Что ты хочешь узнать?

Ответ

История появления термина

Вычислительная техника

Звукозапись и телефония

Электрические измерения

Общая информация

Энергия потока

Взаимное преобразование различных по природе потоков

Отличия дискретного и цифрового сигналов

Виды сигналов

Для чего обрабатывается сигнал

Создание и формирование

Динамический диапазон

Аналоговый сигнал

Цифровой сигнал

Применение цифрового сигнала

Дискретный сигнал

Сравнение цифрового и аналогового сигналов

Аналоговый и цифровой сигналы и цифро-аналоговое преобразование

Видео

Аналоговый сигнал

Что такое дискретный сигнал

Чем отличается непрерывный сигнал от дискретного

Как аналоговый сигнал преобразуется в цифровой и наоборот

Как выглядят спектры аналогового и дискретного сигнала

Какие системы связи используют цифровой сигнал а какие аналоговый

Список книг помогающих разобраться в аналоговых и цифровых сигналах

Дискретные сигналы (Реферат) — TopRef.ru

2. Непрерывные и дискретные сигналы. Дискретизация.

Page

Разница между цифровым сигналом и дискретным сигналом

Непрерывное и дискретное. Непрерывные и дискретные процессы.

1.1 Дискретные и непрерывные сигналы. Цифровая обработка сигналов

Похожие главы из других работ:

1. Непрерывные и дискретные переменные

1.4 Сигналы GPS

1.5 Цифровые сигналы для электронно-лучевых мониторов

2. Сигналы с угловой модуляцией

4. Импульсно-модулированные сигналы

3. Сигналы и цели в радиолокации

2.1.2 Какие сигналы используются в радиолокации

2.1.3 Какие сигналы воздействуют на вход РЛС

5.1 Системы и сигналы синхронизации

1.1 Дискретные сигналы и методы их преобразования

1. Радиотехнические сигналы и цепи

1.1 Радиотехнические сигналы

3. Преобразование двоичных кодовых слов с выхода АЦП в линейные сигналы

2 Линейные частотно — манипулированные сигналы

Что такое непрерывный и дискретный сигнал времени? — Цвета-NewYork.com

Что такое непрерывный и дискретный сигнал времени?

В чем разница между дискретным и цифровым сигналом?

Что такое определение «непрерывный сигнал»?

Что такое пример дискретного сигнала?

Возраст непрерывен или дискретен?

Как узнать, являются ли ваши данные дискретными или непрерывными?

Пол — дискретная или непрерывная переменная?

Деньги непрерывны или дискретны?

Группа крови непрерывная или дискретная?

Стоимость — это дискретная или непрерывная переменная?

В чем разница между дискретной и непрерывной переменной?

Почему деньги — это непрерывная переменная?

Является ли занятость дискретной переменной?

Почтовый индекс непрерывный или дискретный?

Является ли да или нет дискретной переменной?