Дискретные сигналы: основы, преобразования и применения в цифровой обработке

Что такое дискретные сигналы. Как они связаны с аналоговыми сигналами. Какие преобразования применяются к дискретным сигналам. Как используются дискретные сигналы в цифровой обработке.

Содержание

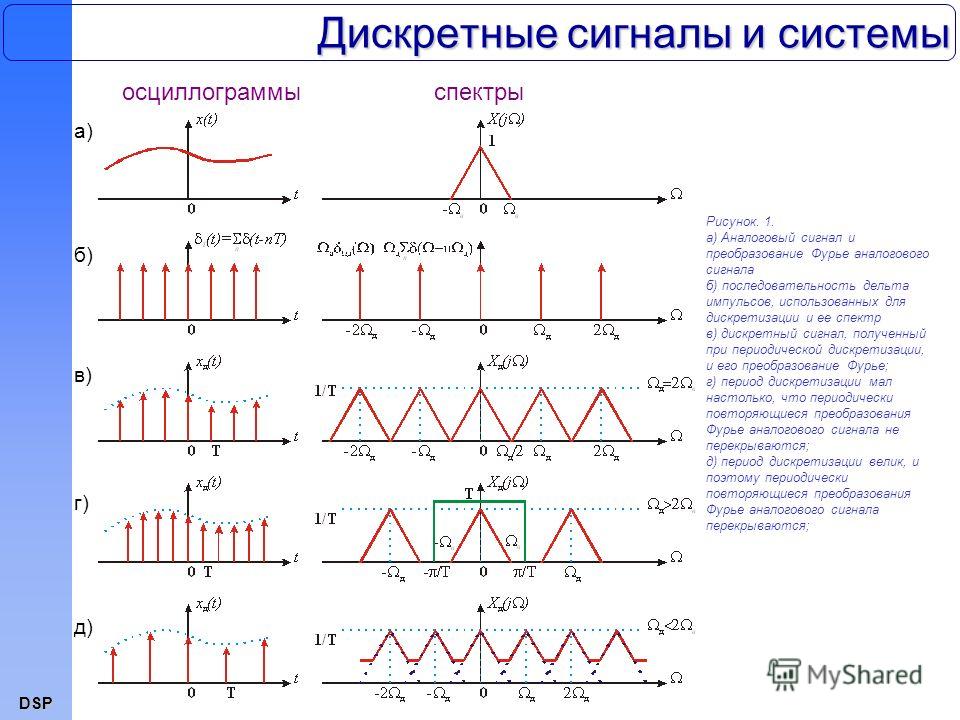
Что такое дискретные сигналы и чем они отличаются от аналоговых

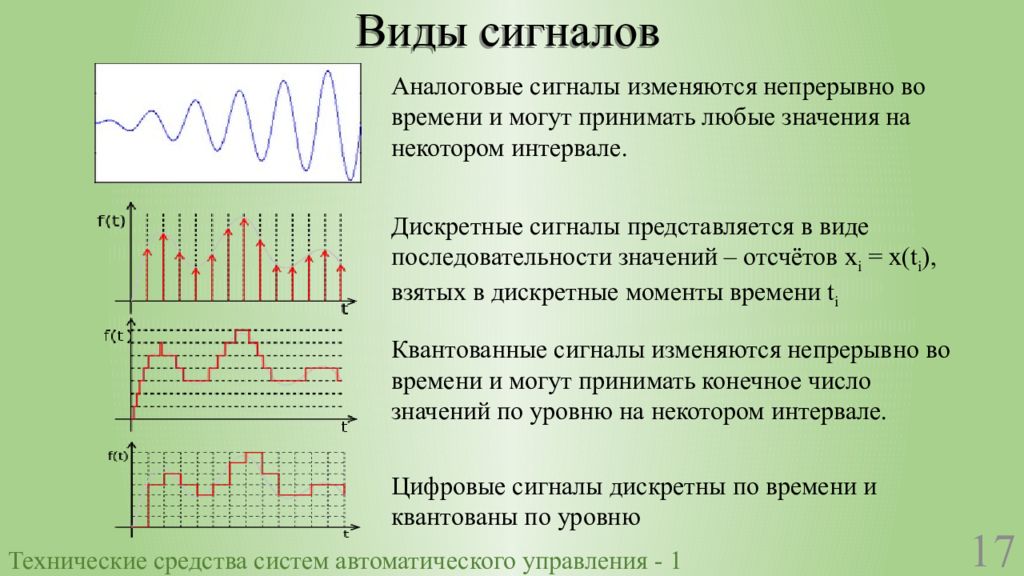
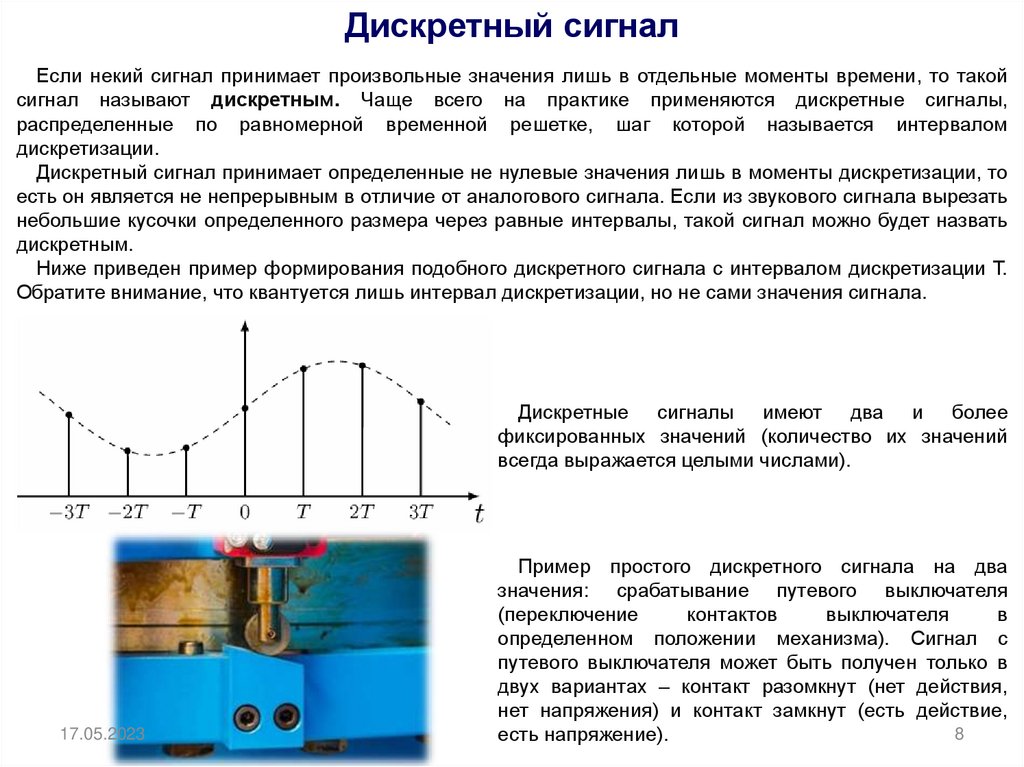
Дискретные сигналы — это сигналы, значения которых определены только в дискретные моменты времени. В отличие от аналоговых сигналов, которые непрерывны во времени, дискретные сигналы представляют собой последовательность отсчетов, взятых через равные промежутки времени.

Основные отличия дискретных сигналов от аналоговых:

Дискретны по времени — значения определены только в фиксированные моменты времени
Представляются последовательностью отсчетов
Описываются дискретными функциями
Спектр периодичен

При этом амплитуда дискретных сигналов может принимать непрерывные значения. Если же амплитуда тоже квантуется (округляется до ближайшего дискретного уровня), то такой сигнал называется цифровым.

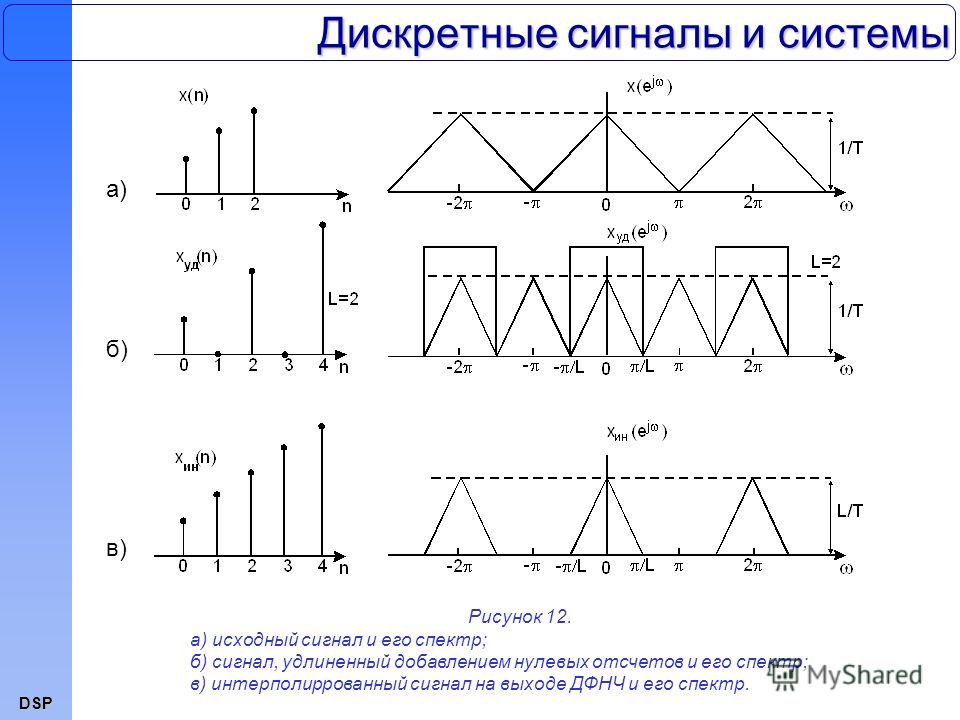
Связь между спектрами аналогового и дискретного сигналов

Между спектрами аналогового сигнала x(t) и его дискретного представления x[n] существует важная связь. Спектр дискретного сигнала X(ω) представляет собой периодическую функцию с периодом 2π и связан со спектром аналогового сигнала X(jΩ) следующим соотношением:

X(ω) = (1/T) Σ X(j(ω/T + 2πk/T))

где T — период дискретизации, k — целое число.

Это означает, что спектр дискретного сигнала является суммой периодических повторений спектра аналогового сигнала, сдвинутых на частоты, кратные частоте дискретизации. Данное соотношение имеет важные практические следствия, в частности, объясняет эффект наложения спектров при дискретизации.

Дискретное преобразование Фурье и его свойства

Дискретное преобразование Фурье (ДПФ) — это основной инструмент анализа дискретных сигналов. ДПФ позволяет перейти от временного представления сигнала к его спектральному представлению.

Прямое ДПФ определяется как:

X[k] = Σ x[n] * e^(-j2πnk/N)

где x[n] — отсчеты сигнала, N — число отсчетов.

Основные свойства ДПФ:

Периодичность по частоте с периодом N
Линейность
Симметрия
Сдвиг во времени приводит к фазовому сдвигу в частотной области
Свертка во временной области соответствует умножению в частотной

ДПФ лежит в основе многих алгоритмов цифровой обработки сигналов и изображений.

Z-преобразование дискретных сигналов

Z-преобразование — это мощный инструмент анализа дискретных систем и сигналов. Оно определяется как:

X(z) = Σ x[n] * z^(-n)

где z — комплексная переменная.

Z-преобразование обладает рядом важных свойств:

Линейность
Сдвиг во времени
Свертка последовательностей
Умножение на экспоненту
Дифференцирование и интегрирование

Z-преобразование широко используется для анализа устойчивости и частотных характеристик дискретных систем, а также для решения разностных уравнений.

Дискретизация аналоговых сигналов

Дискретизация — это процесс преобразования аналогового сигнала в дискретный путем взятия отсчетов через равные промежутки времени. Основные аспекты дискретизации:

Теорема Котельникова

Теорема Котельникова (теорема отсчетов) утверждает, что для точного восстановления аналогового сигнала частота дискретизации должна быть как минимум в 2 раза выше максимальной частоты в спектре сигнала:

fs ≥ 2fmax

где fs — частота дискретизации, fmax — максимальная частота в спектре сигнала.

Эффект наложения спектров

При нарушении теоремы Котельникова возникает эффект наложения спектров (алиасинг), приводящий к искажению сигнала. Для предотвращения этого эффекта используют фильтры нижних частот перед дискретизацией.

Квантование по уровню

При аналого-цифровом преобразовании происходит не только дискретизация по времени, но и квантование по уровню — округление значений отсчетов до ближайших дискретных уровней. Это вносит ошибку квантования, которая проявляется как шум.

Цифровая фильтрация дискретных сигналов

Цифровая фильтрация — одно из основных применений дискретных сигналов. Цифровые фильтры делятся на два основных класса:

Фильтры с конечной импульсной характеристикой (КИХ)

КИХ-фильтры описываются разностным уравнением вида:

y[n] = Σ b[k] * x[n-k]

Основные свойства КИХ-фильтров:

Устойчивы
Могут иметь линейную фазовую характеристику
Требуют большего порядка по сравнению с БИХ

Фильтры с бесконечной импульсной характеристикой (БИХ)

БИХ-фильтры описываются рекурсивным уравнением:

y[n] = Σ b[k] * x[n-k] — Σ a[k] * y[n-k]

Основные свойства БИХ-фильтров:

Могут быть неустойчивы
Нелинейная фазовая характеристика
Меньший порядок по сравнению с КИХ

Выбор типа фильтра зависит от конкретной задачи и требований к характеристикам системы.

Применение дискретных сигналов в цифровой обработке

Дискретные сигналы находят широкое применение в различных областях цифровой обработки:

Цифровая аудио- и видеообработка
Системы связи
Радиолокация и гидролокация
Биомедицинские приложения
Обработка речи и распознавание образов
Сейсмология

Преимущества использования дискретных сигналов:

Высокая точность и повторяемость обработки
Гибкость и адаптивность алгоритмов
Возможность реализации сложных функций

Устойчивость к шумам и помехам
Простота хранения и передачи данных

Развитие технологий цифровой обработки сигналов открывает новые возможности в различных областях науки и техники.

Цифровая обработка сигналов (Оппенгейм А. В.)

Оппенгейм А. В., Шафер Р. В. Цифровая обработка сигналов: Пер. с англ / Под ред. С. Я. Шаца. — М.: Связь, 1979. — 416 с.

В книге достаточно полно систематически изложены математические основы цифровой обработки детерминированных и случайных сигналов методы анализа и синтеза цифровых фильтров идеи алгоритмов быстрого преобразования Фурье, а также преобразование Гильберта и обработка двумерных последовательностей; отдельная глава посвящена гомоморфной обработке сигналов

Книга предназначена для научных работников, занимающихся цифровой обработкой сигналов.

Дискретные сигналы и системы
1.1. ДИСКРЕТНЫЕ СИГНАЛЫ (ПОСЛЕДОВАТЕЛЬНОСТИ)
1.2. ЛИНЕЙНЫЕ СИСТЕМЫ, ИНВАРИАНТНЫЕ К СДВИГУ
1.3. УСТОЙЧИВОСТЬ И ФИЗИЧЕСКАЯ РЕАЛИЗУЕМОСТЬ
1.4. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
1.5. ПРЕДСТАВЛЕНИЕ ДИСКРЕТНЫХ СИГНАЛОВ И СИСТЕМ В ЧАСТОТНОЙ ОБЛАСТИ
1.6. НЕКОТОРЫЕ СВОЙСТВА СИММЕТРИИ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
1.7. ДИСКРЕТИЗАЦИЯ СИГНАЛОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
1.8. ДВУМЕРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И СИСТЕМЫ
ЗАКЛЮЧЕНИЕ
Глава 2. z-преобразование
2.1. ПРЯМОЕ Z-ПРЕОБРАЗОВАНИЕ
2.2. ОБРАТНОЕ Z-ПРЕОБРАЗОВАНИЕ
2.3. ТЕОРЕМЫ О Z-ПРЕОБРАЗОВАНИИ. СВОЙСТВА Z-ПРЕОБРАЗОВАНИЯ
2.4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
2.5. ДВУМЕРНОЕ Z-ПРЕОБРАЗОВАНИЕ
ЗАКЛЮЧЕНИЕ
Глава 3. Дискретное преобразование Фурье
3.1. ПРЕДСТАВЛЕНИЕ ПЕРИОДИЧЕСКИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ДИСКРЕТНЫМ РЯДОМ ФУРЬЕ
3.2. СВОЙСТВА ДИСКРЕТНЫХ РЯДОВ ФУРЬЕ
3.3. СВОЙСТВА ДРФ ПРЕДСТАВЛЕНИЯ ПЕРИОДИЧЕСКИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
3.4. ВЫБОРКИ ИЗ Z-ПРЕОБРАЗОВАНИЯ
3.

5. ПРЕДСТАВЛЕНИЕ ПО ФУРЬЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ КОНЕЧНОЙ ДЛИТЕЛЬНОСТИ — ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
3.6. СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
3.7. ЛИНЕЙНАЯ СВЕРТКА С ИСПОЛЬЗОВАНИЕМ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
3.8. ДВУМЕРНОЕ ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
ЗАКЛЮЧЕНИЕ
Глава 4. Представление цифровых фильтров с помощью графов и матриц
4.1. ПРЕДСТАВЛЕНИЕ ЦИФРОВЫХ ЦЕПЕЙ С ПОМОЩЬЮ НАПРАВЛЕННОГО СИГНАЛЬНОГО ГРАФА
4.2. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ЦИФРОВЫХ ЦЕПЕЙ

4.3. ОСНОВНЫЕ СТРУКТУРНЫЕ СХЕМЫ ПРИ ПОСТРОЕНИИ БИХ-СИСТЕМ
4.4. ОБРАЩЕННЫЕ ФОРМЫ
4.5. ОСНОВНЫЕ СТРУКТУРНЫЕ СХЕМЫ ПРИ ПОСТРОЕНИИ КИХ-СИСТЕМ
4.5.2. КАСКАДНАЯ ФОРМА
4.5.3. СТРУКТУРЫ ДЛЯ ПОСТРОЕНИЯ КИХ-СИСТЕМ С ЛИНЕЙНОЙ ФАЗОВОЙ ХАРАКТЕРИСТИКОЙ
4.5.4. СТРУКТУРЫ С ЧАСТОТНОЙ ВЫБОРКОЙ
4.5.5. СТРУКТУРЫ, ОСНОВАННЫЕ НА ФОРМУЛАХ ИНТЕРПОЛЯЦИОННЫХ ПОЛИНОМОВ
4.6. ЭФФЕКТЫ КВАНТОВАНИЯ ПАРАМЕТРА
4.6.1. ЭФФЕКТЫ КВАНТОВАНИЯ ПАРАМЕТРОВ В БИХ-СИСТЕМАХ
4.6.2. ЭФФЕКТЫ КВАНТОВАНИЯ ПАРАМЕТРОВ В КИХ-СИСТЕМАХ
4.

7. ТЕОРЕМА ТЕЛЕДЖЕНА ДЛЯ ЦИФРОВЫХ ФИЛЬТРОВ И ЕЕ ПРИМЕНЕНИЯ
4.7.1. ВЗАИМНЫЕ И ВЗАИМООБРАТИМЫЕ ЦИФРОВЫЕ ЦЕПИ
4.7.2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ТРАНСПОЗИЦИИ
4.7.3. ФОРМУЛА ЧУВСТВИТЕЛЬНОСТИ ЦЕПИ
ЗАКЛЮЧЕНИЕ
Глава 5. Методы проектирования и расчета цифровых фильтров
5.1. РАСЧЕТ ЦИФРОВЫХ БИХ-ФИЛЬТРОВ ПО ДАННЫМ АНАЛОГОВЫХ ФИЛЬТРОВ

5.1.1. ИНВАРИАНТНОСТЬ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ
5.1.2. МЕТОДЫ РАСЧЕТОВ, ОСНОВАННЫЕ НА ЧИСЛЕННОМ РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
5.1.3. БИЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
5.2. ПРИМЕРЫ РАСЧЕТА ФИЛЬТРОВ НА ОСНОВЕ АНАЛОГО-ЦИФРОВОЙ ТРАНСФОРМАЦИИ
5.2.2. ЦИФРОВЫЕ ФИЛЬТРЫ ЧЕБЫШЕВА
5.2.3. ЭЛЛИПТИЧЕСКИЕ ФИЛЬТРЫ
5.2.4. ЧАСТОТНЫЕ ПРЕОБРАЗОВАНИЯ БИХ-ФИЛЬТРОВ НИЖНИХ ЧАСТОТ
5.3. МАШИННОЕ ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ БИХ-ФИЛЬТРОВ
5.3.1. МИНИМИЗАЦИЯ СРЕДНЕКВАДРАТИЧЕСКОИ ОШИБКИ
5.3.2. КРИТЕРИЙ МИНИМИЗАЦИИ p-ошибки
5.3.3. РАСЧЕТ ОБРАТНОГО ФИЛЬТРА МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
5.4. СВОЙСТВА ЦИФРОВЫХ КИХ-ФИЛЬТРОВ
5.5. РАСЧЕТ КИХ-ФИЛЬТРОВ ПРИ ИСПОЛЬЗОВАНИИ ОКОН
5.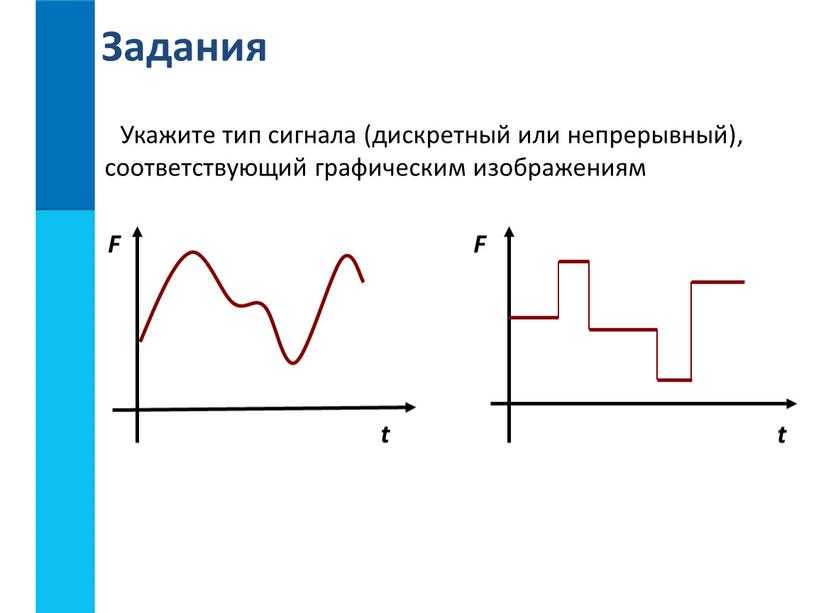

6. МАШИННОЕ ПРОЕКТИРОВАНИЕ КИХ-ФИЛЬТРОВ
5.6.2. АППРОКСИМАЦИИ С РАВНОВЕЛИКИМИ ПУЛЬСАЦИЯМИ ДЛЯ КИХ-ФИЛЬТРОВ
5.7. СРАВНЕНИЕ ЦИФРОВЫХ БИХ- И КИХ-ФИЛЬТРОВ

ЗАКЛЮЧЕНИЕ
Глава 6. Вычисление дискретного преобразования Фурье
6.1. АЛГОРИТМ ГЕРЦЕЛЯ
6.2. АЛГОРИТМЫ БПФ С ПРОРЕЖИВАНИЕМ ПО ВРЕМЕНИ
6.2.1. ВЫЧИСЛЕНИЯ С ЗАМЕЩЕНИЕМ
6.2.2. ДРУГИЕ ФОРМЫ АЛГОРИТМОВ
6.3. АЛГОРИТМЫ БПФ С ПРОРЕЖИВАНИЕМ ПО ЧАСТОТЕ
6.3.1. ВЫЧИСЛЕНИЯ С ЗАМЕЩЕНИЕМ
6.3.2. ДРУГИЕ ФОРМЫ АЛГОРИТМОВ
6.4. АЛГОРИТМЫ БПФ ДЛЯ СОСТАВНОГО ЗНАЧЕНИЯ N
6.5. ОБЩИЕ ОСОБЕННОСТИ АЛГОРИТМОВ БПФ
6.5.3. МНОГОМЕРНОЕ БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
6.6. АЛГОРИТМ ПРЕРЫВИСТОГО Z-ПРЕОБРАЗОВАНИЯ
ЗАКЛЮЧЕНИЕ
Глава 7. Дискретное преобразование Гильберта
7.1. О ДОСТАТОЧНОСТИ ДЕЙСТВИТЕЛЬНОЙ И МНИМОЙ ЧАСТЕЙ ПРЕОБРАЗОВАНИЙ ДЛЯ ПРЕДСТАВЛЕНИЯ ФИЗИЧЕСКИ РЕАЛИЗУЕМЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
7.2. УСЛОВИЕ МИНИМАЛЬНОСТИ ФАЗЫ
7.3. ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА ДЛЯ ДПФ
7.4. ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА ДЛЯ КОМПЛЕКСНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
7.

4.1. СИНТЕЗ ГИЛЬБЕРТОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ
7.4.2. ПРЕДСТАВЛЕНИЕ УЗКОПОЛОСНЫХ СИГНАЛОВ
ЗАКЛЮЧЕНИЕ
Глава 8. Дискретные случайные сигналы
8.1. ДИСКРЕТНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
8.1.1. ПРОЦЕСС БЕРНУЛЛИ
8.1.2. ОПИСАНИЯ СЛУЧАЙНОГО ПРОЦЕССА
8.2. СРЕДНИЕ ЗНАЧЕНИЯ
8.2.2. СРЕДНИЕ ПО ВРЕМЕНИ
8.3. СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ С БЕСКОНЕЧНОЙ ЭНЕРГИЕЙ
8.3.1. СВОЙСТВА КОРРЕЛЯЦИОННОЙ И КОВАРИАЦИОННОЙ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
8.3.2. ПРЕДСТАВЛЕНИЕ С ПОМОЩЬЮ z-ПРЕОБРАЗОВАНИЯ
8.3.3. СПЕКТР МОЩНОСТИ
8.4. РЕАКЦИЯ ЛИНЕЙНЫХ СИСТЕМ НА СЛУЧАЙНЫЕ СИГНАЛЫ
ЗАКЛЮЧЕНИЕ
Глава 9. Эффекты конечной разрядности регистров при цифровой обработке сигналов
9.1. ВЛИЯНИЕ СПОСОБОВ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ НА КВАНТОВАНИЕ
9.1.1. ДВОИЧНЫЕ ЧИСЛА С ФИКСИРОВАННОЙ И ПЛАВАЮЩЕЙ ЗАПЯТЫМИ
9.1.2. ПРЕДСТАВЛЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
9.1.3. ЭФФЕКТ УСЕЧЕНИЯ ИЛИ ОКРУГЛЕНИЯ
9.2. КВАНТОВАНИЕ ПРИ ДИСКРЕТИЗАЦИИ АНАЛОГОВЫХ СИГНАЛОВ
9.3. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ РЕГИСТРА ПРИ ПОСТРОЕНИИ ЦИФРОВЫХ БИХ-ФИЛЬТРОВ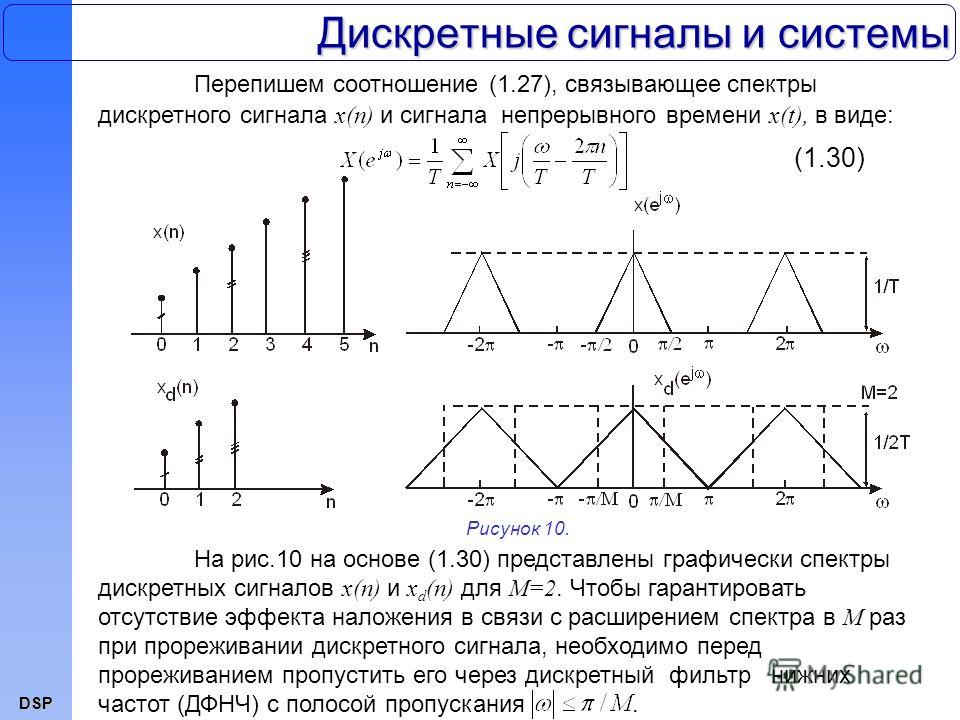

3.1. ПРЕДЕЛЬНЫЕ ЦИКЛЫ НИЗКОГО УРОВНЯ ПРИ ПОСТРОЕНИИ ЦИФРОВЫХ ФИЛЬТРОВ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
9.3.2. СТАТИСТИЧЕСКИЙ АНАЛИЗ КВАНТОВАНИЯ ПРИ ПОСТРОЕНИИ ЦИФРОВЫХ БИХ-ФИЛЬТРОВ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
9.3.3. СТАТИСТИЧЕСКИЙ АНАЛИЗ КВАНТОВАНИЯ ПРИ ПОСТРОЕНИИ ЦИФРОВЫХ БИХ-ФИЛЬТРОВ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
9.4. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ РЕГИСТРОВ ПРИ ПОСТРОЕНИИ ЦИФРОВЫХ КИХ-ФИЛЬТРОВ
9.4.2. СТАТИСТИЧЕСКИЙ АНАЛИЗ ЭФФЕКТОВ КВАНТОВАНИЯ ПРИ ПОСТРОЕНИИ ЦИФРОВЫХ КИХ-ФИЛЬТРОВ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
9.5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ РЕГИСТРОВ ПРИ ВЫЧИСЛЕНИИ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
9.5.2. АНАЛИЗ ЭФФЕКТОВ КВАНТОВАНИЯ В АЛГОРИТМАХ БПФ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
9.5.3. АНАЛИЗ ЭФФЕКТОВ КВАНТОВАНИЯ В АЛГОРИТМАХ БПФ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
9.5.4. ЭФФЕКТЫ КВАНТОВАНИЯ КОЭФФИЦИЕНТОВ В АЛГОРИТМАХ БПФ
ЗАКЛЮЧЕНИЕ
Глава 10. Гомоморфная обработка сигналов
10.2. МУЛЬТИПЛИКАТИВНЫЕ ГОМОМОРФНЫЕ СИСТЕМЫ
10.3. ГОМОМОРФНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
10.4. ГОМОМОРФНЫЕ СИСТЕМЫ ОТНОСИТЕЛЬНО СВЕРТКИ
10.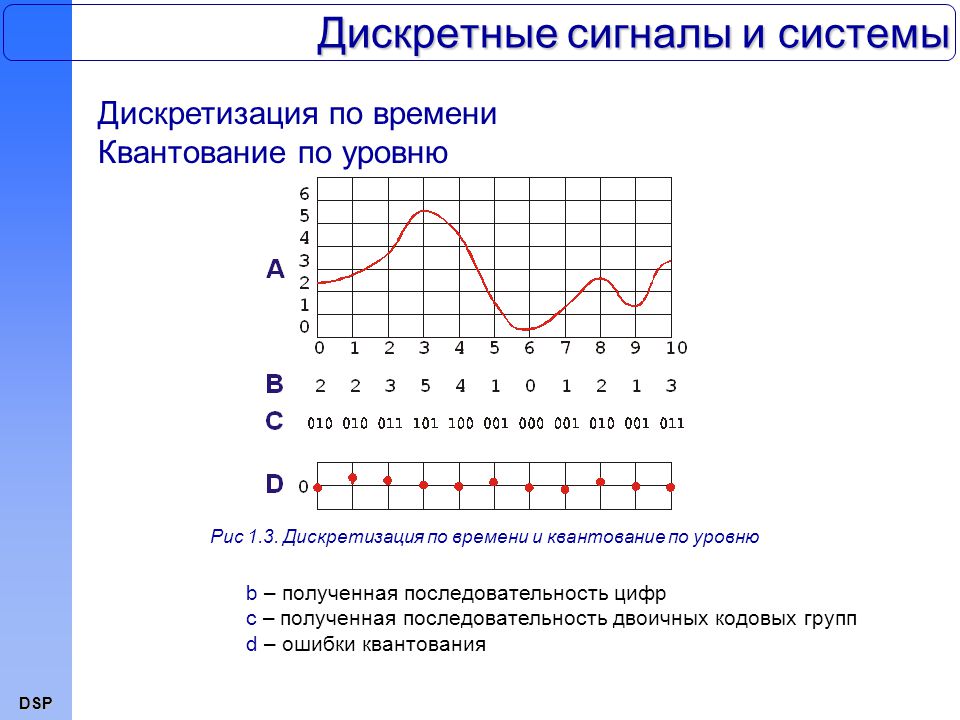

5. СВОЙСТВА КОМПЛЕКСНОГО КЕПСТРА
10.5.2. МИНИМАЛЬНО- И МАКСИМАЛЬНО-ФАЗОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
10.5.3. СЛУЧАЙ, КОГДА ПОЛЮСЫ И НУЛИ НАХОДЯТСЯ НА ЕДИНИЧНОЙ ОКРУЖНОСТИ
10.6. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ ХАРАКТЕРИСТИЧЕСКОЙ СИСТЕМЫ D
10.7. ПРИМЕНЕНИЕ ГОМОМОРФНОЙ РАЗВЕРТКИ
10.7.2. ДЕРЕВЕРБЕРАЦИЯ
10.7.3. ВОССТАНОВЛЕНИЕ ЗВУКОЗАПИСЕЙ
ЗАКЛЮЧЕНИЕ
Глава 11. Оценка спектра мощности
11.1. ОСНОВНЫЕ ПРИНЦИПЫ ТЕОРИИ ОЦЕНОК
11.2. ОЦЕНКИ АВТОКОВАРИАЦИИ
11.3. ПЕРИОДОГРАММА КАК ОЦЕНКА СПЕКТРА МОЩНОСТИ
11.3.2. ДИСПЕРСИЯ ПЕРИОДОГРАММЫ
11.3.3. ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ДИСПЕРСИИ
11.4. СГЛАЖЕННЫЕ ОЦЕНКИ СПЕКТРА
11.4.3. УСРЕДНЕНИЕ МОДИФИЦИРОВАННЫХ ПЕРИОДОГРАММ (МЕТОД УЭЛЧА)
11.5. ОЦЕНКА ВЗАИМНОЙ КОВАРИАЦИИ И ВЗАИМНОГО СПЕКТРА
11.6. ПРИМЕНЕНИЕ БПФ ПРИ ОЦЕНКЕ СПЕКТРА
11.6.1. РЕАЛИЗАЦИЯ МЕТОДОВ БАРТЛЕТА И УЭЛЧА
11.6.2. ВЫЧИСЛЕНИЕ КОРРЕЛЯЦИОННЫХ ОЦЕНОК
11.6.3. ВЫЧИСЛЕНИЕ СГЛАЖЕННЫХ ОЦЕНОК СПЕКТРА
11.7. ПРИМЕРЫ ОЦЕНКИ СПЕКТРА

Дискретные сигналы.

Связь спектров аналогового и дискретного сигналов. Влияние формы тактирующего сигнала на спектр дискретного сигнала. Преобразование Лапласа и Фурье от дискретного сигнала

2.2 Дискретные сигналы

Связь спектров аналогового и дискретного сигналов (1-131)

Аналоговый сигнал .

Отсчеты аналогового сигнала .

Идеальный тактирующий сигнал . (Домножение на — функцию изменяет размерность исходного выражения).

Рис.3.4.

Дискретный сигнал представляем в виде произведения исходного аналогового сигнала на тактирующий сигнал

Так как дельта-функция = 0 везде, кроме t=kT, то можно (1) записать в виде произведения аналогового и тактирующего сигналов.

Тактирующий сигнал – периодическая функция, поэтому

Следовательно,

Умножение сигнала на соответствует сдвигу спектра на . Поэтому искомая связь спектров аналогового и дискретного сигналов:

Рис.3.5.

Теорема Котельникова.

Появление ложных частот.

Рис. 3.6

Необходимость предварительной НЧ фильтрации.

Рис. 3.7.

Влияние формы тактирующего сигнала на спектр дискретного сигнала (4-381).

Рис. 12.31, 12.32

Тактирующий импульс определен на интервале от 0 до Т и =0 вне этого интервала. Его длительность .

Тактирующий сигнал сумме тактирующих импульсов.

Отдельный импульс прямоугольной формы амплитуды s(kT) и длительности Т можно представить как свертку .

Тогда

Следовательно, спектры сигналов связаны следующим образом

Рис. 12.33 (Лучше С.3-10)

Задание. Рассчитать искажение спектра дискретного сигнала при дискретизации тактирующим сигналом прямоугольной формы для и .

Преобразование Лапласа и Фурье от дискретного сигнала (1-145), (2-147).

Преобразование Лапласа (для одностороннего сигнала)

Таким образом,

Спектр, как и сам сигнал, полностью определяется своими отсчетами.

Иногда аргумент спектральной функции записывают в виде

подчеркивая тем самым, что спектр зависит не от p или непосредственно, а от комбинации .

Преобразование Фурье

Задание. Вычислить спектр дискретного сигнала .

Свойства спектров дискретных сигналов (2-147).

Дискретное преобразование Фурье

Было: спектр ДС

— бесконечная последовательность,

— непрерывная периодическая функция с периодом .

Так же для конечных последовательностей

ДПФ бесконечной периодической последовательности

Аналоговый периодический сигнал с периодом может быть представлен рядом Фурье

где

Аналогично дискретный периодический сигнал с периодом

можно представить рядом

Здесь проведены замены

Для нормированного времени

где — номер отсчета, соответствующий частоте .

Спектр периодической последовательности определяется суммой

Заметим, что в (5) и (7) экспоненты — периодические функции как по , так и по с одним и тем же периодом .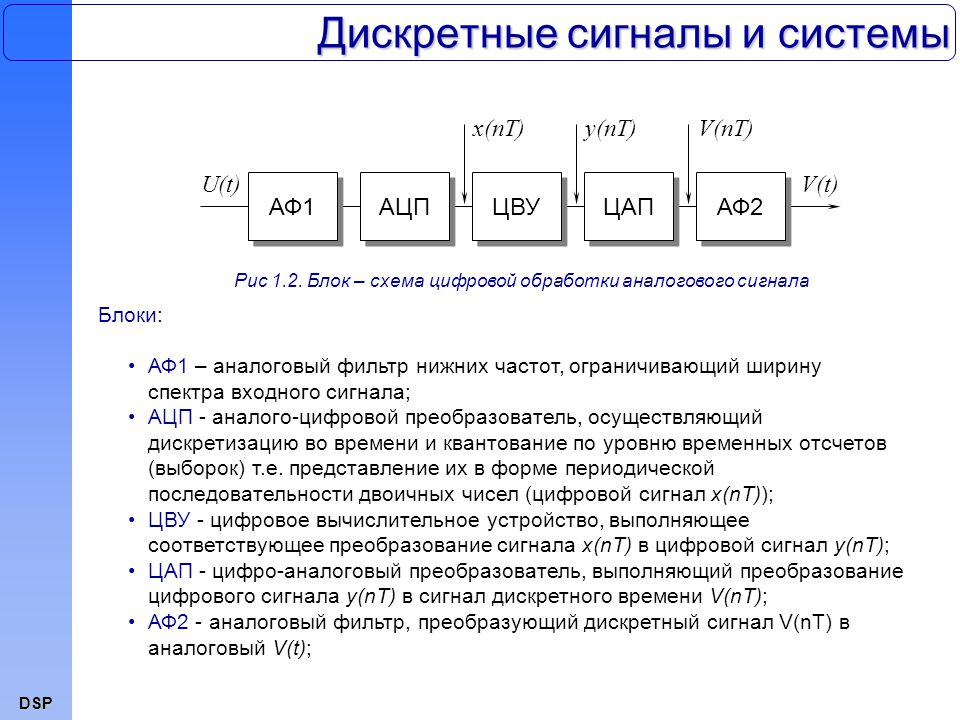 Следовательно, периодическим является не только дискретный сигнал, но и его спектр. В выражениях (6) и (7) мы можем ограничиться частичными суммами (в пределах периода) и записать пару ДПФ в виде (множитель обычно ставится не в (7), а в (6)):

Пара преобразований (8) называется прямым и обратным ДПФ периодической последовательности.

Дискретный сигнал или цифровой сигнал?

спросил 2 года 9 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 580 раз

$\begingroup$

Есть ли разница между ними?

Когда мы говорим о дискретном сигнале, подразумевается ли это только, что ось x или время дискретны? Или это также может означать дискретные амплитуды по оси Y?

Или сигнал называется цифровым только тогда, когда обе его оси дискретны?

дискретные сигналы
цифровые

$\endgroup$

$\begingroup$

Для большей части обработки сигналов используется цифровой сигнал (источник: википедия)

— это представление физического сигнала, который представляет собой выборку и квантованный

Таким образом, он представляет данные как конечных последовательностей дискретных значений.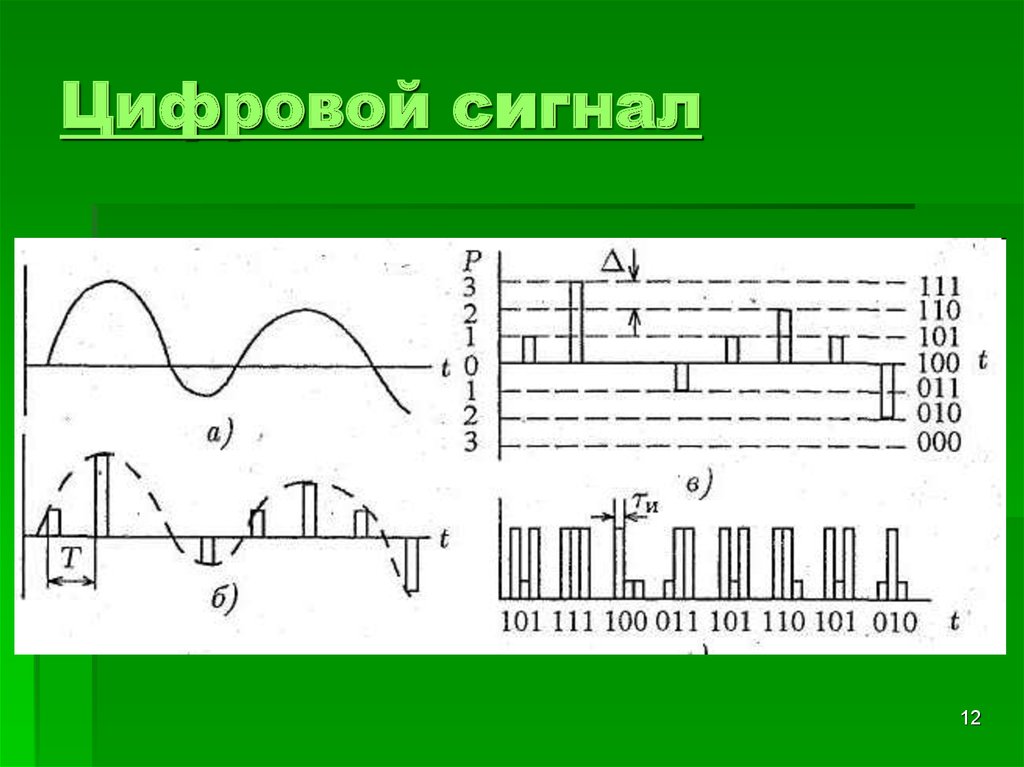 Часто цифровые данные встраиваются в определенный формат для записи/хранения значений (например, 16-битные слова), возможно, с определенным кодированием символов (подумайте о знаковых соглашениях или стандартах с плавающей запятой), чтобы в конечном итоге получить конкретный бит. -мудрое или символьное представление.

Дискретный сигнал — более абстрактная вещь. Это аббревиатура для сигнала дискретного времени . Он может иметь исчисляемое число выборок, и их значения не ограничены дискретностью . Чаще всего интервал времени между выборками постоянный (или равномерный). Для меня лакунарные сигналы, которые имеют однородную выборку, но для которых отсутствуют некоторые выборки, по-прежнему считаются дискретными.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Сигналы дискретного времени — Масштабирование времени и обращение времени

1) Обращение и опережение времени

$x[3-n]$ объединяет две операции:

Обращение времени: $x[n] \rightarrow x[-n] $:
Опережение по времени: $x[-n] \rightarrow x[-n +\tt{3}]$

Визуально

Посмотрите на $x[n]$ и представьте, что вы переворачиваете его вокруг $n=\tt{0}$. Это обращений времени . Выборка при $n=\tt{-4}$ с величиной $-1$ теперь имеет индекс $n = \tt{4}$. То же самое касается выборки при $n=\tt{-3}$ с величиной $-1/2$, которая теперь имеет индекс $n = \tt{3}$. Теперь опережают этот сигнал на $\tt{3}$ отсчетов: тот отсчет в $n=\tt{4}$ с величиной $-1$ теперь равен $n=\tt{4+3} = 7$ . Эта выборка при $n=\tt{3}$ с магнитудой $-1/2$ теперь соответствует $n=\tt{3+3} = 6$ и т. д.

Запишите это

Вы можете сделать это для каждого индекса: давайте выпишем значения для $x[n]$ там, где он определен, т. е. для $-5 \leq n \leq 5$:

\begin{ выровнять} &n &\quad &x[n]\\ \hline -&\tt{5} &\quad &0\\ -&\tt{4} &\quad -&1\\ -&\tt{3} &\quad -&1/2\\ -&\tt{2} &\quad &1/2\\ -&\tt{1} &\квадратный &1\\ &\tt{0} &\квадратный &1\\ &\tt{1} &\квадратный &1\\ &\tt{2} &\quad &1\\ &\tt{3} &\quad &1/2\\ &\tt{4} &\quad &0\\ &\tt{5} &\квадратный &0\\ \end{выравнивание}

Теперь посмотрим на $x[3-n]$. Я начну с $n = -5$, хотя для этого значения $x[3-n] = x[8]$ равно $\text{undefined}$: \начать{выравнивать} &n &\quad &3-n &\quad &x[3-n]\\ \hline -&\tt{5} &\quad &\tt{3} — \tt{(-5) = 8}&\quad &x[8] \text{ не определен}\\ -&\tt{4} &\quad &\tt{3} — \tt{(-4) = 7}&\quad &\text{undefined}\\ -&\tt{3} &\quad &\tt{3} — \tt{(-3) = 6}&\quad &\text{undefined}\\ -&\tt{2} &\quad &\tt{3} — \tt{(-2) = 5}&\quad &0\\ -&\tt{1} &\quad &\tt{4}&\quad &0\\ &\tt{0} &\quad &\tt{3}&\quad &1/2\\ &\tt{1} &\quad &\tt{2}&\quad &1\\ &\tt{2} &\quad &\tt{1} &\quad &1\\ &\tt{3} &\quad &\tt{0}&\quad &1\\ &\tt{4} &\quad &\tt{-1}&\quad &1\\ &\tt{5} &\quad &\tt{-2}&\quad &1/2\\ &\tt{6} &\quad &\tt{-3}&\quad -&1/2\\ &\tt{7} &\quad &\tt{-4}&\quad -&1\\ &\tt{8} &\quad &\tt{-5}&\quad &0\\ \end{выравнивание}

2) Масштабирование по времени

$x[Kn]$ называется прореживанием по масштабному коэффициенту $K>1$ (это называется расширением , если $0

Что такое дискретные сигналы и чем они отличаются от аналоговых

Связь между спектрами аналогового и дискретного сигналов

Дискретное преобразование Фурье и его свойства

Z-преобразование дискретных сигналов