Дискретный сигнал это в информатике. Дискретные и аналоговые сигналы в информатике: ключевые понятия и характеристики

Что такое дискретный и аналоговый сигнал в информатике. Каковы основные отличия между ними. Как происходит дискретизация аналогового сигнала. Где применяются разные типы сигналов.

Понятие сигнала в информатике и теории информации

Сигнал в информатике — это физический процесс, несущий информацию. Сигналы используются для представления и передачи информации в различных системах. Основные характеристики сигнала:

• Амплитуда — максимальное отклонение от среднего значения
• Частота — число колебаний в единицу времени
• Фаза — смещение колебаний относительно начала отсчета
• Спектр — набор частотных составляющих

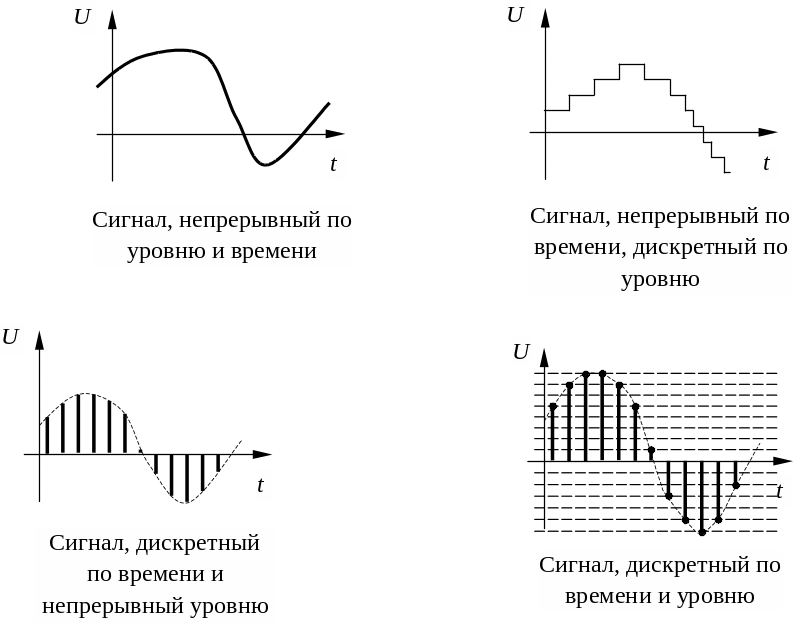
По характеру изменения во времени сигналы делятся на две большие группы: аналоговые (непрерывные) и дискретные.

Аналоговые (непрерывные) сигналы

Аналоговый сигнал — это сигнал, который непрерывно изменяется во времени. Его параметры (амплитуда, частота, фаза) могут принимать любые значения в заданном диапазоне.

Основные свойства аналоговых сигналов:

• Непрерывность изменения во времени
• Бесконечное количество значений в любой промежуток времени
• Плавность переходов между значениями
• Отсутствие разрывов в сигнале

Примеры аналоговых сигналов: звук, изменение температуры, движение стрелки часов, электрическое напряжение в сети.

Дискретные сигналы

Дискретный сигнал — это сигнал, который принимает конечное число значений в заданные моменты времени. Его параметры изменяются скачкообразно.

Ключевые характеристики дискретных сигналов:

• Прерывистость изменения во времени
• Конечное число возможных значений
• Скачкообразные переходы между значениями
• Наличие разрывов в сигнале

Примеры дискретных сигналов: цифровой код, сигналы светофора, показания электронных часов, импульсы в цифровых схемах.

Основные отличия аналоговых и дискретных сигналов

Сравнение ключевых характеристик аналоговых и дискретных сигналов:

Характеристика	Аналоговый сигнал	Дискретный сигнал
Изменение во времени	Непрерывное	Прерывистое
Количество значений	Бесконечное	Конечное
Переходы между значениями	Плавные	Скачкообразные
Наличие разрывов	Отсутствуют	Присутствуют
Математическое описание	Непрерывные функции	Последовательности

Процесс дискретизации аналоговых сигналов

Дискретизация — это процесс преобразования аналогового сигнала в дискретный. При дискретизации непрерывный сигнал заменяется последовательностью отсчетов, взятых через определенные промежутки времени.

Основные этапы дискретизации:

1. Выбор частоты дискретизации
2. Измерение значений сигнала в заданные моменты времени
3. Квантование измеренных значений
4. Кодирование квантованных значений

Качество дискретизации зависит от частоты взятия отсчетов. Согласно теореме Котельникова, для точного восстановления аналогового сигнала частота дискретизации должна быть как минимум в 2 раза выше максимальной частоты в спектре исходного сигнала.

Применение аналоговых и дискретных сигналов

Аналоговые сигналы традиционно используются в следующих областях:

• Аудио- и видеотехника
• Телефонная связь
• Радио- и телевещание
• Аналоговые измерительные приборы
• Аналоговые системы управления

Дискретные сигналы находят применение в:

• Цифровых вычислительных устройствах
• Системах цифровой связи
• Цифровом телевидении
• Цифровой звукозаписи
• Системах передачи данных

Преимущества и недостатки аналоговых и дискретных сигналов

Аналоговые сигналы имеют следующие преимущества:

• Высокая точность представления информации
• Непрерывность во времени
• Простота генерации и обработки

Недостатки аналоговых сигналов:

• Чувствительность к помехам и искажениям
• Сложность хранения и копирования без потерь
• Ограниченные возможности математической обработки

Преимущества дискретных сигналов:

• Высокая помехоустойчивость
• Возможность идеального копирования
• Широкие возможности математической обработки
• Простота хранения и передачи

Недостатки дискретных сигналов:

• Потеря информации при дискретизации
• Ступенчатость формы сигнала
• Необходимость аналого-цифрового преобразования

Области применения различных типов сигналов

Выбор типа сигнала зависит от конкретной задачи и области применения:

• Аналоговые сигналы используются там, где важна плавность и непрерывность: аудиотехника, аналоговое телевидение, аналоговые измерения.
• Дискретные сигналы применяются в цифровых системах: компьютерах, цифровой связи, системах управления.
• В современных системах часто используется комбинация аналоговых и дискретных сигналов с преобразованием между ними.

Заключение

Понимание различий между аналоговыми и дискретными сигналами является ключевым для работы с информационными системами. Каждый тип сигнала имеет свои преимущества и области применения. Выбор оптимального типа сигнала позволяет создавать эффективные системы обработки и передачи информации.

Информация и сигнал (8 класс) Информатика и ИКТ

Информация (от лат. «informatio» -осведомление, разъяснение, изложение) — очень широкое понятие, имеющее множество трактовок. Рассмотрим его с точки зрения субъективного (бытового, человеческого) подхода.

В обыденной жизни под информацией понимают всякого рода сообщения, сведения о чём-либо, которые получают и передают люди. Информация содержится в речи людей, текстах книг, колонках цифр, в звуках и видах природы, в показаниях часов, термометров и других приборов. Каждый материальный объект, с которым происходят изменения, становится источником информации либо об окружающей среде, либо о происходящих в этом объекте процессах. Эту информацию мы получаем в виде сигналов — изменений физических величин (давления, температуры, цвета и др.). Различают световые, звуковые, тепловые, механические, электрические и другие типы сигналов.

Информация для человека — это содержание сигналов (сообщения), воспринимаемых человеком непосредственно или с помощью специальных устройств, расширяющее его знания об окружающем мире и протекающих в нём процессах.

Сигналы могут быть непрерывными или дискретными.

Непрерывный сигнал

принимает бесконечное множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.

Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами. Сравните лестницу и наклонную плоскость. В первом случае имеется строго определённое количество фиксированных высот, равное числу ступенек. Все их можно пронумеровать. Наклонная плоскость соответствует бесконечному количеству значений высоты.

В жизни человек чаще всего имеет дело с непрерывными сигналами. Примерами непрерывных сигналов могут служить речь человека, скорость автомобиля, температура в некоторой географической точке в течение определённого периода времени и многое другое. Примером устройства, подающего дискретные сигналы, является светофор. Сигнал светофора может быть красным, жёлтым или зелёным, т. е. принимать всего три значения.

Самое главное:

• Информация для человека — это содержание сигналов ( сообщения), которые он получает из различных источников.
• Сигналы могут быть непрерывными или дискретными. Непрерывный сигнал принимает бесконечное множество значений из некоторого диапазона. Дискретный сигнал принимает конечное число значений, которые можно пронумеровать.

Вопросы и задания:

1. Что такое информация для человека? Перечислите источники, из которых вы получаете информацию.
2. Приведите примеры непрерывных и дискретных сигналов.

Содержание

Формы представления информации — Технарь

В прошлом пт было сказано, что передача информации делается при помощи сигналов, а самим сигналом является изменение некой свойства носителя со временем. При всем этом зависимо от особенностей конфигурации этой свойства (т.е. параметра сигнала) со временем выделяют два типа сигналов: непрерывные и дискретные.

Сигнал именуется непрерывным (либо аналоговым), если его параметр может принимать хоть какое значение в границах некого интервала.

Если обозначить Z — значение параметра сигнала, a t — время, то зависимость 2(1) будет непрерывной функцией (рис.1.1,а).

Примерами непрерывных сигналов являются речь и музыка, изображение, показание указателя температуры (параметр сигнала — высота столба спирта либо ртути — имеет непрерывный ряд значений) и пр.

Сигнал именуется дискретным, если его параметр может принимать конечное число значений в границах некого интервала.

Пример дискретных сигналов представлен на рис. 1.1,б. Как надо из определения, дискретные сигналы могут быть описаны дискретным и конечным обилием значений характеристик {Z}. Примерами устройств, использующих дискретные сигналы, являются часы (электрические и механические), цифровые измерительные приборы, книжки, табло и пр.

Так как последовательность сигналов есть сообщение, качество прерывности-непрерывности сигналов переносится и на сообщение — есть понятия

«непрерывное сообщение» и «дискретное сообщение». Разумеется, что дискретным будет считаться сообщение, построенное из дискретных сигналов. Еще меньше оснований приписывать данное качество самой инфы, так как информация — категория нематериальная и не может владеть свойством дискретности либо непрерывности. С другой стороны, одна и та же информация, как уже было сказано, может быть представлена средством разных сообщений, в том числе и отличающихся нравом сигналов. К примеру, речь, которую слышим, можно записать в аналоговом виде при помощи магнитофона, а можно и законспектировать средством дискретного набора букв. По этой причине в информатике есть и употребляются сочетания «непрерывная информация» и «дискретная информация». Их необходимо осознавать только как сокращение полных фраз: «информация, представленная средством непрерывных сигналов» и «информация, представленная средством дискретных сигналов» — конкретно в таком контексте эти понятия будут употребляться в предстоящем изложении. Потому когда входит речь о видах инфы, вернее гласить о формах ее представления в сообщении либо о видах сообщений.

Принципным и важным различием непрерывных и дискретных сигналов будет то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного чисел вероятные значения сигнала символ, который будет отличать данный сигнал от другого

Символ — это элемент некого конечного* огромного количества хороших друг от друга сущностей.

* На теоретическом уровне можно было бы обойтись без требования конечности, но, это не имело бы никакого практического значения, так как за конечное время всегда можно передать только сообщения, построенные из конечного числа символов.

Природа знака может хоть какой — жест, набросок, буковка, сигнал светофора, определенный звук и т.д. Природа знака определяется носителем сообщения и формой представления инфы в сообщении.

Вся совокупа символов, применяемых для представления дискретной инфы, именуется набором символов. Таким макаром , набор есть дискретное огромное количество символов.

Набор символов, в каком установлен порядок их следования, именуется алфавитом.

Как следует, алфавит — это упорядоченная совокупа символов. Порядок следования символов в алфавите именуется словарным. Благодаря этому порядку меж знаками инсталлируются дела «больше-меньше»: для 2-ух символов ξ и ψ принимается, что ξ < ψ, если порядковый номер у ξ в алфавите меньше, чем у ψ.

Примером алфавита может служить совокупа арабских цифр 0,1…9 — с его помощью можно записать хоть какое целое число в системах счисления от двоичной до десятичной. Если к этому алфавиту добавить знаки «+» и «-», то сформируется набор символов, применимый для записи хоть какого целого числа, как положительного, так и отрицательного; правда, этот набор нельзя считать алфавитом, так как в нем не определен порядок следования символов. В конце концов, если добавить символ разделителя разрядов («.» либо «,»), то таковой алфавит позволит записать хоть какое вещественное число.

Так как при передаче сообщения параметр сигнала должен изменяться, разумеется, что малое количество разных его значений равно двум и, как следует, алфавит содержит минимум два знака — таковой алфавит именуется двоичным. Верхней границы числа символов в алфавите не существует; примером могут служить иероглифы, любой из которых обозначает целое понятие, и общее их количество исчисляется десятками тысяч.

Знаки, применяемые для обозначения фонем людского языка, именуются знаками, а их совокупа — алфавитом языка.

Сами по для себя символ либо буковка не несут никакого смыслового содержания. Но такое содержание им может быть приписано — в данном случае символ будет называться эмблемой. К примеру, массу в физике принято обозначать буковкой т — как следует, т является эмблемой физической величины «масса» в формулах. Другим примером знаков могут служить пиктограммы, обозначающие в компьютерных программках объекты либо деяния.

Таким макаром, понятия «знак», «буква» и «символ» нельзя считать тождественными, хотя очень нередко различия меж ними не проводят, потому в информатике есть понятия «символьная переменная», «кодировка знаков алфавита», «символьная информация» — во всех приведенных примерах заместо термина «символьный» корректнее было бы использовать «знаковый» либо «буквенный».

Представляется принципиальным снова выделить, что понятия знака и алфавита можно отнести только к дискретным сообщениям.

1)Понятие «информация», сообщение, данные, сигнал

Сообщения. В теории коммуникации сообщение– это предназначенные для передачи высказывание, текст, изображение, физический предмет или поступок. Сообщения состоят из словесных или невербальных сигналов. Одиночный сигнал не может содержать много информации, поэтому для передачи информации используется ряд следующих друг за другом сигналов. Последовательность сигналов и называется сообщением. Таким образом, от источника к приемнику информация передается в виде сообщений. Сообщение выступает в качестве материальной оболочки для представления информации при передаче. Следовательно, сообщение служит переносчиком информации, а информация является содержанием сообщения. Соответствие между сообщением и содержащейся в нем информацией называется правилом интерпретации сообщения.

Существуют понятия непрерывного (аналогового), дискретного, квантованного и цифрового сообщений. Инф-ия данным качеством не обладает, т.к. она нематериальна, хотя одна и та же инф-ия может быть представлена посредством различных сообщений. В информатике иногда используются сочетания инф-ии, представленной посредством непрерывных сигналов, и инф-ии, представленной посредством дискретных сигналов. При формировании сообщения наряду с сигналом используются и такие понятия, как знак, буква и символ.

Знак– это элемент некоторого конечного множества отличных друг от друга сущностей (жест, рисунок, буква, сигнал светофора, звук). Все множество знаков, используемых для представления дискретной инф-ции, назыв. набором знаков (дискретное множество знаков). Набор знаков, в кот. установлен порядок их следования, назыв. алфавитом.Алфавит – это упорядоченная совокупность знаков. Порядок следования знаков в алфавите назыв. лексикографическим  и представляет возможность устанавливать отношения больше-меньше (Г<Д). Знаки, используемые для обозначения фонем человеческого языка, назыв. буквами, а их совокупность – алфавитом языка.Символ– приписанное содержание знаку или букве (напряжение в физике принято обозначать буквой U). Таким образом, понятия «знак», «буква» и «символ» нельзя считать тождественными. Представляется важным еще раз подчеркнуть, что понятия знака и алфавита можно отнести только к дискретным сообщениям. Сигнал. Сигнал – физический процесс или явления, несущий сообщение о каком-либо событии, состоянии объекта либо передающий команды управления. Таким образом, изменение характеристики носителя, кот. используется для представления инф-ии, назыв. сигналом, а значение этой характеристики, отнесенное к некоторой шкале измерений, — параметром сигнала. Например, процессы для передачи инф-ции – волны, параметры сигнала – частота, амплитуда и фаза волны. Различают аналоговые, дискретные, квантовые и цифровые сигналы, кот. могут быть синхронными и асинхронными. Аналоговый (непрерывный). Это сигнал, величина кот. непрерывно изменяется во времени. Он обеспечивает передачу данных путем непрерывного изменения во времени амплитуды, частоты либо фазы. Особенные св-ва: отсутствие избыточности. Аналоговые сигналы используются для представления каких-либо непрерывно изменяющихся физических величин (сигнал с микрофона несет инф-ию о быстрых изменениях давления в звуковой волне). Аналоговые сигналы описываются некоторой математической функцией времени. Например, для гармонического сигнала: Дискретный. Процесс перевод аналогового сигнала в дискретный назыв. дискретизацией, а процесс обратный этому – восстановлением. Непрерывный аналоговый сигнал заменяется здесь последовательностью коротких импульсов-отсчетов, величина кот. = значению сигнала в данный момент времени. Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени.

Данные. Это сведения, полученные путем измерения, наблюдения, логических и арифметических операций и представленные в форме, пригодной для постоянного хранения, передачи и обработки. В процессах сбора, обработки и использования данные расчленяются на отдельные элементарные составляющие – элементы данных. Они могут быть выражены целыми и вещественными числами, словами и булевыми величинами, способными принимать 2 значения: «истина» (1) и «ложь» (0). Экономические данные можно подразделить на: условно постоянные (расценки, нормативы, сведения о производительности оборудования; условно постоянными назыв. т.к. время от времени обновляются; хранятся в массивах картотек или вводятся в память машины) и переменные (сведения о выработке рабочих, о сдаче деталей и продукции, о запасах на складе; после расчета, как правило, изымаются из памяти компьютера). Данные хранятся в базах данных.База данных– совокупность хранимых в памяти компьютера данных, относящихся к определенному объему или кругу дея-ти, специально организованных, обновляемых и логически связанных между собой. Они представляют собой своеобразную информационную модель объекта. Система управления БД – комплекс программных и лингвистических средств общего или специального назначения, реализующий поддержку создания БД, централизованного управления и организации доступа к ним различных пользователей в условиях принятой технологии обработки данных. Она характеризуется используемой моделью, средствами администрирования и разработки прикладных процессов и обеспечивает описание и сжатие данных; манипулирование данными; физическое размещение и сортировка записей; защиту от сбоев, поддержку целостности данных и их восстановление; работу с транзакциями и файлами; безопасность данных. СУБД определяет модель представления данных. Для того, чтобы быть воспринятыми и стать информацией, данные проходят тройной фильтр: физический (ограничения по пропускной способности канала), семантический и прагматический, где оценивается полезность данных. Данные – величина, число или отношение, вводимые в процесс обработки или выводимые из него. Обработка данных – приведение их к такому виду, кот. наиболее удобен для получения их них инф-ии, знания.

Информация. Информация является одной из исходных категорий мироздания, и следовательно, определение «инф-ии вообще» невозможно свести к каким-то простым, исходным терминам. Раньше под инф-ей понимали учение, наставление. Современное понятие инф-ии: — сведения, сообщения о чем-либо, кот. обмениваются люди; — сигналы, импульсы, образы, циркулирующие в технических устройствах; — отражение разнообразия в любых объектах и процессах неживой и живой природы. При методологическом подходе инф-ия рассматривается как абстрактная фикция. Такой подход используется при создании и развитии математической теории инф-ии.

Дискретные сигналы реферат по информатике

Дискретные сигналы А. Т. Бизин Сибирская Государственная Академия телекоммуникаций и информатики Новосибирск 1998 г. Дискретизация непрерывных сигналов Обработка сигналов на цифровых ЭВМ начинается с замены непрерывного сигнала X(t) на дискретную последовательность, для которой применяются такие обозначения x(nT) , x(n) , xn , {x0 ; x1 ; x2 ; … } . Дискретизация осуществляется электронным ключом (ЭК) через равные интервалы времени T (Рис. 1.1). Дискретная последовательность аппроксимирует исходный сигнал X(t) в виде решетчатой функции X(nT). Частота переключения электронного ключа fд и шаг дискретизации T связаны формулой fд = 1 / T . (1.1) Дискретная последовательность или дискретный сигнал выражается через исходный непрерывный (аналоговый) сигнал следующим образом x(nT) = x(t)(t — nT) , (1.2) где (t) — дискретная — функция (Рис. 1.2, а), (t — nT) — последовательность — функций (Рис. 1.2, б). Погрешность, возникающую при замене аналогового сигнала дискретным сигналом, удобно оценить сравнивая спектры этих сигналов. Связь спектров дискретного и непрерывного сигналов. Исходное выражение для спектра дискретного сигнала с учетом (1.2) запишется следующим образом X(j) =x(nT) e-jt dt =x(t)(t — nT) e-jt dt . Периодическую последовательность — функций здесь можно разложить в ряд Фурье (t — nT) =, где с учетом формулы связи спектров периодического и непериодического сигналов , поскольку F(j) = 1 После замены в исходном выражении периодической последовательности — функций ее разложением в ряд Фурье получим X(j) =x(t)() e-jt dt =x(t)e-jt dt . Учитывая здесь теорему смещения спектров, т.е. : если f(t) F(j), то f(t) F[j( 0)] , последнее равенство можно представить в виде формулы, выражающей связь спектров дискретного X(j) и аналогового Xa(j) сигналов X(j) =Xa[j( -)] . (1.3) На основании формулы (1.3) с учетом поясняющих рисунков 1.3, а, б можно сделать следующие выводы : Спектр дискретного сигнала состоит из суммы спектров исходного непрерывного сигнала, сдвинутых друг относительно друга по оси частот на величину равную частоте дискретизации д Спектры аналогового и дискретного сигналов совпадают в диапазоне частот [-0,5д ; 0,5д], если удовлетворяется неравенство в 0,5д , (1.4) где в — верхняя частота спектра аналогового сигнала. Равенство в (1.4) соответствует утверждению теоремы Котельникова о минимальной частоте д. Смежные спектры Xa(j) в (1.3) частично перекрываются, если условие (1.4) не выполняется (Рис 1.3, б). В этом случае спектр дискретного сигнала искажается по отношению к спектру аналогового сигнала. Эти искажения являются неустранимыми и называются ошибками наложения. Аналоговый сигнал можно восстановить полностью по дискретному сигналу с помощью ФНЧ, частота среза которого с = 0,5д. Это утверждение основано но совпадении спектров дискретного сигнала на выходе ФНЧ и непрерывного сигнала. Сигнал восстанавливается без искажений, если выполняется условие (1.4). в противном случае сигнал восстанавливается с искажениями, обусловленными ошибками наложения. Выбор частоты дискретизации осуществляется в соответствии с (1.4). если частота в не известна, то выбор из д определяется расчетом по формуле (1.1), в которой интервал T выбирается приближенно с таким расчетом, чтобы аналоговый сигнал восстанавливался без заметных искажений плавным соединением отсчетов дискретного сигнала. Преобразование Фурье и Лапласа для дискретных сигналов. Для дискретных сигналов формулы Фурье и Лапласа представляется возможным упростить. Действительно, поскольку то после перехода к дискретной переменной пара преобразований Фурье принимает вид Здесь применяются формулы одностороннего преобразования Фурье, так как начало отсчета совмещается с началом действия дискретного сигнала. Формулы Фурье для дискретных сигналов применяются в нормированном виде, поэтому после замены X(nT) X(nT) / T преобразование Фурье принимает окончательный вид (1.5) Формулы Лапласа для дискретных сигналов получаются на основании (1.5) после обобщения частоты на всю плоскость комплексного переменного, то есть j P = + j (1.6) Z — преобразование. Эффективность частотного анализа дискретных сигналов существенно возрастает, если заменить преобразование Лапласа Z — преобразованием. В этом случае изображение сигнала X(p), которое представляет собой трансцендентную функцию переменной P = + j, заменяется Z — изображением сигнала X(Z), которое является рациональной функцией переменной Z = x x(nT) =X(jk1) — обратное ДПФ (1.10) Сигнал с ограниченным спектром имеет, строго говоря, бесконечную протяженность во времени и, соответственно бесконечное число отсчетов и непрерывный спектр. Спектр останется непрерывным, если число отсчетов сигнала ограничить конечным числом N. Формулы (1.10) в этом случае будут выражать связь между N отсчетами дискретного сигнала и N отсчетами его непрерывного спектра, который можно полностью восстановить по его отсчетам. Пример. Определить отсчеты спектра сигнала на Рис. 1.5, а. Здесь N = 2 поэтому X(jk1) =x(nT) e-jkn следовательно X(j01) =x(nT)e-j0 = x(0T) + x(1T) = a + b X(j11) =x(nT)e-jn = x(0T) e-j0 + x(1T) e-j = a — b график отсчетов спектра приведен на Рис. 1.5, б, где 1 = д/N = 0,5д. Сигнал с конечным числом отсчетов N имеет спектр, который повторяет с конечной погрешностью спектр сигнала с бесконечным числом отсчетов : спектры совпадают на отсчетных частотах k1 и отличаются на других частотах. Отличие спектров тем меньше, чем больше N. В самом деле, реальные сигналы обладают конечной энергией и, следовательно, начиная с некоторого номера отсчета остальными номерами можно пренебречь ввиду их малости, что не окажет заметного влияния на спектр сигнала. Пример. Осуществить дискретизацию экспоненциального импульса X(t) = Ae-t = 1 e-10t и сравнить спектры исходного и дискретного сигналов. Решение. График сигнала X(t) представлен на Рис. 1.8 Пусть T = 0,02с. В этом случае плавным соединением отсчетов сигнала (штриховая линия на Рис. 1.8) сигнал восстанавливается удовлетворительно хотя заметны искажения в окрестности точки t = 0, поэтому ошибки наложения будут некоторым образом влиять на спектральные характеристики. Пусть tu = 0,4с. В этом случае N = tu/T = 20. Расчет спектра по формуле прямого ДПФ в точке = 0 (k = 0) запишется так X(j01) = 1,0 + 0,8187 + 0,6703 + 05488 + 0,4493 + 0,368 + 0,3012 + 0,2466 + 0,2019 + 0,1653 + 0,1353 + 0,1108 + 0,09072 + 0,07427 + 0,06081 + 0,04979 + 0,04076 + 0,03337 + 0,02732 + 0,02237 = 5,41 Истинное значение спектра в точке = 0 можно определить зная спектр аналогового экспоненциального импульса Xa(j) = , следовательно Xa(j0) = = 0,1. чтобы сравнить спектры дискретного и непрерывного сигналов, дискретный спектр необходимо денормировать умножением на T, так как формулы Фурье для дискретных сигналов применяются в нормированном виде. Поэтому X(jo1) = 5,41 T = 5,420,02 = 0,1082. Таким образом совпадение спектров Xa(j) и X(j) в точке = 0 вполне удовлетворительное. Некоторая неточность объясняется влиянием ошибок наложения. Уместно заметить, что выбор шага дискретизации достаточно контролировать в точках максимальной крутизны исходной функции X(t). В рассмотренном примере такой точкой является момент времени t = 0. В заключение отметим, что формулы ДПФ упрощают расчетные процедуры по взаимному преобразованию сигналов и их спектров, что особенно важно для технических систем, функционирующих В реальном масштабе времени. В этих случаях применяется алгоритм быстрого преобразования Фурье (БПФ), основанный на формулах ДПФ. Ускоренная процедура расчетов по алгоритму БПФ достигается за счет исключения повторных арифметических операций, характерных для расчетов по формулам ДПФ.

Презентация к уроку информатики в 7 классе «Информация и ее свойства» (УМК Босова Л.Л. и др. 5-9 кл.)

ИНФОРМАЦИЯ И ЕЁ СВОЙСТВА

ИНФОРМАЦИЯ И ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ

КЛЮЧЕВЫЕ СЛОВА

• ИНФОРМАЦИЯ
• СИГНАЛ
• НЕПРЕРЫВНЫЙ СИГНАЛ
• ДИСКРЕТНЫЙ СИГНАЛ
• ВИДЫ ИНФОРМАЦИИ
• СВОЙСТВА ИНФОРМАЦИИ

Информация и сигнал

Информация для человека — это содержание сигналов (сообщения), воспринимаемых человеком непосредственно или с помощью специальных устройств, расширяющее его знания об окружающем мире и протекающих в нём процессах.

В обыденной жизни под информацией понимают сообщения, сведения о чём-либо, которые получают и передают люди.

в показаниях часов и других приборов

Информация содержится

в текстах книг

в речи людей

в звуках и видах природы

Каждый материальный объект, с которым происходят изменения, становится источником информации. Эту информацию мы получаем в виде сигналов.

Различают сигналы

световые

звуковые

тепловые

механические

электрические

Непрерывный сигнал принимает бесконечное множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.

Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.

Речь человека

Виды информации

По способу восприятия человеком информация может быть разделена на следующие виды:

визуальная

аудиальная

обонятельная

тактильная

вкусовая

Полнота

Актуальность

Понятность

Свойства информации

Полезность

Достоверность

Объективность

Самое главное

Информация для человека — это содержание сигналов (сообщения), которые он получает из различных источников.

Сигналы могут быть:

• непрерывными — они принимают бесконечное множество значений из некоторого диапазона;
• дискретными – они принимают конечное число значений, которые можно пронумеровать.

По способу восприятия человеком выделяют визуальную, аудиальную, обонятельную, вкусовую, тактильную информацию .

Объективность, достоверность, полноту, актуальность, полезность и понятность называют свойствами информации .

Одна и та же информация может обладать разными свойствами для разных людей.

Вопросы и задания

Выберите правильный ответ.

е) Об устройстве двигателя каждый водитель автомобиля:

1) должен обладать полной информацией;

2) может иметь неполную информацию.

Выберите правильный ответ.

г) Информация о том, как с помощью подручных средств добыть огонь, будет для вас наиболее полезной:

1) если вы попадёте на необитаемый остров;

2) в нашей повседневной жизни.

Что такое информация для человека? Перечислите источники, из которых вы получаете информацию.

Выберите правильный ответ.

в) Слухи, вымыслы, непроверенные гипотезы — это:

1) достоверная информация;

2) недостоверная информация.

Выберите правильный ответ.

д) О правилах дорожного движения каждый водитель автомобиля:

1) должен обладать полной информацией;

2) может иметь неполную информацию.

Приведите примеры непрерывных и дискретных сигналов.

Перечислите основные виды информации по способу её восприятия человеком.

Выберите правильный ответ.

a) Если вы собираетесь провести выходной день на природе, то своевременной информацией для вас будет:

1) сведения о погоде в такой же день прошлого года;

2) прогноз погоды на выходной день

Выберите правильный ответ.

б) Волга впадает в Каспийское море — это:

1) достоверная информация;

2) недостоверная информация.

Задания

Укажите тип сигнала (дискретный или непрерывный), соответствующий графическим изображениям

F

F

t

t

Задание

Установите соответствие между свойствами информации и их описаниями

Информация выражена на языке,

доступном для получателя

Объективность

Информация позволяет получателю

решать стоящие перед ним задачи

Достоверность

Информация важна, существенна

в настоящий момент времени

Актуальность

Информация достаточна для

понимания ситуации

и принятия решения

Полезность

Понятность

Информация отражает истинное

положение дел

Полнота

Информация не зависит от чьего

либо мнения

Опорный конспект

Информация для человека — это содержание сигналов

(сообщения), которые он получает из различных источников

Дискретные

Виды

информации

Сигналы

Непрерывные

Визуальная

Объективность

Вкусовая

Полнота

Тактильная

Понятность

Свойства

информации

Аудиальная

Актуальность

Обонятельная

Достоверность

Полезность

Информатика и ИКТ ИНФОРМАЦИЯ И ЕЁ СВОЙСТВА

Информатика и ИКТ ИНФОРМАЦИЯ И ЕЁ СВОЙСТВА ИНФОРМАЦИЯ И ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ

Ключевые слова • информация • сигнал • непрерывный сигнал • дискретный сигнал • виды информации • свойства информации

Информация и сигнал Информация для человека — это содержание сигналов (сообщения), воспринимаемых человеком непосредственно или с помощью специальных устройств, расширяющее его знания об окружающем мире и протекающих в нём процессах. В обыденной жизни под информацией понимают сообщения, сведения о чём-либо, которые получают и передают люди.

Информация содержится в текстах и видах природы речи людейчасов и других показаниях звуках книг приборов

Каждый материальный объект, с которым происходят изменения, становится источником информации. Эту информацию мы получаем в виде сигналов. Различают сигналы световые тепловые звуковые электрические механические

Непрерывный сигнал принимает бесконечное Дискретный сигнал принимает конечное число значений. Все значения некоторого диапазона. множество значений из дискретного сигнала можно пронумеровать целыми числами. принимает, нет Между значениями, которые он разрывов. Речь человека

Виды информации По способу восприятия человеком информация может быть разделена на следующие виды: визуальная аудиальная обонятельная тактильная вкусовая

Полнота Актуальность Понятность Свойства информации Достоверность Полезность Объективность

Самое главное Информация для человека — это содержание сигналов (сообщения), которые он получает из различных источников. Сигналы могут быть: • непрерывными — они принимают бесконечное множество значений из некоторого диапазона; • дискретными – они принимают конечное число значений, которые можно пронумеровать. По способу восприятия человеком выделяют визуальную, аудиальную, обонятельную, вкусовую, тактильную информацию. Объективность, достоверность, полноту, актуальность, полезность и понятность называют свойствами информации. Одна и та же информация может обладать разными свойствами для разных людей.

Вопросы и задания Выберите правильный ответ. Что такое информация виды человека? Перечислите Выберите правильный для информации по Приведите правильный ответ. Выберите примеры непрерывных и Перечислите основные ответ. источники, изсигналов. выкак с помощьюгипотезы — е) Информация о том, получаете информацию. которых в) Обеё вы собираетесь провести выходной устройстве двигателя каждый водитель г) Слухи, вымыслы, непроверенные каждый способу. О правилах дорожного движения подручных дискретныхвосприятия человеком. д) Если впадает в Каспийское море — это: a) Волга б) автомобиля: средств добыть огонь, будет для вас наиболее это: водитель автомобиля: деньдостоверная информация; на природе, то своевременной информацией 1) должен полезной: обладать полной информацией; 1) достоверная информация; 1) должен обладать полной информацией; для вас будет: 2) недостоверная информация. 1) если вы попадёте на необитаемый остров; 2) может иметь неполную информацию. 2) недостоверная информация. день прошлого 1) может иметь неполную информацию. сведения о погоде в такой же 2) в нашей повседневной жизни. года; 2) прогноз погоды на выходной день

Задания Укажите тип сигнала (дискретный или непрерывный), соответствующий графическим изображениям F t РТ № 3 (стр. 5)

Задание Установите соответствие между свойствами информации и их описаниями Информация выражена на языке, Объективность доступном для получателя Информация позволяет получателю Достоверность решать стоящие перед ним задачи Информация важна, существенна Актуальность в настоящий момент времени Информация достаточна для Полезность понимания ситуации и принятия решения Понятность Информация отражает истинное положение дел Полнота Информация не зависит от чьего либо мнения РТ № 5 (стр. 6)

Опорный конспект Информация для человека — это содержание сигналов (сообщения), которые он получает из различных источников Дискретные Сигналы Виды информации Непрерывные Визуальная Объективность Вкусовая Полнота Тактильная Понятность Свойства Аудиальная информации Актуальность Обонятельная Достоверность Полезность

Домашнее задание § 1. 1 (стр. 7 -11) РТ № 1, 2, 4, 6 (стр. 3)

Презентация по теме «Информация и ее свойства» | Презентация к уроку по информатике и икт (7 класс):

Слайд 1

Информация и её свойства 7 класс Автор: учитель Информатики и ИКТ Шебанов Я.О.

Слайд 2

Понятие информации Информация – сведения об окружающем нас мире, являющиеся объектом преобразования информации, используемые для создания объективного представления о происходящем вокруг

Слайд 3

Виды информации Визуальная Аудиальная Тактильная Обонятельная Вкусовая

Слайд 4

Источники информации Речь людей Показания приборов Звуки и виды окружающего мира Тексты книг

Слайд 5

Понятие информации в информатике Информация — это содержание сигналов , воспринимаемых человеком непосредственно через органы чувств, или с помощью специальных устройств, расширяющее его знания об окружающем мире и протекающих в нём процессах .

Слайд 6

Виды сигналов Световые Звуковые Тепловые Механические Электрические

Слайд 7

Типы сигналов Непрерывные Дискретные Непрерывный сигнал – принимает бесконечное множество значений из некоторого диапазона. Пример – человеческая речь. Дискретный сигнал – принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами. Пример – светофор.

Слайд 8

Свойства информации Полнота Достоверность Понятность Объективность Полезность Актуальность

Слайд 9

Задания для рефлексии

Слайд 10

Задание 1. Найдите нужный тип сигнала Пример дискретного сигнала: 1) сигнал светофора 2) звучание музыки 3) пение птиц 4) вспышка молнии Пример непрерывного сигнала: 1) азбука Морзе 2) звучание музыки 3) сигналы светофора 4) звук метронома

Слайд 11

Задание 2. Ответьте на вопросы. 1. Наибольший объем информации человек получает при помощи: органов слуха органов зрения органов обоняния органов осязания 2 . По способу восприятия информация о запахах явля­ется: вкусовой обонятельной тактильной аудиальной 3. По способу восприятия информация о форме предмета может быть: вкусовой обонятельной слуховой зрительной

Слайд 12

Задание 3. Установите соответствие между свойствами информации и их описаниями Объективность Достоверность Актуальность Полезность Понятность Полнота Информация выражена на языке, доступном для получателя Информация позволяет получателю решать стоящие перед ним задачи Информация важна, существенна в настоящий момент времени Информация достаточна для понимания ситуации и принятия решения Информация отражает истинное положение дел Информация не зависит от чьего либо мнения

Слайд 13

Спасибо за внимание!

Дискретные и непрерывные системы — Oxford Reference

Системы, с помощью которых сигналы записываются, передаются или отображаются, могут представлять данные в дискретной форме (например, как целые числа) или в непрерывной форме (как «действительные» числа). Важная классификация является результатом выбора дискретного или непрерывного представления амплитуды, а также дискретного или непрерывного представления времени, в которое возникла амплитуда. Аналоговые компьютеры используют физические величины, которые являются приближениями к непрерывным представлениям.Цифровые компьютеры требуют дискретных представлений как времени, так и амплитуды.

Вопрос о том, является ли сигнал (или его источник) внутренне дискретным или внутренне непрерывным, неразрешим: любой эксперимент для определения этого потребовал бы бесконечной полосы пропускания (или бесконечного времени) и бесконечного отношения сигнал / шум, и поэтому был бы невозможен. на практике. Все, что находится под вопросом, — удобнее, полезнее или привлекательнее дискретное или непрерывное представление.

Сигналы, которые интуитивно кажутся непрерывными по времени или с непрерывной амплитудой, но для которых предпочтительно дискретное время или дискретно-амплитудное представление, называются квантованными по времени или квантованными по амплитуде . Временное квантование либо адекватно, либо неадекватно согласно критерию Найквиста. Квантованные по времени сигналы называются дискретизированными , а системы, которые их обрабатывают, называются системами дискретных данных. Квантование по амплитуде ухудшает отношение сигнал / шум, эффект, который можно описать как введение шума квантования.

Время и амплитуда должны быть квантованы для обработки цифровыми компьютерами (или другими цифровыми устройствами), которые работают с конечными скоростями с конечными объемами данных с конечной точностью. Те же физические ограничения действуют, хотя и по-другому, чтобы ограничить степень, в которой аналоговые компьютеры (или другие аналоговые устройства) могут приближаться к непрерывному представлению сигналов.

См. Также квантование.

EECS 4380 — Программа курса цифровой обработки сигналов

EECS 4380 — Программа курса по цифровой обработке сигналов

Кредиты / Контактные часы
3 кредитных часа и два 75-минутных контактных часа лекций в неделю.
Имя преподавателя
Д-р Эззатолла Салари
Учебник
Цифровая обработка сигналов Джона Проакиса и Д. Г. Манолакиса, 4 / E. Pearson, 2006.
Информация о курсе
Дискретное преобразование Фурье (ДПФ), дискретная свертка и корреляция, быстрое преобразование Фурье Преобразование (БПФ) и его приложения, разработка цифровых фильтров БИХ и КИХ, многоскоростной / канал цифровые системы, прореживание и интерполяция.
Предварительное условие: EECS 3210
Элективный курс
Конкретные цели — учебные цели учащихся (SLO)
Учащийся сможет:
1.Продемонстрировать понимание основных систем с дискретным временем, линейности, временной инвариантности, стабильность, импульсная характеристика и дискретная свертка.
2. Реализуйте системы с дискретным временем, рекурсивные и нерекурсивные реализации.
3. Выполните Z-преобразование и найдите обратное Z-преобразование, включая его свойства.
4. Продемонстрировать понимание частотного анализа как непрерывных, так и дискретных сигналы.
5. Продемонстрировать понимание частотной характеристики линейных систем, не зависящих от времени.
6. Продемонстрируйте понимание дискретного преобразования Фурье, его свойств и Приложения.
7. Разработайте цифровые фильтры КИХ и БИХ.
8. Продемонстрируйте понимание многоскоростной обработки сигналов.
Темы
1. Дискретные сигналы времени.
2. Дискретная свертка и корреляция. 3. Z-преобразование.
4. Ряды Фурье, преобразование Фурье.
5. Амплитудно-частотная характеристика систем LTI.
6. Выборка и реконструкция сигналов. 7. Дискретное и быстрое преобразование Фурье.
8. Проектирование цифровых фильтров КИХ и БИХ.
9. Многоскоростная обработка сигналов.

Цифровая обработка сигналов | Департамент компьютерных наук и технологий

Этот модуль может вместить до 24 студентов, включая студентов, участвующих как в Части II, так и в студентах MPhil / Part III

Цели

Этот курс обучает основным принципам обработки сигналов, необходимых для понимания многих современных высокотехнологичных систем, с примерами приложений, ориентированными на обработку звука, кодирование изображений, системы связи и программно-определяемую радиосвязь.Студенты получат практический опыт численных экспериментов по программированию заданий (в MATLAB, NumPy или Julia).

Лекций

• Сигналы и системы. Дискретные последовательности и системы: типы и свойства. Амплитуда, фаза, частота, модуляция, децибелы, среднеквадратичное значение. Линейные инвариантные во времени системы, свертка. Некоторые примеры из электроники, оптики и акустики.
• Фазоры. Собственные функции линейных систем, не зависящих от времени.Обзор сложной арифметики. Фазоры как ортогональные базовые функции.
• преобразование Фурье. Формы и свойства преобразования Фурье. Теорема свертки. Rect и sinc.
• Дельта-функция Дирака. Фурье-представление синусоидальных волн, импульсных гребенок во временной и частотной области. Амплитудная модуляция в частотной области.
• Дискретные последовательности и спектры. Выборка непрерывных сигналов, периодических сигналов, наложение спектров, интерполяция, выборка и реконструкция, преобразование частоты дискретизации, передискретизация, спектральная инверсия.
• Дискретное преобразование Фурье. Непрерывный по сравнению с дискретное преобразование Фурье, симметрия, линейность, БПФ, БПФ с действительным знаком, свертка на основе БПФ, заполнение нулями, повторная выборка на основе БПФ, упражнение по деконволюции.
• Спектральная оценка. Кратковременное преобразование Фурье, явления утечки и волнистости, управление окнами, заполнение нулями. Примеры аудио и голоса. Упражнение DTFM.
• Фильтры конечной импульсной характеристики. Свойства фильтров, формы реализации, оконный дизайн КИХ, использование инверсии частоты для получения фильтров верхних частот, использование модуляции для получения полосовых фильтров.
• Фильтры с бесконечной импульсной характеристикой. Последовательности как полиномы, z -преобразование, нули и полюсы, некоторые методы аналогового БИХ-проектирования (Баттерворта, Чебышева I / II, эллиптические фильтры, каскадная форма второго порядка).
• Полосовые сигналы. Полосовая выборка и реконструкция, повышающее и понижающее преобразование IQ, супергетеродинные приемники, программно-определяемые интерфейсы радио, представление IQ сигналов AM и FM и их демодуляция.
• Цифровая связь. Импульсно-амплитудная модуляция. Детектор согласованного фильтра. Формы импульсов, межсимвольная интерференция, эквализация. IQ-представление сигналов ASK, BSK, PSK, QAM и FSK. [2 часа]
• Случайные последовательности и шум. Случайные переменные, стационарные и эргодические процессы, автокорреляция, взаимная корреляция, детерминированные последовательности взаимной корреляции, фильтрованные случайные последовательности, белый шум, периодическое усреднение.
• Корреляционное кодирование. Энтропия, дельта-кодирование, линейное предсказание, зависимость от корреляции , случайные векторы, ковариация, декорреляция, диагонализация матрицы, собственное разложение, преобразование Карунена-Лоэва, анализ главных компонент.Отношение к кодированию с ортогональным преобразованием с использованием фиксированных базисных векторов, таких как DCT.
• Сжатие с потерями и сжатие без потерь. Какая информация отбрасывается человеческими чувствами и может быть удалена кодировщиками? Шкалы восприятия, маскировка звука, пространственное разрешение, цветовые координаты, некоторые демонстрационные эксперименты.
• Квантование, стандарты кодирования изображений. Равномерное и логарифмическое квантование, кодирование по закону A / µ, сглаживание, JPEG.

Цели

• применять основные свойства неизменных во времени линейных систем;
• разбирается в дискретизации, наложении спектров, свертке, фильтрации, подводных камнях спектральной оценки;
• объясняет вышесказанное в представлениях во временной и частотной областях;
• использовать программное обеспечение для проектирования фильтров;
• визуализировать и обсуждать цифровые фильтры в области z ;
• использовать БПФ для свертки, деконволюции, фильтрации;
• реализует, применяет и оценивает простые приложения DSP;
• знакомство с рядом концепций обработки сигналов, используемых в цифровых системах связи

Рекомендуемая литература

Лион, Р.Г. (2010). Понимание цифровой обработки сигналов. Prentice Hall (3-е изд.).
Оппенгейм, А.В. и Шафер, Р.В. (2007). Цифровая обработка сигналов в дискретном времени. Prentice Hall (3-е изд.).
Stein, J. (2000). Цифровая обработка сигналов — перспектива информатики. Wiley.

Практические занятия

Все практические компоненты представляют собой упражнения по программированию. Если студенты не могут приехать в Кембридж из-за ограничений COVID-19, студентам потребуется собственный ПК / ноутбук с подключением к Интернету, способный загрузить несколько гигабайт образцов данных с www.cl.cam.ac.uk

Оценка

• Контрольная работа по части 1, составляющая 20% от общей оценки.
• Три домашних задания по программированию, каждое из которых составляет 10% от оценки.
• Индивидуальный проект внедрения с письменным отчетом на 8 страницах, тема согласована с преподавателем, составляет 50% оценки.

Дополнительная информация

Из-за COVID-19 метод обучения для этого модуля будет скорректирован с учетом физического дистанцирования и студентов, которые работают удаленно.Как именно будет преподавать модуль, мы уточним ближе к началу семестра.

Этот курс недоступен для бывших студентов бакалавриата Кембриджа, часть II (50%), которые, возможно, уже прошли курс для вопроса Paper 7 DSP в этом году, или бывших студентов части II (75%), которые прошли этот модуль в этом году. .

Односкоростные сигналы и системы с дискретным временем: общий обзор: компьютерные науки и ИТ Глава

Эта глава представляет собой краткий обзор представлений односкоростных сигналов и систем с дискретным временем во временной области и в области преобразования.Сначала мы рассмотрим представление дискретных сигналов и систем во временной области. Представление в области преобразования включает в себя дискретное преобразование Фурье (DTFT), дискретное преобразование Фурье (DFT) и преобразование z . Кратко описаны основные структуры реализации для систем FIR и IIR. Наконец, приведены соотношения между непрерывными и дискретными сигналами.

ДИСКРЕТНЫЕ ВРЕМЕННЫЕ СИГНАЛЫ

Сигнал является функцией по крайней мере одной независимой переменной.В этой книге мы предполагаем, что независимой переменной является время, даже в тех случаях, когда независимой переменной является величина, отличная от времени.

Мы определяем непрерывный сигнал , x _c ( t ) как сигнал, который существует в каждый момент времени t . Непрерывный сигнал с непрерывной амплитудой также называется аналоговым сигналом . Независимая переменная t является непрерывной переменной, а x _c ( t ) может принимать любое значение в непрерывном диапазоне чисел.

Сигнал дискретного времени представляет собой последовательность чисел, обозначенную как { x [ n ]}, где n называется временным индексом , а x [ n ] обозначает значение элемента n ^-й в последовательности. Сигнал с дискретным временем называется дискретным сигналом . Величина x [ n ] также называется значением выборки , а ее временной индекс n называется индексом выборки .Величина x [ n ] может принимать любое значение в некотором непрерывном диапазоне чисел, x _мин. ≤ x [ n ] ≤ x _max .

Дискретные сигналы могут быть определены только для целых значений n из интервала N ₁ ≤ n ≤ N ₂ . Когда значения выборок последовательности { x [ n ]} представлены как двоичные числа с использованием конечного числа битов, сигнал { x [ n ]} представляет собой цифровой сигнал .

Длина последовательности определяется как N ≤ N ₂ — N ₁ + 1. Последовательность { x [ n ]} представляет собой последовательность конечной длины если N имеет конечную длину; в противном случае { x [ n ]} представляет собой последовательность бесконечной длины .

Для целей анализа полезно представить сигналы как комбинацию основных последовательностей. Часто используемые базовые последовательности включены в Таблицу 1.

Таблица 1.

Во многих приложениях сигнал дискретного времени { x [ n ]} генерируется путем дискретизации сигнала непрерывного времени x _c ( t ) через одинаковые интервалы времени. :

. (1)

Временной интервал T называется интервалом выборки или периодом выборки , а обратное значение

(2) представляет собой частоту выборки или частоту выборки .Обычно единицей измерения частоты дискретизации является количество циклов в секунду, и когда T задается в секундах [с], F _T может быть выражено в герцах [Гц].

Понятие частоты в непрерывном и дискретном времени — Цифровая обработка сигналов, Инженерия Компьютерные науки Инженерия (CSE) Примечания

Понятие частоты в непрерывном и дискретном времени.

1) x _a (t) = A Cos (Ом t)

x (нТс) = A Cos (Ом нТс)

= A Cos (wn)

w = Ω Ts

Ω = рад / сек w = рад / выборка

F = циклов / сек f = циклов / выборка

2) Дискретное время — синусоида периодична только в том случае, если ее f является рациональным числом.

x (n + N) = x (n)

Cos 2π f ₀ (n + N) = Cos 2 π f ₀ n

2 π f ₀ N = 2π K => f ₀ = K / N

Пример: A Cos (π / 6) n

f = 1/12 N = 12 выборок / цикл; Fs = частота дискретизации; Ts =

Период выборки

Q. Cos (0,5n) не периодический

Q. x (n) = 5 Sin (2n)

2π f = 2 => f = 1 / π Непериодический

Q. x (n) = 5 Cos (6π n)

2π f = 6π => f = 3 N = 1 для K = 3 Периодический

Q.x (n) = 5 Cos 6πn / 35

2π f = 6π / 35 => f = 3/35 для N = 35 и K = 3 Периодический

Q. x (n) = Sin (0,01π n)

2π f = 0,01π => f = 0,01 / 2 для N = 200 и K = 1 Периодический

Q. x (n) = Cos (3p n) для N = 2 Периодический

fo = GCD (f ₁ , f ₂ ) & T = LCM (T ₁ , T ₂ ) ——- Для аналогового / цифрового сигнала

[Комплексные экспоненциальные и синусоидальные последовательности не обязательно периодичны в ‘n’ с периодом (Wo 2π / ow
) и в зависимости от Wo может вообще не быть периодическим]

N = основной период периодической синусоиды.

3. Наивысшая частота колебаний в дискретной временной синусоиде достигается, когда w = π или -π

Дискретно-временные синусоидальные сигналы с частотами, разделенными целым кратным 2p, идентичны.

4. Fs / 2 ≤ F ≤ Fs / 2

-πFs ≤2p F ≤ π Fs

-π ≤ Ω Ts ≤π

Следовательно — π ≤ w≤ π

5. Увеличение частота дискретной синусоиды не обязательно уменьшает период сигнала.

x ₁ (n) = Cos (πn / 4) N = 8

x ₂ (n) = Cos (3πn) N = 16 3/8> 1/4

2 π f = 3π / 8

⇒ f = 3/16

• Если частота аналогового сигнала = F = 1 / Ts выборок / сек = Гц, то цифровая частота f = 1

W = Ω T _с

2 π f = 2π FT _с => f = 1

2π F = π / 4; 2π f = π / 4

F = 1/8; T = 8; f = 1/8 N = 8

7.Синусоиды с дискретным временем всегда периодичны по частоте.

Q. Сигнал x (t) = 2 Cos (40π t) + Sin (60π t) дискретизируется с частотой 75 Гц. Каков общий период дискретизированного сигнала x (n) и сколько полных периодов x (t) требуется, чтобы получить один период x (n)?

F ₁ = 20 Гц F ₂ = 30 Гц

f ₁ = 20/75 = 4/15 = K1 / N1 f ₂ = 30/75 = 2/5 = K2 / N2

Таким образом, общий период равен N = LCM (N ₁ , N2) = LCM (15, 5) = 15

Основная частота F _o для x (t) равна GCD (20, 30) = 10 Гц

И основной период T = 1 / F0 = 0.1 с

Поскольку N = 15

1 отсчет ———- 1/75 с

15 отсчетов ————? => 15/75 = 0,2S

∴Таким образом, требуется два полных периода x (t), чтобы получить один период x (n) или GCD (K1, K2) = GCD (4, 2) = 2

Частотная область Представление сигналов и систем с дискретным временем

Для систем LTI мы знаем, что представление входной последовательности в виде взвешенной

суммы задержанных импульсов приводит к представлению выходного сигнала в виде взвешенной суммы

задержанных ответы.

Пусть x (n) = e ^jwn

^{y (n) = h (n) * x (n)}

Пусть H — представление системы в частотной области.

∴y (n) = H (e ^jw ) e ^jwn e ^{jwn = собственная функция системы.}

H (e ^jw ) = собственное значение

Q. Найдите частотную характеристику системы порядка 1 ^st y (n) = x (n) + ay (n-1)

(a <1 )

Пусть x (n) = e ^jwn

y _p (n) = C e ^jwn

C e ^jwn = e ^jwn + a C e ^jw (n- 1)

C e ^jwn [1-ae ^-jw ] = e ^jwn

Следовательно, H (e ^jw ) =

Q.Частотная характеристика системы 2-го порядка y (n) = x (n) -1/2 y (n-2)

x (n) = e ^jwn

Цифровая обработка сигналов: перспектива информатики

ПОКАЗЫВАЕТ 1-10 ИЗ 166 ССЫЛОК

СОРТИРОВАТЬ ПО Релевантности Статьи, на которые наибольшее влияние оказали недавнее время

Интерполяция и децимация цифровых сигналов прореживание и интерполяция, а также обсуждает теоретическую модель для таких систем (основанную на теореме выборки) и способы получения различных структур для обеспечения эффективных реализаций этих систем.Разверните

Гаусс и историю быстрого преобразования Фурье

Быстрое преобразование Фурье (Fm стало хорошо известно. Как очень эффективный алгоритм для вычисления дискретного преобразования Фурье (Om последовательности из N чисел. OFT используется во многих дисциплины… Развернуть

Справочник по цифровой обработке сигналов

При параллельной обработке изображений особое внимание уделяется грамматикам изображений для представления и распознавания образов, и ее можно в основном рекомендовать лицам, занимающимся исследованиями, связанными с грамматическим представлением изображений.Развернуть

Адаптивная коррекция

• С. Куреши
• Компьютерные науки
• Протоколы IEEE
• 1985

В этом учебном документе дается обзор современного состояния технологии адаптивной коррекции и обсуждается сходимость и свойства устойчивого состояния алгоритмов адаптации методом наименьшего среднего квадрата (LMS), включая соображения цифровой точности, и три класса быстро сходящихся алгоритмов адаптивного эквалайзера. Разверните

Dsp First: мультимедийный подход

От издателя: Этот практический мультимедийный пакет представляет собой мотивирующее введение в фундаментальные концепции, в частности системы с дискретным временем, для начинающих студентов инженерных специальностей.Это… Развернуть

Линейное предсказание: обзор учебного пособия

• Дж. Махул
• Информатика
• Протоколы IEEE
• 1975

В этой статье дается описание линейного предсказания при анализе дискретных сигналов как линейных комбинация его прошлых значений и настоящих и прошлых значений гипотетического входа в систему, выходом которой является данный сигнал. Expand

CS249 Цифровая связь и обработка сигналов

Вводное описание

Цель модуля — познакомить студентов с принципами и практикой цифровых коммуникаций — от фундаментальных основ коммуникации до того, как сигналы представлены и обрабатываются.
Этот модуль доступен только студентам второго года обучения и не является необычным вариантом для студентов других лет обучения.

Модуль направлен на

Цель модуля — познакомить студентов с принципами и практикой цифровых коммуникаций — от фундаментальных основ коммуникации до того, как сигналы представлены и обрабатываются.
Модуль развивает аналитический подход к проблемам в проектировании и эксплуатации коммуникаций, основанный на элементах теории коммуникации, достаточных для того, чтобы дать студентам понимание проблем, которые влияют на его надежность и эффективность.
Он знакомит с теорией и реализацией подходов к цифровой обработке сигналов, включая представление сигналов в системах связи, методы фильтрации и приложения цифровой обработки сигналов.

План программы

Это ориентировочная схема модуля только для того, чтобы дать представление о том, какие темы могут быть охвачены. Фактические проводимые сеансы могут отличаться.

Источники информации и кодирование: теория информации, кодирование информации для эффективности и защиты от ошибок;
Передача данных: характеристики канала, методы передачи сигналов, помехи и шум, синхронизация, сжатие и шифрование данных;
Представление сигналов: представление сигналов дискретного времени по времени и частоте; z преобразование и представления Фурье; дискретная аппроксимация непрерывных сигналов; отбор проб и квантование; случайные сигналы и шумовые процессы;
Фильтрация: Анализ и синтез дискретных временных фильтров; фильтры с конечной импульсной характеристикой и бесконечной импульсной характеристикой; частотная характеристика цифровых фильтров; полюса и нули; фильтры для корреляции и обнаружения; согласованные фильтры;
Приложения для цифровой обработки сигналов: обработка речевых сигналов с использованием цифровых технологий.

Результаты обучения

К концу модуля студенты должны уметь:

• — Понять структуру процесса коммуникации.
• — Объясните основные проблемы управления в сетях связи.
• — Понимать принципы цифровой обработки сигналов и знать основные области ее применения.
• — Разработка, реализация и анализ поведения простых алгоритмов цифровой обработки сигналов.

Ориентировочный список литературы

Пожалуйста, перейдите по ссылке Talis Aspire, чтобы ознакомиться с наиболее актуальным списком игроков.

Посмотреть список чтения на Talis Aspire

Навыки в зависимости от предмета

По окончании курса студенты должны уметь:
 вычислять информационное содержание и энтропию случайной величины по ее распределению вероятностей;
 связывает энтропии переменных через их вероятности;
 строить эффективные коды для передачи данных по каналам связи;
 понять концепцию цифровых сигналов;
 понимать схемы кодирования и связи с точки зрения спектральных свойств сигналов;
 описывают схемы сжатия и эффективное кодирование с использованием преобразования Фурье и других представлений данных.

Передаваемые навыки

По окончании курса студенты должны уметь:
 использовать MatLab для работы над другими задачами, связанными с математикой
 лучше понимать сложную математику;
 Обладает базовыми знаниями для работы в других областях, таких как аудио, видео и в целом обработка больших данных;
 Приложения в других науках: геномика; нейробиология; астрофизика; классификация зашумленных сигналов; и распознавание образов, включая биометрию.

Время обучения

Тип	Требуется
Лекции	30 сеансов по 1 часу (20%)
Семинары	10 сеансов по 1 часу (7%)
Частное обучение	110 часов (73%)
Итого	150 часов

Описание частного кабинета

Есть много онлайн-материалов, полезных для нашего модуля, таких как учебники по машинному обучению, и в целом вы должны прочитать:

• https: // en.wikipedia.org/wiki/Digital_signal_processing
• Хари Кришна Гарг: Алгоритмы цифровой обработки сигналов, CRC Press, ISBN 0-8493-7178-3
• П. Гайдеки: Основы цифровой обработки сигналов: теория, алгоритмы и проектирование оборудования, институт Инженеры-электрики, ISBN 0-85296-431-5
• Ашфак Хан: Основы цифровой обработки сигналов, Charles River Media, ISBN 1-58450-281-9
• Сен М. Куо, Вун-Сенг Ган: Цифровые сигнальные процессоры: Архитектура , Реализации и приложения, Prentice Hall, ISBN 0-13-035214-4
• Пол А.Линн, Вольфганг Фюрст: вводная цифровая обработка сигналов с компьютерными приложениями, John Wiley & Sons, ISBN 0-471-97984-8
• Ричард Г. Лайонс: понимание цифровой обработки сигналов, Prentice Hall, ISBN 0-13-108989-7
• Виджей Мадисетти, Дуглас Б. Уильямс: Справочник по цифровой обработке сигналов, CRC Press, ISBN 0-8493-8572-5
• Джеймс Х. Макклеллан, Рональд В. Шафер, Марк А. Йодер: Сначала обработка сигналов, Прентис Холл, ISBN 0-13-090999-8
• Бернард Малгрю, Питер Грант, Джон Томпсон: Цифровая обработка сигналов — концепции и приложения, Палгрейв Макмиллан, ISBN 0-333-96356-3
• Боаз Порат: курс цифровой обработки сигналов, Wiley, ISBN 0-471-14961-6
• Джон Г.Проакис, Димитрис Манолакис: Цифровая обработка сигналов: принципы, алгоритмы и приложения, 4-е изд., Пирсон, апрель 2006 г., ISBN 978-0131873742
• Джон Г. Проакис: Руководство для самообучения по цифровой обработке сигналов, Прентис-Холл, ISBN 0- 13-143239-7
• Чарльз А. Шулер: Цифровая обработка сигналов: практический подход, McGraw-Hill, ISBN 0-07-829744-3
• Дуг Смит: Технология цифровой обработки сигналов: основы коммуникационной революции, Американская радиорелейная лига, ISBN 0-87259-819-5
• Смит, Стивен У.(2002). Цифровая обработка сигналов: Практическое руководство для инженеров и ученых. Newnes. ISBN 0-7506-7444-X.
• Стейн, Джонатан Яаков (2000-10-09). Цифровая обработка сигналов, перспектива компьютерных наук. Вайли. ISBN 0-471-29546-9.
• Стергиопулос, Стергиос (2000). Справочник по расширенной обработке сигналов: теория и реализация для радиолокационных, сонарных и медицинских систем реального времени. CRC Press. ISBN 0-8493-3691-0.
• Ван де Вегте, Джойс (2001). Основы цифровой обработки сигналов.Прентис Холл. ISBN 0-13-016077-6.
• Оппенгейм, Алан В .; Шафер, Рональд В. (2001). Обработка сигналов в дискретном времени. Пирсон. ISBN 1-292-02572-7.
• Хейс, Монсон Х. Статистическая цифровая обработка сигналов и моделирование. John Wiley & Sons, 2009. (со сценариями MATLAB)
• Дэвид Маккей Теория информации, логический вывод и алгоритмы обучения (в твердом переплете, 640 страниц, опубликовано в сентябре 2003 г.)
• https://www.cl.cam.ac.uk/ преподавание / 1920 / InfoTheory /
• Обложка, Т.М. и Томас, Дж. А. (2006). Элементы теории информации. Нью-Йорк: Вили.

Дополнительно студенты должны:

• Обзор конспектов лекций
• Выполнение курсовых работ
• Проверка перед экзаменом

Затраты

Никаких дополнительных затрат по этому модулю не определено.

Вам не нужно сдавать все компоненты оценки, чтобы пройти модуль.

Студенты могут зарегистрироваться на этот модуль, не сдавая никаких оценок.

Оценочная группа D2

	Вес	Время обучения
Задание по программированию (Курсовая работа)	20%
Экзамен на территории кампуса	80%
Экзамен CS249 — документ, в котором исследуется содержание курса и обеспечивается достижение результатов обучения. ~ Платформы — AEP Золотая книга ответов (24 страницы) студента могут пользоваться калькулятором

Группа оценки R1

	Вес	Время обучения
Онлайн-экзамен	100%
CS249 повторный экзамен ~ Платформы — AEP Онлайн-экзамен: ответ на вопросы не требуется студента могут пользоваться калькулятором

Отзыв об оценке

Отзывы на семинарах

Прошедшие экзаменационные работы для CS249

Курсы

Этот модуль является основным для:

• 2-й год Вычислительные системы UCSA-G400 BSc
• 2-й год Вычислительные системы MEng UCSA-G402

Этот модуль является дополнительным для:

• 2-й год UCSA-I1N1 Бакалавриат компьютерных наук с бизнес-исследованиями
• 2-й год UCSA-G406 Бакалавриат по разработке компьютерных систем
• 2-й год UCSA-G408 Бакалавриат по разработке компьютерных систем
• 2-й год UCSA-G5N1 бакалавриат компьютерных наук и управления
• 2-й год USTA-G302 Наука о данных для студентов
• 2-й год USTA-G304 Бакалавриат по науке о данных (MSci)

Этот модуль является основным списком опций B для:

• 2-й год UCSA-G5N1 бакалавриат компьютерных наук и управления

Этот модуль представляет собой список опций A для:

• 2-й год UCSA-G500 бакалавриат компьютерных наук
• 2-й год UCSA-G503 Бакалавриат по информатике MEng

Этот модуль представляет собой список опций B для:

• 2-й год UCSA-G4G1 Бакалавриат по дискретной математике
• 2-й год UCSA-G4G3 Бакалавриат по дискретной математике

.