Дискретный сигнал формирует. Дискретные сигналы: формирование, характеристики и применение в цифровой обработке — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое дискретный сигнал и как он формируется. Какие основные характеристики имеют дискретные сигналы. Как применяются дискретные сигналы в цифровой обработке данных. В чем отличие дискретных сигналов от аналоговых.

Содержание

Что такое дискретный сигнал и как он формируется

Дискретный сигнал — это сигнал, значения которого определены только в дискретные моменты времени. В отличие от аналогового сигнала, который является непрерывной функцией времени, дискретный сигнал представляет собой последовательность отсчетов, взятых через определенные интервалы времени.

Формирование дискретного сигнала происходит путем дискретизации аналогового сигнала во времени. При этом непрерывный аналоговый сигнал преобразуется в последовательность мгновенных значений, взятых через равные промежутки времени, называемые периодом дискретизации.

Основные этапы формирования дискретного сигнала:

Выбор частоты дискретизации в соответствии с теоремой Котельникова
Взятие отсчетов аналогового сигнала через равные интервалы времени
Квантование отсчетов по уровню
Кодирование квантованных значений в цифровую форму

Таким образом, дискретный сигнал представляет собой последовательность чисел, соответствующих мгновенным значениям исходного аналогового сигнала в дискретные моменты времени.

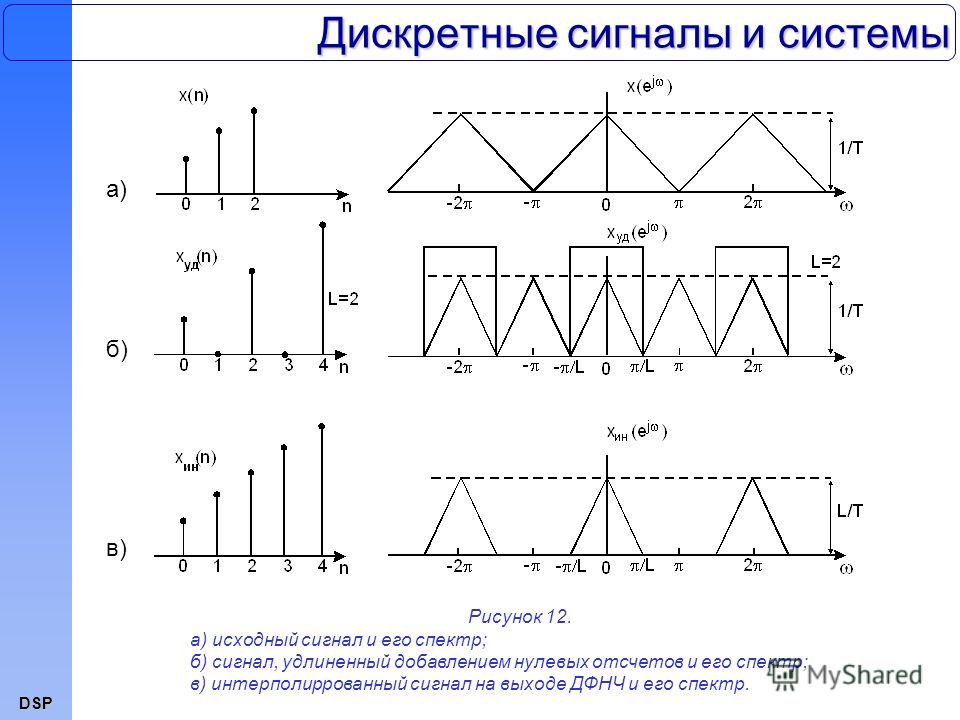
Основные характеристики дискретных сигналов

Дискретные сигналы обладают рядом важных характеристик, которые определяют их свойства и возможности применения в цифровой обработке:

Частота дискретизации

Частота дискретизации — это количество отсчетов в единицу времени, обычно измеряется в герцах (Гц). Она определяет временное разрешение дискретного сигнала и должна выбираться в соответствии с теоремой Котельникова.

Разрядность квантования

Разрядность квантования задает точность представления амплитуды сигнала и измеряется в битах. Чем больше разрядность, тем точнее дискретный сигнал аппроксимирует исходный аналоговый.

Динамический диапазон

Динамический диапазон определяет соотношение между максимальным и минимальным значениями сигнала, которые могут быть представлены. Он зависит от разрядности квантования.

Применение дискретных сигналов в цифровой обработке

Дискретные сигналы нашли широкое применение в различных областях цифровой обработки данных:

Цифровая фильтрация сигналов
Спектральный анализ
Сжатие аудио и видео данных
Распознавание речи и образов
Цифровая связь

Преимущества использования дискретных сигналов включают возможность применения цифровых методов обработки, высокую помехоустойчивость, простоту хранения и передачи информации.

Отличия дискретных сигналов от аналоговых

Основные отличия дискретных сигналов от аналоговых заключаются в следующем:

Параметр	Аналоговый сигнал	Дискретный сигнал
Непрерывность во времени	Непрерывен	Дискретен
Значения сигнала	Непрерывны	Квантованы
Спектр	Непрерывный	Периодический
Помехоустойчивость	Низкая	Высокая

Эти различия определяют особенности обработки и передачи дискретных сигналов по сравнению с аналоговыми.

Преобразование аналоговых сигналов в дискретные

Преобразование аналоговых сигналов в дискретные осуществляется с помощью аналого-цифровых преобразователей (АЦП). Этот процесс включает следующие этапы:

Дискретизация сигнала во времени
Квантование отсчетов по уровню
Кодирование квантованных значений

При этом важно правильно выбрать частоту дискретизации и разрядность квантования, чтобы минимизировать потери информации при преобразовании.

Теорема Котельникова и выбор частоты дискретизации

Теорема Котельникова (теорема отсчетов) устанавливает фундаментальную связь между аналоговыми и дискретными сигналами. Она гласит, что для точного восстановления аналогового сигнала частота дискретизации должна быть как минимум в два раза выше максимальной частоты в спектре исходного сигнала.

Математически это выражается следующим образом:

F_д ≥ 2F_max

где F_д — частота дискретизации, F_max — максимальная частота в спектре сигнала.

Выбор частоты дискретизации в соответствии с теоремой Котельникова позволяет избежать эффекта наложения спектров (алиасинга) и обеспечить точное представление исходного аналогового сигнала в дискретной форме.

Квантование дискретных сигналов

Квантование — это процесс преобразования непрерывных значений отсчетов дискретного сигнала в конечное множество дискретных уровней. Основные характеристики процесса квантования:

Шаг квантования — расстояние между соседними уровнями квантования
Ошибка квантования — разница между исходным значением и ближайшим уровнем квантования

Отношение сигнал/шум квантования — характеризует качество квантования

Существуют различные методы квантования, включая равномерное и неравномерное квантование. Выбор метода зависит от характеристик сигнала и требований к точности его представления.

Спектральные характеристики дискретных сигналов

Спектр дискретного сигнала имеет ряд особенностей по сравнению со спектром аналогового сигнала:

Периодичность спектра с периодом, равным частоте дискретизации
Ограниченность спектра в пределах от 0 до половины частоты дискретизации (частота Найквиста)
Возможность появления эффекта наложения спектров при нарушении теоремы Котельникова

Анализ спектральных характеристик дискретных сигналов осуществляется с помощью дискретного преобразования Фурье (ДПФ) и его быстрых алгоритмов (БПФ).

Заключение

Дискретные сигналы играют ключевую роль в современных системах цифровой обработки информации. Понимание их характеристик, методов формирования и анализа необходимо для эффективного проектирования и использования цифровых систем в различных областях техники и технологий.

Что формирует дискретный сигнал. Дискретный сигнал

ВВЕДЕНИЕ В ЦИФРОВУЮ ОБРАБОТКУ СИГНАЛОВ

Цифровая обработка сигналов (ЦОС или DSP — digital signal processing) является одной из новейших и самых мощных технологий, которая активно внедряется в широкий круг областей науки и техники, таких как коммуникации, метеорология, радиолокация и гидролокация, медицинская визуализация изображений, цифровое аудио- и телевизионное вещание, разведка нефтяных и газовых месторождений и др. Можно сказать, что происходит повсеместное и глубокое проникновение технологий цифровой обработки сигналов во все сферы деятельности человечества. Сегодня технология ЦОС относится к числу базовых знаний, которые необходимы ученым и инженерам всех отраслей без исключения.

Сигналы

Что такое сигнал? В наиболее общей формулировке это зависимость одной величины от другой. Т.е., с математической точки зрения сигнал является функцией. Чаще всего рассматриваются зависимости от времени. Физическая природа сигнала может быть различной. Очень часто это электрическое напряжение, реже – ток.

Формы представления сигнала :

1. временная;

2. спектральная (в частотной области).

Стоимость цифровой обработки данных меньше аналоговой и продолжает снижаться, а производительность вычислительных операций непрерывно возрастает. Немаловажным является и то, что системы ЦОС отличаются высокой гибкостью. Их можно дополнять новыми программами и перепрограммировать на выполнение различных операций без изменения оборудования. Поэтому интерес к научным и к прикладным вопросам цифровой обработки сигналов возрастает во всех отраслях науки и техники.

ПРЕДИСЛОВИЕ К ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ

Дискретные сигналы

Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и др.) преобразуется в последовательность чисел , которая затем подвергается математическим преобразованиям в ВУ.

Аналоговые, дискретные и цифровые сигналы

Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты t, называются аналоговыми .

Какой сигнал называется цифровым? Рассмотрим некоторый аналоговый сигнал (рис. 1.1 а). Он задан непрерывно на всем рассматриваемом временном интервале. Считается, что аналоговый сигнал абсолютно точен, если не учитывать погрешности при измерении.

Рис. 1.1 а) Аналоговый сигнал

Рис. 1.1 б) Дискретизированный сигнал

Рис. 1.1 в) Квантованный сигнал

Для того, чтобы получить цифровой сигнал, нужно провести две операции – дискретизацию и квантование . Процесс преобразования аналогового сигнала в последовательность отсчетов называется

дискретизацией, а результат такого преобразования — дискретным сигналом .Т. обр., дискретизация заключается в составлении выборки из аналогового сигнала (рис. 1.1 б), каждый элемент которой, называемый отсчетом , будет отстоять по времени от соседних отсчетов на некотором интервале Т , называемом интервалом дискретизации или (поскольку интервал дискретизации чаще неизменен) – периодом дискретизации . Величина, обратная периоду дискретизации называется частотой дискретизации и определяется как:

(1.1)

При обработке сигнала в вычислительном устройстве его отсчеты представляются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследствие этого отсчеты могут принимать лишь конечное множество значений и, следовательно, при представлении сигнала неизбежно происходит его округление. Процесс преобразования отсчетов сигнала в числа называется квантованием

. Возникающие при этом ошибки округления называются ошибками или шумами квантования . Т. обр., квантование – это приведение уровней дискретизированного сигнала к некоторой сетке (рис. 1.1 в), чаще обычным округлением в сторону большего. Дискретный во времени и квантованный по уровню сигнал и будет являться цифровым.

Условия, при которых возможно полное восстановление аналогового сигнала по его цифровому эквиваленту с сохранением всей исходно содержавшейся в сигнале информации, выражаются теоремами Найквиста, Котельникова, Шеннона, сущность которых практически одинакова. Для дискретизации аналогового сигнала с полным сохранением информации в его цифровом эквиваленте максимальные частоты в аналоговом сигнале должны быть не менее, чем вдвое меньше, чем частота дискретизации, то есть f max £ (1/2)f d , т.е. на одном периоде максимальной частоты должно быть минимум два отсчета. Если это условие нарушается, в цифровом сигнале возникает эффект маскирования (подмены) действительных частот более низкими частотами. При этом в цифровом сигнале вместо фактической регистрируется «кажущаяся» частота, а, следовательно, восстановление фактической частоты в аналоговом сигнале становится невозможным. Восстановленный сигнал будет выглядеть так, как если бы частоты, лежащие выше половины частоты дискретизации, отразились от частоты (1/2)f d в нижнюю часть спектра и наложились на частоты, уже присутствующие в этой части спектра. Этот эффект называется

наложением спектров или алиасингом (aliasing). Наглядным примером алиасинга может служить иллюзия, довольно часто встречающаяся в кино – колесо автомобиля начинает вращаться против его движения, если между последовательными кадрами (аналог частоты дискретизации) колесо совершает более чем пол-оборота.

Преобразование сигнала в цифровую форму выполняется аналого-цифровыми преобразователями (АЦП). Как правило, они используют двоичную систему счисления с определенным числом разрядов в равномерной шкале. Увеличение числа разрядов повышает точность измерений и расширяет динамический диапазон измеряемых сигналов. Потерянная из-за недостатка разрядов АЦП информация невосстановима, и существуют лишь оценки возникающей погрешности «округления» отсчетов, например, через мощность шума, порождаемого ошибкой в последнем разряде АЦП. Для этого используется понятие отношения «сигнал/шум» — отношение мощности сигнала к мощности шума (в децибелах). Наиболее часто применяются 8-, 10-, 12-, 16-, 20- и 24-х разрядные АЦП. Каждый дополнительный разряд улучшает отношение сигнал/шум на 6 децибел. Однако увеличение количества разрядов снижает скорость дискретизации и увеличивает стоимость аппаратуры. Важным аспектом является также динамический диапазон, определяемый максимальным и минимальным значением сигнала.

Обработка цифровых сигналов выполняется либо специальными процессорами, либо на универсальных ЭВМ и компьютерах по специальным программам. Наиболее просты для рассмотрения линейные системы. Линейными называются системы, для которых имеет место принцип суперпозиции (отклик на сумму входных сигналов равен сумме откликов на каждый сигнал в отдельности) и однородность (изменение амплитуды входного сигнала вызывает пропорциональное изменение выходного сигнала).

Если входной сигнал x(t-t 0) порождает однозначный выходной сигнал y(t-t 0) при любом сдвиге t 0 , то систему называют инвариантной во времени . Ее свойства можно исследовать в любые произвольные моменты времени. Для описания линейной системы вводится специальный входной сигнал — единичный импульс (импульсная функция).

Единичный импульс (единичный отсчет) u 0 (n ) (рис. 1.2):

Рис. 1.2. Единичный импульс

В силу свойства суперпозиции и однородности любой входной сигнал можно представить в виде суммы таких импульсов, подаваемых в разные моменты времени и умноженных на соответствующие коэффициенты. Выходной сигнал системы в этом случае представляет собой сумму откликов на эти импульсы. Отклик на единичный импульс (импульс с единичной амплитудой) называют импульсной характеристикой системы h(n). Знание импульсной характеристики позволяет проанализировать прохождение через дискретную систему любого сигнала. Действительно, произвольный сигнал {x(n)} можно представить в виде линейной комбинации единичных отсчетов.

Лекция № 1

«Аналоговые, дискретные и цифровые сигналы.»

Двумя самыми фундаментальными понятиями в данном курсе являются понятия сигнала и системы.

Под сигналом понимается физический процесс (например, изменяющееся во времени напряжение), отображающий некоторую информацию или сообщение. Математически сигнал описывается функцией определенного типа.

Одномерные сигналы описываются вещественной или комплексной функцией , определенной на интервале вещественной оси (обычно – оси времени) . Примером одномерного сигнала может служить электрический ток в проводе микрофона, несущий информацию о воспринимаемом звуке.

Сигнал x (t ) называется ограниченным если существует положительное число A , такое, что для любого t .

Энергией сигнала x (t ) называется величина

,(1.1)

Если , то говорят, что сигнал x (t ) имеет ограниченную энергию. Сигналы с ограниченной энергией обладают свойством

Если сигнал имеет ограниченную энергию, то он ограничен.

Мощностью сигнала x (t ) называется величина

,(1.2)

Если , то говорят, что сигнал x (t ) имеет ограниченную мощность. Сигналы с ограниченной мощностьюмогут принимать ненулевые значения сколь угодно долго.

В реальной природе сигналов с неограниченной энергией и мощностью не существует. Большинство сигналов, существующих в реальной природе являются аналоговыми.

Аналоговые сигналы описываются непрерывной (или кусочно-непрерывной) функцией , причем сама функция и аргумент t могут принимать любые значения на некоторых интервалах . На рис. 1.1 а представлен пример аналогового сигнала, изменяющегося во времени по закону , где . Другой пример аналогового сигнала, показанный на рис 1.1б, изменяется во времени по закону .

Важным примером аналогового сигнала является сигнал, описываемый т.н. «единичной функцией» , которая описывается выражением

(1.3),

где.

График единичной функции представлен на рис.1.2.

Функцию 1(t ) можно рассматривать как предел семейства непрерывных функций 1(a , t ) при изменении параметра этого семейства a .

(1.4).

Семейство графиков 1(a , t ) при различных значениях a представлено на рис.1.3.

В этом случае функцию 1( t ) можно записать как

(1.5).

Обозначим производную от 1(a , t ) как d (a , t ).

(1.6).

Семейство графиков d (a , t ) представлено на рис.1.4.

Площадь под кривой d (a , t ) не зависит от a и всегда равна 1. Действительно

(1.7).

Функция

(1.8)

называется импульсной функцией Дирака или d — функцией. Значения d — функции равны нулю во всех точках, кроме t =0. При t =0 d -функция равна бесконечности, но так, что площадь под кривой d — функции равна 1. На рис.1.5 представлен график функции d (t ) и d (t — t ).

Отметим некоторые свойства d — функции:

1. (1.9).

Это следует из того, что только при t = t .

2. (1.10) .

В интеграле бесконечные пределы можно заменить конечными, но так, чтобы аргумент функции d (t — t ) обращался в нуль внутри этих пределов.

(1.11).

3. Преобразование Лапласа d -функции

(1.12).

В частности , при t =0

(1.13).

4. Преобразование Фурье d — функции. При p = j v из 1.13 получим

(1.14)

При t =0

(1.15),

т.е. спектр d — функции равен 1.

Аналоговый сигнал f (t ) называется периодическим если существует действительное число T , такое, что f (t + T )= f (t ) для любых t . При этом T называется периодом сигнала. Примером периодического сигнала может служить сигнал, представленный на рис.1.2а, причем T =1/ f . Другим примером периодического сигнала может служить последовательность d — функций, описываемая уравнением

(1.16)

график которой представлен на рис.1.6.

Дискретные сигналы отличаются от аналоговых тем, что их значения известны лишь в дискретные моменты времени.Дискретные сигналы описываются решетчатыми функциями – последовательностями – x д (nT ), где T = const – интервал (период) дискретизации, n =0,1,2,…. Сама функция x д (nT ) может в дискретные моменты принимать произвольные значения на некотором интервале. Эти значения функции называются выборками или отсчетами функции. Другим обозначением решетчатой функции x (nT ) является x (n ) или x n . На рис. 1.7а и 1.7б представлены примеры решетчатых функций и . Последовательность x (n ) может быть конечной или бесконечной, в зависимости от интервала определения функции.

Процесс преобразования аналогового сигнала в дискретный называется временная дискретизация. Математически процесс временной дискретизации можно описать как модуляцию входным аналоговым сигналом последовательности d — функций d T (t )

(1.17)

Процесс восстановления аналогового сигнала из дискретного называется временная экстраполяция.

Для дискретных последовательностей также вводятся понятия энергии и мощности. Энергией последовательности x (n ) называется величина

,(1.18)

Мощностью последовательности x (n ) называется величина

,(1.19)

Для дискретных последовательностей сохраняются те же закономерности, касающиеся ограничения мощности и энергии, что и для непрерывных сигналов.

Периодической называют последовательность x (nT ), удовлетворяющую условию x (nT )= x (nT + mNT ), где m и N – целые числа. При этом N называют периодом последовательности. Периодическую последовательность достаточно задать на интервале периода, например при .

Цифровые сигналы представляют собой дискретные сигналы, которые в дискретные моменты времени могут принимать лишь конечный ряд дискретных значений – уровней квантования. Процесс преобразования дискретного сигнала в цифровой называется квантованием по уровню. Цифровые сигналы описываются квантованными решетчатыми функциями x ц (nT ). Примеры цифровых сигналов представлены на рис. 1.8а и 1.8б.

Связь между решетчатой функцией x д (nT ) и квантованной решетчатой функцией x ц (nT ) определяется нелинейной функцией квантования x ц (nT )= F k (x д (nT )). Каждый из уровней квантования кодируется числом. Обычно для эих целей используется двоичное кодирование, так, что квантованные отсчеты x ц (nT ) кодируются двоичными числами с n разрядами. Число уровней квантования N и наименьшее число двоичных разрядов m , с помощью которых можно закодировать все эти уровни, связаны соотношением

,(1.20)

где int (x ) – наименьшее целое число, не меньшее x .

Т.о., квантование дискретных сигналов состоит в представлении отсчета сигнала x д (nT ) с помощью двоичного числа, содержащего m разрядов. В результате квантования отсчет представляется с ошибкой, которая называется ошибкой квантования

.(1.21)

Шаг квантования Q определяется весом младшего двоичного разряда результирующего числа

.(1.22)

Основными способами квантования являются усечение и округление.

Усечение до m -разрядного двоичного числа состоит в отбрасывании всех младших разрядов числа кроме n старших. При этом ошибка усечения . Для положительных чисел прилюбом способе кодирования . Для отрицательных чисел при использовании прямого кода ошибка усечения неотрицательна , а при использовании дополнительного кода эта ошибка неположительна . Таким образом, во всех случаях абсолютнок значение ошибки усечения не превосходит шага квантования:

.(1.23)

График функции усечения дополнительного кода представлен на рис.1.9, а прямого кода – на рис.1.10.

Округление отличается от усечения тем, что кроме отбрасывания младших разрядов числа модифицируется и m -й (младший неотбрасываемый ) разряд числа. Его модификация заключается в том, что он либо остается неизменным или увеличивается на единицу в зависимости от того, больше или меньше отбрасываемая часть числа величины . Округление можно практически выполнить путем прибавления единицы к ( m +1) – муразряду числа с последующим усечением полученного числа до n разрядов. Ошибка округления при всех способах кодирования лежит в пределах и, следовательно,

.(1.24)

График функции округления представлен на рис. 1.11.

Рассмотрение и использование различных сигналов предполагает возможность измерения значения этих сигналов в заданные моменты времени. Естественно возникает вопрос о достоверности (или наоборот, неопределенности) измерения значения сигналов. Этими вопросами занимается теория информации , основоположником которой является К.Шеннон. Основная идея теории информации состоит в том, что с информацией можно обращаться почти также, как с такими физическими величинами как масса и энергия.

Точность измерений мы обычно характеризуем числовыми значениями полученных при измерении или предполагаемых погрешностей. При этом используются понятия абсолютной и относительной погрешностей. Если измерительное устройство имеет диапазон измерения от x 1 до x 2 , с абсолютной погрешностью ± D , не зависящей от текущего значения x измеряемой величины, то получив результат измерения в виде x n мы записываем его как x n ± D и характеризуем относительной погрешностью .

Рассмотрение этих же самых действий с позиции теории информации носит несколько иной характер, отличающийся тем, что всем перечисленным понятиям придается вероятностный, статистический смысл, а итог проведенного измерения истолковывается как сокращение области неопределенности измеряемой величины. В теории информации тот факт, что измерительный прибор имеет диапазон измерения от x 1 до x 2 означает , что при использовании этого прибора могут бытьполучены показания только в пределах от x 1 до x 2 . Другими словами, вероятность получения отсчетов, меньших x 1 или больших x 2 , равна 0. Вероятность же получения отсчетв где-то в пределах от x 1 до x 2 равна 1.

Если предположить, что все результаты измерения в пределах от x 1 до x 2 равновероятны, т.е. плотность распределения вероятности для различных значений измеряемой величины вдоль всей шкалы прибора одинакова, то с точки зрения теории информации наше знание о значении измеряемой величины до измерения может быть представлено графиком распределения плотности вероятности p (x ).

Поскольку полная вероятность получить отсчет где-то в пределах от x 1 до x 2 равна 1, то под кривой должна быть заключена площадь, равная 1, а это значит, что

(1.25).

После проведения измерения получаем показание прибора, равное x n . Однако, вследствие погрешности прибора, равной ± D , мы не можем утверждать, что измеряемая величина точно равна x n . Поэтому мы записывает результат в виде x n ± D . Это означает, что действительное значение измеряемой величины x лежит где-то в пределах от x n — D до x n + D . С точки зрения теории информации результат нашего измерения состоит лишь в том, что область неопределенности сократилась до величины 2 D и характеризуется намного большей плотностью ве5роятности

(1.26).

Получение каой-либо информации об интересующей нас величине заключается, таким образом, в уменьшении неопределенности ее значения.

В качестве характеристики неопределенности значения некоторой случайной величины К.Шеннон ввел понятие энтропии величины x , которая вычисляется как

(1.27).

Единицы измерения энтропии зависят от выбора основания логарифма в приведенных выражениях. При использовании десятичных логарифмов энтропия измеряется в т.н. десятичных единицах или дитах . В случае же использования двоичных логарифмов энтропия выражается в двоичных единицах или битах .

В большинстве случаев неопределенность знания о значении сигнала определяется действием помех или шумов. Дезинформационное действие шума при передаче сигнала определяется энтропией шума как случайной величины. Если шум в вероятностном смысле не зависит от передаваемого сигнала, то независимо от статистики сигнала шуму можно приписывать определенную величину энтропии, которая и характеризует его дезинформационное действие. При этом анализ системы можно проводить раздельно для шума и сигнала, что резко упрощает решение этой задачи.

Теорема Шеннона о количестве информации . Если на вход канала передачи информации подается сигнал с энтропией H ( x ), а шум в канале имеет энтропию H( D ) , то количество информации на выходе канала определяется как

(1.28).

Если кроме основного канала передачи сигнала имеется дополнительный канал, то для исправления ошибок, возникших от шума с энтропией H (D ), по этому каналу необходтмо передать дополнительное количество информации, не меньшее чем

(1.29).

Эти данные можно так закодировать, что будет возможно скорректировать все ошибки, вызванные шумом, за исключением произвольно малой доли этих ошибок.

В нашем случае, для равномерно распределенной случайной величины, энтропия определяется как

(1.30),

а оставшаяся или условная энтропия результата измерения после получения отсчета x n равна

(1.31).

Отсюда полученное количество информации равное разности исходной и оставшейся энтропии равно

(1.32).

При анализе систем с цифровыми сигналами ошибки квантования рассматриваются как стационарный случайный процесс с равномерным распределением вероятности по диапазону распределения ошибки квантования. На рис. 1.12а, б и в приведены плотности вероятности ошибки квантования при округлении дополнительного кода, прямого кода и усечении соответственно.

Очевидно, что квантование является нелинейной операцией. Однако, при анализе используется линейная модель квантования сигналов, представленная на рис. 1.13.

m – разрядный цифровой сигнал, e (nT ) – ошибка квантования.

Вероятностные оценки ошибок квантования делаются с помощью вычисления математического ожидания

(1.33)

и дисперсии

(1.34),

где p e – плотность вероятности ошибки. Для случаев округления и усечения будем иметь

(1.35),

(1.36).

Временная дискретизация и квантование по уровню сигналов являются неотъемлемыми особенностями всех микропроцессорных систем управления, определяемыми ограниченным быстродействием и конечной разрядностью используемых микропроцессоров.

Мы рассматривали различные определения понятия «информация» и пришли к выводу, что информация может быть определена множеством разных способов в зависимости от выбранного подхода. Но об одном мы можем говорить однозначно: информация — знания, данные, сведения, характеристики, отражения и т.д. — категория нематериальная . Но мы живем в мире материальном. Следовательно, для существования и распространения в нашем мире информация должна быть связана с какой-либо материальной основой. Без нее информация не может передаваться и сохраняться.

Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации , а изменение какой-либо характеристики носителя мы будем называть сигналом .
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).

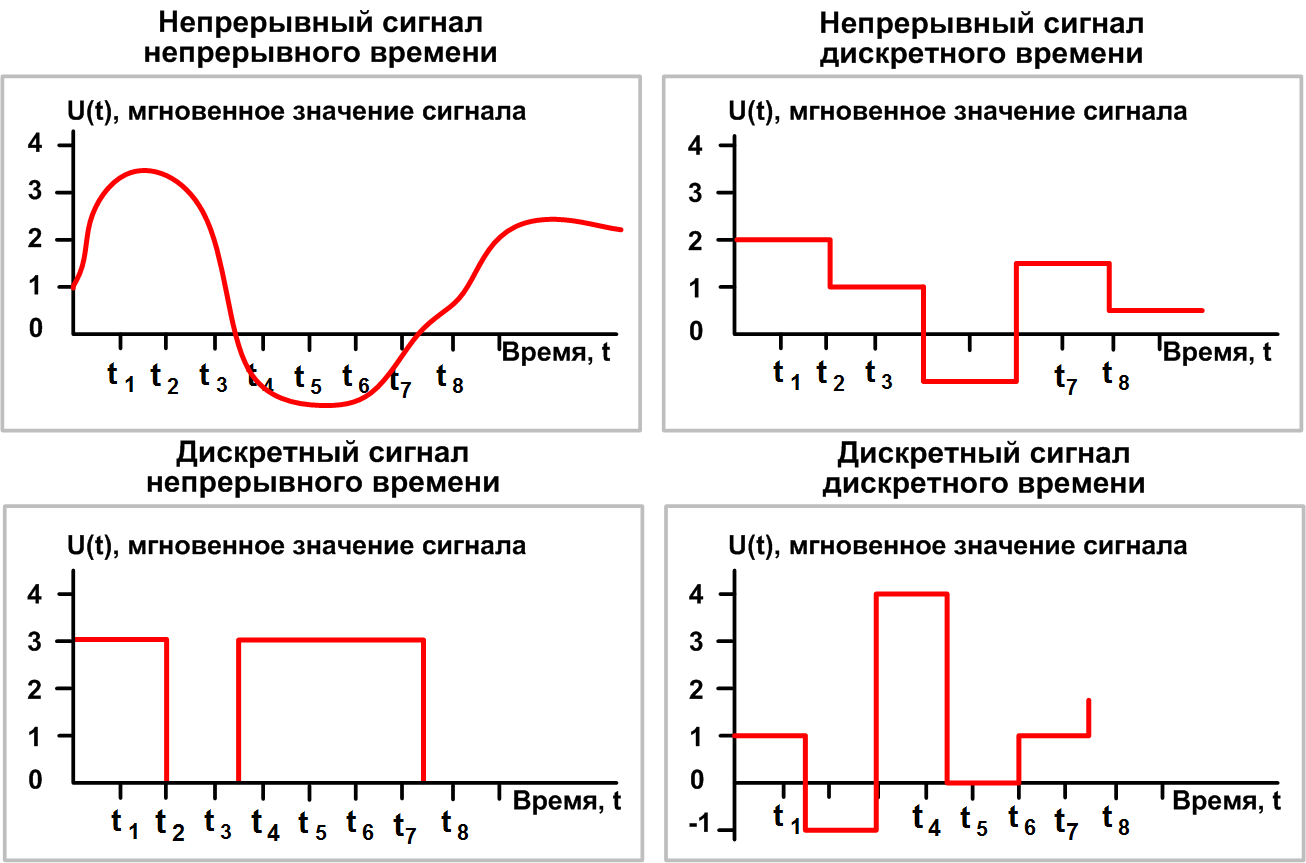
При этом сигналы могут быть двух видов: непрерывный (или аналоговый ) и дискретный .
В учебнике даны следующие определения.

Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.

Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.

Сигнал называется дискретным , если его параметр может принимать конечное число значений в пределах некоторого интервала.

Графики этих сигналов выглядят следующим образом

Примерами непрерывных сигналов могут быть музыка, речь, изображения, показания термометра (высота столба ртути может быть любой и представляет собой ряд непрерывных значений).

Примерами дискретных сигналов могут быть показания механических или электронных часов, тексты в книгах, показания цифровых измерительных приборов и т.д.

Вернемся к примерам, рассмотренным в начале сообщения — мигающая лампочка и человеческая речь. Какой из этих сигналов является непрерывным, а какой дискретным? Ответьте в комментариях и аргументируйте свой ответ. Можно ли непрерывную информацию преобразовать в дискретную? Если да — приведите примеры.

С дискретностью каждый из нас сталкивается ежедневно. Это одно из свойств, присущее материи. В дословном переводе с латинского языка слово discretus означает прерывистость. Например, дискретный сигнал — это способ передачи информации, когда среда-переносчик изменяется во времени, принимая любое из существующего списка допустимых значений.

Конечно, термин «дискретность» применяется в более широком смысле. В частности, сейчас прогресс в микроэлектронике направлен на создание и развитие технологии SOC — «Система на чипе». Предполагается, что все составляющие устройство компоненты между собой тесно интегрированы на единой подложке. Противоположность такого подхода — дискретные схемы, когда элементы сами являются завершенными изделиями, соединяясь линиями связи.

Пожалуй, сейчас невозможно найти человека, который бы не пользовался мобильным телефоном или программой Скайп на компьютере. Одна из их задач — это передача звукового потока (в частности, голоса). Но так как такой звук представляет собой непрерывную волну, для его непосредственной передачи потребовался бы канал с высокой пропускной способностью. Для решения этого вопроса было предложено использовать дискретный сигнал. Формирует он не волну, а ее цифровое представление (помните, речь идет о мобильных телефонах и компьютерах). С волны через определенные промежутки времени выполняются выборки значений данных. То есть, создается дискретный сигнал. Его преимущество очевидно: меньший суммарный и возможность организации пакетной передачи. Целевое приемное устройство объединяет все выборки в единый блок, генерируя исходную волну. Чем больше промежутки между выборками, тем выше вероятность искажения исходной волны. Дискретизация широко используется в вычислительной технике.

Говоря о том, что такое дискретный сигнал, нельзя не воспользоваться замечательной аналогией с обычной печатной книгой. Человек, читая ее, получает непрерывный поток информации. В то же время, содержащиеся в ней данные «закодированы» в виде определенных последовательностей букв — слов — предложений. Получается, что автор из неделимой мысли формирует своеобразный дискретный сигнал, так как выражает ее разбиением на блоки, используя тот или иной способ кодировки (алфавит, язык). Читатель в данном примере получает возможность воспринимать идею автора только после мысленного объединения слов в поток информации.

Наверняка, вы читаете эту статью с экрана компьютера. А ведь даже экран монитора может служить примером, где проявляется дискретность и непрерывность. Вспомним старые модели, основанные на ЭЛТ. В них изображение формировалось последовательностью кадров, которые необходимо было «отрисовывать» несколько десятков раз в секунду. Очевидно, что данное устройство использует дискретный способ построения картинки.

Дискретный сигнал является полной противоположностью непрерывному. Последний представляет собой функцию интенсивности от времени (если представить его на декартовой плоскости). Как уже указывалось, одним из примеров может служить Она характеризуется частотой и амплитудой, однако естественным образом нигде не прерывается. Большинство природных процессов описываются именно таким способом. Несмотря на то, что, все-таки, существует несколько способов обработки непрерывного (или аналогового) сигнала, позволяющих уменьшить поток данных, в современных цифровых системах распространен именно дискретный. Отчасти благодаря тому, что его можно достаточно просто преобразовать в исходный, независимо от конфигурации последнего. Кстати, стоит отметить, что термины «дискретный» и «цифровой» практически равнозначны.

Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT ; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами. Если в цепь микрофона (рис. 1), где ток является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.
Рис. 1 В отличие от непрерывного сигнала дискретный сигнал можно обозначить . Однако, чаще его обозначают , заменяя непрерывное время t дискретными моментами nT , следующими строго через интервал T . Используются и более краткие обозначения: и . Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n . При n = 0 значение равно значению сигнала в момент времени t = 0. При n > 0 отсчеты повторяют форму сигнала , т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT . Рис. 2 Дискретные сигналы можно задавать графиками, как это показано на рис. 1, формулами, например, , в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов. Все средства связи, которые на сегодняшний день используются в мире, основаны на передаче электрического тока из одной точки в другую. Как работа в сети Internet, так и разговор с другом по телефону обеспечиваются за счет постоянного протекания тока по оборудованию телекоммуникационной инфраструктуры. По каналам связи могут передаваться различные типы сигналов. В этой книге рассматриваются два основных типа сигналов: аналоговые и цифровые. Некоторые виды физической передающей среды, как, например, волоконно-оптический кабель, используются для передачи данных в сети провайдера в виде световых сигналов. Принципы цифровой передачи для такой среды такие же, однако для ее организации используются лазеры и светодиоды. Аналоговые и цифровые сигналы коренным образом отличаются друг от друга. Условно можно сказать, что они находятся на разных концах одного и того же спектра. Из-за таких существенных различий между двумя типами сигналов для организации «моста» между ними приходится использовать промежуточные устройства, наподобие цифро-аналоговых преобразователей (они рассматриваются ниже в текущей главе). Основное различие между аналоговыми и цифровыми сигналами заключается в самой структуре сигнального потока. Аналоговые сигналы представляют собой непрерывный поток, характеризующийся изменениями частоты и амплитуды. Это означает, что форма аналогового сигнала обычно похожа на синусоиду (т.е. гармоническую волну), представленную на рис. 1.2. Зачастую на иллюстрациях, изображающих гармоническую волну, весь сигнал характеризуется одним и тем же соотношением частоты и амплитуды, однако при графическом представлении сложной волны видно, что такое соотношение изменяется в зависимости от частоты.
Цифровым сигналам соответствуют дискретные электрические значения, которые передаются индивидуально по некоторой физической передающей среде. В отличие от аналоговых сигналов, в которых количество возможных значений амплитуды почти бесконечно, для цифровых сигналов она может принимать одно из двух (или четырех) различных значений — как положительных, так и отрицательных. Цифровые сигналы передаются в виде единиц и нулей, которые обычно называют двоичными. Более подробно потоки цифровых сигналов рассматриваются в главе 3, «Аналого-цифровое преобразование». Как и в любой другой технологии, для описания аналоговых сигналов используются базовые концепции и собственная терминология. Непрерывные аналоговые сигналы имеют три основные характеристики: амплитуду; длину волны; частоту.

26 вопросов и ответов. Теория электрических цепей. Курс лекций

Сигнал – это физический процесс (например, изменяющиеся во времени токи и напряжения), содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией.

Если в цепь микрофона (рис. 1), где ток является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.

Рис. 1

В отличие от непрерывного сигнала дискретный сигнал можно обозначить . Однако, чаще его обозначают , заменяя непрерывное время t дискретными моментами nT, следующими строго через интервал T. Используются и более краткие обозначения: и . Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n < 0 дискретный сигнал . При n = 0 значение равно значению сигнала в момент времени t = 0. При n > 0 отсчеты повторяют форму сигнала , т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT.

Рис. 2

Дискретные сигналы можно задавать графиками, как это показано на рис. 1, формулами, например, , в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов.

Пример 1.1. Единичный ступенчатый аналоговый сигнал приведен на рис. 2.

Соответствующий ему дискретный сигнал называется ступенчатой последовательностью. Он определяется следующим образом:

Рис. 3

Такая последовательность приведена на рис. 2.

Пример 1.2. Импульс Дирака или d-функция в аналоговой области приведена на рис. 3.

Рис. 4

Дельта-последовательность или дискретная d-функция определяется выражением

Последовательность , приведенная на рис. 3, принимает единственное значение, равное 1, при n = 0. Этот сигнал можно сдвинуть на k интервалов:

Тогда математическая запись любого дискретного сигнала имеет вид

где – отсчеты исходного аналогового сигнала.

Этот сигнал можно получить из аналогового (рис. 4) периодическим замыканием ключа на очень короткое время в моменты t = k.

Самоконтроль

1. Что представляют собой аналоговые, дискретные и цифровые сигналы?

2. Как практически получить дискретный сигнал из аналогового?

3. Что такое ступенчатая последовательность и дельта-последовательность?

4. Изобразите графики дискретных d-функций и .

Дискретным называют сигнал — прерывный информационный сигнал

Сигнал — это любая переменная содержащая какой-либо вид информации. Причем эту информацию можно передавать на расстояние, переносить на устройства хранения, выводить на экран и через динамики или совершать с ней подобные действия. Существующие аналоговый и цифровой кардинально отличаются природой происхождения, способом передачи и хранения.

Аналоговый сигнал

Это природный тип сигналов окружает нас повсеместно и постоянно. Звук, изображение, тактильные ощущения, запах, вкус и команды мозга. Все возникающие, во Вселенной без участия человека, сигналы являются аналоговыми.

В электронике, электротехнике и системах связи аналоговую передачу данных применяют со времени изобретения электричества. Характерной особенностью является непрерывность и плавность изменения параметров. Графически сеанс аналоговой связи можно описать как непрерывную кривую, соответствующую величине электрического напряжения в определённый момент времени. Линия изменяется плавно, разрывы возникают только при обрыве связи. В природе и электронике аналоговые данные генерируются и распространяются непрерывно. Отсутствие непрерывного сигнала означает тишину или черный экран.

В непрерывных системах связи аналогом звука, изображения и любых других данных является электрические или электромагнитные импульсы. Например, громкость и тембр голоса передаются от микрофона на динамик посредством электрического сигнала. Громкость зависит от величины, а тембр от частоты напряжения. Поэтому при голосовой связи сначала напряжение становится аналогом звука, а потом звук аналогом напряжения. Таким же образом происходит передача любых данных в аналоговых системах связи.

Что такое дискретный сигнал

В цифровой системе хранения и передачи данных, отсутствие сигнала, также является формой обмена информацией. В какой-то момент времени он равен нулю, в другой принимает какое-либо значение. Поэтому дискретным называют сигнал прерывный, отсюда и название discretus или разделённый. Аналоговые данные разбиваются на отдельные блоки, обрабатываются и передаются в виде цифрового кода.

Дискретность не подразумевает разрыв связи. В цифровых системах широко используется двоичная система обработки и обмена информацией. Двоичная подразумевает кодировку данных с помощью единицы и нулей. В доли секунды сигнал прерывисто принимает значение 1 или 0. Вместо непрерывной кривой имеем отдельные дискретные значения. Определенный набор нулей и единичек уже несёт в себе какую либо информацию. Примитивный набор это бит или двоичный разряд. Сам по себе он ничего не значит. Данные могут кодироваться только при объединении восьми битов в следующую по сложности комбинацию – байт. Чем больше объединённых байтов, тем больше и точнее можно описать передаваемую информацию.

На качество генерируемых данных влияет не только количество объединённых битов, но и скорость передачи. Непрерывная аналоговая кривая должна быть разбита на как много больше мини участков прерывного сигнала. Полученный таким образом звук и цвет будут соответствовать оригиналу. Качественный дискретный сигнал формирует точную копию аналогового. Например, звуковая дорожка MP3 закодированная со скоростью 320 000 бит в секунду (320 kbps) значительно лучше кодированной в 128 kbps. Дорожки скоростью меньше 128 слушать вообще невозможно.

Чем отличается непрерывный сигнал от дискретного

На первый взгляд отличия в сигналах можно не различить. Оба передаются в виде электрических импульсов по проводам или электромагнитными волнами в эфире. Преобразовываются в звук и изображение, выводятся на динамики и экран. Но разница существенна. Отличие аналогового сигнала от цифрового обусловлено особенностями обработки и передачи данных.

Аналоговые данные не кодируются и не шифруются, просто отображаются в электрические или электромагнитные импульсы. Приёмник преобразовывает импульсы в полном соответствии с полученным сигналом. Передаваемый и принимаемый импульс многогранен и характеризуются постоянным плавным изменением с течением времени. Величина и частота определяют параметры информации. Примером может быть соответствие определённого цвета экрана заданному напряжению. С течением времени цвета плавно меняются следуя изменению напряжения.

Казалось бы, природное происхождение, простота генерации, передачи и приёма благоприятствуют использованию аналогового сигнала. Но в дело вмешиваются электрические и электромагнитные помехи. Это могут быть электромагнитные наводки от электрических сетей, работающих механизмов, рельеф местности, грозы, бури на солнце, шумы создаваемые работой передающего и принимающего оборудования, прочие. Они изменяют плавную кривую. На приёмник информация поступает с изменениями. Шипение, хрипы и искаженное изображение обычная история для аналоговой связи.

Цифровая технология использует совсем иной принцип передачи. Аналоговые данные сначала кодируются и только потом передаются. Кодировка заключается в описании непрерывной кривой аналоговой информации. В каждый конкретный момент времени, передаваемый импульс имеет значение единицы или нуля, и определенная последовательность битов отображает всю полноту оригинальной картинки или звука.

Дискретный сигнал как азбука Морзе, только вместо точек и тире — чёткие биты. Ничего более, шумы и помехи им не мешают. Цифровой информации главное дойти до цели. Цифры без примесей передадут данные и без изменений перевоплотятся в звук и цвет. Но слабый сигнал может не донести полную картину. Как пример — пропадание слов или изображения полностью. Поэтому сотовые передатчики, устанавливают как можно ближе друг от друга, также используют повторители.

Примером непрерывных и дискретных сигналов могут служить старая проводная и новая сотовая связь. Через старые АТС иногда невозможно было разговаривать с соседним домом. Шумы и плохое усиление сигнала мешали слышать друг друга. Что бы вести полноценную беседу, приходилось громко кричать самому и прислушиваться к собеседнику. Другое дело сотовая связь основанная на цифровой технологии. Звук закодирован и хорошо передаётся на далёкие расстояния. Отчетливо слышно собеседника даже с другого континента.

Оба вида связи не лишены недостатков, а ключевыми отличиями являются:

Аналоговый подвержен помехам и поступает с искажениями. В то время как цифровой доходит полностью без искажений или отсутствует вовсе.
Принять или перехватить аналоговое вещание может любой приёмник такого принципа. Дискретная передача адресована конкретному адресату, кодируется и мало доступна к перехвату.
Объём передаваемых данных у аналоговой связи конечен, поэтому она практически исчерпала себя в передаче теле сигнала. Напротив с развитием технологии преобразования аналоговой информации в цифровой код растут объемы и качество трансляции. Например, главным отличием цифрового от аналогового телевидения является превосходное качество изображения.

Цифровая технология выигрывает по всем показателям. Споры идут только среди любителей музыки. Многие меломаны и звукорежиссеры утверждают, что могут различить аналоговый оригинал и цифровую копию. Однако большинство слушателей этого сделать не в состоянии. Да и с развитием цифровых систем аналоговые данные кодируются точнее. Оригинальное звучание и цифровая копия делаются практически неразличимым.

Как аналоговый сигнал преобразуется в цифровой и наоборот

Первой в цифровую форму преобразовали математическую, физическую и компьютерную информацию. Описать формулы и расчеты не составило труда. А вот для преображения аналоговой действительности в цифровые массивы уже потребовались специальные устройства. Ими стали аналого-цифровые преобразователи или сокращенно АЦП. Они предназначены для преобразования различных физических величин в цифровые коды. Обратное действие совершают устройства ЦАП.

Любые цифровые передатчики и приёмники оснащены такими преобразователями. Например, сотовому телефону, поступивший звук необходимо обработать и передать в оцифрованном виде. В то же время необходимо принять от другого абонента код, преобразовать и передать напряжение на динамик. Так же и с изображением на смартфонах и в телевизорах. В любом случае первоначальной информацией выступает напряжение.

Существует много видов АЦП, но самыми распространёнными являются следующие:

параллельного преобразования;
последовательного приближения;
дельта-сигма, с балансировкой заряда.

Преобразования в АЦП понятийно связаны с измерением и сравнением. Кодировка, это процесс сравнения полученных от источника данных с эталоном. То есть полученная аналоговая величина сравнивается с эталонной (с заданным напряжением). Эталоном выступает информация о конкретном цвете, звуке и т.п. Она соответствует заложенным в устройство представлениям о преобразуемом сигнале. Потом данные эталонной величины кодируются для передачи. Во время аналого-цифровой обработки физических превращений сигнала не происходит. С аналогового делается цифровой матрица (модель).

Упрощенно работу любого АЦП можно представить так:

Измерение через определенные интервалы времени амплитуды напряжения.
Сравнение с эталоном и формирование данных.
Отгрузка оцифрованных сведений об изменениях амплитуды на передатчик.

Качество передаваемой информации зависит от двух параметров — точности и частоты измерений. Чем точнее измеряется и зашифровывается входящее напряжение, тем качественней передаваемая информация. Поэтому, имеет большое значение, сколько бит может зашифровать преобразователь. Чем плотнее информационный поток, тем точней передача данных. Это выражается в красках экрана, контрастности картинки и чистоте звука. Следующим важным показателем является дискретизация, то есть частота измерений. Чем чаще, тем меньше провалов в измерениях и необходимости сглаживания. В совокупности, чем чаще и точнее преобразователь может измерять и обрабатывать полученное напряжение, тем он лучше.

Как выглядят спектры аналогового и дискретного сигнала

Изображение сигналов можно представить как две функции. На рисунке наглядно представлено, чем отличается непрерывный сигнал от дискретного. Напряжение исходного изменяется плавно, обработанного прерывисто. Спектр дискретного периодически ступенчато совпадает с непрерывным.

Изменения дискретного происходят резко, через определённый период времени. Уровень в цифровой системе зашифровывается и любую величину напряжения описывают двоичным кодом. От частоты измерений зависит сглаженность преобразования и оригинальность передаваемых данных. Чем точнее описан уровень сигнала и чем чаще проводится и обрабатывается измерение, тем точнее совпадает спектр начального и переданного сигналов.

Какие системы связи используют цифровой сигнал а какие аналоговый

Несмотря на архаичность аналоговая технология ещё используется для телефонной и радио связи. Многие проводные сети до сих пор остаются аналоговыми. В основном это традиционные телефонные линии местных операторов. Но, для магистральной передачи данных связи уже повсеместно используют цифровые каналы. Так же аналоговая технология применяется в простых и дешёвых переносных радиостанциях.

Во всех вновь создаваемых системах используют цифровую технологию обработки сигнала. Это оптоволоконные и проводные линии, сигнализация и телеметрия, военная и гражданская промышленная связь. И конечно же на цифровое вещание переходит телевидение. Аналоговый способ передачи данных исчерпал себя. На смену пришла новая высококачественная и защищенная связь.

Список книг помогающих разобраться в аналоговых и цифровых сигналах

Более подробно изучить и сравнить принципы обработки и передачи данных можно прочитав следующую литературу:

Сато Ю. Обработка сигналов. Первое знакомство. / Пер. с яп.; под ред. Ёсифуми Амэмия. — М: Изд-кий дом «Додэка-XXI», 2002. Книга даёт основы знаний о способах ЦОС. Адресована радиолюбителям, студентам и школьникам, только начинающим изучение систем передачи данных.
Введение в цифровую фильтрацию /под ред. Р. Богнера и А. Константинидиса; перевод с англ. — М: Изд-во «Мир», 1977. В этой книге популярно и доступно изложена информация о различных системах обработки данных. Сравниваются аналоговая и цифровая системы, описаны плюсы и минусы.
Основы цифровой обработки сигналов: Курс лекций /Авторы: А.И. Солонина, Д.А. Улахович, С.М. Арбузов, Е.Б. Соловьев, И.И. Гук. — СПб: Изд-во «БХВ-Петербург», 2005. Книга написана по курсу лекций для студентов ГУТ им. Бонч-Бруевича. Изложены теоретические основы обработки данных, описаны дискретные и цифровые системы разных способов преобразования. Предназначена для изучения в вузах и повышения квалификации специалистов.
Сергиенко А.Б. Цифровая обработка сигналов (второе издание) — СПб: Изд-во «Питер», 2006. Электронный учебно-методический комплекс по дисциплине «Цифровая обработка сигналов». Представлены курс лекций, лабораторный практикум и методические рекомендации по самостоятельной работе. Предназначена для преподавателей и самостоятельного изучения для студентов уровня подготовки бакалавр.
Лайонс Р. Цифровая обработка сигналов. 2-е изд. Пер. с англ. – М.: ООО «Бином-Пресс», 2006. Книга представляет подробную информацию о ЦОС. Написана понятным языком и снабжена большим количеством иллюстрации. Одна из самых простых и понятных книг на русском языке.

Старая добрая аналоговая связь быстро сдаёт позиции. Несмотря на модернизацию и улучшения, возможность обмена данными достигла предела. К тому же, остались старые болезни – искажения и шумы. В то же время цифровая связь лишена этих недостатков, и передаёт большие объёмы информации быстро, качественно, без ошибок.

Дискретный сигнал это ток

Дискретный сигнал

Сигналы могут быть: аналоговые ( непрерывные) и дискретные.

Дискретный сигнал — информационный сигнал. Сигнал называется дискретным, если он может принимать лишь конечное число значений.

См. также

Дискретизация
Квантование
Цифровой сигнал
Теорема Котельникова

Дискретный сигнал — сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи.

Литература

Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. — К. : Вища школа, 1987. — 375 с.

Wikimedia Foundation . 2010 .

Смотреть что такое «Дискретный сигнал» в других словарях:

Дискретный сигнал — сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи. По английски: Discrete signal Синонимы:… … Финансовый словарь

дискретный сигнал — Cигнал, информативный параметр которого может изменяться только прерывисто и иметь только конечное число значений в заданном диапазоне в течение определенного интервала времени. [Источник] EN discretely timed signal discrete signal a signal… … Справочник технического переводчика

Дискретный сигнал — 13. Дискретный сигнал Сигнал, имеющий конечное число значений величин Источник … Словарь-справочник терминов нормативно-технической документации

дискретный сигнал — diskretusis signalas statusas T sritis automatika atitikmenys: angl. sampled signal vok. abgetastetes Signal, n rus. дискретный сигнал, m pranc. signal échantillonné, m; signal discret, m … Automatikos terminų žodynas

дискретный сигнал — Сигнал, описываемый дискретной функцией времени … Политехнический терминологический толковый словарь

дискретный сигнал времени — diskretinamojo laiko signalas statusas T sritis radioelektronika atitikmenys: angl. discrete time signal vok. diskretes Zeitsignal, n rus. дискретный сигнал времени, m pranc. signal discret de temps, m … Radioelektronikos terminų žodynas

Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия

Дискретный — (от лат. discretus раздельный, прерывистый). Это прилагательное может употребляться в разных контекстах: В дискретной математике дискретным называется счётное множество, эта концепция также важна в комбинаторике и теории вероятностей. В общей… … Википедия

дискретный — 4.2.6 дискретный: Относящийся к данным, которые состоят из отдельных элементов, таких как символы, или к физическим величинам, имеющим конечное число различных распознаваемых значений, а также к процессам и функциональным блокам, использующим эти … Словарь-справочник терминов нормативно-технической документации

Источник

Аналоговые, дискретные и цифровые сигналы

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Сигнал называют аналоговым, если он определен на непрерывной оси времени , и в каждый момент может принимать произвольные значения. Аналоговый сигнал может быть представлен непрерывной, или кусочно-непрерывной функции переменной . Пример аналогового сигнала показан на рисунке 1.

Если сигнал принимает произвольные значения только в фиксированные моменты времени , — целое число, то такой сигнал называется дискретным. Наиболее широкое распространение получили дискретные сигналы, определенные на равноотстоящей сетке , где — интервал дискретизации. При этом в моменты дискретизации дискретный сигнал может принимать произвольные значения. Если значения дискретного сигнала также берутся на фиксированной сетке значений, и при этом сами значения могут быть представлены числом конечной разрядности в одной из систем счисления, то такой дискретный сигнал называется цифровым . Часто говорят, что цифровой сигнал представляет собой квантованный по уровню дискретный сигнал. Примеры дискретного и цифрового сигналов также показаны на рисунке 1. Тонкая разница между дискретными и цифровыми сигналами дает возможность их отождествлять практически во всех прикладных задачах. Аналоговый сигнал может быть описан функцией времени, в то время как дискретный и цифровой сигналы могут быть заданы вектором отсчетов :

Указанные преимущества определили повсеместное распространение цифровых систем хранения и обработки сигналов. Но цифровые сигналы также имеют и недостатки по сравнению с аналоговыми.

Во-первых нет возможности передавать цифровые сигналы «как есть», поскольку передача сигналов чаще всего происходит при использовании электромагнитных и акустических волн, которые являются непрерывными во времени. Поэтому для передачи цифровых сигналов требуются дополнительные методы цифровой модуляции, а также цифро-аналоговые преобразователи (ЦАП).

Другим недостатком цифровых сигналов является меньший динамический диапазон сигнала (т.е. отношение самого большого значения к самому маленькому), из-за квантования сигнала на фиксированной сетке значений.

В данном параграфе мы рассмотрим способ выборки дискретных значений аналогового сигнала. Структурная схема устройства дискретизации показана на рисунке 2. Данное устройство называется аналого-цифровой преобразователь (АЦП), потому что оно преобразует аналоговый сигнал в набор оценок дискретных значений , где — целое число, взятых через равноотстоящие промежутки времени .

Временны́е осциллограммы, поясняющие принцип работы устройства показаны на рисунке 3 (см. [1, стр. 475–476], или [2, стр. 438]).

На входе АЦП имеется аналоговый сигнал . Генератор импульсов формирует равноотстоящие стробирующие импульсы , которые управляют ключом, в результате чего на вход усилителя подаются короткие выборки сигнала длительности , взятые через интервал дискретизации .

Оценка дискретного сигнала может быть представлена в виде

Интегрируя на каждом интервале длительности стробирующего импульса получим оценку значения сигнала в момент времени . При конечной величине мы можем говорить об оценке значения сигнала в момент времени с некоторой погрешностью, ввиду изменения сигнала на интервале . Поэтому мы используем шапочку над обозначением , чтобы подчеркнуть приближенную оценку.

При уменьшении длительности погрешность оценки будет уменьшаться, и в пределе мы можем получить дискретный сигнал как:

Бесконечная сумма смещенных дельта-функций называется решетчатой функцией и обозначается [3, стр. 77]:

Тогда математической моделью дискретного сигнала будет произведение исходного аналогового сигнала на решетчатую функцию:

Графически модель дискретного сигнала , с использованием решетчатой функции показана на рисунке 4.

Для получения численных значений дискретного сигнала необходимо проинтегрировать дискретный сигнал (5) в окрестности :

В дальнейшем мы будем широко использовать данную модель дискретного сигнала для перехода от методов анализа и обработки аналоговых сигналов, к цифровым.

Пусть исходный аналоговый сигнал описывает изменение напряжения во времени и имеет размерность вольт . Вспомним, что дельта-функция Дирака имеет размерность, обратную размерности ее аргумента. Тогда решетчатая функция , согласно (4) имеет размерность , а размерность дискретного сигнала (5) будет .

Заметим, что значения дискретного сигнала, полученные из (6) как результат интегрирования дискретного сигнала в окрестности момента времени , будут иметь размерность исходного сигнала .

В данном разделе мы проанализируем спектральную плотность решетчатой функции . Для начала рассмотрим как периодический сигнал. Тогда можно представить в виде разложения в ряд Фурье:

Источник

Аналоговые, дискретные и цифровые сигналы

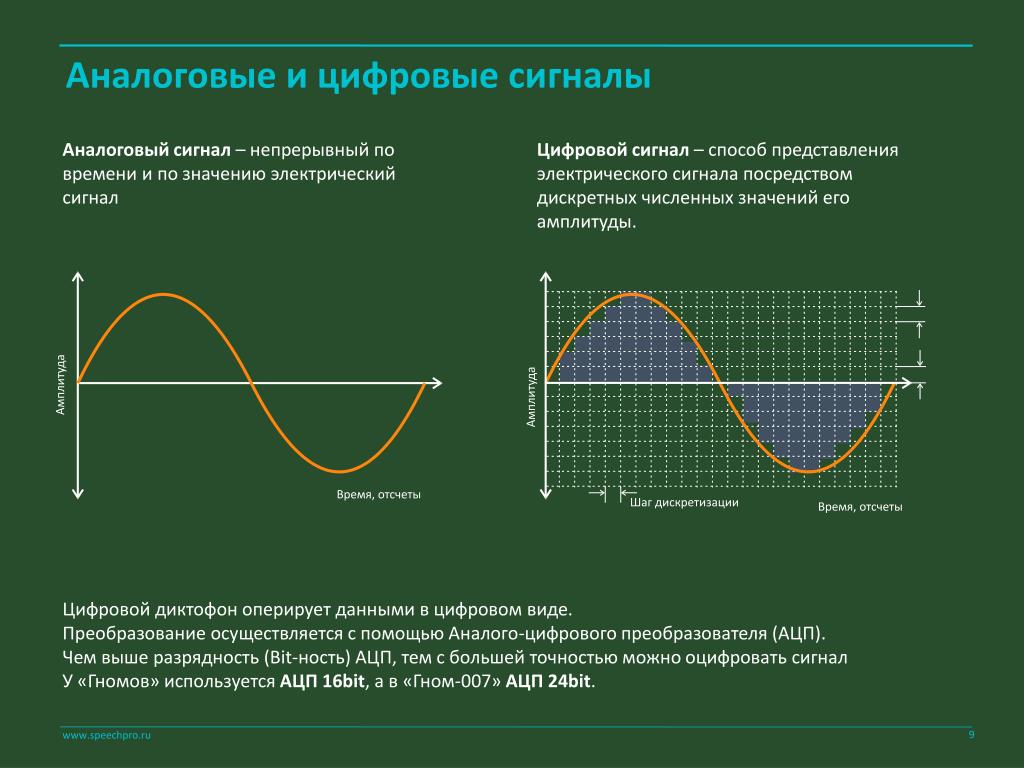
Любая физическая величина по характеру изменения ее значения может быть постоянной (если она имеет только одно фиксированное значение), дискретной (если она может иметь два или более фиксированных значений), или аналоговой (если она может иметь бесчисленное множество значений). Все эти величины могут быть преобразованы в цифровую форму.

Аналоговые сигналы

Аналоговым называется такой сигнал, который может быть представлен непрерывной линией из множества значений, определенных в каждый момент времени относительно временной оси. Значения аналогового сигнала произвольны в каждый момент времени, поэтому он может быть в принципе представлен как некая непрерывная функция (зависящая от времени как от переменной) либо как кусочно-непрерывная функция времени.

Аналоговым сигналом можно назвать, например, звуковой сигнал, генерируемый обмоткой электромагнитного микрофона или ламповым акустическим усилителем, поскольку такой сигнал непрерывен и его значения (напряжение или ток) сильно отличаются друг от друга в каждый момент времени.

На приведенном ниже рисунке изображен пример подобного рода аналогового сигнала.

Аналоговые величины могу иметь бесконечное множество значений в определенных пределах. Они непрерывны и их значения не могут изменяться скачками.

Пример аналогового сигнала: термопара передает в аналоговом виде значение температуры в программируемый логический контроллер, который управляет с помощью твердотельного реле температурой в электрической печи.

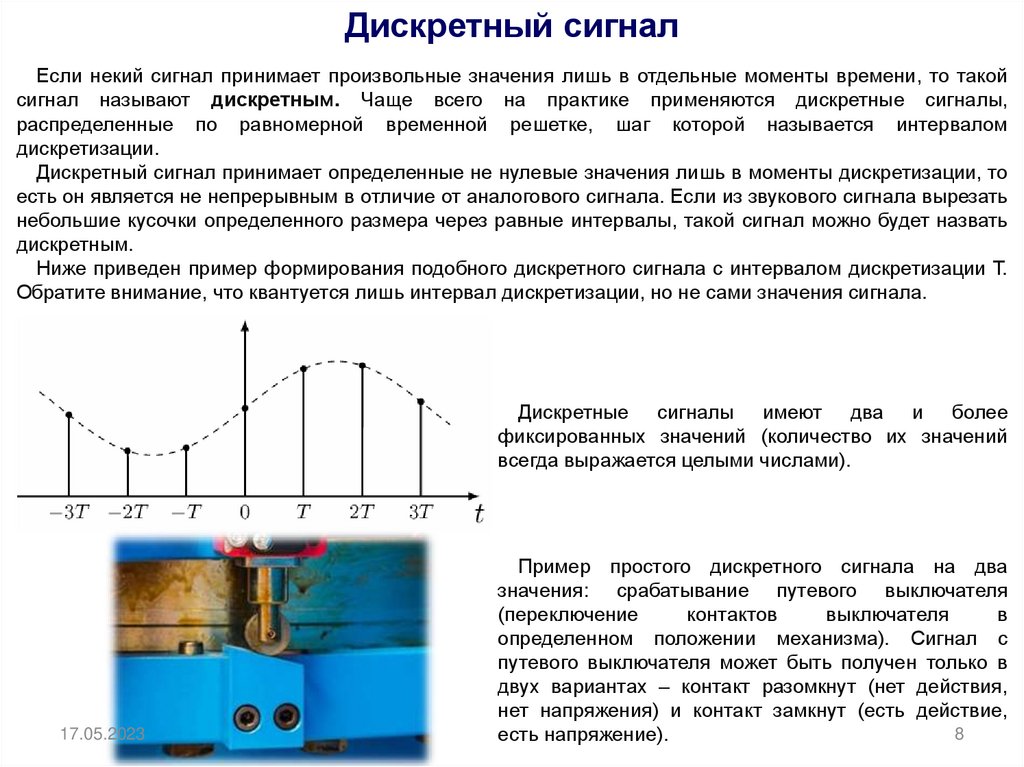
Дискретные сигналы

Если некий сигнал принимает произвольные значения лишь в отдельные моменты времени, то такой сигнал называют дискретным. Чаще всего на практике применяются дискретные сигналы, распределенные по равномерной временной решетке, шаг которой называется интервалом дискретизации.

Дискретный сигнал принимает определенные не нулевые значения лишь в моменты дискретизации, то есть он является не непрерывным в отличие от аналогового сигнала. Если из звукового сигнала вырезать небольшие кусочки определенного размера через равные интервалы, такой сигнал можно будет назвать дискретным.

Ниже приведен пример формирования подобного дискретного сигнала с интервалом дискретизации Т. Обратите внимание, что квантуется лишь интервал дискретизации, но не сами значения сигнала.

Дискретные сигналы имеют два и более фиксированных значений (количество их значений всегда выражается целыми числами).

Пример простого дискретного сигнала на два значения: срабатывание путевого выключателя (переключение контактов выключателя в определенном положении механизма). Сигнал с путевого выключателя может быть получен только в двух вариантах — контакт разомкнут (нет действия, нет напряжения) и контакт замкнут (есть действие, есть напряжение).

Цифровые сигналы

Когда дискретный сигнал принимает только какие-то фиксированные значения (которые могут быть расположены по сетке с определенным шагом), такие что они могут быть представлены как количество квантовых величин, такой дискретный сигнал называется цифровым. То есть цифровой сигнал — это такой дискретный сигнал, который квантован не только по промежуткам времени, но и по уровню.

Практически дискретные и цифровые сигналы в ряде задач отождествляются, и могут быть легко заданы в форме отсчетов с помощью вычислительного устройства.

На рисунке приведен пример формирования цифрового сигнала на базе аналогового. Обратите внимание, что значения цифрового сигнала не могут принимать промежуточных значений, а только определенные — целое количество вертикальных шагов сетки.

Цифровой сигнал легко записывается и перезаписывается в память вычислительных устройств, просто считывается и копируется без потери точности, тогда как перезапись аналогового сигнала всегда сопряжена с утратой некоторой, пусть и незначительной, части информации.

Обработка цифровых сигналов позволяет получать устройства с очень высокими характеристиками благодаря выполнению вычислительных операций совершенно без потерь качества, либо с пренебрежимо малыми потерями.

В силу этих достоинств, именно цифровые сигналы повсеместно распространены сегодня в системах хранения и обработки данных. Вся современная память — цифровая. Аналоговые носители информации (такие как пленочные кассеты и т.д.) давно ушли в прошлое.

Аналоговый и цифровой приборы для измерения напряжения:

Но даже у цифровых сигналов есть свои недостатки. Их невозможно передать напрямую как есть, ибо передача обычно реализуется посредством непрерывных электромагнитных волн. Поэтому при передаче и приеме цифровых сигналов необходимо прибегать к дополнительной модуляции и аналого-цифровому преобразованию. Меньший динамический диапазон цифровых сигналов (отношение наибольшего значения к наименьшему), обусловленный квантованностью значений по сетке, является еще одним их недостатком.

Существуют и такие области, где аналоговые сигналы незаменимы. Например аналоговый звук никогда не сравнится с цифровым, поэтому ламповые усилители и пластинки до сих пор не выходят из моды, несмотря на обилие цифровых форматов записи звука с самой высокой частотой дискретизации.

Источник

Дискретный (цифровой) и аналоговый сигнал: отличия

p, blockquote 1,0,0,0,0 —>

p, blockquote 2,0,0,0,0 —>

Аналоговый сигнал

p, blockquote 3,0,0,0,0 —>

p, blockquote 4,0,0,0,0 —>

p, blockquote 5,0,0,0,0 —>

Что такое дискретный сигнал

p, blockquote 6,0,0,0,0 —>

p, blockquote 7,0,0,0,0 —>

p, blockquote 8,0,1,0,0 —>

p, blockquote 9,0,0,0,0 —>

Чем отличается непрерывный сигнал от дискретного

p, blockquote 10,0,0,0,0 —>

Аналоговые данные не кодируются и не шифруются, просто отображаются в электрические или электромагнитные импульсы. Приёмник преобразовывает импульсы в полном соответствии с полученным сигналом. Передаваемый и принимаемый импульс многогранен и характеризуются постоянным плавным изменением с течением времени. Величина и частота определяют параметры информации. Примером может быть соответствие определённого цвета экрана заданному напряжению. С течением времени цвета плавно меняются следуя изменению напряжения.

p, blockquote 12,0,0,0,0 —>

Цифровая технология использует совсем иной принцип передачи. Аналоговые данные сначала кодируются и только потом передаются. Кодировка заключается в описании непрерывной кривой аналоговой информации. В каждый конкретный момент времени, передаваемый импульс имеет значение единицы или нуля, и определенная последовательность битов отображает всю полноту оригинальной картинки или звука.

p, blockquote 14,0,0,0,0 —>

p, blockquote 15,0,0,0,0 —>

p, blockquote 16,1,0,0,0 —>

Оба вида связи не лишены недостатков, а ключевыми отличиями являются:

p, blockquote 17,0,0,0,0 —>

Аналоговый подвержен помехам и поступает с искажениями. В то время как цифровой доходит полностью без искажений или отсутствует вовсе.
Принять или перехватить аналоговое вещание может любой приёмник такого принципа. Дискретная передача адресована конкретному адресату, кодируется и мало доступна к перехвату.
Объём передаваемых данных у аналоговой связи конечен, поэтому она практически исчерпала себя в передаче теле сигнала. Напротив с развитием технологии преобразования аналоговой информации в цифровой код растут объемы и качество трансляции. Например, главным отличием цифрового от аналогового телевидения является превосходное качество изображения.

p, blockquote 18,0,0,0,0 —>

Как аналоговый сигнал преобразуется в цифровой и наоборот

p, blockquote 19,0,0,0,0 —>

p, blockquote 20,0,0,0,0 —>

p, blockquote 21,0,0,0,0 —>

Существует много видов АЦП, но самыми распространёнными являются следующие:

p, blockquote 22,0,0,0,0 —>

параллельного преобразования;
последовательного приближения;
дельта-сигма, с балансировкой заряда.

p, blockquote 23,0,0,0,0 —>

Упрощенно работу любого АЦП можно представить так:

p, blockquote 24,0,0,1,0 —>

Измерение через определенные интервалы времени амплитуды напряжения.
Сравнение с эталоном и формирование данных.
Отгрузка оцифрованных сведений об изменениях амплитуды на передатчик.

p, blockquote 25,0,0,0,0 —>

Как выглядят спектры аналогового и дискретного сигнала

p, blockquote 26,0,0,0,0 —>

p, blockquote 27,0,0,0,0 —>

p, blockquote 28,0,0,0,0 —>

p, blockquote 29,0,0,0,0 —>

Какие системы связи используют цифровой сигнал а какие аналоговый

p, blockquote 30,0,0,0,0 —>

p, blockquote 31,0,0,0,0 —>

Список книг помогающих разобраться в аналоговых и цифровых сигналах

Более подробно изучить и сравнить принципы обработки и передачи данных можно прочитав следующую литературу:

p, blockquote 32,0,0,0,0 —>

Сато Ю. Обработка сигналов. Первое знакомство. / Пер. с яп.; под ред. Ёсифуми Амэмия. — М: Изд-кий дом «Додэка-XXI», 2002. Книга даёт основы знаний о способах ЦОС. Адресована радиолюбителям, студентам и школьникам, только начинающим изучение систем передачи данных.
Введение в цифровую фильтрацию /под ред. Р. Богнера и А. Константинидиса; перевод с англ. — М: Изд-во «Мир», 1977. В этой книге популярно и доступно изложена информация о различных системах обработки данных. Сравниваются аналоговая и цифровая системы, описаны плюсы и минусы.
Основы цифровой обработки сигналов: Курс лекций /Авторы: А.И. Солонина, Д.А. Улахович, С.М. Арбузов, Е.Б. Соловьев, И.И. Гук. — СПб: Изд-во «БХВ-Петербург», 2005. Книга написана по курсу лекций для студентов ГУТ им. Бонч-Бруевича. Изложены теоретические основы обработки данных, описаны дискретные и цифровые системы разных способов преобразования. Предназначена для изучения в вузах и повышения квалификации специалистов.
Сергиенко А.Б. Цифровая обработка сигналов (второе издание) — СПб: Изд-во «Питер», 2006. Электронный учебно-методический комплекс по дисциплине «Цифровая обработка сигналов». Представлены курс лекций, лабораторный практикум и методические рекомендации по самостоятельной работе. Предназначена для преподавателей и самостоятельного изучения для студентов уровня подготовки бакалавр.
Лайонс Р. Цифровая обработка сигналов. 2-е изд. Пер. с англ. – М.: ООО «Бином-Пресс», 2006. Книга представляет подробную информацию о ЦОС. Написана понятным языком и снабжена большим количеством иллюстрации. Одна из самых простых и понятных книг на русском языке.

p, blockquote 33,0,0,0,1 —>

Источник

Дискретность. Принципы и применение. Сигнал и работа. Особенности

Дискретность в переводе с латинского языка обозначает прерывистость. Данное понятие применяется в различных отраслях науки, в частности электронике, физике, биологии, математике и так далее. В электронике существует понятие дискретного сигнала, предусматривающее передачу информации в условиях изменения возможных значений передающей среды. Кроме этого прерывистость используется и в других более щепетильных сферах, к примеру, в микроэлектронике. В частности при разработке дискретных схем представляющих собой элементы линий связи.

Как применяется дискретность в электронике

Существующие современные технологии связи, в том числе и разработанные для этого компьютерные программы, обеспечивают передачу голоса, являющегося звуковым потоком. При этом разработчики подобного оборудования и программного обеспечения сталкиваются с тем, что голосовой поток это непрерывная волна, передача которой возможна только на канале с высокой пропускной способностью. Его применение слишком затратно как в плане ресурсов, так и финансово. Эта проблема решается использованием принципов дискретности.

Дискретный сигнал представляет собой вместо стандартной непрерывной волны специальное цифровое выражение, способное ее описать. С установленной частотой параметры волны конвертируются в цифровую информацию и отправляются для приема. Фактически, получается обеспечить связь с минимальным применением ресурсов и энергии.

Дискретность позволяет существенно уменьшить суммарный поток данных, формируя из него пакетную передачу. При этом благодаря тому, что соблюдается выборка волны с промежутками между работой и паузами, то исключается вероятность искажения. Создается гарантия, что отправленная часть пакетных данных будет доставлена по предназначению, а за ней уже передастся следующая часть. В случае же с обыкновенными волнами, возможность помех намного выше.

Примеры простейшей дискретности

Учебники по физике для объяснения понятия дискретности при применении его к сигналу зачастую приводят аналогию с печатной книгой. Так, при ее чтении воспринимается непрерывный поток изложенной информации. При этом фактически вся изложенная в ней информация это код, состоящий из набора букв, пробелов и знаков препинания. Изначально способ общения человека – это голос, но посредством письма возможно записать звук с помощью буквенного кода. При этом, если рассматривать в плане емкости в килобайтах или мегабайтах, то объем напечатанного текста будет занимать меньше места, чем его звуковая запись.

Возвращаясь к примеру с книгой получается, что ее автор создает определенный дискретный сигнал, разбивая звуковой поток на блоки и излагая их определенным способом кодирования, то есть письменным языком. Сам читатель открывающий книгу посредством своих знаний в кодировании и мысли объединяет дискретные буквы в непрерывный информационный поток. Данный пример весьма удачно помогает упрощенным языком объяснить зачем нужна дискретность и почему она так тесно связана с сигналами, применяемыми в электронике.

Простым примером визуальной дискретности можно назвать старые рисованные мультфильмы. Их кадр состоял из десятков картинок, которые шли друг за другом с небольшими паузами. Каждая последующая картинка немного изменяется, поэтому глазу человека кажется, что персонажи на экране двигаются. Именно благодаря дискретности вообще возможно формировать движущееся изображение.

Пример с рисованными мультфильмами отображает лишь часть свойства дискретности. Аналогичная технология применяется и при создании видео. Стоит вспомнить диафильмы или старые кинопленки, когда на одной длинной ленте идет множество маленьких картинок, при изменении которых создается эффект движения на экране. Хотя современные технологии и отошли от материальных носителей кадров такого плана, но по-прежнему используется принцип дискретности, хотя и видоизмененный.

Дискретный сигнал

Данное понятие позволяет отобразить противоположное явления непрерывному сигналу. При использовании непрерывности одним из проявлений выступает звуковая волна с определенной амплитудой и частотой, которая транслируется постоянно без пауз. Хотя и существует несколько вполне эффективных способов обработки непрерывного или так называемого аналогового сигнала, позволяющих уменьшить объем информационного потока, но они не так действенны. Использование дискретной переработки позволяет делать оборудование менее объемным и отказаться от дорогостоящих коммуникаций. В электронике понятие дискретный и цифровой сигнал это практически одно и то же.

К неоспоримым достоинствам дискретного сигнала можно отнести:

Возможность избежать искажения информации.
Обеспечение высокой помехоустойчивости, что возможно в результате применения кодирования информации.
Возможность архивирования данных для сохранения ресурсов носителей.
Обеспечение возможности трансляции информации из различных источников по единому каналу.
Наличие упрощенного математического описания.

Не лишена дискретность и недостатков. При ее использовании требуется применение высоких технологий, в связи с чем ответственные детали электронных механизмов теряют возможность проведения кустарного ремонта. При серьезной поломке требуется замена отдельных агрегатов. Кроме этого возможна частичная потеря информации, которая заключена в дискретном сигнале.

Способы реализации дискретности при работе с сигналами

Как уже было выяснено, дискретный сигнал представляет собой последовательность цифровых закодированных значений. Существуют различные способы кодирования, но одним из самых популярных считаются двоичные цифровые сигналы. Они используются практически во всех электронных устройствах, поскольку легко кодируются и декодируются.

Дискретный цифровой сигнал имеет два значения «1» и «0». Для передачи данных создается импульсное напряжение. После генерации импульса принимающее его устройство воспринимает часть сигнала как «1», а последующую после этого паузу как «0». Декодирующая аппаратура оценивает частоту подаваемых импульсов и проводит их восстановление в изначальные данные. Если рассматривать график дискретного сигнала, можно увидеть, что переход между нулевым и максимальным значением происходит мгновенно. График состоит из прямоугольных углов, когда линия между верхним и нижним значением не имеет плавного перехода. Благодаря этому принимающая аппаратура считывает информацию четко, тем самым исключаются помехи, поскольку даже слабо принятый импульс будет читаться как максимум, то есть «1», а пауза как «0».

Хотя дискретность и способна значительно уменьшить образование помех, но не может исключить их полное отсутствие. Если имеется большой уровень шума цифрового потока, то восстановить данные из полученных сигналов невозможно. В случае же с непрерывными аналоговыми сигналами можно применять различные фильтры, чтобы убрать искажения и восстановить информацию. Именно поэтому принцип дискретности применяется далеко не всегда.

Техническая реализация принципов дискретности

Дискретные сигналы используются для записи на известные носители, такие как CD, DVD и так далее. Их читают цифровые проигрыватели, мобильные телефоны, модемы и практически любое техническое оборудование, которым все пользуются ежедневно. Все мультимедийные технологии состоят из устройств сжатия, кодировки и декодировки, что и позволяет работать с дискретными сигналами.

Даже те сферы, которые изначально использовали непрерывные технологии передачи данных, начинают отказываться от такого способа и внедряют дискретность. Вся современная аудиотехника работает именно по такому способу. Также происходит постепенный отказ от аналового телевещания. Отсутствие резкого перехода с одной технологии на вторую наблюдается благодаря тому, что дискретный сигнал можно обратно конвертировать в аналоговый. Это обеспечивает определенную совместимость разных систем.

Если рассматривать еще примеры оборудования, где применяются принципы дискретности, то к таким примерам можно отнести:

Звуковые карты.
Электронные музыкальные инструменты.
Навигаторы.
Цифровые фотоаппараты.

Сфера применения принципа дискретности очень обширна. В связи с этим оборудование, где он внедряется, значительно прогрессирует, при этом удобство применения такой аппаратуры многократно возрастает.

Источник

Аналоговые, дискретные и цифровые сигналы

Содержание

Обнаружили ошибку? Выделите ее мышью и нажмите

Вводные понятия

Рисунок 1. Аналоговый, дискретный и цифровой сигналы

(1)

Вектор отсчетов цифрового сигнала может быть помещен в память вычислительного устройства с возможность многократной перезаписи и копирования без потери точности, в то время как перезапись и копирование аналоговых сигналов неизбежно сопровождается потерей части информации. Кроме того, обработка цифровых сигналов позволяет добиться потенциально-возможных характеристик устройств, ввиду возможности выполнения вычислительных операций без потерь, или с пренебрежимо малыми потерями качества.

Дискретизация аналоговых сигналов. Математическая модель дискретного сигнала

Рисунок 2. Структурная схема аналого-цифрового преобразователя

Рисунок 3. Временны́е осциллограммы АЦП

Оценка дискретного сигнала может быть представлена в виде

(2)

где — прямоугольный импульс длительности единичной амплитуды, который мы уже рассматривали в предыдущих разделах.

(3)

где — смещенная на дельта-функция Дирака, которую мы подробно рассматривали в одном из предыдущих разделов.

Бесконечная сумма смещенных дельта-функций называется решетчатой функцией и обозначается [3, стр. 77]:

(4)

где индекс указывает временной интервал следования дельта-функций.

(5)

Заметим, что (5) уже не является приближенной оценкой, а представляет собой истинную модель дискретного сигнала.

Графически модель дискретного сигнала , с использованием решетчатой функции показана на рисунке 4.

Рисунок 4. Модель дискретного сигнала
на основе решетчатой функции

(6)

где — конечный интервал интегрирования дискретного сигнала в окрестности .

Размерность дискретного сигнала

Преобразование Фурье решетчатой функции

(7)

где , рад/с — частота дискретизации,

(8)

Тогда (7) с учетом (8):

(9)

Заметим, что знак аргумента комплексной экспоненты выражения (9) можно изменить, потому что суммирование ведется от минус бесконечности до бесконечности с положительными и отрицательными . Тогда:

(10)

Выражение (10) представляет как бесконечную сумму комплексных экспонент.

Рассмотрим теперь преобразование Фурье решетчатой функции:

(11)

Поменяем операции интегрирования и суммирования и применим фильтрующее свойство дельта-функции:

(12)

Выражение (12) также представляет собой бесконечную сумму комплексных экспонент. Учтем, что и получим:

(13)

Сравнивая (13) с (10) можно заключить, что:

(14)

Таким образом, спектральная плотность решетчатой функции представляет собой также решетчатую функцию.

Период повторения дельта-функций в частотной области равен , при этом дельта-функции масштабируются в раз, как это показно на рисунке 5.

Рисунок 5. Решетчатая функция:
а — временно́е представление; б — спектральная плотность

Заметим, что умножение на в частотной области изменяет размерность спектральной плотности , в результате чего спектральная плотность переходит в безразмерный спектр (что не удивительно, потому что исходная решетчатая функция — периодическая).

Спектральная плотность дискретного сигнала

\label{discrete_introduction:ft_discrete} Пусть дан аналоговый сигнал , спектральная плотность которого равна . В данном параграфе мы рассмотрим процесс равноотстоящей дискретизации сигнала в частотной области.

Преобразование Фурье дискретного сигнала (5) равно:

(15)

Применим свойство преобразования Фурье произведения сигналов, тогда представляет собой свертку спектральной плотности решетчатой функции и спектральной плотности исходного сигнала :

(16)

Преобразуем (16), используя фильтрующее свойство дельта-функции:

(17)

Уравнение (17) задает спектральную плотность дискретного сигнала как бесконечную сумму масштабированных копий спектральной плотности , отстоящих друг от друга на рад/с по частоте, как это показано на рисунке 6.

Рисунок 6. Спектральная плотность дискретного сигнала

Заметим, что мы не накладываем никаких ограничений ни на интервал дискретизации , ни на сигнал , ни на спектральную плотность . Вне зависимости от частоты дискретизации рад/с, и формы , спектральная плотность дискретного сигнала всегда будет представлять собой сумму масштабированных копий , отстоящих друг от друга на величину частоты дискретизации рад/с.

Размерность спектра дискретного сигнала

Проанализируем выражение (17) на предмет размерности , в предположении, что исходный аналоговый сигнал имеет размерность :

(18)

Таким образом, из (18) можно заключить, что при дискретизации сигнала, его спектральная плотность переходит в спектр, а размерность спектра дискретного сигнала совпадает с размерностью исходного аналогового сигнала .

Если аналоговый сигнал описывает изменения напряжения во времени и измеряется в единицах вольт, то при дискретизации аналогового сигнала, получим дискретные отсчеты, также измеряемые в вольт, и спектр дискретного сигнала также будет измеряться в единицах вольт. Тогда функцию мы можем назвать спектром, а не спектральной плотностью.

Главный вывод: преобразование Фурье дискретного сигнала не изменяет размерности дискретных отсчетов сигнала, в отличии от преобразования Фурье аналогового сигнала, которое возвращает спектральную плотность .

Выводы

В данном разделе мы ввели понятие дискретного и цифрового сигналов. Мы опеределили, что дискретный сигнал может быть представлен как результат произведения решетчатой функции и аналогового сигнала.

Были детально рассмотрены свойства решетчатой функции и показано, что спектральная плотность решетчатой функции также представляет собой масштабированную по амплитуде решетчатую функцию.

В результате свойств решетчатой функци получили, что спектральная плотность дискретного сигнала представляется бесконечной суммой копий спектральных плотностей исходного сигнала, отставленных дург от друга на величину равную частоте дискретизации.

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Информация была полезна? Поделитесь с друзьями!

Facebook

Twitter

Мой мир

Вконтакте

Одноклассники

Список литературы

[1] Гоноровский И.С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[2] Баскаков, С.И. Радиотехнические цепи и сигналы. Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3] Bracewell R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 07.02.2021 (14:06:14)

Страница создана Latex to HTML translator ver. 5.20.11.14

9 Дискретные сигналы — СтудИзба

9. Дискретные сигналы

Мы рассмотрели в предыдущих разделах методы описания аналоговых сигналов и ряд способов их преобразования: модуляцию, детектирование и фильтрацию. После осуществления модуляции сигнала, его усиления, высокочастотной фильтрации, демодуляции и низкочастотной фильтрации формируется сигнал постоянного тока, пропорциональный первичному сообщению. В таком виде сигнал может быть выведен на отчетное устройство или на самописец с целью его регистрации.

Теперь обратимся к другому классу сигналов – к дискретным сигналам и способам их преобразований. Аналоговый сигнал преобразуют в дискретный сигнал с целью его ввода в цифровой процессор. Здесь можно осуществить в цифровой форме самую изощренную обработку сигналов с целью выделения из них максимума информации, необходимой для решения поставленных перед Вами целей.

9.1 Аналого-цифровое и цифро-аналоговое преобразования

Обобщенная структура системы цифровой обработки сигналов представлена на рис. 9.1.

На вход поступает аналоговый сигнал x(t).

Дискретный потенциальный сигнал — Большая Энциклопедия Нефти и Газа, статья, страница 1

Дискретный потенциальный сигнал

Cтраница 1

Дискретный потенциальный сигнал, представляемый скачкообразным изменением постоянного ( а) тока или постоянной составляющей периодического ( б) тока. [1]

Дискретные потенциальные сигналы Um, Us и UB поступают в логическую часть ЛЧ синхронизаторов, которая разрешает или запрещает формирование управляющего воздействия УВ на включение выключателя. [2]

При параллельном коде импульсы или дискретные потенциальные сигналы появляются одновременно на соответствующих выходах функционального элемента. Рассмотренные сигналы целесообразно объединить в две основные группы — аналоговую и дискретную. К аналоговым относятся непрерывные и дискретно-непрерывные сигналы, к дискретным — собственно дискретные, в частности цифровые, и непрерывно — дискретные. Таким образом, две основные группы сигналов определяются непрерывностью или дискретностью информационных параметров несущих процессов вне зависимости от непрерывности или дискретности времени. [3]

Как выполняется логический элемент запоминания дискретного потенциального сигнала ( статический триггер) на интегральных микроэлементах ИЛИ-НЕ ( далее см. гл. [4]

Как выполняется логический элемент запоминания дискретного потенциального сигнала ( статический триггер) на интегральных микроэлементах ИЛИ — НЕ. [5]

Различие состояний потенциального триггера определяется наличием или отсутствием на его выходе дискретного потенциального сигнала. Входной сигнал может быть как потенциальным, так и импульсным. Потенциальный триггер осуществляется на основе усилителя постоянного тока с сильной положительной обратной связью, обеспечивающей релейность его проходной характеристики. Отличительной особенностью характеристики триггера является ее симметричное положение относительно вертикальной оси. [7]

Элемент DX2 имеет третий — инверсный вход для выполнения логической операции ЗАПРЕТ дискретным потенциальным сигналом неисправности СН от автоматического устройства контроля АУК — автоматической диагностики. [8]

В функциональной схеме автоматического устройства РПВ ( рис. 48.26) применяются контактные элементы формирования дискретных потенциальных сигналов, а именно: элемент пуска ЭП, запрета действия ЗД, разрешения подготовки к новому действию — возврату в исходное состояние РВ, защитного сигнала, предотвращающего ложные действия РПВ при перерывах его питания от источника постоянного напряжения Еп — элемент ЗП, элемент управления ЭУ выходным реле KL и элемент информационных сигналов ИС о действии РПВ. [9]

В зависимости от этого угла элемент ЭСФ формирует соответствующий сигнал и на выходах реле KF1 — KF3 появляются дискретные потенциальные сигналы, соответствующие частоте срабатывания реле. [10]

Схема времяимпульсного ЭС, приведенная на рис. 12.16, а, функционирует по способу сравнения длительности tal ВИП, в частности арккосинусного типа ( см. рис. 8.2), с импульсом эталонной длительности устанавливаемой элементом временной задержкиDT1 формирования дискретного потенциального сигнала U и — задержки действия ЭС. [11]

Как указывалось, напряжение на выходе инвертора 1) с / ( рис. 13.22) при срабатывании реле дискретно изменяется от С / вых0 — Еп — 15 В до U j 0, что и соответствует формированию выходного дискретного потенциального сигнала. [12]

Более сложной является логическая часть ЛЧ автоматического устройства ликвидации асинхронного режима ( рис. 14.7), содержащего четыре измерительных реле: направленных реле сопротивления KZ1, KZ2, KZ3 и измерительного реле активной мощности KW с двумя выходами с дискретными потенциальными сигналами ( логическими единицами), формируемыми при превышениях мощностями различных направлений предписанных ( установленных) значений. Они выявляют асинхронный режим в отличие от синхронных качаний в электроэнергетической системе и коротких замыканий. [13]

Орган сравнения фаз токов КАВ на выводах фильтров ZA (, двух полукомплектов устройства защиты представляет собой элемент сравнения фаз двух синусоидальных величин ( см. § 12.3) релейного действия ЭСФ РД. Он формирует дискретный потенциальный сигнал при углах сдвига фаз между токами соответствующих КЗ на защищаемой ВЛ. Сигнал поступает на верхний вход элемента DA ( И) логической части ЛЧ, на нижний вход которого приходит дискретный сигнал от элемента DfF2 ( ИЛИ) при поступлении на его вход одного ( или всех) сигнала orKAZ2 0, КА или KZ. При этом электромеханическими ( реле KL) или тиристорными исполнительными элементами формируются отключающие воздействия Ху2 на выключатели Q, Q2 линии. [14]

Страницы: 1 2

Discrete Signal — обзор

Periodic-Discrete

Это дискретные сигналы, которые периодически повторяются от отрицательной до положительной бесконечности. Этот класс преобразования Фурье иногда называют дискретным рядом Фурье, но чаще всего его называют дискретным преобразованием Фурье .

Вы могли подумать, что названия, данные этим четырем типам преобразований Фурье, сбивают с толку и плохо организованы. Ты прав; имена эволюционировали довольно бессистемно за 200 лет.Вы ничего не можете сделать, кроме как запомнить их и двигаться дальше.

Все эти четыре класса сигналов простираются до положительной и отрицательной бесконечности . Вы говорите, держитесь! Что, если у вас есть только конечное количество образцов, хранящихся в вашем компьютере, скажем, сигнал, сформированный из 1024 точек. Нет ли версии преобразования Фурье, которая использует сигналы конечной длины? Нет, нет. Волны синуса и косинуса определены как как простирающиеся от отрицательной бесконечности до положительной бесконечности. Вы не можете использовать группу бесконечно длинных сигналов, чтобы синтезировать что-то конечной длины.Чтобы решить эту дилемму, нужно сделать так, чтобы конечные данные выглядели как — сигнал бесконечной длины. Это делается путем представления, что сигнал имеет бесконечное количество выборок слева и справа от фактических точек. Если все эти «воображаемые» выборки имеют нулевое значение, сигнал выглядит дискретным и апериодическим , и применяется дискретное временное преобразование Фурье. В качестве альтернативы воображаемые образцы могут быть дублированием реальных 1024 точек. В этом случае сигнал выглядит дискретным и периодическим с периодом 1024 отсчета.Это требует использования дискретного преобразования Фурье.

Как оказалось, для синтеза сигнала апериодического требуется бесконечное количество синусоид . Это делает невозможным вычисление дискретного преобразования Фурье в компьютерном алгоритме. По исключению единственный тип преобразования Фурье, который может использоваться в DSP, — это DFT. Другими словами, цифровые компьютеры могут работать только с информацией, длина которой составляет дискретных и конечных длины.Когда вы боретесь с теоретическими проблемами, решаете домашние задания и размышляете над математическими загадками, вы можете обнаружить, что используете первых трех членов семейства преобразований Фурье. Когда вы садитесь за компьютер, вы будете использовать только DFT. Мы кратко рассмотрим эти другие преобразования Фурье в следующих главах. А пока сконцентрируйтесь на понимании дискретного преобразования Фурье.

Вернитесь к примеру разложения ДПФ на рис. 8-1. На первый взгляд, это сигнал из 16 точек, разложенный на 18 синусоид, каждая из которых состоит из 16 точек.Говоря более формально, 16-точечный сигнал, показанный на (а), следует рассматривать как один период бесконечно длинного периодического сигнала. Аналогично, каждая из 18 синусоид, показанных на (b), представляет собой сегмент из 16 точек из бесконечно длинной синусоиды. Имеет ли значение, рассматриваем ли мы это как 16-точечный сигнал, синтезируемый из 16-точечных синусоид, или как бесконечно длинный периодический сигнал, синтезируемый из бесконечно длинных синусоид? Ответ: обычно нет, но иногда да . В следующих главах мы встретимся со свойствами ДПФ, которые кажутся сбивающими с толку, если рассматривать сигналы как конечные, но станут очевидными, если учесть периодический характер.Ключевым моментом для понимания является то, что эта периодичность вызывается для использования математического инструмента , то есть ДПФ. Обычно это бессмысленно с точки зрения того, где возник сигнал или как он был получен.

Каждое из четырех преобразований Фурье можно разделить на реальных и комплексных версий. Реальная версия является самой простой, с использованием обычных чисел и алгебры для синтеза и разложения. Например, рис. 8-1 представляет собой пример реального ДПФ .Сложные версии четырех преобразований Фурье намного сложнее и требуют использования комплексных чисел и . Это такие числа, как: 3+ 4j , где j равно -1 (инженеры-электрики используют переменную j , а математики используют переменную i ). Сложная математика может быстро стать непосильной даже для тех, кто специализируется на DSP. Фактически, основная цель этой книги — представить основы DSP без использования сложных математических вычислений, что позволит понять материал более широкому кругу ученых и инженеров.Сложные преобразования Фурье — это область деятельности тех, кто специализируется на DSP и готов погрузиться в болото математики. Если вы так склонны, главы 30–3330313233 доставят вас туда.

Математический термин преобразование широко используется в цифровой обработке сигналов, например: преобразование Фурье, преобразование Лапласа, преобразование Z, преобразование Гильберта, дискретное косинусное преобразование и т. Д. Что такое преобразование? Чтобы ответить на этот вопрос, вспомните, что такое функция .Функция — это алгоритм или процедура, которые изменяют одно значение на другое значение. Например, y = 2 x + 1 — это функция. Вы выбираете какое-то значение для x , вставляете его в уравнение, и выдает значение для y . Функции также могут преобразовывать несколько значений в одно значение, например: y = 2 a + 3 b + 4 c , где a, b и c заменяются на y .

Преобразования

являются прямым продолжением этого, позволяя как входу, так и выходу иметь нескольких значений .Предположим, у вас есть сигнал, состоящий из 100 выборок. Если вы разработаете какое-то уравнение, алгоритм или процедуру для преобразования этих 100 выборок в другие 100 выборок, у вас есть преобразование. Если вы считаете, что он достаточно полезен, у вас есть полное право прикрепить к нему свою фамилию и изложить его достоинства своим коллегам. (Это лучше всего работает, если вы выдающийся французский математик 18 века.) Преобразования не ограничиваются каким-либо конкретным типом или количеством данных. Например, у вас может быть 100 выборок дискретных данных для входа и 200 выборок дискретных данных для выхода.Точно так же у вас может быть непрерывный сигнал для входа и непрерывный сигнал для выхода. Также разрешены смешанные сигналы, дискретные входящие и непрерывные выходящие и наоборот. Короче говоря, преобразование — это любая фиксированная процедура, которая преобразует один фрагмент данных в другой. Давайте посмотрим, как это применимо к рассматриваемой теме: дискретное преобразование Фурье.

2.4: Сигналы в дискретном времени — Engineering LibreTexts

Цели обучения

Сигналы могут быть представлены дискретными величинами, а не функцией непрерывной переменной.
Эти дискретные временные сигналы не обязательно должны принимать действительные числовые значения.
Многие свойства непрерывных сигналов передаются почти напрямую в дискретную область.

До сих пор мы рассматривали так называемые аналоговые сигналы и системы . Математически аналоговые сигналы — это функции, имеющие в качестве независимых переменных непрерывные величины, такие как пространство и время. Сигналы дискретного времени — это функции, определенные на целых числах; это последовательности.Один из фундаментальных результатов теории сигналов детализирует условия, при которых аналоговый сигнал может быть преобразован в сигнал с дискретным временем и получить без ошибки . Этот результат важен, потому что дискретными сигналами времени можно управлять с помощью систем, созданных как компьютерные программы. Последующие модули описывают, как практически вся обработка аналоговых сигналов может выполняться с помощью программного обеспечения.

Какими бы важными ни были такие результаты, сигналы с дискретным временем носят более общий характер и включают сигналы, полученные из аналоговых сигналов и , которые таковыми не являются.Например, символы, образующие текстовый файл, образуют последовательность, которая также является сигналом дискретного времени. Мы также должны иметь дело с такими символически значимыми сигналами и системами.

Как и в случае с аналоговыми сигналами, мы ищем способы разложения сигналов дискретного времени с действительным знаком на более простые компоненты. Благодаря этому подходу, ведущему к лучшему пониманию структуры сигнала, мы можем использовать эту структуру для представления информации (создавать способы представления информации с помощью сигналов) и для извлечения информации (извлекать информацию, представленную таким образом).Для сигналов с символическими значениями используется другой подход: мы разрабатываем общее представление всех сигналов с символическим значением, чтобы объединить содержащуюся в них информацию. С точки зрения представления информации наиболее важным вопросом становится эффективность как для сигналов с действительным, так и для символьных значений; Каков наиболее экономичный и компактный способ представления информации для последующего извлечения.

Реальные и комплексные сигналы

Сигнал с дискретным временем представлен символически как с (n), , где n = {…, — 1,0,1 …}. Обычно мы рисуем сигналы с дискретным временем в виде основных графиков, чтобы подчеркнуть тот факт, что это функции, определенные только для целых чисел. Мы можем задержать дискретный сигнал на целое число, как и с аналоговыми. Отсроченная единичная выборка имеет выражение

δ (n − m) δ (n − m) \ [\ delta (n-m) \]

и равняется единице, если n = m .

Рис. 2.4.1 Косинусоидальный сигнал в дискретном времени отображается в виде основного графика. Вы можете найти формулу этого сигнала?

Комплексные экспоненты

Самым важным сигналом, конечно же, является комплексная экспоненциальная последовательность .{i2 \ pi fn} \]

Синусоиды

Синусоиды дискретного времени имеют очевидную форму

\ [s (n) = A \ cos (2 \ pi fn + \ varphi) \]

В отличие от аналоговых комплексных экспонент и синусоид, частота которых может быть любой действительной величиной, частоты их аналогов в дискретном времени дают уникальные формы сигнала только , когда f лежит в интервале (-½, ½). Это свойство можно легко понять, заметив, что добавление целого числа к частоте комплексной экспоненты с дискретным временем не влияет на значение сигнала.{i2 \ pi fn} \]

Этот вывод следует из того, что комплексная экспонента, вычисленная как целое число, кратное 2π , равна единице.

Единица Образец

Вторым по важности сигналом дискретного времени является единичная выборка , которая определена как

\ [\ delta (n) = 1 \; если\; п = 0 \\ \ дельта (п) = 0 \; в противном случае \]

Рис. 2.4.2. Единичная выборка

Исследование графика дискретного сигнала, аналогичного графику косинусоидального сигнала, показанного на рис.{\ infty} s (m) \ delta (n-m) \]

Этот вид разложения уникален для сигналов с дискретным временем и впоследствии окажется полезным.

Системы с дискретным временем могут воздействовать на сигналы с дискретным временем таким же образом, как и в аналоговых сигналах и системах. Из-за роли программного обеспечения в системах с дискретным временем можно представить и «сконструировать» гораздо больше различных систем с помощью программ, чем с помощью аналоговых сигналов. Фактически, особый класс аналоговых сигналов может быть преобразован в сигналы с дискретным временем, обработан с помощью программного обеспечения и преобразован обратно в аналоговый сигнал, и все это без появления ошибки.Для таких сигналов системы могут быть легко созданы в программном обеспечении с эквивалентными аналоговыми реализациями, которые трудно, если не невозможно, спроектировать.

Символьные сигналы

Еще один интересный аспект сигналов с дискретным временем состоит в том, что их значения не обязательно должны быть действительными числами. У нас есть действительные сигналы с дискретным временем, такие как синусоида, но у нас также есть сигналы, которые обозначают последовательность символов, набранных на клавиатуре. Такие символы определенно не являются действительными числами, и как набор возможных значений сигналов они имеют небольшую математическую структуру, кроме того, что они являются членами набора.Более формально, каждый элемент символьного сигнала s (n) принимает одно из значений {a ₁, …. a _K} , которые составляют алфавит A . Эта техническая терминология не означает, что мы ограничиваем символы только членами английского или греческого алфавита. Они могут представлять символы клавиатуры, байты (8-битные величины), целые числа, передающие суточную температуру. Независимо от того, управляются ли они программным обеспечением или нет, системы с дискретным временем в конечном итоге состоят из цифровых схем, которые состоят из полностью аналоговых схемных элементов.Кроме того, передача и прием сигналов с дискретным временем, таких как электронная почта, осуществляется с помощью аналоговых сигналов и систем. Понимание того, как взаимосвязаны дискретные и аналоговые сигналы и системы, возможно, является основной целью этого курса.

Дискретная связь | теория информации

В теории информации: четыре типа связи

Дискретные сигналы могут представлять только конечное число различных распознаваемых состояний. Например, буквы английского алфавита обычно считаются дискретными сигналами.Непрерывные сигналы, также известные как аналоговые сигналы, обычно используются для передачи величин, которые могут изменяться в пределах… \ n

Подробнее

Бесшумная связь

В теории информации: от алфавита сообщений к алфавиту сигналов
Для бесшумной связи декодер на принимающая сторона получает в точности символы, отправленные кодировщиком. Однако эти передаваемые символы обычно не входят в алфавит исходного сообщения. Например, в азбуке Морзе короткие и длинные электрические импульсы, световые вспышки или звуки с надлежащим интервалом … \ n
Подробнее

шумная связь

В теории информации: коды для исправления и обнаружения ошибок
… работают в область дискретной, зашумленной связи указала на возможность построения кодов с исправлением ошибок.Коды с исправлением ошибок добавляют дополнительные биты для исправления ошибок и, таким образом, работают в направлении, противоположном сжатию. Коды обнаружения ошибок, с другой стороны, указывают на то, что ошибка произошла, но не происходит автоматически… \ n
Подробнее
В теории информации: дискретная, зашумленная связь и проблема ошибки
\ nВ обсуждении выше это нереально предположить, что все сообщения передаются без ошибок. В реальном мире, однако, ошибки передачи неизбежны — особенно с учетом присутствия в любом канале связи шума, который является суммой… \ n
Подробнее

появление в нервной системе

В теории информации: физиология
После в целом нервная система — это, прежде всего, канал передачи информации, а мозг — это, помимо прочего, центр обработки информации и обмена сообщениями.Поскольку нервные сигналы обычно состоят из импульсов электрической энергии, нервная система является примером… \ n
Подробнее

«,» url «:» Introduction «,» wordCount «: 0,» sequence «: 1} , «imarsData»: {«INFINITE_SCROLL»: «», «HAS_REVERTED_TIMELINE»: «false»}, «npsAdditionalContents»: {}, «templateHandler»: {«name»: «INDEX», «metered»: false}, » paginationInfo «: {» previousPage «: null,» nextPage «: null,» totalPages «: 1},» seoTemplateName «:» PAGINATED INDEX «,» infiniteScrollList «: [{» p «: 1,» t «: 709369} ], «familyPanel»: {«topicLink»: {«title»: «Дискретное общение», «url»: «/ topic / diste-communication»}, «tocPanel»: {«title»: «Directory», «itemTitle «:» Ссылки «,» toc «: null},» groups «: [],» showCommentButton «: false,» fastFactsItems «: null},» byline «: {» members «: null,» allContributorsUrl «: null, «lastModificationDate»: null, «contentHistoryUrl»: null, «warningMessage»: null, «warningDescription»: null}, «citationInfo»: {«участники»: null, «title»: «Дискретное общение», «lastModification»: null , «url»: «https: // www.britannica.com/topic/discrete-communication»},»websites»:null,»lastArticle»:false}

Узнайте об этой теме в этих статьях:

дискретных сигналов

В теории информации: четыре типа связи
Дискретные сигналы могут представлять только конечное число различных распознаваемых состояний.Например, буквы английского алфавита обычно считаются дискретными сигналами. Непрерывные сигналы, также известные как аналоговые сигналы, обычно используются для передачи величин, которые могут изменяться в пределах…
Подробнее

Бесшумная связь

Теория информации: От алфавита сообщений к алфавиту сигналов
Для бесшумной связи декодер на принимающей стороне принимает точно символы, отправленные кодировщиком. Однако эти передаваемые символы обычно не входят в алфавит исходного сообщения.Например, в азбуке Морзе, правильно распределенные короткие и длинные электрические импульсы, световые вспышки или звуки…
Подробнее

шумная связь

В теории информации: Коды исправления и обнаружения ошибок
… работа в области дискретной, зашумленной связи указала на возможность построения кодов исправления ошибок. Коды с исправлением ошибок добавляют дополнительные биты для исправления ошибок и, таким образом, работают в направлении, противоположном сжатию.Коды обнаружения ошибок, с другой стороны, указывают на то, что ошибка произошла, но не автоматически…
Подробнее
В теории информации: дискретная, шумная связь и проблема ошибки
В приведенном выше обсуждении нереалистично предполагается, что все сообщения передаются без ошибок. Однако в реальном мире ошибок передачи невозможно избежать — особенно с учетом присутствия в любом канале связи шума, который является суммой…
Подробнее

Возникновение в нервной системе

В теории информации: физиология
В конце концов, нервная система — это, прежде всего, канал для передачи информации, а мозг — это, помимо прочего, информация центр обработки и обмена сообщениями.Поскольку нервные сигналы обычно состоят из импульсов электрической энергии, нервная система кажется примером …
Подробнее

Аналоговые и цифровые сигналы: использование, преимущества и недостатки | Статья

Получайте ценные ресурсы прямо на свой почтовый ящик — рассылается раз в месяц

Мы ценим вашу конфиденциальность

Сигнал — это электромагнитный или электрический ток, по которому данные передаются из одной системы или сети в другую.В электронике сигнал часто представляет собой изменяющееся во времени напряжение, которое также является электромагнитной волной, несущей информацию, хотя он может принимать другие формы, например ток. В электронике используются два основных типа сигналов: аналоговые и цифровые. В этой статье обсуждаются соответствующие характеристики, использование, преимущества и недостатки, а также типичные применения аналоговых и цифровых сигналов.

Аналоговый сигнал

Аналоговый сигнал изменяется во времени и обычно привязан к диапазону (например,грамм. От +12 В до -12 В), но в этом непрерывном диапазоне существует бесконечное количество значений. Аналоговый сигнал использует заданное свойство среды для передачи информации о сигнале, например, электричество, движущееся по проводу. В электрическом сигнале напряжение, ток или частота сигнала могут изменяться для представления информации. Аналоговые сигналы часто представляют собой рассчитанные реакции на изменения света, звука, температуры, положения, давления или других физических явлений.

При построении графика зависимости напряжения отНа временном графике аналоговый сигнал должен давать плавную и непрерывную кривую. Не должно быть никаких дискретных изменений значения (см. Рисунок 1) .

Рисунок 1: Аналоговый сигнал

Цифровой сигнал

Цифровой сигнал — это сигнал, который представляет данные как последовательность дискретных значений. Цифровой сигнал может принимать только одно значение из конечного набора возможных значений в данный момент времени. В случае цифровых сигналов физическая величина, представляющая информацию, может быть различной:

Переменный электрический ток или напряжение
Фаза или поляризация электромагнитного поля
Акустическое давление
Намагничивание магнитного носителя информации

Цифровые сигналы используются во всей цифровой электронике, включая вычислительное оборудование и устройства передачи данных.При нанесении на график зависимости напряжения от времени цифровые сигналы имеют одно из двух значений и обычно находятся в диапазоне от 0 В до VCC (обычно 1,8 В, 3,3 В или 5 В) (см. Рисунок 2) .

Аналоговая электроника

Большинство основных электронных компонентов — резисторы, конденсаторы, катушки индуктивности, диоды, транзисторы и операционные усилители (операционные усилители) — по своей сути являются аналоговыми компонентами. Схемы, построенные из комбинации этих компонентов, представляют собой аналоговые схемы (см. Рисунок 3) .

Рисунок 3: Аналоговая схема

Аналоговые схемы могут иметь сложную конструкцию с несколькими компонентами или могут быть простыми, например, двумя резисторами, которые образуют делитель напряжения. Как правило, аналоговые схемы проектировать сложнее, чем цифровые схемы, выполняющие ту же задачу. Чтобы разработать аналоговый радиоприемник или аналоговое зарядное устройство для батареи, потребуется проектировщик, знакомый с аналоговыми схемами, поскольку для упрощения этих конструкций были приняты цифровые компоненты.

Аналоговые схемы обычно более восприимчивы к шуму, а «шум» — это любые небольшие нежелательные изменения напряжения.Небольшие изменения уровня напряжения аналогового сигнала могут привести к значительным ошибкам при обработке.

Аналоговые сигналы обычно используются в системах связи, которые передают голос, данные, изображение, сигнал или видеоинформацию с использованием непрерывного сигнала. Существует два основных типа аналоговой передачи, которые основаны на том, как они адаптируют данные для комбинирования входного сигнала с сигналом несущей. Двумя методами являются амплитудная модуляция и частотная модуляция. Амплитудная модуляция (AM) регулирует амплитуду несущего сигнала.Частотная модуляция (FM) регулирует частоту несущего сигнала. Аналоговая передача может быть достигнута разными способами:

Через витую пару или коаксиальный кабель
Через оптоволоконный кабель
По радио
По воде

Подобно тому, как человеческое тело использует глаза и уши для захвата сенсорной информации, аналоговые схемы используют эти методологии для взаимодействия с реальным миром, а также для точного захвата и обработки этих сигналов в электронике.

MPS производит множество аналоговых ИС и компонентов, таких как MP2322, синхронный понижающий преобразователь с низким I _Q в крошечном корпусе QFN размером 1,5 x 2 мм.

Цифровая электроника

Цифровые схемы реализуют такие компоненты, как логические вентили или более сложные цифровые ИС. Такие ИС представлены прямоугольниками с выходящими из них выводами (см. Рисунок 4) .

Рисунок 4: Цифровая схема

Цифровые схемы обычно используют двоичную схему.Хотя значения данных представлены только двумя состояниями (0 и 1), большие значения могут быть представлены группами двоичных битов. Например, в 1-битной системе 0 представляет значение данных 0, а 1 представляет значение данных 1. Однако в 2-битной системе 00 представляет 0, 01 представляет 1, 10 представляет 2, а 11 представляет 3. В 16-битной системе наибольшее число, которое может быть представлено, равно 216 или 65 536. Эти группы битов могут быть захвачены либо как последовательность последовательных битов, либо через параллельную шину.Это позволяет легко обрабатывать большие потоки данных.

В отличие от аналоговых схем, наиболее полезные цифровые схемы являются синхронными, что означает наличие опорных часов для координации работы схемных блоков, поэтому они работают предсказуемым образом. Аналоговая электроника работает асинхронно, то есть обрабатывает сигнал по мере его поступления на вход.

Большинство цифровых схем используют цифровой процессор для обработки данных. Это может быть простой микроконтроллер (MCU) или более сложный процессор цифровых сигналов (DSP), который может фильтровать и обрабатывать большие потоки данных, например видео.

Цифровые сигналы обычно используются в системах связи, где цифровая передача может передавать данные по каналам передачи «точка-точка» или «точка-многоточка», таким как медные провода, оптические волокна, средства беспроводной связи, носители данных или компьютерные шины. Передаваемые данные представлены в виде электромагнитного сигнала, например микроволнового, радиоволны, электрического напряжения или инфракрасного сигнала.

В общем, цифровые схемы легче спроектировать, но они часто стоят дороже, чем аналоговые схемы, предназначенные для тех же задач.

Каталог цифровых компонентов

MPS включает MP2886A, цифровой многофазный ШИМ-контроллер с интерфейсом PWM-VID, совместимый со спецификацией NVIDIA Open VReg.

Преобразование аналогово-цифрового (АЦП) и цифро-аналогового (ЦАП) сигнала

Многие системы должны обрабатывать как аналоговые, так и цифровые сигналы. Во многих системах связи обычно используется аналоговый сигнал, который действует как интерфейс для среды передачи для передачи и приема информации.Эти аналоговые сигналы преобразуются в цифровые, которые фильтруют, обрабатывают и сохраняют информацию.

Рисунок 5 показывает общую архитектуру, в которой аналоговый РЧ-интерфейс (AFE) состоит из всех аналоговых блоков для усиления, фильтрации и усиления аналогового сигнала. Между тем, секция процессора цифровых сигналов (DSP) фильтрует и обрабатывает информацию. Для преобразования сигналов из аналоговой подсистемы в цифровую подсистему в тракте приема (RX) используется аналого-цифровой преобразователь (ADC).Для преобразования сигналов из цифровой подсистемы в аналоговую подсистему в тракте передачи (TX) используется цифро-аналоговый преобразователь (DAC).

Рисунок 5: Система связи с аналоговыми и цифровыми подсистемами

Цифровой сигнальный процессор (DSP) — это специализированный микропроцессорный чип, который выполняет операции цифровой обработки сигналов. DSP изготавливаются на интегральных схемах MOSFET и широко используются в обработке аудиосигналов, телекоммуникациях, цифровой обработке изображений, телевизионных продуктах высокой четкости, обычных бытовых электронных устройствах, таких как мобильные телефоны, и во многих других важных приложениях.

DSP используется для измерения, фильтрации или сжатия непрерывных реальных аналоговых сигналов. Выделенные DSP часто имеют более высокую энергоэффективность, что делает их пригодными в портативных устройствах из-за ограничений по энергопотреблению. Большинство микропроцессоров общего назначения также могут выполнять алгоритмы цифровой обработки сигналов.

Работа АЦП

Рисунок 6 показывает работу АЦП. На вход поступает аналоговый сигнал, который обрабатывается схемой удержания выборки (S / H) для создания приближенного цифрового представления сигнала.Амплитуда больше не имеет бесконечных значений и была «квантована» до дискретных значений в зависимости от разрешения АЦП. АЦП с более высоким разрешением будет иметь более мелкие размеры шага и более точно представлять входной аналоговый сигнал. Последний каскад АЦП кодирует оцифрованный сигнал в двоичный поток битов, который представляет амплитуду аналогового сигнала. Цифровой вывод теперь можно обрабатывать в цифровом виде.

Рисунок 6: Типичная архитектура АЦП для преобразования аналогового сигнала в цифровой

Работа ЦАП

ЦАП обеспечивает обратную работу.Вход ЦАП представляет собой двоичный поток данных из цифровой подсистемы и выводит дискретное значение, которое аппроксимируется как аналоговый сигнал. По мере увеличения разрешения ЦАП выходной сигнал все больше приближается к истинному плавному и непрерывному аналоговому сигналу (см. Рисунок 7). Обычно в цепи аналогового сигнала есть постфильтр для дальнейшего сглаживания формы волны.

Рисунок 7: 6-битный ЦАП для цифро-аналогового преобразования сигнала

Как упоминалось ранее, многие системы, используемые сегодня, представляют собой «смешанные сигналы», что означает, что они полагаются как на аналоговые, так и на цифровые подсистемы.Эти решения требуют, чтобы АЦП и ЦАП преобразовывали информацию между двумя доменами.

Сравнение цифровых сигналов и аналоговых сигналов: преимущества и недостатки

Как и в большинстве инженерных тем, у аналоговых и цифровых сигналов есть свои плюсы и минусы. Конкретное приложение, требования к производительности, среда передачи и операционная среда могут определять, следует ли использовать аналоговую или цифровую сигнализацию (или их комбинацию).

Цифровые сигналы: преимущества и недостатки

Преимущества использования цифровых сигналов, включая цифровую обработку сигналов (DSP) и системы связи, включают следующее:

Цифровые сигналы могут передавать информацию с меньшим шумом, искажениями и помехами.
Цифровые схемы можно легко воспроизводить в массовых количествах при сравнительно небольших затратах.
Цифровая обработка сигналов более гибкая, поскольку операции DSP можно изменять с помощью систем с цифровым программированием.
Цифровая обработка сигналов более безопасна, поскольку цифровая информация может быть легко зашифрована и сжата.
Цифровые системы более точны, и вероятность появления ошибок можно снизить за счет использования кодов обнаружения и исправления ошибок.
Цифровые сигналы могут быть легко сохранены на любом магнитном носителе или оптическом носителе с использованием полупроводниковых микросхем.
Цифровые сигналы могут передаваться на большие расстояния.

К недостаткам использования цифровых сигналов, в том числе систем цифровой обработки сигналов (DSP) и систем связи, относятся следующие:

Для цифровой связи требуется более широкая полоса пропускания по сравнению с аналоговой передачей той же информации.
DSP обрабатывает сигнал на высоких скоростях и содержит больше внутренних аппаратных ресурсов.Это приводит к более высокому рассеянию мощности по сравнению с обработкой аналогового сигнала, которая включает пассивные компоненты, потребляющие меньше энергии.
Цифровые системы и обработка обычно более сложные.

Аналоговые сигналы: преимущества и недостатки

Преимущества использования аналоговых сигналов, включая системы обработки аналоговых сигналов (ASP) и связи, включают следующее:

Аналоговые сигналы легче обрабатывать.
Аналоговые сигналы лучше всего подходят для передачи аудио и видео.
Аналоговые сигналы имеют гораздо более высокую плотность и могут предоставлять более точную информацию.
Аналоговые сигналы используют меньшую полосу пропускания, чем цифровые сигналы.
Аналоговые сигналы обеспечивают более точное представление изменений физических явлений, таких как звук, свет, температура, положение или давление.
Аналоговые системы связи менее чувствительны с точки зрения электрических допусков.

Недостатки использования аналоговых сигналов, включая системы обработки аналоговых сигналов (ASP) и системы связи, включают следующее:

Передача данных на большие расстояния может привести к нежелательным помехам сигнала.
Аналоговые сигналы склонны к потере генерации.
Аналоговые сигналы подвержены шумам и искажениям, в отличие от цифровых сигналов, которые имеют гораздо более высокую устойчивость.
Аналоговые сигналы обычно имеют более низкое качество, чем цифровые сигналы.

Аналоговые и цифровые сигналы: системы и приложения

В традиционных аудиосистемах и системах связи используются аналоговые сигналы. Однако с развитием технологий обработки кремния, возможностей цифровой обработки сигналов, алгоритмов кодирования и требований к шифрованию — в дополнение к увеличению эффективности использования полосы пропускания — многие из этих систем стали цифровыми.Они по-прежнему являются некоторыми приложениями, в которых аналоговые сигналы имеют устаревшее использование или преимущества. Большинство систем, которые взаимодействуют с реальными сигналами (такими как звук, свет, температура и давление), используют аналоговый интерфейс для захвата или передачи информации. Несколько приложений аналогового сигнала перечислены ниже:

Запись и воспроизведение звука
Датчики температуры
Датчики изображения
Радиосигналы
Телефоны
Системы управления

MPS предлагает широкий ассортимент аналоговых компонентов, включая MP2322, MP8714, MP2145 и MP8712.

Хотя многие оригинальные системы связи использовали аналоговую сигнализацию (телефоны), современные технологии используют цифровые сигналы из-за их преимуществ, таких как помехоустойчивость, шифрование, эффективность использования полосы пропускания и возможность использования ретрансляторов для передачи на большие расстояния. Ниже перечислены несколько приложений для цифровых сигналов:

Системы связи (широкополосная, сотовая)
Сеть и передача данных
Цифровые интерфейсы для программирования

Посетите наш веб-сайт, чтобы узнать больше о цифровых компонентах MPS, таких как MP2886A, MP8847, MP8868, MP8869S и MP5416.

Заключение

В этой статье представлены некоторые основные концепции аналоговых и цифровых сигналов и их использование в электронике. У каждой технологии есть явные преимущества и недостатки, и знание потребностей вашего приложения и требований к производительности поможет вам определить, какой сигнал (ы) выбрать.

_________________________

Вам это показалось интересным? Получайте ценные ресурсы прямо на свой почтовый ящик — рассылайте их раз в месяц!

Получить техническую поддержку

Разделение сигнала структуры посредством дискретного вейвлет-преобразования максимального перекрытия и быстрого преобразования Фурье

Спектральная плотность мощности (PSD) используется для оценки процесса вибрации конструкции.Более того, PSD не только показывает дискретную форму вибрации, но также представляет различные компоненты в структуре вибрации. Наложение нескольких шаблонов вибрации на один и тот же спектр затрудняет анализ спектральной информации таким образом, чтобы найти дискретную вибрацию конструкции. В этой статье предлагается метод разделения синтетического вибрационного сигнала на дискретную вибрацию конструкции и другие посторонние колебания с использованием метода дискретного вейвлет-преобразования с максимальным перекрытием (MODWT) в сочетании с методом быстрого преобразования Фурье (FFT).С помощью комбинации этих двух алгоритмов, MODWT и FFT, сигналы синтезированной вибрации были разделены на составляющие сигналы с различными частотными диапазонами. Это означает, что будет сформирован PSD, который основан на комбинации отдельных спектров мощности компонентных сигналов. Таким образом, единый спектр каждого из этих построенных компонентов может использоваться для оценки типов дискретных колебаний, сосуществующих в процессе вибрации конструкции. Результаты исследования в этой статье показывают чувствительность и пригодность выбранных типов дискретных колебаний, которые необходимо выделить во время оценки структурных изменений, чтобы достичь наилучшего возможного плана по устранению нежелательных и неожиданных шумовых и вибрационных компонентов.

1. Введение

Извлечение информации из сигналов измерения вибрации конструкции довольно популярно для краткосрочных исследований [1–3]. Фактические сигналы вибрации часто используются во временной области, чтобы оценить изменение сигнала, соответствующее времени. Во временной области параметры, извлеченные из принятого сигнала, будут оценивать изменения качественной структуры во время процедуры работы [4, 5]. Многие исследования перешли из временной области в частотную, чтобы оценить количественные изменения [6–9].Этот аналитический метод будет использовать количественные значения процесса вибрации внутри конструкции. Характеристики вибросигнала обычно выражаются следующим образом: значение дискретной частоты колебаний [10–12], амплитуда колебаний [13], максимальная мощность [14], демпфирование [15] и деформация при удлинении [16]. В лаборатории любая конструкция, подвергнутая достаточно сильной внешней силе, будет вибрировать. Теоретически конструкция примет уникальную вибрацию, соответствующую действию заданной приложенной силы [17].Многие вибрации являются результатом воздействия на конструкцию начальной внешней силы. Но многие другие вибрации могут проявляться как эффект накопления движущих и демпфирующих сил или различных граничных условий. Таким образом, необходимо исключить эти типы посторонних вибраций компонентов, особенно шумовых компонентов, чтобы точно оценить наиболее характерную вибрацию конструкции. Этот анализ позволяет получить больше информации о сигнале за прошедшее время, а также больше информации об изменениях в самой структуре.Для разделения компонентов сигналов используется множество различных алгоритмов, таких как анализ Фурье [18, 19], анализ Калмана [20–22], анализ фильтра Гаусса шума [23–25] и, наиболее широко применяемый алгоритм, вейвлет-анализ [26–31] и многие методы оказались очень эффективными [32, 33]. Объединение вейвлет-анализа с другими алгоритмами повышает эффективность обработки [34]. Однако вейвлет-исследования еще не прояснили существование и влияние шума из-за посторонних вибраций.Кроме того, текущий вейвлет-анализ еще не указывал конкретно на взаимосвязь между компонентами и общими сигналами. С той же точки зрения на исследования в лаборатории, экспериментально наблюдаемые колебания конструкции являются результатом воздействия различных приложенных сил или других случайных сил. И в процессе несения нагрузки на конструкцию, сама конструкция будет испытывать множество форм вибраций, возможно, включая большое количество шумовой вибрации. Это означает, что конструкция будет одновременно совершать множество типов колебаний, включая как дискретные, так и когерентные колебания, в результате чего общий сигнал осциллографа будет содержать слишком много информации.Таким образом, полученный сигнал не совсем подходит для оценки структурных изменений или определения информации, необходимой в измеренное время. Синтез, возникающий в результате множества различных вибраций, делает результаты оценки менее точными, и, одновременно, используемые параметры становятся менее чувствительными, чем ожидалось изначально.

При таком распознавании результаты оценки будут лучше в случае разделения этих синтетических сигналов на дискретные. В этой статье реализован комбинированный метод MODWT и FFT, чтобы анализировать спектр сигнала реальной вибрации путем четкого разделения характеристик каждой вибрации.Это означает, что в статье по-прежнему оценивается изменение сигнала по спектру вибрации, как и в предыдущих исследованиях, но без использования характеристик, извлеченных из общего спектра вибрации [35–37]. Настоящее исследование разделяет этот спектр на дискретные формы, соответствующие формам различных колебаний, и одновременно устраняет составляющие шумовой вибрации. Эта процедура повысит качество оцениваемых параметров, полученных от каждого типа дискретной вибрации для структурных изменений.Результаты этого исследования покажут уникальную частоту вибрации каждой формы вибрации компонентов. Соответственно, эти дискретные колебания можно разделить по их собственным частотам. Кроме того, они образуют резонансную область, в которой будет сосредоточена большая часть образующейся энергии. Таким образом, в исследовании предлагается использовать дискретное вейвлет-преобразование с максимальным перекрытием (MODWT) на основе БПФ, чтобы решить проблему идентификации и разделения этих компонентов. Это исследование также определяет изменение сигнала как во временной области, так и в частотной области.В ходе исследования сигнал исходной вибрации был разделен на составляющие и одновременно аппроксимирован каждый из этих сигналов сигналом либо шума, либо отсутствия шума. Таким образом, каждый отдельный сигнал может представлять колебательную форму исходного сигнала, соответствующую каждой силовой ситуации, действующей на конструкцию. Извлеченный сигнал содержит область частоты вибрации с характеристиками условий ее вибрации, которые можно считать основной формой вибрации.И наоборот, разделенный сигнал не находится в области дискретной частоты вибрации и может рассматриваться как форма шума. Это исследование поможет определить структурные изменения за прошедшее время и внезапные изменения в спектре мощности. Этот обзор поможет выявить тенденцию, порождаемую формами вибрации, встроенными в спектр дискретной мощности вибрации.

2. Теоретическая основа

2.1. Недостатки метода обычного вейвлет-преобразования

Дискретные вейвлет-преобразования считаются анализом с множественным разрешением.Этот анализ применяется к фильтрации шума и разделению полей во время обработки данных [38]. В реальной вибрации каждый вибрирующий сигнал имеет свою частотную характеристику. Однако некоторые типы сигналов являются посторонними и часто называются шумовыми сигналами. Как правило, сигнал, анализируемый с помощью вейвлет-преобразования, обычно состоит из двух дискретных компонентов в зависимости от области распределенной частоты: области низких частот и области высоких частот. Однако во многих предыдущих исследованиях [26–31] высокочастотное значение в значительной степени вызвано шумом или нежелательными внешними факторами окружающей среды.Дискретное вейвлет-преобразование способно разложить исходный сигнал на две составляющие, аппроксимацию и подробные компоненты, представленные следующим образом:

В соответствии с методикой анализа множественного разложения, любые сигналы x ( t ) могут быть переписаны как сумма сигналов последовательного приближения и детальных составляющих. Это означает, что функция x ( t ) ограничена суммой разложенных сигналов и ее собственным последовательным приближением.Следовательно, с предложением из этой статьи для разницы между двумя последовательными сигналами с разрешением 2 ^{j −1} и 2 ^j разрешение представляет собой подробный сигнал с разрешением 2 ^j. Функция ϕ ( t ) обозначает пропорциональную функцию двух последовательных сигналов, а ψ ( t ) обозначает вейвлет-функцию с вейвлет-коэффициентом { d _{j , n}} , заданный следующим уравнением:

В то же время приближенная функция или коэффициент отношения между двумя последовательными сигналами { c _{j , n}} представлен в следующем уравнении:

Соотношение коэффициента отношения и вейвлет-коэффициента вейвлет-сигнала определяется с помощью уравнений (4a) и (4b): в которых представляет фильтр низкочастотной области, h _k представляет фильтр высокочастотной область, а k — дискретное вейвлет-преобразование для уровней M ^th.Уравнения (4a) и (4b) представляют приблизительный и подробный сигнал с уровнем разрешения j , и он разложен на приблизительный сигнал с уровнем разрешения j -1. В случае проведения обратного анализа во время фазы восстановления сигнала приблизительный сегмент сигнала с уровнем разрешения j -1 рассчитывается из приблизительного сигнала и подробного сигнала с разрешением j по следующему уравнению:

Уравнения (4a), (4b) и (5) реализуются посредством дискретного вейвлет-преобразования (DWT).Для случая, когда данные получены в течение достаточно длительного времени, метод дискретного вейвлет-преобразования больше не является правильным или эффективным, потому что количество шума сигнала будет увеличиваться, когда время измерения сигнала слишком велико [39 , 40]. В этой статье предлагается использовать вместо этого MODWT, который также считается неопределенным дискретным вейвлет-преобразованием.

2.2. Дискретное вейвлет-преобразование с максимальным перекрытием (MODWT)

MODWT [41] строится путем изменения размера фильтров в соответствии со значениями фильтра для заданных низкочастотных и высокочастотных областей из уравнений (4a) и (4b) до и .Тогда значение вейвлет-фильтров MODWT должно соответствовать следующим свойствам: в котором r является ненулевым целым числом, а K обозначает длину вейвлет-волнового фильтра. Фильтр будет масштабирован на {} пропорции с требованием, аналогичным. Граничное условие сигнала во временной области равно. Преобразование MODWT создаст приблизительную функцию сигнала {} и подробную функцию сигнала {} с разрешением j приблизительного сигнала, когда разрешение составляет j — 1, что означает {}.в котором N — ширина выборки сигнала во временной области. Уравнения (7a) и (7b) также можно рассматривать как периодический фильтр исходного сигнала { x _n} с использованием фильтра, как показано на рисунке 1. и, в частности, следующим образом:

Рисунок 1 показано, как исходный сигнал может быть восстановлен следующим образом: при n = 0, 1, 2,…, N — 1. Сосредоточившись на разрешении j , среднее значение вейвлет-коэффициента MODWT { } равен нулю: где и — среднее значение сигнала, проанализированного во временной области.А собственно в уравнении (10). Атрибут, определенный в этой статье, используется при обнаружении изменения сигнала на основе вейвлетов. Уравнение (10) может обнаруживать внезапные скачки среднего значения принятого сигнала. Как правило, метод множественного разрешения MODWT, представленный в статье, помогает разложить исходный сигнал на приблизительные и подробные поля без дискретизации во время такого процесса фильтрации, а также не влияет ни на количество, ни на качество принятого сигнала. Следовательно, случаи разложенных данных могут быть связаны, чтобы восстановить исходный сигнал путем суммирования разложенных сигналов, как показано на рисунке 2.

2.3. Теория настройки спектра плотности мощности с помощью быстрого преобразования Фурье
В статье, построенной на модели, пространство сигнала преобразуется из временной области в частотную, чтобы учесть затухание исходного сигнала методом MODWT. Исходный полученный сигнал представляет собой необработанные данные с большим количеством информации, которую нельзя использовать, если использовать только во временной области. Таким образом, в этой статье показано, как сигналы передаются из временной области в частотную, что будет иметь преимущества по сравнению с их использованием только во временной области.Сигналы, которые в основном используются в частотной области, представляют собой сигналы, реализованные посредством спектрального анализа, и в этом исследовании мы используем спектры плотности мощности. Спектры плотности мощности, необходимые для преобразования Фурье корреляционной функции сигнала во временной области t в двух временных точках τ и T + τ находятся из которых x — данные, соответствующие времени τ и y — данные, соответствующие времени T + τ .Таким образом, уравнение (11) позволяет соотнести два момента сигнала вибрации. Функция корреляции будет оценивать случайность сигнала по разнице между двумя наборами данных. Это помогает оценить стабильность измеренных сигналов вибрации. Согласно теории, Фурье может разделять любые функции на множество различных подкомпонентов, поэтому в этой статье будет применен метод анализа Фурье, чтобы разделить синтезированный сигнал на множество подкомпонентных сигналов с разными соответствующими частотами.Это означает, что исходный сигнал во временной области может быть полностью переписан как сумма сгенерированных из него подфункций. Следовательно, преобразование Фурье сигнала обычно определяется следующей формулой:
Если вы хотите выполнить обратное преобразование из частотной области во временную, выполните следующие действия в соответствии с уравнением
Чтобы решить уравнение (13), предполагая, что числа a и b достаточно велики ( a <0, b > 0), уравнение (13) реализуется следующим образом:
Уравнение (15) называется преобразованием Фурье, и из этого , в статье будет сгенерирована концепция преобразования дискретного анализа Фурье.Соответственно, мы разделим сегмент [ a , b ] на последовательность из N элементов, чтобы вычислить приближенное уравнение (15):
Затем приближенная функция Φ ( ω ) от F ( ω ) дается выражением coining
Подстановка уравнения (18) в уравнение (17) дает
Уравнение (19) приводит к дискретному преобразованию Фурье:
Алгоритм решателя БПФ в этой статье применяется только в случае N = 2 ^s,.При четном N уравнение суммы (20) может быть проанализировано на две суммы подкомпонентов, включая четные и нечетные компоненты h _I сигнала f ( t ), в которой последовательность — это последовательность с четным порядком, а h _I — это последовательность с нечетным порядком. Общие компоненты каждой последовательности имеют N /2 элемента:
Применение дискретного Фурье из уравнения (20) к каждой последовательности в уравнении (21) дает результат
Подстановка уравнения (24) в уравнения (20) — (22) , получаем
Таким образом, значение S _n может быть вычислено согласно известным значениям как и H _n.Однако приведенное выше выражение является правильным только в том случае, если
и H _n не будут определены, когда n велико. Итак, для S _n может быть вычислено в соответствии с периодическими свойствами дискретного преобразования Фурье:
Мы рассматриваем
Из уравнений (28) и (29) получаем
Итак, когда Преобразование Фурье вычисляется следующим образом:
Таким образом, БПФ может обрабатывать автокорреляционную функцию сигналов, чтобы получить спектр плотности мощности в частотной области быстрее, чем это может сделать обычное преобразование Фурье.Мы можем анализировать скрытые компоненты в сигнале, которые иначе не были бы обнаружены при обработке во временной области, путем преобразования сигналов из временной области в частотную. Изменение сигнала также приведет к изменению спектра плотности мощности.
3. Результаты и обсуждение
3.1. Разделение спектра плотности мощности с помощью MODWT модели
Спектр плотности мощности представляет собой преобразование вибрации сигнала из временной области в частотную область посредством преобразования БПФ для функции автокорреляции исходного сигнала.Таким образом, спектр, полученный из вариации исходного сигнала, будет спектром с постоянной частотой. Эта частотная последовательность может содержать различные дискретные частоты разных типов сигналов. Соответственно, этот спектр представляет собой комбинацию спектров плотности мощности дискретных сигналов, которые появляются при получении от некоторой структуры. Кроме того, посредством анализа дискретных вейвлетов с максимальным перекрытием дискретные сигналы и спектры плотности мощности этих дискретных сигналов от типичного спектра могут быть отделены с целью представления общей формы сигнала, как показано на рисунке 3.

Видно, что спектры плотности мощности покрывают каждую дискретную область колебаний. Это показывает, что комбинированный анализ между MODWT и FFT, описанный в этой статье, помог отделить дискретные сигналы от общего принятого сигнала. Как показано на рисунке 3, компонент сигнала разлагается на уровне 4, и на этом уровне типы сигналов почти разлагаются, чтобы показать посторонние вибрации и их влияние на общий кластер сигнала. Следовательно, этот процесс разделения также имеет эффект фильтрации значений помех или нежелательных сигналов в общем сигнале.Исходя из этого, мы можем легко найти типы сигналов, которые необходимо исследовать, а также сигналы конкретных воздействий. Согласно сигналам на Рисунке 4, исследование разделения из общего спектра будет генерировать трехкомпонентные спектры со следующими характеристиками: два спектра имеют гораздо большую спектральную амплитуду, чем другие. Два спектра с большими амплитудами, распределенными по двум различным частотным областям, включают низкочастотную область с диапазоном 5–15 Гц и высокочастотную область, распределенную в диапазоне 30–50 Гц.Однако спектр покрывается в диапазоне 10–40 Гц с очень малой амплитудой, определяемой как количество шума, вызванного во время измерения и обработки данных, или сигналы слишком малы для наблюдения и исследования. Таким образом, два спектра с большими амплитудами, распределенные в двух разных областях в частотной последовательности, являются спектральными формами, сформированными специально рассмотренным нами исходным сигналом. Эти сигналы могут напрямую влиять на субъектов, опрошенных и оцениваемых в этом исследовании.

Таким образом, в ходе исследования были получены два разных типа спектров вибрации для одного и того же исходного сигнала с использованием метода анализа с множественным разрешением MODWT, в котором полученные спектры показали две разные причины ударов по конструкции подшипника.В то же время результаты исследования показывают, что общая PSD является только суммой компонентных спектров, или, другими словами, на основе компонентных спектров мы можем оценить изменение структуры под каждым воздействующим агентом.
3.2. Модель PSD и MODWT в фактическом результате
В действительности спектр мощности сигнала, полученный из структуры, весьма разнообразен, в котором спектр также подвержен влиянию большого количества помех, помимо влияния основных факторов на структуру. .Это вопрос, который уже давно вызывает значительный интерес исследователей. Кроме того, в практических условиях работы, например, при воздействии на мосты, дороги, дома и гражданские постройки, конструкции будут одновременно подвергаться воздействию множества различных факторов. Эти факторы могут быть активными агентами, а это означает, что различные причины активно влияют на строительство сооружений в соответствии с определенными целями и четкими тенденциями. Однако, помимо факторов, вызывающих прямые эффекты, косвенные факторы также могут существенно повлиять на работу проекта.На рисунке 5 показан эксперимент с транспортным средством с рабочими параметрами, показанными в таблице 1, которое проезжает по пролету моста с приблизительно постоянной скоростью в течение рассматриваемого временного интервала.

al
Модуль упругости 207 ГПа
Масса на единицу длины 20,000 кг / м
м
Второй момент площади 0.174 м ⁴
Коэффициент сдвига 5/6
Вязкостное демпфирование балки 1750 Н · с / м
Длина балки 100 м 75 eq 434,39 (кг)
Жесткость пружины K _eq 19097,32 (Н · м ⁻¹)
Коэффициент демпфирования C
84 (Н · с · м ⁻¹)
Скорость 20 (м · с ⁻¹)
Основное влияние на пролет моста критическое воздействие колес, движущихся по мосту, с его колесной системой, как показано на рисунке 5. Система демпфирования оказывает непосредственное влияние во время работы и вызывает вибрацию моста под действием пружинной системы. На рис. 5 показано, что во время работы транспортное средство создает множество различных вибраций, которые воздействуют на конструкцию.В положениях, в которых конструкция контактирует с колесами, основная вибрация в механической системе ( м ₁, C ₁ и k ₁ и м ₂, C ₂ и k ₂), а также генерируется серия шумовых сигналов. Эти типы шумовых сигналов включают количество шума в процессе измерения, шум, создаваемый оборудованием, как показано на рисунке 6, и количество шума, генерируемого во время обработки данных, как показано на рисунке 7.Кроме того, масса транспортного средства ( м ₃) под действием инерции образует третью вибрацию транспортного средства, влияющую на конструкцию. На основании двух положений передних и задних колес и самой массы транспортного средства в ходе исследования были получены сигналы вибрации, вызванной воздействием на пролет моста, путем анализа общей вибрации транспортного средства, воздействующей на мост. Если только один объект влияет на структуру, как показано на рисунке 5, полученные спектры будут такими, как показано на рисунке 8.

Как показано на рисунке 8, для случая, когда конструкция находится под воздействием только одного объекта, в разных положениях измерения по всей структуре результаты аналогичны, а результаты сравнения показаны на Таблица 2. Это свидетельствует о том, что при достаточно сильном воздействии объекта на конструкцию возбудители в близких точках будут похожи друг на друга. Напротив, количество шума, генерируемого в разных положениях, очень различается из-за ограничений граничных условий между объектами, и они показаны на рисунке 8.Однако, хотя это количество шума присутствует непосредственно в измеренных данных, его можно устранить во время обработки данных, как видно из результатов исследования рукописи, с помощью модели разложения MODWT. Следовательно, мы можем полностью удалить составляющие шума, те компоненты, которые не влияют напрямую на структуру, и сохранить только основные составляющие воздействия посредством преобразования вейвлет-преобразователя и спектра мощности.
Габаритные размеры
Корпус Параметры модели автомобиля Значения частот Шум (%)
Габаритные размеры автомобиля Ш × В (мм)
4425 × 1730 × 1475
Габаритные внутренние размеры: ( Г × Ш × C ) (мм) 1895 × 1420 × 1205
Колесная база (мм) 2550
Колесная база ( перед / зад) 1,475 / 1,460 = 50 км / ч 32.5 (Гц) 10
= 65 км / ч 33,3 (Гц) 6,5
= 70 км / ч 33,2 (Гц) 6
2,5-тонный грузовик Hyundai mighty 3735 (мм)
Протектор Передний / задний: 1.650 / 1,495 (мм) = 50 км / ч 25,7 (Гц) 7
= 65 км / ч 24,3 (Гц) 8
= 70 км / ч 24,7 (Гц) 5
5-тонный грузовик Hyundai Размеры D × W × H (мм)
6175 × 2050 × 2260 Размеры автомобиля
D × R × C (мм)
4340 × 1920 × 390
Размер дорожного просвета: 220 (мм)
Вес без нагрузки: 3205 кг
Вес брутто: 8440 кг
Грузоподъемность: 5 тонн = 50 км / ч 12.5 (Гц) 8
= 65 км / ч 11,4 (Гц) 6
= 70 км / ч 11,6 (Гц) 6
20-тонный грузовик Модель железного цилиндра: ZZ1317M3861 V
Полная допустимая нагрузка (кг): 31000
Тип нагрузки (кг): 17800
Габаритные размеры D × W × H (мм)
11182 × 2496 × 4735
Размер ствола D × W × H (мм)
10300 × 2726 × 800
Колесная база (мм): 1800 + 3800 + 1350
Колея передних / задних колес (мм): 2022 ( 2041) / 1830 = 30 км / ч 8.5 (Гц) 6
= 40 км / ч 7,9 (Гц) 5
= 50 км / ч 7,8 (Гц) 5
При съемке одного и того же объекта для модели транспортного средства, много раз движущейся по одной и той же конструкции, результаты показаны на рисунках 9 и 10 в двух случаях (случай 1: ускорение во время движения и случай 2: замедление во время движения). движущийся). В обоих случаях одинаковый спектр получается со значением репрезентативного спектра мощности.Однако разница в этих двух случаях заключается во влиянии шума, величина которого часто меняется в зависимости от характера движения транспортного средства.

В первом случае, когда модель транспортного средства пересекает балку моста с большим ускорением, величина шума резко изменяется в конце сигнала. Это можно объяснить тем, что при разгоне количество инерции уменьшается, шум переходит в отрицательную часть оси промежуточного вала, и тогда конструкция работает в сжатом состоянии.Напротив, инерция увеличивается в случае замедления из-за увеличения шума в положительной части оси промежуточного вала, что приводит к тому, что большая часть системы находится под напряжением во время работы. При практическом применении модели количество шума увеличивается и усложняется. Помимо исследуемого объекта, на Рисунке 11 показаны многие другие типы ударов.

Результаты на Рисунке 11 показывают, что каждая группа различных объектов, воздействующих на конструкцию, будет формировать сигнал разного типа.Это указывает на то, что конструкция моста постоянно подвергается воздействию множества различных воздействий транспортных средств и деятельности человека. Однако необходимо оценить причину основных вибраций конструкции, чтобы точно оценить и спрогнозировать ее срок службы, а также процесс ее эксплуатации. Для вышеприведенного обзора транспортные средства, будь то небольшие грузовики или более тяжелые автомобили, являются основными факторами, вызывающими вибрацию конструкции пролетного строения моста. Небольшие транспортные средства и другие виды деятельности человека не влияют на работу конструкции, но несут значительный шум в сигнале вибрации моста.Обзоры некоторых реальных моделей транспортных средств, движущихся по мостам, показаны на рисунках 12 и 13. На рисунке 10 показан сигнал вибрации пролета моста в фактическом состоянии циркуляции при случайной нагрузке на него. Второй случай осуществляется в статусе пролета моста в час пик, когда проезжают автомобили. Разделив MODWT в сочетании с методом преобразования БПФ, как представлено в этой рукописи, можно показать, что основным взаимным воздействием на пролет моста по-прежнему является величина нагрузки, создаваемой транспортными средствами со значительным весом.Несмотря на обследование в час пик, форма спектра, разделенная на два случая, практически не изменилась. Это показывает, что, несмотря на пробки или многолюдное движение по мосту в час пик, изменения в транспортном потоке мало влияют, и рабочий процесс остается в основном обычным.

4. Заключение
Таким образом, метод MODWT в сочетании с методом преобразования БПФ использовался в этом исследовании для определения фактических спектров плотности мощности во время разделения сигналов.Спектры плотности мощности, соответствующие дискретным колебаниям, отделенные от общего исходного спектра, могут эффективно выявить факторы, оказывающие основное влияние на конструкцию во время эксплуатации. Процесс разделения сигналов с использованием метода анализа с множественным разрешением с помощью MODWT позволяет захватывать необходимые сигналы и устранять шумовые сигналы, которые мало влияют на структуру. Основные результаты, полученные в этой статье, резюмируются следующим образом: (1) Сигнал измерения общей вибрации фактически представляет собой общий сигнал, объединенный с различными дискретными вибрациями, которые существуют в виде значительного шума.Мы можем разделить исходный полученный сигнал на сигналы дискретной вибрации, используя метод анализа MODWT, одновременно устраняя шумовую составляющую в сигнале. Это делает информацию, извлеченную из этого сигнала, более эффективной с более высокой чувствительностью, чем неразделенные сигналы. (2) Спектр плотности мощности, полученный в результате преобразования общего сигнала вибрации от конструкции, фактически также является синтезом спектров плотности мощности дискретные колебания и наведенный шум.Следовательно, исследование изменения спектра мощности не сможет полностью учесть изменение сигнала. Вместо этого нам просто нужно исследовать дискретные спектры каждого агента, чтобы найти причину изменения структуры. Это делает параметры, полученные на основе теории, представленной в этой статье, гораздо более чувствительными, чем параметры, полученные на основе общего сигнала. (3) Высокая достоверность и применимость этого исследования были продемонстрированы в этой статье, демонстрируя результаты процесса извлечения данных в реальных условиях. конструкции.Исследование успешно упростило процесс извлечения данных из метода MODWT в сочетании с методом преобразования FFT. Данные можно многократно использовать и оценивать для множества различных случаев. Измеренные сигналы тщательно и эффективно используются, чтобы удовлетворить спрос на использование больших данных в современном мире.
Доступность данных
Данные, использованные для подтверждения результатов этого исследования, включены в статью.
Раскрытие информации
Автор подтверждает, что интеллектуальное содержание этой статьи является оригинальным продуктом их работы.
Конфликт интересов
Автор заявляет, что конфликта интересов нет.
Сравнение аналоговых и цифровых — learn.sparkfun.com
Добавлено в избранное Любимый 61
Обзор
Мы живем в аналоговом мире. Есть бесконечное количество цветов, которыми можно нарисовать объект (даже если разница незаметна для нашего глаза), есть бесконечное количество тонов, которые мы можем слышать, и существует бесконечное количество запахов, которые мы можем почувствовать.Общей темой для всех этих аналоговых сигналов является их бесконечных возможностей.
Цифровые сигналы и объекты имеют дело с областью дискретных или конечных , что означает ограниченный набор значений, которыми они могут быть. Это может означать всего два возможных значения: 255, 4 294 967 296 или что угодно, если только это не ∞ (бесконечность).
Реальные объекты могут отображать данные, собирать входные данные с помощью аналоговых или цифровых средств. (Слева направо): часы, мультиметры и джойстики могут иметь любую форму (аналоговая вверху, цифровая внизу).
Работа с электроникой означает работу как с аналоговыми, так и с цифровыми сигналами, входами и выходами. Наши проекты электроники должны каким-то образом взаимодействовать с реальным аналоговым миром, но большинство наших микропроцессоров, компьютеров и логических устройств являются чисто цифровыми компонентами. Эти два типа сигналов похожи на разные электронные языки; некоторые компоненты электроники двуязычны, другие могут понимать и говорить только на одном из двух языков.
В этом руководстве мы рассмотрим основы работы с цифровыми и аналоговыми сигналами, включая примеры каждого из них.Мы также поговорим об аналоговых и цифровых схемах и компонентах.
и nbsp
и nbsp
Рекомендуемая литература
Концепции аналоговой и цифровой аппаратуры существуют сами по себе и не требуют больших предварительных знаний в области электроники. Тем не менее, если вы еще этого не сделали, вам следует просмотреть некоторые из этих руководств:
Аналоговые сигналы
Определение: сигналы
Прежде чем идти слишком далеко, мы должны немного поговорить о том, что на самом деле представляет собой сигнал , в частности, об электронных сигналах (в отличие от сигналов светофора, альбомов Ultimate Power-Trio или общих средств связи).Сигналы, о которых мы говорим, представляют собой изменяющихся во времени «величин», которые передают какую-то информацию. В электротехнике величина , величина , которая изменяется во времени, обычно равна напряжению (если не то, то обычно току). Поэтому, когда мы говорим о сигналах, просто думайте о них как о напряжении, которое меняется со временем.
Сигналы передаются между устройствами для отправки и получения информации, которая может быть видео, аудио или каким-либо видом закодированных данных. Обычно сигналы передаются по проводам, но они также могут проходить по воздуху с помощью радиочастотных (RF) волн.Аудиосигналы, например, могут передаваться между звуковой картой вашего компьютера и динамиками, а сигналы данных могут передаваться по воздуху между планшетом и маршрутизатором WiFi.
Графики аналоговых сигналов
Поскольку сигнал меняется во времени, полезно нанести его на график, где время отложено по горизонтали, x -оси, а напряжение — по вертикали, y -оси. Глядя на график сигнала, как правило, проще всего определить, аналоговый он или цифровой; График зависимости напряжения аналогового сигнала от времени должен быть плавным и непрерывным .
Хотя эти сигналы могут быть ограничены диапазоном максимальных и минимальных значений, в этом диапазоне все еще существует бесконечное количество возможных значений. Например, аналоговое напряжение, выходящее из настенной розетки, может быть ограничено от -120 В до + 120 В, но по мере увеличения разрешения вы обнаруживаете бесконечное количество значений, которыми на самом деле может быть сигнал (например, 64,4 В. , 64,42 В, 64,424 В и бесконечные, все более точные значения).
Пример аналоговых сигналов
Видео и аудио передачи часто передаются или записываются с использованием аналоговых сигналов.Например, композитный видеосигнал, выходящий из старого разъема RCA, представляет собой кодированный аналоговый сигнал, обычно в диапазоне от 0 до 1,073 В. Незначительные изменения сигнала имеют огромное влияние на цвет или расположение видео.
Аналоговый сигнал, представляющий одну строку составных видеоданных.
Чистые аудиосигналы также являются аналоговыми. Сигнал, исходящий из микрофона, полон аналоговых частот и гармоник, которые в совокупности создают прекрасную музыку.
Цифровые сигналы
Цифровые сигналы должны иметь конечный набор возможных значений.Число значений в наборе может быть от двух до очень большого числа, которое не может быть бесконечным. Чаще всего цифровые сигналы будут иметь одно из двух значений — например, 0 В или 5 В. Временные графики этих сигналов выглядят как прямоугольных волн .
Или цифровой сигнал может быть дискретным представлением аналоговой формы волны. При взгляде издалека приведенная ниже волновая функция может показаться гладкой и аналоговой, но если вы присмотритесь, вы увидите крошечные дискретные шагов , поскольку сигнал пытается приблизиться к значениям:
В этом большая разница между аналоговыми и цифровыми волнами.Аналоговые волны бывают плавными и непрерывными, цифровые волны — ступенчатыми, квадратными и дискретными.
Пример цифровых сигналов
Не все аудио- и видеосигналы являются аналоговыми. Все стандартизованные сигналы, такие как HDMI для видео (и аудио) и MIDI, I ² S или AC’97 для аудио, передаются в цифровом виде.
Большая часть обмена данными между интегральными схемами осуществляется в цифровом формате. Такие интерфейсы, как последовательный, I ² C и SPI, все передают данные в виде кодированной последовательности прямоугольных сигналов.
Последовательный периферийный интерфейс (SPI) использует множество цифровых сигналов для передачи данных между устройствами.
Аналоговые и цифровые схемы
Аналоговая электроника
Большинство основных электронных компонентов — резисторы, конденсаторы, катушки индуктивности, диоды, транзисторы и операционные усилители — все по своей сути аналоговые. Схемы, построенные из комбинации только этих компонентов, обычно являются аналоговыми.
Аналоговые схемы обычно представляют собой сложные комбинации операционных усилителей, резисторов, конденсаторов и других основных электронных компонентов.Это пример аналогового аудиоусилителя класса B.
Аналоговые схемы могут иметь очень элегантную конструкцию с множеством компонентов или могут быть очень простыми, например, два резистора, объединяемых в делитель напряжения. В целом, тем не менее, аналоговые схемы намного сложнее разработать , чем те, которые выполняют ту же задачу в цифровом виде. Для создания аналогового радиоприемника или аналогового зарядного устройства требуется специальный мастер аналоговых схем; цифровые компоненты существуют, чтобы сделать эти конструкции намного проще, .
Аналоговые цепи обычно намного более восприимчивы к шуму (небольшие нежелательные колебания напряжения). Небольшие изменения уровня напряжения аналогового сигнала могут привести к значительным ошибкам при обработке.
Цифровая электроника
Цифровые схемы работают с использованием дискретных цифровых сигналов. Эти схемы обычно состоят из комбинации транзисторов и логических вентилей, а на более высоких уровнях — микроконтроллеров или других вычислительных микросхем. Большинство процессоров, будь то большие мощные процессоры в вашем компьютере или крошечные микроконтроллеры, работают в цифровой сфере.
Цифровые схемы используют такие компоненты, как логические вентили или более сложные цифровые ИС (обычно представленные в виде прямоугольников с маркированными выводами, отходящими от них).
Цифровые схемы обычно используют двоичную схему для цифровой сигнализации. Эти системы назначают два разных напряжения как два разных логических уровня — высокое напряжение (обычно 5 В, 3,3 или 1,8 В) представляет одно значение, а низкое напряжение (обычно 0 В) представляет другое.
Хотя цифровые схемы, как правило, проще спроектировать, они, как правило, на дороже , чем аналоговые схемы с такими же задачами.
Комбинированный аналоговый и цифровой
Нередко можно увидеть смесь аналоговых и цифровых компонентов в схеме. Хотя микроконтроллеры, как правило, цифровые звери, они часто имеют внутреннюю схему, которая позволяет им взаимодействовать с аналоговыми схемами (аналого-цифровыми преобразователями, широтно-импульсной модуляцией и цифро-аналоговыми преобразователями. Аналого-цифровой преобразователь (АЦП) ) позволяет микроконтроллеру подключаться к аналоговому датчику (например, фотоэлементам или датчикам температуры) для считывания аналогового напряжения.Менее распространенный цифро-аналоговый преобразователь позволяет микроконтроллеру генерировать аналоговые напряжения, что удобно, когда ему нужно воспроизводить звук.
Ресурсы и дальнейшее развитие
Теперь, когда вы знаете разницу между аналоговыми и цифровыми сигналами, мы предлагаем ознакомиться с учебным пособием по преобразованию аналогового сигнала в цифровое. Работа с микроконтроллерами или любой другой логической электроникой означает большую часть времени работать в цифровой сфере. Если вы хотите измерять свет, температуру или сопрягать микроконтроллер с множеством других аналоговых датчиков, вам нужно знать, как преобразовать аналоговое напряжение, которое они производят, в цифровое значение.
Также рекомендуется прочитать наше руководство по широтно-импульсной модуляции (ШИМ). ШИМ — это уловка, с помощью которой микроконтроллеры могут сделать цифровой сигнал аналоговым.
Вот еще несколько вопросов, которые серьезно относятся к цифровым интерфейсам:
Или, если вы хотите глубже погрузиться в аналоговую сферу, подумайте о проверке этих руководств:
Дискретный и аналоговый ввод / вывод для ПЛК
Так что вы думаете, этот стакан наполовину полон или наполовину пуст? Для меня это может быть немного сложно ответить и может варьироваться в зависимости от дня, который у меня есть, но если мы спрашиваем об уровне, почему бы не позволить ПЛК ответить? На самом деле, почему бы ПЛК не сообщать нам уровень, температуру воды, скорость потока, с которой она была заполнена, доступную емкость стакана и давление, оказываемое на дно? Хорошо, обычно вы не будете использовать ПЛК для такого небольшого приложения, но в более крупном масштабе, например, резервуар, ПЛК может ответить на все эти вопросы.Но как заставить ПЛК «видеть» этот резервуар, не говоря уже о том, насколько он полон? Что ж, я рад, что ты спросил, или я спросил, или что-то в этом роде. Нам нужно устройство, которое может позволить ПЛК получать информацию из своего окружения и обрабатывать ее. Нам также нужно устройство, которое позволит ПЛК влиять на свое окружение по мере необходимости. Нам нужен ввод-вывод, а под вводом-выводом я подразумеваю вводы и выводы. В этом обсуждении мы сосредоточимся на двух основных типах ввода-вывода: аналоговом и дискретном.
Дискретный ввод / вывод
Давайте сначала возьмем самое простое, дискретное.Дискретные сигналы — это сигналы, которые либо включены, либо выключены, истинны или ложны. Подумайте о выключателе в вашем доме. Выключатель либо включает свет, либо выключает его, если это не люминесцентная лампа — тогда он, вероятно, все еще мигает. Поскольку дискретные сигналы существуют в одном из этих двух состояний, они представлены прямоугольной волной, как показано ниже. В мире ПЛК существует множество применений дискретного ввода-вывода. Некоторые из устройств, которые подают сигналы включения / выключения, — это кнопки, фотоэлементы, концевые выключатели, поплавковые выключатели и бесконтактные выключатели.В дни стартапа я много работал с определенной службой доставки посылок. Они используют множество датчиков включения / выключения и контроля, чтобы отслеживать посылки и доставлять их в нужное место назначения или на грузовик. Фотоэлементы, которые представляют собой устройства, которые излучают инфракрасный световой луч и могут определять, когда этот луч был прерван, широко используются для обнаружения и отслеживания пакетов в процессе их сортировки. Применение вашей системы управления определит типы дискретных устройств, которые вы выберете. Существует множество дискретных оконечных устройств и модулей, которые можно использовать в системе ПЛК для отправки и приема сигналов включения / выключения.Эти устройства могут быть переменного или постоянного тока и доступны в различных диапазонах напряжения. 0–24 В постоянного тока и 0–230 В переменного тока — это два доступных диапазона напряжения, где 0 — сигнал ВЫКЛ, а 24 В постоянного тока или 230 В переменного тока — сигнал ВКЛ. Обычно существует порог обнаружения, при котором модуль 0-24 В постоянного тока обнаруживает все, что выше 22 В постоянного тока, как сигнал ВКЛ, и все, что ниже 2 В постоянного тока, как ВЫКЛ. Теперь давайте посмотрим на аналог.
Аналоговый ввод / вывод
Аналоговые сигналы — это сигналы, которые могут изменяться или изменяться. Мы живем в аналоговом мире, и наши чувства — аналоговые приемники.«Почувствуй, как жарко!», «Ты можешь говорить?» и «Посмотрите на все цвета!» это утверждения, которые показывают, как вариации аналоговых сигналов, таких как температура, звук и свет, могут влиять на наши чувства. Вернемся к примеру с выключателем света; Давайте теперь установим в нашем доме небольшую декоративную подсветку. Вместо штатного выключателя мы будем использовать диммер. Переключатель диммера будет изменять сопротивление в линии, заставляя свет тускнеть или становиться ярче по нашему выбору. Новые диммерные переключатели усовершенствованы, чтобы быть более эффективными, но в этом примере мы придерживаемся старой школы.Напряжение, подаваемое на светильник, не будет постоянным уровнем, а будет изменяться между верхним и нижним пределами. Обычно это синусоида.
Использование датчиков
Положение, уровень, температура, давление, расход и скорость — это лишь некоторые из измерений, которые аналоговые устройства могут предоставить системе управления. Вы, вероятно, спрашиваете себя: «Как давление, являющееся физической величиной, становится электрическим сигналом?» Это отличный вопрос! Преобразование выполняется с помощью преобразователей.Преобразователь принимает физическую величину, например давление, и преобразует ее в электрический сигнал. Многие преобразователи используют физическую величину для управления сопротивлением в электрической цепи. Например, RTD (датчик температуры сопротивления) будет изменять значение сопротивления в зависимости от нагрева. По мере увеличения тепла увеличивается и сопротивление в цепи, изменяя подаваемое напряжение или ток. То же самое верно и для датчиков давления, в которых используются тензодатчики. При приложении давления к тензодатчику сопротивление в цепи увеличивается, а уровень напряжения или тока изменяется.Некоторые детекторы потока будут использовать поток жидкости для толкания ребра, соединенного с поворотным потенциометром. Более быстрый поток означает большее изменение сопротивления. Одним из самых крутых датчиков, с которыми я столкнулся в дни работы в морской нефтяной промышленности, был детектор песка. Этот преобразователь был акустическим и крепился к трубам, по которым нефть выводилась со дна моря. Он действительно слышал, как песок трется о внутреннюю часть трубы. Уровень звука был преобразован в аналоговый сигнал, используемый для предупреждения персонала, если при бурении извлекается слишком много песка, что может привести к обрушению скважины.Электрические сигналы, которые выдают преобразователи, могут быть основаны на напряжении или токе. От 4 до 20 мА, от 0 до 20 мА, от 0 до 10 В постоянного тока и от -10 до +10 В постоянного тока — вот лишь некоторые из доступных диапазонов, производимых датчиками. ПЛК подает напряжение или ток, а датчик возвращает значение в заданном диапазоне. Это значение будет пропорционально имеющемуся давлению, потоку и т. Д. Теперь мы подошли к двум важным частям этого обсуждения: масштабированию и разрешению.
Масштабирование
Масштабирование — это когда мы берем необработанное возвращаемое значение напряжения или тока и преобразуем его в значимое измерение.Допустим, у меня есть расходомер 4–20 мА, который возвращает сигнал 8 мА на ПЛК. Это будет означать, что в это время течет 8 мА жидкости, верно? Конечно, нет. Нам нужно взять необработанное значение и масштабировать его до чего-то значимого, скажем, галлонов в минуту. Мы знаем от производителя, что расходомер откалиброван для считывания расхода от 0 до 200 галлонов в минуту. Следовательно, мы можем масштабировать исходное значение 4-20 мА до 0-200 галлонов в минуту в нашей системе. Обычно это можно сделать с помощью программного обеспечения для программирования, как показано ниже, и после масштабирования нашего значения 8 мА мы видим, что в настоящее время поток составляет 50 галлонов в минуту.
Разрешение
Теперь посмотрим на разрешение. Разрешение и точность идут рука об руку; чем больше у вас разрешение, тем точнее будут ваши измерения. Аналоговые модули имеют разрешение, которое они обеспечивают. Доступны 12-битные, 13-битные и 16-битные разрешения. Итак, что значит иметь модуль 4-20 мА с 12-битным разрешением? 12-битное двоичное слово может иметь 4096 различных комбинаций. Следовательно, наш модуль с 12-битным разрешением может иметь 4096 (4095 со знаком) различных измерений в диапазоне 4-20 мА.Другими словами, диапазон 4-20 можно разбить на 4096 различных частей. Чем больше штук, тем точнее. Насколько точно? Что ж, наш общий диапазон составляет 16 мА (20 минус 4), и если мы разделим наш общий диапазон на 4096 частей, мы увидим, что наш модуль может обнаруживать каждые 0,003 мА изменения.
Шум
И последнее: при использовании аналоговых сигналов важно помнить, что они очень чувствительны к шуму. Шум может привести к неправильным показаниям и неустойчивому поведению системы управления.

Что такое дискретный сигнал и как он формируется

Основные этапы формирования дискретного сигнала:

Основные характеристики дискретных сигналов

Частота дискретизации

Разрядность квантования

Динамический диапазон

Применение дискретных сигналов в цифровой обработке

Отличия дискретных сигналов от аналоговых

Преобразование аналоговых сигналов в дискретные

Теорема Котельникова и выбор частоты дискретизации

Квантование дискретных сигналов

Спектральные характеристики дискретных сигналов

Заключение

Что формирует дискретный сигнал. Дискретный сигнал

26 вопросов и ответов. Теория электрических цепей. Курс лекций

Дискретным называют сигнал — прерывный информационный сигнал

Аналоговый сигнал

Что такое дискретный сигнал

Чем отличается непрерывный сигнал от дискретного

Как аналоговый сигнал преобразуется в цифровой и наоборот

Как выглядят спектры аналогового и дискретного сигнала

Какие системы связи используют цифровой сигнал а какие аналоговый

Список книг помогающих разобраться в аналоговых и цифровых сигналах

Дискретный сигнал это ток

Дискретный сигнал

См. также

Литература

Смотреть что такое «Дискретный сигнал» в других словарях:

Аналоговые, дискретные и цифровые сигналы

Аналоговые, дискретные и цифровые сигналы

Дискретный (цифровой) и аналоговый сигнал: отличия

Аналоговый сигнал

Что такое дискретный сигнал

Чем отличается непрерывный сигнал от дискретного

Как аналоговый сигнал преобразуется в цифровой и наоборот

Как выглядят спектры аналогового и дискретного сигнала

Какие системы связи используют цифровой сигнал а какие аналоговый

Список книг помогающих разобраться в аналоговых и цифровых сигналах

Дискретность. Принципы и применение. Сигнал и работа. Особенности

Как применяется дискретность в электронике

К неоспоримым достоинствам дискретного сигнала можно отнести:

Если рассматривать еще примеры оборудования, где применяются принципы дискретности, то к таким примерам можно отнести:

Аналоговые, дискретные и цифровые сигналы

9 Дискретные сигналы — СтудИзба

Рекомендуемые файлы

Дискретный потенциальный сигнал — Большая Энциклопедия Нефти и Газа, статья, страница 1

Дискретный потенциальный сигнал

Discrete Signal — обзор

Periodic-Discrete

2.4: Сигналы в дискретном времени — Engineering LibreTexts

Реальные и комплексные сигналы

Комплексные экспоненты

Синусоиды

Единица Образец

Символьные сигналы

Дискретная связь | теория информации

Бесшумная связь

шумная связь

появление в нервной системе

дискретных сигналов

Бесшумная связь

шумная связь

Возникновение в нервной системе

Аналоговые и цифровые сигналы: использование, преимущества и недостатки | Статья

Аналоговый сигнал

Цифровой сигнал

Аналоговая электроника

Цифровая электроника

Преобразование аналогово-цифрового (АЦП) и цифро-аналогового (ЦАП) сигнала

Работа АЦП

Работа ЦАП

Сравнение цифровых сигналов и аналоговых сигналов: преимущества и недостатки

Цифровые сигналы: преимущества и недостатки

Аналоговые сигналы: преимущества и недостатки

Аналоговые и цифровые сигналы: системы и приложения

Заключение

Разделение сигнала структуры посредством дискретного вейвлет-преобразования максимального перекрытия и быстрого преобразования Фурье

1. Введение

2. Теоретическая основа

2.1. Недостатки метода обычного вейвлет-преобразования