Что такое дискретная математика. Какие разделы включает дискретная математика. Как применяется дискретная математика. Чем отличается дискретная математика от непрерывной.
Что такое дискретная математика и почему она важна?
Дискретная математика — это раздел математики, изучающий дискретные математические структуры, то есть объекты, которые можно пересчитать. В отличие от непрерывной математики, оперирующей непрерывными величинами, дискретная математика имеет дело с объектами, принимающими отдельные, изолированные значения.
Почему дискретная математика так важна в современном мире? Есть несколько ключевых причин:
- Она является основой компьютерных наук и программирования
- Применяется в криптографии для защиты информации
- Используется в теории кодирования для передачи данных
- Необходима в теории алгоритмов и анализе их сложности
- Применяется в теории графов для моделирования сетей и процессов
Таким образом, дискретная математика играет важнейшую роль в развитии информационных технологий и цифровой экономики. Без нее невозможно представить современную науку и технику.
Основные разделы дискретной математики
Дискретная математика включает несколько ключевых разделов, каждый из которых изучает определенные дискретные структуры и связанные с ними задачи:
1. Теория множеств
Теория множеств изучает свойства множеств — наборов объектов. Она включает операции над множествами (объединение, пересечение, разность), отношения между множествами, мощность множеств. Это базовый раздел, на котором строятся остальные области дискретной математики.
2. Комбинаторика
Комбинаторика занимается подсчетом количества элементов в конечных множествах. Сюда входят перестановки, сочетания, размещения, правило произведения и суммы. Комбинаторика широко применяется в теории вероятностей и статистике.
3. Теория графов
Теория графов изучает свойства графов — наборов вершин, соединенных ребрами. Графы позволяют моделировать различные структуры и процессы в науке, технике и экономике. В теории графов решаются задачи о путях, циклах, раскрасках, потоках в сетях и другие.
4. Математическая логика
Математическая логика исследует методы рассуждений и доказательств. Она включает логику высказываний, логику предикатов, теорию доказательств. Логика лежит в основе проектирования электронных схем и верификации программ.
5. Теория кодирования
Теория кодирования разрабатывает методы эффективного и надежного представления информации. Она применяется для сжатия данных, обнаружения и исправления ошибок при передаче информации, в криптографии.
Применение дискретной математики в различных областях
Дискретная математика находит широкое применение в самых разных сферах науки и техники. Рассмотрим некоторые важные области ее использования:
Компьютерные науки и программирование
Это основная область применения дискретной математики. Она используется для:
- Анализа алгоритмов и оценки их сложности
- Проектирования структур данных
- Разработки языков программирования
- Верификации программ
- Проектирования архитектуры компьютеров
Криптография и защита информации
Дискретная математика лежит в основе современной криптографии. Она применяется для:
- Разработки криптографических алгоритмов
- Анализа криптостойкости шифров
- Построения систем электронной подписи
- Протоколов безопасного обмена ключами
Теория кодирования и передача данных
В этой области дискретная математика используется для:
- Разработки помехоустойчивых кодов
- Сжатия информации
- Обнаружения и исправления ошибок
- Оптимизации систем связи
Исследование операций и теория принятия решений
Здесь дискретная математика применяется для:
- Решения оптимизационных задач
- Построения моделей принятия решений
- Анализа и оптимизации сетей
- Теории расписаний
Отличия дискретной математики от непрерывной
Чем же отличается дискретная математика от классической непрерывной? Рассмотрим ключевые различия:
Объекты изучения
Дискретная математика изучает дискретные структуры — множества, графы, последовательности. Непрерывная математика имеет дело с непрерывными величинами и функциями.
Методы
В дискретной математике используются комбинаторные, алгебраические, логические методы. Непрерывная математика опирается на методы математического анализа, дифференциальных уравнений.
Характер зависимостей
Дискретная математика рассматривает дискретные зависимости между объектами. В непрерывной математике изучаются непрерывные функции и процессы.
Области применения
Дискретная математика в основном применяется в информатике, криптографии, теории кодирования. Непрерывная математика используется в физике, механике, экономике.
Базовые понятия и структуры дискретной математики
Рассмотрим некоторые фундаментальные понятия и структуры, изучаемые в дискретной математике:
Множества
Множество — это совокупность различных объектов, рассматриваемых как единое целое. Множества являются базовым понятием дискретной математики. Над множествами определены различные операции — объединение, пересечение, разность, симметрическая разность.
Отношения
Отношение — это связь между элементами множеств. Примеры отношений: «больше», «делится нацело», «является подмножеством». Отношения могут обладать различными свойствами — рефлексивностью, симметричностью, транзитивностью.
Графы
Граф — это совокупность вершин, некоторые из которых соединены ребрами. Графы позволяют моделировать сложные структуры и процессы. Различают ориентированные и неориентированные, взвешенные и невзвешенные графы.
Деревья
Дерево — это связный граф без циклов. Деревья широко используются в информатике для представления иерархических структур данных. Важную роль играют бинарные и сбалансированные деревья.
Конечные автоматы
Конечный автомат — это математическая модель устройства с конечным числом состояний. Автоматы применяются для описания и анализа различных процессов с дискретными состояниями.
Алгоритмы в дискретной математике
Важнейшую роль в дискретной математике играют алгоритмы для решения различных задач. Рассмотрим некоторые классические алгоритмы:
Алгоритмы на графах
- Поиск в глубину и в ширину
- Алгоритм Дейкстры поиска кратчайшего пути
- Алгоритм Крускала построения минимального остовного дерева
- Алгоритм Форда-Фалкерсона нахождения максимального потока
Комбинаторные алгоритмы
- Генерация всех перестановок
- Генерация всех подмножеств множества
- Алгоритм поиска ближайших соседей
Алгоритмы сортировки
- Быстрая сортировка
- Сортировка слиянием
- Пирамидальная сортировка
Алгоритмы на строках
- Алгоритм Кнута-Морриса-Пратта поиска подстроки
- Алгоритм Рабина-Карпа поиска подстроки
- Алгоритм сжатия данных Хаффмана
Анализ и разработка эффективных алгоритмов — одна из ключевых задач дискретной математики и информатики в целом.
Перспективы развития дискретной математики
Дискретная математика — быстро развивающаяся область. Каковы перспективы ее дальнейшего развития?
Квантовые вычисления
Развитие квантовых компьютеров требует разработки новых дискретных структур и алгоритмов для квантовых вычислений.
Машинное обучение
Методы дискретной математики находят все более широкое применение в алгоритмах машинного обучения и искусственного интеллекта.
Большие данные
Анализ больших объемов данных требует разработки новых эффективных дискретных алгоритмов и структур данных.
Криптография и кибербезопасность
Развитие криптографических систем и методов защиты информации остается важнейшей задачей дискретной математики.
Таким образом, дискретная математика продолжает играть ключевую роль в развитии информационных технологий и цифровой экономики. Ее методы и подходы находят все новые области применения.
Дискретное и непрерывное «живут» в разных областях мозга
Наука
|
Поделиться
Согласно результатам исследований, область мозга, которая ранее считалась ответственной за обработку числовой информации в целом, на самом деле поделена на две области, у которых имеются различные функции. Первая участвует в дискретных оценках, вторая в оценке неисчисляемых величин.
Открытие было сделано под руководством профессора Брайана Баттеруорта (Brian Butterworth) признанного специалиста в области изучения дискалькулии. Проф. Баттеруорт, опубликовавший книгу «Математический мозг», считает, что результаты исследований помогут в дальнейшем проводить более точную диагностику этого заболевания с помощью метода магнитно-резонансного сканирования (fMRI), сообщает Physorg.
«Теперь, когда нам известно, в каких именно областях мозга следует искать признаки, отличающие пациентов, страдающих дискалькулией, мы сможем точнее поставить диагноз и выработать более эффективные методы лечения этого заболевания», полагает профессор.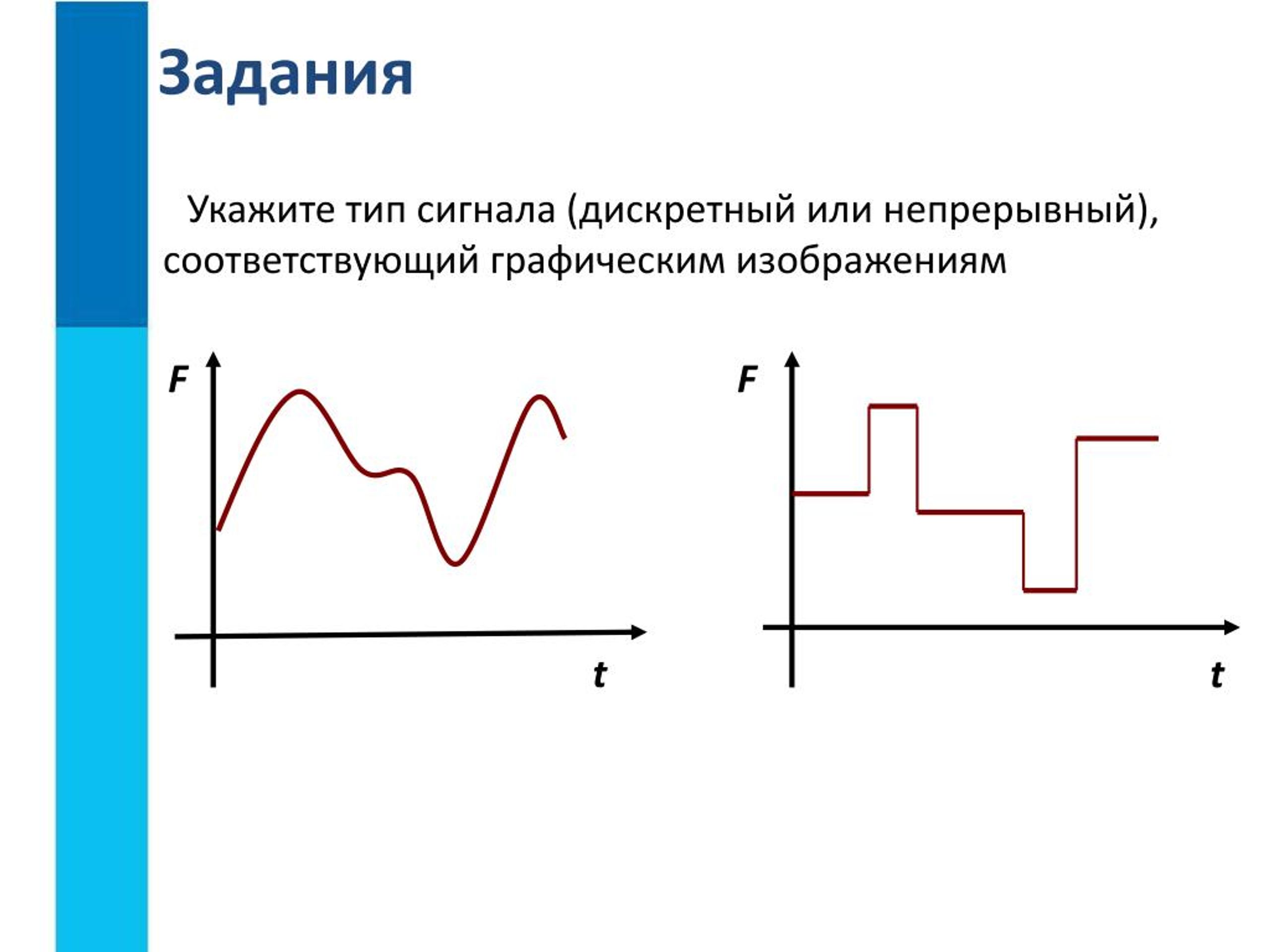
Несколько лет назад коллеги проф. Баттеруорта провели ряд экспериментов по выявлению области мозга, связанной с возникновением дислексии. Их открытие явилось важным шагом в диагностике и разработке новых методов лечения заболевания. Ученые надеются, что в области изучения и лечения дискалькулии можно будет достигнуть столь же впечатляющих успехов.
Специалисты провели два эксперимента по исследованию деятельности мозга в области межтеменной борозды большого мозга (intraparietal sulcus, IPS) с помощью fMRI-сканирования. Область IPS ответственна за обработку числовой информации. В первом эксперименте анализировалась мозговая деятельность пациента во время анализа дискретных (исчисляемых), во втором неисчисляемых величин.
Новые правила аккредитации и получения налоговых льгот для ИТ-компаний: что важно знать
Поддержка ИТ-отрасли
Суть первого эксперимента состояла в следующем.
Пациентам показывали голубые и зеленые квадраты, возникающие на экране дисплея последовательно друг за другом, или одновременно все квадраты на экране. Функциональная магнитно-резонансная томография мозга показала, что в обоих случаях была задействована одна и та же область мозга, ответственная за дискретные количественные оценки.
Однако когда во втором эксперименте пациентам были показаны плавно перетекающие из одного в другой цвета, либо квадрат с плавными цветовыми переходами, трудилась совсем иная область мозга оценка предмета с помощью дискретных методов счета оказалась невозможной. На основании полученных данных ученые сделали вывод, что у больных дискалькулией могут быть выявлены нарушения в работе именно той области мозга, которая отвечает за счет.
Магнитно-резонансное сканирование активно применяется в исследованиях функций
различных областей мозга, изучении методов биологической обратной связи
и принципа работы человеческой памяти.
- Бесплатный фотошоп: лучшие программы для обработки фото онлайн
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 32 дискретных транзисторных выхода 1х32DO = 24В/ 0,5А, SIEMENS, 6ES73221BL000AA0
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 16 дискретных транзисторных выходов 16х1DO, 24-48В UC/ 0,5А
202605 руб/шт
202605 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 16 дискретных транзисторных выходов 1х16DO ~120/230ВАС/1А
133771 руб/шт
133771 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 16 дискретных транзисторных выходов 2х8DO = 24В/ 0,5А
87510 руб/шт
87510 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 16 дискретных транзисторных выходов 2х8DO=24В/0,5А, быстродейств
105624 руб/шт
105624 руб/шт
Купить
Simatic S7-300 SM322 Модуль вывода дискретных сигналов, 16вых.
DC24V/0,5A, с диагностикой
147149 руб/шт
147149 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 32 дискретных транзисторных выхода 4х8DO, 230В АС/1А
267821 руб/шт
267821 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 8 дискретных транзисторных выходов 2х4DO = 24В/2А
70787 руб/шт
70787 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 8 дискретных транзисторных выходов 2х4DO ~120/230ВАС/1А
92246 руб/шт
92246 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 8 дискретных транзисторных выходов 8х1DO ~120/230ВАС/2А
111755 руб/шт
111755 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 64 дискретных транзисторных выхода 16х4DO = 24В/ 0,3А, m-ключ
265312 руб/шт
265312 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 64 дискретных транзисторных выхода 16х4DO = 24В/ 0,3А, р-ключ
265312 руб/шт
265312 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 4×1 DO Namur =24В/20мА, Ex(i)
157079 руб/шт
157079 руб/шт
Купить
Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 4×1 DO Namur =15В/20мА, Ex(i)
157079 руб/шт
157079 руб/шт
Купить
SIMATIC S7/PCS7, МОДУЛЬ ДИСРЕТНОГО ВЫВОДА SM 322, 16 DO, =24 В / 0,5A, ДИАГНОСТИЧЕСКИЕ ВОЗМОЖНОСТИ, ОБРЫВ ПРОВОДОВ, ОПРЕДЕЛЕНИЕ 0/1, ДЛЯ РАБОТЫ ТРЕБУЕТСЯ 40-ПОЛЮСНЫЙ ФРОНТШТКЕР И IM 153-X HF
354184 руб/шт
354184 руб/шт
Купить
Модуль вывода дискретных сигналов SM 1222 для Simatic S7-1200, 8 дискретных транзисторных выходов 8DO = 24В/ 0,5А
29619 руб/шт
29619 руб/шт
Купить
Модуль вывода дискретных сигналов SM 1222 для Simatic S7-1200, 16 дискретных транзисторных выходов 16DO = 24В/ 0,5А
47341 руб/шт
47341 руб/шт
Купить
Дискретный модуль расширения Logo! DM16 230R, Uпит=115-240VAC/DC, 8 дискретных входов, 8 релейных выходов
18106 руб/шт
18106 руб/шт
Купить
Модуль ввода аналоговых сигналов SM 1231, 8 аналоговых входов ±10 B, ±5 B, ±2,5 B, 0/4…20мА, 13Бит
99294 руб/шт
99294 руб/шт
Купить
Модуль ввода дискретных сигналов SM 321 для Simatic S7-300, 32 дискретных входа 1х32DI =24 В
126805 руб/шт
126805 руб/шт
Купить
Цифровой модуль расширения Logo! DM8 230R, Uпит=115-240VAC/DC, для ввода-вывода дискретных сигналов, 4 вх, 4 релейных вых
ДИСКРЕТНЫЙ Синонимов: 15 синонимов и антонимов для ДИСКРЕТНЫЙ
См.
определение дискретный на Dictionary.com
- прил. individual
synonyms for discrete
- disconnected
- distinct
- various
- detached
- different
- discontinuous
- diverse
- separate
- several
- unattached
See also synonyms for: discretely / discreteness
antonyms for discrete
MOST RELEVANT
- connected
- similar
- attached
- combined
- joined
Roget’s 21st Century Thesaurus, Third Edition Copyright © 2013 Филип Лиф Групп.
ПОПРОБУЙТЕ ИСПОЛЬЗОВАТЬ дискретный
Посмотрите, как выглядит ваше предложение с разными синонимами.
Символов: 0/140
ВИКТОРИНА
Не нужно раздувать эту викторину «Слово дня»!
НАЧАТЬ ВИКТОРИНУКак использовать дискретный в предложении
В 1990 году Керестели Корради и Шандор Сабо придумали именно такой дискретный объект.
КОМПЬЮТЕРНЫЙ ПОИСК РЕШАЕТ МАТЕМАТИЧЕСКУЮ ЗАДАЧУ 90-ЛЕТНЕЙ СТАРНОСТИ старение.
СЕКРЕТ ДОЛГОЙ ЗДОРОВОЙ ЖИЗНИ В ГЕНАХ СТАРЕЙШИХ ЛЮДЕЙ ALIVESHELLY FANAGUST 10, 2020SINGULARITY HUB
Обратные ссылки должны быть включены дискретным и осмысленным образом.
ДЕВЯТЬ ОШИБОК, КОТОРЫХ СЛЕДУЕТ ИЗБЕГАТЬ ПРИ ОБРАЩЕНИИ С ВЕБ-САЙТАМИ ДЛЯ ОБРАТНЫХ ССЫЛОК 29 ИЮЛЯ 2020 г. SEARCH ENGINE WATCH
Молекулярные биологи должны точно определить, какие гены из многих тысяч взаимодействуют как дискретная сеть, чтобы произвести данный признак.
ЧТО ТАКОЕ ИНДИВИДУАЛЬНОЕ ЛИЦО? БИОЛОГИЯ ИЩЕТ ПОДСКАЗКИ В ТЕОРИИ ИНФОРМАЦИИ0005
Чтобы разбить эти задачи на небольшие отдельные работы, которые можно было бы выполнять без особых навыков или знаний.
ДОРОГАЯ, Я ВЫРОСЛА ЭКОНОМИКУ (ЭП. 399) СТИВЕН Дж. ДАБНЕР 5 ДЕКАБРЯ 2019 ФРЕКОНОМИКА
Поражения при этом заболевании обычно дискретны — отдельно одно от другого — но они могут быть скучены вместе.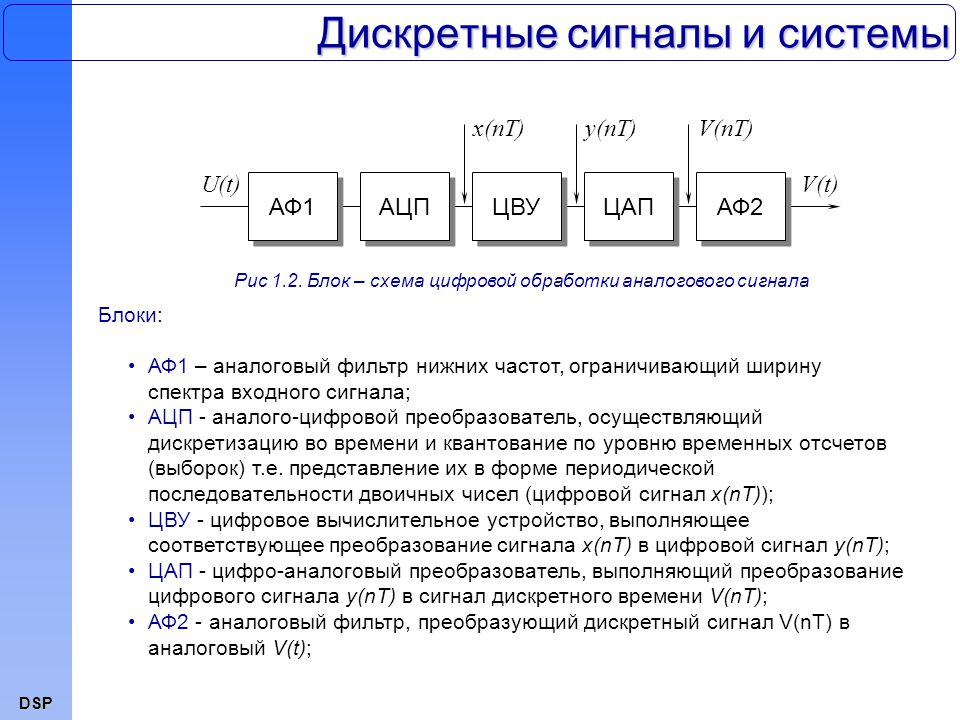
ОПЫТЫ ПАСТЫРСКОЙ МЕДИЦИНЫ ОСТИН МЭЛЛИ
Кажется, что выше мы рассмотрели количество и классифицировали как дискретное, так и непрерывное количество38 среди других «существ».
ПЛОТИН: ПОЛНОЕ СОБРАНИЕ, Т. 3ПЛОТИН (ПЛОТИН)
Это элемент, общий для числа (дискретная величина) и для непрерывного измерения.
ПЛОТИН: ПОЛНОЕ СООБРАЖЕНИЕ, Т. 3ПЛОТИН (PLOTINUS)
Музыкальные тона дискретны,— голос переходит от высоты к высоте через интервалы молча.
ЧИТАТЕЛИ ОНТАРИО: ЧИТАТЕЛЬ ВЫСШЕЙ ШКОЛЫ, 1886МИНИСТЕРСТВО ОБРАЗОВАНИЯ
Даже нервная система, которая, по-видимому, действует как координирующий центр, сама по себе представляет собой совокупность отдельных клеток.
ФОРМА И ФУНКЦИЯ. S. (EDWARD STUART) RUSSELL
WORDS RELATED TO DISCRETE
- cogent
- conclusive
- detailed
- diagnostic
- discrete
- dissecting
- explanatory
- expository
- inquiring
- inquisitive
- interpretive
- следственный
- рассудительный
- логический
- организованный
- проникающий
- perceptive
- perspicuous
- precise
- problem-solving
- questioning
- ratiocinative
- rational
- reasonable
- scientific
- searching
- solid
- sound
- studious
- subtle
- systematic
- testing
- тщательный
- действительный
- обоснованный
- аналитический
- cogent
- conclusive
- detailed
- diagnostic
- discrete
- dissecting
- explanatory
- expository
- inquiring
- inquisitive
- interpretive
- investigative
- judicious
- logical
- organized
- penetrating
- perceptive
- заметный
- точный
- решающий проблемы
- задающий вопросы
- ratiocinative
- rational
- reasonably
- scientific
- searching
- solid
- sound
- studious
- subtle
- systematic
- testing
- thorough
- valid
- alone
- apart
- discrete
- разобщенные
- разделенные
- эмансипированные
- свободные
- изолированные
- изолированные
- loose
- loosened
- removed
- separate
- severed
- unaccompanied
- unconnected
- another
- another story
- atypical
- bizarre
- discrete
- diverse
- especial
- express
- необычный
- индивидуальный
- новый
- оригинальный
- другой
- необычный
- particular
- peculiar
- rare
- several
- singular
- something else
- special
- specialized
- specific
- startling
- strange
- uncommon
- unconventional
- unique
- unusual
- various
- отдельный
- отдельный
- разный
- разный
- разный
- disunited
- divergent
- diverse
- especial
- individual
- offbeat
- particular
- peculiar
- poles apart
- separate
- separated
- several
- single
- sole
- special
- specific
- отдельный
- отдельный
- уникальный
- разный
- характеристика
- cool
- diacritic
- diagnostic
- discrete
- distinguishing
- excellent
- extraordinary
- far cry
- gnarly
- idiosyncratic
- individual
- like night and day
- offbeat
- original
- outstanding
- особый
- идеальный
- полюса друг от друга
- собственный
- отдельный
- одиночный
- единственного числа
- Специальный
- Верхний
- Типичный
- Необычный
- UNREAL
- Weird
- Wicked
Roget’s 21 -й век.
Дискретная математика | Brilliant Math & Science Wiki
Содержание
- Комбинаторика
- Теория множеств
- Теория графов
- Вероятность
- Статистика
- Биекции
- Логика
Основная статья: Комбинаторика
Комбинаторика — это математика счета и упорядочивания. Конечно, большинство людей умеет считать, но комбинаторика применяет математические операции для подсчета вещей, которые слишком велики, чтобы их можно было считать обычным способом.
Комбинаторика особенно полезна в информатике. Комбинаторные методы можно использовать для оценки того, сколько операций потребуется для компьютерного алгоритма. Комбинаторика также важна для изучения дискретной вероятности. Методы комбинаторики можно использовать для подсчета возможных исходов в однородном вероятностном эксперименте.
Комбинаторику часто интересует, как устроены вещи. В этом контексте расположение — это способ группировки объектов. Самыми основными правилами, касающимися договоренностей, являются правило произведения и правило суммы. Эти правила определяют, как подсчитывать аранжировки с использованием операций умножения и сложения соответственно.
В местном гастрономе предлагаются следующие варианты бутербродов:
- Типы хлеба: Белый, Ржаной, Пшеничный
- Типы сыра: Швейцарский, Чеддер, Хаварти, Проволоне
- Типы мяса: ростбиф, индейка, ветчина, солонина, рваная свинина
Если покупатель выберет ровно по одному продукту каждого типа, то сколько возможных бутербродов можно приготовить?
Более специфичным типом расположения является перестановка.
\text{rd}.\) порядок \(\text{ABC}\) будет отличаться от \(\text{ACB}.\)
Сколько существует возможных полей для размещения лошадей?
Комбинация (не путать с комбинацией или ) — это еще один тип расположения, связанный с перестановками. Комбинация — это расположение объектов без учета порядка.
12 разных игроков собираются сыграть в футбол. Двумя капитанами команд являются Брэндон и Мередит (входят в число 12). Каждый из них будет по очереди выбирать игрока в свою команду, пока не будут выбраны все игроки.
Сколькими способами можно разделить игроков на команды?
Как область математики, комбинаторика почти так же широка, как дискретная математика. Другие темы комбинаторики включают
расстройства: перестановка, при которой ни один объект не находится на своем первоначальном месте в порядке;
обходов по прямоугольной решетке: определение количества способов обхода прямоугольной решетки;
распределение объектов по ячейкам: определение того, как объекты могут быть сгруппированы по ячейкам.
Основная статья: Теория множеств
См. также:
Мощность
Объединение и пересечение
Комплектация
Принцип включения и исключения
Законы Де Моргана
Теория множеств — это раздел математики, изучающий наборы объектов. Наборы могут быть дискретными или непрерывными; дискретная математика в первую очередь занимается первым. На базовом уровне теория множеств занимается тем, как можно упорядочивать, комбинировать и подсчитывать множества.
Мощность конечного множества — это количество элементов в этом множестве. Для данного множества \(A,\) его мощность обозначается через \(|A|.\)
Какова мощность множества простых чисел меньше 25?
Набор простых чисел меньше 25 равен
\[\{2,3,5,7,11,13,17,19,23\}.\]
В этом наборе 9 элементов, поэтому мощность равна 9.
\(_\квадрат\)Мощность также может быть распространена на бесконечные множества. Хотя этот вид кардинальности нельзя сосчитать, каждую кардинальность можно сравнить с другой кардинальностью.
Пусть \(A\) и \(B\) — множества. Их мощности сравниваются следующим образом:
Если существует биекция между \(A\) и \(B,\), то \(|A|=|B|.\)
Если существует инъективная функция из \(A\) в \(B, \), но нет биективной функции, то \(|A|<|B|.\)
Покажите, что множество целых чисел и множество четных целых чисел имеют одинаковую мощность.
Может показаться странным, что эти множества имеют одинаковую мощность. В конце концов, четные числа более «редки». Однако эти наборы оба бесконечный . Следовательно, «здравый смысл», предполагающий конечных множеств, должен быть отброшен. Вместо этого цель состоит в том, чтобы получить биективную функцию из набора целых чисел в набор четных целых чисел:
\[f(n)=2n, \n\in\mathbb{Z}.
Приведенная выше функция дает однозначное соответствие между каждым целым числом \(n\) и каждым четным целым числом \(2n.\). Поскольку биекция установлена, множество целых чисел и множество четных целых чисел имеют одинаковую мощность . \(_\квадрат\)
\]Дополнение множества \(A\) — это множество элементов, не входящих в \(A.\). Изучение дополнений множества дает ряд эффективных методов для вычисления мощностей конечных множеств. Например, можно эффективно получить мощность набора, который содержит «по крайней мере один» элемент другого набора.
Дэвид — лидер Комитета Дэвида. Он хочет назначить 3 человек в состав Главного совета. Ему предстоит выбрать из 9 претендентов, трое из которых Томми, Джек и Майкл. Сколькими способами он может выбрать людей в Совет так, чтобы хотя бы один из Томми, Джека и Майкла был выбран?
Объединение и пересечение позволяют описать, как можно комбинировать наборы.
Целое положительное число меньше 1000 является не только полным квадратом, но и полным кубом.
Сколько таких чисел?
6% 36% 42% 54% 60%
Человек «А» говорит правду в 60% случаев, а человек «Б» делает это 90% времени.
В каком проценте случаев они могут противоречить друг другу, констатируя один и тот же факт?
Законы Де Моргана дают тождества для дополнений объединений и пересечений.
300 400 600 900
Сколько целых чисел от 1 до 1000 (включительно) не являются ни кратными 2, ни кратными 5? 96\) (включительно) не являются ни совершенными квадратами, ни совершенными кубами, ни совершенными четвертыми степенями?
Основная статья: Теория графов
Теория графов — это изучение графов , которые представляют собой совокупность связанных узлов.
Базовый график 3-Cycle
Графики полезны для представления всех видов реальных проблем.
от 4 до 5 до 8 с 4 по 7 по 3 с 4 по 5 с 4 по 9От 4 до 7 от 2 до 10
Если существует жадный алгоритм, который будет проходить по графу, выбирая наибольшее значение узла в каждой точке, пока не достигнет листа графа, по какому пути пойдет жадный алгоритм на приведенном ниже графе?
Джон живет на Деревах Десяти Домов, и это самое идеальное и идиллическое место для него и других обитателей сени. Они потратили огромное количество времени на проектирование этих домов, и, чтобы ни один дом не чувствовал себя изолированным от других, они построили новый, искусно сделанный мост между каждым домом!
К сожалению, Деревья Десяти Домов не были застрахованы от гроз, и мосты не были хорошо спроектированы.
Ночь была коварной, завывающей от ветра и замерзающей от дождя, так что шансы на мосты были невелики — казалось, что каждый мост скорее уцелеет, чем рухнет!
К счастью, поскольку на Деревах Десяти Домов было очень много мостов, когда Джон проснулся на следующее утро, он обнаружил, что может добраться до каждого дома, используя только существующие мосты, хотя и окольными путями. маршруты, возможно, были необходимы. Когда они начали восстанавливать, Джону стало любопытно… каковы были шансы, что им всем так повезет? 9{10} P \большой\rэтаж?\)
Детали и предположения:
- Деревья десяти домов на самом деле содержат ровно 10 домов.
- До бури существует единственный мост между каждой уникальной парой домов.
- Шторм разрушит каждый мост с независимой вероятностью \(\frac{1}{2}\).
- Джону разрешено проходить через чужие дома, чтобы попытаться добраться до них всех, но он должен использовать только уцелевшие мосты, чтобы добраться туда. Не допускается раскачивание виноградной лозы.
Не допускается раскачивание виноградной лозы.Отмечен #ComputerScience, так как без него решить эту задачу довольно утомительно, хотя и не невозможно.
Изображение предоставлено: http://hdscreen.me/wallpaper/2645876-bridges-fantasy-art-landscapes-mountains
Основная статья: Вероятность
Вероятность — это число от 0 до 1 включительно, представляющее вероятность события. Дискретная вероятность — это вероятность, основанная на дискретных наборах результатов. Самым основным типом вероятности является равномерная вероятность. Если каждый исход в наборе равновероятен, то вероятность события равна отношению кардинальностей.
Пусть \(S\) — выборочное пространство исходов. Если каждый исход в этом множестве равновероятен, то вероятность события \(A\) в \(S\) равна
.\[P(A)=\frac{|A|}{|S|}.\]
Какова вероятность того, что в високосном году будет 53 воскресенья?
Многие правила вероятности аналогичны правилам комбинаторики.
Вероятностные правила произведения, суммы и дополнения работают аналогично тем же правилам комбинаторики. Кроме того, структура вероятностного принципа включения и исключения такая же, как у ПИС для множеств.
\[\dfrac{121}{243}\] \[\dfrac{122}{243}\] \[\dfrac{124}{243}\] \[\dfrac{125}{243}\]
Многократно подбрасывается смещенная монета. Предположим, что исходы различных бросков независимы и вероятность выпадения орла равна \(\frac{2}{3}\) для каждого броска. Какова вероятность выпадения четного числа голов за 5 бросков?
Дискретное распределение вероятностей — это функция, которая принимает числовой результат в качестве аргумента и дает в результате вероятность. Дискретные распределения вероятностей могут быть созданы с использованием правил и указаний, описанных выше. Есть также некоторые дискретные распределения вероятностей, которые проявляются во многих задачах:
- Геометрическое распределение: Учитывая повторяющиеся испытания, в которых вероятность успеха каждый раз одинакова, это дает вероятность того, что первый успех будет достигнут в определенном испытании. Пример : Вы бросаете кости, пока не выпадете 6. Какова вероятность того, что первые 6 выпадут при третьем броске?
- Биномиальное распределение: Учитывая определенное количество испытаний, в которых вероятность успеха каждый раз одинакова, это дает вероятность определенного количества успехов. Пример : Вы подбрасываете монету 10 раз. Какова вероятность того, что выпадет ровно 5 орлов?
- Распределение Пуассона: Учитывая период времени, в течение которого событие происходит определенное среднее количество раз, это дает вероятность того, что событие произойдет определенное количество раз. Пример : Ресторан быстрого питания принимает 3 клиентов в минуту. Какова вероятность того, что они получат 4 клиентов в следующую минуту?
Пример : Вы бросаете кости, пока не выпадете 6. Какова вероятность того, что первые 6 выпадут при третьем броске?Хотя базовые вероятности основаны на дискретных множествах, понятие вероятности можно распространить на непрерывные множества, используя концепции исчисления.
На единичном отрезке случайным образом отмечается точка.
Найдите математическое ожидание суммы квадратов длин двух частей.
Основная статья: биекция, инъекция и сюръекция
Биекция — это отношение между двумя наборами, такое, что каждый элемент в наборе связан ровно с одним элементом в другом наборе, и наоборот. Биекции можно применять для решения проблем, устанавливая биекцию между набором, который трудно перечислить, и хорошо понятной дискретной структурой. Устанавливая биекцию, можно воспользоваться известными формулами и теоремами, которые дает дискретная структура.
Трое братьев и сестер Моллой, Эйприл, Брэдли и Кларк, имеют целый возраст, который в сумме равен 15. Сколько существует возможных распределений возрастов?
Примечание : Возможно, что возраст может быть равен 0, что означает, что ребенок только что родился.
Можно установить биекцию между множеством распределений возрастов и множеством комбинаций. Рассмотрим расположение звездочек и полосок ниже:
\[\star \star \mid \star \star \star \star \mid \star \star \star \star \star \star \star \star \star\]
Это расположение соответствует следующему распределению возрастов: апрель — 2, Брэдли — 4, Кларк — 9.
Количество раздач возрастов
\[\binom{17}{2}=136.\ _\квадрат\]
Обратите внимание, что в приведенном выше расположении 15 звезд и 2 полосы. Это дает в общей сложности 17 объектов, 2 из которых являются барами. Размещение полосок в разных местах среди 17 мест даст новое распределение возрастов. Таким образом, можно установить биекцию между множеством распределений возрастов и множеством комбинаций 2 объектов из 17.На парковке 10 свободных мест подряд.
Прибывают 6 автомобилей, каждый из которых занимает ровно 1 парковочное место, выбранное случайным образом из числа доступных мест. Затем прибывает Робби на своем пикапе, для парковки которого требуется 2 пустых соседних места.
Если вероятность того, что Робби сможет припарковаться, равна \(\frac{a}{b},\), где \(a\) и \(b\) взаимно простые положительные целые числа, то что такое \(a+ б?\)
Основные статьи:
Логические головоломки
Логика высказываний
Булева алгебра
Предложение — это утверждение, которое может быть либо истинным, либо ложным.
Логика высказываний направлена на то, чтобы наметить правила того, как эти утверждения могут быть изменены и объединены.
Какие из следующих утверждений верны, а какие ложны, зная, что весь набор непротиворечив?
С1. Утверждения 2 и 3 либо оба верны, либо оба ложны.
С2. Ровно одно из утверждений 4 и 5 верно.
С3. Ровно одно из утверждений 4 и 6 верно.
С4. Ровно одно из утверждений 1 и 6 верно.
С5. Утверждения 1 и 3 относятся к одному типу (оба истинны или оба ложны).
С6. Ровно одно утверждение из утверждений 2 и 5 верно.
Ответ запишите в виде конкатенации цифр 1 и 0 для значений истинности утверждений (истинно и ложно), начиная с S1 до S6, где значению истинно соответствует 1, а значению ложно соответствует 0. Например, если бы первые 2 утверждения были истинными, а остальные ложными, ответ был бы 110000.
Если правильный ответ начинается с некоторого количества начальных нулей, удалите его из записи ответа.
