Два резистора. Анализ соединения резисторов в электрической цепи: последовательное и параллельное подключение — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как определить тип соединения резисторов в электрической схеме. Какие признаки указывают на последовательное подключение резисторов. Как отличить параллельное соединение от последовательного. Какие правила расчета параметров цепи применяются при разных типах соединения.

Содержание

Основные типы соединения резисторов в электрических цепях

В электротехнике выделяют два основных способа соединения резисторов в цепи:

Последовательное соединение
Параллельное соединение

Понимание различий между этими типами соединений критически важно для правильного анализа и расчета электрических цепей. Давайте рассмотрим каждый тип подробнее.

Последовательное соединение резисторов: ключевые признаки

При последовательном соединении резисторы включаются один за другим, образуя единую цепь. Основные признаки такого соединения:

Через все резисторы протекает один и тот же ток
Общее напряжение распределяется между резисторами
Общее сопротивление цепи равно сумме сопротивлений отдельных резисторов

Как определить последовательное соединение на схеме? Если резисторы соединены «встык», без ответвлений между ними, это указывает на последовательное подключение.

Параллельное соединение резисторов: что нужно знать

При параллельном соединении резисторы подключаются к одним и тем же точкам цепи. Ключевые особенности:

На всех резисторах одинаковое напряжение
Общий ток разветвляется между резисторами
Обратная величина общего сопротивления равна сумме обратных величин сопротивлений резисторов

Визуально на схеме параллельное соединение можно определить по наличию узлов, от которых отходят несколько ветвей с резисторами.

Как не спутать последовательное и параллельное соединение?

Иногда на первый взгляд бывает сложно определить тип соединения. Вот несколько советов:

Проследите путь тока — при последовательном соединении он проходит через все элементы поочередно
Проверьте напряжение — при параллельном оно одинаково на всех резисторах

Мысленно замените один резистор проводником — если это не изменит схему, соединение параллельное

Помните, что расположение элементов на схеме может быть обманчивым. Всегда анализируйте электрические соединения, а не визуальное размещение.

Расчет параметров цепи при разных типах соединения

Тип соединения резисторов определяет, какие формулы нужно применять для расчета параметров цепи:

Последовательное соединение:

Общее сопротивление: R = R1 + R2 + R3 + …
Общий ток: I = U / R, где U — общее напряжение
Напряжение на каждом резисторе: Un = I * Rn

Параллельное соединение:

Обратная величина общего сопротивления: 1/R = 1/R1 + 1/R2 + 1/R3 + …
Общее напряжение равно напряжению на каждом резисторе
Общий ток: I = I1 + I2 + I3 + …

Практический пример анализа схемы

Рассмотрим схему с двумя резисторами R1 и R2, подключенными к источнику напряжения V. Как определить тип соединения?

Проверяем узлы схемы — есть ли общие точки подключения резисторов?
Анализируем путь тока — проходит ли он через оба резистора последовательно?
Оцениваем распределение напряжения — одинаково ли оно на обоих резисторах?

Ответив на эти вопросы, мы сможем точно определить тип соединения и применить соответствующие формулы для расчета.

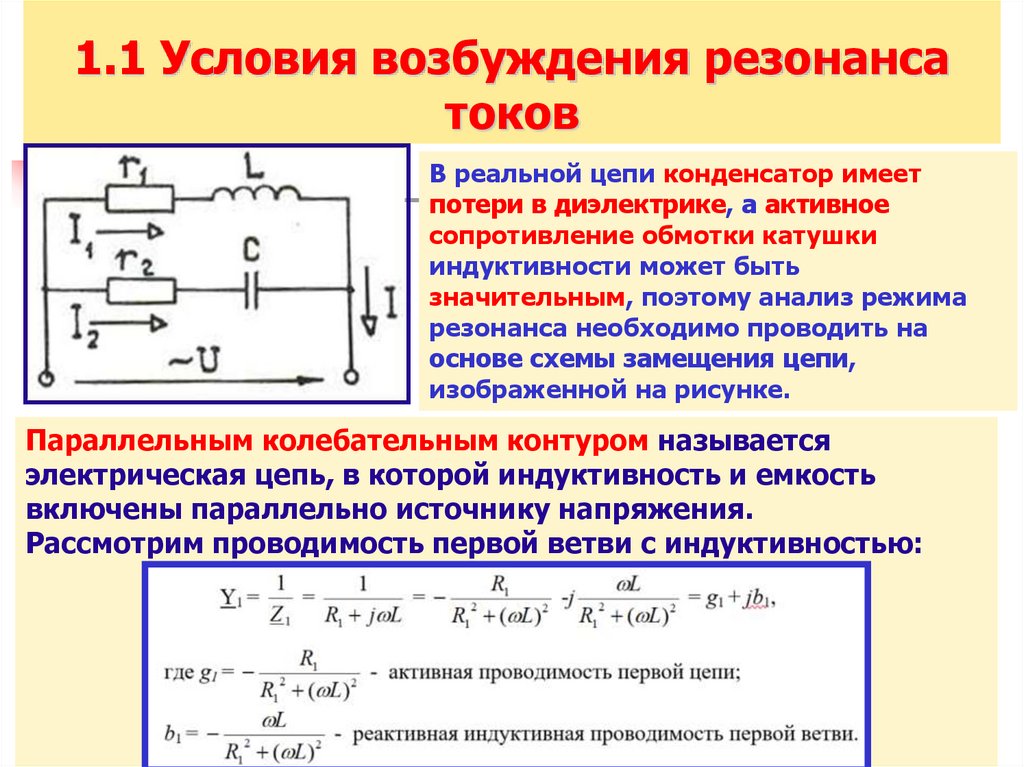
Смешанное соединение резисторов: как анализировать?

В реальных схемах часто встречается смешанное соединение, сочетающее последовательные и параллельные участки. Алгоритм анализа такой схемы:

Разбейте схему на участки с однотипным соединением
Рассчитайте эквивалентное сопротивление для каждого участка
Замените участки эквивалентными резисторами
Повторяйте процесс, пока не получите простую схему

Этот метод позволяет упростить сложные схемы и провести их корректный анализ.

Влияние типа соединения на характеристики цепи

Выбор способа соединения резисторов существенно влияет на свойства электрической цепи:

Последовательное соединение увеличивает общее сопротивление
Параллельное соединение уменьшает общее сопротивление
При последовательном соединении легче контролировать ток
Параллельное соединение позволяет распределять нагрузку между резисторами

Понимание этих особенностей помогает правильно проектировать электрические схемы для различных применений.

Два резистора, сопротивлениями соответственно 20 Ом и 40 Ом, соединен… — Учеба и наука






Лучший ответ по мнению автора

Т.к. сопротивления соединены последовательно, то
Rоб=R1+R2=20+40=60 Ом
Сила тока в цепи I=Uоб/Rоб=120/60=2 А
Мощность выделяемая на резисторах
P1=I^2R1=2^2*20=80 Вт
P2=I^2R2=2^2*40=160 Вт

26.

04.15

Лучший ответ по мнению автора

Михаил Александров

Читать ответы

Андрей Андреевич

Читать ответы

Владимир

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Физика

Похожие вопросы

УСЛОВИЕ: Два точечных положительных заряда: q1=30 нКл и q2=10 нКл находятся в вакууме на расстоянии L=0,5 м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А.

Два точечных отрицательных заряда: q1 -20 нКл и q2 -40 нКл находятся в вакууме на расстоянии L 1,5 м друг от друга. Определите величину…

Решено

интенсивность света

Решено

Сколько электронов нужно «перенести» с одной пылинки на другую чтобы сила кулоновского притяжения между пылинками на расстоянии 1см равнялась 10 мкН?

в двух противоположных вершинах квадрата…

Пользуйтесь нашим приложением

Два резистора с сопротивлениями R1 и R2 подключены к источнику тока с внутренним сопротивлением r (см. рисунок). Напряжение на втором резисторе равно U2. Чему равны напряжение на первом резисторе и ЭДС источника?Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

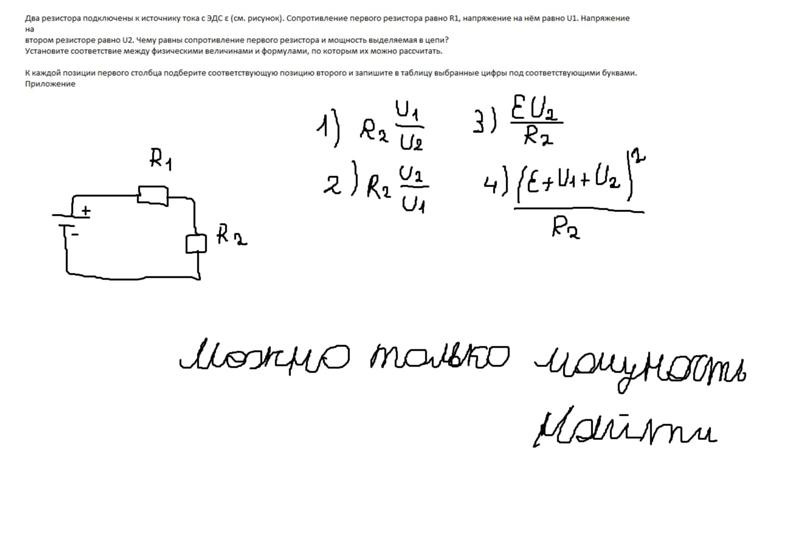К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) ЭДС источника Б) напряжение на резисторе R1 ФОРМУЛЫ 1) $ {U_2} \cdot \frac{{{R_1}}}{{{R_2}}} $ 2) $ {U_2} \cdot \frac{{{R_2}}}{{{R_1}}} $ 3) $ \frac{{{U_2}}}{{{R_2}}} \cdot \left( {{R_1} + {R_2} + r} \right) $ 4) $ \frac{{{U_2}}}{{{R_1}}} \cdot \left( {{R_1} + {R_2} + r} \right) $ Два резистора с сопротивлениями R1 и R2 подключены к источнику тока с внутренним сопротивлением r (см. рисунок). Напряжение на втором резисторе равно U2. Чему равны напряжение на первом резисторе и ЭДС источника?Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) ЭДС источника Б) напряжение на резисторе R1 ФОРМУЛЫ 1) $ {U_2} \cdot \frac{{{R_1}}}{{{R_2}}} $ 2) $ {U_2} \cdot \frac{{{R_2}}}{{{R_1}}} $ 3) $ \frac{{{U_2}}}{{{R_2}}} \cdot \left( {{R_1} + {R_2} + r} \right) $ 4) $ \frac{{{U_2}}}{{{R_1}}} \cdot \left( {{R_1} + {R_2} + r} \right) $

Учебник Курсы Книги Тесты Вопросы Личный кабинет

Учебник Курсы Книги Тесты Вопросы

Личный кабинет

Новогодние скидки 50% на все курсы

Задание ЕГЭ по физике
Линия заданий — 19
Наслаждайтесь интересным учебником и решайте десятки тестов на Studarium,
мы всегда рады вам! =)

15517. Два резистора с сопротивлениями R₁ и R₂ подключены к источнику тока с внутренним сопротивлением r (см. рисунок). Напряжение на втором резисторе равно U₂. Чему равны напряжение на первом резисторе и ЭДС источника?
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) ЭДС источника
Б) напряжение на резисторе R₁
ФОРМУЛЫ
1) $ {U_2} \cdot \frac{{{R_1}}}{{{R_2}}} $
2) $ {U_2} \cdot \frac{{{R_2}}}{{{R_1}}} $
3) $ \frac{{{U_2}}}{{{R_2}}} \cdot \left( {{R_1} + {R_2} + r} \right) $
4) $ \frac{{{U_2}}}{{{R_1}}} \cdot \left( {{R_1} + {R_2} + r} \right) $
Верный ответ: 31
P. S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке 😉
При обращении указывайте id этого вопроса — 15517.

Математическая задача: Два резистора — вопрос № 25291, Электротехника
Два резистора, 20 Ом и 60 Ом, соединены последовательно, и к ним подключено внешнее напряжение 400 В. Каковы электрические напряжения на соответствующих резисторах? Прокомментируйте, пожалуйста!
Правильный ответ:
U ₁ = 100 В
U ₂ = 300 В
=R1+R2=20+60=80 Ом I=U/R=400/80=5 A U1=I⋅ R1=5⋅ 20=100 В
U2=I⋅ R2=5⋅ 60=300=300 В Проверка решения: R1:R2=U1:U2 r1=R1/R2=20/60=31≐0,3333 r2 =U1/U2=100/300=31≐0,3333 U=U1+U2

Нашли ошибку или неточность? Не стесняйтесь
пишите нам
. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Воспользуйтесь нашим калькулятором коэффициентов.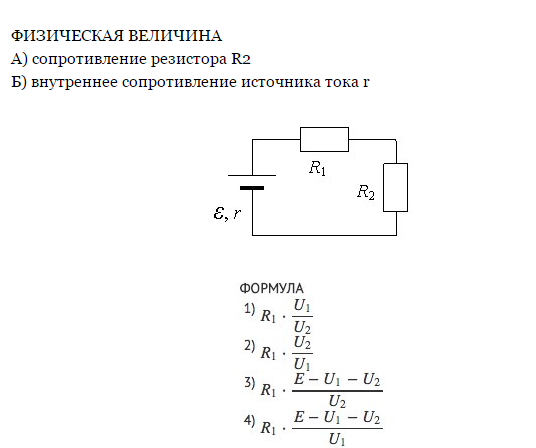
Для решения этой математической задачи вам необходимо знать следующие знания:
основные функции
Соотношение
Темы, темы:
Основы физики
Закон Ом
Электрои Инженер
Оценка слов. Проблема:
.
Наименьшее напряжение
Три резистора с резисторами R1 = 10 кОм, R2 = 20 кОм, R3 = 30 кОм соединены последовательно и к ним подключено внешнее напряжение U = 30 В. На каком резисторе самое низкое напряжение?
Сопротивления 80604
Резисторы сопротивлением 6 Ом и 10 Ом соединены последовательно на напряжение 24 В. а) Какой ток проходит через них? б) Каковы напряжения на отдельных резисторах?
Сопротивления 66064
Два резистора с сопротивлениями 40 Ом и 60 Ом соединены последовательно и подключены к напряжению 150В. A) полное сопротивление B) ток в цепи C) напряжение на обоих резисторах
Индивидуальное 46993
Мы измерили напряжение U= 75 В между внешними клеммами цепи с помощью вольтметра. Значения сопротивления цепи отдельных резисторов (последовательно) составляют 50 Ом и 100 Ом. Узнаем, какое напряжение мы будем измерять на 1-м и 2-м резисторе
Закон Кирхгофа
Два резистора сопротивлением 100 Ом и 300 Ом соединены последовательно. Ток 1,8 А проходит через первый резистор 100 Ом. Какой ток протекает через второй резистор?
Заряд А
Заряд 9 Кл проходит через последовательно соединенные резисторы сопротивлениями 40 Ом и 60 Ом за 1 минуту. а) К какому напряжению они подключены? б) Рассчитайте напряжение на каждом резисторе.
Сопротивление 5938
Если сопротивление первого резистора 100 Ом и отношение напряжений на первом и втором резисторах 2:1. Чему будет равно сопротивление второго последовательно включенного резистора?
Напряжение цепи
Рассчитайте напряжение замкнутой цепи. Рассчитайте мощность на резисторах. R1 = 30 Ом, R2 = 10 Ом. я = 0,1А. У =?. Резисторы соединены последовательно, один за другим.
Резисторы
Два параллельно соединенных резистора дают результирующее сопротивление 240 Ом и 57,6 Ом. Определить сопротивление этих резисторов.
Последовательное соединение
Если напряжение на первом резисторе равно 6 В и отношение сопротивлений первого и второго резисторов равно 1:3, каково будет напряжение на втором резисторе, если их соединить последовательно?
Индивидуальный 31411
На источниках с напряжением U=12В последовательно соединены резисторы R1=1 Ом, R2=2 Ом и R3=9 Ом. Определить ток I, протекающий от источника, и падения напряжения U1, U2 и U3 на отдельных резисторах.
Действующее и среднее напряжение
Делитель напряжения, состоящий из резисторов R1 = 103000 Ом и R2 = 197000 Ом, подключен к идеальному источнику синусоидального напряжения, R2 подключен к вольтметру, который измеряет среднее напряжение и имеет внутреннее сопротивление R3 = 200300 Ом, измеренное значение i
Короткое замыкание 22841
Внешняя цепь сопротивлением 3,8 Ом подключена к источнику электрического напряжения с Ue=12 В. По цепи протекает ток силой 3 А. Укажите: напряжение на клеммах источника, внутреннее сопротивление источника, максимальный ток короткого замыкания.
Вентилятор
Вентилятор с сопротивлением 20 Ом подключен к источнику питания. Ток, протекающий по цепи, равен 2,5 А. Какое напряжение источника питания?
Рассчитать 80467
Рассчитайте ток I, протекающий через резистор R5 (720 Ом), резистор R2 (220 Ом) и светодиод (U=2 В) от источника постоянного тока 6 В. Резисторы соединены последовательно.
Сопротивление 5939
Если сопротивление первого резистора 200 Ом, а сопротивление второго резистора 600 Ом. Каково будет отношение электрического напряжения на первом резисторе к электрическому напряжению на втором резисторе (оба соединены
Резистор
Резистор 1 сопротивлением 100 Ом и резистор 2 сопротивлением 400 Ом соединены параллельно стороны в цепи. Между выводами резистора имеется напряжение 80 В. а) Начертите принципиальную схему и запишите в нее введенные величины б)
all math problems16163
algebra 4723
arithmetic 3198
basic functions 5037
combinatorics 862
geometry 2718
goniometry and trigonometry 486
numbers 4901
physical quantity 5179
planimetrics 2960
solid геометрия 2059
статистика 623
темы, темы 2491

Новые задачи по математике
Самые просматриваемые задачи по математике
Самые сложные задачи
Самые простые задачи со словами
Анализ схемы — Как соединить два резистора с источником напряжения
спросил 2 года, 6 месяцев назад
Изменено 2 года, 6 месяцев назад
Просмотрено 3к раз
\$\начало группы\$

^{имитация этой цепи – Схема создана с помощью CircuitLab}
^{имитация этой цепи}
Эти две схемы одинаковы? Если нет, не могли бы вы также указать, почему?
анализ цепей
\$\конечная группа\$
2
\$\начало группы\$
В самом начале ваш мозг легко обмануть расположением предметов, а не тем, что они есть на самом деле. Бок о бок не означает автоматически параллельно.
Что, если я возьму вашу «параллельную» схему:
^{смоделирую эту схему — Схема, созданная с помощью CircuitLab}
, и просто изменю ее на эту. Он по-прежнему кажется вам параллельным? Или сериал, если на то пошло? Помните, ток может течь в цепь по этим шлейфам извне.

^{имитация этой цепи}
Параллельное = напряжение на всех компонентах одинаковое
Серия
= ток через все компоненты одинаков
Пусть вас не обманывает расположение элементов на странице.
\$\конечная группа\$
\$\начало группы\$
^{смоделируйте эту цепь – схема создана с помощью CircuitLab}
0227 Р1 + Р2 .
^{смоделируйте эту схему}
Рис. 2. В этом случае резисторы R1 и R2 включены параллельно.
\$\конечная группа\$
3
\$\начало группы\$

Есть хороший способ понять, является ли комбинация последовательной или параллельной. Например, взгляните на схему ниже.
^{смоделируйте эту схему – Схема создана с помощью CircuitLab}
Левая сторона R ₁ напрямую соединена с положительной клеммой аккумуляторной батареи. Допустим, напряжение равно _В . Точно так же правая сторона R ₁ подключена к отрицательной клемме аккумулятора. Допустим, напряжение V _b.
Таким образом, разность потенциалов между R ₁ равна (V _a — V _b )
Аналогично, напряжение на R ₂ также будет (V _a — V _b )
Если два резистора соединены параллельно, то они будут иметь одинаковую разность потенциалов между их клеммами.
^{имитация этой схемы}
Теперь для этой новой схемы верхняя сторона резистора R ₁ напрямую подключена к положительной клемме батареи. Напряжение этого терминала обозначено как V _a .
Теперь будет падение напряжения, вызванное резистором R ₁ (примечание: закон Ома V=IR). Таким образом, новый уровень напряжения V _c появится на нижней стороне R ₁ . А нижняя сторона R ₂ напрямую связана с отрицательной клеммой аккумулятора, которая обозначена как V _b .
Все комбинации последовательностей вызовут такое изменение напряжения.
Возьмем сложный пример.
^{имитация этой схемы}
Просто при осмотре понять довольно сложно. Но если отметить напряжения узлов, то вы увидите, что все они имеют одинаковую разность потенциалов, которая составляет (V _а — В _б). Это означает, что все они параллельны друг другу.
\$\конечная группа\$
\$\начало группы\$
Иногда, когда вы еще новичок во всем этом, просто не ясно, параллельно (или последовательно) соединены два элемента схемы.
Если вы не уверены, есть простой способ проверить, подключены ли два резистора параллельно: рассмотрите возможность установки одного из резисторов на ноль Ом.
Например, установите \$R_1=0\Omega\$ (по сути, замените \$R_1\$ проводом).
Понятно, что источник напряжения видит резистор \$R_2\$ в качестве нагрузки.
Но это не так, если \$R_1\$ и \$R_2\$ соединены параллельно, так как при \$R_1=0\$ имеем
$$R_1||R_2 = \frac{ 0\cdot R_2}{0 + R_2} = 0\Omega$$
То есть ноль омов параллельно с \$R\$ омами равняется нулю омов .
Так как источник не видит ноль Ом с \$R_1=0\Omega\$, то два резистора не подключены параллельно.
\$\конечная группа\$
\$\начало группы\$
Возможно, ваша путаница связана с эквивалентной схемой Thevenin той, которую вы показываете (источник напряжения Vth=V*R2/(R1+R2) последовательно с резистором Rth=R1//R2).