Как переводить числа между десятичной, двоичной и шестнадцатеричной системами счисления. Какие существуют методы и алгоритмы перевода. Как использовать калькулятор и Excel для перевода чисел между системами счисления. Какие есть особенности и тонкости при переводе чисел.
Основные понятия систем счисления
Прежде чем рассматривать методы перевода чисел между системами счисления, давайте вспомним ключевые понятия:
- Система счисления — это способ записи чисел с помощью заданного набора символов и правил их использования.
- Позиционная система счисления — система, в которой значение цифры зависит от ее положения (позиции) в записи числа.
- Основание системы счисления — количество различных цифр, используемых для записи чисел в данной системе.
- Алфавит системы счисления — набор символов, используемых для записи чисел.
Наиболее распространенные системы счисления:
- Десятичная (основание 10, цифры 0-9)
- Двоичная (основание 2, цифры 0 и 1)
- Шестнадцатеричная (основание 16, цифры 0-9 и буквы A-F)
Перевод из десятичной системы в двоичную
Для перевода целого десятичного числа в двоичную систему используется метод последовательного деления на 2:
- Разделить число на 2
- Записать остаток от деления (0 или 1)
- Если частное не равно 0, повторить шаги 1-2 для частного
- Полученные остатки записать в обратном порядке
Пример перевода числа 75 в двоичную систему:
- 75 / 2 = 37 (остаток 1)
- 37 / 2 = 18 (остаток 1)
- 18 / 2 = 9 (остаток 0)
- 9 / 2 = 4 (остаток 1)
- 4 / 2 = 2 (остаток 0)
- 2 / 2 = 1 (остаток 0)
- 1 / 2 = 0 (остаток 1)
Записываем остатки в обратном порядке: 7510 = 10010112
Перевод из двоичной системы в десятичную
Для перевода двоичного числа в десятичную систему нужно:
- Пронумеровать разряды справа налево, начиная с нуля
- Умножить значение каждого разряда на 2 в степени номера разряда
- Сложить полученные значения
Пример перевода числа 10010112 в десятичную систему:
- 1*26 + 0*25 + 0*24 + 1*23 + 0*22 + 1*21 + 1*20
- 64 + 0 + 0 + 8 + 0 + 2 + 1 = 75
Итак, 10010112 = 7510
Перевод между двоичной и шестнадцатеричной системами
Перевод между двоичной и шестнадцатеричной системами основан на том, что каждая шестнадцатеричная цифра соответствует 4 битам:

- Для перевода из двоичной в шестнадцатеричную нужно разбить двоичное число на группы по 4 бита справа налево и заменить каждую группу соответствующей шестнадцатеричной цифрой.
- Для перевода из шестнадцатеричной в двоичную нужно заменить каждую шестнадцатеричную цифру соответствующей группой из 4 бит.
Пример перевода 10010112 в шестнадцатеричную систему:
- Разбиваем на группы по 4 бита: 100 1011
- Дополняем первую группу нулями слева: 0100 1011
- Заменяем группы на шестнадцатеричные цифры: 4B
Итак, 10010112 = 4B16
Использование калькулятора для перевода чисел
Стандартное приложение «Калькулятор» в Windows имеет режим «Программист», который позволяет легко переводить числа между системами счисления:
- Откройте калькулятор и переключите его в режим «Программист»
- Выберите систему счисления, в которой вы хотите ввести число (Dec, Bin, Oct, Hex)
- Введите число
- Выберите нужную систему счисления для просмотра результата перевода
Этот метод удобен для быстрой проверки результатов ручного перевода или при работе с небольшими числами.

Перевод чисел в Excel
Microsoft Excel предоставляет функции для перевода чисел между системами счисления:
- DEC2BIN(число) — перевод из десятичной в двоичную
- BIN2DEC(число) — перевод из двоичной в десятичную
- DEC2HEX(число) — перевод из десятичной в шестнадцатеричную
- HEX2DEC(число) — перевод из шестнадцатеричной в десятичную
Пример использования:
- =DEC2BIN(75) вернет 1001011
- =BIN2DEC(1001011) вернет 75
- =DEC2HEX(75) вернет 4B
- =HEX2DEC(«4B») вернет 75
Excel удобен для работы с большим количеством чисел или при необходимости выполнять дополнительные вычисления.
Особенности и тонкости перевода чисел
При переводе чисел между системами счисления следует учитывать несколько важных моментов:
- Перевод дробных чисел: для перевода дробной части используется метод умножения на основание новой системы счисления с выделением целой части.
- Ограничения разрядности: при переводе больших чисел или дробей с большим количеством знаков после запятой может возникнуть потеря точности из-за ограничений разрядности.
- Отрицательные числа: при работе с отрицательными числами нужно учитывать способ их представления в разных системах счисления (например, дополнительный код в двоичной системе).
- Системы счисления с основанием больше 10: при работе с такими системами (например, шестнадцатеричной) используются буквы для обозначения цифр больше 9.
Понимание этих особенностей поможет избежать ошибок при переводе чисел и работе с разными системами счисления.

Практические применения перевода чисел между системами счисления
Умение переводить числа между различными системами счисления находит применение во многих областях:
- Программирование: двоичная и шестнадцатеричная системы широко используются в программировании для работы с битовыми операциями, представления цветов, IP-адресов и т.д.
- Компьютерные сети: IP-адреса и маски подсети часто записываются в двоичном или шестнадцатеричном виде.
- Криптография: многие алгоритмы шифрования работают с данными в двоичном или шестнадцатеричном представлении.
- Цифровая электроника: проектирование цифровых схем часто требует работы с двоичными числами.
- Компьютерная графика: цвета в цифровых изображениях часто кодируются шестнадцатеричными значениями.
Практика перевода чисел между системами счисления развивает логическое мышление и улучшает понимание принципов работы компьютерных систем.
Заключение
Перевод чисел между системами счисления — важный навык для специалистов в области информационных технологий. Понимание принципов работы различных систем счисления и методов перевода между ними позволяет эффективно решать многие задачи в программировании, компьютерных сетях и других областях. Регулярная практика и использование различных инструментов, таких как калькулятор или Excel, помогут закрепить этот навык и применять его в реальных проектах.

Онлайн калькулятор дробей с решением со степенями со скобками с буквами
Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и десятичных дробей.
Основные возможности:
- Сложение, вычитание, деление и умножение дробей.
- Расчет дробей с подробнейшим решением.
- Расчет дробей со степенями, скобками и буквами.
- Сокращение дробей.
- Поддержка до трех дробей онлайн.
На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей.
Калькулятор умеет:
- Вносить целую часть дроби в числитель для смешанных дробей.
- Расчет дробей со скобками- поддержка до двух уровней вложенности скобок.
- Расчет дробей со степенями — степенью может быть только число.
- Расчет дробей с буквами — любые анг.
 (-2) +1.
(-2) +1. - При сложении дробей состоящих только из чисел калькулятор вычисляет НОД и НОК.
- При расчете сразу трех дробей сначала выполняется операция умножение(деления), затем сложения(вычитания). Для изменения этого порядка поставьте галочку в поле «Большие скобки» и выберите нужный порядок расчета. В этом случае первой будет выполняться операция в больших скобках.
Перевод чисел из одной системы счисления в любую другую онлайн
- Главная
- Конвертеры
- Инструменты
- Перевод чисел из одной системы счисления в любую другую онлайн
Для перевода чисел из десятичной с/с в любую другую, необходимо делить десятичное число на основание системы, в которую переводят, сохраняя при этом остатки от каждого деления. Результат формируется справа налево. Деление продолжается до тех пор, пока результат деления не станет меньше делителя.
Калькулятор переводит числа из одной системы счисления в любую другую. Он может переводить числа из двоичной в десятичную или из десятичной в шестнадцатеричную, показывая подробный ход решения. Вы с легкостью можете перевести число из троичной в пятеричную или даже из семеричной в семнадцатеричную. Калькулятор умеет переводить числа из любой системы счисления в любую другую.
Он может переводить числа из двоичной в десятичную или из десятичной в шестнадцатеричную, показывая подробный ход решения. Вы с легкостью можете перевести число из троичной в пятеричную или даже из семеричной в семнадцатеричную. Калькулятор умеет переводить числа из любой системы счисления в любую другую.
Онлайн калькулятор перевода чисел из одной системы счисления в любую другую
Способы перевода чисел из одной системы счисления в другую
В программу ЕГЭ по информатике входят несколько задач, связанных с переводом чисел из одной системы в другую. Как правило, это преобразование между 8- и 16-ричными системами и двоичной. Это разделы А1, В11. Но есть и задачи с другими системами счисления, как например, в разделе B7
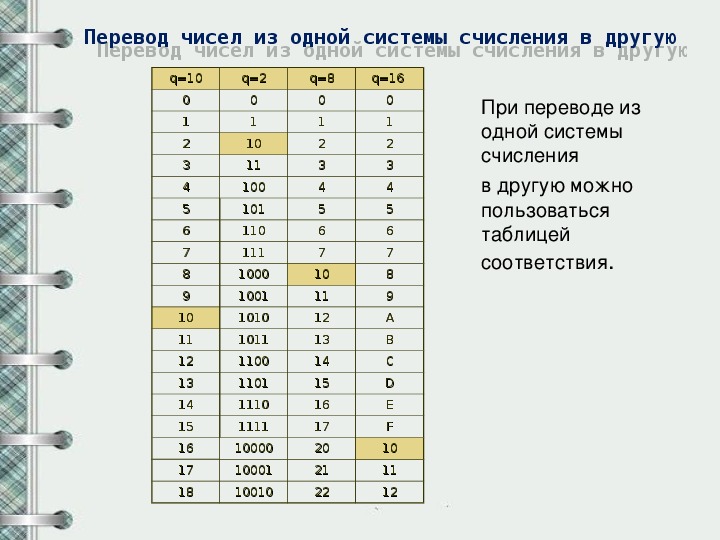
.Для начала напомним две таблицы, которые хорошо бы знать наизусть тем, кто выбирает информатику своей дальнейшей профессией.
Таблица степеней числа 2:
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 |
| 2 | 4 | 8 | 16 | 64 | 128 | 256 | 512 | 1024 |
Она легко получается умножением предыдущего числа на 2. Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Таблица двоичных чисел от 0 до 15 c 16-ричным представлением:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Недостающие значения тоже нетрудно вычислить, прибавляя по 1 к известным значениям.
Арифметические операции в двоичной системе счисления
|
Сложение |
Вычитание |
Умножение |
|
0+0=0 |
0-0=0 |
0*0=0 |
|
1+0=1 |
1-0=1 |
1*0=0 |
|
0+1=1 |
0-1=1 |
0*1=0 |
|
1+1=10 |
1-1=0 |
1*1=1 |
При сложении двух чисел, равных 1, в данном разряде получается 0, а 1-ца переносится в старший разряд.
Перевод целых чисел
Итак, начнем с перевода сразу в двоичную систему. Возьмём то же число 81010. Нам нужно разложить это число на слагаемые, равные степеням двойки.
- Ищем ближайшую к 810 степень двойки, не превосходящую его. Это 29 = 512.
- Вычитаем 512 из 810, получаем 298.
- Повторим шаги 1 и 2, пока не останется 1 или 0.
- У нас получилось так: 810 = 512 + 256 + 32 + 8 + 2 = 29 + 28 + 25 + 23 + 21.
Далее есть два способа, можно использовать любой из них. Как легко увидеть, что в любой системе счисления её основание всегда 10. Квадрат основания всегда будет 100, куб 1000. То есть степень основания системы счисления — это 1 (единица), и за ней столько нулей, какова степень.
Способ 1: Расставить 1 по тем разрядам, какие получились показатели у слагаемых. В нашем примере это 9, 8, 5, 3 и 1. В остальных местах будут стоять нули. Итак, мы получили двоичное представление числа 81010 = 11001010102. Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Итак, мы получили двоичное представление числа 81010 = 11001010102. Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Способ 2: Распишем слагаемые как степени двойки друг под другом, начиная с большего.
810 =
| 29 = | 1000000000 | (1 и девять нулей) + |
| 28 = | 100000000 | (1 и восемь нулей) + |
| 25 = | 100000 | (1 и пять нулей) + |
| 23 = | 1000 | (1 и три нуля) + |
| 21 = | 10 | (1 и один ноль) |
А теперь сложим эти ступеньки вместе, как складывают веер: 1100101010.
Вот и всё. Попутно также просто решается задача «сколько единиц в двоичной записи числа 810?».
Ответ — столько, сколько слагаемых (степеней двойки) в таком его представлении. У 810 их 5.
Теперь пример попроще.
Переведём число 63 в 5-ричную систему счисления. Ближайшая к 63 степень числа 5 — это 25 (квадрат 5). Куб (125) будет уже много. То есть 63 лежит между квадратом 5 и кубом. Тогда подберем коэффициент для 52. Это 2.
Получаем 6310 = 50 + 13 = 50 + 10 + 3 = 2 * 52 + 2 * 5 + 3 = 2235.
Ну и, наконец, совсем лёгкие переводы между 8- и 16-ричными системами. Так как их основанием является степень двойки, то перевод делается автоматически, просто заменой цифр на их двоичное представление. Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.
Переведем в двоичную систему число 5478.
| 5478= | 101 | 100 | 111 |
| 5 | 4 | 7 |
Ещё одно, например 7D6A16.
| 7D6A16= | (0)111 | 1101 | 0110 | 1010 |
| 7 | D | 6 | A |
Переведем в 16-ричную систему число 7368. Сначала цифры запишем тройками, а потом поделим их на четверки с конца: 7368 = 111 011 110 = 1 1101 1110 = 1DE16. Переведем в 8-ричную систему число C2516. Сначала цифры запишем четвёрками, а потом поделим их на тройки с конца: C2516 = 1100 0010 0101 = 110 000 100 101 = 60458. Теперь рассмотрим перевод обратно в десятичную. Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем. E6816 = 14 * 162 + 6 * 16 + 8 = 3688. 7328 = 7 * 82 + 3*8 + 2 = 474.
Перевод отрицательных чисел
Здесь нужно учесть, что число будет представлено в дополнительном коде. Для перевода числа в дополнительный код нужно знать конечный размер числа, то есть во что мы хотим его вписать — в байт, в два байта, в четыре. Старший разряд числа означает знак. Если там 0, то число положительное, если 1, то отрицательное. Слева число дополняется знаковым разрядом. Беззнаковые (unsigned) числа мы не рассматриваем, они всегда положительные, а старший разряд в них используется как информационный.
Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1.
Итак, переведем число -79 в двоичную систему. Число займёт у нас один байт.
Переводим 79 в двоичную систему, 79 = 1001111. Дополним слева нулями до размера байта, 8 разрядов, получаем 01001111. Меняем 1 на 0 и 0 на 1. Получаем 10110000. К результату прибавляем 1, получаем ответ 10110001.
Получаем 10110000. К результату прибавляем 1, получаем ответ 10110001.
Попутно отвечаем на вопрос ЕГЭ «сколько единиц в двоичном представлении числа -79?».
Ответ — 4.
Прибавление 1 к инверсии числа позволяет устранить разницу между представлениями +0 = 00000000 и -0 = 11111111. В дополнительном коде они будут записаны одинаково 00000000.
Перевод дробных чисел
Дробные числа переводятся способом, обратным делению целых чисел на основание, который мы рассмотрели в самом начале. То есть при помощи последовательного умножения на новое основание с собиранием целых частей. Полученные при умножении целые части собираются, но не участвуют в следующих операциях. Умножаются только дробные. Если исходное число больше 1, то целая и дробная части переводятся отдельно, потом склеиваются.
Переведем число 0,6752 в двоичную систему.
| 0 | ,6752 |
| *2 | |
| 1 | ,3504 |
| *2 | |
| 0 | ,7008 |
| *2 | |
| 1 | ,4016 |
| *2 | |
| 0 | ,8032 |
| *2 | |
| 1 | ,6064 |
| *2 | |
| 1 | ,2128 |
Процесс можно продолжать долго, пока не получим все нули в дробной части или будет достигнута требуемая точность. Остановимся пока на 6-м знаке.
Остановимся пока на 6-м знаке.
Получается 0,6752 = 0,101011.
Если число было 5,6752, то в двоичном виде оно будет 101,101011.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Перевод из двоичной системы в десятичную
1. Перевод из двоичной системы в десятичную
Как переводить из двоичной системы в десятичнуюДвоичная система счисления («по основанию два») — система
счисления, которая имеет два возможных значения для
каждого разряда; часто эти значения представляются как 0
или 1. И наоборот, десятичная (по основанию десять)
система счисления имеет десять возможных значений
(0,1,2,3,4,5,6,7,8 или 9) для каждого разряда. Чтобы не
запутаться при использовании различных систем счисления,
основание каждого отдельного числа можно записывать
после числа нижним индексом. Например, двоичное число
10011100 можно записать по основанию два как 100111002.
 А
Адесятичное число 156 может быть записано как 15610,
читаться оно будет так: «сто пятьдесят шесть, по основанию
десять». Так как двоичная система является внутренним
языком компьютеров, то серьезные программисты должны
понимать, как переводить из двоичной системы в десятичную.
Обратный перевод из десятичной в двоичную зачастую
сложнее освоить первым.
Запишите число в двоичной системе
счисления, а степени двойки справа
налево. Например, мы хотим
преобразовать двоичное число
100110112 в десятичное. Сначала
запишем его. Затем запишем степени
двойки справа налево. Начнем с 20, что
равно «1». Увеличиваем степень на
единицу для каждого следующего числа.
Останавливаемся, когда число
элементов в списке равно числу цифр в
двоичном числе. Наше число для
примера, 10011011, включает в себя
восемь цифр, поэтому список из восьми
элементов будет выглядеть так: 128, 64,
32, 16, 8, 4, 2, 1
2
Запишите цифры двоичного числа
под соответствующими степенями
двойки.
 Теперь просто запишите
Теперь просто запишите10011011 под числами 128, 64, 32, 16, 8,
4, 2, и 1, с тем чтобы каждая двоичная
цифра соответствовала своей степени
двойки. Самая правая «1» двоичного
числа должна соответствовать самой
правой «1» из степеней двоек, и так
далее. Если вам удобнее, вы можете
записать двоичное число над степенями
двойки. Самое важное – чтобы они
соответствовали друг другу.
3
Соедините цифры в двоичном числе
с соответствующими степенями
двойки. Нарисуйте линии (справа
налево), которые соединяют каждую
последующую цифру двоичного числа
со степенью двойки, находящейся над
ней. Начните построение линий с
соединения первой цифры двоичного
числа с первой степенью двойки над
ней. Затем нарисуйте линию от второй
цифры двоичного числа ко второй
степени двойки. Продолжайте соединять
каждую цифру с соответствующей
степенью двойки. Это поможет вам
визуально увидеть связь между двумя
различными наборами чисел.

4
Запишите конечное значение каждой
степени двойки. Пройдитесь по каждой
цифре двоичного числа. Если эта цифра
1, запишите соответствующую степень
двойки под цифрой. Если эта цифра 0,
запишите под цифрой 0.Так как «1»
соответствует «1», она остается «1». Так
как «2» соответствует «1», она остается
«2». Так как «4» соответствует «0», она
становится «0». Так как «8» соответствует
«1», она становится «8», и так как «16»
соответствует «1» она становится «16».
«32» соответствует «0» и становится «0»,
«64» соответствует «0» и поэтому
становится «0», в то время как «128»
соответствует «1» и становится 128.
Сложите получившиеся
значения. Теперь сложите
получившиеся под линией цифры. Вот
что вы должны сделать: 128 + 0 + 0 + 16
+ 8 + 0 + 2 + 1 = 155. Это десятичный
Запишите ответ вместе с нижним
индексом, равным системе
счисления. Теперь все, что вам
осталось сделать – это записать 15510,
чтобы показать, что вы работаете с
десятичным ответом, который оперирует
степенями десятки.
 Чем больше вы
Чем больше выбудете преобразовывать двоичные
числа в десятичные, тем проще вам
будет запомнить степени двойки, и тем
быстрее вы сможете выполнять данную
задачу.
7
Используйте данный метод, чтобы
преобразовать двоичное число с
десятичной точкой в десятичную
форму. Вы можете использовать
данный метод даже если вы хотите
преобразовать двоичное число, такое
как 1.12 в десятичное. Все, что вам
необходимо знать – это то, что число в
левой части десятичного числа – это
обычное число, а число в правой части
десятичного числа – это число «делений
надвое», или 1 x (1/2).»1″ слева от
десятичного числа соответствует 20, или
1. 1 справа от десятичного числа
соответствует 2-1, или .5. Сложите 1 и .5
и вы получите 1.5, которое является
эквивалентом 1.12 в десятичном виде.
Перевод чисел из десятичной системы счисления в двоичную и наоборот. Использование приложения Калькулятор(и программы EXCEL)
ГКОУ « Ахтининская средняя общеобразовательная школа» РД
Урок информатики в 8 классе с использованием информационно-коммуникативных технологий (ИКТ)
2017г.
Цели урока:
Обучающая
Обобщить способ перевода десятичных чисел в двоичную систему счисления, двоичных чисел в десятичную систему счисления, расширить представления учащихся о возможностях приложения Калькулятор.
Развивающая
Продолжить развитие у учащихся умения самостоятельно делать выводы, обосновывать и высказывать свое мнение.
Воспитывающая
Продолжить формирование навыков самостоятельной работы на компьютере. Развивать культуру общения, умение работать в паре.
Задачи:
Повторить способ перевода десятичных чисел в двоичную систему счисления, показать другие способы перевода двоичных чисел в десятичную систему счисления: использование приложения Калькулятор, перевод чисел в программе Excel
Оборудование:
Презентация к данному уроку, компьютер, мультимедийный проектор
Карточки
Тип урока:
Комбинированный урок
Форма работы: фронтальная, групповая, индивидуальная.
Знания и навыки учащихся:
Уметь переводить целые десятичные числа в двоичную систему счисления и обратно. Умение работать на компьютере с приложением Калькулятор.
Ход урока
1.Организационный момент.
2.Актуализация опорных знаний учащихся.
Учитель:
Здравствуйте. На прошлых занятиях мы занимались с вами переводом чисел из десятичной системы счисления в двоичную и наоборот, используя алгоритм перевода. Какие возникли у вас вопросы при выполнении домашнего задания?
(Проверка домашнего задания. Выяснить, какие задания вызывали затруднения, какие вопросы возникли у учеников. )
Давайте вспомним некоторые понятия. Скажите, пожалуйста, что такое система счисления?
Ответ: система счисления – это принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса:
позиционные – количественное значение каждой цифры зависит от ее место положения (позиции) в числе;
непозиционные – цифры не меняют своего количественного значения при изменении их положения в числе.

Учитель: А, что такое алфавит системы счисления?
Ответ: знаки, с помощью которых записываются числа, называют цифрами, а их совокупность алфавитом системы счисления.
Учитель: почему система счисления называется двоичной, десятичной?
Ответ: система счисления называется двоичной, потому что алфавит системы счисления состоит из двух цифр: 0 и 1, а алфавит десятичной системы составляют цифры 0,1,2,3,4,5,6,7,8,9.
Учитель: что называют основанием системы счисления?
Ответ: для записи чисел в различных системах счисления используется определенное количество знаков или цифр. Число таких знаков в позиционной системе счисления называется основанием системы счисления.
Учитель: а теперь вспомним алгоритм перевода чисел из десятичной в двоичную и наоборот.
Двое учащихся показывают алгоритм перевода на слайде№3
Учитель: я предлагаю вам несколько заданий, решив устно, вы должны выбрать правильный ответ слайды №4-11
1. Двоичное число 1010000 в десятичной записи имеет вид:
Двоичное число 1010000 в десятичной записи имеет вид:
А) 81
Б) 92
В) 80
Г) 78
2.Десятичное число 118 в двоичной записи имеет вид:
А) 1110010
Б) 1110011
В) 1110110
Г) 1111001
3.Двоичное число 1001 в десятичной записи имеет вид:
А) 9
Б) 8
В) 17
Г) 10
Значит, чтобы перевести числа из двоичной системы в десятичную и наоборот мы должны ….
Слайды 12-13
Учитель: Мы с вами повторили, как переводятся десятичные числа в двоичную систему счисления и наоборот. Сейчас мы рассмотрим с вами другие способы перевода чисел из десятичной системы в двоичную и наоборот с помощью приложения Калькулятор, и в программе Exsel
Для этого вы должны включить компьютеры. Работая на компьютере, ребята, помните правила техники безопасности и давайте будем следовать им при работе за компьютером (вспомнить некоторые правила по ТБ). Сейчас мы будем работать с приложением Калькулятор. Давайте посмотрим, как его найти и как настроить для работы. (Слайд 14-17)
Давайте посмотрим, как его найти и как настроить для работы. (Слайд 14-17)
Пуск/ Стандартные/Калькулятор
Запускаем приложение Калькулятор и выполняем команду (Вид- инженерный). Обратите внимание на группу переключателей, определяющих систему счисления:
Убедимся, что Калькулятор настроен на работу в десятичной системе счисления. С помощью клавиатуры или мыши вводим в поле ввода произвольное число. Активизируем переключатель Bin и в поле ввода видим новое число в двоичной системе счисления.
Настроим Калькулятор на работу в двоичной системе счисления. Обратите внимание, какие кнопки и цифровые клавиши нам доступны. Вводим двоичное число и с помощью переключателя Dec переводим его в десятичную систему счисления.
Пример №1 ( 128)10=(?)2
Пример№2 (1110111)2=(?)10
Закрепление.
Учитель: Теперь можно приступить вам к выполнению практической работы
Нарисуй фигуру
Каждой паре выдается карточка, содержащая таблицу с координатами точек, записанными в двоичной системе счисления, и система координат. Для выполнения задания необходимо:
Для выполнения задания необходимо:
а) перевести координаты точек в десятичную систему с помощью приложения Калькулятор
б) построить по ним фигуру в координатной плоскости
Для выполнения этого задания вам понадобятся не только знания, полученные сегодня на уроке, но и математические знания. Каждому ученику выдается тетрадный лист с нанесенной на нем системой координат (заранее подготавливается учителем)
Пояснение к заданию: каждая координата точки записана в двоичной системе координат. Вам надо перевести координаты точек в десятичную систему счисления и, применяя знания по математике, построить точки на системе координат, соединить их.
I вариант (буква Г)
Отметьте и последовательно соедините на координатной плоскости точки, координаты которых приведены в двоичной системе счисления.
Ответ: (5;5), (5;40), (25;40), (25;35), (10;35), (10;5), (5;5).2 вариант. Звезда
Ответ: (2;15), (8;16), (11; 22), (14; 16), (20; 15), (16; 10), (18; 4), (11; 7), (4;4), (6;10), (2;15)3 вариант. Ракета
Ракета
Учитель: давайте немного отдохнем (физминутка) слайд№22
Учитель: Откройте все программу Excel. Посмотрим, как легко перевести числа в этой программе слайд№23
Ну а сейчас, ребята, поиграем «Попробуй открой открытку»(PROEKT 1и PROEKT 2). Можете пользоваться любым способом перевода
Слайд №24
Итог урока.
Что нового узнали на уроке? (В виде беседы с классом.)
Рефлексия.
Вам понравился урок? Чтобы узнать мнение учащихся, учесть их интересы и лучше подготовиться к следующему уроку, можно подготовить два вида смайликов. Учащиеся выбирают тот смайлик, который соответствует их настроению.
Слайд25
Домашнее задание слайд №26
Вывод:
Данный урок сопровождается презентацией.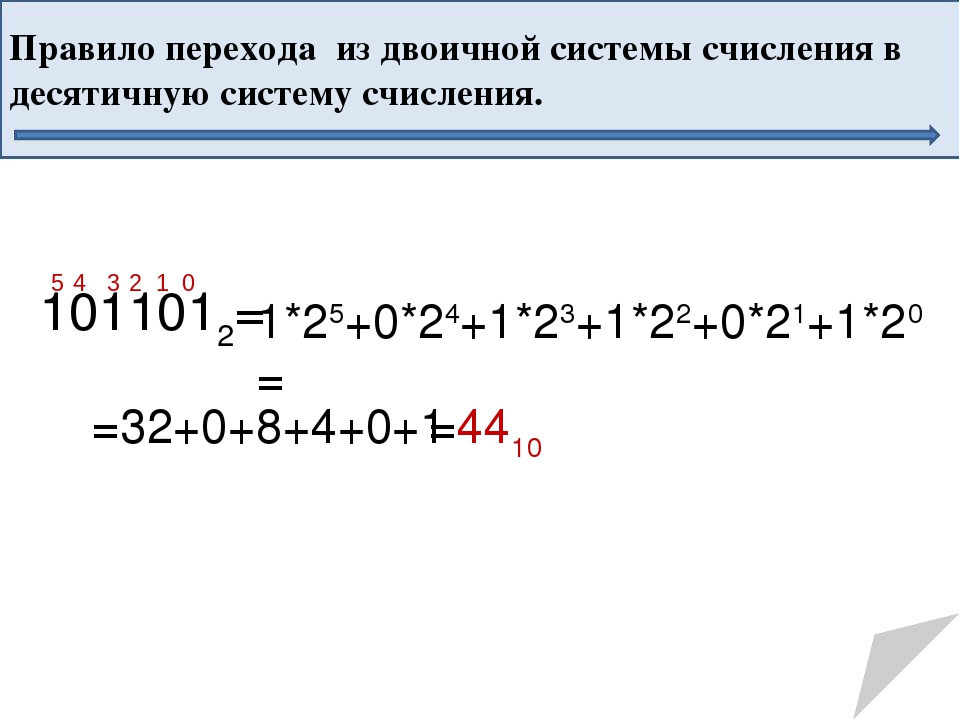 С помощью мультимедийного проектора на экране учащиеся наглядно видят весь теоретический и практический материал данного урока, что повышает результативность и усвояемость данного материала.
С помощью мультимедийного проектора на экране учащиеся наглядно видят весь теоретический и практический материал данного урока, что повышает результативность и усвояемость данного материала.
Данная методическая разработка урока предназначена в помощь учителю, работающему по новому учебно-методическому комплекту по информатике
(автор Босова Л.Л., издательство «Бином. Лаборатория знаний»), имеющему гриф «Допущено» Министерства образования РФ.
Учебное пособие:
Информатика: Учебник
/Л.Л. Босова. – 4-е изд., испр. – М.: Бином. Лаборатория знаний, 2006.
Используемая методическая литература:
Уроки информатики в 8-9 классах: Методическое пособие/ Л.Л. Босова, А.Ю. Босова. – М.:Бином. Лаборатория знаний, 2004.
Занимательные задачи по информатике
/ Л.Л.Босова, А.Ю.Босова, Ю.Г. Коломенская. – 2-е изд., испр. – М.: Бином. Лаборатория знаний, 2006.
Быстро учимся считать в двоичной и шестнадцатеричной системе
Введение
Иногда возникает потребность быстро прочитать или записать числа в двоичной или шестнадцатеричной системе счисления, например, работая с различными байтовыми редакторами,при расчете формул с побитовыми операциями или работе с цветом. Часто в таких ситуациях нет возможности долго переводить числа с помощью формул или калькулятора. О быстрых способах перехода между системами счисления пойдет речь в данной статье.
Переход от десятичной системы к двоичной
Первый случай – считаем от десятичной системы к двоичной. Основное, что нужно помнить в данном случае – это ряд степеней двойки (1, 2, 4, 8, 16, 32, 64, 128 и т.д.). Даже если его вы не знаете, то ничего не стоит каждое следующее число умножать на двойку. Так как младшие разряды идут справа, а старшие – слева, то будем их записывать в обратном порядке справа налево.
Для примера будем переводить число 115. Дальше смотрим, если значение разряда помещается в число, то вычитаем из него это значение и ставим в этом разряде 1, иначе ставим 0.
Обратный перевод еще проще – нужно просуммировать все значения разрядов, которые отмечены единичками: 64+32+16+2+1 = 115.
Переход к шестнадцатеричной системе
Теперь давайте разберемся с шестнадцатеричной системой. Имея ввиду то, что количество чисел, которые кодируются тетрадой (4 бита) и одним шестнадцатеричным символом совпадают, то соответственно каждый символ кодирует одну двоичную тетраду.
В результате получили число 0х73. Главное помнить, что А = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Если есть потребность перевести десятичное число в шестнадцатеричное или наоборот, то здесь проще всего будет сначала перевести число в двоичное представление, а затем только в шестнадцатеричное или десятеричное соответственно.
В итоге мы научились быстро переводить числа из одной системы счисления в другую. Главное, что нужно помнить — степени двойки и уметь хорошо складывать и вычитать. Детальнее о машинной математике вы можете узнать во втором уроке курса C# Стартовый.
Попрактикуйтесь самостоятельно и переведите несколько чисел из одной системы в другую, сверяясь с калькулятором. Немного практики — и вы всему научитесь.
Вычитание в столбик в любой системе
Вычитание в столбик в любой системе счисления
Система счисления – это форма записи чисел по определенным правилам. Мы пользуемся в быту десятичной системой, но бывают и другие позиционные системы счисления (двоичная, пятеричная, восьмеричная, 16-ичная и т.д.).
Вы можете просмотреть цикл видеоуроков по системе счисления, чтобы понять, что к чему (автор видеоуроков – Максим Семенихин, он же автор данного сайта):
- Введение в системы счисления.
- Перевод чисел из десятичной системы в недесятичную.
- Быстрый переход из двоичной системы в восьмеричную.
- Шестнадцатеричная система счисления.
Вычитание в столбик в любой системе счисления производится по тому же принципу, что и в десятичной системе. Отличаются лишь сами по себе правила вычитания цифр.
Если уменьшаемая цифра больше вычитаемой, то разницы не наблюдается: 5 – 3 = 2, например, в любой системе счисления, в которой существуют цифры 5, 3 и 2.
Если же уменьшаемая цифра меньше вычитаемой, то нужно занять единицу из ближайшего следующего (старшего) разряда, цифра которого не равна нулю, и выполнить вычитание по правилам n-ичной системы. При этом все следующие разряды-нули, начиная от того, из которого заняли, и заканчивая уменьшаемым разрядом, становятся вместо нулей равными основанию системы счисления, уменьшенному на единицу (как и в десятичной системе).
Онлайн калькулятор
для вычитания в столбик
в любой системе счисления
Для того, чтобы вычесть любые два числа в любой системе счисления, вы можете воспользоваться калькулятором, который находится на данной странице вверху. Введите любые два числа, а затем нажмите кнопку «Вычесть».
Замечание. Иногда калькулятор будет выдавать нули впереди числа в результате, например 00123. Это НЕ специфика записи числа в другой системе счисления (в любой системе число не может начинаться с нуля). Это лишь объяснение подробностей вычитания (на самом деле 00123 – это просто число 123).
Двоичный калькулятор онлайн
Если вам необходимо произвести математические операции над двоичными числами воспользуйтесь нашим двоичным онлайн калькулятором:
Просто введите целые двоичные числа, выберите операцию и получите результат.
Данный калькулятор может производить следующие действия над двоичными числами:
- сложение +
- вычитание −
- умножение ×
- деление ÷
- логическое И (AND)
- логическое ИЛИ (OR)
- исключающее ИЛИ (XOR)
Сложение двоичных чисел
Сложение двух двоичных чисел производится столбиком поразрядно. Начиная с младшего разряда (справа на лево), как и при сложении столбиком десятичных чисел. Но так как цифр всего две (0 и 1), их сложение происходит по следующим правилам:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Пример
Для примера сложим 1011 и 101:
| + | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 0 | 0 | |
10112 + 1012 = 100002
(1110 + 510 = 1610)
Вычитание двоичных чисел
Вычитание двоичных чисел производится аналогично сложению – столбиком, но по следующим правилам:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1
Пример
Для примера вычтем из числа 1011 число 101:
10112 − 1012 = 1102
(1110 − 510 = 610)
Умножение двоичных чисел
Умножение двоичных чисел производится в столбик аналогично умножению в десятичной системе, но по следующим правилам:
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Пример
Для примера перемножим числа 1011 и 101:
| × | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||||
| + | 1 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | |||
| 1 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 1 | 1 | 1 | |
10112 × 1012 = 1101112
(1110 × 510 = 5510)
Деление двоичных чисел
Внешне деление двоичных чисел похоже на деление десятичных чисел, но тут есть свои нюансы: такое деление производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Чтобы понять этот процесс рассмотрим пример:
Пример
Для примера разделим число 11110 на 110:
111102 ÷ 1102 = 1012
(3010 ÷ 610 = 510)
См. также
▷ Преобразователь двоично-десятичного числа
Вам нужно преобразовать двоичное число в десятичное число ?
Ниже приведен бесплатный преобразователь двоичных чисел в десятичные числа , который позволяет преобразовывать двоичные числа в их десятичное представление.
И если вы хотите научиться преобразовывать двоичные числа в десятичные, прочтите или посмотрите наш учебник о процессе преобразования двоичных чисел в десятичные числа.
Оцените этот конвертер
[Всего: 64 Среднее: 4.7/5]Как использовать двоично-десятичный преобразователь
- Введите двоичное число в первое поле.
- Нажмите кнопку «Преобразовать».
- Выходное десятичное число появится во втором поле.
- Дополнительно , вы можете скопировать вывод в буфер обмена или сохранить его как файл на вашем устройстве.
Попробуйте также преобразователь из десятичного в двоичный код !
Как преобразовать двоичное в десятичное
Итак, вам нужно знать, как преобразовать двоичное в десятичное? Все эти единицы и нули могут напугать.Здесь вы можете найти преобразователь из двоичного в десятичный формат или научиться преобразовывать самостоятельно — компьютер не требуется.
Кредит видео
Если вы думали, что для преобразования двоичного числа в десятичное необходимы сложные формулы, вы можете вздохнуть с облегчением. Чтобы преобразовать двоичное в десятичное, вам действительно нужно знать три вещи . Первый , помните, что единицы и нули, составляющие двоичный код, можно рассматривать как ответ на вопрос «да» или «нет».Один за «да» и ноль за «нет». Следующий , если у вас есть понимание силы двойки, это будет пустяк. Последний шаг — это базовое дополнение.
(Супер) силы 2
Мы можем поблагодарить степень двойки за то, что это так просто. Если вы не знакомы с ними, таблица для справки сделает вашу работу еще проще. Вам не понадобится обширная таблица, если вы не конвертируете очень большие двоичные числа. Например, если двоичное число, которое вы хотите преобразовать, состоит из трехзначного числа , вам понадобится только первых трех степеней 2 (2 0 , 2¹ и 2²).
Давайте посмотрим на трехзначное двоичное число, 101 .
Чтобы преобразовать 101 из двоичной системы в десятичную, мы должны использовать первые три степени двойки. Самый простой способ визуализировать это — написать свое двоичное число, а над ним заполнить степень двойки. начните с 2 0 справа и продолжайте двигаться влево, пока у вас не закончатся двоичные цифры.
У нас есть 1, 0 и 1, и степень 2 для каждой двоичной цифры.Посмотрите на 2 0 ; что под ним? Один. Это означает, что мы будем использовать 2 0 в десятичном выводе.
А теперь давайте поработаем. Что ниже 2¹? Ноль. Это означает, что мы будем использовать , а не , 2¹. А меньше 2²? Еще один. Чтобы узнать, что такое 101 в десятичной системе, нам понадобится 2 0 и 2².
В остальном все просто — 2 0 и 2² равны 1 и 4 соответственно. Теперь просто сложите 1 + 4. Двоичное число 101 является десятичным 5 .
Это невероятно просто, если вы можете думать о 1 как о «да» и о 0 как о «нет». Точно так же работают и большие числа. Давайте добавим в смесь несколько дополнительных нулей и возьмем 100001. Он длинный, но метод тот же. На этот раз нам нужно всего 6 степеней двойки; по одному на каждую цифру двоичного числа.
Какие степени двойки соответствуют единице? Только 2 6 и 2 0 . Теперь мы складываем эти степени двойки вместе. 100001 в десятичном формате — это 33 .
Чтобы доказать, насколько просто преобразовать двоичное в десятичное, давайте рассмотрим еще более длинную двоичную цифру: 11001100 . Для этого преобразования нам нужно пройти весь путь до 2 7 .
Все, что нам нужно сделать, это добавить использованные степени двойки. Помните, мы «используем» их только тогда, когда они соответствуют единице. В этом случае нам нужно сложить 128, 64, 8 и 4, чтобы найти десятичную дробь. Все остальное обозначается нулем, поэтому нам не нужно их включать! 11001100 в двоичном формате — это десятичное 204 .
Если вы хотите попробовать это сами, вы можете использовать двоично-десятичный калькулятор на этой странице, чтобы проверить свою работу. Потренируйтесь несколько раз, и вы с легкостью заговорите на языке компьютеров.
Вопросы и ответы о преобразовании двоичного числа в десятичное
👉 Как использовать двоичный преобразователь в десятичный?Преобразователь двоичных чисел в десятичные числа на ConvertBinary.com действительно прост в использовании.
Просто выполните следующие действия: введите двоичное число в первое поле, затем нажмите кнопку «Преобразовать».
Десятичное представление вашего двоичного числа немедленно появится в поле ниже.
✏️ Как преобразовать двоичное в десятичное?Чтобы преобразовать двоичные числа в их десятичный эквивалент, у вас есть два варианта: вы можете либо использовать онлайн-конвертер (например, тот, который предоставляется бесплатно на ConvertBinary.com), либо вы можете сделать это вручную.
Если вы хотите научиться преобразовывать двоичное в десятичное вручную, вы можете прочитать это руководство или просмотреть соответствующее руководство.
⚙️ Как работает двоично-десятичный преобразователь?Он использует функцию сценария, которая анализирует ввод (в нашем случае двоичное число) и возвращает целое число.
Вызов функции указывает, что следует использовать двоичную систему.
Процесс автоматический и настолько быстрый, что кажется, будто он мгновенный, даже для очень больших чисел.
🔟 Могу ли я преобразовать числа из десятичного в двоичное?Конечно! Если вы хотите преобразовать любое десятичное число в двоичное, вы можете использовать Decimal to Binary Converter at ConvertBinary.com.
Преобразователь двоичного числа в десятичный— w3resource
Двоичное число:
[Введите двоичное число, например 1110, в следующее поле и нажмите кнопку «Преобразовать». ]
Десятичное число:
Преобразование: двоичное в десятичное
Двоичная система счисления:
В математике и цифровой электронике двоичное число — это число, выраженное в двоичной системе счисления или системе счисления с основанием 2, которое представляет числовые значения с использованием двух разных символов: обычно 0 (ноль) и 1 (единица).Система с основанием 2 представляет собой позиционную систему счисления с основанием 2. Из-за ее простой реализации в цифровых электронных схемах с использованием логических вентилей двоичная система используется внутри почти всех современных компьютеров и компьютерных устройств. Каждая цифра называется битом.
Десятичная система счисления:
Десятичная система счисления (также называемая основанием десять) имеет основу десять, которая в десятичной системе счисления записывается как 10, как и база в любой позиционной системе счисления.Это числовая база, наиболее широко используемая современными цивилизациями.
Таблица преобразования двоичного числа в десятичное
| Двоичный Число |
Десятичное число Число |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 10010 | 18 |
| 10011 | 19 |
| 10100 | 20 |
| 10101 | 21 |
| 10110 | 22 |
| 10111 | 23 |
| 11000 | 24 |
| 11001 | 25 |
| 11010 | 26 |
| 11011 | 27 |
| 11100 | 28 |
| 11101 | 29 |
| 11110 | 30 |
| 11111 | 31 |
| 100000 | 32 |
| 1000000 | 64 |
| 10000000 | 128 |
| 100000000 | 256 |
Далее: Преобразовать двоичное в шестнадцатеричное
Десятичный / двоичный преобразователь — изучение двоичного кода
из десятичного в двоичное
Введите десятичное число (например,g., 3.1415) (без запятых, пробелов, показателей, дробей, операторов) Преобразуется в это двоичное число: Числовые цифры:Опции:
Двоичное в десятичное
Введите двоичное число (например, 110.001) (без запятых, пробелов, показателей степени, дробей, операторов) Преобразуется в это десятичное число: Числовые цифры:(Хотите преобразовать в двоичный код с плавающей запятой ? Попробуйте мой конвертер с плавающей запятой.)
(Хотите, чтобы вычислили с двоичными числами? Попробуйте мой двоичный калькулятор.)
(Хотите преобразовать числа между произвольными основаниями ? Попробуйте мой конвертер оснований.)
О десятичном / двоичном преобразователе
Это преобразователь из десятичного в двоичное и из двоичного в десятичное . Он отличается от большинства десятичных / двоичных преобразователей, таких как калькулятор Google или калькулятор Windows, потому что:
- Может преобразовывать как дробные, так и целые числа.
- Может преобразовывать очень большие и очень маленькие числа — до сотен цифр.
Десятичные числа преобразуются в «чистые» двоичные числа, а не в компьютерные числовые форматы, такие как дополнение до двух или двоичные числа с плавающей запятой IEEE.
Преобразование осуществляется с помощью арифметики произвольной точности, что дает преобразователю возможность преобразовывать числа, большие, чем те, которые могут соответствовать стандартным размерам компьютерных слов (например, 32 или 64 бита).
Как использовать десятичный / двоичный преобразователь
Ввод
- Введите положительное или отрицательное число без запятых и пробелов, не выраженное в виде дроби или арифметических вычислений, а также в экспоненциальном представлении.Дробные значения обозначаются точкой счисления (‘.’, , а не ‘,’)
- Измените количество битов, которое вы хотите отображать в двоичном результате, если оно отличается от значения по умолчанию (применяется только при преобразовании дробного десятичного значения).
- Нажмите «Преобразовать», чтобы преобразовать.
- Нажмите «Очистить», чтобы сбросить форму и начать с нуля.
Если вы хотите преобразовать другое число, просто введите исходное число и нажмите «Преобразовать» — нет необходимости сначала нажимать «Очистить».
Выход
Помимо результата преобразования отображается количество цифр как в исходном, так и в преобразованном числах. Например, при преобразовании десятичного числа 43,125 в двоичное 101011.001 количество цифр отображается как «от 2,3 до 6,3». Это означает, что десятичный ввод имеет 2 цифры в своей целой части и 3 цифры в своей дробной части, а двоичный вывод имеет 6 цифр в своей целой части и 3 цифры в дробной части.
Десятичные дробные значения, которые являются двоичными, преобразуются в конечные дробные двоичные значения и отображаются с полной точностью.Десятичные дробные значения, которые не являются двоичными, преобразуются в бесконечные (повторяющиеся) дробные двоичные значения, которые усекаются, а не округляются до указанного числа битов. В этом случае к концу двоичного числа добавляется многоточие (…), а количество цифр дробной части отмечается как бесконечное с помощью символа «∞».
Исследование свойств десятичного / двоичного преобразования
Конвертер настроен так, что вы можете исследовать свойства преобразования десятичного числа в двоичное и преобразования двоичного числа в десятичное.Вы можете скопировать выход десятичного преобразователя в двоичный на вход двоичного преобразователя в десятичный и сравнить результаты (не копируйте часть числа «…» — двоичный преобразователь пометит его как недопустимый).
Десятичное целое или двоичное дробное значение, преобразованное в двоичное, а затем обратно в десятичное, соответствует исходному десятичному значению; недиадическое значение преобразуется обратно только в приближенное значение своего исходного десятичного значения. Например, 0,1 в десятичной системе счисления — до 20 бит — это 0.00011001100110011001 в двоичном формате; 0,00011001100110011001 в двоичном формате — это 0,09999942779541015625 в десятичном. Увеличение числа битов точности сделает преобразованное число ближе к исходному.
Вы можете изучить разницу в количестве цифр в десятичном и двоичном представлении числа. Большие двоичные целые числа имеют примерно log 2 (10), или примерно в 3,3 раза больше цифр, чем их десятичные эквиваленты. У двоичных десятичных дробей такое же количество цифр, как и у их двоичных эквивалентов.Недиадические десятичные значения, как уже отмечалось, имеют бесконечные двоичные эквиваленты.
Прочие преобразователи дробных значений произвольной точности
Вот хороший конвертер, который можно использовать, если вы хотите отображать повторяющиеся дробные части в виде столбиков; например, 0,1 10 преобразуется в 0,00011 2 . (Этот преобразователь также выполняет преобразование между основанием, отличным от двоичного и десятичного.)
Двоичный преобразовательв десятичный, демонстрирующий и поясняющий его работу
Что такое двоичное число?
Двоичное число — это число, состоящее только из единиц и нулей.Двоичные числа используют систему с основанием 2 (отсюда и «bi» в двоичной системе), в отличие от десятичных чисел, использующих систему с основанием 10.
Другими словами, десятичная система (основание 10) использует только цифры 0,1,2,3,4,5,6,7,8 и 9, тогда как двоичная система (основание 2) использует только цифры 0 и 1.
Чтобы различать число с основанием 2 и число с основанием 10, числа с основанием 2 обычно записываются с 2 в качестве нижнего индекса. Например, 101 2 сообщит вам, что это двоичное число один-ноль-один, а не десятичное число сто-один.
Как преобразовать двоичное в десятичное
Чтобы помочь вам понять, как преобразовать двоичное в десятичное, может быть полезно посмотреть, как мы переводим значение десятичного числа. Давайте возьмем десятичное число 1234 (1234 10 или одна тысяча двести тридцать четыре) в качестве примера:
Преобразование значения десятичного (с основанием 10) числа← проведите пальцем влево и вправо → ← проведите пальцем влево и вправо →
| A | Мощность 10: | 10 3 | 10 2 | 10 1 | 10 0 | ||||
| B Место 9020 значение (результат A): | 1000 | 100 | 10 | 1 | |||||
| C | Введенная десятичная цифра: | 1 | 2 | 3 | 4 | D | |||
| 1000 | 200 | 30 | 4 | ||||||
| E | Кумулятивная сумма D: | 1000 | 1200 | 1230 | 1234 |
| A | Мощность 2: | 2 3 | 2 2 | 2 1 | 2 0 |
| B | Разрядное значение (результат A): | 8 | 4 | 2 | 1 |
| C | Введенная двоичная цифра: | 1 | 1 | 1 | |
| D | Продукт B * C: | 8 | 4 | 2 | 1 |
| E | Совокупная сумма D: | 8 12 | 15 |
Добавление val В строке D мы получаем число 15 по основанию 10.Другими словами, число 1111 2 переходит в число 15 10 .
Как видите, преобразование двоичного числа в десятичное — это простой процесс определения значения разряда каждой цифры, умножения каждой цифры на ее значение разряда и последующего сложения всех произведений.
Преобразование чисел с основанием 2, имеющими десятичные точки
Если основание 2, которое вы хотите преобразовать, имеет десятичную точку, вы просто продолжаете вычитать 1 из каждой экспоненты (строка A ниже) при перемещении слева направо.Например, вот как можно преобразовать 111.101 2 в его эквивалент по основанию 10:
Преобразование двоичного файла с десятичной точкой← проведите пальцем влево и вправо → ← проведите пальцем влево и вправо →
| A | Мощность 2: | 2 2 | 2 1 | 2 0 | 2 -1 | 2 -2 | 2 -3 | ||
| B | Разместите значение (результат A): | 4 | 2 | 1 | 0.5 | 0,25 | 0,125 | ||
| C | Введенная двоичная цифра: | 1 | 1 | 1 | 1 | 0 | 1 | D | 4 | 2 | 1 | 0,5 | 0 | 0,125 |
| E | Совокупная сумма D: | 4 | 6 | 7 | 7,5 | 7 | 7,5 | 25 |
Складывая значения строки D, мы получаем десятичное число 7,625. Другими словами, число 111.101 2 переходит в число 7.625 10 . Обратите внимание, что красные показатели в строке A указывают цифры, расположенные справа от десятичной точки.
Итак, вы видите, что в двоичном числе каждое разрядное значение справа от десятичной точки уменьшается на 1/2 (-> 1/2, 1/4, 1/8 и т. Д.) В отличие от разрядных значений. слева от десятичной точки, значения которой удваиваются с каждым перемещением влево (8, 4, 2, 1 <-).
Двоично-десятичный преобразователь в двоичный | Математические калькуляторы
Двоичные числа — это основание 2, представленное 1 и 0, десятичное число — основание 10, представленное числами от 0 до 9
★ ★ ★ ★ ★ [Нет голосов]
Как преобразование двоичного числа в десятичное может быть более эффективным
Преобразователь двоичного числа в десятичное очень помогает при преобразовании заданного двоичного числа в соответствующее десятичное число. Преобразователь двоичного кода в десятичный очень прост в использовании и помогает выполнять ряд десятичных преобразований чисел в течение нескольких секунд.Вы получите свои результаты сразу после нажатия «Enter». Это очень быстро и всегда точно.
Преобразование двоичного числа в десятичное — одна из важнейших операций в мире цифровой электроники и связи. С помощью этого калькулятора вы можете выполнять преобразования, которые помогут вам читать двоичные числа более удобным для человека способом. Десятичные числа являются самой популярной и общей системой счисления, используемой во всем мире, и, как люди, мы считаем, что с десятичной системой относительно легко работать, особенно при использовании степени 10.Двоичный формат отлично подходит для компьютеров, но большинству людей будет сложно вычислить двоичное математическое уравнение.
Давайте посмотрим на двоичную и десятичную системы счисления, и как мы можем преобразовать двоичное число в десятичное число, и их важность.
Двоичная система счисления
Двоичная система счисления — это система счисления, в которой в качестве основания используется число «2» (также известное как основание системы счисления). Поскольку основание каждого двоичного числа — «2», это просто означает, что каждое двоичное число состоит только из двух чисел i.е., 0 и 1.
Использование двоичной системы счисления в цифровом мире
Основное использование этой системы состоит в выполнении операции «ИСТИНА» или «ЛОЖЬ» или для определения состояния «ВКЛ» или «ВЫКЛ». Наиболее эффективное использование этой системы — обнаружение состояний «ВКЛ» и «ВЫКЛ» электрической системы, поэтому двоичная система часто встречается в электронике и инженерных расчетах.
Двоичная система счисления считается основой любой компьютерной системы, поскольку компьютеры принимают входные данные только в двух формах: i.е., 0 и 1. Он также используется для компоновки данных в компьютерах и машинах с компьютерным управлением в ряде отраслей. Даже этот цифровой текст, который вы сейчас читаете, состоит только из двоичной системы счисления. Этот инструмент преобразования, который вы собираетесь использовать для преобразования двоичного числа в десятичное, также будет использовать ту же систему счисления для выполнения любых операций.
Как читать двоичное число
Считывание двоичного числа — не сложная задача. Это намного проще, чем кажется.Если вы хотите преобразовать двоичное число в десятичное и также хотите понять его концепцию, вам необходимо иметь базовые знания об этой системе, например, как мы читаем двоичное число, как мы его представляем и т. Д. Двоичная система счисления — это позиционная система, и поэтому каждое число в этой системе возведено в степень «2». Самая правая цифра будет в позиции 20.
Например, (1101) 2 можно записать как-
(1 * 23) + (1 * 22) + (0 * 21) + (1 * 20)
Десятичная система счисления
Эта система счисления является самой популярной и наиболее часто используемой системой счисления в мире, в основе которой лежит число «10».Всего в этой системе используется 10 чисел, т.е. от 0 до 9.
Как преобразовать двоичное число в десятичное
Существует два метода преобразования двоичного числа в десятичное. В первом способе преобразование выполняется с помощью позиций. Второй метод известен как «Double Dabble». Первый метод является наиболее популярным и широко применяемым. Второй метод сложен и используется для более быстрого преобразования более длинной двоичной строки.Мы собираемся обсудить наиболее распространенный из них.
Преобразование двоичных чисел в десятичные с использованием позиций
- Первый шаг — записать число и определить позиции, а именно степень двойки, которой принадлежит цифра.
- Следующим шагом будет представление числа в виде позиций.
- Последний шаг — вычислить окончательное полученное вами число.
Преобразование двоичных чисел в десятичные Пример
(10110) 2
(1 * 24) + (0 * 23) + (1 * 22) + (1 * 21) + (0 * 20)
16 + 0 + 4 + 2 + 0
(22) 10
| двоичных | десятичных | |||
|---|---|---|---|---|
| 0000 | 0 | |||
| 0001 | 9020 | 2 | ||
| 0011 | 3 | |||
| 0100 | 4 | |||
| 0101 | 5 | |||
| 0110 | 6 | 8 | ||
| 1001 | 9 | |||
| 1010 | 10 | |||
| 1011 | 11 | |||
| 1100 | 12 | |||
| 1110 | 14 | |||
| 1111 | 15 |
Резюме
Двоичная система счисления стала языком компьютеров и электроники в современном мире.Обычный человек не может понять все, что написано на двоичном языке. Вот почему преобразователь двоичных чисел в десятичные используется для преобразования двоичных чисел в десятичные единицы, чтобы мы могли понять это более эффективно. Вы можете использовать этот онлайн-интерфейс в любое время, чтобы получить мгновенные и точные результаты.
Математические калькуляторы
Вам также могут пригодиться следующие математические калькуляторы.
Двоично-десятичный преобразователь
Преобразователь двоично-десятичного числа
Преобразователь двоично-десятичного числа делает то, что мы всегда хотели делать за секунды.Это помогает в мгновение ока преобразовать двоичное в десятичное. Преобразование двоичного числа в десятичное преобразование двоичного числа в число (основание 2 в основание 10) является важной концепцией для понимания, поскольку двоичная система счисления образует основу для всех компьютеров и цифровых систем.
Что такое десятичная система счисления?
В двоичной системе счисления с основанием 10 система счисления по основанию 10 называется десятичной или «денарной» системой счисления, где каждая цифра в числе принимает одно из десяти возможных значений, называемых «цифрами», от 0 до 9, е.грамм. 213 10 (Двадцать первая сотня).
Но, помимо 10 цифр (от 0 до 9), десятичная система счисления также имеет сложение, вычитание, умножение и деление.
Каждая цифра имеет значение, в десять раз превышающее ее предыдущее число в десятичной системе, и эта десятичная система счисления использует набор символов b вместе с основанием q для определения веса каждой цифры в пределах число. Шесть из шестидесяти, например, имеют меньший вес, чем шесть из шестисот.
N = b i q i
Где: N — действительное положительное число
b — это цифра
q — базовое значение, а — базовое значение целое число (i) может быть положительным, отрицательным или нулевым N = b n q n … b 3 q 3 + b 2 q 2 + b 1 q 1 + b 0 q 0 + b -1 q -1 + b -2 q -2 … и т. Д. Каждый столбец с целыми числами имеет значения единиц, десятки, сотни, тысячи и т. Д. В десятичной системе счисления, десятичной системе счисления (den) или десятичной системе счисления, когда мы перемещаемся по числу справа налево. Эти значения записываются математически как 10 0 , 10 1 , 10 2 , 10 3 и т. Д. Тогда каждая позиция слева от десятичной точки означает увеличение на 10. Аналогичным образом, вес число становится более отрицательным для дробных чисел при движении слева направо, 10 -1 , 10 -2 и 10 -3 и т. д. Преобразование двоичного числа в десятичное может быть выполнено путем нанесения каждого двоичного значения, соответствующего его десятичному значению, в каждом столбце или с помощью преобразователя двоичных чисел. Каждый столбец представляет собой показатель степени 2. Показатель увеличивается на единицу справа налево. Вы можете добавить значение этих столбцов, помеченных как ON или эквивалентное 1, чтобы получить общее значение. Например, двоичное число 101100101 преобразуется в десятичное число следующим образом: Показатель степени = 2 8 2 7 2 6 2 5 2 4 2 3 2 2 2 1 2 0 Общее значение = (256 + 64 + 32 + 4 + 1) = 357 Таким образом, двоичное число 101100101 равно 357 в десятичных числах. Калькулятор двоичного числа в десятичный преобразует двоичное число в целое, что упрощает его использование для пользователей двоичного десятичного числа. Что еще мы можем предложить, кроме от bin до dec? Мы разработали передовые инструменты двоичного преобразования, такие как преобразователь из шестнадцатеричного в десятичный, преобразователь из десятичного в шестнадцатеричный, двоичный переводчик, преобразователь текста в двоичный и преобразователь из десятичного в двоичный . Теперь преобразовать разные системы счисления друг в друга несложно, поскольку для этой цели мы предлагаем несколько инструментов преобразования. Подавляющее большинство из нас знакомы с десятичной дробью и десятичной системой счисления. В повседневном счете мы используем десятичную систему счисления. Меньше людей знакомы с двоичной системой. Двоичная — это система счисления, которая играет важную роль в хранении информации для компьютеров. В этой статье мы поговорим о десятичных дробях, двоичных файлах и способах преобразования между ними. Десятичная система счисления или система счисления с основанием 10 — это система счисления, с которой мы сталкиваемся чаще всего. В десятичной системе счисления 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Каждый столбец целых чисел в десятичной системе счисления имеет значение единиц. Каждая позиция слева от десятичной точки имеет увеличенную положительную степень 10. Каждая позиция справа от десятичной точки становится более отрицательной на степень десяти. Возьмем число 549. Крайнее правое число, 9, находится в столбце единиц. Это ближайшее к десятичной запятой.Цифра 9 означает, что их девять. Следующая цифра справа, 4, находится в столбце 10. Число 4 там означает, что на самом деле число 40. Последнее число, 5, находится в разряде сотен. Это означает, что их 5 сотен (500). С другой стороны, двоичная система является системой с основанием 2. В то время как десятичная система имеет значения от 0 до 9, система с основанием 2 (или двоичная) имеет только значения 0 или 1. В этой двоичной системе счисления каждая цифра справа налево имеет значение в два раза больше, чем предыдущая цифра. Итак, значения двоичных позиций, начиная справа, равны: 1, 2, 4, 8, 16, 32, 64 и т. Д. Давайте посмотрим на двоичное число 11. 1 в столбце 1 и 1 в столбце 2. Итак, 1 + 2 = 3. Число 11 = 3. Давайте попробуем другой номер: 1101. 1 в столбце 1, 0 в столбце 2, 1 в столбце 4 и 1 в столбце 8. Итак, имеем 1 + 4 + 8 = 13. Число 1101 = 13. Вот удобная диаграмма, которая показывает вам числа 0–9, преобразованные в двоичные Десятичное двоичный 0 0 1 1 2 10 3 11 4 100 5 101 6 110 7 111 8 1000 9 1001 Вы можете легко преобразовать двоичный код в десятичный, используя стратегию, называемую методом остатка.Давайте посмотрим на эти шаги. Начнем с 29. 29/2 = 14, остаток 1 14/2 = 7, остаток 0 7/2 = 3, остаток 1 3/2 = 1, остаток 1 1/2 = 0, остаток 1 0 29 = 11101 Для преобразования двоичного числа в десятичное необходимо умножить значение цифры на заполнитель в числе. Давай попробуем. 101110 Помните, что в двоичной системе счисления каждая цифра справа налево имеет значение вдвое больше, чем предыдущая цифра. Итак, значение двоичных позиций, начиная справа, составляет: 1, 2, 4, 8, 16, 32, 64 и т. Д. 0 Х 1 = 0 1 Х 2 = 2 1 Х 4 = 4 1 Х 8 = 8 0 Х 16 = 0 1 Х 32 = 32 Возьмите значения, которые вы определили, и сложите их все вместе 2 + 4 + 8 + 32 = 46 101110 двоичный = 46 десятичный Преобразование двоичного числа в десятичное (или наоборот) может быть непростым делом.Вот несколько советов, которые нужно запомнить, как делать каждый из них. Одна из самых больших проблем, с которыми вы можете споткнуться в своем преобразователе двоичных чисел в десятичные, — это использование неправильного разряда для двоичных разрядов. Помните, что каждая двоичная позиция имеет двойную ценность перед ней. Если вы обнаружите, что ошиблись или забыли, какое значение есть какое, вам может потребоваться … Наш второй совет — сделать стол. Если вы забываете о ценностях, вам может помочь составление таблицы. Запишите значение двоичного разряда, затем оставьте строку для ввода значения 1 или 0. Таким образом вы легко сможете увидеть, что такое ценность. Вот некоторые проблемы с десятичным и двоичным образцами. Попробуйте написать их и посмотрите, получите ли вы правильный ответ. Решение: 10000 Решение: 110001 Решение: 10011 Двоичные и десятичные числа — это две разные системы счисления.
Как преобразовать двоичное в десятичное?
Таблицы
Двоичные Десятичные 0000 0 0001 1 0010 0010 4 0101 5 0110 6 0111 7 1000 100 10 1011 11 1100 12 1101 13 1110 14 Двоичное в десятичное, двоичное в десятичном, двоичное в десятичном, Binario a decimal, Binario para decimal, Окончательный инструмент преобразования десятичных чисел в двоичные
Что такое десятичные дроби?
Что такое двоичные файлы?
: эквиваленты
Как преобразовать двоичное в десятичное
# 1: Запишите десятичное число
# 2: разделите число на 2 и обратите внимание на остаток
# 3: Разделите результат целого числа на 2 и обратите внимание на остаток
# 4: повторяйте шаг 3, пока результат деления не будет 0
# 5: Прочитать остаток снизу вверх
Как преобразовать двоичное в десятичное
# 1: Запишите число
# 2: умножить каждую цифру на ее заполнитель
# 3: Сложить все результаты
# 4: Результат — ваше десятичное число
Как преобразовать двоичное в десятичное: основные советы
# 1: Запомните значения для каждого двоичного разряда
# 2: Сделайте стол
Десятичный преобразователь в двоичный: примеры задач
# 1: написать 16 в базе 2
# 2: написать 33 в базе 2
# 3: написать 19 в базе 2
Конвертер двоичного числа в десятичный: последние мысли

