Эдс в катушке: Самоиндукция. Энергия магнитного поля.

Самоиндукция. Энергия магнитного поля.

Определение 1

Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.

В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).

Собственный магнитный поток Φ, который проходит через контур или катушку с током, является пропорциональным силе тока I: Φ=LI.

Определение 2

Коэффициент пропорциональности L в формуле Φ=LI есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в СИ носит название генри (Гн). Индуктивность контура или катушки равна 1 Гн, когда при силе постоянного тока 1 А собственный поток составляет 1 Вб: 1 Гн=1 Вб1 А.

Расчет индуктивности

Пример 1

Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l. Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:

B=μ0nI,

где I является обозначением тока в соленоиде, n = Ne указывает число витков на единицу длины соленоида.

Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:

Φ=B·S·N=μ0n2Sl

Таким образом, индуктивность соленоида будет выражена формулой:

L=μ0n2S·l=μ0n2V,

где V=Sl – объем соленоида, содержащий магнитное поле.

Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость μ, при заданном токе

I индукция магнитного поля будет возрастать по модулю в μ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в μ раз:

Lμ=μ·L=μ0·μ·n2·V.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Определение 3

ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:

δинд=δL=-∆Φ∆t=-L∆I∆t.

ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.

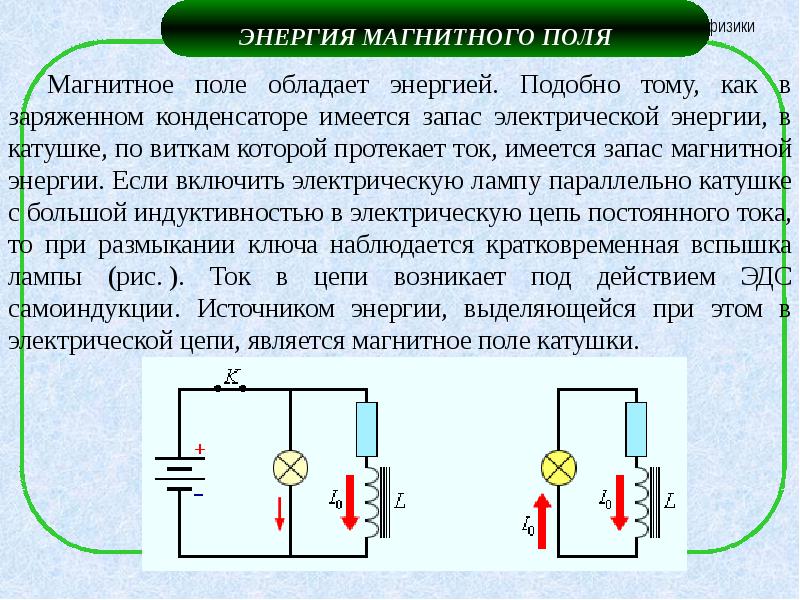
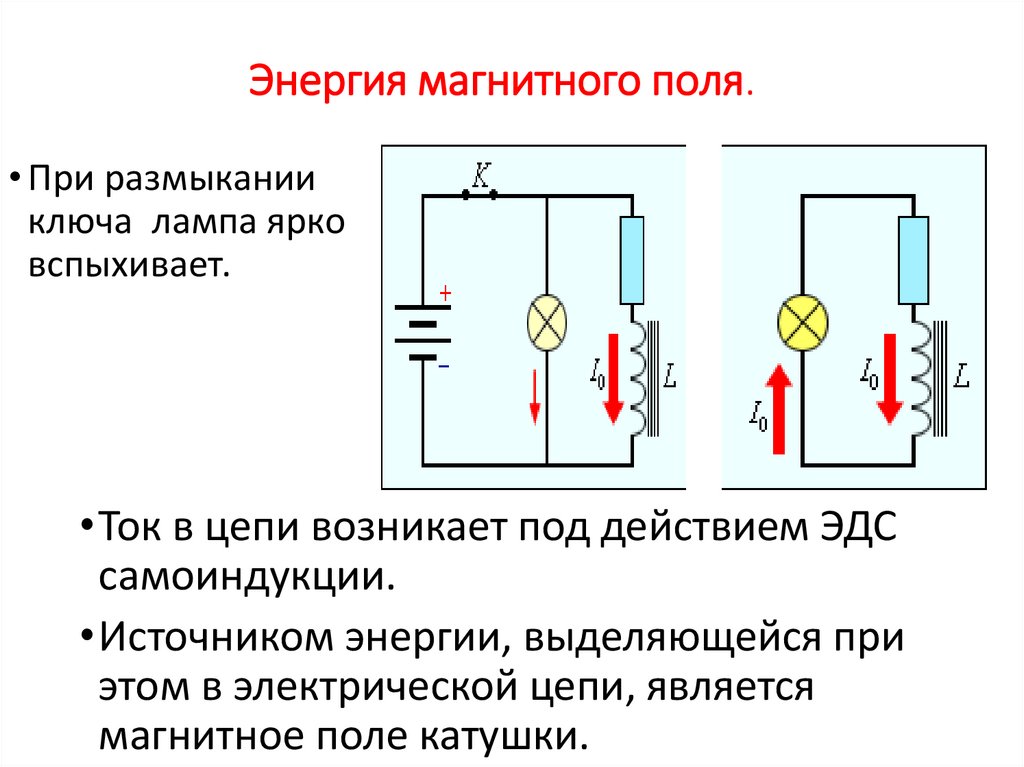
Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1.21.1). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.

Рисунок 1.21.1. Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.

Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как Rполное сопротивление цепи, тогда за время Δt будет выделено количество теплоты ΔQ=I2·R·Δt.

Ток в цепи составляет:

I=δLR=-LR∆I∆t

Выражение для ΔQ можем записать так:

∆Q=-L·I·∆I=-Φ(I)∆I

В данной записи ΔI < 0; значение тока в цепи постепенно снижается от изначального I0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I0 до 0. Тогда получим:

Q=LI022

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока

I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:

Рисунок 1.21.2. Вычисление энергии магнитного поля.

В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:

Wм=ΦI2=LI22=Φ22L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:

Wм=μ0·μ·n2·I22V=B22μ0·μV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

Методы защиты устройств (датчиков, приборов, контроллеров) с транзисторными выходами от токов самоиндукции

Введение

В данной статье будет рассмотрено явление самоиндукции, проявляющееся зачастую при коммутации индуктивных нагрузок. Также будут рассмотрены способы защиты и используемое для этого оборудование.

Техника безопасности

ВНИМАНИЕ! К работам по монтажу, наладке, ремонту и обслуживанию технологического оборудования допускаются лица, имеющие техническое образование и специальную подготовку (обучение и проверку знаний) по безопасному производству работ в электроустановках с группой не ниже 2 для ремонтного персонала, а также имеющие опыт работ по обслуживанию оборудования, в конструкцию которого вносятся изменения и дополнения, либо производится модернизация. За неисправность оборудования и безопасность работников при неквалифицированном монтаже и обслуживании ООО «КИП‑Сервис» ответственности не несет.

1. Электромагнитная индукция. Определение. Физический смысл

Электромагнитная индукция — явление возникновения электрического тока, при изменении во времени магнитного поля. Изменение магнитного поля, в силу закона электромагнитной индукции, приводит к возбуждению в контуре индуктивной электродвижущей силы (ЭДС). Процесс возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию, а при убывании тока — препятствует убыванию. Величина ЭДС самоиндукции определяется уравнением:

E=−L×dI/dtE= -L times dI / dt

где:
E — ЭДС самоиндукции
L — индуктивность катушки
dI/dt — изменение тока во времени.

Знак «минус» означает, что ЭДС самоиндукции действует так, что индукционный ток препятствует изменению магнитного потока. Этот факт отражён в правиле Ленца:

Индукционный ток всегда имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Явление самоиндукции можно наблюдать при включении и последующем выключении катушек соленоидов, промежуточных реле, электромагнитных пускателей. При подаче напряжения на катушку создается электромагнитное поле, в следствии чего образуется электродвижущая сила, которая препятствует мгновенному росту тока в катушке. Согласно принципу суперпозиции, основной ток в катушке можно представить в виде суммы токов, один из которых вызван внешним напряжением и сонаправлен с основным током, а второй вызван ЭДС самоиндукции и имеет противоположное направление основному току. Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки. При протекании тока катушка «запасает» энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдает запасенную энергию, стремясь поддержать величину тока в цепи. Это, в свою очередь, вызывает всплеск напряжения обратной полярности на катушке. Данный всплеск может достигать значений во много раз превышающих номинальное напряжение источника питания, что может помешать нормальной работе электронных устройств, вплоть до их разрушения.

Разберем более подробно, почему скачок ЭДС самоиндукции будет иметь обратную полярность. На рисунке 1 изображены две схемы, на которых стрелками обозначено направление движения тока, а так же потенциалы на всех элементах схемы при закрытом и открытом ключе.

а — закрытый ключб — открытый ключ

Рисунок 1 — Направление тока при закрытом и открытом ключе

При закрытом ключе потенциалы на всех элементах совпадают с потенциалом источника питания (рисунок 1, а). Во время размыкания ключа, из схемы исключается источник питания, и ЭДС самоиндукции стремится поддержать ток в катушке. Для того, что бы сохранить направление тока в катушке, ЭДС меняет свой потенциал на противоположный по знаку источнику питания (рисунок 1, б). Именно поэтому всплеск ЭДС самоиндукции будет иметь обратную полярность.

Более наглядно этот всплеск показан на рисунке 2. На графике изображено напряжение источника питания Uпит, ток возникающий в катушке I, ЭДС самоиндукции.

Рисунок 2 — График изменения тока и напряжения при коммутации

2. Теоретический расчет ЭДС самоиндукции

Рассмотрим явление самоиндукции на примере работы электромагнитной катушки при пропускании через нее постоянного тока. Включение катушки происходит при помощи бесконтактного датчика. Катушку можно заменить на последовательно соединенные активное Rk и индуктивное Lk сопротивления (рисунок 3).

Рисунок 3 — Эквивалентная схема электромагнитной катушки

Тогда электрическая схема будет иметь вид, представленный на рисунке 4.

Рисунок 4 — Схема включения электромагнитной катушки

При сработавшем датчики падение напряжения U на катушке составляет 24 В. При коммутации индуктивной нагрузки в первый момент времени ток остается равным току до коммутации, а после изменяется по экспоненциальному закону. Таким образом, при переходе управляющего транзистора в закрытое состояние катушка начинает генерировать ЭДС самоиндукции, предотвращающую падение тока. Попробуем рассчитать величину генерируемого катушкой напряжения.

На рисунке 5 показано направление тока при открытом транзисторе. Переход транзистора в закрытое состояние фактически означает что цепь катушки с генерируемым ЭДС самоиндукции замыкается через подтягивающий резистор. Обозначим его Ro. По документации датчика это сопротивление составляет 5,1 кОм.

Рисунок 5 — Направление тока при открытом транзистореРисунок 6 — Направление тока после перехода транзистора в закрытое состояние

На рисунке 6 видно что ток на резисторе Ro поменял направление — это обусловлено возникновением ЭДС самоиндукции в катушке. Для полученного замкнутого контура выполняется следующее уравнение:

UR0+URk+ULk=0U_R0+U_Rk+U_Lk=0

Выражая напряжение через ток и сопротивление, получим:

I×R0+I×Rk+ULk=0I times R_0 + I times R_k +U_Lk=0 ULk=−I×(Rk+R0)U_Lk= -I times ( R_k + R_0 )

При этом ток в цепи стремится к значению тока при открытом транзисторе:

Подставим данное выражение в предыдущую формулу, получим величину генерируемого напряжения самоиндукции:

ULk=−U×(Rk+R0)/Rk=−U×(1+R0/Rk)U_Lk= -U times ( R_k + R_0 ) / R_k = -U times ( 1 + R_0 / R_k )

Все переменные из этой формулы известны:
U = 24В — напряжение питания
R_o = 5,1кОм — сопротивление подтягивающего резистора датчика
R_k = 900 Ом — активное сопротивление катушки (данные из документации).

Подставив значения в формулу, рассчитаем примерное значение напряжения самоиндукции:

ULk=−U×(1+R0/Rk)=−24×(1+5100/900)=−160ВU_Lk= -U times ( 1 + R_0/R_k ) = -24 times ( 1 + 5100 / 900 )=-160 В

Данный расчет упрощен и не учитывает индуктивность катушки, от которой так же зависит ЭДС самоиндукции. Но даже из упрощенного расчета видно, что величина генерируемого напряжения оказывается во много раз больше номинального напряжения 24В.

Воздействие ЭДС самоиндукции может повредить устройства, имеющие общие с индуктивной нагрузкой цепи питания. На рисунке 7 приведена некорректная схема, на которой от одного источника питания подключен бесконтактный датчик и катушка соленоидного клапана.

Рисунок 7 — Некорректная схема подключения

На первый взгляд, данная схема может работать без каких-либо сбоев. Однако, при выключении катушки клапана возникает всплеск напряжения в результате самоиндукции. Всплеск распространяется по цепи питания на клемму «минус» датчика. В результате, разница потенциалов между коллектором и эмиттером закрытого транзистора превышает максимальное значение, что приводит к его пробою.

3. Практическое измерение ЭДС самоиндукции

Чтобы проверить правдивость приведенных выше теоретических расчетов, проведем измерение ЭДС самоиндукции. Для проведения измерений необходимо собрать схему, для которой мы проводили расчеты. При помощи осциллографа на клеммах катушки произведем измерение напряжения (рисунок 8).

Рисунок 8 — Измерение ЭДС самоиндукции

На рисунке 9 изображена осциллограмма значений напряжения самоиндукции катушки с питанием 24 В. На графике видно, что реальный всплеск напряжения при отключении катушки в несколько раз больше напряжения питания и составляет 128 В. Как следствие, транзисторный ключ выйдет из строя. Возникающий скачок ЭДС приводит к пробою транзисторных ключей, бесконтактных датчиков, слаботочных коммутирующих элементов и другим нежелательным эффектам в схемах управления.

Рисунок 9 — ЭДС самоиндукции при выключении катушки с питанием 24 В

4. Методы и средства защиты от ЭДС самоиндукции

Для подавления ЭДС самоиндукции и предотвращения выхода из строя оборудования необходимо принимать специальные меры. Для подавления пиков напряжения на катушке во время выключения, необходимо параллельно катушке включить в схему диод (для постоянного напряжения) или варистор (для переменного напряжения). ЭДС самоиндукции будет ограничиваться этими элементами, тем самым они будут обеспечивать защиту схемы.

Диод включается параллельно катушке против напряжения питания (рисунок 10). Таким образом, в установившемся режиме он не оказывает никакого воздействия на работу схемы. Однако при отключении питания на катушке возникает ЭДС самоиндукции, имеющая полярность, противоположную рабочему напряжению. Диод открывается и шунтирует катушку индуктивности.

а — включение диода в схему PNPб — включение диода в схему NPN

Рисунок 10 — Схема включения диода для защиты от самоиндукции

Варистор также включается параллельно катушке (рисунок 11).

Рисунок 11 — Схема включения варистора для защиты от самоиндукции

При увеличении напряжения выше пороговой величины, сопротивление варистора резко уменьшается, шунтируя индуктивную нагрузку. Соответственно, при броске тока варистор быстро срабатывает и обеспечивает надежную защиту схемы.

На рисунке 12 изображен график напряжения во время включения и выключения индуктивной катушки с использованием защитного диода для напряжения 24 В.

Рисунок 12 — ЭДС самоиндукции с использованием диода

На графике видно, что использование защитных диодов сглаживает переходную характеристику напряжения.

Для защиты от ЭДС самоиндукции существует целый ряд готовых устройств. Их выбор зависит от применяемой катушки и типа напряжения питания. Для гашения ЭДС самоиндукции на катушках промежуточных реле используют модули FINDER серии 99 (рисунок 13):

Рисунок 13 — Защитный модуль Finder/99.02.9.024.99

99.02.0.230.98 Finder/ Модуль защитный(светодиод+варистор)~/=110…240

99.02.9.024.99 Finder/ Модуль защитный(светодиод+диод), =6…24В

Модули устанавливаются непосредственно на колодку реле, не требуют дополнительного изменения схемы управления.

В случае подключения катушек пускателей, либо катушек соленоидных клапанов, необходимо использовать защитные клеммники Klemsan серии WG-EKI (рисунок 14):

Рисунок 14 – Защитный клеммник WG-EKI

110 220 Клеммник WG-EKI с варистором (0,5…2,5 мм2, рабочее напряжение до 30В, рабочий ток до 10А)

110 040 Клеммник WG-EKI с защитным диодом (0,5…2,5 мм2, рабочее напряжение до 1000В, рабочий ток до 10А, ток диода 1А)

Клеммники позволяют осуществить подключение индуктивной катушки без дополнительного изменения схемы. Клеммник имеет два яруса, соединенных между собой защитным диодом либо варистором. Для осуществления защиты необходимо провести провода питания катушки через этот клеммник. При использовании клеммника с защитным диодом необходимо соблюдать полярность при подключении (рисунок 15).

Рисунок 15 — Схема подключения клеммника WG-EKI с защитным диодом

Заключение

В рамках данной статьи было рассмотрено явление самоиндукции, приведен теоретический расчет ЭДС и практическое подтверждение этого расчета. Применяя модули Finder серии 99 и клеммники Klemsan серии WG-EKI, можно избавиться от пагубного воздействия самоиндукции и сохранить целостность коммутирующих элементов цепей управления.

Инженер ООО «КИП-Сервис»
Хоровец Г.Н.

Список использованной литературы:

1. Сивухин, Д.В. Общий курс физики. Электричество. Том III / Сивухин Д.В — М.: Наука, 1977. — 724.с.
2. Калашников, С.Г. Электричество / Калашников С.Г. — 6-е изд., стереот. — М.: Физматлит, 2003.-624.с.
3. Алексеев Н.И., Кравцов А.В. Лабораторный практикум по общей физике (электричество и магнетизм). Самоиндукция / Лицей No1580 при МГТУ им. Н.Э. Баумана, 2012. — 16 с.

Читайте также:

расчет электродвижущей силы по формуле

Электромагнитная индукция – генерирование электротоков магнитными полями, изменяющимися во времени. Открытие Фарадеем и Генри этого феномена ввело определенную симметрию в мир электромагнетизма. Максвеллу в одной теории удалось собрать знания об электричестве и магнетизме. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.

Эксперименты Фарадея

Законы Фарадея и Ленца

Электрические токи создают магнитные эффекты. А возможно ли, чтобы магнитное поле порождало электрическое? Фарадей обнаружил, что искомые эффекты возникают вследствие изменения МП во времени.

Когда проводник пересекается переменным магнитным потоком, в нем индуцируется электродвижущая сила, вызывающая электроток. Системой, которая генерирует ток, может быть постоянный магнит или электромагнит.

Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца.

Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности.

Важно! Направление индуцированной ЭДС такое, что вызванный ею ток стремится противостоять создающей его причине.

Фарадей заметил, что интенсивность индуцированного тока растет, когда быстрее изменяется число силовых линий, пересекающих контур. Другими словами, ЭДС электромагнитной индукции находится в прямой зависимости от скорости движущегося магнитного потока.

ЭДС индукции

Формула ЭДС индукции определена как:

Е = — dФ/dt.

Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью.

Получена общая формулировка закона электромагнитной индукции, из которой можно вывести выражения для частных случаев.

Движение провода в магнитном поле

Когда провод длиной l движется в МП, имеющем индукцию В, внутри него будет наводиться ЭДС, пропорциональная его линейной скорости v. Для расчета ЭДС применяется формула:

• в случае движения проводника перпендикулярно направлению магнитного поля:

Е = — В x l x v;

• в случае движения под другим углом α:

Е = — В x l x v х sin α.

Индуцированная ЭДС и ток будут направлены в сторону, которую находим, пользуясь правилом правой руки: расположив руку перпендикулярно силовым линиям магнитного поля и указывая большим пальцем в сторону перемещения проводника, можно узнать направление ЭДС по оставшимся четырем распрямленным пальцам.

Перемещение провода в МП

Вращающаяся катушка

Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков.

ЭДС индуцируется в электроцепи всегда, когда магнитный поток ее пересекает, в соответствии с определением магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на поверхностную площадь, через которую проходит МП, и косинус угла, образованного вектором В и перпендикулярной линией к плоскости S).

Из формулы следует, что Ф подвержен изменениям в следующих случаях:

• меняется интенсивность МП – вектор В;
• варьируется площадь, ограниченная контуром;
• изменяется ориентация между ними, заданная углом.

В первых опытах Фарадея индуцированные токи были получены путем изменения магнитного поля В. Однако можно индуцировать ЭДС, не двигая магнит или не меняя ток, а просто вращая катушку вокруг своей оси в МП. В данном случае магнитный поток меняется из-за изменения угла α. Катушка при вращении пересекает линии МП, возникает ЭДС.

Если катушка вращается равномерно, это периодическое изменение приводит к периодическому изменению магнитного потока. Или количество силовых линий МП, пересекаемых каждую секунду, принимает равные значения с равными интервалами времени.

Вращение контура в МП

Важно! Наведенная ЭДС меняется вместе с ориентацией с течением времени от положительной до отрицательной и наоборот. Графическое представление ЭДС представляет собой синусоидальную линию.

Для формулы ЭДС электромагнитной индукции применяется выражение:

Е = В х ω х S x N x sin ωt, где:

• S – площадь, ограниченная одним витком или рамкой;
• N – количество витков;
• ω – угловая скорость, с которой вращается катушка;
• В – индукция МП;
• угол α = ωt.

На практике в генераторах переменного тока часто катушка остается неподвижной (статор), а электромагнит вращается вокруг нее (ротор).

ЭДС самоиндукции

Когда через катушку проходит переменный ток, он генерирует переменное МП, обладающее изменяющимся магнитным потоком, индуцирующим ЭДС. Этот эффект называется самоиндукцией.

Поскольку МП пропорционально интенсивности тока, то:

Ф = L x I,

где L – индуктивность (Гн), определяемая геометрическими величинами: количеством витков на единицу длины и размерами их поперечного сечения.

Для ЭДС индукции формула принимает вид:

Е = — L x dI/dt.

Взаимоиндукция

Если две катушки расположены рядом, то в них наводится ЭДС взаимоиндукции, зависящая от геометрии обеих схем и их ориентации относительно друг друга. Когда разделение цепей возрастает, взаимоиндуктивность снижается, так как уменьшается соединяющий их магнитный поток.

Взаимоиндукция

Пусть имеется две катушки. По проводу одной катушки, обладающей N1 витками, протекает ток I1, создающий МП, проходящее через катушку с N2 витками. Тогда:

1. Взаимоиндуктивность второй катушки относительно первой:

М21 = (N2 x F21)/I1;

2. Магнитный поток:

Ф21 = (М21/N2) x I1;

3. Найдем индуцированную ЭДС:

Е2 = — N2 x dФ21/dt = — M21x dI1/dt;

4. Идентично в первой катушке индуцируется ЭДС:

Е1 = — M12 x dI2/dt;

Важно! Электродвижущая сила, вызванная взаимоиндукцией в одной катушке, всегда пропорциональна изменению электротока в другой.

Взаимную индуктивность можно признать равной:

М12 = М21 = М.

Соответственно, E1 = — M x dI2/dt и E2 = M x dI1/dt.

М = К √ (L1 x L2),

где К – коэффициент связи между двумя индуктивностями.

Явление взаимоиндукции используется в трансформаторах – электроаппаратах, позволяющих изменить значение напряжения переменного электротока. Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот.

Кроме генерирования, трансформации электроэнергии магнитная индукция применяется в иных устройствах. Например, в магнитных левитационных поездах, которые двигаются не в непосредственном контакте с рельсами, а на несколько сантиметров выше из-за электромагнитной силы отталкивания.

Видео

Оцените статью:

Электричество и магнетизм

Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле. Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока

Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре

Введем коэффициент пропорциональности L

(8.16)

Коэффициент пропорциональности L называется индуктивностью контура. 

Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока.

 

Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.  

В системе СИ единицей измерения индуктивности является генри (Гн)

Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции. 

Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции.

 

Видео 8.13.  Закон Фарадея. Явление самоиндукции.

Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.

Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.  

Выведем формулу для ЭДС самоиндукции . Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени

(8.17)

Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нём и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков

,

что необходимо учитывать при дифференцировании

Подставляя это выражение в (8.17), получаем для неподвижного контура всреде

(8.18)

 

Если же индуктивность контура не зависит от силы тока в нём, то имеем

(8.19)

Мы приходим к закону самоиндукции. В этом простейшем случае: 

В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи.

Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна

где — магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как

(8.20)

где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между  и I, получаем величину индуктивности длинного соленоида (рис. 8.31)

(8.21)

 

Рис. 8.31. Индуктивность соленоида 

При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.

Самоиндукция простыми словами: определение, формулы, примеры

Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.

Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.

Определение

Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.

Рис. 1. Магнитное поле катушки

Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.

Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.

Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.

Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.

Рис. 2. Явление самоиндукции

Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.

Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).

Рис. 3. Схема опыта с лампочками

Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.

На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.

График на рисунке 4 красноречиво объясняет эффект задержки.

Рис. 4. Иллюстрация задержки изменения тока в цепи индуктивности

Обратите внимание на нелинейность изменения силы тока по времени.

Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.

Рис. 5. Возникновение самоиндукции

Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.

В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.

Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.

Формулы

Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.

При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:

где E_{самоинд.} – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.

Индуктивность

Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.

Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.

Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.

Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.

Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.

Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: W_м = LI²/2.

Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.

Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.

Примеры использования на практике

Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.

Работает этот важный узел следующим образом:

1. На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
2. Электрическая цепь резко обрывается специальным прерывателем.
3. Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
4. Искровой разряд зажигает топливную смесь, приводя в движение поршень.

В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.

Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.

В блоках питания электронной аппаратуры таким же способом убирают:

• шумы:
• пульсации;
• нежелательные частоты.

Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.

Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.

В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.

В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.

Видео в помощь

Явление самоиндукции — определение, формулы, примеры

Магнитный поток

Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.

Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.

Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению:

• модуля вектора магнитной индукции ​B​,
• площади поверхности ​S​, которую пронизывает поток,
• и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).

Магнитный поток Ф — магнитный поток [Вб] B — магнитная индукция [Тл] S — площадь пронизываемой поверхности [м2] n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.

Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.

Вот что показали эти опыты:

1. Индукционный ток возникает только при изменении линий магнитной индукции.


2. Направление тока различается при увеличении числа линий и при их уменьшении.


3. Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Самоиндукция

Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.

Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток [Вб] L — индуктивность контура [Гн] I — сила тока в контуре [А]

Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.

Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.

Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:

• первая лампа загорится практически сразу,
• вторая лампа загорится с заметным запаздыванием.

При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.

ЭДС самоиндукции ξis — ЭДС самоиндукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность [Гн]

Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.

Индуктивность

Индуктивность — это способность накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.

Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.

Можно ли увеличивать индуктивность катушки?

Конечно! Можно увеличить число витков, например. Или поместить в центр катушки железный сердечник.

Как работает катушка

Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.

Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.

Задачка раз

На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.

Решение

За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:

Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.

Задачка два

По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб. Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?

Решение

При протекании тока через катушку индуктивности возникает магнитный поток, численно равный Ф = LI.

Отсюда индуктивность катушки равна:

Тогда для достижения значений потока вектора магнитной индукции в 6 мВб ток будет равен:

Ответ: для достижения значений потока вектора магнитной индукции в 6 мВб необходим ток в 3 А.

Формула эдс через индуктивность

Самоиндукция: — явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур. Самоиндукция — частный случай электромагнитной индукции.

Индуктивность: L — коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком. Индуктивность — величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. 1 Гн = 1 Вб / 1 А.

ЭДС самоиндукции: ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Индуктивность соленоида:Магнитное поле соленоида определяется формулой: , .

Магнитный поток, пронизывающий все N витков соленоида, равен: .

Следовательно, индуктивность катушки равна: .

Электродвижущая сила(ЭДС) это работа сторонних сил по перемещению единичного положительного заряда по замкнутому контору.

Энергия взаимодействия токов. Энергия и плотность энергии магнитного поля.

Энергия взаимодействия токов:

Для n токов: i = от 1 доn

Энергия магнитного поля:При отсутствии ферромагнетиков контур с индуктивностью L, по которому течет ток I, обладает магнитной энергией (собственной энергией тока), т. е.

Плотность энергии магнитного поля:— физическая величина, равная отношению:

— энергии магнитного поля в некотором объеме; к

— величине этого объема.

, — плотность энергии магнитного поля соленоида.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8561 — | 7411 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​ ( S ) ​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​ ( B ) ​, площади поверхности ​ ( S ) ​, пронизываемой данным потоком, и косинуса угла ​ ( alpha ) ​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​ ( Phi ) ​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​ ( alpha ) ​ магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​ ( N ) ​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​ ( R ) ​:

При движении проводника длиной ​ ( l ) ​ со скоростью ​ ( v ) ​ в постоянном однородном магнитном поле с индукцией ​ ( vec ) ​ ЭДС электромагнитной индукции равна:

где ​ ( alpha ) ​ – угол между векторами ​ ( vec ) ​ и ( vec ) .

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​ ( varepsilon_ ) ​, возникающая в катушке с индуктивностью ​ ( L ) ​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​ ( Phi ) ​ через контур из этого проводника пропорционален модулю индукции ​ ( vec ) ​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​ ( L ) ​ между силой тока ​ ( I ) ​ в контуре и магнитным потоком ​ ( Phi ) ​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность [1] , краем которой является этот контур. [2][3][4] .

— магнитный поток, — ток в контуре, — индуктивность.

Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока [4] :

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током [4] :

.

Обозначение и единицы измерения

В системе единиц СИ индуктивность измеряется в генри [7] , сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 10 9 см) [4] . Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.

Символ , используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz) [ источник не указан 1017 дней ] . Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry) [8] . Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года [ источник не указан 1017 дней ] .

Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре: (1) где коэффициент пропорциональности L называетсяиндуктивностью контура. При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называетсясамоиндукцией. Из выражения (1) задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В

Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ_{μ(N 2 I/l)S . Подставив в (1), найдем (2) т. е. индуктивность соленоида зависит от длиныl солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида. Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды. Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и(3) где знак минус, определяемый правилом Ленца, говорит о том, чтоналичие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем увеличивается, то (dI/dt 0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξs >1), обладающей боль­шой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникнове­ние значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.}

43. Явление взаимной индукции. Трансформатор.

Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I₁, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I₁. Обозначим через Ф₂₁ часть потока,пронизывающая контур 2. Тогда (1) где L₂₁ — коэффициент пропорциональности.

Если ток I₁ меняет свое значение, то в контуре 2 индуцируется э.д.с. ξ_i2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, который создается током в первом контуре и пронизыващет второй: Аналогичным образом, при протекании в контуре 2 тока I₂ магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф₁₂ — часть этого потока, который пронизывает контур 1, то Если ток I₂ меняет свое значение, то в контуре 1 индуцируется э.д.с. ξ_i1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, который создается током во втором контуре и пронизывает первый: Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е. (2) Коэффициенты пропорциональности L₁₂ и L₂₁ зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн). Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N₁, током I₁ и магнитной проницаемостью μ сердечника, B = μμ_{(N1I1/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф2 = BS = μμ(N1I1/l)S}

Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N₂ витков, Поток Ψ создается током I₁, поэтому, используя (1), найдем (3) Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L₁₂ получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

Наведенная ЭДС и магнитный поток

Цели обучения

К концу этого раздела вы сможете:

• Рассчитайте поток однородного магнитного поля через петлю произвольной ориентации.
• Опишите методы создания электродвижущей силы (ЭДС) с помощью магнитного поля или магнита и проволочной петли.

Аппарат, использованный Фарадеем для демонстрации того, что магнитные поля могут создавать токи, показан на рисунке 1.Когда переключатель замкнут, магнитное поле создается в катушке в верхней части железного кольца и передается катушке в нижней части кольца. Гальванометр используется для обнаружения любого тока, наведенного в катушке внизу. Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр обнаруживает ток в одном направлении в катушке внизу. (Вы также можете наблюдать это в физической лаборатории.) Каждый раз, когда переключатель открывается, гальванометр обнаруживает ток в противоположном направлении.Интересно, что если переключатель остается замкнутым или разомкнутым в течение некоторого времени, через гальванометр нет тока. Замыкание и размыкание переключателя индуцирует ток. Это изменение в магнитном поле, которое создает ток. Более важным, чем текущий ток, является ЭДС, которая его вызывает. Ток является результатом ЭДС , индуцированной изменяющимся магнитным полем , независимо от того, есть ли путь для протекания тока.

Рисунок 1.Аппарат Фарадея для демонстрации того, что магнитное поле может производить ток. Изменение поля, создаваемого верхней катушкой, вызывает ЭДС и, следовательно, ток в нижней катушке. Когда переключатель разомкнут и замкнут, гальванометр регистрирует токи в противоположных направлениях. Когда переключатель остается замкнутым или разомкнутым, через гальванометр не течет ток.

Эксперимент, который легко проводится и часто проводится в физических лабораториях, показан на рисунке 2. ЭДС индуцируется в катушке, когда стержневой магнит толкается внутрь и из нее.ЭДС противоположных знаков создаются движением в противоположных направлениях, и ЭДС также меняются на противоположные за счет изменения полюсов. Те же результаты будут получены, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, и когда магнит неподвижен относительно катушки, ЭДС отсутствует.

Рис. 2. Движение магнита относительно катушки создает ЭДС, как показано. Такие же ЭДС возникают при перемещении катушки относительно магнита.Чем больше скорость, тем больше величина ЭДС, и при отсутствии движения ЭДС равна нулю.

Метод создания ЭДС, используемый в большинстве электрических генераторов, показан на рисунке 3. Катушка вращается в магнитном поле, создавая ЭДС переменного тока, которая зависит от скорости вращения и других факторов, которые будут исследованы в следующих разделах. Обратите внимание, что генератор очень похож по конструкции на двигатель (другая симметрия).

Рис. 3. Вращение катушки в магнитном поле создает ЭДС.Это основная конструкция генератора, в котором работа, выполняемая по вращению катушки, преобразуется в электрическую энергию. Обратите внимание, что генератор очень похож по конструкции на двигатель.

Итак, мы видим, что изменение величины или направления магнитного поля вызывает ЭДС. Эксперименты показали, что существует критическая величина, называемая магнитным потоком , Φ , определяемым

.

Φ = BA cos θ ,

, где B — напряженность магнитного поля над площадью A под углом θ к перпендикуляру к области, как показано на рисунке 5. Любое изменение магнитного потока Φ индуцирует ЭДС. Этот процесс определяется как электромагнитная индукция . Единицы магнитного потока Φ Т ⋅ м ² . Как видно на рисунке 4, B cos θ = B _⊥ , который является составляющей B , перпендикулярной области A . Таким образом, магнитный поток равен Φ = B _⊥ A , произведению площади и составляющей магнитного поля, перпендикулярной ей.

Рис. 4. Магнитный поток Φ связан с магнитным полем и площадью, на которой оно существует. Поток Φ = BA cos θ связан с индукцией; любое изменение Φ вызывает ЭДС.

Вся индукция, включая приведенные до сих пор примеры, возникает из-за некоторого изменения магнитного потока Φ . Например, Фарадей изменил B и, следовательно, Φ при открытии и закрытии переключателя в своем устройстве (показано на рисунке 1).Это также верно для стержневого магнита и катушки, показанных на рисунке 2. При вращении катушки генератора угол θ и, следовательно, Φ изменяется. Насколько велика ЭДС и какое направление она принимает, зависит от изменения в Φ и от того, как быстро это изменение выполняется, как будет рассмотрено в следующем разделе.

Сводка раздела

• Ключевой величиной в индукции является магнитный поток Φ , определяемый как Φ = BA cos θ , где B — напряженность магнитного поля на площади A под углом θ к перпендикуляру к площади. .
• Единицы магнитного потока Φ Т м ² .
• Любое изменение магнитного потока Φ индуцирует ЭДС — процесс определяется как электромагнитная индукция.

Концептуальные вопросы

1. Каким образом многоконтурные катушки и железное кольцо в версии аппарата Фарадея, показанной на рисунке 1, улучшают наблюдение наведенной ЭДС?

2. Когда магнит вставляется в катушку, как показано на рисунке 2 (а), в каком направлении катушка воздействует на магнит? Нарисуйте диаграмму, показывающую направление тока, индуцируемого в катушке, и создаваемое ею магнитное поле, чтобы обосновать вашу реакцию.Как величина силы зависит от сопротивления гальванометра?

3. Объясните, как магнитный поток может быть равен нулю, когда магнитное поле не равно нулю.

4. Индуцируется ли ЭДС в катушке на рис. 5, когда она растягивается? Если да, укажите причину и укажите направление индуцированного тока.

Рис. 5. Круглая катушка с проволокой натянута в магнитном поле.

Задачи и упражнения

1. Какое значение магнитного потока в катушке 2 на рисунке 6 из-за катушки 1?

Рисунок 6.(а) Плоскости двух катушек перпендикулярны. (б) Проволока перпендикулярна плоскости катушки.

2. Какое значение магнитного потока, проходящего через катушку на Рисунке 6 (b), обусловлено проводом?

Глоссарий

магнитный поток:

величина магнитного поля, проходящего через конкретную область, рассчитанная с помощью Φ = B A cos θ , где B — напряженность магнитного поля на площади A под углом θ к перпендикуляру к площадь

электромагнитная индукция:

Процесс наведения ЭДС (напряжения) с изменением магнитного потока

Электромагнитная индукция и закон Фарадея

Если затем намотать провод в катушку, магнитное поле значительно усиливается, создавая вокруг себя статическое магнитное поле, формирующее форму стержневого магнита, дающего отчетливые северный и южный полюсы.

Полая катушка с воздушным сердечником

Магнитный поток, развиваемый вокруг катушки, пропорционален величине тока, протекающего в обмотках катушек, как показано. Если дополнительные слои проволоки намотаны на одну и ту же катушку с тем же током, протекающим через них, напряженность статического магнитного поля будет увеличиваться.

Следовательно, напряженность магнитного поля катушки определяется амперными витками катушки. Чем больше витков провода внутри катушки, тем больше напряженность статического магнитного поля вокруг нее.

Но что, если бы мы изменили эту идею, отключив электрический ток от катушки и вместо полого сердечника мы поместили стержневой магнит внутрь сердечника катушки с проволокой. Перемещая этот стержневой магнит «внутрь» и «наружу» из катушки, в катушку будет индуцироваться ток за счет физического движения магнитного потока внутри нее.

Аналогичным образом, если бы мы удерживали стержневой магнит в неподвижном состоянии и перемещали катушку вперед и назад в магнитном поле, в катушке индуцировался бы электрический ток.Затем, перемещая провод или изменяя магнитное поле, мы можем индуцировать напряжение и ток внутри катушки, и этот процесс известен как Электромагнитная индукция и является основным принципом работы трансформаторов, двигателей и генераторов.

Электромагнитная индукция была впервые обнаружена еще в 1830-х годах Майклом Фарадеем . Фарадей заметил, что когда он перемещал постоянный магнит внутрь и из катушки или одиночной петли провода, он индуцировал электродвижущую силу или ЭДС, другими словами, напряжение, и, следовательно, создавался ток.

Итак, Майкл Фарадей открыл способ создания электрического тока в цепи с использованием только силы магнитного поля, а не батарей. Затем это привело к очень важному закону, связывающему электричество с магнетизмом, Закон электромагнитной индукции Фарадея . Так, как это работает?.

Когда магнит, показанный ниже, перемещается «к» катушке, стрелка или стрелка гальванометра, который по сути представляет собой очень чувствительный амперметр с подвижной катушкой с нулевым центром, отклоняется от своего центрального положения только в одном направлении.Когда магнит перестает двигаться и остается неподвижным по отношению к катушке, стрелка гальванометра возвращается к нулю, поскольку нет физического движения магнитного поля.

Аналогичным образом, когда магнит перемещается «от катушки» в другом направлении, стрелка гальванометра отклоняется в противоположном направлении относительно первого, указывая на изменение полярности. Затем, перемещая магнит назад и вперед по направлению к катушке, стрелка гальванометра будет отклоняться влево или вправо, в положительную или отрицательную сторону относительно направленного движения магнита.

Электромагнитная индукция движущимся магнитом

Аналогично, если магнит теперь удерживается в неподвижном состоянии и ТОЛЬКО катушка перемещается к магниту или от него, стрелка гальванометра также будет отклоняться в любом направлении. Затем движение катушки или петли через магнитное поле индуцирует в катушке напряжение, величина которого пропорциональна скорости или скорости движения.

Тогда мы можем видеть, что чем быстрее движение магнитного поля, тем больше будет индуцированная ЭДС или напряжение в катушке, поэтому для выполнения закона Фарадея должно быть «относительное движение» или движение между катушкой и магнитным полем. и либо магнитное поле, либо катушка, либо и то, и другое могут двигаться.

Закон индукции Фарадея

Из приведенного выше описания мы можем сказать, что существует взаимосвязь между электрическим напряжением и изменяющимся магнитным полем, о которой говорится в известном законе Майкла Фарадея об электромагнитной индукции: «что напряжение индуцируется в цепи всякий раз, когда существует относительное движение между проводником и проводником. магнитное поле и что величина этого напряжения пропорциональна скорости изменения магнитного потока ».

Другими словами, Электромагнитная индукция — это процесс использования магнитных полей для создания напряжения, а в замкнутой цепи — тока.

Итак, какое напряжение (ЭДС) может быть наведено в катушку, используя только магнетизм. Это определяется следующими тремя различными факторами.

• 1). Увеличение количества витков провода в катушке — за счет увеличения количества отдельных проводников, прорезающих магнитное поле, количество создаваемой наведенной ЭДС будет суммой всех отдельных витков катушки, поэтому, если есть 20 витков в в катушке будет в 20 раз больше наведенной ЭДС, чем в одном куске проволоки.
• 2). Увеличение скорости относительного движения между катушкой и магнитом — если одна и та же катушка с проволокой прошла через то же магнитное поле, но ее скорость или скорость увеличились, проволока перережет линии потока с большей скоростью, что приведет к большей наведенной ЭДС. будет произведено.
• 3). Увеличение силы магнитного поля. Если ту же катушку с проволокой перемещать с той же скоростью через более сильное магнитное поле, будет возникать большая ЭДС, потому что есть больше силовых линий, которые нужно разрезать.

Если бы мы могли перемещать магнит на приведенной выше диаграмме внутрь и наружу катушки с постоянной скоростью и на постоянное расстояние без остановки, мы бы генерировали непрерывно индуцированное напряжение, которое чередовалось бы между одной положительной полярностью и отрицательной полярностью, создавая переменную или отрицательную полярность. Выходное напряжение переменного тока, и это основной принцип работы электрического генератора, аналогичного тем, которые используются в динамо-машинах и автомобильных генераторах.

В небольших генераторах, таких как велосипедное динамо, небольшой постоянный магнит вращается под действием велосипедного колеса внутри фиксированной катушки.В качестве альтернативы, электромагнит, питаемый фиксированным постоянным напряжением, может вращаться внутри фиксированной катушки, например, в больших генераторах энергии, вырабатывающих в обоих случаях переменный ток.

Простой генератор с использованием магнитной индукции

Простой генератор типа динамо, представленный выше, состоит из постоянного магнита, который вращается вокруг центрального вала, с катушкой с проволокой, размещенной рядом с этим вращающимся магнитным полем. Когда магнит вращается, магнитное поле вокруг верхней и нижней части катушки постоянно меняется между северным и южным полюсами.Это вращательное движение магнитного поля приводит к тому, что в катушке индуцируется переменная ЭДС, как определено законом электромагнитной индукции Фарадея.

Величина электромагнитной индукции прямо пропорциональна плотности потока β, количеству петель, определяющих общую длину проводника, l в метрах, и скорости или скорости, ν, с которой изменяется магнитное поле внутри проводника в метрах / секунды или м / с, что выражается выражением двигательной ЭДС:

Движение ЭДС Фарадея Выражение

Если проводник не движется под прямым углом (90 °) к магнитному полю, то к приведенному выше выражению будет добавлен угол θ °, что приведет к уменьшению выходной мощности при увеличении угла:

Закон электромагнитной индукции Ленца

Закон Фарадея говорит нам, что наведение напряжения в проводник может быть выполнено либо путем пропускания его через магнитное поле, либо путем перемещения магнитного поля мимо проводника, и что, если этот проводник является частью замкнутой цепи, электрический ток будет течь. .Это напряжение называется индуцированной ЭДС , поскольку оно было индуцировано в проводнике изменяющимся магнитным полем из-за электромагнитной индукции с отрицательным знаком в законе Фарадея, указывающим нам направление индуцированного тока (или полярность наведенной ЭДС).

Но изменяющийся магнитный поток создает переменный ток через катушку, которая сама создает собственное магнитное поле, как мы видели в учебнике по электромагнитам. Эта самоиндуцированная ЭДС противодействует вызывающему ее изменению, и чем выше скорость изменения тока, тем больше противоположная ЭДС.Эта самоиндуцированная ЭДС по закону Ленца будет противодействовать изменению тока в катушке, и из-за ее направления эту самоиндуцированную ЭДС обычно называют обратной ЭДС .

Закон Ленца гласит: «Направление индуцированной ЭДС таково, что она всегда будет противодействовать вызывающему ее изменению». Другими словами, индуцированный ток всегда будет ПРОТИВ движению или изменению, которое в первую очередь привело к возникновению индуцированного тока, и эта идея обнаруживается в анализе индуктивности.

Аналогично, если магнитный поток уменьшается, то наведенная ЭДС будет противодействовать этому уменьшению, создавая индуцированный магнитный поток, который добавляется к исходному потоку.

Закон Ленца является одним из основных законов электромагнитной индукции для определения направления потока индуцированных токов и связан с законом сохранения энергии.

Согласно закону сохранения энергии, который гласит, что общее количество энергии во Вселенной всегда будет оставаться постоянным, поскольку энергия не может быть создана или уничтожена.Закон Ленца выводится из закона индукции Майкла Фарадея.

Последний комментарий к закону Ленца об электромагнитной индукции. Теперь мы знаем, что когда существует относительное движение между проводником и магнитным полем, внутри проводника индуцируется ЭДС.

Но проводник на самом деле может не быть частью электрической цепи катушек, но может быть железным сердечником катушек или какой-либо другой металлической частью системы, например, трансформатором. Индуцированная ЭДС внутри этой металлической части системы заставляет циркулирующий ток течь вокруг нее, и этот тип тока сердечника известен как Eddy Current .

Вихревые токи, генерируемые электромагнитной индукцией, циркулируют вокруг сердечника катушек или любых соединительных металлических компонентов внутри магнитного поля, поскольку для магнитного потока они действуют как одиночная петля из проволоки. Вихревые токи ничего не вносят в полезность системы, но вместо этого они противодействуют потоку индуцированного тока, действуя как отрицательная сила, вызывая резистивный нагрев и потери мощности внутри сердечника. Однако существуют электромагнитные индукционные печи, в которых для нагрева и плавления ферромагнитных металлов используются только вихревые токи.

Вихревые токи, циркулирующие в трансформаторе

Изменяющийся магнитный поток в железном сердечнике вышеуказанного трансформатора будет индуцировать ЭДС не только в первичной и вторичной обмотках, но и в железном сердечнике. Железный сердечник является хорошим проводником, поэтому токи, индуцируемые в твердом железном сердечнике, будут большими. Кроме того, вихревые токи текут в направлении, которое, согласно закону Ленца, ослабляет поток, создаваемый первичной катушкой. Следовательно, ток в первичной катушке, необходимый для создания заданного поля B, увеличивается, поэтому кривые гистерезиса становятся более толстыми по оси H.

Ламинирование железного сердечника

Потери на вихревые токи и гистерезис нельзя полностью исключить, но их можно значительно уменьшить. Вместо использования твердого железного сердечника в качестве материала магнитного сердечника трансформатора или катушки, магнитный путь является «ламинированным».

Эти пластинки представляют собой очень тонкие полосы изолированного (обычно покрытого лаком) металла, соединенные вместе для образования твердого сердечника. Пластины увеличивают сопротивление железного сердечника, тем самым увеличивая общее сопротивление потоку вихревых токов, поэтому индуцированные потери мощности на вихревые токи в сердечнике уменьшаются, и именно по этой причине цепь магнитного железа трансформаторов и электрические машины все ламинированы.

23,1 Индуцированная ЭДС и магнитный поток — Физика колледжа: OpenStax

Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии

Сводка

• Рассчитайте поток однородного магнитного поля через петлю произвольной ориентации.
• Опишите методы создания электродвижущей силы (ЭДС) с помощью магнитного поля или магнита и проволочной петли.

Устройство, использованное Фарадеем для демонстрации того, что магнитные поля могут создавать токи, показано на рисунке 1. Когда переключатель замкнут, магнитное поле создается в катушке в верхней части железного кольца и передается на катушку в нижней части. часть кольца. Гальванометр используется для обнаружения любого тока, наведенного в катушке внизу. Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр обнаруживает ток в одном направлении в катушке внизу.(Вы также можете наблюдать это в физической лаборатории.) Каждый раз, когда переключатель открывается, гальванометр обнаруживает ток в противоположном направлении. Интересно, что если переключатель остается замкнутым или разомкнутым в течение некоторого времени, через гальванометр нет тока. Замыкание и размыкание переключателя индуцирует ток. Это изменение магнитного поля, которое создает ток. Более важным, чем текущий ток, является вызывающая его ЭДС . Ток является результатом ЭДС , индуцированной изменяющимся магнитным полем , независимо от того, есть ли путь для протекания тока.

Рис. 1. Аппарат Фарадея для демонстрации того, что магнитное поле может производить ток. Изменение поля, создаваемого верхней катушкой, вызывает ЭДС и, следовательно, ток в нижней катушке. Когда переключатель разомкнут и замкнут, гальванометр регистрирует токи в противоположных направлениях. Когда переключатель остается замкнутым или разомкнутым, через гальванометр не течет ток.

Эксперимент, который легко проводится и часто проводится в физических лабораториях, показан на рисунке 2.ЭДС индуцируется в катушке, когда стержневой магнит вставляется и выходит из нее. ЭДС противоположных знаков создаются движением в противоположных направлениях, и ЭДС также меняются на противоположные за счет изменения полюсов. Те же результаты будут получены, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, и когда магнит неподвижен относительно катушки, ЭДС отсутствует.

Рис. 2. Движение магнита относительно катушки создает ЭДС, как показано.Такие же ЭДС возникают при перемещении катушки относительно магнита. Чем больше скорость, тем больше величина ЭДС, и при отсутствии движения ЭДС равна нулю.

Метод создания ЭДС, используемый в большинстве электрических генераторов, показан на рисунке 3. Катушка вращается в магнитном поле, создавая ЭДС переменного тока, которая зависит от скорости вращения и других факторов, которые будут исследованы в следующих разделах. Обратите внимание, что генератор очень похож по конструкции на двигатель (другая симметрия).

Рис. 3. При вращении катушки в магнитном поле возникает ЭДС. Это основная конструкция генератора, в котором работа, выполняемая по вращению катушки, преобразуется в электрическую энергию. Обратите внимание, что генератор очень похож по конструкции на двигатель.

Итак, мы видим, что изменение величины или направления магнитного поля вызывает ЭДС. Эксперименты показали, что существует критически важная величина, называемая магнитным потоком, [латекс] \ boldsymbol {\ phi} [/ latex], определяемый

[латекс] \ boldsymbol {\ phi = BA \; \ textbf {cos} \; \ theta}, [/ латекс]

где [латекс] \ boldsymbol {B} [/ latex] — это напряженность магнитного поля над областью [латекс] \ boldsymbol {A} [/ latex] под углом [латекс] \ boldsymbol {\ theta} [/ latex ] с перпендикуляром к области, как показано на рисунке 4.2} [/ латекс]. Как видно на рисунке 4, [latex] \ boldsymbol {B \; \ textbf {cos} \; \ theta = B _ {\ perp}} [/ latex], который является компонентом [latex] \ boldsymbol {B} [ / latex] перпендикулярно области [латекс] \ boldsymbol {A} [/ latex]. Таким образом, магнитный поток — это [латекс] \ boldsymbol {\ phi = B _ {\ perp} A} [/ latex], произведение площади и составляющей магнитного поля, перпендикулярной ей.

Рис. 4. Магнитный поток Φ связан с магнитным полем и площадью, на которой оно существует.Поток Φ = BA cos θ связан с индукцией; любое изменение Φ вызывает ЭДС.

Вся индукция, включая приведенные до сих пор примеры, возникает из-за некоторого изменения магнитного потока [латекс] \ boldsymbol {\ phi} [/ латекс]. Например, Фарадей изменил [латекс] \ boldsymbol {B} [/ latex] и, следовательно, [латекс] \ boldsymbol {\ phi} [/ latex] при открытии и закрытии переключателя в своем устройстве (показано на рисунке 1). Это также верно для стержневого магнита и катушки, показанных на рисунке 2.При вращении катушки генератора угол [латекс] \ boldsymbol {\ theta} [/ latex] и, следовательно, [латекс] \ boldsymbol {\ phi} [/ latex] изменяется. Насколько велика ЭДС и какое направление она принимает, зависит от изменения [latex] \ boldsymbol {\ phi} [/ latex] и от того, как быстро это изменение будет выполнено, как будет рассмотрено в следующем разделе.

• Ключевой величиной в индукции является магнитный поток [латекс] \ boldsymbol {\ phi} [/ latex], определяемый как [латекс] \ boldsymbol {\ phi = BA \; \ textbf {cos} \; \ theta} [ / latex], где [latex] \ boldsymbol {B} [/ latex] — это напряженность магнитного поля над областью [latex] \ boldsymbol {A} [/ latex] под углом [латекс] \ boldsymbol {\ theta} [ / латекс] с перпендикуляром к площади.2} [/ латекс].
• Любое изменение магнитного потока [латекс] \ boldsymbol {\ phi} [/ latex] вызывает ЭДС — процесс определяется как электромагнитная индукция.

Концептуальные вопросы

1: Каким образом многопетлевые катушки и железное кольцо в версии аппарата Фарадея, показанной на рисунке 1, усиливают наблюдение наведенной ЭДС?

2: Когда магнит вставляется в катушку, как показано на рисунке 2 (а), в каком направлении катушка воздействует на магнит? Нарисуйте диаграмму, показывающую направление тока, индуцируемого в катушке, и создаваемое ею магнитное поле, чтобы обосновать вашу реакцию.Как величина силы зависит от сопротивления гальванометра?

3: Объясните, как магнитный поток может быть равен нулю, когда магнитное поле не равно нулю.

4: Индуцируется ли ЭДС в катушке на рис. 5, когда она растягивается? Если да, укажите причину и укажите направление индуцированного тока.

Рис. 5. Круглая катушка с проволокой натянута в магнитном поле.

Задачи и упражнения

1: Какое значение магнитного потока в катушке 2 на рисунке 6 из-за катушки 1?

Рисунок 6. (a) Плоскости двух катушек перпендикулярны. (б) Проволока перпендикулярна плоскости катушки.

2: Какое значение магнитного потока, проходящего через катушку на рис. 6 (b), обусловлено проводом?

Глоссарий

магнитный поток

величина магнитного поля, проходящего через определенную область, рассчитывается с помощью [latex] \ boldsymbol {\ phi = BA \; \ textbf {cos} \; \ theta} [/ latex] где [latex] \ boldsymbol {B} [/ latex] — это напряженность магнитного поля над областью [латекс] \ boldsymbol {A} [/ latex] под углом [латекс] \ boldsymbol {\ theta} [/ latex] с перпендикуляром к площади

электромагнитная индукция

Процесс наведения ЭДС (напряжения) с изменением магнитного потока

Решения

Задачи и упражнения

1: Ноль

Электродвижущая сила в индукторах — MagLab

Электродвижущая сила (ЭДС) и ее помощник, обратная ЭДС, представляют собой интересные электромагнитные явления, которые на самом деле вовсе не являются силами.

ЭДС — это аббревиатура от электродвижущей силы. Ученые склонны не использовать расширенную версию этого термина, отчасти потому, что это может вводить в заблуждение: на самом деле ЭДС не является силой в том, как физики используют этот термин. Скорее, это энергия, производимая взаимодействием между током и магнитным полем, когда одно (или оба) изменяется. Оно измеряется в вольтах и ​​иногда приравнивается к напряжению или разности потенциалов.

В приведенном ниже руководстве описывается как ЭДС, так и связанное с ней явление, против ЭДС (или против ЭДС ).EMF объясняет внезапное мигание лампочки в изображенной схеме как при подключении, так и при отключении.

Учебное пособие содержит простую схему из батареи, рубильника и лампочки (действующей как резистор , препятствующий прохождению тока). Он также содержит индуктор в виде проволочной катушки. Индукторы хранят энергию в виде магнитных полей, которые генерируются вокруг них током, проходящим через провод.

Посмотрите, как это работает, нажав на синюю кнопку Turn On , чтобы нажать рубильник и включить цепь, обозначенную желтым свечением в цепи.Обратите внимание на синие силовые линии магнитного поля (проявление ЭДС), которые формируются вокруг катушки индуктора, что объясняется законом индукции Фарадея. Также обратите внимание, что лампочка на мгновение мигает, а затем гаснет. Этот эффект объясняется обратной ЭДС.

Когда электричество проходит по цепи, его первоначальное предпочтение — избегать лампочки и двигаться по пути наименьшего сопротивления через спиральный провод. Но, по крайней мере, на несколько мгновений, электричество действительно проходит через лампочку, вызывая короткую вспышку.Это происходит, когда катушка на короткое время создает собственное сопротивление току в виде обратной ЭДС. Эта обратная ЭДС создается в результате закона Ленца , который гласит, что в цепи с наведенной ЭДС, вызванной изменением в магнитном поле, наведенная ЭДС вызывает протекание тока в направлении, противоположном . изменение потока. Другими словами, если увеличивающееся магнитное поле индуцирует ЭДС, результирующий ток будет препятствовать дальнейшему увеличению.

По мере того, как магнитное поле в индукторе растет, он индуцирует ток, который противодействует току, генерируемому батареей.В результате ток батареи легче протекает через лампочку — по крайней мере, до тех пор, пока магнитное поле индуктора не достигнет устойчивого состояния (не перестанет меняться), что положит конец обратной ЭДС.

Эффекты обратной ЭДС можно также увидеть, если нажать красную кнопку Turn Off , чтобы прервать цепь. Обратите внимание, что силовые линии магнитного поля начинают разрушаться по мере замедления электрического тока. В этом проявлении закона Ленца уменьшающееся магнитное поле индуцирует ЭДС, а результирующий ток препятствует дальнейшему уменьшению.Результирующий ток течет по цепи к лампочке, которая вспыхивает с этим скачком, а затем гаснет, когда электричество полностью исчезает из цепи.

---

Спасибо нашему научному консультанту на этой странице, г-ну Джеймсу Энди Пауэллу, инженеру-электронику в отделе КИП и эксплуатации MagLab.

13.6 Электрические генераторы и обратная ЭМП — Университетская физика, Том 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните, как работает электрогенератор
• Определить наведенную ЭДС в контуре на любом временном интервале, вращающемся с постоянной скоростью в магнитном поле
• Показать, что вращающиеся катушки имеют наведенную ЭДС; в двигателях это называется обратной ЭДС, потому что она противодействует входной ЭДС в двигатель
.

С помощью закона Фарадея можно понять множество важных явлений и устройств.В этом разделе мы рассмотрим два из них.

Электрогенераторы

Электрические генераторы индуцируют ЭДС, вращая катушку в магнитном поле, как кратко обсуждается в Движущей ЭДС. на магнитное поле изначально равна cosθ, cosθ, и она вставляется по определению скалярного произведения.Величина магнитного поля и площадь контура фиксируются во времени, что позволяет быстро упростить интеграцию. Индуцированная ЭДС записывается по закону Фарадея:

ε = NBAsinθdθdt.ε = NBAsinθdθdt.

Решение

Нам дано, что N = 200, N = 200, B = 0.80T, B = 0.80T, θ = 90 ° θ = 90 °, dθ = 90 ° = π / 2dθ = 90 ° = π / 2 и dt = 15.0 мс. Dt = 15.0 мс. Площадь петли A = πr2 = (3,14) (0,0500 м) 2 = 7,85 × 10−3м2. A = πr2 = (3,14) (0,0500 м) 2 = 7,85 × 10−3м2.

Ввод этого значения дает

ε = (200) (0,80T) (7,85 × 10−3m2) sin (90 °) π / 215.0 × 10−3s = 131V. Ε = (200) (0,80T) (7,85 × 10−3m2) sin (90 °) π / 215,0 × 10−3s = 131V.

Значение

Это практическое среднее значение, подобное 120 В, используемому в бытовой электросети.

ЭДС, вычисленная в примере 13.9, является средним значением за четверть оборота. Какова ЭДС в каждый момент времени? Он меняется в зависимости от угла между магнитным полем и перпендикуляром к катушке. Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной × и высотой × в однородном магнитном поле, как показано на рисунке 13.28.

Рисунок 13.28 Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, синусоидально изменяющуюся во времени. Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для выработки тока, а не наоборот.

На заряды в проводах петли действует магнитная сила, потому что они движутся в магнитном поле. Заряды в вертикальных проводах испытывают силы, параллельные проводу, вызывая токи.Но те, кто находится в верхнем и нижнем сегментах, ощущают силу, перпендикулярную проводу, которая не вызывает тока. Таким образом, мы можем найти наведенную ЭДС, рассматривая только боковые провода. ЭДС движения задается равной ε = Blvε = Blv, где скорость v перпендикулярна магнитному полю B . Здесь скорость находится под углом θθ к B , так что ее составляющая, перпендикулярная B , равна v sin θθ (см. Рисунок 13.28). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ε = Blvsinθε = Blvsinθ, и они направлены в одном направлении.Суммарная ЭДС вокруг контура тогда составляет

. ε = 2Blvsinθ.ε = 2Blvsinθ.

13,13

Это выражение допустимо, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью ωω. Угол θθ связан с угловой скоростью соотношением θ = ωt, θ = ωt, так что

ε = 2Blvsin (ωt). ε = 2Blvsin (ωt).

13,14

Итак, линейная скорость v связана с угловой скоростью ωω соотношением v = rω.v = rω. Здесь r = w / 2, r = w / 2, так что v = (w / 2) ω, v = (w / 2) ω и

ε = 2Blw2ωsinωt = (lw) Bωsinωt.ε = 2Blw2ωsinωt = (lw) Bωsinωt.

13,15

Заметив, что площадь петли A = lw, A = lw, и учитывая N петель, мы находим, что

ε = NBAωsin (ωt) .ε = NBAωsin (ωt).

13,16

Это ЭДС, индуцированная в катушке генератора из N, витков и площади A, , вращающейся с постоянной угловой скоростью ωω в однородном магнитном поле B . Это также может быть выражено как

. ε = ε0sinωt, ε = ε0sinωt,

13,17

где

— пиковая ЭДС, так как максимальное значение sin (wt) = 1 sin (wt) = 1.Обратите внимание, что частота колебаний равна f = ω / 2πf = ω / 2π, а период равен T = 1 / f = 2π / ω.T = 1 / f = 2π / ω. На рисунке 13.29 показан график зависимости ЭДС от времени, и теперь кажется разумным, что переменное напряжение синусоидально.

Рис. 13.29 ЭДС генератора направляется на лампочку с показанной системой колец и щеток. График показывает ЭДС генератора как функцию времени, где ε0ε0 — пиковая ЭДС. Период равен T = 1 / f = 2π / ω, T = 1 / f = 2π / ω, где f — частота.

Тот факт, что пиковая ЭДС равна ε0 = NBAωε0 = NBAω, имеет смысл.Чем больше катушек, тем больше их площадь и чем сильнее поле, тем больше выходное напряжение. Интересно, что чем быстрее вращается генератор (больше ωω), тем больше ЭДС. Это заметно на велосипедных генераторах — по крайней мере, на более дешевых моделях.

На рис. 13.30 показана схема, с помощью которой генератор может вырабатывать импульсный постоянный ток. Более сложные конструкции из нескольких катушек и разрезных колец могут обеспечить более плавный постоянный ток, хотя для создания постоянного тока без пульсаций обычно используются электронные, а не механические средства.

Рисунок 13.30 Разделенные кольца, называемые коммутаторами, в этой конфигурации создают импульсный выходной сигнал ЭДС постоянного тока.

В реальной жизни электрические генераторы сильно отличаются от рисунков в этом разделе, но принципы те же. Источником механической энергии, вращающей катушку, может быть падающая вода (гидроэнергия), пар, образующийся при сжигании ископаемого топлива, или кинетическая энергия ветра. Рисунок 13.31 показывает паровую турбину в разрезе; пар движется по лопастям, соединенным с валом, который вращает катушку внутри генератора.Производство электрической энергии из механической энергии — основной принцип всей энергии, которая направляется через наши электрические сети в наши дома.

Рисунок 13.31 Паровая турбина / генератор. Пар, образующийся при сжигании угля, ударяется о лопатки турбины, вращая вал, соединенный с генератором.

Генераторы

, показанные в этом разделе, очень похожи на двигатели, показанные ранее. Это не случайно. Фактически, двигатель становится генератором, когда его вал вращается.В некоторых ранних автомобилях стартер использовался в качестве генератора. В следующем разделе мы подробнее исследуем действие двигателя как генератора.

Задний Emf

Генераторы преобразуют механическую энергию в электрическую, а двигатели преобразуют электрическую энергию в механическую. Таким образом, неудивительно, что двигатели и генераторы имеют одинаковую общую конструкцию. Двигатель работает, посылая ток через проволочную петлю, находящуюся в магнитном поле. В результате магнитное поле оказывает крутящий момент на петлю.Это вращает вал, тем самым извлекая механическую работу из первоначально подаваемого электрического тока. (Обратитесь к разделу «Сила и крутящий момент в токовой петле», чтобы обсудить двигатели, которые помогут вам лучше понять их, прежде чем продолжить.)

Когда катушка двигателя поворачивается, магнитный поток через катушку изменяется, и индуцируется ЭДС (в соответствии с законом Фарадея). Таким образом, двигатель действует как генератор всякий раз, когда его катушка вращается. Это происходит независимо от того, поворачивается ли вал под действием внешнего источника, например ременной передачи, или под действием самого двигателя.То есть, когда двигатель выполняет работу и его вал вращается, возникает ЭДС. Закон Ленца говорит нам, что ЭДС противодействует любому изменению, так что входной ЭДС, питающей двигатель, противостоит самогенерируемая ЭДС двигателя, называемая обратной ЭДС двигателя (рис. 13.32).

Рис. 13.32 Катушка двигателя постоянного тока представлена ​​на этой схеме как резистор. Обратная ЭДС представлена ​​как переменная ЭДС, которая противодействует ЭДС, приводящей в движение двигатель. Обратная ЭДС равна нулю, когда двигатель не вращается, и увеличивается пропорционально угловой скорости двигателя.

Выходная мощность генератора двигателя — это разница между напряжением питания и обратной ЭДС. При первом включении двигателя обратная ЭДС равна нулю, что означает, что катушка получает полное управляющее напряжение, а двигатель потребляет максимальный ток, когда он включен, но не вращается. По мере того, как двигатель вращается быстрее, обратная ЭДС возрастает, всегда противодействуя управляющей ЭДС, и снижает как напряжение на катушке, так и величину потребляемого ею тока. Этот эффект заметен во многих обычных ситуациях.При первом включении пылесоса, холодильника или стиральной машины свет в той же цепи на короткое время тускнеет из-за падения IR , возникающего в питающих линиях из-за большого тока, потребляемого двигателем.

Когда двигатель впервые включается, он потребляет больше тока, чем когда он работает с нормальной рабочей скоростью. Когда на двигатель оказывается механическая нагрузка, например, электрическая инвалидная коляска, поднимающаяся в гору, двигатель замедляется, обратная ЭДС падает, течет больше тока и можно выполнять больше работы.Если двигатель работает на слишком низкой скорости, больший ток может его перегреть (из-за резистивной мощности в катушке, P = I2R), P = I2R), возможно, даже сжечь его. С другой стороны, если на двигатель нет механической нагрузки, он увеличивает свою угловую скорость ωω до тех пор, пока противоЭДС не станет почти равной управляющей ЭДС. Тогда двигатель использует достаточно энергии только для преодоления трения.

Вихревые токи в железных сердечниках двигателей могут вызывать серьезные потери энергии. Их обычно сводят к минимуму, собирая сердечники из тонких электрически изолированных листов железа.На магнитные свойства сердечника практически не влияет ламинация изолирующего листа, в то время как резистивный нагрев значительно снижается. Рассмотрим, например, катушки двигателя, представленные на рисунке 13.32. Катушки имеют эквивалентное сопротивление 0,400 Ом 0,400 Ом и управляются ЭДС 48,0 В. Вскоре после включения они потребляют ток

. I = V / R = (48,0 В) / (0,400 Ом) = 120 AI = V / R = (48,0 В) / (0,400 Ом) = 120 А

и, таким образом, рассеивают P = I2R = 5,76 кВт = I2R = 5,76 кВт энергии в качестве теплопередачи.При нормальных условиях работы для этого двигателя предположим, что противоэдс составляет 40,0 В. Тогда при рабочей скорости полное напряжение на катушках составляет 8,0 В (48,0 В минус противоэдс 40,0 В), а потребляемый ток равен

. I = V / R = (8,0 В) / (0,400 Ом) = 20 А. I = V / R = (8,0 В) / (0,400 Ом) = 20 А.

Таким образом, при нормальной нагрузке рассеиваемая мощность составляет P = IV = (20A) (8,0 В) = 160 Вт. P = IV = (20 A) (8,0 В) = 160 Вт. Это не вызывает проблем для этого двигателя, тогда как прежние 5,76 кВт сожгли бы катушки, если бы продолжали работать.

Пример 13.10

Двигатель с последовательной обмоткой в ​​работе

Полное сопротивление (Rf + Ra) (Rf + Ra) двигателя постоянного тока с последовательной обмоткой составляет 2,0 Ом 2,0 Ом (рисунок 13.33). При подключении к источнику 120 В (εSεS) двигатель потребляет 10 А при работе с постоянной угловой скоростью. (а) Какая обратная ЭДС индуцируется во вращающейся катушке εi? εi? б) Какова механическая мощность двигателя? (c) Какая мощность рассеивается на сопротивлении катушек? (d) Какова выходная мощность источника 120 В? (e) Предположим, что нагрузка на двигатель увеличивается, заставляя его замедляться до точки, в которой он потребляет 20 А.Ответьте на вопросы от (a) до (d) в этой ситуации.

Рисунок 13.33. Схема двигателя постоянного тока с последовательной обмоткой.

Стратегия

Обратная ЭДС рассчитывается на основе разницы между подаваемым напряжением и потерями из-за тока через сопротивление. Мощность каждого устройства рассчитывается по одной из формул мощности на основе данной информации.

Решение

1. ЭДС обратная εi = εs − I (Rf + Ra) = 120V− (10A) (2.0Ω) = 100V. εi = εs − I (Rf + Ra) = 120V− (10A) (2.0 Ом) = 100 В.
2. Поскольку потенциал на якоре составляет 100 В при токе через него 10 А, выходная мощность двигателя равна Pm = εiI = (100 В) (10 A) = 1,0 × 103 Вт. Pm = εiI = (100 В) (10 A) = 1,0 × 103 Вт.
3. Ток 10 А протекает через катушки, общее сопротивление которых составляет 2,0 Ом 2,0 Ом, поэтому мощность, рассеиваемая в катушках, равна PR = I2R = (10 A) 2 (2,0 Ом) = 2,0 × 102 Вт. PR = I2R = (10 A) 2 (2,0 Ом) = 2,0 × 102 Вт.
4. Поскольку 10 А потребляется от источника 120 В, его выходная мощность составляет Ps = εsI = (120V) (10A) = 1,2 × 103Вт. Ps = εsI = (120V) (10A) = 1.2 × 103 Вт.
5. Повторяя те же вычисления с I = 20AI = 20A, находим εi = 80 В, Pm = 1,6 × 103 Вт, PR = 8,0 × 102 Вт и Ps = 2,4 × 103 Вт. εi = 80 В, Pm = 1,6 × 103 Вт, PR = 8,0 × 102 Вт и Ps = 2,4 × 103 Вт. В этом случае двигатель вращается медленнее, поэтому его выходная мощность и мощность источника больше.

Значение

Обратите внимание, что у нас есть баланс энергии в части (d): 1,2 × 103 Вт = 1,0 × 103 Вт + 2,0 × 102 Вт. {\ circ} \)) в 15.0 мс. Круглая катушка с 200 витками имеет радиус 5,00 см и находится в однородном магнитном поле 1,25 Тл. Какая средняя наведенная ЭДС?

Рисунок \ (\ PageIndex {1} \): Когда катушка генератора вращается на одну четверть оборота, магнитный поток \ (\ Phi \) изменяется от максимального до нуля, вызывая ЭДС.

Стратегия:

Мы используем закон индукции Фарадея, чтобы найти среднюю ЭДС, индуцированную за время \ (\ Delta t \): \ [emf = -N \ frac {\ Delta \ Phi} {\ Delta t}. \ Label {23.6.{-3} s} = 131V. \]

Обсуждение:

Это практическое среднее значение, аналогичное 120 В, используемому в бытовой электросети.

ЭДС, вычисленная в этом примере, представляет собой среднее значение за четверть оборота. Какова ЭДС в каждый момент времени? Он меняется в зависимости от угла между магнитным полем и перпендикуляром к катушке. Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной \ (\ w \) и высотой \ (l \) в однородном магнитном поле, как показано на рисунке \ (\ PageIndex {2} \).

Рисунок \ (\ PageIndex {2} \): Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, синусоидально изменяющуюся во времени. Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для выработки тока, а не наоборот.

На заряды в проводах петли действует магнитная сила, потому что они движутся в магнитном поле. Заряды в вертикальных проводах испытывают силы, параллельные проводу, вызывая токи.Но те, кто находится в верхнем и нижнем сегментах, ощущают силу, перпендикулярную проводу, которая не вызывает тока. Таким образом, мы можем найти наведенную ЭДС, рассматривая только боковые провода. Движущаяся ЭДС равна \ (ЭДС = Blv \), где скорость \ (v \) перпендикулярна магнитному полю \ (B \). Здесь скорость находится под углом \ (\ theta \) к \ (B \), так что ее составляющая, перпендикулярная \ (B \), равна \ (v \ sin {\ theta} \) (Рисунок \ (\ PageIndex { 2} \)). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна \ (emf = Blv \ sin {\ theta} \), и они направлены в одном направлении.Суммарная ЭДС вокруг контура тогда составляет

.

\ [emf = 2Blv \ sin {\ theta}. \ Label {23.6.4} \]

Это выражение допустимо, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью \ (\ omega \). Угол \ (\ theta \) связан с угловой скоростью соотношением \ (\ theta = \ omega t \), так что

\ [emf = 2Blv \ sin {\ omega t}. \ Label {23.6.5} \]

Итак, линейная скорость \ (v \) связана с угловой скоростью \ (\ omega \) соотношением \ (v = r \ omega \).Здесь \ (r = \ omega / 2 \), так что \ (v = \ left (w / 2 \ right) \ omega \) и

\ [emf = 2Bl \ frac {w} {2} \ omega \ sin {\ omega t} = \ left (w \ right) B \ omega \ sin {\ omega t}. \ Label {23.6.6} \ ]

Заметив, что площадь петли равна \ (A = w \), и учитывая \ (N \) петель, мы находим, что

\ [emf = NAB \ omega \ sin {\ omega t} \ label {23.6.7} \]

— это ЭДС , индуцированная в катушке генератора из \ (N \) витков и области \ (A \), вращающейся с постоянной угловой скоростью \ (\ omega \) в однородном магнитном поле \ (B \).Это также может быть выражено как

.

\ [emf = emf_ {0} \ sin {\ omega t}, \ label {23.6.8} \]

, где \ [emf_ {0} = NAB \ omega \ label {23.6.9} \] — максимальная (пиковая) ЭДС . Обратите внимание, что частота колебаний равна \ (f = \ omega / 2 \ pi \), а период равен \ (T = 1 / f = 2 \ pi / \ omega \). На рисунке \ (\ PageIndex {3} \) показан график зависимости ЭДС от времени, и теперь кажется разумным, что напряжение переменного тока является синусоидальным.

Рисунок \ (\ PageIndex {3} \): ЭДС генератора направляется в лампочку с показанной системой колец и щеток.График показывает зависимость ЭДС генератора от времени. \ (emf_0 \) — пиковая ЭДС. Период равен \ (T = 1 / f = 2π / ω \), где \ (f \) — частота. Обратите внимание, что сценарий E означает emf.

Тот факт, что пиковая ЭДС, \ (emf_0 = NABω \), имеет смысл. Чем больше катушек, тем больше их площадь и чем сильнее поле, тем больше выходное напряжение. Интересно, что чем быстрее вращается генератор (больше ω), тем больше ЭДС. Это заметно на велосипедных генераторах — по крайней мере, на более дешевых моделях.Один из авторов, будучи подростком, находил забавным ездить на велосипеде достаточно быстро, чтобы погасить его свет, пока ему не пришлось ехать домой без света одной темной ночью.

На рисунке показана схема, с помощью которой генератор может вырабатывать импульсный постоянный ток. Более сложные конструкции из нескольких катушек и разрезных колец могут обеспечить более плавный постоянный ток, хотя для создания постоянного тока без пульсаций обычно используются электронные, а не механические средства.

Рисунок \ (\ PageIndex {4} \): Разделенные кольца, называемые коммутаторами, в этой конфигурации создают импульсный выходной сигнал ЭДС постоянного тока.

Пример \ (\ PageIndex {2} \): расчет максимальной ЭДС генератора

Рассчитайте максимальную ЭДС, ЭДС0 генератора, который был предметом примера.

Стратегия

После определения \ (ω \), угловой скорости, \ (emf_0 = NABω \) можно использовать для определения \ (emf_0 \). Все остальные количества известны.

Решение

Угловая скорость определяется как изменение угла в единицу времени:

\ (ω = \ frac {Δθ} {Δt} \).2) (1,25T) (104,7рад / с) = 206V \).

Обсуждение

Максимальная ЭДС больше, чем средняя ЭДС 131 В, найденная в предыдущем примере, как и должно быть.

В реальной жизни электрические генераторы выглядят совсем иначе, чем на рисунках в этом разделе, но принципы те же. Источником механической энергии, вращающей катушку, может быть падающая вода (гидроэнергия), пар, образующийся при сжигании ископаемого топлива, или кинетическая энергия ветра. \ (\ PageIndex {5} \) показывает вид паровой турбины в разрезе; пар движется по лопастям, соединенным с валом, который вращает катушку внутри генератора.

Рисунок \ (\ PageIndex {5} \): Паровая турбина / генератор. Пар, образующийся при сжигании угля, ударяет по лопаткам турбины, вращая вал, соединенный с генератором. (кредит: Nabonaco, Wikimedia Commons)

Генераторы, показанные в этом разделе, очень похожи на двигатели, показанные ранее. Это не случайно. Фактически, двигатель становится генератором, когда его вал вращается. В некоторых ранних автомобилях стартер использовался в качестве генератора. В Back Emf мы подробнее рассмотрим действие двигателя как генератора.

Сводка

• Электрический генератор вращает катушку в магнитном поле, вызывая ЭДС, заданную как функцию времени на
.

\ (ЭДС = NABωsinωt, \)

где \ (A \) — площадь \ (N \) витка катушки, вращающейся с постоянной угловой скоростью ω в однородном магнитном поле \ (B \).

• Пиковая ЭДС \ (ЭДС_0) генератора

\ (emf_0 = NABω \).

Глоссарий

электрогенератор

устройство для преобразования механической работы в электрическую энергию; он индуцирует ЭДС, вращая катушку в магнитном поле

ЭДС, индуцированная в обмотке генератора

\ (emf = NABωsinωt \), где \ (A \) — площадь \ (N \) витка катушки, вращающейся с постоянной угловой скоростью \ (ω \) в однородном магнитном поле \ (B \), за период времени \ (t \)

пиковая ЭДС

(ЭДС_0 = NABω \) 0 = NABω

Авторы и авторство

• Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Физика — Электродвижущая сила — Бирмингемский университет

Электродвижущая сила (ЭДС) равна разности потенциалов на клеммах при отсутствии тока. ЭДС и разность потенциалов на клеммах ( В, ) измеряются в вольтах, но это не одно и то же. ЭДС ( ϵ ) — это количество энергии ( E ), обеспечиваемое батареей для каждого проходящего кулон заряда ( Q ).

Как рассчитать ЭДС?

ЭДС можно записать через внутреннее сопротивление батареи ( r ) где: ϵ = I (r + R )

Что из закона Ома, мы можем затем изменить это с точки зрения оконечного сопротивления: ϵ = В + Ir

ЭДС ячейки может быть определена путем измерения напряжения на ячейке с помощью вольтметра и тока в цепи с помощью амперметра для различных сопротивлений.Затем мы можем настроить схему для определения ЭДС, как показано ниже.

ЭДС и внутреннее сопротивление электрических элементов и батарей

Исследование ЭМП

Как закон Фарадея соотносится с ЭМП?

Закон Фарадея гласит, что любое изменение магнитного поля катушки будет индуцировать в катушке ЭДС (а следовательно, и ток). Он пропорционален минус скорости изменения магнитного потока ( ϕ ) (примечание N — количество витков в катушке).

Согласно закону Фарадея, общество извлекло выгоду из таких важных технологий, как трансформаторы, которые используются для передачи электроэнергии в национальной энергосистеме Великобритании, которая сейчас необходима в наших домах. Также он используется в электрических генераторах и двигателях, таких как плотины гидроэлектростанций, которые производят электричество, которое сейчас является неотъемлемой частью наших современных технологических потребностей. Текущий исследовательский проект MAG-DRIVE в Бирмингеме направлен на поиск способов разработки и улучшения материалов с постоянными магнитами, которые можно использовать в электромобилях следующего поколения.ЭМП также генерируется солнечными батареями, поэтому они важны для исследований в области возобновляемых источников энергии.

Лабораторные признания

Исследователи подкаста «In the Laboratory Confessions» рассказывают о своем лабораторном опыте в контексте практических экзаменов A Level. Эпизоды, которые касаются надлежащего использования цифровых инструментов (простое гармоническое движение), правильного построения принципиальных схем (удельное сопротивление в проводе) и использования источников питания постоянного тока (конденсаторов), имеют отношение к эксперименту по ЭДС, ниже вы можете услышать удельное сопротивление. в проводном подкасте.

Как мы интерпретируем наши данные?

По мере увеличения сопротивления переменного резистора величина тока будет уменьшаться. График зависимости напряжения от тока должен давать линейную зависимость, где градиент линии дает отрицательное внутреннее сопротивление ячейки ( -r ), а точка пересечения дает ЭДС (напряжение, при котором ток равен 0).

Выполнение нескольких измерений при разных значениях сопротивления даст больше точек на графике V-I, что сделает подбор более надежным.Также рекомендуется повторить измерения, так как ячейка будет постепенно стекать, что повлияет на показания. Во избежание разряда элемента / батареи ее следует отключать между измерениями. В качестве альтернативы в схему можно включить выключатель. Также не рекомендуется использовать аккумуляторные батареи, так как они имеют низкое внутреннее сопротивление.

Хотя этот эксперимент довольно прост, он поможет вам отличить конечную разницу от ЭДС, что может быть трудной для понимания концепцией учащимся.Поскольку люди все больше полагаются на электричество, исследования, связанные с ЭМП, важны для развития и технического прогресса электричества.

Следующие шаги

Эти ссылки предоставлены только для удобства и в информационных целях; они не означают одобрения или одобрения Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте. Бирмингемский университет не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок.Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы относительно его содержания.

.