Эффект холла лабораторная работа. Эффект Холла в полупроводниках: принцип работы, применение и лабораторные исследования — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое эффект Холла и как он проявляется в полупроводниках. Какие параметры можно определить с помощью эффекта Холла. Как проводятся лабораторные исследования эффекта Холла в полупроводниках. Каковы основные применения эффекта Холла в современной электронике.

Содержание

Физическая природа эффекта Холла

Эффект Холла — это явление возникновения поперечной разности потенциалов (ЭДС Холла) в проводнике с током, помещенном в магнитное поле. Он был открыт американским физиком Эдвином Холлом в 1879 году.

В чем заключается физическая сущность этого эффекта? Когда проводник с током помещается в магнитное поле, на движущиеся носители заряда начинает действовать сила Лоренца:

F = q[v x B]

где q — заряд носителя, v — его скорость, B — индукция магнитного поля.

Под действием этой силы носители заряда отклоняются к одной из граней проводника, создавая на ней избыточный заряд. На противоположной грани возникает заряд противоположного знака. В результате в направлении, перпендикулярном току и магнитному полю, возникает электрическое поле и соответствующая ему ЭДС Холла.

Особенности эффекта Холла в полупроводниках

В полупроводниках эффект Холла проявляется значительно сильнее, чем в металлах. Это связано с тем, что:

Концентрация носителей заряда в полупроводниках на несколько порядков меньше, чем в металлах
В полупроводниках могут присутствовать носители заряда обоих знаков — электроны и дырки
Подвижность носителей заряда в полупроводниках выше, чем в металлах

Благодаря этим особенностям, измерение эффекта Холла позволяет определить важнейшие параметры полупроводников:

Тип проводимости (электронная или дырочная)
Концентрацию основных носителей заряда
Подвижность носителей заряда

Постоянная Холла и ее связь с параметрами полупроводника

Основной характеристикой эффекта Холла является постоянная Холла R

H. Она связывает ЭДС Холла U_H с плотностью тока j и индукцией магнитного поля B:

U_H = R_HjB

Для полупроводников с одним типом носителей заряда постоянная Холла равна:

R_H = 1/nq

где n — концентрация носителей, q — элементарный заряд.

Зная постоянную Холла, можно определить концентрацию носителей заряда:

n = 1/R_Hq

А измерив дополнительно удельную проводимость σ, можно рассчитать подвижность носителей:

μ = R_Hσ

Методика измерения эффекта Холла в лабораторных условиях

Типичная схема для измерения эффекта Холла в полупроводниках включает в себя:

Образец полупроводника в форме тонкой пластины
Источник постоянного тока
Электромагнит для создания магнитного поля
Вольтметр для измерения ЭДС Холла

Порядок проведения измерений:

Через образец пропускается постоянный ток известной величины
Образец помещается в магнитное поле, перпендикулярное току
Измеряется возникающая ЭДС Холла
По измеренным значениям тока, магнитной индукции и ЭДС Холла рассчитывается постоянная Холла
На основе постоянной Холла определяются концентрация и подвижность носителей заряда

Применение эффекта Холла в современной электронике

Эффект Холла нашел широкое применение в различных областях электроники и измерительной техники:

Датчики Холла для измерения магнитных полей
Бесконтактные датчики тока
Датчики положения и перемещения
Измерители мощности в СВЧ-технике
Магнитометры
Измерители параметров полупроводников

Благодаря своей простоте и надежности, датчики на основе эффекта Холла широко используются в автомобильной электронике, промышленной автоматике, бытовой технике и других областях.

Эффект Холла в наноструктурах

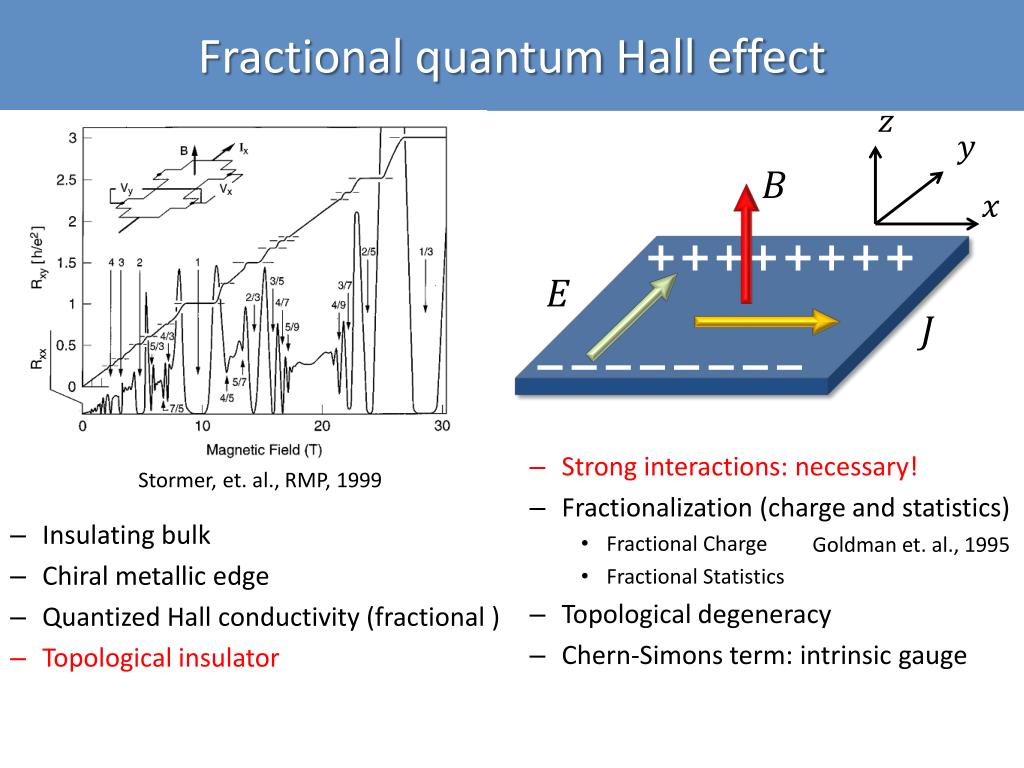
В последние годы активно изучается проявление эффекта Холла в низкоразмерных структурах — квантовых ямах, проволоках и точках. В таких системах наблюдается ряд интересных квантовых эффектов:

Целочисленный квантовый эффект Холла
Дробный квантовый эффект Холла
Спиновый эффект Холла

Исследование этих явлений позволяет глубже понять квантовую природу твердых тел и создавать новые типы электронных устройств.

Заключение

Эффект Холла является мощным инструментом для исследования свойств полупроводников и создания различных электронных устройств. Его изучение в лабораторных условиях позволяет студентам глубже понять физику твердого тела и освоить современные методы измерений. Дальнейшие исследования эффекта Холла в наноструктурах открывают новые перспективы как для фундаментальной науки, так и для практических приложений.

Лабораторная работа № 1 изучение эффекта холла в полупроводниках

Цель работы. Определить концентрацию и подвижность носителей заряда в Ge n- и р-типа, используя эффект Холла. Определить ширину запрещенной зоны Ge из температурной зависимости постоянной Холла в области собственной проводимости.

Рассмотрим действие магнитного поля на полупроводники помещенные в магнитное поле по которым протекает электрический ток. В перпендикулярное направлению движения зарядов. Пусть полупроводники имеют вид параллелепипеда сечением db. Электрическое поле (Е) направлено вдоль оси у, а магнитное поле (В) — вдоль оси: (рис.1.1). Под действием электрического поля носители заряда получают скорость направленного движения V_д — дрейфовую скорость: по полю — для дырок и против поля — для электронов.

Если носители заряда — дырки (рис. 1.1 а), то под действием магнитного поля B

z (силы Лоренца) они будут отклоняться на левую грань образца и на этой грани накопится положительный электрический заряд, а на противоположной грани останется нескомпенсированный отрицательный заряд.

Рис.1.1. Схема возникновения ЭДС Холла в полупроводниках с проводимостью: а — дырочная проводимость; б – электронная проводимость; в — смешанная проводимость

Если носители заряда — электроны (рис. 1.1 б), то под действием магнитного поля В (силы Лоренца) они будут также отклоняться на левую грань и накапливаться там, создавая отрицательный заряд, а на противоположной грани будет оставаться некомпенсированный положительный заряд.

Сила Лоренца F, действующая на движущийся электрон или дырку, перпендикулярна скорости движения электрона или дырки V_д и индукции магнитного поля В:

; (1.1)

нo

, (1.2)

поэтому

, (1.3)

где q_о — заряд электрона;

μ- дрейфовая подвижность;

m^* — эффективная масса носителя заряда;

— усредненное время релаксации.

То есть сила Лоренца не зависит от знака носителей заряда, а определяется только направлением полей Е и В или плотностью тока j и В. Для случаев, представленных на рисунках 1.1 а и б, сила F направлена вдоль оси х. Носители заряда — электроны и дырки — отклоняются в одну и ту же сторону, если их скорость определяется электрическим полем Е.

Если в переносе электрического тока участвуют и дырки и электроны (смешанная проводимость, рис. 1.1 в), то картина значительно усложняется. Если и подвижности и концентрация электронов и дырок одинаковы, то за счет взаимной компенсации электронов и дырок у боковых граней пластинки суммарный заряд будет равен 0. Если же это равенство не имеет места, т.е. концентрация или подвижность носителей одного знака больше, чем другого, то у боковых граней пластинки происходит частичная взаимная компенсация зарядов электронов и дырок и на гранях накапливаются заряды противоположных знаков, не равные нулю. Если противоположные грани полупроводникового образца заряжаются (рис.

1.1 а, б и в), то возникают поперечное по отношению к Е_у и B_z электрическое поле Холла Е_х и соответствующая разность потенциалов ЭДС U_x. Явление возникновения поперечной напряженности электрического поля Е_х в полупроводнике вследствие отклонения электронов или дырок проводимости, создающих электрический ток плотностью j в поперечном магнитном поле с индукцией В_z, называется эффектом Холла. Поле Е_х носит название поля Холла, а соответствующая ЭДС U_x — ЭДС Холла. Направление поля Холла Е_х зависит от знака носителей заряда, в рассматриваемых нами случаях (рис.1.1 а и б) Е_х направлено вправо в р-образце и влево в n-образце.

Численное значение ЭДС Холла для случая примесной проводимости можно получить исходя из следующих соображений. Процесс накопления заряда на боковых гранях (рис. 1.1 а и б) будет продолжаться до тех пор, пока возникающая при этом сила электрического поля Холла q_оЕ_х не уравновесит силу Лоренца F (см. формулу 1.1.):

, (1.4)

откуда для напряженности электрического поля Холла получаем выражение

(1.5)

Учитывая, что V_д=μЕ_у , a U_x=E_xb, для ЭДС Холла в однородном магнитном поле В получим выражение

. (1.6)

Выражая подвижность носителей заряда (электронов или дырок) через плотность тока j

_,(1.7)

и учитывая, что ,

получим выражение для ЭДС Холла в виде

, (1.8)

где d -толщина образца в направлении магнитного поля;

n — концентрация носителей заряда.

Обозначив

, (1.

получим для ЭДС Холла выражение

. (1.10)

Коэффициент пропорциональности R называется постоянной Холла или коэффициентом Холла.

При выводе выражения (1.10) не был учтен статистический характер распределения носителей заряда по скоростям, в результате чего ход рассуждений оказался неправильным по крайней мере по двум причинам:

— равенство (1.4) не может выполняться одновременно для всех электронов (дырок), имеющих различные по величине и по направлению скорости;

— в действительности стационарное состояние наступает не тогда, когда сила Лоренца уравновешивает силу электрического поля Холла для каждого электрона, чего вообще не может быть, а тогда, когда перестает накапливаться заряд на боковых гранях образца, т.е. когда ток, создаваемый холловским полем, компенсирует ток на боковую грань, создаваемый магнитным полем.

Более строгое математическое описание эффекта Холла в слабых магнитных полях основано на решении кинетического уравнения Больцмана. Менее строгий, но более наглядный вывод можно получить из условия стационарности, т.е. холловское поле Ех (рис. 1.1) должно создать ток, равный и противоположный току, создаваемому магнитным полем.

Для случаев, представленных на рис. 1.1, носители заряда — электроны и дырки — отклонятся в одну и ту же сторону, если их скорость определяется электрическим полем. В результате действия полей Е_у и B_z и столкновений электроны и дырки будут двигаться по траектории в виде прямой линии, усредняющей отрезки циклоид, под углом φ к полю Е_у, т.е. вектор плотности тока j будет повернут на угол φ относительно вектора Е_у (рис. 1.2 а и б), причем направление поворота зависит от знака носителей заряда. Таким образом должно протекать явление в неограниченном образце.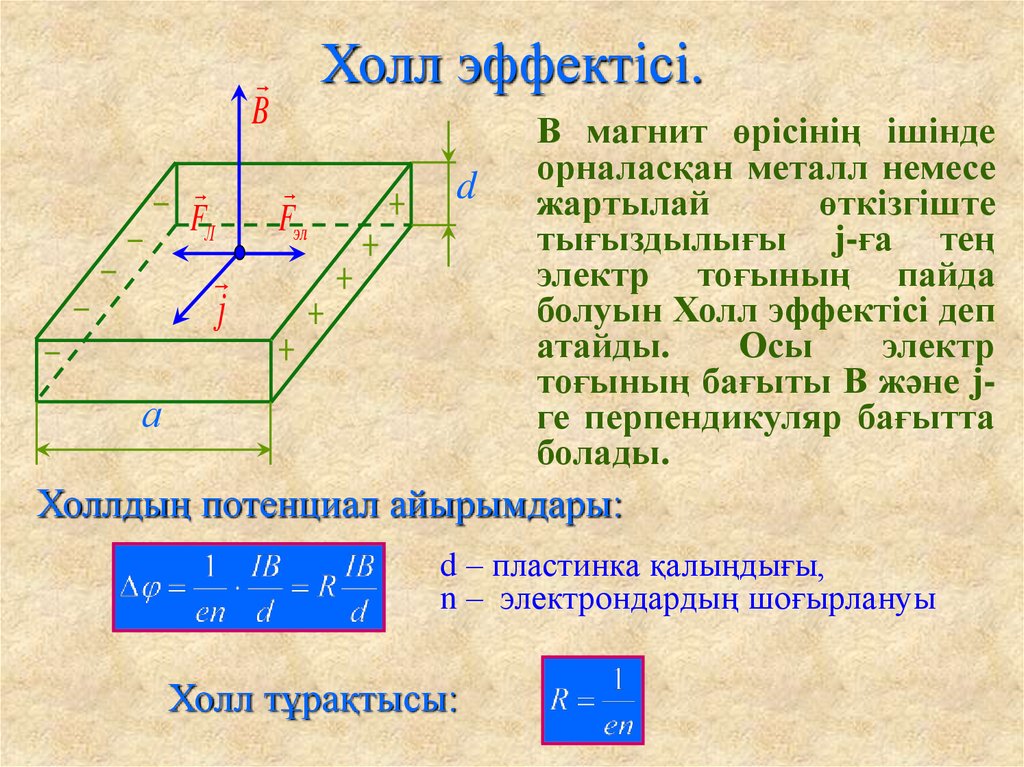

Если полупроводник имеет конечные размеры в направлении оси ОХ, то в результате смещения зарядов (электронов и дырок) происходит накопление заряда на противоположных гранях и возникает поле Холла Е_х, перпендикулярное и плотности тока j и магнитному полю В. При этом суммарное электрическое поле (Е=Е_х+Е_у) будет повернуто на угол φ_р или φ_n (рис. 1.2 в и г) относительно плотности тока j.

Рис. 1.2 Угол Холла в неограниченном (о, б) и ограниченном (в, г) полупроводниках

Плотность тока дырок по оси OY

. (1.11)

Под действием магнитного поля происходит отклонение вектора j_p от первоначального положения на угол φ_р (φ_р =μ В ) и создается составляющая тока по оси ОХ:

. (1.12)

Аналогичные выражения можно записать для плотности тока электронов:

; (1.13)

. (1.14)

Так как электроны и дырки отклоняются в одном направлении, то результирующий ток по оси ОХ равен их разности.

. (1.15)

Для плотности тока, создаваемого вдоль оси OX полем Е_х, можно записать выражение

j_x=σE_x=q₀E_x(μ_pp+μ_nn). (1.16)

Следовательно, для того чтобы заряды не накапливались, необходимо выполнение условия

j_x=j^x;(1. 17)

или

; (1.18)

. (1.19)

Выразив Е_y через плотность тока j, протекающего через полупроводник, учитывая, что, получим выражение для коэффициента Холла из формул (1.10) и (1.19):

. (1.20)

При строгом расчете с учетом распределения скоростей носителей заряда по закону Максвелла для невырожденных полупроводников

, (1.21)

где А_р и А_n — постоянные, зависящие от механизма рассеяния носителей заряда в полупроводниках, называемые Холл-факторами. В случае упругого рассеяния для любого механизма рассеяния A_n = А_р =А.

В атомной решетке длина свободного пробега носителей заряда не зависит от энергии, а коэффициент А имеет значение

В случае рассеяния на ионах примеси

А ≈ 1,93 .

В вырожденных полупроводниках, так же как и в металлах, в электропроводности принимают участие только электроны или дырки, находящиеся на самых высоких энергетических уровнях вблизи уровня Ферми, следовательно, в этом случае не нужно учитывать распределение электронов или дырок по скоростям, так как можно считать, что все носители заряда обладают одной и той же скоростью.

В металлах и вырожденных полупроводниках A=1.

Нетрудно убедиться, что в случае примесной проводимости, когда n=0 или р= 0, формула (1.21) примет вид:

для электронного полупроводника

^,(1.22)

для дырочного полупроводника

. (1. 23)

Если n = р (собственный полупроводник) и μ_p = μ_n , то в случае cобственной проводимости постоянная Холла равна нулю. Если n = р , а μ_p ≠ μ_n , то при А_n=A_p=A

. (1.24)

Согласно выражению (1.24), в области собственной проводимости знак ЭДС Холла соответствует знаку носителей, подвижность которых больше, т.е. знаку электронов.

Для вырожденных примесных полупроводников для коэффициента Холла имеем выражение (1.9).

Значение коэффициента Холла определяется свойством примесного образца: он обратно пропорционален концентрации носителей заряда, и его знак совпадает со знаком носителей заряда (см. формулы (1.22) и (1.23)). У электронных полупроводников R отрицателен, у дырочных — положителен.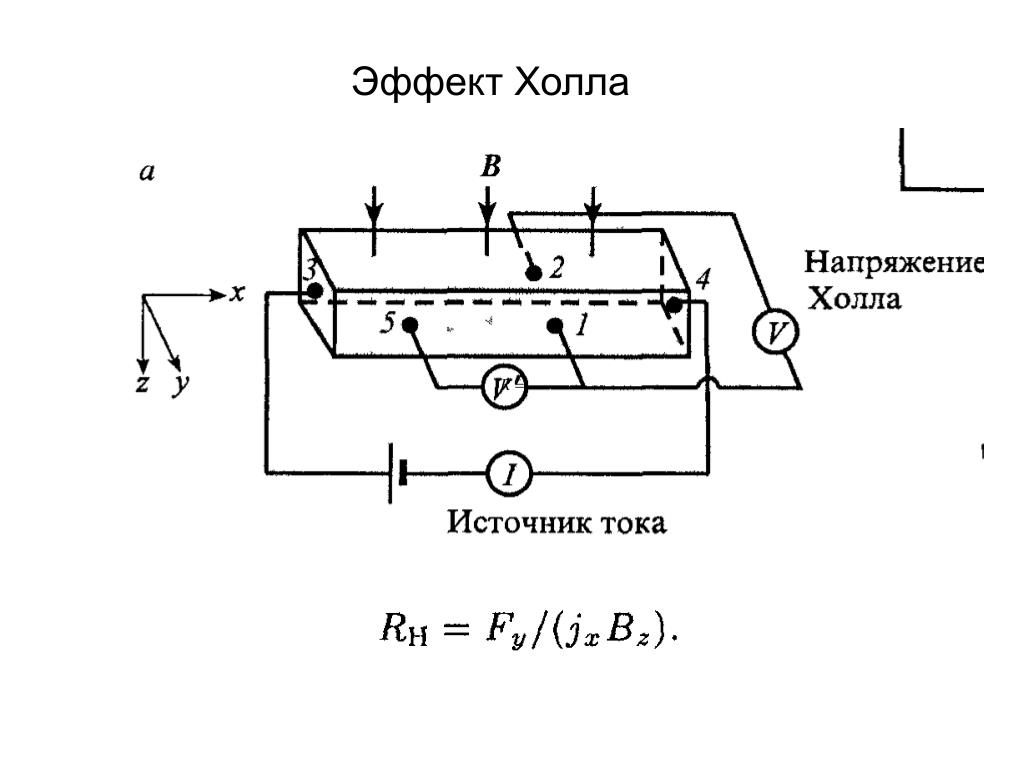 Определив знак R, можно найти тем самым знак носителей заряда или тип проводимости. Знак R определяется по знаку ЭДС Холла.

Измерив на опыте величины U_x, В, I, d, входящие в формулу (1.10), можно вычислить коэффициент Холла R, а зная R, можно найти из выражения (1.9) или из выражений (1.22) и (1.23) концентрацию свободных электронов или дырок в исследуемом примесном полупроводнике в области примесной проводимости.

Измеряя, кроме того, удельную электропроводность примесного полупроводника (σ=q₀n μ), можно определить подвижность носителей заряда:

μ=Rσ/A (1.25)

Таким образом, одновременные измерения удельной электропроводности и коэффициента Холла позволяют получить все основные сведения о носителях заряда примесного полупроводника в области примесной проводимости: знак, концентрацию, подвижность.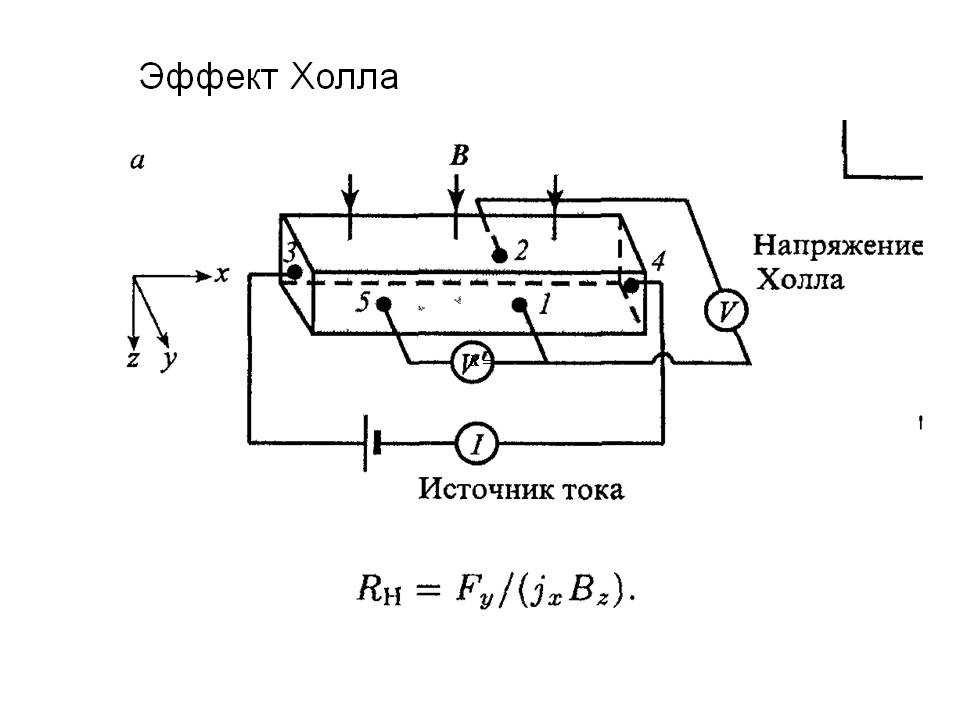

В случае смешанной проводимости одновременное измерение постоянной Холла и удельной электропроводности не дает достаточных данных для определения подвижности и концентрации электронов.

Лабораторная работа №16 эффект холла

Целью работы является выяснение физической природы эффекта Холла, определение постоянной Холла и типа проводимости исследуемого полупроводника, концентрации и подвижности носителей тока в полупроводнике.

Эффект Холла^¹ относится к числу гальваномагнитных явлений, связанных с влиянием магнитного поля на электрические свойства металлов и полупроводников.

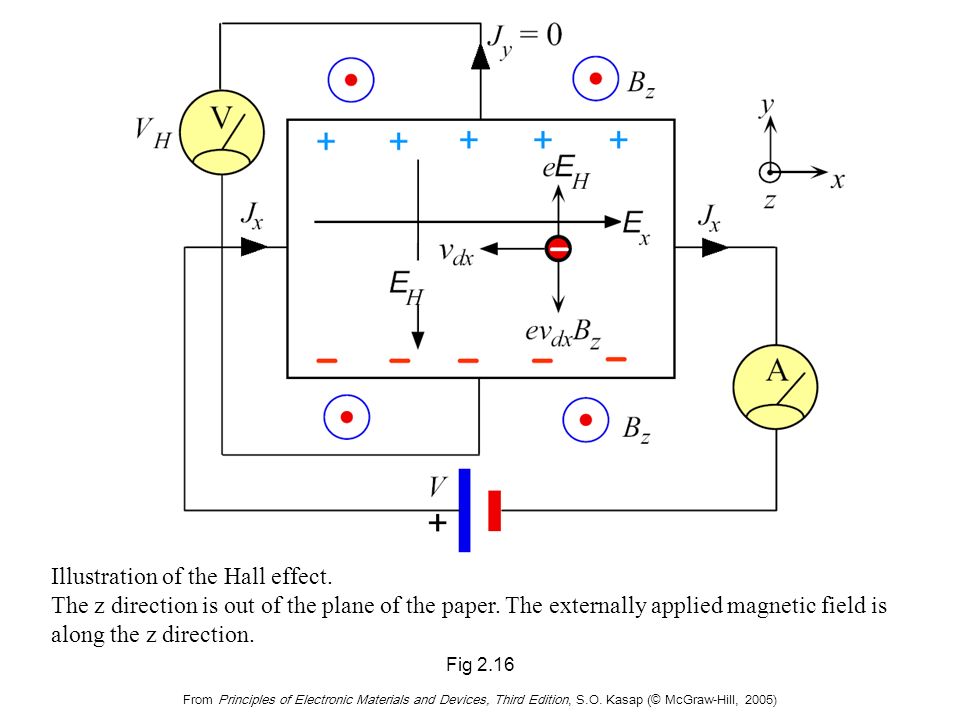
Рис. 16.1. Схема, поясняющая появление холловской разности потенциалов в металлическом проводнике

Эффект Холла заключается в следующем. Пусть по пластинке проводника, имеющего ширину а и толщину b, течет ток плотностью . Выберем на боковых сторонах пластины точки C и D, разность потенциалов между которыми равна нулю. Если эту пластину поместить перпендикулярно в магнитное поле с индукцией , то между точками C и D возникнет разность потенциалов U_H, которая называется холловской разностью потенциалов или ЭДС Холла. Опыт показывает, что в не слишком сильных полях выполняется следующее соотношение:

U_H=R_HBja (16.1)

Коэффициент пропорциональности R_H называется коэффициентом Холла или постоянной Холла.

Рассмотрим физическую природу эффекта Холла. Возникновение холловской разности потенциалов вызвано тем, что на электрический заряд q, движущийся в магнитном поле со скоростью, действует сила Лоренца:

. (16.2)

При сила Лоренца равна:

(16.3)

В случае если рассматриваемый проводник является металлом, то электрический ток вызван упорядоченным движением электронов^². Под действием силы Лоренца электроны отклоняются к внешней грани пластины (пунктир на рисунке 16.1), заряжая ее отрицательно. Противоположная грань, из-за оголения ионного остова, заряжается положительно. Это приводит к возникновению электрического поля, направленного от D к C, и равного:

, (16.4)

где U_H – разность потенциалов между точками С и D (э.д.с. Холла).

В свою очередь это электрическое поле действует на электроны с силой

, (16.5)

где q – заряд электрона, .

Под действием силы Лоренца плотность зарядов на внешних гранях пластины непрерывно увеличивается. В результате увеличивается и напряженность поперечного электрического поля. Когда напряженность этого электрического поля достигнет такого значения, что его действие на электроны будет уравновешивать силу Лоренца, установится стационарное распределение зарядов в поперечном направлении.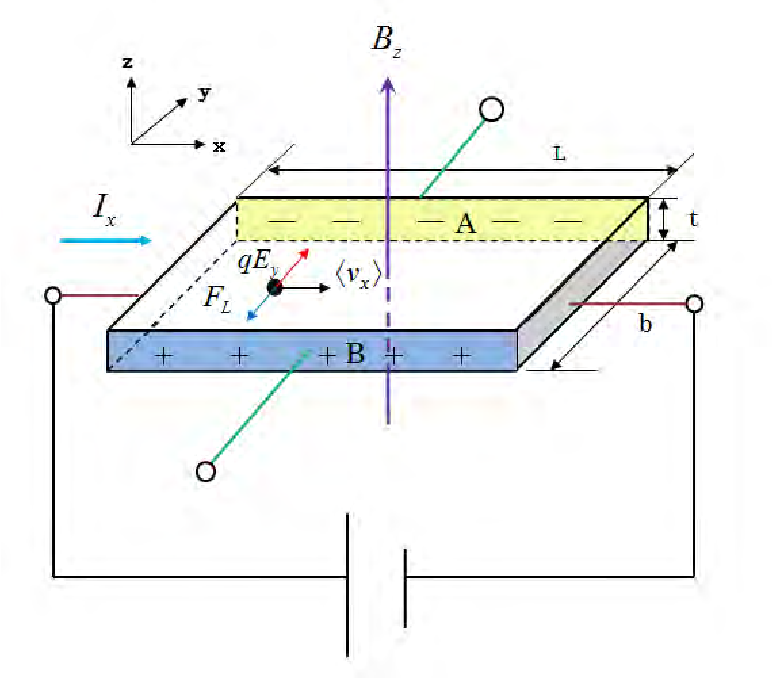 Из условия равновесия

(16.6)

найдем

. (16.7)

Здесь – средняя скорость упорядоченного движения электронов.

Умножив это соотношение на расстояние а между точками C и D, получим

. (16.8)

Учтем, что , и, следовательно,. Здесь j – плотность тока в проводнике, n – число носителей тока в единице объема (концентрация носителей тока).

Отсюда получим:

. (16.9)

Полученное выражение для холловской разности потенциалов, как видно, совпадает с выражением, полученным экспериментально. Постоянная Холла оказывается при этом равной

. (16.10)

Выражение для холловской разности потенциалов можно записать и по другому, используя вместо плотности тока j силу тока I ():

. (16.11)

Эффект Холла наблюдается не только в металлах, но и в полупроводниках. В полупроводниках по знаку эффекта (по знаку заряда боковых пластин) можно судить о принадлежности полупроводника к n– или p–типу (в полупроводниках n-типа знак носителей тока отрицателен, p-типа – положителен).

Т.о., по измеренной холловской разности потенциалов можно определить тип проводимости и концентрацию носителей тока в исследуемом материале.

Если наряду с постоянной Холла определить удельное сопротивление проводника, то можно вычислить еще такую важную характеристику, как подвижность носителей тока.

Подвижностью  называется отношение средней скорости упорядоченного движения носителей тока к величине напряженности электрического поляЕ, создающего ток

. (16.12)

Иными словами, подвижность носителей тока численно равна средней скорости упорядоченного движения носителей тока, которую они приобретают находясь в электрическом поле с напряженностью 1 В/м.

По закону Ома

. (16.13)

Здесь  – удельная электропроводность вещества, которая является обратной величиной удельному сопротивлению .

Если концентрация носителей тока n, заряд q, то плотность электрического тока через образец равна

. (16.14)

Подставив все это в выражение, определяющую подвижность носителей тока, получим:

. (16.15)

Примечание

Физическая природа эффекта Холла была выяснена на основе классической электронной теории металлов. Полученное выражение постоянной Холла позволило провести экспериментальную проверку этой модели для металлов в предположении, что концентрация электронного газа равна числу валентных электронов в единице объема.

Сравнение расчетных и экспериментальных значений постоянной Холла показало, что удовлетворительное согласие наблюдается только для элементов первой группы таблицы Менделеева. Значительно менее удовлетворительное согласие наблюдается для элементов других групп. Но основная трудность возникла в объяснении знака эффекта Холла для ряда металлов. Так как все металлы обладают электронной проводимостью, то, казалось бы, что знак эффекта Холла у всех металлов должен быть одинаков, так как под действием магнитного поля поток электронов отклоняется вполне определенным образом. Тем не менее, у ряда металлов (Be, Cd, Zn и др.) знак эффекта Холла оказался противоположным. Эта трудность была преодолена в квантовой теории твердого тела

В лабораторной работе эффект Холла изучается в полупроводнике, поскольку в них эффект Холла имеет в основном классическую природу и, следовательно, полученные выражения для постоянной Холла справедливы. Но тем не менее необходимо помнить следующее. Выражения для постоянной Холла, концентрации носителей тока, подвижности получены в предположении, что носители тока имеют одинаковую скорость движения, которая, к тому же, не изменяется при движении носителей тока в веществе. Кроме того, не учтено то обстоятельство, что при своем движении в реальном веществе носители тока испытывают столкновения и потому рассеиваются на примесях, колебаниях решетки. Учет этого обстоятельства приводит в классической модели эффекта Холла к появлению коэффициента А для постоянной Холла:

. (16.2)

Устройство для установки на эффекте Холла: особенности, процедура и наблюдение

Содержание

В настоящее время доступно несколько операторов и инструментов для внедрения практических знаний в лабораториях. Одним из таких инструментов, помогающих изучать эффект Холла в полупроводниках, является установка на эффекте Холла .

Это один из самых полезных инструментов наблюдения, используемых в лаборатории. Дайте нам подробную информацию о Установка на эффекте Холла здесь:

Установка на эффекте Холла — это инструмент для измерения эффекта Холла, который помогает изучать магнитные поля и токи в соленоидах и других линейных магнитопроводящих областях.

Но прежде чем мы узнаем больше об устройстве, давайте кратко расскажем об эффекте Холла.

Эффект Холла создает разность потенциалов (известную как напряжение Холла) на электрическом проводнике, движущемся перпендикулярно однородному магнитному полю. Эдвин Х. Холл — физик, открывший его в 1879 году.

Теперь на ум приходит вопрос: как возникает этот эффект?

Эффект Холла – это возникновение разности электрических потенциалов между двумя точками в магнитном поле из-за движения проводника в магнитном поле.

Может помочь измерить разность потенциалов, подав напряжение между этими точками и измерив результирующий ток.

Таким образом, прибор создает магнитное поле, в котором электрический ток течет перпендикулярно его направлению, и измеряет силу магнитного поля.

Из чего состоит установка на эффекте Холла ?

Основной целью установки на эффекте Холла является создание магнитного поля, которое может изменяться по величине и направлению путем подачи внешнего напряжения на его клеммы. Несколько компаний производят лабораторное оборудование, и они предлагают установку на эффекте Холла, которая обеспечивает всю структуру аппарата.

Эти настройки обычно состоят из:

Electromagnet
Блок измерения
Tesla и Gaussmeter
Зал зонд с духовкой
Струкция
Цифровые метеры
Power Power Supply
Цифровые метеры
Power Power Supply
Цифровые метеры
Power Power Power Supply
. Читайте также: Программное обеспечение Automation Studio: использование, функции, загрузка и руководство по установке Вот некоторые из стандартных функций, предлагаемых большинством производителей:
- Большая часть установок на эффекте Холла поставляется с полным набором в полупроводнике.
- Он также поставляется с блоком измерения источника постоянного тока с ЖК-дисплеем.
- Установка также поставляется с электромагнитом и датчиком InAs для измерения магнитного поля.
- Поставляется с германиевым кристаллом, печью и интерфейсом ПК для измерения тока зонда и напряжения Холла.
- Установка поставляется с Tesla M, Gauss M и т. д.
Схема установки на эффекте Холла
Объем обучения для установки на эффекте Холла (примеры экспериментов)
Изучение установки на эффекте Холла очень важно, в которой можно проводить множество экспериментов, таких как перемещение магнита к соленоиду и от него. .
Мы можем наблюдать, что количество силовых линий магнитного поля, проходящих через катушку, увеличивается и уменьшается в зависимости от изменения расстояния между магнитом и соленоидом.
Объем обучения представляет собой объем и пределы знаний учащегося и, следовательно, является одним из наиболее важных факторов в обучении. Вот некоторые из экспериментов, которые можно проводить с помощью этой установки:
- Определение коэффициента Холла полупроводниковых кристаллов, измерение напряжения Холла в зависимости от температуры образца, тока образца и плотности магнитного потока.
- Нахождение плотности и подвижности носителей заряда
- Рассчитать магнитное поле с помощью измерителя Гаусса и Тесла, входящего в комплект поставки.
- Откройте полюса электромагнита с помощью датчика Холла и гауссметра, входящих в комплект поставки
- Измерение напряжения Холла
- Оценить коэффициент Холла кристалла Ge ‘p-типа, а также подвижность частиц носителей заряда
- Изучить напряжение Холла как часть тока в постоянном магнитном поле, а также зависимость коэффициента эффекта Холла от температуры.
См. также: Комплект для обучения ПЛК: все, что вам нужно знать от производителей
Процедура эксперимента с установкой на эффекте Холла, наблюдение и расчет: батарея. Магнитное поле, создаваемое током, протекающим по виткам проволоки, индуцирует электрический ток в широкой части металла.
В присутствии магнитного поля электрический ток, протекающий по проводнику, перпендикулярному этому полю, испытывает силу, усиливающую ветер.
Эта сила действует на каждый электрон отдельно, не создавая макроскопического напряжения. Выходное напряжение этого усилителя будет пропорционально напряженности магнитного поля.
Так почему же это происходит?
Намагниченность ферромагнитных материалов заставляет пространство заполняться циркулирующими электрическими токами, известными как магнитные поля. Когда такой намагниченный материал присутствует во внешнем магнитном поле, сила, действующая на электроны внутри, создает ЭДС на его концах, что помогает пропускать ток через внешнюю цепь. Процедура эксперимента по установке эффекта Холла требует оборудования для исследования:
Инструменты должны иметь ассоциацию электромагнита, который должен подключаться к источнику питания.
Установка требует размещения датчика Холла на электромагните, и он должен подключаться между полюсными наконечниками электромагнита.
Плата и датчик Холла должны устанавливаться вертикально между полюсами электромагнита.
Наблюдение и расчет эксперимента на эффекте Холла:
Теперь вопрос, как это работает? Рабочий механизм эксперимента на эффекте Холла зависит от магнитного поля, создаваемого при пропускании тока через проволочную петлю. Изменяющееся магнитное поле индуцирует электрическое поле, которое создает напряжение на концах круга. Генерируемое напряжение может быть измерено для различных значений тока.
Если проводник с током находится в перпендикулярном магнитном поле, разность потенциалов будет генерироваться перпендикулярно магнитному полю и проводнику.
Это явление, которое происходит здесь, называется эффектом Холла. Эффект Холла имеет множество применений в физике твердого тела и полупроводниках, где он определяет как знак, так и плотность носителей заряда.
Расскажите нам больше об эксперименте с эффектом Холла с помощью примера здесь:
Рассмотрим проводник прямоугольной формы толщиной «t», удерживаемый в плоскости XY. Электрическое поле прикладывается в направлении X с помощью генератора постоянного тока (CCG), так что ток «I» протекает через образец.
Пусть w — ширина модели, t — ее толщина. Здесь мы предполагаем, что магнитное поле «i» присутствует вдоль отрицательной оси z.
В этом случае он генерирует электрическое поле в плоскости Xz, которое ускоряет носители заряда (скажем, электроны) в направлении Y. Это вызывает накопление носителей заряда на верхней кромке образца.
В результате внутри проводника возникает электрическое поле Ey, вызывающее колебания напряжения вдоль оси Y пропорционально плотности тока I и площади A, заключенной в ограничивающих стенках.
Это явление, также известное как эффект Холла или напряжение Фарадея Холла, представляет собой переходную разницу напряжений между контактами, покрывающими обе стороны узкого канала, по которому протекает ток «i». Между двумя пластинами конденсатора присутствует напряжение, и заряды на нижней пластине будут двигаться к положительному выводу.
Это движение заряда создает электрическое поле с потенциалом, который можно измерить с помощью вольтметра.
Эксперимент на эффекте Холла Заключение:
Эксперимент на эффекте Холла помогает наблюдать явления магнетизма и электричества. При исследовании стержневой магнит должен крепиться к электромагниту, который при протекании через него тока создает замкнутую цепь, и этот ток отклоняет стрелку вольтметра.
Как мы уже знаем, эффект Холла создает разность потенциалов на электрическом проводнике, поперечную электрическому току в проводнике, когда он вступает в контакт с магнитным полем.
Это происходит из-за относительного движения между носителями (носителями заряда) и электронами, которое заставляет их создавать электродвижущую силу (ЭДС) в направлении, перпендикулярном как их скорости, так и магнитному полю.
Эффект Холла помогает продемонстрировать эксперимент, поместив полупроводник с приложенным напряжением на его клеммах. Знак носителей заряда в токе противоположен знаку приложенного напряжения. После этого на полупроводник будет действовать сила, и она обусловлена этим накоплением заряда.
Эксперимент на эффекте Холла – производитель, поставщик, экспортер:
Когда мы просматриваем Интернет, мы можем найти множество производителей и экспортеров, которые поставляют лабораторное оборудование. Но основная проблема, с которой приходится сталкиваться, заключается в том, где найти поставщика, который предлагает высококачественный продукт по разумной цене.
Tesca global — это компания, в которой вы можете рассчитывать на поставку оборудования из материалов мирового класса по конкурентоспособной цене. Tesca является надежным поставщиком оборудования для создания эффекта Холла.
Они известны как самый надежный и известный производитель, экспортер и поставщик установки на эффекте Холла, состоящей из трех основных частей:
1) Датчик Холла
2) Датчик Холла
3) Генератор магнитного поля.
Компания предлагает широкий спектр решений для измерения эффекта Холла. Изделия отличаются высокой точностью, долговечностью и прочной конструкцией, способной выдерживать суровые условия окружающей среды с колебаниями температуры. Так что приобретите подходящий аппарат с Tesca Global, выбрав правильный вариант в соответствии с вашим бюджетом!
Узнайте больше
Читайте также: Производители лабораторного оборудования: Tesca Global
Team Tesca
Вклад в достижение Целей устойчивого развития Организации Объединенных Наций в области качественного образования, промышленности, инноваций и инфраструктуры.
Просмотреть все сообщения
Расширенная лаборатория — Эффект Холла: Эксперимент на эффекте Холла
Расширенная лаборатория — Эффект Холла: Эксперимент на эффекте ХоллаГлавная Следующий Предыдущий Содержание

2. Эксперимент на эффекте Холла
В этой части описывается аппарат на эффекте Холла, а также процедуры компьютерного управления и сбора данных.
2.1 Список приборов и оборудования

Рисунок 1: Аппарат на эффекте Холла.

Рисунок 2: Деталь датчика Холла
Оборудование
Магнит с водяным охлаждением Alpha и блок питания (Перед включением питания включите воду. Не превышайте ток магнита 10 А).
Зонд Холла, арсенид индия (InAs), красный и черный токоподводы, зеленый и белый провода Холла для измерения напряжения, устанавливается в печь, на подставке.
Дополнительный датчик Холла для исследования со штативом.
Печь для нагрева датчика Холла.
Цифровой термометр с термопарой и дисплеем.
Источник питания постоянного тока для подачи тока на датчик Холла; настроить только регулятор «напряжение»; ток датчика не должен превышать 0,4 А.
Variac для управления переменным током в духовке; заблокирован для ограничения температуры до 100°C.
Амперметр для измерения тока датчика Холла.
Вольтметр с высоким входным сопротивлением для измерения напряжения Холла.
Магнитный компас для определения направления магнитного поля.
Гауссметр для измерения магнитного поля.
Зонд на эффекте Холла и калиброванный блок управления с подставкой для зонда.
Компьютер и плата сбора данных.
2.2 Меры предосторожности
Персональный
Источник питания магнита может обеспечивать большие токи при опасном уровне напряжения; не прикасайтесь к открытым контактам катушки магнита.
Духовка нагревается.
Кабели переменного тока от Variac к духовке могут быть опасны; они не должны быть выставлены напоказ.
Устройство
Никогда не прерывайте внезапно и не подавайте питание на большой магнит. Большие индуктивные скачки напряжения могут повредить изоляцию. Начните с установки элементов управления на нулевой ток и постепенно увеличивайте ток. При выключении плавно уменьшите ток до нуля и затем выключите.
Включите воду перед включением катушки магнита.
Не превышайте ток магнита 10 А.
Не превышайте ток датчика Холла 0,4 А.
Не превышайте температуру духовки 100°C (еще несколько градусов на короткое время не причинят вреда).
Не оставляйте ток магнита на высоком значении в течение времени сверх минимально необходимого для сбора данных — это влияет на монитор (очевидно).
2.3 Процедура
Шаги, перечисленные ниже, описывают процедуру получения данных с помощью компьютера для исследования как эффекта Холла, так и эффекта магнитосопротивления. Полные наборы данных должны быть получены при трех температурах: комнатной температуре, между 65-70°C и 100°C. Раздел «Примечания» содержит рисунок, который поможет найти подходящие настройки вариака. Температура должна достичь равновесия, прежде чем вы начнете снимать данные.
Данные Этапы сбора данных об эффекте Холла:
Измерьте напряжение Холла (VHall) для каждого из четырех токов зонда (0,1, 0,2, 0,3 и 0,4 А) для каждого из пяти магнитных токов (1,3,5,7 и 9 А). При каждом магнитном токе используйте гауссметр для определения магнитного поля. Для проведения полевых измерений датчик Холла — печь — термометр необходимо снять и заменить датчиком гауссметра. Сборка датчика Холла и печи не очень прочная, обращайтесь с ней осторожно.
Данные Этапы сбора данных об эффекте магнитосопротивления:
Для каждого из пяти магнитных токов, перечисленных выше, и нулевой напряженности магнитного поля (снимите датчик Холла с магнита, чтобы свести к минимуму любые поля рассеяния) измерьте сопротивление датчика Холла.
Процедура управления аппаратом и сбора данных прогоны
Прежде чем что-либо делать, включите охлаждающую воду, чтобы магнит не перегревался!
Включите компьютер. (пароль для входа «taisgood»).
Запустите программу Hall Effect, показанную на рабочем столе.
Установите желаемую температуру с помощью регулятора температуры. Не забудьте записать это значение.
Убедитесь, что «Магнитный ток» на экране компьютера установлен на ноль ампер.
На источнике питания для «Магнитного тока» установите переключатель в положение «включено».
Оба экрана на дисплее «Magnetic Current» должны показывать ноль (или что-то очень близкое к этому)
Вернуться к компьютеру: С помощью мыши наведите указатель мыши на кнопку в верхнем левом углу экрана (чуть ниже слово «Файл» в строке меню), у которого есть всплывающее окно с надписью «Выполнять непрерывно». Нажмите на эту кнопку.
Дождитесь появления экрана ошибки. Нажмите «Продолжить».
Примечание: это сообщение об ошибке не означает ничего важного, так что не беспокойтесь об этом.
Нажмите один раз на кнопку «Сделай это!» кнопку так, чтобы загорелась зеленая лампочка на кнопке.
Увеличьте магнитный ток до желаемого значения в амперах. (не забудьте записать значение магнитного поля на гауссметре) (это понадобится позже) (также обратите внимание на единицы измерения на гауссметре. В лабораторной части анализа требуется, чтобы они были в теслах)
Примечание. Посмотрите на правый экран блока питания, чтобы увидеть, как «Магнитный ток» увеличивается по мере увеличения магнитного тока на экране компьютера. Очевидно, это ток, протекающий через магнит. Не повышайте его слишком быстро или выше 9 ампер, потому что блок питания отключится и заблокируется. Если это произойдет, выключите источник питания на мгновение и вернитесь к шагу 5.
Перейдите к экрану меню «Получить кривую ВАХ» и установите параметры для эксперимента.
Установите максимальный ток на 0,4 А
Установите значение тока для увеличения с шагом 0,1 А
Установите число для усреднения эксперимента равным 20 (чем выше это число, тем точнее данные, но тем медленнее будет выполняться эксперимент… 20 — это хороший номер).
При отображении экрана меню «Получить кривую ВАХ» нажмите «Сделать это!» дважды, чтобы свет погас, а затем снова загорелся.
Подождите, пока компьютер выполнит тест.
Наблюдайте за красным дисплеем «Ток и напряжение датчика» (куда подключены красный и черный провода), пока компьютер выполняет тест. Обратите внимание, как программа останавливается на каждом шаге тока и выполняет указанное количество измерений при этом количестве ампер. Также следите за изменением показаний напряжения Холла (где подключены белый и зеленый провода), когда компьютер выполняет тест.
После того, как программа выполнила тест, сохраните файл в папке на компьютере.
(Когда вы позже запустите файл для проведения анализа в лабораторной работе, его следует открыть в Microsoft Excel или какой-либо другой программе подобного типа, которая поместит данные в таблицы и столбцы. После открытия четыре столбца данных с пятью каждая строка будет в сохраненном файле:
Первый столбец — это напряжение Холла в вольтах.
Во втором столбце указан соответствующий ток зонда в амперах. Он должен читаться от 0,0 до 0,4 с шагом 0,1.
Третий столбец представляет собой сопротивление датчика Холла в Омах, которое представляет собой напряжение на датчике, деленное на соответствующий ток датчика (столбец 4, разделенный на столбец 2).
Четвертая колонка представляет собой напряжение на датчике Холла (напряжение датчика) в вольтах из-за носителей тока (т. е. напряжение на красной цифровой индикации тока датчика Холла).

Нажмите на красный знак остановки («Прервать выполнение») в верхней левой строке меню (рядом с кнопкой «Выполнить непрерывно» из шага 6). Если этого не сделать, эксперимент будет продолжаться непрерывно и несколько раз будет запрашиваться сохранение данных.
Поздравляем, вы провели свой первый тест.
Вернуться к первому экрану меню.
Вернитесь к шагу 8, чтобы запустить еще один тест, установив новую температуру, магнитный ток или и то, и другое на желаемые значения.
2.4 Примечания
Нуль гауссметра необходимо контролировать и корректировать по мере необходимости. Для этого отодвиньте щуп гауссметра подальше от магнита и проверьте ноль шкалы, которая используется в настоящее время. Ноль может смещаться при изменении масштаба. Чтобы обнаружить влияние поля рассеяния, наблюдайте за нулем при изменении ориентации зонда примерно на 9°.0 градусов.
Во время эксперимента исследуйте геометрию установки. Обратите внимание на направление магнитного поля, ток зонда и напряжение Холла, это поможет в анализе. В этом вам поможет дополнительный зонд (см. также рис. 2).
Постоянно используйте блоки MKSC. Магнитные поля должны быть выражены в теслах (T = Ns/mC = кг/Cs). В литературе по физике магнитные поля часто выражают в гауссах, где 1 Тл = 10 000 гаусс. Обратите внимание на единицы измерения на гауссметре. Всегда записывайте данные в тех же единицах, которые используются измерительным прибором, но с единицами, указанными в паспорте. Сделайте необходимые преобразования позже.
Ом = Js/C ² ; единицы проводимости (Ом-м) ^-1 .
Используйте рис. 3, чтобы определить правильную настройку Variac для требуемой температуры зонда:

Рисунок 3.