Как работают цепи переменного тока с активным сопротивлением. Какие законы электротехники применяются для их анализа. Каковы основные характеристики и особенности таких цепей.
Понятие активного сопротивления в цепях переменного тока
Активное сопротивление в цепях переменного тока представляет собой сопротивление, которое преобразует электрическую энергию в тепловую. Это происходит из-за столкновения свободных электронов с атомами проводника при протекании тока.
Основные свойства активного сопротивления в цепях переменного тока:
- Не зависит от частоты тока
- Не создает сдвига фаз между током и напряжением
- Рассеивает электрическую энергию в виде тепла
- Измеряется в омах (Ом)
В отличие от реактивных элементов (индуктивность, емкость), активное сопротивление не накапливает энергию магнитного или электрического поля.
Закон Ома для цепи переменного тока с активным сопротивлением
Для цепи переменного тока с активным сопротивлением справедлив закон Ома, аналогичный закону для цепей постоянного тока:

I = U / R
где:
- I — действующее значение силы тока (А)
- U — действующее значение напряжения (В)
- R — активное сопротивление (Ом)
Закон Ома для мгновенных значений:
i(t) = u(t) / R
где i(t) и u(t) — мгновенные значения тока и напряжения соответственно.
Векторная диаграмма и фазовые соотношения
В цепи переменного тока с чисто активным сопротивлением ток и напряжение совпадают по фазе. Это означает, что:
- Векторы тока и напряжения направлены в одну сторону
- Максимумы и минимумы тока и напряжения наступают одновременно
- Угол сдвига фаз между током и напряжением равен нулю
Векторная диаграмма для такой цепи выглядит следующим образом:
«` «`Здесь вектор напряжения U и вектор тока I совпадают, что отражает отсутствие сдвига фаз между ними.
Мощность в цепи переменного тока с активным сопротивлением
В цепи с активным сопротивлением вся потребляемая энергия преобразуется в тепло. Мощность, выделяемая на активном сопротивлении, называется активной мощностью.
Мгновенное значение мощности:

p(t) = u(t) * i(t) = Um * Im * sin2(ωt)
Среднее значение мощности (активная мощность):
P = U * I = I2 * R = U2 / R
где U и I — действующие значения напряжения и тока.
Коэффициент мощности для цепи с чисто активным сопротивлением равен единице:
cos φ = 1
Это означает, что вся потребляемая энергия преобразуется в полезную работу (в данном случае — в тепло).
Временные диаграммы тока, напряжения и мощности
Графики мгновенных значений тока, напряжения и мощности для цепи с активным сопротивлением имеют следующий вид:
«` «`На этой диаграмме:
- Синяя кривая — напряжение u(t)
- Красная кривая — ток i(t)
- Зеленая кривая — мгновенная мощность p(t)
Как видно из графиков, кривые тока и напряжения совпадают по фазе. Мгновенная мощность всегда положительна и имеет удвоенную частоту по сравнению с током и напряжением.
Особенности расчета цепей переменного тока с активным сопротивлением
При расчете цепей переменного тока с активным сопротивлением следует учитывать следующие особенности:

- Используются действующие значения тока и напряжения
- Применяются те же методы расчета, что и для цепей постоянного тока (законы Ома и Кирхгофа)
- Не учитывается сдвиг фаз между током и напряжением
- Мощность рассчитывается как произведение действующих значений тока и напряжения
Пример расчета: определить ток в цепи с активным сопротивлением R = 100 Ом при приложенном напряжении U = 220 В.
Решение:
I = U / R = 220 В / 100 Ом = 2.2 А
Применение цепей переменного тока с активным сопротивлением
Цепи переменного тока с активным сопротивлением широко используются в различных областях техники и быта:
- Электрические нагреватели и обогреватели
- Лампы накаливания
- Электрические плиты и духовки
- Резисторы в электронных схемах
- Электрические водонагреватели
В этих устройствах активное сопротивление используется для преобразования электрической энергии в тепловую.
Сравнение с цепями, содержащими реактивные элементы
В отличие от цепей с чисто активным сопротивлением, цепи с реактивными элементами (индуктивностью и емкостью) имеют следующие особенности:

- Наличие сдвига фаз между током и напряжением
- Зависимость сопротивления от частоты
- Наличие реактивной мощности
- Более сложные методы расчета (использование комплексных чисел)
Сравнительная таблица:
| Характеристика | Активное сопротивление | Индуктивность | Емкость |
|---|---|---|---|
| Сдвиг фаз | 0° | +90° | -90° |
| Зависимость от частоты | Нет | Прямая | Обратная |
| Тип мощности | Активная | Реактивная | Реактивная |
Заключение
Цепи переменного тока с активным сопротивлением являются простейшим типом цепей переменного тока. Они характеризуются отсутствием сдвига фаз между током и напряжением, преобразованием всей электрической энергии в тепловую и относительной простотой расчета. Понимание принципов работы таких цепей является основой для изучения более сложных цепей переменного тока, содержащих реактивные элементы.
4. Электрическая цепь с активным сопротивлением
Электрический ток проводимости в металлах представляет собой направленное движение свободных электронов. Скорость электронов и направление их движения определяется значением и полярностью приложенного к проводнику напряжения.
При движении электроны сталкиваются с атомами проводника, и их кинетическая энергия превращается в тепловую энергию, которая идет на нагрев проводника и рассеивание в окружающую среду. Этот активный процесс является необратимым и количественно определяется сопротивлением R. Поэтому его называют активным сопротивлением. Как правило, различают активное и омическое сопротивления. При рассмотрении цепей переменного тока сопротивление R называют активным, так как оно больше сопротивления постоянному току. При рассмотрении цепей постоянного тока сопротивление R называют омическим.
(Если через один и тот же проводник
пропускать переменный и постоянный
ток, то для того, чтобы выделилось одно
и то же количество теплоты, величина
переменного тока должна быть больше,
чем постоянного).
Элементы электрической цепи, обладающие только активным сопротивлением R, называют резисторами. Все элементы электрической цепи – провода, обмотки, реостаты – обладают активным сопротивлением, все они нагреваются при пропускании тока.
Кроме активного сопротивления существует еще индуктивное, емкостное, реактивное, полное.
Пусть к зажимам цепи с активным сопротивлением R приложено напряжение источника питания.
По закону Ома для мгновенных значений для этой цепи
, отсюда
– закон Ома для амплитудных значений.
Разделив левую и правую части этого выражения на , получим
– закон Ома для действующих значений
( , – связь действующего значения с амплитудным).
– закон Ома в комплексной форме.
Комплексное действующее значение тока .
Поскольку ток и напряжение совпадают по фазе, как видно из формул для мгновенных значений, то можно представить изменение тока и напряжения на временной диаграмме следующим образом:
5.
 Мощность в цепи с активным сопротивлением
Мощность в цепи с активным сопротивлением Мгновенная мощность
Мощность определяет скорость расхода энергии, и для цепей переменного тока также является переменной величиной.
Т.к. , то
Из формулы видно:мгновенная мощность остается всегда положительной и колеблется около уровня UI (см. график).
С энергетической точки зрения, положительная мощность – это мощность, которая поступает из генератора в нагрузку, а отрицательная – та, которая возвращается обратно. Первая мощность называется активной, вторая – реактивной. Через активное сопротивление проходит только активная мощность.
Средняя мощность
Для определения расхода энергии за длительное время пользуются средним значением мощности. Такую мощность еще называют активной
P = UI.
Активная мощность
обозначается [P],
единица измерения Ватт (Вт), (кВт), (МВт).
6. Электрическая цепь с индуктивностью
Индуктивность можно определить как меру магнитной инерции элемента в отношении электромагнитного поля. По смыслу индуктивность в электротехнике можно сравнить с массой в механике. Чем больше индуктивность элемента, тем медленнее и тем большую энергию магнитного поля он запасает.
Индуктивностью, индуктивным сопротивлением обладают в разной мере все элементы электрической цепи переменного тока. Особенно велика она у обмоток или катушек, состоящих из большого числа витков. В цепях постоянного тока индуктивность равна нулю, поскольку ток не меняется со временем и проявляется лишь при переходных режимах.
Рассмотрим электрическую цепь, состоящую из источника и катушки индуктивности.
|
Под действием синусоидального напряжения в цепи протекает синусоидальный ток |
В результате этого
вокруг катушки возникает переменное
магнитное поле, и в катушке наводится
э. д.с. самоиндукции.
д.с. самоиндукции.
Если R = 0, то напряжение источника целиком идет на уравновешивание этой э.д.с. Следовательно,
Т.к. по закону электромагнитной индукции , то
или , где .
Сопоставив выражения для мгновенных значений тока и напряжения, можно видеть, что напряжение в цепи с индуктивностью опережает по фазе ток на .
Т.О, временная диаграмма для тока и напряжения выглядит:
|
Векторная диаграмма тока и напряжения для цепи с индуктивностью |
,
– индуктивное сопротивление цепи;
: видно, что с увеличением частоты увеличивается индуктивное сопротивление.
Закон Ома для цепи с индуктивностью
Закон Ома для амплитудных значений для цепи с индуктивностью: .
Разделив левую и
правую части этого выражения на
,
получим закон Ома для действующих
значений
.
Закон Ома в комплексной форме
,
j обеспечивает сдвиг фаз на между I и U на комплексной плоскости.
| Цепь переменного тока с активным и индуктивным сопротивлениями
Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально емкости.
Таким образом. емкостное сопротивление:
где Хс — емкостное сопротивление, ом;
ώ — угловая частота переменного тока, рад/сек;
С —емкость, ф.
Известно, что угловая частота . Поэтому емкостное сопротивление можно определить так:
где f— частота переменного тока, гц.
Если включенная емкость измеряется в микрофарадах, то емкостное сопротивление
Если емкость измеряется в пикофарадах, то
Следует подчеркнуть, что имеется существенное различие между емкостным и активным сопротивлениями. Как известно, активная нагрузка безвозвратно потребляет энергию генератора переменного тока.
Если же к источнику переменного тока присоединена емкость, то, как было рассмотрено выше, энергия генератора расходуется при заряде конденсатора на создание электрического поля между пластинами и возвращается обратно генератору при разряде конденсатора.
Следовательно, емкостная нагрузка не потребляет энергию генератора, а в цепи с емкостью происходит «перекачивание» энергии из генератора в конденсатор и обратно. По этой причине емкостное сопротивление, как и индуктивное, называется реактивным.
Пример. Конденсатор емкостью С=2 мкф включен в цепь переменного тока, частота которого 50 гц. Определить:
1) его емкостное сопротивление при частоте f=50 гц;
2) емкостное сопротивление этого конденсатора переменному току, частота которого 500 гц.
Решение. Емкостное сопротивление конденсатора переменному току при частоте f=50 гц
При частоте f=500 гц
Из приведенного примера видно, что емкостное сопротивление конденсатора уменьшается с повышением частоты, а с уменьшением частоты переменного тока емкостное сопротивление возрастает.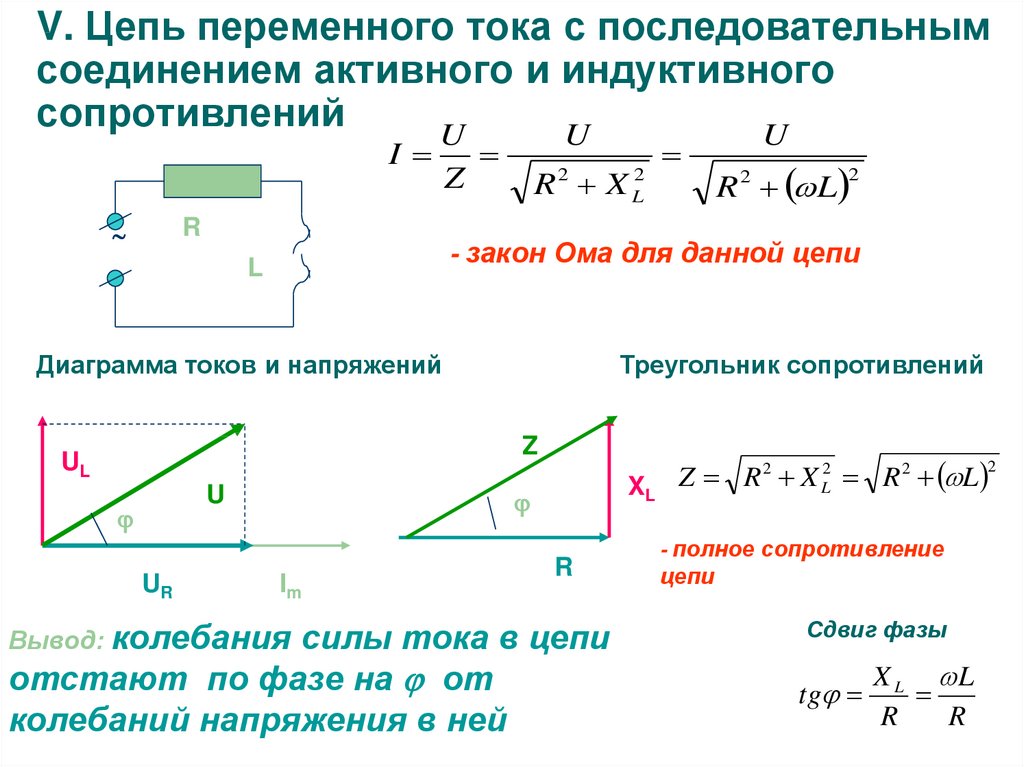 Для постоянного тока, когда напряжение на зажимах цепи не изменяется, конденсатор практически обладает бесконечно большим сопротивлением и поэтому он постоянного тока не пропускает.
Для постоянного тока, когда напряжение на зажимах цепи не изменяется, конденсатор практически обладает бесконечно большим сопротивлением и поэтому он постоянного тока не пропускает.
§ 55. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ И ИНДУКТИВНЫМ СОПРОТИВЛЕНИЯМИ
Любая проволочная катушка, включенная в цепь переменного тока, обладает активным сопротивлением, зависящим от материала, Длины и сечения проволоки , и индуктивным сопротивлением, которое зависит от индуктивности катушки и частоты переменного тока, протекающего по ней (ХL=ωL=2πfL). Такую катушку можно рассматривать как приемник энергии, в котором активное и индуктивное сопротивления соединены последовательно.
Рассмотрим цепь переменного тока, в которую включена катушка индуктивности (рис. 56, а) с активным r и индуктивным ХL сопротивлением. Падение напряжения на активном сопротивлении
Падение напряжения на индуктивном сопротивлении
Построим векторную диаграмму тока и напряжения (рис. 56, б) для рассматриваемой цепи.
56, б) для рассматриваемой цепи.
Отложим по горизонтали вектор тока I в выбранном масштабе. Известно, что ток и напряжение в цепи с активным сопротивлением совпадают по фазе, поэтому вектор падения напряжения на активном сопротивлении откладываем по вектору тока.
В цепи с индуктивностью ток отстает от напряжения на угол =90°. Поэтому вектор падения напряжения на индуктивном сопротивлении откладываем на диаграмме вверх под углом 90° к вектору тока.
Для определения общего напряжения, приложенного к цепи, сложим векторы Ua. и UL Суммой этих векторов будет диагональ параллелограмма — вектор U. Треугольник АОБ, стороны которого выражают соответственно напряжения Uа, UL и общее напряжение и, называется треугольником напряжений. На основании теоремы Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов — следует, что общее напряжение на зажимах цепи
Пример. Падение напряжения на активном сопротивлении Ua=15в. Напряжение на индуктивном сопротивлении UL=26 в. Вычислить общее напряжение, приложенное к цепи.
Напряжение на индуктивном сопротивлении UL=26 в. Вычислить общее напряжение, приложенное к цепи.
Решение. Общее напряжение на зажимах цепи переменного тока с последовательно соединенными активным и индуктивным сопротивлениями.
Чтобы определить полное сопротивление цепи переменного тока с активным и индуктивным сопротивлениями, следует разделить векторы Ua=Ir и UL =IXL на число I, выражающее силу тока в цепи, и построить треугольник А’О’В’ (рис. 56, в), стороны которого меньше сторон треугольника напряжений в I раз. Образованный треугольник называется треугольником сопротивлений. Его сторонами являются сопротивления r и ХL и полное сопротивление цепи Z.
Пользуясь теоремой Пифагора, можно написать что,
отсюда полное сопротивление цепи
Пример. Активное сопротивление катушки r=7 ом, а ее индуктивное сопротивление ХL=24 ом. Вычислить полное сопротивление катушки.
Решение. Полное сопротивление катушки переменному току
Сила тока в цепи с активным и индуктивным сопротивлениями определяется по закону Ома:
На векторной диаграмме видно, что в цепи переменного тока с активным и индуктивным сопротивлениями ток и напряжение не совпадают по фазе.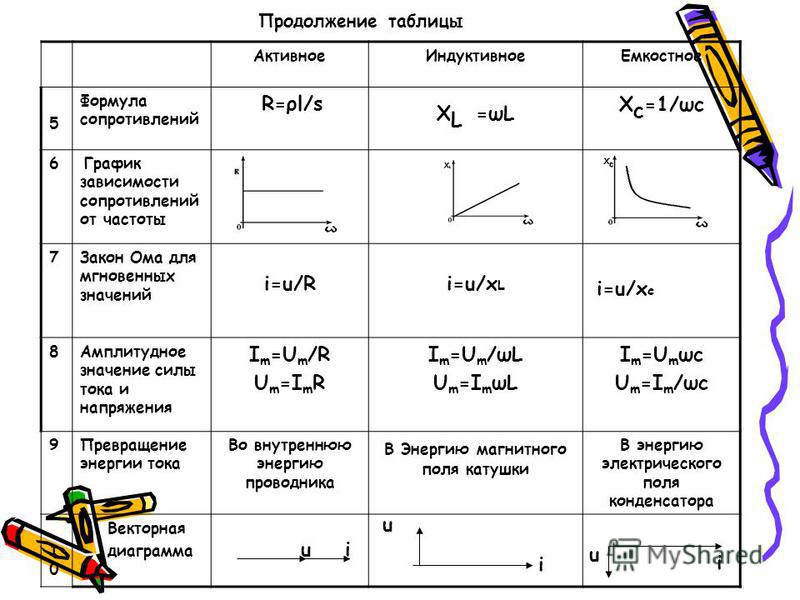 Ток отстает от напряжения — на угол .
Ток отстает от напряжения — на угол .
Угол сдвига между током и напряжением можно определить, если известен косинус этого угла.
Из треугольника напряжений косинус угла сдвига фаз
Теперь можно, пользуясь таблицей тригонометрических функций, определить угол .
Пример. Падение напряжения на активном сопротивлении катушки Ua =30 в. Общее напряжение на ее зажимах U=60в. Определить угол сдвига фаз между током и напряжением в цепи.
Решение. На основании данных найдем
По таблице тригонометрических функций угол сдвига фаз при со =0,5 составляет 60°.
Резистивные цепи переменного тока
Однонаправленная величина, будь то напряжение или ток, известна как величина постоянного или постоянного тока, которая имеет постоянную величину во времени, поэтому ее также называют неизменной во времени величиной. С другой стороны, переменная величина является величиной, изменяющейся во времени, поскольку величина и полярность периодически меняются через равные промежутки времени.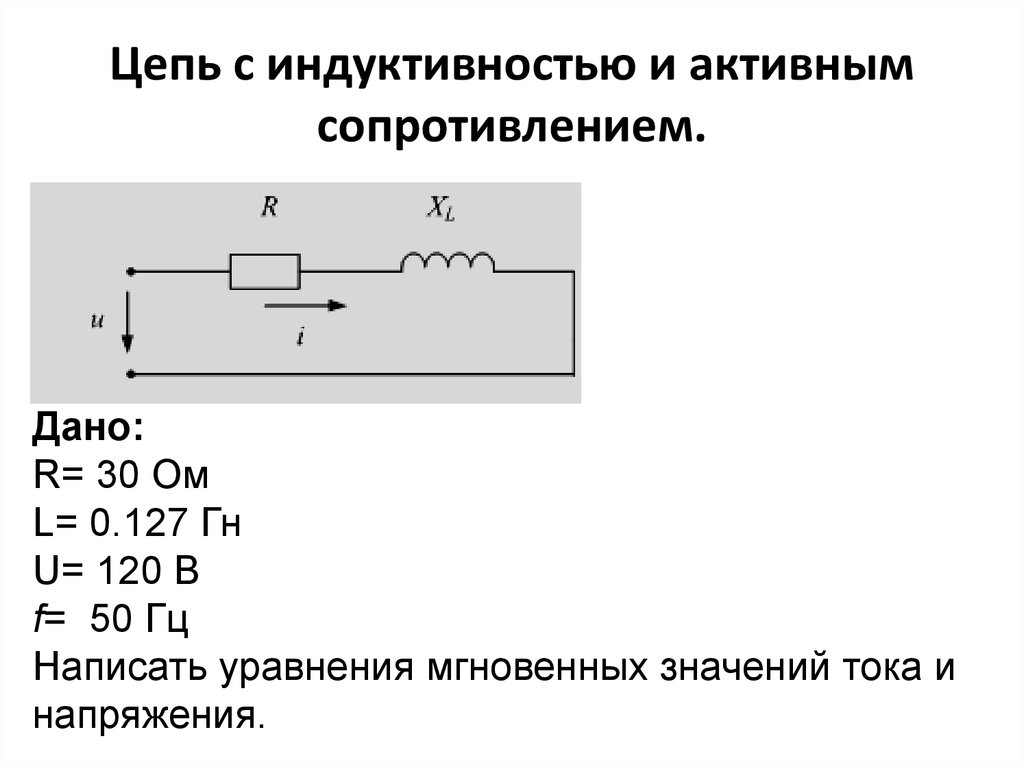
[adsense1]
Синусоидальная величина, например напряжение, может быть выражена как V = Vm sin (ωt + θ)
Где
В = мгновенное значение напряжения
Вм = максимальное значение напряжения
ω = угловая скорость = 2π f
θ = фазовый угол
Основными элементами цепи переменного тока являются сопротивление, индуктивность и емкость . В цепях переменного тока используется комбинация этих элементов (любых двух или трех) в последовательных и параллельных комбинациях.
Работа каждой отдельной цепи с отдельными элементами отличается от работы цепи, состоящей из комбинации этих элементов. В этой статье мы собираемся обсудить поведение цепи переменного тока с резистивной нагрузкой.
[adsense2]
Схема
Переменный ток, подаваемый через чистый резистор
В этом случае чистое сопротивление подключается к источнику переменного тока, что эквивалентно схеме, которая подает переменный ток на резистор, лампу или нагреватель или любую другую резистивную нагрузку. Это простейший тип цепи переменного тока, в которой нет ни индуктивности, ни емкости.
Это простейший тип цепи переменного тока, в которой нет ни индуктивности, ни емкости.
Эта чисто резистивная цепь ведет себя как цепь постоянного тока, предлагая такой же тип противодействия переменному току, как и в случае постоянного тока. На рисунке ниже показана резистивная цепь переменного тока с осциллограммами напряжения и тока.
Когда на резистивную нагрузку подается переменное напряжение, ток в цепи зависит от приложенного напряжения, и это значение тока можно определить с помощью закона Ома. Эта величина тока зависит от действующих значений приложенного напряжения и сопротивления в цепи.
Пусть мгновенное значение напряжения v = Vm sin ωt
Тогда ток в цепи по закону Ома определяется как
i = V/R = Vm sin ωt / R
При ωt = 90 0 значение i равно Im, следовательно, Im= Vm/R
Таким образом, ток может быть записан как , i = Im sin ωt
Следовательно, и напряжение, и ток имеют синусоидальную форму а также имеют одинаковую частоту. Это означает, что направление тока изменяется таким же образом, как и приложенное напряжение, и, следовательно, они находятся в фазе друг с другом.
Это означает, что направление тока изменяется таким же образом, как и приложенное напряжение, и, следовательно, они находятся в фазе друг с другом.
Таким образом, кривые напряжения и тока достигают своих максимальных и минимальных значений в одно и то же время. Однако амплитуды этих сигналов отличаются друг от друга.
Ниже показано векторное представление резистивной цепи переменного тока, в которой сигналы тока и напряжения совпадают по фазе.
Мощность и коэффициент мощности
Мощность в резистивной цепи является произведением напряжения и тока. Средняя мощность в резистивной цепи переменного тока может быть рассчитана как
Поскольку нет разности фаз между сигналами напряжения и тока, фазовый угол равен нулю (θ = 0), и, следовательно, коэффициент мощности будет равен единице.
Коэффициент мощности, cos θ = cos 0 0 = 1
Пример 1
Если в цепи есть источник переменного напряжения 280 В и нагревательный элемент 40 Ом, каков эффективный ток, потребляемый от источника? А также определить мощность, потребляемую нагревательным элементом.
Ток, потребляемый от источника питания,
I = V/R
= 280/40
= 7 ампер
Активная мощность, потребляемая сопротивлением переменного тока, равна
P = i2 R = 42 × 60 = 960 Вт
Пример 1 для резистивной цепи переменного тока
Если переменное синусоидальное напряжение V (t) = 200 x cos (ωt + 60 0 ) подключено к сопротивлению 40 Ом, то какой ток протекает через схема?
Преобразование данного выражения напряжения из временной области в векторную область. Мы получаем VR (t) = 200 cos (ωt + 60 0 ) → VR = 200 ∠60 0 вольт
Применяя закон Ома, ток в цепи можно рассчитать как
IR = VR / R = 200 ♂ 60 0
= 200 ♂ 60 0 /40
= 5om 60 0 AMPS
Схема переменного тока с резитивными нагрузками
На рисунке показано на рисунке. простая цепь переменного тока, состоящая из последовательно соединенных резисторов поперек источника питания. Ток через каждый элемент или в любой точке цепи имеет одинаковое значение из-за последовательного соединения, а его величина зависит от приложенного напряжения и общего сопротивления в цепи.
Ток через каждый элемент или в любой точке цепи имеет одинаковое значение из-за последовательного соединения, а его величина зависит от приложенного напряжения и общего сопротивления в цепи.
Независимо от количества последовательно соединенных резисторов ток всегда совпадает по фазе с приложенным напряжением.
В приведенной выше схеме напряжение на каждом сопротивлении можно определить, применяя закон Ома. Сумма падений напряжения на каждом сопротивлении дает общее напряжение, приложенное к цепи.
Соотношение фаз между приложенным напряжением и током этой цепи показано на диаграмме ниже, где как отдельные падения напряжения, так и общее напряжение совпадают по фазе с током.
Пример
Предположим, если в цепи имеется источник переменного напряжения 280 В и два нагревательных элемента соответственно 40 Ом и 60 Ом, то каково падение напряжения на каждом нагревательном элементе.
Полное сопротивление в цепи, Ом Тл = R1 + R2
= 40 + 60 = 100 Ом 280/ 100 = 2,8 А
Следовательно, I T = IR1 = IR2
Тогда Падение напряжения на нагревательном элементе-1, V1 = I T R1 = 2,8 × 40 = 112 В
Падение напряжения на нагревательном элементе-2, V2 = I T R2 = 2,8 × 60 = 168 В
Параллельная цепь переменного тока с резистивными нагрузками
В параллельной цепи переменного тока различные резистивные нагрузки подключены к источнику переменного напряжения, поэтому напряжение на каждой ветви остается постоянным, а общий ток распределяется между отдельными резистивными ветвями.
Таким образом, общий ток можно определить, сложив все отдельные токи, протекающие через каждое сопротивление. Эти отдельные токи находятся в фазе с приложенным напряжением, поскольку цепь состоит из чисто резистивной нагрузки.
На приведенном выше рисунке показано синфазное соотношение между напряжением и отдельными токами в параллельной цепи переменного тока с чисто резистивной нагрузкой. Величина отдельного тока через резистор зависит от приложенного напряжения и сопротивления, предлагаемого этим резистором.
Чем больше номинал резистора, тем меньше ток через него, и наоборот. Однако эти токи следуют форме волны напряжения (т. Е. В фазе с ней) независимо от их величины.
Пример
Если в цепи есть источник переменного напряжения 240 В, подключенный к двум параллельным нагревательным элементам 390 Ом и 1 кОм соответственно, то каков эффективный ток, протекающий через каждый из нагревательных элементов?
В параллельной цепи напряжение на каждом резисторе одинаковое, т. е. V = V1 = V2
е. V = V1 = V2
По закону Ома ток через ТЭН-1,
IR1 = V1 / R1 = 240/390 = 0,615 = 615 мА
Аналогично, IR2 = V2 / R2 = 240/1000 = 0,24 = 240 мА
Поэтому токи через нагревательные элементы составляют 615 мА и 240 мА соответственно.
Что такое чисто резистивная цепь? — Векторная диаграмма и форма волны
Цепь, содержащая только чистое сопротивление омов в цепи переменного тока, известна как Чистая резистивная цепь переменного тока 9.0186 . Наличие индуктивности и емкости не существует в чисто резистивной цепи. Переменный ток и напряжение движутся как вперед, так и назад в обоих направлениях цепи. Следовательно, переменный ток и напряжение имеют форму синусоидальной волны или известную как синусоидальная форма волны.
Содержимое:
- Описание резистивной цепи
- Фазовый угол и форма сигнала резистивной цепи
- Мощность в чисто резистивной цепи
В чисто резистивной цепи мощность рассеивается резисторами, а фазы напряжения и тока остаются одинаковыми, т.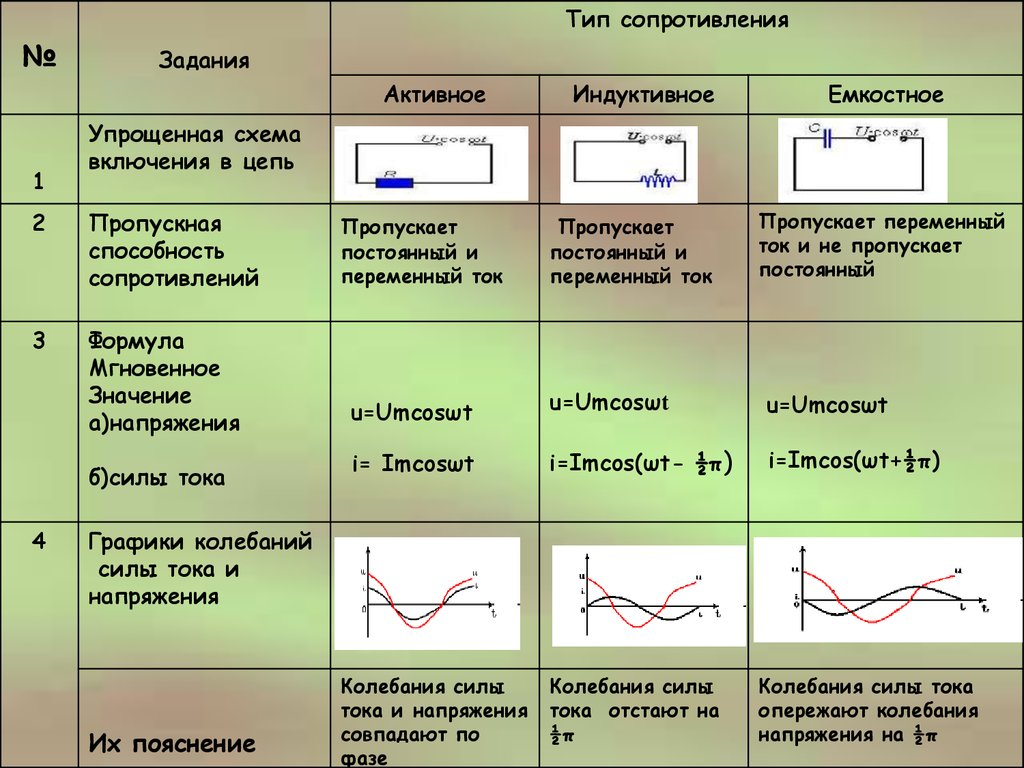 е. и напряжение, и ток достигают своего максимального значения одновременно. Резистор является пассивным устройством, которое не производит и не потребляет электроэнергию. Он преобразует электрическую энергию в тепло .
е. и напряжение, и ток достигают своего максимального значения одновременно. Резистор является пассивным устройством, которое не производит и не потребляет электроэнергию. Он преобразует электрическую энергию в тепло .
Пояснение к резистивной цепи
В цепи переменного тока отношение напряжения к току зависит от частоты питания, фазового угла и разности фаз. В резистивной цепи переменного тока значение сопротивления резистора будет одинаковым независимо от частоты питания.
Пусть переменное напряжение, приложенное к цепи, определяется уравнением
Тогда мгновенное значение тока, протекающего через резистор, показанный на рисунке ниже, будет:
Значение тока будет максимальным, когда ωt= 90° или sinωt = 1
Подставив значение sinωt в уравнение (2), получим
Фазовый угол и форма сигнала резистивной цепи
Из уравнений (1) и (3) видно, что существует нет разности фаз между приложенным напряжением и током, протекающим через чисто резистивную цепь, т. е. угол сдвига фаз между напряжением и током равен ноль . Следовательно, в цепи переменного тока, содержащей чистое сопротивление, ток совпадает по фазе с напряжением, как показано на рисунке ниже.
е. угол сдвига фаз между напряжением и током равен ноль . Следовательно, в цепи переменного тока, содержащей чистое сопротивление, ток совпадает по фазе с напряжением, как показано на рисунке ниже.
Мощность в чисто резистивной цепи
Три цвета: красный, синий и розовый, показанные на кривой мощности или форме волны, обозначают кривую тока, напряжения и мощности соответственно. Из векторной диаграммы видно, что ток и напряжение находятся в фазе друг с другом, что означает, что значение тока и напряжения достигает своего пика в один и тот же момент времени, а кривая мощности всегда положительна для всех значений тока. и напряжение.
Как и в цепи питания постоянного тока, произведение напряжения и тока известно как мощность в цепи. Точно так же мощность одинакова и в цепи переменного тока, с той лишь разницей, что в цепи переменного тока учитываются мгновенные значения напряжения и тока.
Таким образом, мгновенная мощность в чисто резистивной цепи определяется уравнением, показанным ниже:0213 Поскольку клапан cosωt равен нулю.

