Электростатическое поле источники: Основные источники электростатических полей — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Электрическое поле: определение, классификация, характеристики

Нас окружает материальный мир. Материю мы воспринимаем с помощью зрения и других органов чувств. Отдельным видом материи является электрическое поле, которое можно выявить только через его влияние на заряженные тела или с помощью приборов. Оно порождает магнитные поля и взаимодействует с ними. Эти взаимодействия нашли широкое практическое применение.

Содержание

Определение

Электрическое поле неразрывно связано с магнитным полем, и возникает в результате его изменения. Эти два вида материи являются компонентами электромагнитных полей, заполняющих пространство вокруг заряженных частиц или заряженных тел.

Таким образом, данный термин означает особый вид материи, обладающий собственной энергией, являющийся составным компонентом векторного электромагнитного поля. У электрического поля нет границ, однако его силовое воздействие стремится к нулю, при удалении от источника – заряженного тела или точечных зарядов [1].

Важным свойством полевой формы материи является способность электрического поля поддерживать упорядоченное перемещение носителей зарядов.

Рис. 1. Определение понятия «электрическое поле»

Энергия электрического поля подчиняется действию закона сохранения. Её можно преобразовать в другие виды или направить на выполнение работы.

Силовой характеристикой полей выступает их напряжённость – векторная величина, численное значение которой определяется как отношение силы, действующей на пробный положительный заряд, к величине этого заряда.

Характерные физические свойства:

реагирует на присутствие заряженных частиц;
взаимодействует с магнитными полями;
является движущей силой по перемещению зарядов – как положительных ионов, таки отрицательных зарядов в металлических проводниках;

поддаётся определению только по результатам наблюдения за проявлением действия.

Оно всегда окружает неподвижные статичные (не меняющиеся со временем) заряды, поэтому получило название – электростатическое. Опыты подтверждают, что в электростатическом поле действуют такие же силы, как и в электрическом.

Электростатическое взаимодействие поля на заряженные тела можно наблюдать при поднесении наэлектризованной эбонитовой палочки к мелким предметам. В зависимости от полярности наэлектризованных частиц, они будут либо притягиваться, либо отталкиваться от палочки.

Сильные электростатические поля образуются вблизи мощных электрических разрядов. На поверхности проводника, оказавшегося в зоне действия разряда, происходит перераспределение зарядов.

Вследствие распределения зарядов проводник становится заряженным, что является признаком влияния электрического поля.

Классификация

Электрические поля бывают двух видов: однородные и неоднородные.

Однородное электрическое поле

Состояние поля определяется пространственным расположением линий напряжённости. Если векторы напряжённости идентичны по модулю и они при этом сонаправлены во всех точках пространства, то электрическое поле – однородно. В нём линии напряжённости расположены параллельно.

В качестве примера является электрическое поле, образованное разноимёнными зарядами на участке плоских металлических пластин (см. рис. 2).

Рис. 2. Пример однородности

Неоднородное электрическое поле

Чаще встречаются поля, напряжённости которых в разных точках отличаются. Линии напряжённости у них имеют сложную конфигурацию. Простейшим примером неоднородности является электрический диполь, то есть система из двух разноимённых зарядов, влияющих друг на друга (см. рис. 3). Несмотря на то, что векторы напряжённости электрического диполя образуют красивые линии, но поскольку они не равны, то такое поле неоднородно. Более сложную конфигурацию имеют вихревые поля (рис 4). Их неоднородность очевидна.

Рис. 3. Электрический диполь

Рис. 4. Вихревые поля

Характеристики

Основными характеристиками являются:

потенциал;
напряжённость;
напряжение.

Потенциал

Термин означает отношение потенциальной энергии W, которой обладает пробный заряд q′ в данной точке к его величине. Выражение φ =W/q′. называется потенциалом электрического поля в этой точке.

Другими словами: количество накопленной энергии, которая потенциально может быть потрачена на выполнение работы, направленной на перемещение единичного заряда в бесконечность, или в другую точку с условно нулевой энергией, называется потенциалом рассматриваемого электрического поля в данной точке.

Энергия поля учитывается по отношению к данной точке. Её ещё называют потенциалом в данной точке. Общий потенциал системы равен сумме потенциалов отдельных зарядов. Это одна из важнейших характеристик поля. Потенциал можно сравнить с энергией сжатой пружины, которая при высвобождении способна выполнить определённую работу.

Единица измерения потенциала – 1 вольт. При бесконечном удалении точки от наэлектризованного тела, потенциал в этой точке уменьшается до 0: φ_∞=0.

Напряжённость поля

Достоверно известно, что электрическое поле отдельно взятого заряда q действует с определённой силой F на точечный пробный заряд, независимо от того, на каком расстоянии он находится. Сила, действующая на изолированный положительный пробный заряд, называется напряжённостью и обозначается символом

Напряжённость – векторная величина. Значение модуля вектора напряжённости: E=F/q′.

Линиями напряжённости электрического поля (известные как силовые линии), называются касательные, которые в точках касания совпадают с ориентацией векторов напряжённости. Плотность силовых линий определяет величину напряжённости.

Рис. 5. Электрическое поле положительного и отрицательного вектора напряжённости

Напряженность вокруг точечного заряда Q на расстоянии r от него, определяется по закону Кулона: E = 14πε

0⋅Qr2. Такие поля называют кулоновскими.

Векторы напряженности положительного точечного заряда направлены от него, а отрицательного – до центра (к заряду). Направления векторов кулоновского поля видно на рис. 6.

Рис. 6. Направление линий напряжённости положительных и отрицательных зарядов

Для кулоновских полей справедлив принцип суперпозиции. Суть принципа в следующем:вектор напряжённости нескольких зарядов может быть представлен в виде геометрической суммы напряжённостей, создаваемых каждым отдельно взятым зарядом, входящих в эту систему.

Для общего случая распределения зарядов имеем:

Линии напряжённости схематически изображены на рисунке 7. На картинке видно линии, характерные для полей:

электростатического;
дипольного;
системы и одноимённых зарядов;
однородного поля.

Рис. 7. Линии напряжённости различных полей

Напряжение

Поскольку силы электрического поля способны выполнять работу по перемещению носителей элементарных зарядов, то наличие поля является условием для существования электрического тока. Электроны и другие элементарные заряды всегда двигаются от точки, обладающей более высоким потенциалом, к точке с низшим потенциалом. При этом часть энергии расходуется на выполнение работы по перемещению.

Для поддержания постоянного тока (упорядоченного движения носителей элементарных зарядов) необходимо на концах проводника поддерживать разницу потенциалов, которую ещё называют напряжением. Чем больше эта разница, тем активнее выполняется работа, тем мощнее ток на этом участке. Функции по поддержанию разницы потенциалов возложены на источники тока.

Методы обнаружения

Органы чувств человека не воспринимают электрических полей. Поэтому мы не можем их увидеть, попробовать на вкус или определить по запаху. Единственное, что может ощутить человек – это выпрямление волос вдоль линий напряжённости. Наличие слабых воздействий мы просто не замечаем.

Обнаружить их можно через воздействие на мелкие кусочки бумаги, бузиновые шарики и т.п. Электрическое поле воздействует на электроскоп – его лепестки реагируют на такие воздействия.

Очень простой и эффективный метод обнаружения с помощью стрелки компаса. Она всегда располагается вдоль линий напряжённости.

Существуют очень чувствительные электронные приборы, с лёгкостью определяющие наличие электростатических полей.

Методы расчета электрического поля

Для расчётов параметров используются различные аналитические или численные методы:

метод сеток или конечных разностей;
метод эквивалентных зарядов;
вариационные методы;
расчёты с использованием интегральных уравнений и другие.

Выбор конкретного метода зависит от сложности задачи, но в основном используются численные методы, приведённые в списке.

Использование

Изучение свойств электрического поля открыло перед человечеством огромные возможности. Способность поля перемещать электроны в проводнике позволила создавать источники тока.

На свойствах электрических полей создано различное оборудование, применяемое в медицине, химической промышленности, в электротехнике. Разрабатываются приборы, применяемые в сфере беспроводной передачи энергии к потребителю. Примером могут послужить устройства беспроводной зарядки гаджетов. Это пока только первые шаги на пути к передачи электричества на большие расстояния.

Сегодня, благодаря знаниям о свойствах полевой формы материи, разработаны уникальные фильтры для очистки воды. Этот способ оказался дешевле, чем использование традиционных сменных картриджей.

К сожалению, иногда приходится нейтрализовать силы полей. Обладая способностью электризации предметов, оказавшихся в зоне действия, электрические поля создают серьёзные препятствия для нормальной работы радиоэлектронной аппаратуры. Накопленное статическое электричество часто является причиной выхода из строя интегральных микросхем и полевых транзисторов.

Электростатическое поле, напряженность, силовые линии. Тест

Всего вопросов: 13

Вопрос 1. Источником электростатического поля является…

Вопрос 2. На рисунке приведено графическое изображение электрического поля с помощью линий напряженности. На каком из рисунков изображено однородное электрическое поле?

Вопрос 3. Физическая векторная величина, определяемая отношением силы, с которой электростатическое поле действует на положительный электрический заряд, к числовому значению этого заряда, называется:

Вопрос 4. За направление вектора напряженности электростатического поля принято:

Вопрос 5. По какой формуле из приведенных ниже можно рассчитать модуль напряженности электростатического поля точечного заряда q, находящегося в однородном диэлектрике?

Вопрос 6. Электрическое поле создано положительным зарядом. Какое направление имеет вектор напряженности в точке а?

Вопрос 7. На рисунке изображено однородное электрическое поле и протон. В каком направлении на протон действует сила и каков характер движения частицы?

Вопрос 8. На рисунке изображено однородное электрическое поле и электрон. В каком направлении на электрон действует сила и каков характер движения частицы?

Вопрос 9. Как изменится по модулю напряженность электрического поля в данной точке при уменьшении заряда, создающего поле, в 3 раза?

Вопрос 10. Какой из графиков на рисунке соответствует зависимости модуля напряженности электрического поля, созданного уединенным точечным зарядом, от квадрата расстояния до него?

Вопрос 11. Одинаковые по величине и по знаку заряды расположены в двух вершинах равностороннего треугольника. Вектор напряженности в третьей вершине треугольника направлен…

Вопрос 12. Одинаковые по величине и по знаку заряды расположены в двух вершинах равностороннего треугольника. Вектор напряженности в третьей вершине треугольника направлен…

Вопрос 13. На каком расстоянии от небольшого заряженного шара напряженность электростатического поля в воде с диэлектрической проницаемостью 81 будет такой же, как в вакууме на расстоянии 18 см от центра шара?

Тема 1. Электростатическое поле и его источники — КиберПедия

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ЗАКОНЫ И ФОРМУЛЫ

(содержание тестовых заданий)

Часть 2. ЭЛЕКТРОМАГНЕТИЗМ

МОСКВА — 2012

Часть 2. ЭЛЕКТРОМАГНЕТИЗМ

НАЗВАНИЯ РАЗДЕЛОВ

6.ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

7 ПОСТОЯННЫЙ ТОК. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ в ВЕЩЕСТВЕ

8. МАГНИТНОЕ ПОЛЕ

9. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

10. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Раздел 6.ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

Тема 1. Электростатическое поле и его источники

П. 1. Электрический заряд. Объемная плотность заряда

П. 2. Электростатическое поле. Линии поля. Принцип суперпозиции

П. 3. Напряженность электрического поля. Закон Кулона

П. 4. Потенциал электрического поля

Тема 2. Поток и циркуляция электрического поля

П. 1. Поток электрического поля

П. 2. Циркуляция электрического поля

П. 3. Закон Гаусса для электрического поля

П. 4. Схема решения задач с использованием закона Гаусса

П. 5. Расчет напряженности электрического поля заряженной нити

Тема 3. Проводники в электрическом поле

П. 1. Проводники в электрическом поле. Электростатическая индукция

П. 2. Электроемкость тела. Емкость шара

П. 3. Взаимная емкость. Емкость плоского конденсатора

Тема 1. Электростатическое поле и его источники

1. СОХРАНЯЕМОСТЬ ЗАРЯДА ОЗНАЧАЕТ, ЧТО СУММАРНЫЙ ЗАРЯД В ИЗОЛИРОВАННОЙ СИСТЕМЕ НЕ МЕНЯЕТСЯ.

2. ОБЪЕМНАЯ ПЛОТНОСТЬ ЗАРЯДОВ ОПРЕДЕЛЯЕТСЯ ФОРМУЛОЙ

r = dQ / dV .

3. ЛИНИЕЙ ПОЛЯ НАЗЫВАЕТСЯ ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК, В КАЖДОЙ ИЗ КОТОРЫХ ВЕКТОР НАПРЯЖЕННОСТИ НАПРАВЛЕН ПО КАСАТЕЛЬНОЙ К ЛИНИИ ПОЛЯ.

4. НАПРЯЖЕННОСТЬ ЕСТЬ ВЕКТОРНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ, ЧИСЛЕННО РАВНАЯ СИЛЕ, ДЕЙСТВУЮЩЕЙ НА ЕДИНИЧНЫЙ ЗАРЯД .

5. НАПРЯЖЕННОСТЬ в ТОЧКЕ с РАДИУС-ВЕКТОРОМ ЭЛЕКТРИЧЕСКОГО ПОЛЯ, СОЗДАННОГО ТОЧЕЧНЫМ ЗАРЯДОМ q, РАСПОЛОЖЕННЫМ в НАЧАЛЕ СИСТЕМЫ КООРДИНАТ, по ВЕЛИЧИНЕ РАВНА

Е = ———— .

4p e e₀ r²

6. ПОТЕНЦИАЛ ЕСТЬ СКАЛЯРНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ, ЧИСЛЕННО РАВНАЯ РАБОТЕ по ПЕРЕМЕЩЕНИЮ ЕДИНИЧНОГО, ПОЛОЖИТЕЛЬНОГО ЗАРЯДА из ДАННОЙ ТОЧКИ в ФИКСИРОВАННУЮ ТОЧКУ ₀, в КОТОРОЙ ПОТЕНЦИАЛ ПРИНЯТ ЗА 0.

7. ПОТЕНЦИАЛ в ТОЧКЕ С РАДИУС-ВЕКТОРОМ ЭЛЕКТРИЧЕСКОГО ПОЛЯ, СОЗДАННОГО ТОЧЕЧНЫМ ЗАРЯДОМ q, РАСПОЛОЖЕННЫМ в НАЧАЛЕ КООРДИНАТ, РАВЕН

j = ———— .

4p e e₀ r

Тема 2. Поток и циркуляция электрического поля

8. ПОТОК НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Фе = .

9. ЦИРКУЛЯЦИЯ НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Се = .

10. ЗАКОН ГАУССА ДЛЯ ЭЛ.СТАТИЧЕСКОГО ПОЛЯ:

= r dV.

11. При решении задачи о поле заряженной нити в качестве поверхности интегрирования S_о выбирается цилиндр с радиусом, равным расстоянию до точки наблюдения , осью которого является нить.

12. Напряженность поля на расстоянии r от заряженной нити по величине равна

Е(r) = ——— .

2p ee₀ r

Тема 2.Примеры расчета магнитного поля

8. ЗАКОН ЦИРКУЛЯЦИИ МАГНИТНОГО ПОЛЯ: = m₀.

9. НА ПОВЕРХНОСТИ ПРОВОДА ДИАМЕТРОМ 1 мм С ТОКОМ ___ А ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ РАВНА 1 мТл .

УКАЗАНИЯ: ИСПОЛЬЗУЙТЕ ФОРМУЛУ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ПРЯМОГО БЕСКОНЕЧНО ДЛИННОГО ПРОВОДНИКА С ТОКОМ.

ВЕЛИЧИНА МАГНИТНОЙ ПОСТОЯННОЙ РАВНА 4p·10^-7 Гн/м.

10. ВНУТРИ СОЛЕНОИДА, НАМОТАННОГО В ОДИН СЛОЙ ПРОВОДОМ ДИАМЕТРОМ 1 мм, ПО КОТОРОМУ ТЕЧЕТ ТОК 5 А, ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ РАВНА ____ мТл .

УКАЗАНИЯ: ИСПОЛЬЗУЙТЕ для РАСЧЕТА ФОРМУЛУ МАГНИТНОГО ПОЛЯ ВНУТРИ БЕСКОНЕЧНО ДЛИННОГО СОЛЕНОИДА. ПО ИЗВЕСТНОМУ ДИАМЕТРУ ПРОВОДА ОПРЕДЕЛИТЕ КОЛИЧЕСТВО ВИТКОВ на ЕДИНИЦУ ДЛИНЫ. ПРИ ВВОДЕ ОТВЕТА ОБРАТИТЕ ВНИМАНИЕ на РАЗМЕРНОСТЬ.

ВЕЛИЧИНА МАГНИТНОЙ ПОСТОЯННОЙ РАВНА 4p·10^-7 Гн/м.

11. В ЦЕНТРЕ ВИТКА РАДИУСА 10 см, ИМЕЮЩЕГО МАГНИТНЫЙ МОМЕНТ 0.012 А·м МАГНИТНОЕ ПОЛЕ РАВНО ___ мкТл .

УКАЗАНИЯ: ИСПОЛЬЗУЙТЕ ФОРМУЛЫ для ИНДУКЦИИ МАГНИТНОГО ПОЛЯ в ЦЕНТРЕ КРУГОВОГО ВИТКА с ТОКОМ и ФОРМУЛУ МАГНИТНОГО МОМЕНТА ВИТКА с ТОКОМ. ОБРАТИТЕ ВНИМАНИЕ НА РАЗМЕРНОСТЬ ОТВЕТА.

ВЕЛИЧИНА МАГНИТНОЙ ПОСТОЯННОЙ РАВНА 4p·10^-7 Гн/м.

Тема 1.Законы индукции

1 Общий вид закона индукции: C₀ = const (F) .

2 ЗАКОН МАГНИТОЭЛЕКТРИЧЕСКОЙ ИНДУКЦИИ в ВАКУУМЕ:

C₀_m = m₀ e₀ (Ф_е) .

3. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ:

C₀_e = — (Ф_m) .

4 ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ для ПРОВОДЯЩЕГО КОНТУРА: e_ИНД = — .

5 ЗАКОН САМОИНДУКЦИИ: ЭДС САМОИНДУКЦИИ e_С.И. = — L (I) .

6 Формула индуктивности соленоида: L = m₀ V n² .

7 Закон взаимной индукции: e_ИНД.1 = — L₁₂ (I₂)

Тема 3.Колебательный контур

12 ФОРМУЛА КВАДРАТА РЕЗОНАНСНОЙ ЧАСТОТЫ ПОСЛЕДОВАТЕЛЬНОГО КОЛЕБАТЕЛЬН. КОНТУРА: = — 2 b² .

13 ФОРМУЛА КВАДРАТА ХАРАКТЕРИСТИЧЕСКОГО СОПРОТИВЛЕНИЯ КОНТУРА: r² = L / С .

14 ФОРМУЛА КВАДРАТА РЕЗОНАНСНОЙ ЧАСТОТЫ ПАРАЛЛЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА: = — 4 b² .

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ЗАКОНЫ И ФОРМУЛЫ

(содержание тестовых заданий)

Часть 2. ЭЛЕКТРОМАГНЕТИЗМ

МОСКВА — 2012

Часть 2. ЭЛЕКТРОМАГНЕТИЗМ

НАЗВАНИЯ РАЗДЕЛОВ

6.ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

7 ПОСТОЯННЫЙ ТОК. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ в ВЕЩЕСТВЕ

8. МАГНИТНОЕ ПОЛЕ

9. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

10. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Раздел 6.ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

Тема 1. Электростатическое поле и его источники

П. 1. Электрический заряд. Объемная плотность заряда

П. 2. Электростатическое поле. Линии поля. Принцип суперпозиции

П. 3. Напряженность электрического поля. Закон Кулона

П. 4. Потенциал электрического поля

Тема 2. Поток и циркуляция электрического поля

П. 1. Поток электрического поля

П. 2. Циркуляция электрического поля

П. 3. Закон Гаусса для электрического поля

П. 4. Схема решения задач с использованием закона Гаусса

П. 5. Расчет напряженности электрического поля заряженной нити

Тема 3. Проводники в электрическом поле

П. 1. Проводники в электрическом поле. Электростатическая индукция

П. 2. Электроемкость тела. Емкость шара

П. 3. Взаимная емкость. Емкость плоского конденсатора

Тема 1. Электростатическое поле и его источники

1. СОХРАНЯЕМОСТЬ ЗАРЯДА ОЗНАЧАЕТ, ЧТО СУММАРНЫЙ ЗАРЯД В ИЗОЛИРОВАННОЙ СИСТЕМЕ НЕ МЕНЯЕТСЯ.

2. ОБЪЕМНАЯ ПЛОТНОСТЬ ЗАРЯДОВ ОПРЕДЕЛЯЕТСЯ ФОРМУЛОЙ

r = dQ / dV .

Е = ———— .

4p e e₀ r²

j = ———— .

4p e e₀ r

Понятие электростатического поля — fiziku5.ru

где dS − элементарная поверхность, занятая зарядом dq, а − поверхностная плотность заряда.

c) в случае непрерывного распределения заряда по линии:

где dl − элементарный отрезок линии, занятый зарядом dq, а − линейная плотность заряда.

§12.2. Понятие электростатического поля

Электростатическое поле − это особый вид материи, не имеющей массы покоя, заполняющий пространство вокруг его источников — электрических зарядов и воздействующий на электрические заряды. Любой заряд по отношению к данному полю выступает либо в роли источника, либо в роли пробного заряда. Источниками данного поля выступают заряды, благодаря которым поле возникло (подобно тому, как вода в озере порождается родниками, бьющими на дне). Пробным по отношению к данному полю зарядом называется заряд, не входящий в число источников. В рамках нашего курса вопрос взаимодействия источника со своим собственным полем не рассматривается.

Таким образом, электростатическое поле является материальным посредником, передающим воздействие источника на окружающие его заряды. Иными словами, благодаря полю происходит взаимодействие зарядов, пространственно отделённых друг от друга: поле одного заряда воздействует на другой заряд, поле второго − на первый.

Электростатическое поле является частным случаем электрического поля, которое в свою очередь входит в пятёрку физических полей, известных на данный момент человечеству. Кроме электрического известны магнитное, гравитационное, сильное и слабое физические поля. Каждое из этих полей является материальным посредником, переносящим взаимодействие того или иного вида через пространство. Неслучайно невидимая и невесомая материя, заполняющая пространство вокруг источников, изучаемая в физике, получила название, заимствованное из математики.

Каждое физическое поле можно представить как непрерывное распределение той или иной физической величины в пространстве, то есть как математическое поле.

Векторная физическая величина, непрерывное распределение которой в пространстве представляет электростатическое поле, называется электрической напряженностью или напряжённостью электрического поля . Это значит, что для описания данного электрического поля необходимо и достаточно знать соответствующее векторное поле .

Рис.12.2

Что же такое напряжённость электрического поля? Дадим определение: вектор электрической напряжённости в данной точке пространства , заполненного электрическим полем, совпадает с силой , которая действовала бы со стороны электрического поля на точечный единичный положительный пробный заряд, если его поместить в данную точку.

Неверно было бы сказать, что является такой силой. Дело в том, что напряжённость − это характеристика электрического поля самого по себе независимо от того, существуют ли какие-либо пробные заряды, «купающиеся» в нём, или нет. Если в точке пространства, заполненного полем, есть единичный положительный пробный заряд, то этой точке соответствуют два физических вектора: вектор силы и равный ему вектор напряжённости . Если же в данной точке нет никакого пробного заряда, то вектор силы отсутствует, а вектор напряжённости по-прежнему имеет место (рис.12.3).

Рис.12.3

Из опыта известно, что электрическая сила, то есть сила, действующая со стороны электрического поля на пробный заряд, прямо пропорциональна его величине. Это значит, что если в точку поместить не единичный положительный, а произвольный пробный заряд q, то сила , действующая на него, будет в q раз больше чем . То есть

Þ .

Только нужно понимать, что в первом равенстве q выступает как физически безразмерное число, а во втором − как физическая величина, имеющая размерность. Отсюда можно получить физическую размерность электрической напряжённости: . Более традиционным, впрочем, является другое представление размерности напряжённости, о чем мы поговорим позже.

Для любого векторного поля можно ввести понятие лини поля. Линия в пространстве, заполненном векторным полем, в каждой точке которой вектор поля направлен по касательной, называется линией поля. Линии физических полей называются силовыми линиями. Силовые линии необходимы для изображения пространственной конфигурации поля. Вспомните, как Вы схематически изображаете текущую воду. На самом деле движущаяся жидкость представляется векторным полем скорости, и линии которые Вы рисуете, − это линии этого поля. Конечно, изображение физического поля с помощью силовых линий условно, хотя каждая силовая линия реальна. Дело в том, что через каждую точку пространства, заполненного полем, проходит силовая линия, и при том только одна. Кроме этого, силовые линии никогда не пересекают сами себя. Значит, силовых линий бесконечно много, и изобразить их всех невозможно. Более того, попытка изобразить как можно больше силовых линий вредна, так как неизбежно приведёт к такому рисунку:

Рис.12.4

Условным при изображении поля является выбор изображаемых силовых линий. Иными словами, неверный выбор изображаемых правильных силовых линий приведёт к неправильному изображению поля. Для примера приведём неправильное и правильное изображение поля одного точечного заряда Q>0 (рис.12.5).

Рис.12.5

На обоих рисунках изображено по шесть правильных силовых линий. Но левый рисунок неверен, а правый верен. При выборе изображаемых силовых линий необходимо воспроизвести пространственную симметрию поля. Поле точечного источника обладает сферической симметрией, то есть все радиальные направления, идущие из точки источника равноправны. Это требование будет автоматически выполнено, если следовать правилу густоты. Под густотой силовых линий в данной области пространства dV понимается отношение количества силовых линий dN, пронизывающих эту область, к её объёму, то есть .

При правильном изображении физического поля густота силовых линий должна быть пропорциональна модулю вектора поля в данной области.

Рис.12.6

Количество изображённых силовых линий должно быть достаточным для выполнения правила густоты и, следовательно, воспроизведения пространственной симметрии поля. Например, для изображения однородного поля достаточно трёх силовых линий (рис.12.7).

Рис.12.7

Электрическое поле – FIZI4KA

Электродинамика – раздел физики, изучающий свойства и взаимодействия электрических зарядов, осуществляемые посредством электромагнитного поля.

Электростатикой называется раздел электродинамики, в котором рассматриваются свойства и взаимодействия неподвижных электрически заряженных тел или частиц.

Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макротелами.

Точечный заряд – заряженное тело, размер которого мал по сравнению с расстоянием, на котором оценивается его действие.

Электризация тел

Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.

Способы электризации:

трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
при ударе;
под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.

Взаимодействие зарядов. Два вида зарядов

Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.

Обозначение – \( q \), единица измерения в СИ – кулон (Кл).

Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10^-19 Кл), наименьший положительный заряд (1,6·10^-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.

Величина заряда тела будет равна

где \( N \) — число избыточных или недостающих электронов;
\( e \) — элементарный заряд, равный 1,6·10^-19 Кл.

Важно!
Частица может не иметь заряда, но заряд без частицы не существует.

Электрические заряды взаимодействуют:

заряды одного знака отталкиваются:

заряды противоположных знаков притягиваются:

Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.

Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.

Закон сохранения электрического заряда

Систему называют замкнутой (электрически изолированной), если в ней не происходит обмена зарядами с окружающей средой.

В любой замкнутой (электрически изолированной) системе сумма электрических зарядов остается постоянной при любых взаимодействиях внутри нее.

Полный электрический заряд \( (q) \) системы равен алгебраической сумме ее положительных и отрицательных зарядов \( (q_1, q_2 … q_N) \):

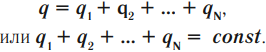
Важно!
В природе не возникают и не исчезают заряды одного знака: положительный и отрицательный заряды могут взаимно нейтрализовать друг друга, если они равны по модулю.

Закон Кулона

Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.

Закон Кулона формулируется так:
сила взаимодействия \( F \) двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям \( q_1 \) и \( q_2 \) и обратно пропорциональна квадрату расстояния между ними \( r \):

где \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (Н·м²)/Кл² – коэффициент пропорциональности,
\( \varepsilon_0=8.85\cdot10^{-12} \) Кл²/(Н·м²) – электрическая постоянная.

Коэффициент \( k \) численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.

Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.

Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:

где \( \varepsilon \) – диэлектрическая проницаемость среды.

Закон Кулона применим к взаимодействию

неподвижных точечных зарядов;
равномерно заряженных тел сферической формы.

В этом случае \( r \) – расстояние между центрами сферических поверхностей.

Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции).

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

материально;
создается зарядом;
обнаруживается по действию на заряд;
непрерывно распределено в пространстве;
ослабевает с увеличением расстояния от заряда.

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

где \( \vec{E} \) – напряженность электрического поля, \( q \) – заряд.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
записать для заряда условие равновесия или основное уравнение динамики материальной точки;
выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
записать математически все вспомогательные условия;
решить полученную систему уравнений относительно неизвестной величины;
проверить решение

Напряженность электрического поля

Напряженность электрического поля \( \vec{E} \) – векторная физическая величина, равная отношению силы \( F \), действующей на пробный точечный заряд, к величине этого заряда \( q \):

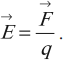
Обозначение – \( \vec{E} \), единица измерения в СИ – Н/Кл или В/м.

Напряженность поля точечного заряда в вакууме вычисляется по формуле:

где \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (Н·м²)/Кл²,
\( q_0 \) – заряд, создающий поле,
\( r \) – расстояние от заряда, создающего поле, до данной точки.

Напряженность поля точечного заряда в среде вычисляется по формуле:

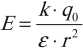
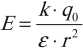
где \( \varepsilon \) – диэлектрическая проницаемость среды.

Важно!
Напряженность электрического поля не зависит от величины пробного заряда, она определяется величиной заряда, создающего поле.

Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку.

Линией напряженности электрического поля называется линия, касательная к которой в каждой точке направлена вдоль вектора напряженности \( \vec{E} \).

Линии напряженности электростатического поля начинаются на положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность от положительного заряда и приходят из бесконечности к отрицательному заряду.

Распределение линий напряженности вокруг положительного и отрицательного точечных зарядов показано на рисунке.

Определяя направление вектора \( \vec{E} \) в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.

Поле, в котором напряженность одинакова по модулю и направлению в любой точке, называется однородным электрическим полем. Однородным можно считать электрическое поле между двумя разноименно заряженными металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу.

Принцип суперпозиции электрических полей

Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов.

Принцип суперпозиции электрических полей: напряженность электрического поля системы \( N \) зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности:

Электрические поля от разных источников существуют в одной точке пространства и действуют на заряд независимо друг от друга.

Потенциальность электростатического поля

Электрическое поле с напряженностью \( \vec{E} \) при перемещении заряда \( q \) совершает работу. Работа \( A \) электростатического поля вычисляется по формуле:

где \( d \) – расстояние, на которое перемещается заряд,
\( \alpha \) – угол между векторами напряженности электрического поля и перемещения заряда.

Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле.

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным.

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой \( W \), так как буквой \( E \) обозначают напряженность поля:

Потенциальная энергия заряда \( q \), помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – \( \varphi \), единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – \( \Delta\varphi \), единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой \( U \) и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле.

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда \( q \) в точке, удаленной от него на расстояние \( r \), вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (\( r =R \), где \( R \) – радиус шара). Напряженность поля внутри шара равна нулю.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

установить характер и особенности электростатических взаимодействий объектов системы;
ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
записать законы сохранения и движения для объектов;
выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
составить систему уравнений и решить ее относительно искомой величины;
проверить решение.

Проводники в электрическом поле

Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.

Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.

Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.

Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.

Важно!
Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей. На этом основана электростатическая защита.

Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.

Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.

Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны).

Диэлектрики в электрическом поле

Диэлектриками называют вещества, не проводящие электрический ток. Диэлектриками являются стекло, фарфор, резина, дистиллированная вода, газы.

В диэлектриках нет свободных зарядов, все заряды связаны. В молекуле диэлектрика суммарный отрицательный заряд электронов равен положительному заряду ядра. Различают полярные и неполярные диэлектрики.

В молекулах полярных диэлектриков ядра и электроны расположены так, что центры масс положительных и отрицательных зарядов не совпадают и находятся на некотором расстоянии друг от друга. То есть молекулы представляют собой диполи независимо от наличия внешнего электрического поля. В отсутствие внешнего электрического поля из-за теплового движения молекул диполи расположены хаотично, поэтому суммарная напряженность поля всех диполей диэлектрика равна нулю.

Если в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов в молекуле диэлектрика совпадают, то он называется неполярным. Пример такого диэлектрика – молекула водорода. Если такой диэлектрик поместить во внешнее электрическое поле, то направления векторов сил, действующих на положительные и отрицательные заряды, будут противоположными. В результате молекула деформируется и превращается в диполь. При внесении диэлектрика в электрическое поле происходит его поляризация.

Поляризация диэлектрика – процесс смещения в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества в электрическом поле.

Если диэлектрик неполярный, то в его молекулах происходит смещение положительных и отрицательных зарядов. На поверхности диэлектрика появятся поверхностные связанные заряды. Связанными эти заряды называют потому, что они не могут свободно перемещаться отдельно друг от друга.

Внутри диэлектрика суммарный заряд равен нулю, а на поверхностях заряды не скомпенсированы и создают внутри диэлектрика поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Это значит, что внутри диэлектрика поле имеет меньшую напряженность, чем в вакууме.

Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:

В полярном диэлектрике во внешнем электрическом поле происходит поворот диполей, и они выстраиваются вдоль линий напряженности.

Если внесенный в электрическое поле диэлектрик разрезать, то его части будут электрически нейтральны.

Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – \( C \), единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

Формула для вычисления электроемкости:

где \( q \) – заряд проводника, \( \varphi \) – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

где \( q \) – модуль заряда одной из обкладок,
\( U \) – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью \( S \), находящиеся на расстоянии \( d \) друг от друга.

Электроемкость плоского конденсатора:

где \( \varepsilon \) – диэлектрическая проницаемость вещества между обкладками,
\( \varepsilon_0 \) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

Виды конденсаторов:

по типу диэлектрика – воздушный, бумажный и т. д.;
по форме – плоский, цилиндрический, сферический;
по электроемкости – постоянной и переменной емкости.

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

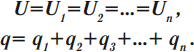
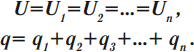
Общая емкость:

Последовательное соединение конденсаторов

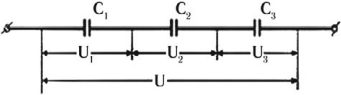
При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

Общее напряжение:

Величина, обратная общей емкости:

При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости.

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Энергия электрического поля конденсатора

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:

Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.

Плотность энергии электрического поля:

где \( V \) – объем пространства между обкладками конденсатора.

Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.

Основные формулы раздела «Электрическое поле»

Электрическое поле

5 (100%) 1 vote

Электростатическое поле, напряженность, силовые линии, их свойства. Принцип суперпозиции, сумма векторов

Тестирование онлайн

Электростатическое поле

Электростатическое поле — это особая форма материи, которая возникает вокруг неподвижного электрического заряда. Это поле нет возможности увидеть, понюхать. Поле можно представить при помощи линий напряженности (силовых линий).

На рисунке видно, какое условное направление имеют силовые линии: начинаются на положительных зарядах и заканчиваются на отрицательных. Изображено и то, как линии напряженности распределяются при взаимодействии одноименных и разноименных зарядов.

В реальности силовые линии можно увидеть при помощи железных опилок.

Чем дальше удаляться от заряда, тем меньше сила поля (силовые линии редеют), тем слабее взаимодействуют заряженные тела, посредством создаваемого ими поля.

Поле бывает однородным. В этом случае линии напряженности параллельные.

Поле однородное между пластинами в центре

Напряженность поля

Как оценить силу поля вокруг некоторого заряда? Для этого используют пробный заряд q₀. Пробный заряд — это всегда положительный заряд, его собственное электростатическое поле ничтожно мало, относительно исследуемого поля.

Сила, с которой поле действует на пробный заряд в данной точке поля, называется напряженностью электростатического поля в этой точке

Напряженность поля — векторная величина. Вектора — это касательная к линиям напряженности в данной точке поля. Направлен вектор туда же, куда силовая линия (линия напряженности).

Вектор напряженности в различных точках поля: А, B, C и D

Вектор напряженности в точках 1, 2 и 3

Можно вывести формулу

— напряженность поля точечного заряда q на расстоянии r от него.

Принцип суперпозиции

Если поле создается несколькими зарядами, то напряженность в некоторой точке равна векторной сумме напряженностей каждого из полей в отдельности

Т. Электростатическое поле — PhysBook

Электростатическое поле

Закон Кулона определяет силу взаимодействия между электрическими зарядами, но не объясняет, как это взаимодействие передается на расстояние от одного тела к другому.

Опыты показывают, что это взаимодействие наблюдается и тогда, когда наэлектризованные тела находятся в вакууме. Значит, для электрического взаимодействия не нужна среда. По теории, развитой М. Фарадеем и Дж. Максвеллом, в пространстве, где находится электрический заряд, существует электрическое поле.

Электростатическое поле — особый вид материи, ее источником являются неподвижные относительно рассматриваемой инерциальной системы отсчета (ИСО) заряды, посредством которой осуществляется их взаимодействие.

Таким образом, электростатическое поле — материально. Оно непрерывно в пространстве. Исходя из современных представлений, неподвижная заряженная частица является источником электростатического поля, а наличие поля — признаком существования самой заряженной частицы. Взаимодействие электрических зарядов сводится к следующему: поле заряда q₁ действует на заряд q₂, а поле заряда q₂ действует на заряд q₁. Эти взаимодействия передаются не мгновенно, а с конечной скоростью, равной скорости света с = 300000 км/с. Электрическое поле, создаваемое неподвижными электрическими зарядами, относительно рассматриваемой ИСО называется электростатическим.

Мы не можем непосредственно воспринимать электростатическое поле с помощью наших органов чувств. О существовании электростатического поля мы можем судить по его действиям. Электростатическое поле заряда действует с некоторой силой на любой другой заряд, оказавшийся в поле данного заряда.

Сила, с которой электростатическое поле действует на внесенный в него электрический заряд, называется электрической силой.

Действие электростатического поля на заряд зависит от расположения заряда в этом поле.

Если есть несколько заряженных тел, расположенных в различных точках пространства, то в любой точке этого пространства будет проявляться совместное действие всех зарядов, т.е. электростатического поля, создаваемого всеми этими заряженными телами.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 214-215.

90000 Electrostatic fields — Wikiversity 90001 90002 A static field [edit] 90003 90004 We call a field static field when it does not change with time explicitly. Electric fields due to static or stationary charge distributions are electrostatic fields. For example, if we have a charge held fixed somewhere in the space, it creates an electrostatic field. And when it is moving, it creates an electrodynamic field (the charge distribution changes with time explicitly). But when I have a static current of charges in a wire, it creates an electrostatic field (and later it will be seen that moving charges create magnetic field too) because although the charges are moving, the charge distribution in the space is not changing with time as we have a fixed current.90005 90004 The idea of static field must not be confused as it is the same always. Sometimes in electrostatics we encounter problems when the charge distribution do change but we wish to study the final theme when everything is static (as example, when we place a small charge near a conducting surface, it creates induced charges on the conducting surface and thus changes the charge distribution; but in study of electrostatics we are concerned about what the ultimate charge distribution or field will be there and not about what was happening when the charge distribution was changing).90005 90002 Electric Field [edit] 90003 90004 The electric force acting on a charged object can be interpreted as being produced by some property of the space where that object is located. That property of space that leads to forces over the electrostatic charges is called Electric field denoted as E 90005 90004 In mathematical terms, the electric field can be defined precisely in the following way: at any point in space the electric field is a vector E → {\ Displaystyle {\ vec {E}}} obtained by dividing the force F → {\ Displaystyle {\ vec {F}}} acting on a point charge q 0 {\ Displaystyle q_ {0}} placed in that point, over the value of the charge: 90005 90004 E → = F → q 0 {\ Displaystyle {\ vec {E}} = {\ frac {\ vec {F}} {q_ {0}}}} 90005 90004 With 90005 90018 90019 E → {\ Displaystyle {\ vec {E}}} Vector Electric field 90020 90019 F {\ Displaystyle F} Electric force 90020 90019 q 0 {\ Displaystyle q_ {0}} Point charge 90020 90025 90002 Electric Potential [edit] 90003 90004 The source of the electric field can be either other electrostatic charges, or a varying magnetic field.If the field is produced by static electric charge distribution, it is called electrostatic field. In that case, it can be shown that is is a conservative field; namely, the path integral of the field between two points is independent of the path. As a consequence, it is possible to define a potential function: the potential in any point of space ( x , y , z ) {\ Displaystyle (x, y, z)} is equal to the path integral of the electrostatic field from an arbitrary reference point P 0 {\ Displaystyle P_ {0}} until the point ( x , y , z ) {\ Displaystyle (x, y, z)} .90005 90004 V ( x , y , z ) = — ∫ P 0 ( x , y , z ) E → ⋅ d l → {\ Displaystyle V (x, y, z) = — \ int _ {P_ {0}} ^ {(x, y, z)} {\ vec {E}} \ cdot d {\ vec {l}}} 90005 90004 Thus, the electrostatic potential (also known as voltage) is a scalar field and it can be proved that the gradient of that scalar field is equal to minus the electrostatic field: 90005 90004 E → = — ∇ → V {\ Displaystyle {\ vec {E}} = — {\ vec {\ nabla}} V} 90005 .90000 Electrostatic Fields: Coulomb s Law & the Electric Field Intensity 90001 90002 Electromagnetism Laws and Equations 90003 90004 90005 Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields……………………………………… Electrostatic Force …. …………………………………. 2 90006 More information 90007 90002 Exam 1 Practice Problems Solutions 90003 90004 90011 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8 Spring 13 Exam 1 Practice Problems Solutions Part I: Short Questions and Concept Questions Problem 1: Spark Plug Pictured at right is a typical 90006 More information 90007 90002 Chapter 22: The Electric Field.Read Chapter 22 Do Ch. 22 Questions 3, 5, 7, 9 Do Ch. 22 Problems 5, 19, 24 90003 90004 90017 Chapter: The Electric Field Read Chapter Do Ch. Questions 3, 5, 7, 9 Do Ch. Problems 5, 19, 4 The Electric Field Replaces action-at-a-distance Instead of Q 1 exerting a force directly on Q at a distance, 90006 More information 90007 90002 Chapter 7: Polarization 90003 90004 90023 Chapter 7: Polarization Joaquín Bernal Méndez Group 4 1 Index Introduction Polarization Vector The Electric Displacement Vector Constitutive Laws: Linear Dielectrics Energy in Dielectric Systems Forces 90006 More information 90007 90002 State of Stress at Point 90003 90004 90029 State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention, 90006 More information 90007 90002 CHAPTER 24 GAUSS S LAW 90003 90004 90035 CHAPTER 4 GAUSS S LAW 4.The net charge shown in Fig. 4-40 is Q. Identify each of the charges A, B, C shown. A B C FIGURE 4-40 4. From the direction of the lines of force (away from positive and toward 90006 More information 90007 90002 Part A Electromagnetism 90003 90004 90041 Part A Electromagnetism James Sparks [email protected] Hilary Term 2009 E = ρ ǫ 0 B = 0 E = B () E B = μ 0 J + ǫ 0 Contents 0 Introduction ii 0.1 About these notes …………………………… 90006 More information 90007 90002 Chapter 6 Circular Motion 90003 90004 90047 Chapter 6 Circular Motion 6.1 Introduction … 1 6.2 Cylindrical Coordinate System … 2 6.2.1 Unit Vectors … 3 6.2.2 Infinitesimal Line, Area, and Volume Elements in Cylindrical Coordinates … 4 Example 90006 More information 90007 90002 Chapter 28 Fluid Dynamics 90003 90004 90053 Chapter 28 Fluid Dynamics 28.1 Ideal Fluids … 1 28.2 Velocity Vector Field … 1 28.3 Mass Continuity Equation … 3 28.4 Bernoulli s Principle … 4 28.5 Worked Examples: Bernoulli s Equation … 7 Example 90006 More information 90007 90002 Vector Spaces; the Space R n 90003 90004 90059 Vector Spaces; the Space R n Vector Spaces A vector space (over the real numbers) is a set V of mathematical entities, called vectors, U, V, W, etc, in which an addition operation + is defined and in which 90006 More information 90007 90002 Faraday s Law of Induction 90003 90004 90065 Chapter 10 Faraday s Law of Induction 10.1 Faraday s Law of Induction … 10-10.1.1 Magnetic Flux … 10-3 10.1. Lenz s Law … 10-5 10. Motional EMF … 10-7 10.3 Induced Electric Field … 10-10 10.4 Generators … 10-1 90006 More information 90007 90002 P.A.M. Dirac Received May 29, 1931 90003 90004 90071 P.A.M. Dirac, Proc. Roy. Soc. A 133, 60 1931 Quantised Singularities in the Electromagnetic Field P.A.M. Dirac Received May 29, 1931 1. Introduction The steady progress of physics requires for its theoretical 90006 More information 90007 90002 Kyu-Jung Kim Mechanical Engineering Department, California State Polytechnic University, Pomona, U.S.A. 90003 90004 90077 MECHANICS: STATICS AND DYNAMICS Kyu-Jung Kim Mechanical Engineering Department, California State Polytechnic University, Pomona, U.S.A. Keywords: mechanics, statics, dynamics, equilibrium, kinematics, 90006 More information 90007 90002 Charges, voltage and current 90003 90004 90083 Charges, voltage and current Lecture 2 1 Atoms and electrons Atoms are built up from Positively charged nucleus Negatively charged electrons orbiting in shells (or more accurately clouds or orbitals) — 90006 More information 90007 90002 Electric Fields in Dielectrics 90003 90004 90089 Electric Fields in Dielectrics Any kind of matter is full of positive and negative electric charges.In a dielectric, these charges can not move separately from each other through any macroscopic distance, 90006 More information 90007 90002 8.2 Elastic Strain Energy 90003 90004 90095 Section 8. 8. Elastic Strain Energy The strain energy stored in an elastic material upon deformation is calculated below for a number of different geometries and loading conditions. These expressions for 90006 More information 90007 90002 Solutions for Review Problems 90003 90004 90101 olutions for Review Problems 1.Let be the triangle with vertices A (,,), B (4 ,, 1) and C (,, 1). (A) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (C) Find a vector 90006 More information 90007 90002 Conceptual: 1, 3, 5, 6, 8, 16, 18, 19. Problems: 4, 6, 8, 11, 16, 20, 23, 27, 34, 41, 45, 56, 60, 65. Conceptual Questions 90003 90004 90107 Conceptual: 1, 3, 5, 6, 8, 16, 18, 19 Problems: 4, 6, 8, 11, 16, 20, 23, 27, 34, 41, 45, 56, 60, 65 Conceptual Questions 1.The magnetic field can not be described as the magnetic force per unit charge 90006 More information 90007 90002 Chapter 33. The Magnetic Field 90003 90004 90113 Chapter 33. The Magnetic Field Digital information is stored on a hard disk as microscopic patches of magnetism. Just what is magnetism? How are magnetic fields created? What are their properties? These 90006 More information 90007 90002 Eðlisfræði 2, vor 2007 90003 90004 90119 [Assignment View] [Pri Eðlisfræði 2, vor 2007 May 28.Sources of Magnetic Field Assignment is due at 2:00 am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline 90006 More information 90007 90002 Elasticity Theory Basics 90003 90004 90125 G22.3033-002: Topics in Computer Graphics: Lecture # 7 Geometric Modeling New York University Elasticity Theory Basics Lecture # 7: 20 October 2003 Lecturer: Denis Zorin Scribe: Adrian Secord, Yotam Gingold 90006 More information 90007 90002 Chapter 27 Static Fluids 90003 90004 90131 Chapter 27 Static Fluids 27.1 Introduction … 1 27.2 Density … 1 27.3 Pressure in a Fluid … 2 27.4 Pascal s Law: Pressure as a Function of Depth in a Fluid of Uniform Density in a Uniform Gravitational 90006 More information 90007 90002 Differentiation of vectors 90003 90004 90137 Chapter 4 Differentiation of vectors 4.1 Vector-valued functions In the previous chapters we have considered real functions of several (usually two) variables f: D R, where D is a subset of R n, where 90006 More information 90007 90002 Specific Intensity.I ν = 90003 90004 90143 Specific Intensity Initial question: A number of active galactic nuclei display jets, that is, long, nearly linear, structures that can extend for hundreds of kiloparsecs. Many have two oppositely-directed 90006 More information 90007 90002 Chapter 9 Circular Motion Dynamics 90003 90004 90149 Chapter 9 Circular Motion Dynamics 9. Introduction Newton s Second Law and Circular Motion… 9. Universal Law of Gravitation and the Circular Orbit of the Moon … 9 .. Universal Law of Gravitation … 3 90006 More information 90007 90002 Unified Lecture # 4 Vectors 90003 90004 90155 Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann, 90006 More information 90007 90002 LINEAR ALGEBRA W W L CHEN 90003 90004 90161 LINEAR ALGEBRA W W L CHEN c W W L Chen, 1982, 2008.This chapter originates from material used by author at Imperial College, University of London, between 1981 and 1990. It is available free to all individuals, 90006 More information 90007 90002 At the skate park on the ramp 90003 90004 90167 At the skate park on the ramp 1 On the ramp When a cart rolls down a ramp, it begins at rest, but starts moving downward upon release covers more distance each second When a cart rolls up a ramp, it rises 90006 More information 90007 .90000 Revision Notes on Electrostatic | askIITians 90001 90002 90003 90004 90005 90006 90007 90008 90009 90010 Electrostatic Force and Electrostatic field: — 90011 90012 90013 90014 90015 90016 90017 F = K 90018 q 90019 90020 1 90021 90018 q 90019 90020 2 90021/90018 r 90019 90028 2 90029 90030 90017 Here, K = 1 / 4π 90018 ε 90019 90020 0 90021 = 9 × 10 90028 9 90029 90018 Nm 90019 90028 2 90029 90018 C 90019 90028 -2 90029 (in free space) 90030 90047 90048 90010 Relative Permittivity (90018 ε 90019 90020 r 90021): — 90011 90055 90056 90017 The relative permittivity (90018 ε 90019 90020 r 90021) of a medium is defined as the ratio between its permittivity of the medium (90018 ε 90019) and the permittivity (90018 ε 90019 90020 0 90021) of the free space.90030 90017 90018 ε 90019 90020 r 90021 = 90018 ε 90019/90018 ε 90019 90020 0 90021 90030 90047 90048 90010 Coulomb force in vector form: — 90011 The force on charge q 90020 1 90021 due to q 90020 2 90021 is, 90055 90056 90017 90092 90030 90017 If 90018 q 90019 90020 1 90021 90018 q 90019 90020 2 90021> 0, R.H.S is positive. 90030 90017 If 90018 q 90019 90020 1 90021 90018 q 90019 90020 2 90021 <0, a negative sign from 90018 q 90019 90020 1 90021 90018 q 90019 90020 2 90021 will change 90121 and 90122.The relation will again be true, since, in that case have same directions. 90030 90017 C.G.S, 90018 q 90019 = ± 1 stat-coulomb 90030 90017 S.I, 90018 q 90019 = ± 1 Coulomb 90030 90047 90048 90010 Relation between coulomb and stat-coulomb: - 90011 90055 90056 90017 1 coulomb = 3 × 10 90028 9 90029 stat-coulomb 90030 90017 1 coulomb = (1/10) ab-coulomb (e.m.u of charge) 90030 90047 90048 90010 Dielectric constant: - 90011 The dielectric constant (90018 ε 90019 90020 r 90021) of a medium can be defined as the ratio of the force between two charges separated by some distance apart in free space to the force between the same two charges separated by the same distance apart in that medium.90055 90056 90017 So, 90018 ε 90019 90020 r 90021 = 90018 ε 90019/90018 ε 90019 90020 0 90021 = 90018 F 90019 90020 1 90021/90018 F 90019 90020 2 90021 90030 90017 Here, 90018 F 90019 90020 1 90021 and 90018 F 90019 90020 2 90021 are the magnitudes of the force between them in free space and in a medium respectively. 90030 90017 90010? 90011 Line charge, 90018 λ 90019 = 90018 q 90019/90018 L 90019 90030 90017 Surface charge, 90018 σ 90019 = 90018 q 90019/90018 A 90019 90030 90017 Volume charge, 90018 ρ 90019 = 90018 q 90019/90018 V 90019 90030 90047 90048 90010 Electric field (90213) 90011 90010: - 90011 The strength of an electric field is measured by the force experienced by a unit positive charge placed at that point.The direction of field is given by the direction of motion of a unit positive charge if it were free to move. 90055 90056 90017 90220 90030 90017 90018 E 90019 = [Newton / Coulomb] or [Joule / (Coulomb) (meter)] 90030 90047 90048 90010 Electric lines of force: - 90011 An electric line of force is defined as the path 90010, 90011 straight or curved 90010, 90011 along which a unit positive charge is urged to move when free to do so in an electric field.The direction of motion of unit positive charge gives the direction of line of force. 90055 90056 90017 90237 90030 90017 90010 Properties: - 90011 90030 90017 (a) The lines of force are directed away from a positively charged conductor and are directed towards a negatively charged conductor. 90030 90017 (b) A line of force starts from a positive charge and ends on a negative charge. This signifies line of force starts from higher potential and ends on lower potential.90030 90047 90048 90010 Electric field intensity due to a point charge: - 90011 90018 E 90019 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 r 90019 90028 2 90029) 90055 90048 90010 Electric field Intensity due to a linear distribution of charge: - 90011 90055 90056 90017 90270? 90030 90017 (a) At point on its axis. 90030 90017 E = (90018 λ 90019 / 4π 90018 ε 90019 90020 0 90021) [1/90018 a 90019 - 1/90018 a 90019 + 90018 L 90019] 90030 90017 Here, 90018 λ 90019 is the linear charge density.90030 90017 (b) At a point on the line perpendicular to one end. 90030 90017? 90295 90030 90017 Here 90018 λ 90019 is the line charge. 90030 90047 90048 90010 Electric field due to ring of uniform charge distribution: - 90011 90055 90056 90017 90308 90030 90017 At a point on its axis, 90018 E 90019 = (1 / 4π 90018 ε 90019 90020 0 90021) [90018 qx 90019 / (90018 a 90019 90028 2 90029 + 90018 x 90019 90028 2 90029) 90028 3/2 90029] 90030 90047 90048 90010 Electric field due to uniformly charged disc: - 90011 90055 90056 90017 90337 90030 90017 Here 90018 σ 90019 is the surface charge.90030 90047 90048 90010 Electric field due to thin spherical shell: - 90011 90055 90056 90017 (a) 90018 E 90019 90020 out 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 r 90019 90028 2 90029) 90030 90017 (b) 90018 E 90019 90020 in 90021 = 0 90030 90017 90372 90030 90047 90048 90010 Electric field of a non-conducting solid sphere having uniform volume distribution of charge: - 90011 90055 90056 90017 90381 90030 90017 (a) Outside Point: - 90018 E 90019 90020 out 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 Q 90019/90018 r 90019 90028 2 90029) 90030 90017 (b) Inside Point: - 90018 E 90019 90020 in 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 Qr 90019/90018 R 90019 90028 3 90029) 90030 90017 (c) On the Surface: - 90018 E 90019 90020 surface 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 Q 90019/90018 R 90019 90028 2 90029) 90030 90017 Here, 90018 Q 90019 is the total charge 90030 90047 90048 90010 Electric field of a cylindrical conductor of infinite length having line charge 90018 λ 90019: - 90011 90055 90056 90017 90444 90030 90017 (a) Outside the cylinder: - E = λ / 2πε0r 90030 90017 (b) Inside the cylinder: - 90018 E 90019 = 0 90030 90047 90048 90010 Electric field of a non-conducting cylinder having uniform volume density of charge: - 90011 90055 90056 90017 (a) Outside the cylinder: - 90018 E 90019 = 90018 λ 90019 / 2π 90018 ε 90019 90020 0 90021 90018 r 90019 90030 90017 (b) Inside a point: - 90018 E 90019 = 90018 ρr 90019/2 90018 ε 90019 90020 0 90021 90030 90047 90048 90010 Electric field of an infinite plane sheet of charge surface charge (90018 σ 90019): - 90011 90018 E 90019 = 90018 σ 90019/2 90018 ε 90019 90020 0 90021 90055 90056 90017 90497 90030 90047 90048 90010 Electric field due to two oppositely infinite charged sheets: - 90011 90055 90056 90017 (a) Electric field at points outside the charged sheets: - 90030 90017 E 90020 P 90021 = 90018 E 90019 90020 R 90021 = 0 90030 90017 (b) Electric field at point in between the charged sheets: - 90030 90017 E 90020 Q 90021 = 90018 σ 90019/90018 ε 90019 90020 0 90021 90030 90047 90048 90010 Electric Dipole: - 90011 An electric dipole consists of two equal and opposite charges situated very close to each other.90055 90056 90047 90048 90010 Dipole Moment: - 90011 Dipole moment (90537) of an electric dipole is defined as the product of the magnitude of one of the charges and the vector distance from negative to positive charge. 90055 90056 90017 90541 90030 90047 90048 90010 Unit of Dipole Moment: - 90011 coulomb meter (S.I), stat coulomb cm (non S.I) 90055 90056 90047 90048 90010 Electric field due to an electric dipole: - 90011 90055 90056 90017 (a) At any point on the axial line: - 90030 90017 90558 90030 90017 Alt Tag: Electric field due to an electric dipole on the axial line.90030 90017 90563 90030 90017 (b) At a point on the equatorial line (perpendicular bisector): - 90030 90017 90568 90030 90017 90571 90030 90017 (c) At any point: - 90030 90017 90576 90030 90017 90579 90030 90047 90048 90010 Torque (90011 90585 90010) acting on a electric dipole in a uniform electric field (90018 E 90019): - 90011 90055 90056 90017 90585 = 90018 pE 90019 sin 90018 θ 90019 90030 90017 90018 90019 Here, 90018 p 90019 is the dipole moment and 90018 θ 90019 is the angle between direction of dipole moment and electric field 90018 E 90019.90030 90047 90048 90010 Electric Flux: - 90011 Electric flux 90018? 90019 90020 E 90021 for a surface placed in an electric field is the sum of dot product of 90213 and 90618 for all the elementary areas constituting the surface. 90055 90056 90017 90622 90030 90047 90048 90010 Gauss Theorem: - 90011 It states that, for any distribution of charges, the total electric flux linked with a closed surface is 1/90018 ε 90019 90020 0 90021 times the total charge with in the surface.90055 90056 90017 90635 90030 90047 90048 90010 Electric field (90018 E 90019) of an infinite rod at a distance (90018 r 90019) from the line having linear charge density (90018 λ 90019): - 90011 90055 90056 90017 E = 90018 λ 90019 / 2π 90018 ε 90019 90020 0 90021 90018 r 90019 90030 90017 The direction of electric field 90018 E 90019 is radially outward for a line of positive charge. 90030 90047 90048 90010 Electric field of a spherically symmetric distribution of charge of Radius 90018 R 90019: - 90011 90055 90056 90017 90672 90030 90017 (a) Point at outside (90018 r 90019> 90018 R 90019): — 90018 E 90019 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 r 90019 90028 2 90029), Here 90018 q 90019 is the total charge.90030 90017 (b) Point at inside (90018 r 90019 <90018 R 90019): - 90018 E 90019 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 qr 90019/90018 R 90019 90028 3 90029), Here 90018 q 90019 is the total charge. 90030 90047 90048 90010 Electric field due to an infinite non-conducting flat sheet having charge σ: - 90011 90055 90056 90017 E = 90018 σ 90019/2 90018 ε 90019 90020 0 90021 90030 90017 90729 90030 90017 This signifies, the electric field near a charged sheet is independent of the distance of the point from the sheet and depends only upon its charge density and is directed normally to the sheet.90030 90047 90048 90010 Electric field due to an infinite flat conductor carrying charge: - 90011 90055 90056 90017 90010? 90011 E 90010 = 90018 σ 90019/90018 ε 90019 90020 0 90021 90011 90030 90047 90048 90010 Electric pressure (90018 P 90019 90020 elec 90021) on a charged conductor: - 90011 90055 90056 90017 90018 P 90019 90020 elec 90021 = (½ 90018 ε 90019 90020 0 90021) 90018 σ 90019 90028 2 90029 90030 90005 90006 90007 90008 90009 90010 Electro-Static Potential and Capacitance: - 90011 90012 90013 90014 90015 90016 90017 (a) Electric potential, at any point, is defined as the negative line integral of electric field from infinity to that point along any path.90030 90017 90790 90030 90017 90018 (b) V 90019 (90018 r 90019) = 90018 kq 90019/90018 r 90019 90030 90017 90018 (c) 90019 Potential difference, between any two points, in an electric field is defined as the work done in taking a unit positive charge from one point to the other against the electric field. 90030 90017 90018 W 90019 90020 AB 90021 = 90018 q 90019 [90018 V 90019 90020 A 90021 - 90018 V 90019 90020 B 90021] 90030 90017 So, 90018 V 90019 = [90018 V 90019 90020 A 90021 - 90018 V 90019 90020 B 90021] = 90018 W 90019/90018 q 90019 90030 90017 Units: - volt (S.I), stat-volt (C.G.S) 90030 90017 Dimension: - [90018 V 90019] = [ML 90028 2 90029 T 90028 -3 90029 A 90028 -1 90029] 90030 90017 Relation between volt and stat-volt: - 1 volt = (1/300) stat-volt 90030 90047 90048 90010 Relation between electric field (90018 E 90019) and electric potential (90018 V 90019): - 90011 90055 90056 90017 90018 E 90019 = - 90018 dV 90019/90018 dx 90019 = - 90018 dV 90019/90018 dr 90019 90030 90047 90048 90010 Potential due to a point charge: - 90011 90055 90056 90017 90018 V 90019 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 r 90019) 90030 90047 90048 90010 Potential at point due to several charges: - 90011 90055 90056 90017 90018 V 90019 = (1 / 4π 90018 ε 90019 90020 0 90021) [90018 q 90019 90020 1 90021/90018 r 90019 90020 1 90021 + 90018 q 90019 90020 2 90021/90018 r 90019 90020 2 90021 + 90018 q 90019 90020 3 90021/90018 r 90019 90020 3 90021] 90030 90017 = 90018 V 90019 90020 1 90021 + 90018 V 90019 90020 2 90021 + 90018 V 90019 90020 2 90021 + ....90030 90047 90048 90010 Potential due to charged spherical shell: - 90011 90055 90056 90017 (a) Outside, 90018 V 90019 90020 out 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 r 90019) 90030 90017 (b) Inside, 90018 V 90019 90020 in 90021 = - (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019 / R) 90030 90017 (c) On the surface, 90018 V 90019 90020 surface 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 R 90019) 90030 90047 90048 90010 Potential due to a uniformly charged non-conducting sphere: - 90011 90055 90056 90017 (a) Outside, 90018 V 90019 90020 out 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 r 90019) 90030 90017 (b) Inside, 90018 V 90019 90020 in 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) [90018 q 90019 (3 90018 R 90019 90028 2 90029 - 90018 r 90019 90028 2 90029) / 2 90018 R 90019 90028 3 90029] 90030 90017 (c) On the surface, 90018 V 90019 90020 surface 90021 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 R 90019) 90030 90017 (d) In center, 90018 V 90019 90020 center 90021 = (3/2) [(1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019/90018 R 90019)] = 3/2 [90018 V 90019 90020 surface 90021] 90030 90047 90048 90010 Common potential (two spheres joined by thin wire): - 90011 90055 90056 90017 (a) Common potential, 90018 V 90019 = (1 / 4π 90018 ε 90019 90020 0 90021) [(90018 Q 90019 90020 1 90021 + 90018 Q 90019 90020 2 90021) / (90018 r 90019 90020 1 90021 + 90018 r 90019 90020 2 90021)] 90030 90017 (b) 90018 q 90019 90020 1 90021 = 90018 r 90019 90020 1 90021 (90018 Q 90019 90020 1 90021 + 90018 Q 90019 90020 2 90021) / (90018 r 90019 90020 1 90021 + 90018 r 90019 90020 2 90021) = 90018 r 90019 90020 1 90021 90018 Q 90019/90018 r 90019 90020 1 90021 + 90018 r 90019 90020 2 90021; 90018 q 90019 90020 2 90021 = 90018 r 90019 90020 2 90021 90018 Q 90019/90018 r 90019 90020 1 90021 + 90018 r 90019 90020 2 90021 90030 90017 (c) 90018 q 90019 90020 1 90021/90018 q 90019 90020 2 90021 = 90018 r 90019 90020 1 90021/90018 r 90019 90020 2 90021 or 90018 σ 90019 90020 1 90021/90018 σ 90019 90020 2 90021 = 90018 r 90019 90020 1 90021/90018 r 90019 90020 2 90021 90030 90047 90048 90010 Potential at any point due to an electric dipole: - 90011 90055 90056 90017 90018 V 90019 (90018 r 90019, 90018 θ 90019) = 90018 qa 90019 cos 90018 θ 90019 / 4π 90018 ε 90019 90020 0 90021 90018 r 90019 90028 2 90029 = 90018 p 90019 cos 90018 θ 90019 / 4π 90018 ε 90019 90020 0 90021 90018 r 90019 90028 2 90029 90030 90017 (a) Point lying on the axial line: - 90018 V 90019 = 90018 p 90019 / 4π 90018 ε 90019 90020 0 90021 90018 r 90019 90028 2 90029 90030 90017 (b) Point situated on equatorial lines: - 90018 V 90019 = 0 90030 90047 90048 90010 If 90018 n 90019 drops coalesce to form one drop, then, 90011 90055 90056 90017 (a) 90018 R 90019 = 90018 n 90019 90028 1/3 90029 90018 r 90019 90030 90017 (b) 90018 Q 90019 = 90018 nq 90019 90030 90017 (c) 90018 V 90019 = 90018 n 90019 90028 2/3 90029 90018 V 90019 90020 small 90021 90030 90017 (d) 90018 σ 90019 = 90018 n 90019 90028 1/3 90029 90018 σ 90019 90020 small 90021 90030 90017 (e) 90018 E 90019 = 90018 n 90019 90028 1/3 90029 90018 E 90019 90020 small 90021 90030 90047 90048 90010 Electric potential energy 90018 U 90019 or work done of the system 90018 W 90019 having charge 90018 q 90019 90020 1 90021 and 90018 q 90019 90020 2 90021 90011: - 90055 90056 90017 90018 W 90019 = 90018 U 90019 = (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019 90020 1 90021 90018 q 90019 90020 2 90021/90018 r 90019 90020 12 90021) = 90018 q 90019 90020 1 90021 V 90020 1 90021 90030 90047 90048 90010 Electric potential energy 90018 U 90019 or work done of the system 90018 W 90019 of a three particle system having charge 90018 q 90019 90020 1 90021, 90018 q 90019 90020 2 90021 and 90018 q 90019 90020 3 90021 90011: - 90055 90056 90017 90018 W = U = 90019 (1 / 4π 90018 ε 90019 90020 0 90021) (90018 q 90019 90020 1 90021 90018 q 90019 90020 2 90021/90018 r 90019 90020 12 90021 + 90018 q 90019 90020 1 90021 90018 q 90019 90020 3 90021/90018 r 90019 90020 13 90021 + 90018 q 90019 90020 2 90021 90018 q 90019 90020 3 90021/90018 r 90019 90020 23 90021) 90030 90047 90048 90010 Electric potential energy of an electric dipole in an electric field: - 90011 Potential energy of an electric dipole, in an electrostatic field, is defined as the work done in rotating the dipole from zero energy position to the desired position in the electric field .90055 90056 90017 91423 90030 90017 (a) If 90018 θ 90019 = 90º, then 90018 W 90019 = 0 90030 90017 (b) If 90018 θ 90019 = 0º, then 90018 W 90019 = - 90018 pE 90019 90030 90017 (c) If 90018 θ 90019 = 180º, then 90018 W 90019 = 90018 pE 90019 90030 90047 90048 90010 Kinetic energy of a charged particle moving through a potential difference: - 90011 90055 90056 90017 K. E = ½ 90018 mv 90019 90028 2 90029 = 90018 eV 90019 90030 90047 90048 90017 90010 Conductors: - 90011 Conductors are those substance through which electric charge easily.90030 90055 90048 90017 90010 Insulators: - 90011 Insulators (also called dielectrics) are those substances through which electric charge can not pass easily. 90030 90055 90048 90017 90010 Capacity: 90011 - The capacity of a conductor is defined as the ratio between the charge of the conductor to its potential 90030 90055 90056 90017 C = 90018 Q 90019/90018 V 90019 90030 90017 90010 Units: - 90011 90030 90017 S.I - farad (coulomb / volt) 90030 90017 C.G.S - stat farad (stat-coulomb / stat-volt) 90030 90017 90010 Dimension of 90018 C 90019: - 90011 [M 90028 -1 90029 L 90028 -2 90029 T 90028 4 90029 A 90028 2 90029] 90030 90047 90048 90010 Capacity of an isolated spherical conductor: - 90011 90055 90056 90017 90018 C 90019 = 4π 90018 ε 90019 90020 0 90021 90018 r 90019 90030 90047 90048 90017 90010 Capacitor: - 90011 A capacitor or a condenser is an arrangement which provides a larger capacity in a smaller space.90030 90055 90048 90017 90010 Capacity of a parallel plate capacitor: - 91535 90011 90030 90055 90056 90017 C 90020 air 90021 = 90018 ε 90019 90020 0 90021 90018 A 90019/90018 d 90019 90030 91552 90030 90017 C 90020 med 90021 = 90018 Kε 90019 90020 0 90021 90018 A 90019/90018 d 90019 90030 90017 Here, 90018 A 90019 is the common area of the two plates and 90018 d 90019 is the distance between the plates.90030 90047 90048 90010 Effect of dielectric on the capacitance of a capacitor: - 90011 90055 90056 90017 90018 C 90019 = 90018 ε 90019 90020 0 90021 90018 A 90019 / [90018 d 90019 - 90018 t 90019 + (90018 t 90019 / K)] 90030 90017 Here 90018 d 90019 is the separation between the plates, 90018 t 90019 is the thickness of the dielectric slab 90018 A 90019 is the area and 90018 K 90019 is the dielectric constant of the material of the slab. 90030 90017 If the space is completely filled with dielectric medium (90018 t 90019 = 90018 d 90019), then, 90030 90017 90018 C 90019 = 90018 ε 90019 90020 0 90021 90018 KA 90019/90018 d 90019 90030 90047 90048 90010 Capacitance of a sphere: - 90011 90055 90056 90017 (a) 90018 C 90019 90020 air 90021 = 4π 90018 ε 90019 90020 0 90021 90018 R 90019 90030 90017 (b) 90018 C 90019 90020 med 90021 = 90018 K 90019 (4π 90018 ε 90019 90020 0 90021 90018 R 90019) 90030 90047 90048 90010 Capacity of a spherical condenser: - 90011 90055 90056 90017 (a) When outer sphere is earthed: 90010 - 90011 90030 90017 C 90020 air 90021 = 4π 90018 ε 90019 90020 0 90021 [90018 ab 90019 / (90018 b 90019 - 90018 a 90019)] 90030 90017 C 90020 med 90021 = 4π 90018 ε 90019 90020 0 90021 [K 90018 ab 90019 / (90018 b 90019 - 90018 a 90019)] 90030 90017 (b) When the inner sphere is earthed: - 90030 90017 C 90020 1 90021 = 4π 90018 ε 90019 90020 0 90021 [90018 ab 90019 / (90018 b 90019 - 90018 a 90019)] 90030 90017 C 90020 2 90021 = 4π 90018 ε 90019 90020 0 90021 90018 b 90019 90018? 90019 90030 90017 Net Capacity, 90018 C 90019 '= 4π 90018 ε 90019 90020 0 90021 [90018 b 90019 90028 2 90029/90018 b 90019 - 90018 a 90019] 90030 90017 Increase in capacity, Δ 90018 C 90019 = 4π 90018 ε 90019 90020 0 90021 90018 b 90019 90030 90017 It signifies, by connecting the inner sphere to earth and charging the outer one we get an additional capacity equal to the capacity of outer sphere.90030 90047 90048 90010 Capacity of a cylindrical condenser: - 90011 90055 90056 90017 90018 C 90019 90020 air 90021 = 90018 λl 90019 / [(90018 λ 90019 / 2π 90018 ε 90019 90020 0 90021) (log 90020 e 90021 90018 b 90019/90018 a 90019)] = [2π 90018 ε 90019 90020 0 90021 90018 l 90019 / (log 90020 e 90021 90018 b 90019/90018 a 90019)] 90030 90017 C 90020 med 90021 = [2π 90018 Kε 90019 90020 0 90021 90018 l 90019 / (log 90020 e 90021 90018 b 90019/90018 a 90019)] 90030 90047 90048 90010 Potential energy of a charged capacitor (Energy stored in a capacitor): - 90011 90055 90056 90017 90018 W 90019 = ½ 90018 QV 90019 = ½ 90018 Q 90019 90028 2 90029/90018 C 90019 = ½ 90018 CV 90019 90028 2 90029 90030 90047 90048 90010 Energy density of a capacitor: - 90011 90055 90056 90017 90018 U 90019 = ½ 90018 ε 90019 90020 0 90021 90018 E 90019 90028 2 90029 = ½ (90018 σ 90019 90028 2 90029/90018 ε 90019 90020 0 90021) 90030 90017 This signifies the energy density of a capacitor is independent of the area of plates of distance between them so long the value of 90018 E 90019 does not change.90030 90017 90010? (A) 90011 90030 90017 (i) Capacitors in parallel: - 90018 C 90019 = 90018 C 90019 90020 1 90021 + 90018 C 90019 90020 2 90021 + 90018 C 90019 90020 3 90021 + ... .. + 90018 C 90019 90020 n 90021 90030 90017 90020 90021 91881 The resultant capacity of a number of capacitors, connected in parallel, is equal to the sum of their individual capacities. 90030 90017 (ii) 90018 V 90019 90020 1 90021 = 90018 V 90019 90020 2 90021 = 90018 V 90019 90020 3 90021 = 90018 V 90019 90030 90017 (iii) 90018 q 90019 90020 1 90021 = 90018 C 90019 90020 1 90021 90018 V 90019, 90018 q 90019 90020 2 90021 = 90018 C 90019 90020 2 90021 90018 V 90019, 90018 q 90019 90020 3 90021 = 90018 C 90019 90020 3 90021 90018 V 90019 90030 90017 (iv) Energy Stored, 90018 U 90019 = 90018 U 90019 90020 1 90021 + 90018 U 90019 90020 2 90021 + 90018 U 90019 90020 3 90021 90030 90017 (b) 90030 90017 (i) Capacitors in Series: - 1/90018 C 90019 = 1/90018 C 90019 90020 1 90021 + 1/90018 C 90019 90020 2 90021 + ...... + 1/90018 C 90019 90020 n 90021 90030 90017 91966? The reciprocal of the resultant capacity of a number of capacitors, connected in series, is equal to the sum of the reciprocals of their individual capacities.90030 90017 90018 (ii) 90019 90018 q 90019 90020 1 90021 = 90018 q 90019 90020 2 90021 = 90018 q 90019 90020 3 90021 = 90018 q 90019 90030 90017 90018 (iii) V 90019 90020 1 90021 = 90018 q 90019/90018 C 90019 90020 1 90021, 90018 V 90019 90020 2 90021 = 90018 q 90019/90018 C 90019 90020 2 90021, 90018 V 90019 90020 3 90021 = 90018 q 90019 / 90018 C 90019 90020 3 90021 90030 90017 (iv) Energy Stored, 90018 U 90019 = 90018 U 90019 90020 1 90021 + 90018 U 90019 90020 2 90021 + 90018 U 90019 90020 3 90021 90030 90047 90048 90010 Energy stored in a group of capacitors: - 90011 90055 90056 90017 (a) Energy stored in a series combination of capacitors: - 90030 90017 90018 W 90019 = ½ (90018 q 90019 90028 2 90029/90018 C 90019 90020 1 90021) + ½ (90018 q 90019 90028 2 90029/90018 C 90019 90020 2 90021) + ½ (90018 q 90019 90028 2 90029/90018 C 90019 90020 3 90021) = 90018 W 90019 90020 1 90021 + 90018 W 90019 90020 2 90021 + 90018 W 90019 90020 3 90021 90030 90017 Thus, net energy stored in the combination is equal to the sum of the energies stored in the component capacitors.90030 90017 (b) Energy stored in a parallel combination of capacitors: - 90030 90017 W = ½ 90018 C 90019 90020 1 90021 90018 V 90019 90028 2 90029 + ½ 90018 C 90019 90020 2 90021 90018 V 90019 90028 2 90029 + ½ 90018 C 90019 90020 3 90021 90018 V 90019 90028 2 90029 = 90018 W 90019 90020 1 90021 + 90018 W 90019 90020 2 90021 + 90018 W 90019 90020 3 90021 90030 90017 The net energy stored in the combination is equal to sum of energies stored in the component capacitors.90030 90047 90048 90010 Force of attraction between plates of a charged capacitor: - 90011 90055 90056 90017 90018 (a) F 90019 = ½ 90018 ε 90019 90020 0 90021 90018 E 90019 90028 2 90029 90018 A 90019 90030 90017 90018 (b) F 90019 = σ 90028 2 90029 90018 A 90019/2 90018 ε 90019 90020 0 90021 90030 90017 90018 (c) F = Q 90019 90028 2 90029/2 90018 ε 90019 90020 0 90021 90018 A 90019 90030 90047 90048 90010 Force on a dielectric in a capacitor: - 90011 90055 90056 90017 90018 F 90019 = (90018 Q 90019 90028 2 90029/2 90018 C 90019 90028 2 90029) (90018 dC 90019/90018 dx 90019) = ½ 90018 V 90019 90028 2 90029 (90018 dC 90019/90018 dx 90019) 90030 90047 90048 90010 Common potential when two capacitors are connected: - 90011 90055 90056 90017 V = [90018 C 90019 90020 1 90021 90018 V 90019 90020 1 90021 + 90018 C 90019 90020 2 90021 90018 V 90019 90020 2 90021] / [90018 C 90019 90020 1 90021 + 90018 C 90019 90020 2 90021] = [90018 Q 90019 90020 1 90021 + 90018 Q 90019 90020 2 90021] / [90018 C 90019 90020 1 90021 + 90018 C 90019 90020 2 90021] 90030 90047 90048 90010 Charge transfer 90011 90010 when two capacitors are connected: - 90011 90055 90056 90017 Δ 90018 Q 90019 = [90018 C 90019 90020 1 90021 90018 C 90019 90020 2 90021/90018 C 90019 90020 1 90021 + 90018 C 90019 90020 2 90021] [90018 V 90019 90020 1 90021 - 90018 V 90019 90020 2 90021] 90030 90047 90048 90010 Energy loss 90011 90010 when two capacitors are connected: - 90011 90055 90056 90017 Δ 90018 U 90019 = ½ [90018 C 90019 90020 1 90021 90018 C 90019 90020 2 90021/90018 C 90019 90020 1 90021 + 90018 C 90019 90020 2 90021] [90018 V 90019 90020 1 90021 - 90018 V 90019 90020 2 90021] 90028 2 90029 90030 90047 90048 90010 Charging of a capacitor: - 90011 90055 90056 90017 (a) 90018 Q 90019 = 90018 Q 90019 90020 0 90021 (1-e 90028 - 90018 t 90019/90018 RC 90019 90029) 90030 90017 (b) 90018 V 90019 = 90018 V 90019 90020 0 90021 (1-e 90028 - 90018 t 90019/90018 RC 90019 90029) 90030 90017 (c) 90018 I 90019 = 90018 I 90019 90020 0 90021 (1-e 90028 - 90018 t 90019/90018 RC 90019 90029) 90030 90017 (d) 90018 I 90019 90020 0 90021 = 90018 V 90019 90020 0 90021/90018 R 90019 90030 90047 90048 90010 Discharging of a capacitor: - 90011 90055 90056 90017 (a) 90018 Q = Q 90020 0 90021 (e 90028 -t / RC 90029) 90019 90030 90017 (b) 90018 V 90019 = 90018 V 90019 90020 0 90021 (e 90028 - 90018 t 90019/90018 RC 90019 90029) 90030 90017 (c) 90018 I 90019 = 90018 I 90019 90020 0 90021 (e 90028 - 90018 t 90019/90018 RC 90019 90029) 90030 90047 90048 90010 Time constant: - 90011 92428 90055 90056 90017 Title: 90030 90017 Revision Notes on Electrostatic | askIITians 90030 90017 Meta description: 90030 90017 Revision Notes on electrostatic force, electrostatic field, electro static potential, electrostatic energy and capacitance provides by askIITians.90030 90017 92440 90030 92442 92440 92444 Course Features 92445 90047 90048 728 Video Lectures 90055 90048 Revision Notes 90055 90048 Previous Year Papers 90055 90048 Mind Map 90055 90048 Study Planner 90055 90048 NCERT Solutions 90055 90048 Discussion Forum 90055 90048 Test paper with Video Solution 90055 90056 92440 .

Определение

Классификация

Однородное электрическое поле

Неоднородное электрическое поле

Характеристики

Потенциал

Напряжённость поля

Напряжение

Методы обнаружения

Методы расчета электрического поля

Использование

Понятие электростатического поля — fiziku5.ru

Электрическое поле – FIZI4KA

Электризация тел

Взаимодействие зарядов. Два вида зарядов

Закон сохранения электрического заряда

Закон Кулона

Действие электрического поля на электрические заряды

Напряженность электрического поля

Принцип суперпозиции электрических полей

Потенциальность электростатического поля

Потенциал электрического поля. Разность потенциалов

Проводники в электрическом поле

Диэлектрики в электрическом поле

Электрическая емкость. Конденсатор

Энергия электрического поля конденсатора

Основные формулы раздела «Электрическое поле»

Тестирование онлайн

Электростатическое поле

Напряженность поля

Принцип суперпозиции

Т. Электростатическое поле — PhysBook

Электростатическое поле

Литература

Похожие записи

Coocox: CooCox. Текущее состояние дел. / CoIDE / Pluslab

Приборы для измерения давления жидкости: Манометр — из чего состоит? Виды и типы

Регулируемая индуктивность: Регулируемая катушка индуктивности на кольцевом сердечнике

Добавить комментарий Отменить ответ