Что такое логические элементы и как они работают. Какие бывают виды логических элементов. Как используются таблицы истинности. Чем отличаются элементы И, ИЛИ, НЕ и их комбинации. Как применяются логические элементы в цифровой технике.
Что такое логические элементы и для чего они нужны
Логические элементы являются базовыми «кирпичиками», из которых строятся все цифровые устройства и микросхемы. Это простейшие электронные схемы, выполняющие элементарные логические операции над двоичными сигналами.
Основные характеристики логических элементов:
- Имеют несколько входов и один выход
- Работают с двоичными сигналами (0 и 1)
- Выполняют строго определенную логическую функцию
- Описываются таблицей истинности
Логические элементы позволяют реализовывать сложные цифровые устройства, выполняющие обработку и преобразование цифровой информации. Они являются основой всей современной цифровой электроники.
Основные виды логических элементов
Существует несколько базовых типов логических элементов, на основе которых строятся более сложные цифровые схемы:

Элемент И (AND)
Выполняет операцию логического умножения. Выдает 1 на выходе только если на всех входах 1.
Элемент ИЛИ (OR)
Реализует логическое сложение. Выдает 1 если хотя бы на одном входе 1.
Элемент НЕ (NOT)
Инвертирует входной сигнал. Преобразует 0 в 1 и наоборот.
Элемент И-НЕ (NAND)
Комбинация И и НЕ. Выдает 0 только если на всех входах 1.
Элемент ИЛИ-НЕ (NOR)
Комбинация ИЛИ и НЕ. Выдает 0 если хотя бы на одном входе 1.
Элемент «Исключающее ИЛИ» (XOR)
Выдает 1 если входные сигналы не равны.
Таблицы истинности логических элементов
Работа логических элементов описывается с помощью таблиц истинности. Они показывают значение выходного сигнала для всех возможных комбинаций входных сигналов.
Например, таблица истинности для элемента И:
| Вход A | Вход B | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таблицы истинности позволяют однозначно описать поведение логического элемента и являются важным инструментом при проектировании цифровых схем.
Как используются логические элементы на практике
Логические элементы находят широкое применение в различных областях цифровой электроники:
- Проектирование процессоров и микроконтроллеров
- Создание запоминающих устройств
- Разработка интерфейсов и шин данных
- Реализация цифровых фильтров и преобразователей сигналов
- Построение схем управления в автоматике
На основе базовых логических элементов создаются более сложные цифровые узлы — триггеры, счетчики, регистры, сумматоры и т.д. Из них в свою очередь строятся законченные цифровые устройства.
Реализация логических элементов на транзисторах
Физически логические элементы реализуются на основе полупроводниковых приборов — диодов и транзисторов. Существует несколько технологий:
- Транзисторно-транзисторная логика (ТТЛ)
- Эмиттерно-связанная логика (ЭСЛ)
- Комплементарная МОП-логика (КМОП)
Например, простейшая схема элемента И-НЕ на биполярных транзисторах:
«` «`Такая реализация позволяет создавать компактные и быстродействующие логические схемы на интегральных микросхемах.
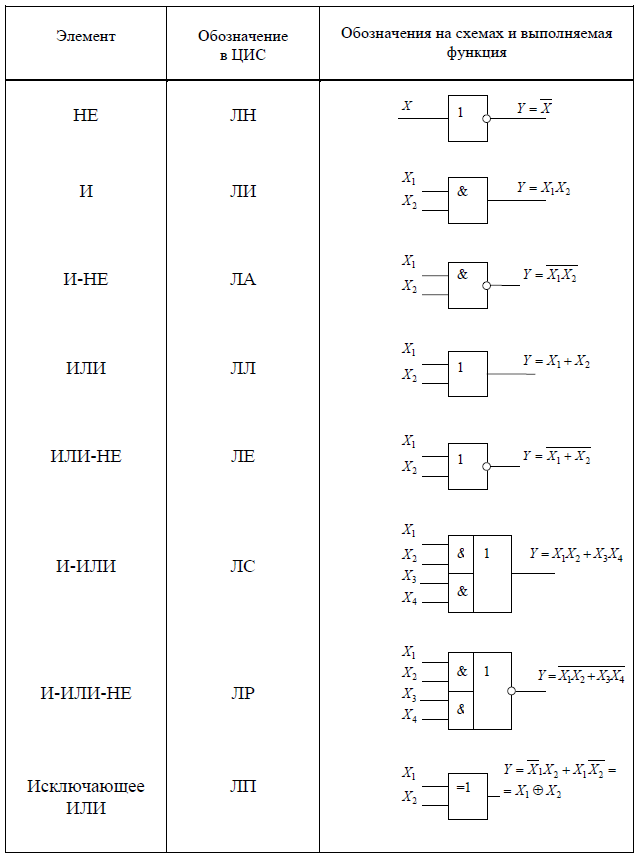
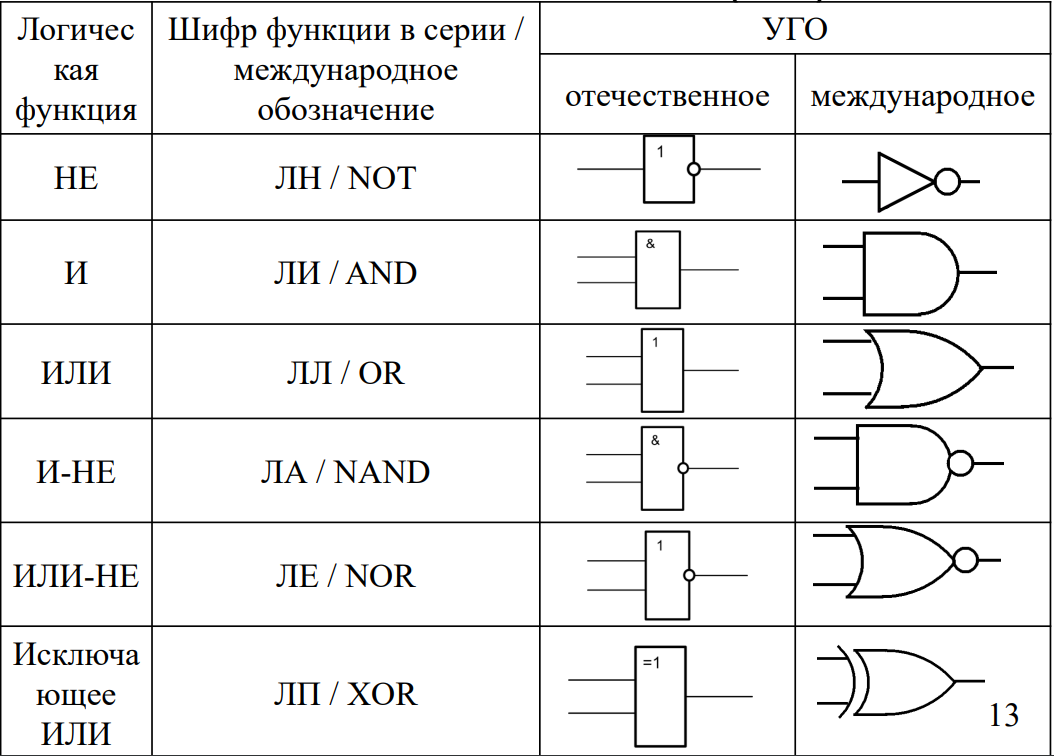
Условные графические обозначения логических элементов
Для изображения логических элементов на принципиальных схемах используются специальные условные графические обозначения (УГО). Существуют российские и международные стандарты обозначений.

Основные обозначения логических элементов:
«` «`Знание этих обозначений необходимо для чтения и разработки принципиальных схем цифровых устройств.
Преимущества и недостатки различных типов логических элементов
Каждый тип логических элементов имеет свои особенности:
Элементы И, ИЛИ, НЕ
Преимущества:
- Простота и наглядность
- Легкость проектирования схем
Недостатки:
- Требуется больше элементов для сложных функций
- Низкая помехоустойчивость
Элементы И-НЕ, ИЛИ-НЕ
Преимущества:
- Функциональная полнота
- Высокая помехоустойчивость
- Простота аппаратной реализации
Недостатки:
- Сложнее в понимании
- Требуют дополнительных инверторов
Перспективы развития логических элементов
Современные тенденции в области логических элементов:
- Уменьшение размеров транзисторов до единиц нанометров
- Снижение энергопотребления
- Увеличение быстродействия
- Разработка квантовых логических элементов
- Создание элементов на основе углеродных нанотрубок
Развитие технологий производства логических элементов открывает новые возможности для создания более мощных и эффективных цифровых устройств.
Базовые логические элементы.
И, ИЛИ, НЕ и их комбинации
В Булевой алгебре, на которой базируется вся цифровая техника, электронные элементы должны выполнять ряд определённых действий. Это так называемый логический базис. Вот три основных действия:
ИЛИ – логическое сложение (дизъюнкция) – OR;
И – логическое умножение (конъюнкция) – AND;
НЕ – логическое отрицание (инверсия) – NOT.
Примем за основу позитивную логику, где высокий уровень будет «1», а низкий уровень примем за «0». Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.
Логический элемент И.
На рисунке представлена таблица истинности элемента «И» с двумя входами. Хорошо видно, что логическая единица появляется на выходе элемента только при наличии единицы на первом входе и
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
На принципиальных схемах логический элемент «И» обозначают так.

На зарубежных схемах обозначение элемента «И» имеет другое начертание. Его кратко называют AND.

Логический элемент ИЛИ.
Элемент «ИЛИ» с двумя входами работает несколько по-другому. Достаточно логической единицы на первом входе или на втором как на выходе будет логическая единица. Две единицы так же дадут единицу на выходе.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
На схемах элемент «ИЛИ» изображают так.

На зарубежных схемах его изображают чуть по-другому и называют элементом OR.

Логический элемент НЕ.
Элемент, выполняющий функцию инверсии «НЕ» имеет один вход и один выход. Он меняет уровень сигнала на противоположный. Низкий потенциал на входе даёт высокий потенциал на выходе и наоборот.
| Вход X | Выход Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Вот таким образом его показывают на схемах.

В зарубежной документации элемент «НЕ» изображают следующим образом. Сокращённо называют его NOT.

Все эти элементы в интегральных микросхемах могут объединяться в различных сочетаниях. Это элементы: И–НЕ, ИЛИ–НЕ, и более сложные конфигурации. Пришло время поговорить и о них.
Логический элемент 2И-НЕ.
Рассмотрим несколько реальных логических элементов на примере серии транзисторно-транзисторной логики (ТТЛ) К155 с малой степенью интеграции. На рисунке когда-то очень популярная микросхема К155ЛА3, которая содержит четыре независимых элемента 2И – НЕ. Кстати, с помощью её можно собрать простейший маячок на микросхеме.

Цифра всегда обозначает число входов логического элемента. В данном случае это двухвходовой элемент «И» выходной сигнал которого инвертируется. Инвертируется, это значит «0» превращается в «1», а «1» превращается в «0». Обратим внимание на кружочек на выходах – это символ инверсии. В той же серии существуют элементы 3И–НЕ, 4И–НЕ, что означает элементы «И» с различным числом входов (3, 4 и т.д.).
Как вы уже поняли, один элемент 2И-НЕ изображается вот так.

По сути это упрощённое изображение двух объёдинённых элементов: элемента 2И и элемента НЕ на выходе.
Зарубежное обозначение элемента И-НЕ (в данном случае 2И-НЕ). Называется NAND.

Таблица истинности для элемента 2И-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
В таблице истинности элемента 2И – НЕ мы видим, что благодаря инвертору получается картина противоположная элементу «И». В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И – НЕ» часто называют элементом Шеффера.
Логический элемент 2ИЛИ-НЕ.
Логический элемент 2ИЛИ – НЕ представлен в серии К155 микросхемой 155ЛЕ1. Она содержит в одном корпусе четыре независимых элемента. Таблица истинности так же отличается от схемы «ИЛИ» применением инвертирования выходного сигнала.

Таблица истинности для логического элемента 2ИЛИ-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
Изображение на схеме.

На зарубежный лад изображается так. Называют как NOR.

Мы имеем только один высокий потенциал на выходе, обусловленный подачей на оба входа одновременно низкого потенциала. Здесь, как и на любых других принципиальных схемах, кружочек на выходе подразумевает инвертирование сигнала. Так как схемы И – НЕ и ИЛИ – НЕ встречаются очень часто, то для каждой функции имеется своё условное обозначение. Функция И – НЕ обозначается значком «&«, а функция ИЛИ – НЕ значком «1«.
Для отдельного инвертора таблица истинности уже приведена выше. Можно добавить, что количество инверторов в одном корпусе может достигать шести.
Логический элемент «исключающее ИЛИ».
К числу базовых логических элементов принято относить элемент реализующий функцию «исключающее ИЛИ». Иначе эта функция называется «неравнозначность».
Высокий потенциал на выходе возникает только в том случае, если входные сигналы не равны. То есть на одном из входов должна быть единица, а на другом ноль. Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная – «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.
Таблица истинности.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Эти логические элементы находят своё применение в сумматорах. «Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей «=1«.

На зарубежный манер «исключающее ИЛИ» называют XOR и на схемах рисуют вот так.

Кроме вышеперечисленных логических элементов, которые выполняют базовые логические функции очень часто, используются элементы, объединённые в различных сочетаниях. Вот, например, К555ЛР4. Она называется очень серьёзно 2-4И-2ИЛИ-НЕ.

Её таблица истинности не приводится, так как микросхема не является базовым логическим элементом. Такие микросхемы выполняют специальные функции и бывают намного сложнее, чем приведённый пример. Так же в логический базис входят и простые элементы «И» и «ИЛИ». Но они используются гораздо реже. Может возникнуть вопрос, почему эта логика называется транзисторно-транзисторной.
Если посмотреть в справочной литературе схему, допустим, элемента 2И – НЕ из микросхемы К155ЛА3, то там можно увидеть несколько транзисторов и резисторов. На самом деле ни резисторов, ни диодов в этих микросхемах нет. На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный транзистор.
Главная » Цифровая электроника » Текущая страница
Также Вам будет интересно узнать:
Логические элементы

 В данной статье расскажем что такое логические элементы, рассмотрим самые простые логические элементы.
В данной статье расскажем что такое логические элементы, рассмотрим самые простые логические элементы.
Любое цифровое устройство — персональный компьютер, или современная система автоматики состоит из цифровых интегральных микросхем (ИМС), которые выполняют определённые сложные функции. Но для выполнения одной сложной функции необходимо выполнить несколько простейших функций. Например, сложение двух двоичных чисел размером в один байт происходит внутри цифровой микросхемы называемой «процессор» и выполняется в несколько этапов большим количеством логических элементов находящихся внутри процессора. Двоичные числа сначала запоминаются в буферной памяти процессора, потом переписываются в специальные «главные» регистры процессора, после выполняется их сложение, запоминание результата в другом регистре, и лишь после результат сложения выводится через буферную память из процессора на другие устройства компьютера.
Процессор состоит из функциональных узлов: интерфейсов ввода-вывода, ячеек памяти – буферных регистров и «аккумуляторов», сумматоров, регистров сдвига и т.д. Эти функциональные узлы состоят из простейших логических элементов, которые, в свою очередь состоят из полупроводниковых транзисторов, диодов и резисторов. При конструировании простых триггерных и других электронных импульсных схем, сложные процессоры не применить, а использовать транзисторные каскады – «прошлый век». Тут и приходят на помощь – логические элементы.
Логические элементы, это простейшие «кубики», составные части цифровой микросхемы, выполняющие определённые логические функции. При этом, цифровая микросхема может содержать в себе от одного, до нескольких единиц, десятков, …и до нескольких сотен тысяч логических элементов в зависимости от степени интеграции. Для того, чтобы разобраться, что такое логические элементы, мы будем рассматривать самые простейшие из них. А потом, наращивая знания, разберёмся и с более сложными цифровыми элементами.
Начнём с того, что единица цифровой информации это «один бит». Он может принимать два логических состояния – логический ноль «0», когда напряжение равно нулю (низкий уровень), и состояние логической единицы «1», когда напряжение равно напряжению питания микросхемы (высокий уровень).
Поскольку простейший логический элемент это электронное устройство, то это означает, что у него есть входы (входные выводы) и выходы (выходные выводы). И входов и выходов может быть один, а может быть и больше.
Для того, чтобы понять принципы работы простейших логических элементов используется «таблица истинности». Кроме того, для понимания принципов работы логических элементов, входы, в зависимости от их количества обозначают: Х1, Х2, … ХN, а выходы: Y1, Y2, … YN.
Функции, выполняемые простейшими логическими элементами, имеют названия. Как правило, впереди функции ставится цифра, обозначающая количество входов. Простейшие логические элементы всегда имеют лишь один выход.
Рассмотрим простейшие логические элементы



 — «НЕ» (NOT) – функция отрицания (инверсии сигнала). Потому его чаще называют — «инвертор». Графически, инверсия обозначается пустым кружочком вокруг вывода элемента (микросхемы). Обычно кружок инверсии ставится у выхода, но в более сложных логических элементах, он может стоять и на входе. Графическое обозначение элемента «НЕ» и его таблица истинности представлены на рисунке слева.
— «НЕ» (NOT) – функция отрицания (инверсии сигнала). Потому его чаще называют — «инвертор». Графически, инверсия обозначается пустым кружочком вокруг вывода элемента (микросхемы). Обычно кружок инверсии ставится у выхода, но в более сложных логических элементах, он может стоять и на входе. Графическое обозначение элемента «НЕ» и его таблица истинности представлены на рисунке слева.
У элемента «НЕ» всегда один вход и один выход. По таблице истинности следует, что при наличии на входе элемента логического нуля, на выходе будет логическая единица. И наоборот, при наличии на входе логической единицы, на выходе будет логический ноль. Цифра «1» внутри прямоугольника обозначает функцию «ИЛИ», её принято рисовать и внутри прямоугольника элемента «НЕ», но это ровным счётом ничего абсолютно не значит.

 Обозначение D1.1 означает, что D — цифровой логический элемент, 1 (первая) — номер микросхемы в общей схеме, 1 (вторая) — номер элемента в микросхеме. Точно также расшифровываются и другие логические элементы.
Обозначение D1.1 означает, что D — цифровой логический элемент, 1 (первая) — номер микросхемы в общей схеме, 1 (вторая) — номер элемента в микросхеме. Точно также расшифровываются и другие логические элементы.
Часто, чтобы отличить цифровые микросхемы от аналоговых микросхем, применяют обозначения из двух букв: DD – цифровая микросхема, DA – аналоговая микросхема. В последующем, мы не будем заострять внимание на это обозначение, а вернёмся лишь тогда, когда это будет необходимым.
Самой распространённой микросхемой «транзисторно-транзисторной логики» (ТТЛ), выполняющей функцию «НЕ», является интегральная микросхема (ИМС) К155ЛН1, внутри которой имеется шесть элементов «НЕ». Нумерация выводов этой микросхемы показана справа.



 — «И» (AND) – функция сложения (если на всех входах единица, то на выходе будет единица, в противном случае, если хотя бы на одном входе ноль, то и на выходе всегда будет ноль). В алгебре-логике элемент «И» называют «конъюнктор». Графическое обозначение элемента «2И» и его таблица истинности представлены слева.
— «И» (AND) – функция сложения (если на всех входах единица, то на выходе будет единица, в противном случае, если хотя бы на одном входе ноль, то и на выходе всегда будет ноль). В алгебре-логике элемент «И» называют «конъюнктор». Графическое обозначение элемента «2И» и его таблица истинности представлены слева.
Название элемента «2И» обозначает, что у него два входа, и он выполняет функцию «И». На схеме внутри прямоугольника микросхемы рисуется значок «&», что на английском языке означает «AND» (в переводе на русский — И).
По таблице истинности следует, что на выходе элемента «И» будет логическая единица только в одном случае — когда на обоих входах будет логическая единица. Если хотя бы на одном входе ноль, то и на выходе будет ноль.

 Самой распространённой микросхемой «транзисторно-транзисторной логики» (ТТЛ), выполняющей функцию «2И», является интегральная микросхема (ИМС) К155ЛИ1, внутри которой имеется четыре элемента «2И». Нумерация выводов этой микросхемы показана справа.
Самой распространённой микросхемой «транзисторно-транзисторной логики» (ТТЛ), выполняющей функцию «2И», является интегральная микросхема (ИМС) К155ЛИ1, внутри которой имеется четыре элемента «2И». Нумерация выводов этой микросхемы показана справа.
 Для того, чтобы вам было понятнее что такое «2И», «3И», «4И», и т.д., приведу графическое обозначение и таблицу истинности элемента «3И».
Для того, чтобы вам было понятнее что такое «2И», «3И», «4И», и т.д., приведу графическое обозначение и таблицу истинности элемента «3И».
По таблице истинности следует, что на выходе элемента «3И» будет логическая единица только в том случае — когда на всех трёх входах будет логическая единица. Если хотя бы на одном входе будет логический ноль, то и на выходе элемента также будет логический ноль. Самой распространённой микросхемой ТТЛ, выполняющей функцию «3И», является микросхема К555ЛИ3, внутри которой имеется три элемента «3И».



 — «И-НЕ» (NAND) – функция сложения с отрицанием (если на всех входах единица, то на выходе будет ноль, в противном случае на выходе всегда будет единица). Графическое обозначение элемента «2И-НЕ» и его таблица истинности приведены слева.
— «И-НЕ» (NAND) – функция сложения с отрицанием (если на всех входах единица, то на выходе будет ноль, в противном случае на выходе всегда будет единица). Графическое обозначение элемента «2И-НЕ» и его таблица истинности приведены слева.
По таблице истинности следует, что на выходе элемента «2И-НЕ» будет логический ноль только в том случае, если на обоих входах будет логическая единица. Если хотя бы на одном входе ноль, то на выходе будет единица.

 Самой распространённой микросхемой ТТЛ, выполняющей функцию «2И-НЕ», является ИМС К155ЛА3, а микросхемами КМОП (комплементарный металлооксидный полупроводник) – ИМС К561ЛА7 и К176ЛА7, внутри которых имеется четыре элемента «2И-НЕ». Нумерация выводов этих микросхем показана справа.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2И-НЕ», является ИМС К155ЛА3, а микросхемами КМОП (комплементарный металлооксидный полупроводник) – ИМС К561ЛА7 и К176ЛА7, внутри которых имеется четыре элемента «2И-НЕ». Нумерация выводов этих микросхем показана справа.
Сравнив таблицы истинности элемента «2И-НЕ» и элемента «2И» можно догадаться об эквивалентности схем:


Добавив к элементу «2И» элемент «НЕ» мы получили элемент «2И-НЕ». Так можно собрать схему, если нам необходим элемент «2И-НЕ», а у нас в распоряжении имеются только элементы «2И» и «НЕ».
И наоборот:


Добавив к элементу «2И-НЕ» элемент «НЕ» мы получили элемент «2И». Так можно собрать схему, если нам необходим элемент «2И», а у нас в распоряжении имеются только элементы «2И-НЕ» и «НЕ».
Аналогичным образом, путём соединения входов элемента «2И-НЕ» мы можем получить элемент «НЕ»:


Обратите внимание, что было введено новое в обозначении элементов – дефис, разделяющий правую и левую часть в названии «2И-НЕ». Этот дефис непременный атрибут при инверсии на выходе (функции «НЕ»).


 — «ИЛИ» (OR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – единица, в противном случае на выходе всегда будет ноль). В алгебре-логике, элемент «ИЛИ» называют «дизъюнктор». Графическое обозначение элемента «2ИЛИ» и его таблица истинности приведены слева.
— «ИЛИ» (OR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – единица, в противном случае на выходе всегда будет ноль). В алгебре-логике, элемент «ИЛИ» называют «дизъюнктор». Графическое обозначение элемента «2ИЛИ» и его таблица истинности приведены слева.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2ИЛИ», является ИМС К155ЛЛ1, внутри которой имеется четыре элемента «2ИЛИ». Нумерация выводов этой микросхемы показана справа.

 Предположим, что нам в схеме необходим элемент, выполняющий функцию «2ИЛИ», но у нас есть в распоряжении только элементы «НЕ» и «2И-НЕ», тогда можно собрать схему, которая будет выполнять функцию «2ИЛИ»:
Предположим, что нам в схеме необходим элемент, выполняющий функцию «2ИЛИ», но у нас есть в распоряжении только элементы «НЕ» и «2И-НЕ», тогда можно собрать схему, которая будет выполнять функцию «2ИЛИ»:





 — «ИЛИ-НЕ» (NOR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – ноль, в противном случае на выходе всегда будет единица). Как вы поняли, элемент «ИЛИ-НЕ» выполняет функцию «ИЛИ», а потом инвертирует его функцией «НЕ».
— «ИЛИ-НЕ» (NOR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – ноль, в противном случае на выходе всегда будет единица). Как вы поняли, элемент «ИЛИ-НЕ» выполняет функцию «ИЛИ», а потом инвертирует его функцией «НЕ».
Графическое обозначение элемента «2ИЛИ-НЕ» и его таблица истинности приведена слева.

 Самой распространённой микросхемой ТТЛ, выполняющей функцию «2ИЛИ-НЕ», является ИМС К155ЛЕ1, а микросхемами КМОП – К561ЛЕ5 и К176ЛЕ5, внутри которых имеется четыре элемента «2ИЛИ-НЕ». Нумерация выводов этих микросхем показана справа.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2ИЛИ-НЕ», является ИМС К155ЛЕ1, а микросхемами КМОП – К561ЛЕ5 и К176ЛЕ5, внутри которых имеется четыре элемента «2ИЛИ-НЕ». Нумерация выводов этих микросхем показана справа.
Предположим, что нам в схеме необходим элемент, выполняющий функцию «2ИЛИ-НЕ», но у нас есть в распоряжении только элементы «НЕ» и «2И-НЕ», тогда можно собрать следующую схему, которая будет выполнять функцию «2ИЛИ-НЕ»:


По аналогии с элементом «2И-НЕ», путём соединения входов элемента «2ИЛИ-НЕ» мы можем получить элемент «НЕ»:





 — «Исключающее ИЛИ» (XOR) — функция неравенства двух входов (если на обоих входах элемента одинаковые сигналы, то на выходе – ноль, в противном случае на выходе всегда будет единица). Операция, которую он выполняет, часто называют «сложение по модулю 2».
— «Исключающее ИЛИ» (XOR) — функция неравенства двух входов (если на обоих входах элемента одинаковые сигналы, то на выходе – ноль, в противном случае на выходе всегда будет единица). Операция, которую он выполняет, часто называют «сложение по модулю 2».
Графическое обозначение элемента «Исключающее ИЛИ» и его таблица истинности приведены слева.

 Самой распространённой микросхемой ТТЛ, выполняющей функцию «Исключающее ИЛИ», является ИМС К155ЛП5, а микросхемами КМОП – К561ЛП2 и К176ЛП2, внутри которых имеется четыре элемента «Исключающее ИЛИ». Нумерация выводов этих микросхем показана справа.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «Исключающее ИЛИ», является ИМС К155ЛП5, а микросхемами КМОП – К561ЛП2 и К176ЛП2, внутри которых имеется четыре элемента «Исключающее ИЛИ». Нумерация выводов этих микросхем показана справа.
Предположим, что нам в схеме необходим элемент, выполняющий функцию «Исключающее ИЛИ», но у нас есть в распоряжении только элементы «2И-НЕ», тогда можно собрать следующую схему, которая будет выполнять функцию «Исключающее ИЛИ»:



 В цифровой схемотехнике процессоров главная функция — «Суммирование двоичных чисел», поэтому сложный логический элемент – «Сумматор» является неотъемлемой частью арифметико-логического устройства любого, без исключения процессора. Составной частью сумматора является набор логических элементов, выполняющих функцию «Исключающее ИЛИ с переносом остатка». Что это такое? В соответствии с наукой «Информатика», результатом сложения двух двоичных чисел, две единицы одного разряда дают ноль, при этом формируется «единица переноса» в следующий старший разряд, который участвует в операции суммирования в старшем разряде. Для этого в схему добавляется ещё один вывод «переноса» — «Р».
В цифровой схемотехнике процессоров главная функция — «Суммирование двоичных чисел», поэтому сложный логический элемент – «Сумматор» является неотъемлемой частью арифметико-логического устройства любого, без исключения процессора. Составной частью сумматора является набор логических элементов, выполняющих функцию «Исключающее ИЛИ с переносом остатка». Что это такое? В соответствии с наукой «Информатика», результатом сложения двух двоичных чисел, две единицы одного разряда дают ноль, при этом формируется «единица переноса» в следующий старший разряд, который участвует в операции суммирования в старшем разряде. Для этого в схему добавляется ещё один вывод «переноса» — «Р».
Графическое обозначение элемента «Исключающее ИЛИ с переносом» и его таблица истинности представлена слева.
Такая функция сложения одноразрядных чисел в простых устройствах обычно не используется, и как правило, интегрирована в состав одной микросхемы – сумматора, с минимальным количеством разрядов – четыре, для сложения четырехбитных чисел. По причине слабого спроса, промышленность таких логических элементов не выпускает. Поэтому, в случае необходимости, функцию «Исключающее ИЛИ с переносом» можно собрать по следующей схеме из элементов «2И-НЕ» и «2ИЛИ-НЕ», которая активно применяется как внутри простых сумматоров, так и во всех сложных процессорах (в том числе Pentium, Intel-Core, AMD и других, которые появятся в будущем):


Вышеперечисленные логические элементы выполняют статические функции, а на основе них строятся более сложные статические и динамические элементы (устройства): триггеры, регистры, счётчики, шифраторы, дешифраторы, сумматоры, мультиплексоры.
Для выполнения логических операций и решать логические задачи с помощью средств электроники были изобретены логические элементы. Их создают с помощью диодов, транзисторов и комбинированных элементов (диодно-транзисторные). Такая логика получила название диодной логики (ДЛ), транзисторной (ТЛ) и диодно–транзисторной (ДТЛ). Используют как полевые, так и биполярные транзисторы. В последнем случае предпочтение отдается устройствам типа n-p-n, так как они обладают большим быстродействием.
Логический элемент «ИЛИ»
Схема логического элемента «ИЛИ» представлена на рисунке 1 а. На каждый из входов может подаваться сигнал в виде какого-то напряжения (единица) или его отсутствия (ноль). На резисторе R появиться напряжение даже при его появлении на каком – либо из диодов.
 Рис. 1
Рис. 1
Элементы или могут иметь несколько логических входов. Если используются не все входы, то те входы которые не используются следует соединять с землей (заземлять), чтобы избежать появления посторонних сигналов.
На рисунке 1б показано обозначение на электрической схеме элемента, а на 1в таблица истинности.
Логический элемент «И»
Схема элемента приведена на рис. 2. Если хотя – бы к одному из входов будет сигнал равный нулю, то через диод будет протекать ток. Падение напряжения на диоде стремится к нулю, соответственно на выходе тоже будет ноль. На выходе сможет появится сигнал только при условии, что все диоды будут закрыты, то есть на всех входах будет сигнал. Рассчитаем уровень сигнала на выходе устройства:
 Рис.2
Рис.2
на рис. 2 б – обозначение на схеме, в – таблица истинности.
Логический элемент «НЕ»
В логическом элементе «НЕ» используют транзистор (рис.3 а). при наличии положительного напряжения на входе х=1 транзистор открывается и напряжение его коллектора стремится к нулю. Если х=0 то положительного сигнала на базе нет, транзистор закрыт, ток не проходит через коллектор и на резисторе R нет падения напряжения, соответственно на коллекторе появится сигнал Е. условное обозначение и таблица истинности приведены на рис. 3 б,в.
 Рис.3
Рис.3
Логический элемент «ИЛИ-НЕ»
При создании различных схем на логических элементах часто применяют элементы комбинированные. В таких элементах совмещены несколько функций. Принципиальная схема показана на рис. 4 а.
 Рис.4
Рис.4
Здесь диоды Д1 и Д2 выполняют роль элемента «ИЛИ», а транзистор играет роль инвертора. Обозначение элемента на схеме и его таблица истинности рис. 4б и в соответственно.
Логический элемент «И-НЕ»
Показана схема на рис. 5 а. Здесь диод Д3 выполняет роль так сказать фильтра во избежание искажения сигнала. Если на вход х1 или х2 не подан сигнал (х1=0 или х2=0), то через диод Д1 или Д2 будет протекать ток. Падение на нем не равно нулю и может оказаться достаточным для открытия транзистора. Последствием чего может стать ложное срабатывание и на выходе вместо единицы мы получим ноль. А если в цепь включить Д3, то на нем упадет значительная часть напряжения открытого на входе диода, и на базу транзистора практически ничего не приходит. Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов. На рис. 5б и в показаны таблица истинности и схемное обозначение данного устройства.
 Рис.5
Рис.5
Логические элементы получили широчайшее применение в электронике и микропроцессорной технике. Многие системы управления строятся с использованием именно этих устройств.
РадиоКот :: Логические элементы
РадиоКот >Обучалка >Цифровая техника >Основы цифровой техники >Логические элементы
Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас.
Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.
Итак, какие бывают элементы?
Смотрим:
Элемент «И» (AND)
Иначе его называют «конъюнктор».
Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется « таблица истинности ». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем.
Вот так выглядит элемент «И» и его таблица истинности:
Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам.
Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.
Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем. Идем дальше.
Элемент «ИЛИ» (OR)
По другому, его зовут «дизъюнктор».
Любуемся:
Опять же, название говорит само за себя.
На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.
Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.
Элемент «НЕ» (NOT)
Чаще, его называют «инвертор».
Надо чего-нибудь говорить по поводу его работы?
Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ».
Элемент «И-НЕ» (NAND)
Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» — единица. И наоборот. Э то легко понять по эквивалентной схеме элемента:
Элемент «ИЛИ-НЕ» (NOR)
Та же история – элемент «ИЛИ» с инвертором на выходе.
Следующий товарищ устроен несколько хитрее:
Элемент «Исключающее ИЛИ» (XOR)
Он вот такой:
Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.
Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый.
Эквивалентная схема примерно такая:
Ее запоминать не обязательно.
Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4.
Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем.
Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питание подается на ножки 7 (-) и 14 (+). Напряжение питания – смотри в таблице в предыдущем параграфе.
<<—Вспомним пройденное—-Поехали дальше—>>
|
Как вам эта статья? |
Заработало ли это устройство у вас? |
НОУ ИНТУИТ | Лекция | Логические основы ЭВМ
Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.
Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 — это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864 гг.), она является основой всех методов упрощения булевых выражений.
Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Логическое умножение (конъюнкция) — функция И
Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:
- на входе схемы разомкнутое состояние соответствующего ключа, например,
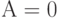 ;
; - на выходе схемы (
 ) — такое ее состояние, когда через сопротивление R ток не протекает.
) — такое ее состояние, когда через сопротивление R ток не протекает.
Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.

Рис. 1.1. Трёх-входовой логический элемент И
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа —  ,
,  и
и  . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно
. Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно 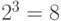 . Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и
. Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и  , и
, и  , и
, и  . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
. Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа —  и
и  . Количество сочетаний этих переменных равно
. Количество сочетаний этих переменных равно  . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или
. Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или  , или
, или  . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
. Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.

Рис. 1.2. Логический элемент ИЛИ на два входа
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая 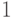 , то на его выходе будет логическая 1.
, то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо
 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
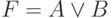 — с использованием знака дизъюнкции.
— с использованием знака дизъюнкции.
Логическое отрицание (инверсия) — функция НЕ
Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход —  . Количество вариантов для единственной логической переменной равно
. Количество вариантов для единственной логической переменной равно 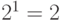 . Очевидно, что через сопротивление R ток протекает (
. Очевидно, что через сопротивление R ток протекает (  ) тогда, когда
) тогда, когда  не замкнут, т.е.
не замкнут, т.е. 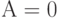 . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет
только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
. Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет
только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
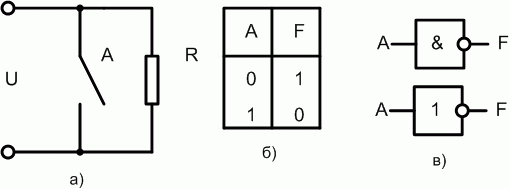
Рис. 1.3. Логический элемент НЕ
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
В логических выражениях применяется единственный вариант обозначения инверсии:

К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
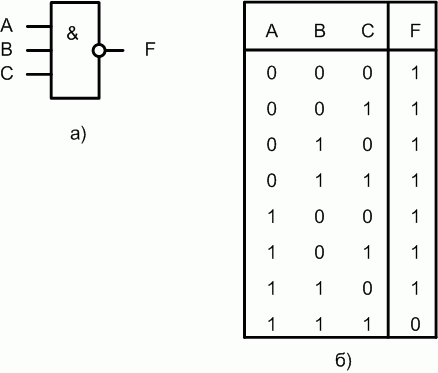
Рис. 1.4. Логический элемент И-НЕ на три входа
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо
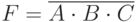 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое; - либо
 ;
; - либо
 ;
; - либо
 .
.
Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо
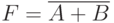 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
 .
.
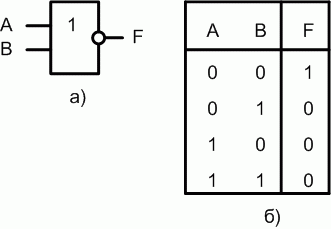
Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно логических функций и соответствующих им логических элементов, где — основание системы счисления, — число входов (аргументов), — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
|
Содержание
|
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
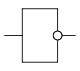 Инвертор, НЕ
Инвертор, НЕ
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение, ДА
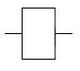
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)
 2И
2И
| ٨ | ||
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)
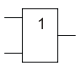 2ИЛИ
2ИЛИ
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)
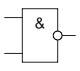 2И-НЕ
2И-НЕ
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)
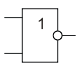 2ИЛИ-НЕ
2ИЛИ-НЕ
| ↓ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
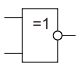 ИСКЛ-ИЛИ-НЕ
ИСКЛ-ИЛИ-НЕ
| ↔ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует четное количество,
- «0» тогда и только тогда, когда на входе действует нечетное количество
Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.
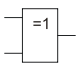 ИСКЛ-ИЛИ
ИСКЛ-ИЛИ
В англоязычной литературе 2XOR.
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации логических элементов
Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
 Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Ссылки
Литература
Аннотация: Рассматривается различные технологии реализации логических элементов.
Логические элементы транзисторно-транзисторной логики
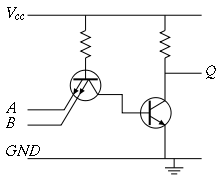
Схемы транзисторно-транзисторной логики (ТТЛ) базируются на биполярных транзисторах npn-структуры. Базовым элементом (рис. 16.1) данной технологии является схема И-НЕ. Логическое умножение осуществляется за счет свойств многоэмиттерного транзистора VT1 [1]. При подаче хотя бы одного логического нуля на эмиттеры этого транзистора замыкается цепь: +5 В, сопротивление R1, переход база-эмиттер, земля на входе. При этом транзисторы VT2 и VT3 остаются закрытыми. Поэтому выходная цепь не замкнута, падения напряжения в ней нет, следовательно, в точке F на выходе схемы будет потенциал источника питания, т.е. логическая единица. Выполняется правило И-НЕ [2]: при подаче хотя бы одного нуля на выходе схемы получили логическую единицу.
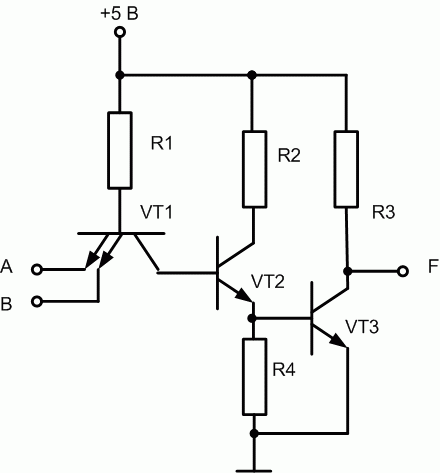
Рис. 16.1. Базовый элемент И-НЕ на ТТЛ
При подаче логической единицы на все входы схемы замыкается цепь: +5 В, сопротивление R2, транзистор VT2, сопротивление R3 , земля. Следовательно, на базу выходного транзистора VT3 подается потенциал, достаточный для его открытия (соответствует падению напряжения на сопротивлении R3). Через открытый транзистор VT3 замыкается буферная цепь: +5 В, сопротивление R4, транзистор VT3, земля. Следовательно, на выходе F будет потенциал, соответствующий падению напряжения на открытом транзисторе VT3, т.е. 0.4 В. Таким образом, F=0.
На рис. 16.2 представлен логический элемент ИЛИ-НЕ. Логическое сложение осуществляется за счет монтажного соединения транзисторов VT3 и VT4. Замыкание буферной цепи (состояние F=0 ) в этом случае возможно при замыкании хотя бы одной из цепей, проходящих через сопротивления R2 и R3. Эти цепи замыкаются в том случае, если на входы подается хотя бы одна логическая единица. Таким образом, выполняется правило ИЛИ-НЕ [2]: при подаче хотя бы одной единицы на выходе схемы получим логический ноль.
При замене в схеме И-НЕ многоэмиттерного транзистора VT1 на одноэмиттерный получается инвертор (рис. 16.3).

Рис. 16.3. Логический элемент НЕ на ТТЛ
Буферная часть схем логических элементов ТТЛ-технологии может быть реализована по-разному. В частности, резистор в буферной части может быть вынесен за пределы интегральной схемы, при этом существенно уменьшаются потери и нагрев кристалла. Такие схемы называются схемами «с открытым коллектором «. Пример такой схемы приведен на рис. 16.4.
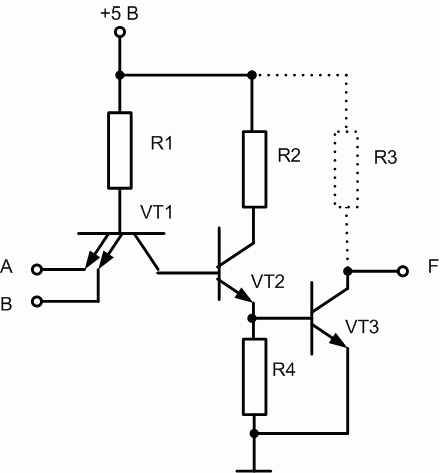
Рис. 16.4. Базовый элемент И-НЕ на ТТЛ с открытым коллектором
В схемах с активной нагрузкой (рис. 16.5) состояние буферной цепи определяется состоянием не одного, а двух транзисторов.
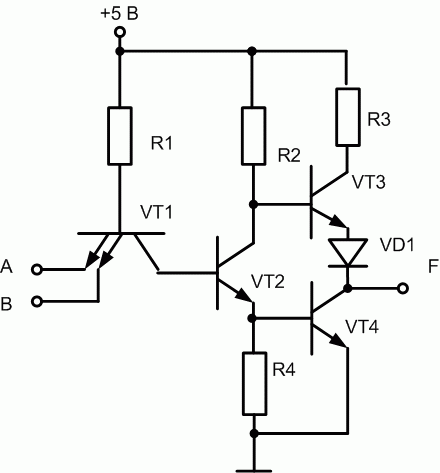
Рис. 16.5. Базовый элемент И-НЕ на ТТЛ с активной нагрузкой
Буферные схемы на три состояния (первые два – логический 0 и логическая 1 ) имеют помимо информационных, разрешающий вход Е (рис. 16.6). При Е=1 диод VD2 подключен на обратное напряжение, поэтому дополнительная цепь, включающая в себя диод VD2 и вход Е, разомкнута и не влияет на работу логического элемента. Таким образом, осуществляется «разрешение» работы элемента. При отсутствии такового разрешения Е=0. Диод VD2 оказывается подключенным на прямое напряжение, замыкается цепь + 5 В, сопротивление R2, открытый диод VD2, земля на входе E. Следовательно, на базу транзистора VT3 в буферной части схемы подается потенциал, соответствующий падению напряжения на открытом диоде, т.е. 0.2 В. При таких условиях данный транзистор закрыт, поэтому выход F оказывается отключенным от источника питания. Кроме того, независимо от состояния информационных входов A и B, замкнется входная цепь +5 В, сопротивление R1, переход база-эмиттер транзистора VT1, земля на входе E. Поэтому, как было описано выше, транзисторы VT2 и VT4 будут закрыты. Вследствие закрытия VT4 выход F будет отключен также и от земли. Таким образом, схема будет не в нулевом и не в единичном, а в «третьем» состоянии, которое называется состоянием высокого сопротивления, Z-состоянием, высокоимпедансным состоянием. Все перечисленные термины обозначают одно и то же: выход схемы отключен и от источника питания, и от земли.
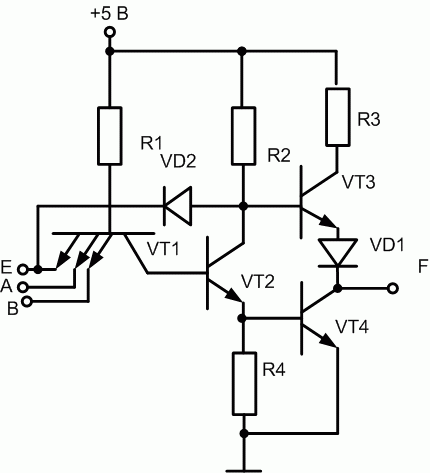
Рис. 16.6. Базовый элемент И-НЕ на ТТЛ с выходом на три состояния
Логические элементы nМОП-технологии
Схемы nМОП-технологии базируются на полевых (МОП) транзисторах с индуцированным каналом n-типа. Базовым элементом (рис. П16.7) данной технологии является схема И-НЕ. Логическое умножение осуществляется за счет последовательного соединения каналов транзисторов VT1 и VT2. Канал между истоком и стоком в nМОП-транзисторе индуцируется в том случае, когда на затвор (вход схемы) подается положительный относительно подложки потенциал. Цепь от +5 В до земли замкнется только в одном случае, когда A=B=1, поскольку в этом случае оба транзистора открываются и образуется единый канал, замыкающий цепь.

Рис. 16.7. Логический элемент И-НЕ nМОП-технологии
Функция ИЛИ-НЕ осуществляется за счет параллельного соединения таких транзисторов (рис. 16.8): при подаче хотя бы на один вход единицы индуцируется канал в соответствующем транзисторе и замыкается цепь от +5 В до земли. Следовательно, на выходе будет потенциал, соответствующий падению напряжения в канале транзистора, т.е. 0,2 В, при этом F=0.
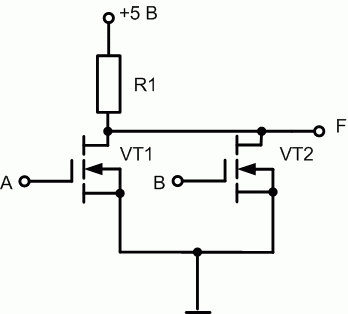
Рис. 16.8. Логический элемент ИЛИ-НЕ nМОП-технологии
Схема инвертора (рис. 16.9) строится на базе одного транзистора.

Рис. 16.9. Логический элемент НЕ nМОП-технологии
Java — Что такое элемент, а что не элемент в DOM?
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
Загрузка…
- Авторизоваться зарегистрироваться
-
текущее сообщество
HTML-элементов
HTML-элемент определяется начальным тегом, некоторым содержимым и конец тега.
HTML-элементов
HTML-элемент определяется начальным тегом, некоторым содержимым и конечным тегом:
Элемент HTML — это все от начального тега до конечного тега:
Мой Первый заголовок
Мой первый абзац.
| Начальная метка | Содержание элемента | Конечная метка |
|---|---|---|
| |
Моя первая рубрика | |
|
|
Мой первый абзац. | |
| |
нет | нет |
Примечание: Некоторые элементы HTML не имеют содержимого (например,
элемент).Эти элементы называются пустыми элементами. Пустые элементы не имеют конечного тега!
вложенных элементов HTML
HTML-элементы могут быть вложенными (это означает, что элементы могут содержать другие элементы).
Все документы HTML состоят из вложенных элементов HTML.
Следующий пример содержит четыре элемента HTML ( Мой первый абзац. Элемент Он имеет начальный тег Затем внутри элемента Мой первый абзац.
Элемент Он имеет начальный тег Затем внутри элемента
Мой первый абзац. Элемент Он имеет начальный тег
Элемент Имеет начальный тег
Мой первый абзац.
Некоторые элементы HTML будут отображаться правильно, даже если вы забудете конечный тег: Однако никогда не полагайтесь на это! Неожиданные результаты и ошибки могут возникнуть, если вы забудете конечный тег! HTML-элементы без содержимого называются пустыми элементами. Тег Теги HTML не чувствительны к регистру: Стандарт HTML не требует строчных тегов, но W3C
рекомендует нижний регистр в HTML, а требует строчный для более строгих типов документов, таких как XHTML. В W3Schools мы всегда используем имена тегов в нижнем регистре. W3Schools содержит дополнительную информацию об этих тегах и их атрибутах. Фредрик Лунд | Последнее обновление июль 2007 г. В этой заметке представлены типы Element, SubElement и ElementTree
доступно на сайте effbot.org
библиотека элементов. Обзор, ссылки на статьи и дополнительную документацию см. В
Обзор ElementTree Страница . Справочную информацию по API см. В Модуль elementtree.ElementTree . Вы можете скачать библиотеку с сайта efffot.org
стр. В этой статье: Тип элемента является гибкий контейнерный объект, разработанный
хранить иерархические структуры данных в памяти. Тип может быть
описывается как нечто среднее между списком и словарем. Каждый элемент имеет ряд свойств, связанных с ним: Все элементы должны иметь тег, но все остальные свойства
по желанию. Все строки могут быть либо строками Unicode, либо 8-битными
строки, содержащие только US-ASCII. Чтобы создать элемент, вызовите конструктор Element и передайте
строка тега в качестве первого аргумента: Вы можете получить доступ к строке тега с помощью атрибута тега : Чтобы построить дерево, создайте дополнительные элементы и добавьте их в
родительский элемент: Поскольку это очень распространенная операция, библиотека предоставляет
вспомогательная функция под названием SubElement , которая создает
новый элемент и добавляет его к своему родителю, за один шаг: Для доступа к подэлементам вы можете использовать обычный список (последовательность)
операции. Это включает в себя лен (элемент) , чтобы получить количество
субэлементы, элемент [i] для извлечения i-го субэлемента и использование
оператор for-in для зацикливания на подэлементах: Тип элемента также поддерживает нарезку (включая срез
присвоение), а также к стандартным , добавляются , , вставляются и
удалить методы: Обратите внимание, что remove принимает элемент, а не тег. Чтобы найти
элемент для удаления, вы можете либо перебрать родительский элемент, либо использовать один из
найти методов, описанных ниже. В ElementTree 1.2 и более ранних версиях поведение последовательности
означает, что элемент без каких-либо подэлементов проверяется как ложный (так как он
пустая последовательность), даже если она содержит текст или атрибуты.
Чтобы проверить возвращаемое значение из функции или метода, которые могут
вернуть None вместо узла, вы должны использовать явный тест. Примечание:
Это поведение, вероятно, несколько изменится в ElementTree 1.3. Написать
код, совместимый в обоих направлениях, используйте «element is None» для проверки
для отсутствующего элемента и «len (element)» для проверки непустых элементов.
Структура элемента не имеет родительских указателей.Если вам нужно сохранить
отслеживать отношения ребенка / родителя, вы можете структурировать свою программу
работать на родителей, а не на детей: Функция getiterator более подробно описана ниже. Если вы делаете это много, вы можете обернуть код итератора в генератор
функция: Другой подход заключается в использовании отдельной структуры данных для сопоставления с
дочерние элементы их родителям. В Python 2.4 и более поздних версиях следующий однострочный создает дочернюю / родительскую карту для всего дерева: , , ):
Пример
Пример объяснения
является корневым элементом
и это определяет весь документ HTML. и конечный тег .
<корпус>
элемент:
определяет
тело документа. и конечный тег . есть два других элемента:
:
:
определяет абзац. и конечный тег <900/9007:
Никогда не пропускайте конечную метку
Пустые элементы HTML
- определяет разрыв строки, и
пустой элемент без закрывающего тега:
HTML не чувствителен к регистру
означает то же самое, что .
Справочник по тегам HTML
Справочник по тегам
тег
Описание
Определяет корень HTML-документа
Определяет тело документа
Определяет заголовки HTML
,
, Элементов и Деревьев Элементов
Тип элемента #
из elementtree.ElementTree import Element
root = Element ("root")
print root.tag
root = элемент ("корень")
root.append (Element ( "один"))
root.append (Element ( "два"))
корень.append (Element ("three"))
from elementtree.ElementTree import Element, SubElement
root = элемент ("корень")
SubElement (root, "one")
SubElement (root, "two")
SubElement (root, "three")
для узла в корне:
узел печати
узлы = узел [1: 5]
узел.Append (подузел)
node.insert (0, подузел)
node.remove (subnode)
Проверка правды #
def fetchnode ():
...
узел = fetchnode ()
если не узел:
выведите «узел не найден, или узел не имеет подузлов»
если узел None:
печать "узел не найден" Доступ к родителям #
для родителя в tree.getiterator ():
для ребенка в родителе:
... работа над родительским / дочерним кортежем
def iterparent (дерево):
для родителя в tree.getiterator ():
для ребенка в родителе:
уступать родителю, ребенку
для родителя, потомок в iterparent (дерево):
,.. работа над родительским / дочерним кортежем

