Что такое логические элементы. Какие бывают виды логических элементов. Как работают основные логические операции. Где применяются логические элементы в электронике. Какие существуют реализации логических элементов.
Что такое логические элементы и для чего они нужны
Логические элементы — это основные «кирпичики», из которых строятся все цифровые электронные устройства. Они выполняют простейшие логические операции над входными сигналами и формируют выходной сигнал в соответствии с заданной логической функцией.
Основное назначение логических элементов:
- Обработка и преобразование цифровых сигналов
- Реализация логических функций и операций
- Построение более сложных цифровых устройств и систем
Логические элементы оперируют двоичными сигналами — логическим нулем (низкий уровень напряжения) и логической единицей (высокий уровень напряжения). На основе комбинации простейших логических элементов можно реализовать любые, сколь угодно сложные логические функции.

Основные виды логических элементов
Существует несколько базовых видов логических элементов, выполняющих элементарные логические операции:
- НЕ (инвертор) — выполняет операцию отрицания
- И (конъюнктор) — выполняет операцию логического умножения
- ИЛИ (дизъюнктор) — выполняет операцию логического сложения
- И-НЕ — комбинация операций И и НЕ
- ИЛИ-НЕ — комбинация операций ИЛИ и НЕ
- Исключающее ИЛИ — выполняет сложение по модулю 2
Рассмотрим подробнее работу каждого из этих логических элементов.
Как работают основные логические операции
Элемент НЕ (инвертор)
Элемент НЕ имеет один вход и один выход. Он инвертирует входной сигнал:
- Если на входе 0, на выходе 1
- Если на входе 1, на выходе 0
Таблица истинности элемента НЕ:
| Вход | Выход |
|---|---|
| 0 | 1 |
| 1 | 0 |
Элемент И
Элемент И имеет два или более входа и один выход. Выходной сигнал равен 1 только если на всех входах 1, иначе 0.
Таблица истинности двухвходового элемента И:
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Элемент ИЛИ
Элемент ИЛИ имеет два или более входа и один выход. Выходной сигнал равен 1, если хотя бы на одном из входов 1, иначе 0.

Таблица истинности двухвходового элемента ИЛИ:
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Практическое применение логических элементов
Логические элементы находят широкое применение в цифровой электронике и вычислительной технике:
- Построение арифметико-логических устройств
- Реализация устройств управления
- Создание схем памяти
- Организация интерфейсов и шин данных
- Реализация цифровых фильтров
- Построение дешифраторов, мультиплексоров, компараторов
Практически все современные цифровые устройства, от простейших до сложнейших, построены на основе логических элементов.
Физические реализации логических элементов
Существует несколько технологий физической реализации логических элементов:
- Резисторно-транзисторная логика (РТЛ)
- Диодно-транзисторная логика (ДТЛ)
- Транзисторно-транзисторная логика (ТТЛ)
- КМОП-логика
- Эмиттерно-связанная логика (ЭСЛ)
Наиболее распространенными на сегодняшний день являются ТТЛ и КМОП технологии. Они обеспечивают хорошее быстродействие при низком энергопотреблении.
Комбинационные и последовательностные логические устройства
На основе базовых логических элементов строятся более сложные цифровые устройства, которые делятся на два класса:
Комбинационные устройства
В комбинационных устройствах выходные сигналы в любой момент времени однозначно определяются комбинацией входных сигналов. К ним относятся:
- Шифраторы и дешифраторы
- Мультиплексоры и демультиплексоры
- Сумматоры
- Компараторы
Последовательностные устройства
В последовательностных устройствах выходные сигналы зависят не только от текущих входных сигналов, но и от предыдущих состояний. Они обладают памятью. К ним относятся:
- Триггеры
- Регистры
- Счетчики
- Запоминающие устройства
Комбинируя комбинационные и последовательностные устройства, можно создавать сложные цифровые системы любого назначения.
Перспективы развития логических элементов
Современные тенденции в развитии логических элементов включают:
- Уменьшение размеров транзисторов до нанометровых масштабов
- Снижение энергопотребления
- Повышение быстродействия
- Увеличение степени интеграции элементов
- Разработка новых технологий (квантовые вычисления, спинтроника и др.)
Несмотря на развитие новых вычислительных парадигм, классические логические элементы еще долго будут оставаться основой цифровой электроники.
Урок 8.3 — Логические элементы
8.3. Логические элементы
Все, абсолютно все электронные компоненты, обрабатывающие цифровые сигналы, состоят из небольшого набора одинаковых «кирпичиков». В микросхемах малой степени интеграции могут быть единицы и десятки таких элементов, а в современных процессорах их может быть очень и очень много. Они называются логические элементы. Логическим элементом называется электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.
Тем не менее, принцип работы цифровой логики остается неизменным – на входе логического элемента (входов может быть несколько) должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.
Конечно, логические элементы строятся, в свою очередь, из уже рассмотренных в предыдущих уроках резисторов, транзисторов и других электронных компонентов, но с точки зрения разработки цифровых схем именно логический элемент является их «элементарной» частицей.
При анализе работы логических элементов используется так называемая булева алгебра . Начала этого раздела математики было изложено в работах Джорджа Буля – английского математика и логика 19-го века, одного из основателей математической логики. Основами булевой алгебры являются высказывания, логические операции, а также функции и законы. Для понимания принципов работы логических элементов нет необходимости изучать все тонкости булевой алгебры, мы освоим ее основы в процессе обучения с помощью таблиц истинности.
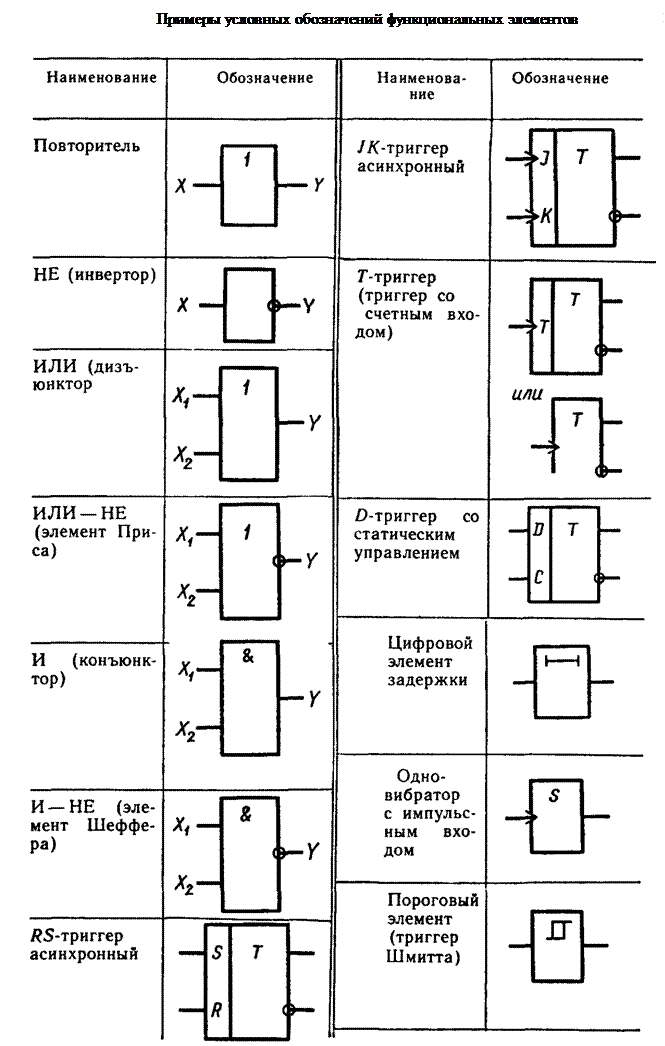
Еще несколько замечаний. Логические элементы (как, впрочем, и другие элементы электронных схем) принято обозначать так, чтобы входы были слева, а выходы справа. Число входов может быть, вообще говоря, любым, отличным от нуля. Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Какие же бывают логические элементы?
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
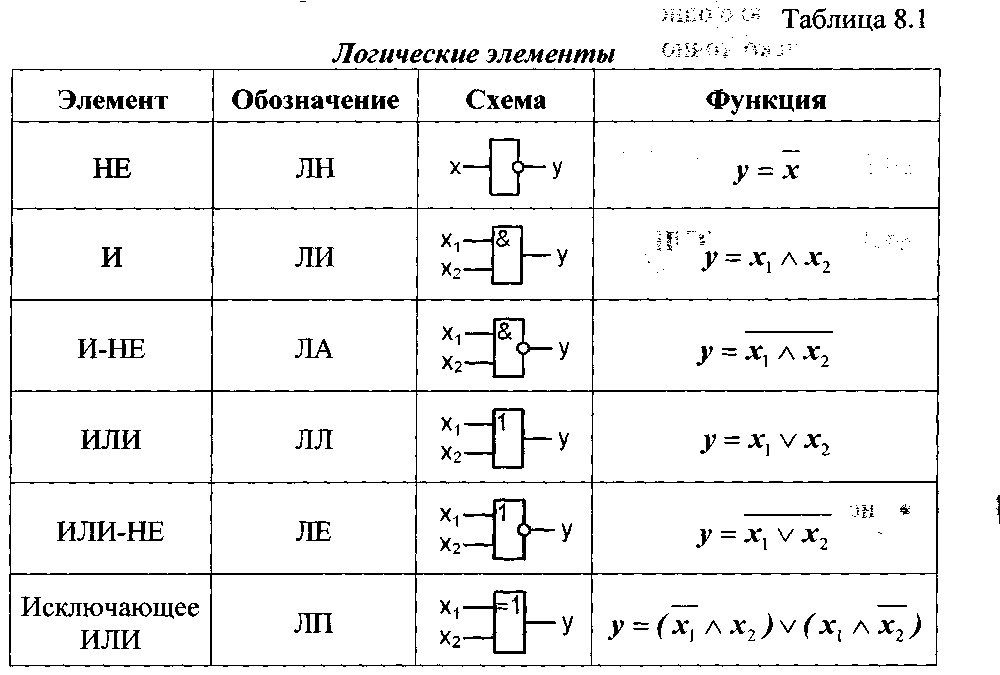
Элемент «И» (AND), он же конъюнктор, выполняет операцию логического умножения:
Условное обозначение — Таблица истинности
Здесь изображен логический элемент «2И» (цифра перед буквой «И» означает число входов). Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент «И». Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема (Digital), цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.
Состояние входов в таблице обозначаются «0» и «1» («ложь» и «истина»). Из таблицы видно, что выход «Y» будет иметь состояние «1» только в том случае, когда на обоих входах «Х1» и «Х2» будут «1». Это легко запомнить: умножение на «0» всегда дает «0».
Элемент «ИЛИ» (OR), он же дизъюнктор, выполняет операцию логического сложения:
Условное обозначение — Таблица истинности
Состояние «1» на выходе будет всегда, пока есть хотя бы одна «1» на входах.
Элемент «НЕ» (NOT), он же инвертор, выполняет операцию логического отрицания:
Условное обозначение — Таблица истинности
Состояние на входе обратно состоянию на входе.
Вот из этих трех элементов строятся все цифровые устройства!
Рассмотрим еще три логических элемента, которые можно получить, комбинируя уже рассмотренные. В силу исторически сложившихся схемотехнических решений эти скомбинированные схемы тоже считаются логическими элементами.
Элемент «И-НЕ» (NAND), конъюнктор с отрицанием:
Условное обозначение — Таблица истинности
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» будет единица. И наоборот.
Элемент «ИЛИ-НЕ» (NOR), дизъюнктор с отрицанием:
Условное обозначение — Таблица истинности
Элемент работает так же как и «ИЛИ», но с инверсией выхода.
Элемент «Исключающее ИЛИ» (XOR), сумматор по модулю 2:
Условное обозначение — Таблица истинности
В этом элемента «1» на выходе будет только тогда, когда на входах разные состояния.
На таких элементах строят сумматоры двоичных многоразрядных чисел. Для этого используется еще один дополнительный выход, на котором при появлении на входах двух «1» появляется сигнал переноса разряда.
Мы рассмотрели логические элементы, которые применяются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут делать одну крайне важную работу – они не умеют хранить информацию. Для хранения используется более сложный класс устройств, называемый элементами с памятью или конечными автоматами. В этот класс входят триггеры, регистры, счетчики, шифраторы (дешифраторы), мультиплексоры (демультиплексоры) и сумматоры. Некоторый из этих устройств мы рассмотрим в следующем уроке.
Программа-тренажер «Логика» для изучения логических элементов: сайт Константина Полякова
Логика
Что это такое?
Тренажер «Логика» предназначен для проведения практических занятий по теме «Математическая логика» в игровой форме. Подобная игра была ранее написана для компьютеров «Ямаха» (программисты П. Меняйло и М. Щекочихин). Оригинал программы вместе с имитатором MSX-компьютера можно скачать здесь (спасибо Михаилу Бондаревскому).
Программа работает под управлением операционных систем линейки Windows 95/98/NT/2000/XP/2003 на любых современных компьютерах. После распаковки архива она находится в работоспособном состоянии и не требует никаких дополнительных настроек.
Скачать
Программа является бесплатной для некоммерческого использования. Исходные тексты программы не распространяются.
Программа поставляется «as is», то есть, автор не несет никакой ответственности за всевозможные последствия ее использования, включая моральные и материальные потери, вывод оборудования из строя, физические и душевные травмы.
Программа содержит конструктор, позволяющий создавать новые схемы и подключать их в качестве уровней. Здесь можно скачать готовые схемы всех уровней, а также схемы триггеров на элементах «И-НЕ» и «ИЛИ-НЕ».
Достоинства
- игровая форма закрепления учебного материала;
- программа имеет встроенный набор логических схем (задач) для каждого из 10 уровней;
- существует возможность составлять новые схемы и проверять их работу, не выходя из программы;
- с каждым уровнем можно связать свою схему; список нестандартных схем хранится в файле инициализации LOGIC.INI; таким образом, можно составить несколько ini-файлов с разнотипными заданиями;
- кроме стандартного набора логических элементов (И, ИЛИ, НЕ) в схемах можно использовать включенные (непонятно почему) в школьную программу элементы «импликация», «эквивалентность», а также полусумматор, сумматор и RS-триггер.
Правила игры
Задача заключается в том, чтобы последовательно передавать кристалл с верхней площадки на нижнюю. Подавая ток на вход механизмов в правой части схемы, можно выдвигать
площадки на пути кристалла. Если на входе механизма нет тока, площадка убирается.Для управления механизмами используют выключатели в левой части поля. Их состояние изменяется щелчком мыши. Если выключатель включен, по цепи идет ток и поступает на логические схемы, включенные в эту цепь (средняя часть поля). Логические схемы преобразуют входные сигналы по следующим правилам:
- схема НЕ: на выходе будет ток (сигнал 1), если на входе тока нет (сигнал 0), и наоборот;
- схема И: на выходе будет 1, если на обоих входах 1;
- схема ИЛИ: на выходе будет 1, если хотя бы на одном входе 1;
- схема XOR (исключающее ИЛИ): на выходе будет 1, если только на одном входе 1;
- схема импликация (1—>2): на выходе будет 0, если на первом входе 1, а на втором — 0; иначе на выходе 1;
- схема эквивалентность (<—>
Кристалл нельзя передавать сразу через несколько «пролетов» — в этом случае он разбивается и приходится начинать уровень заново. Кроме того, у вас есть только 5 кристаллов на всю игру, если вы разобьете их все, задание считается невыполненным.
Игра состоит из 10 уровней. Если вы сможете пройти все уровни, сохранив хотя бы один кристалл и наберете больше нуля очков, вы увидите картинку.
Логические элементы — это… Что такое Логические элементы?
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно логических функций и соответствующих им логических элементов, где — основание системы счисления, — число входов (аргументов), — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
|
Содержание
|
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
Инвертор, НЕ| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение, ДА
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)
2И| ٨ | ||
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)
2ИЛИМнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)
2И-НЕМнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)
2ИЛИ-НЕ| ↓ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
ИСКЛ-ИЛИ-НЕ| ↔ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует четное количество,
- «0» тогда и только тогда, когда на входе действует нечетное количество
Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.
ИСКЛ-ИЛИВ англоязычной литературе 2XOR.
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации логических элементов
Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Ссылки
Литература
Использование логики ветвей в Microsoft Forms
К опросу или тесту можно применить логику ветвления, чтобы он изменялся в зависимости от ответов. В ветвящемся опросе или тесте отображаются только вопросы, подходящие для конкретного респондента. Если подходящих вопросов нет, респондент может пропустить набор вопросов или перейти к другому набору.
Добавление логики ветвинга в форму
Прежде всего убедитесь, что все вопросы уже созданы. Когда вы будете готовы добавить ветвление, выполните следующие действия:
-
Перейдите к вопросу, для которого нужно добавить ветвление. Нажмите Дополнительные параметры вопроса и выберите Добавить ветвь.
Примечание: При добавлении разделов в форму можно также добавить ветвление в раздел. В разделе, в который нужно добавить ветвление, нажмите Дополнительные параметры раздела и выберите Добавить ветвь.
-
На странице Параметры ветвления выберите раскрывающийся список рядом с вопросом, для которого требуется ветвление.
-
Выберите вопрос, к которому должна вести ветвь. В этом примере, если респондент отвечает «Да», #5 вопрос, можно перенаправить его на следующий вопрос (#6). Однако если респондент ответит нет на вопрос, #5 ответ, вы будете иметь его ветвь или пропустить, чтобы #7.
Примечания:
-
Вы можете направлять ветвь только к следующему вопросу, а не к предыдущему. Например, если у вас в форме семь вопросов и вы хотите добавить ветвление для вопроса 4, ветвь от него может вести к вопросам 5, 6, 7 или в конец формы. В этом же примере ветвь от вопроса 5 может вести только к вопросам 6, 7 или в конец формы.
-
Если вы попытаетесь направить ветвь к предыдущему вопросу, например от вопроса 4 к вопросу 2, это прекратит взаимодействие с вашим респондентом путем пропуска вопросов с 5 по 7 и его направления сразу в конец формы с кнопкой Отправить. Чтобы избежать этого, направляйте ветвь только к следующим вопросам.
-
-
Чтобы добавить в опрос или тест другие ветви, повторите действия 2–3. Если вы хотите, чтобы определенный вопрос был последним в опросе или тесте, откройте раскрывающийся список рядом с ним и выберите Конец формы.
Если вы хотите сбросить форму и удалить ветвление, нажмите Дополнительные параметры и выберите Сброс.
Отзыв о Microsoft Forms
Мы ждем ваших отзывов! Чтобы отправить отзыв о Microsoft Forms, перейдите в правый верхний угол формы и выберите Другие параметры формы > Отзыв.
См. также
Добавление разделов в форму
элементов логики
элементов логики Центр Жака Маритена: Чтенияпо
Его Преосвященство кардинал Мерсье
Третье издание
Переведено
Юэн Макферсон
Нью-Йорк
Манхэттенвиль Пресс
1912
Nihil Obstat.
РЕМИГИУС ЛАФОРТ, Д.Д.
Цензор
Imprimatur
ДЖОН КАРДИНАЛ ФАРЛИ
Архиепископ Нью-Йоркский
Авторское право 1912
Манхэттенвильская пресса
Введение
Глава I
Эффективная причина логического порядка
Глава II
Суть или материальная причина логического порядка
Арт.I. Концепты
§ 1. Понятие, его объект и свойства
§ 2. Разделение понятий
Арт. II. Условия.
§ 1. Термин, его предмет и свойства
§ 2 Классификация терминов
Глава III
Формальная причина логического порядка
Арт. I. Решение и предложение
§ 1. Понятие решения и предложения
§ 2. Решения и предложения
И.Классификация простых предложений
II. Классификация сложных предложений
§ 3. Соотношение предложений
Арт. II. Рассуждение
§ 1. Рассуждение и силлогизм
§ 2. Силлогизмы
I. Рассмотрение силлогизмов относительно их формы
II. Рассмотрение силлогизмов по существу
Различные виды демонстрации
Вероятные аргументы
Ошибочные и софистические аргументы
Арт.III. Научная систематизация
Предварительные замечания
§ 1. Научные процессы
§ 2. Метод и методы
Глава IV
Последняя причина логического порядка
Заключение
<< ======= >>
элементов логики | работа Whately
В истории логики: Другие логики 18-го века… эта традиция возникла из книги Ричарда Уэйтли Elements of Logic (1826) и, в той же традиции, из чрезвычайно популярной книги Джона Стюарта Милля A System of Logic (1843).Несимволический учебник Уэйтли, который сейчас в значительной степени отнесен к сноске, переформулировал многие концепции таким продуманным и ясным образом, что в целом (и во-первых…
Подробнееобзор Милля
- В книге Джона Стюарта Милля: Общественная жизнь и письмо
… (1828 г.) Ричарда Уэйтли « Элементы логики », он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики.Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла».”В течение нескольких лет он тщетно искал…
Подробнее
Узнайте об этой теме. , Чрезвычайно популярная книга Джона Стюарта Милля A System of Logic (1843).Несимволический учебник Уэйтли, который сейчас в значительной степени отнесен к сноске, переформулировал многие концепции таким продуманным и ясным образом, что в целом (и сначала… Подробнее
обзор Милля
- В книге Джона Стюарта Милля: Общественная жизнь и письмо
… (1828 г.) из книги Ричарда Уэйтли «Элементы логики », он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики.Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». Несколько лет он тщетно искал…
Подробнее
элементов логического рассуждения | Логика
. Некоторые из наших первых опытов убедительной силы аргумента пришли из школьной математики: столкнувшись с математическим доказательством, мы не можем отрицать вывод, если исходные посылки приняты. За такими аргументами скрывается более общий образец «доказательных аргументов», который изучается в науке логики.Логические рассуждения применяются на всех уровнях, от повседневной жизни до продвинутых наук, и в повседневных логических рассуждениях достигается замечательный уровень сложности, даже если лежащие в их основе принципы остаются интуитивно понятными. Ян фон Платон дает доступное, но строгое введение в важный аспект современной логики: ее дедуктивный механизм. Он показывает, что при анализе форм логического рассуждения оказывается, что ограниченный набор основных принципов может представлять любой логический аргумент.Его книга будет ценна для студентов, изучающих логику, математику и информатику.
- Включает уникальный исторический обзор дедуктивных систем от Аристотеля до наших дней.
- Дает введение в дедуктивный механизм металогики.
- Раскрывает набор первых принципов для представления логических аргументов
Обзоры и подтверждения
«Элементы логического мышления заполняют пробел, предоставляя столь необходимые объяснения и мотивацию для сухой литературы.’ Генри Тауснер, The Mathematical Intelligencer
Отзывы клиентов
Еще не просмотрел
Оставьте отзыв первым
Отзыв не размещен из-за ненормативной лексики
×Подробная информация о продукте
- Дата публикации: январь 2014 г.
- формат: Мягкая обложка
- isbn: 9781107610774
- длина: 271 страница
- размеры: 246 x 173 x 13 мм
- вес: 0,56 кг
- наличие: в наличии
Содержание
Часть I.Первые шаги в логическом рассуждении:
1. Начальные точки
2. Правила доказательства
3. Естественный вывод
4. Поиск доказательства
5. Классический естественный вывод
6. Поиск доказательства в классической логике
7. Семантика логики высказываний
Часть II. Логические рассуждения с помощью кванторов:
8. Кванторы
9. Выводы в логике предикатов
10. Семантика логики предикатов
Часть III. Beyond Pure Logic:
11. Равенство и аксиоматические теории
12.Элементы теории доказательств арифметики
Часть IV. Дополнительные темы:
13. Нормализация и устранение отсечений
14. Дедуктивный механизм от Аристотеля до Гейтинга.
Автор
Ян фон Платон , Университет Хельсинки
Ян фон Платон — профессор философии Хельсинкского университета. Он является автором книги «Создание современной вероятности» (Cambridge University Press, 1994) и, вместе с Сарой Негри, «Теории структурных доказательств» (Cambridge University Press, 2001) и «Анализ доказательств» (Cambridge University Press, 2011).
логический элемент Определение
Наименьшая логическая единица, расположенная в ЛАБОРАТОРИИ, из всех устройств Intel, поддерживаемых Программное обеспечение Quartus ® Prime. Логический элемент также известен как логический элемент. клетка.
В поддерживаемом устройстве ( Серия Arria ® , Циклон серии ® и Stratix ® серия ), логический элемент состоит из четырехвходовой LUT, программируемый регистр и цепочка переноса.Поддерживаемые логические элементы семейства устройств также поддерживает режим динамического однобитового сложения или вычитания, который выбирается В ЛАБОРАТОРИИ управляющий сигнал. Каждый логический элемент управляет локальной, строкой, столбцом, цепочкой переноса, регистром цепи и межсоединения с прямым звеном.
Каждый программируемый регистр поддерживаемого устройства ( Серия Arria ® , Циклон серии ® и Stratix ® series) семейный логический элемент может быть сконфигурирован для работы D, T, JK или SR или полностью отключен для чисто комбинационной логика.Часы регистра, очистка, включение часов, предварительная установка, асинхронная загрузка и управление асинхронными данными может осуществляться с помощью выводов ввода-вывода общего назначения или любых внутренних логика. Часы и сброс регистра также могут управляться глобальными сигналами.
Вы можете назначить логическую функцию конкретному логическому элементу в поддерживаемых ( Серия Arria ® , Циклон серии ® и Stratix ® серии) семейные устройства.Вы также можете назначить логическую функцию для пользовательской области, чтобы убедиться, что в Функция реализована в логическом элементе в этой настраиваемой области.
Логические элементы имеют «числа» следующего формата для следующих устройства:
|
Семейство устройств |
Формат для логического элемента «Числа» |
Описание переменных и чисел |
|
|---|---|---|---|
|
Серия Arria ® , Циклон серии ® и Stratix ® серия |
|
|
Номер столбца, который содержит LAB, содержащую логический элемент. |
|
|
Номер строки, содержащей LAB, содержащую логику элемент. |
||
|
|
Номер логического элемента от 0 до 10. |
||
Элементы аргументов: введение в критическое мышление и логику
Элементы аргументов знакомит с такими центральными темами критического мышления, как неформальные заблуждения, разница между достоверностью и истиной, базовая формальная логика высказываний и способы извлечения аргументов из текстов. Турецкий стремится предотвратить распространенные заблуждения, четко объясняя ряд важных различий, в том числе суждения vs.пропозициональные установки, предложения против положения дел, логика против риторики против психологии. Повсюду предлагаются упражнения, включая многочисленные неформальные аргументы, которые можно оценить, используя навыки и стратегии, представленные в тексте.
Комментарии
«По сравнению с другими книгами в этой области я считаю, что The Elements of Arguments является почти лучшим по качеству. Что касается обучения разнообразной группы студентов с разным опытом и разными способностями, я считаю это исключительным.Автор чрезвычайно чувствителен к традиционным проблемам и недоразумениям, которые окружают предмет, что затрудняет преподавание. Он дал высшему образовательному сообществу стандарт высочайшего уровня с замечательной пользой для студентов, которых мы обслуживаем ». — Деннис Брэндон, Калифорнийский государственный университет, Нортридж
«Среди множества вводных текстов выделяется Элементы аргументов . Турецкий достиг в одном томе удивительно четкого представления как «критического мышления», так и «логики» как отдельных, но пересекающихся дисциплин.Инструкторы извлекут большую пользу из ясных определений в книге, четких различий и многочисленных упражнений. Студенты найдут свое чтение вознагражденным разнообразными и доступными примерами, а также проницательными разделами, относящимися к логике и другим областям, таким как психология, риторика и философия языка. Используя этот текст, студенты будут хорошо подготовлены к аргументации и аргументации по любому предмету ». — Тайлер Уилл, Государственный университет Колорадо
Введение для студентов
Введение для преподавателей
Глава I: ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И СТРУКТУРА ТЕКСТА
Часть I: Аргументы
Часть II: Некоторые типы аргументов и стандарты оценки
- (A) Стандарты оценки аргументов
- (B) Стандарты оценки дедуктивных аргументов
- (C) Недедуктивные аргументы и стандарты их оценки
Глава II: ПРЕДЛОЖЕНИЯ
Часть I: Истина и ложность предположений
Часть II: Обозначение предложений
- (A) Истина и ложь: суждения всегда о чем-то
- (B) Положения и установки
- (C) Логика и психология
- (D) Факты и мнения
Часть III: Логика и риторика
- (A) Важность логики и критического мышления
- (B) Убедительный язык
Часть IV: Неформальные заблуждения
- (A) Апелляция к мотивам или эмоциям вместо поддержки
- (B) Обращение к властям
- (C) Нападение на человека: аргументы Ad hominem
- (D) Заблуждение субъективизма (или заблуждение релятивизма)
Упражнения: неформальные заблуждения
Глава III: СОСТАВНЫЕ ПРЕДЛОЖЕНИЯ И ИСТИННЫЕ ФУНКЦИОНАЛЬНЫЕ СОЕДИНЕНИЯ
Часть I: Логическое отрицание
Часть II: Логическая связь
- Неформальная ошибка: сложный вопрос
Часть III: Логическая дизъюнкция
- Неформальная ошибка: ложная дилемма
Часть IV: Функциональные условия истины
- (A) Различные варианты использования условных операторов
- (B) Функциональные условные выражения истины
- (C) Необходимые и достаточные условия
- (D) Определение условных обозначений
- (E) Истинные функциональные двусмысленные условия и определения
- (F) Неформальная ошибка: скользкий склон
Краткое описание логического оператора и логических связок: их символы, правила и таблицы истинности
Упражнения
Приложение: Допустимые формы категориальных силлогизмов
Глава IV: ЛОГИЧЕСКИЕ ОТНОШЕНИЯ
Часть I: Определения некоторых логических отношений
- (A) Логически несовместимые утверждения
- (B) Тавтологии, логически непротиворечивые предложения и условные предложения
- (C) Логическое следствие
- (D) Логическая эквивалентность
Часть II: Модальные концепции
- (A) Модальные концепции и логические отношения
- (B) Последствия среди модальностей
- (C) Различные типы возможности и невозможности
Часть III: Неформальные ложные утверждения
Упражнения: неформальные заблуждения
Глава V: ФОРМЫ АРГУМЕНТОВ И ИХ ОЦЕНКА
Часть I: Формы аргумента
Часть II: Проверка действительности
- (A) Использование таблиц истинности для определения действительности
- (B) Более короткая процедура определения действительности
- (C) Некоторые стандартные формы аргумента
- (D) Проверка действительности более сложных форм аргумента
Часть III: От действительности к обоснованности
- (A) Предоставление аргументов, подтверждающих посылку аргумента
- (B) Оценка неподдерживаемых помещений
- (C) Предварительное принятие посылок аргумента в качестве предположений
Упражнения: проверка действительности
Приложение: Действительность форм аргумента для проверки адекватности определяющих предложений
Глава VI: АРГУМЕНТЫ НА ОБЫЧНОМ ЯЗЫКЕ
Часть I: Определение аргументов
Часть II: Схема потока помещений и выводы
Часть III: Принципы интерпретации: энтимемы
- Неформальная ошибка: Ошибка соломенного человека
- Шаги для анализа аргументов
Часть IV: Стратегии оценки аргументов
- (A) Оценка действительности аргументов на обычном английском языке
- (B) Оценка индуктивных аргументов
Упражнения: полный анализ аргументов
Филип Турецки преподавал философию в Государственном университете Колорадо, Университете Южной Дакоты, Рипон-колледже и других высших учебных заведениях.Он является автором Time (Routledge, 1998) и множества научных статей.
Символическая логика для Lega »Ричарда Д. Фридмана
Аннотация
Мы можем с радостью согласиться с Холмсом в том, что логика — это не жизнь закона », и все же утверждать, что логика должна играть значительную роль в юридическом дискурсе. Логика не может продемонстрировать истинность посылок, а значит, сама по себе не может продемонстрировать достоинства юридического аргумента. Более того, даже с учетом предпосылок может оказаться, что прыжок веры или интуиции играет непреодолимую роль, по крайней мере, в некоторых хороших юридических аргументах.2 Но, по крайней мере, здравый юридический аргумент не будет нелогичным. Аргумент не будет убедительным, если окажется, что он нарушает основные принципы логики. Если провозглашение принципа права должно иметь хоть какую-то надежду на стабильность, он должен иметь возможность последовательного применения в ситуациях, которые материально схожи, и если формулировка не является логически последовательной, это условие вряд ли будет преобладать. В этой статье я исследую использование символической логики при обсуждении понятия элементов иска или защиты.Я буду использовать термин «иск» в общем смысле, имея в виду не только основания, лежащие в основе иска — то, что утверждается в жалобе или документе о предъявлении обвинения — но также и любое требование о судебной защите. Таким образом, я буду говорить о претензии о предварительном облегчении или о санкциях за раскрытие информации. В Части I я предполагаю, что попытка изложить юридический аргумент путем символического изложения элементов иска или защиты часто может способствовать поиску ясности. В части U я исследую некоторые ограничения этого метода, показывая, что в некоторых случаях само понятие элементов иска или защиты не работает.В Части I я предложу схемы логики юридической аргументации, которая работает безрезультатно и поэтому значительно отличается от классической логики, ярко и увлекательно представленной в замечательном новом тексте «Предпосылки и выводы» Роберта Родса и Говарда Поспезеля. 3
Рекомендуемое цитирование
Фридман, Ричард Д. «Логика и элементы. (Предпосылки и выводы: символическая логика для юридического анализа)». Нотр-Дам Л. Rev.73, вып. 3 (1998): 575-601.
Project MUSE — Элементы логики Винсента Э.Смит, доктор философии (обзор)
210 ОТЗЫВЫ КНИГ, защищающие цензуру. «Эти действия, — сообщают нам, — опасны, потому что небольшая энергичная группа способна навязывать последствия своих суждений и предубеждений сообществу, часто без того, чтобы большая часть сообщества узнала о том, что произошло». (стр. 37) Комиссия не могла более точно описать, что она делает. Колледж Провиденс, Провиденс, Р. И. ДЭВИД А. О’КОННЕЛЛ, О. П. Элементы логики.ВИНСЕНТ Э. СМИТ, PH. Д. Милуоки: Брюс, 1957. Стр. Q98. 3,50 доллара США. Доктор Винсент Смит с факультета Университета Нотр-Дам осмелился отличаться, написав довольно новый тип руководства по логике для студентов колледжей. Хорошо зная об изобилии учебников по логике с аристотелевским колоритом и не забывая о популярности, которой в последние несколько десятилетий пользовались книги по символической логике в большинстве университетских городков США и других стран, автор искренне и успешно включил некоторые новые возможности. в · этот учебник, который должен оказаться очень привлекательным для преподавателей и студентов колледжей логики.Среди множества отличительных целей этой книги главная заключалась в том, чтобы дать студентам колледжа возможность «сформировать беспристрастное суждение о том, насколько хорош или плох метод любого, кто представляет аргумент». (стр. 20). Эта благородная цель должна была быть достигнута за счет того, что искусство искусств «стало более живым для студентов, представив его в терминах историй логических операций» и за счет выхода «значительно дальше чисто формальной трактовки силлогизма». и познакомить студентов с некоторыми современными приложениями логики и научных методов.»(стр. vii, предисловие) Эта книга имеет ряд выдающихся особенностей. Совершенно очевидно, что автор провел много часов в классе, преподавая этот предмет, поскольку у него есть приятный способ предвидеть и осознавать многие трудности, которые обычно возникают в умах студентов колледжей. Он также знает, что очень немногие группы колледжей смогут за один семестр идеально охватить тридцать пять глав. Он достаточно честен, чтобы предложить определенные компромиссы в акцентах. проводиться каждым инструктором в соответствии с потребностями и способностями обучаемых групп, если основная цель достигнута.«Истории болезни», основанные в основном на важнейших вопросах нашей западной культуры, можно найти в каждой главе. Эти цитаты самых известных ученых древности, средневековья и современности представляют собой нововведение, достойное большой похвалы. Его КНИЖНЫЕ ОБЗОРЫ замечателен плохим выбором текстов из столь разнообразных интеллектуальных традиций. и должен значительно повысить привлекательность этого учебника для студентов. Тем не менее, доктор Смит призывает инструкторов часто использовать передовые статьи в местных газетах и еженедельных национальных журналах.Все это согласуется с его основной задачей при создании учебника. Его объяснения логических сущностей окажутся в уме этого рецензента столь же понятными, сколь и интересными для обычного коллеги, прошедшего курс науки о короретном мышлении. Любые упущения в предметах, которые традиционно преподаются (например, возражение, категорические силлогизмы, редукция к первой фигуре и т. Д. :), делаются неохотно только на том основании, что они не вносят значительного вклада в достижение основной цели этой книги.Хотя было бы несправедливо, если бы кто-либо написал «обжигающий обзор» (стр. ~ 66) на этот счет, тем не менее, многие преподаватели схоластики сочтут с немалым оправданием, что такие упущения представляют собой неудачное решение в свете подробного рассмотрения других предметы, которые, строго говоря, не логичны, как указано в Части VI. Его сверхъестественная манера соотносить с логикой такое огромное количество фактов в гуманитарных и естественных науках убеждает студента-читателя в том, насколько практичной может быть логика в повседневной жизни.Наконец, одна из наиболее ценных особенностей книги — это обширное рассмотрение индукции и популярного «научного метода». Структурно этот учебник удобно разделен на семь основных частей, каждая из которых обычно подразделяется на от трех до девяти глав.

