Емкость параллельно подключенных конденсаторов: формулы, расчеты и применение

Как рассчитать общую емкость при параллельном соединении конденсаторов. Чем отличается от последовательного соединения. Где применяется параллельное подключение конденсаторов. Какие преимущества дает такое соединение.

Что такое параллельное соединение конденсаторов

Параллельное соединение конденсаторов — это способ подключения, при котором все конденсаторы присоединяются к одним и тем же двум точкам электрической цепи. При этом на всех конденсаторах будет одинаковое напряжение, равное напряжению источника.

Основные характеристики параллельного соединения конденсаторов:

• Напряжение на всех конденсаторах одинаково и равно напряжению источника
• Общий заряд равен сумме зарядов отдельных конденсаторов
• Общая емкость увеличивается и равна сумме емкостей всех конденсаторов

Формула расчета общей емкости при параллельном соединении

Для расчета общей емкости при параллельном соединении конденсаторов используется следующая формула:

C = C1 + C2 + C3 + … + Cn

Где:

• C — общая емкость
• C1, C2, C3, …, Cn — емкости отдельных конденсаторов

Как видно из формулы, при параллельном соединении емкости просто складываются. Это значительно проще, чем расчет для последовательного соединения.

Сравнение с последовательным соединением конденсаторов

В чем основные отличия параллельного и последовательного соединения конденсаторов:

Параметр	Параллельное соединение	Последовательное соединение
Напряжение	Одинаковое на всех конденсаторах	Делится между конденсаторами
Заряд	Суммируется	Одинаковый на всех конденсаторах
Общая емкость	Увеличивается	Уменьшается
Формула расчета	C = C1 + C2 + C3 + …	1/C = 1/C1 + 1/C2 + 1/C3 + …

Как видим, параллельное соединение позволяет увеличить общую емкость, в отличие от последовательного.

Пример расчета емкости при параллельном соединении

Рассмотрим простой пример расчета общей емкости для трех параллельно соединенных конденсаторов:

• C1 = 10 мкФ
• C2 = 22 мкФ
• C3 = 47 мкФ

Используем формулу: C = C1 + C2 + C3

C = 10 мкФ + 22 мкФ + 47 мкФ = 79 мкФ

Таким образом, общая емкость трех параллельно соединенных конденсаторов составит 79 мкФ.

Где применяется параллельное соединение конденсаторов

Параллельное соединение конденсаторов широко используется в различных электронных устройствах и схемах. Основные области применения:

• Увеличение общей емкости в схеме
• Фильтрация высокочастотных помех
• Сглаживание пульсаций в блоках питания
• Накопление энергии в импульсных схемах
• Создание временных задержек в RC-цепях

Параллельное подключение позволяет гибко комбинировать конденсаторы разной емкости для получения требуемых характеристик.

Преимущества параллельного соединения конденсаторов

Параллельное соединение конденсаторов дает ряд важных преимуществ:

1. Увеличение общей емкости — можно получить большую емкость, комбинируя несколько конденсаторов меньшей емкости
2. Снижение эквивалентного последовательного сопротивления (ESR)
3. Увеличение максимального рабочего тока
4. Улучшение фильтрации высокочастотных помех
5. Повышение надежности — при выходе из строя одного конденсатора схема продолжит работать

Эти преимущества делают параллельное соединение очень востребованным в различных электронных устройствах.

Особенности выбора конденсаторов для параллельного соединения

При выборе конденсаторов для параллельного соединения следует учитывать несколько важных моментов:

• Рабочее напряжение всех конденсаторов должно быть не меньше напряжения в схеме
• Желательно использовать конденсаторы одного типа и производителя
• Для снижения ESR лучше применять несколько параллельных конденсаторов меньшей емкости
• Необходимо учитывать температурные характеристики конденсаторов
• Для фильтрации в широком диапазоне частот используют конденсаторы разной емкости

Правильный выбор конденсаторов позволит максимально эффективно использовать преимущества параллельного соединения.

Расчет параметров при параллельном соединении конденсаторов

При параллельном соединении конденсаторов важно уметь рассчитывать не только общую емкость, но и другие параметры:

Расчет общего заряда

Q = Q1 + Q2 + Q3 + … + Qn

Где Q — общий заряд, Q1, Q2 и т.д. — заряды отдельных конденсаторов

Расчет тока через конденсаторы

I = I1 + I2 + I3 + … + In

Где I — общий ток, I1, I2 и т.д. — токи через отдельные конденсаторы

Расчет энергии, запасенной в конденсаторах

W = W1 + W2 + W3 + … + Wn

Где W — общая энергия, W1, W2 и т.д. — энергия, запасенная в отдельных конденсаторах

Эти формулы помогут более точно рассчитать характеристики схемы с параллельно соединенными конденсаторами.

Параллельное соединение конденсаторов – общая емкость, заряд, формула кратко

4.6

Средняя оценка: 4.6

Всего получено оценок: 54.

4.6

Средняя оценка: 4.6

Всего получено оценок: 54.

Компоненты электрической цепи могут быть соединены различными способами, чаще всего используется параллельное и последовательное соединение. Рассмотрим работу параллельно соединенных конденсаторов.

Виды соединений в электрической цепи

Любая электрическая цепь состоит из одного или нескольких источников тока и одного или нескольких потребителей. Все эти компоненты связаны между собой проводниками.

Как бы ни сложна была электрическая цепь, в ней всегда можно выделить узлы и звенья:

• узел — это точка, в которой сходятся три и более проводника;
• звено — это участок цепи между двумя соседними узлами.

Каждое звено может быть простым проводником, может состоять из одного потребителя, а может содержать несколько потребителей, соединенных «цепочкой», один за другим. Такое соединение потребителей называется последовательным.

Если несколько звеньев подключаются к одним и тем же двум узлам, такое соединение называется параллельным.

Если три и более звена соединяются так, что некоторые звенья будут соединены параллельно, а некоторые — последовательно, то такое соединение называется смешанным.

Рис. 1. Виды соединений в электрической цепи.

Параллельное соединение конденсаторов

При параллельном соединении к двум выводам звена подключается каждый из соединенных конденсаторов. Получается, что при подключении к внешней цепи электрический ток будет поступать сразу на все конденсаторы. Произведем расчет емкости такой батареи конденсаторов.

Напомним, что емкость конденсатора показывает, насколько легко сообщить конденсатору заряд, и равна отношению заряда к напряжению на обкладках:

$$C={q\over U}$$

Если сообщить батарее конденсаторов некоторый заряд, то по закону сохранения этот заряд может лишь распределиться между конденсаторами, однако суммарно он останется прежним:

$$q_{общ}=q_1+q_2+…+q_n$$

При параллельном соединении конденсаторов напряжение на каждом из них будет одинаково. Действительно, если на каком-то из конденсаторов напряжение было бы больше, то заряд из этого конденсатора сразу же перешел бы к другому, тем самым уменьшив напряжение на первом и увеличив на втором.

Таким образом, общая емкость батареи конденсаторов равна:

$$C_{общ}={q_1+q_2+…+q_n\over U}={q_1\over U}+{q_2\over U}+…+{q_n\over U}$$

Каждый компонент полученной суммы равен отношению заряда на одном из конденсаторов к напряжению на нем, а это — емкость данного конденсатора. Заменяя каждую дробь на соответствующую емкость, получаем формулу для определения общей емкости параллельно соединенных конденсаторов:

$$C_{общ}=C_1+C_2+…+Cn$$

При параллельном соединении конденсаторов общая емкость батареи равна сумме емкостей отдельных элементов.

Рис. 2. Параллельное соединение конденсаторов.

Использование параллельного соединения конденсаторов

Казалось бы, смысла в параллельном соединении конденсаторов нет. Зачем брать два конденсатора, если можно взять один, большей емкости?

Основная причина состоит в том, что выпускаемые номиналы конденсаторов имеют не любые значения.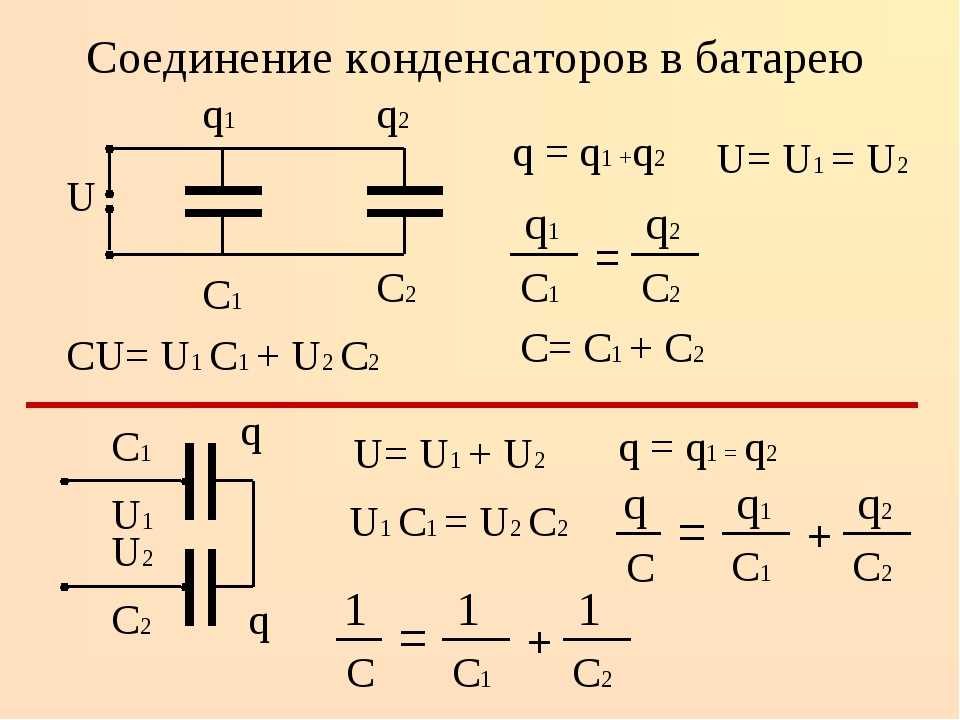 Например, конденсаторы емкостью 7 мкФ не выпускаются. Однако выпускаются конденсаторы емкостью 6,8 мкФ и 0,2 мкФ. Соединив их параллельно, можно получить требуемые 7 мкФ.

Рис. 3. Стандартные ряды номиналов радиодеталей.

Существует еще одна причина использования параллельного соединения конденсаторов — их неидеальность. Например, у больших конденсаторов имеется заметная на высоких частотах паразитная индуктивность. Из-за этого высокочастотная составляющая сигнала, которая в идеале должна легко проходить через большую емкость конденсатора, не проходит через него. Поэтому в этом случае параллельно конденсатору большой емкости ставится еще один, малой емкости, но имеющий очень малую паразитную индуктивность, которой можно пренебречь. В результате высокочастотная составляющая будет проходить через него.

Что мы узнали?

Общая емкость конденсаторов при параллельном соединении равна сумме емкостей отдельных конденсаторов. Такое соединение используется чаще всего для того, чтобы получить номиналы, не выпускающиеся промышленностью.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 54.

---

А какая ваша оценка?

При отсутствии необходимого номинала конденсаторов используют параллельное и последовательное соединение конденсаторов.

Когда в нашем распоряжении нет конденсатора нужной емкости или напряжение на конденсаторе превышает допускаемое, возникает необходимость использовать параллельное и последовательное соединение конденсаторов.

Содержание

• 1 Последовательное соединение конденсаторов
• 2 Параллельное соединение конденсаторов

Последовательное соединение конденсаторов

Сообщим равные по величине разноименные заряды крайним обкладкам (внешним электродам) цепочке из двух последовательно соединенных конденсаторов с емкостью С1 и С2.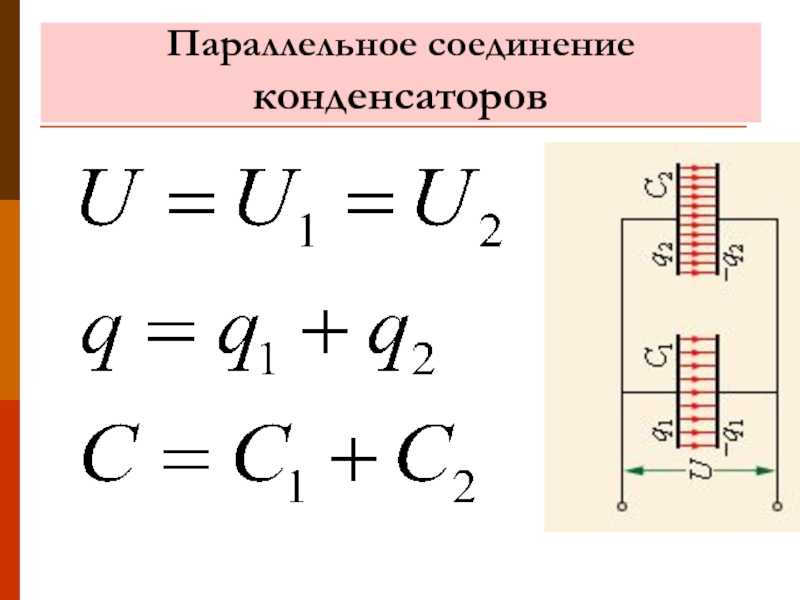

В результате взаимодействия зарядов на соединенных проводником внутренних обкладках возникнут также равные по величине и обратные по знаку заряды, так что на каждой из четырех обкладок будут одинаковые по величине заряды Q. Согласно формуле C = Q/U напряжения между обкладками каждого конденсатора будут:
U = Q/C1 и U2 = Q/C2,
т. е. при различных значениях емкостей напряжения на конденсаторах будут различны.
Сложив напряжения U1 и U2, мы получим напряжение U между внешними обкладками (напряжение на зажимах цепочки). Таким образом,
U = U1 + U2. (1-9)
Подставив в выражение (1-9) вместо напряжений отношение зарядов к емкостям, получим:
Q/C = Q/C1 + Q/C2
где С — общая или эквивалентная емкость.
Сокращая на Q, будем иметь:
1/C = 1/C1 + 1/C2,                          (1-10)
откуда емкость конденсатора, заменяющая цепочку, или общая емкость двух последовательно соединенных конденсаторов.
1/C = C2 + C1 / C1C2 или C = C1C2 / C1+C2               (1-11)

В случае последовательного соединения трех конденсаторов общую емкость можно найти из формулы, аналогичной (1-10):
1/C = 1/C1 + 1/C2 + 1/C3                   (1-12)
Тем же путем можно вычислить общую емкость любого числа последовательно соединенных конденсаторов.

 

Параллельное соединение конденсаторов

При параллельном соединении, например, трех конденсаторов (рис. 1-11) получаются две группы обкладок разных конденсаторов. Каждая группа обкладок представляет собой равнопотенциальное проводящее тело, поэтому разности потенциалов (или напряжения) между обкладками отдельных конденсаторов будут одинаковы. Заряды на обкладках при неодинаковых емкостях конденсаторов имеют разные значения:
Ql = C1U;  Q2 = C2U;  Q3 = C3U.
Заряд на группе объединенных обкладок
Q = Q1 + Q2 + Q3,
откуда емкость конденсатора, заменяющего три параллельно соединенных конденсатора, или общая емкость
С = Q/U = Q1 + Q2 + Q3/U = C1 + C2 + C3, (1-13)
т. е. равна сумме емкостей отдельных конденсаторов. Это и есть формула при параллельном соединение конденсаторов.

При другом числе параллельно соединенных конденсаторов общая емкость вычисляется аналогично.
Пример:
Определить общую емкость двух конденсаторов при последовательном и параллельном их соединении, если С1 = 2 мкф, а С2 = 4 мкф.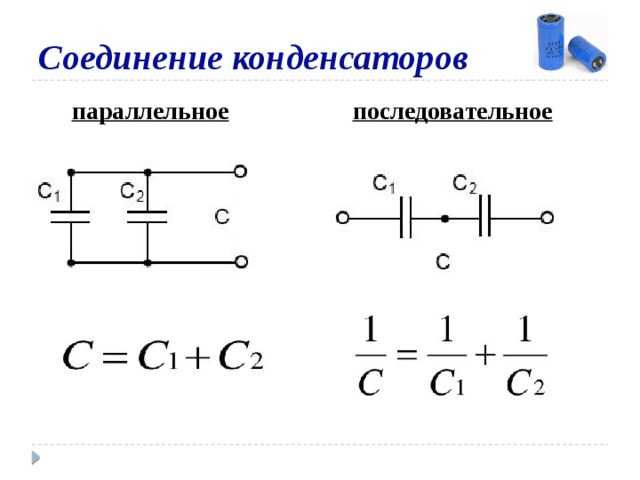
Емкость при последовательном соединении
C = C1C2/C1+C2 = 2×4/2+4 = 1,33 мкф.
Емкость при параллельном соединении
С = С1 + С2 = 2 + 4 = 6 мкф.

Видеофильм о последовательном и параллельном их соединении конденсаторов смотрите ниже:

Объяснение урока: Конденсаторы последовательно и параллельно

В этом объяснении мы узнаем, как рассчитать общую емкость нескольких конденсаторов, соединенных последовательно и параллельно.

Для начала вспомним законы Кирхгофа, которые помогут нам понять эффекты объединения конденсаторов разными способами:

1. Ток в переходе равен току из перехода.
2. Сумма перепадов напряжения вокруг замкнутого контура равна нулю.

Мы начнем обсуждение с рассмотрения конденсаторов, соединенных параллельно, как показано на схеме ниже.

Обратите внимание, что оба конденсатора находятся на отдельной ветви этой цепи, и помните, что каждая ветвь параллельной цепи получает одинаковое напряжение или разность потенциалов. Второй закон Кирхгофа подтверждает это. Таким образом, разность потенциалов на конденсаторе 1, которую мы можем назвать 𝑉, равна разности потенциалов второго конденсатора, 𝑉, и разности потенциалов, обеспечиваемой батареей, 𝑉общ. Это общее соотношение сформулировано математически ниже.

На приведенной выше диаграмме у нас есть два конденсатора, но пунктирное продолжение уравнения ниже (и других в этом объяснении) подразумевает, что соотношение сохраняется для любого количества конденсаторов, которое мы, возможно, захотим рассмотреть: 𝑉=𝑉=𝑉=⋯.total

Первый закон Кирхгофа утверждает, что ток, входящий и выходящий из ответвления в цепи, равен. Кроме того, помните, что количество заряда, протекающего через ветвь цепи, является произведением тока в ветви и времени, в течение которого протекает заряд.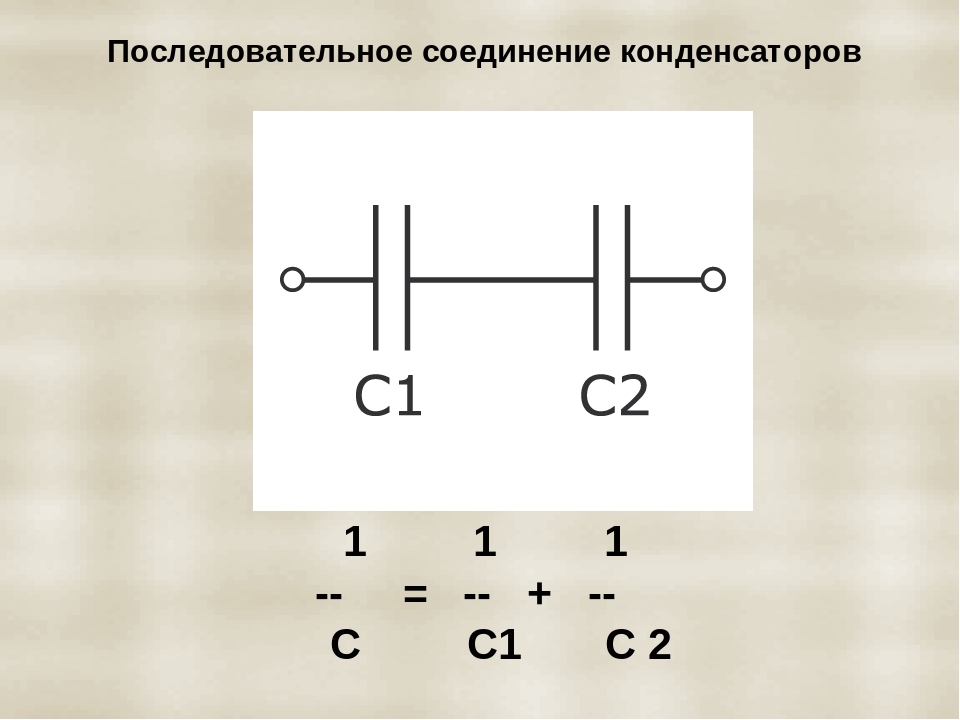 Таким образом, когда цепь замкнута и конденсаторы могут заряжаться в течение некоторого времени, заряды на всех конденсаторах (здесь 𝑄 и 𝑄) складываются в общий заряд во всей цепи, 𝑄total, следующим образом: 𝑄=𝑄+𝑄+⋯.всего

Мы уже знаем, что можем связать разность потенциалов и заряд с емкостью, используя уравнение 𝐶=𝑄𝑉, которое можно переписать как 𝑄=𝐶𝑉.

Применим это к приведенному выше уравнению для заряда, заменив «𝑄» на «𝐶𝑉» следующим образом: 𝑄=𝐶𝑉=𝐶𝑉+𝐶𝑉+⋯.totaltotaltotal

Помните, что значения разности потенциалов для всех элементов в параллельной комбинации эквивалентны, поэтому мы можем разделить все это уравнение на разность потенциалов. Это приводит к уравнению, которое мы используем, чтобы связать значение общей емкости с емкостью каждого конденсатора в параллельной комбинации.

Определение: Общая емкость для параллельной комбинации

Общая емкость для параллельной комбинации конденсаторов определяется выражением 𝐶=𝐶+𝐶+⋯.total

В следующих примерах мы будем практиковать параллельное соединение конденсаторов.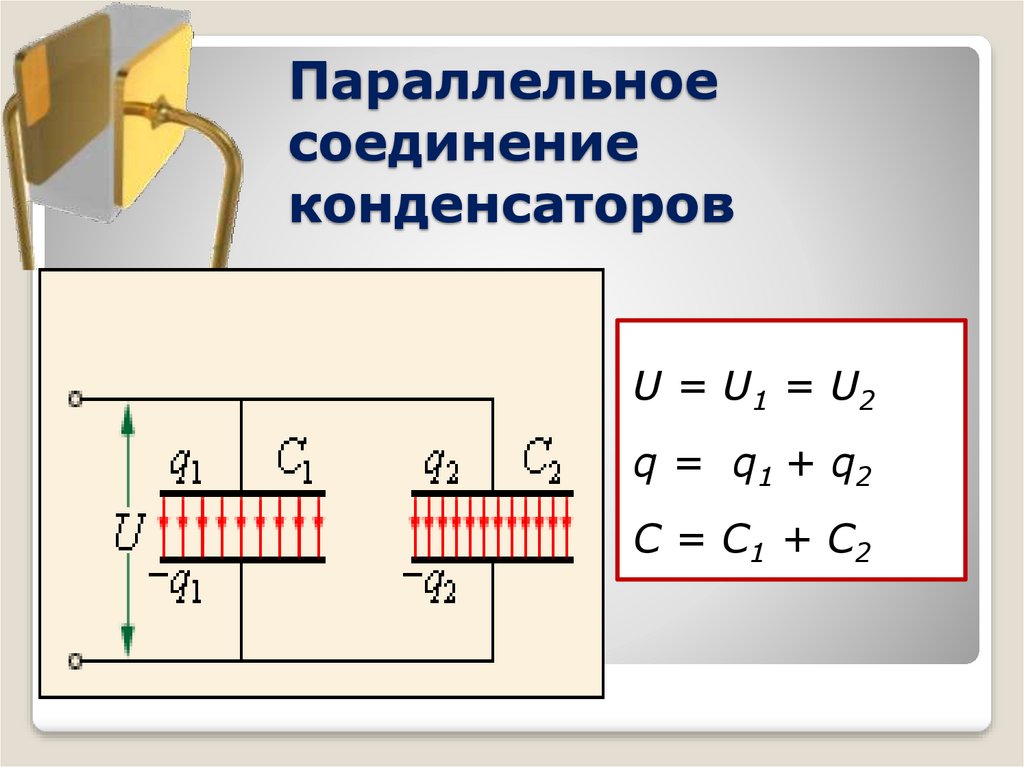

Пример 1: Параллельное соединение конденсаторов

Схема на схеме содержит два конденсатора, соединенных параллельно. Какова общая емкость цепи?

Ответ

Начнем с того, что вспомним уравнение для параллельно соединенных конденсаторов: 𝐶=𝐶+𝐶+⋯.всего

Поскольку здесь у нас есть два конденсатора, включенных параллельно, и мы знаем их значения, мы готовы сложить их, чтобы найти общую емкость цепи: 𝐶=35+65=100.totalµFµFµF

Таким образом, мы нашли, что общая емкость этой цепи составляет 100 мкФ.

Пример 2: Параллельное соединение конденсаторов

Схема на схеме содержит два конденсатора, соединенных параллельно. Суммарная емкость цепи 240 мкФ. Какая емкость 𝐶?

Ответ

Здесь нам нужно определить неизвестное значение емкости 𝐶, и мы можем начать с рассмотрения уравнения для полной емкости параллельной комбинации: 𝐶=𝐶+𝐶+⋯.total

Таким образом, отдельные значения емкости просто добавляются к общему значению емкости.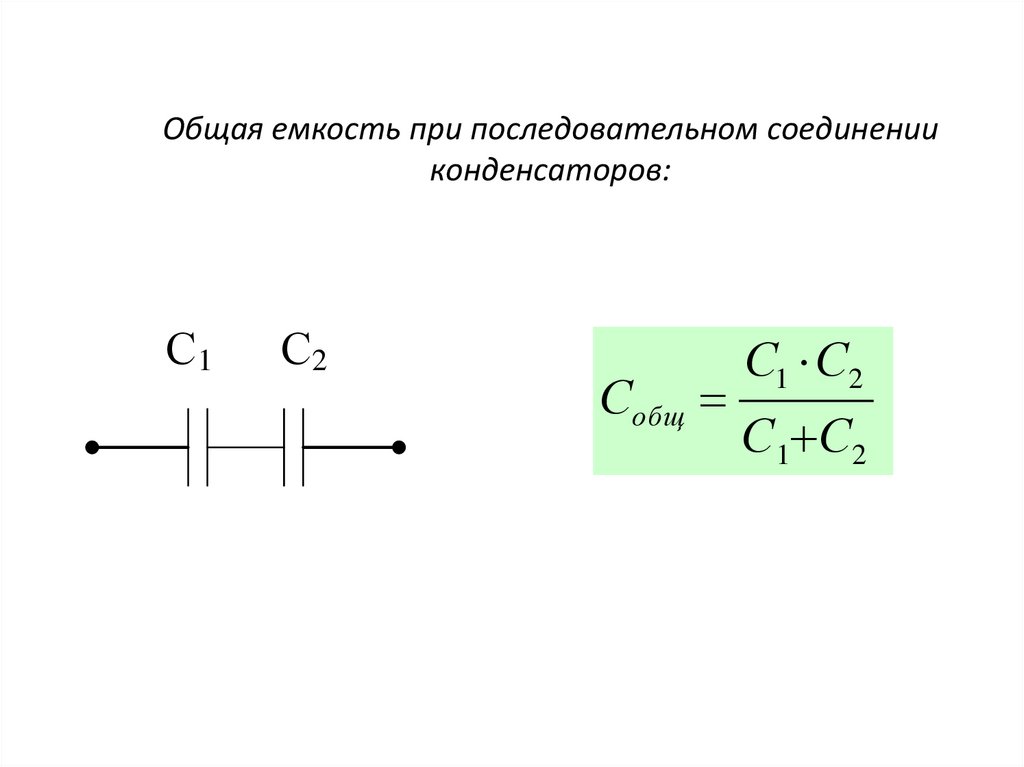 Подставляя значения, которые нам дали, уравнение становится 240=𝐶+135.µFµF

Мы можем найти 𝐶, вычитая 135 µF из обеих частей уравнения: 𝐶=240−135=105.мкФµFµФ

Таким образом, мы нашли, что емкость 𝐶 равна 105 мкФ.

Давайте теперь сосредоточимся на последовательном соединении конденсаторов, как показано на схеме ниже.

Напомним, что ток во всех точках последовательной цепи одинаков, что подтверждается первым законом Кирхгофа. Это означает, что последовательно соединенные конденсаторы накапливают одинаковые заряды. Таким образом, для серийной комбинации 𝑄=𝑄=𝑄=⋯.total

Из-за второго закона Кирхгофа мы знаем, что сумма разностей потенциалов между элементами в замкнутом контуре равна нулю. Последовательная комбинация представляет собой один большой замкнутый контур, поэтому разность потенциалов на конденсаторах должна суммироваться с разностью потенциалов на батарее. Так, 𝑉=𝑉+𝑉+⋯.всего

Еще раз напомним, что емкость, разность потенциалов и заряд любого конденсатора задаются формулой 𝐶=𝑄𝑉, которую можно преобразовать как 𝑉=𝑄𝐶.

Мы можем подставить это в приведенное выше уравнение разности потенциалов, чтобы соотношение было записано как 𝑉=𝑄𝐶=𝑄𝐶+𝑄𝐶+⋯.totaltotaltotal

Мы уже определили, что заряды на всех последовательных элементах цепи эквивалентны, поэтому мы можем разделить все уравнение на заряд. И у нас есть отношение для описания значений емкости в последовательной комбинации.

Определение: Общая емкость для последовательного соединения

Общая емкость для последовательного соединения конденсаторов определяется выражением 1𝐶=1𝐶+1𝐶+⋯.total

Обратите внимание на обратную природу этого уравнения, которая означает, что при последовательном добавлении большего количества конденсаторов общая емкость уменьшается. Мы рассмотрим эту концепцию в следующих нескольких примерах.

Пример 3: Объединение конденсаторов в серию

Два конденсатора, 𝐶 и 𝐶, соединены последовательно, где 𝐶>𝐶. Какое из следующих утверждений правильно связывает общую емкость, 𝐶total, с 𝐶 и 𝐶?

1. 𝐶 = 𝐶+𝐶total
2. 𝐶 = (𝐶+𝐶) Всего
3. 𝐶 = 𝐶𝐶total
4. 𝐶𝐶𝐶total
5. 𝐶𝐶𝐶total

Ответ

Выбор A может выглядит знакомо, но это уравнение было бы применимо, если бы два конденсатора были добавлены параллельно, а не последовательно. Следовательно, А неверно. Уравнение для полной емкости двух последовательно соединенных конденсаторов: 1𝐶=1𝐶+1𝐶.total

Это уравнение не преобразуется и не упрощается ни до уравнения B, ни до C, поэтому эти два варианта неверны. Хотя приведенное выше уравнение прямо не указано ни в одном варианте ответа, мы можем использовать его для сравнения 𝐶total, 𝐶 и 𝐶 по размеру и определить, является ли правильным D или E.

Из-за обратных свойств в приведенном выше уравнении мы можем сказать, что по мере последовательного добавления конденсаторов эквивалентная или общая емкость уменьшается. Таким образом, при последовательном соединении конденсаторов общая емкость меньше емкости любого одного конденсатора в цепи. Это означает, что 𝐶𝐶всего и что 𝐶𝐶всего.

Следовательно, выбор E правильный.

Пример 4: Объединение конденсаторов в серию

Схема на схеме содержит два последовательно соединенных конденсатора. Какова общая емкость цепи? Ответ с точностью до микрофарад.

Ответ

Начнем с того, что вспомним уравнение для нахождения эквивалентной емкости последовательно соединенных конденсаторов: 1𝐶=1𝐶+1𝐶+⋯.total

Теперь подставим значения для двух показанных выше конденсаторов: 1𝐶=1𝐶+1𝐶=1150+1250.totalµFµF

Чтобы сложить дроби в правой части уравнения, мы будем использовать 750 µF как наименьший общий знаменатель: 1𝐶=5750+3750=8750.totalµFµFµF

Теперь мы можем взять обратную или перевернуть обе части уравнения, чтобы найти окончательное значение 𝐶total: 𝐶=7508=93,75.totalµFµF

Округляя до микрофарад, получаем, что общая емкость цепи равна 94 мкФ.

Поскольку теперь мы увидели, как добавлять конденсаторы последовательно и параллельно, давайте проверим оба навыка на следующих примерах.

Пример 5: последовательное и параллельное соединение конденсаторов

Конденсатор емкостью 135 мкФ и конденсатор емкостью 264 мкФ можно соединять либо последовательно, либо параллельно. Найдите отношение полной емкости при параллельном соединении к полной емкости при последовательном соединении.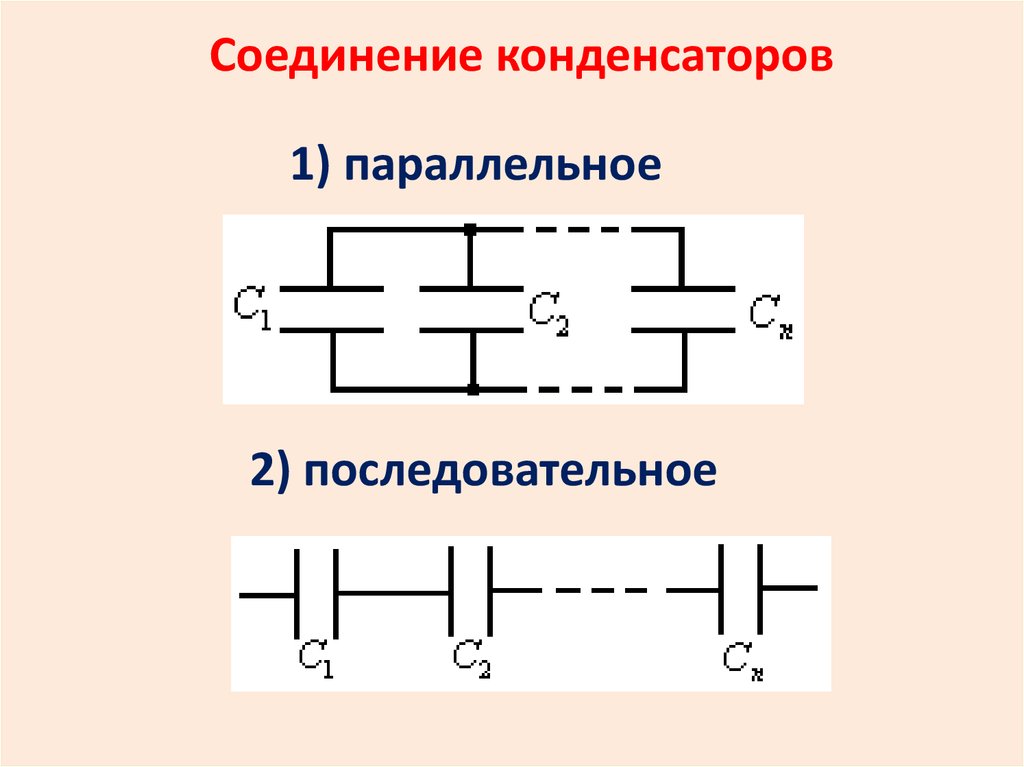 Дайте ответ с точностью до двух знаков после запятой.

Ответ

Здесь мы изучим влияние объединения двух конденсаторов различными способами на их общую емкость. Начнем с того, что вспомним уравнение для параллельного соединения конденсаторов: 𝐶=𝐶+𝐶+⋯.total

Таким образом, мы можем сказать, прежде чем подставлять какие-либо значения для 𝐶 или 𝐶, что общая емкость будет больше, чем любое отдельное значение емкости любого конденсатора. Теперь, подставив два значения, которые нам дали, мы можем найти общую емкость для параллельной комбинации, которую мы можем назвать 𝐶параллельной: 𝐶=135+264=399.parallelµFµFµF

Теперь мы можем посмотреть на уравнение для последовательного соединения конденсаторов: 1𝐶=1𝐶+1𝐶+⋯.total

Мы видим, что общая емкость для последовательной комбинации, которую мы можем назвать 𝐶рядом, будет меньше, чем отдельные значения емкости 𝐶 или 𝐶. Таким образом, можно ожидать, что 𝐶параллельность будет больше 𝐶серии и что отношение их значений будет больше единицы.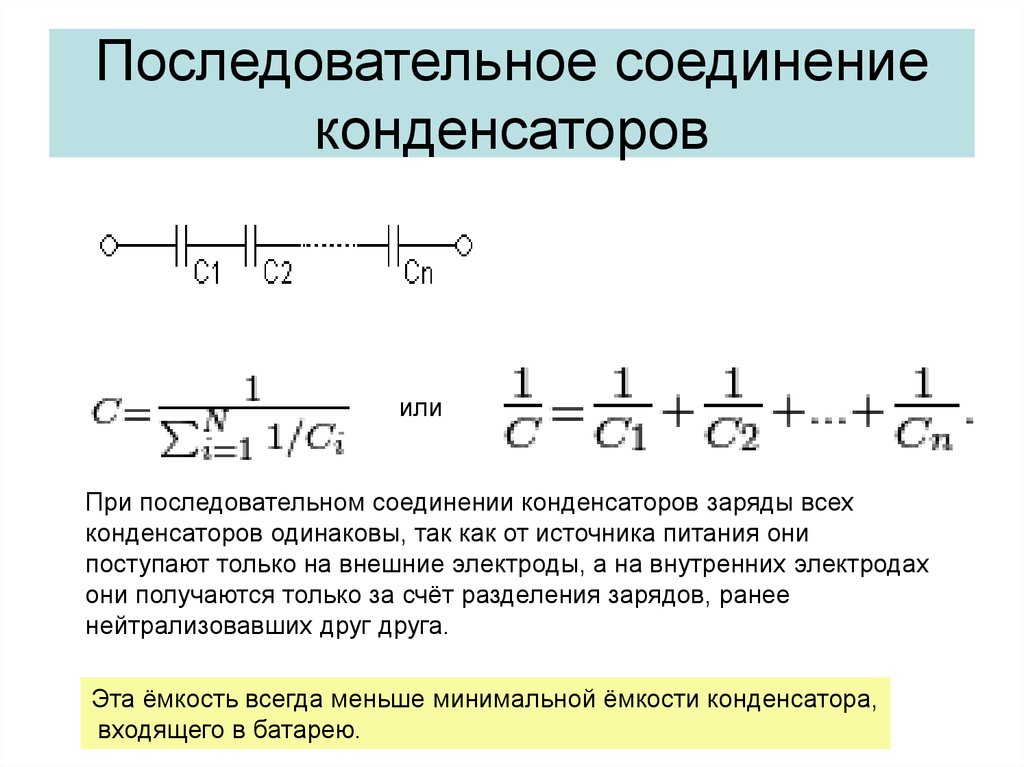

Теперь найдем значение общей емкости последовательно: 1𝐶=1135+1264.ряд мкФмкФ

Переписав уравнение так, чтобы мы могли складывать дроби, используя наименьший общий знаменатель, мы имеем 1𝐶=8811880+4511880=13311880.seriesµFµFµF

Возьмем обратное или перевернем все уравнение для решения 𝐶ряда, переместив его из знаменателя в числитель: 𝐶=11880133=89.32.seriesµFµF

Теперь, когда мы знаем 𝐶параллель и 𝐶ряд, мы можем найти отношение их значений: 𝐶𝐶=39989,32=4,4671.parallelseriesµFµF

Округляя до двух знаков после запятой, получаем, что отношение полной емкости параллельно к полной емкости последовательно равно 4,47.

Пример 6: Соединение конденсаторов последовательно и параллельно

Схема на схеме содержит конденсаторы, соединенные последовательно и параллельно. Какова общая емкость цепи? Дайте свой ответ с точностью до микрофарад.

Ответ

Здесь у нас есть цепь, содержащая последовательно и параллельно соединенные конденсаторы.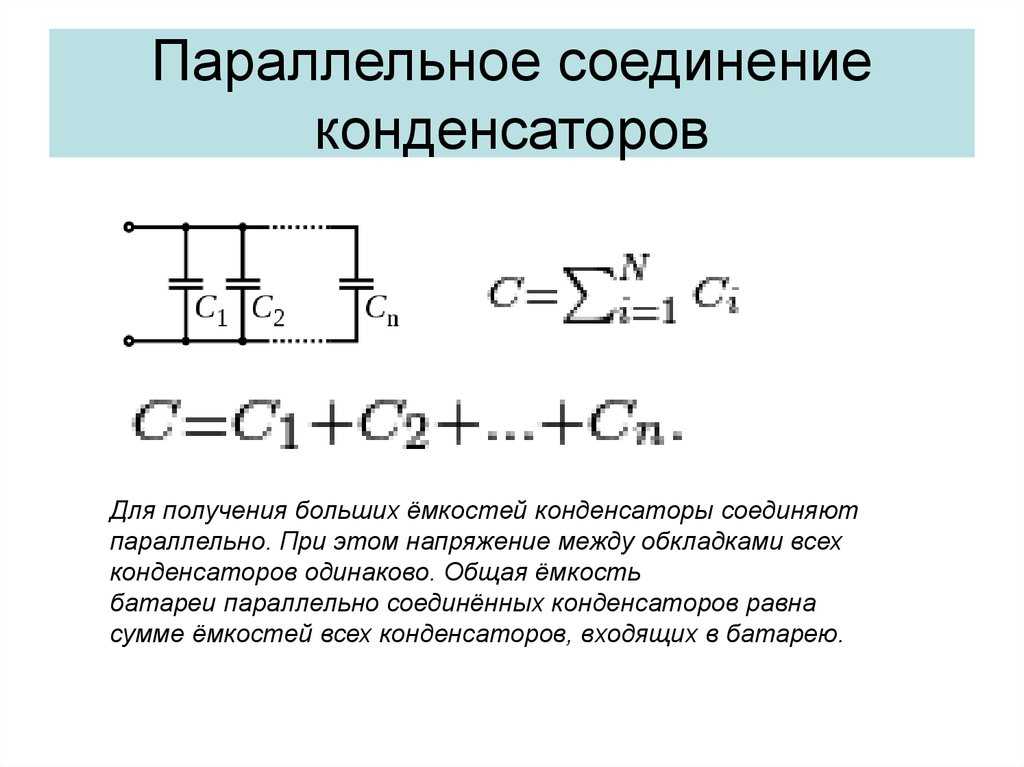 Мы будем работать с этой схемой по частям и обозначим три конденсатора как A, B и C, как показано на диаграмме ниже.

Конденсаторы A и B соединены последовательно, поэтому сначала найдем их эквивалентную емкость. Эта эквивалентная емкость, которую мы можем назвать 𝐶AB, будет представлять собой общую емкость среднего провода этой параллельной цепи. Мы можем начать с уравнения для нахождения общей емкости последовательной комбинации и подставить наши значения для конденсаторов A и B: наименьший общий знаменатель этих дробей равен 825 мкФ: 1𝐶=11825+15825=26825.ABµFµFµF

Теперь мы обратим или перевернем все уравнение и вычислим значение эквивалентной емкости A и B: 𝐶=82526=31,73.ABµFµF

Теперь мы можем представить, что цепь состоит из двух параллельно соединенных конденсаторов, как показано на схеме ниже.

Теперь у нас есть два конденсатора, соединенных параллельно, поэтому мы можем подставить их значения и найти общую емкость всей цепи: 𝐶=𝐶+𝐶+⋯total𝐶=𝐶+𝐶=31,73+35=66,73. totalABCµFµFµF

Округляя до микрофарад, находим, что общая емкость этой цепи равна 67 мкФ.

Давайте закончим резюмированием некоторых важных понятий.

Ключевые моменты

• При параллельном соединении конденсаторов используйте 𝐶=𝐶+𝐶+⋯total.
• При последовательном соединении конденсаторов используйте 1𝐶=1𝐶+1𝐶+⋯total.
• Параллельно соединенные конденсаторы имеют одинаковую разность потенциалов.
• Конденсаторы, соединенные последовательно, накапливают одинаковые заряды.

Вопрос Видео: Нахождение полной емкости последовательно и параллельно соединенных конденсаторов

Стенограмма видео

Цепь на схеме содержит конденсаторы, соединенные последовательно и параллельно. Какова общая емкость цепи? Дайте свой ответ с точностью до микрофарад.

На схеме, которую нам дали, показана цепь, в которой ячейка подключена к комбинации конденсаторов. Мы видим, что эта схема имеет две параллельные ветви с включенными конденсаторами. Вот эта ветвь посередине, которую мы обозначим как ветвь А. И мы видим, что на ней есть конденсаторы. Есть один с емкостью 75 мкФ и другой с емкостью 55 мкФ. Затем есть вот эта ветвь, которую мы обозначим как ветвь B. И она содержит только один конденсатор на 35 мкФ.

Нас просят найти общую емкость цепи. А для этого нам нужно будет вспомнить, как мы соединяем конденсаторы последовательно и параллельно. При последовательном соединении нескольких конденсаторов обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. То есть, если мы соединим последовательно кучу конденсаторов с емкостями 𝐶 один, 𝐶 два, 𝐶 три и так далее, то один сверх общей емкости 𝐶 нижний индекс Т будет равен единице больше 𝐶 один плюс один больше 𝐶 два плюс один больше 𝐶 три и так далее.

Между тем, если у нас есть несколько конденсаторов, соединенных параллельно, то мы просто добавляем отдельные емкости, чтобы получить общую емкость. На нашей диаграмме видно, что ветвь, обозначенная буквой А, состоит из двух последовательно соединенных конденсаторов.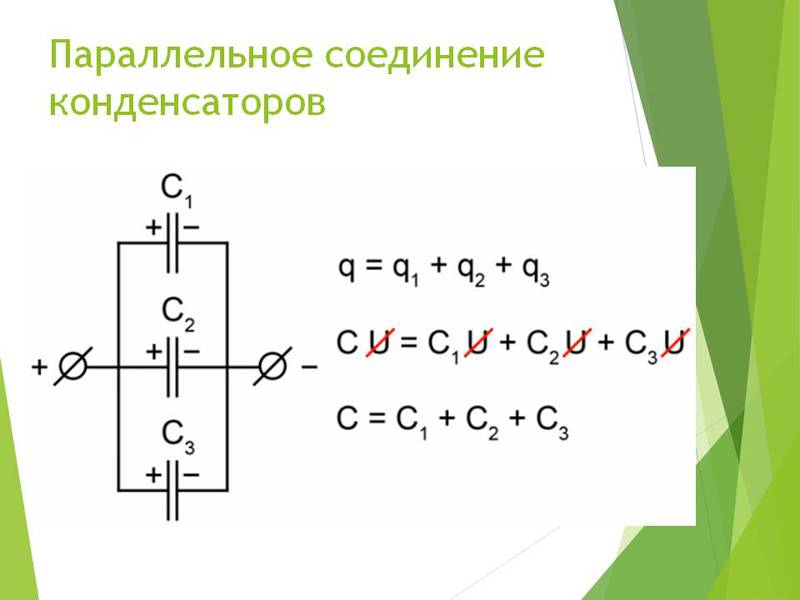 Обозначим общую емкость этой ветви, так что это общая емкость этих двух последовательно соединенных конденсаторов, как 𝐶 нижний индекс A. Мы также обозначим эту емкость 75 мкФ как 𝐶 один, а эту емкость 55 мкФ как 𝐶 два. Тогда из нашего общего выражения для конденсаторов, соединенных последовательно, мы знаем, что один над 𝐶 нижним индексом A равен одному над 𝐶 единицей плюс один над 𝐶 двумя.

Поскольку мы знаем значения как 𝐶 единицы, так и 𝐶 двойки, мы можем использовать это уравнение, чтобы найти значение 𝐶 нижнего индекса A. Для этого мы хотим сделать 𝐶 нижний индекс A предметом уравнения . Мы начнем с умножения обеих частей уравнения на 𝐶 нижний индекс A, 𝐶 один и 𝐶 два. Раскрыв скобки в правой части, мы можем переписать уравнение следующим образом. В этой дроби слева индекс 𝐶 A в числителе сокращается с индексом 𝐶 A в знаменателе. В этой первой дроби справа 𝐶 в числителе и знаменателе сокращаются. И в этой второй дроби справа две 𝐶 в числителе и знаменателе сокращаются.

Как только мы избавимся от отмененных терминов, мы получим вот это выражение. Затем мы можем вынести индекс 𝐶 A, который появляется в обоих терминах справа. Последний шаг, который нам нужно сделать, чтобы получить 𝐶 индекс A как субъект этого уравнения, — это разделить обе части на 𝐶 один плюс 𝐶 два, так что справа 𝐶 один плюс 𝐶 два в числителе сокращается с единицей в знаменатель. Если мы затем напишем уравнение наоборот, мы получим, что 𝐶 Нижний индекс A равен 𝐶 один раз 𝐶 два, деленное на 𝐶 один плюс 𝐶 два.

Итак, это уравнение говорит нам, как рассчитать общую емкость 𝐶 индекс А двух конденсаторов, 𝐶 одного и 𝐶 двух, соединенных последовательно.

Давайте теперь освободим место, чтобы мы могли подставить наши значения 𝐶 один и 𝐶 два из этой схемы. Подставив сюда 𝐶 единица равна 75 мкФ и 𝐶 двойка равна 55 мкФ, получим такое выражение для 𝐶 индекса А. В числителе имеем 75 мкФ умножить на 55 мкФ. И это получается как 4125 единиц микрофарад в квадрате. Затем в знаменателе у нас есть 75 микрофарад плюс 55 микрофарад, что дает 130 микрофарад.

С точки зрения единиц, мы можем сократить один из двух множителей микрофарад из числителя с микрофарадами из знаменателя.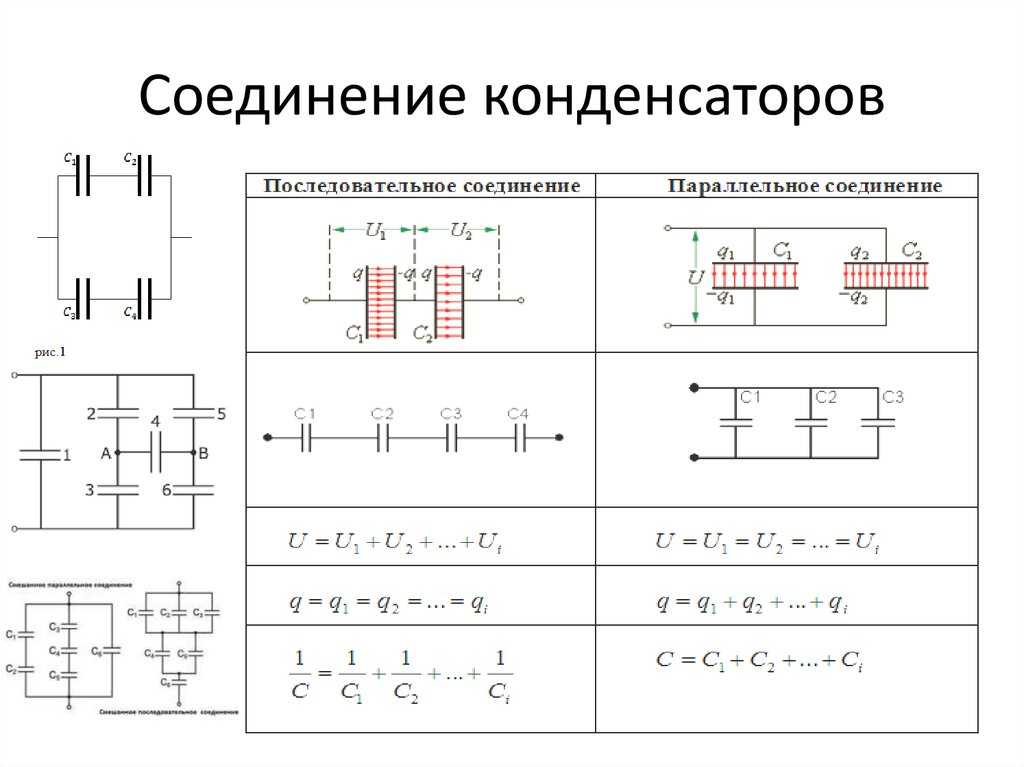 Это оставляет нам единицы для 𝐶 нижнего индекса A микрофарад. Тогда вычисление выражения дает результат с точностью до двух знаков после запятой 31,73 мкФ. Итак, мы нашли значение индекса 𝐶 A, которое представляет собой емкость ветви, которую мы обозначили как A на нашей принципиальной схеме. Так как ветвь В содержит всего один конденсатор, то мы знаем, что его емкость как раз равна этой величине 35 мкФ. Обозначим это как 𝐶 индекс B.

Теперь у нас есть две параллельные ветви. Это ветвь A и ветвь B. И мы знаем емкость каждой ветви. Это наши значения для 𝐶 нижнего индекса A и 𝐶 нижнего индекса B. Если мы теперь освободим место на доске, то сможем использовать наше общее выражение для конденсаторов, соединенных параллельно, чтобы найти общую емкость этих двух ветвей. .

Это общее выражение говорит нам, что для конденсаторов, соединенных параллельно, мы просто добавляем отдельные емкости. В нашем случае это значения для 𝐶 нижнего индекса A и 𝐶 нижнего индекса B. Таким образом, общая емкость 𝐶 нижнего индекса T равна 𝐶 нижнему индексу A плюс 𝐶 нижнему индексу B.