Емкостное сопротивление определяется по формуле. Емкостное сопротивление в цепи переменного тока: формула, расчет и применение

Что такое емкостное сопротивление конденсатора. Как рассчитать емкостное сопротивление по формуле. От чего зависит величина емкостного сопротивления. Как применяется емкостное сопротивление на практике.

Что такое емкостное сопротивление конденсатора

Емкостное сопротивление — это сопротивление, которое оказывает конденсатор переменному току в электрической цепи. В отличие от активного сопротивления резисторов, емкостное сопротивление является реактивным и не приводит к рассеиванию энергии в виде тепла.

Основные особенности емкостного сопротивления:

• Возникает только в цепях переменного тока
• Измеряется в омах (Ом)
• Зависит от емкости конденсатора и частоты тока
• Уменьшается с ростом частоты
• Создает сдвиг фаз между током и напряжением на 90°

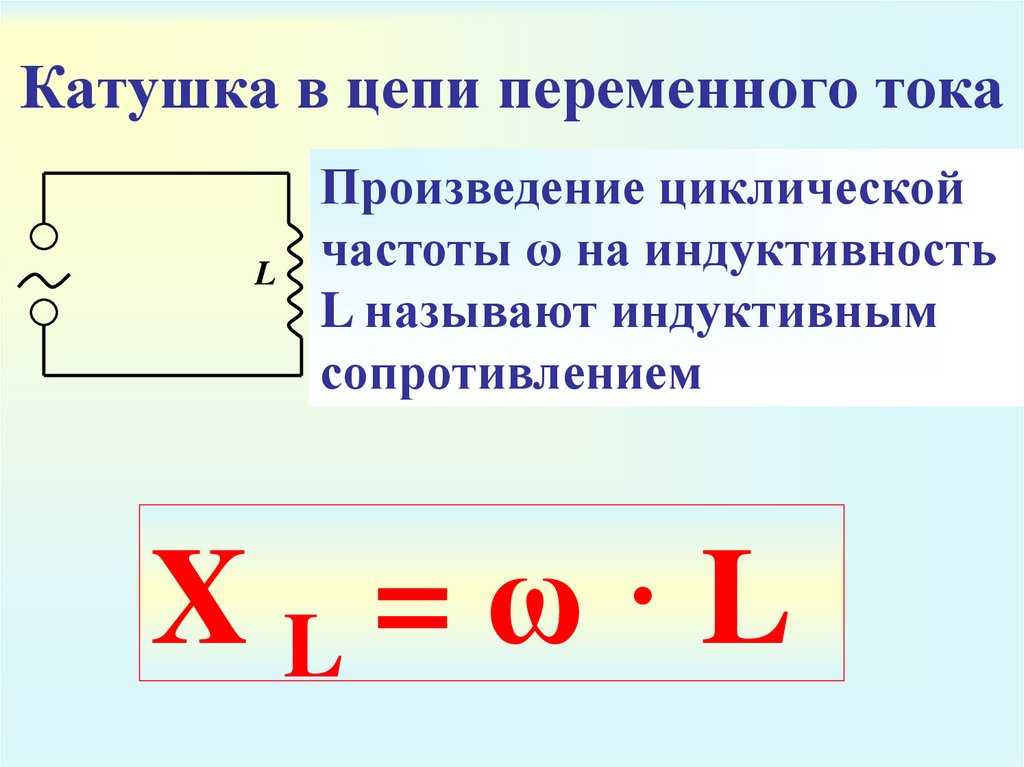
Формула расчета емкостного сопротивления

Емкостное сопротивление конденсатора (Xc) рассчитывается по формуле:

Xc = 1 / (2πfC)

где:

• Xc — емкостное сопротивление в омах (Ом)
• π — число пи (≈3,14)
• f — частота переменного тока в герцах (Гц)
• C — емкость конденсатора в фарадах (Ф)

Примеры расчета емкостного сопротивления

Рассмотрим несколько примеров расчета емкостного сопротивления конденсаторов:

Пример 1

Дано: конденсатор емкостью 10 мкФ, частота тока 50 Гц.

Xc = 1 / (2 * 3,14 * 50 * 10 * 10^-6) = 318,3 Ом

Пример 2

Дано: конденсатор емкостью 100 нФ, частота тока 1 кГц.

Xc = 1 / (2 * 3,14 * 1000 * 100 * 10^-9) = 1591,5 Ом

От чего зависит величина емкостного сопротивления

Анализируя формулу, можно выделить ключевые факторы, влияющие на величину емкостного сопротивления:

• Емкость конденсатора — чем больше емкость, тем меньше сопротивление
• Частота тока — с ростом частоты сопротивление уменьшается

Рассмотрим эти зависимости подробнее:

Зависимость от емкости

При увеличении емкости конденсатора его сопротивление переменному току уменьшается. Это объясняется тем, что конденсатор большей емкости способен накапливать и отдавать больший заряд за период переменного тока.

Зависимость от частоты

С ростом частоты переменного тока емкостное сопротивление уменьшается. При высоких частотах конденсатор не успевает полностью зарядиться и разрядиться за период, что эквивалентно уменьшению его сопротивления.

Применение емкостного сопротивления на практике

Знание особенностей емкостного сопротивления позволяет эффективно применять конденсаторы в различных электрических схемах:

Фильтрация сигналов

Емкостное сопротивление используется для создания фильтров высоких и низких частот. Например, конденсатор в цепи питания пропускает высокочастотные помехи на землю, отфильтровывая их.

Разделение постоянной и переменной составляющих

Конденсатор не пропускает постоянный ток, но пропускает переменный. Это свойство применяется для разделения постоянной и переменной составляющих сигнала.

Сдвиг фаз

Емкостное сопротивление создает сдвиг фаз между током и напряжением на 90°. Это используется в фазосдвигающих цепях и генераторах сигналов.

Сравнение емкостного и индуктивного сопротивлений

Емкостное и индуктивное сопротивления имеют ряд схожих и отличительных черт:

Общие свойства

• Являются реактивными сопротивлениями
• Зависят от частоты переменного тока
• Не рассеивают энергию в виде тепла
• Создают сдвиг фаз между током и напряжением

Отличия

• Емкостное сопротивление уменьшается с ростом частоты, индуктивное — увеличивается
• Ток в конденсаторе опережает напряжение на 90°, в катушке индуктивности — отстает на 90°
• Конденсатор накапливает энергию в электрическом поле, катушка — в магнитном

Емкостное сопротивление в колебательном контуре

Колебательный контур — это электрическая цепь, состоящая из конденсатора и катушки индуктивности. В таком контуре происходит периодический обмен энергией между электрическим полем конденсатора и магнитным полем катушки.

Роль емкостного сопротивления в колебательном контуре:

• Определяет частоту собственных колебаний контура
• Влияет на добротность контура
• Участвует в процессе обмена энергией между конденсатором и катушкой

Резонансная частота колебательного контура определяется формулой:

f = 1 / (2π√LC)

где L — индуктивность катушки, C — емкость конденсатора.

Измерение емкостного сопротивления

Для измерения емкостного сопротивления используются различные методы и приборы:

Измерительные мосты

Позволяют точно измерить емкостное сопротивление путем сравнения с эталонным сопротивлением.

Измерители RLC

Специализированные приборы для измерения параметров пассивных компонентов, включая емкостное сопротивление.

Осциллографы

Позволяют наблюдать сдвиг фаз между током и напряжением, вызванный емкостным сопротивлением.

Влияние температуры на емкостное сопротивление

Температура может оказывать влияние на емкостное сопротивление конденсатора:

• Изменение размеров обкладок и диэлектрика приводит к изменению емкости
• Изменение свойств диэлектрика влияет на емкость конденсатора
• Некоторые типы конденсаторов имеют специальные температурные коэффициенты емкости

При проектировании устройств необходимо учитывать температурную зависимость емкостного сопротивления и выбирать компоненты с подходящими характеристиками.

Емкостное сопротивление конденсатора формула расчёта и последовательность соединения в цепи

Содержание:

Емкостное сопротивление конденсатора – величина, измеряемая в омах, создается непосредственно самим конденсатором, который включен в любую цепь. Оно должно иметь большую величину, то есть быть большим. Если на них происходит подача переменного тока, в устройстве происходят процессы заряда и последующего разряда. Последнее происходит по требованию цепи. При включении электрического тока, напряжение будет равно 0. Само устройство при этом начнет заряжаться, следовательно его величина напряжения постепенно растет. В случае необходимости, при достижении максимального заряда, произойдет разряд конденсатора.

В статье, посвященной теме расчета сопротивления конденсатора, приведена вся информация о процессе, как происходит заряд-разряд. В качестве бонуса есть интересный материал по теме, который можно скачать, и видеоролик в конце статьи.

Формула сопротивления конденсаторов.

Формула сопротивления

Формула ёмкостного сопротивления выводится следующим образом:

• Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
• Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.

Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление. Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

Формула сопротивления.

Применение на практике

Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:

• Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
• Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
• Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.

В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.

Измерение сопротивления конденсаторов.

Характеристики прибора

Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:

C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:

• удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
• рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
• температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
• сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
• эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
• абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
• ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
• полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
• эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

Таблицы максимальных значений емкости конденсаторов.

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.

[stextbox id=’info’]Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.[/stextbox]

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) ² ) ^½, где

• Xl — индуктивность;
• Xс — ёмкость;
• R — активная составляющая.

Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

Материал в тему: все о переменном конденсаторе.

Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

• X > 0, в элементе проявляются индуктивные свойства;
• X = 0, в ёмкости присутствует только активная величина;
• X < 0, в элементе проявляется ёмкостное сопротивление.

Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.

Импеданс элемента.

Пример расчёта

Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R ² +Xc ² ) ^½.

Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.

Стоит почитать: все об электролитических конденсаторах.

В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет

Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 ⁻⁶ ) = 3,2 кОм.

По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.

Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 ⁻³ + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (5000²+3200²)½ = 5 936 Ом =5,9 кОм.

[stextbox id=’info’]Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.[/stextbox]

Свойства ёмкостей

Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.

Свойства ёмкостей.

Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.

[stextbox id=’info’]Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.[/stextbox]

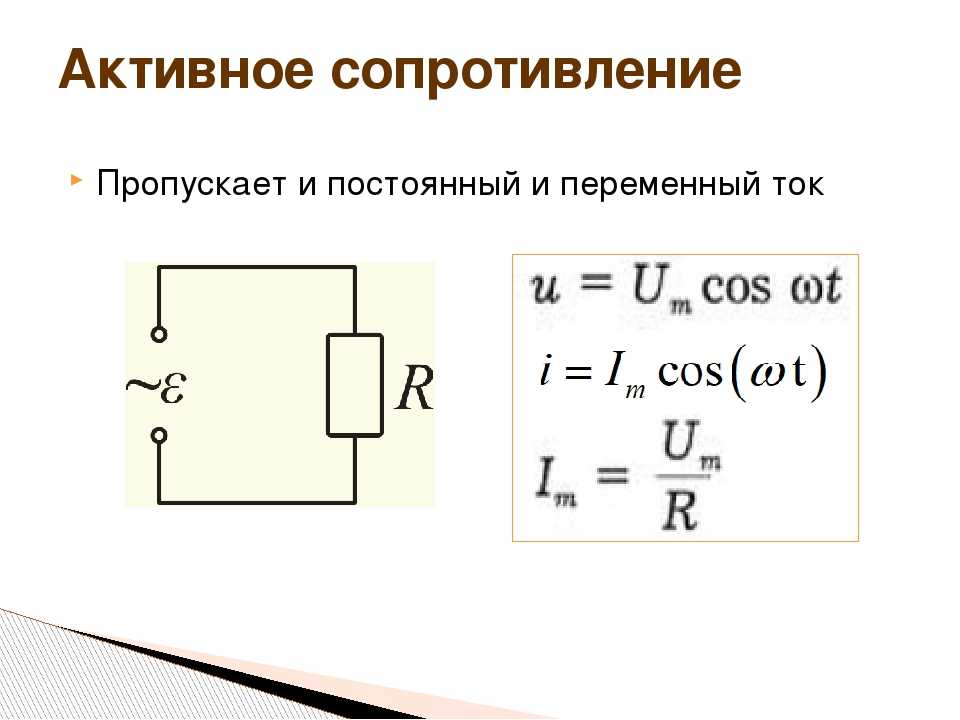
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле.  Сопротивление конденсатора вычисляется по формуле:

Расчет сопротивления.

В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.

Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:

• X > 0 – элемент проявляет свойства индуктивности .
• X = 0 – элемент имеет чисто активное сопротивление .
• X < 0 – элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.

Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.

Заключение

В данной статье были рассмотрены основные вопросы расчета сопротивления конденсаторов.  Больше информации можно найти в скачиваемой версии учебника по электромеханике “Что такое конденсаторы”

В нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессиональных электронщиков. Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vk.com/electroinfonet. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:

www.amperof.ru

www.eduspb.com

www.beasthackerz. ru

www.electroandi.ru

www.websor.ru

Предыдущая

КонденсаторыСколько стоят керамические конденсаторы?

Следующая

КонденсаторыЧто такое ионистор?

Емкостное и индуктивное сопротивление в цепи переменного тока; Школа для электриков: Электротехника и электроника

Емкостное и индуктивное сопротивления называются пассивными сопротивлениями. Энергия не тратится на реактивное сопротивление, как на активное. Энергия, запасенная в конденсаторе, периодически отдается обратно источнику, когда электрическое поле в конденсаторе исчезает.

Содержание

Емкостное и индуктивное сопротивление в цепи переменного тока

Если мы включим конденсатор в цепь постоянного тока, то обнаружим, что он имеет бесконечное сопротивление, потому что постоянный ток просто не может пройти через диэлектрик между витками, так как диэлектрик по определению не проводит постоянный ток.

Конденсатор разрывает цепь постоянного тока. Однако если тот же конденсатор включить в цепь переменного тока, мы обнаружим, что конденсатор не разрывается полностью, а попеременно заряжается и разряжается, т.е. Электрический заряд перемещается, а ток во внешней цепи поддерживается.

Исходя из теории Максвелла, в этом случае можно сказать, что переменный ток, проходящий внутри конденсатора, замыкается, за исключением того, что в данном случае это реактивный ток. Таким образом, конденсатор в цепи переменного тока действует как своего рода сопротивление конечной величины. Это сопротивление называется емкость ..

Практика давно показала, что величина переменного тока, протекающего через провод, зависит от формы провода и магнитных свойств окружающей среды. Прямой провод будет иметь наибольший ток, но если тот же провод намотать в катушку с большим количеством витков, сила тока будет меньше.

А если в ту же катушку вставить ферромагнитный сердечник, ток еще больше уменьшится. Поэтому проводник имеет не только омическое (активное) сопротивление переменному току, но и некоторое дополнительное сопротивление, которое зависит от индуктивности проводника. Это сопротивление называется индуктивное сопротивление ..

Его физический смысл заключается в том, что изменение тока в проводнике, обладающем определенной индуктивностью, вызывает в этом проводнике ЭДС самоиндукции, которая стремится предотвратить изменение тока, то есть стремится уменьшить ток. Это эквивалентно увеличению сопротивления проводника.

Емкость в цепи переменного тока

Давайте сначала подробнее рассмотрим емкостное сопротивление. Предположим, что конденсатор емкостью C подключен к источнику синусоидально переменного тока, ЭДС этого источника будет описываться следующей формулой:

Падение напряжения на соединительных проводах будет опущено, так как оно обычно очень мало и при необходимости может быть рассмотрено отдельно. Теперь предположим, что напряжение на катушках конденсатора равно напряжению источника переменного тока. Следующий:

В любой момент времени заряд на конденсаторе зависит от его емкости и напряжения между его катушками. Затем, для заданного известного источника, о котором говорилось выше, мы получаем выражение для нахождения заряда на катушках конденсатора через напряжение источника:

Пусть за бесконечно долгое время dt заряд на конденсаторе изменится на величину dq, тогда ток I будет равен току, который течет по проводам от источника к конденсатору:

Значение амплитуды тока будет равно:

Тогда окончательное выражение для тока будет выглядеть следующим образом:

Перепишем формулу для амплитуды тока следующим образом:

Это уравнение является законом Ома, где обратная величина угловой частоты, умноженная на емкость, играет роль сопротивления, и по сути является выражением для нахождения емкости конденсатора в цепи синусоидально переменного тока:

Таким образом, емкость обратно пропорциональна угловой частоте тока и емкости конденсатора. Легко понять и физический смысл этих отношений.

Чем больше емкость конденсатора в цепи переменного тока и чем чаще меняется направление тока в цепи, тем больше общий заряд, который в итоге проходит за единицу времени через поперечное сечение проводников, соединяющих конденсатор с источником переменного тока. Таким образом, ток пропорционален произведению емкости и угловой частоты.

В качестве примера рассчитаем емкость конденсатора 10 мкФ для цепи синусоидально переменного тока с частотой 50 Гц:

Если бы частота была 5000 Гц, тот же конденсатор представлял бы собой сопротивление около 3 Ом.

Из приведенных выше формул ясно, что ток и напряжение в цепи переменного тока с конденсатором всегда изменяются в разных фазах. Фаза тока на пи/2 (90 градусов) раньше, чем фаза напряжения. Это означает, что максимальный ток по времени всегда на четверть периода опережает максимальное напряжение. Поэтому в емкостном резисторе ток находится на четверть периода по времени или на 90 градусов по фазе перед напряжением.

Давайте объясним физическое значение этого явления. В первый момент конденсатор полностью разряжен, поэтому малейшее приложенное к нему напряжение перемещает заряды на пластинах конденсатора, создавая ток.

По мере заряда конденсатора напряжение на его катушках увеличивается, что препятствует дальнейшему протеканию заряда, поэтому ток в цепи уменьшается независимо от дальнейшего увеличения напряжения, приложенного к катушкам.

Таким образом, если ток был максимальным в начальный момент времени, то когда напряжение достигнет максимума через четверть периода, ток вообще перестанет течь.

В начале периода ток максимален, а напряжение минимально и начинает расти, но через четверть периода напряжение достигает максимума, а ток к тому времени падает до нуля. Поэтому ток на четверть периода раньше, чем напряжение.

Индуктивное сопротивление в цепи переменного тока

Давайте теперь вернемся к индуктивному сопротивлению. Предположим, что через катушку индуктивности протекает синусоидально переменный ток. Это можно выразить следующим образом:

Ток вызывается изменяющимся напряжением, приложенным к катушке. Это означает, что катушка будет иметь ЭДС самоиндукции, которая выражается следующим образом:

Опять же, давайте пренебрежем падением напряжения на проводах, соединяющих источник ЭДС с катушкой. Их омическое сопротивление очень мало.

Пусть изменяющееся напряжение, приложенное к катушке, в каждый момент времени полностью уравновешивается результирующей ЭДС самоиндукции, равной по величине, но противоположной по направлению:

Тогда у нас есть закон обозначений:

Поскольку амплитуда напряжения, приложенного к катушке, равна:

Выразим максимальный ток следующим образом:

Это выражение на самом деле является законом Ома. Величина, равная произведению индуктивности на угловую частоту, здесь выступает как сопротивление и является ничем иным, как индуктивным сопротивлением катушки индуктивности:

Поэтому индуктивное сопротивление пропорционально индуктивности катушки и угловой частоте переменного тока, протекающего через катушку.

Это происходит потому, что индуктивное сопротивление обусловлено влиянием самоиндуцированного электромагнитного поля на напряжение источника – самоиндуцированное электромагнитное поле стремится уменьшить ток и тем самым вносит сопротивление в цепь. Известно, что величина ЭДС самоиндукции пропорциональна индуктивности катушки и скорости изменения протекающего через нее тока.

В качестве примера рассчитаем индуктивное сопротивление катушки с индуктивностью 1 Гн, включенной в цепь с частотой тока 50 Гц:

Если бы частота была 5000 Гц, то сопротивление той же катушки было бы около 31400 Ом. Напомним, что омическое сопротивление провода катушки обычно указывается в единицах Ом.

Из приведенных формул видно, что изменения тока и напряжения в катушке происходят в разных фазах, причем фаза тока всегда меньше фазы напряжения на pi/2. Поэтому максимум тока наступает на четверть периода позже, чем максимум напряжения.

В индуктивном резисторе ток отстает от напряжения на 90 градусов из-за тормозящего эффекта ЭДС самоиндукции, которая препятствует изменению тока (как увеличению, так и уменьшению), поэтому максимальный ток в цепи катушки наступает позже, чем максимальное напряжение.

Катушка и конденсатор работают вместе

Когда индуктор и конденсатор соединены последовательно в цепи переменного тока, напряжение на индукторе будет превышать напряжение на конденсаторе на половину периода, т.е. 180 градусов по фазе.

Емкостное и индуктивное сопротивления называются пассивными сопротивлениями. В реактивном сопротивлении энергия расходуется не так, как в активном. Энергия, запасенная в конденсаторе, периодически отдается обратно источнику, когда электрическое поле в конденсаторе исчезает.

То же самое справедливо и для катушки: пока магнитное поле катушки создается током, энергия накапливается в катушке в течение четверти периода, а затем возвращается к источнику в течение следующей четверти периода. В этой статье мы рассматриваем синусоидально переменный ток, для которого эти положения строго соблюдаются.

В цепях синусоидального переменного тока для ограничения тока традиционно используются индукционные катушки с сердечниками, называемые дросселями. Их преимущество перед реостатами заключается в том, что энергия не рассеивается в больших количествах в виде тепла.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это поможет нашему сайту сильно вырасти!

C – размер конденсатора в фарадах.

От чего зависит сопротивление конденсаторов в цепях переменного тока?

Его величина зависит не только от емкостных характеристик последнего, но и от частотной характеристики электрического тока, протекающего по цепи. Когда мы говорим о сопротивлении резистора, мы имеем в виду параметры самого резистора, например, материал, форму, но нет абсолютно никакой связи между его сопротивлением и электрической частотой цепи (мы говорим об идеальном резисторе, который не характеризуется паразитными параметрами). Когда мы говорим об устройстве для хранения энергии и зарядки электрическим полем – все по-другому. Конденсатор с одинаковой емкостью имеет разный уровень сопротивления при разных частотах тока. Амплитуда тока, протекающего через него при постоянной амплитуде напряжения, имеет другое значение.

Расчет Xc

Какие выводы можно сделать из этой формулы для сопротивления конденсатора в цепи переменного тока? По мере увеличения частоты сигнала электрическое сопротивление конденсатора уменьшается.

По мере увеличения емкости накопителя заряда энергия электрического поля Xc переменного электричества, протекающего через него, будет иметь тенденцию к уменьшению.

График, представляющий величину этого конденсатора при непостоянном токе в цепи, имеет форму гиперболы

По мере приближения значений частоты к нулю на оси (когда переменный ток становится похожим по своим параметрам на постоянный), это сопровождается увеличением Xc конденсатора до бесконечных значений. Это действительно так: известно, что конденсатор в сети постоянного тока на самом деле является разомкнутой цепью. Фактическое электрическое сопротивление, конечно, не бесконечно; оно ограничено коэффициентом утечки конденсатора. Однако его ценности остаются на высоком уровне, который нельзя игнорировать.

При увеличении числа частот до бесконечных значений емкость электрического конденсатора стремится к нулю. Это характеризует идеальные модели. В реальной жизни конденсатор обладает неприятными свойствами (такими как индуктивность и сопротивление утечки), поэтому емкость уменьшается до определенных значений, а затем увеличивается.

Пожалуйста, обратите внимание! Когда конденсатор подключен к переменной электрической цепи, его энергия не расходуется, поскольку фазовые характеристики напряжения и тока сдвинуты на 90° относительно друг друга. В течение одной четверти периода конденсатор заряжен (энергия накапливается в его электрическом поле), в течение следующего он разряжен, энергия отдается обратно в цепь. Его электрическое сопротивление без ваты, реактивное.

В этом случае сопротивление конденсатора в цепи переменного тока составляет 96,5 кОм. Если мы запишем все расчеты, то получим следующие результаты.

Векторное представление емкости

Для простого понимания процессов, происходящих в конденсаторе под воздействием источника переменного тока, удобно использовать векторное представление емкости.

В начальный момент зарядки конденсатора потенциал U на его катушках равен нулю (точка a). В то же время ток I имеет максимальное значение (точка b). В этот момент уже заметна задержка. Ток начинает уменьшаться от своего пикового значения (точка bd). Напряжение в этой точке еще не увеличилось и только приближается к своему максимальному значению (ac).

То же самое отражено на диаграмме справа. В точке, где напряжение U имеет наименьшее значение (e), ток I только начал переходить в отрицательную область (f).

Таким образом, в конце второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет своего наибольшего, амплитудного значения.

Емкость конденсатора

Мы уже видели, что ток в цепи с конденсатором может течь только при изменении приложенного к нему напряжения, и ток, протекающий через цепь при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС.

Конденсатор в цепи переменного тока влияет на ток, протекающий через цепь, то есть ведет себя как сопротивление. Чем выше емкость и чем выше частота переменного тока, тем меньше значение емкостного сопротивления. И наоборот, сопротивление конденсатора для переменного тока увеличивается с уменьшением емкости и снижением частоты.

Рисунок 2. Зависимость емкости конденсатора от частоты.

Для постоянного тока, т.е. когда его частота равна нулю, емкостное сопротивление бесконечно велико; поэтому постоянный ток не может протекать через цепь с емкостью.

Значение емкости определяется по следующей формуле:

где Xc – емкость конденсатора в Ом;

f – частота переменного тока в гц;

ω – угловая частота переменного тока;

C – емкость конденсатора в ф.

Когда конденсатор подключен к цепи переменного тока, в нем не расходуется энергия, как в индуктивности, поскольку фазы тока и напряжения смещены на 90° относительно друг друга. Энергия накапливается в электрическом поле конденсатора в течение одной четверти периода – когда конденсатор заряжается – и в течение другой четверти периода – когда конденсатор разряжается – она высвобождается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.

Следует отметить, однако, что практически в каждом конденсаторе, когда через него проходит переменный ток, потребляется больше или меньше активной мощности из-за изменений в диэлектрическом состоянии конденсатора. Кроме того, между пластинами конденсатора никогда не бывает абсолютно идеальной изоляции; утечки в изоляции между пластинами приводят к тому, что конденсатор подключается параллельно с каким-либо активным сопротивлением, через которое протекает ток, и, следовательно, потребляется некоторая мощность. В обоих случаях мощность бесполезно расходуется на нагрев диэлектрика и поэтому называется мощностью потерь.

Потери из-за изменения состояния диэлектрика называются диэлектрическими потерями, а потери из-за несовершенства изоляции между пластинами – потерями утечки.

Ранее мы сравнивали электрическую емкость с емкостью герметично закрытого сосуда или с площадью дна открытого сосуда с вертикальными стенками.

Конденсатор в цепи переменного тока можно сравнить с упругостью пружины. Чтобы избежать возможного недопонимания, под упругостью следует понимать не эластичность (“твердость”) пружины, а ее противоположность, “мягкость” или “податливость” пружины.

Представьте себе, что мы периодически сжимаем и растягиваем свернутую пружину, которая одним концом плотно прикреплена к стене. Время, которое нам потребуется для завершения полного цикла сжатия и растяжения пружины, будет соответствовать периоду переменного тока.

Таким образом, мы сожмем пружину в первом квартале периода, отпустим ее во втором квартале периода, растянем в третьем квартале периода и снова отпустим в четвертом квартале периода.

Кроме того, предположим, что наши усилия в течение периода будут неравномерными, а именно, они будут увеличиваться от нуля до максимума в первом и третьем кварталах периода и уменьшаться от максимума до нуля во втором и четвертом кварталах периода.

Сжимая и растягивая пружину таким образом, вы заметите, что в начале первой четверти периода свободный конец пружины будет двигаться довольно быстро при относительно небольшом усилии с нашей стороны.

В конце первой четверти периода (когда пружина сжата), наоборот, несмотря на увеличение силы, неприкрепленный конец пружины будет двигаться очень медленно.

Во второй четверти периода, когда мы постепенно уменьшаем давление на пружину, свободный конец пружины будет отходить от стены в нашу сторону, несмотря на то, что наши сдерживающие силы направлены в сторону стены. В этом случае наши силы в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины – наименьшей. В конце второй четверти периода, когда наши силы будут наименьшими, скорость пружины будет наибольшей, и так далее.

Продолжая аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и строя графики (рис. 1, б) изменения нашей силы и скорости движения незакрепленного конца пружины, мы увидим, что эти графики точно соответствуют графикам ЭДС и тока емкостной цепи (рис. 1, а), график силы будет соответствовать графику ЭДС, а график скорости – графику тока.

Рисунок 3. (a) Процессы, происходящие в цепи переменного тока с конденсатором и (b) Сравнение между конденсатором и пружиной.

Легко видеть, что пружина, как и конденсатор, накапливает энергию за одну четверть периода и отдает ее за другую четверть периода.

Также очевидно, что чем менее упругой является пружина, тем более упругой она является и тем большую силу она будет оказывать на нас. То же самое верно и для электрической цепи: чем меньше емкость, тем больше сопротивление цепи на данной частоте.

Наконец, чем медленнее мы сжимаем и растягиваем пружину, тем меньше скорость движения ее свободного конца. Аналогично, чем ниже частота, тем меньше ток при данной ЭДС.

При постоянном давлении пружина будет только сжиматься и тем самым останавливать свое движение, так же как при постоянной ЭДС конденсатор будет только заряжаться и тем самым останавливать дальнейшее движение электронов в цепи.

Теперь вы можете увидеть, как ведет себя конденсатор в цепи переменного тока на видео ниже:

ПОНРАВИЛАСЬ ЛИ ВАМ СТАТЬЯ? ПОДЕЛИТЕСЬ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Если R = 0, то напряжение на конденсаторе равно приложенному напряжению и u = q/C.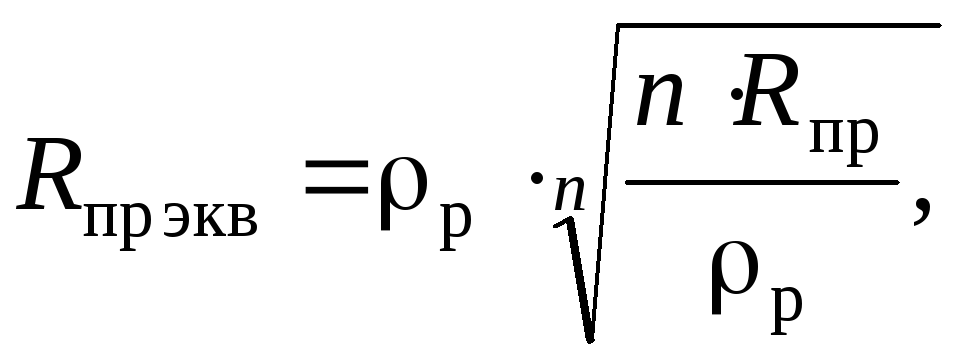 Мгновенное значение тока задается выражением:

Емкость

Конденсатор с емкостью C имеет бесконечное сопротивление в цепи постоянного тока. Однако если к конденсатору приложить переменное напряжение, он будет периодически заряжаться, и в цепи потечет ток. Напряжение на конденсаторе достигает своего максимального значения в те моменты, когда ток равен нулю.

Если R = 0, то напряжение на конденсаторе равно приложенному напряжению и u = q/C. Мгновенное значение тока задается выражением:

Между напряжением и током существует разность фаз -π/2.

В чисто емкостной цепи переменного тока ток превышает напряжение на π/2 (или T/4).

Из приведенного выше уравнения следует, что амплитуда тока I_m = ωCU_m. Сравнение с законом Ома U = RI показывает, что 1/ωC действует как сопротивление.

Цепь переменного тока, содержащая емкость C, имеет сопротивление переменному току; это называется емкость Х_C.

Единица СИ для емкостного сопротивления: [X_C] = Ом.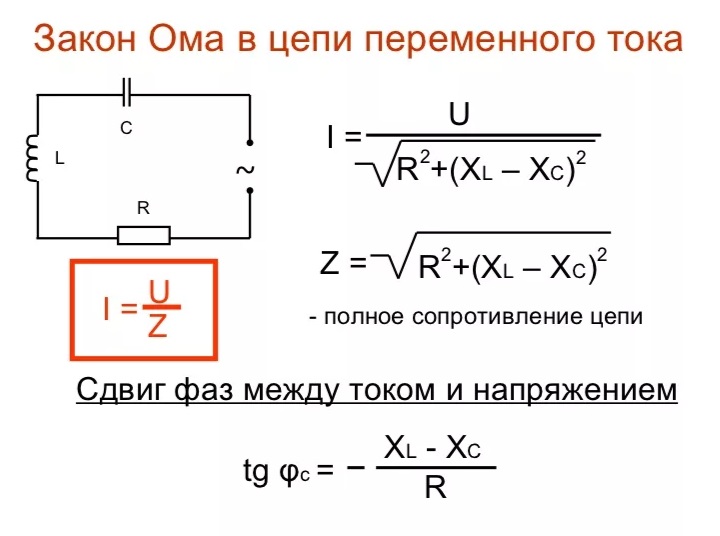

ХC	емкость цепи переменного тока,	Ом
ω = 2πf	круговая частота переменного тока,	радиан/секунда
C	емкость,	Фарад

С увеличением частоты емкость уменьшается. Для постоянного тока (f = 0) она бесконечно велика.

Ток в цепи с одной только емкостью дается выражением

После этого можно легко определить значение емкости или реактивного сопротивления конденсатора: xc = 1/2π x f x C = 1/ ω x C. Этот показатель рассчитывается, когда конденсатор подключен к цепи переменного тока. Поэтому, согласно закону Ома, в цепи переменного тока с подключенным конденсатором значение тока будет следующим: I = U/xc, а напряжение на катушках составит: Uc = Ic x xc.

Емкость в цепи переменного тока

Когда конденсатор подключается к цепи постоянного тока, через него в течение короткого периода времени протекает зарядный ток. После завершения зарядки, когда напряжение конденсатора совпадет с напряжением источника тока, протекание тока в цепи на короткое время прекратится. Таким образом, полностью заряженный конденсатор при постоянном токе будет представлять собой своего рода разомкнутую цепь или сопротивление бесконечной величины. При переменном токе конденсатор будет вести себя совсем по-другому. В такой цепи он будет заряжаться в переменном направлении. Протекание переменного тока в цепи не прерывается в этой точке.

Более внимательное рассмотрение этого процесса показывает, что в момент включения конденсатор имеет нулевое напряжение. При подаче напряжения сети переменного тока начинается зарядка. В это время напряжение в сети будет расти в течение первой четверти этого периода. По мере накопления заряда на катушках напряжение самого конденсатора будет увеличиваться. Когда напряжение в сети достигнет максимума в конце первого квартала, зарядка закончится, и ток в цепи будет равен нулю.

Существует формула для определения тока в цепи конденсатора: I = ∆q/∆t, где q – количество электроэнергии, протекающей через цепь в момент времени t. Согласно законам электростатики, количество электричества в приборе составит: q = C x Uc = C x U. В этой формуле C – емкость конденсатора, U – напряжение сети, а Uc – напряжение на катушках элемента. Окончательная формула для тока в цепи будет такой: i = C x (∆Uc/∆t) = C x (∆U/∆t).

В начале второго квартала напряжение в сети упадет, и конденсатор начнет разряжаться. Ток в цепи изменит направление и потечет в противоположном направлении. В следующем полупериоде напряжение сети изменит направление, ячейка зарядится, а затем снова начнет разряжаться. Ток, присутствующий в цепи конденсатора, будет опережать напряжение на катушках на 90 градусов.

Установлено, что ток конденсатора изменяется со скоростью, пропорциональной угловой частоте ω. Поэтому, согласно уже известной формуле для тока в цепи i = C x (∆U/∆t), по аналогии получается, что среднеквадратичное значение тока также является пропорциональной зависимостью между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.

После этого можно легко определить значение емкости или реактивного сопротивления конденсатора: xc = 1/2π x f x C = 1/ ω x C.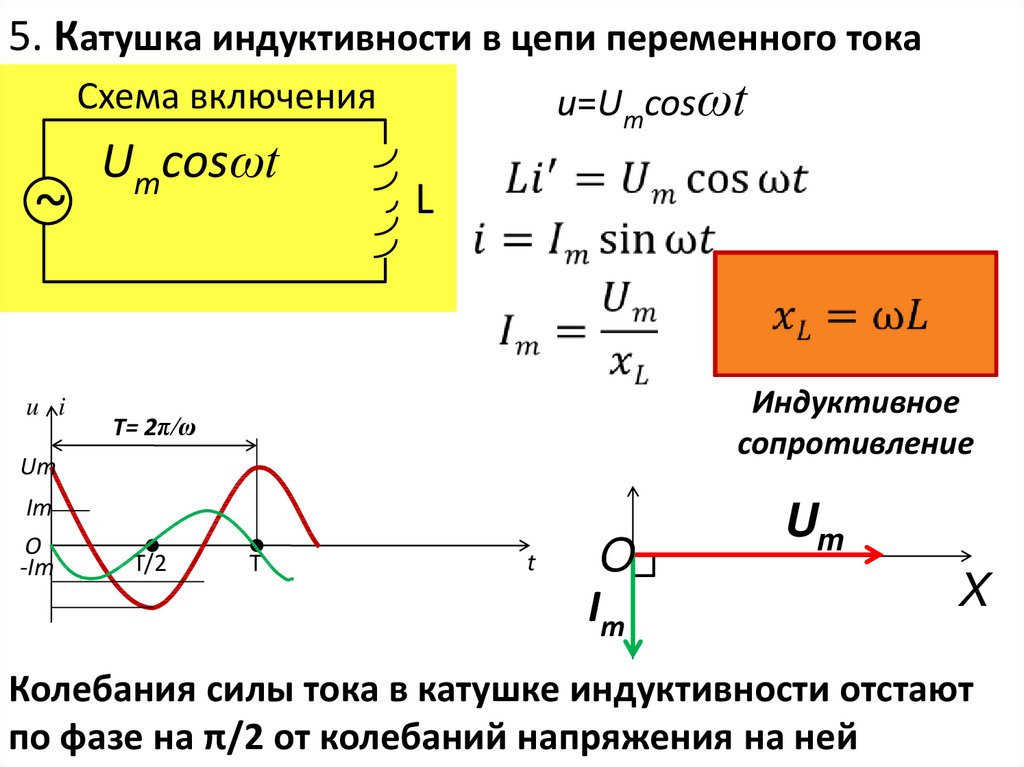 Этот показатель рассчитывается, когда конденсатор подключен к цепи переменного тока. Поэтому, согласно закону Ома, в цепи переменного тока с подключенным конденсатором значение тока будет следующим: I = U/xc, а напряжение на катушках составит: Uc = Ic x xc.

Часть сетевого напряжения, падающая на конденсатор, называется емкостным падением напряжения. Она также известна как реактивная составляющая напряжения, обозначаемая символом Uc. Значение емкости xc и значение индуктивного сопротивления xi напрямую зависят от частоты переменного тока.

Читайте далее:

• Полное сопротивление цепи переменного тока – Основы электроники.
• Лекции по ТЭ – #27 Явление резонанса в электрических цепях.
• Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
• Урок 28 Электрическая емкость. Конденсатор – Физика – 10 класс – Российская электронная школа.
• 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
• Форум RadioCat; Просмотр темы – Измерение индуктивности простыми методами.
• Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.

Конденсатор и емкость — формулы и уравнения

Следующие формулы и уравнения могут быть использованы для расчета емкости и соответствующих величин конденсаторов различной формы следующим образом.

Содержание

Емкость конденсатора:

Емкость – это количество заряда, накопленного в конденсаторе, на вольт потенциала между его пластинами. Емкость можно рассчитать, если известны заряд Q и напряжение V конденсатора:

C = Q/V

Заряд, накопленный в конденсаторе:

Если известны емкость C и напряжение V, то заряд Q можно рассчитать по формуле:

Q = C V

Напряжение конденсатора10: 9000

И вы можете рассчитать напряжение конденсатора, если известны две другие величины (Q и C):

В = Q/C

Где

• Q — заряд, накопленный между пластинами в кулонах
• Кл — емкость в фарадах
• В — разность потенциалов между пластинами в
Вольт.

Реактивное сопротивление конденсатора:

Реактивное сопротивление – это сопротивление конденсатора переменному току, которое зависит от его частоты и измеряется в Омах, как сопротивление. Емкостное реактивное сопротивление рассчитывается по формуле:

Где

• X _C — емкостное реактивное сопротивление
.
• F — применяемая частота
• Кл — емкость

Коэффициент добротности конденсатора:

Коэффициент добротности или добротность – это эффективность конденсатора с точки зрения потерь энергии, которая определяется по формуле:

QF = X _C /ESR

23 Где

3

X _C — емкостное реактивное сопротивление

ESR — эквивалентное последовательное сопротивление конденсатора.

Коэффициент рассеивания конденсатора:

D-фактор или коэффициент рассеяния является обратным значением добротности, он показывает рассеивание мощности внутри конденсатора и определяется как:

DF = tan δ = ESR/X _C

Где

• DF — коэффициент рассеяния
• δ — угол между емкостной реактивностью победителя и отрицательной осью.
• X _C — емкостное реактивное сопротивление
.
• ESR — эквивалентное последовательное сопротивление цепи.

Похожие сообщения:

• Емкость и индуктивность из калькулятора реактивного сопротивления
• Почему ток увеличивается при увеличении емкости или уменьшении емкостного реактивного сопротивления?

Энергия, накопленная в конденсаторе:

Энергия E, запасенная в конденсаторе, определяется по формуле:

E = ½ CV ²

Кл — емкость в фарадах

В это напряжение в вольтах

Средняя мощность конденсатора

Средняя мощность конденсатора определяется по формуле:

P _av  = CV ²  / 2t

, где

• t – время в секундах.

Напряжение конденсатора во время заряда/разряда:

Когда конденсатор заряжается через резистор R, для полного заряда требуется до 5 постоянных времени или 5 Тл. Напряжение в любой момент времени можно найти с помощью следующих формул зарядки и разрядки:

Во время зарядки:

Напряжение конденсатора в любой момент зарядки определяется по формуле:

Во время разрядки:

Напряжение конденсатора в любой момент разрядки определяется по формуле:

Где

• В
  C
 
• Vs — подаваемое напряжение
• t — время, прошедшее после подачи напряжения.
• RC = τ — постоянная времени RC-цепи зарядки
.

Похожие сообщения:

• Что произойдет, если мы неправильно подключим полярный конденсатор?
• Какова роль конденсатора в потолочном вентиляторе?

Формулы емкости

Емкость между двумя проводящими пластинами с диэлектриком между ними можно рассчитать по формуле:

Где

• k — диэлектрическая проницаемость
• ε _d – диэлектрическая проницаемость диэлектрика
• ε ₀ — диэлектрическая проницаемость пространства, равная 8,854 x 10 ^-12 Ф/м
• А — площадь пластин
• d — расстояние между пластинами

Емкость пластинчатого конденсатора Формула

Где:

• C – емкость в фарадах
• А — площадь площадки
• n — количество пластин
• d — расстояние между пластинами
• ε _r — относительная проницаемость вещества между пластинами
• ε _o абсолютная диэлектрическая проницаемость

Self Capacitance of a Coil (Medhurst Formula)

C ₂ ≈ (0.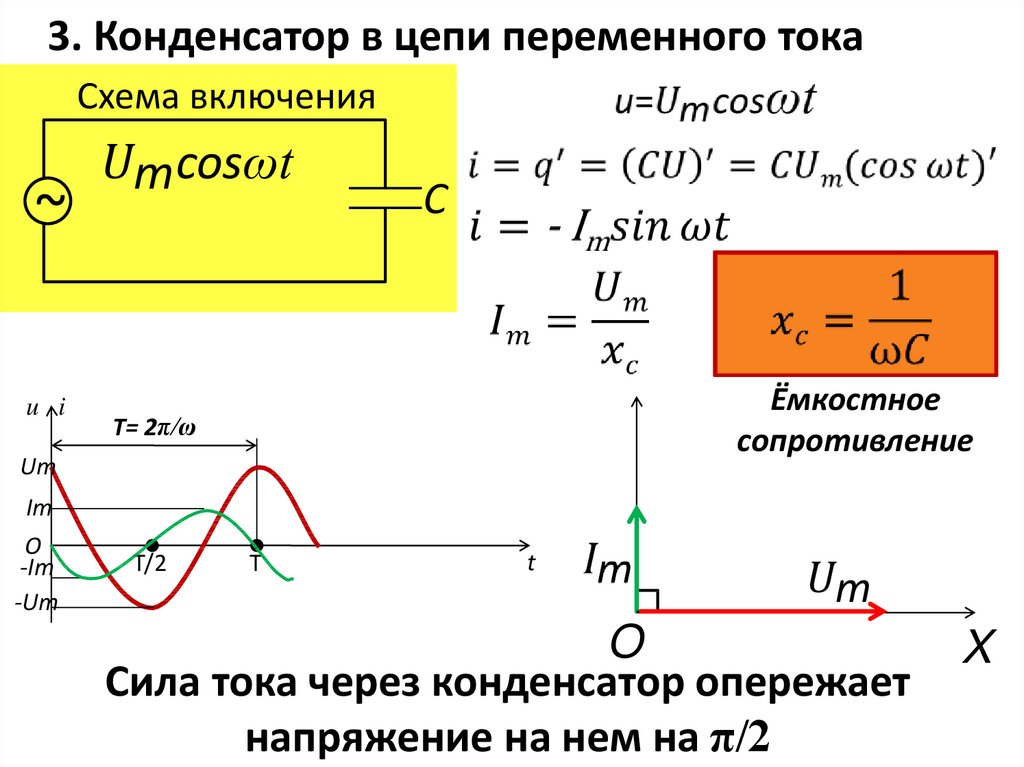 256479 h ₂ + 1.57292 r ₂ ) pF

Where:

• h ₂ and r ₂ в дюймах

Формула собственной емкости сферы

C _2b ≈ 4πε _o r

Где:

90 радиус сферы

Собственная емкость тороидального индуктора Формула

Где:

• r — малый радиус
• R большой радиус

Закон Ома для конденсатора:

Q = CV

Дифференцируя уравнение, получаем:

где

• i — мгновенный ток через конденсатор
• Кл — емкость конденсатора
• Dv/dt — мгновенная скорость изменения приложенного напряжения.

Связанные формулы и уравнения Сообщений:

• Формула и уравнения для индуктора и индуктивности
• Основные формулы и уравнения электротехники
• Сопротивление, емкость и индуктивность в последовательно-параллельном соединении – уравнения и формулы
• Основные формулы электрических величин
• Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока
• Потери в электрических машинах – формулы и уравнения
• Формулы и уравнения генератора постоянного тока
• Уравнение мощности, напряжения и ЭДС двигателя постоянного тока – формулы
• Формулы и уравнения синхронного генератора и генератора переменного тока
• Формулы и уравнения синхронных, шаговых и двигателей переменного тока
• Асинхронный двигатель и линейные асинхронные двигатели Формулы и уравнения
• Трансформаторные формулы и уравнения
• Формулы и уравнения в области электротехники и электроники
• Символы конденсаторов
• Электрические и электронные элементы и символы

URL скопирован

Показать полную статью

Связанные статьи

Кнопка «Вернуться к началу»

Формула емкостного реактивного сопротивления Известно, что конденсатор определяется как устройство, которое накапливает ток и имеет возможность влиять на величину заряда, которую он может достичь.

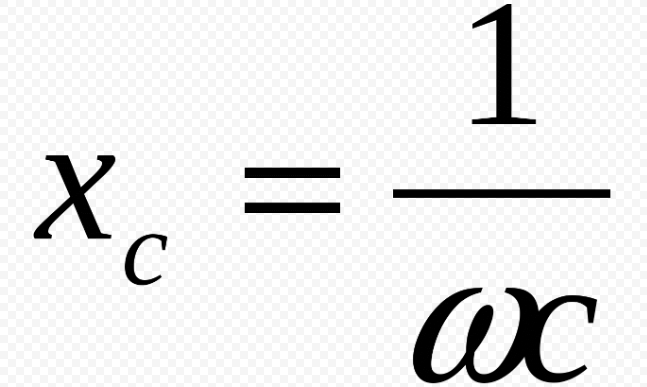Величина его емкости определяется частотой f проходящего через него электрического сигнала. Это сопротивление элемента цепи изменениям тока или напряжения. Его стандартная единица измерения Ом (Ом). Обозначается символом X _c , а его размерная формула определяется как [M ¹ L ² T ^-3 I ^-2 ]. Его математическая формула равна единице, деленной на удвоенное произведение пи, частоты и емкости конденсатора.

емковая формула реактивной способности

x _C = 1/2πfc

, где

x _C — емкостная реактивная реакция,

π — констант с значением 3.14,

π —

9,

.0002 f — частота,

c — емкость.

Примеры задач

Задача 1. Найдите емкостное сопротивление, если емкость равна 5 Ф при частоте 20 Гц.

Решение:

. × 20 × 5)

= 1/628

= 0,0016 Ом

Задача 2. Найти емкостное сопротивление, если емкость равна 4 Ф для частоты 50 Гц.

Решение:

Мы имеем,

F = 50

C = 4

, используя формулу,

x _C = 1/2πfc

= 1/(2 × 3,14. × 50 × 4)

= 1/2512

= 0,00039 Ом

Задача 3. Найти емкостное реактивное сопротивление, если емкость равна 0,5 Ф за время 10 с.

Решение:

. Используя полученную формулу,

X _c = 1/2πfc

= 1/(2 × 3,14 × 0,1 × 0,5)

= 1/0,314

= 3,183 Ом 3 9004 Найти задачу. емкостное реактивное сопротивление, если емкость равна 2,5 Ф в течение 16 с.

Решение:

Мы имеем,

T = 16

C = 2,5

с использованием формулы F = 1/T Мы имеем

x _C = 1/2πfc

= 1/(2 × 3,14 × 0,0625 × 2,5)

= 1/0,98125

= 1,0186 Ом

.