Емкостное сопротивление в чем измеряется. Емкостное сопротивление конденсатора: что это такое, формула расчета и применение

Что такое емкостное сопротивление конденсатора. Как рассчитать его по формуле. Где применяется емкостное сопротивление на практике. От чего зависит величина емкостного сопротивления.

Что такое емкостное сопротивление конденсатора

Емкостное сопротивление — это свойство конденсатора препятствовать прохождению переменного электрического тока. Данная характеристика присуща только переменному току, при постоянном токе конденсатор выступает в роли разрыва цепи.

Чем обусловлено возникновение емкостного сопротивления? При подаче переменного напряжения на обкладки конденсатора происходят циклические процессы заряда и разряда. Это создает противодействие протеканию тока, которое и называется емкостным сопротивлением.

Формула для расчета емкостного сопротивления

Емкостное сопротивление конденсатора рассчитывается по следующей формуле:

Xc = 1 / (2πfC)

где:

• Xc — емкостное сопротивление в Омах
• f — частота переменного тока в Герцах
• C — емкость конденсатора в Фарадах
• π ≈ 3,14

Из формулы видно, что емкостное сопротивление обратно пропорционально частоте тока и емкости конденсатора. То есть при увеличении частоты или емкости, сопротивление уменьшается.

От чего зависит величина емкостного сопротивления

Основные факторы, влияющие на величину емкостного сопротивления конденсатора:

• Частота переменного тока — чем выше частота, тем ниже сопротивление
• Емкость конденсатора — чем больше емкость, тем меньше сопротивление
• Диэлектрическая проницаемость диэлектрика между обкладками
• Площадь пластин конденсатора
• Расстояние между обкладками

Как можно заметить, на емкостное сопротивление влияют как параметры самого конденсатора, так и характеристики протекающего через него тока.

Применение емкостного сопротивления на практике

Свойство емкостного сопротивления конденсаторов широко используется в электротехнике и электронике:

• Создание частотных фильтров для разделения сигналов разной частоты
• Сглаживание пульсаций в выпрямителях
• Разделение постоянной и переменной составляющих сигнала
• Создание времязадающих RC-цепей
• Компенсация реактивной мощности в электросетях
• Настройка колебательных контуров в радиотехнике

Понимание принципов емкостного сопротивления позволяет грамотно применять конденсаторы в различных электрических схемах.

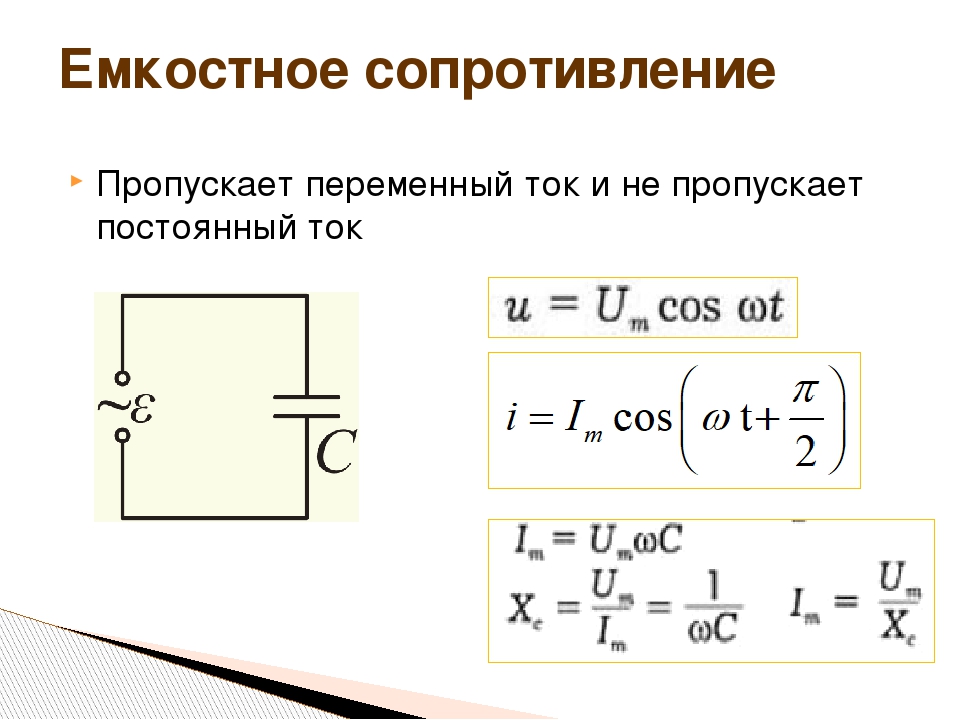
Особенности емкостного сопротивления конденсатора

Важно отметить несколько ключевых особенностей емкостного сопротивления:

• Является реактивным сопротивлением, то есть не приводит к потерям энергии
• Создает сдвиг фаз между током и напряжением на 90°
• При увеличении частоты до бесконечности стремится к нулю
• При частоте 0 (постоянный ток) стремится к бесконечности
• Измеряется в Омах, как и активное сопротивление

Учет этих особенностей необходим при проектировании электрических цепей с конденсаторами.

Сравнение емкостного и индуктивного сопротивления

Емкостное и индуктивное сопротивления являются двумя видами реактивного сопротивления. Основные отличия:

• Емкостное сопротивление уменьшается с ростом частоты, индуктивное — увеличивается
• Емкостное создает опережение тока относительно напряжения, индуктивное — отставание
• Емкостное сопротивление обратно пропорционально емкости, индуктивное прямо пропорционально индуктивности

При последовательном соединении конденсатора и катушки индуктивности их сопротивления вычитаются. Это используется для создания резонансных контуров.

Расчет полного сопротивления цепи с конденсатором

В реальных электрических цепях конденсатор обычно используется совместно с резисторами, катушками и другими элементами. Для расчета полного сопротивления такой цепи используется понятие импеданса.

Импеданс учитывает как активную, так и реактивную составляющие сопротивления:

Z = √(R² + (XL — XC)²)

где:

• Z — полное сопротивление (импеданс)
• R — активное сопротивление
• XL — индуктивное сопротивление
• XC — емкостное сопротивление

Эта формула позволяет рассчитать полное сопротивление любой цепи, содержащей конденсаторы.

Практические примеры расчета емкостного сопротивления

Рассмотрим несколько примеров расчета емкостного сопротивления конденсатора:

1. Конденсатор емкостью 100 мкФ в цепи с частотой 50 Гц:

Xc = 1 / (2π * 50 * 100 * 10^-6) = 31.8 Ом

2. Тот же конденсатор при частоте 1 кГц:

Xc = 1 / (2π * 1000 * 100 * 10^-6) = 1.59 Ом

3. Конденсатор 1 нФ при частоте 1 МГц:

Xc = 1 / (2π * 10^6 * 1 * 10^-9) = 159 Ом

Как видно из примеров, емкостное сопротивление сильно зависит от частоты и емкости конденсатора.

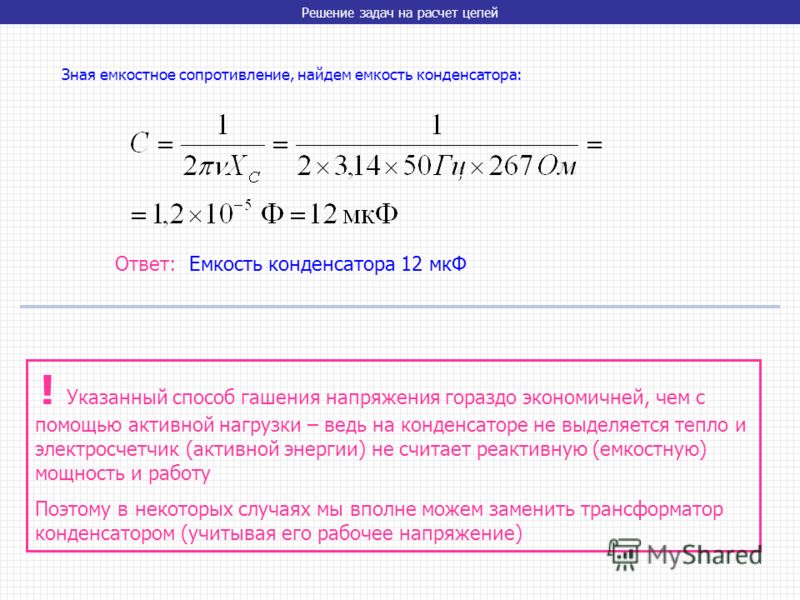
Емкостное сопротивление | Формулы и расчеты онлайн

Конденсатор емкостью C имеет в цепи постоянного тока бесконечно большое сопротивление. Если же приложить к конденсатору переменное напряжение, то он будет периодически перезаряжаться, и в цепи потечет ток. Напряжение на конденсаторе достигает максимального значения в те моменты, когда ток равен нулю.

Если R = 0, то напряжение на конденсаторе совпадает с приложенным напряжением и u = q/C. Мгновенное значение тока определяется выражением:

\[ i = \frac{dq}{dt} = C \frac{du}{dt} = C \frac{d}{dt}(U_{m} \sin(ωt)) \]

Отсюда следует

\[ i = ωCU_{m} \cos(ωt) = ωCU_{m} \sin(ωt + \frac{π}{2}) \]

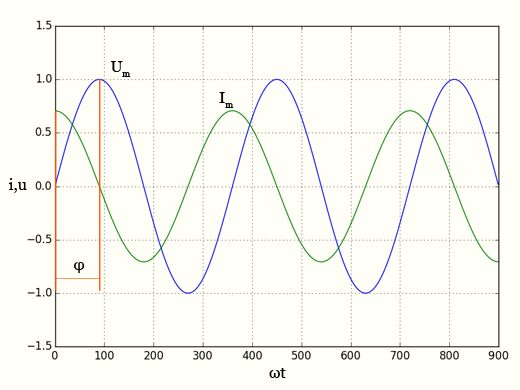
Емкостное сопротивление — график тока и напряжения

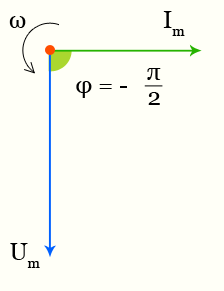
Между напряжением и током имеется разность фаз —π/2.

В чисто емкостной цепи переменного тока ток опережает напряжение на π/2 (или Т/4).

В соответствии с приведенным выше уравнением амплитуда тока I_m = ωCU_m. Сравнение с законом Ома U = RI показывает, что величина 1/ωС играет роль сопротивления.

Цепь переменного тока, содержащая емкость C, обладает сопротивлением переменному току; оно называется емкостным сопротивлением Х_C.

Единица СИ емкостного сопротивления: [X_C] = Ом.

Если

ХC	емкостное сопротивление цепи переменного тока,	Ом
ω = 2πf	круговая частота переменного тока,	радиан/Секунда
C	емкость,	Фарад

то

\[ X_{C} = \frac{1}{ωC} \]

$ $

Ток в цепи, обладающей только емкостным сопротивлением, определяется выражением

\[ I = UωC \]

Вычислить, найти емкостное сопротивление

Емкостное сопротивление	стр. 687

конденсатора в цепи переменного тока, формула

Электросопротивление — это параметр в электротехнике, характеризующий возможность вещества препятствовать прохождению электричества. В зависимости от качеств материала, электросопротивляемость может уменьшаться до крайне маленьких величин (микро\милиОмы — у проводников, металлов) или повышаться до огромных значений (ГигаОмы — изоляторов, диэлектриков). Величина противоположная сопротивлению — проводимость.

Что такое

Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.

Формула вычисления

Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.

Графическое отображение формулы

Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами. Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.

Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.

Дополнительная информация: Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения. По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства.

По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда.

От чего зависит сопротивление конденсаторов цепей переменного тока

Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.

Вычисление Xc

Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.

При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.

График, отображающий эту величину конденсатора при непостоянном токе цепи, имеет форму гиперболы

Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.

При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.

Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.

Причины ёмкостного сопротивления

Причиной возникновения сопротивления емкостного считается уровень напряжения, возникающий на конденсаторе в процессе его заряда. Вектор его действия встречен вектору напряжения источника электричества, потому создает помеху воспроизведению электротока этим источником.

Как рассчитать Xc

Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.

Формула вычисления показателя напряжения за одну секунду

 

Формула расчета величины силы электротока за мгновение

Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.

По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:

Наибольшие величины напряженности и силы тока можно рассчитывать по формулеОкончательная формула расчета емкостного сопротивления в цепи переменного тока

ω = 2πf.

f — показатель частоты непостоянного тока, измеряется в герцах;

ω — показатель угловой частоты тока;

С — размер конденсатора в фарадах.

Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока.

Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).

Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц. Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.

После введения данных в формулу, определяющую Xc, и получаются значения:

Результат для частоты 50 ГцРезультат для 1 кГц

Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.

В чем измеряется емкостное электросопротивление

R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома. Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.

Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства. Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.

Емкостное сопротивление конденсатора формула расчёта и последовательность соединения в цепи

Емкостное сопротивление конденсатора – величина, измеряемая в омах, создается непосредственно самим конденсатором, который включен в любую цепь. Оно должно иметь большую величину, то есть быть большим. Если на них происходит подача переменного тока, в устройстве происходят процессы заряда и последующего разряда. Последнее происходит по требованию цепи. При включении электрического тока, напряжение будет равно 0. Само устройство при этом начнет заряжаться, следовательно его величина напряжения постепенно растет. В случае необходимости, при достижении максимального заряда, произойдет разряд конденсатора.

В статье, посвященной теме расчета сопротивления конденсатора, приведена вся информация о процессе, как происходит заряд-разряд. В качестве бонуса есть интересный материал по теме, который можно скачать, и видеоролик в конце статьи.

Формула сопротивления конденсаторов.

Формула сопротивления

Формула ёмкостного сопротивления выводится следующим образом:

• Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
• Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.

Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление. Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

Формула сопротивления.

Применение на практике

Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:

• Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
• Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
• Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.

В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.

Измерение сопротивления конденсаторов.

Характеристики прибора

Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:

C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:

• удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
• рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
• температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
• сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
• эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
• абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
• ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
• полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
• эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

Таблицы максимальных значений емкости конденсаторов.

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.

Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) ² ) ^½, где

• Xl — индуктивность;
• Xс — ёмкость;
• R — активная составляющая.

Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

Материал в тему: все о переменном конденсаторе.

Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

• X > 0, в элементе проявляются индуктивные свойства;
• X = 0, в ёмкости присутствует только активная величина;
• X < 0, в элементе проявляется ёмкостное сопротивление.

Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.

Импеданс элемента.

Пример расчёта

Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R ² +Xc ² ) ^½.

Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.

Стоит почитать: все об электролитических конденсаторах.

В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет

Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 ⁻⁶ ) = 3,2 кОм.

По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.

Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 ⁻³ + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (5000²+3200²)½ = 5 936 Ом =5,9 кОм.

Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.

Свойства ёмкостей

Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.

Свойства ёмкостей.

Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.

Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.

Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:

Расчет сопротивления.

В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.

Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:

• X > 0 – элемент проявляет свойства индуктивности .
• X = 0 – элемент имеет чисто активное сопротивление .
• X < 0 – элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.

Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.

Заключение

В данной статье были рассмотрены основные вопросы расчета сопротивления конденсаторов.  Больше информации можно найти в скачиваемой версии учебника по электромеханике “Что такое конденсаторы”

В нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессиональных электронщиков. Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vk.com/electroinfonet. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:

www.amperof.ru

www.eduspb.com

www.beasthackerz.ru

www.electroandi.ru

www.websor.ru

Предыдущая

КонденсаторыСколько стоят керамические конденсаторы?

Следующая

КонденсаторыЧто такое ионистор?

емкостное сопротивление — это… Что такое емкостное сопротивление?



• condensance
• hydrody-namic resistance

Смотреть что такое «емкостное сопротивление» в других словарях:

• ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью цепи (или ее участка). Емкостное сопротивление синусоидальному току хс=1/?С, где ? угловая частота, С емкость. Измеряется в омах …   Большой Энциклопедический словарь

• ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ — в цепи переменного тока реактивная часть сопротивления двухполюсника (см. Импеданс), в к ром синусоидальный ток опережает по фазе приложенное напряжение подобно тому, как это имеет место в обычном электрич. конденсаторе. В идеальном случае, когда …   Физическая энциклопедия

• емкостное сопротивление — Реактивное сопротивление, обусловленное емкостью элемента электрической цепи и равное абсолютному значению величины, обратной произведению значений этой емкости и угловой частоты. [ГОСТ Р 52002 2003] EN capacitive reactance reactance having a… …   Справочник технического переводчика

• емкостное сопротивление — 149 емкостное сопротивление Реактивное сопротивление, обусловленное емкостью элемента электрической цепи и равное абсолютному значению величины, обратной произведению значений этой емкости и угловой частоты Источник: ГОСТ Р 52002 2003:… …   Словарь-справочник терминов нормативно-технической документации

• емкостное сопротивление — talpinė varža statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. capacitive reactance vok. kapazitive Reaktanz, f; kapazitiver Widerstand, m rus. емкостное… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• Емкостное сопротивление — 1. Реактивное сопротивление, обусловленное емкостью элемента электрической цепи и равное абсолютному значению величины, обратной произведению значений этой емкости и угловой частоты Употребляется в документе: ГОСТ Р 52002 2003 Электротехника.… …   Телекоммуникационный словарь

• емкостное сопротивление электрической цепи — Абсолютное значение реактивного сопротивления, обусловленное емкостью цепи и равное величине, обратной произведению этой емкости и угловой частоты …   Политехнический терминологический толковый словарь

• сопротивление электрическое — величина, характеризующая противодействие электрической цепи (или её участка) электрическому току. Электрическое сопротивление обусловлено преобразованием электрической энергии в другие виды энергии; при необратимом преобразовании… …   Энциклопедический словарь

• сопротивление пластической деформации — [strain resistance] напряжение одноосного растяжения или сжатия при данных температурно скоростных параметрах пластического формоизменения. Сопротивление пластической деформации важнейшая механическая характеристика материала, определяющая… …   Энциклопедический словарь по металлургии

• сопротивление материалов — [strength of materials] наука о прочности и деформируемости элементов (деталей) сооружений и машин. Основные объекты изучения сопротивления материалов стержни и пластины, для которых устанавливаются соответствующие методы расчета на прочность,… …   Энциклопедический словарь по металлургии

основные понятия, формула для расчёта

Конденсатор оказывает определённое сопротивление переменному току и совершенно не проводит постоянный. Это свойство находит применение в различных областях радиоэлектроники и электротехники. Ёмкостное сопротивление в цепи переменного тока зависит от частоты последнего и ёмкости конденсатора.

Основные понятия

Ёмкостное сопротивление — это величина, которая создаётся конденсатором, включённым в цепь. Сопротивление подводящих проводов должно быть непренебрежимо большим. При подаче переменного тока возникают процессы, обусловленные периодическим зарядом и разрядом конденсатора.

Период разбивается на четыре четверти. В течение первой четверти напряжение растёт. В этот момент по цепи проходит зарядный ток, сила которого будет уменьшаться, достигнув нуля, когда электродвижущая сила достигнет положительного максимума. Конденсатор полностью заряжен. После этого начнётся спад напряжения. Конденсатор будет разряжаться через подключённую к нему нагрузку. По цепи потечёт ток.

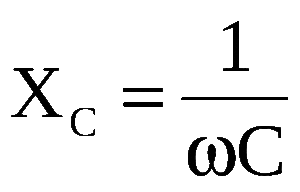К концу полупериода величина напряжения будет равна нулю, а сила тока будет наибольшей. Разрядка завершена. В начале третьей четверти электродвижущая сила будет возрастать, изменив своё направление. Вновь начнётся процесс заряда. Направление зарядного тока в третью четверть будет таким же, как и в предыдущую. По мере зарядки конденсатора эта величина будет убывать. К концу третьей четверти процесс зарядки будет завершён.

Электродвижущая сила достигнет своего наибольшего отрицательного значения. А на той обкладке, на которой в течение первого полупериода был положительный заряд, теперь будет отрицательный. Во время четвёртой четверти значение электродвижущей силы снова будет стремиться к нулю. Конденсатор будет разряжаться. Соответственно, в цепи появится постепенно нарастающий ток. Процесс повторяется. Таким образом, фаза переменного тока в конденсаторной цепи опережает фазу напряжения на 90 градусов.

Формула сопротивления

Формула ёмкостного сопротивления выводится следующим образом:

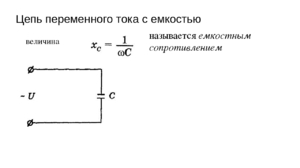• Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
• Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.

Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление.

Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

Применение на практике

Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:

• Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
• Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.

Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.

В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.

Благодаря своим свойствам конденсаторы используются в тех случаях, когда необходимо передать и постоянный, и переменный ток по одним и тем же проводам. Источник постоянного напряжения подключается к общему проводу и второму выводу ёмкости, через которую присоединяется источник переменного напряжения. На другой стороне происходит разделение: потребитель переменного подключается через конденсатор той же ёмкости, а потребитель постоянного — напрямую, до выводов детали.

Распространённый пример подобного использования — это телевизионная наружная антенна с усилителем. Сам телевизор или подключаемое к кабелю устройство, называемое «инжектором», подаёт напряжение питания. В антенном усилителе происходит разделение и фильтрация сигналов. Таким образом, ёмкостное сопротивление конденсатора находит широкое применение. Фильтры обеспечивают задержку одних сигналов и прохождение — других.

Благодаря этому свойству, можно передавать сразу и переменное, и постоянное напряжение, что имеет немаловажное значение при построении некоторых линий связи.

Т. Емкостное сопротивление — PhysBook

Емкостное сопротивление

Опыт показывает, что если последовательно с лампочкой соединить конденсатор и подключить их к генератору постоянного напряжения, то лампочка не горит. Это понятно, так как обкладки конденсатора разделены диэлектриком, и цепь оказывается разомкнутой. При подключении конденсатора к источнику постоянного тока возникает кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Но если эту цепь подключить к источнику переменного напряжения, то лампочка горит. Переменный ток представляет собой вынужденные электромагнитные колебания, происходящие под действием переменного электромагнитного поля генератора. При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается, и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор снова заряжается, но знак заряда на его обкладках изменяется на противоположный и т.д. Через диэлектрик, разделяющий обкладки конденсатора, как и в цепи постоянного тока, электрические заряды не проходят. Но по проводам, соединяющим обкладки конденсатора с источником напряжения, течет переменный ток разрядки и зарядки конденсатора. Поэтому лампочка, включенная последовательно с конденсатором, будет гореть непрерывно. Если теперь конденсатор отсоединить, то лампочка горит ярче. Следовательно, конденсатор оказывает переменному току сопротивление, которое называется емкостным сопротивлением.

Рассмотрим цепь (рис. 1), состоящую из конденсатора и подводящих проводов, сопротивление которых пренебрежительно мало, и генератора переменного напряжения.

Рис. 1

Пусть напряжение на конденсаторе изменяется по закону \(~U = U_0\sin wt.\) Как известно, заряд на обкладках конденсатора можно определить по формуле \(~q = CU = CU_0\sin wt.\) Сила тока \(~I = q’.\) Следовательно,

\(~I = -wCU_0\cos wt = wCU_0\sin(wt+\frac {\pi}2).\)

Отсюда \(~I=I_0\sin (wt +\frac {\pi}2),\)

где \(~I_0=wCU_o\) — амплитудное значение силы тока:

\(~I_0=\frac {U_0}{\frac 1{wC}}; I_0 =\frac {U_0}{X_C},\)

где \(~X_C = \frac 1{wC}.\)

Выразив амплитудные значения через действующие \(~I_0 = \sqrt2 I \) и \(~U_0 = \sqrt2 U,\) получим \(~I= \frac U{X_C}, \) т.е. действующее значение силы тока связано с деиству-Хс ющим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение на участке цепи постоянного тока. Это позволяет рассматривать величину Хс как сопротивление конденсатора переменному току:

\(~X_C = \frac 1{wC}\) — емкостное сопротивление.

В СИ единицей емкостного сопротивления является ом (Ом).

Как видно из полученной выше формулы, если в цепи включено только емкостное сопротивление, колебания силы тока в этой цепи опережают по фазе колебания напряжения на конденсаторе на \(~\frac {\pi}2,\) что изображено на графике и на векторной диаграмме (рис. 2).

Рис. 2

Мгновенная мощность

\(~P=IU = I_0\sin (wt +\frac {\pi}2)U_0\sin wt = I_0U_0\sin wt \cos wt =\frac {I_0U_0}2 \sin 2wt,\)

т.е. мощность периодически изменяется с двойной частотой, а среднее значение мощности — за период \(\mathcal h P \mathcal i =0,\) так как \(~\mathcal h \sin 2wt \mathcal i = 0.\) Первую и третью четверти периода, когда конденсатор заряжается, он получает энергию от генератора, а вторую и четвертую четверти периода, когда конденсатор разряжается, он отдает энергию генератору.

Таким образом, так же, как активное сопротивление, емкостное сопротивление ограничивает силу тока в цепи, но в отличие от активного сопротивления на емкостном сопротивлении электрическая энергия не превращается необратимо в другие виды энергии.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 402-404.

Расчёт реактивного сопротивления

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U_ampsin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U_ampωCsin(ωt+π/2).

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.

---

Онлайн-калькулятор расчёта реактивного сопротивления

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Реактивное сопротивление ёмкости XC = 1 /(2πƒC)

Реактивное сопротивление индуктивности XL = 2πƒL

Расчитать ёмкость или индуктивность для реактивного сопротивления:

Расчёт ёмкости: C = 1 /(2πƒXC)

Расчёт индуктивности: L = XL /(2πƒ)

---

Похожие страницы с расчётами:

Расcчитать импеданс.
Расcчитать частоту резонанса колебательного контура LC.
Расcчитать реактивную мощность и компенсацию.

Емкостное реактивное сопротивление | Примечания по электронике

Емкостное реактивное сопротивление — это влияние конденсатора на протекание переменного тока.

---

Емкостное руководство В комплект входит:
Емкость Формулы конденсатора Емкостное реактивное сопротивление Параллельные конденсаторы Последовательные конденсаторы Диэлектрическая проницаемость и относительная диэлектрическая проницаемость Коэффициент рассеяния, тангенс угла потерь, СОЭ Таблица преобразования конденсаторов

---

Важно знать, какое влияние конденсатор окажет на любую цепь, в которой он работает.Он не только предотвращает прохождение компонента постоянного тока сигнала, но также влияет на любой переменный сигнал, который может появиться.

Реактивное сопротивление

В цепи постоянного тока, где могут быть батарея и резистор, именно резистор препятствует прохождению тока в цепи. Это основной закон Ома. То же верно и для цепи переменного тока с конденсатором. Конденсатор с небольшой площадью пластины сможет накапливать только небольшой заряд, и это будет препятствовать протеканию тока.Конденсатор большего размера позволит протекать большему току. Говорят, что конденсатор имеет определенное реактивное сопротивление. Это имя выбрано, чтобы отличаться от названия резистора, но оно точно так же измеряется в Ом. Реактивное сопротивление конденсатора зависит от номинала конденсатора, а также от рабочей частоты. Чем выше частота, тем меньше реактивное сопротивление.

Фактическое реактивное сопротивление можно рассчитать по формуле:

X _c = 1 / (2 pi f C)

где

X _c — емкостное реактивное сопротивление в омах
f — частота в герцах
C — емкость в фарадах

Расчет тока

Реактивное сопротивление конденсатора, рассчитанное по приведенной выше формуле, измеряется в Ом.Затем ток, протекающий в цепи, можно рассчитать обычным способом, используя закон Ома:

.

V = I X _c

Суммирование сопротивления и реактивного сопротивления

Хотя сопротивление и реактивное сопротивление очень похожи, и значения обоих измеряются в Омах, они не совсем одинаковы. В результате их невозможно напрямую сложить. Вместо этого их нужно суммировать «векторно». Другими словами, необходимо возвести каждое значение в квадрат, а затем сложить их вместе и извлечь квадратный корень из этого числа.В более математическом формате:

X _итого ² = X _c ² + R ²

Дополнительные основные понятия:
Напряжение Текущий Сопротивление Емкость Мощность Трансформеры RF шум Децибел, дБ Q, добротность
Вернуться в меню «Основные понятия». . .

.

емкостных и резистивных сенсорных экранов: в чем разница?

MakeUseOf — Политика конфиденциальности

Мы уважаем вашу конфиденциальность и обязуемся защищать вашу конфиденциальность во время работы в сети на нашем сайт. Ниже раскрываются методы сбора и распространения информации для этой сети. сайт.

Последний раз политика конфиденциальности обновлялась 10 мая 2018 г.

Право собственности

MakeUseOf («Веб-сайт») принадлежит и управляется Valnet inc.(«Нас» или «мы»), корпорация зарегистрирован в соответствии с законодательством Канады, с головным офисом по адресу 7405 Transcanada Highway, Люкс 100, Сен-Лоран, Квебек h5T 1Z2.

Собранные персональные данные

Когда вы посещаете наш веб-сайт, мы собираем определенную информацию, относящуюся к вашему устройству, например, ваше IP-адрес, какие страницы вы посещаете на нашем веб-сайте, ссылались ли вы на другие веб-сайт, и в какое время вы заходили на наш веб-сайт.

Мы не собираем никаких других персональных данных.Если вы заходите на наш сайт через учетной записи в социальной сети, пожалуйста, обратитесь к политике конфиденциальности поставщика социальных сетей для получения информации относительно их сбора данных.

Файлы журнала

Как и большинство стандартных серверов веб-сайтов, мы используем файлы журналов. Это включает интернет-протокол (IP) адреса, тип браузера, интернет-провайдер (ISP), страницы перехода / выхода, тип платформы, дата / время и количество кликов для анализа тенденций, администрирования сайта, отслеживания пользователей движение в совокупности и собирать широкую демографическую информацию для совокупного использования.

Файлы cookie

Файл cookie — это фрагмент данных, хранящийся на компьютере пользователя, связанный с информацией о пользователе. Мы и некоторые из наших деловых партнеров (например, рекламодатели) используем файлы cookie на нашем веб-сайте. Эти файлы cookie отслеживают использование сайта в целях безопасности, аналитики и целевой рекламы.

Мы используем следующие типы файлов cookie:

• Основные файлы cookie: эти файлы cookie необходимы для работы нашего веб-сайта.
• Функциональные cookie-файлы: эти cookie-файлы помогают нам запоминать выбор, который вы сделали на нашем веб-сайте, запоминать ваши предпочтения и персонализировать ваш опыт работы с сайтом.
• Аналитические и рабочие файлы cookie: эти файлы cookie помогают нам собирать статистические и аналитические данные об использовании веб-сайта.
• Файлы cookie социальных сетей: эти файлы cookie позволяют вам взаимодействовать с контентом на определенных платформах социальных сетей, например, «лайкать» наши статьи. В зависимости от ваших социальных сетей настройки, сеть социальных сетей будет записывать это и может отображать ваше имя или идентификатор в связи с этим действием.
• Рекламные и таргетированные рекламные файлы cookie: эти файлы cookie отслеживают ваши привычки просмотра и местоположение, чтобы предоставить вам рекламу в соответствии с вашими интересами. См. Подробности в разделе «Рекламодатели» ниже.

Если вы хотите отключить файлы cookie, вы можете сделать это в настройках вашего браузера. Для получения дополнительной информации о файлах cookie и способах управления ими, см. http://www.allaboutcookies.org/.

Пиксельные теги

Мы используем пиксельные теги, которые представляют собой небольшие графические файлы, которые позволяют нам и нашим доверенным сторонним партнерам отслеживать использование вашего веб-сайта и собирать данные об использовании, включая количество страниц, которые вы посещаете, время, которое вы проводите на каждой странице, то, что вы нажимаете дальше, и другую информацию о посещении вашего веб-сайта.

Рекламодатели

Мы пользуемся услугами сторонних рекламных компаний для показа рекламы, когда вы посещаете наш веб-сайт. Эти компании могут использовать информацию (не включая ваше имя, адрес, адрес электронной почты или номер телефона) о ваших посещениях этого и других веб-сайтов для размещения рекламы товаров и услуг, представляющих для вас интерес. Если вы хотите получить дополнительную информацию об этой практике и узнать, как можно отказаться от использования этой информации этими компаниями, щелкните здесь.

Рекламодатели, как сторонние поставщики, используют файлы cookie для сбора данных об использовании и демографических данных для показа рекламы на нашем сайте. Например, использование Google Файлы cookie DART позволяют показывать рекламу нашим пользователям на основе их посещения наших сайтов и других сайтов в Интернете. Пользователи могут отказаться от использования DART cookie, посетив политику конфиденциальности Google для рекламы и содержательной сети.

Мы проверили все политики наших рекламных партнеров, чтобы убедиться, что они соответствуют всем применимым законам о конфиденциальности данных и рекомендуемым методам защиты данных.

Мы используем следующих рекламодателей:

Ссылки на другие веб-сайты

Этот сайт содержит ссылки на другие сайты. Помните, что мы не несем ответственности за политика конфиденциальности таких других сайтов. Мы призываем наших пользователей знать, когда они покидают нашу сайт, и прочитать заявления о конфиденциальности каждого веб-сайта, который собирает лично идентифицируемая информация. Это заявление о конфиденциальности применяется исключительно к информации, собираемой этим Интернет сайт.

Цель сбора данных

Мы используем информацию, которую собираем, чтобы:

• Администрирование нашего веб-сайта, включая устранение неполадок, статистический анализ или анализ данных;
• Для улучшения нашего Веб-сайта и повышения качества обслуживания пользователей, обеспечивая вам доступ к персонализированному контенту в соответствии с вашими интересами;
• Анализируйте использование пользователями и оптимизируйте наши услуги.
• Для обеспечения безопасности нашего веб-сайта и защиты от взлома или мошенничества.
• Делитесь информацией с нашими партнерами для предоставления таргетированной рекламы и функций социальных сетей.

Данные передаются третьим лицам

Мы не продаем и не сдаем в аренду ваши личные данные третьим лицам. Однако наши партнеры, в том числе рекламные партнеры, может собирать данные об использовании вашего веб-сайта, как описано в настоящем документе. См. Подробности в разделе «Рекламодатели» выше.

Как хранятся ваши данные

Все данные, собранные через наш Веб-сайт, хранятся на серверах, расположенных в США.Наши серверы сертифицированы в соответствии с Соглашением о защите конфиденциальности ЕС-США.

IP-адрес и строковые данные пользовательского агента от всех посетителей хранятся в ротационных файлах журнала на Amazon. сервера на срок до 7 дней. Все наши сотрудники, агенты и партнеры стремятся сохранить ваши данные конфиденциальны.

Мы проверили политику конфиденциальности наших партнеров, чтобы убедиться, что они соответствуют аналогичным политикам. для обеспечения безопасности ваших данных.

Согласие в соответствии с действующим законодательством

Если вы проживаете в Европейской экономической зоне («ЕЭЗ»), окно согласия появится, когда доступ к этому сайту.Если вы нажали «да», ваше согласие будет храниться на наших серверах в течение двенадцать (12) месяцев, и ваши данные будут обработаны в соответствии с настоящей политикой конфиденциальности. После двенадцати месяцев, вас снова попросят дать согласие.

Мы соблюдаем принципы прозрачности и согласия IAB Europe.

Вы можете отозвать согласие в любое время. Отзыв согласия может ограничить вашу возможность доступа к определенным услугам и не позволит нам обеспечить персонализированный опыт работы с сайтом.

Безопасность данных

Наши серверы соответствуют ISO 27018, сводам правил, направленных на защиту личных данных. данные в облаке. Мы соблюдаем все разумные меры предосторожности, чтобы гарантировать, что ваши данные безопасность.

В случае, если нам станет известно о любом нарушении безопасности данных, изменении, несанкционированном доступе или раскрытие каких-либо личных данных, мы примем все разумные меры предосторожности для защиты ваших данных и уведомит вас в соответствии с требованиями всех применимых законов.

Доступ, изменение и удаление ваших данных

Вы имеете право запросить информацию о данных, которые у нас есть для вас, чтобы запросить исправление и / или удаление вашей личной информации. пожалуйста, свяжитесь с нами в [email protected] или по указанному выше почтовому адресу, внимание: Отдел соблюдения требований данных.

Возраст

Этот веб-сайт не предназначен для лиц младше 16 лет. Посещая этот веб-сайт. Вы настоящим гарантируете, что вам исполнилось 16 лет или вы посещаете Веб-сайт под присмотром родителей. надзор.

Заявление об отказе от ответственности

Хотя мы прилагаем все усилия для сохранения конфиденциальности пользователей, нам может потребоваться раскрыть личную информацию, когда требуется по закону, когда мы добросовестно полагаем, что такие действия необходимы для соблюдения действующего судебное разбирательство, постановление суда или судебный процесс, обслуживаемый на любом из наших сайтов.

Уведомление об изменениях

Каждый раз, когда мы изменяем нашу политику конфиденциальности, мы будем публиковать эти изменения на этой странице Политики конфиденциальности и других места, которые мы считаем подходящими, чтобы наши пользователи всегда знали, какую информацию мы собираем, как мы ее используем, и при каких обстоятельствах, если таковые имеются, мы ее раскрываем.

Контактная информация

Если у пользователей есть какие-либо вопросы или предложения относительно нашей политики конфиденциальности, свяжитесь с нами по адресу [email protected] или по почте на указанный выше почтовый адрес, внимание: Департамент соответствия данных.

.