Фазные токи. Фазные и линейные токи в трехфазных системах: ключевые понятия и расчеты

Что такое фазный и линейный ток в трехфазной системе. Как рассчитать фазный ток при известном линейном напряжении. Каковы соотношения между фазными и линейными величинами при соединении звездой и треугольником. Как измерить мощность в трехфазной цепи.

Фазные и линейные токи: основные определения

В трехфазных системах различают фазные и линейные токи:

• Фазный ток — ток, протекающий по отдельной фазе.
• Линейный ток — ток, протекающий по линейному проводу между источником и нагрузкой.

Соотношения между фазными и линейными токами зависят от схемы соединения:

• При соединении звездой: I_л = I_ф
• При соединении треугольником: I_л = √3 * I_ф

Расчет фазного тока при известном линейном напряжении

Для расчета фазного тока при известном линейном напряжении и сопротивлении нагрузки в схеме треугольник используется следующая формула:

I_ф = U_л / (√3 * Z_ф)

Где:

• I _ф — фазный ток
• U_л — линейное напряжение
• Z_ф — полное сопротивление фазы нагрузки

Особенности схемы соединения треугольником

При соединении нагрузки треугольником:

• Напряжения на фазах равны линейным напряжениям
• Токи в фазах могут быть различными при несимметричной нагрузке
• Линейные токи определяются по первому закону Кирхгофа для узлов схемы

Измерение мощности в трехфазных цепях

Для измерения мощности в трехфазных цепях применяются следующие методы:

• Метод трех ваттметров — для несимметричной нагрузки
• Метод двух ваттметров (схема Арона) — для симметричной и несимметричной нагрузки в трехпроводной системе
• Метод одного ваттметра — для симметричной нагрузки

Метод двух ваттметров (схема Арона)

Схема Арона позволяет измерять мощность в трехпроводной линии двумя ваттметрами. Полная мощность равна алгебраической сумме показаний ваттметров:

P = W₁ + W₂

Где W₁ и W₂ — показания двух ваттметров.

Расчет мощности в трехфазных цепях

Для расчета мощности в трехфазных цепях используются следующие формулы:

Активная мощность

P = √3 * U_л * I_л * cos φ

Реактивная мощность

Q = √3 * U_л * I_л * sin φ

Полная мощность

S = √(P² + Q²)

Где:

• U_л — линейное напряжение
• I_л — линейный ток
• cos φ — коэффициент мощности

Соотношения между фазными и линейными величинами

Соотношения между фазными и линейными величинами зависят от схемы соединения:

Соединение звездой

• U_л = √3 * U_ф
• I_л = I_ф

Соединение треугольником

• U_л = U_ф
• I _л = √3 * I_ф

Практическое применение фазных и линейных токов

Понимание соотношений между фазными и линейными токами важно для:

• Выбора сечения проводников
• Расчета потерь мощности
• Настройки защитных устройств
• Анализа несимметричных режимов работы

Например, при выборе автоматического выключателя для защиты трехфазной нагрузки, соединенной треугольником, необходимо учитывать, что линейный ток будет в √3 раз больше фазного.

Влияние несимметрии нагрузки на фазные и линейные токи

При несимметричной нагрузке в трехфазной системе:

• Фазные токи могут существенно различаться
• Возникает ток в нейтральном проводе (при соединении звездой с нейтралью)
• Появляются дополнительные потери мощности
• Возможно появление высших гармоник

Для оценки степени несимметрии используется коэффициент несимметрии токов:

K_2I = I₂ / I₁ * 100%

Где I₂ — ток обратной последовательности, I

1 — ток прямой последовательности.

Векторные диаграммы фазных и линейных токов

Векторные диаграммы наглядно показывают соотношения между фазными и линейными токами:

• При соединении звездой векторы линейных токов совпадают с векторами фазных токов
• При соединении треугольником векторы линейных токов образуются как разность соответствующих векторов фазных токов

Анализ векторных диаграмм позволяет:

• Определить угол сдвига фаз между током и напряжением
• Оценить симметричность нагрузки
• Рассчитать активную и реактивную составляющие тока

Особенности измерения фазных и линейных токов

При измерении фазных и линейных токов в трехфазных системах следует учитывать:

• Линейные токи измеряются в линейных проводах
• Фазные токи измеряются непосредственно на нагрузке
• При соединении звездой измерение линейного тока эквивалентно измерению фазного
• При соединении треугольником для определения фазных токов требуются дополнительные измерения или расчеты

Для точного измерения токов рекомендуется использовать токовые клещи или амперметры с соответствующими трансформаторами тока.

Расчет параметров трехфазной цепи по известным фазным и линейным токам

Зная фазные и линейные токи, можно рассчитать различные параметры трехфазной цепи:

• Полное сопротивление нагрузки: Z = U_ф / I_ф
• Активное сопротивление: R = Z * cos φ
• Реактивное сопротивление: X = Z * sin φ
• Коэффициент мощности: cos φ = P / S

Эти расчеты позволяют оценить характер нагрузки и ее влияние на энергосистему.

Влияние гармоник на фазные и линейные токи

Наличие гармоник в трехфазной системе может существенно влиять на соотношения между фазными и линейными токами:

• Гармоники кратные трем (3-я, 9-я и т.д.) суммируются в нейтральном проводе
• Несимметрия нагрузки усиливает влияние гармоник
• Возможно появление токов, превышающих номинальные значения

Для анализа влияния гармоник используется коэффициент искажения синусоидальности кривой тока:

K_I = √(Σ(I_n²) / I₁²) * 100%

Где I_n — действующее значение тока n-й гармоники, I₁ — действующее значение тока основной гармоники.

22. Как рассчитать фазный ток, если известны линейное напряжение и сопротивление нагрузки в схеме треугольник.

Схема треугольник

В этой схеме (рис. 10.2,) токи в фазах при несимметричной нагрузке различны но напряжения остаются неизменными (номинальные). Линейные токи определяют по закону Кирхгофа

Мощность трехфазной несимметричной цепи.

Для измерения активной мощности трехфазной нагрузки в общем случае, когда нагрузка несимметрична, используют 3 ваттметра (рис. 10.3, 

а), и тогда полная мощность равна сумме показаний ваттметров. При симметричной нагрузке достаточно одного ваттметра, включенного в одну из фаз.

Трехфазную цепь с тремя проводами, соединяющими генератор с потребителем, всегда можно рассматривать как две двухпроводные линии, имеющие один общий провод, например как линии АВ и СВ с общим проводом В (рис.   10.3, б), в котором ток . При этом по первой линии при напряженииидет ток, а по второй линии при напряженииидет ток.

Рис. 10.3

Мощность, передаваемая по первой линии ,

а мощность, передаваемая по второй линии,

Полная мощность, передаваемая по трехпроводной линии, S = S₁ 

+ S₂.

Из сказанного вытекает возможность измерять мощность, передаваемую по трехпроводной линии трехфазной системы, двумя ваттметрами, каждый из которых определяет мощность, передаваемую по одной из двух двухпроводных линий. Такая схема включения ваттметров (схема Арона) изображена на рис. 10.3, б.

При выводе не делалось никаких предположений о симметрии системы, следовательно, найденный метод измерения мощности двумя ваттметрами применим как в случае симметричной, так и в случае несимметричной трехфазной трехпроводной системы.

При чисто активной нагрузке (=0) показания обоих ваттметров одинаковы.

Полное значение передаваемой (активной) мощности равно алгебраической сумме показаний обоих ваттметров. На практике часто два ваттметра ставятся на общую ось. Показания такого сдвоенного ваттметра непосредственно равны всей (активной) мощности, передаваемой по трехпроводной линии.

Если определить разность показаний ваттметров W₂–W₁=U_ЛI_Лsin, то по ней можно определить реактивную мощность . На основании последних выражений легко вывести формулу, позволяющую определить угол по показаниям ваттметров:

Вычисление величины полной мощности. Расчет полной мощности электрической цепи требует знания ее активной и реактивной составляющих, соотношение которых в любой схеме описывается треугольником мощностей.

Для вычисления активной (Р) и реактивной (Q)

 составляющих 3-х фазной цепи проводится суммирование их величин в каждой фазе по формулам:

   Р=Р_A+Р_B+Р_C=U_AI_Acosφ_A+U_ВI_Вcosφ_В+U_СI_AСcosφ_С;    Q=Q_A+Q_B+Q_C=U_AI_Asinφ_A+U_ВI_Вsinφ_В+U_СI_AСsinφ_С.

I_A, I_В, I_С, U_A, U_В, U_С – вектора токов и напряжений в фазах,

Φ – угол сдвига фаз векторов тока относительно напряжения.

Для симметричного режима работы схемы во всех фазах выполняется равенство мощностей. Поэтому общую величину мощности можно получить простым умножением фазной составляющей на количество фаз в системе:

   Р=3Р_Ф=3U_Ф∙I_Ф∙cosφ;    Q=3Q=3U_Ф∙I_Ф∙sinφ;    S=3S_Ф=(Р2+Q2)=3U_ФI_Ф.

Делаем замену фазных составляющих линейными по их соотношениям для схемы звезды: I_Л=I_Ф, U_Ф=U_Л/√3.

В результате получаем:

   Р=3U_Ф∙I_Ф∙cosφ=(3U_Л∙I_Л/√3)∙cosφ=√3∙U_Л∙I_Л∙cosφ.

Заменяем фазные составляющие линейными для схемы треугольника по их соотношениям: I_Ф=I_Л/√3, U_Ф=U_Л.

Итог вычисления:

   Р=3U_Ф∙I_Ф∙cosφ=(3U_Л∙I_Л/√3)∙cosφ=√3∙U_Л∙I_Л∙cosφ.

Таким образом, получилось, что зависимость от вариантов соединения элементов цепи схемой γ либо Δ в 3-х фазной симметричной системе значения мощностей отсутствует. Они вычисляются по одним и тем же формулам:

   Р=√3∙U∙I∙cosφ [Вт];    Q=√3∙U∙I∙sinφ [вар];    S=√(Р²+Q²) [ВА].

Для данных выражений сложилось правило: подставлять линейные значения векторов U и I без указания их линейных индексов.

Способы измерений мощности В энергетике существует постоянная необходимость измерения электрических величин. Активная составляющая полной мощности замеряется ваттметром, а реактивная – варметром. Ваттметр работает по алгоритму, описанному формулой:

   W=U_W∙I_W∙cos(U_W^I_W)=Re│U_W∙I_W*│.

U_W, I_W – те вектора, которые подвели к клеммам прибору для замера активной составляющей.

Практика электрических измерений предлагает несколько вариантов подключения к электросети ваттметров. Они выбираются в зависимости от схемы выполненный коммутации нагрузок и ее характеристик.

В симметричной 3-х фазной системе достаточно включить один ваттметр в любую фазу для постоянного замера активной мощности с последующим утроением полученного результата по алгоритму Р=3W=3U_Ф∙I_Ф∙cosφ.

Однако, этот простой способ только ориентировочно оценивает замеряемые величины, имеет большие погрешности. Поэтому, он малоприемлем для выполнения замеров, требующих высокой точности и в решении коммерческих задач.

Более точные замеры активной составляющей для звезды с нейтральным проводом обеспечивает использование в измерении трех ваттметров.

Фазные и линейные токи и напряжения.

Численные соотношения между фазными и линейными величинами. — Студопедия

Поделись с друзьями: 

Каждая часть многофазной системы, имеющая одинаковую характеристику тока, называется фазой.

Фазное напряжение – возникает между началом и концом какой-либо фазы. По другому его еще определяют, как напряжение между одним из фазных проводов и нулевым проводом.

Линейное — которое определяют еще как межфазное или между фазное – возникающее между двумя проводами или одинаковыми выводами разных фаз. Показатель фазного напряжения составляет примерно 58% от параметров линейного. Таким образом, при нормальных условиях эксплуатации показатели линейных одинаковы и превышают фазные в 1,73 раза. В трехфазной сети напряжение, как правило, оценивают по данным линейного напряжения. Для трехфазных линий, которые отходят от подстанции, устанавливается линейное напряжение номиналом 380 вольт. Это соответствует фазному в 220 вольт.

Так, токи, протекающие в каждой фазе, именуют фазными и условно обозначают IА, IB, IC либо условно Iф. Токи в ветвях нагрузки именуют линейными. Их величина обуславливается величиной фазных напряжений, типом нагрузки. При сугубо активной нагрузке токи идентичны с напряжениями по фазе, а при индуктивной либо емкостной нагрузке, токи могут опережать или отставать от напряжения.

В традиционных электросетях имеет место 2 метода соединения:

— треугольник;

— звезда.

При соединении ветвей схемы треугольником конец одной обмотки подключается к началу другой, т.е. получается замкнутый контур. Для каждого узла схемы выполняется баланс – сумма входящих токов равна сумме исходящих. При таком подключении и симметричной нагрузке выполняется соотношение:

Iл = v3 Iф.

При соединении ветвей элементов схемы звездой все окончания обмоток фаз подключают в один узел 0. Ввиду того, что фазы генератора соединяются последовательно с фазами электроприемников (нагрузки), то линейные токи по величине равны фазным:

Iф = Iл.

Соединение потребителей трехфазного тока по схеме «звезда».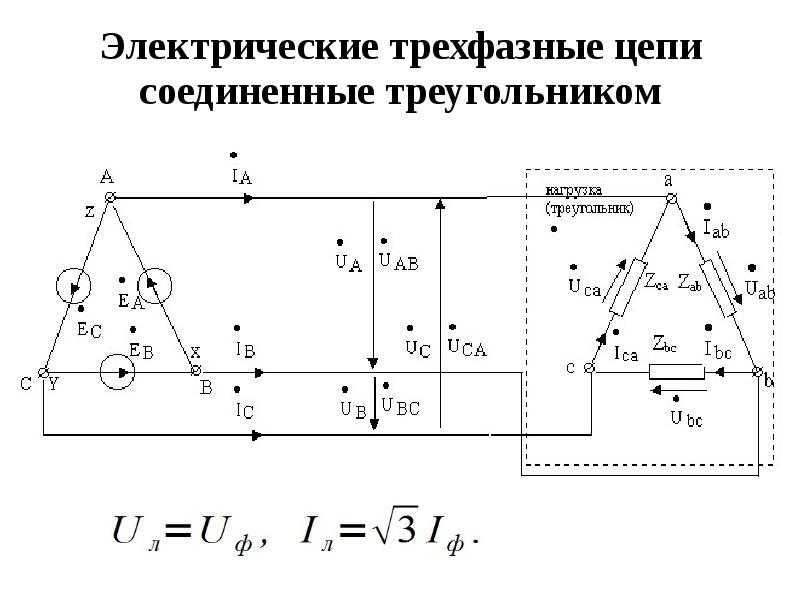 Симметричный и несимметричный режимы.

При соединение фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников (Z_a, Z_b, Z_c) также соединяют в одну точку n. Такое соединение называется соединение звезда.

Провода A−a, B−b и C−c, соединяющие начала фаз генератора и приемника, называются линейными, провод N−n, соединяющий точкуN генератора с точкой n приемника, – нейтральным.

Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной.

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---



Значения трехфазного тока в 3-фазной или многофазной системе

Для понимания разделения Трехфазный ток в трехфазной системе можно отметить следующие моменты и I _B ) на рис. 1 и 2 не указывает направления токов в конкретный момент, но показывает направления токов, когда мы принимаем их положительными. Можно отметить, что не существует момента, когда направление всех трех фазных токов одинаково, т. е. не существует возможного момента, когда все три фазных тока одновременно идут или выходят в общую точку.

Символы со стрелками показывают, что первый ток выходит из фазы R , затем, после времени фазы 120°, этот ток покидает фазу Y , а для следующих 120° он покидает фазу B .

2. В любом одном или двух проводниках выходной ток равен входному току в этом проводнике (или проводниках). Другими словами, каждый проводник обеспечивает обратный путь для токов других проводников. Таким образом, текущее деление постоянно меняется в трех строках. Следовательно, алгебраическая сумма трех токов равна Ноль (0) в любой момент.

Рис. Значения трехфазного тока в трехфазной системе.

Объяснение трехфазных токов в многофазной системе:

Трехфазные токи показаны на приведенном выше рисунке с одинаковым пиковым значением 8A , но смещены друг от друга на 120° .

На рисунке выше в точке «а» значения токов в фазах R и B равны +4А и направление этих токов наружу, а значение фазы Y равно -8А . Его средний ток фазы Y обеспечивает обратный путь к токам фаз R и B .

Аналогично,

• В точке «b» = I _R =+6A, I _Y = +2A, I _B =-8A …. Теперь B обеспечивает обратный путь для токов Y и R
• В точке «C» = I _Y =+6A, I _B = +2A, I _R =-8A …. Теперь R обеспечивает обратный путь для токов Y и B
• В точке «d» = I _R =0A, I _B = +6,9A, I _Y =-6,9A …. т.е. Ток B исходит, а Y возвращается с пути Y

Таким образом, можно отметить, что хотя распределение тока в трех фазах непрерывно изменяется , но в любой момент их алгебраическая сумма мгновенных значений равна нулю (0) т.е.

I _R + I _Y + I _B = 0    ……………. Алгебраически

Вы также можете прочитать:

• Значения напряжения, тока и мощности при соединении звездой (Y)
• Значения напряжения, тока и мощности при соединении треугольником (Δ)
• Сравнение соединения звездой (Y) и треугольником (Δ)
• Метод пуска трехфазного двигателя по схеме «звезда-треугольник» (Y-Δ) с помощью автоматического пускателя по схеме «звезда-треугольник» с таймером.
• Подключение трехфазного двигателя по схеме ЗВЕЗДА/ТРЕУГОЛЬНИК без таймера Схемы питания и управления

URL-адрес скопирован

Показать полную статью

Связанные статьи

Кнопка «Вернуться к началу»

Объяснение: линейное напряжение, линейный ток, фазное напряжение, фазный ток

Термины «линия» и «фаза» относятся к системе электропитания переменного или переменного тока. Эти термины используются, в частности, в трехфазной системе электроснабжения, при соединении по схеме «звезда» и «треугольник». Вы должны знать об этих терминах, чтобы понимать систему электрического баланса и несбалансированную систему. Напряжение — это разность потенциалов на проводнике, которая фактически заставляет начать протекание тока, с другой стороны, ток — это поток электронов через проводник.

В трехфазной энергосистеме используются два типа соединений: 1. Соединение звездой 2. Соединение треугольником.

Соединение по схеме «звезда» — это соединение одной клеммы всех трех фаз с нейтральной точкой. Соединение треугольником — это когда все три фазы соединены в замкнутую систему, окончание одной фазы связано с началом другой фазы. Здесь вы можете увидеть схему соединений «звезда» и «треугольник».

Что такое линейное напряжение?

В трехфазной системе разность потенциалов или напряжение между любыми двумя фазами или клеммой под напряжением называется линейным напряжением. Итак, если три фазы R, Y, B, то линейное напряжение может проходить через R-Y, Y-B или B-R. Линейное напряжение обозначается VL. Как правило, линейное напряжение представляет собой более высокое напряжение трехфазной энергосистемы. Линейное напряжение доступно на уровне 440 В в Индии. Линейное напряжение больше фазного.

В энергосистеме, соединенной звездой, линейное напряжение в три (√3) раза выше, чем фазное напряжение. Итак, VL = √3*VPh или VL = 1,732VPh

В энергосистеме, соединенной треугольником, линейное напряжение равно фазному напряжению. Таким образом, VL = VPh

Пример линейного напряжения: 33 кВ, 11 кВ и 440 В являются примерами линейного напряжения. 440 В в основном используется для питания потребителей, а другие напряжения используются для передачи электроэнергии.

Что такое фазное напряжение?

В энергосистеме разность потенциалов или напряжение между любой фазой и нейтральной точкой называется фазным напряжением. Фазное напряжение обозначается VPh. Если три фазы — R, Y и B, а нейтральная точка — N, то фазное напряжение может проходить через R-N, Y-N или B-N. В энергосистеме фазное напряжение в Индии составляет 230 В. Фазное напряжение ниже сетевого напряжения.

В энергосистеме, соединенной звездой, фазное напряжение VPh = VL/√3

В энергосистеме, соединенной треугольником, фазное напряжение равно линейному напряжению или VPh = VL

Фазное напряжение Пример: Однофазное питание 230 В является примером фазного напряжения.

Разница между линейным напряжением и фазным напряжением

1. Линейное напряжение является высоким, тогда как фазное напряжение является низким.

2. Для получения линейного напряжения необходимы обе клеммы под напряжением, тогда как для получения фазного напряжения требуется любая клемма фазы.

Читайте также:  

Что такое линейный ток?

Протекание тока через любую линию между трехфазным источником питания и нагрузкой называется линейным током. Линейный ток обозначается IL. Здесь нейтраль не требуется для измерения линейного тока.

При соединении по схеме «звезда» линейный ток равен фазному току или IL = IPh

При соединении по схеме «треугольник» линейный ток в √3 раза больше фазного тока или IL = √3IPh

Что такое фазный ток?

Поток тока через любой компонент трехфазной системы к нагрузке называется фазным током. Фазный ток обозначается IPh.

При соединении звездой фазный ток равен линейному току или IPh = IL

При соединении треугольником фазный ток IPh = IL/√3

Разница между линейным током и фазным током

1. Линия ток течет от любой одной линии ко всей трехфазной системе через нагрузку, тогда как фазный ток течет от любой одной линии к нагрузке.

2. Линейный ток можно назвать протеканием тока вне нагрузки, с другой стороны, фазный ток можно назвать протеканием тока внутри нагрузки.

Читайте также:  

• Что такое падение напряжения? Формула, причины, последствия, примеры
• Что такое конденсатор переменного тока? Рейтинги, приложения, свойства
• Что такое дроссельная катушка? Типы, применение, свойства, схема

Благодарим вас за посещение веб-сайта.