Физический смысл емкостного сопротивления: обзор ключевых аспектов

Что такое емкостное сопротивление. Как оно связано с электрическим зарядом и напряжением. Почему емкость измеряется в фарадах. Какова физическая сущность этого явления.

Что такое емкостное сопротивление и его физический смысл

Емкостное сопротивление — это способность элемента электрической цепи накапливать электрический заряд при приложении к нему напряжения. Физический смысл емкостного сопротивления заключается в следующем:

• Оно характеризует способность проводников накапливать электрический заряд
• Определяет соотношение между накопленным зарядом и приложенным напряжением
• Зависит от геометрических размеров и свойств диэлектрика между проводниками
• Создает сдвиг фаз между током и напряжением в цепи переменного тока

Таким образом, емкостное сопротивление отражает фундаментальное свойство проводников накапливать заряд под действием электрического поля.

Почему емкость измеряется в фарадах (Кл/В)

Единица измерения емкости — фарад (Ф) — определяется как отношение заряда к напряжению (Кл/В). Это обусловлено следующими причинами:

• Емкость характеризует способность накапливать заряд при заданном напряжении
• Существует линейная зависимость между зарядом и напряжением для конденсатора
• Напряжение создается разделением зарядов и пропорционально величине заряда
• Отношение Q/V остается постоянным для данного конденсатора

Таким образом, определение емкости через Q/V позволяет количественно охарактеризовать способность элемента накапливать заряд при заданном напряжении.

Связь емкостного сопротивления с электрическим зарядом

Емкостное сопротивление напрямую связано с накоплением электрического заряда:

• Величина накопленного заряда пропорциональна емкости и приложенному напряжению: Q = CV
• Чем больше емкость, тем больший заряд накапливается при том же напряжении
• При увеличении напряжения растет и накопленный заряд
• Максимальный накопленный заряд ограничен пробивным напряжением диэлектрика

Следовательно, емкость определяет способность элемента накапливать и хранить электрический заряд в зависимости от приложенного напряжения.

Роль напряжения в определении емкостного сопротивления

Напряжение играет ключевую роль в определении емкостного сопротивления по нескольким причинам:

• Напряжение создает электрическое поле, разделяющее заряды в конденсаторе
• Величина накопленного заряда прямо пропорциональна приложенному напряжению
• Отношение Q/V остается постоянным для данного конденсатора
• Напряжение определяет энергию, запасенную в электрическом поле конденсатора

Таким образом, напряжение является ключевым параметром, характеризующим работу конденсатора и его способность накапливать заряд.

Физическая сущность емкостного сопротивления

Физическая сущность емкостного сопротивления заключается в следующем:

• Это мера способности проводников накапливать электрический заряд
• Отражает свойство разделения зарядов под действием электрического поля
• Характеризует накопление энергии в электрическом поле между проводниками
• Определяет инерционность изменения напряжения при протекании тока

Таким образом, емкостное сопротивление является фундаментальным свойством, связанным с накоплением заряда и энергии электрического поля.

Практическое применение емкостного сопротивления

Емкостное сопротивление находит широкое применение в электротехнике и электронике:

• Конденсаторы используются для накопления заряда и энергии
• Емкостные элементы применяются для фильтрации сигналов
• Емкостное сопротивление позволяет создавать частотно-зависимые цепи
• На основе емкости строятся генераторы сигналов и таймеры
• Емкостные датчики используются для измерения различных величин

Понимание физической сущности емкостного сопротивления важно для эффективного применения конденсаторов в электрических схемах.

Влияние параметров конденсатора на емкостное сопротивление

Емкостное сопротивление конденсатора зависит от нескольких ключевых параметров:

• Площадь пластин — чем она больше, тем выше емкость
• Расстояние между пластинами — при его уменьшении емкость растет
• Диэлектрическая проницаемость материала между пластинами
• Геометрическая форма электродов конденсатора
• Наличие примесей и дефектов в диэлектрике

Изменяя эти параметры, можно создавать конденсаторы с различной емкостью для разных применений.

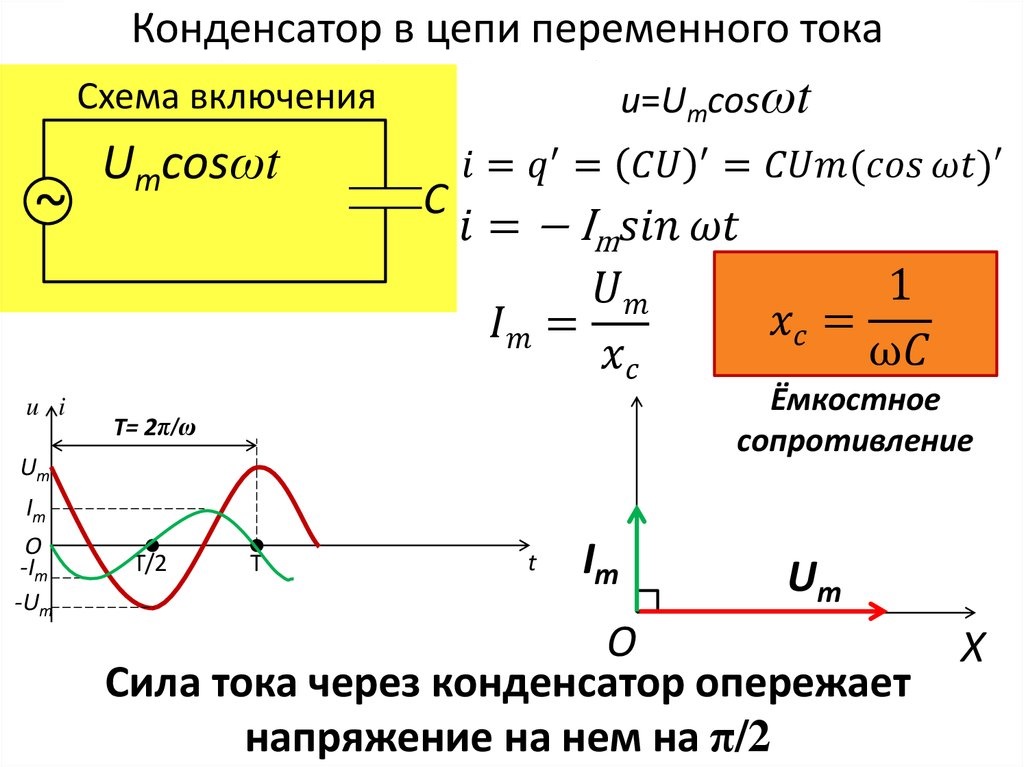
Емкостное сопротивление в цепях переменного тока

В цепях переменного тока емкостное сопротивление проявляет ряд важных свойств:

• Создает сдвиг фаз между током и напряжением на 90°
• Ток через конденсатор опережает напряжение по фазе
• Емкостное сопротивление обратно пропорционально частоте тока
• На высоких частотах конденсатор становится проводником
• Емкостное и индуктивное сопротивления могут компенсировать друг друга

Эти свойства широко используются при проектировании фильтров, резонансных контуров и других устройств.

Курс физики (Грабовский Р.И.)

Курс физики (Грабовский Р.И.)

Грабовский Р.И. Курс физики. Учеб. пособие для с/х ин-тов. Изд. 4-е, перераб. и доп. М., «Высш. школа», 1974. — 552 с. Учебник составлен в соответствии с программой по физике для сельскохозяйственных институтов. В нем приводится достаточное количество примеров, связанных с агробиологическими науками и сельскохозяйственным производством. Настоящее издание (3-е вышло в 1970 г.) отличается от предыдущих некоторыми (небольшими по объему) дополнениями и изменениями, способствующими улучшению содержания. Предназначается для студентов неинженерных факультетов сельскохозяйственных вузов. Многие разделы учебника могут быть использованы и студентами инженерных факультетов. Оглавление Предисловие Введение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 10. Силы упругости § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III. Работа и энергия § 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика § 35. Основные положения молекулярно-кинетической теории § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа § 43. О числе степеней свободы. Внутренняя энергия газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50. Внутреннее трение (вязкость) Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 53. Тепловое расширение твердых и жидких тел § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 65. Сжижение газов. Эффект Джоуля-Томсона § 66. Испарение и конденсация. Кипение § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором § 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции § 83. Конденсатор. Энергия электрического поля Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 91. Ток в жидкостях. Электролиз. Законы Фарадея § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов § 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 100. Действие магнитного поля на проводник с током. Определение ампера § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока § 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122. Об интерференции света, отраженного от прозрачных пленок § 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии

21(А).

Схема замещения линий электропередачи.

1) Для выполнения расчётов электрической сети составляется её схема замещения. При рассмотрении симметричных рабочих режимов схема замещения составляется на одну фазу трёхфазной сети. Общей для всей схемы является нейтраль. Схема замещения составляется с таким расчётом, чтобы отразить достаточно точно энергетические характеристики явлений, происходящих в сети.

Схема замещения воздушной линии электропередачи.

Схема замещения ЛЭП содержит следующие параметры: активное сопротивление R , реактивное сопротивление X, активную проводи­мость G, реактивную проводимость В. Указанные параметры равно­мерно распределены вдоль линии электропередачи. Для линий срав­нительно небольшой длины, в которых длина волны несоизмерима с длиной линии, обычно не учитывается распределённость параметров линии. Равно­мерно распределённые параметры линии заменяются сосредоточен­ными. Установлено, что с достаточной степенью точности можно полагать проводимости сосредоточенными в середине линии, а её сопротивления — по концам, или, наоборот, сопротивления — в середине, а проводимости — по концам линии.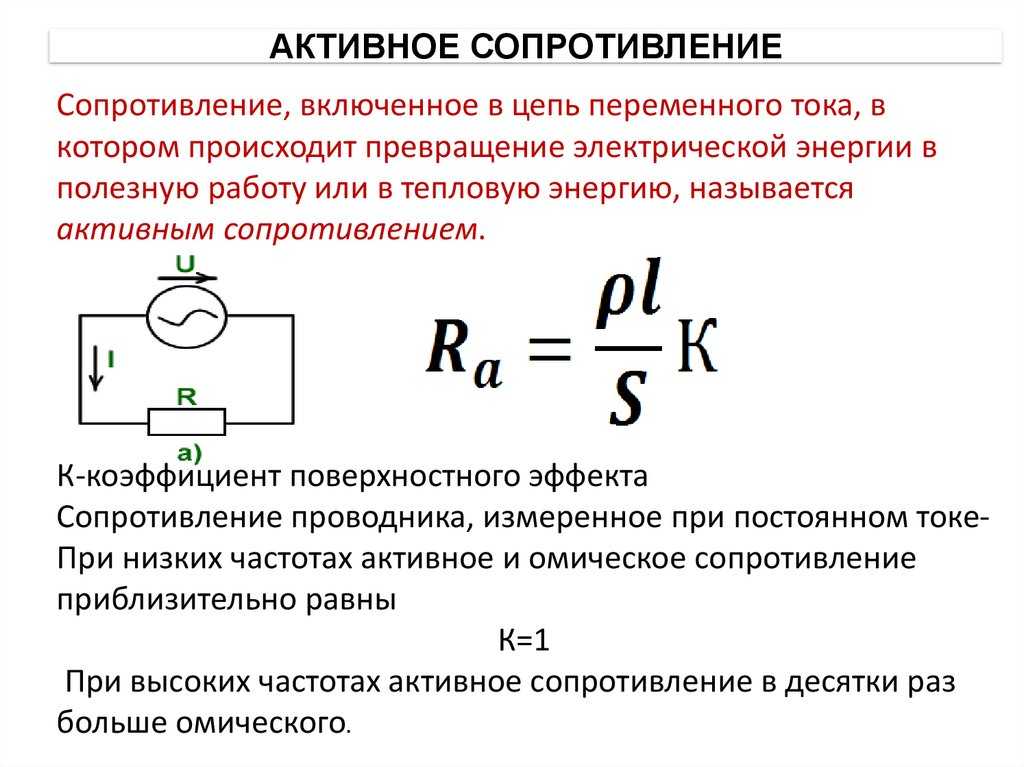

Исходя из указанных вариантов упрощения возможны две схе­мы замещения: Т — образная, П — образная (рие.8).

О пыт показал, что для расчётов удобнее использовать П — образную схему замещения. Параметры линии определяются через её погонные параметры следующим образом:

21(Б). Параметры схемы замещения воздушной линии электропередачи и их физический смысл.

2 ) Активное сопротивление линии.

Активное сопротивление проводов и кабелей определяется материалом токоведущих жил и их сечениями. Существует два способа определения R0:

1. По таблицам

2. На основании удельных сопротивлений и проводимостей материала провода по формуле

Где F – сечение провода.

Определяемое указанным выше способом погонное омическое сопротивление для голых проводов ВЛ и кабелей относится к тем­пературе +20°С. Температурные колебания могут существенно изме­нить омическое сопротивление. Если температура в реальных усло­виях отличается от + 20°С, то сопротивление определяется по формуле:

Индуктивное сопротивление.

Физическая суть индуктивного сопротивления: при протека­нии тока по проводу переменного напряжения вокруг и внутри него появляется переменное магнитное поле. Магнитные силовые линии переменного направления пересекают материал провода и в нём в силу закона электромагнитной индукции появляется ЭДС самоин­дукции. В соответствии с принципом Ленца эта ЭДС направлена так, чтобы воспрепятствовать изменению тока.

Транспозиция — в нескольких точках трассы линии фазные провода на опорах меняются местами. Каждый провод пооче­рёдно занимает все три возможных положения при примерно одинаковой протяжённости в каждом из этих положений. ЭДС, наводимые в фазных проводах, выравниваются. Индуктивные сопротивления прово­дов становятся одинаковыми.

Активная проводимость линии.

При включении линии может возникнуть ионизация слоя воздуха вблизи поверхности провода, когда напряжённость электрического поля на поверхности провода превосходит некоторое критическое значение. На поверхности провода образуются электрические разря­ды. Этот процесс называется короной и сопровождается образовани­ем светящегося нимба вокруг проводника и потрескиванием. Активная проводимость соответствует потерям энергии, связан­ным с появлением короны на проводах BЛ, а также потерям от не­совершенства изоляции (утечки). Корона зависит от трёх факторов: напряжения передачи, радиуса провода и атмосферных условий.

Ёмкостная проводимость

Любую пару проводов ВЛ или КЛ, а также каждый провод такой линии и землю можно рассматривать как конденсатор с соответствующей ёмкостью. Ёмкостная проводимость линии обусловлена наличием ёмкостных связей между проводами и землёй, определяется рабочей ёмко­стью фазы линии (ёмкостью между проводами и землёй) и равна при частоте 50 Гц для ВЛ

Наличие ёмкостной проводимости позволяет рассматривать ли­нию передачи как потребителя реактивной ёмкостной мощности. Эта мощность называется зарядной мощностью линии. Зарядная мощность, имея противоположный знак, уменьшает индуктивную составляющую на­грузки, передаваемой по линии к потребителю.

электромагнетизм — Что такое емкость вообще?

В общей физической системе мы обычно имеем от до переменных и от до переменных. У нас также есть потока и усилий переменных. См. Справочник по вибрации и ударам — Silva.

В электрической сети ток через и расход переменная и напряжение через и усилие переменная. В сетевой картине электрической цепи узлы — это идеальные провода (т. е. межсоединения), а линейные элементы цепи — ребра между этими узлами. Каждый узел имеет соответствующее напряжение, поэтому мы говорим о напряжении через элемент. Через каждое ребро протекает ток, поэтому мы говорим о текущем элементе от до .

В механической сети скорость — это через и расход переменная и сила это через и усилие переменная. В сетевой картине механической цепи узлы представляют собой куски материи, а ребра между узлами — пружины и амортизаторы между узлами. Каждый узел имеет связанную с ним скорость, поэтому, думая о разнице напряжений между двумя узлами, соединенными ребром, мы говорим о разнице скоростей через элемент. Каждый элемент имеет силу, действующую на два элемента, которые он соединяет, поэтому мы говорим о силе от до элемента (это немного натянуто, но это не так уж плохо).

В электричестве есть ток $I$, его интегральный заряд $Q$ и его производная изменения тока во времени $\dot{I}$.

В механике есть скорость $v$, ее интегральное положение $x$ и ее производное ускорение $a$.

В электричестве конденсатор связывает $Q$ и $V$: $$ C = \ frac {Q} {V} = \ frac {\ int I dt} {V} = \ frac {1} {s} \ frac {I} {V} $$ $Q$ — интеграл от переменной расхода $I$.

Аналогичным элементом для механической цепи является пружинный элемент Хука. $$ \ frac {1} {k} = \ frac {x} {F} = \ frac {\ int xdt} {F} = \ frac {1} {s} \ frac {v} {F} $$

Обычно импеданс представляет собой отношение усилия к переменной расхода. $$ Z \ sim \ frac {V} {I} \ sim \ frac {F} {v} \ sim \ frac {\ text {Effort}} {\ text {Flow}} $$ Мы видим, что если импеданс высок, большое усилие приводит лишь к небольшому потоку. Итак, мы видим, что электрическое сопротивление конденсатора равно $1/Cs$, а механическое сопротивление пружины равно $k/s$.

Что же такое вообще емкость? Емкость — это тип импеданса. В физической системе, которую вы можете параметризовать как сеть (т. е. граф), которая имеет сквозные переменные, связанные с каждым ребром, и сквозные переменные в каждом узле, вы также можете идентифицировать эти переменные как переменные усилия и потока. Таким образом, импеданс — это то, как связаны переменные усилия и потока для краевого элемента. Емкость – это особый тип импеданса, который связывает ИНТЕГРАЛ переменной расхода со значением переменной усилия. То есть в частотной области емкость представляет собой тип импеданса, который пропорционален $1/s$.

Электрическая емкость говорит нам, сколько заряда может храниться при данном напряжении. Механическая емкость говорит нам, какое смещение положения может быть выдержано при заданной силе.

Другим случаем системы, которую можно рассматривать по аналогии с цепью, является система сверхвысокого вакуума при равновесном давлении. Переменные через / усилие представляют собой давление в камере, переменные через / расхода представляют собой скорость потока между камерами. Дифференциальные отверстия накачки действуют как резисторы.

электростатика. Почему емкость определяется как отношение заряда к напряжению?

спросил 6 лет, 9 месяцев назад

Изменено 6 лет, 9 месяцев назад

Просмотрено 16 тысяч раз

$\begingroup$

Насколько я понимаю, емкость — это способность тела накапливать электрический заряд, а формула $C=\frac{Q}{V}$.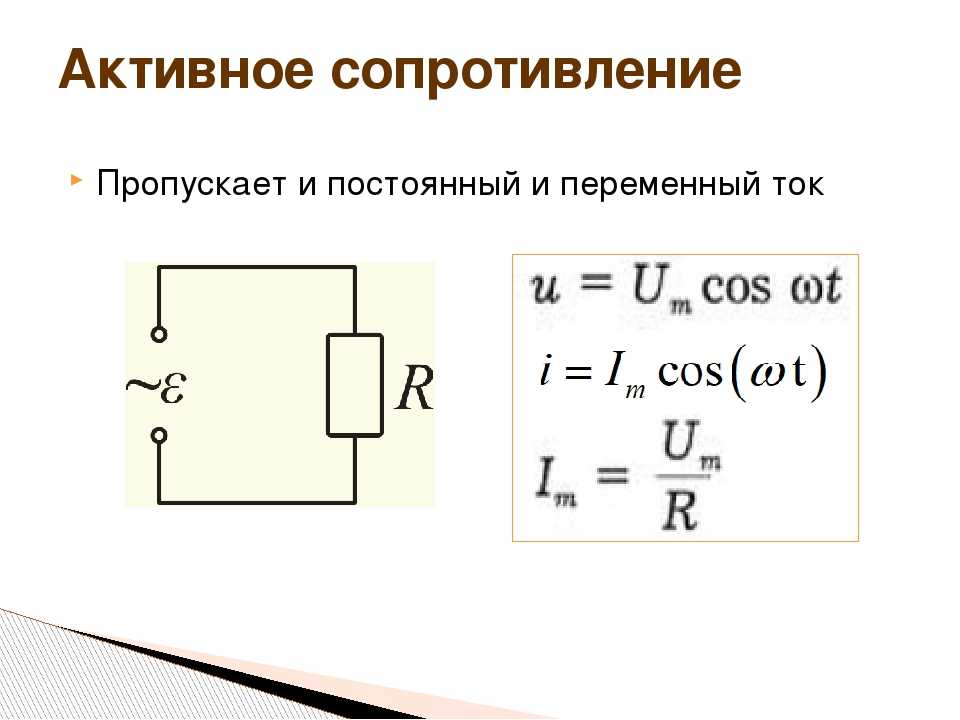 Однако я не понимаю, почему он определяется как 9 кулонов.0003 на вольт . Конечно, заряд в числителе имеет смысл, но я не понимаю, почему емкость измеряется по отношению к напряжению. Например, почему бы не измерить способность хранить что-либо объемом, который он занимает, так почему бы не взимать плату за единицу объема. Или, согласно уравнению $C=\frac{Q}{V}$, почему повышение напряжения при сохранении постоянного заряда влияет на способность тела накапливать заряд. Надеюсь, вы можете дать мне некоторую интуицию по этой теме.

• электростатика
• электричество
• электрические цепи
• заряд
• емкость

$\endgroup$

3

$\begingroup$

Вы можете использовать высокую вертикальную трубу для хранения воды (наполняйте ее снизу, вталкивая воду)

Сколько воды вы можете хранить? Это, очевидно, зависит от давления, которое вы прикладываете, чтобы протолкнуть его внутрь. Если вы нажмете сильнее, будет храниться больше воды.

Тюбик характеризуется не количеством воды, а тем, насколько легко ее хранить. Его «емкость» — это поперечное сечение на этом рисунке. Чем шире, тем больше воды вы храните при заданном усилии .

Вот это прямая аналогия. Конденсатор никогда не бывает полным (= трубка очень высокая), вы всегда можете накопить больше заряда, вам просто нужно сильнее надавить.

Действительно, есть верхний край трубки, когда вода вытекает. Вот тогда проскакивает искра и частично разряжает конденсатор. Но это другая история. 92$?
Один ответ: эксперимент показывает, что данный конденсатор будет иметь линейную зависимость накопленного заряда от приложенного напряжения.
Другой ответ: поле, создаваемое зарядом, линейно пропорционально $Q$ (закон Кулона). Таким же будет и напряжение (это интеграл поля).

… Видите ли, я могу рассматривать систему с разных точек зрения, каково причинно-следственное направление. Вы можете сказать, что высокий водяной столб создает высокое давление, или вы можете сказать, что высокое давление толкает водяной столб высоко.
С таким же успехом можно сказать, что конденсатор накапливает напряжение, а не заряд; оба правы. Энергию дает продукт, и это то, о чем вы действительно заботитесь.

$\endgroup$

4

$\begingroup$

Емкость — это «заряд сверх напряжения», а один фарад — это «кулон на вольт», потому что емкость конденсаторов (то, что определяет их «качество») — это способность сохранять максимальный заряд на пластине ($+Q$ с одной стороны, $-Q$ с другой стороны) при фиксированном напряжении.

Когда вы пытаетесь разделить заряды, вы неизбежно создаете электрические поля ($\vec E$ от положительно заряженной части к отрицательно заряженной части), и когда вы интегрируете это электрическое поле $\vec E$ по $d\vec r$, расстояние между разделенными положительными и отрицательными зарядами, вы получаете напряжение. (Электрическое поле измеряется в вольтах на метр.)

Таким образом, напряжение неизбежно индуцируется разделенными положительными и отрицательными зарядами. А для фиксированного конденсатора — с фиксированной геометрией — существует закон пропорциональности. Чем больше заряды $+Q$ и $-Q$, которые мы разделили (заметим, что электрические поля и силы пропорциональны $Q$, например, по закону Кулона), тем больше электрические поля $\vec E$ в предыдущем абзаце, и чем больше напряжение (интеграл от $\vec E$, в основном $V=\vec E\cdot \Delta \vec r$), тоже. Эта пропорциональность сводится к линейности уравнений Максвелла в электрических полях; и в источниках (и токах).

Из-за этой пропорциональности должен существовать закон $Q=CV$ для заряда как функции напряжения для фиксированной «конструкции» конденсатора, а коэффициент называется просто емкостью. Мы хотим, чтобы напряжение было фиксированным, например. потому что конденсатор является частью цепи, и его целью является создание некоторого фиксированного напряжения в цепи при определенных обстоятельствах. Чем больше емкость, тем больший заряд способен выделить конденсатор при фиксированном напряжении.

Соотношение заряда и объема точно не определено, поскольку фиксированные конденсаторы могут нести в основном любого заряда – но напряжение соответственно возрастет в соответствии с законом $V=Q/C$, который мы вывели выше. Таким образом, заряд на единицу объема просто не может быть фиксированным для данного конденсатора.

Даже если бы существовал способ записать заряд «в расчете на что-то еще» (некоторая функция размеров конденсатора), который был бы постоянным для данного конденсатора, это было бы не очень полезно, потому что назначение конденсатора влиять на напряжения и токи в цепи. Нас просто не интересует, как конденсатор выполняет свою работу. Мы хотим добавить этот компонент в соответствии с на что он способен .

Заряд в основном равен $Q=I\cdot t$, произведению тока и времени, в течение которого конденсатор может производить этот ток, а напряжение важно во всех цепях. Мы хотим знать, как связаны ток $I$ и напряжение $V$, потому что это две самые важные величины в каждой цепи. У резисторов $U=RI$, закон Ома, у конденсаторов что-то похожее, в принципе $$Q\equiv I\cdot t = C\cdot V$$ Ток, умноженный на время, в течение которого конденсатор способен его производить, равен емкости, умноженной на напряжение в начале, до того, как он разрядится. Мы хотим знать, как компоненты схемы влияют на токи и напряжения, потому что это основные величины, с которыми работают схемы. Токи проходят по проводам, а напряжения обеспечиваются, например. по батареям. Резисторы влияют на поведение цепей по своим правилам, а константы $R,C$ описывают, как это делается.

Индуктивность индукторов (катушек и т. д.) аналогична, за исключением того, что время отображается в обратном порядке: $V=L \cdot dI/dt$. Напряжение катушки индуктивности пропорционально производной тока по времени (скорость, с которой ток изменяется во времени), и этот коэффициент известен как индуктивность. Таким образом, компоненты цепей имеют некоторое влияние на напряжения и токи — единственные основные «внутренне электромагнитные величины», которые имеют отношение к току, — и цепи также работают во времени, что означает, что мы можем захотеть знать, как токи или напряжения изменяются или как эти изменения соотносятся с другими вещами. Схема выполняет определенную работу, и конденсаторы и катушки индуктивности (и особенно транзисторы!) могут быть уменьшены, в то время как функциональность схемы остается прежней. Вот почему нам нужно знать соответствующие или обязательные параметры, чтобы «сохранить функциональность прежней».

$\endgroup$

$\begingroup$

Мы используем $C=Q/V$, потому что это полезно для измерения. Часто легко забыть, но многие из используемых нами уравнений выбраны потому, что они работают, а другие уравнения не работают. Никогда не недооценивайте эту часть реальности.

Мы не используем «плата за единицу объема», потому что это число непостоянно. Вы можете зарядить конденсатор, не изменяя его объема. Заряд, деленный на напряжение, остается постоянным.

Я думаю, что самый важный вопрос, который вы задали:

Или, согласно уравнению $C=\frac{Q}{V}$, почему повышение напряжения при сохранении постоянного заряда влияет на способность тела накапливать заряд.

Мне нравится этот вопрос, потому что он немного задом наперед, предполагая, что вы думаете об этом по-другому. Мне нравится, когда люди думают о чем-то задом наперед, потому что это показывает, что они действительно думают и готовы попытаться понять, что происходит!

Хитрость заключается в том, что вы обнаружите, что не можете увеличить напряжение на конденсаторе, сохраняя при этом постоянный заряд, без каких-либо физических модификаций самого конденсатора. Реальность просто не позволит вам. Если вы попытаетесь увеличить напряжение, вы обнаружите, что в конденсатор будет поступать ровно столько заряда, чтобы сбалансировать напряжение.

Что еще интереснее, рассмотрим случай, когда вы мгновенно меняете напряжение, скажем, с 1 В на 10 В. Теоретически это должно «увеличить напряжение без увеличения заряда», потому что не было времени для протекания тока. Вы можете нарисовать это в симуляторе схемы, таком как PSPICE, и изменить напряжение при t = 0. Похоже надо менять емкость.

В реальности мы видим другой эффект. Мы видим, что, несмотря на то, что мы увеличили напряжение в системе, напряжение на конденсаторе фактически останется прежним! Это имеет смысл из уравнения, потому что мы знаем, что заряд и емкость не изменились, поэтому напряжение не может измениться. Но теперь похоже, что у нас разорвана цепь: почему-то у нас на входе 10В, а на конденсаторе всего 1В! Все знают, что это не сходится.

На самом деле мы обнаруживаем, что в каждом устройстве, которое мы используем, есть «паразитические сопротивления». Батарея имеет сопротивление, конденсатор имеет сопротивление, даже те провода, которыми вы их соединяете, имеют сопротивление. Итак, ваша реальная схема — это не просто источник напряжения и конденсатор, это источник напряжения, конденсатор и набор небольших резисторов.

В 99% случаев мы можем игнорировать эти резисторы, потому что они не сильно меняют схему. Однако в этой слегка патологической ситуации они на самом деле имеют большое значение. Именно они «впитывают» это дополнительное напряжение. Вы получите 1 В на конденсаторе и 9 В на сумме всех этих резисторов. Теперь начинается самое интересное. поскольку ток через резистор использует $V=IR$, мы можем рассчитать ток, проходящий через систему. Чем более идеальными были провода и батареи, тем больший ток нам придется использовать для учета 9V. Этот ток является потоком заряда. Куда оно течет? Конденсатор. Вы сразу же начнете видеть, как заряд на конденсаторе растет, поскольку через него протекает ток, пока, в конце концов, на конденсаторе не будет достаточно заряда, чтобы создать на нем потенциал 10 В. В этот момент на резисторах больше нет напряжения, поэтому ток падает до 0, и цепь остается постоянной.

(На самом деле там есть некоторые экспоненциальные члены, и технически это никогда не достигает точно 10 В, но в реалистичных сценариях мы склонны подбираться достаточно близко, чтобы отмахнуться от этого набора дополнительных сложностей)

$\endgroup$

1

$\begingroup$

Конденсатор используется для хранения энергии в виде электрических полей. Это электрическое поле создается зарядами на пластинах конденсатора.

Итак, вы накапливаете заряд на конденсаторах.

Пусть кто-нибудь спросит вас, сколько заряда вы можете хранить в своем конденсаторе. Что бы вы ответили?

Очевидно, вы отвечаете: «Я могу хранить 1 мКл или 100 мКл, в зависимости от разности потенциалов, которую вы прикладываете к конденсатору. »

Итак, вам нужен стандарт, чтобы определить, сколько заряда вы можете хранить при некоторых универсальных условиях.

Стандарт — 1 В. Следовательно, заряд, хранящийся в конденсаторе при стандартном напряжении 1 В, называется емкостью конденсатора.

Почему стандартом был 1В, потому что расчеты стали проще. 92}$

Итак, для объема тоже есть зависимость. Но связь не слишком прямая. Если вы сохраняете d постоянным и увеличиваете заряд V, вы можете сохранить увеличение.

Вместо этого, если вы оставите A постоянным, а затем измените V, оно уменьшится.

Заряд, хранящийся на единицу объема, на самом деле ему могут быть присвоены другие имена, такие как плотность заряда (или имя Смит :-), как хотите).

Этот термин может быть полезен для расчета размера конденсатора, необходимого для любого устройства. Но более прямое использование — разность потенциалов на конденсаторе.

Изменить V для хранения заряда намного проще, чем изменить объем конденсаторов.

Или, согласно уравнению $C=\frac{Q}{V}$, почему повышение напряжения при сохранении постоянного заряда влияет на способность тела накапливать заряд.

Вы накапливаете заряд в конденсаторе. Если вы применяете больше PD, вы можете хранить больше заряда (мне не нужно это объяснять).

Если вы можете хранить больше заряда и, следовательно, больше энергии для одного и того же частичного разряда, разве это не сделает вас счастливым? Таким образом, емкость накапливает заряд, и если вы можете хранить больше заряда для того же PD в 1 В, вы говорите, что емкость больше.

$\endgroup$

1

$\begingroup$

Я так понимаю, что емкость это способность тела накапливать электрический заряд и формула $C = {Q \over V}$

Возможно, вам просто нужно подумать о емкости как таковой. «Емкость» звучит как «емкость», что приводит к интуитивно понятной ловушке вроде этой:

Если у меня есть корзина вместимостью 2 яблока, то корзина большей вместимости может вместить более 2 яблок. Итак, если у меня есть конденсатор с большей емкостью, он может удерживать больше электрического заряда, верно?

Я вижу, что это недоразумение довольно часто возникает в контексте электротехники. Возьмем, к примеру, этот вопрос. Несмотря на то, что вопрос не ставится прямо и не озвучивается, то, как он написан, предполагает, что автор подозревает, что если он сможет найти «достаточно большой» конденсатор («большой» означает «большой емкости»), то этот достаточно большой конденсатор может иметь достаточно энергии для своих нужд.

Но дело в том, что идеальный конденсатор никогда не бывает «полным», вне зависимости от его емкости. Вы можете вложить в него столько заряда или энергии, сколько захотите. Точно так же, как вы можете растянуть «идеальную» пружину настолько, насколько вам захочется. Таким образом, любое понимание «емкости», похожее на «емкость корзины для яблок», интуитивно неверно и никогда не будет иметь смысла.

Конечно, настоящие пружины в какой-то момент деформируются, а настоящие конденсаторы в какой-то момент выходят из строя. Но мы обсуждаем идеальный случай. И хотя я использую слово «конденсатор» как электрическое устройство с двумя пластинами, то же самое относится к одному объекту и его собственной емкости. В идеальном случае нет предела тому, насколько заряженным может быть один объект.

Емкость просто показывает, насколько увеличится напряжение на единицу заряда. Вот почему фарад равен кулону на вольт. Один фарад означает, что на каждый кулон приходится изменение на один вольт.

Таким образом, вы можете думать о емкости как об аналоге силовой постоянной пружины. В то время как силовая постоянная говорит вам, какая сила требуется для растяжения пружины, емкость говорит вам, какое напряжение требуется для зарядки конденсатора. Меньшая емкость похожа на более жесткую пружину.

С небольшой перестановкой закон Гука и формула для емкости очень похожи:

$$ F = k X \\ Q = CV $$

Для более высокой силовой постоянной потребуется больше силы для заданного изменения удлинения. Для более высокой емкости потребуется больше заряда для данного изменения электрического потенциала.

$\endgroup$

$\begingroup$

почему повышение напряжения при сохранении постоянного заряда имеет какое-либо значение? влияние на способность тела накапливать заряд.

(1) Конденсаторы хранят не заряд, а электрическую энергию. Для конденсатора подразумевается, что одна пластина имеет заряд $Q$, а другая пластина имеет заряд $-Q$, поэтому суммарный электрический заряд отсутствует.

(2) Если увеличить напряжение на конденсаторе, заряд $Q$ должен увеличить , если только вы физически не изменяете расположение двух пластин определенным образом.

Например, если расстояние между двумя пластинами плоского конденсатора увеличивается (что уменьшает емкость) по мере увеличения напряжения (например, за счет источника переменного напряжения), $Q$ может Остаются неизменными.

Но имейте в виду, что не увеличение напряжения изменяет емкость, а физическое изменение расстояния между пластинами.

Теперь — это устройств, которые демонстрируют емкость, зависящую от напряжения, например варакторные диоды, но это выходит за рамки этого ответа.

$\endgroup$

$\begingroup$

Например, почему бы не измерить способность что-либо хранить с помощью объем, который он занимает, так почему бы не взимать плату за единицу объема.

Нет ничего плохого в том, что вы определили параметр, который является «платой за единицу объема», но после его определения что вы собираетесь с ним делать? 9{-3}$.

Я спрашиваю: «Что произойдет с зарядом на единицу объема, если удвоить разность потенциалов на клеммах?»
Ваш параметр не поможет вам получить ответ, и вам нужно будет использовать идею о том, что для вашего конденсатора заряд пропорционален разности потенциалов.

Спрашиваю «Что будет, если вдвое уменьшить объем конденсатора?»
Без какой-либо дополнительной информации вы не сможете ответить на вопрос, а для ответа на вопрос вам, вероятно, будет легче вернуться к определению емкости обычным способом.

«Заряд на единицу объема» может быть полезен в некоторых приложениях, но для подавляющего большинства случаев гораздо полезнее $Q=CV$ как мера емкости накопления заряда (энергии).

$\endgroup$

$\begingroup$

Читая ваши высказывания, у меня складывается впечатление, что вам непонятна разница между ёмкостью и ёмкостью. Емкость конденсатора равна , определяемой его «физической» конструкцией (длина, ширина, площадь, объем, материал и т. д. C = кА/д). Однако емкость является мерой того, насколько сложно/легко конденсатору хранить заряд (C = Q/V, аналогично R = E/I). Хотя они связаны, это не одно и то же.