Что такое активное сопротивление в цепи переменного тока. Как рассчитать активное сопротивление. Какие характеристики имеет активное сопротивление в переменном токе. Чем отличается от реактивного сопротивления.
Что такое активное сопротивление в цепи переменного тока
Активное сопротивление в цепи переменного тока — это сопротивление, на котором происходит необратимое преобразование электрической энергии в другие виды энергии, например, в тепловую. Основные характеристики активного сопротивления:
- Вызывает падение напряжения на участке цепи
- Приводит к безвозвратным потерям электрической энергии
- Не зависит от частоты переменного тока
- Напряжение и ток на активном сопротивлении совпадают по фазе
Активным сопротивлением обладают проводники, нагревательные элементы, лампы накаливания и другие устройства, преобразующие электроэнергию в тепло.
Формула для расчета активного сопротивления
Активное сопротивление в цепи переменного тока рассчитывается по закону Ома:
R = U / I
где:
- R — активное сопротивление, Ом
- U — напряжение на участке цепи, В
- I — сила тока, А
При этом используются действующие (эффективные) значения напряжения и тока.
Характеристики активного сопротивления в переменном токе
Основные характеристики активного сопротивления в цепи переменного тока:
- Не зависит от частоты переменного тока
- Напряжение и ток совпадают по фазе
- Активная мощность P = I^2 * R
- Коэффициент мощности cosφ = 1
- Векторная диаграмма напряжения и тока — прямая линия
Активное сопротивление вызывает необратимые потери энергии в виде тепла. На нем происходит преобразование электрической энергии в другие виды энергии.
Отличие активного сопротивления от реактивного
Основные отличия активного сопротивления от реактивного в цепи переменного тока:
| Характеристика | Активное сопротивление | Реактивное сопротивление |
|---|---|---|
| Зависимость от частоты | Не зависит | Зависит |
| Сдвиг фаз напряжения и тока | 0° | ±90° |
| Потери энергии | Есть | Нет |
| Преобразование энергии | Необратимое | Обратимое |
Таким образом, активное сопротивление вызывает потери энергии, а реактивное — только её перераспределение между магнитным и электрическим полями.
Как измерить активное сопротивление в цепи переменного тока
Существует несколько способов измерения активного сопротивления в цепи переменного тока:
- С помощью амперметра и вольтметра:
- Подключить амперметр последовательно с нагрузкой
- Подключить вольтметр параллельно нагрузке
- Измерить ток I и напряжение U
- Рассчитать R = U / I
- С помощью омметра:
- Отключить исследуемый участок от цепи
- Подключить омметр к выводам участка
- Измерить сопротивление
- С помощью измерителя RLC:
- Подключить прибор к исследуемому участку
- Выбрать режим измерения активного сопротивления
- Считать показания
При измерениях в цепи переменного тока важно использовать приборы, рассчитанные на переменный ток нужной частоты.
Активное сопротивление в различных элементах цепи
Различные элементы электрической цепи обладают разным активным сопротивлением:
- Проводники — небольшое активное сопротивление, зависит от материала и сечения
- Резисторы — специально созданы для получения заданного активного сопротивления
- Лампы накаливания — активное сопротивление зависит от температуры нити
- Нагревательные элементы — большое активное сопротивление для выделения тепла
- Катушки индуктивности — небольшое активное сопротивление обмотки
- Конденсаторы — очень малое активное сопротивление, обычно им пренебрегают
При расчетах цепей переменного тока важно учитывать активное сопротивление всех элементов.
Влияние активного сопротивления на работу цепи переменного тока
Активное сопротивление оказывает следующее влияние на работу цепи переменного тока:
- Вызывает падение напряжения на участках цепи
- Приводит к потерям электроэнергии в виде тепла
- Уменьшает амплитуду тока в цепи
- Вызывает нагрев проводников и элементов
- Снижает КПД электрических устройств
- Изменяет фазовые соотношения между током и напряжением
Для снижения негативного влияния активного сопротивления применяют провода большего сечения, используют материалы с меньшим удельным сопротивлением, оптимизируют конструкцию устройств.
Зависимость активного сопротивления от параметров проводника
Активное сопротивление проводника зависит от следующих параметров:
- Удельное сопротивление материала ρ
- Длина проводника l
- Площадь поперечного сечения S
- Температура T
Зависимость выражается формулой:
R = ρ * l / S * (1 + α * ΔT)
где α — температурный коэффициент сопротивления, ΔT — изменение температуры.
Таким образом, для уменьшения активного сопротивления нужно выбирать материал с меньшим ρ, уменьшать длину и увеличивать сечение проводника.
Применение активного сопротивления в электротехнике
Активное сопротивление находит широкое применение в электротехнике:- Нагревательные элементы (электроплиты, обогреватели)
- Лампы накаливания
- Резисторы для ограничения тока
- Шунты для измерительных приборов
- Реостаты для регулировки тока
- Балластные сопротивления
- Токоограничивающие резисторы
Активное сопротивление используется везде, где нужно преобразовать электрическую энергию в тепловую или ограничить ток в цепи.
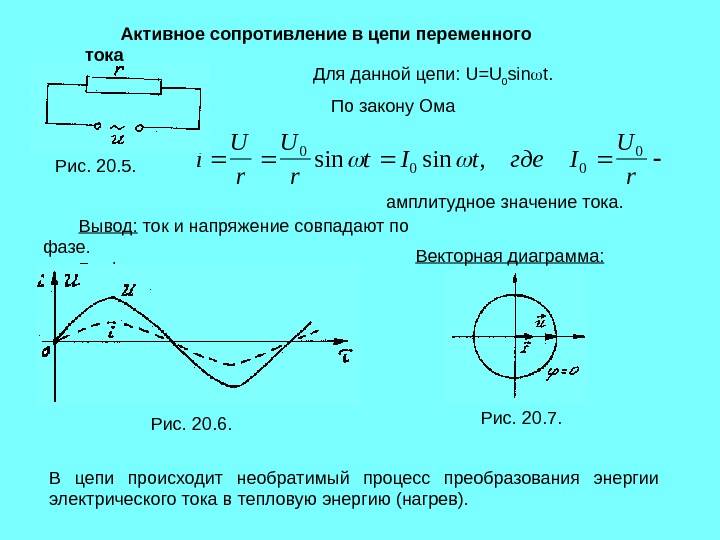
Активное сопротивление в цепи переменного тока
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
u = Umsinωt
Найдём ток и мощность в цепи.
Ток в цепи переменного тока с активным сопротивлением.
По закону Ома найдем выражение для мгновенного тока:
где Im = Um/R — амплитуда тока
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).
Действующий ток найдем, разделив амплитуду на √ 2:
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём 
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I2R = U2R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
Активное сопротивление в цепи переменного тока
На векторных диаграммах можно показать, что ток и напряжение совпадают по фазе (рис. 52,а) или э. д.с. сдвинуты по фазе на некоторый угол (рис. 52,6). Условно принято считать, что векторы перемещаются в направлении против движения часовой стрелки.
Если векторы имеют различную длину, следовательно, их действующие значения разные (см. рис. 52, б).
§ 52. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
Рассмотрим цепь переменного тока (рис. 53), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в Цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в Цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (=0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
Пример. К цепи переменного тока с активным сопротивлением r=55 ом подключен генератор, максимальное значение напряжения которого Um=310,2 в.
Определить:
показание вольтметра, подключенного к зажимам генератора; показание амперметра, включенного в цепь; среднее значение мощности, потребляемой сопротивлением.
Решение. Известно, что электроизмерительные приборы, включенные в цепь переменного тока, измеряют действующие значения. Поэтому показание вольтметра, измеряющего напряжение,
Показание амперметра, измеряющего действующее значение тока,
Среднее значение активной мощности, потребляемой сопротивлением, Р=220х4 = 880 вт или Р=I2r=42×55=16×55=880 вт.
§ 53. ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Прохождение электрического тока по проводнику или катушки сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока (рис. 54,а), в которую включена катушка индуктивности, имеющая небольшое количество витком проволоки сравнительно большого сечения, активное сопротивления которой можно считать практически равным нулю.
Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции
(55)
где L — индуктивность катушки,
в омах. Таким образом, индуктивное сопротивление катушки ХL зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ) и от индуктивности катушки L:
где XL, — индуктивное сопротивление, ом,
ώ — угловая частота переменного тока, рад/сек,
L — индуктивность катушки, гн.
Так как угловая частота переменного тока , то индуктивное сопротивление
где, f—-частота переменного тока, гц.
Пример. Катушка, обладающая индуктивностью L=0,5 гн, присоединена к источнику переменного тока, частота которого f=50 гц. Определить:
1) индуктивное сопротивление катушки при частоте f=50 гц;
2) индуктивное сопротивление этой катушки переменному току, частота которого f=800 гц.
Решение. Индуктивное сопротивление переменному току при f=50 гц
При частоте тока f=800 гц
Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока, протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает. Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки, э. д. с. самоиндукции не возникает, индуктивное сопротивлений катушки ХL равно нулю. Катушка индуктивности для постоянного тока представляет собой лишь сопротивление
Выясним, как изменяется э. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток.
Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.
На графике (рис. 54, в) переменный ток показан в виде синусоиды (сплошная линия). В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции ес, согласно правилу Ленца, препятствует увеличению тока в цепи. Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д.с. самоиндукции изменяет свое направление и увеличивается препятствуя убыванию силы тока. В третью четверть периода том изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с. самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы тока в цепи.
Сопротивление в цепи переменного тока принимает разные формы, что связано с тем, что в ней существует как явление необратимой трансформации энергетического ресурса, так и перетекание его от одного компонента к другому. Чтобы произвести правильный выбор радиодеталей и определить, к каким классам они должны принадлежать и какими характеристиками обладать, электротехник должен знать, как проявляет себя такая физическая величина, как сопротивление.
Резисторы – элементы, обладающие значительным активным противодействием
Что такое активное сопротивление
Активное нагрузочное сопротивление – это та его форма, которая наблюдается при безвозвратной трансформации электрической энергии в другие ее виды, например, тепловую (как в электроплите), световую или механического движения. На элементе, имеющем активное сопротивление, падает цепное напряжение, притом, чем больше падение, тем больше значение резистивности. Кроме того, когда по такому компоненту идет ток, происходят безвозвратные потери мощности. В качестве иллюстрации можно упомянуть выделение тепла на резисторе. Таким противодействием обладают также проводники и конфигурации из них, в том числе кабели, которыми компоненты цепи соединяют друг с другом, и обмотки электрических моторов.
Важно! У той детали, которая имеет только активную компоненту резистивности, фазы тока и напряжения будут совпадать.
Определение значения осуществляется посредством формулы:
R=U/I.
Напряжение на детали делится на проходящий через нее электроток. На результат влияют различные характеристики провода: материал, конфигурация, геометрические параметры, температура.
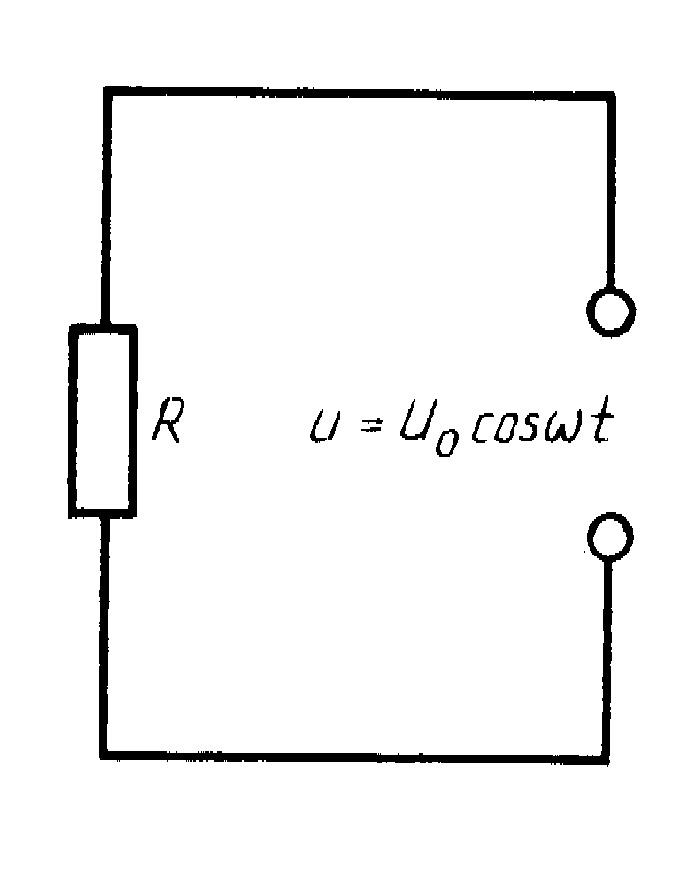
Цепь с резисторным компонентом
Реактивное сопротивление
Эта разновидность описывает не привязанное к расходу электроэнергии соотношение между напряженностью и током на индуктивных элементах или деталях, обладающих емкостью. Существует это явление только в цепях переменного тока. Реактивная компонента может иметь и отрицательное значение: это наблюдается в случае, если так обгоняет напряжение. В катушках индуктивности наличие такого явления обусловлено электродвижущей силой самоиндукции, возвращающей энергию магнитного поля в электроцепь. Присутствует реактивная компонента и у конденсатора. При накоплении заряда он потребляет энергию извне, потом возвращает ее в электроцепь. В схемах элементы с наличием такого эффекта могут соединяться как исключительно друг с другом, так и с резисторами.
Важно! У активной компоненты величина падения напряжения во всех случаях имеет противоположное направление. У реактивной – она может быть направлена как в одну сторону с током, так и в противоположную. В последнем случае возникает препятствие изменению электротока.
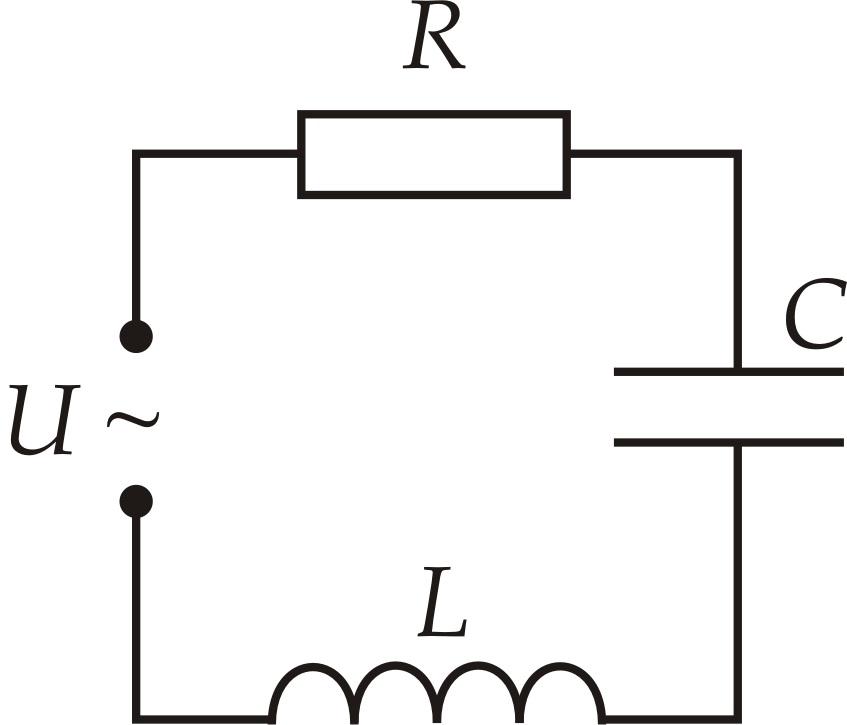
Цепь включает детали с реактивной компонентой
Активное и реактивное сопротивление
Реактивная составляющая встречается в двух формах: емкостной (она присуща конденсаторным устройством) и индуктивной (свойственна трансформаторам, катушкам и обмоткам). Для определения отношения между напряжением и токовой силой требуется знать показатели всех видов оказываемого проводником сопротивления.
Когда конденсатор подсоединен в электроцепь, за временной период до смены полярности он успевает набрать только некоторый процент заряда. Частота тока прямо пропорциональна величине заряда, набираемой элементом. Реактивный эффект на конденсаторном элементе наблюдается из-за того, что у него есть емкость. Когда частота возрастает, емкостное противодействие падает. Благодаря этому эффекту, данные детали хорошо подходят для использования в роли шунта с меняющейся величиной.
У катушки при увеличении токовой частоты растет и индуктивное противодействие. Помимо частоты, на значение также сильно влияет обмоточная индуктивность.
Важно! Бывает, что результирующая реактивная составляющая в цепи с несколькими обмотками и конденсаторами оказывается равной нулю. В таком случае фазы напряжения и электротока совпадают. Если между ними есть хоть какая-то разница фаз в ту или другую сторону, реактивная компонента будет отличной от нуля.
В реальности детали электрической цепи имеют как активную, так и обе реактивных составляющих. Но в ряде случаев одной или двумя из них принято пренебрегать из-за очень малых показателей, незначительно влияющих на общую ситуацию в сети. К примеру, обычно принимают, что конденсатор (если пренебречь энергетическими потерями) имеет исключительно емкостное противодействие. У лампочек накаливания, в свою очередь, принимается во внимание только активная компонента. У обмоточных элементов выделяются активная и индуктивная составляющие.
Треугольник сопротивлений
Для электроцепи, по которой проходит переменный ток, общий показатель резистивности принято определять как корень из суммы квадратов активного и реактивного показателей. Графически это проще всего представить в форме прямоугольного треугольника. Катеты такой фигуры являют собой резистивность активной нагрузки и суммарный реактивный показатель цепи, а гипотенуза – общее значение цепного противодействия.
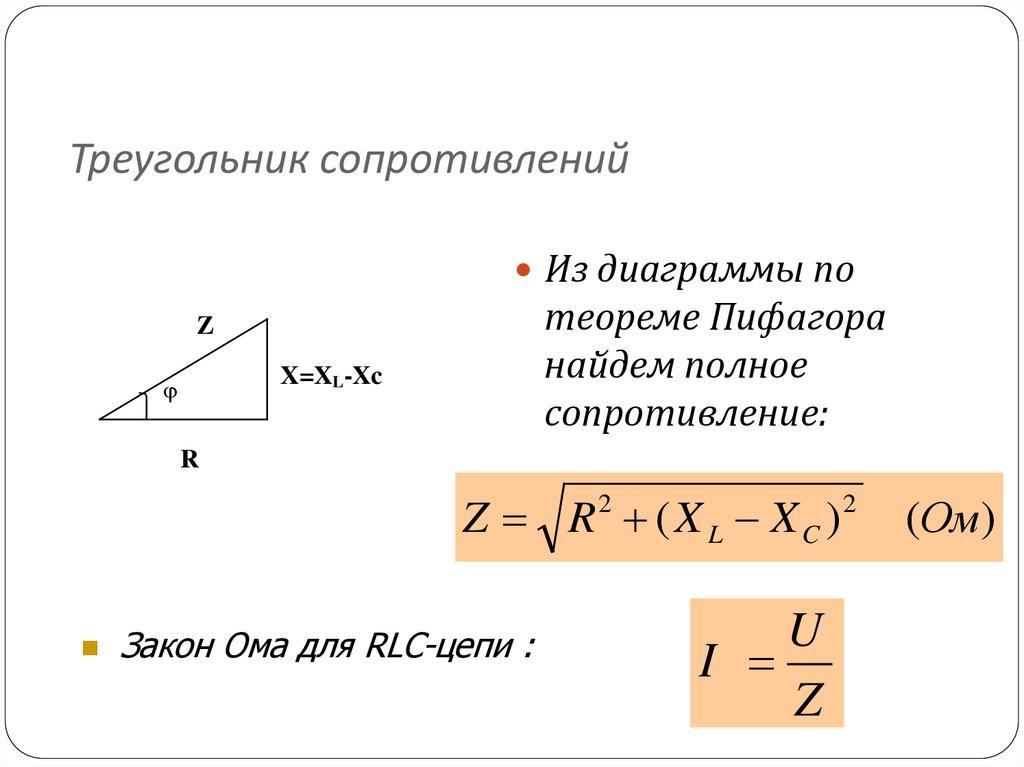
Треугольник сопротивлений
Характеристики потерь
При подсчете мощностного значения на компоненте цепи всегда принимаются во внимание потери, возникающие в сопротивлениях. Мощностные потери, характерные для активных сопротивлений, связаны с характеристиками проводниковых компонентов и качествами изоляционного покрытия. Реактивные потери в сети связаны с индуктивными противодействиями проводов, а также особенностями задействованных емкостных и катушечных элементов.
Чтобы суметь правильно рассчитать требуемые характеристики элементов сети, нужно знать, на какие составляющие делится сопротивление. Активная компонента связана с необратимым переходом энергии из одной формы в другую.
Видео
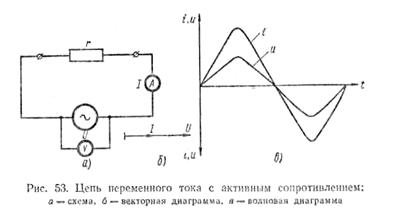Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением. К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства. Рассмотрим цепь переменного тока , в которую включено активное сопротивление. в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе. Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения U. Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (=0), откладываем вектор тока I по направлению вектора напряжения. Сила тока в такой цепи определяется по закону Ома: I=U/R.
Билет 20. Вопрос 1. Переменный ток: понятие, получение, характеристики, единицы измерения.
Переме́нный ток, электрический ток, который периодически изменяется по модулю и направлению. Для передачи и распределения электрической энергии преимущественно используется Переменный ток благодаря простоте трансформации его напряжения почти без потерь мощности .Генераторы и двигатели Переменный токпо сравнению с машинами постоянного тока при равной мощности меньше по габаритам, проще по устройству, надёжнее и дешевле. Переменный ток может быть выпрямлен, например полупроводниковыми выпрямителями, а затем с помощью полупроводниковых инверторов преобразован вновь в Переменный ток другой, регулируемой частоты; это создаёт возможность использовать простые и дешёвые безколлекторные двигатели . Характеристики переменного тока.Средняя мощность переменного тока за период T равна:Pср. = Im*Umcos()/2, где — сдвиг фаз между током и напряжением, Um и Im — максимальные (амплитудные) значения напряжения и силы тока.В цепи переменного тока с активной нагрузкой колебания силы тока совпадают по фазе с колебаниями напряжения. Если U = Umsin(wt), то I = Imsin(wt) и cos() =1.Действующие (эффективные) значения силы тока и напряжения рассчитываются по формулам:Iд = Im/корень 2,Uд =Um/корень2 .
Билет 21. Вопрос 1.. Режимы работы трансформатора: режим холостого хода, рабочий режим, режим короткого замыкания. КПД трансформатора. Режимом холостого хода трансформатора называют режим работы при питании одной из обмоток трансформатора от источника с переменным напряжением и при разомкнутых цепях других обмоток. Такой режим работы может быть у реального трансформатоpa, когда он подключен к сети, а нагрузка, питаемая от его вторичной обмотки, еще не включена. Рабочий режим — это работа трансформатора при подключенных потребителях или под нагрузкой (под нагрузкой понимается ток вторичной цепи — чем он больше, тем больше нагрузка). К трансформатору подключаются различного рода потребители: электрические двигатели, освещение и т. п. Режим короткого замыкания, возникающий случайно в процессе эксплуатации при номинальном первичном напряжении, является аварийным процессом, сопровождающимся весьма большими токами в обмотках. Многократное повышение токов по сравнению с номинальными (в 10-20 раз) может привести к повреждению изоляции обмоток в следствии нагрева и к разрушению обмоток механическими силами, возникающими при этом режиме между обмотками. Коэффициентом полезного действия трансформатора называется отношение активной мощности, передаваемой нагрузке, к активной мощности, подводимой к трансформатору. КПД трансформатора имеет высокое значение. У силовых трансформаторов небольшой мощности он составляет примерно 0,95, а у трансформаторов мощностью в несколько десятков тысяч киловольт-ампер доходит до 0,995. Определение КПД по формуле с использованием непосредственно измеренных мощностей P1 и P2 даёт большую погрешность. Удобнее эту формулу представить в другом виде:КПД=P2/P1 +сумарное дельта Р.
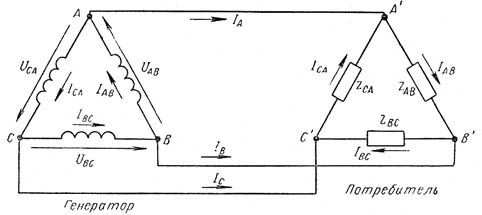Билет 22. Вопрос 1.Соединение фаз генератора и потребителей треугольником: симметричная и несимметричная нагрузка, векторная диаграмма.
АВС начало фазы, хуz – конец фазы, АА’ –линейный провод. При соединении треугольником начало фазы соединяется с концом предидущей фазы и смещается на 120 градусов. при симметричной нагрузке, соединенной треугольником, линейный ток в √3 раз больше фазного тока. Iл=корень 3 >Iф. Uл=Uф. В трехфазных цепях различают симметричную (сопротивление в каждой фазе нагрузке одинаковое) несимметричную (сопротивление нагрузки хотя бы в одной фазе отличается) нагрузок. При симметричной нагрузки достаточно иследовать одну фазу и все умножить на 3. При несимметричной необходимо иследовать каждую фазу а потом сложить. При симметричной нагрузке фазные напряжения отдельных фаз равны между собой. При несимметричной нагрузке трехфазной системы симметрия токов и напряжений нарушается. Однако в четырехпроводных цепях часто пренебрегают незначительной несимметрией фазных напряжений. В этих случаях между линейными и фазными напряжениями существует зависимость: Uл=sqrtUф.
P=корень3 Uл Iлcosфи =3Uф Iф COSфи. ВТ; Q=sqrt3 Uл Iл SINфи = 3Uф Iф SINфи. ВАР
S=sqrt3 Uл Iл =3Uф Iф ВА
Полное сопротивление цепи переменного тока
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
Или
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
А также цифровой осциллограф:
С помощью него мы будем смотреть напряжение и силу тока .
Что?
Силу тока?
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.
Кто не помнит – напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 😉
Осциллограмма силы тока на активном сопротивлении
В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Поэтому, наша схема примет вот такой вид:
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма – это напряжение с генератора Uген , а желтая осциллограмма – это напряжение с шунта Uш , в нашем случае – сила тока. Смотрим, что у нас получилось:
Частота 28 Герц:
Частота 285 Герц:
Частота 30 Килогерц:
Как вы видите, с ростом частоты сила тока у нас осталась такой же.
Давайте побалуемся формой сигнала:
Как мы видим, сила тока полностью повторяет форму сигнала напряжения.
Итак, какие можно сделать выводы?
1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.
2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.
3) С ростом частоты ничего не меняется (если только на очень высоких частотах).
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.
Смотрим осциллограммы:
Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.
Вспоминаем алгебру старшие классы. Итак, полный период T – это 2П
Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:
Где-то примерно П/2 или 90 градусов.
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
Красная осциллограмма – это напряжение, которое мы подаем на конденсатор, а желтая – это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
50 Герц.
100 Герц
200 Герц
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Реактивное сопротивление конденсатора
Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:
где
Хс – реактивное сопротивление конденсатора, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
С – емкость конденсатора, Фарад
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка – это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
34 Килогерца
17 Килогерц
10 Килогерц
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Реактивное сопротивление катушки индуктивности
Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле
где
ХL – реактивное сопротивление катушки, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
L – индуктивность, Генри
Мощность в цепи с реактивными радиоэлементами
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность – это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком “плюс”, а напряжение со знаком “минус”. В итоге плюс на минус дает минус. Получается мощность со знаком “минус”. А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем “плющить” пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно – это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо – это уже другая история.
В третий промежуток времени t3 и ток и напряжение у нас со знаком “минус”. Минус на минус – это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL – это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L – собственно сама индуктивность катушки
С – межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r – сопротивление диэлектрика и корпуса между обкладками
С – собственно сама емкость конденсатора
ESR – эквивалентное последовательное сопротивление
ESI (ESL) – эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Резюме
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.
В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.
Сопротивление катушки вычисляется по формуле
Сопротивление конденсатора вычисляется по формуле:
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.
Сопротивлением в электротехнике называют такую величину, которая характеризует противодействие отдельность части электрической сети или ее элементов электрическому току. Это основано на том, что сопротивление изменяет электрическую энергию и конвертирует ее в другие типы. Например, в сетях с переменных электротоком происходят необратимые изменения энергии и ее передача между участниками этой электроцепи.
Сопротивление как физическую величину трудно переоценить, так как она является одной из ключевых характеристик электричества в сети и прямо или пропорционально определяет силу тока и напряжение. Этот материал познакомит с такими понятиями как: активное сопротивление и реактивное сопротивление в цепи переменного тока, как проявляется зависимость активного сопротивления от частоты.
Векторное изображение полного импедансаКакое сопротивление называется реактивным, какое активным
Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.
Типы рассматриваемой величины и формулы ее расчетаРеактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии. Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.
Течение переменного электротока не зависит от типа сопротивляемости элементов и всей сетиКакие отличия
Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.
Индуктивная величина и ее формулыВажно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть.
Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.
Комплексная сопротивляемость отдельного элетроэлемента сети RВ активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.
Активная сопротивляемость в цепи переменного синусоидального токаОт чего зависит активное сопротивление
Активное электросопротивление зависит от сечения проводника. Это значит, что полезным сечением при электротоке с высокой частотой будет только тонкий наружный слой проводника. Из этого исходит также то, что активностное электросопротивление только возрастает с увеличением частоты электротока переменного типа.
Для того чтобы уменьшить поверхностный эффект проводника, по которому течет электроток высокой частоты, его изготавливают трубчатым и покрывают напылением металла, хорошо проводящего электрический ток, например, серебром.
Схема косвенного метода амперметра, вольтметра и ваттметраВ чем измеряется реактивное сопротивление
Само по себе, явление реактанса характерно только для цепей с электрическим током переменного типа. Обозначается оно латинской буквой «X» и измеряется в Омах. В отличие от активностного варианта, реактанс может иметь как положительное, так и отрицательное значение. Знак «+» или «-» соответствует знаку, по которому сдвигается фаза электротока и напряжения. Знак положительный, когда ток отстает от напряжения и отрицателен, когда кот опережает напряжение.
Важно! Абсолютно чистое реактивное электросопротивление имеет сдвиг фазы на ± 180/2. То есть, фаза «двигается» на π/2.
Примером активной сопротивляемости — линия электропередачКак правильно измерять сопротивление
При работе с радиоаппаратурой иногда требуется измерять не только активностное, но и реактивное электросопротивление (индуктивность и емкость). Для измерений применяют косвенный метод использования мультиметра, а более точные значения получают при мостовом методе.
Активом сопротивляемости может выступать любой резисторКосвенный метод наиболее прост в своей реализации, так как не требует дополнительных схем включения. Одна требуется наличие трех отдельных приборов: амперметра, вольтметра и ваттметра. Если измерить напряжение и силу электротока в цепи, то можно получить полное электросопротивление: Z=U*I После измерения активностной мощности P, можно получить величину активного сопротивления отдельного элемента: R= P/I².
Обмотка трансформатора — один из примеров актива по превращению электроэнергииОбласти проявления
Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.
Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя. Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление. Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.
Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.
Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.
Индукция ЭДС может наблюдаться в дросселеТаким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.
Цепи переменного тока
Переменный ток (а.с.) является основой современного распределения электроэнергии. В этой статье я рассмотрю некоторые из наиболее важных концепций. Это незавершенная работа, и я буду добавлять к ней постепенно, когда начну закрывать страницы в вики. Надеемся, что к моменту полной амортизации Wiki у нас должна появиться разумная статья.
Теория переменного тока
Синусоида Переменное напряжение или ток имеют форму синусоиды и задаются:
и
Где: время
V, время 1000 (момент времени) — момент времени — t — t) — это мгновенное напряжение в момент времени, t
Vm — это максимальное значение мгновенного напряжения
Im — это максимальное значение мгновенного тока
ω — это угловая частота в радианах
— это фазовый угол напряжения
— это фазовый угол тока
Количество полных циклов в секунду является частотой (f) и измеряется в герцах (Гц).Период (T) синусоидальной волны — это время завершения цикла в секундах, которое связано с частотой:
Примечание: В Европе частота составляет 50 Гц (период до 20 мс), в то время как в США оно составляет 60 Гц (период 16,67 мс) .
Угловая частота ω определяется следующим образом:
. Основы питания в цепях переменного тока (вы НЕ ДОЛЖНЫ забывать) — фоторепортаж: electrosound.co.uk
