Что такое активное сопротивление в цепи переменного тока. Как оно связано с выделением тепла. Какова формула для расчета активного сопротивления. Чем оно отличается от реактивного сопротивления. Как проявляется поверхностный эффект при высоких частотах.
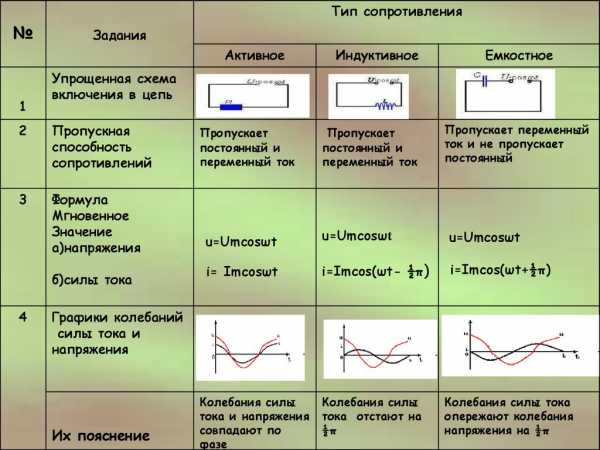
Что такое активное сопротивление в цепи переменного тока
Активное сопротивление в цепи переменного тока — это сопротивление, на котором происходит необратимое преобразование электрической энергии в другие виды энергии, чаще всего в тепловую. Оно обозначается буквой R и измеряется в Омах (Ом).
Основные характеристики активного сопротивления в цепи переменного тока:
- Вызывает выделение тепла при прохождении тока
- Не зависит от частоты переменного тока
- Ток и напряжение на активном сопротивлении совпадают по фазе
- Определяется материалом и геометрическими размерами проводника
Формула активного сопротивления в цепи переменного тока
Для расчета активного сопротивления в цепи переменного тока используется та же формула, что и для постоянного тока:

R = U / I
Где:
- R — активное сопротивление (Ом)
- U — действующее значение напряжения (В)
- I — действующее значение силы тока (А)
Важно отметить, что в этой формуле используются действующие (эффективные) значения напряжения и тока, а не амплитудные.
Чем активное сопротивление отличается от реактивного
Активное и реактивное сопротивления имеют ряд существенных отличий:
| Активное сопротивление | Реактивное сопротивление |
|---|---|
| Вызывает необратимые потери энергии | Не вызывает потерь энергии |
| Не зависит от частоты | Зависит от частоты |
| Ток и напряжение совпадают по фазе | Есть сдвиг фаз между током и напряжением |
| Определяется свойствами проводника | Определяется свойствами катушек и конденсаторов |
Как проявляется поверхностный эффект при высоких частотах
При высоких частотах переменного тока проявляется так называемый поверхностный эффект (скин-эффект). Он заключается в том, что ток вытесняется к поверхности проводника.
Основные особенности поверхностного эффекта:
- Плотность тока максимальна у поверхности проводника и уменьшается к центру
- Эффективное сечение проводника уменьшается
- Активное сопротивление проводника увеличивается
- Эффект усиливается с ростом частоты тока
- Наиболее заметен в проводниках большого диаметра
Для уменьшения влияния поверхностного эффекта при высоких частотах используют полые проводники или многожильные провода из тонких изолированных жил.

Какие факторы влияют на активное сопротивление в цепи переменного тока
На величину активного сопротивления в цепи переменного тока влияют следующие основные факторы:
- Материал проводника — удельное сопротивление материала
- Температура — с ростом температуры сопротивление металлов обычно увеличивается
- Частота тока — при высоких частотах проявляется поверхностный эффект
- Наличие ферромагнитных материалов вблизи проводника
- Качество контактных соединений в цепи
Учет этих факторов позволяет более точно рассчитывать активное сопротивление при проектировании и анализе цепей переменного тока.
Практическое применение знаний об активном сопротивлении
Понимание свойств активного сопротивления в цепях переменного тока важно во многих практических приложениях:
- Расчет потерь энергии в линиях электропередач
- Проектирование систем электроснабжения
- Разработка нагревательных элементов
- Создание измерительных приборов
- Расчет защитного заземления
- Проектирование антенн и СВЧ-устройств
Правильный учет активного сопротивления позволяет повысить эффективность и надежность электрических устройств и систем.

Методы измерения активного сопротивления в цепях переменного тока
Для измерения активного сопротивления в цепях переменного тока используются различные методы:
- Метод амперметра-вольтметра
- Мостовые методы (мост Уитстона, мост Максвелла)
- Резонансные методы
- Метод вольтметра
- Использование специализированных измерителей импеданса
Выбор конкретного метода зависит от требуемой точности, диапазона измеряемых сопротивлений, частоты тока и других факторов. При измерениях важно учитывать возможное влияние паразитных параметров и соблюдать правила техники безопасности.
Активное сопротивление, индуктивность, емкость
а) Активное сопротивление R, r – это идеализированный элемент цепи, в котором происходят необратимые превращения электрической энергии в тепловую:
 ,
(3.5)
,
(3.5)
 А.
А.
б) Индуктивность L – идеализированный элемент цепи, который характеризуется способностью накапливать энергию магнитного поля. Индуктивность численно равна отношению потокосцепления к току, которым это потокосцепление обусловлено:
 ,
(3.6)
,
(3.6)
где
 — поток сцепления катушки индуктивности,
— поток сцепления катушки индуктивности,
N –число витков катушки,
Ф– магнитныйпоток.
.
в) Емкость C– идеализированный элемент электрической цепи, который характеризуетсяспособностью накапливать энергию электрического поля.
 ,
(3.7)
,
(3.7)
где
 –
заряд на обкладках или пластинах
конденсатора,
–
заряд на обкладках или пластинах
конденсатора,
 – разность потенциалов между пластинами
конденсатора.
– разность потенциалов между пластинами
конденсатора.
Емкость
С – не зависит от
 ,
а определяется размерами, формой
конденсатора, а также диэлектрическими
свойствами среды, находящейся между
обкладками конденсатора.
,
а определяется размерами, формой
конденсатора, а также диэлектрическими
свойствами среды, находящейся между
обкладками конденсатора.
 .
.
Действующее значение переменного тока
Колебания, возникающие под воздействием внешней периодически изменяющейся ЭДС, называются вынужденными электромагнитными колебаниями. Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание переменного тока в цепи, содержащей резистор, катушку индуктивности и конденсатор.
На рис. 3.5 представлен график переменного синусоидального тока.
Рис. 3.5. График переменного тока
Действующее значение переменного тока равно такому значению постоянного тока, которое за время, равное периоду переменного тока, выделяет в том же сопротивлении такое же количество теплоты, что и данный ток. Определяется по формуле 3.8.
 . (3.8)
. (3.8)
Активное, реактивное и полное сопротивление в цепях переменного тока
Ток в активном сопротивлении

где Ir, Ur — действующие значения тока и напряжения на активном сопротивлении R.
Сдвиг фаз между током и напряжением на резисторе равен нулю (см. рис. 3.6).
Рис. 3.6. Векторная диаграмма тока и напряжения на резисторе
Ток в индуктивности
 ,
(3.10)
,
(3.10)
где IL, UL — действующие значения тока и напряжения на индуктивном сопротивлении хL.
, (3.11)
где ω – циклическая частота, равна нуль, поэтому при постоянном токе катушка индуктивности не имеет сопротивления.
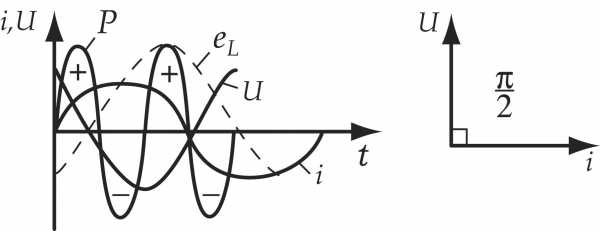
В индуктивном сопротивлении ток отстает от напряжения на угол 90° (рис. 3.7).
Рис. 3.7. Векторная диаграмма тока и напряжения на индуктивности
Величина хC называется реактивным емкостным сопротивлением.
 .
(3.12)
.
(3.12)
При емкостном сопротивлении напряжение отстает от тока на угол 90° (рис. 3.8).
Рис. 3.8. Векторная диаграмма тока и напряжения на емкости
Для постоянного тока ω равна нулю и хC=∞, т.е. постоянный ток через конденсатор течь не может.
, (3.13)
где Z – полное сопротивление цепи,
х – реактивное сопротивление: .
studfiles.net
Цепи переменного тока с активным сопротивлением
|
|
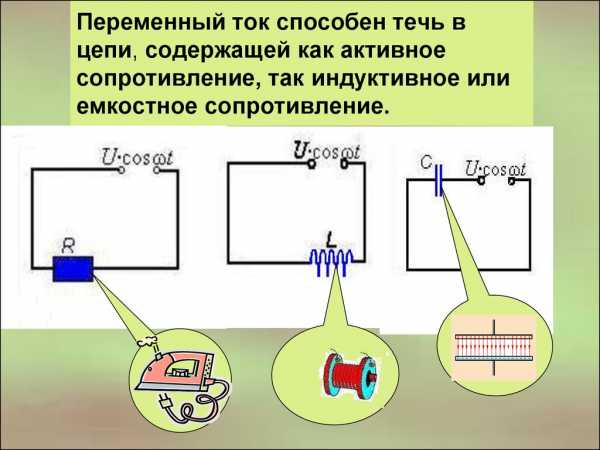
На величину тока и его характер в цепях переменного тока оказывает влияние не только сопротивление, определяемое материалом и геометрическими размерами, но и наличием в цепи емкости и индуктивности. Любая электрическая цепь обладает сопротивлением, индуктивностью и емкостью. Однако, часто тот или иной элемент преобладает над другим, поэтому их влиянием можно пренебречь.
Один и тот же проводник имеет различное сопротивление в цепях постоянного и переменного тока, причем, в цепях переменного тока это сопротивление больше.
|
— постоянный ток | |
|
— переменный ток |
Это объясняется тем, что переменный ток в отличие от постоянного, который протекает по сечению проводника с равномерной плотностью, частично вытесняется из внутренних слоев проводника к наружным. В результате чего плотность тока в различных слоях неодинакова. Это явление называется поверхностным эффектом.Это объясняется тем, что внутренние слои проводника сцеплены с большим числом магнитных силовых линий, чем наружные, и поэтому в них наводится большая ЭДС самоиндукции, которая препятствует протеканию тока и вытесняет его к наружным слоям, где ЭДС самоиндукции меньше.
Разделив обе части
равенства на
 ,
получим действующие значения
,
получим действующие значения .
.
Ток и напряжение в цепи с активным сопротивлением совпадают по фазе.
Таким
образом, мощность состоит из постоянной
составляющей
 и переменной составляющей,
среднеезначение которых за период
равно нулю. Таким образом, постоянная
составляющая мощности
и переменной составляющей,
среднеезначение которых за период
равно нулю. Таким образом, постоянная
составляющая мощности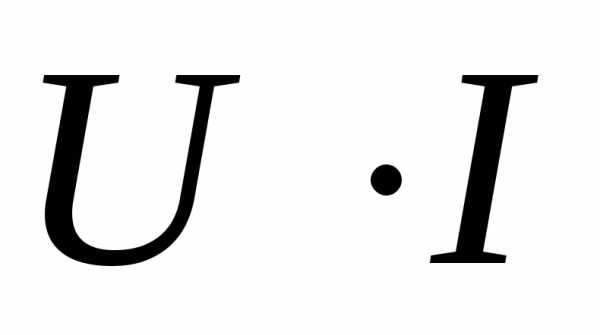 выражает среднее за период значение
мощности и называетсяактивной
мощностью:
выражает среднее за период значение
мощности и называетсяактивной
мощностью:
Мощность в оба полупериода положительна. Это означает, что цепь с сопротивлением rтолько потребляет энергию из сети и назад ее не возвращает, т.к. она преобразуется в другие виды энергии.
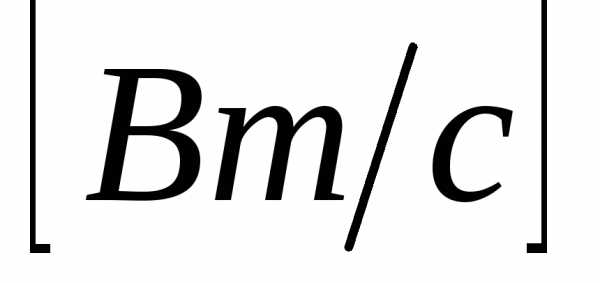
Цепи переменного тока с индуктивностью
|
|
Допустим, что под действием напряжения в этой цепи протекает ток. Под действием переменного тока в катушке возникает переменный магнитный поток, который наводи в ней ЭДС самоиндукции. |
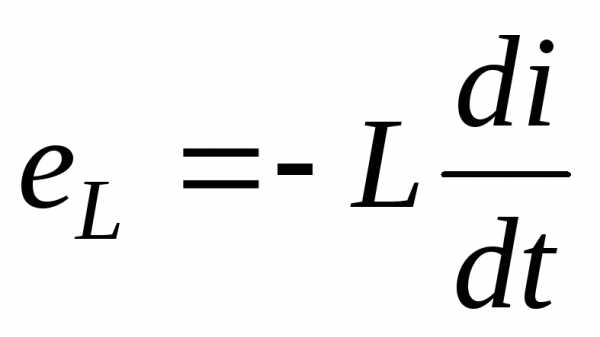
ЭДС самоиндукции
 в любой момент времени уравновешивается
напряжением:
в любой момент времени уравновешивается
напряжением:
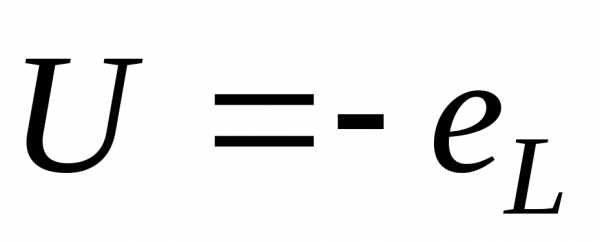
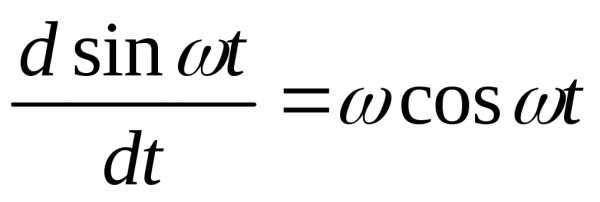
Т.о. в цепи с индуктивностью напряжение опережает ток на угол 900.
 —
индуктивное (реактивное) сопротивление.
—
индуктивное (реактивное) сопротивление.
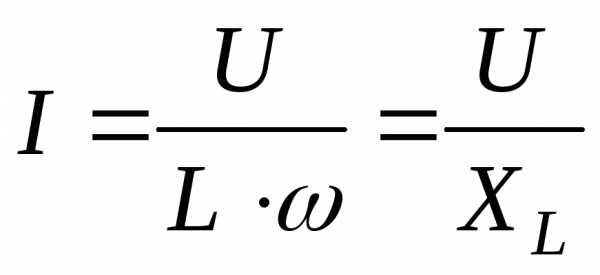 — закон Ома для
цепи с индуктивностью.
— закон Ома для
цепи с индуктивностью.
Физически индуктивное сопротивление характеризует препятствие, оказываемое переменному току в результате наличия ЭДС самоиндукции.
Мощность цепи:
Т.о. мощность изменяется с двойной частотой и может быть положительной и отрицательной. Когда она «+» индуктивность потребляет электрическую энергию от источника и запасает ее от магнитного поля. Когда мощность «-» индуктивность возвращает запасенную энергию обратно к источнику.
Т.о. между источником и индуктивностью происходит непрерывный обмен энергией, при котором:
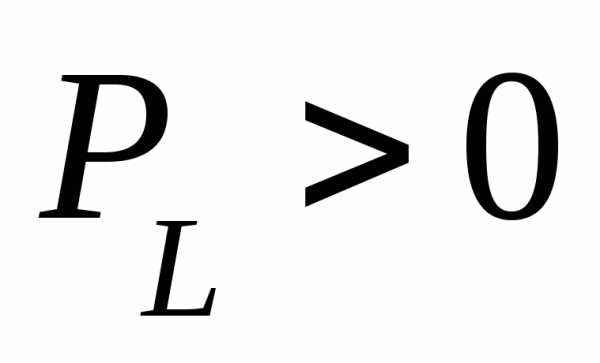 — цепь работает
потребителем
— цепь работает
потребителем
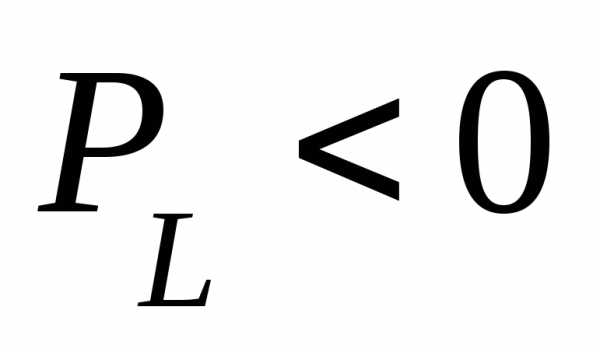 — цепь работает
генератором.
— цепь работает
генератором.
Максимальное значение мощности цепи индуктивности называется реактивной мощностью:
Энергия, запасенная в магнитном поле катушки, равна
studfiles.net
Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока
Активное сопротивление
Определение 1
Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:
\[I\left(t\right)=I_m{sin \left(\omega t\right)\ \left(1\right).\ }\]Рисунок 1.
Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:
\[U=IR=I_m{Rsin \left(\omega t\right)\ \left(2\right),\ }\]где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:
\[U_m=RI_m\left(3\right),\]где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.
Ёмкостное сопротивление
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.
Рисунок 2.
Мы можем использовать следующие соотношения:
Если $I(t)$ определена уравнением (1), то заряд выражен как:
где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:
Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $\frac{\pi }{2}.$ Амплитуда напряжения на емкости равна:
Величину $X_C=\frac{1}{\omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=\infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.
Индуктивное сопротивление
Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.
Рисунок 3.
Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:
По условию $R=0. \mathcal E$ самоиндукции можно выразить как:
Из выражений (8), (9) следует, что:
Амплитуда напряжения в данном случае равна:
где $X_L-\ $индуктивное сопротивление (кажущееся сопротивление индуктивности).
Закон Ома для цепей переменного тока
Определение 2
Выражение вида:
\[I_m=\frac{U_m}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}\left(12\right).\]где
\[Z=\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}(13)\]называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.
Пример 1
Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $\nu$.
Решение:
Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.
Амплитудное значение силы тока выражается «законом Ома для переменного тока»:
\[I_m=\frac{U_m}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}\left(1.1\right)\]оно связано с действующим значением силы тока как:
\[I=\frac{I_m}{\sqrt{2}}\left(1.2\right).\]В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:
\[U=\frac{U_m}{\sqrt{2}}\to U_m=\sqrt{2}U\left(1.3\right).\]Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:
\[I=\frac{1}{\sqrt{2}}\frac{\sqrt{2}U}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}=\frac{U}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}=\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},\]где $\omega =2\pi \nu .$
Ответ: $I=\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.$
Пример 2
Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).
Решение:
Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой:
\[U_L=I\omega L=2 \pi \nu L\frac{U}{\sqrt{R^2+{\left(2 \pi \nu L-\frac{1}{2 \pi \nu C}\right)}^2}}.\]Напряжение на активном сопротивлении ($U_R$) равно:
\[U_R=IR=\frac{UR}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.\]Напряжение на конденсаторе ($U_C$) определяется как:
\[U_C=\frac{I}{C2 \pi \nu}=\frac{1}{C2 \pi \nu}\frac{U}{\sqrt{R^2+{\left(2 \pi \nu L-\frac{1}{2 \pi \nu C}\right)}^2}}.\]Ответ: $U_L=2\pi \nu L\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},\ U_R=\frac{UR}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},U_C=\frac{1}{C2\pi \nu }\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.$
spravochnick.ru
|
Емкостное сопротивление в цепи переменного тока |
|
|
При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ? 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока. |
|
|
Мгновенное значение напряжения равно . Мгновенное значение силы тока равно: Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2. |
|
|
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: , где — емкостное сопротивление. |
|
|
Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты). |
|
|
Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току). |
|
|
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной. |
|
|
Индуктивное сопротивление в цепи переменного тока |
|
|
В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения. |
|
|
Мгновенное значение силы тока: |
|
|
Мгновенное значение напряжения можно установить, учитывая, что u = — εi, где u – мгновенное значение напряжения, а εi – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению. |
|
|
. Следовательно , где амплитуда напряжения. Напряжение опережает ток по фазе на π/2. |
|
|
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой. |
|
|
Величина — индуктивное сопротивление. |
|
|
Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления. |
|
|
В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка. |
|
|
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной. |
|
www.eduspb.com
§50. Активное сопротивление в цепи переменного тока
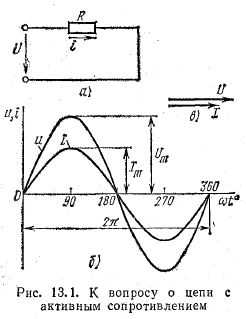
Ток и напряжение. При включении в цепь переменного тока активного сопротивления R (рис. 175, а) напряжение и источника создает в цепи ток i. Если напряжение и изменяется по синусоидальному закону u = Uт sin ?t, то ток i также изменяется синусоидально:
i = Iт sin ?t
При этом
Iт = Uт / R
Таким образом, ток и напряжение изменяются по одному и тому же закону; они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 175,б). Следовательно, при включении в цепь переменного тока активного сопротивления ток и напряжение совпадают по фазе (рис. 175, в).
Если обе части равенства Iт = Uт / R разделить на ?2, то получим выражение закона Ома для рассматриваемой цепи для действующих значений напряжения и тока:
I = U / R
Следовательно, для цепи переменного тока, содержащей только активное сопротивление, этот закон имеет такую же математическую форму, как и для цепи постоянного тока.
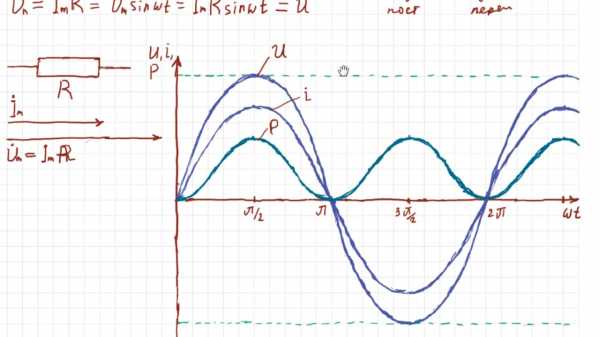
Электрическая мощность. Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения и. Следовательно, мгновенная мощность р не является постоянной величиной, как при постоянном токе, а изменяется по кривой (см. рис. 175,б). Эту кривую можно также получить графически, перемножая ординаты кривых силы тока i и напряжения и при различных углах ?t. Изменение мощности происходит с двойной частотой ?t по отношению к изменению тока и напряжения, т. е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности являются положительными. Физически положительное значение мощности означает, что энергия передается от источника электрической энергии к приемнику. Максимальное значение мощности при ?t = 90° и ?t = 270°
Pmax = UтIт = 2UI
Рис. 175. Схема включения в цепь переменного тока активного сопротивления (а), кривые тока i, напряжения и, мощности р (б) и векторная диаграмма (в)
Практически об энергии W, создаваемой электрическим током, судят не по максимальной мощности, а по средней мощности Рср = Р, так как эта энергия может быть выражена как произведение среднего значения мощности Р на время протекания тока:
W = Pt.
Кривая мгновенной мощности симметрична относительно линии АБ, которая соответствует среднему значению мощности Р. Поэтому
P = Pmax / 2 = UI
Используя формулу (67) закона Ома, активную мощность можно выразить также в виде P = I2R или P=U2/R.
В электротехнике среднюю мощность, потребляемую активным сопротивлением, обычно называют активной мощностью, или просто мощностью, и обозначают буквой Р.
Поверхностный эффект. Следует отметить, что активное сопротивление проводников в цепи переменного тока всегда больше их сопротивления в цепи постоянного тока. Переменный ток i не протекает равномерно по всему поперечному сечению проводника, как постоянный ток i, а вытесняется на его поверхность (рис. 176, а). Поэтому полезное сечение проводника как бы уменьшается и сопротивление его при переменном токе возрастает. Это явление носит название поверхностного эффекта. Неравномерное распределение переменного тока по поперечному сечению проводника объясняется действием э. д. с. самоиндукции, индуцированной в проводнике магнитным полем, которое создается проходящим по проводнику током I. Это магнитное поле действует не только в пространстве, окружающем проводник (внешний поток Ф2), но и внутри самого проводника (внутренний поток Ф2) (рис. 176,б). Поэтому слои проводника, расположенные ближе к его центру, будут охватываться большим магнитным потоком, чем слои, расположенные ближе к его поверхности, и э. д. с. самоиндукции, индуцированная во внутренних слоях, будет большей, чем во внешних. Поскольку э. д. с. самоиндукции препятствует изменению
Рис. 176. Схема протекания постоянного I и переменного i токов по проводнику (а) и возникновение поверхностного эффекта (б)
Рис. 177. Схема термообработки деталей токами высокой частоты: 1 — высокочастотный индуктор; 2 — закаливаемая деталь; 3 — разогретый слой
тока, последний будет стремиться пройти там, где э. д. с. самоиндукции имеет наименьшее значение, т. е. пройдет преимущественно по поверхностным слоям проводника. В результате этого плотность тока У в поверхностных слоях будет больше, чем во внутренних. Чем больше частота тока, тем больше э. д. с. самоиндукции индуцируется во внутренних слоях проводника и тем в большей степени ток вытесняется на поверхность.
При частоте 50 Гц увеличение сопротивления медных и алюминиевых проводников при малом их диаметре практически ничтожно, и сопротивление таких проводников в цепях переменного и постоянного тока можно считать одинаковым. Но для медных и алюминиевых проводников диаметром свыше 10 мм, а для стальных проводников при еще меньших диаметрах необходимо при расчетах учитывать влияние поверхностного эффекта на их активное сопротивление.
При токах высокой частоты, принятых в радиотехнике, телевидении и различных высокочастотных установках, с целью лучшего использования металла проводников их обычно изготовляют полыми.
На свойстве переменного тока высокой частоты протекать, главным образом, по поверхности проводников основаны различные методы высокочастотной закалки и термообработки. Например, при высокочастотной термообработке деталей вихревыми токами (рис. 177) эти токи индуцируются в основном в поверхностном слое металла. Они быстро разогревают поверхностные слои обрабатываемой детали, раньше, чем ее внутренняя часть успеет заметно нагреться за счет теплопроводности металла.
electrono.ru
Активное сопротивление цепи переменного тока
Активным или ваттным сопротивлением называется всякое сопротивление, поглощающее электрическую энергию или вернее превращающее ее в другой вид энергии, например в тепловую, световую или химическую.
Потери энергии, а, следовательно, и активное сопротивление в электрической цепи при переменном токе всегда больше потерь энергии в этой же цепи при постоянном токе. Причина этого заключается в том, что в цепях переменного тока потери энергии обусловлены не только обычным омическим сопротивлением проводников, но и многими другими причинами.
Рассмотрим некоторые из этих.
Так, например, наличие конденсатора в цепи переменного тока связано с дополнительными потерями энергии в результате периодического (с частотой переменного тока) изменения поляризации диэлектрика или, попросту говоря, в результате непрерывного переворачивания взад и вперед молекулярных парных зарядов. При этом происходит нагревание диэлектрика, т. е. электрическая энергия превращается в тепловую. Эти потери энергии называются диэлектрическими потерями.
Кроме диэлектрических потерь, как уже говорилось раньше, происходят потери энергии из-за утечки тока вследствие несовершенства изоляции между пластинами конденсаторов. Эти потери называются потерями утечки.
Вокруг всякого переменного тока существует переменное магнитное поле. Следовательно, во всех окружающих железных предметах происходит непрерывное переворачивание молекулярных магнитиков в такт с частотой переменного тока. В результате железные предметы, находящиеся в поле переменного тока, нагреваются, т. е электрическая энергия превращается в тепловую. Эти потери называются потерями на гистерезис.
Благодаря электромагнитной индукции переменный электрический ток наводит в близлежащих замкнутых электрических цепях индукционные токи, что связано с нагреванием этих цепей, т. е. с дополнительными потерями энергии.
Кроме того, такие же индукционные круговые токи возникают не только в замкнутых электрических цепях, но и в близлежащих металлических предметах и нагревают их. Эти токи называются токами Фуко. Возникновение токов Фуко также сопряжено с потерями электрической энергии.
Токи Фуко не всегда являются вредными. Например, на принципе токов Фуко основана защита радиоприборов медными или алюминиевыми экранами от переменных магнитных полей высокой частоты.
Наконец, при очень высоких частотах цепь переменного тока может излучать электромагнитные волны (радиоволны), что связано с потерями на излучение.
Наличие всех этих потерь увеличивает активное сопротивление цепи переменному току.
Опыт показывает, что при высоких частотах и омическое сопротивление проводника оказывается значительно большим, чем при постоянном токе.
Для объяснения этого явления увеличим мысленно сечение проводника (рис. 1) и посмотрим, что происходит в нем при прохождении по нему переменного тока. Вдоль проводника взад и вперед с частотой переменного тока движется огромное количество электронов.
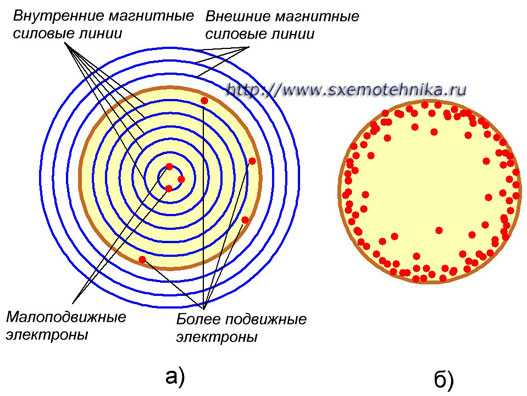
Рисунок 1. Поверхностный эффект, как фактрор увеличения активного сопротивления в цепи переменного тока. Ток вытесняется магнитным полем на поверхность проводника (а), поэтому у поверхности проводника плотность тока больше, чем внутри проводника (б).
До сих пор нам было известно, что движущийся по проводнику переменный поток электронов создает вокруг него переменное магнитное поле. Теперь же, когда мы заглянем внутрь проводника, мы увидим, что магнитное поле имеется и внутри проводника. Это вызвано тем, что каждый электрон при движении создает вокруг себя магнитное поле, а так как часть электронов движется вблизи оси проводника, то они создают магнитное поле не только во вне, но и внутри проводника.
Продолжая присматриваться к происходящему внутри проводника, мы заметим, что наиболее быстро движутся электроны, находящиеся у поверхности проводника, а по мере приближения к середине проводника амплитуда (размах) колебаний электронов становится все меньше и меньше.
Почему же электроны колеблются с различными амплитудами в разных точках сечения проводника?
Это явление также имеет свое объяснение. Вспомним, что при всяком изменении скорости движения электрона на него действует ЭДС самоиндукции, противодействующая этому изменению. Вспомним также, что ЭДС самоиндукции зависит от числа магнитных силовых линий вокруг движущегося электрона. Чем большим числом магнитных силовых линий охватывается электрон, тем труднее ему совершать колебательное движение.
Теперь становится ясным, почему электроны, находящиеся у поверхности проводника, колеблются с большой амплитудой, а электроны, находящиеся глубоко внутри проводника, — с малой. Ведь первые охватываются только теми магнитными силовыми линиями, которые расположены вне проводника, а вторые охватываются и внешними и внутренними магнитными силовыми линиями.
Таким образом, плотность переменного тока получается большей у поверхности проводника и меньшей внутри его.
На рис. 1,б плотность тока характеризуется количеством красных точек. Как видим, наибольшая плотность тока получается около самой поверхности проводника.
При очень высоких частотах противодействие ЭДС самоиндукции внутри проводника становится настолько сильным, что все электроны движутся только по поверхности проводника. Это явление и называется поверхностным эффектом. Так как активное сопротивление проводника зависит от его сечения, а полезным сечением при токе высокой частоты оказывается только тонкий наружный слой проводника, то вполне понятно, что его активное сопротивление увеличивается с повышением частоты переменного тока.
Для уменьшения поверхностного эффекта проводники, по которым протекают токи высокой частоты, делают трубчатыми и покрывают их слоем хорошо проводящего металла, например серебра.
В целях борьбы с явлением поверхностного эффекта применяют также провода специальной конструкции, так называемый литцендрат.
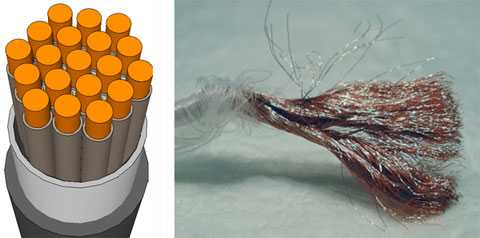
Такой проводник свивают из отдельных тонких медных жилок, имеющих эмалевую изоляцию, причем скрутка жилок производится таким образом, чтобы каждая из них проходила поочередно то внутри проводника, то снаружи его.
Явление поверхностного эффекта особенно сильно сказывается в железных проводах, в которых вследствие большой магнитной проницаемости железа внутренний магнитный поток оказывается особенно большим и поэтому явление поверхностного эффекта становится очень заметным даже при сравнительно низких (звуковых) частотах.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
Активное сопротивление в цепи переменного тока
Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.

Активное сопротивление в цепи переменного тока.
Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т. е. имеют место явления индуктивности. Ток возникает под действием электрического поля на заряды, следовательно, проводник должен обладать емкостью, так как в диэлектрической среде вокруг него возникает поток смещения.
Однако в ряде случаев относительная роль двух из трех параметров R, L, С в электрической цепи практически незначительна. Это позволяет рассматривать подобную цепь как обладающую только сопротивлением, или только индуктивностью, или только емкостью. Мы рассмотрим поочередно условия в трех таких простейших цепях переменного тока.
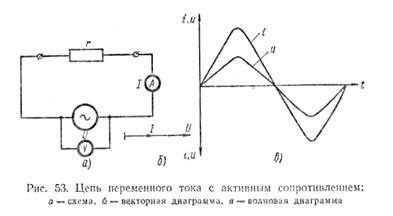
В цепи, содержащей только сопротивление г, синусоидальное напряжени u = Um sin ?t источника электроэнергии создает ток:
i = u : r = (Um : r ) sin ?t
Так как сопротивление r от времени не зависит, то в этой цепи ток совпадает по фазе с напряжением (рис. 1) и изменяется также синусоидально:
i = Im sin ?t
здесь:
Im = Um : r
Рисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.
Разделив последнее выражение на , получим формулу закона Ома для действующих значений напряжения и тока:
I = U : r
Как видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.
В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.). Оно может существенно отличаться от сопротивления r при постоянном токе. Сопротивление для постоянного тока называют омическим, чтобы отличить его от активного сопротивления для переменного тока.
Различие между активным и омическим сопротивлениями обуславливается рядом причин. Одна из них — поверхностный эффект, частичное вытеснение переменного тока в поверхностные слои проводника. Чем больше частота переменного тока, тем это вытеснение значительнее. Из-за поверхностного эффекта сопротивление r оказывается уже существенно большим, чем вычисленное по формуле:
r = ? (l : S)
Поверхностный эффект создается тем, что переменное магнитное поле индуктирует во внешних слоях проводника меньшую ЭДС самоиндукции, чем во внутренней его части. Особенно сильно поверхностный эффект увеличивает активное сопротивление стальных проводов. На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв.мм).
Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.
fazaa.ru



