Формула для определения сопротивления. Формула электрического сопротивления: принципы расчета и применение

Как рассчитать электрическое сопротивление проводника. Какие факторы влияют на сопротивление материалов. От чего зависит удельное сопротивление веществ. Как применять формулы сопротивления на практике.

Что такое электрическое сопротивление

Электрическое сопротивление — это свойство проводника препятствовать прохождению электрического тока. Оно характеризует способность материала противодействовать движению заряженных частиц под действием электрического поля.

Единицей измерения электрического сопротивления в Международной системе единиц (СИ) является Ом. Один Ом равен сопротивлению участка электрической цепи, на котором при силе тока 1 Ампер возникает напряжение 1 Вольт.

Основная формула для расчета сопротивления

Основная формула для расчета электрического сопротивления проводника выглядит следующим образом:

R = ρ * L / S

Где:

• R — электрическое сопротивление проводника (Ом)
• ρ (ро) — удельное сопротивление материала проводника (Ом·м)
• L — длина проводника (м)
• S — площадь поперечного сечения проводника (м²)

Эта формула позволяет рассчитать сопротивление однородного проводника правильной геометрической формы, зная его параметры и свойства материала.

Факторы, влияющие на электрическое сопротивление

На величину электрического сопротивления проводника влияют следующие основные факторы:

1. Материал проводника. Разные вещества имеют различное удельное сопротивление.
2. Длина проводника. Чем длиннее проводник, тем больше его сопротивление.
3. Площадь поперечного сечения. Чем толще проводник, тем меньше его сопротивление.
4. Температура. С повышением температуры сопротивление большинства проводников увеличивается.
5. Наличие примесей и дефектов кристаллической решетки.

Знание этих факторов позволяет управлять электрическим сопротивлением проводников при разработке электрических цепей и устройств.

Удельное электрическое сопротивление

Удельное электрическое сопротивление (ρ) — это физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока. Оно зависит от природы материала и его состояния.

Удельное сопротивление измеряется в Ом·м и численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м².

Вот значения удельного сопротивления для некоторых распространенных материалов при 20°C:

• Серебро: 1.59 × 10⁻⁸ Ом·м
• Медь: 1.68 × 10⁻⁸ Ом·м
• Алюминий: 2.82 × 10⁻⁸ Ом·м
• Железо: 9.71 × 10⁻⁸ Ом·м
• Константан: 49 × 10⁻⁸ Ом·м

Чем меньше удельное сопротивление, тем лучше материал проводит электрический ток.

Температурная зависимость сопротивления

Электрическое сопротивление большинства проводников зависит от температуры. Для металлов эта зависимость описывается формулой:

R = R₀(1 + αΔT)

Где:

• R — сопротивление при температуре T
• R₀ — сопротивление при начальной температуре T₀
• α — температурный коэффициент сопротивления
• ΔT — изменение температуры (T — T₀)

Для большинства металлов α положительно, то есть их сопротивление растет с повышением температуры. Однако у некоторых материалов, например у полупроводников, наблюдается обратная зависимость.

Последовательное и параллельное соединение резисторов

При расчете сложных электрических цепей важно учитывать способ соединения резисторов:

Последовательное соединение:

R = R₁ + R₂ + R₃ + …

Общее сопротивление равно сумме сопротивлений всех резисторов.

Параллельное соединение:

1/R = 1/R₁ + 1/R₂ + 1/R₃ + …

Обратная величина общего сопротивления равна сумме обратных величин сопротивлений всех резисторов.

Применение формул сопротивления на практике

Знание формул расчета электрического сопротивления необходимо во многих областях техники и электроники:

• Проектирование электрических цепей
• Расчет параметров проводов и кабелей
• Разработка резисторов и других электронных компонентов
• Анализ тепловых потерь в электрических системах
• Создание измерительных приборов

Правильный расчет сопротивления позволяет оптимизировать работу электрических устройств, повысить их эффективность и безопасность.

Измерение электрического сопротивления

Для измерения электрического сопротивления используются специальные приборы — омметры. Существует несколько методов измерения:

1. Прямой метод — измерение падения напряжения на резисторе при пропускании через него известного тока.
2. Мостовой метод — сравнение неизвестного сопротивления с эталонным.
3. Компенсационный метод — уравновешивание падения напряжения на измеряемом сопротивлении.

Выбор метода зависит от требуемой точности измерения и диапазона измеряемых сопротивлений.

Заключение

Формулы расчета электрического сопротивления являются фундаментальными в электротехнике и электронике. Они позволяют анализировать и проектировать электрические цепи, выбирать оптимальные материалы и размеры проводников, рассчитывать тепловые потери. Понимание принципов формирования электрического сопротивления необходимо для эффективной работы с электрическими системами любой сложности.

что это такое, формула, как измерять

Электрическое сопротивление характеризует свойство проводника оказывать противодействие направленному движению заряженных частиц.

Влияние электрического сопротивления на электрический ток можно представить следующим образом:

• Движение свободных носителей электрического заряда внутри проводника приводит к тому, что свободные носители заряда сталкиваются с атомами и нарушают их поток.
• Этот эффект называется сопротивлением, которое обладает свойством ограничивать электрический ток в электрической цепи.
• Столкновение носителей электрического заряда с атомами также имеет тепловой эффект. Соответствующий элемент электрической цепи становится теплым или даже горячим. Если он перегреется, он может выйти из строя.

Электрическое сопротивление говорит о том, какое напряжение U необходимо, чтобы заставить электрический ток определенной силы тока I протекать через проводник. В физике для обозначения электрического сопротивления в формуле используется прописная буква R (от английского слова “Resistor” или “Resistance”).

Аналогия с потоком воды

Когда речь идет об электрическом сопротивлении в физике, необходимо различать два случая:

1. Электрические сопротивления как элементы электрической цепи (см. пример на рисунке 2). То есть, если вы называете элемент в электротехнике резистором, то вы имеете в виду конкретный элемент, предназначенный для целей ограничения протекания электрического тока в электрической цепи.
2. Электрическое сопротивление как физическая величина. Вы также можете спросить, насколько сильно тот или иной элемент препятствует протеканию электрического тока или вообще как можно рассчитать электрическое сопротивление. Здесь вы говорите об электрическом сопротивлении как о физической величине.

Примечание. Резистор – это прибор с постоянным сопротивлением. Если необходимо регулировать силу тока в электрической цепи, то используют для этой цели реостаты – приборы с переменным сопротивлением. В составе реостата имеется подвижный контакт, при помощи которого изменяется длина участка, включённого в цепь. Реостат используется, например, в регуляторах громкости радиоприёмников.

Вы можете проиллюстрировать работу резистора как элемента (т.е. случай 1) с помощью модели протекания воды в трубе.

Если представить поток электрического тока как поток воды через трубу, то резистор, имеющий электрическое сопротивление R, выполняет функцию сужения трубы. Сужение в трубе препятствует потоку воды, подобно тому, как резистор препятствует потоку электрического тока. Если вы сильнее сузите трубу, то сопротивление потоку воды увеличится. Тем самым труба будет больше препятствовать потоку воды.

Рис. 1. Суть электрического сопротивления на примере модели протекания воды в трубе

Формулы для определения электрического сопротивления

Согласно закона Ома для участка электрической цепи следует, что если вы измеряете напряжение U на проводнике и через него течет ток силой I, то проводник имеет электрическое сопротивление R, равное U, деленное на I, т.е. R = U / I. Единицей измерения электрического сопротивления в СИ является Ом, которая названа в честь немецкого физика Георга Симона Ома. То есть, 1 Ом – это сопротивление проводника, в котором при напряжении 1 В проходит ток силой 1 А. Поэтому, иногда, электрическое сопротивление ещё могут называть “омическим сопротивлением”.

Рис. 2. Определение электрического сопротивления

Для очень малых или очень больших сопротивлений используются такие дополнения, как милли-, кило- или мегаом. Применяются следующие отношения:

• 1 Миллиом = 1 мОм = 1*10^-3 Ом;
• 1 Килоом = 1 кОм = 1*10³ Ом;
• 1 Мегаом = 1 МОм = 1*10⁶ Ом.

Интересный факт! Электрическое сопротивление человеческого тела может изменяться от 20000 Ом до 1800 Ом.

Также вы можете рассчитать электрическое сопротивление проводников с помощью их геометрических характеристик. Формула для этого следующая (см. также рисунок 3):

R = (ρ * l) / S, где

• R – электрическое сопротивление проводника;
• l – длина проводника;
• S – площадь поперечного сечения проводника;
• ρ – удельное сопротивление вещества проводника (выбирается по таблицам).

Рис. 3. Электрическое сопротивление проводника

Другими словами, чем тоньше и длиннее проводник, тем больше его сопротивление электрическому току. Весомое значение имеет также материал, из которого изготовлен проводник.

Как измерять электрического сопротивление?

Для измерения электрического сопротивления необходимо придерживаться следующих правил:

• Измерение проводить нужно параллельно элементу электрического цепи;
• Элемент должен быть обесточен;
• Элемент не должен быть подключен к электрической цепи;
• Измерение имеет смысл только для обычного резистора.

Значение омического сопротивления лучше всего определять с помощью цифрового мультиметра, чтобы избежать ошибок и неточностей в показаниях.

При измерении с помощью измерительного прибора измеряемый элемент не должен быть подключен к источнику напряжения во время измерения. Измеряемый элемент должен быть отпаян от электрической цепи, по крайней мере, с одной стороны. В противном случае расположенные параллельно элементы будут влиять на результат измерения.

формула расчета удельного сопротивления и закон Ома

Закон Ома является основным законом электрических цепей. При этом он позволяет объяснять многие явления природы. Например, можно понять, почему электричество не «бьет» птиц, которые сидят на проводах. Для физики закон Ома является крайне значимым. Без его знания невозможно было бы создавать стабильно работающие электрические цепи или вовсе не было бы электроники.

Зависимость I = I(U) и ее значение

История открытия сопротивления материалов напрямую связана с вольт-амперной характеристикой. Что это такое? Возьмем цепь с постоянным электрическим током и рассмотрим любой ее элемент: лампу, газовую трубку, металлический проводник, колбу электролита и т. д.

Меняя напряжение U (часто обозначается как V), подаваемое на рассматриваемый элемент, будем отслеживать изменение силы тока (I), проходящего через него. Как итог, мы получим зависимость вида I = I (U), которая носит название «вольт-амперная характеристика элемента» и является прямым показателем его электрических свойств.

Вольт-амперная характеристика может выглядеть по-разному для различных элементов. Самый простой ее вид получается при рассмотрении металлического проводника, что и сделал Георг Ом(1789 — 1854).

Вольт-амперная характеристика — это линейная зависимость. Поэтому ее графиком служит прямая линия.

Закон в простой форме

Исследования Ома по изучению вольт-амперных характеристик проводников показали, что сила тока внутри металлического проводника пропорциональна разности потенциалов на его концах (I ~ U) и обратно пропорциональна некоему коэффициенту, то есть I ~ 1/R. Этот коэффициент стал называться «сопротивление проводника», а единица измерения электрического сопротивления — Ом или В/А.

Стоит отметить еще вот что. Закон Ома часто используется для расчета сопротивления в цепях.

Формулировка закона

Закон Ома говорит, что сила тока (I) отдельно взятого участка цепи пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.

Следует заметить, что в таком виде закон остается верным только для однородного участка цепи. Однородной называется та часть электрической цепи, которая не содержит источника тока. Как пользоваться законом Ома в неоднородной цепи, будет рассмотрено ниже.

Позже опытным путем было установлено, что закон остается справедливым и для растворов электролитов в электрической цепи.

Физический смысл сопротивления

Сопротивление — это свойство материалов, веществ или сред препятствовать прохождению электрического тока. Количественно сопротивление в 1 Ом означает, что в проводнике при напряжении 1 В на его концах способен проходить электрический ток силой 1 А.

Удельное электрическое сопротивление

Экспериментальным методом было установлено, что сопротивление электрического тока проводника зависит от его размеров: длина, ширина, высота. А также от его формы (сфера, цилиндр) и материала, из которого он сделан. Таким образом, формула удельного сопротивления, например, однородного цилиндрического проводника будет: R = р*l/S.

Если в этой формуле положить s = 1 м² и l = 1 м, то R численно будет равен р. Отсюда вычисляется единица измерения для коэффициента удельного сопротивления проводника в СИ — это Ом*м.

В формуле удельного сопротивления р — это коэффициент сопротивления, определяемый химическими свойствами материала, из которого изготовлен проводник.

Для рассмотрения дифференциальной формы закона Ома, необходимо рассмотреть еще несколько понятий.

Плотность тока

Как известно, электрический ток — это строго упорядоченное движение любых заряженных частиц. Например, в металлах носителями тока выступают электроны, а в проводящих газах — ионы.

Возьмем тривиальный случай, когда все носители тока однородны — металлический проводник. Мысленно выделим в этом проводнике бесконечно малый объем и обозначим через u среднюю (дрейфовую, упорядоченную) скорость электронов во взятом объеме. Далее пусть n обозначает концентрацию носителей тока в единице объема.

Теперь проведем бесконечно малую площадь dS перпендикулярно вектору u и построим вдоль скорости бесконечно малый цилиндр с высотой u*dt, где dt — обозначает время, за которое все носители скорости тока, содержавшиеся в рассматриваемом объеме, пройдут сквозь площадку dS.

При этом электронами сквозь площадку будет перенесен заряд, равный q = n*e*u*dS*dt, где e — заряд электрона. Таким образом, плотность электрического тока — это вектор j = n*e*u, обозначающий количество заряда, переносимого в единицу времени через единицу площади.

Один из плюсов дифференциального определения закона Ома заключается в том, что часто можно обойтись без расчета сопротивления.

Электрический заряд. Напряженность электрического поля

Напряженность поля наряду с электрическим зарядом является фундаментальным параметром в теории электричества. При этом количественное представление о них можно получить из простых опытов, доступных школьникам.

Для простоты рассуждений будем рассматривать электростатическое поле. Это электрическое поле, которое не изменяется со временем. Такое поле может быть создано неподвижными электрическими зарядами.

Также для наших целей необходим пробный заряд. В его качестве будем использовать заряженное тело — настолько малое, что оно не способно вызывать какие-либо возмущения (перераспределение зарядов) в окружающих объектах.

Рассмотрим поочередно два взятых пробных заряда, последовательно помещенных в одну точку пространства, находящуюся под воздействием электростатического поля. Получается, что заряды будут подвергаться неизменному во времени воздействию с его стороны. Пусть F₁ и F₂ — это силы, воздействующие на заряды.

В результате обобщения опытных данных было установлено, что силы F₁ и F₂ направлены либо в одну, либо в противоположные стороны, а их отношение F₁/F₂ является независимым от точки пространства, куда были поочередно помещены пробные заряды. Следовательно, отношение F₁/F₂ является характеристикой исключительно самих зарядов, и никак не зависит от поля.

Открытие данного факта позволило охарактеризовать электризацию тел и в дальнейшем было названо электрическим зарядом. Таким образом, по определению получается q₁/q₂ = F₁/F₂, где q₁ и q₂ — величина зарядов, помещаемых в одну точку поля, а F₁ и F₂ — силы, действующие на заряды со стороны поля.

Из подобных соображений были экспериментально установлены величины зарядов различных частиц. Условно положив в соотношение один из пробных зарядов равным единице, можно вычислить величину другого заряда, измерив соотношение F₁/F₂.

Через известный заряд можно охарактеризовать любое электрическое поле. Таким образом, сила, действующая на единичный пробный заряд, находящийся в состоянии покоя, называется напряженностью электрического поля и обозначается E. Из определения заряда получаем, что вектор напряженности имеет следующий вид: E = F/q.

Связь векторов j и E. Другая форма закона Ома

В однородном проводнике упорядоченное движение заряженных частиц будет происходить по направлению вектора E. А это значит, что векторы j и E будут сонаправлены. Как и при определении плотности тока, выделим в проводнике бесконечно малый цилиндрический объем. Тогда через поперечное сечение этого цилиндра будет проходить ток, равный j*dS, а напряжение, приложенное к цилиндру, будет равно E*dl. Также известна формула удельного сопротивления цилиндра.

Тогда, записав формулу силы тока двумя способами, получим: j = E/р, где величина 1/р носит название удельной электрической проводимости и является обратной к удельному электрическому сопротивлению. Ее принято обозначать σ (сигма) или λ (лямбда). Единицей измерения проводимости является См/м, где См — это Сименс. Единица, обратная Ом.

Таким образом, можно ответить на вопрос, поставленный выше, о законе Ома для неоднородной цепи. В таком случае на носителей тока будет действовать сила со стороны электростатического поля, которая характеризуется напряженностью E₁, и другие силы, воздействующие на них со стороны другого источника тока, которые можно обозначить E₂. Тогда Закон Ома применительно к неоднородному участку цепи будет иметь вид: j = λ(E₁ + E₂).

Подробнее о проводимости и сопротивлении

Способность проводника проводить электрический ток характеризуется его удельным сопротивлением, которое можно найти через формулу удельного сопротивления, или удельной проводимостью, рассчитывающейся как обратное проводимости. Величина данных параметров определяется как химическими свойствами материала проводника, так и внешними условиями. В частности температурой окружающей среды.

Для большинства металлов удельное сопротивление при нормальной температуре пропорционально ей, то есть р ~ T. Однако при низких температурах наблюдаются отклонения. У большого ряда металлов и сплавов при температурах, близких к 0°К, расчет сопротивления показывал нулевые значения. Это явление получило название сверхпроводимости. Таким свойством обладают, например, ртуть, олово, свинец, алюминий и др. Для каждого металла существует свое критическое значение температуры T_k, при которой наблюдается явление сверхпроводимости.

Также отметим, что определение удельного сопротивления цилиндра можно обобщить для проводов, состоящих из одного материала. В таком случае площадь поперечного сечения из формулы удельного сопротивления будет равна сечению провода, а l — его длине.

Рациональная формула для определения тягового сопротивления плуга — тезисы доклада

Рациональная формула для определения тягового сопротивления плугатезисы доклада Исследовательская статья

• Автор: Чиненова В. Н.
• Сборник: Институт истории естествознания и техники им. С.И.Вавилова. Годичная научная конференция, посвященная 85-летию ИИЕТ РАН
• Том: 23
• Тезисы
• Год издания: 2017
• Место издания: Янус-К Москва
• Первая страница: 169
• Последняя страница: 172
• Аннотация: В.
  П.Горячкину принадлежит открытие рациональной формулы для тягового сопротивления плуга. Горизонтальную составляющую Rx сопротивления плуга при вспашке В. П. Горячкин назвал тяговым сопротивлением и выразил ее трехчленом: Rx=fПG + kПabn+εabnV2. (1) Первое слагаемое — fПG- сопротивление перекатыванию опорных колес плуга и трению о дно и стенку борозды, пропорциональное весу G плуга. Коэффициент пропорциональности fП назван коэффициентом сопротивления протаскиванию. Силу fПG определяют протаскиванием плуга в открытой борозде. Значение коэффициента fП, зависит от типа почв, их агрофона, конструкции плугов и находится в пределах 0,4… 1,0. Второе слагаемое — kПabn- вызвано сопротивлением подрезанию, разрушению и укладыванию пласта в борозду. Действие этой составляющей общего сопротивления считается полезным. Коэффициент kП оценивает удельное сопротивление почвы, определяемое из соотношения kП=RX / abn, где RX- горизонтальная составляющая силы сопротивления почвы при вспашке плугом; а— глубина вспашки; b— ширина захвата корпуса; n— число корпусов.
  Силу RX находят при динамометрировании (осциллографировании) без учета первого и третьего слагаемых формулы (1). Величина kП зависит от типа почв и степени их освоенности. Так, для глинистых и дерново-подзолистых почв значение kП в 2,3…2,6 раза больше, чем для легкосуглинистых и супесчаных. При вспашке после уборки зерновых значение kП на 10…20 % меньше в сравнении с обработкой травяного пласта. Третье слагаемое — εabnV2- скоростное сопротивление, зависящее от кинематической энергии, сообщаемой почвенным пластом. Эта составляющая не оказывает существенного влияния на полезное деформирование почвы. Коэффициентεскоростного сопротивления зависит от типа почв, геометрических форм рабочих поверхностей плужных корпусов. При скоростях вспашки до 5 км/ч коэффициентεнезначительно (2…3 %) изменяет общую силу RX С увеличением скорости движения до 12 км/ч сопротивление плугов с традиционными корпусами существенно возрастает. Для пахоты на скоростях 12… 15 км/ч применяют скоростные рабочие поверхности плужных корпусов, в которых уменьшено значение коэффициента ε. Формула Горячкина (1) выражает физическую сущность взаимодействия плуга с почвой, но определение силы RX и ее составляющих требует многочисленных трудоемких экспериментов, поэтому в практических расчетах широко применяют упрощенное выражение для тягового сопротивления плуга Rx= kabn, где k— удельное сопротивление плуга. Значение к рассчитывают по формуле k = Rx/abn, замерив среднее тяговое сопротивление Rx, глубину а пахоты и ширину bn захвата плуга. Коэффициент k отражает все три составляющие тягового сопротивления плуга, входящие в выражение (3.9). На величину k влияют технологические свойства почвы, конструктивные параметры плуга и скорость его движения. В зависимости от коэффициента k почвы разделяют на легкие — k< 30 кН/м2, средние — 30…50, среднетяжелые — 50…70, тяжелые — 70…120 и очень тяжелые — k> 120 кН/м2.
• Добавил в систему: Чиненова Вера Николаевна

Прикрепленные файлы

---

№	Имя	Описание	Имя файла	Размер	Добавлен
1.	Краткий текст		Kratkoe_soderzh_k_rats-formule.doc	50,5 КБ	17 декабря 2017 [Chinenova]

Формула электрического сопротивления — GeeksforGeeks

Когда к любому проводнику прикладывается напряжение, электрические заряды начинают течь по проводнику, и скорость потока заряда называется током. Свойство материалов, которое измеряет количество протекающего через него заряда, известно как электрическое сопротивление, а также на основе которого материалы классифицируются как хорошие или плохие проводники электричества.

Электрическое сопротивление

Электрическое сопротивление является свойством использования, мы выделяем тепло и имеем различные применения в нашей повседневной жизни.

Электрическое сопротивление: Свойство электрического проводника противодействовать (сопротивляться) потоку электрического тока известно как электрическое сопротивление . Все материалы имеют собственное электрическое сопротивление. Он представлен R , а его единица СИ равна Ом Ω (греческая буква Омега)

Георг Симон Ом был немецким физиком, который вывел закон, известный как закон Ома, а также дает связь между током, напряжением и сопротивление. Согласно закону Ома, сила тока, протекающего через проводник, прямо пропорциональна разности потенциалов на нем.

V ∝ I

или

V = IR

Следовательно, из вышеуказанных уравнений мы получаем отношение:

R = V/I

Где

• V является разность потенциалов на проводнике (в вольтах),
• I — ток через проводник (в амперах), а
• R — константа пропорциональности, называемая сопротивлением (в омах).

Удельное электрическое сопротивление (удельное сопротивление)

Удельное электрическое сопротивление или удельное сопротивление — это фундаментальное свойство материала, которое измеряет, насколько сильно он сопротивляется электрическому току. Низкое удельное сопротивление указывает на то, что материал легко пропускает электрический ток. Удельное сопротивление определяется как сопротивление, предлагаемое материалом на единицу длины для единицы поперечного сечения, и обратно пропорционально сопротивлению.

• Удельное сопротивление обычно обозначается греческой буквой ρ (ро).
• Единицей удельного электрического сопротивления в системе СИ является ом-метр (Ом-м) или мОм.

Математически, удельное сопротивление определяется как

ρ = (R × A)/L

или

R = (ρ × L)/A

, где

• R — сопротивление. ,
• L — длина,
• A — площадь поперечного сечения проводника.

Из приведенного выше соотношения видно, что сопротивление проводника зависит от следующих факторов:

1. Площадь поперечного сечения проводника
2. Длина проводника
3. Материал проводника
4. Температура проводящего материала

Материалы с низким значением удельного электрического сопротивления очень хорошо проводят электричество, являются проводниками и изоляторами будет иметь более высокое значение удельного сопротивления, чем у проводников. Некоторые материалы и их стандартное удельное сопротивление (сопротивление) при 20° ^C:

Material	Resistivity (in Ω-m)
Aluminium	2.8 × 10 -8
Copper	1,7 × 10 -8
Gold	2,4 × 10 -8
(GRAPTIT0010	1 × 10 -5
Germanium	4. 6 × 10 -1
Iron	1.0 × 10 — 7
Lead	1.9 × 10 -7
Nichrome	1.1 × 10 -6
Silver	1,6 × 10 -8

.

R = (ρ×L)/A

где R — сопротивление, V — напряжение, I — ток, ρ — удельное сопротивление, L — длина, а A — поперечное сечение площадь проводника.

Примеры задач на электрическое сопротивление

Задача 1. Каково сопротивление цепи, в которой приложено напряжение 12 В, а через нее протекает ток 4 А?

Решение:

В соответствии с соотношением:

V = IR

или

R = V/I

Следовательно,

R = 12 В/4 A

R = 3 ω,

R = 12 В/4 A

R = 3 ω.

Задача 2: Какой ток протекает в цепи, в которой приложенное напряжение равно 12 В, а сопротивление проводника равно 3 Ом?

Решение:

В соответствии с соотношением:

V = IR

или

I = V/R

Это подразумевает,

I = 12 V/3 T

I = 4 A

Задача 3. Какое напряжение приложено к цепи, в которой ток, проходящий через проводник, равен 4 А, а сопротивление проводника равно 3 Ом?

Решение:

Согласно соотношению:

В = IR

Следовательно,

В = 4 А × 3 Ом

В = 12 В

секция 10 ^-6 м ² . Удельное сопротивление меди 1,7·10 ^-8 Ом·м.

Решение:

По формуле

R = (ρ×L)/A

R = (1,7 x 10 ^-8 Ом·м) × 4 м 92 -6 ^{0126 2}

R = 6,8×10 ^-2 Ом

Задача 5. Медный провод длиной 4 м и площадью поперечного сечения 10 а9026 -6 м 6,8×10 ^-2 Ом. Вычислите удельное сопротивление меди.

Решение:

Использование Формулы

ρ = (R × A) / L

ρ = (6,8 × 10 ^-2 ) × 10 ^-6 /4

ρ = 1.76 -6 /4

ρ = 1.7 × 10 ^-8 Ом·м.

Расчет сопротивления — AP Physics C Electricity

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  Репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочее

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Мы открыты в субботу и воскресенье!

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

All AP Physics C Electricity Resources

1 Диагностический тест 46 практических тестов Вопрос дня Карточки Learn by Concept

AP Physics C Электричество Помощь » Экзамен по электричеству и магнетизму » Электрические схемы » Резисторы » Расчет сопротивления

Три резистора и батарея образуют следующую цепь.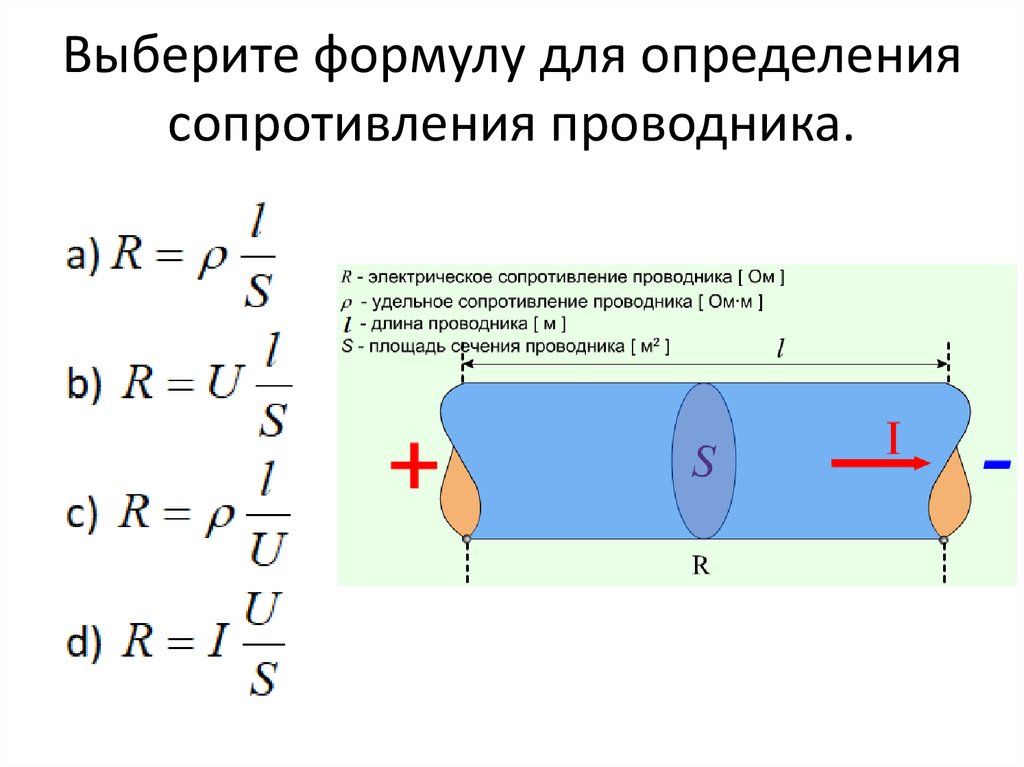

Рассчитайте эквивалентное сопротивление, если резисторы имеют следующие значения.

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала рассчитайте эквивалентное сопротивление  и . Поскольку эти два резистора расположены последовательно, мы просто берем сумму их номиналов.

С резисторами 2 и 3, объединенными вместе в одно значение, формируется следующая схема.

 

Обратите внимание, что  и  располагаются параллельно. Чтобы вычислить эквивалентное сопротивление этой параллельной пары, мы используем следующее уравнение.

Подставьте значения и найдите .

Это похоже на схему, показанную ниже.

Сообщить об ошибке

Уведомление об авторских правах

Посмотреть репетиторов

Латаша
Сертифицированный репетитор

Университет Нового Орлеана, бакалавр медицинских наук, общий. Университет Арканзаса, доктор наук, клеточная физика…

Просмотреть преподавателей

Мохаммад
Сертифицированный преподаватель

Джамия Миллия Исламия, магистр наук, физика.

Посмотреть репетиторов

Доссеви
Сертифицированный репетитор

Коул Сте Женевив Версаль, бакалавр наук, математика. Гренобльский национальный политехнический институт, магистр наук…

All AP Physics C Resources Electricity

1 Диагностический тест 46 практических тестов Вопрос дня Карточки Learn by Concept

Формула внутреннего сопротивления – объяснение, примеры с решениями

Соотношение между внутренним сопротивлением, обозначаемым r, и ЭДС, обозначаемой e ячейки, определяется следующим образом:

e = I (r + R)

Где мы можем заметить, что термин, обозначаемый буквой e = ЭДС, известный как электродвижущая сила Вольт, записывается как: I = ток, который обозначается буквой A, буква, обозначающая R = сопротивление нагрузки, а буква, обозначающая r, является внутренним сопротивлением.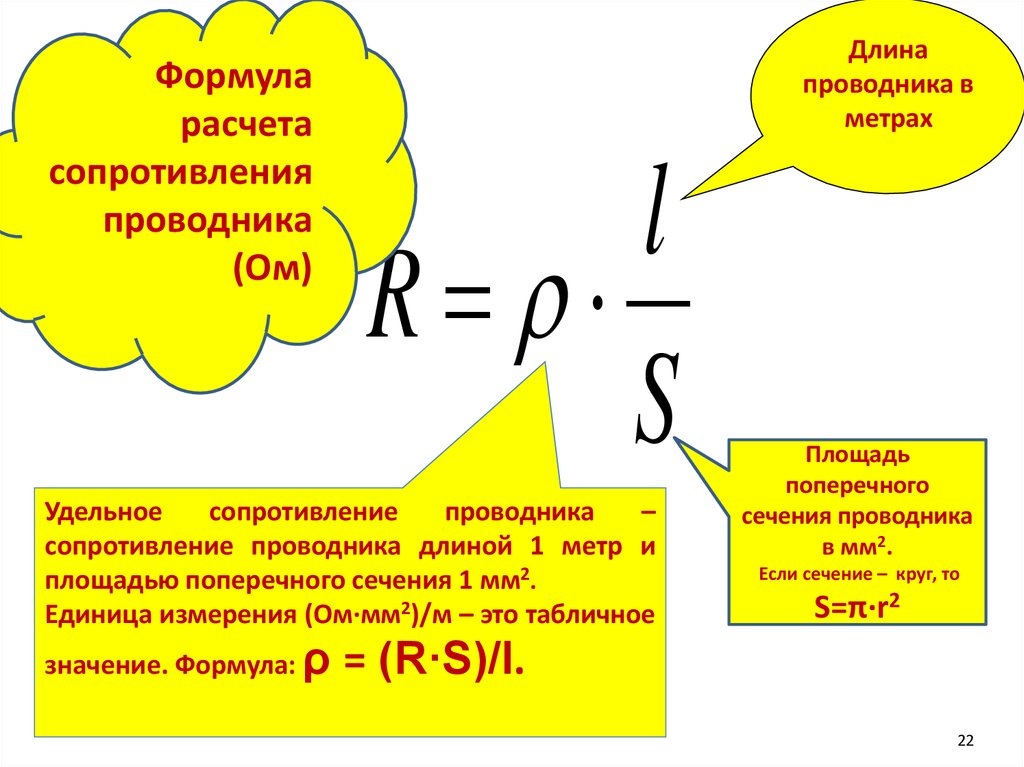 ячейки измеряется в омах.

Преобразовав приведенное выше уравнение, мы получим следующее:

То есть e = IR + Ir или, e = V + Ir

Формула внутреннего сопротивления

В приведенном выше уравнении мы можем сказать, что буква  V равна клемма разности потенциалов на ячейке, когда ток, обозначенный буквой I, протекает через цепь.

Мы можем отметить: ЭДС, обозначаемая буквой e ячейки, всегда больше, чем разность потенциалов, обычно на конце ячейки.

Пример: 1 — это разность потенциалов на ячейке, когда через цепь не протекает ток, равный 3 В. Когда протекает ток I = 0,37, т. е. ток в амперах, эта разность потенциалов на клеммах падает до 2,8. вольт. Определить внутреннее сопротивление, обозначенное буквой r ячейки?

Решение:

То есть e = V + Ir

Или мы видим e – V = Ir

Или это (e – V)/I = r

Следовательно, мы видим, что r = (3,0 – 2,8)/ 0,37 = 0,54 Ом.

Теперь, благодаря внутреннему сопротивлению ячейки, то есть электронам, движущимся через ячейку, что превращает часть электрической энергии в тепловую. Следовательно, мы видим, что разность потенциалов доступна для остальной части цепи, то есть:

То есть V = E, что означает ЭДС ячейки – Ir, то есть p.d. через внутренний резистор

Электродвижущая сила, которая обозначается буквой e или э.д.с. это энергия, которая обычно обеспечивается элементом или батареей на кулон проходящего через них заряда. Таким образом, мы можем сказать, что оно измеряется в вольтах, то есть в В. Говорят, что оно равно разности потенциалов на клеммах ячейки, когда ток не течет.

ε=E/Q

• Можно сказать, что e = электродвижущая сила в вольтах, В

• И тогда E = энергия в джоулях, Дж

• Тогда буква Q = заряд в

Батареи и элементы имеют внутреннее сопротивление, обозначаемое буквой r, которое измеряется в омах, обозначаемых буквой W. Когда поток электричества проходит по цепи, внутреннее сопротивление, которое представляет собой сам элемент, сопротивляется потоку тока и, следовательно, тепловому это называется теплом, то есть энергия тратится впустую в самой клетке.

ε=I(R+r)

• Буква e = электродвижущая сила в вольтах, В

• Буква I = ток в амперах, А

• Буква R = сопротивление нагрузки в цепь в омах, Вт

• Буква r = внутреннее сопротивление ячейки в омах, Вт

(Изображение будет загружено в ближайшее время)

IR+Ir

, а затем на следующее: 

ε=V+Ir

В этом уравнении появляется буква V, которая представляет собой разность потенциалов на клеммах, которая обычно измеряется в вольтах, т. е. В. Это разность потенциалов, которая, как говорят, находится на клеммах ячейке, когда в цепи протекает ток, т. е. он всегда меньше э.д.с. клетки.

Мы можем сказать Например:

1. Мы можем сказать, что p.d. То есть на клеммах ячейки 3,0 вольта, когда она не подключена к цепи и ток не течет. Здесь, когда говорят, что ячейка подключена к цепи и через клемму p.d. течет ток 0,37 А. Это обычно падает до 2,8 В. Мы можем сказать, что такое внутреннее сопротивление ячейки?

Граф терминала, который имеет p.d. против тока

Таким образом, мы можем сказать, что если мы построим график разности потенциалов на клеммах, обозначенной буквой V, в зависимости от тока в цепи, обозначенного буквой I, мы получим прямую линию с отрицательным градиентом.

(Изображение скоро будет загружено)

Здесь можно сказать, что они вообще перестраивают Э.Д.С. уравнение, приведенное выше, чтобы соответствовать общему выражению для прямой линии, то есть мы можем сказать y = mx +c.

(Изображение будет загружено в ближайшее время)

Мы можем отметить, что это из красных прямоугольников, что выше:

Мы можем сказать, что Physics net Site Search.

Формула внутреннего сопротивления клетки

Электродвижущая сила, называемая ЭДС, незнакома большинству учащихся. Эти вещи тесно связаны с более привычной концепцией напряжения. Понимание разницы между ними и того, что обычно означает ЭДС, дает нам инструменты, необходимые для решения многих задач в физике, а также в электронике. Также будет введено понятие внутреннего сопротивления батареи. Здесь снова мы можем сказать, что ЭДС говорит о напряжении батареи без учета внутреннего сопротивления, уменьшающего значение. Говорят, что в этой теме объясняется формула ЭДС с примерами. Итак, снова мы можем видеть, что давайте учиться этому.

Уже сказано, что электродвижущая сила определяется как разность потенциалов на клеммах батареи, то есть мы можем сказать, когда через нее не протекает ток. Говорят, что это не похоже на это, поскольку это имело бы значение, но мы можем сказать, что каждая батарея имеет внутреннее сопротивление. Можно сказать, что оно похоже на обычное сопротивление, уменьшающее ток в цепи, но существует внутри самой батареи.

Через ячейку, которая называется внутренним сопротивлением, не протекает ток, который ничего не изменит, потому что нет тока, который мог бы ее замедлить.

Определение внутреннего сопротивления

Формула внутреннего сопротивления — это математическое уравнение, которое можно использовать для расчета сопротивления движущегося объекта. Внутреннее сопротивление вызвано потерей тепла, трением и другими процессами, которые замедляют или останавливают движение. Формула внутреннего сопротивления часто используется в инженерных приложениях при проектировании двигателей и силовых агрегатов для легковых или грузовых автомобилей, но ее также можно применять во многих других ситуациях. В этой статье я объясню, что означает формула внутреннего сопротивления, как она рассчитывается, и приведу примеры с решениями, чтобы вы поняли, как работает внутреннее сопротивление!

Внутреннее сопротивление важно изучать следующими способами:

1. Чтобы повысить эффективность электродвигателя или любого другого электрического устройства, важно понять, какое внутреннее сопротивление имеет это устройство и как его можно уменьшить. уменьшенный.

2. Внутреннее сопротивление применяется при изучении внутреннего сопротивления батарей. Внутреннее сопротивление является важным понятием в электротехнике, и его можно применять ко многим типам проектов или экспериментов, связанных с электричеством.

3. Внутреннее сопротивление также имеет важное значение при проектировании двигателей легковых, грузовых и других крупногабаритных транспортных средств. Внутреннее сопротивление может применяться в двигателях внутреннего сгорания (ДВС) для повышения производительности и топливной экономичности двигателя.

Вот несколько важных советов по изучению внутреннего сопротивления:

1. Изучите основы. Формула внутреннего сопротивления — это концепция, которую можно применять ко многим типам двигателей и электрических устройств. Для начала следует понять формулы внутреннего сопротивления в их простейшей форме, прежде чем пробовать более сложные приложения. Формула внутреннего сопротивления показывает взаимосвязь между напряжением, током, потребляемой мощностью и внутренним сопротивлением: Внутреннее сопротивление = напряжение – ток

2. Практика внутреннего сопротивления. Формулу внутреннего сопротивления можно применять ко многим различным типам проектов и экспериментов, но Формулы внутреннего сопротивления следует сначала практиковать на более простых задачах, прежде чем переходить к более сложным. Практикуйте формулы внутреннего сопротивления, используя их в простых цепях или используя батареи, для которых вы знаете внутреннее сопротивление! Это поможет формуле внутреннего сопротивления стать второй натурой, когда вам понадобится использовать ее позже в дороге.

3. Поймите, где применять Формулу внутреннего сопротивления можно применять разными способами, но важно понимать, где и как следует применять внутреннее сопротивление.